The Nature of Hydrogen Bonds: A Delineation of the Role of Different Energy Components on Hydrogen Bond Strengths and Lengths

Abstract

Hydrogen bonds are a complex interplay between different energy components, and their nature is still subject of an ongoing debate. In this minireview, we therefore provide an overview of the different perspectives on hydrogen bonding. This will be done by discussing the following individual energy components: 1) electrostatic interactions, 2) charge‐transfer interactions, 3) π‐resonance assistance, 4) steric repulsion, 5) cooperative effects, 6) dispersion interactions and 7) secondary electrostatic interactions. We demonstrate how these energetic factors are essential in a correct description of the hydrogen bond, and discuss several examples of systems whose energetic and geometrical features are not captured by easy‐to‐use predictive models.

1. Introduction

Hydrogen bonds (HBs) are still often seen as electrostatic interactions between an electronegative atom A and a hydrogen atom attached to a second electronegative atom H‐D.1 However, this purely electrostatic interpretation cannot account for all experimental and theoretical observations, such as the change in H‐D stretching frequency, the NMR downfield chemical shift and cooperative effects upon HB formation. This has led the IUPAC task force2, 3 and others4 to advice to change the official IUPAC gold book definition, which still defines HBs as electrostatic interactions.1

Interestingly, this complex nature of HBs was already recognized by Linus Pauling in 1949, who proposed that hydrogen bonds in ice have partly covalent character.5 Already in the 1950s, Coulson decomposed the HB energy into four different components, namely (1) electrostatic interaction, (2) delocalization effects, (3) repulsive forces and (4) dispersion force.6 In 1954, Tsubomura stated that we cannot say that HBs are predominantly electrostatic in nature, simply because the sum of the other components is practically zero.7 A complete understanding of the hydrogen bond energy, he argued, would only be attained if we would calculate or estimate all these energy terms precisely. As the properties of self‐assembled systems can be tuned by manipulating their energetic features, a complete understanding is indeed essential.8

This focus review is intended to provide experimental and theoretical chemists with a general overview of the different energy components that can influence the HB mechanism. Describing the HB energy in terms of different energy components requires the HB energy to be decomposed. This can be done in many ways (see for example, ref. 9), but this review is not intended to review the available energy decomposition schemes. Instead, we hope to give a balanced view of the different perspectives on H bonding. The following individual energy components will be discussed: 1) electrostatic interactions, 2) orbital interactions, 3) π‐resonance assistance, 4) cooperative effects, 5) steric repulsion, 6) dispersion interactions and 7) secondary electrostatic interactions (Figure 1). For the sake of brevity, not all computational settings are mentioned explicitly but can instead be found in the given references.

Figure 1.

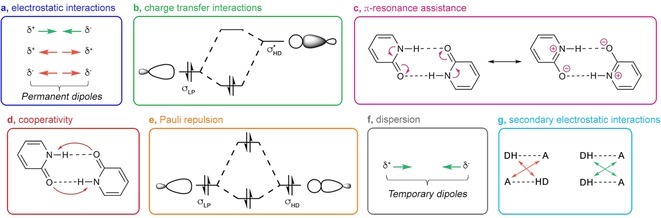
Schematic representation of a) electrostatic interaction, b) charge transfer interactions, c) π‐resonance assistance, d) Pauli (steric) repulsion, e) dispersion, f) cooperativity and g) secondary electrostatic interactions. Adapted with permission from ref. 10. Copyright 2019, ACS.

2. Energy components in hydrogen bonds

2.1. Electrostatic Interaction

HBs are usually formed between atoms that are electronically complementary, that is, between a proton acceptor atom with partial negative charge and an opposing proton atom with partial positive charge. The electrostatic interaction (Figure 1 a) will generally become stronger when the partial charges on the frontier atom are enhanced, which can be achieved by modifying the molecular structure.6, 11, 12, 13, 14

The electrostatic interaction ΔV _elstat between two hydrogen‐bonded monomers A and B can be written as

$${\displaystyle \Delta {\mathrm{V}}_{\mathrm{elstat}}={\sum }_{\begin{array}{c}\alpha ϵA\\ \beta ϵB\end{array}}\frac{{\mathrm{Z}}_{\alpha }{\mathrm{Z}}_{\beta }}{{\mathrm{R}}_{\alpha \beta }}-\int {\sum }_{\alpha ϵ\mathrm{A}}\frac{{\mathrm{Z}}_{\alpha }{\rho }_{\mathrm{B}}\left(\mathrm{r}\right)}{\left|\mathrm{r}-{\mathrm{R}}_{\alpha }\right|}\mathrm{dr}-\int {\sum }_{\beta ϵ\mathrm{B}}\frac{{\mathrm{Z}}_{\beta }{\rho }_{\mathrm{A}}\left(\mathrm{r}\right)}{\left|\mathrm{r}-{\mathrm{R}}_{\beta }\right|}\mathrm{dr}+\int \int \frac{{\rho }_{\mathrm{A}}\left({\mathrm{r}}_1\right){\rho }_{\mathrm{B}}\left({\mathrm{r}}_2\right)}{{\mathrm{r}}_{12}}\mathrm{d}{\mathrm{r}}_1\mathrm{d}{\mathrm{r}}_2}$$

where Z _α and R _α are the nuclear charge and position of atom α, respectively, and ρ(r) is the molecule's electronic density. The first term is the repulsive Coulombic interaction between the nuclei of monomer A with those in monomer B, the second and third terms are the attractive Coulombic interactions between the electrons of monomer A with the nuclei in monomer B and vice versa, and the last term is the repulsive Coulombic interaction between the electrons in monomer A with those in monomer B. However, as it is computationally demanding to obtain an accurate electronic density, particularly for large molecular systems, the electrostatic interaction has been approximated by simpler models. The simplest approach would be to represent the interacting nuclei as point charges, but this does not account for the directional preferences15 that are seen in HBs. Therefore, a more complete description of the charge distribution is necessary. Lennard‐Jones and Pople used point charges to represent the lone pair (LP) orbital as a finite dipole and the electrons on the H‐D bond as an asymmetrical quadrupole, which gave reasonable values for the HB energy of (H₂O)₂.16 Buckingham and Fowler modeled the monomeric charge distribution by a set of point multipoles while mimicking the steric repulsion by embedding the atoms in hard spheres,17 which correctly predicted the geometry of 29 van der Waals complexes. The successful application of these simple charge models supported the idea that the electrostatic interaction is a good descriptor for the HB strength and directionality.15, 17, 18, 19, 20 However, these oversimplified models cannot account for all experimental and theoretical observations.2, 3 Clark, Politzer and Murray21, 22 argue that simple electrostatic models fail because they neglect the polarization by using the unperturbed monomeric electronic density. By using the Hellman‐Feynman theorem, they show that noncovalent interactions could be described by classical electrostatics, but only when the exact electronic density (or a good approximation) is known.

Another way to describe HBs is by viewing the monomers as interacting dipole moments. This so‐called monomeric polarity model has been used successfully to qualitatively explain the bonding trends in complexes with more than one HB. Šponer and co‐workers23 studied 30 DNA base pairs and found that their bonding energy is strongly influenced by the polarities of the monomers and the mutual alignment of their dipole moments. This explains, for example, why πκ base pairs are less stable than normal base pairs, or why the mismatched guanine (G) base pair GG1 is considerably more stable than GG4 (Figure 2).23, 24

Figure 2.

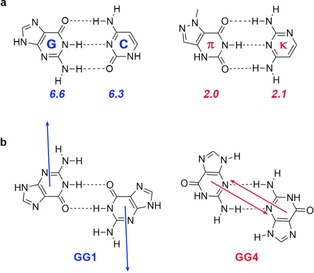
a) GC and πκ‐base pairs with their monomeric dipole moments in italic [in Debye]; b) Mutual alignment of monomeric dipole moments in GG1 and GG4. Data were taken from ref. 23 and 24.

However, there are also cases in which this dipole‐dipole interpretation fails to explain the geometrical and energetic trends, such as the nonlinearity of the HF dimer14 or the large energetic differences between dimers with similar dipole moments.10 More recently, Tiwari and Vanka25 proposed to use the electrostatic force (which has directionality) rather than the electrostatic interaction for the description of noncovalent interactions. Good correlations were found between the electrostatic forces and the binding energy for a wide range of systems, including 28 base pairs that were studied in ref. 26.

2.2. Charge Transfer Interactions

Charge transfer (CT) interactions are defined as the transfer of electron density from one monomer to the other monomer upon formation of the HB. The charge is usually transferred from the lone pair (LP) orbital on the HB acceptor atom to the opposing antibonding σ*_D‐H orbital (Figure 1 b), but can also be donated by other electron‐rich regions.2, 3, 4, 27, 28, 29, 30, 31, 32, 33, 34 The magnitude of these CT interactions is proportional to35

$${\displaystyle \mathrm{CT}\propto -\frac{{\mathrm{S}}_{\mathrm{occ},\mathrm{virt}}^2}{\left|{ϵ}_{\mathrm{occ}}-{ϵ}_{\mathrm{virt}}\right|}}$$

where S is the orbital overlap and ϵ is the energy difference between the occupied‐virtual orbitals. The orbital interactions are thus enhanced by a larger orbital overlap (which makes this term strongly angular‐ and distance dependent14, 36, 37) and smaller orbital energy gap, which can be tuned by modifying the molecular structure. These substituent effects were for example studied by Fonseca Guerra et al.11, 12, 13 by introducing substituents on remote positions in the DNA base pairs guanine‐cytosine (GC) and adenine‐thymine (AT) and by Gilli and Gilli37 for enaminones derivatives.

The covalent nature of HBs has been highlighted in many studies. In 2000, Gilli and Gilli introduced the Electrostatic‐Covalent HB Model (ECHBM) based on a large number of structural and spectroscopic data.37 This model states that HBs become increasingly covalent with increasing strength, up to very strong homonuclear HBs that are essentially three‐center‐four‐electron covalent bonds. Furthermore, several groups have shown that the electrostatic interaction alone is not always capable of overcoming the repulsive steric interactions at equilibrium distance, which emphasizes the importance of CT interactions in Watson–Crick (WC) and mismatched DNA base pairs,32, 33, 38 formamide dimers and derivatives,29 smaller analogues of WC base pairs28 and other dimers containing two to four HBs.30 Another way to probe the importance of CT interactions is by switching off any orbital interactions and reoptimize the system of interest subsequently.4, 27, 39 This was for example done by Weinhold and Klein4 for H₃N⋅⋅⋅H₄N⁺, which resulted in a significant elongation of the N‐N distance, shortening of the H−N bond and almost four times less stable HB energy. Another phenomenon that highlights the importance of covalency is cooperativity, which will be further discussed in Chapter 2.4.

HB formation often results in an elongation of the D−H bond, which is accompanied by a decrease of its stretching vibrational frequency. This so‐called redshifting effect has been one of the criteria for the experimental detection of HBs,2, 40 and can be understood from both electrostatic and covalent arguments. From a purely electrostatic perspective, Joseph and Jemmis argue that the electrostatic attraction between H and A (H⋅⋅⋅A) promotes elongation of the D−H bond.41 However, a more popular explanation is based on covalent arguments, which states that the redshifting comes from the donation of charge into the D−H σ* orbital upon HB formation. This accumulation of charge increases its antibonding character and therefore results in a weakening of the D−H bond.2, 39, 42 Redshifting is therefore seen as evidence for the covalent character of HBs.2 Wang, Mo, Shaik et al.27 have shown that inhibiting CT interactions results in a shortening of the D−H bond, which shows that these covalent interactions are crucial for the redshifting to occur.

Despite all these studies that highlight the importance of orbital interactions, a general consensus of the amount of covalency in HBs is still missing. This is partly because not all EDA schemes are able to separate the intermolecular CT from the intramolecular polarization interaction (i.e. the reorganization of electronic density within one monomer due to the presence of the other monomer), but also because the many available EDA schemes are not always in agreement with each other. For example, according to the natural bond order (NBO) method the HF dimer has a CT interaction of −6.6 kcal mol⁻¹ and is primarily responsible for HB formation.43 On the other hand, the same CT interaction is estimated to be only −0.4 kcal mol⁻¹ by using the symmetry‐adapted perturbation theory (SAPT) variant SAPT(DFT), leading to the opposing conclusion that CT interactions do not play a dominant role in HB formation.44 Nevertheless, there are many different EDA schemes that find significant CT interactions. Second‐generation absolutely localized molecular orbital (ALMO)‐EDA estimates that 40 % of the total interaction energy in the water dimer is composed of CT interactions.38 Galbraith et al. used a valence bond (VB) theory‐based EDA and concluded that the HBs in F−H⋅⋅⋅FH, F−H⋅⋅⋅OH₂, F−H⋅⋅⋅NH₃, HO−H⋅⋅⋅OH₂, HO−H⋅⋅⋅NH₃ and H₂N−H⋅⋅⋅NH₃ are predominantly covalent in nature.45 They argue that the importance of CT is further supported by the fact that the HB becomes stronger when going from the acceptors FH<OH₂<NH₃, because this correlates with the electron donating ability of the proton acceptor atom.

Interestingly, the nature of HBs was even further questioned by Weinhold and Klein46 by introducing the concept of anti‐electrostatic HBs (AEHBs). AEHBs are kinetically stable HBs between monomers with like charges. As the Coulombic interaction between these monomers must be repulsive, they argued that these systems proved the dominant covalent nature of HBs and that the electrostatic contribution is even irrelevant. This was objected by Frenking and Caramori,47 who showed that not only the orbital interactions, but also the electrostatic interactions are stabilizing with respect to the transition state. The attractive electrostatic interaction in AEHBs was later confirmed by Shaik and Mo48 and others,38 and can be understood from polarization upon formation of the dimer which makes the proton acceptor more negative and proton itself more positive.48 These groups thus concluded that both the electrostatic and orbital interaction contribute significantly to the AEHB energy.38, 47, 48

2.3. π‐Resonance Assistance

The concept of π‐resonance (Figure 1 c) was first proposed by Gilli et al. in 1989.49, 50 In this so‐called resonance‐assisted H‐bonding (RAHB) model, they proposed that “the interplay between HB and (.) heteroconjugated systems can strengthen remarkably the HB itself”. The model thus suggests that there is a synergistic reinforcement between π‐resonance and H‐bonding.

The nature of this π‐delocalization has been interpreted in multiple ways, and is still a subject of an ongoing debate.51, 52, 53, 54, 55, 56 One interpretation is that resonance in the π‐electron system makes the HB donor more positively charged and the HB acceptor atom more negatively charged (Figure 3), which results in an overall reinforcement of the HB strength. Another interpretation is that there is a synergistic interplay between the donor‐acceptor interactions in the σ‐ and delocalization in the π‐electron system. In this exposition, the π‐resonance assists the HB by destabilizing the σ_LP of the HB acceptor and stabilizing the σ* of the HB donor atom, resulting in a smaller σ HOMO–LUMO gap and thus a stronger σ CT interaction. Both interpretations will be discussed in this subchapter for both intermolecular and intramolecular HBs.

Figure 3.

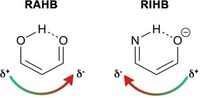
The π‐resonance in RIHB makes the H acceptor more positive and H donor more negative, which opposes the favorable π‐charge flow in RAHBs.

The nature of π‐resonance assistance in the DNA base pairs GC and AT was studied by Fonseca Guerra et al.33, 57 By analyzing the atomic charge rearrangements associated with dimer formation (Figure 4), they showed that the acceptor atoms gain π‐density while the opposing N−H bonds lose π‐density (Figure 4). A similar charge rearrangement was found by Ziegler and co‐workers in a number of doubly to quadruply H‐bonded systems,30 and for systems with intramolecular HBs.51, 54 The π‐resonance thus counteracts the build‐up of charge that arises from charge‐transfer interaction in the σ system. For GC and AT, these π‐orbital interactions amount to −4.8 and −1.7 kcal mol⁻¹, respectively, which is a small but significant contribution to the total orbital interaction of −22.4 (AT) and −34.1 (GC) kcal mol⁻¹.33 For the systems in ref. 30, values between −1.8 and −6.4 kcal mol⁻¹ were found for the RAHB, which is about four times as small as the stabilization from the σ orbital interaction. The role of the aromatic ring in A and T was more recently studied by Guillaumes et al. by removing the aromatic rings of both monomers.28 They found that the charge rearrangements in the π‐electron system are not exclusively due to aromaticity, but that the sp ²‐hybridization of the proton‐ donor and acceptor atoms already accounts for the π‐charge delocalization.

Figure 4.

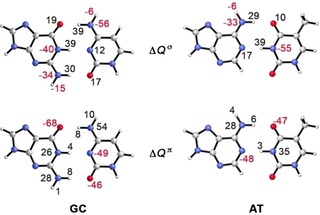
Atomic charge rearrangement ΔQ (in milli‐electrons) upon HB formation in GC (left) and AT (right) in the σ (up) and π (down) electron systems. Data were taken from ref. 56.

When polarization in the π‐electron system is inhibited in GC and AT, the σ orbital interactions remain practically unchanged.33 This indicates that there is almost no synergistic reinforcement between the σ and π‐electron system, and that the σ and π interactions thus take place independently from each other. Also for the smaller analogues of AT, the simultaneous occurrence of the σ and π interactions was found to be only slightly stronger than the sum of these interactions occurring individually.28 However, the π‐resonance does play an important role for the structure of the DNA bases. By computing the HB energy with and without π‐polarization as a function of the base‐base distance, it was found that the equilibrium HB distance expands for both bases by circa 0.1 Å when π‐polarization is inhibited.33

The intramolecular HB in unsaturated systems is generally stronger than in their saturated analogues. Different reasons have been proposed for this enhanced HB strength. Alkorta et al.55 have argued that the increased HB strength in unsaturated systems is actually associated with the σ‐skeleton which allows the HB donor‐ and acceptor atoms A and D to be in closer proximity. In a later study by Yáñez and co‐workers54 on forty different systems with intramolecular HBs, it was shown that when the D and A atom in saturated systems are constrained to have the same position as in their unsaturated analogues, their HBs were of similar strength or even stronger than the HBs in the unsaturated systems. They therefore concluded that the increased stability of RAHB systems comes indeed from the structure of the σ‐skeleton. However, these findings were contradicted by Mo and co‐workers, who demonstrated that the π‐resonance actually decreases the HB distance and therefore increases the HB strength.52 This shortening of the bond occurs because π‐resonance makes the proton donor more positive and proton acceptor more negative, resulting in shorter and stronger HBs. Furthermore, they argue that the σ‐framework is even unfavorable for some unsaturated systems in comparison with their saturated analogues because it is less flexible. A recent study by Grosch et al. on malonaldehyde (MA) and its saturated analogue 3‐OH showed that π‐resonance reduces its HB distance and therefore increases its strength, which is in line with the findings by Mo et al.51

Grosch et al. also studied the synergistic interplay between the σ‐ and π‐electron system in malonaldehyde (MA) and its saturated analogue 3‐OH.51 No significant changes were found in the σ orbital interactions when π‐delocalization was inhibited, which led them to conclude that there is no synergistic interplay between the σ‐ and π‐orbital interactions.

Resonance can also weaken the HB (Figure 3). These so‐called resonance‐impaired or resonance‐inhibited HBs (RIHBs) have been studied by numerous groups.58, 59, 60 For example, the 3‐amino acrylaldehyde (right structure in Figure 3) forms significantly shorter HBs with stronger N‐H red shifting when the π‐resonance is quenched.57 Furthermore, comparing this unsaturated system with its saturated counterpart shows that the HB in the saturated system is significantly stronger, which indicates again that the π‐resonance has a destabilizing impact on the HB energy. The either weakening or strengthening contribution of π‐resonance can be exploited by substituting electron donating or withdrawing groups to tune the HB strength.58

2.4. Cooperative Effects

Cooperativity is defined as the simultaneous occurrence of two or more interactions being stronger than the sum of each of these interactions occurring individually (Figure 1 d). An example is the cooperative reinforcement between the σ‐ and π‐electron system, which has been discussed in the previous subchapter. Another form of cooperativity is found in oligomers with n>2 in which the HBs are stronger than the HBs in the dimer. These cooperative effects play an important role in chemistry, biology and material science, and have therefore been studied extensively (see for example the excellent review by Mahadevi and Sastry, 201661).

A high degree of cooperativity was found in H‐bonded formamide chains, in which the outer HBs in the decamer are 2.5 times stronger than the HBs in the dimer.62 The HB energy changes less significantly in the middle of the chain upon the lengthening of the chain. As the HB strength depends on both the length of the chain and the position in the chain, Dannenberg concludes that it is inadequate to model these interactions by simple pairwise interactions between individual HBs, which has important implications for the modeling of, for example, protein folding by using molecular dynamics. Similar cooperative effects were later found in 4‐pyridone chains.63 Cooperative effects have also been observed in C−H⋅⋅⋅O bonds by Scheiner et al.64 For HFCO, the individual HB energy increases by 57 % when going from the dimer to the infinite chain. Interestingly, the increase in HB energy for H₂O is of similar magnitude (66 %), even though the individual HB strength of the HFCO dimer is more than twice as weak as the H₂O dimer.

A significant cooperative reinforcement has also been observed in guanine quartets G₄, which was initially attributed to π‐resonance assistance.65 However, as no cooperativity was found in xanthine quartets X₄, even though both systems share similar π‐electron systems (Figure 5), this interpretation was questioned.66 Fonseca Guerra et al. demonstrated that the cooperative reinforcement in G₄ instead originates from the charge separation that goes with donor‐acceptor orbital interactions in the σ‐electron system.66 Since the donor‐acceptor interactions between the guanine bases induce a charge separation, the HB accepting base in G₂ builds up a positive charge, while the HB donating base builds up a negative charge. The build‐up of charge results in a larger partial positive charge on the HB donor groups N‐H and a larger negative charge on the HB acceptor atoms N and O. This translates into a strengthening of 1) the electrostatic interaction and 2) the orbital interaction because the charge accumulation reduces the HOMO–LUMO gap. Cooperative effects in specific guanine ribbon arrangements in vacuo and gold surfaces67 and cyclic water trimers and tetramers68 have also been attributed to CT interactions.

Figure 5.

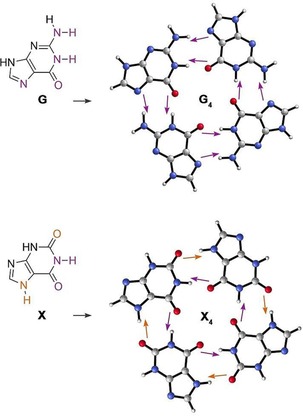
Guanine (G) and xanthine (X) monomers (left) and quartets (right). The purple and orange arrows represent the direction of σ charge flow due to HB formation, and explain why there is a favorable charge separation in G₄.

Filot et al. studied the cooperative effect in supramolecular polymers that are composed of trialkylbenzene‐1,3,5,‐tricarboxamide (BTA) monomers.69 They found that the threefold HBs go from 9.2 kcal mol⁻¹ in the dimer to 27.7 kcal mol⁻¹ in the central bond in the heptamer, which was for the largest part attributed to the increase in polarization and CT interactions upon the growth of the polymer chain. These effects were visualized by electrostatic potential surfaces, which show that the outer two monomers in the BTA heptamer have a larger accumulation of charge than the BTA dimer, making them better HB partners for the next incoming monomer.

Besides cooperative, systems can also be anticooperative, in which HBs reduce the strengths of each other. This occurs for example in systems with double HB donors such as H₂O. Steiner has attributed this effect to the repulsion between two roughly parallel dipole moments.70 However, a later study by Rocha‐Rinza et al. in different water structures attributed the weakening to CT interactions.68 For A₁⋅⋅⋅H₁‐D‐H₂⋅⋅⋅A₂ systems, the transfer of charge from A₁ to H₁ makes H₂ more negative, which weakens its resulting HB with A₂. Similarly, in D‐H₁⋅⋅⋅A⋅⋅⋅H₂‐D systems, the transfer of charge from A to H₁ makes A less negative, which makes it a less suitable H₂ proton acceptor.68

2.5. Pauli Repulsion

The Pauli repulsion is defined as the repulsive interactions between the monomer's filled orbitals (Figure 1 e), and originates from the fact that electrons with the same spin cannot be at the same position in space. Obeying the Pauli principle results in a depletion of electron density around the hydrogen atom, which explains the downfield ¹H chemical shift upon HB formation.71 Furthermore, Pauli repulsion has been shown to be crucial for a correct description of the HB strengths and lengths.

Adhikari and Scheiner72 studied the angular dependence for (among others) H₃N⋅⋅⋅Z (Z=HOH, HOF, HF and HCl) by distorting the N⋅⋅⋅H−D angle. By using SAPT, they found that only the exchange repulsion goes up in energy when the angle is distorted, which implies that the exchange repulsion is actually the driving force behind the HB directionality in these systems. A similar result was found by Head‐Gordon et al. for the near‐linear O−H⋅⋅⋅O bond of the water dimer. They demonstrated with ALMO‐EDA that this near‐linearity is already preferred without CT and polarization, which shows that the linearity comes from an interplay between the electrostatic interaction and Pauli repulsion.73

Van der Lubbe and Fonseca Guerra demonstrated74 that the Pauli repulsion can also be a decisive factor for relative HB strengths. They found that the mismatched DNA base pair GG is significantly stronger bound than CC, even though the latter has more favorable electrostatic and orbital interactions. The higher stability for GG follows entirely from the Pauli repulsion, which is significantly less repulsive for GG than for CC. This difference was traced back to the direction of the lone pair orbitals (Figure 6), which results in a significant larger overlap with the opposing filled N‐H orbitals in CC than in GG.

Figure 6.

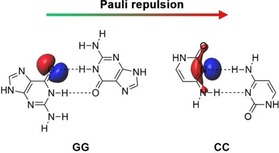
The lone pair on N has a better alignment with the opposing H−N bond, which results in a larger Pauli repulsion for CC than for GG.73

2.6. Dispersion Interactions

Dispersion is defined as the attractive interaction between temporary dipoles, which arise from the correlated motion between electrons in monomer A with those in monomer B (Figure 1 f). Dispersion interactions are important to include for a correct description of the geometric and energetic HB properties in large bulky systems, and are affected by the size, shape and relative distance of the H‐bonded moieties.75, 76, 77, 78, 79 When these factors are comparable, the dispersion interactions are usually of similar strength.10, 76 However, when one or more of these factors are significantly different, dispersion might even determine the trend in interaction strength. This was shown by Hoja et al. by studying (XOH)₂ with X=H, Me, Et, nPr, nBu, iPr and tBu.76 They found that the interaction energy between two H‐bonded monomers becomes 58 % stronger when going from the smallest dimer (H₂O)₂ to the bulkiest dimer (tBuOH)₂ (Figure 7). Interestingly, this trend becomes virtually the opposite when the dispersion interaction between the alkyl substituents is not taken into account. This demonstrates that the dispersion energy can be crucial for a correct description of the bonding trends.

Figure 7.

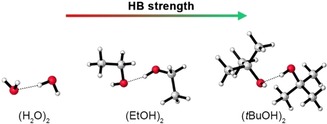
The HB interaction energy becomes stronger when going to bulkier dimers.76

2.7. Secondary Electrostatic Interactions

The secondary electrostatic interaction (SEI) model was formulated in 1990 by Jorgensen and Pranata to explain differences in binding strengths between multiple H‐bonded arrays.80 SEIs are defined as the diagonal interactions between the HB donor (D) and acceptor (A) atoms of adjacent HBs, and can either be attractive or repulsive (Figure 1 g). For doubly H‐bonded systems, there are thus two possible configurations, that is, DD‐AA and DA‐AD, of which the former is predicted to be the most stable. The model oversimplifies the HB mechanism by describing them as interacting point charges, but nevertheless, the SEI model has been widely used to predict and explain differences in experimental binding strengths.

The model was questioned by Popelier and Joubert26 who studied the interactions in 27 DNA base pairs. They demonstrated that the SEI model ignores many significant (long‐range) interactions, which led them to conclude that primary and secondary interactions constitute “a rather arbitrary subset”. The importance of considering additional atom‐atom pairwise interactions has been confirmed by other groups.25, 81, 82, 83 Lukin and Leszczynski84 studied seventeen multiply H‐bonded complexes to test the applicability of the SEI model, and concluded that “the stability information of a single complex could not be directly used to obtain stability data for H‐bonded assemblies in general.” Wu et al.84 showed with 26 triply and 20 quadruply H‐bonded systems that the predictions made by the SEI model do not always hold. That is, the systems with attractive SEIs are not always the strongest bound, and dimers with the same net number of SEIs may still vary significantly in binding strength.

Despite these valid criticisms, experimental binding strengths are often in line with the model's predictions.10, 86, 87 Recently, we showed that this predictive power can be understood from the charge separation in the monomers.10 When HB donor atoms (which are electron donating in nature) are grouped, there is a larger accumulation of positive charge around their frontier atoms. Likewise, when HB acceptor atoms (which are electron withdrawing in nature) are grouped, there is a larger accumulation of negative charge around their frontier atoms (Figure 8). This larger accumulation of charge results in 1) a stronger electrostatic interaction and 2) a stronger orbital interaction because the charge accumulation decreases the HOMO–LUMO gap. Since the grouping of proton donor‐ and acceptor groups is typical for systems with attractive SEIs, these dimers are often stronger bound than dimers with repulsive SEIs in which the proton donor‐ and acceptor groups are alternating.

Figure 8.

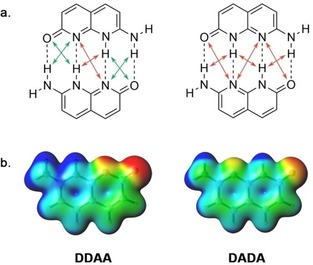
When the HB donors and acceptor are grouped (as in DDAA), there is a larger monomeric charge accumulation than in systems with alternating donors and acceptors (as in DADA), which results in stronger HBs.10

In line with these results are the recent findings by Hernández‐Rodríguez, Rocha‐Rinza and co‐workers, who developed the acidity‐basicity interplay (ABI) model to explain the difference in association constants.82, 83 In this model, the HB strength increases with the acidity of the proton donor and basicity of the proton acceptor groups. The ABI model was not only capable to explain the order of stability or triply H‐bonded systems (AAA‐DDD>AAD‐DDA>ADA‐DAD), but also the relative order of dimers with the same HB pattern. As a larger accumulation of charge is associated with stronger acidities and basicities, the findings in ref. 10 explain the ABI model from a molecular orbital perspective.

3. Conclusion and perspectives

The HB mechanism is a complex interplay between different energy terms, whose importance depend on the molecular system. In this review, we have seen several examples of systems whose energetic features are not captured by easy‐to‐use predictive models, including the relative stability of the mismatched DNA base pairs GG and CC (entirely governed by the difference in steric repulsion),74 the energetic trends in (XOH)₂ with X=H up to tBu (entirely determined by dispersion interactions),76 the HB strength in oligomer chains in which the HB strength depends on both the length of and the position in the chain (resulting from cooperative effects)62, 69 and the significant atom‐atom pairwise interactions that are not considered by the SEI model.26, 81, 83 This emphasizes the importance of using quantum‐chemical calculations such as density functional theory (DFT) or post‐Hartree–Fock methods for a correct description of the HB. As our understanding of the HB mechanism is improving, we expect that the rational tuning of individual energy components will start to play a more important role in the artificial design of self‐assembled systems.

Conflict of interest

The authors declare no conflict of interest.

Biographical Information

Célia Fonseca Guerra received her PhD in Theoretical Chemistry with E. J. Baerends and J. G. Snijders on parallelization of the ADF program. Afterwards, she worked with F.M. Bickelhaupt on chemical bonding and became Assistant Professor. Currently, she holds Chairs in Supramolecular Quantum Biochemistry at the Vrije Universiteit Amsterdam and Applied Theoretical Chemistry at Leiden University.

Biographical Information

Stephanie C. C. van der Lubbe obtained her bachelor's degree in Forensic Science in 2014 and master's degree in Theoretical Chemistry in 2016. She is currently doing her PhD under the supervision of professor Fonseca Guerra at the Vrije Universiteit in Amsterdam, in which she studies the nature of hydrogen bonds from a Kohn–Sham molecular orbital perspective.

S. C. C. van der Lubbe, C. Fonseca Guerra, Chem. Asian J. 2019, 14, 2760.