Quantification of hydroxyl exchange of D‐Glucose at physiological conditions for optimization of glucoCEST MRI at 3, 7 and 9.4 Tesla

Abstract

Aims

To determine individual glucose hydroxyl exchange rates at physiological conditions and use this information for numerical optimization of glucoCEST/CESL preparation. To give guidelines for in vivo glucoCEST/CESL measurement parameters at clinical and ultra‐high field strengths.

Methods

Five glucose solution samples at different pH values were measured at 14.1 T at various B₁ power levels. Multi‐B₁‐Z‐spectra Bloch‐McConnell fits at physiological pH were further improved by the fitting of Z‐spectra of five pH values simultaneously. The obtained exchange rates were used in a six‐pool Bloch‐McConnell simulation including a tissue‐like water pool and semi‐solid MT pool with different CEST and CESL presaturation pulse trains. In vivo glucose injection experiments were performed in a tumor mouse model at 7 T.

Results and discussion

Glucose Z‐spectra could be fitted with four exchanging pools at 0.66, 1.28, 2.08 and 2.88 ppm. Corresponding hydroxyl exchange rates could be determined at pH = 7.2, T = 37°C and 1X PBS. Simulation of saturation transfer for this glucose system in a gray matter‐like and a tumor‐like system revealed optimal pulses at different field strengths of 9.4, 7 and 3 T. Different existing sequences and approaches are simulated and discussed. The optima found could be experimentally verified in an animal model at 7 T.

Conclusion

For the determined fast exchange regime, presaturation pulses in the spin‐lock regime (long recover time, short yet strong saturation) were found to be optimal. This study gives an estimation for optimization of the glucoCEST signal in vivo on the basis of glucose exchange rate at physiological conditions.

Abbreviations used

AR

anomeric ratio

BM

Bloch‐McConnell

CESL

chemical exchange sensitive spin‐lock

CEST

chemical exchange saturation transfer

CNR

contrast‐to‐noise ratio

GM

gray matter

MT

magnetization transfer

SNR

signal‐to‐noise ratio

ssMT

semi‐solid MT

1. INTRODUCTION

Chemical exchange saturation transfer (CEST) MRI enables the indirect detection of metabolites in small concentrations via exchange of protons in functional groups and water protons. CEST effects were observed in vivo for amide protons of proteins, amine protons of glutamate, guanidyl protons of creatine,1, 2, 3 and also for hydroxyl protons of glycosaminoglycans and myo‐inositol.4, 5 As hydroxyls of sugars also showed significant CEST effects in vitro, in vivo experiments could be performed to detect the uptake of injected glucose and glucose analogs in animal models using CEST,6, 7, 8, 9, 10, 11 and also the related chemical exchange sensitive spin‐lock (CESL) technique.12, 13 GlucoCEST/CESL imaging using natural D‐glucose has already been shown to be feasible in human brain tumors at 7 T.14, 15, 16, 17 Although proof of concept has been provided, to date there is no comprehensive study investigating the optimal CEST/CESL presaturation parameters. A major problem is that optimization in vivo is complicated, especially in human subjects, as only a few protocols can be tested reliably during one examination. Moreover, exchange rates for each individual hydroxyl proton of the glucose molecule have not been determined, nor their pH dependence, thus preventing a proper and accurate simulation and investigation of saturation conditions for optimizing the attainable CEST contrast. To overcome this problem a numerical approach is followed in the present work: by quantification of glucose exchange rates at physiological conditions in vitro, a tissue‐like two‐pool model of water and a semi‐solid magnetization transfer (ssMT) can be extended by the determined glucose hydroxyl pools. This in silico pool model is then used in Bloch‐McConnell simulations to gain insight into the expected signal and contrast‐to‐noise of a glucose injection experiment as near as possible to an in vivo experiment.

The present work consists of three major parts. In the first part, glucose exchange rates are determined at physiological conditions using Bloch‐McConnell (BM) fitting of Z‐spectra. While BM fitting of Z‐spectra with separated pools and lower exchange rate has been shown to be successful for exchange rate quantification,18 the glucose system has two additional challenges: (i) the hydroxyl resonances are very close to each other and to the water proton resonance; and (ii) exchange rates are in the intermediate to fast exchange regime, thus peaks are coalescent. To gain more insight into and reliability in the nonlinear BM fit, in addition to physiological conditions, lower pH values are also quantified to get a valid extrapolation to the fast exchange regime and thus to the more difficult to fit physiological situation. In the second part, the obtained glucose pool model is used to create a gray matter (GM)‐like system including realistic water relaxation rates and a ssMT component. As the fast hydroxyl exchange requires relatively strong saturation, proper modeling of the B₁‐sensitive direct saturation and ssMT is crucial for obtaining reliable predictions for in vivo effect strength. This allowed for optimization of the presaturation parameters and analysis of previous approaches; optimal parameters are presented for the static field strengths of 3, 7 and 9.4 T. In the third part, the gained insights are translated to in vivo application in a mouse model with tumors measured at 7 T, where a small range of saturation parameters could be tested and the corresponding CEST effects directly compared.

2. METHODS

2.1. Glucose hydroxyl pool model

In solution, D‐glucopyranose (D‐glucose) is predominantly in the form of a pyranose ring with two possible anomeric conformations, α and β (Figure 1). At equilibrium the anomeric ratio (AR), which is the ratio of concentration of both forms in solution, is AR/(1‐AR) = 0.36/0.64 for α:β.

Figure 1.

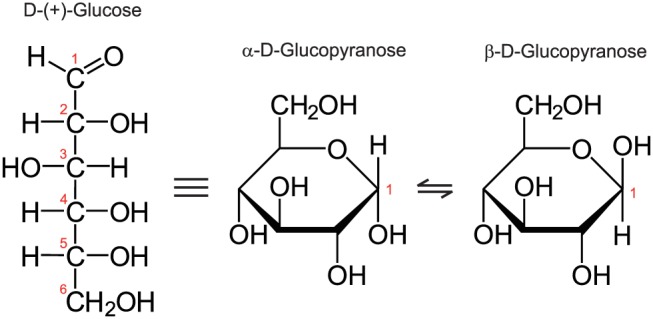
Glucose structure and anomers

In both anomeric conformations, the –OH at the sixth carbon atom (numbering as in Figure 1) has a chemical shift from water of 0.66 ppm; the three –OH groups at positions 2, 3 and 4 have very similar chemical shifts of ~ 1.28 ppm.19 The chemical shift of the hydroxyl at position 1 depends on the anomeric conformation: it is 2.08 ppm for the α form and 2.88 ppm for the β form. The chemical shifts relative to water are assumed to be independent of pH and temperature.

With the assumption that each proton site with the same chemical shift shows the same exchange rate to water (assumption 1), we can build a four‐pool model for a glucose solution in water.

We label the –OH sites using the letters B, D, E and F, in the order of increasing chemical shift relative to water; thus the chemical shifts of these pools are δ_B = 0.66 ppm, δ_D = 1.28 ppm, δ_E = 2.08 ppm and δ_F = 2.88 ppm (pool A is the water pool; pool C is omitted here as it is reserved in the BM simulation for the ssMT pool).

We now define the fraction of glucose molecules relative to water protons:

$${\mathrm{f}}_{\mathrm{glc}}=\left[\mathrm{Glc}\right]/\left(2\left[{\mathrm{H}}_2\mathrm{O}\right]\right)=\left[\mathrm{Glc}\right]/11\text{1M}$$

With this, the proton fractions of each pool can be written by using f_glc and the AR:

$${\mathrm{f}}_{\mathrm{B}}={\mathrm{f}}_{\mathrm{glc}};{\mathrm{f}}_{\mathrm{D}}=3{\mathrm{f}}_{\mathrm{glc}};{\mathrm{f}}_{\mathrm{E}}=\mathrm{AR}·{\mathrm{f}}_{\mathrm{glc}};{\mathrm{f}}_{\mathrm{F}}=\left(1-\mathrm{AR}\right)·{\mathrm{f}}_{\mathrm{glc}}$$

To decrease the number of unknowns, the chemical shifts of these pools are set to the aforementioned fixed values; also, the proton fractions are fixed and directly given by the glucose concentration fraction; the only degree of freedom for the concentrations is the AR, which depends on the pH or temperature of the solution.

We also neglect intramolecular exchange between the individual hydroxyl groups (assumption 2), only considering an exchange directly to the water pool (that can still be base‐, acid‐ or water‐catalyzed at this point). We also assume that the transverse and longitudinal relaxation rates of the hydroxyl protons are negligible compared with the exchange with water (assumption 3). Thus the only free parameters of the fit are the exchange rates, k_B, k_D, k_E and k_F, and the AR, as well as the transverse relaxation rate of water, R_2A. The R_1A values for the water pool were measured by a saturation recovery sequence and provided to the fit.

In a second model, we extend the Bloch equations by pH as a parameter, by assuming that the exchange rate can be expressed as a sum of base‐ and water‐catalyzed exchange (assumption 4).

$${\mathrm{k}}_{\mathrm{x}}={\mathrm{k}}_{\mathrm{x}1}\cdot {10}^{\mathrm{pH}-7}+{\mathrm{k}}_{\mathrm{x}0}$$ (1)

Then, for each pool, x = B, D, E, F, two unknowns are added, k_x1 and k_x0. This seems like an introduction of more parameters, yet multiple pH Z‐spectra can then be fitted simultaneously. Thus, for five pH values and four pools, the previous model required (5 x 4) 20 exchange rates, but now only (2 x 4) 8 unknown exchange constants must be determined by the fit. In addition, the better defined exchange rates at low pH values are then implicitly used for better extrapolation and determination of the exchange rates at high pH values, and therefore an increased stability is expected.

2.2. Simulation and full Bloch‐McConnell fitting

The underlying equations used for fitting are the six‐pool BM equations, including a ssMT pool. The matrix equations were described in detail previously,18 and further details on ssMT are also available.20 Numerical solutions of these equations and corresponding fits are realized as custom‐written scripts in Matlab version 8.2.0.701 (MathWorks Inc., Natick, MA, USA) following previously reported procedures.18, 21 In vitro glucose data were fitted in Matlab employing the full BM equations and the optimization function lsqcurvefit. The simulation files can be found and downloaded from the websites, cest‐sources.org or github.org: https://github.com/cest‐sources/BM_sim_fit.

2.3. Tissue‐like simulation

As CEST and CESL are almost equivalent experiments, with CESL being more general,22, 23 only CESL Z‐spectra were simulated using n ideal spin‐lock (SL) pulses with pulse duration (t_p) and amplitude B_1. With that, saturation parameters can be optimized, but also the comparison with on‐resonant SL can easily be performed by looking at short saturation durations, t_p. An applied readout will change the initial magnetization Z_i = M_i/M₀ before the subsequent saturation phase; for 90° excitation methods like spin‐echo this initial magnetization would be close to Z_i = 0 for a low angle gradient‐echo at Ernst condition Z_i ~ 1/(2‐T_R/T₁) ~ 0.5; here it was set to Z_i = M_i/M₀ = 0.1 as a compromise. Each simulation started from Z_i with a recovery period of duration T_rec, followed by the saturation period of duration t_sat = n·t_p/DC. To account for SAR and amplifier limits, a duty‐cycle (DC) of 50 % was assumed for the simulations. Using the tissue parameters of Table 1 and optimized exchange rates derived (Table 2), a tissue‐like full six pool simulation, including water and ssMT (two pools) and the glucose hydroxyls (four pools), was established.

Table 1.

Tissue model parameters at different field strengths. T₁ and T₂ values were taken from the multi‐field study of Zhu et al.24 MT parameters (pool C) were adapted from Stanisz et al25; f_C = 0.05, T_2c = 9.1 μs, k_CA = 40 Hz, δ_C = 0; Super‐Lorentzian lineshape

Tissue\B0	3 T	7 T	9.4 T
tissue model 1 (GM)	T1 = 1.31 s; T2 = 0.071 s; fC = 5%	T1 = 1.67 s; T2 = 0.043 s; fC = 5%	T1 = 2.002 s; T2 = 0.035 s; fC = 5%
tissue model 2 (tumor)	T1 = 1.31 s; T2 = 0.2 s; fC = 2%	T1 = 1.67 s; T2 = 0.2 s; fC = 2%	T1 = 2.002 s; T2 = 0.2 s; fC = 2%
PBS model 37°C	‐	T1 = 4.4 s, T2 = 2.6 s, fC = 0%	‐

Table 2.

Exchange rate estimations at physiological conditions: 1X PBS, 37°C, pH = 7.2. As a compromise between blood pH = 7.4 and intracellular tissue pH = 7, we use pH = 7.2 as physiological pH here for simplification. GOF, goodness‐of‐fit parameter adjusted R² (ranging from 0 to 1 with 1 being a perfect fit); Jin et al,12 Aroulmoji et al26

Method\exchange rate	kB (Hz)	kD (Hz)	kE (Hz)	kF (Hz)	AR	R2A (Hz)	GOF adjusted R2
Multi‐B1	1570 ± 220	7360 ± 476	5662 ± 2660	10 000 ± 3800	0.5 ± 0.5	0.41 ± 0.13	0.9953 (pH 6.8) 0.9946 (pH 7.2)
Multi‐B1‐multi‐pH	2900 ± 500	6500 ± 170	5200 ± 500	14 000 ± 650	0.374 ± 0.01	0.43 ± 0.01	0.99551
Jin et al7		6000	for single pool at 1.5 ppm and with concentration 5·fglc
Aroulmoji et al21		3421	For single pool, glucose 10%, 25 °C

To simulate pre‐ and postinfusion experiments two Z‐spectra are generated, one with the glucose pools activated (Z_post: six‐pool simulation) and one without (Z_pre: two‐pool simulation). We assume that the endogenous CEST effects are negligible for the optimization outcome (assumption 5).

The glucose contrast is then calculated by

$${\mathrm{Z}}_{\text{diff}}\left(\mathrm{\Delta \omega }\right)={\mathrm{Z}}_{\text{post}}\left(\mathrm{\Delta \omega }\right)-{\mathrm{Z}}_{\mathrm{pre}}\left(\mathrm{\Delta \omega }\right)$$ (2)

Assuming constant noise, the CNR is given by

$$\mathrm{CNR}={\mathrm{\Delta Z}}_{\text{diff}}\left(\mathrm{\Delta \omega }\right)\propto {\mathrm{Z}}_{\text{diff}}\left(\mathrm{\Delta \omega }\right).\sqrt{2}·{\mathrm{SNR}}_{\text{M0}}$$

Thus optimizing Z_diff also optimizes CNR for a constant SNR.

2.4. Experimental preparation of glucose

Seven model solutions containing 20 mM of glucose were prepared at different pH values ranging from 6.2 to 7.4. Model solutions were buffered using phosphate‐buffered saline (PBS) defined according to Cold Spring Harb Protoc.27 All model solutions were pipetted from highly concentrated stock solutions to ensure a precise adjustment of the concentrations, and pH values were adjusted to the final values using hydrochloric acid (HCl) at 90 % of the final volume, to take into account the added amounts of HCl. Final pH values were checked by means of a calibrated pH electrode. Experiments were performed after a waiting time of more than two hours to ensure that the anomeric equilibrium was reached.

2.5. Experimental CEST data acquisition and processing

Acquisition and processing of CEST data were performed in a similar manner as previously reported.28, 29 Model solutions were examined on a 14.1 T (600 MHz for ¹H) Avance II narrow‐bore spectrometer (Bruker BioSpin, Karlsruhe‐Rheinstetten, Germany). A 5 mm probe was used for RF irradiation and signal acquisition. To avoid radiation damping, the probe was operated detuned. The samples were stabilized at 37°C using the internal heating and cooling device. For CEST measurements, off‐resonance presaturation was achieved by a rectangular (rect) continuous wave (cw) pulse of length 12 seconds and different amplitudes, B₁, ranging from 1 to 5 μT. Signal acquisition was realized by a 90° rect pulse. Prior to repetition of the presaturation at another off‐resonance frequency, Δω, a relaxation interval of one second was included. Z‐values were calculated by integration of the water resonance (M_sat) and normalization with the equilibrium magnetization (M₀). M₀ was acquired at different time points and interpolated to obtain an individual M₀ for each presaturation cycle. Z‐spectra were sampled at 117 frequency offsets in unequal steps between ±5 ppm relative to the water peak. Z_initial was obtained after acquisition of M₀ and switching off the presaturation pulse. A T₁ measurement was achieved by a saturation recovery pulse sequence.

2.6. In vivo glucose injection experiments

For in vivo experiments, six‐week‐old female BALB/c mice (Charles River Laboratories Italia S.r.l., Calco, Italy) were maintained in the animal facility of the Department of Molecular Biotechnology and Health Sciences, University of Turin, under specific pathogen‐free conditions. All animal studies were approved by the University Ethics Committee in accordance with the European guidelines under directive 2010/63. Mice were injected subcutaneously with 2.5 x 10⁵ TS/A cells (cell line derived from a mammary adenocarcinoma spontaneously arising in BALB/c mice) and 15 days after the inoculation MRI acquisitions were performed with a Bruker 7 T Avance 300 MRI scanner equipped with a 30 mm ¹H birdcage coil. Animals were anesthetized by injecting a mixture of xylazine 5 mg/kg (Rompun, Bayer, Milan, Italy) and tiletamine/zolazepam 20 mg/kg (Zoletil 100, Virbac, Milan, Italy) and the breath rate was monitored by an air pillow placed below the animal (SA Instruments, Stony Brook, NY, USA). Glucose (dose: 3 g/kg) was administered through the tail vein using a programmable infusion pump (PHD 22/2000, Harvard Apparatus, Inc., USA) as a bolus followed by a continuous infusion for 30 minutes (at an infusion rate of 360 μl/h).

After acquisition of scout images, a T₂‐weighted anatomical reference image was acquired using a fast spin echo (FSE) sequence and the same geometry was used for the CESL experiments. Briefly, CESL Z‐spectra were acquired by using an adiabatic SL pulse, as reported by Herz et al,30 before and after the glucose injection with several saturation power levels (range: 0.6–5.0 μT) and irradiation times (range: 0.1–5.0 s). A single‐shot FSE‐centric encoding readout was used with the following parameters: TR = 6 s, TE = 3.5 ms, FOV = 3 x 3 cm, slice thickness = 2 mm, matrix size = 64 x 64.31

Z‐spectra were interpolated, on a voxel‐by‐voxel basis, by smoothing splines for B₀ correction32 and glucose contrast calculated as Z_diff values at 1.2 ppm.

3. RESULTS AND DISCUSSION

3.1. Glucose hydroxyls exchange rates at 14 T – individual pH

In a first attempt, multi‐B₁‐Z‐spectra for each pH were fitted by the numerical Bloch‐McConnell solution individually including the transverse relaxation of water R_2A as a free parameter. Figure 2 shows the fitted Z‐spectra and fitting results for the exchange rates, R_2A, and the AR. The fits are less stable at high pH values where exchange rates are faster and peaks coalesce, even at such high B₀. The AR is close to the literature value of 0.37 for low pH, yet shows an implausible pH dependence, decreasing to almost 0 for pH 6.8. Also, the fit output for the exchange rate of the anomeric proton E at high pH values is too low and hints at inaccuracies or instabilities of the fit at high pH.

Figure 2.

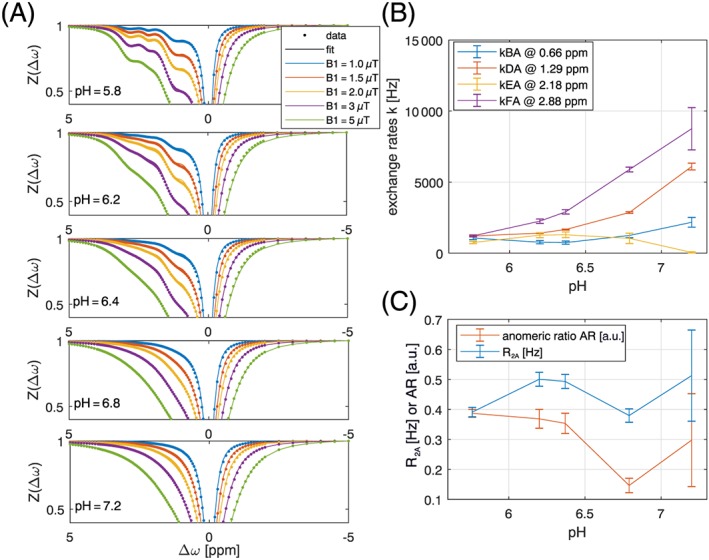
(A) Simultaneous multi‐B₁‐fit of five Z‐spectra of 20mM glucose model solutions acquired at 14.1 T yields glucose hydroxyl exchange rates for each pH at T = 37°C (B) and R_2A and anomeric ratio (C)

3.2. Glucose hydroxyls exchange rates at 14 T – multi‐pH

To overcome the instabilities, a second model was used that combined the multi‐pH measurements in the Bloch equations. Thus a stack of 25 multi‐pH‐multi‐B₁ Z‐spectra were fitted simultaneously by employing Equation 1. A pH‐independent but variable AR was used, and the results are shown in Figure 3; this resulted in a more reliable exchange rate estimation, k_B = (2900 ± 500) Hz, k_D = (6500 ± 170) Hz, k_E = (5200 ± 500) Hz, k_F = (14000 ± 650) Hz, R_2A = (0.43 ± 0.01) Hz, and AR = 0.374 ± 0.01 at physiological conditions of pH = 7.2 and T = 37°C (see again Table 2, the full parametrization k(pH) can be found in Supporting information Table S1). Table 2 also shows that both results compare relatively well with the averaged results of Jin et al12, who assumed a single exchanging pool and used on‐resonant SL for quantification of this fictional pool, which was then found at 1.5 ppm with an exchange rate of 6000 Hz. It is also in plausible agreement with the relaxometric studies at 25°C of Aroulmoji et al21 with an average exchange rate of ~ 3400 Hz for T = 25°C (Table 2).

Figure 3.

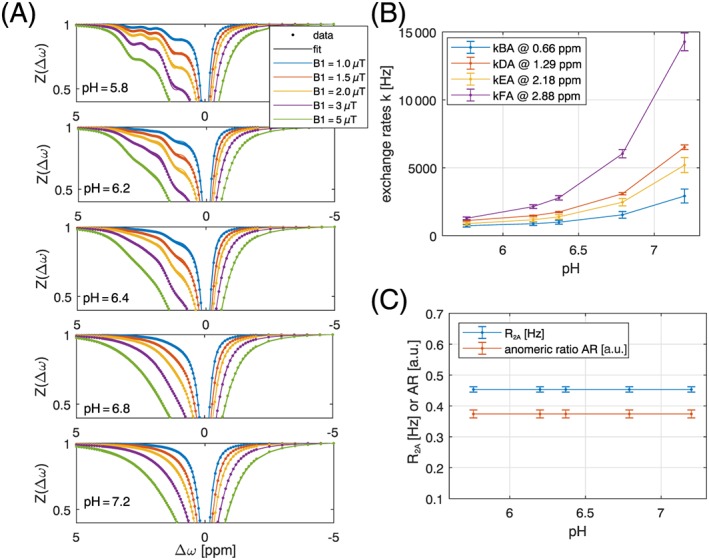
(A) Simultaneous multi‐B₁‐pH‐fit of 25 Z‐spectra of 20mM glucose model solutions acquired at 14.1 T yields glucose hydroxyl exchange rates as a function of pH at T = 37°C (B) and R_2A and anomeric ratio (C)

The proposed multi‐pH‐multi‐B₁ method can also be applied to other CEST active metabolites such as glucose analogs. A prerequisite is that a suitable pool model is found, which can be trickier if more anomers or protons affected by the anomeric structure are present. Also, in vivo coalesced effects are reported33, 34, 35; conceivably, ex vivo multi‐pH‐multi‐B₁ experiments can improve exchange rate determination.

For our purpose, to optimize the glucoCEST saturation, the exchange parameters given describe the multi‐pH multi‐B₁ data best (GOF in Table 2). Thus a glucose pool model is created by the data in Table 2 (row 2) and changes in the Z‐spectrum are studied at B₀ = 7 T using only individual pools (Figure 4). Initially, none of the pools shows a peak at their respective resonance frequencies, but instead saturation transfer effects coalesce completely with their on‐resonant T_2ex contribution (see also36). As expected by their concentrations, pools D and F are the strongest contributors to the saturation transfer effects of this model. Pools E and F show higher CEST signals than pool B due to the higher chemical shift. Investigating the difference spectra (Z_diff, Equation 2), shows that the contribution of hydroxyl exchange on the negative ppm side is of the same order of magnitude as that on the positive side for all hydroxyl pools. The exchange dependent relaxation value, R_ex (full details in36), of each hydroxyl can be calculated,21 as shown in Figure 4 (bottom row). Here, it can be seen that the strongest contribution of all hydroxyls is still on‐resonant, yet this broad peak is asymmetric: only the direct water saturation lets these effects appear as selective off‐resonant effects. Thus, in terms of selectivity, it is difficult to talk about hydroxyl proton “peaks” in the Z‐spectrum. The peak appears where the labeling and spillover effects have equal influence, thus the peak position is mostly dependent on B₁ and the type of reference used. We can conclude from this that: (i) asymmetry is not optimal to measure changes by glucose administration as effect size is decreased by the effects from the negative side; (ii) even the difference Z‐spectra are governed by direct water saturation, thus methods that have reduced direct saturation are of benefit, and lowering B₁ and saturation time in vivo could be the most crucial optimization step; and (iii) on‐resonant methods with access to R_ex such as SL must be evaluated as its exchange contribution is highest.

Figure 4.

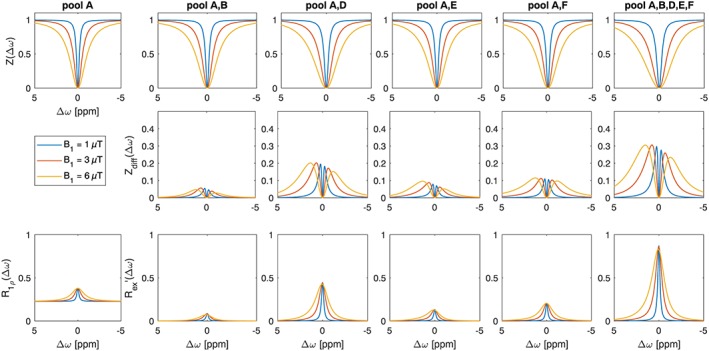
Simulation of glucose model at 7 T in PBS. Top row: Z‐spectra; middle row: Z_diff for the derived physiological glucose model with different number of pools; bottom row: R_1ρ of water, R_ex contribution for each pool separately and combined (details about R_1p and R_ex are in reference36)

Most important for the simulation are the actual tissue parameters for relaxation and ssMT. As spillover and ssMT will each have a very important contribution at the required powers, the optimal parameters will strongly depend on the tissue of interest. To reduce the number of hypotheses in the tested models, we assumed two tissue types, one healthy GM including semi‐solid MT, and one more liquid tissue type based on GM but with a long T₂ of 200 ms and decreased ssMT concentration (this could reflect either tumorous tissue or also a vascular compartment, but at least it shows what influence a reduced direct saturation and MT has on the optimal parameters). How strong the influence of the tissue parameters is can be seen when comparing Figures 5E and 5F, which show CEST effects of the same pools in PBS and in GM: the same CEST pool system yields CEST effects of an order of magnitude lower when the tissue relaxation parameters are altered from PBS‐like to tissue‐like.

Figure 5.

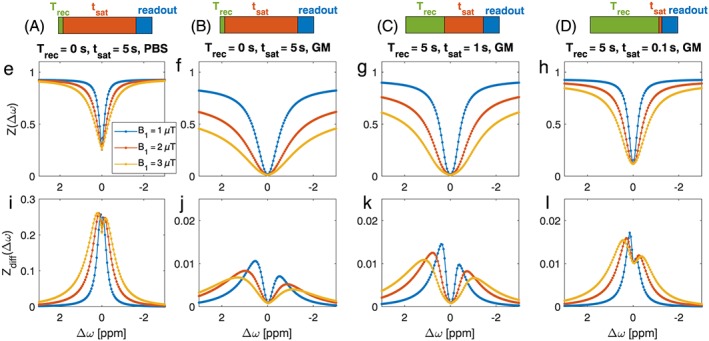
(A‐D) Schemes of different saturation approaches used in each column: long steady‐state saturation (A,B), intermediate saturation with precedent recovery phase (C), and short saturation after long recovery (D). In silico model of four glucose hydroxyl pools for different saturation regimes at 7 T in PBS (E,I) and tissue‐like GM environment (F‐H,J‐L). Z‐spectra (E‐H) and Z_diff (I‐L) in the steady‐state CEST regime (E,F,I,J), the intermediate regime with only one second of saturation (G,K), and the spin‐lock regime with 100 ms of saturation (H,L)

Before we look at the optimization outcome, we must gain insight into the simulation for GM and the four glucose hydroxyl pools for three typical CEST/CESL protocols. One is the typical long saturation to steady state (t_sat = 25 x 2 x 100 ms = 5 s) without any recovery time (T_rec) before saturation (Figure 5A,B). Second is the shorter saturation sequence with a T_rec = 5 s before one second of saturation (Figure 5C). Third is saturation in the SL regime with only 100 ms of saturation after five seconds of recovery (Figure 5D). To be able to compare the parameters, all of the simulations were performed as spin‐lock experiments, only with different parameters, which also enabled a direct comparison of off‐resonant CESL (more CEST‐like) with on‐resonant CESL. Figure 5 shows the Z‐spectra and the difference spectra Z_diff. Obviously the four parameters, T_rec, t_sat, saturation amplitude B₁ and saturation frequency offset, are nonlinearly related and have to be optimized simultaneously. From this first simulation we can already conclude that the optimal parameters may be closer to the on‐resonant SL regime with relatively short saturation.

As the parameters are interrelated and maximal effect strengths can be at different offsets, automatic optimization is not that easy. In a manual iterative process, we repeatedly performed the following steps: (i) find the optimal B₁ for long t_sat; (ii) fix this B₁ level; (iii) find the optimal t_sat for this B₁ level; (iv) fix t_sat; and (v) repeat the steps from (i) until no further visible changes occur. The optimal saturation parameters were defined by finding the maxima shown in Figure 6. In addition, we tested if the T_rec affected the optimum. The result was that generally longer T_rec lead to a stronger signal, independent of t_sat or B₁. To avoid missing a global optimum along this path, all signal strengths for each iteration were stored in a table, and subsequently checked if the converged optimum was local or global. All reported values were global optima along this path.

Figure 6.

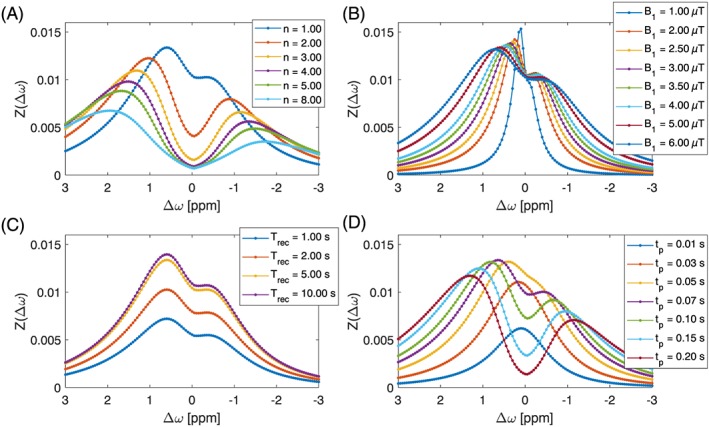
Results of the manual optimization process. Z_diff of in silico model of glucose in tissue model 1 for different saturation parameters at 7 T. Optimal parameters: B₁ = 5.00 μT, n = 1, T_rec = 5.0 s, t_p = 0.07 s; these were also the unchanged standard parameters for each subplot

The optimal parameters in GM were found to be T_rec = 10 s, n = 1, t_p = 0.07 s, B₁ = 2 μT. Yet, for practical reasons of limited scan time, we kept T_rec = 5 s. Also, for 2 μT, the signal is high yet relatively sharp and close to water. When moving to higher B₁ the signal is also broader, which makes it more stable against B₀ artifacts. Thus for GM at 7 T the simulation suggests: T_rec = 5 s, n = 1, t_p = 0.07 s, B₁ = 5 μT for 1.3% effect at 0.6 ppm.

In the more liquid environment of tissue model 2 (Figure 7), B₁ = 5 μT, n = 2, T_rec = 5.0 s, t_p = 0.1 s are optimal and yield 5.7% effect at 0.3 ppm.

Figure 7.

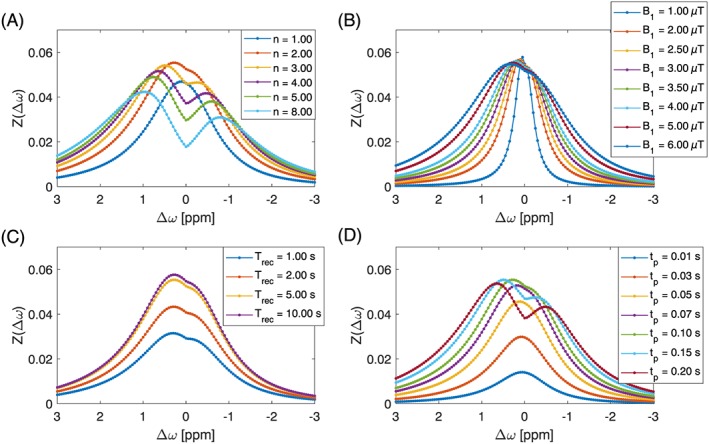
Results of the manual optimization process. Z_diff of in silico model of glucose in tissue model 2 for different saturation parameters at 7 T. Optimal parameters: B₁ = 5.00 μT, n = 2, T_rec = 5.0 s, t_p = 0.10 s; these were also the unchanged standard parameters for each subplot

Similar plots for 9.4 and 3 T can be found in the supporting information; here, the optimal parameters slightly changed, as summarized in Table 3. The effects strength observed varies between field strengths, as shown in Figures S1‐S4; the effects strength drops sharply when decreasing from 7 to 3 T.

Table 3.

Optimal glucoCEST/CESL parameters

Tissue model\B0	3 T, DC = 50%	7 T, DC = 50%	9.4 T, DC = 50%
tissue model 1 (GM)	B1 = 4.00 μT, n = 1, Trec = 5.0 s, tp = 0.10 s Maximum 0.55% at 0.8 ppm	B1 = 5.00 μT, n = 1, Trec = 5.0 s, tp = 0.07 s Maximum 1.3% at 0.6 ppm	B1 = 5.00 μT, n = 1, Trec = 5.0 s, tp = 0.07 s Maximum 1.7% at 0.6 ppm
tissue model 2 (tumor)	B1 = 4.00 μT, n = 2, Trec = 5.0 s, tp = 0.10 s Maximum 1.5% at 0.4 ppm	B1 = 5.00 μT, n = 2, Trec = 5.0 s, tp = 0.1 s Maximum 5.7% at 0.3 ppm	B1 = 5.00 μT, n = 2, Trec = 5.0 s, tp = 0.10 s Maximum 8.3% at 0.25 ppm

n, number of saturation pulses; t_p, saturation pulse duration; B₁, saturation block pulse amplitude; T_rec, recovery time before saturation starting from initial magnetization; Z_i, M_i/M₀ = 0.1

Comparing the less and more liquid tissue models reveals that there is a different optimal set of parameters for each tissue. However, the contrast is so much higher in the less structured tissue that we believe optimization should be performed primarily for the more structured tissue. Optimizing for less structured tissue or CSF will lead to parameters that strongly suppress signals of structured tissues. Yet for some applications such an optimization might make sense, and as a general rule we can state that the less structured, the longer the optimal saturation duration.

Having established the chemical exchange properties of all hydroxyl groups, we then set out to compare the signal theoretically achieved with published glucoCEST approaches at 7 T (Figure 8A). One caveat is that we used the pulse train parameters, but simulated all methods with ideal SL pulses. In tissue model 1, the proposed parameters lead to Z_diff = 1.3%, compared with the approach of Schuenke et al16 (Z_diff = 1.2%), followed by Xu et al14 with Z_diff = 0.7%. In tissue model 2, the proposed parameters here achieve Z_diff = 5.7%, the approach of Xu et al14 achieves Z_diff = 3.8% and that of Schuenke et al16 with Z_diff = 3.0%. This estimation hints that slight optimization in saturation time, recover time or evaluated offset is possible to further optimize the glucose‐weighted contrast. A final question to be answered is translation of these findings from an ideal SL to pulsed CEST or CESL on a whole‐body system. The on‐resonant adiabatic SL approach of Schuenke et al16 will generate strong artifacts when used off‐resonance. Also, rectangular pulses will not be able to yield stable results for such short saturation regimes due to induced Rabi oscillations (Figure 9A). Shaped pulses will have strong flip‐angle‐like oscillations close to water, yet even at 3 T for offsets at 1 ppm these oscillations are minor and the pulses behave adiabatically (Figure 9B). Recently proposed matched adiabatic SL pulses30, 42 can be used both on‐ and off‐resonant and are shown to perform well under the optimized conditions (Figure 9C). Thus, shaped off‐resonant pulses or adiabatic matched SL pulses can both realize the proposed optimal parameters.

Figure 8.

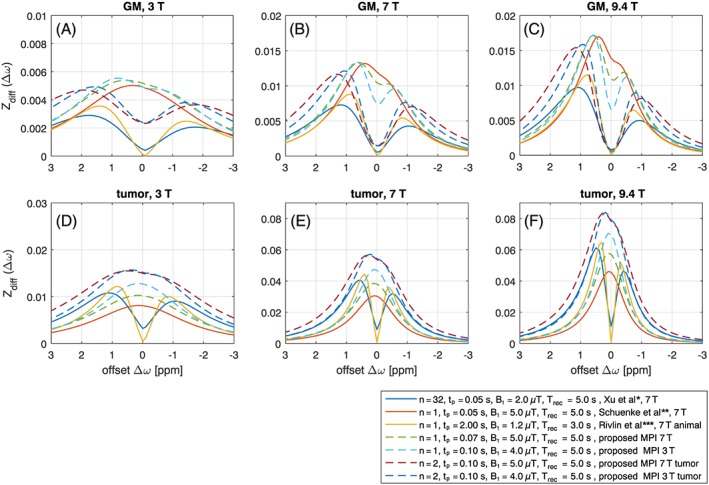
Comparison of existing irradiation conditions at 7 T, all realized using ideal SL pulses, showing Z_diff at 3 T (A,D), 7 T (D,E) and 9.4 T (C,F) for tissue model 1 (A‐C) and tissue model 2 (D‐F). *Xu et al14; **Schuenke et al16; ***Rivlin et al8

Figure 9.

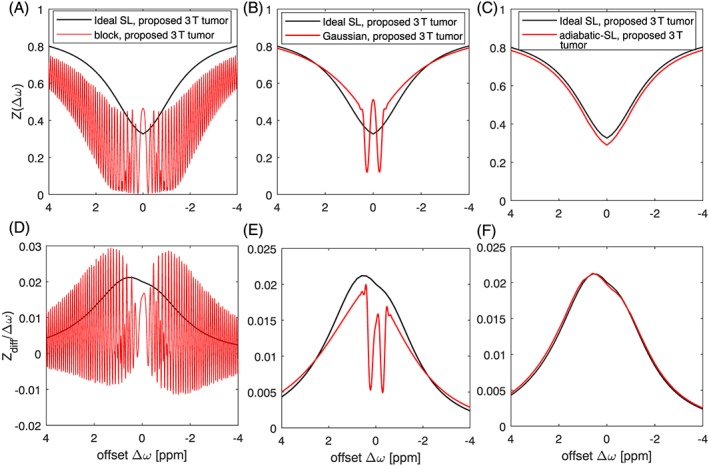
Nonideal methods (red) compared to the ideal spinlock simulation (black) for proposed 3 T saturation (B₁ = 4 μT, n = 2, T_rec = 5.0 s, t_p = 0.10 s): (A,D) block pulses, (B,E) Gaussian pulses, (C,F) matched‐adiabatic SL pulses

When comparing on‐ and off‐resonant signals, Z_diff shows only slightly higher signals for the off‐resonant case. Thus the simpler to implement on‐resonant SL seems a reasonable choice for glucose exchange weighting. However, the Z‐value and thus the MR image intensity is lowest for on‐resonant SL (see again Figure 5D), as here the direct saturation is strongest. Thus frequency offsets Δω > 0 ppm are beneficial for both effect strength and imaging SNR.

In conclusion, we can demonstrate that CEST in the SL regime with slight off‐resonance of ~ 0.3–1.0 ppm should optimize the glucose‐weighted imaging contrast. In this regime, MTR_asym is not the optimal evaluation technique, as hydroxyl CEST effects are broad and also appear at the negative side, but a difference analysis of B₀ corrected pre‐ and postglucose injection scans can be performed and yields higher contrast by a factor of 2. More often than not, sequences are optimized in very liquid model solutions; herein we showed that it is important to take tissue T₂ and ssMT contribution into account in the optimization. Direct saturation and ssMT effects dilute the effect strength by an order of magnitude and lower saturation power and saturation time, as well as making recovery before preparation a necessity. Comparison with existing approaches showed that the differently obtained glucoCEST signals are in the same order of magnitude, yet it is possible to gain another factor of 1.5 to 2 by optimizing for the tissue and field strength of interest.

It should be noted that the optimal parameters will depend on the optimal offset where the data has to be acquired and evaluated, thus if larger offsets are chosen for other reasons (eg, to have fewer B₀ artifacts), then parameters can be slightly different.

Herein we compared only on‐and off‐resonant SL preparation, however T₂ also changes upon addition of exchanging sites, as given by the Swift‐Connick equation37 and shown experimentally in vivo by Yadav et al38 and Goldenberg et al.39 Comparing the exchange contribution in the Swift‐Connick equation and in SL theory,36 one observes that the exchange weighting of on‐resonant T_1ρ and T₂ are actually very similar, and an even higher exchange weighting is expected for T₂ compared with T_1ρ. We can conclude that optimal T₂‐weighting for glucose detection must be similar to our on‐resonant SL optima. While no saturation power is needed for T₂‐weighting, an echo time between 70 to 200 ms, with respect to tissue and field strength (Table 3), is expected to be optimal for a spin‐echo experiment.

At ultra‐high fields amplifier limits might tighten the range of possible parameters and it may be that slightly lower B₁ values are beneficial. On the other hand, adiabatic SL techniques require a certain B₁ level to behave adiabatically. Therefore, only lower DC or lower saturation duration can decrease the applied power further, and the possible limits have to be achieved following the guidelines provided.

As a final optimization, T_rec can be shortened and traded against averages. Dietrich35 showed for repeated FID scans that choosing 0.7293·T₁ < T_rec < 2.0882·T₁ optimizes this trade‐off between recovery and averaging. This can be translated to our findings, leading to an optimal short T_rec in GM of 1.4–1.6 seconds.

• Finally, we want to discuss the assumptions made for the fitting:

  • assumption 1: same chemical shift = same exchange rate.

  • assumption 2: no intramolecular exchange.

  • assumption 3: transverse relaxation of CEST pools can be neglected.

  • assumption 4: base‐ and water‐catalyzed exchange rate relation.

  • assumption 5: endogenous CEST effects are negligible for optimization.

Assumption 1 seems to hold relatively well, as the B₁ dispersion is described well; still, some deviations, especially around the 1.3 ppm peak, are observed, which might originate from the artificial fusion of these pools. This is unlikely to have a huge influence on our optimization, but could be investigated in greater detail at lower temperatures. Assumption 2 is plausible, as we did not see large deviations in the B₁ dispersions, thus the first order Bloch‐McConnell system appears to also be accurate for multiple proton pools nearby. Assumption 3 might only alter the obtained exchange rates in the range of the R₂ of the individual pools, thus we can assume that deviations due to this assumption are smaller than ~ 50 Hz. Assumption 4 is questionable, especially around pH 7, where an acid catalysis can begin. But as the individual fits showed a similar exchange rate behavior, we believe that this assumption is sufficient and helps substantially in improving the fit stability. We tested the dependency of the 0.66 ppm pool as a function of pH, as it has been shown to be potentially partially acid‐catalyzed below pH = 7,41 yet any addition of an acid‐catalyzed component to the equation did not improve the fit and resulted in a lower adjusted R². Assumption 5, consisting of neglecting endogenous CEST effects, might alter the optimal parameters slightly, yet direct water saturation outweighs typical CEST effects by at least an order of magnitude. In an actual glucose injection experiment, in addition to changes due to glucose, a small ΔR _1ρ will be introduced due to osmolality changes. According to Jin et al,12 this contribution is rather small for glucose. Still, it would increase the apparent glucose effect size if measured by Z_diff, as both osmotic effects and glucose concentration would lower the Z‐value after injection. How this would affect the optimal saturation parameters can only be estimated by making assumptions regarding the underlying rate constants of the osmotic effects. For now, we can only estimate that the change of the optimal parameters would also be rather small.

This numerical study is based on several plausible assumptions investigating the theoretical signal of glucose in tissue. It does not take into account the fact that glucose alters osmolality, gets metabolized, and creates CEST active metabolite products that might also contribute to the signal after glucose injection. Also, altered tissue pH values in pathologies are not considered. The present parameters reflect estimations of the actual in vivo signal assuming all the glucose injected is delivered and stored in the tissue. Thus it can only be used as guidance and a starting point for in vivo optimization as described in the following.

To validate our findings in vivo, three mice bearing mammary adenocarcinoma tumors were examined with an off‐resonant SL protocol including glucose injection at a field strength of 7 T. Figure 10 shows images and ROI evaluations of the calculated Z_diff contrast; to be able to compare other CEST approaches Z_diff was evaluated at 1.2 ppm. In a first experiment we could demonstrate that, as predicted by the simulation, when going from a long saturation of 5 s to a shorter saturation of 0.5 s, the glucose weighting increased (Figure 10A). Also in agreement with the simulation, it was found that the CEST effect further increased when the power was increased from 3 to 5 μT (Figure 10A). The higher effect strength compared with our simulations is probably due to the higher dose of glucose used in the animal experiments. In a second experiment we observed reproducible results for two repeated settings, but also a decrease in signal when reaching lower saturation times or power levels (Figure 10B). In contrast to our predictions, the optimal saturation time was not found to be 200 ms, but was visible at ~ 500 ms in the third experiment (Figure 10C). This disagreement could have several origins, the most probable being that the larger offset leads to more effect for longer saturation, but also the different tissue type with other relaxation and ssMT parameters compared with the simulation can alter this optimum. Still, the outcome for the optimum is fairly close and supports the fact that our simulations provide a good starting point for the optimization, and that higher saturation B₁ and shorter saturation duration improve the glucose weighting. Herein, just three in vivo samples were shown and more in vivo experiments are needed to further verify the optimal parameters. Recently, a study in human brain tumor patients at 3T showed glucose uptake signals using similar SL preparation.42 Finally, certain saturation parameter regions need to be sampled more densely to find the global optimum, although this probably has to be repeated for each and every tissue or disease of interest.

Figure 10.

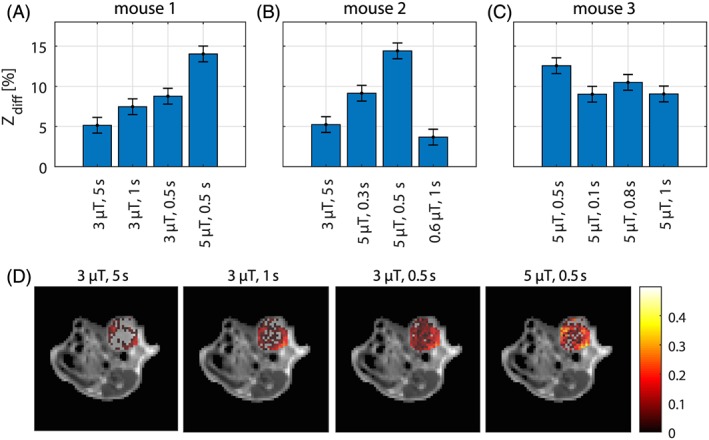
In vivo glucose injection experiments in three mice bearing TS/A tumor xenografts using adiabatic SL prepared acquisition at 7 T. Data acquired at different saturation pulse power levels and durations were compared and evaluated using Z_diff at 1.2 ppm (Z_diff = Z_post‐Z_pre). Bar plots of the average Z_diff calculated in ROI encompassing the whole tumor region for the experiments in (A) mouse 1, (B) mouse 2 and (C) mouse 3; (D) Z_diff images overlaid onto the T₂w anatomical image for mouse 1 showing the effect of different saturation power levels and duration times on the calculated glucoCEST contrast upon CESL acquisition. CESL acquisition with B₁ = 5 μT and t_sat = 0.5 s yielded an average Z_diff of 13.7 ± 0.98% in the three investigated mice. Error bars in (A‐C) show this determined standard deviation

4. CONCLUSIONS

With glucose exchange rates determined at physiological conditions at 14.1 T, an in silico tissue model including glucose pools was generated. This allowed quasi in‐vivo optimization of presaturation parameters and comparison of existing approaches at 7 T, as well as predictions for optimum glucose weighting at 3 and 9.4 T. Glucose weighting was strongest in the SL regime with long recovery before a short and strong saturation. This optimum predicted by simulation could be experimentally verified. For the intermediate exchange system, the optimal frequency offset of highest contrast is not governed by the exact hydroxyl chemical shift, but by the interplay of direct saturation and labeling, and is found between 0.5 and 1.0 ppm from water.

Supporting information

Table S1: Multi‐B1‐multi‐pH fit result and full parametrization of glucose hydroxyl exchange rates at T=37°C as a function of pH following the equation k_x = k_x1·10^pH−7 + k_x0. In addition, anomeric ratio AR, fitted transverse water proton relaxation rate R2A and measured longitudinal water proton relaxation R1A at B₀ = 14.1 T, T=37°C. Together with the proton fractions f_B = f_glc; f_D = 3 f_glc; f_E = AR· f_glc; f_F = (1‐AR)·f_glc, and the ratio f_glc = [Glc]/(2[H₂O]) = [Glc]/111 M these parameters can be and were used for Z‐spectra simulation with arbitrary water and MT pool parameters, and arbitrary saturation parameters.

Figure S1: Results of the manual optimization process. Z_diff of in silico model of glucose in tissue model 1 for different saturation parameters at 9.4 T. Optimal parameters: B1 = 5.00 μT, n = 1, Trec = 5.0 s, tp = 0.1 s

Figure S2: Results of the manual optimization process. Z_diff of in silico model of glucose in tissue model 2 for different saturation parameters at 9.4 T. Optimal parameters: B1 = 5.00 μT, n = 2, Trec = 5.0 s, tp = 0.1 s

Figure S3: Results of the manual optimization process. Z_diff of in silico model of glucose in tissue model 1 for different saturation parameters at 3 T. Optimal parameters: B1 = 4.00 μT, n = 1, Trec = 5.0 s, tp = 0.1 s

Figure S4: Results of the manual optimization process. Z_diff of in silico model of glucose in tissue model 2 for different saturation parameters at 3 T. Optimal parameters: B1 = 4.00 μT, n = 1, Trec = 5.0 s, tp = 0.1 s

Figure S5: Glucose exchange rates as a function of pH obtained by multi‐B1‐multi‐pH fit for T = 21°C

Table S2: Glucose exchange rates obtained by multi‐B1‐multi‐pH fit for different pH values for T = 21°C; a relative arror of approximatley ±30% for kBA,kEA, and kFA, and a relative arror of approximatley ±7% for kDA must be assumed

Zaiss M, Anemone A, Goerke S, et al. Quantification of hydroxyl exchange of D‐Glucose at physiological conditions for optimization of glucoCEST MRI at 3, 7 and 9.4 Tesla. NMR in Biomedicine. 2019;32:e4113 10.1002/nbm.4113