Abstract
Migration, the recurring movement of individuals between a breeding and a non‐breeding habitat, is a widespread phenomenon in the animal kingdom. Since the life cycle of migratory species involves two habitats, they are particularly vulnerable to environmental change, which may affect either of these habitats as well as the travel between them.
In this study, we aim to reveal the consequences of environmental change affecting older life‐history stages for the population dynamics and the individual life history of a migratory population.
We formulate a population model based on the individual energetics and life history to study how increased energetic cost of the breeding travel and reduced survival and food availability in the non‐breeding habitat affect an anadromous fish population.
These unfavourable conditions have impacts at the individual and the population level. First, when conditions deteriorate individuals in the breeding habitat have a higher body growth rate as a consequence of reductions in spawning that reduce competition. Second, population abundance decreases, and its dynamics change from a regular annual cycle to oscillations with a period of four years. The oscillations are caused by the density‐dependent feedback between individuals within a cohort through the food abundance in the breeding habitat, which results in alternation of a strong and a weak cohort.
Our results explain how environmental change, by affecting older life‐history stages, has multiple consequences for other life stages and for the entire population. We discuss these results in the context of empirical data and highlight the need for mechanistic understanding of the interactions between life‐history and population dynamics in response to environmental change.
Keywords: anadromy, Atlantic salmon, body size, energy budget, environmental change, life history, population dynamics
1. INTRODUCTION
Animals from all major animal taxa set out every year on a journey between habitats in step with seasonal changes. Generally, these seasonal changes also define the timing of breeding; therefore, the habitats occupied by animals during different seasons are known as breeding and non‐breeding habitat. Since migratory animals utilize multiple habitats and resources, they appear to be particularly vulnerable to environmental change (Vagg & Hepworth, 2006). Furthermore, given the spatial separation between the habitats, the effect of environmental change may differ across the habitats used by individuals at different stages of their life cycle. As a consequence, a change in ecological conditions in one of the habitats directly impacts individual life history. Life history, in turn, has large effects on population processes (de Roos & Persson, 2013), which strongly influence the realized life history of organisms through the population feedback on, for example, food conditions (De Roos, Persson, & McCauley, 2003). Therefore, environmental change has the potential to affect the interaction between life history and population ecology of migratory and in particular anadromous species.
Anadromous individuals begin their life cycle in the breeding habitat in freshwater and later migrate to the non‐breeding habitat in the ocean (this migration we from here on refer to as habitat switch), where they grow larger and eventually become mature. Mature individuals migrate back to the breeding habitat in order to reproduce (hereafter breeding travel). Many anadromous fishes including salmons, sturgeons and shads are of both economic and cultural importance. However, like many other commercially exploited fish, they are in decline and their conservation is a major concern (Pauly et al., 2002).
Anadromous species have shown major declines in the last decades due to multiple threats such as damming, overfishing and climate change (Limburg & Waldman, 2009). Damming increases the cost of the breeding travel to the spawning grounds that negatively affects individual fecundity as it leads to larger depletion of energy reserves (Jonsson, Jonsson, & Hansen, 1997). Overfishing increases mortality in later life stages as especially mature individuals are targeted by fishing. And climate change, among many other impacts, is predicted to reduce ocean productivity (Hoegh‐Guldberg & Bruno, 2010), which results in reduced growth rate in the marine phase of the life cycle. These threats have negative impacts on the life history of individuals by affecting their fecundity, survival and growth rate during the life stage after the habitat switch. This raises the question how these threats, by influencing the life history of individuals in a late life‐history stage, affect the dynamics of the entire population and, in turn, the realized life history of individuals. To address this question, we use a theoretical approach to study the consequences of increased energetic cost of the breeding travel and reduced survival and food availability in the non‐breeding habitat on an anadromous population. Since these threats have an effect on the population by affecting the life history of individuals after their first habitat switch, the representation of the individual life history in our model is crucial. Hence, we use a dynamic energy budget model to describe how individuals acquire and utilize energy (Nisbet, Muller, Lika, & Kooijman, 2000) and to translate these individual‐level energetics into different life‐history trajectories. In the present study, we use data from Atlantic salmon to parameterize the dynamic energy budget model and consider its ecology to build the model at the population level. In addition, available data of wild populations of Atlantic salmon are used to test predictions of the model.
2. MATERIALS AND METHODS
2.1. The model
We formulate a model that accounts for an anadromous population migrating between two habitats (Figure 1). We assume that in each habitat (breeding and non‐breeding), the individuals exploit a different resource. The migratory population is structured by age, individual body size and energy reserves and follows semi‐discrete dynamics: continuous dynamics describe the resource consumption, somatic growth, stored energy reserves and survival, and a discrete map describes the pulsewise reproduction (Persson, Leonardsson, de Roos, Gyllenberg, & Christensen, 1998).
Figure 1.
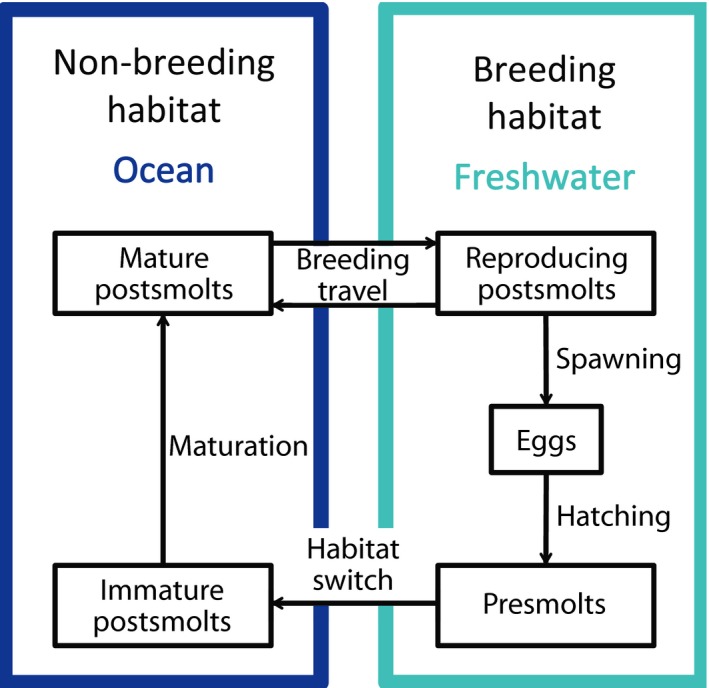
Schematic representation of the modelled anadromous life cycle
2.1.1. Yearly cycle and life‐history events
Salmon utilizes freshwater streams to breed; therefore, its first life stages occur in this habitat. In the model female salmon are assumed to spawn in autumn at day of the year, the eggs develop throughout winter and hatch at age (in spring) (Hendry & Cragg‐Hine, 2003). After hatching, individuals remain in the stream until they reach an age , when they smolt and migrate to the ocean (Hendry & Cragg‐Hine, 2003) (hereafter, individuals younger than are referred to as presmolts, in contrast to older individuals that are referred to as postsmolts). Every autumn, sexually mature individuals in the ocean return to the stream and start migrating upstream at day to spawn somewhat later at day . After spawning, postsmolts return to the ocean and finish downstream migration at day of the year. Atlantic salmon is an iteroparous species; hence, in the model repeated migration and spawning are allowed.
2.1.2. Habitats
Density dependence is strong in the breeding habitat (Jonsson, Jonsson, & Hansen, 1998) and directly affects growth in body size in salmonids (Walters, Copeland, & Venditti, 2013). Therefore, we incorporate density dependence effects on the growth rate of presmolts via competition for food. In the absence of consumers, the biomass of assimilates density (hereafter food density) is assumed to follow a semi‐chemostat growth dynamics with maximum density and growth rate (for an explanation and justification of this type of growth dynamics, see Persson et al. (1998)):
| (1) |
The food density is depleted by the consumption of individuals in this habitat (presmolts). Therefore, high density of presmolts results in a lower food density in the breeding habitat (see Appendix S1).
In contrast, in the non‐breeding habitat, postsmolts do not experience density dependence (Jonsson et al., 1998); therefore, we assume a constant biomass of assimilates density which translates into a constant feeding level.
In both habitats, temperature is assumed to oscillate during the year around the average temperature with an amplitude and a period equal to the length of the year. Therefore, the temperature reaches its maximum in summer (middle of the year) and its minimum in winter.
| (2) |
where is the current time in days, and is the number of days of the year.
2.1.3. Individual dynamics
The core part of the model is the description of the individual behaviour, that is feeding, growth, reproduction and mortality as a function of the individual state (age, body size and energy reserves) and the state of the environment (food availability and temperature). In the following sections, we describe the individual‐level dynamics.
Feeding
In the breeding habitat, individuals are assumed to feed on the food resource following a Holling type II functional response. So their feeding level (or scaled functional response) is given by:
| (3) |
where K is the half‐saturation food density.
However, in the non‐breeding habitat density dependence is assumed to be negligible so individuals feed at a constant feeding level .
Dynamic energy budget model: individual states
The model follows the bioenergetics approach introduced by Kooijman and colleagues (Kooijman & Metz, 1984; Nisbet et al., 2000) in which the energy allocation to somatic and reproductive metabolism is proportional to a fraction κ and a 1−κ of the total energy assimilation rate, respectively. More specifically, we adopt the model developed and described in detail by Martin, Heintz, Danner, and Nisbet (2017). Below we provide only a concise synopsis of the model.
Individuals are characterized by three state variables: individual age , structural mass and energy reserve storage . The acquisition and utilization of energy are described by Equations (4) to (12).
The energy assimilation flux is given by:
| (4) |
where is the feeding level in either the breeding or the non‐breeding habitat introduced above, is the maximum area‐specific assimilation rate, and the surface area for assimilation is assumed to scale with structural mass to the power of 2/3.
Metabolic maintenance cost is the product of the mass‐specific maintenance cost and the structural mass:
| (5) |
Assimilates are assumed to split into two energy fluxes: the flux and the 1 − κ flux. The flux is first used to cover metabolic maintenance cost, while the remaining flux is used to synthesize structural mass. On the other hand, the 1 − κ flux is allocated to energy reserve storage. Thus,
| (6) |
| (7) |
If the metabolic maintenance cost is larger than the flux, the individual starves, stops growing and depletes its storage if necessary to cover the deficit in maintenance requirements; thus, in case of starvation :
| (8) |
| (9) |
Therefore, the individual state dynamics of structural mass and energy reserve storage are described by the following system of differential equations:
| (10) |
| (11) |
The parameter in Equation (10) represents the efficiency with which assimilates are converted into structural mass.
The rate constants (, ) are assumed to be temperature‐dependent and scale from the reference temperature to the actual temperature at time , , following the Arrhenius relationship. Hence, both rate constants are multiplied by the temperature correction factor :
| (12) |
where is the Arrhenius temperature.
Maturation, reproduction and breeding travel
Individuals mature when they have reached a fixed structural mass . The storage:structure ratio at maturity is the threshold for reproductive investment; therefore, the excess of energy reserves above the amount that equals the storage:structure ratio is used for reproduction. Reproduction occurs at a discrete time . The number of offspring produced by an adult individual with structural mass and energy reserve storage , hence, equals:
| (13) |
Simultaneously, if reproduction occurs the energy reserve storage value of the reproducing individuals is reduced to . The number of offspring produced is dependent on the yield for the conversion of storage into eggs and the egg mass . During the egg stage individuals do not feed; therefore, we assumed newly hatched individuals to be born with a structural mass equal to and an energy reserve storage .
During the breeding, travel individuals are assumed to cease feeding, stop growing and use their energy reserves (Jonsson et al., 1997) to meet their basic metabolic maintenance cost as well as the energetic cost of the travel, which we assumed to be proportional to the metabolic maintenance cost:
| (14) |
Here is the proportionality constant relating the cost of the breeding travel to the metabolic maintenance cost. Individuals travel to the spawning grounds and reproduce if their storage:structure ratio when arriving at the spawning grounds is larger than the storage:structure ratio with which they matured. They can repeat the breeding travel and spawn several times during their life span as long as they meet this condition.
Survival
Individuals may die from either starvation or background mortality. The mortality rate of starving individuals with a storage:structural mass ratio smaller than a threshold level increases with decreasing values of :
| (15) |
where is a positive proportionality constant (Persson et al., 1998). Once they have depleted their storage () completely, starving individuals die instantaneously.
In addition to starvation mortality, individuals die at a rate during the egg stage, at a rate if they are presmolts and if they are postsmolts. The total per capita death rate is the sum of the different sources of mortality.
2.1.4. Population dynamics
Since reproduction occurs as a discrete event at a specific time in the year, all individuals that are born in the same reproductive event are lumped into a single cohort and assumed to grow at the same rate. Thus, we can describe the dynamics of every cohort by using a system of ordinary differential equations, which keeps track of the density of individuals, their structural mass and their energy reserve storage (see Appendix S1). Therefore, the dynamics of the population can be followed by numerically integrating the ordinary differential equations for each cohort separately. When a reproductive event occurs, a new cohort is added to the population, which implies additional differential equations describing the population dynamics. In addition, food density in the breeding habitat increases by an intrinsic growth process (following semi‐chemostat dynamics, see Persson et al. (1998)) and decreases by consumption; these changes in food density can be followed by numerical integration of the ordinary differential equation that accounts for food resource growth and consumption. The numerical integration is carried out using the EBT (Escalator Boxcar Train) (de Roos, 1988), a numerical integration method specifically designed to handle the system of differential equations that describes a physiologically structured population.
We parameterized the model for Atlantic salmon based on literature data of its individual life history and the characteristics of the breeding and non‐breeding habitats. All parameter values and their sources are presented in Table 1, while Appendix S1 provides details about the population‐level formulation of the model.
Table 1.
Parameter values
| Description | Symbol | Value | Unit | References | |
|---|---|---|---|---|---|
| Environment | |||||
| Year |
|
365 | day | ||
| Average temperature |
|
10 | °C | ||
| Amplitude of temperature variation |
|
5 | °C | ||
| Events within the season | |||||
| Day of the beginning of breeding travel |
|
205 | Doucett, Booth, Power, and McKinley (1999) | ||
| Day of reproduction (spawning) |
|
215 | Thorpe, Mangel, Metcalfe, and Huntingford (1998) | ||
| Day of the end of breeding travel |
|
225 | Doucett et al. (1999) | ||
| Age‐dependent events during life cycle | |||||
| Age at hatching |
|
150 | day | Thorpe et al. (1998) | |
| Age at smolting |
|
545 | day | Mccormick, Hansen, Quinn, and Saunders (1998) | |
| Food resource in the breeding habitat | |||||
| Food resource growth rate |
|
0.1 | day−1 | ||
| Maximum food resource density |
|
varied | g/m3 | ||
| Half‐saturation food resource density |
|
1 | g/m3 | ||
| Population | |||||
| Functional response of postsmolts |
|
varied | – | ||
| Fraction of assimilation flux to structural mass and maintenance |
|
0.8 | Kooijman 2010 | ||
| Maximum area‐specific assimilation rate |
|
0.18 | g g−2/3 day−1 | Calculated with method of (Jager, Martin, & Zimmer, 2013) from regressions of (Sutton, Bult, & Haedrich, 2000) | |
| Mass‐specific maintenance cost |
|
0.006 | g g−1 day−1 | Calculated with method of (Jager et al., 2013) from regressions of (Sutton et al., 2000) | |
| Reference temperature |
|
293 | K | ||
| Arrhenius temperature |
|
8,000 | K | ||
| Yield of structural mass on assimilates |
|
0.8 | g/g | Jager et al. (2013) | |
| Yield of egg buffer on storage |
|
0.95 | g/g | Jager et al. (2013) | |
| Mass of a single egg |
|
0.1 | g | Potts and Rudy () | |
| Mass of a newborn |
|
0.06 | g | Shearer, Asgard, Andorsdottir, and Aas (1994) | |
| Structural mass at maturity |
|
74 | g | Kooijman 2010; Pecquerie, Johnson, Kooijman, and Nisbet (2011) | |
| Cost of breeding travel |
|
varied | – | ||
| Mortality rate of eggs |
|
0.0125 | day−1 | Bley and Moring (1988) | |
| Mortality rate of presmolts |
|
0.0025 | day−1 | Bley and Moring (1988) | |
| Mortality rate of postsmolts |
|
varied | day−1 | Bley and Moring (1988) | |
| Minimum storage/structural mass ratio that individuals stand without starvation mortality |
|
0.1 | Persson et al. (1998) | ||
| Scaling coefficient for starvation mortality |
|
0.2 | day−1 | Persson et al. (1998) | |
2.2. Model analysis
Our main interest is to investigate the consequences of three unfavourable conditions on the population and the realized life history of individuals: the effects of (a) increased cost of the breeding travel, (b) low survival and (c) food availability in the non‐breeding habitat. To do so, we vary the feeding rate in the non‐breeding habitat between ad libitum food and 0.3 times the amount of food ad libitum, the background mortality rate of postsmolt individuals between 0.0063 and 0.0107 per day, equivalent to annual survival probabilities of 0.1 and 0.02, respectively, and lastly, the cost of the breeding travel between 0 and 1 times the basal metabolic maintenance cost for the period that the breeding travel lasts (between and ). In addition, we evaluate the effect of within‐yearclass growth rate variation. To do so, we assume that within a yearclass the maximum area‐specific assimilation rate follows a truncated normal distribution with a mean value of 0.18 and a minimum value and maximum value of equal to 80% and 120% of this mean, respectively.
All model results presented correspond to the values of the population statistics after transient dynamics have disappeared.
2.3. Data analysis
In order to test predictions of the model regarding the relationship between growth rates of presmolts and postsmolts, we estimated growth rates of presmolts and postsmolts based on data of wild population of Atlantic salmon presented by Hutchings and Jones (1998) (see Table 2). The growth rate of presmolts is estimated as the difference in length between 1‐year‐old individuals (1 + parr) and individuals at the time of smolting (smolt), divided by the age of these smolting individuals minus 1. Growth rate of postsmolts is estimated as the difference in length between smolts and grilse (individuals that spend one winter in the sea after smolting to migrate upstream to spawn) as well as smolt and 2SW fish (individuals returning to spawn after two winters in the sea). Hutchings and Jones (1998) present data for smolt age and length of 1‐year‐old individuals, smolt and grilse for 25 populations and of length of 2SW for 22 populations. We tested the correlation between the growth rate of presmolts and the growth rate of postsmolts with a Pearson correlation test.
Table 2.
Atlantic salmon life‐history data
| Region | River | Parr + 1 length | Smolt length | Smolt age | Grilse length | 2SW length | Smolt‐grilse survival | References |
|---|---|---|---|---|---|---|---|---|
| Labrador | Sandhill | 16 | 4.44 | 0.0815 | Hutchings and Jones (1998) | |||
| Maritimes | Miramichi | 9.39 | 12.8 | 2.8 | 55.3 | 73.4 | Hutchings and Jones (1998) | |
| Newfoundland | Conne | 14.8 | 3.28 | 0.0578 | Hutchings and Jones (1998) | |||
| Newfoundland | Highlands | 8.27 | 13.1 | 2.9 | 53.3 | 73.4 | Hutchings and Jones (1998) | |
| Newfoundland | Little Codroy | 8.59 | 15 | 2.66 | 54.1 | 75.1 | 0.0229 | Bley and Moring (1988), Hutchings and Jones (1998) |
| Newfoundland | NE Trepassey | 3.67 | 0.0622 | Hutchings and Jones (1998) | ||||
| Newfoundland | North Hr | 8.43 | 15.1 | 3.2 | 55.1 | 76.3 | Hutchings and Jones (1998) | |
| Newfoundland | West Arm Bk | 7.54 | 16.8 | 3.68 | 52.9 | 0.0489 | Hutchings and Jones (1998) | |
| Newfoundland | Wings Bk | 7.63 | 16.4 | 4 | 51 | Hutchings and Jones (1998) | ||
| Quebec | Bec‐Scie | 2.97 | 0.0283 | Hutchings and Jones (1998) | ||||
| Quebec | Bouleau | 8.36 | 13.1 | 3.14 | 50.6 | 74.6 | Hutchings and Jones (1998) | |
| Quebec | Kosoak | 7 | 20.6 | 5.6 | 62.3 | 80.3 | Hutchings and Jones (1998) | |
| Quebec | Matamek | 8.59 | 15 | 3.11 | 52.9 | 72.9 | Hutchings and Jones (1998) | |
| Quebec | Moisie | 6.31 | 12 | 3.57 | 48.7 | 74.6 | Hutchings and Jones (1998) | |
| Quebec | Pigou | 9.62 | 15.1 | 2.93 | 53.1 | 72.7 | Hutchings and Jones (1998) | |
| Quebec | Saint‐Jean | 5.42 | 11.5 | 3.52 | 54.4 | 73.3 | Hutchings and Jones (1998) | |
| Quebec | Trinité | 8.06 | 12.1 | 3 | 54.2 | 74.7 | 0.0237 | Hutchings and Jones (1998) |
| Norway | Figgenelva | 8.4 | 11.7 | 2.28 | 54.3 | 77.1 | Hutchings and Jones (1998) | |
| Norway | Haelva | 8.9 | 12.5 | 2.47 | 60.2 | 80 | Hutchings and Jones (1998) | |
| Norway | Imsa | 15.4 | 1.95 | 0.0357 | Hutchings and Jones (1998) | |||
| Norway | Laerdalselva | 8.2 | 11.9 | 2.82 | 67.96 | 89.26 | Hutchings and Jones (1998) | |
| Norway | Mandalselva | 8.5 | 13.3 | 2.82 | 54 | 79.3 | Hutchings and Jones (1998) | |
| Norway | Namsen | 8 | 11.9 | 2.67 | 58.49 | 86.75 | Hutchings and Jones (1998) | |
| Norway | Nummendals | 7.2 | 10.5 | 2.47 | 65.4 | 84.5 | Hutchings and Jones (1998) | |
| Norway | Ogna | 8.8 | 13.2 | 2.65 | 54.6 | 78.6 | Hutchings and Jones (1998) | |
| Norway | Orkla | 7.8 | 11.4 | 2.82 | 56.8 | 81.6 | Hutchings and Jones (1998) | |
| Norway | Otra | 8.6 | 12.8 | 2.63 | 60.1 | 86.8 | Hutchings and Jones (1998) | |
| Norway | Tengselva | 9.3 | 14.1 | 2.92 | 60.8 | 75.8 | Hutchings and Jones (1998) | |
| Norway | Tovdalselva | 8.7 | 13 | 2.72 | 52.8 | 76.1 | Hutchings and Jones (1998) | |
| Norway | Varhaugelva | 8.6 | 12.1 | 2.73 | 49.3 | Hutchings and Jones (1998) | ||
| Ireland | Burrishoole | 12.1 | 2.24 | 0.0375 | Bley and Moring (1988), Hutchings and Jones (1998) | |||
| Ireland | Corrib | 13.4 | 1.75 | 0.0266 | Hutchings and Jones (1998) | |||
| Scotland | North Esk | 12.6 | 2.33 | 0.0601 | Hutchings and Jones (1998) |
In addition, from Hutchings and Jones (1998), we selected data of populations with annual survival rates of smolt–grilse below 0.1 to ensure survival is a critical factor in the dynamics of those populations. Given that data on smolt–grilse survival are only available for a small number of populations (11 populations) and that for these populations the data on smolt age and length of 1‐year‐old individuals and smolt are incomplete, we use only the smolt age and smolt length (if available) as a proxy of growth rate of presmolts. Smolt age is an approximate measure of the growth rate of presmolts, so the higher the smolt age, the lower the growth rate as presmolts (Hutchings & Jones, 1998; Metcalfe & Thorpe, 1990; Power, 1981). The growth rate was calculated as the ratio between the smolt length and the smolt age. For those populations without information on smolt length (2 populations), we use the smolt length average of all populations (14.8 cm [Hutchings & Jones, 1998]). We tested the correlation between the growth rate of presmolts and the survival rate of postsmolts with a Pearson correlation test.
3. RESULTS
Under most conditions studied, the population model exhibits a regular annual cycle (annual fixed‐point dynamics), meaning that the same values of population abundance and biomass, as well as food density in the breeding habitat, occur every year at a particular point of the year cycle (i.e. start of the year, spawning day, hatching day), even though within the year these densities, of course, vary. The population also exhibits 4‐year cycles when conditions for postsmolts are very unfavourable, meaning a particular value of population abundance and biomass, and food density in the breeding habitat repeats itself every 4 years.
3.1. Unfavourable conditions for postsmolts increase presmolt growth rate and affect life‐history trajectories
When the food in the non‐breeding habitat is abundant (high feeding levels), the survival in the non‐breeding habitat is high and the cost of the breeding travel is low, the offspring production by the population is high. High food levels and survival in the non‐breeding habitat as well as low energetic cost of the breeding travel (favourable conditions) result in high offspring production due to the combination of (a) high growth rate of postsmolts which reach a large body size and hence a high fecundity (Figure 2a), (b) long life span that increases the opportunities to reproduce (Figure 2c) and (c) low energy expenditure during the breeding travel resulting in more energy reserves available for reproduction at arrival at the spawning grounds (Figure 2e). High offspring production means a large number of presmolts competing for food in the next generation, which by foraging deplete the food abundance in the non‐breeding habitat to a low level and therefore causes a low growth rate during the presmolt stage (Figure 2b,d,f).
Figure 2.
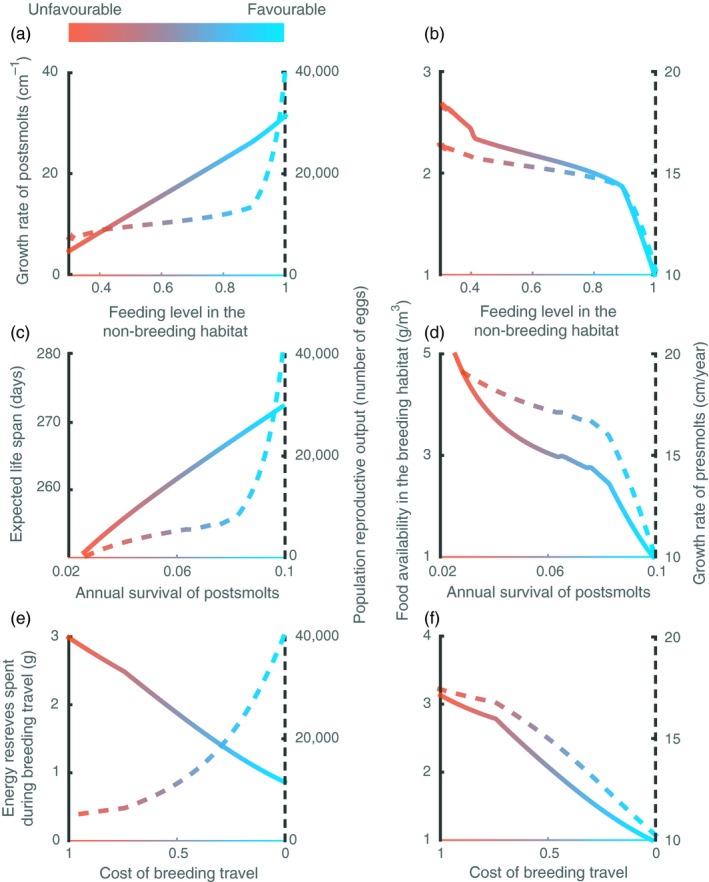
Effects of variation in feeding level in the non‐breeding habitat (top row), annual survival of postsmolts (middle row) and cost of the breeding travel (bottom row) on life‐history traits of postsmolts (growth rate, expected life span and proportion of energy reserves at the beginning of the breeding travel spent during travelling, solid lines in left column plots), population reproductive output (dashed lines in left column plots), food availability in the breeding habitat (solid lines in right column plots) and growth rate of presmolts (dashed lines in right column plots). Default values representing favourable conditions (feeding level in the non‐breeding habitat = 1, annual survival of postsmolts = 0.1 and cost of the breeding travel = 0) are used for parameters that are not varied. = 5 g/m3, other parameter values as in Table 2. The values correspond to the average population statistics after the transient dynamics have disappeared
In contrast, low food abundance in the non‐breeding habitat (low feeding levels) results in a decrease in the growth rate of postsmolts, which in turn causes a reduction in the population offspring production (Figure 2a). Similarly, low survival of postsmolts reduces the individual life span and therefore the opportunities to reproduce, causing a low offspring production (Figure 2c). Likewise, high cost of the breeding travel causes the individuals to spend a larger amount of their energy reserves during the migration (about 37%), leaving less energy available for reproduction upon their arrival at the spawning grounds (63%). Consequently, it results in low offspring production, and therefore in low densities of presmolts in the next generation (Figure 2e). Since a low number of presmolts means less competition in the breeding habitat, the food availability in this habitat is higher, and therefore, presmolts of the next generation grow at higher rate (Figures 2b,d,f and 4). Hence, unfavourable conditions for postsmolts including low food abundance and survival in the non‐breeding habitat and high cost of the breeding travel cause high growth rate of presmolts in the next generation. This result is robust to intracohort growth rate variation (See Appendix S2).
Interestingly, despite that the three types of unfavourable conditions have the same consequence for presmolts, that is result in a high presmolt growth rate, their impacts on the life‐history trajectories of postsmolts differ. While low food abundance and low survival in the non‐breeding habitat result in younger spawners (Figure 3a,b), high cost of the breeding travel does not reduce the age at spawning (Figure 3c). In the former case, the lower age at first spawning is a direct consequence of a high growth rate in the breeding habitat, which enables individuals to reach the maturation size faster and therefore to reproduce earlier. However, when the cost of the breeding travel is high, although the individuals after 1 year in the sea have reached the maturation size, the energy reserves they have accumulated after maturation only cover the high costs of the breeding travel, leaving no energy for offspring production. Effectively, they therefore postpone spawning until the reproductive season in the following year.
Figure 3.
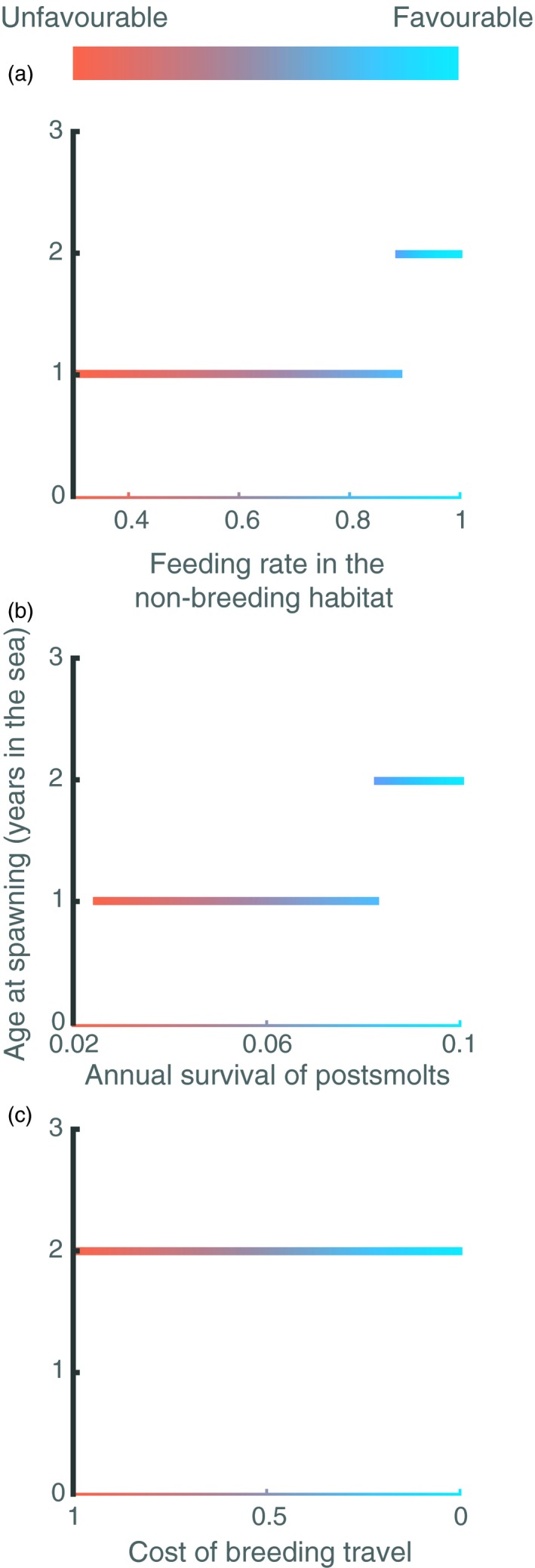
Effects of variation in feeding level in the non‐breeding habitat (top row), annual survival of postsmolts (middle row) and cost of the breeding travel (bottom row) on sea age at first spawning. Same parameters as in Figure 2. The values correspond to the average population statistics after the transient dynamics have disappeared. The lower age at first spawning (in top and middle plot) is a direct consequence of a high growth rate in the breeding habitat
3.2. Unfavourable conditions for postsmolts affect population dynamics
Unfavourable conditions for postsmolts have effects on the population by affecting its abundance and its dynamics. For instance, a decrease in food abundance in the non‐breeding habitat not only causes a decrease in the total population biomass, but also leads to the occurrence of population cycles with a period of 4 years when feeding levels are low (feeding level below 0.5 in Figure 4a,b). Similarly, low survival of postsmolts or high cost of the breeding travel can also lead to the occurrence of such cycles (Figure 4c,d). These 4‐year cycles are caused by the alternation of a fast‐ and a slow‐growing presmolt cohort. As mentioned above, unfavourable conditions for postsmolts result in low offspring production, which is very low when the conditions are extremely unfavourable, such as very low feeding levels in the non‐breeding habitat. Very low offspring numbers result in low competition in the breeding habitat and therefore high growth rates of presmolts in the next generation. Those individuals can reach large sizes before smolting and therefore accumulate sufficient energy for a high fecundity. This fast‐growing cohort, therefore, produces a large number of offspring experiencing high competition in the breeding habitat, which causes the next‐generation cohort to grow slowly and accumulate less energy. As a consequence, this slow‐growing cohort has low fecundity and produces an offspring cohort of small number that experiences low competition in the non‐breeding habitat, resulting in a fast‐growing cohort. The period cycle equals twice the average age at first spawning of the fast‐growing cohort (2 years). The destabilization of the system from a regular annual cycle to regular 4‐year cycles involves a transition of irregular dynamics with a period of approximately 4 years (Figure 4c,d).
Figure 4.
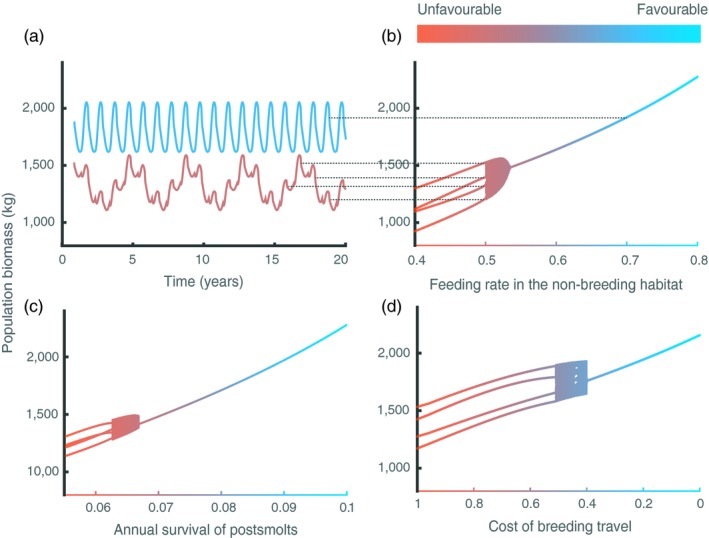
(a,b) Effect of feeding level in the non‐breeding habitat, (c) annual survival of postsmolts and (d) cost of the breeding travel on population biomass dynamics. (a) Annual fixed‐point dynamics (blue) and 4‐year cycles (brown) occur when feeding level in the non‐breeding habitat equals 0.7 and 0.5, respectively. Dotted lines in (a) indicate the time points in the dynamics at which the yearly census the population biomass occurs, resulting in the values shown in (b). In (b–d), irregular dynamics with a period of approximately 4 years occur in the transition from a regular annual cycle to regular 4‐year cycles. Default values representing favourable conditions (feeding level in the non‐breeding habitat = 1, annual survival of postsmolts = 0.1 and cost of the breeding travel = 0) are used for parameters that are not varied. = 8 g/m3, other parameter values as in Table 2. The values in plots (b–d) correspond to the population biomass census occurring every year at the time of hatching after the transient dynamics have disappeared
Intracohort growth rate variation dampens the oscillatory dynamics when survival of postsmolts is low while it has only slight quantitative effects when food abundance is low in the non‐breeding habitat. Changes in the cost of the breeding travel make that the regular 4‐year cycles become irregular dynamics with a period of approximately 4 years in the presence of intracohort growth rate variation. In addition, the presence of intracohort growth rate variation affects the values of cost of the breeding travel at which the transition from a regular annual cycle to irregular dynamics with a period of approximately 4 years occurs (See Appendix S2).
The regular 4‐year population cycles also occur as a consequence of favourable conditions in conjunction with high maximum food density (food resource productivity) in the breeding habitat (See Appendix S3). Higher maximum food density in the breeding habitat results in higher growth potential of presmolts. Hence, very low offspring production due to extremely unfavourable conditions in the non‐breeding habitat is not necessary to achieve high growth rate in the breeding habitat. In this case, a fast‐growing cohort can reach large body sizes and fecundity and consequently produce numerous offspring. Large number of individuals in the next generation means strong competition for food in the breeding habitat and therefore slow growth rate during the presmolt stage. This slow‐growing cohort can reach smaller body size and lower fecundity, and consequently, it produces a less numerous offspring cohort that experiences less strong competition in the breeding habitat and therefore grows fast during the presmolt stage. This fast‐growing cohort will give rise to a slow‐growing cohort in the next generation, and the alternation between fast‐ and slow‐growing cohorts is maintained over generations.
3.3. Data from wild populations
Data from wild populations show that low survival of postsmolts and low food abundance in the non‐breeding habitat are correlated with high growth rates of presmolts. The growth rate of postsmolts (taken as a proxy for the food availability in the non‐breeding habitat) is negatively correlated with the growth rate of presmolts (Figure 5a). Thus, when the food available in the non‐breeding habitat is high and consequently the growth rate of postsmolts is high, the growth rate of presmolts is low. Conversely, a high growth rate of presmolts occurs when the growth rate of postsmolts is low. Similarly, the survival rate of postsmolts is negatively correlated with the growth rate of presmolts (Figure 5b). These correlations support our model prediction that unfavourable conditions for postsmolts cause high growth rate of presmolts in the next generation.
Figure 5.
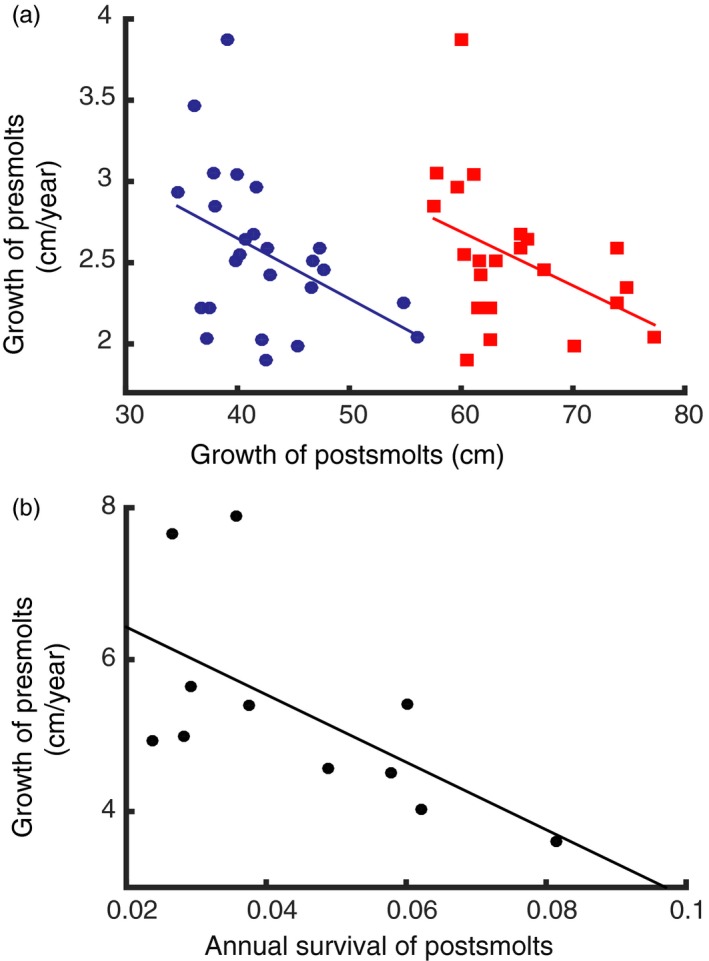
(a) Growth rate of presmolts vs growth rate of postsmolts of 25 populations based on length of grilse (regression: p < 0.05, R‐squared = −0.42, blue circles) and of 22 populations based on length of 2SW fish (regression: p < 0.05, R‐squared = −0.43, red squares). (b) Growth of presmolts vs annual survival of postsmolts of 11 wild populations (regression: p < 0.05, R‐squared = −0.61). Data are shown in Table 2 from Bley and Moring (1988) and Hutchings and Jones (1998)
4. DISCUSSION
Although relations between postsmolt conditions and presmolt growth rates in salmonids have rarely been studied in wild populations, the negative correlation between postsmolts and presmolts growth rates was previously described in a wild population (Einum, Thorstad, & Naesje, 2002). Similarly, the growth rate of postsmolts from the Drammen River has decreased in the last decades while the growth rate of presmolts has increased (McCarthy, Friedland, & Hansen, 2008). Yet, the mechanism that causes this difference in growth rates between different stages was not clear and different explanatory hypotheses have been proposed: the presence of traits having opposing effects on growth in different environments (Einum et al., 2002) or a different growth rate in each environment due to a different necessity of escapement from different predation risk (Abrahams & Sutterlin, 1999). Here, we describe a simple mechanism arising from the interaction between individuals, in particular the intimate link between the strength of density dependence in the breeding habitat and the reproductive output of postsmolts (Figure 6). Furthermore, given that the strength of the density dependence in the breeding area determines the presmolt growth rate while the postsmolt growth rate directly affects the reproductive output and thus the strength of density dependence in the next generation, the presmolt and postsmolts growth rates are negatively correlated in a population. Moreover, farmed Atlantic salmon that are not limited by food grow faster as presmolts compared to wild salmon (McGinnity et al., 2003), whereas both farmed and wild Atlantic salmon have similar growth rates in the ocean (Jonsson, Jonsson, & Hansen, 2003). Therefore, the difference in growth rates of individuals in wild populations in the two habitats is not an individual trait but is more likely arising from the interaction between individuals. This supports our hypothesis that density dependence in the breeding habitat is the main cause of the negative correlation in growth rates rather than individual traits or predation risk.
Figure 6.
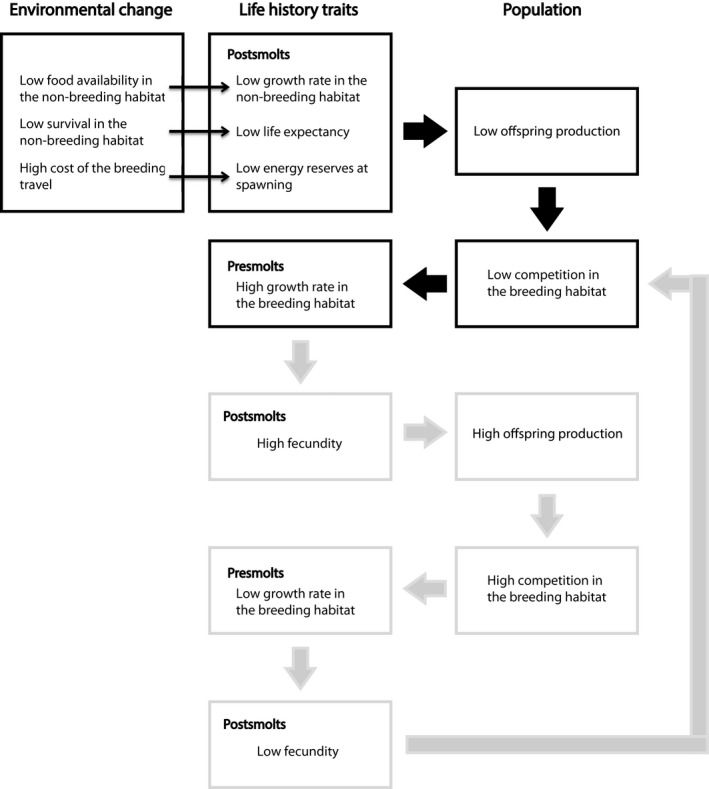
Direct (narrow arrows) and indirect (thick arrows) effects of environmental change on life‐history traits and population processes. Life‐history traits and population processes causing 4‐year cycles in grey arrows and boxes
Likewise, based on data of Atlantic salmon presented by Hutchings and Jones (1998), we show that low survival of postsmolts is correlated with high growth rate of presmolts as well, which is also predicted by our model as a consequence of reduced competition in the breeding habitat. Low food abundance and survival of postsmolts in the non‐breeding habitat also have an impact on the life‐history trajectory of individuals by reducing the sea age at first spawning from 2 to 1 year. In fact, the average sea age at first spawn has decreased in recent decades and this decrease coincides with a decline in the growth rate of postsmolts (Jonsson & Jonsson, 2004).
The effects of environmental change on wild populations, both in abundance (Lane, Kruuk, Charmantier, Murie, & Dobson, 2012; Ozgul et al., 2010) and in dynamics (Cornulier et al., 2013; Nelson & Yamanaka, 2013), have become increasingly documented. However, most analyses are phenomenological. Here, we focus on the mechanisms leading to changes in population abundance and dynamics of anadromous fishes facing environmental change through variation in food abundance, survival and cost of the breeding travel. In particular, we predict a change of dynamics from regular annual cycles to 4‐year cycles in the face of unfavourable conditions for postsmolts or favourable conditions in combination with high food carrying capacity in the breeding habitat. Interestingly, cyclic dynamics have been observed in wild populations of other salmonid species. For instance, four‐year oscillations in some populations of Sockeye salmon (Oncorhynchus nerka) have motivated theoretical studies that explained the occurrence of this dynamics to be caused by tritrophic interactions (Guill, Drossel, Just, & Carmack, 2011), stochastic processes (Myers, Mertz, Bridson, & Bradford, 1998), depensatory predation or genetic effects (Levy & Wood, 1992). Our model successfully predicts the oscillations as a result of the density‐dependent feedback between individuals within a cohort through the food density in the breeding habitat that causes the alternation of a fast‐ and a slow‐growing cohort (Figure 6). The 4‐year cycles in populations of sockeye salmon occur in case of a breeding habitat with high food carrying capacity rather than unfavourable conditions of postsmolts, according to empirical evidence and in line with previous theoretical studies (Guill et al., 2011). To our knowledge, there are no reported examples of transitions from stable annual to multi‐annual cyclic dynamics in anadromous populations to date. However, under a scenario of declining ocean productivity due to climate change (Hoegh‐Guldberg & Bruno, 2010), we may observe in the future a destabilization of populations into cyclical dynamics. Such changes in population dynamics potentially will have consequences for the entire marine community the salmon is part of (Millon et al., 2014).
Simultaneous changes in life‐history traits and population dynamics in response to environmental change are common in nature (Parmesan, 2006). However, the causes underlying these joint responses remain largely unidentified. Few studies have shown the causal relation between coupled responses of individual traits and population dynamics to environmental change (Ozgul et al., 2010; Thompson & Ollason, 2001). In this study, we demonstrate how changes in life‐history traits and population dynamics are intimately linked. In particular, we show how environmental change, by affecting individuals in a specific life stage, has multiple consequences for other life stages and for the entire population. This is particularly relevant for species with complex life cycles involving more than one habitat, because they are exposed to different impacts of environmental change across the habitats and, therefore, across their life cycle. In this context, we provide a mechanistic understanding of the interactions between life‐history and population dynamics based on individual energy budgets for anadromous fishes. If we hope to accurately predict the biological consequences of environmental change, this mechanistic understanding is certainly required.
AUTHORS’ CONTRIBUTIONS
P.C.C.‐P. and A.M.R. conceived the ideas, designed methodology, contributed critically to the drafts and gave final approval for publication; P.C.C.‐P. analysed the results and led the writing of the manuscript.
Supporting information
ACKNOWLEDGEMENTS
This research was supported by funding from the European Research Council (ERC) under the European Union's Seventh Framework Programme (FP/2007‐2013)/ERC Grant Agreement No. 322814.
Chaparro‐Pedraza PC, de Roos AM. Environmental change effects on life‐history traits and population dynamics of anadromous fishes. J Anim Ecol. 2019;88:1178–1190. 10.1111/1365-2656.13010
Footnotes
Data from Bowerman, Pinson‐Dumm, Peery, and Caudill (2017) show that female Chinook Salmon spend more than 50% of their energy content during the spawning migration.
DATA ACCESSIBILITY
The model was parameterized with published data, and references are indicated in Table 1. Data used in Figure 5 are published, and references are indicated in Table 1.
REFERENCES
- Abrahams, M. , & Sutterlin, A. (1999). The foraging and antipredator behaviour of growth‐enhanced transgenic Atlantic salmon. Animal Behaviour, 58, 933–942. 10.1006/anbe.1999.1229 [DOI] [PubMed] [Google Scholar]
- Bley, P. , & Moring, J. (1988). Freshwater and ocean survival of Atlantic salmon and steelhead: A synopsis (Vol. 88). Orono, ME: U.S. Fish and Wildlife Service, Biological Report. [Google Scholar]
- Bowerman, T. E. , Pinson‐Dumm, A. , Peery, C. A. , & Caudill, C. C. (2017). Reproductive energy expenditure and changes in body morphology for a population of Chinook salmon Oncorhynchus tshawytscha with a long distance migration. Journal of Fish Biology, 90(5), 1–20. 10.1111/jfb.13274 [DOI] [PubMed] [Google Scholar]
- Cornulier, T. , Yoccoz, N. G. , Bretagnolle, V. , Brommer, J. E. , Butet, A. , Ecke, F. , … Lambin, X. (2013). Europe‐wide dampening of population cycles in keystone herbivores. Science, 340(6128), 63–66. 10.1126/science.1228992 [DOI] [PubMed] [Google Scholar]
- de Roos, A. M. (1988). Numerical methods for structured population models: The Escalator Boxcar Train. Numerical Methods for Partial Differential Equations, 4(3), 173–195. 10.1002/num.1690040303 [DOI] [Google Scholar]
- de Roos, A. M. , & Persson, L. (2013). Population and community ecology of ontogenetic development. Princeton, NJ: Princeton University Press. [Google Scholar]
- De Roos, A. M. , Persson, L. , & McCauley, E. (2003). The influence of size‐dependent life‐history traits on the structure and dynamics of populations and communities. Ecology Letters, 6(5), 473–487. 10.1046/j.1461-0248.2003.00458.x [DOI] [Google Scholar]
- Doucett, R. R. , Booth, R. K. , Power, G. , & McKinley, R. S. (1999). Effects of the spawning migration on the nutritional status of anadromous Atlantic salmon (Salmo salar): Insights from stable‐isotope analysis. Canadian Journal of Fisheries and Aquatic Sciences, 56(11), 2172–2180. 10.1139/cjfas-56-11-2172 [DOI] [Google Scholar]
- Einum, S. , Thorstad, E. B. , & Naesje, T. F. (2002). Growth rate correlations across life‐stages in female Atlantic salmon. Journal of Fish Biology, 60(3), 780–784. 10.1006/jfbi.2002.1895 [DOI] [Google Scholar]
- Guill, C. , Drossel, B. , Just, W. , & Carmack, E. (2011). A three‐species model explaining cyclic dominance of Pacific salmon. Journal of Theoretical Biology, 276(1), 16–21. 10.1016/j.jtbi.2011.01.036 [DOI] [PubMed] [Google Scholar]
- Hendry, K. , & Cragg‐Hine, D. (2003). Ecology of the Atlantic salmon. Conserving Natura 2000 rivers. Ecology series, 7 .
- Hoegh‐Guldberg, O. , & Bruno, J. F. (2010). The impact of climate change on the world's marine ecosystem. Science, 328, 1523–1528. 10.1080/00330124.2015.1124788 [DOI] [PubMed] [Google Scholar]
- Hutchings, J. A. , & Jones, M. E. B. (1998). Life history variation and growth rate thresholds for maturity in Atlantic salmon, Salmo salar . Canadian Journal of Fisheries and Aquatic Sciences, 55, 22–47. 10.1139/cjfas-55-S1-22 [DOI] [Google Scholar]
- Jager, T. , Martin, B. T. , & Zimmer, E. I. (2013). DEBkiss or the quest for the simplest generic model of animal life history. Journal of Theoretical Biology, 328, 9–18. 10.1016/j.jtbi.2013.03.011 [DOI] [PubMed] [Google Scholar]
- Jonsson, N. , & Jonsson, B. (2004). Size and age of maturity of Atlantic salmon correlate with the North Atlantic Oscillation Index (NAOI). Journal of Fish Biology, 64(1), 241–247. 10.1046/j.1095-8649.2004.00269.x [DOI] [Google Scholar]
- Jonsson, N. , Jonsson, B. , & Hansen, L. P. (1997). Changes in proximate composition and estimates of energetic costs during upstream migration and spawning in Atlantic salmon Salmo salar . Journal of Animal Ecology, 66(3), 425–436. 10.2307/5987 [DOI] [Google Scholar]
- Jonsson, N. , Jonsson, B. , & Hansen, L. P. (1998). The relative role of density‐dependent and density‐independent survival in the life cycle of Atlantic salmon Salmo salar . Journal of Animal Ecology, 67(5), 751–762. 10.1046/j.1365-2656.1998.00237.x [DOI] [Google Scholar]
- Jonsson, N. , Jonsson, B. , & Hansen, L. P. (2003). The marine survival and growth of wild and hatchery‐reared Atlantic salmon. Journal of Applied Ecology, 40(5), 900–911. [Google Scholar]
- Kooijman, S. A. L. M. (2010). Dynamic energy budget theory for metabolic organisation. Cambridge, UK: Cambridge University Press. [DOI] [PubMed] [Google Scholar]
- Kooijman, S. A. L. M. , & Metz, J. A. J. (1984). On the dynamics of chemically stressed populations: The deduction of population consequences from effects on individuals. Hydrobiological Bulletin, 17(1), 88–89. 10.1007/BF02255198 [DOI] [PubMed] [Google Scholar]
- Lane, J. E. , Kruuk, L. E. B. , Charmantier, A. , Murie, J. O. , & Dobson, F. S. (2012). Delayed phenology and reduced fitness associated with climate change in a wild hibernator. Nature, 489(7417), 554–557. 10.1038/nature11335 [DOI] [PubMed] [Google Scholar]
- Levy, D. A. , & Wood, C. C. (1992). Review of proposed mechanisms for sockeye salmon population cycles in the Fraser river. Bulletin of Mathematical Biology, 54(2–3), 241–261. 10.1007/BF02464832 [DOI] [Google Scholar]
- Limburg, K. E. , & Waldman, J. R. (2009). Dramatic declines in North Atlantic diadromous fishes. BioScience, 59(11), 955–965. 10.1525/bio.2009.59.11.7 [DOI] [Google Scholar]
- Martin, B. , Heintz, R. , Danner, E. , & Nisbet, R. (2017). Integrating lipid storage into general representations of fish energetics. Journal of Animal Ecology, 86(2), 812–825. 10.1111/1365-2656.12667 [DOI] [PubMed] [Google Scholar]
- McCarthy, J. L. , Friedland, K. D. , & Hansen, L. P. (2008). Monthly indices of the post‐smolt growth of Atlantic salmon from the Drammen River, Norway. Journal of Fish Biology, 72(7), 1572–1588. 10.1111/j.1095-8649.2008.01820.x [DOI] [Google Scholar]
- Mccormick, S. D. , Hansen, L. P. , Quinn, T. P. , & Saunders, R. L. (1998). Movement, migration, and smolting of Atlantic salmon (Salmo salar). Canadian Journal of Fisheries and Aquatic Sciences, 55, 77–92. 10.1139/d98-011 [DOI] [Google Scholar]
- McGinnity, P. , Prodöhl, P. , Ferguson, A. , Hynes, R. , Maoiléidigh, N. O. , Baker, N. , … Cross, T. (2003). Fitness reduction and potential extinction of wild populations of Atlantic salmon, Salmo salar, as a result of interactions with escaped farm salmon. Proceedings of the Royal Society B: Biological Sciences, 270(1532), 2443–2450. 10.1098/rspb.2003.2520 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metcalfe, N. B. , & Thorpe, J. E. (1990). Determinants of geographical variation in the age of seaward‐migrating salmon, Salmo salar . Journal of Animal Ecology, 59(1), 135–145. 10.2307/5163 [DOI] [Google Scholar]
- Millon, A. , Petty, S. J. , Little, B. , Gimenez, O. , Cornulier, T. , & Lambin, X. (2014). Dampening prey cycle overrides the impact of climate change on predator population dynamics: A long‐term demographic study on tawny owls. Global Change Biology, 20(6), 1770–1781. 10.1111/gcb.12546 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myers, R. A. , Mertz, G. , Bridson, J. M. , & Bradford, M. J. (1998). Simple dynamics underlie sockeye salmon (Oncorhynchus nerka) cycles. Canadian Journal of Fisheries and Aquatic Sciences, 55, 2355–2364. 10.1139/cjfas-55-10-2355 [DOI] [Google Scholar]
- Nelson, W. A. , & Yamanaka, T. (2013). Recurrent insect outbreaks caused by temperature‐driven changes in system stability. Science, 341(6147), 796–799. 10.1126/science.1238477 [DOI] [PubMed] [Google Scholar]
- Nisbet, R. M. , Muller, E. B. , Lika, K. , & Kooijman, S. A. L. M. (2000). From molecules to ecosystems through dynamic energy budget models. Journal of Animal Ecology, 69(6), 913–926. 10.1046/j.1365-2656.2000.00448.x [DOI] [Google Scholar]
- Ozgul, A. , Childs, D. Z. , Oli, M. K. , Armitage, K. B. , Blumstein, D. T. , Olson, L. E. , … Coulson, T. (2010). Coupled dynamics of body mass and population growth in response to environmental change. Nature, 466(7305), 482–485. 10.1038/nature09210 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parmesan, C. (2006). Ecological and evolutionary responses to recent climate change. Annual Review of Ecology, Evolution, and Systematics, 37(1), 637–669. 10.1146/annurev.ecolsys.37.091305.110100 [DOI] [Google Scholar]
- Pauly, D. , Christensen, V. , Guénette, S. , Pitcher, T. J. , Sumaila, U. R. , Walters, C. J. , … Zeller, D. (2002). Towards sustainability in world fisheries. Nature, 418(6898), 689–695. 10.1038/nature01017 [DOI] [PubMed] [Google Scholar]
- Pecquerie, L. , Johnson, L. R. , Kooijman, S. A. L. M. , & Nisbet, R. M. (2011). Analyzing variations in life‐history traits of Pacific salmon in the context of dynamic energy budget (DEB) theory. Journal of Sea Research, 66(4), 424–433. 10.1016/j.seares.2011.07.005 [DOI] [Google Scholar]
- Persson, L. , Leonardsson, K. , de Roos, A. M. , Gyllenberg, M. , & Christensen, B. (1998). Ontogenetic scaling of foraging rates and the dynamics of a size‐structured consumer‐resource model. Theoretical Population Biology, 54(3), 270–293. 10.1006/tpbi.1998.1380 [DOI] [PubMed] [Google Scholar]
- Potts, W. T. W. , & Rudy, P. P. (1969). Water balance in the eggs of the Atlantic salmon Salmo salar . The Journal of Experimental Biology, 50(1), 223–237. [DOI] [PubMed] [Google Scholar]
- Power, G. (1981). Stock characteristics and catches of Atlantic salmon (Salmo salar) in Quebec, and Newfoundland and Labrador in relation to environmental variables. Canadian Journal of Fisheries and Aquatic Sciences, 38(12), 1601–1611. 10.1139/f81-210 [DOI] [Google Scholar]
- Shearer, K. , Asgard, T. , Andorsdottir, G. , & Aas, G. (1994). Whole body elemental and proximate composition of Atlantic salmon (Salmo salar) during the life cycle. Journal of Fish Biology, 44, 785–797. 10.1111/j.1095-8649.1994.tb01255.x [DOI] [Google Scholar]
- Sutton, S. G. , Bult, T. P. , & Haedrich, R. L. (2000). Relationships among fat weight, body weight, water weight, and condition factors in wild Atlantic salmon parr. Transactions of the American Fisheries Society, [DOI] [Google Scholar]
- Thompson, P. M. , & Ollason, J. C. (2001). Lagged effects of ocean climate change on fulmar population dynamics. Nature, 413(6854), 417–420. 10.1038/35096558 [DOI] [PubMed] [Google Scholar]
- Thorpe, J. E. , Mangel, M. , Metcalfe, N. B. , & Huntingford, F. A. (1998). Modelling the proximate basis of salmonid life‐history variation, with application to Atlantic salmon, Salmo salar L. Evolutionary Ecology, 12(5), 581–599. 10.1023/A:1022351814644 [DOI] [Google Scholar]
- Vagg, R. , & Hepworth, H. (2006). Migratory species and climate change: Impacts of a changing environment on wild animals. Bonn, Germany: UNEP/CMS Secretariat. [Google Scholar]
- Walters, A. W. , Copeland, T. , & Venditti, D. A. (2013). The density dilemma: Limitations on juvenile production in threatened salmon populations. Ecology of Freshwater Fish, 22(4), 508–519. 10.1111/eff.12046 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The model was parameterized with published data, and references are indicated in Table 1. Data used in Figure 5 are published, and references are indicated in Table 1.


