Evaluation of Deep Learning Strategies for Nucleus Segmentation in Fluorescence Images

Abstract

Identifying nuclei is often a critical first step in analyzing microscopy images of cells and classical image processing algorithms are most commonly used for this task. Recent developments in deep learning can yield superior accuracy, but typical evaluation metrics for nucleus segmentation do not satisfactorily capture error modes that are relevant in cellular images. We present an evaluation framework to measure accuracy, types of errors, and computational efficiency; and use it to compare deep learning strategies and classical approaches. We publicly release a set of 23,165 manually annotated nuclei and source code to reproduce experiments and run the proposed evaluation methodology. Our evaluation framework shows that deep learning improves accuracy and can reduce the number of biologically relevant errors by half. © 2019 The Authors. Cytometry Part A published by Wiley Periodicals, Inc. on behalf of International Society for Advancement of Cytometry.

Image analysis is a powerful tool in cell biology to collect quantitative measurements in time and space with precision, speed, and sensitivity. From image‐based assays to high‐content screening 1, 2, microscopy images have led to understanding genetic perturbations, pursuing drug discovery, and phenotyping cells in biomedical applications and cell biology research 3, 4. The most widely used quantitative imaging technique in biological laboratories is fluorescence imaging; with automation it can easily produce terabytes of primary research data 5. Accurate and automated analysis methods are key to successfully quantify relevant biology in such large image collections.

One critical step in quantifying fluorescence images is often the identification of the nucleus of each cell with a DNA stain, and there is a long history of research efforts to design and improve nuclear and cellular segmentation 6. One of the most commonly used strategies for nucleus segmentation is Otsu's thresholding method 7 followed by seeded watershed 8, 9, because of its effectiveness, simplicity of use and computational efficiency. Machine learning‐based segmentation methods have also been introduced for segmenting cells 10, which typically require annotated examples in the form of segmentation masks or interactive scribbles. Many of these strategies are readily available in various bioimage software packages 11, including open source options such as CellProfiler 12, Ilastik 10, and ImageJ/Fiji 13, facilitating their adoption in routine biological research.

Despite widespread adoption, segmentation tools in biology generally do yield nontrivial amounts of segmentation error. These may silently propagate to downstream analyses, yielding unreliable measures or systemic noise that is difficult to quantify and factor out. There are several causes for segmentation errors. First, existing algorithms have limitations due to the assumptions made in the computational design that do not always hold, such as thresholding methods that assume bimodal intensity distributions, or region growing that expects clearly separable boundaries. Second, the most popular solutions for nucleus segmentation were originally formulated and adopted several decades ago when the biological systems and phenotypes of interest were often simpler; however, as biology pushes the limits of high‐throughput cellular and tissue models, natural and subtle variations of biologically meaningful phenotypes are more challenging to segment. Finally, algorithms are usually configured using a few—hopefully representative—images from the experiment, but variations in signal quality and the presence of noise pose challenges to the robustness and reliability of the solution at large scale.

The ideal approach to nucleus segmentation would be a generic, robust, and fully automated solution that is as reliable as modern face detection technologies deployed in mobile applications and social networks. The current state of the art in face detection and many other computer vision tasks is based on deep learning 14, which has demonstrated high accuracy, even surpassing human‐level performance in certain tasks 15. Several models based on deep learning have already been proposed for cell segmentation in biological applications, most notably U‐Net 16 and DeepCell 17, which are based on convolutional neural networks (CNNs).

In this article, we present an evaluation framework, including a new metric, to answer the question of how much improvement is obtained when adopting deep learning models for nucleus segmentation. The most commonly‐used metric for nucleus/cell segmentation evaluation is the Jaccard index 17, 18, 19, which measures pixel‐wise overlap between ground truth and segmentations estimated by an algorithm. From a cell biology perspective, pixel‐wise overlap alone is not useful to diagnose the errors that actually impact the downstream analysis, such as missing and merged objects (Fig. S1). Thus, we recommend the use of metrics that explicitly count correctly segmented objects as true positives and penalize any instance‐level error, similar to practice in diagnostic applications 20, 21. These include object‐level F1‐score and false positives, among others.

We demonstrate the utility of this methodology by evaluating two deep learning methods proposed for cell segmentation and comparing them against classical machine learning and image processing algorithms. The goal of our study is to investigate the potential of deep learning algorithms to improve the accuracy of nucleus segmentation in fluorescence images. Expert biologists on our team hand‐annotated more than 20,000 nuclei in an image collection of 200 images of the DNA channel from a large image‐based chemical screen, sampled from a diverse set of treatments 22. We apply our evaluation framework to analyze different types of segmentation errors, computational efficiency, and the impact of quantity and quality of training data for creating deep learning models.

Our study is restricted to segmenting the nucleus of cells in fluorescence images, which is different from the more general cell segmentation problem. We also assume the availability of a large dataset of annotated images for training the machine learning models. We note that the deep learning techniques evaluated in our experiments were designed for different settings: general purpose cell segmentation with limited training data. Nevertheless, both deep learning methods (DeepCell and U‐Net) showed improved ability for segmenting nuclei and fix errors that are relevant to experimental biology when trained with a large image set.

Materials

Image Collection

The image set is a high‐throughput experiment of chemical perturbations on U2OS cells, comprising 1,600 bioactive compounds 22. The effect of treatments was imaged using the Cell Painting assay 23 which labels cell structures using six stains, including Hoechst for nuclei. From this image collection, we randomly sampled 200 fields of view of the DNA channel, each selected from a different compound. By doing so, phenotypes induced by 200 distinct chemical perturbations were sampled.

The original image collection is part of the Broad Bioimage Benchmark Collection, with accession number BBBC022, and the subset used for this study has been made publicly available with accession number BBBC039 at https://data.broadinstitute.org/bbbc/BBBC039/.

Expert Annotations

Each image in the sampled subset was reviewed and manually annotated by PhD‐level expert biologists. Annotators were made to label each single nucleus as a distinguishable object, even if nuclei happen to be clumped together or appear to be touching each other. Nuclei of all sizes and shapes were included as our goal was to densely annotate every single nucleus that can be recognized in the sampled images, regardless of its phenotype. In this way, a wide variety of phenotypes was covered, including micronuclei, toroid nuclei, fragmented nuclei, round nuclei, and elongated nuclei, among others 22.

We included tiny fragments of nuclei as part of the annotated objects in our dataset, which correspond to small blobs of DNA‐stained material that appear to be membrane bound, primarily micronuclei. The biological relevance of micronuclei is abundantly documented in the literature 24, 25, 26, 27, 28, 29 and these are frequently quantified using fluorescent imaging for projects involving cancer research, congenital disorders, and therapy toxicity, among others. Adding these tiny objects to the dataset is useful to stimulate computational research that detects and quantifies them better.

Creating a resource of manually annotated images is time consuming, and existing tools for annotating natural images are not ideal for microscopy. In order to improve and simplify the image annotation experience for experts in our team, we created a prototype annotation tool to assign single‐object masks in images. Our user interface allowed the experts to zoom in and out to double check details, and also presented the annotation masks overlaid on top of the original image using a configurable transparency layer. Importantly, our annotation tool was based on assisted segmentation based on superpixels, which are computed on intensity features to facilitate user interactions.

Our prototype tool was useful to collect nucleus annotations for this research; however, significant development is needed to improve it. Alternative methods for collecting image annotations now exist, such as the Quanti.us system 30 for distributing manual annotations to nonexpert workers on the internet. This may enable the annotation process for new projects to be scaled up quickly to many more images, and, according to their findings, reaching similar precision to experts when multiple workers provide independent annotation replicates.

Methods

Identifying nuclei in an image is best framed as an “instance segmentation” problem 31, where the challenge is to find distinct regions corresponding to a single class of objects: the nucleus. Semantic segmentation 32, which splits an image to regions of various classes without requiring objects to be separated, is not helpful for nucleus segmentation because there is only one class, and touching nuclei would not be distinguished from each other. Both of the deep learning strategies evaluated in this article are cases of instance segmentation that formulate nucleus segmentation as a boundary detection problem.

The boundary detection problem consists of identifying three different types of pixels in an image of nuclei: (a) background, (b) interior of nuclei, and (c) boundaries of nuclei. This formulation simplifies the problem of instance segmentation into a three‐class, pixel‐wise classification problem (Fig. 1), which can be understood as a semantic segmentation solution to identify the structural elements of the image. The critical class to separate single objects is the boundary class: failure to classify boundaries correctly will result in merged or split objects. The actual segmentation masks are obtained from the interior class, which covers the regions where objects are located. This requires additional postprocessing steps over classification probability maps to recover individual instances using the connected components algorithm 33 and morphological operators 34 (Supporting Information S2). Note that while we pose this as a pixel‐wise classification problem of boundaries, we evaluate the performance on the success of identifying entire objects.

Figure 1.

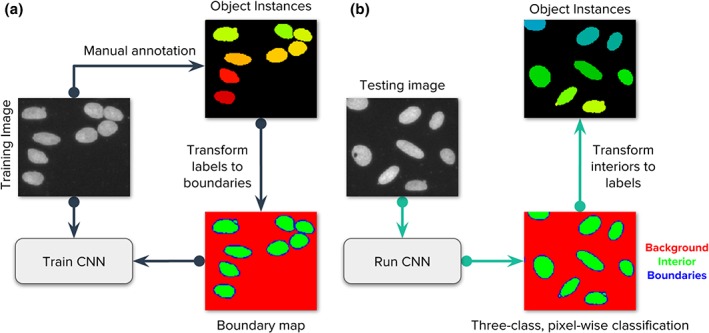
Strategy of the evaluated deep learning approaches. Our main goal is to follow the popular strategy of segmenting each nucleus and micronucleus as a distinct entity, regardless of whether it shares the same cell body with another nucleus. It is generally possible to group nuclei within a single cell using other channels of information in a postprocessing step if the assay requires it. (a) Images of the DNA channel are manually annotated, labeling each nucleus as a separate object. Then, labeled instances are transformed to masks for background, nucleus interior, and boundaries. A convolutional neural network (CNN) is trained using the images and their corresponding masks. (b) The trained CNN generates predictions for the three class classification problem. Each pixel belongs to only one of the three categories. In postprocessing, the predicted boundary mask is used to identify each individual instance of a nucleus. [Color figure can be viewed at wileyonlinelibrary.com]

The ground truth to solve the boundary detection problem starts with masks individually assigned to each object (Section 2.2) and then transformed to three‐class annotations. The boundary annotations are initially obtained from ground truth annotations using a single pixel contour around each nucleus. We then expand this contour with two more pixels, one inside and another outside the boundary to cover natural pixel intensity variations of the input image and also to compensate for errors in manual annotations. We tested with boundaries of different sizes but did not observe any significant benefits of further adjusting this configuration.

Various CNNs can be used for nucleus segmentation, including the Mask‐RCNN model 35, which decomposes images into regions first and then predicts object masks. The automatic design of neural networks by searching the space of architectures with an optimization procedure 36 may also be used to create generic nucleus segmentation networks. However, in this work we do not propose novel architectures, instead, we develop an evaluation methodology to identify errors and improve performance of existing models. Specifically, we evaluate two architectures, representing two prominent models designed and optimized for segmenting biological images: DeepCell 17 and U‐Net 16. We use the same preprocessing and postprocessing pipeline when evaluating both CNN models (Supporting Information S2), so differences in performance are explained by architectural choices only.

DeepCell

DeepCell 17 is a framework designed to perform general‐purpose biological image segmentation using neural networks. Its driving philosophy is to get deep learning operational in biological laboratories using well‐constructed models that can be trained with small datasets using modest hardware requirements, making them usable in a small data regime. The DeepCell library is open source and features a Docker container with guidelines for training and testing models with new data via Jupyter Notebooks, and more recently, user‐friendly functionalities to run a deep learning application in the cloud 37.

The DeepCell model evaluated in our work is a CNN that segments images of cells using a patch‐based, single pixel classification objective. The network architecture has seven convolutional layers, each equipped with a ReLu nonlinearity 38 and batch normalization 39; three max‐pooling layers to progressively reduce the spatial support of feature maps; and two fully connected layers; totaling about 2.5 million trainable parameters per network (a full DeepCell model is an ensemble of five networks). Note that DeepCell was designed to be trained in a sample wise fashion and then executed in a fully convolutional way. During training, the incoming feature layer is flattened, and during execution a tensor product using the same weight matrix is used. This architecture has a receptive field of 61 × 61 pixels, which is the approximate area needed to cover a single cell (of a diameter up to 40 μm, imaged at 20× at a resolution of 0.656 μm/pixel), and produces as output a three‐class probability distribution for the pixel centered in the patch.

In our evaluation, we use the recommended configuration reported by Van Valen et al. 17, which was demonstrated to be accurate on a variety of cell segmentation tasks, including mammalian cell segmentation and nuclei. Their configuration include training an ensemble of five replicate networks to make predictions in images. The final segmentation mask is the average of the outputs produced by each individual network. The ensemble increases processing time and the number of trainable parameters, but can also improve segmentation accuracy. The settings of the DeepCell system that we used in our experiments can be reproduced using the following Docker container: https://hub.docker.com/r/jccaicedo/deepcell/.

U‐Net

The U‐Net architecture 16 resembles an autoencoder 40 with two main sub‐structures: (a) an encoder, which takes an input image and reduces its spatial resolution through multiple convolutional layers to create a representation encoding. (b) A decoder, which takes the representation encoding and increases spatial resolution back to produce a reconstructed image as output. The U‐Net introduces two innovations to this architecture: First, the objective function is set to reconstruct a segmentation mask using a classification loss; and second, the convolutional layers of the encoder are connected to the corresponding layers of the same resolution in the decoder using skip connections.

The U‐Net evaluated in our work consists of eight convolutional layers and three max pooling layers in the encoder branch, and eight equivalent convolutional layers with upscaling layers in the decoder branch. We note that batch normalization layers were not part of the original U‐Net design, so we added one after all convolutional layers in our implementation. The skip connections copy the feature maps from the encoder to the decoder. The receptive field of the U‐Net is set to 256 × 256 pixels during training, which can cover a large group of cells at the same time. This architecture has a total of 7.7 million trainable parameters.

We adapted the objective function as a weighted classification loss, giving 10 times more importance to the boundary class. We did not introduce a different weighting scheme for edges between two cells, giving all boundary pixels the same weight regardless of their context (background or another cell). We apply basic data augmentation during training, including random cropping, flips, 90° rotations, and illumination variations. Also, we apply additional data augmentation using elastic deformations, as discussed by the authors 16. The training parameters for this network were tuned using the training and validation sets, and the final model is applied to the test set to report performance. The source code of our U‐Net implementation can be found in https://github.com/carpenterlab/2019_caicedo_cytometryA, with an optional CellProfiler 3.0 plugin of this nucleus‐specific model 41. Also, a U‐Net plugin was independently developed for ImageJ for running generic cell segmentation and quantification tasks 42.

Evaluation Metrics

Measuring the performance of cell segmentation has been generally approached as measuring the difference between two segmentation masks: a reference mask with ground truth objects representing the true segmentation, versus the predicted/estimated segmentation mask. These metrics include root‐mean‐square deviation 43, Jaccard index 17, and bivariate similarity index 18, among others. However, these metrics focus on evaluating pixel‐wise segmentation accuracy only, and fail to quantify object‐level errors explicitly (such as missed or merged objects).

In our evaluation, we adopt an object‐based accuracy metric that uses a measure of area coverage to identify correctly segmented nuclei. Intuitively, the metric counts the number of single objects that have been correctly separated from the rest using a minimum area coverage threshold. The metric relies on the computation of intersection‐over‐union between ground truth objects T and estimated objects E:

$$\mathit{IoU}\left(T,E\right)=\frac{T\cap E}{T\cup E}$$

Consider n true objects and m estimated objects in an image. A matrix C _n × m is computed with all IoU scores between true objects and estimated objects to identify the best pairing. This is a very sparse matrix because only a few pairs share enough common area to score a nonzero IoU value.

To complete the assignment, a threshold greater than 0.5 IoU is applied to the matrix to identify segmentation matches. In our evaluation, we do not accept overlapping objects, that is, one pixel belongs only to a single nucleus. Thus, a threshold greater than 0.5 ensures that for each nucleus in the ground truth there is no more than one match in the predictions, and vice versa. We also interpret this threshold as requiring that at least half of the nucleus is covered by the estimated segmentation to call it a true positive. In other words, segmentations smaller than half the target object are unacceptable, raising the bar for practical solutions. This differs from a previous strategy 44 that takes a similar approach but does not impose this constraint, potentially allowing for very low object coverage. At a given IoU threshold t, the object‐based segmentation F ₁‐score is then computed as:

$$F_1=\frac{2\mathit{TP}}{2\mathit{TP}+\mathit{FN}+\mathit{FP}}.$$

We compute the average F ₁‐score across all images, and then across multiple thresholds, starting at t = 0.50 up to t = 0.90 with increments Δt = 0.05. This score summarizes the quality of segmentations by simultaneously looking at the proportion of correctly identified objects as well as the pixel‐wise accuracy of their estimated masks.

Our evaluation metric is similar in spirit to other evaluation metrics used in computer vision problems, such as object detection in the PASCAL challenge 45 and instance segmentation in the COCO challenge 31, 46. One important difference between these metrics and ours is that our problem considers a single object category (the nucleus), and therefore, it is more convenient to adopt the F ₁‐score instead of precision. Precision and recall have been used in previous studies of nucleus segmentation in fluorescent images 47, and F ₁‐score has also been adopted to measure segmentation performance in tissue samples 48. But we note that our score is evaluated across multiple intersection‐over‐union thresholds, which is the practice in modern computer vision research to simultaneously measure object detection accuracy as well as shape alignment accuracy.

In our evaluation, we also measure other quality metrics, including the number and type of errors to facilitate performance analysis 49. The following are different types of errors that a segmentation algorithm can make: false negatives (missed objects); merges (under‐segmentations), which are identified by several true objects being covered by a single estimated mask; and splits (over‐segmentations), which are identified by a single true object being covered by multiple estimated masks. We identify these errors in the matrix C of IoU scores using a fixed threshold for evaluation, and keep track of them to understand the difficulties of an algorithm to successfully segment an image.

Baseline Segmentations

Classic image processing

We use CellProfiler 3.0 41 pipelines to create baseline segmentations. CellProfiler was used as a baseline over other tools because it offers great flexibility to configure multi‐step image processing pipelines that connect different algorithms for image analysis, and it is widely used in biology labs and high‐throughput microscopy facilities. The pipelines are configured and tested by an expert image analyst using images from the training set, and then run in the validation and test set for evaluation. We refer to two CellProfiler pipelines for obtaining baseline segmentations: basic and advanced.

The basic pipeline relies only on the configuration of the module IdentifyPrimaryObjects, which is frequently used to identify nuclei. The module combines thresholding techniques with area and shape rules to separate and filter objects of interest. This is the simplest way of segmenting nuclei images when the user does not have extensive experience with image analysis operations, yet it is complete enough to allow them to configure various critical parameters.

The advanced pipeline incorporates other modules for preprocessing the inputs and postprocessing the outputs of the IdentifyPrimaryObjects module. In our advanced configuration, we included illumination correction, median filters and opening operations, to enhance and suppress features in the input images before applying thresholding. These operations are useful to remove noise and prepare images to the same standard for segmentation using the same configuration. The postprocessing steps include measuring objects to apply additional filters and generate the output masks.

A single pipeline was used for segmenting images in the BBBC039 dataset, while Van Valen's set required to split the workflow in two different pipelines. We observed large signal variation in Van Valen's set given that these images come from different experiments and reflect realistic acquisition modes. Two settings were needed for thresholding, the first for normal single mode pixel intensity distributions and another one for bimodal distributions. The latter is applied to cases where subpopulations of nuclei are significantly brighter than the rest, requiring two thresholds. We used a clustering approach to automatically decide which images needed which pipeline. The pipelines used in our experiments are released together with the data and code.

Segmentation using classic machine learning

We used Ilastik 10 to train a supervised machine‐learning model as an additional benchmark in this evaluation. Ilastik is effective at balancing memory and CPU requirements, allowing users to run segmentations in real time with sparse annotations over the images (scribbles). We loaded the full set of existing annotated training images, and trained a Random Forest classifier with the default parameters. The feature set included intensity, edge, and texture features in three different scales. The annotated images used the same three categories used for deep‐learning‐based segmentation: background, interior, and boundaries of nuclei. In addition, we subsampled pixels in the background and interior categories to balance annotations and reduce the impact of redundant pixels.

After the Random Forest model is trained, the validation and test images were loaded into Ilastik for predictions. We obtained the probability maps for each category and applied the same postprocessing steps used for deep‐learning‐based segmentations (Supporting Information S2).

Results

Deep Learning Improves Nucleus Segmentation Accuracy

Overall, we find that deep learning models exhibit higher accuracy than classical segmentation algorithms, both in terms of the number of correctly identified objects, as well as the localization of boundaries of each nucleus (Fig. 2). We evaluate these properties using the F ₁‐score (the harmonic average of precision and recall) averaged over increasingly stringent thresholds of overlap between the ground truth and prediction. U‐Net and DeepCell obtained higher average F ₁‐scores (Fig. S1), yielding 0.898 and 0.858, respectively, versus 0.840 for Random Forests, 0.811 for advanced CellProfiler and 0.790 for the basic CellProfiler pipeline. This improvement is a significant margin when experiments are run at large scale with thousands of images. Deep learning models yield a higher average F1‐score across higher thresholds (Fig. 2a), indicating that the boundaries of objects are more precisely mapped to the correct contours compared to the other methods.

Figure 2.

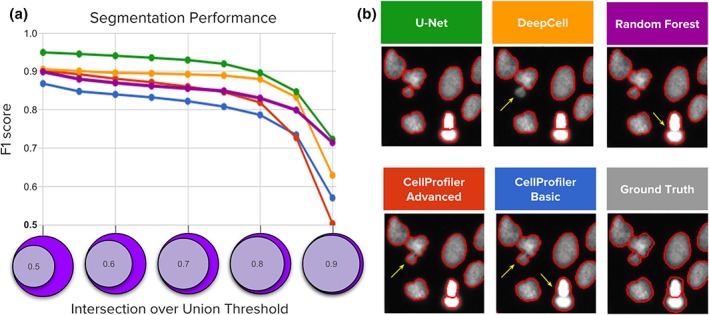
Segmentation performance of five strategies compared against ground‐truth expert segmentations. (a) Average F ₁‐score versus nucleus coverage for U‐Net (green), DeepCell (yellow), Random Forest (purple), CellProfiler advanced (red), and CellProfiler basic (blue). The y axis is average F ₁‐score (higher is better), which measures the proportion of correctly segmented objects. The x axis represents intersection‐over‐union (IoU) thresholds as a measurement of how well aligned the ground truth and estimated segmentations must be to count a correctly detected nucleus. Higher thresholds indicate stricter boundary matching. Notice that average F ₁‐scores remain nearly constant up to IoU = 0.80; at higher thresholds, performance decreases sharply, which indicates that the proportion of correctly segmented objects decreases when stricter boundaries are required to count a positive detection. (b) Example segmentations obtained with each of the five evaluated methods sampled to illustrate performance differences. Segmentation boundaries are in red, and errors are indicated with yellow arrows. [Color figure can be viewed at wileyonlinelibrary.com]

The most common errors for all methods are merged objects, which occur when the segmentation fails to separate two or more touching nuclei (yellow arrows in Fig. 2b). Deep learning strategies tend to reduce this type of error (more in Fig. 3c) and provide tighter and smoother segmentation boundaries than those estimated by global Otsu thresholding and declumping, which is at the core of the baseline CellProfiler pipelines for nucleus segmentation.

Figure 3.

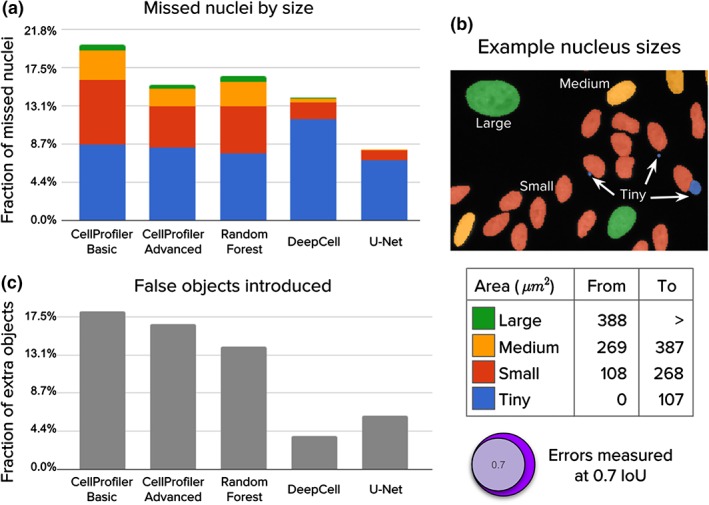
Analysis of segmentation errors (missed and extra objects). The 5,720 nuclei in the test set were used in this analysis. (a) Fraction of missed nuclei by object size (see table). Missed objects in this analysis were counted using an IoU threshold of 0.7, which offers a good balance between strict nucleus coverage and robustness to noise in ground truth annotations. (b) Example image illustrating sizes of nuclei. (c) Fraction of extra or false objects introduced by algorithms. [Color figure can be viewed at wileyonlinelibrary.com]

Qualitatively, nucleus boundaries predicted by deep learning appear to define objects better than those produced by human annotators using an assistive annotation tool, which can introduce boundary artifacts. Neural nets can learn to provide edges closer to the nuclei with fewer gaps and better‐delineated shapes, despite being trained with examples that have such boundary artifacts, showing ability to generalize beyond noise. Overcoming the limitation of assisted annotations is a major strength of this approach because fixing boundary artifacts by hand in the training data is very time consuming. We suspect that the accuracy drop observed in the segmentation performance plot at IoU = 0.85 (Fig. 2a) may be partly explained by inaccurate boundaries in ground truth annotations, that is, improved segmentations may be unfairly scored at high thresholds.

Deep Learning Excels at Correct Splitting of Adjacent Nuclei

Deep learning methods make fewer segmentation mistakes compared to classical pipelines, effectively correcting most of their typical errors (Figs. 3 and 4). Here, an error is defined as when a nucleus in the ground truth is missed in an estimated segmentation mask after applying a minimum IoU threshold of 0.7. By this metric, U‐Net achieves an error rate of 8.1%, DeepCell 14.0%, Random Forest 16.5%, advanced CellProfiler 15.5%, and basic CellProfiler 20.1% (Fig. S2). These results are consistent with the evaluation of accuracy performed at multiple IoU thresholds, indicating that deep learning obtains improved performance.

Figure 4.

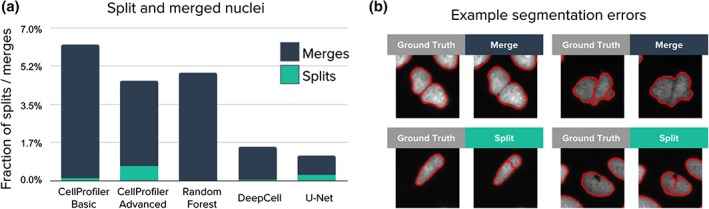
Analysis of segmentation errors (splits and merged objects). The 5,720 nuclei in the test set were used in this analysis. (a) Fraction of merged and split nuclei. These errors are identified by masks that cover multiple objects with at least 0.1 IoU. (b) Example merges and splits. [Color figure can be viewed at wileyonlinelibrary.com]

To understand the performance differences among the evaluated methods, we categorized missed objects by size (Fig. 3a,b) and segmentation errors by type (merges vs. splits; Fig. 4a,b). An object is missed when the segmentation does not meet the minimum IoU threshold criterion. A merge is counted when one estimated mask is found covering more than one ground truth mask. Similarly, a split is counted when a ground truth mask is being covered by more than one estimated mask. Note that splits and merges are a subset of the total number of errors, and partially overlap with the number of missed objects. That is, some splits and all merges result in one or more missing objects, but not all missing objects are a result of a split or merge.

Deep learning corrects almost all of the errors made by classical pipelines for larger nuclei. We also note that all methods usually fail to capture tiny nuclei correctly (generally, micronuclei, which are readily confounded with debris or artifacts, and represent about 15% of all objects in the test set; Fig. 3a). Interestingly, deep learning tends to accumulate errors for tiny nuclei only, while the CellProfiler pipelines and Random Forests tend to make errors across all sizes (Fig. 3b). Tiny nuclei are missed for several reasons, including merging with bigger objects, confounding with debris, or failing to preserve enough object signal for the postprocessing routines. Some of these issues can be addressed by developing multi‐scale segmentation methods or by increasing the resolution of the input images either optically or computationally.

Both deep learning approaches are effective at recognizing boundaries to separate touching nuclei and correct typical error modes of classical algorithms: merges and splits (Fig. 4a). Split errors produced by the advanced CellProfiler pipeline reveal a trade‐off when configuring the parameters of classical algorithms: in order to fix merges we have to accept some more splits. A similar situation happens with U‐Net: it has learned to separate clumped nuclei very effectively because the boundary class has 10 times more weight in the loss function, which at the same time forces the network to make some splits to avoid the cost of missing real boundaries (Fig. 3a,c).

We observe different types of errors produced by the two deep learning models. U‐Net detects nuclei of all sizes better than DeepCell (Fig. 3a), but also sees imaginary objects more often (Fig. 3c). Also, U‐Net is more sensitive than DeepCell at detecting intra‐cell edges, which helps introduce fewer merge errors. However, U‐Net also see edges where it should not, leading to more splitting errors as well (Fig. 4a). Computationally, two main differences between the methods are the use of multiresolution and how spatially coarse feature maps are created. However, we did not investigate the impact on performance of these or other differences (such as filter sizes) in detail in this work.

More Training Data Improves Accuracy and Reduces Errors

We found that training deep learning models with just two images performs already more accurately than an advanced CellProfiler pipeline (Fig. 5a). This is consistent with previous experiments conducted in the DeepCell study 17, demonstrating that the architecture of neural networks can be designed and optimized to perform well in the small data regime. Since training a CNN requires the additional effort of manually annotating example images for learning, limiting the investment of time from expert biologists is valuable.

Figure 5.

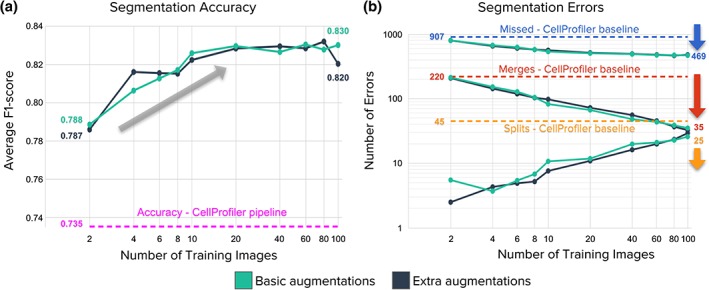
Impact of the number of annotated images used for training a U‐Net model. Basic augmentations include flips, 90° rotations, and random crops. Extra augmentations include the basic plus elastic deformations. (a) Accuracy improves as a function of the number of training images, up to a plateau around 20 images (representing roughly 2,000 nuclei). (b) Segmentation errors are reduced overall as the number of training images increases, but the impact differs for merges versus splits. The advanced CellProfiler pipeline is shown as dotted lines throughout. Results are reported using the validation set to prevent over‐optimizing models in the test set (holdout). For all experiments, we randomly sampled (with replacement) subsets (n = 2, 4, 6, 8, 10, 20, 40, 60, 80, 100) of images from the training set (n = 100) and repeated 10 times to evaluate performance. Data points in plots are the mean of repetitions. Although the percent overlap between the random samples increases with increasing sample size, and is 100% for n = 100, we nonetheless kept the number of repeats fixed (=10) for consistency. The numbers below each arrow indicate the reduction in number of errors for each category of errors. [Color figure can be viewed at wileyonlinelibrary.com]

Data augmentation plays an important role for achieving good generalization results with a small number of images. DeepCell classifies the center pixel of cell‐sized patches, creating a large dataset with thousands of examples obtained from each image. Basic augmentations include image rotations, flips, contrast, and illumination variations. When combined all together, it results in thousands of training points drawn from an image manifold around the available annotated examples. U‐Net follows a similar approach but using larger crops and additional data augmentation based on elastic deformations.

Providing more annotated examples improved segmentation accuracy and reduced the number of errors significantly (Fig. 5). Accuracy improves with more data, gaining a few points of performance as more annotated images are used, up to the full 100 images in the training set (Fig. 5a). We found little difference in this trend whether using basic data augmentation versus using extra augmentations based on elastic deformations.

Segmentation errors are reduced significantly with more annotated examples, by roughly half (Fig. 5b), but as above, even training with two images produces results better than the advanced CellProfiler baseline. Touching nuclei particularly benefit from more training data, which helps to reduce the number of merge errors. As a model learns to fix difficult merge errors by correctly predicting boundaries between touching objects, a trade‐off occurs: some split errors appear in ambiguous regions where no boundaries should be predicted. This effect makes the number of split errors increase with more data, albeit at a slower rate and representing a very small fraction of the total number of errors, while being still fewer than the number of splits made by the advanced CellProfiler pipeline.

Providing a Variety of Training Images Improves Generalization

Preventing overfitting is an important part of training deep learning models. In our study, we followed the best practices, discussed in detail in the DeepCell work, to mitigate the effect of overfitting: (a) collection of a large annotated dataset for training; (b) the use of pixel normalization and batch normalization to control data and feature variations, respectively; (c) the adoption of data augmentation; (d) weight decay to control parameter variations. Besides all these known strategies, we also found that including example images with technical variations in the training set (such as experimental noise or the presence of artifacts) can prevent overfitting, serving as an additional source of regularization.

We found that training with images that exhibit different types of noise produces models that transfer better to other sets (Fig. 6a). In contrast, training on an image set that has homogeneous acquisition conditions does not transfer as well to other experiments (Fig. 6b). We tested U‐Net models trained on one image set and evaluated their performance when transferring to another set. In one case we took images of nuclei from a prior study (“Van Valen's Set”)17, representing different experiments and including representative examples of diverse signal qualities, cell lines, and acquisition conditions (Fig. 6d). In the other case we used the BBBC039 image collection which exhibits homogeneous signal quality and was acquired under similar technical conditions (Fig. 6c).

Figure 6.

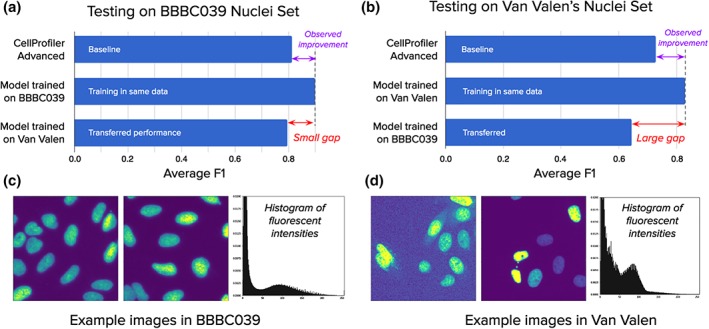
Signal quality is the main challenge when transferring models across experiments: Performance differences when models are trained and evaluated in different experiments. (a) Models evaluated on the BBBC039 test set, including a U‐Net trained on the same set, another U‐Net trained on Van Valen's set, and a CellProfiler pipeline. The results indicate that transferring the model from one screen to another can bring improved performance. (b) Models evaluated in Van Valen's test set, including CellProfiler baselines adapted to this set, a U‐Net trained on the same set, and another U‐Net trained on BBBC039. The results illustrate the challenges of dealing with large signal variation. (c) Example images from BBBC039 showing homogeneous signal with uniform background, which is reflected in the aggregated histogram of fluorescent intensities for this dataset, with a bimodal distribution and easily separable peaks. (d) Example images from Van Valen's set illustrating various types of realistic artifacts, such as background noise and high signal variance, also observed in the corresponding histogram with higher density between the peaks of the bimodal distribution. Number of training images: 100 in BBBC039 and 9 in Van Valen. Number of test images: 50 in BBBC039 and 3 in Van Valen. [Color figure can be viewed at wileyonlinelibrary.com]

A model trained only on the 9 diverse images of Van Valen's set generalizes well to test images in BBBC039, improving performance over the baseline (Fig. 6a) and reaching comparable performance to the model trained on BBBC039 training images. Note that training a network on images of BBBC039 improves performance with respect to the CellProfiler baseline. The transferred model does not fix all the errors, likely because the number of training examples is limited. Nevertheless, the transferred performance indicates that it is possible to reuse models across experiments to improve segmentation accuracy.

A transfer from the more homogenous BBBC039 set to the more diverse Van Valen's set is less successful: a model trained with 100 examples from the BBBC039 set fails to improve on the test set of Van Valen's images despite the availability of more data (Fig. 6b). This demonstrates the challenges of dealing with varying signal quality, which is a frequent concern in high‐throughput and high‐content screens. The large gap in performance is explained by varying signal conditions (Fig. 6c,d): because the model did not observe these variations during training, it fails to correctly segment test images.

The CellProfiler pipelines also confirm the difficulty of handling noisy images. A single pipeline cannot deal with all variations in Van Valen's test set, requiring the adjustment of advanced settings and the splitting of cases into two different pipelines. In BBBC039, a single pipeline works well due in part to the homogeneity of signal in this collection; the errors are due to challenging phenotypic variations, such as tiny nuclei or clumped objects.

Deep Learning Needs More Computing and Annotation Time than Classical Methods

Although we found the performance of deep learning to be favorable in terms of improving segmentation accuracy, we also found that this comes at higher computational cost and annotation time. First, deep learning requires significantly more time to prepare training data with manual annotations (Fig. 7a). Second, deep learning needs the researchers to train a model and tune its parameters (Fig. 7b), usually with special hardware. Third, when a model has been trained, it is slower to run on new images than classical algorithms (Fig. 7c). However, running times can be accelerated using graphic cards, which makes the technique usable in practice.

Figure 7.

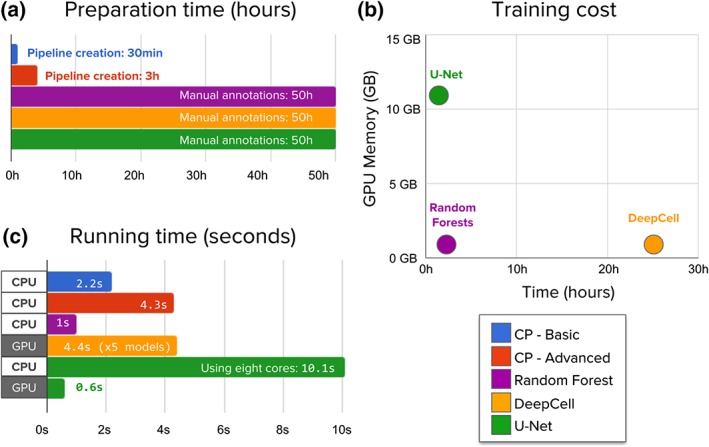
Evaluation of the time needed to create annotations, train, and run segmentation models. (a) Preparation time measures hands on, expert time annotating images or creating CellProfiler pipelines. Manually annotating 100 training images with about 11,500 nuclei requires significantly longer times. (b) Machine learning models need to be trained while CellProfiler pipelines do not need additional processing. Neural network training was run on a single NVIDIA Titan X GPU. DeepCell trains an ensemble of five models, which was used in all evaluations. (c) CellProfiler pipelines and Random Forests are run on new images using CPU cores to measure the computational cost of segmenting a single image. Deep learning needs significantly more resources to accomplish the task, but can be accelerated using GPUs, which have thousands of computing cores that allow algorithms to run operations in parallel. This reduces significantly the elapsed time, making it practical and even faster than classical solutions. [Color figure can be viewed at wileyonlinelibrary.com]

We observed that the time invested by experts for annotating images is significantly longer than configuring CellProfiler segmentation pipelines (Fig. 7a). We estimate that manually annotating 100 images for training (~11,500 objects) takes 50 h of work using an assisted‐segmentation tool. In contrast, a basic CellProfiler pipeline can be calibrated in 15–30 min of interaction with the tool, setting up a configuration that even users without extensive experience nor computational expertise could complete. CellProfiler is very flexible and allows users to add more modules in order to correct certain errors and factor out artifacts, creating an advanced pipeline that can take from 1 to 3 h.

Training deep learning models takes substantial computing time on GPUs, while CellProfiler pipelines do not need any additional training or postprocessing (Fig. 7b). In our study, the deep learning models under evaluation are big enough to need a GPU for training, but light enough to be trained in a few hours. In particular, a U‐Net can be trained in a single NVIDIA Titan X GPU in just 1 h, while DeepCell takes 25 h for an ensemble of five networks (as suggested in the original work 17). Also, training models may need preliminary experiments to calibrate hyperparameters of the neural network (e.g., learning rate, batch size, epochs), which adds more hands‐on time.

Notice the trade‐off between memory and training time of deep learning models. DeepCell trains a compact neural network with small memory requirements, which makes it ideal for running experiments efficiently in modest hardware configurations. This design has the additional advantage of allowing strategic pixel sampling for training, resulting in a balanced selection of pixels from the background, boundary, and interior of cells. In contrast, U‐Net trains larger neural network models that process all the pixels simultaneously using a fully convolutional approach resulting in high memory requirements and, therefore, needing expensive GPU hardware for training. This can be constraining for laboratories not equipped to run computationally heavy experiments.

When segmenting new images using CPU cores, deep learning models are slower than CellProfiler pipelines (Fig. 7c). The computational complexity in terms of space (memory) and time (operations) of a CNN is proportional to the number of layers, the number of filters, and the size of images. As these architectures get deeper and more complex, they involve more operations to produce the final result, and thus require more computing power. This is in contrast to classical segmentation algorithms whose thresholding and filtering operations have relatively limited computing requirements that scale well with the size of images. Even with 8 times more cores, a U‐Net takes 10.1 s to segment a single image, which results in about 20 times more computing power requirements than the advanced CellProfiler pipeline. CellProfiler pipelines are run in a single CPU core and take 2.2 and 4.3 s for the basic and advanced pipelines respectively.

Using GPU acceleration can significantly speed up the computations of deep learning models, making them very usable and efficient in practice (Fig. 7c). Segmenting a single image with a U‐Net model takes only 0.6 s on a Nvidia Titan X GPU, improving computation times by a factor of 16×. Note that no batching was used for prediction, which can accelerate computation of groups of images even further. In our experiments, a single DeepCell network ran at 4.4 s per image with GPU acceleration, which has been sped up using a custom implementation of dilated convolution and pooling operations in Theano. Even faster versions of these operations are available in modern deep learning frameworks, such as TensorFlow. These results show that deep learning models are faster than classical algorithms when using appropriate hardware and efficient implementations.

Better Segmentations Improve High‐Content Cytometry Screens

Accurate nucleus segmentation improves the sensitivity of cytometry screens in real world high‐throughput applications. To quantify this effect, we evaluated the performance of the segmentation using the Z’‐factor in a high‐content experiment. The goal of this experiment is to identify compounds that disrupt normal cell cycle, thus, we measured the DNA content of single cells using the total integrated intensity within each segmented nucleus as a readout.

We selected a subset of 10 compounds screened with high‐replicates in the BBBC022 image collection (Fig. S3) to measure their effect to the cell cycle compared to DMSO treated wells (negative controls). For each image, we measured the integrated intensity of nuclei and estimated the proportion of cells with 4N DNA content. After controlling for potential batch effects, we observed that none of the compounds yield a sufficiently high Z’‐factor that indicates cell cycle disruption. It should be noted that the compounds selected are not known to have effects on the cell cycle—thus, we did not expect them all to yield a detectable phenotype in this assay. However, the measurements were a good choice for our purposes, because we wanted a nucleus‐based readout whose baseline quality was not so high so as to leave no room for improvement with better segmentation. For 7 out of the 10 selected compounds we observed improved Z’‐factor scores when the segmentation was carried out with a deep learning model, indicating more sensitivity of the screen for detecting interesting compounds.

Other studies have also observed improved assay quality when using deep learning for cell segmentation. For instance, analyzing the structure of tumors in tissues using multiplexed ion beam imaging reveals the spatial organization and response of immune cells in cancer patients 50. These results were obtained with a computational workflow powered by the DeepCell library, demonstrating that deep learning can accurately segment single cells in challenging imaging conditions.

Discussion

Previous studies of cell segmentation observed minor improvements when comparing deep learning methods versus classical algorithms using the Jaccard index 17. Also, a recent cell tracking challenge analysis noted that thresholding approaches are still the top solutions for segmenting cells 19; their ranking score is also the Jaccard index. We argue that these evaluation methods do not satisfactorily capture biologically important error modes, making it difficult to appropriately assess cell and nuclei segmentation algorithms. We presented an evaluation framework focused on object level accuracy, which captures biological interpretations more naturally than pixel‐level scores (Fig. S1).

The objects of interest in biology are full instances of nuclei that experts can identify by eye. Our results show that deep learning strategies improve segmentation accuracy and reduce the number of errors significantly as compared to baselines based on classical image processing and machine learning. However, we show that these methods still make mistakes that experts do not. Being able to quantify these mistakes explicitly will drive future research toward better methods that could match human performance. In our benchmark, deep learning provided improved performance in all the tests that measured accuracy and error rates. Despite requiring significant annotation effort and computational cost, deep learning methods can have a positive impact on the quality and reliability of the measurements extracted from fluorescence images.

Improved Accuracy

The proposed evaluation metrics are able to distinguish biologically meaningful errors, helping to better differentiate the performance of segmentation models. The results of our benchmark show that deep learning methods can bring significant advantages for segmenting single objects in new images, compared to manually configured image processing algorithms and classic machine learning. Both DeepCell and U‐Net are able to improve the segmentation accuracy (Figs. 2 and S1) and reduce the total number of errors (Figs. 3, 4, and S2). This shows that even though these models were created for generic cell segmentation and optimized for learning from small datasets, they can be trained to successfully identify nuclei using large sets of images.

The analysis of errors indicates that deep learning can fix most of the segmentation errors observed in classical algorithms, especially merges. One special type of error that represents a challenge for both deep learning models is the segmentation of tiny nuclei (micronuclei and other debris, if of interest in an experiment). In extensive experiments conducted in the DeepCell study 17, the size of the receptive field has been shown to be a key parameter to improve performance, suggesting that crops that fully cover single cells are sufficiently informative for accurate segmentation. Increasing the resolution of images, either during acquisition 51 or with computational methods such as resizing images to make objects look bigger, may help fix these errors. Alternatively, different loss functions adapted to this problem might be designed.

Training Data

In our evaluation, the amount of training data was shown to be an important factor to reduce the number of errors. Our results confirm that training a neural network with only a few images is enough to get improved performance relative to nondeep learning baselines. However, in order to improve accuracy and leverage the learning capacity of deep learning models, more data is required. Importantly, a neural network can also be reused across experiments, as long as the training data incorporates variations in morphological phenotypes as well as variations in signal quality and acquisition conditions.

Datasets used for training supervised machine learning models are prone to contain human errors and subjective biases. Errors include accidentally overlooking real objects, and biases include differences in opinion about precise boundaries. We used multiple annotators for practical reasons and also to reflect real differences of opinion among biologists. When multiple annotators are used, it is recommended to agree upon best practices to minimize errors and curate useful ground truth. A useful dataset is one that has enough examples of varied situations and where the real signal is not dominated by subjective noise. We believe our dataset is such a resource, where biologists agreed on covering all possible nuclei phenotypes and worked hard to be as consistent as possible, while allowing for individual variation that might arise from subjectivity or even screen brightness during annotation. Although assigning two or more annotators to the same image can create a very high‐quality dataset, given the amount of inherent subjectivity among annotators, we decided it would be more useful to have twice the amount of good‐quality ground truth with a single annotator per image. Future efforts to fix existing issues and to expand the dataset would be welcome.

We argue that a single deep learning model might be constructed to address all the challenges of nucleus segmentation in fluorescence images if a diverse database of annotated examples were to be collected to incorporate these two critical axes of variation. We advocate for collecting that data collaboratively from different research labs, so everyone will benefit from a shared resource that can be used for training robust neural networks. We have begun such an effort via the 2018 Data Science Bowl https://www.kaggle.com/c/data-science-bowl-2018/.

Computational Cost

Deep learning models generally run a higher computational cost. GPUs can be useful in microscopy laboratories for accelerating accurate neural network models; if acquisition or maintenance is prohibitive, cloud computing allows laboratories to run deep learning models using remote computing resources on demand. Adopting these solutions will equip biologists with essential tools for many other image analysis tasks based on artificial intelligence in the future.

Author Contributions

JCC contributed experiments, data analysis, software development, and manuscript writing. JR contributed experiments, data preparation, data analysis, and software development. AG contributed experimental design, data preparation, and software development. TB contributed experiments, software development, and manuscript writing. KWK contributed experiments, data preparation, and data analysis. MB contributed experiments and data analysis. MC contributed experiments. CM contributed data preparation and software development. SS contributed experimental design and manuscript writing. FT contributed experimental design and manuscript writing. AEC contributed experimental design, data interpretation, and manuscript writing.

Supporting information

Data S1 The main dataset in this paper, BBBC039, was split in three subsets, using 50% of the images for training, 25% for validation, and 25% for testing (holdout set). All optimization steps of the deep learning strategies were tuned using the training and validation sets, and the reported results are obtained with final evaluations using the holdout test set (unless otherwise indicated). We evaluate five segmentation strategies, two based on deep learning, one based on classical machine learning, and two baseline pipelines based on the CellProfiler software. The deep learning strategies are U‐Net (16), representing a family of neural networks originally designed for segmentation; and DeepCell (17), representing another family of neural networks for patch‐based, pixel‐wise classification. Random Forest was selected as the classical machine learning algorithm using the implementation provided by Ilastik (10), which is specialized for segmentation. The baseline segmentation pipelines include an advanced settings mode and a basic settings mode. With trained deep learning models and calibrated CellProfiler pipelines, we proceeded to segment all images in the test set. To evaluate and compare the estimated masks we use the average F ₁‐score and modes of error.

Data S2 The following are the post‐processing steps used to recover single object instances from pixel classification probability maps: (a) max‐binarization: the prediction for each pixel is a three‐way probability distribution. These predictions are binarized by assigning 1 to the category with maximum probability and 0 to the rest. (b) Isolation of the interior channel. The other channels only serve the purpose of indicating where the boundaries and background are located, thus they are ignored after determining binary values for each pixel. (c) Use the connected components algorithm (33) to label single objects in the interior channel. After removing the boundaries and background, single nuclei are separated in a binary map. Each of these regions is assigned a different number. (d) Dilation of single objects. The dilation morphological operation (34) is applied to all objects using a square structuring element of 3 × 3 pixels to compensate for the loss of boundaries. This procedure was used for the two evaluated deep learning models: DeepCell and U‐Net. No additional boundary refinement algorithms––such as watershed or similar––were applied.

Figure S1 F ₁‐score has better resolution for detecting performance differences than the Jaccard index. In addition, the F ₁‐score is penalized by biologically relevant errors that can be explained in terms of missing, merged and split objects. (a) F ₁‐score and Jaccard index are highly correlated measures of segmentation performance, but F ₁‐score displays more resolution to distinguish biologically meaningful errors. Each dot in the plot is an image in the test set segmented with the CellProfiler advanced pipeline. (b) Example images that get similar Jaccard indexes but have very different segmentation errors as shown by the yellow arrows. F ₁‐score captures these differences more naturally, which is explained by the number of false negatives resulting from the merges. (c) Performance of the evaluated methods on the entire test set. The Jaccard index reports little difference between the two CellProfiler baselines, and also between Random Forest and the two deep learning methods. With average F ₁‐score, the biologically relevant errors are measured more explicitly, and performance differences can be observed more clearly.

Figure S2 Total number of missed (false negative) and extra (false positive) objects generated by each segmentation model in the test set. The total number of objects in the test set is 5,720. Deep learning algorithms reduce both missed and extra objects with respect to the baseline. U‐Net misses 47% less objects than the CellProfiler advanced pipeline, while Random Forest misses 6% more. Similarly, DeepCell introduces 77% less extra objects, providing cleaner segmentations. Deep learning algorithms display a tradeoff between accurately recovering all relevant objects and not introducing segmentation artifacts (by splits or debris).

Figure S3 Z’‐factor values for a set of 10 compounds selected for evaluation. (a) The Z’‐factor values indicate whether a compound has an observable cell cycle disruption in a population of cells with respect to negative controls. To compute the Z’‐factor, images are first segmented using CellProfiler or a U‐Net model. Then, the DNA content is measured within each nucleus using the integrated intensity of pixels. The distribution of DNA content reflects the expected 2N/4N cell cycle. (b) Z’‐factor values obtained for the two evaluated methods. Higher values are better. (c) Scatter plot of the values reported in b. The y axis presents the result obtained with deep learning and the x axis presents the result with CellProfiler segmentations.