Structure and Energetics of Ligand–Fluorine Interactions with Galectin‐3 Backbone and Side‐Chain Amides: Insight into Solvation Effects and Multipolar Interactions

Abstract

Multipolar fluorine–amide interactions with backbone and side‐chain amides have been described as important for protein–ligand interactions and have been used to improve the potency of synthetic inhibitors. In this study, fluorine interactions within a well‐defined binding pocket on galectin‐3 were investigated systematically using phenyltriazolyl‐thiogalactosides fluorinated singly or multiply at various positions on the phenyl ring. X‐ray structures of the C‐terminal domain of galectin‐3 in complex with eight of these ligands revealed potential orthogonal fluorine–amide interactions with backbone amides and one with a side‐chain amide. The two interactions involving main‐chain amides seem to have a strong influence on affinity as determined by fluorescence anisotropy. In contrast, the interaction with the side‐chain amide did not influence affinity. Quantum mechanics calculations were used to analyze the relative contributions of these interactions to the binding energies. No clear correlation could be found between the relative energies of the fluorine–main‐chain amide interactions and the overall binding energy. Instead, dispersion and desolvation effects play a larger role. The results confirm that the contribution of fluorine–amide interactions to protein–ligand interactions cannot simply be predicted, on geometrical considerations alone, but require careful consideration of the energetic components.

Introduction

The success of structure‐based ligand design is closely tied to structural information about the biological target and biophysical understanding of the molecular recognition processes. Analysis of protein–ligand complexes by X‐ray crystallography provides structural information, and fluorescence polarization (FP) or other methods such as isothermal titration calorimetry can provide affinity and thermodynamic data. Quantum chemical calculations of selected subsets of the ligand atoms can provide valuable information about the different energetic components that contribute to the enthalpy and entropy of binding. Organofluorine compounds are common in drug discovery because fluorine atoms are known to have diverse effects on the physicochemical and conformational properties of ligands. Introduction of fluorine atoms at key positions in ligands has been proven to be a promising strategy in lead optimization.1 The position and degree of fluorination can have a strong effect on protein–ligand interactions.1, 2 Fluorines impart increased hydrophobicity, and the highly polarized C−F bond can form dipole–dipole interactions with moieties in the protein that have a partial positive charge. Such distinct fluorophilic environments in proteins are peptide bonds, which can participate in multipolar C−F⋅⋅⋅H−N, C−F⋅⋅⋅C=O, and C−F⋅⋅⋅H−Cα interactions, as well as the side‐chain amide moieties of Asn and Gln.3 Fluorines enhance ligand affinity by interacting with both the polar electropositive and the hydrophobic groups in proteins.4 In particular, orthogonal multipolar C−F⋅⋅⋅C=O interactions with both peptide backbone and side‐chain carbonyl groups have been described as important for fluorine. Amides are abundant in proteins, and orthogonal multipolar fluorine–amide interactions between ligand fluorines and backbone amides (Figure 1 a) have been reported.1, 3, 4, 5 The fluorine–amide interaction is proposed to arise from an attractive dipole interaction between the C−F and C=O groups,1 and the geometric preferences have also been determined in a model system6 using chemical double‐mutant cycles. At shorter F⋅⋅⋅C=O distances (<3.0 Å), the F⋅⋅⋅C=O angle (denoted a2 in Figure 1 a) tends toward 90°,1 whereas at longer distances, the angular dependence is weaker. The C−F⋅⋅⋅C=O angle (denoted a1 in Figure 1 a) is more variable.1 In apolar environments, the orthogonal multipolar fluorine–amide interaction with backbone amides can contribute −0.8 to −1.5 kJ mol⁻¹ in binding free energy (ΔΔG).6

Figure 1.

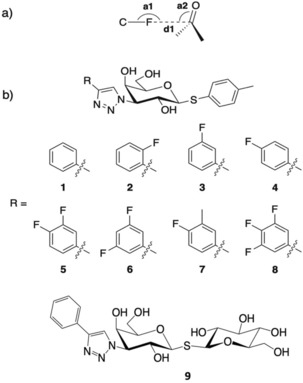
a) Schematic view of an orthogonal fluorine–amide interaction with a backbone amide with the F⋅⋅⋅C=O distance d1 and the C−F⋅⋅⋅C and F⋅⋅⋅C=O angles of the interaction indicated by a1 and a2 respectively. b) Chemical structures of thiogalactosides 1–9.

Fluorine–amide interactions with side‐chain amides, for example in asparagine and glutamine, are less discussed in the literature, but a Protein Data Bank (PDB) search in 2007 revealed several such interactions.3 Based on a statistical analysis, the angular dependence is weaker for side‐chain amides than in backbone amides. The C−F⋅⋅⋅C=O angles (a1 in Figure 1 a) were <120°, whereas the F⋅⋅⋅C=O angles (a2) were 60°<a2<150°. Furthermore, fluorine–side‐chain amide interactions found in database searches are described as being “frontal”, that is, approaching the amide group approximately in the same plane rather than laterally.3

Systematic studies of the contribution of fluorine–amide interactions to ligand affinity are relatively infrequent. One early study on tricyclic thrombin inhibitors showed that the introduction of a single such interaction could improve the IC₅₀ value by a factor of five.7 A more recent analysis on two regions of a ligand binding pocket in the protein menin showed good correlation between the introduction of fluorine atoms that were well poised to make such orthogonal multipolar interactions and modest increases in inhibition of protein–peptide interactions.4 The same study analyzed eight previously determined systems containing such interactions and found a positive relationship between fluorine–amide interactions and affinity for six of them (2‐ to 24‐fold increases). In contrast, for two systems the introduction of such interactions could be related to modest decreases in inhibitory activity, leading to the conclusion that predictions based solely on geometrical criteria may have limitations.4

Galectin‐3 is a β‐d‐galactopyranoside‐binding protein that, by cross‐linking glycoconjugates, plays important roles in modulating the behavior of proteins in, for example, the immune system,8 as well as in tumor growth and metastasis.9 Fluorinated phenyltriazolyl‐thiogalactosides have been reported with varying galectin‐3 affinities, depending on the position of the fluorine atom.5 A binding pocket for the aryl moiety of 3‐substituted galactosyl inhibitors is created by displacement of the side chain of Arg144 from a water‐mediated salt bridge on the protein surface such that it stacks on top of the aryl moiety. Within this pocket, the position of the aryl group is relatively invariant. This pocket in galectin‐3C presents an excellent model system for a thorough study of fluorine–amide interactions due to the presence of several appropriately oriented main‐chain and side‐chain amide groups. To study the geometric and energetic differences in fluorine interactions with backbone and side‐chain amides, herein we report structural and quantum mechanical analyses of the galectin‐3 C‐terminal domain (galectin‐3C) binding to eight monosaccharide ligands singly or multiply substituted at the ortho, meta, and para positions of a phenyl group (Figure 1) such that the fluorine atoms are oriented toward either backbone or side‐chain amides in the pocket.

Results

Ligand affinity measurements by fluorescence polarization

The affinities of 1–9 were measured using fluorescence polarization (Table 1).10 The K _d values for 1–8 have already been published,5 but they are reproduced in Table 1 for clarity.

Table 1.

Affinities of ligands 1–9 as measured by fluorescence polarization.

Ligand	R	K d [μm]5
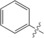
1		88±3
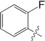
2		92±5
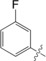
3		22±0.7
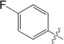
4		31±1.3
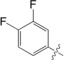
5		8.8±0.3
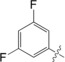
6		15±0.3
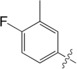
7		23±1.0
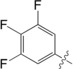
8		5.2±0.3
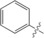
9 [a]		4.5±0.2

[a] The affinity of compound 9 is not directly comparable with the others due to its glucose moiety.

The unsubstituted phenyl group in 1 has a K _d value of 88±3 μm. Addition of fluorine at the ortho position in 2 has no effect on affinity (92±5 μm). In contrast, a fourfold improvement in affinity (22±0.7 μm) is gained by the addition of fluorine at the meta position in 3, and approximately threefold (31±1.3 μm) by para‐addition in 4. The combination of meta‐ and para‐fluorines in 5 gives a further 2.5‐ to 3.5‐fold improvement over the single substitutions (8.8±0.3 μm). Combination of two meta substitutions in 6 has a more modest 1.5‐ to 2‐fold effect (15±0.3 μm). The trisubstituted m,p,m compound 8 has the highest affinity, at 5.2±0.3 μm. The combination of a meta‐methyl group with a para‐fluoro group in 7 gives slightly better affinity than the single para‐fluoro substitution in 4 (23±1.0 vs. 31±1.3 μm).

Structural analysis of galectin‐3C in complex with thiogalactosides 2–9

X‐ray structures for thiogalactosides 2–9 in complex with galectin‐3C were obtained at very high resolution (Table S1, Supporting Information), with excellent electron density for all compounds (Figure S2), revealing highly similar binding modes of the galactose and phenyltriazole units (Figure 2), with all phenyl rings coplanar, as observed in thiodigalactoside complexes reported earlier.11 In contrast, electron density for the p‐tolyl moiety was poorly defined, presumably due to rotational disorder. We could not obtain a structure of the complex with compound 1 because of its limited solubility. Thus, we modified ligand 1 by replacing the p‐tolyl group with a glucopyranosyl moiety (9), which increased the solubility without affecting the binding mode in the Arg144 pocket. The binding mode of 9 is shown in Supporting Information Figure S3 to avoid any confusion, as it is overall slightly different from the rest of the ligands. We use the more soluble glucose analogue 9 as a proxy for 1 in the following discussions. In all of the crystal structures with 2–9, the protein side chains in the binding pocket have identical conformations, with the exception of the flexible Arg144, which exhibits relatively high B‐factors in all structures, and which was found to move slightly along the top face of the phenyl moiety.

Figure 2.

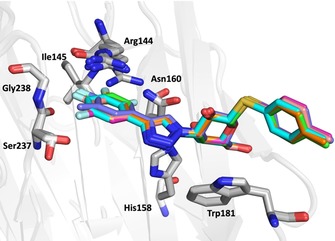
Binding mode of ligands 2–8 in the pocket bounded by the side chains of Arg144, Asn160, and Ala146 (the latter not shown), as well as the main‐chain atoms of Arg144, Ile145, Ser237, and Gly238. Key residues are labeled.

The crystal structures (Figures 2 and Figure 3) of the three monofluorinated phenyltriazoles 2–4 confirmed previously reported orthogonal multipolar fluorine–amide interactions with backbone amides.5, 11 The meta‐fluorine in 3, positioned 3.0 and 3.5 Å from the carbonyl carbon atoms of Ile145 and Arg144, respectively, forms potential fluorine–amide interactions with each backbone amide. For these interactions, the a1 and a2 angles are 154.5°/100.3° and 137.6°/89.5°, respectively. Thus, both interactions are near‐orthogonal (a2≈90°). The para‐fluorine in 4, 3.2 Å from the carbonyl carbon of Ser237, forms one orthogonal fluorine–amide interaction with the backbone amide of Ser237, with angles a1=132.1° and a2=89.7°. Moreover, it also makes a favorable C−F⋅⋅⋅H−Cα interaction with the α‐carbon of Gly238, as the observed distance between the fluorine and hydrogen atoms on the α‐carbon is only 2.9 Å (Figure 3 c). In contrast, the ortho‐fluorine in 2 is not directed toward any backbone amide, but is positioned 3.5 Å (F⋅⋅⋅C distance) from the side‐chain amide of Asn160, oriented almost orthogonally, suggesting a fluorine–amide interaction. The orientation of Asn160 is unambiguous due to a hydrogen bond between its side‐chain carbonyl group and the side chain of Arg162 (not shown). Superimposing the crystal structures (Figure 3 d) reveals a slight inward shift of the phenyl ring with the para‐fluorine in 4, relative to the others, due to the lack of bulky atoms on the protein‐facing side, which may optimize the interactions of the para‐fluorine with Ser237 and Gly238.

Figure 3.

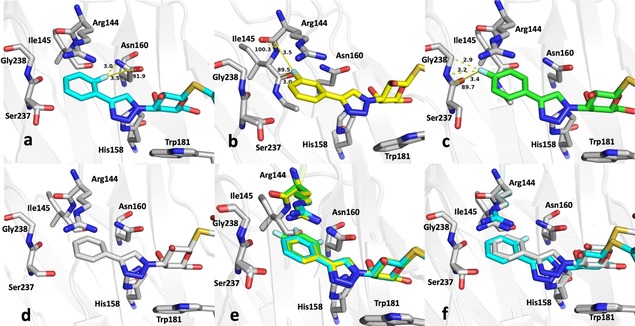
Close‐up view of the fluorinated phenyl moiety in the crystal structures of galectin‐3C in complex with phenyltriazoles a) 2, b) 3, c) 4, d) 9, e) 2, 3 and 4, and f) 2 and 9. Key fluorine interactions described in the text are indicated with yellow dashed lines. Distances and F⋅⋅⋅C=O angles a2 are shown in panels a)–c).

The crystal structures allow partial rationalization of the affinities of compounds 1–8 for galectin‐3. The meta and para analogues 3 and 4 had similar affinities: K _d=22 μm for 3 and 31 μm for 4. On the other hand, the affinity of the ortho analogue 2 was 3‐ to 4‐fold lower (K _d=92 μm), in fact no better than that of the unsubstituted phenyl compound (1, K _d=88 μm),5 which suggests a lack of a favorable fluorine–amide interaction with the side‐chain amide of Asn160. Figure 3 f compares the binding of 2 and 9 (equivalent to 1, except for the solubility‐enhancing glucose group distant from the binding pocket). The unsubstituted ligand 9 binds slightly further toward the interior of the binding pocket due to the lack of a fluorine atom on the inward‐facing side.

To investigate the observed additive effect on binding affinity of the fluorine interactions of 3 and 4, the crystal structures of the m,p‐difluoro‐ (5), m,m‐difluoro‐ (6), o‐methyl‐p‐fluoro‐ (7), and m,p,m‐trifluorophenyl‐ (8) thiogalactosides (Figure 4) in complex with galectin‐3C were also determined. Orthogonal multipolar fluorine–amide interactions with Arg144, Ile145, and Ser237 and the C−F⋅⋅⋅H−Cα multipolar interaction with the hydrogen at the α‐carbon of Gly238 at a distance of 2.9 Å were observed as in the singly substituted compounds (Figure 4). Compound 5 has both meta‐ and para‐fluorine atoms, and it recapitulates both the expected interactions from the monosubstituted compounds (Figure 4 a). Compound 6 has two meta‐fluorines, of which only the inward‐facing one makes a fluorine–amide interaction, correlating with its similar binding affinity to that of meta compound 3. The affinity of the m,p,m‐trifluorinated compound 8 (K _d=5.2 μm)5 is fourfold higher than for the meta analogue 3 and very similar to that of 5, again suggesting the importance of the inner meta‐ and para‐fluorine atoms, but a negligible contribution from the outer meta‐fluorine. Compound 7 has one methyl group at the meta position, and in the structure (Figure 4 e) the methyl group is found outside the binding pocket for steric reasons and due to the absence of a favorable fluorine–amide interaction.

Figure 4.

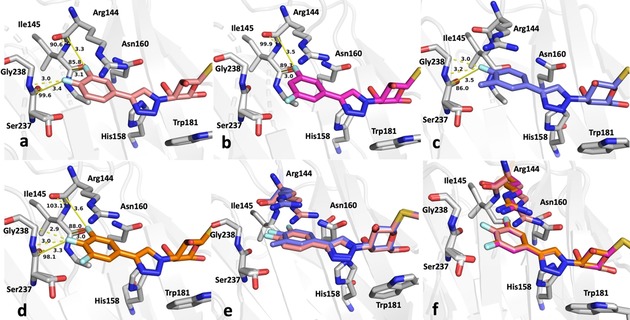
Close‐up view of the fluorinated phenyl moiety in the crystal structures of galectin‐3C in complex with a) 5, b) 6, c) 7, d) 8, and e) 5 and 7. f) Superimposed structures of 5, 6, and 8 show nearly identical modes of binding. Key fluorine interactions described in the text are indicated with yellow dashed lines. Distances and F⋅⋅⋅C=O angles a2 are shown in panels a)–d).

Quantum mechanical calculations

To rationalize the binding properties of the seven thiogalactosides 1–6 and 8, we performed quantum‐mechanical (QM) calculations on the interactions between the corresponding fluoro‐substituted benzene rings and small models of the backbone of Arg144‐Ile145 and Ser237‐Gly238 (both modelled by CH₃NHCOCH₂NHCOCH₃), as well as the side chain of Asn160 (modelled by CH₃C(O)NH₂). Examples of the models are given in Figure 5. The results are presented in Table 2 and Figure 6.

Figure 5.

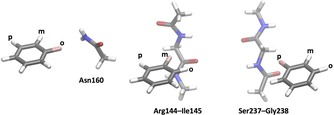
Examples of models used for the QM calculations, showing from left to right, compound 1 with Asn160, compound 2 with Arg144‐Ile145, and compound 3 with Ser237‐Gly238.

Table 2.

Calculated interaction energies between the ligand fragments and the side chain of Asn160, the backbone of Arg144+Ile145, or Ser237+Gly238.^[a]

	ΔG exp [b]	Solv[c]	Dispersion				QM				QM+dispersion
	[kJ mol−1]		Asn	R+I	S+G	Sum	Asn	R+I	S+G	Sum	Asn	R+I	S+G	Sum
2	−23.2	−3.3	−4.7	−9.1	−8.0	−21.8	2.7	1.4	3.2	7.3	−2.0	−7.7	−4.8	−14.6
3	−26.7	−3.3	−5.3	−11.6	−8.3	−25.3	−4.2	1.7	3.5	1.0	−9.5	−9.9	−4.9	−24.3
4	−25.9	−3.3	−7.2	−14.3	−8.6	−30.0	1.9	1.0	2.8	5.7	−5.2	−13.3	−5.8	−24.3
6	−27.7	−2.3	−5.4	−12.0	−8.9	−26.4	−2.5	2.1	2.4	2.1	−7.9	−9.9	−6.5	−24.3
5	−29.0	−2.8	−5.6	−11.7	−8.4	−25.8	−2.7	2.8	2.0	2.1	−8.3	−8.9	−6.5	−23.7
8	−30.3	−1.5	−5.9	−12.0	−8.7	−26.5	−2.5	2.9	1.3	1.7	−8.4	−9.1	−7.4	−24.9
1	−23.3	−3.8	−5.5	−9.8	−6.8	−22.1	1.0	−0.4	1.9	2.5	−4.5	−10.2	−4.9	−19.7
R [d]		−0.85	0.24	0.54	0.72	0.57	0.75	−0.87	0.48	0.60	0.82	−0.05	0.89	0.79
slope[d]		−0.2	0.1	0.3	0.2	0.6	0.8	−0.4	0.1	0.5	0.8	0.0	0.3	1.1

[a] The energies are divided into dispersion (DFT‐D3) and QM contributions, as well as their sums. [b] The second column contains the measured binding free energy from the fluorescence polarization experiments. [c] The third column lists the calculated COSMO‐RS solvation free energy values. [d] The last two rows contain the correlation (R) between the calculated energy and the experimental binding free energy and its slope.

Figure 6.

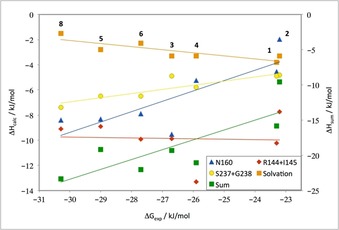
Calculated QM interaction and solvation energies for the seven substituted benzene groups plotted on the y‐axis against the experimental binding free energy on the x‐axis. Interaction energies were calculated for the three amino acid models shown in Figure 5, that is, with models of the side chain of Asn160, the backbone of Arg144‐Ile145 or the backbone of Ser237‐Gly238. “Sum” is the sum of these three interaction energies minus the solvation energy of the ligand and with an entropy penalty of 1.7 kJ mol⁻¹ for the asymmetric ligands; it is shown on the right‐hand‐side axis. Best‐fit lines are shown in the same color as the symbols for each set of data.

The calculations conclusively confirm that the interaction between the ortho‐fluoro substituent in 2 and Asn160 does not improve the affinity relative to the other ligands. The calculated interaction energy is favorable, but only by 2 kJ mol⁻¹, which is less than for the corresponding interaction energy between Asn160 and the other compounds (−4 to −10 kJ mol⁻¹). In particular, the meta‐fluorine has an interaction energy with Asn160 that is almost five times that of the ortho‐fluorine. There is a reasonable correlation between the interaction energies of the various model compounds with Asn160 and the experimentally measured net binding free energy (R=0.82; the slope of the correlation line is 0.8), but the effect is largest for the monosubstituted compounds (Figure 6). This is probably because the fluorine atom in 2 is in a far‐from‐ideal geometry. In fact, it is closer to the side‐chain nitrogen atom of Asn160 (3.0 Å), which has a partial negative charge like the fluorine, than it is to the side‐chain carbon atom (3.5 Å) and also quite close to the side‐chain oxygen atom (2.7 Å) with a strongly negative charge. In the other ligands, instead a phenyl hydrogen atom, with a positive partial charge, resides at this position, giving more favorable interactions. Moreover, the meta‐fluorine atom in 3 is rather close to one of the amide hydrogen atoms (3.4 Å), giving an additional attractive interaction. The above observations show that it is hard to interpret fluorine interactions from individual distances in crystal structures.

There is also a good correlation between the interaction energies of the various fluoro‐substituted benzene rings with the backbone model of the Ser237‐Gly238 dipeptide (R=0.89) and the binding free energy, but with a slope of only 0.3. The interaction energies are slightly larger for the para‐substituted compound 4 than for those with an ortho, meta, or no substituent (2, 3, and 1). However, the difference is only 1 kJ mol⁻¹.

On the other hand, we found no correlation between the binding free energies and the interaction energies between the seven ligands and the Arg144‐Ile145 dipeptide. In particular, the meta‐substituted model system does not give the strongest binding to this dipeptide (−10 kJ mol⁻¹), as was expected from the crystal structure. It is stronger than that of the corresponding ortho‐fluorinated system (−8 kJ mol⁻¹), but is weaker than both the corresponding para system (−13 kJ mol⁻¹) and the unsubstituted benzene molecule (−11 kJ mol⁻¹). The reason for this is probably that the partial charge of the fluorine atom (obtained by a fit to the QM electrostatic potential sampled with the Merz–Kollman approach)12 is actually slightly smaller than that of the hydrogen atoms on the phenyl ring (e.g., −0.30 e for F in 3, compared with 0.35 e on the H atom in 4 that is directed toward the amide groups). Moreover, many atoms of both positive and negative charge are close to the fluorine or hydrogen atoms in these orthogonal interactions (for 3, the distance to the carbonyl C atom is 3.0 Å, but the distances to the N and O atoms in the same group are only 3.3 Å and the distance to the N atom in the other amide group is the same; for 4, there is one H⋅⋅⋅O distance of 3.1 Å and one H⋅⋅⋅N distance of 3.2 Å, as well as two H⋅⋅⋅C carbonyl distances of 3.1–3.2 Å between the ligand the two amide groups). This confirms that it is very difficult to estimate the interaction energies from only some measured distances.

Summing up the three potential fluorine interactions with the protein gives a net interaction energy that is essentially constant (−24 to −25 kJ mol⁻¹) for all ligands, except those with no substitution or an ortho substitution (1 and 7; −15 and −20 kJ mol⁻¹). Thus, the QM calculations support the suggestion that fluorine interactions with the side chain of Asn160 do not stabilize the binding of the ortho‐substituted 2 relative to the unsubstituted ligand, but they also indicate that the specific fluorine–amide interactions observed in the crystal structures do not explain the observed differences in the binding energies for the other ligands 3–7, contrary to what would have been predicted from geometrical considerations. We thus hypothesized that the situation could be more complicated, in that the fluorine interactions are partly compensated by other effects, for example, dispersion and desolvation. Therefore, we separated the dispersion contribution (from the DFT‐D3 term) from the QM interaction energies (mainly electrostatic and exchange–repulsion contributions). The results (Table 2) show that the interaction energy is completely dominated by the dispersion energy. In fact, for the two backbone models, the remaining QM interaction energy is positive for all ligands and only 0–3 kJ mol⁻¹. For the interaction with Asn160, the interaction energy is attractive for all ligands involving a meta‐fluorine substituent (by 2–4 kJ mol⁻¹), whereas it is still positive for the ortho‐ and para‐substituted benzene rings as models of 1 and 3, as well as without any substituent (i.e., 7; 1–4 kJ mol⁻¹).

Finally, we also calculated the solvation free energies for the fluoro‐substituted phenyl moieties of all ligands with the COSMO‐RS approach.13, 14 This showed a small solvation energy for all compounds, −1.5 to −3.8 kJ mol⁻¹. It was most negative for the unsubstituted group and decreased with the number of fluorine groups. Therefore, the solvation free energy showed a good anticorrelation to the binding free energies (R=−0.85), although the slope is only 0.2. Nevertheless, the decreased desolvation penalty can explain why the di‐ and trisubstituted ligands have more negative binding free energies.

It should be noted that for the asymmetric ligands (2, 3, 5, and 7), there is an additional entropic effect. They can only bind in a single conformation to the protein, determined by the position of the fluorine group. This gives an entropic penalty factor of RT ln2=1.7 kJ mol⁻¹ for the asymmetric ligands, compared to the symmetric ligands.

Discussion

Structural and theoretical analyses of galectin‐3 ligands containing fluorinated phenyltriazolyl‐thiogalactosides were carried out to study fluorine–amide interactions in the galectin‐3 binding pocket and to attempt to correlate these with binding affinity as measured by fluorescence polarization. Fluorine–amide C−F⋅⋅⋅C=O interactions with the backbone amides of Arg144, Ile145, and Ser237, as well as a multipolar C−F⋅⋅⋅H−N and C−F⋅⋅⋅H−Cα interaction with the amide group of Gly238 were identified in the crystal structures. These correspond well to interactions previously observed and postulated to be important for ligand binding.5, 11 QM calculations confirm an approximate linear dependence between the binding free energies and interaction energies between the substituted benzene rings and the Ser237‐Glu238 backbone. However, this dependence seems to have no clear relationship to the geometry of the fluorine–amide interactions, in that the fluorine atom that is directed toward the amide is not the largest contributor to the binding energy. The calculations show that the interaction with the backbone of Arg144‐Ile145 is not more favorable with the meta‐fluoro than the para‐fluoro group, which is further away. A fluorine interaction with the side‐chain amide of Asn160 was observed, but it contributed little to affinity or calculated binding energy relative to the unsubstituted phenyl group. In fact, the QM calculations show that the interaction between the ortho‐fluoro substituent and the side chain of Asn160 is less favorable than for the meta and para positions, where the fluorine interaction is with main‐chain atoms. On the other hand, it was possible to rationalize the stronger binding of the ligands with two or three fluoro groups from the fact that they have a smaller desolvation penalty than the monosubstituted and unsubstituted ligands. Finally, the calculations indicate that the observed fluoride–amide interactions are dominated by dispersion, rather than electrostatics.

Further quantum‐chemical calculations indicate that the orthogonal fluorine–amide interactions play a quite secondary role for the interaction of the ligands with the active site. We optimized freely, in the absence of other restraints such as the stacking interaction to Arg144, the structures of mono‐fluorobenzene with the three models of Asn160, Arg144‐Ile145, or Ser237‐Gly238 (starting from the ligand with the most pronounced fluorine–amide interaction, that is, those shown in Figure 5). The resulting structures (Figure 7) did not contain any such interactions. Instead, all structures reveal a short interaction between the hydrogen atom ortho to the fluorine atom and a carbonyl oxygen atom (2.2–2.4 Å). In the model with Asn160, the fluorine atom forms a rather normal hydrogen bond with the amide NH₂ group (2.05 Å), whereas for the complex with Arg144‐Ile145, the fluorine atom is closest to the terminal methyl group (2.6 Å; in this complex the ligand stacks with one of the two amide groups, indicating a complex dominated by dispersion). In the complex with Ser237‐Gly238, the fluorine atom is closest to the CH₂ group between the two amides (2.6 Å). However, in the latter two complexes, the fluorine is also rather close also to one of the carbonyl atoms of the amide groups (3.0–3.1 Å), but the C−F⋅⋅⋅C angle is far from straight at 102–112°. Thus, it seems that the binding of all ligands in this study is determined by other effects, in particular dispersion, desolvation, and polar interactions with other parts of the ligand. The fluorine group is involved only in the fine‐tuning the position of the substituted benzene group, and also in this process it is not more significant than the hydrogen atoms on the benzene ring. However, fluorine slightly yet significantly decreases the solvation energy of the ligand (reflecting that it is actually less polar than hydrogen atoms), which promotes the binding to a hydrophobic site.

Figure 7.

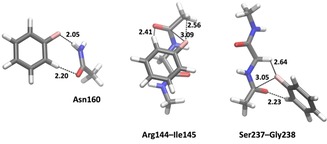
Optimized QM structures of the models in Figure 5, that is, F‐benzene with models of Asn160, Arg144‐Ile145, or Ser237‐Gly238. The figures show the shortest contacts between the ligand and the amino acid models, but also the closest F−C carbonyl distances. Note that we have not made an exhaustive conformational search of the complexes, but only started the optimizations from the structures in Figure 5, that is, the crystal conformations with the most pronounced fluorine–amide interactions.

Conclusions

In summary, the current work confirms that the energetic contributions of protein–ligand interactions are difficult to predict on intuitive grounds based on visual inspection of ligand binding pockets or on simple geometrical consideration of orthogonal multipolar interactions, but should be backed up by thorough theoretical calculations for each ligand.

Experimental Section

General: All reagents and solvents were dried prior to use according to standard methods. Purification of compounds was carried out by preparative HPLC (Agilent 1260 infinity system, SymmetryPrep C18 column, 17 mL min⁻¹ flow rate, H₂O/MeCN gradient 10–100 %, 15 min with 0.1 % formic acid). Specific rotations were measured on a PerkinElmer model 341 polarimeter. NMR spectra ¹H, ¹³C, 2D COSY and HMQC were recorded with a Bruker Avance II 400 MHz spectrometer (400 Hz for ¹H and 100 Hz for ¹³C) at ambient temperature. Chemical shifts (δ) are reported in parts per million (ppm). HRMS data were determined by direct infusion on a Waters XEVO‐G2 QTOF mass spectrometer using electrospray ionization (ESI). Compound 9 was of >95 % purity according to UPLC analysis (Waters Acquity UPLC system, Waters Acquity CSH C18 column, 0.5 mL min⁻¹ flow rate, H₂O/MeCN gradient 5–95 %, 10 min with 0.1 % formic acid). The synthesis of compounds 1–8 was described by Peterson et al.5

Synthesis of 3′‐deoxy‐3′‐[4‐phenyl‐1H‐1,2,3‐triazol‐1‐yl]‐β‐d‐galactopyranosyl 1‐thio‐β‐d‐glucopyranoside 9: To a solution of 3′‐azido‐3′‐deoxy‐β‐d‐galactopyranosyl 1‐thio‐β‐d‐glucopyranoside (10 mg, 0.026 mmol) and CuI (1 mg, 0.007 mmol) in MeCN (3 mL) were added phenylacetylene (4 μL, 0.039 equiv) and diisopropylethylamine (5 μL, 0.026 mmol). The mixture was stirred for 20 h at 50 °C before quenching with saturated aqueous NH₄Cl followed by evaporation of the solvent. The residue was purified by preparative HPLC to give the product (5 mg, 40 %) as an amorphous white solid. ${\left[\alpha \right]}_{\mathrm{D}}^{20}$ =17.8 (c=0.36, CH₃OH); ¹H NMR (CD₃OD, 400 MHz): δ=8.41 (s, 1 H, Ph), 7.84 (dd, J=8.4, 1.4 Hz, 2 H, Ph), 7.44 (t, J=7.6 Hz, 2 H, Ph), 7.34 (tt, J=7.4, 2.0 Hz, 1 H, Ph), 4.94 (d, J=9.6 Hz, 1 H, H‐1), 4.87 (obscured by water H‐3), 4.79 (d, J=9.8 Hz, 1 H, H‐1′), 4.33 (t, J=10.1 Hz, 1 H, H‐2), 4.13 (d, J=2.8 Hz, 1 H, H‐4), 3.90 (dd, J=12.2, 1.7 Hz, 1 H, H‐6′), 3.86–3.78 (m, 2 H, H‐5 and H‐6), 3.71–3.64 (m, 2 H, H‐6 and H‐6′), 3.43–3.32 ppm (m, 4 H, H‐2′, H‐3′, H‐4′ and H‐5′); ¹³C NMR (CD₃OD, 100 MHz): δ=148.4, 131.9, 130.0, 129.3, 126.7, 121.8, 86.0, 84.5, 82.2, 81.2, 79.6, 74.7, 71.5, 69.8, 69.2, 68.5, 63.0, 62.6 ppm; HRMS calculated for [C₂₀H₂₈N₃O₉S]⁺: 486.1546, found: 486.1552.

Co‐crystallization of galectin‐3C with compounds 2–9: Galectin‐3C (C‐terminal domain) solution (9.2 mg mL⁻¹ in 1× phosphate buffered saline (PBS) pH 7.4 with 10 mm β‐mercaptoethanol) was mixed with crystallization solution (20 % PEG 4000, 0.1 m Tris⋅HCl pH 7.5, 0.4 m NaSCN, 10 mm β‐mercaptoethanol). Crystallization drops of 2+2 μL were set up over 0.5 mL reservoir solution. Crystals obtained were soaked with compounds. All compounds were dissolved in DMSO to obtain uniform and highly concentrated stock. These stocks were then diluted with PEG 400 (final concentration 30 %), and then ligand soaking solution was prepared by mixing crystallization solution and ligands to make a 10 mm solution. Crystals were placed in 4 μL of these cocktails and left for 15–20 h. These soaked crystals were flash‐frozen in cryo‐solution (20 % PEG 400, 20 % w/v PEG 4000, 400 mm NaSCN, 100 mm Tris⋅HCl pH 7.5).

Data collection and structure solution of galectin‐3C in complex with compounds 2–9: Data for compounds 2–7 were collected at 100 K at station I911‐3 of the MAX‐II synchrotron (Lund, Sweden) (λ=1.0000 Å), equipped with a marMosaic 225 mm CCD detector.15 Three hundred images with 1° rotation were collected with exposure times of 1–3 s. Data for 8 were collected at beamline ID23‐1 ESRF (Grenoble, France), and data for 9 were collected at the BioMAX beamline, MAX IV (Lund, Sweden). Six hundred images were collected with 0.1° rotation and 0.1 s exposure for 8 and 1800 images with 0.05 s exposure for 9. Data for all structures were integrated using XDS and scaled using XSCALE.16 The structures were refined using phenix.refine17 and PDB ID: 3ZSL (stripped of water molecules and alternate conformations)18 as starting model. Five percent of the total reflections were randomly set aside for cross‐validation. Models were subjected to rigid body refinement until the R‐factors converged, then they were refined atomically at the maximum data resolution. After initial refinement of the protein coordinates in phenix.refine,17 the coordinates of ligands were fitted to the respective electron density using Coot.19 Further model building and manipulations were done in Coot. Restraints were generated using eLBOW20 from Phenix. The structures were refined until convergence and individual anisotropic atomic displacement parameters for each atom were refined. Water molecules were added to positive difference density peaks more than 4.5 or 5.0 σ above the mean and also present in the 2mF _o−DF _c map at the 1 σ level. Riding hydrogen atoms were added in the final stages of refinement. Refinement statistics are listed in Table S1. Molecular images were generated using PyMOL (Schrödinger LLC). Model validation and analysis were performed using MolProbity21 and PDB_REDO.22

Quantum‐mechanical calculations: Two sets of quantum‐mechanical (QM) calculations were used to explain the differences in binding affinity of the seven studied ligands. All QM calculations were performed with the Turbomole 7.2 software package.23, 24 In all calculations, the ligands were modelled as isolated fluorine‐substituted benzene rings by truncating the ligands with a hydrogen atom.

In the first set of calculations, we calculated the interaction energy between the seven ligands and one or two nearby residues: the side chain of Asn160 and the backbone of Arg144 and Ile145 or Ser237 and Gly238. The side chain of Asn160 was modelled as CH₃C(O)NH₂, whereas the backbones of the two dipeptides were modelled by CH₃CONHCH₂CONHCH₃. All coordinates were taken directly from the crystal structures. For residues that had two conformations, we performed calculations on each of the conformations and weighted the final average of the interaction energies by the occupancies of the two conformations. All calculations were performed with the TPSS‐D3 method.25, 26 The geometry optimizations in Figure 7 used the def2‐SV(P) basis set, whereas all the energy calculations used the much larger def2‐QZVPD basis set.27, 28 The interaction energy for each system was calculated from three single‐point calculations as ΔE=E _complex−E _residue−E _ligand.

In the second set of calculations, we obtained the solvation free energies for the ligands, using the conductor‐like screening model for real solvents (COSMO‐RS)13, 14 with optimized radii for all atoms.29 These calculations were based on two single‐point BP‐D3 calculations26, 30, 31 with the TZVP basis set,32 as is requested by the method,30, 31 one in vacuum and one in a continuum solvent with an infinite dielectric constant.

Conflict of interest

U.J.N. and H.L. are shareholders in Galecto AB, which develops inhibitors against galectins.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

R. Kumar, M. M. Ignjatović, K. Peterson, M. Olsson, H. Leffler, U. Ryde, U. J. Nilsson, D. T. Logan, ChemMedChem 2019, 14, 1528.