Abstract
Purpose
Intravoxel incoherent motion (IVIM) modeling for estimation of the diffusion coefficient (D) and perfusion fraction (f) is increasingly popular, but no consensus on standard protocols exists. This study provides a framework for optimization of b‐value schemes for reduced estimation uncertainty of D and f from segmented model fitting.
Theory
Analytical expressions for uncertainties of D and f from segmented model fitting were derived as Cramer‐Rao lower bounds (CRLBs).
Methods
Optimized b‐value schemes were obtained for 3 to 12 acquisitions and in the limit of infinitely many acquisitions through constrained minimization of the CRLBs, with b‐values constrained to be 0 or 200 to 800 s/mm2. The optimized b‐value scheme with eight acquisitions was compared with b‐values linearly distributed in the allowed range using simulations and in vivo liver data from seven healthy volunteers.
Results
All optimized b‐value schemes contained exactly three unique b‐values regardless of the total number of acquisitions (0, 200, and 800 s/mm2) with repeated acquisitions distributed approximately as 1:2:2. Compared with linearly distributed b‐values, the variability of estimates of D and f was reduced by approximately 30% as seen both in simulations and in repeated in vivo measurements.
Conclusion
The uncertainty of IVIM D and f estimates can be reduced by the use of optimized b‐value schemes.
Keywords: Cramer‐Rao lower bound, diffusion‐weighted imaging, error propagation, experiment design, IVIM, MRI
1. INTRODUCTION
The concept of intravoxel incoherent motion (IVIM) aims to describe the effect of both diffusion and microcirculation on the MR signal in a diffusion‐weighted imaging experiment.1 The mathematical model commonly used to describe the diffusion‐weighted signal is given by:
| (1) |
where D is the diffusion coefficient, D* is the pseudo‐diffusion coefficient, f is the perfusion fraction, and S 0 is the signal with no diffusion weighting.1
Because of the flexibility of a biexponential model and typical values of the IVIM parameters, IVIM parameter estimation is inherently difficult.2, 3 To deal with the problematic estimation, several methods have been proposed including a number of least‐squares approaches and some Bayesian ones.3, 4, 5, 6 One of the most commonly used approaches is the segmented model fitting, also called stepwise, asymptotic or oversegmented.3, 7, 8 It has multiple times shown superiority in terms of estimation accuracy, precision, and repeatability to full least‐squares fitting; has a relatively low computational cost; and is simple to implement.7, 9 It proceeds in three steps: 1) estimate D using b‐values above a certain threshold where the magnitude of the second exponential in Equation 1 is negligible, 2) use the model parameters estimated in step 1 to extrapolate the signal to b = 0 and compare with the measured signal at b = 0 to estimate f, and 3) fix the values of D and f obtained in step 1 and 2 and estimate D* and S 0 using nonlinear least squares.3 The main benefits of this approach are that a robust estimate of D is obtained and that f is estimated without explicit estimation of D*. It has even been proposed to limit the analysis to the first two steps, i.e. to use a simplified approach including estimation of only D and f. 1, 10 By avoiding the estimation of D*, the number of b‐values and demands on data quality are reduced. This enables extraction of both diffusion and perfusion information in a clinically feasible scan time.11, 12
Optimization of acquisition parameters has the potential to reduce the parameter estimation error13 and thereby either reduce scan time or improve quality of parametric maps. Optimization techniques have been used to find optimal measurement parameters in several aspects of quantitative MRI, for example, diffusion MRI,14 magnetization‐transfer imaging,15 and DIXON imaging.16 Optimal choices of b‐values and the number of repeated acquisitions of each b‐value have been studied extensively for the monoexponential diffusion model, mainly using error propagation or similar techniques.17, 18, 19 Some studies have performed similar work with the IVIM model.9, 20, 21, 22, 23, 24 However, these studies on the IVIM model have focused on minimizing the error of parameters estimated simultaneously from the biexponential model and not the segmented procedure nor for estimation of only D and f. Optimization of acquisition of data for segmented model fitting is to our knowledge hitherto limited to choice of intermediate b‐value in three‐b‐value protocols.11, 25
The aim of this work was to develop a framework for optimization of b‐value schemes for diffusion‐weighted imaging data used to estimate IVIM parameters D and f with segmented model fitting. The proposed framework includes optimization of number of b‐values and their magnitude as well as the number of acquisitions of each b‐value. An optimized b‐value scheme was generated for typical diffusion and perfusion values in healthy liver and the impact on parameter estimation error was studied through simulations and in vivo measurements.
2. THEORY
Assuming D* >> D and using b‐values either equal to zero or large enough to regard the signal fraction from the perfusion compartment as negligible, the IVIM model (Equation 1) may be simplified to:
| (2) |
where δ is the discrete delta function. This exact formulation was introduced by Sénégas et al.,10 but the concept was given already by le Bihan et al. in the seminal IVIM paper.1 The simplified IVIM model may equivalently be formulated as:
| (3) |
where b thr is the threshold b‐value where the signal fraction from the perfusion compartment is considered negligible. The important observation to make here is that the least‐squares estimate of D based on Equation 2 is determined only from b ≥ b thr, i.e. a monoexponential model fit using only b‐values that are high enough not to include signal from the perfusion compartment. This corresponds to the first step in the segmented procedure.3 The least‐squares estimate of f based on Equation 2 is uniquely defined and equals the result from the second step in the segmented procedure. The signal extrapolated to b = 0 [A = S 0(1 – f)] as is estimated in step 1 is used to calculate the estimate of f as f = 1 – A/S 0, where S 0 is given directly by the measurements with b = 0. Parameter estimation based on Equation 2 is thus equivalent to the first two steps of the segmented procedure.25 Since D* is omitted in Equation 2, the final step of the segmented procedure has no analog. If only D and f are of interest, one can thus potentially find an optimal b‐value scheme for Equation 2 and use it for the segmented model fitting procedure.
In the case of only three unique b‐values, i.e. b 0 = 0 and b 1, b 2 > 0, closed form solutions for D and f exist26:
| (4) |
| (5) |
In this case, the variability of parameter estimates can be calculated through error propagation resulting in:
| (6) |
| (7) |
where ni is the number of acquisitions of the ith b‐value and SNR equals S0/σ, where σ is the standard deviation of the noise. Derivations of Equations 6 and 7 are found in the Supporting Information.
If more than three unique b‐values are used, the model parameters instead have to be estimated using a nonlinear least‐squares method and the standard methods for error propagation cannot be used. A popular alternative in these cases is the CRLB, which is a lower limit of the variance of the parameter estimate.14 These bounds are given by the diagonal elements of the inverse of the Fisher matrix for the particular model (here Equation 2). For a Gaussian noise distribution the elements of the Fisher matrix are given by:
| (8) |
with p ∈ {D, f, S 0} and N + 1 is the number of unique b‐values.14 The partial derivatives found in Equation 8 are given in the Supporting Information. The Fisher matrix is thus a 3 × 3 matrix, which can be inverted analytically. The diagonal elements of interest are:
| (9) |
| (10) |
If N = 2, i.e. if three b‐values are used, Equations 9 and 10 simplify to the results given by error propagation (i.e. Equations 6 and 7) as noted for D previously by Brihuega‐Moreno et al.19
3. METHODS
In this paper, optimization of b‐value schemes refers to finding b‐values and the proportion of acquisitions with these b‐values such that the variability of IVIM parameter estimates is minimized. The optimization was conditioned by lower and upper limits on the b‐values and a fixed number of total signal acquisitions. The presented optimization framework is in principle general; however, its potential was demonstrated by optimization for the specific situation of a liver examination.
3.1. Optimization of b‐value schemes
The presented optimization framework assumes that Equation 2 is a proper model of the diffusion‐weighted signal at the chosen b‐values. This assumption was justified by setting a lower and upper limit on the nonzero b‐values. The lower limit should be set high enough that the signal contribution from the perfusion compartment is negligible. In this study it was set to 200 s/mm2, which essentially removes all signal from the perfusion compartment in typical liver tissue (D* = 70 µm2/ms).27 This threshold is also commonly seen in literature3, 28, 29, 30 although other choices occur as well.7, 9 The upper limit should be set low enough to ensure that the signal decay due to diffusion weighting in the diffusion compartment is well approximated by a monoexponential model. In this study it was set to 800 s/mm2, which is a standard choice of the highest b‐value in clinical liver studies. Given an SNR of 15 in the b = 0 image, which is typical in abdominal diffusion‐weighted imaging, the chosen upper limit also ensures that the noise is well approximated by a Gaussian distribution since the SNR at all b‐values is at least 5, as predicted by inserting typical liver IVIM parameters into Equation 2.31 An approximately Gaussian noise distribution makes the expressions for the CLRBs and methods for model fitting substantially less complicated14, 32 and is assumed for model fitting in most studies.
Because of the finite diffusion encoding gradient strength, increasing the highest b‐value results in a longer echo time and thereby a decreased SNR. To account for this, an echo‐time‐dependent expression for SNR was defined; it was inserted into Equations 9 and 10:
| (11) |
where SNR 0 is the SNR at TE = 0, and = 40 ms and = 80 ms are the T2‐relaxation times in the diffusion and perfusion compartments, respectively.33 A derivation of the expression is found in the Supporting Information. On the basis of the use of an SE‐EPI sequence, which was utilized in this study, the echo time that was inserted into Equation 11 was calculated as . Given the maximum available gradient strength G max, δ (G max, b max) is the shortest possible gradient duration needed to generate the maximum b‐value. t nodiff is the time from excitation to the main echo in the EPI readout when diffusion encoding is not applied. On the basis of the MR scanner and pulse sequence used in the subsequent examinations the fixed parameters were set to G max = 41.6 mT/m, t nodiff = 19.6 ms.
Optimization of b‐values and number of acquisitions for a finite total number of acquisitions was based on CRLB (Equation 9 and 10). The objective function used in the optimization was the average error over a range of values of D and f (D ∊ [1.0 1.2] µm2/ms, f ∊ [0.15 0.30]), with error defined as the sum of the coefficients of variation as follows:
| (12) |
where (F −1)DD and (F −1)ff are obtained from Equations 9 and 10, respectively. The average error was calculated by summing CV tot over 100 × 100 linearly distributed values of D and f on the specified range, which were based on previously reported parameter values in healthy liver.27
Optimal sets of b‐values were found through constrained minimization using the MATLAB function fmincon. The adjustable parameters in the optimization were the b‐value of each signal acquisition, b i. To avoid local minima, 10 random initializations were used. The optimization procedure was performed for 3 to 12 signal acquisitions, with the requirements of at least one acquisition with b = 0 and at least two acquisitions in the interval 200 to 800 s/mm2. Note that the number of acquisitions of each b‐value was not explicitly included in the optimization, i.e. n i = 1 in Equations 9 and 10. Instead, it was obtained as the number of times the same b‐value repeated in the solution. Since SNR 0 in Equation 11 is a positive constant, which can be chosen arbitrarily without affecting the SNR dependence in the optimization, it was omitted in the expression used in the optimization.
To study the behavior of the optimization at a large number of acquisitions, a similar optimization procedure was set up in the limit of infinitely many acquisitions. Since the total number of acquisitions (n tot = Σi ni) can be considered a constant in the optimization, Equation 8 can be divided by n tot without affecting the solution. The resulting ratios ai = ni/n tot are the proportion of acquisitions acquired at each b‐value. These were added as adjustable parameters in the optimization with the constraints that ai was allowed to vary between 0 and 1 and that they summed up to 1.
The MATLAB code for optimization of b‐value schemes is available at http://mathworks.com/matlabcentral/profile/authors/3680885-oscar-jalnefjord.
3.2. Simulations
Two b‐value schemes with eight acquisitions were compared to study the usefulness of the optimization procedure; the optimized scheme (bopt; 2 × 0, 3 × 200, 3 × 800 s/mm2; see Table 1) was compared with b‐values linearly distributed in the available range (blin; 1 × 0, 1 × 200, 1 × 300, 1 × 400, 1 × 500, 1 × 600, 1 × 700, 1 × 800 s/mm2).
Table 1.
Optimal number of acquisitions of each optimal b‐value for different total number of acquisitions (n tot) and the proportions for the limiting case of an infinite total number of acquisitions
| n tot | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ∞ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| n 0 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 19% |
| n 1 | 1 | 2 | 2 | 3 | 3 | 3 | 4 | 4 | 5 | 5 | 43% |
| n 2 | 1 | 1 | 2 | 2 | 3 | 3 | 3 | 4 | 4 | 5 | 38% |
The optimal b‐values were b 0 = 0, b 1 = 200, and b 2 = 800 s/mm2 regardless of the value of n tot. Corresponding results from optimization when omitting the upper b‐value limit or the echo‐time dependence are provided as supporting material (Supporting Information Tables S1 to S3).
A set of Monte Carlo simulations with accompanying analyses was used 1) to validate the use of CRLB minimization for optimization of b‐value schemes for segmented IVIM model fitting and 2) to compare the b‐value schemes in terms of estimation variability.
The simulations were performed on a grid of 20 × 20 values of D and f linearly distributed in the ranges D ∊ [0.5 1.5] µm2/ms and f ∊ [0.05 0.40]. The ranges were somewhat wider than what was used in the optimization to enable study of the effect of optimization on parameter estimation error also outside the parameter ranges typically found in healthy liver. For each combination of D and f, and for each of the two b‐value schemes 20 000 data series were generated using the IVIM model (Equation 1) with Rician noise at an SNR of 15. Three sets of simulations were run with D* = 10, 20, or 50 µm2/ms to study the impact of the size of D*, i.e. the size of the signal contribution from the perfusion compartment for b > 0. The parameters D and f were estimated using the segmented fitting procedure where D was first estimated using nonlinear least squares and f was estimated from extrapolation as described in the Theory section. The estimated parameters were constrained to the ranges D ∊ [0 3] µm2/ms, f ∊ [0 1] and S 0 ∊ [0 2S max], where S max is the maximum measured signal value.
The CRLB gives a lower limit rather than an actual level of parameter variability. Minimization of the CRLB is therefore not guaranteed to reduce the actual parameter estimation variability. To validate the use of CRLB minimization for optimization of b‐value schemes for segmented IVIM model fitting, the error based on CRLB was compared with that obtained from fitting simulated data. Specifically, the sum of coefficients of variation for the estimates of D and f from simulated data was obtained (equivalent to Equation 12) and compared with the total relative error based on CRLB (Equation 12). This was done for each combination of D, f, D*, and b‐value scheme.
The two b‐value schemes were compared by calculating the standard deviation of the estimated parameter values from each b‐value scheme and combination of D, f, and D*. Although not part of the b‐value optimization, the estimation bias was also calculated for comparison between b‐value schemes for each combination of D, f, and D* as the mean difference between estimated and simulated parameter value.
3.3. In vivo measurements
To assess the impact of b‐value optimization on in vivo data, diffusion‐weighted MR images of the upper part of the abdomen were acquired in eight healthy subjects (median age 27 years, range 22–43 years, four males). The study was approved by the regional ethical review board in Gothenburg, Sweden. The MR images were acquired on a 3T Philips Achieva dStream (Best, the Netherlands) with software release 5.1.7. A respiratory triggered single shot SE‐EPI sequence was used to acquire images with the same b‐values as were used in the simulations (Δ = 26.5 ms, δ = 17.7 ms), with the exception that b = 1 s/mm2 was used instead of b = 0. This change was applied because of practical difficulties in acquiring an odd number of acquisitions experimentally for b = 0 and should have had a minimal effect on the final parameter estimates. In the subsequent analysis the measurements at b = 1 s/mm2 were treated as being measured at b = 0. Other imaging parameters were TE = 55 ms, TR = 3000 ms, half‐scan factor = 0.7, acquisition pixel size = 3 × 3 mm2, slice thickness = 6 mm, slice gap = 0.6 mm, 32 slices, SENSE factor = 2 (anterior‐posterior direction), slice‐selective gradient reversal and spectral presaturation with inversion recovery for fat suppression. To enable a study on the repeatability of parameter estimates, the examination was repeated four times with the same planning without moving the subject. One subject was excluded because of incorrect triggering, which resulted in images heavily corrupted by motion artifacts. A region of interest (ROI) was drawn that comprised of a major part of the right liver lobe and model fitting was performed on a voxel level. The SNR was estimated in each voxel by calculating the mean and standard deviation of the signal in the repeated acquisitions of b = 1 s/mm2 used for the optimal scheme. The median SNR in each subject was 11 ± 3 (mean ± SD).
Parameter estimation variability was quantified by calculating the standard deviation of parameter estimates obtained from the four repetitions of the examination. Specifically, the mean and standard deviation over the four repetitions were calculated for each voxel separately. Then, for each subject the median standard deviation within the ROI was calculated and compared for the two b‐value schemes.
4. RESULTS
4.1. Optimization
No more than three unique b‐values were found in the optimized b‐value schemes regardless of the total number of acquisitions. These b‐values were always 0 (preset) and the lower and upper limits set in the optimization, i.e. 200 and 800 s/mm2. The optimal number of acquisitions of each b‐value was approximately twice as many for the middle and high b‐values (200 and 800 s/mm2) as for b = 0 (Table 1), although the exact results depended on the total number of acquisitions. As the number of acquisitions was increased, the distribution of acquisitions over b‐values approximately matched the distribution over b‐values for infinite numbers of acquisitions (Table 1).
Optimized b‐value schemes were also generated without an upper b‐value limit and without adjusting for the echo‐time dependence on SNR. Omitting either the upper b‐value limit or the TE‐related SNR penalty had no effect on the solution other than a slightly higher value of the high b‐value (b 2 ≈ 850 s/mm2) (Supporting Information Tables S1 and S2). Omitting both the upper b‐value limit and the TE‐related SNR penalty resulted in minor effects on the proportions of acquisitions at each b‐value, but resulted in a substantially higher value of the high b‐value (b 2 ≈ 1300 s/mm2) (Supporting Information Table S3).
4.2. Simulations
An approximately monotonically increasing relationship was seen between total relative error derived from CRLB (Equation 12) and from segmented model fitting of simulated data (Figure 1). This relationship justifies the use of CRLB in the optimization procedure since it indicates that a lower CRLB implies a lower estimation error from segmented model fitting. The relationship was mainly unaffected by the magnitude of D* (Figure 1 and Supporting Information Figures S1 and S2).
Figure 1.
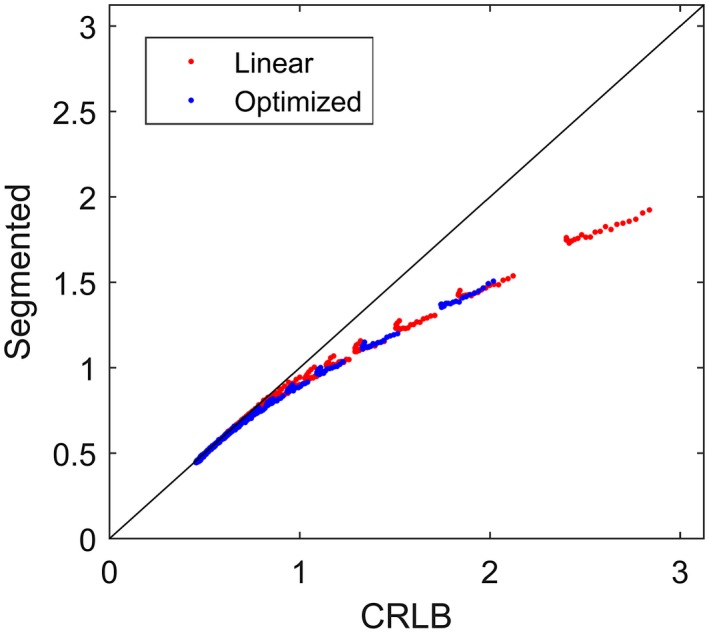
Comparison between estimation variability based on CRLB and segmented model fitting based on simulated data with D* = 50 µm2/ms. The red and blue markers show results based on the linear and optimized b‐value schemes, respectively. Each data point represents the total relative error (Equation 12 and its equivalent measure derived from segmented model fitting) for a given combination of D and f. Note the monotonic behavior of the data points. The line of unity is shown in black. Supporting Information Figures S1 and S2 show the corresponding plots based on data with D* = 20 µm2/ms and D* = 10 µm2/ms respectively. CRLB, Cramer‐Rao lower bound
The optimized b‐value scheme produced parameter estimates with smaller estimation variability for all simulated combinations of D and f. The standard deviation of D was 18% to 40% smaller with the larger differences for smaller values of D, while the standard deviation of f was 25% to 45% smaller with the larger differences for larger values of f (Figure 2). The same level of reduction in estimation variability was seen for all simulated magnitudes of D* (Figure 2 and Supporting Information Figures S3 to S5).
Figure 2.
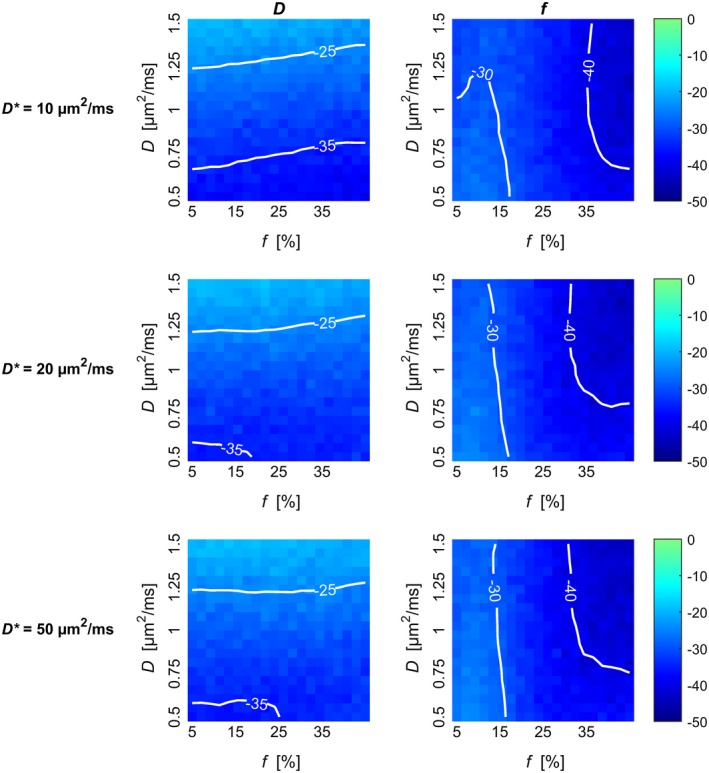
Relative difference between estimate standard deviation observed with the linear and the optimized b‐values schemes. The relative difference for estimation of D (left column) and f (right column) from simulated data is plotted for each combination of D, f, and D*. Negative values imply less variability with the optimized b‐value scheme. Contours are superimposed on the color maps for improved visualization. Plots showing the estimation variability of each b‐value scheme separately are shown in Supporting Information Figures S3 to S5
The estimation bias was only weakly affected by the size of D (Supporting Information Figures S6 to S8). A positive bias on D and a negative bias on f could be seen for parameters estimated from data generated with D* = 10 µm2/ms (Figure 3). The bias increased in magnitude with increasing size of f used for data generation. Larger values of D* were in general not associated with any noticeable biases, except for a small negative bias on D, which was caused by the Rician noise distribution. The bias could only be seen for data generated with D* = 50 µm2/ms, but was presumably present for all values of D*.
Figure 3.
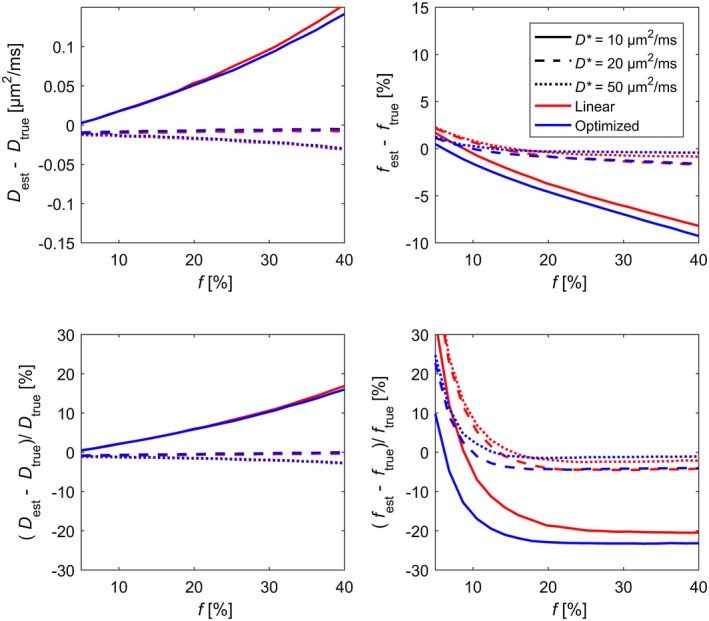
Estimation bias for estimation of D (left column) and f (right column) from simulated data based on the two studied b‐value schemes plotted versus true values of f for different values of D*. The top row shows bias in absolute units, while the bottom row shows relative bias. The plotted bias is an average across the simulated values of D. Plots showing the joint dependence on D and f are found in Supporting Information Figures S6 to S8
4.3. In vivo measurements
The b‐value schemes produced similar estimates of D and f on a group level, but the estimation uncertainty was lower with the optimized scheme (Figure 4). On the individual level there were variations between schemes due to interscan variability (Figures 4, 5, 6 and Supporting Information Figures S9 to S15). Nevertheless, the median parameter uncertainty was lower with the optimized b‐value scheme for all subjects. The median relative difference for D and f was 36% and 22%, respectively (Figure 4).
Figure 4.
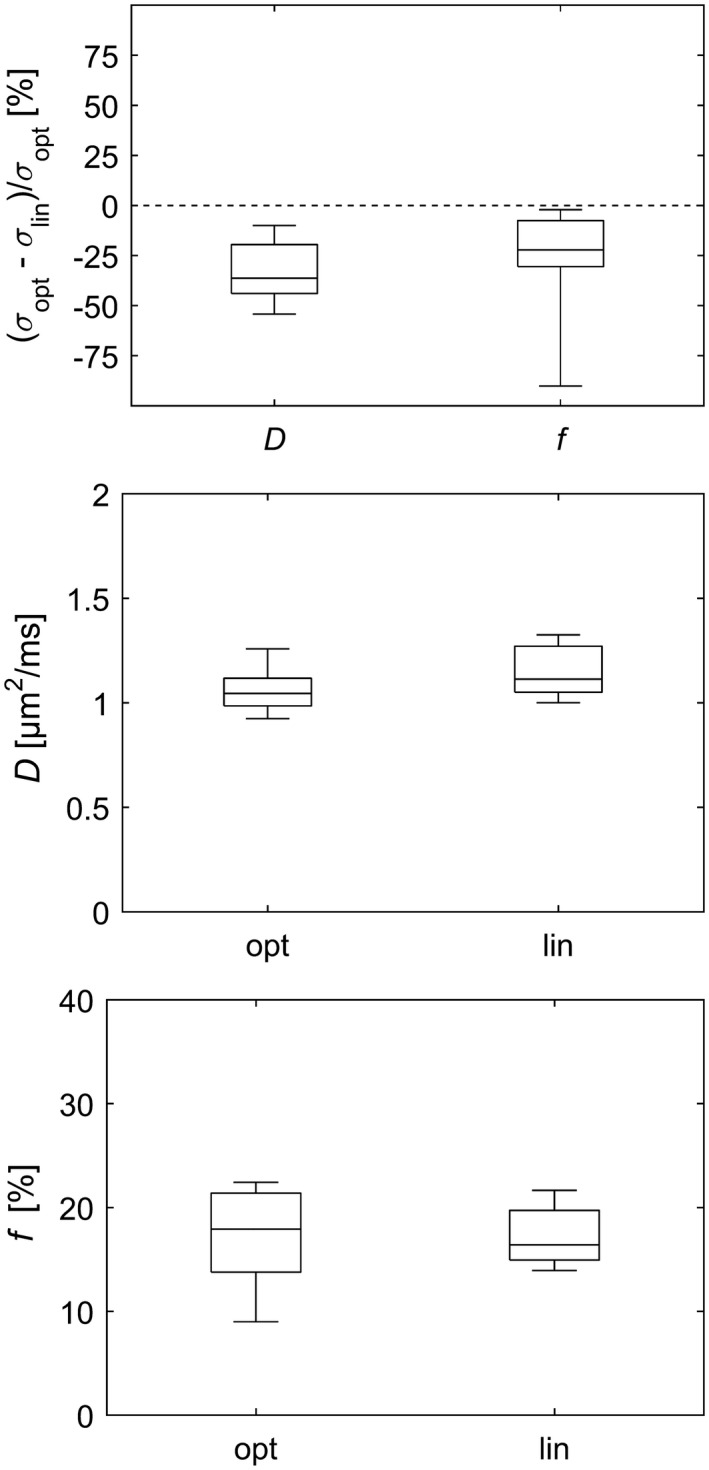
Comparison of b‐value schemes for in vivo data with respect to standard deviation of parameter estimates (top plot) and with respect to the estimated diffusion coefficient (middle plot) and the estimated perfusion fraction (bottom plot). The box plots show the distribution across subjects of ROI median of either parameter estimate variability or parameter estimate, depending on the context. The whiskers show the minimum and maximum values. Note that negative values in the top plot imply less variability with the optimized b‐value scheme. ROI, region of interest
Figure 5.
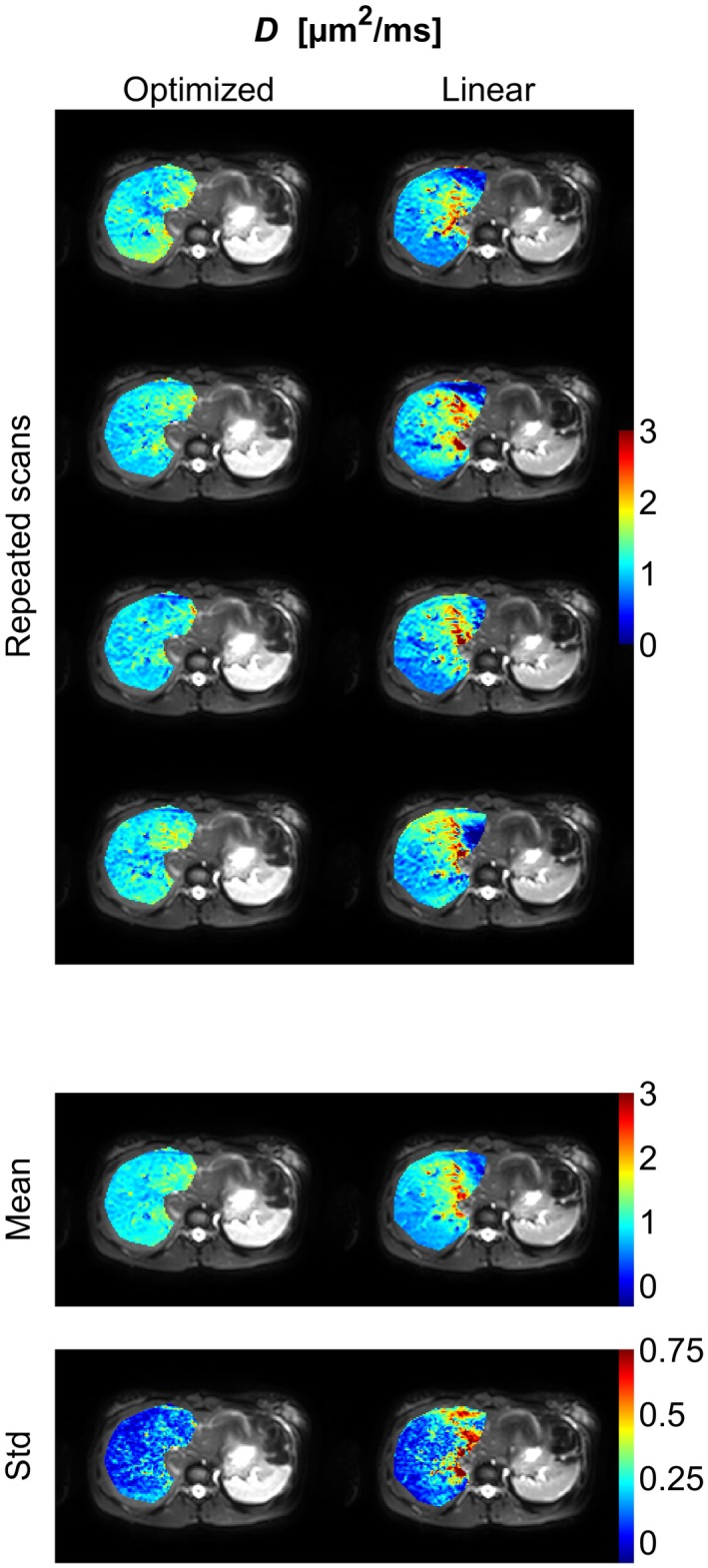
Diffusion‐coefficient (D) parameter maps (color) of the right part of the liver superimposed on the b = 1 s/mm2 image (gray scale) from an example subject. The figure shows parameter maps from repeated scans as well as the mean and the standard deviation of these maps. Corresponding figures for the remaining subjects are found in Supporting Information Figures S9 to S14
Figure 6.
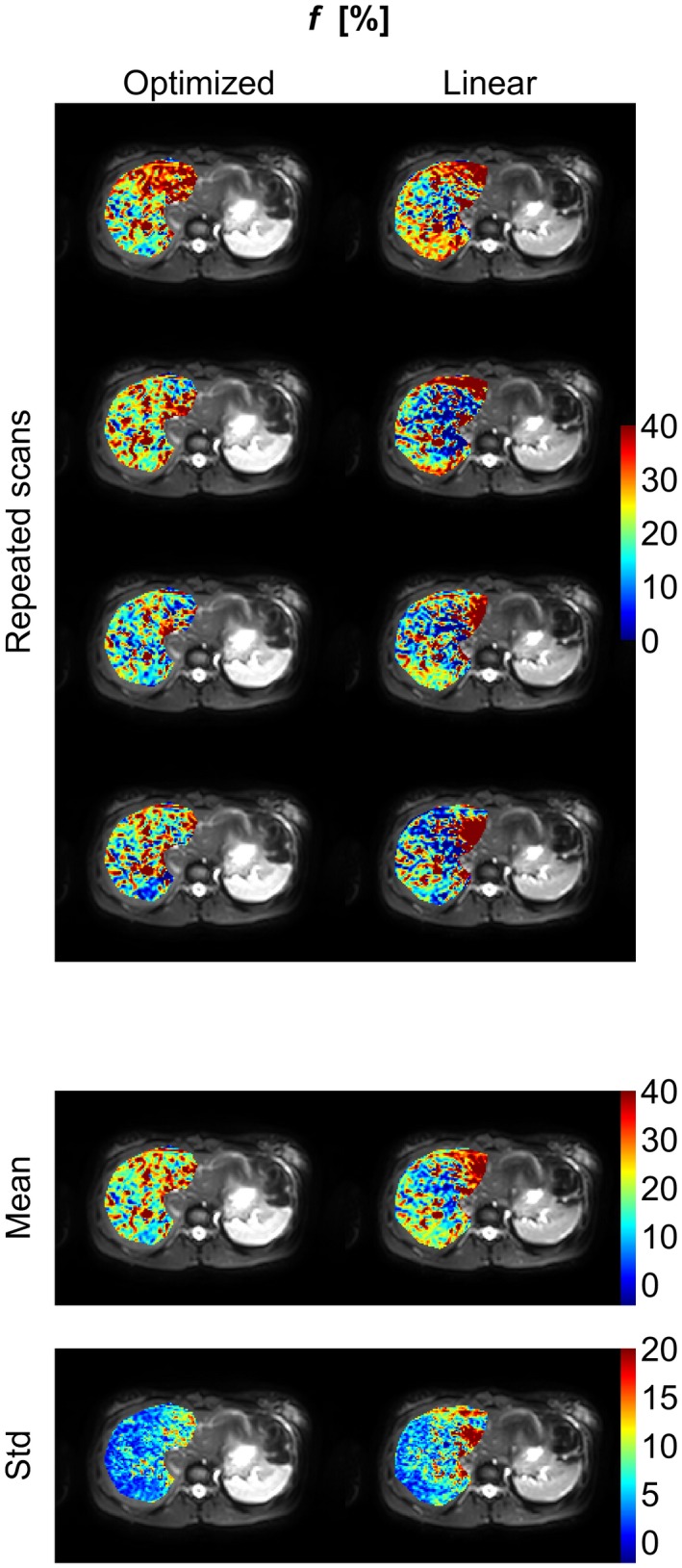
Perfusion‐fraction (f) parameter maps (color) of the right part of the liver superimposed on the b = 1 s/mm2 image (gray scale) from an example subject. The figure shows parameter maps from repeated scans as well as the mean and the standard deviation of these maps. Corresponding figures for the remaining subjects are found in Supporting Information Figures S9 to S14
5. DISCUSSION
This work presents a framework for optimization of b‐value schemes for segmented IVIM model fitting. Analytical expressions are given for estimation of D and f along with their errors from error propagation based on a three‐b‐value protocol. The CRLB‐based analogs are given for general protocols, thus enabling error analysis in the cases of four or more b‐values. Application of the optimized b‐value schemes shows improved estimation performance for both D and f in simulations as well as in in vivo measurements, as demonstrated by reduced parameter estimation uncertainty and improved parameter repeatability.
5.1. The optimized b‐value schemes
Previous studies on optimal b‐values for segmented model fitting for estimation of D and f have focused on the choice of the intermediate b‐value in a protocol containing three unique b‐values.11, 25 The current study provides complementary results regarding choice and number of b‐values including repeated acquisitions of b‐values. Most importantly, the optimal number of unique b‐values was always found to be three, regardless of the total number of acquisitions. This is in agreement with previous similar studies regarding the monoexponential model17, 18, 19 and the full IVIM model,20, 21 where the optimal number of unique b‐values also equaled the number of parameters in the model. Larger optimal numbers of unique b‐values have been reported for the monoexponential model, but only when the range of D values was very large and no upper limit on the b‐values was applied.19 In the case of the monoexponential model, acquisition of the high b‐value is emphasized with an approximate 1:3 ratio.17 In contrast, the results in the current work place less weight on the highest b‐value with an approximate 1:2:2 relationship. This is reasonable since the information on f is mainly contained in the low and intermediate b‐values. It is also in concordance with results reported for the full IVIM model,20 although those results emphasized the intermediate b‐values even more since D* also was to be estimated.
A distinctly reduced parameter uncertainty was observed for all subjects when using the optimized b‐value scheme. Also, the median improvement closely resembled what was predicted by simulations for the particular tissue type and corresponding parameter values used in this study. Although the general trend agreed well with what was predicted, a substantial spread in improvement was seen between subjects. This is likely due to the inherent difficulty of diffusion imaging of the upper abdomen where respiratory and cardiac motion often result in image artifacts. Improvements on motion compensation and imaging robustness are therefore important.34, 35
While the repeatability of IVIM parameters estimates was improved by the use of an optimized b‐value scheme, the estimated parameter values were similar for the two b‐value schemes on the group level and agreed well with previous results on healthy liver.27
5.2. Optimization based on CRLB
The simulation results justify the optimization approach since a lower CRLB was associated with a lower estimation error from segmented model fitting. Although the error from segmented model fitting was lower than the CRLB, likely because of the constraint f ≥ 0, thus contradicting the theory that CRLB is the lower limit of the estimation error, CRLB could be seen still to serve as a useful indicator of the actual error. Furthermore, the deviations from a fully monotonically increasing relationship between estimation errors derived from CRLB and segmented fitting were small and should therefore have minimal effects on the resulting b‐value schemes. Furthermore, the agreement between the results from simulations and in vivo measurements also suggests that the optimization provides important improvements in in vivo measurements.
However, the optimization of b‐value schemes was performed under the assumption that Equation 2 is a proper model for the signal behavior. If the signal contribution from the perfusion compartment is nonnegligible for the b‐values larger than zero, the parameter estimates will be biased.11, 25 Similarly, if too‐high b‐values are used, a bias due to diffusional variance36 or low SNR, which results in a non‐Gaussian noise distribution,31 may be introduced. For the liver scenario that was studied in this paper, the chosen b‐value limits had minimal impact on the results other than a bias seen for very low values of D*. The decreased estimation variability obtained when using the optimized b‐value scheme was essentially unaffected by the value of D* and the upper b‐value limit only played a marginal role when the TE‐related SNR penalty was included in the optimization. When applied to other tissue types or scan situations, the lower and upper limits of the b‐values used in the optimization should be chosen carefully on the basis of expected IVIM parameter values and SNR to ensure a bias of acceptably low magnitude and ensure that a Gaussian noise approximation is appropriate. The Gaussian noise distribution was assumed in the optimization and model fitting in this study while simulated and in vivo data have non‐Gaussian noise characteristics at low SNR. However, the desired reduction in parameter estimation variability was still achieved while only a minimal bias was introduced as seen in the simulation results (see Figure 3).
5.3. The objective function
An important step when setting up the optimization for obtaining an optimal set of b‐values is the choice of objective function. Several aspects must be taken into account when the objective function is formulated. Some of the most important aspects are whether the estimation error should be minimized directly or indirectly by use of for example CRLB, whether estimation bias or just variability should be minimized, and how errors of different parameters are combined into a single measure. Since the specific choices related to many of this kind of aspects make the objective function different rather than better or worse, choosing a preferable objective function is more or less a subjective choice. It is instead important to know the implications of these methodological choices when setting up the optimization or analyzing the results.
Direct minimization of the estimation error can be performed by running Monte Carlo simulations and model fitting in each iteration as suggested by Lemke et al.2 Such an approach can easily incorporate e.g. complex characteristics of the model‐fitting method and noise distribution, but is associated with a high computational cost, which may necessitate simplifications such as an incremental build of the b‐value scheme that may result in a suboptimal solution. Indirect minimization of the estimation error based on e.g. CRLB or some other closed form approximation of the parameter estimation error is computationally cheaper, but often builds on several assumptions. If the specific assumptions do not hold for a particular experiment setup, the effects on the obtained b‐value scheme may be nontrivial to predict. Nevertheless, optimization based on CRLB has been successfully applied to diffusion MRI for several methods.14, 19, 20, 37 However, as available computational power increases, Monte Carlo‐based methods may become more tractable.
It is typically preferable to minimize not only the estimation variability but also the bias. To accomplish this, the bias may be included as part of the objective function or the optimization can be constrained to avoid solutions that cause substantial bias. However, if the bias is to be included in the objective function, it is necessary to define a way of combining it with the estimation variability into a single measure, where the weights of the two factors are not necessarily equal. Furthermore, expressions related to the bias may be difficult to obtain depending on the error measure that is used. On the other hand, explicit constraints are easier to apply to the optimization, but it may be harder to relate them to the actual bias of the model parameters. In addition, the importance of minimization of variability relative to bias may vary depending on application.
To enable optimization for multiparametric models, a method must be chosen for combining errors of multiple parameters. In the current study, the errors of parameters were combined as a sum of the relative errors similar to previous studies.2, 20 However, there are several other possible alternatives such as a sum of squared relative errors,14 a weighted sum of relative errors,21 or a weighted sum of absolute errors. While the use of squared errors provides cleaner analytical expressions, it also places a strong weight on minimizing the largest parameter error. Similarly, the use of relative errors may place a stronger emphasis on minimization of errors of small parameter values. This is especially important if the presented optimization framework is used for low‐perfused tissue, where the errors of small value of f would be given a comparatively strong impact.11
5.4. Limitations
A limitation of this work is that even if the presented framework is general in principle, the in vivo verification in this study was limited to a single tissue type, the liver. Confirmation of the results in other tissue types is thus needed and should include careful evaluation regarding the choice of b‐value limits. Another limitation is that the optimized b‐value scheme was only compared with a scheme with linearly distributed b‐values. The reduction in estimation uncertainty will depend on the reference b‐value scheme, and the linear b‐value scheme is not common among studies limited to D and f. However, the linear b‐value scheme serves as a contrast to a b‐value scheme based on repeated acquisition of a few key b‐values, such as the scheme found to be optimal in this study.
6. CONCLUSIONS
A substantially reduced estimation uncertainty of the IVIM parameters D and f, derived from segmented model fitting, can be achieved by the use of optimal b‐value schemes. The optimal b‐value schemes, as obtained from CRLB optimization, were always composed of three unique b‐values, with approximately twice as many acquisitions for the middle and high b‐value as for b = 0. The improved estimation certainty was seen in results from simulations as well as from in vivo data.
Supporting information
FIGURES S1‐S2 Comparison of CRLB‐derived estimation error and the corresponding measure obtained from simulations. Equivalent to Figure 1, but with simulated D* = 10 µm2/ms or D* = 20 µm2/ms. CRLB, Cramer‐Rao lower bound
FIGURES S3‐S5 Estimation variability obtained from simulations with different combinations of D, f, and D* for each of the two b‐value schemes, showing data that underlie what is shown in Figure 2
FIGURES S6‐S8 Estimation bias obtained from simulations with different combinations of D, f, and D* for each of the two b‐value schemes, showing data that underlie what is shown in Figure 3
FIGURES S9‐S14 IVIM parameter maps from repeated scans as well as the mean and the standard deviation of those maps. Equivalent to Figures 5 and 6, but showing the remaining six subjects and both D and f shown in the same figure IVIM, intravoxel incoherent motion
FIGURES S15 Median standard deviation of parameter estimates over repeated measurements for each subject and b‐value scheme
TABLES S1‐S3 Optimized b‐value schemes as in Table 1, but without the upper b‐value limit, without the SNR penalty or without any of the two SNR, signal‐to‐noise ratio
Jalnefjord O, Montelius M, Starck G, Ljungberg M. Optimization of b‐value schemes for estimation of the diffusion coefficient and the perfusion fraction with segmented intravoxel incoherent motion model fitting. Magn Reson Med. 2019;82:1541–1552. 10.1002/mrm.27826
REFERENCES
- 1. Le Bihan D, Breton E, Lallemand D, Aubin ML, Vignaud J, Laval‐Jeantet M. Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging. Radiology. 1988;168:497–505. [DOI] [PubMed] [Google Scholar]
- 2. Lemke A, Stieltjes B, Schad LR, Laun FB. Toward an optimal distribution of b values for intravoxel incoherent motion imaging. Magn Reson Imaging. 2011;29:766–776. [DOI] [PubMed] [Google Scholar]
- 3. Barbieri S, Donati OF, Froehlich JM, Thoeny HC. Impact of the calculation algorithm on biexponential fitting of diffusion‐weighted MRI in upper abdominal organs. Magn Reson Med. 2016;75:2175–2184. [DOI] [PubMed] [Google Scholar]
- 4. Orton MR, Collins DJ, Koh D‐M, Leach MO. Improved intravoxel incoherent motion analysis of diffusion weighted imaging by data driven Bayesian modeling. Magn Reson Med. 2014;71:411–420. [DOI] [PubMed] [Google Scholar]
- 5. Gustafsson O, Montelius M, Starck G, Ljungberg M. Impact of prior distributions and central tendency measures on Bayesian intravoxel incoherent motion model fitting. Magn Reson Med. 2018;79:1674–1683. [DOI] [PubMed] [Google Scholar]
- 6. Freiman M, Perez‐Rossello JM, Callahan MJ, et al. Reliable estimation of incoherent motion parametric maps from diffusion‐weighted MRI using fusion bootstrap moves. Med Image Anal. 2013;17:325–336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Merisaari H, Movahedi P, Perez IM, et al. Fitting methods for intravoxel incoherent motion imaging of prostate cancer on region of interest level: repeatability and Gleason Score Prediction. Magn Reson Med. 2017;77:1249–1264. [DOI] [PubMed] [Google Scholar]
- 8. Pekar J, Moonen C, van Zijl P. On the precision of diffusion/perfusion imaging by gradient sensitization. Magn Reson Med. 1992;23:122–129. [DOI] [PubMed] [Google Scholar]
- 9. Cho GY, Moy L, Zhang JL, et al. Comparison of fitting methods and b‐value sampling strategies for intravoxel incoherent motion in breast cancer. Magn Reson Med. 2015;74:1077–1085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Sénégas J, Perkins TG, Keupp J, et al. Towards organ‐specific b‐values for the IVIM‐based quantification of ADC: in vivo evaluation in the liver In Proceedings of the 20th Annual Meeting of ISMRM, Melbourne, Australia, 2012. p. 1891. [Google Scholar]
- 11. Meeus EM, Novak J, Dehghani H, Peet AC. Rapid measurement of intravoxel incoherent motion (IVIM) derived perfusion fraction for clinical magnetic resonance imaging. Magn Reson Mater Phy. 2018;31:269–283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Mürtz P, Sprinkart AM, Reick M, et al. Accurate IVIM model‐based liver lesion characterisation can be achieved with only three b‐value DWI. Eur Radiol. 2018: 1-11.%2010.1007/s00330-018-5401-7. [DOI] [PubMed] [Google Scholar]
- 13. MacKay D. Information‐based objective functions for active data selection. Neural Comput. 1992;4:589–603. [Google Scholar]
- 14. Alexander DC. A general framework for experiment design in diffusion MRI and its application in measuring direct tissue‐microstructure features. Magn Reson Med. 2008;60:439–448. [DOI] [PubMed] [Google Scholar]
- 15. Cercignani M, Alexander DC. Optimal acquisition schemes for in vivo quantitative magnetization transfer MRI. Magn Reson Med. 2006;56:803–810. [DOI] [PubMed] [Google Scholar]
- 16. Pineda AR, Reeder SB, Wen Z, Pelc NJ. Cramér‐Rao bounds for three‐point decomposition of water and fat. Magn Reson Med. 2005;54:625–635. [DOI] [PubMed] [Google Scholar]
- 17. Bito Y, Hirata S, Yamamoto E. Optimum Gradient Factors for Apparent Diffusion Coefficient Measurements In Proceedings of the 3rd Annual Meeting of ISMRM, Nice, France, 1995. p. 913. [Google Scholar]
- 18. Xing D, Papadakis NG, Huang CL, Lee VM, Carpenter TA, Hall LD. Optimised diffusion‐weighting for measurement of apparent diffusion coefficient (ADC) in human brain. Magn Reson Imaging. 1997;15:771–784. [DOI] [PubMed] [Google Scholar]
- 19. Brihuega‐Moreno O, Heese FP, Hall LD. Optimization of diffusion measurements using Cramer‐Rao lower bound theory and its application to articular cartilage. Magn Reson Imaging. 2003;50:1069–1076. [DOI] [PubMed] [Google Scholar]
- 20. Leporq B, Saint‐Jalmes H, Rabrait C, et al. Optimization of intra‐voxel incoherent motion imaging at 3.0 Tesla for fast liver examination. J Magn Reson Imaging. 2015;41:1209–1217. [DOI] [PubMed] [Google Scholar]
- 21. Zhang JL, Sigmund EE, Rusinek H, et al. Optimization of b‐value sampling for diffusion‐weighted imaging of the kidney. Magn Reson Med. 2012;67:89–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Slator PJ, Hutter J, Ianus A, et al. A framework for calculating time‐efficient diffusion MRI protocols for anisotropic IVIM and an application in the placenta In 2018 MICCAI Workshop on Computational Diffusion MRI (CDMRI'18), Granada, Spain, 2018. [Google Scholar]
- 23. Dyvorne H, Jajamovich G, Kakite S, Kuehn B, Taouli B, Taouli B. Intravoxel incoherent motion diffusion imaging of the liver: optimal b‐value subsampling and impact on parameter precision and reproducibility. Eur J Radiol. 2014;83:2109–2113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Chen W, Zhang J, Long D, Wang Z, Zhu J‐M. Optimization of intra‐voxel incoherent motion measurement in diffusion‐weighted imaging of breast cancer. J Appl Clin Med Phys. 2017;18:191–199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. While PT, Teruel JR, Vidic I, Bathen TF, Goa PE. Relative enhanced diffusivity: noise sensitivity, protocol optimization, and the relation to intravoxel incoherent motion. Magn Reson Mater Phy. 2018;31:425–438. [DOI] [PubMed] [Google Scholar]
- 26. Taouli B. ed. Extra‐Cranial Applications of Diffusion‐Weighted MRI. Cambridge: Cambridge University Press; 2010. [Google Scholar]
- 27. Li YT, Cercueil J‐P, Yuan J, Chen W, Loffroy R, Wáng Y. Liver intravoxel incoherent motion (IVIM) magnetic resonance imaging: a comprehensive review of published data on normal values and applications for fibrosis and tumor evaluation. Quant Imaging Med Surg. 2017;7:59–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Cho GY, Moy L, Kim SG, et al. Evaluation of breast cancer using intravoxel incoherent motion (IVIM) histogram analysis: comparison with malignant status, histological subtype, and molecular prognostic factors. Eur Radiol. 2016;26:2547–2558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Park HJ, Sung YS, Lee SS, et al. Intravoxel incoherent motion diffusion‐weighted MRI of the abdomen: The effect of fitting algorithms on the accuracy and reliability of the parameters. J Magn Reson Imaging. 2017;45:1637–1647. [DOI] [PubMed] [Google Scholar]
- 30. Liu C, Liang C, Liu Z, Zhang S, Huang B. Intravoxel incoherent motion (IVIM) in evaluation of breast lesions: comparison with conventional DWI. Eur J Radiol. 2013;82:782–789. [DOI] [PubMed] [Google Scholar]
- 31. Gudbjartsson H, Patz S. The Rician distribution of noisy MRI data. Magn Reson Med. 1995;34:910–914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Andersson J. Maximum a posteriori estimation of diffusion tensor parameters using a Rician noise model: why, how and but. NeuroImage. 2008;42:1340–1356. [DOI] [PubMed] [Google Scholar]
- 33. Jerome NP, d'Arcy JA, Feiweier T, et al. Extended T2‐IVIM model for correction of TE dependence of pseudo‐diffusion volume fraction in clinical diffusion‐weighted magnetic resonance imaging. Phys Med Biol. 2016;61:667–680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Ozaki M, Inoue Y, Miyati T, et al. Motion artifact reduction of diffusion‐weighted MRI of the liver: use of velocity‐compensated diffusion gradients combined with tetrahedral gradients. J Magn Reson Imaging. 2013;37:172–178. [DOI] [PubMed] [Google Scholar]
- 35. Aliotta E, Wu HH, Ennis DB. Convex optimized diffusion encoding (CODE) gradient waveforms for minimum echo time and bulk motion‐compensated diffusion‐weighted MRI. Magn Reson Med. 2017;77:717–729. [DOI] [PubMed] [Google Scholar]
- 36. Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K. Diffusional kurtosis imaging: The quantification of non‐Gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med. 2005;53:1432–1440. [DOI] [PubMed] [Google Scholar]
- 37. Lampinen B, Szczepankiewicz F, van Westen D, et al. Optimal experimental design for filter exchange imaging: apparent exchange rate measurements in the healthy brain and in intracranial tumors. Magn Reson Med. 2017;77:1104–1114. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
FIGURES S1‐S2 Comparison of CRLB‐derived estimation error and the corresponding measure obtained from simulations. Equivalent to Figure 1, but with simulated D* = 10 µm2/ms or D* = 20 µm2/ms. CRLB, Cramer‐Rao lower bound
FIGURES S3‐S5 Estimation variability obtained from simulations with different combinations of D, f, and D* for each of the two b‐value schemes, showing data that underlie what is shown in Figure 2
FIGURES S6‐S8 Estimation bias obtained from simulations with different combinations of D, f, and D* for each of the two b‐value schemes, showing data that underlie what is shown in Figure 3
FIGURES S9‐S14 IVIM parameter maps from repeated scans as well as the mean and the standard deviation of those maps. Equivalent to Figures 5 and 6, but showing the remaining six subjects and both D and f shown in the same figure IVIM, intravoxel incoherent motion
FIGURES S15 Median standard deviation of parameter estimates over repeated measurements for each subject and b‐value scheme
TABLES S1‐S3 Optimized b‐value schemes as in Table 1, but without the upper b‐value limit, without the SNR penalty or without any of the two SNR, signal‐to‐noise ratio


