Task-Dependent Constraints in Motor Control: Pinhole Goggles Make the Head Move Like an Eye

Abstract

In the 19th century, Donders observed that only one three-dimensional eye orientation is used for each gaze direction. Listing's law further specifies that the full set of eye orientation vectors forms a plane, whereas the equivalent Donders' law for the head, the Fick strategy, specifies a twisted two-dimensional range. Surprisingly, despite considerable research and speculation, the biological reasons for choosing one such range over another remain obscure. In the current study, human subjects performed head-free gaze shifts between visual targets while wearing pinhole goggles. During fixations, the head orientation range still obeyed Donders' law, but in most subjects, it immediately changed from the twisted Fick-like range to a flattened Listing-like range. Further controls showed that this was not attributable to loss of binocular vision or increased range of head motion, nor was it attributable to blocked peripheral vision; when subjects pointed a helmet-mounted laser toward targets (a task with goggle-like motor demands but normal vision), the head followed Listing's law even more closely. Donders' law of the head only broke down (in favor of a “minimum-rotation strategy”) when head motion was dissociated from gaze. These behaviors could not be modeled using current “Donders' operators” but were readily simulated nonholonomically, i.e., by modulating head velocity commands as a function of position and task. We conclude that the gaze control system uses such velocity rules to shape Donders' law on a moment-to-moment basis, not primarily to satisfy perceptual or anatomic demands, but rather for motor optimization; the Fick strategy optimizes the role of the head as a platform for eye movement, whereas Listing's law optimizes rapid control of the eye (or head) as a gaze pointer.

Although the eye is mechanically able to rotate torsionally (i.e., about the nasal–occipital axis), the oculomotor system normally chooses just one angle of ocular torsion for any one gaze direction (Donders, 1848). Since its discovery, this Donders' law has been extended to apply to several motor systems whose motion is restricted by the brain to eliminate needless degrees of freedom (Straumann et al., 1991; Hore et al., 1992; Theeuwen et al., 1993; Crawford and Vilis, 1995). For example, Donders' law also applies to the head, which is mechanically able to rotate torsionally but which normally adopts just one torsional angle for any one facing direction (Straumann et al., 1991; Glenn and Vilis 1992; Tweed and Vilis 1992). However, what are the functional advantages of Donders' law that caused it to develop in these different motor systems? Surprisingly, after a century of research and speculation, the answer is unknown.

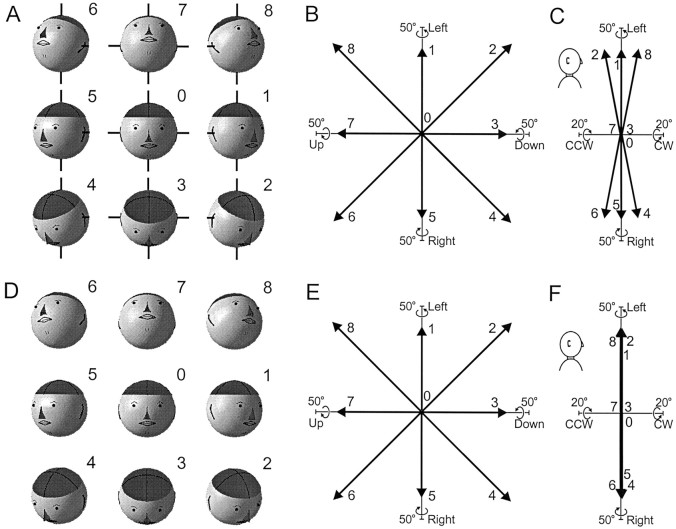
One clue, however, is that different body parts obey different forms of the law. For example, the eye obeys a form of Donders' law called Listing's law, which means that it assumes only those orientations that can be reached from a central reference position by rotation about a fixed axis in a plane (von Helmholtz, 1867; Ferman et al., 1987;Tweed and Vilis, 1990a). Some geometric consequences of Listing's law are that the torsional angle of the eye is always zero (when rotational position is expressed using quaternions) (Westheimer, 1957) and that the vectors representing the three-dimensional (3-D) orientations of the eye are not spread out in a 3-D volume but instead fall in a single flat surface known as Listing's plane. (See Fig.1, E and F, for an illustration of such vectors.) In contrast, the head tends toward a form of Donders' law called the Fick strategy (Glenn and Vilis, 1992;Theeuwen et al., 1993; Radau et al., 1994; Tweed et al., 1995;Medendorp et al., 1998; Misslisch et al., 1998; Crawford et al., 1999). As a result of this strategy, the vectors representing 3-D head orientation do not fall within a plane but rather in a twisted, saddle-shaped surface, with non-zero torsional components at oblique facing directions (Fig. 1A–C).

Fig. 1.

Two possible forms of Donders' law of the head: the Fick pattern (A–C) and Listing's law (D–F). A, In the Fick pattern, purely horizontal rotations occur about the illustrated torso-fixed vertical axis and purely vertical rotations about the illustrated head-fixed horizontal axis (note the foreshortening of the horizontal axis in head positions 5 and 1). Shown are the head positions that would be used to view the nine dots in the standard target array used in this experiment. B, Front view (showing horizontal and vertical components) of orientation vectors for head positions in A, plotted in space-fixed coordinates. These vectors describe orientation by specifying the virtual axis of rotation relative to a central reference position; the vector's length is proportionate to the angle of that rotation. The right-hand rule applies, e.g., to interpret position 1in A, point your right thumb upward; then, your fingers curl leftward, in the direction of rotation. Orientation vectors are labeled with their corresponding number, e.g., 1 inB is the orientation vector for final head position1 in A. C, Same distribution of orientation vectors in B but viewed from the side (i.e., vertical vs torsional axes). Note that the torsional axis in orientation vector coordinates is fixed in space, independent of head movement. As a result, vectors for positions with zero torsion in Fick coordinates have non-zero components in these coordinates, particularly at the corner positions (2,4, 6, and 8). As shown previously, the total set of such vectors falls within a twisted, saddle-shaped distribution (Glenn and Vilis, 1992; Radau et al., 1994).D, Head positions hypothetically obeying Listing's law. Same convention as in A. E,F, Front and side views of head orientation vectors for head positions in D. Same convention as inB and C. The side view shows that the orientation vectors now lie in a plane in this coordinate system. (For the head traces in A and D, Matlab coding courtesy of W. P. Medendorp, J. A. M. Van Gisbergen, M. W. I. M. Horstink, and C. C. A. M. Gielen, as reported in Medendorp et al., 1999).

Various suggestions have been made as to the functional purpose of Listing's law, for instance that it optimizes the perception of radial lines (Hering, 1868), binocular vision (Crawford and Vilis, 1991), saccade paths to and from center (Tweed and Vilis, 1990a), a combination of the latter two (Tweed, 1997b), the visuomotor transformation (Hepp et al., 1997), or the workload on the eye muscles (Fick, 1858; Tweed and Vilis, 1990; Radau et al., 1994). Similarly, the Fick strategy for the head could optimize the perception of lines on the horizon (Glenn and Vilis, 1992; Hore et al., 1992), binocular alignment of the eyes with the horizon (Crawford and Vilis, 1995), perceived tilt in visual and/or vestibular stimuli (Rock et al., 1981; Crawford and Vilis, 1995; Crawford et al., 1999), the workload on the neck muscles (Glenn and Vilis 1992; Radau et al., 1994), the motion of cervical vertebrae (the top two of which are linked anatomically like Fick gimbals) (Glenn and Vilis, 1992), or eye–arm coordination (Straumann et al., 1991; Theeuwen et al., 1993). However, these arguments remain speculative.

Recently, an opportunity to test between most of these possibilities has presented itself. Crawford et al. (1999) found that, when monkeys made gaze shifts while wearing pinhole goggles (opaque glasses that reduced the visual range to a monocular 8° disk), the twisted, Fick-like twist distribution of head orientation vectors observed during gaze fixations (Fig. 1A–C) flattened into something resembling Listing's plane (Fig.1D–F). Here, we demonstrate a similar phenomenon in humans, showing that pinhole goggles alter the form of Donders' law used to restrict head orientation during gaze fixations. We then use variations on the goggle experiment to determine which of the following factors are important in shaping this law: binocular vision, peripheral vision, range of head motion, or motor demands on the head.

MATERIALS AND METHODS

Ten subjects (six female, four male; aged 23–44; without known eye or head movement disorders) participated, and all signed informed consent papers before the experiments. The study was preapproved by the Human Participants Review Subcommittee of York University.

Subjects performed gaze shifts in a lighted room with their torsos fixed via seatbelts to a stationary chair within three mutually perpendicular magnetic fields (frequencies 90, 124, and 250 kHz) generated by Helmholtz coils 2 m across. Three-dimensional head orientations were measured using magnetic search coils, as described previously (Tweed et al., 1990; Glenn and Vilis, 1992). Unless otherwise stated below, we used a homemade, 3-D coil attached to a snug swim cap. The three voltages from each coil were sampled at 100 Hz. Subjects reported that our gaze-related tasks were easy to perform, but for additional confirmation, we measured orientation of the right eye using Skalar (Delft, The Netherlands) search coils. This was done in the first three subjects in experiment 1 and in four subjects in experiment 4. Calibration and accuracy were as described previously (Henriques et al., 1998; Klier and Crawford, 1998).

Target arrays. Subjects made eye–head gaze shifts between white dots (1 cm diameter) on a black tangent screen 1.1 m in front of them. The “standard target array” consisted of nine dots arranged in a square grid centered in front of the right eye. The central target was placed at the intersection of the horizontal meridian and the parasagittal plane, the four cardinal targets were 40° right, left, above, and below it, and the four oblique targets were 48° from center, in the corners. This array of targets was selected to clearly distinguish between the Fick and Listing strategies, which give position ranges that mainly differ at the corners. Some experiments also used a “reduced target array” of two dots 25° left and right of center, two dots 20° above and below center, and four oblique targets 28° from center, in the corners. These dimensions were selected to match the typical range of head positions seen during normal gaze shifts to targets of the standard array.

At the start of every task (defined in the next section), subjects fixated the center target to define a reference position. Then, at 2 sec intervals, they were verbally instructed to redirect their gaze to specific targets, e.g., up–left, down–right, middle–center, as in a previous gaze-control experiment (Glenn and Vilis, 1992). Sessions were divided into 20 sec blocks, each randomized block including one gaze shift to each of the nine targets, and each task consisted of five blocks for a total of 100 sec and 45 fixations. Subjects were allowed to briefly practice each such task before the experiment just to the point of familiarizing themselves with the instructions.

Experiments. Four experiments were performed, each composed of a set of tasks designed to test between different hypotheses of Donders' law of the head. Experiment 1 measured the basic effect of pinhole goggles on head motion. Subjects performed two tasks: control and goggle. In the control task (CT), subjects made head-free gaze shifts to the targets of the standard array. This was done both before and after other manipulations to account for hysteresis effects, such as fatigue and practice. In the goggle task (GT), subjects wore opaque goggles that blocked all vision except through a single monocular aperture, 5 mm across, that reduced the visual range to 10°. The aperture was positioned over the right eye at the median of the eye positions that the first six subjects used when they looked straight ahead without goggles (in a preliminary test). Wearing the goggles, subjects made head-free gaze shifts to the targets of the standard array. Note that the goggles did not allow for peripheral vision of any target beyond the current fixation point, so subjects had to acquire these targets based on remembered representations formed during previous control and practice runs. Only subjects who showed a significant effect (i.e., an altered Donders' law of the head) in this experiment went on to participate in the remaining experiments, which were designed to determine why the effect occurred.

Experiment 2 explored which aspect of the goggle task caused the changes in head motion: monocular vision, enlarged head movements, factors related to memory, peripheral vision, and/or motor task constraints. Subjects performed five tasks: the CT; the patch task (PT), wearing no goggles but a patch over the left eye; the GT; the binocular-goggle task (BG), wearing modified pinhole goggles with an aperture centered in front of each eye; and the reduced range goggle task (RG) in which subjects made gaze shifts with the standard goggles to targets in the reduced array. Subjects also performed a memory control task (MT) in which they performed gaze shifts between remembered targets in the dark. This was done after standard controls but before donning the goggles to avoid contaminating their cognitive set.

Experiment 3 tested whether it was the loss of peripheral vision with pinhole goggles that altered the pattern of head motion. Subjects wore a light-weight bicycle helmet (380 gm), which fit tightly over the swimming cap and was fastened with chin-straps. Attached to the helmet were a 3-D coil and a laser pointer mounted on top via a universal joint positioner. Before testing, subjects fixated the center target with the helmet and goggles on, and the laser was adjusted to point at the center target. The goggles were then removed, and the subjects performed three tasks: the control helmet task (CH) in which the laser was off and subjects made unencumbered gaze shifts to the targets of the standard array while wearing the helmet; the standard laser task (LT) in which subjects pointed the laser at targets of the standard array; and the reduced laser task (RL), using the reduced target array. Finally, subjects removed the helmet and repeated the control and goggle tasks (using the standard target array) for comparison.

Experiment 4 tested the idea that head movements obey Donders' law only when they are part of a gaze shift. Subjects repeated the control helmet task and then performed a gaze-fixation task (GF) by keeping their eyes on the center target while turning their heads to point the laser at targets of the reduced range, i.e., gaze was stationary and only the head moved. CH and RL were also repeated here as controls.

Data analysis. Reference positions of the head and right eye were defined by having subjects look straight ahead at the center target. From the raw coil signals, we then computed quaternions (Tweed and Vilis, 1990a; Tweed et al., 1990) to represent the orientations of the eye in space (E_s) and head in space (H_s) with respect to their reference positions (Tweed et al., 1990, 1995). These quaternions,E_s andH_s, were expressed in a right-handed coordinate system that was aligned with the Helmholtz coils. Orientation of the eye in the head (E_h) were computed fromE_s andH_s orientations as described previously (Glenn and Vilis, 1992). Gaze direction and head-facing direction were expressed as unit vectors that were computed from quaternions (Tweed et al., 1990). For 2-D display, these vectors were projected onto a frontal plane aligned with the horizontal and vertical magnetic fields.

Previous experiments have shown that, strictly speaking, Donders' law of the head only holds during head fixations between movements (Crawford et al., 1999). In contrast, head movement trajectories do not generally obey Donders' law (with the possible exception of pure horizontal or vertical movements). In particular, large oblique movements clearly violate the Fick constraint, transiently leaving the twisted Fick surface to take the shortest path between two corners with a similar torsional twist (Fig. 1C). Moreover, several of our experiments, such as restricting the visual range, were primarily relevant to stable fixation points at which the visual information is gathered, so that any effect on trajectories would only be secondary. Thus, movement trajectories were not the focus of our analysis.

Instead, to characterize Donders' law, we quantified the 3-D range of head orientations at fixation points at which head velocity was <10°/sec. This was done by computing theH_s surface, which is a second-order surface of best fit to the H_squaternions (Tweed and Vilis, 1990a; Tweed et al., 1990; Glenn and Vilis, 1992; Theeuwen et al., 1993; Radau et al., 1994; Medendorp et al., 1998; Misslisch et al., 1998; Crawford et al., 1999). A second-order surface is described by the following equation, which expresses torsional position (q₁) as a function of vertical (q₂) and horizontal (q₃) position:

$$q_1=a_1+a_2{q}_2+a_3{q}_3+a_4(q_2{)}^2+a_5{q}_2{q}_3+a_6(q_3{)}^2.$$ Equation 1

For each task, we also computed its torsional variability, which quantifies how closely the head orientations cluster around theirH_s surface (Tweed et al., 1990;Crawford et al., 1999). The smaller the torsional variability, the closer the H_s quaternions adhere to their surface and therefore the better they conform to Donders' law.

Note that the Fick strategy owes its name to its resemblance, at least at points of fixation, to the set of orientations describing the zero-torsion space in Fick coordinates, sometimes implemented mechanically with the use of a nested set of axes called Fick gimbals. In this instance, the vertical axis would be fixed in the body and the horizontal axis would be fixed in the head (Fig. 1A). To quantify the twist in the H_ssurface of fixation points, we computed its gimbal score (s) (Glenn and Vilis, 1992; Crawford et al., 1999), which describes the dependence of torsion on vertical and horizontal position as follows:

$$q_1=s(q_2{q}_3/q_0).$$ Equation 2

This allowed us to compare surface shapes along a continuum ranging from the twisted saddle generated by Fick gimbals (gimbal score of −1), through the plane produced by a system that follows Listing' law (gimbal score of 0), to the oppositely twisted saddle generated by Helmholtz gimbals (gimbal score of +1) in which the horizontal axis is fixed in the body and the vertical in the head. (Intermediate scores and scores of greater than ±1 are also possible.) Statistical analysis was performed with the SPSS (Chicago, IL) Statistical Package and consisted of two-tailed paired-sample t tests unless otherwise specified.

RESULTS

General observations: 2-D eye–head coordination

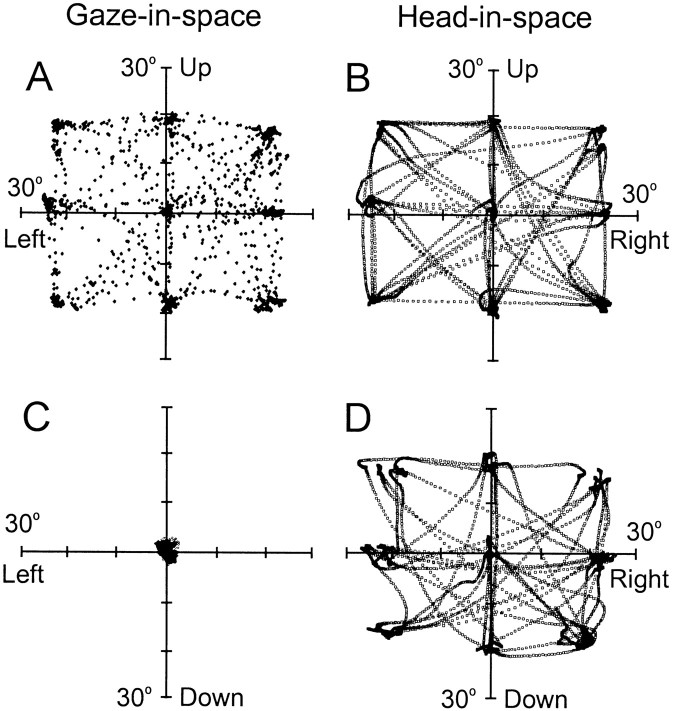
As a prelude to our 3-D analysis, Figure2 shows the basic way that pinhole goggles alter 2-D coordination of the eyes and head. These results confirm previous observations reported for the human (Misslisch et al., 1998) and monkey (Crawford and Guitton, 1997). The three rows of Figure 2 plot three 2-D variables: the gaze direction of the eye in space (E_s), the facing direction of the head in space (H_s), and the pointing direction of the eye relative to the head (E_h), all sampled while a subject fixated the nine targets of the standard array. Subjects were able to accurately aim the eye in space, E_s, at the nine targets both under normal conditions (A) and with pinhole goggles (D). The difference between the two conditions was in the relative contributions of the eyes and head to gaze direction.

Fig. 2.

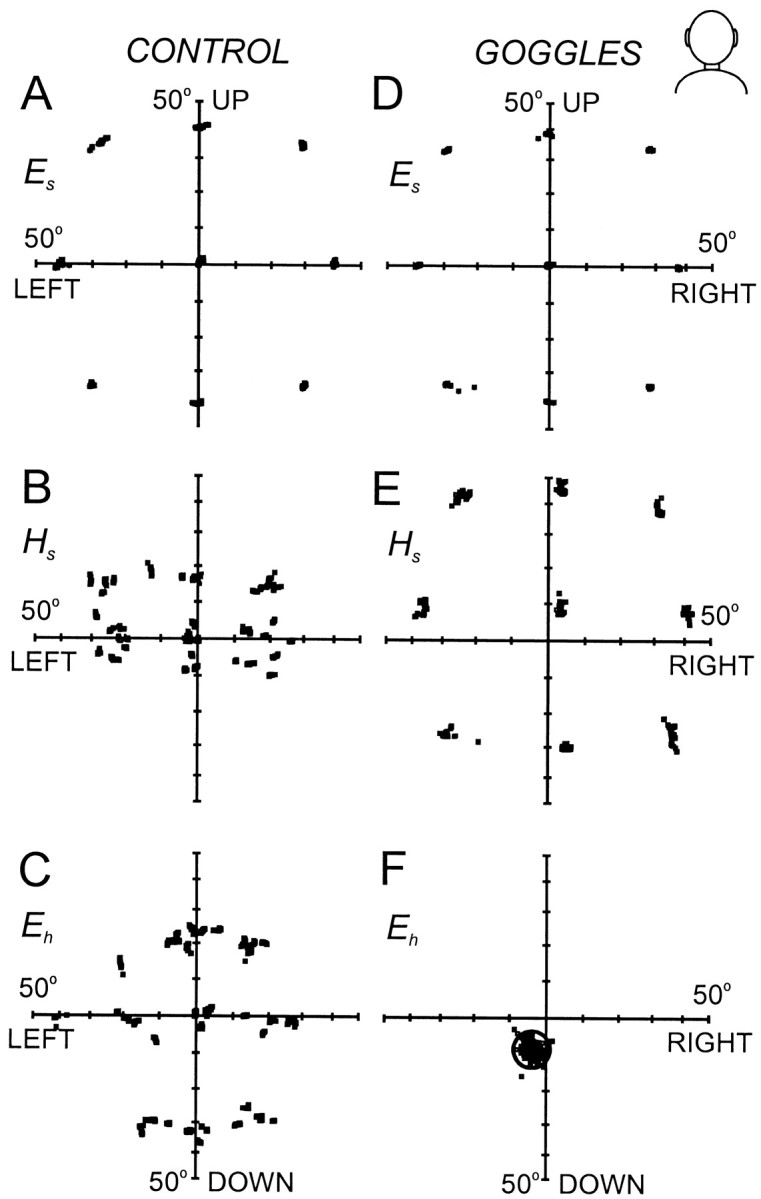
Frontal projections of two-dimensional pointing vectors: distribution of gaze, E_s(top row), head, H_s(middle row), and eye, E_h(bottom row) positions during control (A–C) and goggle (D–F) conditions, as viewed from behind one subject during head-free fixations toward the nine targets. Data points were selected as final fixation points at which eye, head, and gaze were <10°/sec. Cardinal targets were placed at 40° eccentricity and the oblique targets at 48°. Goggles restricted the effective visual range to ∼10° (denoted by the ring in F). Subject M.C.

Without goggles (B), the positions of the head in space, H_s, were variable and rather close to center, especially vertically, whereas with goggles (E), H_s positions were highly consistent and as eccentric as the target dots (with a slight shift related to eye–pinhole position), as of course they had to be to get the pinhole pointed at the targets. Without goggles (C), the positions of the eye relative to the head,E_h, were variable and covered a wide range, especially vertically, as in most previous studies (Glenn and Vilis, 1992; Crawford and Guitton, 1997; Freedman et al., 1997), whereas with goggles (F),E_h positions were tightly clustered so as to look through the small aperture (ring inF). Thus, subjects wearing pinhole goggles could still look at targets with great accuracy, but their pattern of eye–head coordination was changed so that the head was now the prime mover of gaze (Crawford and Guitton, 1997; Misslisch et al., 1998).

Experiment 1: do goggles alter Donders' law of the head in humans?

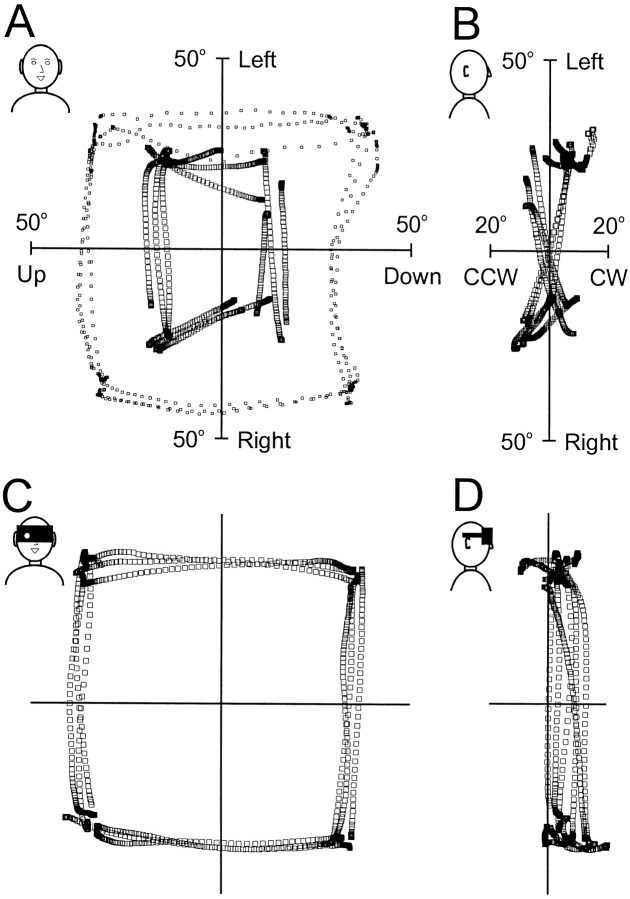
In monkeys, pinhole goggles alter the 3-D pattern of head motion (Crawford et al., 1999). Figure 3 shows a similar effect in humans: it plots 12 head movements (large squares) made by one subject in the control task (top row) and with goggles (bottom row). For the sake of clarity, we have only shown horizontal and vertical movements between the four corner targets. These trajectories, viewed from the front (A and C) and the side (B andD), represent the tips of orientation vectors like those explained in Figure 1. Thus, the right-hand rule applies, e.g., upward points on the vertical axis signify leftward head and gaze positions.

Fig. 3.

Three-dimensional head-in-space trajectories during movements in the control (A, B) and goggle (C, D) tasks. Shown are three horizontal and three vertical movements to each of the four oblique targets in the standard array. A, C, 2-D kinematics of head-in-space (large squares) and eye-in-space (small squares, only in A) orientations viewed from the front (head–shoulder caricature indicates space-fixed coordinates) of quaternions during control (A) and goggle (C) tasks, using the right-hand rule (horizontal axis flipped because of frontal view, see Fig. 1 legend).B, D, 3-D kinematics of head-in-space orientations showing side projection of quaternion vectors, i.e., horizontal position as a function of torsion during the control (B) and goggle (D) tasks. Subject M.C.

In the control task (A), the gaze point (plotted assmaller squares) was accurately controlled, but the vertical and horizontal components of head movement were highly variable. However, these vertical and horizontal movements should stay fairly close to the Donders' surface of the head (Glenn and Vilis, 1992;Crawford et al., 1999). Indeed, when viewed from the side perspective (B), these head trajectories formed the classic Fick twist, like that in Figure 1C. In contrast, with the goggle task (C), the head movements were larger, as expected, but more importantly, in the side view (D), the surface defined by their trajectories was less twisted than the control surface, and therefore more similar to the plane displayed in Figure 1F. Could this mean that the head had switched from the Fick strategy to Listing's law?

To answer this question, we will henceforth focus on head fixation points, at which Donders' law is known to hold with the greatest accuracy (Crawford et al., 1999). Figure4 plots such end positions for one subject, recorded in the control task (A) and with goggles (B). Recall that each task repetition consisted of nine targets fixated five times each, so the data set for each such file is derived from 45 independent fixations. Unfortunately, it is difficult to visually derive the 3-D shape of these ranges by looking at their 2-D projections (Fig.4A,B). Therefore, as in previous studies, surfaces of best fit were computed (Eq. 1) (Glenn and Vilis, 1992; Crawford et al., 1999; Medendorp et al., 1999).

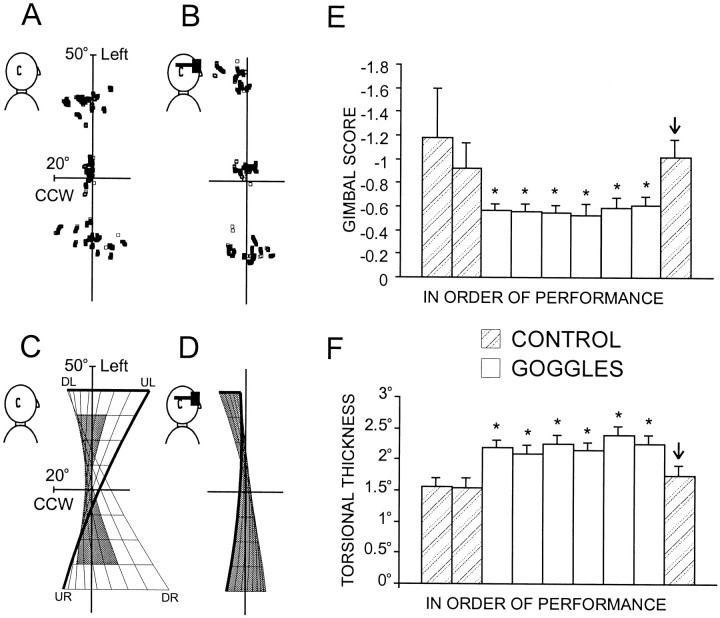
Fig. 4.

Head orientation during fixation of the nine targets in the control (A, C) and goggle (B, D) tasks of experiment 1.A, B, Quaternion vectors as viewed from the side (see caricatures) for subject S.P. during the control (A) and goggle (B) tasks. Only fixation points were considered, i.e., at which head speed was <10°/sec. C, D,H_s surfaces for the data in Aand B. Each grid indicates 10° horizontal–vertical across the surface, with a 40 × 40° limit (extent of the range of data for the goggle condition). The shaded areareflects the actual data range (i.e., data range of Aand B). Thick lines correspond to the upper and leftward edges of the fit according to gaze direction.CCW, Counterclockwise torsion. E, Gimbal scores (see Materials and Methods). Each bar represents the average gimbal score across all 10 subjects with SE, for each paradigm (100 sec intervals), presented in order of their performance during the experiment. *p < 0.05 indicates a significant difference from the final control task (↓); two-tailedt test. F, Torsional variability. Each bar shows the average torsional variability, in degrees, and its SE across all 10 subjects for each task, presented in order of performance. *p < 0.05 indicates a significant difference from the control task; two-tailedt test.

Figure 4, C and D, shows theH_s surfaces of best fit for the same data sets. Each square in the grids marks 10°. Thedarkened patches on the surfaces approximate the actual ranges of head motion, but to facilitate comparison, we draw all surfaces extended over the same 40 × 40° range, which corresponds to the largest head motions seen. In the control task (C), the H_s surface shows the twist characteristic of Fick gimbals;H_s assumes a counterclockwise orientation in the down–left (DL) and up–right positions (UR), and a clockwise orientation in the up–left (UL) and down–right (DR) positions. However, in the goggle task (D), theH_s surface becomes much less twisted.

To quantify the twist, we calculated gimbal scores with and without goggles. Figure 4E shows the average gimbal scores (and SE) for 10 subjects across all task repetitions, in order of their performance during the experiment, with the hatched barsrepresenting the control and the white bars representing the goggle task. During analysis of this experiment (and others with more than one control), we noticed that the size and intersubject variance of the control gimbal score dropped after its initial repetition, presumably because of practice. Therefore, for statistical analysis, we used the control whose gimbal score was most stable across subjects. In Figure 4E and subsequent similar figures, significant differences from this control (↓) are indicated byasterisks. On average, goggles reduced the gimbal score by 56%. This effect was significant compared with controls when tested across all 10 subjects (p = 0.021). Moreover, individually, 7 of the 10 subjects showed a statistically significant flattening of their range. This was accompanied by a slight but significant increase in torsional variance of the range (Fig.4F). Thus, in humans as in monkeys (Crawford and Guitton, 1997; Crawford et al., 1999), pinhole goggles flattened theH_s surface.

Experiment 2: task dependence

The rest of our experiments were designed to determine which aspect of the goggle task led to the alteration in Donders' law, i.e., to determine why this effect occurred. Therefore, these subsequent experiments were only performed on the seven subjects who individually showed a significant effect in experiment 1. Typical surfaces fit to the fixation ranges from experiment 2 are shown in Figure5A, with gimbal scores for these surfaces shown in B and torsional thickness scores in C. Once again, when retested in this experiment, these subjects showed the surface flattening effect in the GT compared with CT (Fig. 5A,B). But why?

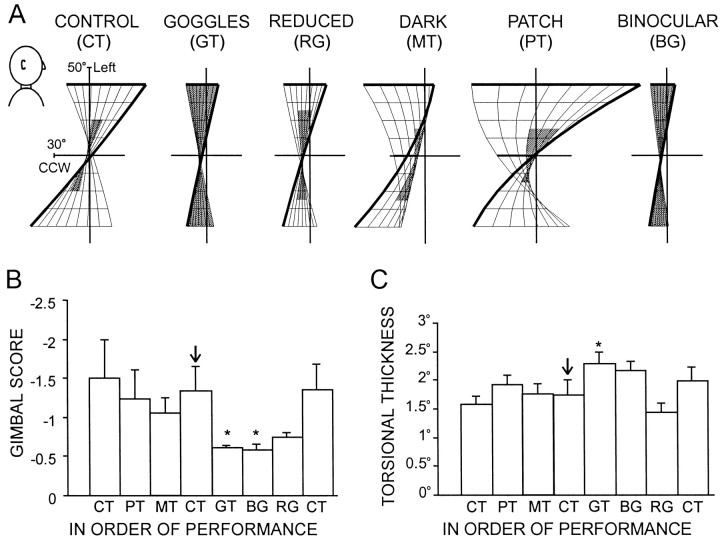
Fig. 5.

Head orientation in the ranges during fixation of the nine targets during the various task-constrained paradigms of experiment 2. A,H_s surfaces for each of the six tasks, viewed from the side of subject M.C. Shaded regionsreflect the actual data range with each surface fitted with a 40 × 40° range for standardization. CCW, Counterclockwise torsion. B, Quantitative comparison of the gimbal score. Each bar represents the average gimbal score across all seven subjects with SE, for each paradigm (100 sec intervals). *p < 0.05 indicates a significant difference from the control task (↓); two-tailed ttest. C, Quantitative comparison of the torsional thickness score of the head orientation range to the second-order surface. Each bar represents the average torsional thickness score, in degrees, across all seven subjects with SE, for each paradigm (100 sec intervals) with the above designations. *p < 0.05 indicates a significant difference from the control task; two-tailed t test. The surface fits (A) are ordered to follow the logical flow of Results, whereas the quantitative data (B, C) are arranged to document the actual order in which tasks were performed during the experiment.

We first examined the possibility that the change in the Donders' surfaces was simply attributable to a change in the 2-D range of head-facing directions. For instance, subjects wearing pinhole goggles make unusually large horizontal and vertical head movements. Might this extended range be what flattens theirH_s surfaces? We shrank the range by presenting a reduced target array, just 50° across and 40° high (see Materials and Methods). When subjects looked at these targets while wearing goggles, their head movements were, on average, no larger than in the control task. Yet their H_ssurfaces (RG) were still flattened (Fig.5A,B), with gimbal scores averaging just −0.61 versus −1.44 in the control case (p= 0.089). Therefore, the size of the head movements did not appear to be the crucial factor affecting the form of Donders' law.

Another possibility is that the flattening of the Donders' surfaces in the goggle paradigm (experiment 1) (Fig.4D,E) was simply attributable to the concomitant increase in torsional variance (Fig.4F). In other words, the goggles may have made Donders' law less precise, and the resulting noise or variability could have hidden the twist in the H_ssurface. That this was not the case is shown by Figure 5C, which plots torsional variability from this surface, a measure of the deviation from Donders' law (see Materials and Methods), for different tasks. It is true that the torsional variability is larger with goggles than without (2.2 vs 1.6°; p < 0.005), but this comparison is unfair because, with goggles, theH_s surface is also much larger horizontally and vertically. When we used the reduced target array so that the range of head motion with goggles was approximately the same as in the control condition without goggles, the torsional variability was actually slightly smaller than normal (1.5 vs 1.6°). Thus, for a given range of head motion, adherence to Donders' law was not degraded by wearing goggles, and therefore the surface-flattening effect could not be attributed to such a degradation.

Furthermore, the effect could not be attributed to the use of memory-guided movements rather than visually guided movements, because subjects failed to show the same flattening effect in our MT (Fig.5A). Although it is true that MT gimbal scores were reduced slightly relative to controls (Fig. 5B), this difference was not significant compared with any of the control gimbal scores (smallest, p = 0.135), whereas it was significantly higher (p = 0.042) than the equivalent goggle score. This issue will be addressed again in the next section.

A fourth possible reason for the flattening is that the goggles allowed only monocular vision. However, when subjects made gaze shifts (in the standard target array) with no goggles but with a patch over the left eye (PT), their H_s surfaces were still strongly twisted (Fig. 5A,B). Although the average gimbal score did shrink slightly, from −1.44 to −1.23, the change was not significant (p = 0.415). Thus, blocking vision in one eye did not flatten theH_s surface, nor did the opposite task (binocular vision with goggles) twist the surface (Fig.5A,B, BG); when subjects wore modified pinhole goggles with a hole for each eye, theirH_s surfaces were still flattened to the same degree as with the one-hole goggles (average gimbal scores in both cases being −0.58) and were much flatter than with no goggles (p = 0.031). Therefore, the presence or absence of binocular vision did not significantly affect the form of Donders' law.

Experiment 3: peripheral vision versus motor task constraints

A fifth possibility is that Donders' law has something to do with orienting the peripheral visual field to features in the environment and that pinhole glasses flatten theH_s surface because they block out the periphery. To test this idea, we required a task with the same motor requirements as the goggle task but with full peripheral vision. For this, we mounted a laser on a helmet and had subjects point it at targets of the standard array. This task also had the advantage of getting rid of the need for memory controls, because the visual aspect of the task was the same as in normal gaze shifts.

In a control condition (CH), subjects made normal eye–head gaze shifts to the standard targets array with the helmet on but the laser turned off. In this task, the H_s surface was twisted in the normal Fick-like manner (Fig.6A). However, when subjects pointed the laser toward the same targets (LT), the surface was much flatter (Fig. 6B) and the average gimbal score (Fig. 6D) was significantly smaller (−0.25 vs −1.07; p = 0.01). Thus, theH_s surface still flattened out, even with full peripheral vision.

Fig. 6.

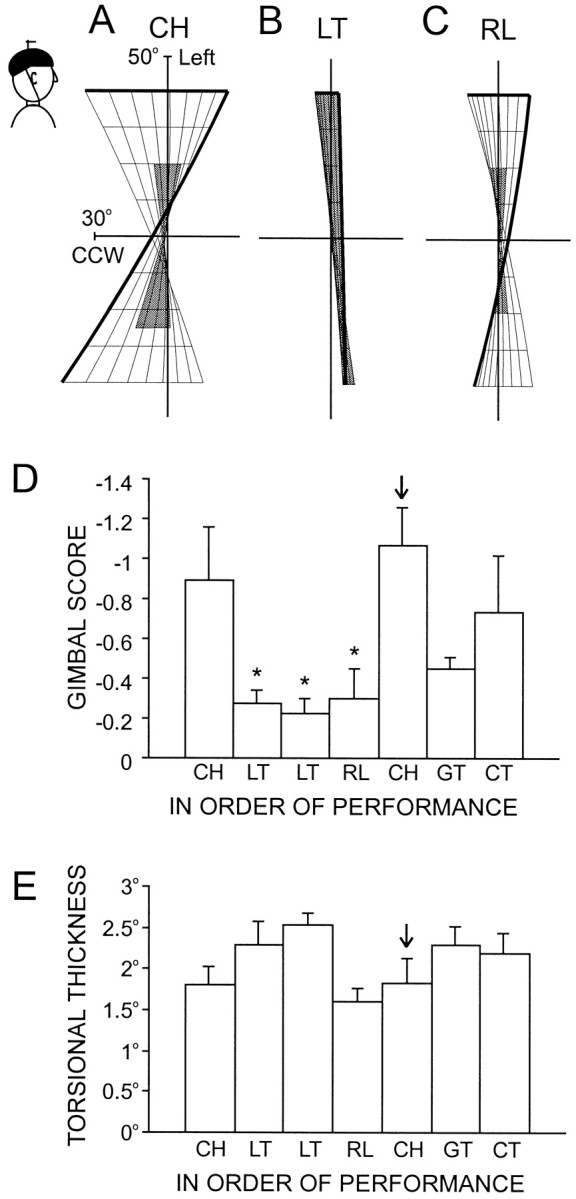
3-D head orientation in the tasks of experiment 3.A–C, H_s surfaces of subject M.S., viewed from the side. A, Control helmet task.B, Laser task. C, Reduced laser task.D, Gimbal scores. E, Average torsional variability across subjects. *p < 0.05 indicates significance of laser tasks relative to the second control helmet task (↓); two-tailed t test. Otherwise, conventions as Figure 5.

To check again for range effects, we asked subjects to point the laser at targets of the reduced array. The resultingH_s surface was still relatively flat (Fig. 6C). The average gimbal score of −0.30 was only slightly larger than in the LT and significantly smaller (p = 0.021) than in the CH. In addition, the gimbal scores for both the LT and RL tasks were even lower than in the GT, repeated here as a further control (Fig. 6D). Figure 6E shows that torsional variability, i.e., the deviation from Donders' law, was slightly but not significantly larger during the standard LT than in the control helmet and goggle tasks but again was even lower than normal in the RL. Thus, the head obeyed Listing's law even more closely in the laser task than in the goggle task, precluding the idea that this effect is attributable to the loss of peripheral vision, either for its role in perceiving initial target direction or in orienting the head to earth-fixed visual structures.

Experiment 4: Donders' law during head-gaze dissociation

In all of our experiments so far in which Donders' law held, head motion helped to transport the gaze point. For example, gaze and head-facing direction followed fairly similar 2-D trajectories during the laser task, as illustrated in Figure7, A and B. However, what if the orienting head movement were not part of a gaze shift? Would Donders' law now break down? To test this hypothesis, we had subjects fix their eyes on the center target and move their heads to point the laser at the other targets of the reduced array. As seen in Figure 7, subjects had no trouble maintaining fixation in this task (C) while pointing their heads with reasonable accuracy toward the targets (D). The SDs of horizontal and vertical fixation direction for the entire duration of this task were only 1.1 and 1.7°, respectively (averaged across the four subjects who wore eye coils in this task). Thus, this paradigm effectively dissociated head motion from gaze shifts.

Fig. 7.

Comparison of gaze control during reduced range laser task (A, B) and gaze-fixation task (C, D). 2-D pointing directions are plotted for gaze (left column) and head-facing direction (right column) during the entire duration of each task, showing both trajectories and fixation points in subject M.C. 2-D head trajectories were slightly more variable in the gaze-fixation task, but this does not contribute to torsional variability when Donders' law is being obeyed (Crawford et al., 1999).

The result of this dissociation was immediately evident, even without sophisticated surface fits (Fig. 8,top row). Whereas the LT produced a flat, compact range of data points (B), the gaze fixation task produced a torsionally scattered range of positions (C). This was not because of a twist in the range; the gaze fixation task produced an H_s surface (F) that was less twisted than normal (D), with a gimbal score (Fig. 8G,GF) of just 0.29, significantly smaller than in the control helmet task (p = 0.005). Instead, as predicted, the torsional thickness of the head range showed a substantial increase (Fig. 8H). The SD of this range from its surface of best fit, at 3.14°, was significantly larger than the CH (1.86°; p = 0.031; one-tailed ttest) and the RL (1.59°; p = 0.029; one-tailedt test). Thus, when head movement was dissociated from gaze, Donders' law of the head broke down.

Fig. 8.

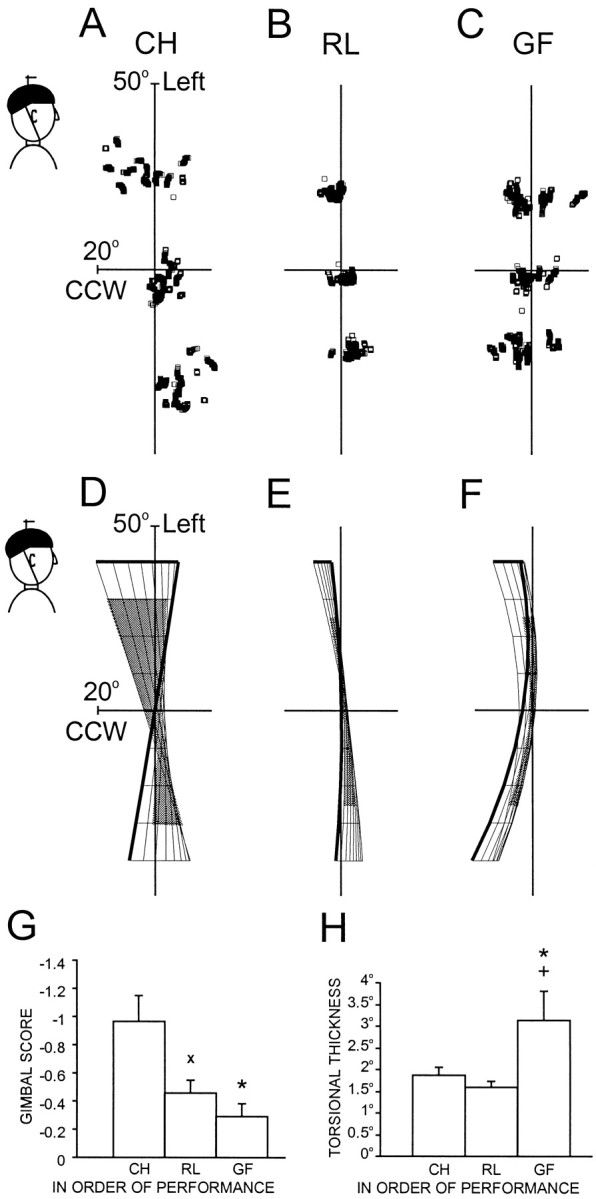
3-D head orientation in the tasks of experiment 4.A–C, Quaternion vectors in side view for subject S.P.A, Control helmet task. B, Reduced laser task. C, Gaze-fixation task. D–F,H_s surfaces for the data inA–C. G, Gimbal scores. *p < 0.05 indicates a significant difference from the control helmet task; two-tailed t test. ×p < 0.05 indicates a significant difference from the control helmet task; one-tailed t test.H, Torsional variabilities. *p < 0.05 indicates a significant difference from the control helmet; one-tailed t test. +p < 0.05 a significant difference from the reduced laser task; one-tailedt test. Otherwise, conventions as in Figures 4 and5.

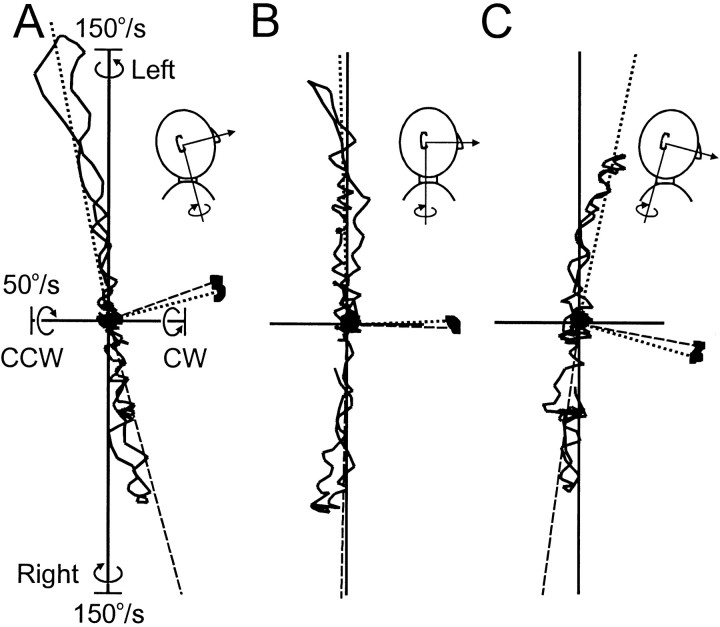
To understand this relaxation or violation of Donders' law, we looked at the axes of head rotation. Because angular velocity (i.e., the instantaneous axes of rotation) determines changes in orientation, kinematic constraints can be described in terms of either orientation or velocity (Tweed and Vilis, 1990). However, velocity axes are more useful for illustrating certain aspects of these constraints. For example, in the Fick strategy, the vertical axis (for horizontal head rotation) stays fixed in space independent of head position (Glenn and Vilis, 1992; Crawford et al., 1999), whereas for Listing's law, the vertical axis tilts by half the angle of vertical eye position (Tweed and Vilis, 1990). In contrast to both of these strategies, axes of head rotation remained head-fixed (orthogonal to facing direction) in our gaze dissociation task (Fig.9A–C), a strategy that transports the facing direction using the smallest possible head rotation. It is well known that such a strategy is inconsistent with Fick, Listing, or indeed with any form of Donders' law, because it produces torsional tilts as a function of initial position (Tweed and Vilis, 1990, 1992). However, such torsional deviations must cancel out across randomly directed movements, producing the thick, flat distribution that was observed in Figure 8C.

Fig. 9.

Minimum-rotation strategy observed during the head-gaze dissociation task. A, Head facing upward targets. B, Head facing forward targets.C, Head facing downward targets. Eachpanel shows two oppositely elongated (one upward and one downward) angular velocity loops, for one leftward and one rightward head movement, respectively. Each point along these loops defines the instantaneous axis and speed of head rotation, as a vector emanating from the origin. Vectors pointing rightward (i.e., forward for the subject) show the facing direction of the head during the rightward (hatched line) and leftward (dotted line) movements. Corresponding vertical linesshow the perpendiculars to these facing vectors, which aligned closely with the angular velocity loops. Thus, as indicated by thecaricatures, the vertical axis of head rotation remained orthogonal to head-facing direction, in contrast to the space-fixed vertical axes observed during normal random gaze shifts.

Other geometric aspects of theH_s range

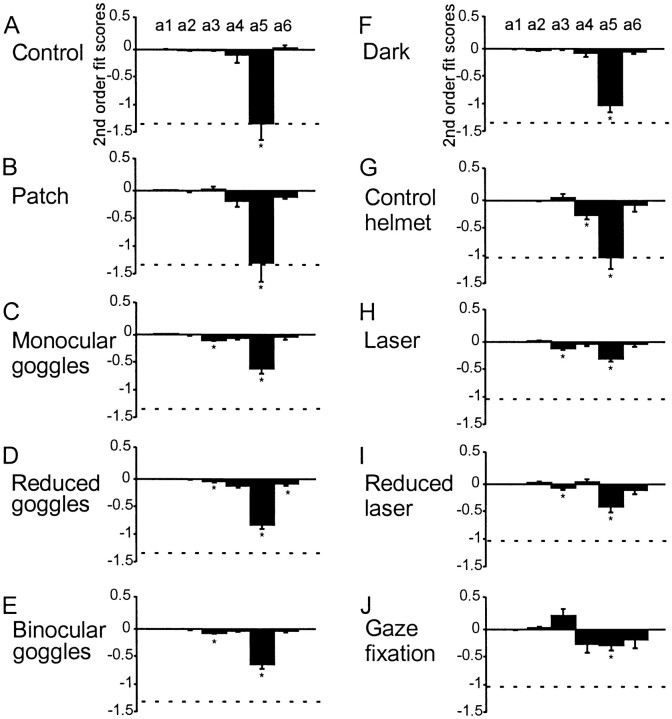
So far, we have quantified H_ssurfaces using only gimbal scores. To measure other properties of these surfaces, we examined the six coefficients of the second-order fit (Eq.1), each of which quantifies some aspect of surface geometry (Glenn and Vilis, 1992; Medendorp et al., 1998; Crawford et al., 1999). Figure10 shows the six parameters for each of the 10 tasks (A–J), averaged across the seven subjects who participated in all four experiments.

Fig. 10.

Average parameters (a₁–a₆) of the H_s surfaces for each task, across all four experiments. A–I, Means and SEs across subjects during control (A), patch (B), monocular goggle (C), reduced range goggle (D), binocular goggle (E), memory control (F), control helmet (G), laser (H), laser reduced (I), and gaze fixation (J) conditions. For comparison, the dotted line in A–F marks the twist score (a₅) for the control task (A) and, in G–J, the twist score (a₅) for the control helmet task (F). *p < 0.05 indicates a significant difference from zero; two-tailed ttest.

The first parameter, a₁, quantifies the torsional shift of the surface away from the reference position. Averaged a₁ scores were small (−0.009 to 0.0042) and never significantly different from 0. Parametera₂ describes the dependence of torsion on vertical H_s position. Averagea₂ scores were also small in all tasks (−0.013 to 0.025) and never significant. Thea₃ scores, quantifying the dependence of torsion on horizontal H_s position, varied more across tasks (−0.118 to 0.239) and differed significantly from zero in several of the tasks: goggle tasks, Figure 10,C (−0.107; p = 0.0015), D(−0.050; p = 0.034), and E (−0.079;p = 0.0073); and laser tasks, H (−0.118;p = 0.0054) and I (−0.078;p = 0.043). These negative scores describe the backward tilts observable in Figures 6B (laser task) and 8E (reduced laser task), which reflect the tendency of the head to roll clockwise when facing right and counterclockwise when facing left.

Parameter a₄ describes the curvature along the torsional axis with vertical eye position. The range ofa₄ scores (−0.269 to 0.03) was small across paradigms and not significantly different from zero, except during the control helmet task (Fig. 10G) in which it was −0.269 (p = 0.009). This negative score means that the head rolled counterclockwise when tilting up or down. Parameter a₆ similarly describes the curvature along the torsional axis with horizontal eye position. Its range (−0.192 to 0.022) was also small across tasks, and it differed significantly from zero for only one task, reduced goggles (D) in which it was −0.09; (p= 0.046). This negative value means that the head rolled counterclockwise when facing left or right.

Finally, the fifth parameter,a₅, describes the twist of theH_s surface. This parameter, which is closely related to our gimbal score, was the largest of the six and the only one that was significantly different from zero in all tasks. It also varied the most between tasks (−0.290 to −1.341), although it was almost always negative, indicating a consistent Fick–gimbal-like twist in the surface. These results, showing little systematic variation in any surface property except twist, suggest that the gimbal score used in Figures 4-8 captured the major effects of our various paradigms.

Simulations

Given that most of the variation in ourH_s surfaces could be described with a single variable, the gimbal score, it follows that an adjustable Donders' operator could be controlled by a neural signal with just one degree of freedom. We called this hypothetical Donders' box the “gimbal operator.” The detailed math for this model is given in the. This model was capable of simulating the main results from experiments 1–3. However, it failed to explain other aspects of head motion, such as the minimum-rotation behavior observed in Figures 8 and9. To fit this third mode into a unified scheme with the Listing and Fick strategies, a new approach was required.

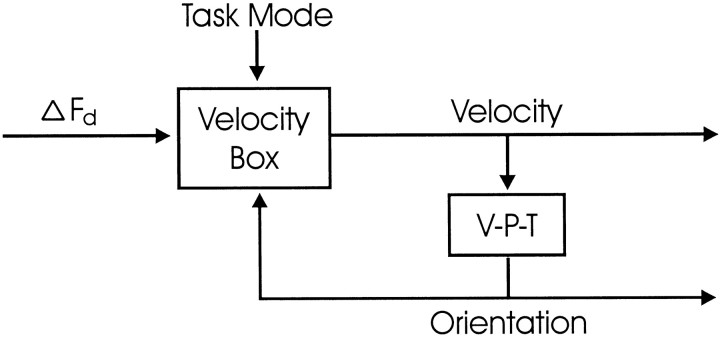
The latter was satisfied by implementing the constraints at the level of velocity commands rather than position commands (Fig.11). All three modes of head control (Fick, Listing, and minimum rotation) can be expressed as velocity rules, so all three can be modeled using an adjustable “velocity box.” The detailed mathematical implementation of this scheme is provided in the legend for Figure 11. In brief, we supposed that head movements are driven by a 2-D command that specifies nothing about head torsion but encodes the desired facing direction or its desired motion. We then assumed a feedback signal that codes current head position. This signal might also be 2-D, but it can be shown that such an arrangement is limited in its capabilities and leads to implausible behavior, so it is more likely that the feedback codes all three dimensions of head position. These two signals, desired facing direction or motion and actual head position, were fed into the velocity box, which computed the correct 3-D velocity command to drive the head toward its target. As shown in Figure12, this arrangement of control signals was capable of simulating the Fick strategy (A,B), Listing's law (C, D), or the random violations of Donders' law produced by the minimum-rotation strategy (E, F), simply by switching the internal parameters of the velocity box with the use of a third, task-dependent input.

Fig. 11.

Velocity rule model of head control during gaze shifts. Desired change in 2-D head facing direction (ΔF_d) is input to a velocity box, which uses information about current head orientation and task mode to compute the correct 3-D velocity command for the head. The latter is also input to a velocity-to-position transformation (V-P-T), which estimates current head orientation (Tweed and Vilis, 1987). This head orientation signal can be used to control head posture in the feedforward direction but is also fed back to the velocity box. As the movement proceeds, the velocity command shrinks toward zero, as in any negative-feedback loop. A task mode input sets the internal parameters of the velocity box, as follows. All three modes of head control (Fick, Listing, and minimum rotation) can be expressed as velocity rules. In each mode, the angular-velocity vector of the head must lie in a certain velocity plane, which is a function of the facing direction. Supposef is a unit vector (a vector of length 1) pointing in the facing direction, N is a unit vector orthogonal to the velocity plane, and i, j, andk are body-fixed unit vectors pointing forward, left and up. Then, the various head constraints we have considered take the following forms. The minimum-rotation strategy says thatN = f, i.e., the velocity vector must be orthogonal to the current facing direction; the Fick pattern says that N is obtained by rotating finto the horizontal plane, i.e., N_Fick= k × (f ×k), if we normalize this vector (stretch it out to make its length 1); the Helmholtz pattern says that N is f rotated into the sagittal plane, i.e.,N_Helmholtz = j × (f × j) normalized; and Listing's law, as usual, is halfway between Fick and Helmholtz:N_Listing bisects the angle betweenN_Fick andN_Helmholtz; equivalently,N_Listing bisects the angle betweenf and i, so thatN_Listing = f +i normalized.

Fig. 12.

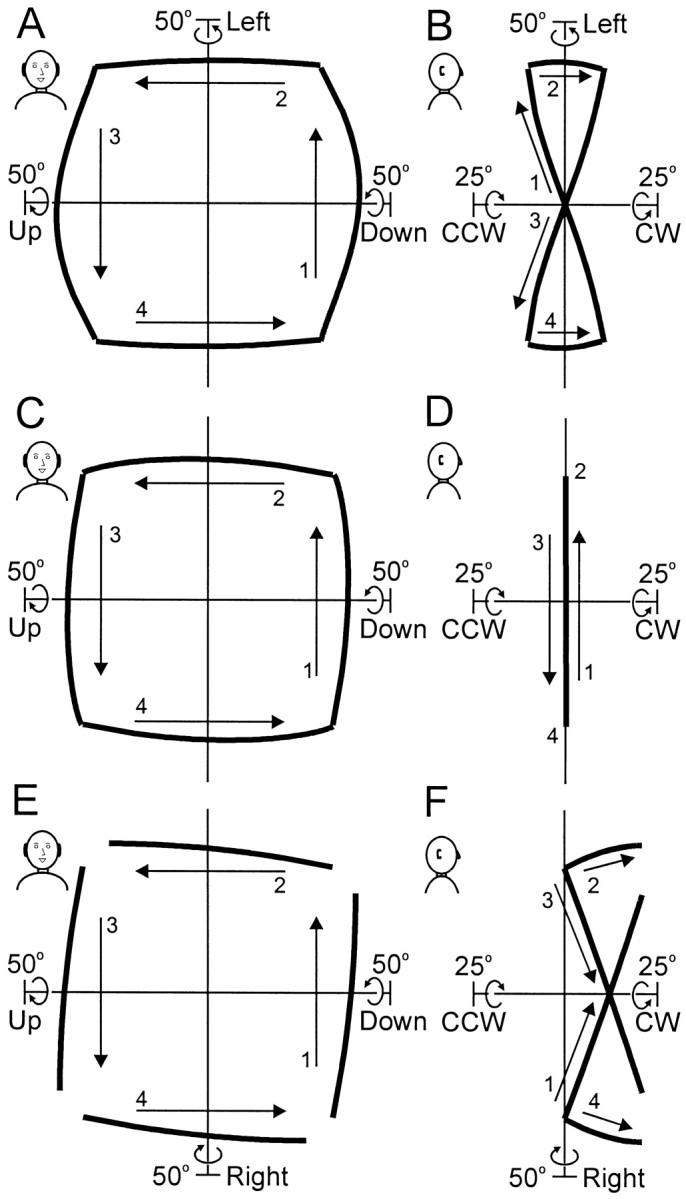
Simulations of the velocity rule model of head control. Each row plots four movements that take the facing direction clockwise between the four oblique targets of the standard array, at 48° eccentricity. Corresponding movements (labeled1–4) are viewed from the front (left column) and side (right column) perspectives.A, B, The model operates in Fick–gimbal mode, so that in the side view the head-position trajectories trace out a twisted bow-tie shape. C, D, In Listing mode, the trajectories stay in the zero torsion Listing's plane.E, F, Minimum-rotation mode puts no bounds on torsion. In these simulations, each movement starts from Listing's plane (torsional starting position is arbitrary in this mode because it would depend on the previous movement history). All four movements carry the head clockwise, so if each started where the previous one ended, clockwise torsion would accumulate. Similarly, movements in the opposite direction would cause counterclockwise accumulation, whereas randomly directed movements would cause a general increase in torsion like that observed in our gaze dissociation task (Fig. 8C). Note that the corner positions of the head differ from mode to mode in the torsional, vertical, and horizontal dimensions, although all of these positions point the facing direction at the same four oblique targets.

DISCUSSION

Our results demonstrate four new findings. First, most people can switch between different patterns of head control depending on the motor task. Obviously, one can move one's head almost any way one likes by voluntarily controlling all three dimensions of its motion, but in some situations, including many orienting tasks, the torsional dimension is instead set automatically by unconscious control modules in the brain. Our results suggest that, in different gaze tasks, these control modules set torsion to obey different forms of Donders' law. Second, more importantly, we have ascertained the functional factors that determine the choice between these laws. Third, when head motion was dissociated from eye motion, Donders' law of the head broke down. This suggests that the mechanisms underlying Donders' law are part of the gaze system, although of course other head motor tasks besides gaze control may obey their own forms of the law. Finally, we have demonstrated a new, more powerful way to model these control systems: with the use of velocity constraints.

Purpose of Listing's law versus the Fick strategy

During normal eye–head gaze shifts, the head moves in a Fick pattern (Glenn and Vilis, 1992; Radau et al., 1994; Misslisch et al., 1998). Here, we have shown that, when a subject dons pinhole goggles, the pattern of head motion usually changes to resemble Listing's law. The same thing was earlier found in monkeys (Crawford et al., 1999), but whereas monkeys had to be trained extensively on the goggle task, humans learned it immediately. Moreover, most of these subjects' head movements showed an immediate switch from the Fick strategy toward something more closely resembling Listing's law. This finding suggests that either their motor control circuits already contained a subcircuit for Listing's law or these circuits are capable of very rapid adaptation. More importantly, the versatility of our human subjects allowed us to use several different tasks to track down the determinants of this pattern switching.

Our second and third experiments showed that the switch was not triggered by altered vision; it occurred whether or not vision in one eye or in the retinal periphery was blocked. So it appears that the choice between the Fick pattern and Listing's law was not primarily guided by factors serving binocular or peripheral vision. Of course Donders' laws of the head and eye do have important implications for these aspects of vision, but our results suggest that vision is not the main factor shaping the range of head motion.

Instead, the crucial factor appears to be the motor role of the head. In normal gaze shifts, the eyes point gaze at visual targets and the head is essentially a platform for the eyes. However, whenever the head becomes a pointer of gaze like the eye, it adopts a motion pattern like that of the eye. This happened with pinhole goggles, when the head became the prime mover of the gaze line, but even more so with a helmet-mounted laser in which the head was solely responsible for pointing the beam. For a pointer, Listing's law is an efficient strategy because it redirects the facing direction using the smallest possible rotations toward and away from some central, primary position. Thus, it helps aim the pointer quickly. In contrast, when the head acts merely as a platform, it plays a smaller role in getting the eye on target quickly and so becomes free to optimize other variables besides speed. In this case, the Fick pattern is attractive because it prevents the head from rolling sideways relative to gravity. The head tilts forward and back, but in the torsional plane, it stays always balanced on the vertebral column, easing the workload on the neck muscles.

If the purpose of Listing's law is to redirect the pointer quickly, why not use other strategies that are even faster? Fastest of all is the minimum-rotation strategy, which always rotates the head about an axis orthogonal to the facing direction (Tweed and Vilis, 1992). However, a problem with this strategy, as demonstrated in our gaze dissociation task, is that it is incompatible with any form of Donders' law, and therefore it allows torsion to accumulate. During gaze shifts, this strategy has only been observed transiently during back-and-forth head motion in which the resulting torsion cancels out (Tweed and Vilis, 1992; Crawford et al., 1999). The only general way to preserve Donders' law and still take the fastest route, i.e., a fixed-axis rotation, between any two head positions is to obey Listing's law. With any other form of Donders' law, one must either violate the law in transit (Crawford et al., 1999) or take an indirect route with a nonfixed axis, so in this sense Listing's is the fastest form of Donders' law. Our data suggest that the choice between these strategies is governed by issues of motor performance, whereas the underlying purpose of Donders' law is to prevent accumulation of torsion.

Implications for the control system

How then does the gaze-control system switch between different forms of Donders' law for the head? One possibility is that the brain contains two Donders' operators for the head, one for Fick and one for Listing. Another possibility is that there is just one Donders' operator, but it is adjustable. By “turning a knob” somewhere in the neural circuit, the brain could twist theH_s surface into a Fick shape or flatten it into a Listing's plane (see for math). Given that most of the variation in our H_ssurfaces could be described with a single variable, the gimbal score, it follows that an adjustable gimbal operator could be controlled by a neural signal with just one degree of freedom. However, the gimbal operator fails to explain some modes of head motion, such as the minimum-rotation behavior that is used when subjects look back and forth repeatedly between two targets (Tweed and Vilis, 1992; Crawford et al., 1999) and that was also observed in our gaze dissociation task.

An attractive alternative is to implement the constraints at the level of velocity commands rather than position commands (Fig. 11). This approach is more general because many constraints, called nonholonomic, simply cannot be expressed in terms of position alone (Wongchaisuwat et al., 1984) but can be expressed in terms of the velocities that are permitted in different positions. An example is the minimum-rotation constraint; transporting the gaze line with the smallest possible rotation is not a matter of staying within some range of positions but of choosing the right velocity given your starting position and the location of the visual target.

Therefore, we modeled this control system as a velocity box (Fig. 11) with inputs encoding both the desired 2-D facing direction of the head (or its desired motion) and a feedback signal encoding 3-D head orientation. This scheme provides considerable flexibility. For example, Crawford et al. (1999) pointed out that previously existing (i.e., holonomic) models cannot account for departures of the head from the Fick surface during oblique movements unless the Donders' operator is outside of the motor feedback loop. However, this is no longer a constraint in nonholonomic modeling. Another major advantage of the velocity-based model over most previous models is that it satisfies position-dependent constraints in motor control without using explicit commands (such as “desired head orientation”) that are not evident in actual brainstem physiology (Freedman and Sparks, 1997).

In the case of gaze tasks, the neural signal coding change in desired facing direction might arise from the superior colliculus, which appears to contain a map of desired gaze shifts (Tomlinson and Bahra, 1986; Galiana and Guitton, 1992; Freedman and Sparks, 1997; Goosens and Van Opstal, 1997). This 2-D gaze error signal could interact with eye- and head-position feedback in the velocity box to produce a 3-D command for head velocity. In our fourth experiment, though, the gaze error was zero, so the head commands likely arose outside the colliculus, perhaps in the basal ganglia (Medendorp et al., 1999). Such commands would seem to bypass any sort of Donders' operator (Medendorp et al., 1999), but they might still pass through the velocity box that we have proposed. In either case, the output of this box would then drive the movement and could also be input to a velocity-to-position transformation (Fig.11) that computes the tonic signals required to maintain final head posture, much like those observed in the oculomotor system (Crawford et al., 1991). For example, as with the eye, the correct level of torsional head tilt appears to require a delicate balance in tonic activity between the right and left midbrain reticular formation (Brandt and Dieterich, 1994; Klier et al., 1999; Wang et al., 1999).

To compute its commands in a flexible way, the velocity box must operate in different modes, including Fick, Listing, minimum rotation, and perhaps others. As illustrated in Figure 11, this could be implemented by a separate “mode” input to the velocity box that specifies which pattern the velocity commands are to fit, adjusting the motion to the current task. The choice between modes may also be influenced by the source of the input, e.g., 2-D gaze error signals from the superior colliculus would normally undergo Fick processing, whereas inputs from elsewhere are handled differently. A similar flexible, nonholonomic system may also control the arms, which, like the head, obey Donders' law in some tasks (Straumann et al., 1991;Hore et al., 1992; Theeuwen et al., 1993) and violate it systematically so as to minimize kinetic energy in other situations (Soechting et al., 1995). In this regard, our model is consistent with the conclusions of a recent study that suggested that the arm is also under the control of velocity constraints (Nishikawa et al., 1999) and thus may have useful applications in other areas of motor control.

Adjustable gimbal operator for the head

The details of this operator depend on the coordinate system, quaternions, Fick angles, etc., that is used to represent head rotations, and apart from some preliminary evidence (Masino and Knudsen, 1993; Klier et al., 1999) few clues exist as to the coordinates used by the brain to represent head motion. To illustrate the idea, we shall assume the simplest case in which head orientation is represented using its torsional (T), vertical (V), and horizontal (H) Helmholtz angles (Tweed et al., 1997). If the brain chooses a desired facing direction for the head, that direction can be represented by the two Helmholtz angles V and H, and the job of the gimbal operator is to fill in the missing torsional angle. If the head is to move in the Fick pattern, torsion must be set according to the formula T = −1 × V ×H, because this is the equation for the Fick pattern in Helmholtz coordinates. If the head is to obey Listing's law, we must have T = −0.5 × V × H. In general, torsion is set equal to γ × V ×H, where γ is the single degree of freedom signal that adjusts the gimbal operator. Note that γ is not equal to the gimbal score, because γ works in Helmholtz coordinates and the gimbal score in quaternions, but the two are closely related, and both carry the same information: they determine the twist in theH_s surface.