Periodicity and Firing Rate As Candidate Neural Codes for the Frequency of Vibrotactile Stimuli

Abstract

The flutter sensation is felt when mechanical vibrations between 5 and 50 Hz are applied to the skin. Neurons with rapidly adapting properties in the somatosensory system of primates are driven very effectively by periodic flutter stimuli; their evoked spike trains typically have a periodic structure with highly regular time differences between spikes. A long-standing conjecture is that, such periodic structure may underlie a subject's capacity to discriminate the frequencies of periodic vibrotactile stimuli and that, in primary somatosensory areas, stimulus frequency is encoded by the regular time intervals between evoked spikes, not by the mean rate at which these are fired. We examined this hypothesis by analyzing extracellular recordings from primary (S1) and secondary (S2) somatosensory cortices of awake monkeys performing a frequency discrimination task. We quantified stimulus-driven modulations in firing rate and in spike train periodicity, seeking to determine their relevance for frequency discrimination. We found that periodicity was extremely high in S1 but almost absent in S2. We also found that periodicity was enhanced when the stimuli were relevant for behavior. However, periodicity did not covary with psychophysical performance in single trials. On the other hand, rate modulations were similar in both areas, and with periodic and aperiodic stimuli, they were enhanced when stimuli were important for behavior, and were significantly correlated with psychophysical performance in single trials. Thus, the exquisitely timed, stimulus-driven spikes of primary somatosensory neurons may or may not contribute to the neural code for flutter frequency, but firing rate seems to be an important component of it.

The sensation of flutter is produced when mechanical vibrations between 5 and 50 Hz are applied to the skin (Mountcastle et al., 1967; Talbot et al., 1968). Earlier studies using vibrotactile stimuli reported four basic observations: (1) that sensation in the flutter range is mediated by primary afferent fibers and S1 neurons with rapidly adapting properties associated with Meissner's mechanoreceptors (Mountcastle et al., 1967; Talbot et al., 1968); (2) that these afferents and cortical neurons are driven very effectively by periodic flutter stimuli, which evoke highly periodic spike trains (Mountcastle et al., 1969, 1990; Recanzone et al., 1992); (3) that psychophysical performance in frequency discrimination, which is similar for humans and monkeys (LaMotte and Mountcastle, 1975), correlates closely with the discriminability of the evoked, periodic interspike intervals (Mountcastle et al., 1969, Recanzone et al., 1992); and (4) that in afferent and S1 units, the firing rate, computed over hundreds of milliseconds, changes little within the flutter range (Talbot et al., 1968; Mountcastle et al., 1969, 1990; Recanzone et al., 1992). In view of these results, it was argued that flutter frequency cannot be encoded by the firing rate of rapidly adapting units and that a subject's capacity to discriminate flutter frequencies has to depend on the periodicity of the evoked interspike intervals (Mountcastle et al., 1967, 1969, 1990; Talbot et al., 1968; Recanzone et al., 1992). This led to the proposal that “frequency discrimination is made by a central neural mechanism capable of measuring the lengths of the dominant periodic intervals in the [evoked] trains of impulses” (Mountcastle et al., 1967).

Nevertheless, the fourth and crucial observation was based on a small number of neurons (Mountcastle et al., 1990) or on responses to a narrow range of frequencies applied to anesthetized animals (Recanzone et al., 1992). Additionally, direct microstimulation of Meissner-type primary afferents produced flutter sensations of frequencies that were perceived to increase with evoked firing rate (Ochoa and Torebjörk, 1983). More recently, we also observed that monkeys can discriminate the mean frequencies of aperiodic stimuli, which lack any temporal regularity. Animals can work with aperiodic stimuli whether these are delivered naturally, by a mechanical probe, or artificially, through microinjection of electrical current into S1 (Romo et al., 1998). These considerations cast doubts on the bold proposal quoted above. Is it true, then, that spike periodicity plays a functional role in frequency discrimination and that firing rate does not? If this were the case, cortical somatosensory neurons would provide a solid demonstration of a temporal neural code (Shadlen and Newsome, 1994, 1998; Singer and Gray, 1995; Ahissar, 1998). Here we try to assess the relation, if any, between behavior and stimulus-driven modulations in firing rate and in periodic interspike timing in S1 and S2. The results suggest that firing rate does play an important role in encoding stimulus frequency in our paradigm.

MATERIALS AND METHODS

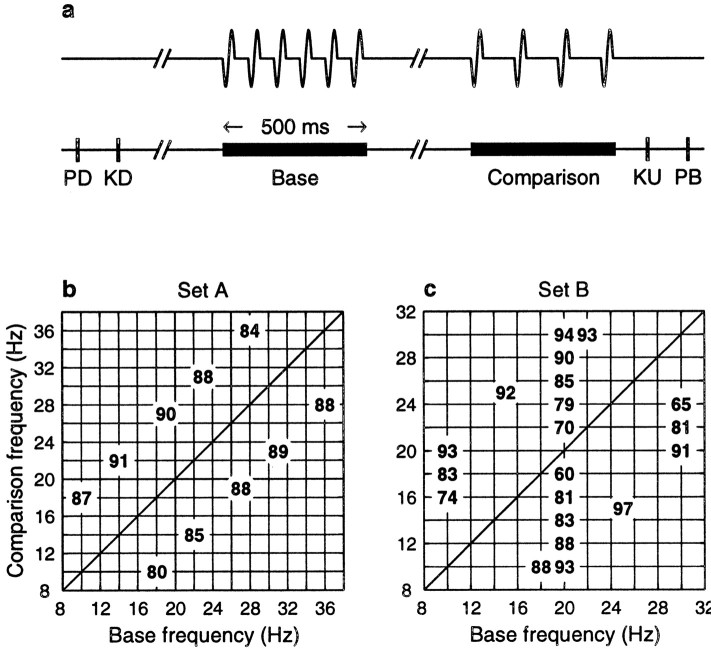
Neurophysiology and behavior. The behavioral task is schematized in Figure 1a [see also Romo et al. (1998);Hernández et al. (1997)]. In each trial the monkey had to compare the frequencies of two vibratory stimuli presented consecutively. The sequence of events was as follows. The mechanical probe was lowered, indenting the glabrous (hairless) skin of one digit of the restrained hand; the monkey reacted, placing its free hand on a lever within 1 sec after indentation; after a delay period (1.5–3 sec), the probe oscillated vertically, periodically, at a base frequency; after an interstimulus interval (1–3 sec), a second stimulus was delivered at a comparison frequency; the monkey had to release the lever within 600 msec and press one of two push-buttons to indicate whether the comparison frequency was higher or lower than the base. Both stimuli lasted 500 msec and were delivered to the distal segment of digits 2, 3, or 4 of the left hand via a computer-controlled Chubbuck linear motor stimulator (Chubbuck, 1966), which had a 2 mm round tip. Initial indentation was 500 μm. Stimulus amplitudes were adjusted to equal subjective intensities (Mountcastle et al., 1990;Hernández et al., 1997). For example, 71 μm at 12 Hz and 51 μm at 34 Hz (∼1.4% per Hertz). In each trial of the task, a pair of base-comparison frequencies was chosen pseudorandomly from a set typically comprising ∼10 pairs. For one full data collection run, at least five trials per pair had to accumulate with the same stimulus set. Typically, each run included 10 trials per pair. Figure 1,b and c, shows two stimulus sets commonly used in the experiments (set A was used much more often; see Fig. 1, legend). The numbers inside the grids indicate the percentage of correct discriminations for each pair of frequencies. In set A, the difference between base and comparison was always 8 Hz, and the monkeys performed between 80 and 91% correct. In set B, smaller and larger differences were combined. In general, monkeys had clear difficulties discriminating when base and comparison frequencies differed by ∼2 Hz or less.

Fig. 1.

Behavioral paradigm and stimulus sets used.a, Schematic diagram of the task. In each trial, the mechanical probe was lowered so that it touched one of the fingertips of the restrained hand (PD, probe down); the monkey reacted, placing its free hand on a lever within 1 sec after indentation (KD, key down); after a delay period (1.5–3 sec) the probe oscillated vertically, delivering a series of pulses at a base frequency; after an interstimulus interval (1–3 sec), a second set of pulses was delivered at a comparison frequency; after the end of the comparison stimulus, the monkey had to release the lever within 600 msec (KU, key up) and press one of two push-buttons (PB). One button indicated that the comparison frequency was higher than the base, and the other indicated that the comparison was lower than the base. b, c, Two stimulus sets frequently used in the experiments. The numbers inside the grid indicate the percentage of correct responses for each base-comparison combination.Set A had constant differences of 8 Hz between base and comparison. Percentages are based on the performance of three monkeys throughout 350 runs with this set. Set B was designed to vary the difficulty of the task in a more systematic manner. The percentages shown correspond to 42 runs from two monkeys.

Sinusoidal stimuli were used initially; 137 S1 neurons were studied in this way. Later we switched to trains of short mechanical pulses like those illustrated in Figure 1a. Each of these pulses consisted of a single-cycle sinusoid lasting 20 msec. For stimulation at 20 Hz, 11 successive pulses were applied, separated by 50 msec. This interval was measured between the beginnings of successive pulses. The data obtained with sinusoidal stimuli were not used in Figure 2 or in comparisons with S2 responses, but they were included in the comparisons between active and passive conditions and between neuronal and psychophysical responses.

Fig. 2.

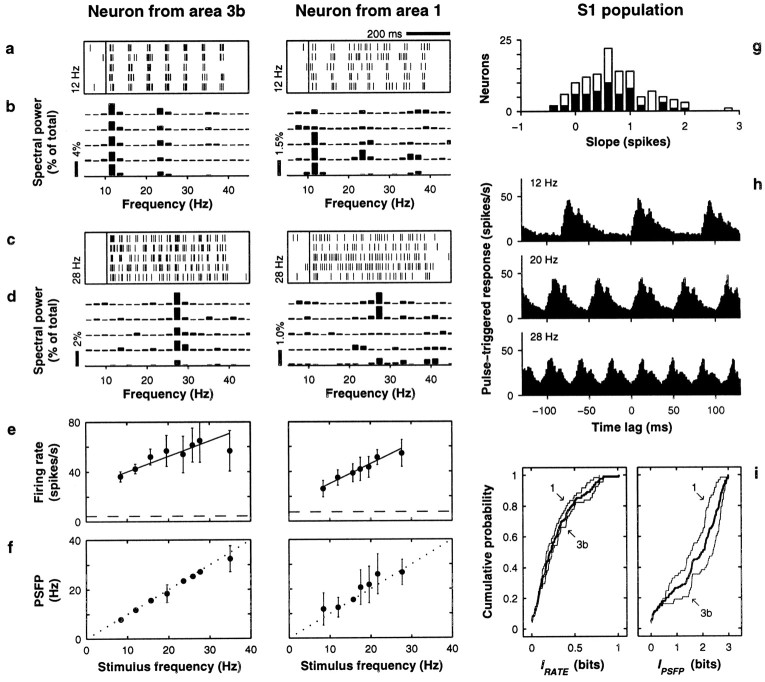
Neuronal responses in S1. Left andmiddle columns show data, in the same format, from two neurons from areas 3b and 1, respectively. The right columnshows population data from 68 neurons in area 3b and 61 neurons in area 1. All plots are based on neuronal activity evoked by the base stimulus. a, c, Raster plots from five trials in which stimulus frequency was 12 Hz (a) and 28 Hz (c).Small vertical ticks indicate spikes; each rowcorresponds to one trial. The long vertical line indicates stimulation onset. b, d, Power spectra of the five spike trains shown immediately above. Power is expressed as percentage of total power across all bins, but only frequencies within the flutter range are shown. e, Mean firing rate (±1 SD) as a function of stimulus frequency. Continuous line indicates best linear fit; dashed line indicates baseline firing rate, computed in the 800 msec preceding stimulation onset. For the neurons on theleft and middle columns, I_RATE = 0.50 ± 0.10 and 0.58 ± 0.09 bits, respectively (both significant). f, Mean PSFP (±1 SD) as a function of stimulus frequency. The diagonal dotted line indicates equality between x and y axes. For the neurons on the left and middle columns, I_PSFP = 2.71 ± 0.03 and 2.08 ± 0.04 bits, respectively (both significant). Because PSFP values were discrete and often distributed bimodally, SDs here suggest more overlap between response distributions than was actually measured.g, Distribution of slopes from linear fits to the rate-versus-frequency curves (as in e). White andblack bars correspond to area 3b and area 1 neurons, respectively. h, Average S1 responses triggered on individual stimulation pulses. The three histogramscorrespond to stimulation at 12, 20, and 28 Hz and were constructed from the responses of 89–102 S1 neurons tested at these frequencies. The y axis indicates the firing rate (in 1 msec time bins), averaged over neurons and trials, x milliseconds before or after the onset of an individual stimulation pulse, where x is called the time lag. Phase-locking is readily apparent at all frequencies. i, Cumulative distributions for I_RATE and I_PSFP. The value on the y axis represents the fraction of neurons with information smaller or equal to the amount indicated on the x axis. Thin lines indicate separate distributions for areas 3b and 1; thick lines correspond to pooled data sets. Note the different scales on the x axes.

Experiments with aperiodic stimuli were also conducted (Romo et al., 1998). In this situation a frequency of 20 Hz still corresponded to 11 mechanical pulses delivered in a 500 msec period, so the mean interval between pulses was 50 msec, but the times between pulses were random. The minimum time between the onsets of consecutive pulses was equal to their width, 20 msec, corresponding to a maximum instantaneous frequency of 50 Hz. In practice, then, the total number of pulses delivered was constant across trials of a particular frequency, as in the periodic case, and given the stimulation period of 500 msec and the pulse width of 20 msec, those pulses were randomly distributed among 500/20 = 25 positions in time (except that the first and last pulses were always delivered at the beginning and end of the stimulation interval). The specific temporal pattern of pulses was chosen randomly in each trial, and the patterns were different even for trials with the same mean frequency. The monkeys had to compare the average frequencies of the base and comparison stimuli exactly as before. By average frequency we mean the total number of stimulation pulses divided by the corresponding 500 msec period. These experiments were of two types: with periodic base and aperiodic comparison, or with both aperiodic. Behavioral results from these two variants of the paradigm were pooled. These experiments were performed in blocks interleaved between blocks of regular discrimination with periodic stimuli.

Passive stimulation tests were also performed in blocks and were also interleaved between blocks of active discrimination. During passive stimulation, the hand used to press the push-buttons was restrained, so there were no behavioral reactions, and no reward was provided. Otherwise, single trials proceeded as with regular discrimination. The same combinations of base-comparison frequencies were used in experiments with periodic and aperiodic vibrations and in passive and active conditions. However, not all neurons could be recorded long enough to complete all the types of tests, so the numbers of recorded neurons varied across conditions.

Recordings were obtained with an array of seven independent microelectrodes of 2–3 MΩ (Mountcastle et al., 1990, 1991). Recording procedures were the same as those described by Mountcastle et al. (1990) (see also Romo et al., 1998, 1999). Microelectrodes were aimed at the hand representations in S1 and S2, and the locations of the penetrations were confirmed with standard histological techniques. For the analysis of simultaneously recorded neurons, only pairs with units from different electrodes were used. Separation between microelectrodes was at least 500 μm. Animals were handled according to the guidelines of the National Institutes of Health and the Society for Neuroscience.

Response measures. The firing rate in each trial was equal to the number of spikes emitted during the 500 msec stimulation period (base or comparison) divided by 0.5 sec. The mean firing rate r was obtained by averaging over trials of equal stimulus frequency; therefore, r and its SD ς were functions of frequency (r and ς correspond, respectively, to the data points and error bars in Figs. 2e, 3e). Response curves of mean firing rate versus stimulus frequency were fitted to linear and Gaussian functions through χ² minimization (Press et al., 1992). Gaussian tuning curves had four parameters, amplitude A , baseline B , center frequency C , and width ς_G, such that:

$$r(s)=B+Aexp\left(-\frac{(s-C{)}^2}{2{\varsigma }_G^2}\right),$$ Equation 1

where s is the stimulus frequency. In the text, angle brackets 〈〉 indicate averaging over all stimulus frequencies. Thus, 〈r〉 indicates the mean firing rate averaged over all frequencies. Similarly, 〈ς〉 corresponds to the SD of the firing rate averaged over all frequencies and measures the mean trial-to-trial variability. That is, r and ς were first calculated independently for each stimulus frequency and then were averaged across frequencies to obtain 〈r〉 and 〈ς〉. We also computed a signal-to-noise ratio for each neuron. This was defined as:

$$SNR=\frac{r_{max}-r_{min}}{\langle \varsigma \rangle },$$ Equation 2

where r_max and r_min are the maximum and minimum values, over all stimulus frequencies, of the mean firing rate.

Fig. 3.

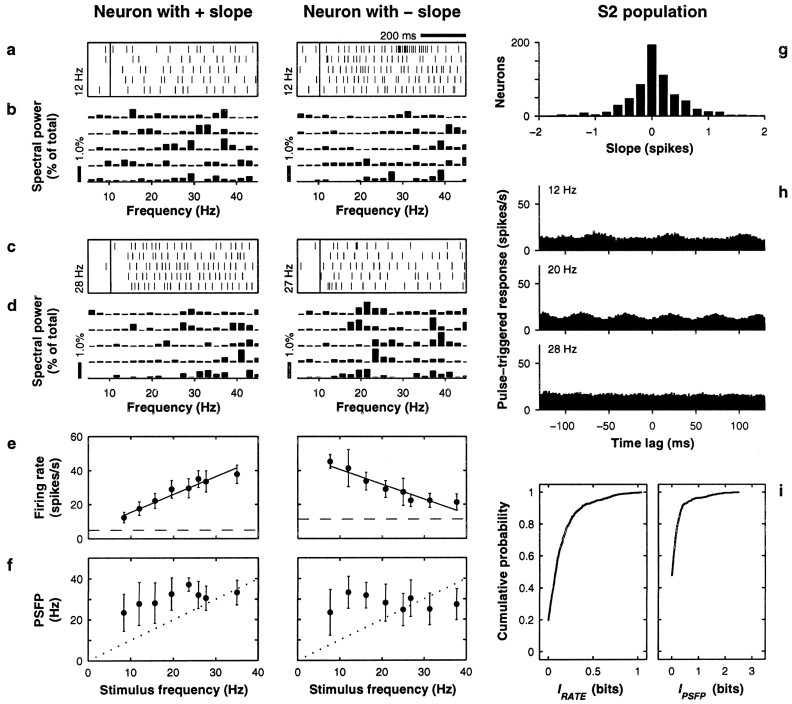
Neuronal responses in S2. Left andmiddle columns show data from two neurons: the firing rate of one increases with increasing stimulus frequency (positive slope), and the firing rate of the other decreases with increasing stimulus frequency (negative slope). Slopes were extracted from the linear fits shown in e. Same format is used as in Figure 2, except ind, middle column, frequency was 27 Hz; in e, I_RATE = 0.89 ± 0.09 and 0.75 ± 0.13 bits for left and middle columns, respectively (both significant); in h, I_PSFP = 0.26 ± 0.18 and I_PSFP = 0 ± 0.30 bits, forleft and middle columns, respectively (both not significant). In h, histograms are averages of 250–287 neurons (note same scale as in Fig. 2). Population data in gand i are based on 689 S2 neurons. All data are based on neuronal activity evoked by the base stimulus.

To relate periodicity to performance, we used several measures based on Fourier decompositions of the time signals formed by the evoked trains of spikes. For each trial, the power spectrum of the spike train evoked during the stimulation period (base or comparison) was computed and normalized, having had the DC component removed, so that the total power summed over all positive frequency bins was 100% (Press et al., 1992). Examples of power spectra for individual trials are shown in Figures 2b,d, 3b,d. In this way the number of spikes contained in each train had little impact on the resulting Fourier amplitudes, which indicated the proportion of power in the corresponding frequency bins. That is, the Fourier amplitudes were mainly determined by the temporal arrangement of the spikes, not by their number (however, the power spectrum could not be computed in trials in which less than two spikes were emitted). The sampling interval for the spike trains was 0.5 msec, and the width of the frequency bins was 1.95 Hz. The latter was limited by the duration of the stimulation period, which for the Fourier analysis we took as 512 msec.

Four quantities were extracted from each power spectrum, that is, at each trial. The first two were the power (or amplitude) at the stimulus frequency (P_S) and the power at twice the stimulus frequency. These two numbers should increase for evoked spikes that are more tightly phase-locked to the stimulation pulses. The third quantity was the maximum power (maximum y coordinate) between 4 and 42 Hz, and its corresponding frequency (x coordinate) was the fourth quantity, which we denominated the power spectrum frequency at peak (PSFP). The three amplitudes measure how periodic a spike train is, whereas the PSFP is an actual estimate of stimulus frequency that depends on the periodicity of the evoked spike trains; this distinction is crucial (notice that the stimulus frequency needs to be known a priori to compute P_S and the amplitude at twice the stimulus frequency). Note that the resolution of the PSFP depends on the width of the frequency bins of the power spectrum. Consider an example that was relatively common in S1. Suppose a neuron is strongly phaselocked to the stimulus and fires spikes somewhat like a clock, one or two spikes per stimulation pulse, in an approximately periodic fashion. In its spectra, the maximum power would be at the stimulus frequency. Thus, the PSFP amplitude would be equal to P_S, the PSFP would be the center of the frequency bin nearest to the stimulus frequency, and all three amplitudes (at the PSFP, at the stimulus frequency, and at twice the stimulus frequency) would be much larger than the average power across all bins. Statistical tests applied to any of these four quantities were always performed also with the other three, but sometimes only the results for the most sensitive one are mentioned.

In each trial, we also computed the average interburst interval (AIBI), which measures how often a burst of spikes is produced. A burst was defined as a group of spikes in which all intervals between consecutive spikes were less than τ msec. Thus, the number of spikes per burst was variable, with a minimum of 1, and all interspike intervals within a given burst had to be smaller than τ. Large τ values produced few bursts with many spikes, whereas small τ values produced many bursts with few or single spikes. Having fixed τ, the AIBI was then computed as the mean value of the time intervals between consecutive burst endings.

Standardized responses. To compare the above responses in correct discrimination trials (hits) versus incorrect discrimination trials (errors), these responses had to be pooled across different base-comparison frequency pairs, because errors were rather infrequent. To illustrate the pooling method, we first consider the firing rate as the response. The standardized rate in a given trial was obtained by taking the original firing rate at that trial, subtracting the mean rate from all trials belonging to the same condition (base-comparison frequency pair), and dividing by the SD from the same subset of trials. The same was done for all trials in the data collection run. This eliminated any differences in response level attributable to preference for one frequency or combination of base and comparison stimulus frequencies—differences across conditions—but left intact any differences within conditions, such as differences between hits and errors. By construction, such a set of standardized rates has zero mean and unit SD. Exactly the same procedure was followed to compute the standardized measures of periodicity, which were the standardized PSFP amplitude, the standardized P_S, and the standardized amplitude at twice the stimulus frequency. In all cases the standardized values in individual trials were obtained from the “raw” values by subtracting the mean of the corresponding condition and dividing by the SD, as explained above. Having obtained the standardized responses for each run, trials were separated into two groups. In trials of type 1, the base frequency was higher than the comparison, and in trials of type 2, the comparison was higher than the base. Thus, for each run and each kind of response, two comparisons between hits and errors were made, one for each set of trials of the same type. In all cases the mean of all standardized responses in error trials was compared with the mean of all standardized responses in hit trials, and the significance of the difference was determined (see Figs. 8, 9). For each type of comparison, a minimum of five error trials was required.

Fig. 8.

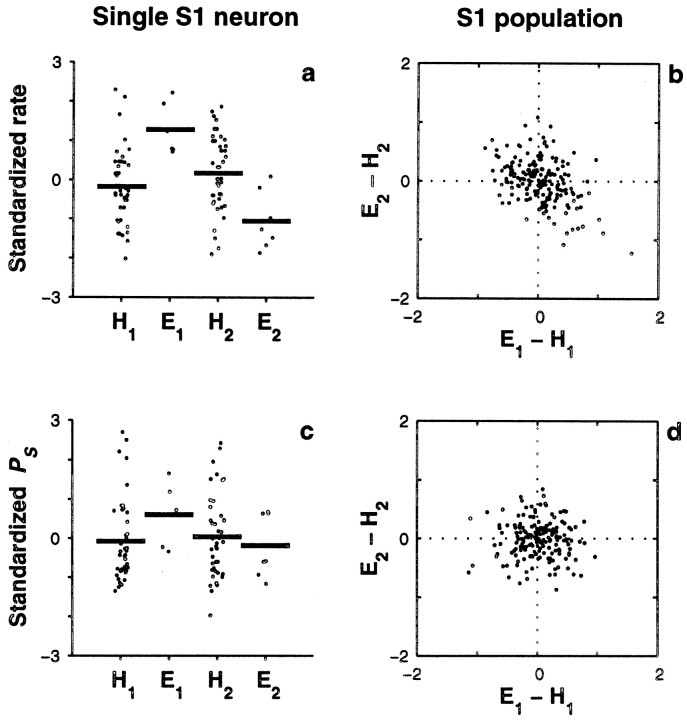
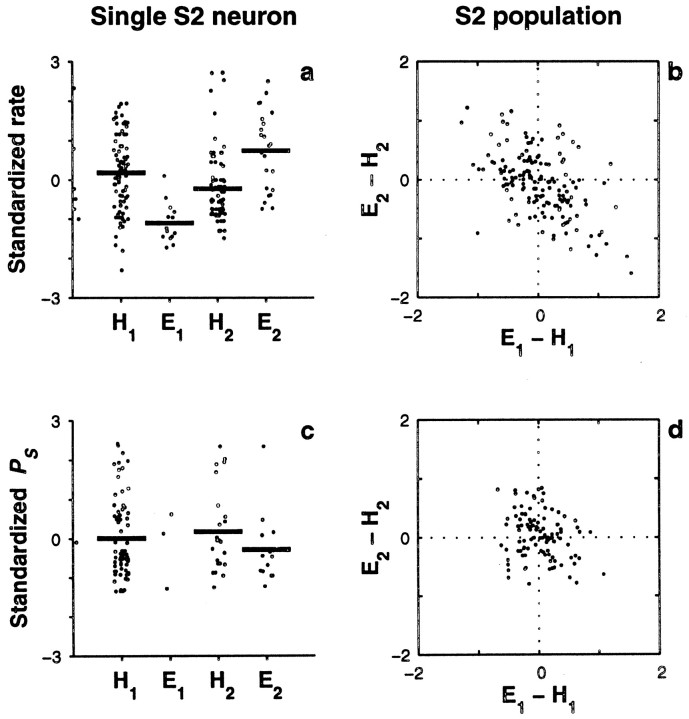
Single-trial covariations between behavioral responses and neuronal responses in S1. This analysis was based on the neuronal activity evoked by the comparison stimulus. a, Standardized firing rates (dots) for a single S1 neuron are shown subdivided into four categories: hits (H₁) and errors (E₁) when the frequency of the base stimulus was higher than the frequency of the comparison stimulus (type 1 trials), and hits (H₂) and errors (E₂) when the frequency of the comparison stimulus was higher than the frequency of the base (type 2 trials).Thick horizontal lines represent mean values for each category. For this neuron, the mean values in error trials were significantly different (p < 0.002) from the mean values in hit trials of the same type. This neuron had a positive slope of 1.17 ± 0.12 spikes. b, The standardized firing rate reveals a negative correlation between error types in S1. Each point represents one of 191 S1 neurons with at least five errors of each type. For each neuron, the mean difference in standardized rate between errors and hits for type 2 trials (E₂ − H₂) was computed and plotted versus the mean difference for type 1 trials (E₁ − H₁). The population shows a negative correlation between error types: Pearson's linear correlation coefficient was −0.42 (p < 0.0002). Dotted lines indicate the origin. c, Standardized power at the stimulus frequency (P_S) for the neuron illustrated in a, with trials subdivided into the same four hit/error categories. The differences in mean between hits and errors of the same type were not significant, although this neuron had significant I_PSFP (0.80 ± 0.14 bits).d, The standardized P_S shows no correlation between error types in S1. The plot shows mean differences in standardized P_S between errors and hits for type 2 versus type 1 trials for 184 S1 neurons. The correlation coefficient was practically zero (0.008, p > 0.9).Dotted lines indicate the origin.

Fig. 9.

Single-trial covariations between behavioral responses and neuronal responses in S2, based on the neuronal activity evoked by the comparison stimulus. Same format as in Figure 8.a, Standardized firing rates (dots) for a single S2 neuron are shown subdivided into four categories: hits (H₁) and errors (E₁) when the frequency of the base stimulus was higher than the frequency of the comparison stimulus (type 1 trials), and hits (H₂) and errors (E₂) when the frequency of the comparison stimulus was higher than the frequency of the base (type 2 trials).Thick horizontal lines represent mean values for each category. For this neuron, the mean values in error trials were significantly different (p < 0.0002) from the mean values in hit trials of the same type. b, The standardized firing rate reveals a negative correlation between error types in S2. Each point represents one of 128 S2 neurons with at least five errors of each type. For each neuron, the mean difference in standardized rate between errors and hits for type 2 trials (E₂ − H₂) was computed and plotted versus the mean difference for type 1 trials (E₁ − H₁). The population shows a negative correlation between error types: Pearson's linear correlation coefficient was −0.52 (p < 0.0002).Dotted lines indicate the origin. c, Standardized power at the stimulus frequency (P_S) for the neuron illustrated in a, with trials subdivided into the same four hit/error categories. The differences in mean between hits and errors of the same type were not significant. d, Mean differences in standardized P_S between errors and hits for type 2 versus type 1 trials for 103 S2 neurons. There was a small, nonsignificant correlation of −0.23 (p > 0.025).Dotted lines indicate the origin.

Trial-to-trial covariations in the firing rates of simultaneously recorded neurons were measured using Pearson's linear correlation coefficient ρ (Press et al., 1992). This coefficient can be computed easily from the same standardized rates described in the previous paragraph. If r_i^a is the standardized rate of neuron a at trial i , the correlation coefficient between neurons a and b is simply:

$${\rho }_{\text{ab}}=\frac{1}{N} \sum _{\text{i}=1}^N r_{\text{i}}^{\text{a}}{r}_{\text{i}}^{\text{b}},$$ Equation 3

where N is the total number of trials in the run, including all stimulus frequencies.

Information estimates and other statistics. Having computed the firing rate, the PSFP, and the AIBI in each trial, we quantified how they varied as functions of stimulus frequency for any given cell. For this we used Shannon's mutual information (Cover and Thomas, 1991; Abbott et al., 1996). Information is a measure of association between two quantities, typically stimulus and response. Its magnitude relates to the accuracy with which one of them can be determined given the other. Thus, by computing the information that they provide about a stimulus, two different responses can be compared in the same units, namely, in terms of their capacity to encode the stimulus.

The information that a response r provides about a stimulus s is computed from the probability distributions relating these two variables. In our case, s is the frequency of the applied flutter stimulus. The function P(r‖s) represents the conditional probability of observing a response r given that the stimulus had a value s . The expression P(r) describes the probability of observing a response r regardless of the value of the stimulus, and P(s) is the probability that the stimulus takes a value s . When all stimuli are presented the same number of times, P(s) is simply a constant. Using these quantities, the information that the response provides about the stimulus can be computed as:

$$I=\sum _{\text{r},\text{s}} P(s)P(r\Vert s){log}_2 \left(\frac{P(r\Vert s)}{P(r)}\right).$$ Equation 4

Here the sums are over all possible values of the stimulus and the response. Information is measured in bits. If the stimulus s can take N different values, the maximum amount of information that can be provided by any signal is log₂(N) bits. A response carrying these many bits of information lets us determine exactly which of the N stimulus values is presented in any trial; stimulus and response are then maximally correlated. Most information results shown below correspond to experiments in which seven or eight frequencies were applied and in which, therefore, the maximum amount of mutual information was log₂ (8) = 3 bits. An exception to this was made in comparisons between active and passive conditions, because here what mattered was the difference in information values (found with identical numbers of frequencies) across conditions; several sets with 9–11 frequencies were allowed in these cases.

The information that the firing rate provided about the stimulus, I_RATE, was computed from the set of firing rates from all trials assuming that the response probability distributions P(r‖s) were Gaussian (Abbott et al., 1996). (These Gaussians are response probability distributions specific to each stimulus frequency and should not be confused with the Gaussian tuning curves mentioned above.) Then, a correction for finite sampling, based on Monte Carlo methods, was applied [Treves and Panzeri (1995); E. Salinas, unpublished results, but see below]. In practice, this meant that I was first computed from Equation 4 and then a correction term, computed separately, was subtracted from it. The information that the AIBI provided about the stimulus,I_AIBI, was computed in a similar way, using the AIBI values in all trials and assuming Gaussian statistics. The information that the PSFP provided about the stimulus, I_PSFP, was computed somewhat differently. Because of the Fourier methods involved, PSFP values were drawn from binned distributions, so I_PSFP was computed using the original PSFP bins between 4 and 42 Hz, which correspond to the flutter range; including higher frequencies only increased the uncertainty in frequency and decreased I_PSFP. Corrections for finite sampling were also applied in this case (see below). For all information estimates, at least five trials per stimulus value were required.

The significance of all information values was computed through Monte Carlo resampling schemes (Efron, 1982; Press et al., 1992) akin to permutation tests (Siegel and Castellan, 1988). The basic procedure consists of shuffling the order of the trials with respect to the stimulus labels, such that the correspondence between stimulus and response is disrupted, made entirely random, and then recomputing the information values as was done originally, before shuffling. This is done repeatedly, with different shufflings, to obtain the fraction of times that the shuffled information was larger or equal to the original information computed previously from the nonshuffled responses. This fraction gives an estimate of the probability of measuring the original amount of information just by chance, when the actual information is really zero. This is precisely the significance: the probability of measuring the original amount of information when the responses are in fact independent from the stimulus. For all significance estimates, 2000 shufflings were used. In tests using synthetic data generated by a computer, we found that this method to obtain the significance of information was extremely robust: its results were accurate even with small numbers of trials (five) and regardless of the distributions from which the data were drawn. A significant amount of information indicates that a real association between stimulus and response probably exists; the amount of information quantifies the strength of this association.

When information is computed from relatively small numbers of data samples, it is typically biased upward with respect to its true value, especially when binned distributions are used (Treves and Panzeri, 1995; Abbott et al., 1996). All of the information calculations for I_RATE, I_PSFP, and I_AIBI were extensively cross-validated through computer simulations to minimize such biases. The simulations essentially consisted of three steps: (1) defining mathematical fits or binned distributions that modeled the measured empirical response distributions (for rate, PSFP, or AIBI); (2) generating, from these model distributions, synthetic data sampled exactly like in the experiments, with the same numbers of stimuli and samples; and (3) comparing the information computed from the full model distributions to the information computed from the synthetic sampled data. This comparison revealed how information estimates from sampled data deviate from the true values on average, depending on the numbers of samples and the type and distribution of the responses considered. In practice, this provided two things: first, an error bar for the information, and second, the term to be subtracted from Equation 4, i.e., the bias.

Overall, the average correction for I_RATE and I_AIBI was approximately −0.11 bits, and it was similar for significant and nonsignificant values. The mean correction was larger for I_PSFP, because it was computed from binned distributions: on average it was approximately −0.4 bits for significant values and approximately −1.1 bits for nonsignificant ones. As a comparison, the largest nonsignificant I_PSFP in the data presented below (after the correction) was of 0.4 bits. Thus, small, nonsignificant I_PSFP values were the most biased and suffered the greatest corrections. Note also that the uncorrected numbers never exceeded the theoretical maximum equal to log₂ of the number of frequencies used. These corrections are important for the results below primarily when I_PSFP is compared with I_RATE or I_AIBI; otherwise, they make little difference.

Unless specified otherwise, other statistical comparisons were based on permutation tests (Siegel and Castellan, 1988). Here the underlying idea is practically the same as for the computation of significance described above. Two distributions are thought to differ in some statistic, for instance in their means. To test the significance of the difference, the two distributions are mixed, and two new shuffled distributions, with the same numbers of elements as the original ones, are obtained. Then the difference in the means is recomputed, as done originally. The procedure is repeated many times with different shufflings, and the end result is an estimate of the probability of measuring the original difference in the means just by chance, under the null hypothesis that the two sample distributions actually came from the same source. This powerful procedure may be applied not only to the mean but to other statistics as well. It was used in all pairwise comparisons reported here. For these tests, 5000 permutations were performed; thus p < 0.0002 was the maximum resolution. Significance was set at the p < 0.01 level.

RESULTS

Firing rate and periodicity modulations in S1

Three monkeys (Macaca mulatta) were trained in the discrimination task. In each trial, the frequencies of two mechanical vibrations delivered successively had to be compared (Romo et al., 1998; Hernández et al., 1997) (Fig.1; and see Materials and Methods). After training, single neurons were recorded extracellularly while the task was performed (Mountcastle et al., 1990; Romo et al., 1998). In primates, processing of somatosensory information from S1 to S2 seems to proceed mostly in a serial fashion (Pons et al., 1987, 1992). We recorded in these two areas to assess any differences in the processing or representation of tactile information. In both areas, a neuron was selected for study if, relative to background activity, it responded in any way to the base or comparison stimulus or during the interstimulus interval. For S1 neurons (areas 3b and 1) the stimulating probe was placed at the receptive field centers. S2 neurons had large receptive fields, often bilateral, spanning all digits and sometimes even reaching the forearm (Pons et al., 1987, 1992; Sinclair and Burton, 1993; Fitzgerald et al., 1999). Stimuli were always applied at the fingertips and, as illustrated in Figure 1a, consisted of trains of short mechanical pulses delivered at various frequencies.

For each neuron, two quantities were computed in each trial: the mean firing rate and the PSFP, which is an estimate of stimulus frequency based on the periodicity of evoked action potentials (see Materials and Methods). We used the PSFP because, just like firing rate, it is a scalar quantity from which stimulus frequency can be estimated on a trial-by-trial basis; however, unlike with firing rate, the accuracy of this estimation depends on the periodicity of the spike trains. Figure 2, a andc, shows examples of S1 spike trains evoked during the base stimulus in individual trials, and Figure 2, b andd, shows the corresponding power spectra. The PSFP is simply the center (x coordinate) of the frequency bin with the most power. As illustrated in these Figures, the PSFP in S1 tends to be the same across trials. This is because the evoked spikes are phase-locked to the individual stimulation pulses. This can be seen more clearly in Figure 2h, which shows average S1 responses triggered at the time of individual pulses, the onset of which occurs at a time lag equal to 0 msec. The evoked activity reflects the periodicity of the sensory input. Curves for mean PSFP versus frequency were also obtained; this was done by averaging the PSFP over trials with equal stimulus frequency. These curves are shown in Figure 2f. Here the points fall close to the x = y line, confirming that the PSFP typically falls near the stimulus frequency. Curves for mean firing rate versus frequency were also obtained; examples are shown in Figure 2e. Notice that these neurons tend to fire more action potentials at higher stimulus frequencies. This was also true for the population: when straight lines were fit (Press et al., 1992) to the rate-versus-frequency data, most neurons had positive slopes, as shown in Figure 2g. Variations in mean rate across the tested range of frequencies were similar to those observed previously in somatosensory cortex using paradigms based on other tactile stimuli, such as textured surfaces or tactile motion (Sinclair and Burton, 1991, 1993; Gardner et al., 1992; Romo et al., 1996).

Curves like those of Figure 2, e and f, give a rough idea of the strength of association between the stimulus and the evoked variations in firing rate and in PSFP, but comparing them against each other is difficult. Instead, a quantitative measure of association was computed: Shannon's mutual information (Cover and Thomas, 1991; Abbott et al., 1996) (see Materials and Methods). This statistic is useful because it allows a direct comparison between the two kinds of response in the same units, that is, in terms of their capacity to encode stimulus frequency. The maximum amount of information in these experiments was 3 bits.

In S1, the information that the PSFP—i.e., periodic spike timing—provided about stimulus frequency, I_PSFP, was extremely high (1.71 ± 0.95 bits, mean ± SD; 107 of 129 values were significant, p < 0.01), as can be seen in Figure 2i (right plot). In 12 cases, I_PSFP >2.8 bits, which means that by computing the PSFPs of any one of these neurons, on average seven frequencies could in principle be distinguished from each other with 100% reliability. The spike rasters of S1 neurons seem to provide a faithful representation of the stimulus as it progresses in time (Fig. 2a, c, h), and the high I_PSFP values agree with this subjective impression. Notice in Figure 2i, however, that the mean I_PSFP dropped considerably from area 3b, which receives the heaviest thalamic projection (Jones, 1975, 1983), to area 1. The average numbers were 1.96 ± 0.97 bits for area 3b (n = 68) and 1.43 ± 0.86 bits for area 1 (n = 61), and the difference was highly significant (p < 0.001). These I_PSFP values represent upper bounds on the information provided by the PSFP that is available to neurons downstream from S1, because neuronal mechanisms that may actually implement an approximate Fourier decomposition—for example, operations based on spike train autocorrelations (Cariani and Delgutte, 1996) or intrinsic oscillators (Ahissar and Vaadia, 1990;Ahissar, 1998)—cannot match the accuracy of the numerical methods (Press et al., 1992) used to compute the PSFP.

In contrast to these numbers, the information about stimulus frequency provided by the firing rate, I_RATE, was approximately sixfold lower, but certainly not negligible (0.28 ± 0.23 bits; 74 of 129 values were significant). The distribution of values is shown in Figure 2i (left). What order of magnitude for I_RATE should we have expected based on rate curves like those in Figure 2e? To get a better idea of the correspondence between the rate-versus-frequency curves and I_RATE, consider the following idealized but representative example. Suppose the applied stimulus frequency s can take one of eight values, 8, 12, 16, 20, 24, 28, 32 or 36 Hz, and consider a neuron whose mean firing rate increases linearly with s with a slope of 0.7 spikes, typical of S1 (Fig. 2g), such that the evoked mean firing rate can be described by:

$$r(s)=22+0.7s+\varsigma \epsilon .$$ Equation 5

Here ε represents random Gaussian noise with zero mean and unit variance, so ς is the SD of the mean firing rate. This ς is equivalent to the ς computed from the experimental data, except that, for simplicity, it is considered independent of frequency s. On average, the mean rate of this ideal neuron is ∼28 spikes/sec when s = 8 Hz and ∼47 spikes/sec when s = 36 Hz; these values are also typical for the minimum and maximum mean rates at which S1 neurons fired during our experiments. For this idealized typical neuron, when the amplitude of the noise is ς = 3.5 spikes/sec, I_RATE = 1 bit; when ς = 8.7 spikes/sec (close to the average measured value, as seen in Fig. 5c), I_RATE = 0.3 bits; and when ς = 16 spikes/sec I_RATE = 0.1 bits. In comparison, a Poisson process, which provides a reasonable first order model for neuronal firing (Softky and Koch, 1993; Shadlen and Newsome, 1998), would give I_RATE = 0.3 bits, assuming that it fired at the same mean rates and that spikes were counted in a 500 msec time window. So, for cortical standards, 1 bit corresponds to an extremely reliable neuron, and 0.3 bits should be more or less typical given the experimental parameters and the measured rates. This is in agreement with the information values computed from the data.

Fig. 5.

Behavioral context modulates neuronal activity in S1. In all plots, responses during active discrimination (y axes) are compared with responses during passive stimulation (x axes). Diagonal lines indicate equality between x and y axes. All comparisons are based on the responses of 77 S1 neurons tested in both situations. All quantities were computed from the responses to the comparison stimulus. a, The mean I_RATE was significantly higher during active discrimination (p < 0.0004); note that higher values tend to fall above the x = y line. Circles correspond to 50 neurons with I_RATE significantly different from zero in at least one of the two conditions, and dots indicate nonsignificant neurons. Crosses indicate the mean uncertainty in the information values; they correspond to ±1 average SD in each direction. b, Circles correspond to 63 neurons with I_PSFP significantly different from zero in at least one of the two conditions, and dots indicate nonsignificant neurons. The mean I_PSFP was higher during active discrimination, and the effect was close to but below the significance threshold (p > 0.025).Crosses correspond to ±1 average SD in each direction.c, Trial-to-trial variability in the firing rate, quantified by 〈ς〉, was significantly smaller during active discrimination (p < 0.0002); note that small values, which correspond to higher reliability, tend to fall below the x = yline. d, The mean amplitude of the Fourier spectrum at the stimulus frequency (mean P_S) was significantly higher during active discrimination (p < 0.005). This indicates that in this condition, the evoked spikes were more phase-locked to the stimulus.

Taken together, these results confirm that S1 spikes are precisely time-locked to the stimulation pulses (Mountcastle et al., 1969, 1990;Recanzone et al., 1992), but they also show that although periodic firing can in principle provide a better code for stimulus frequency, firing rate cannot be dismissed.

Differences between S1 and S2

Figure 3 shows results, displayed in the same format as those in Figure 2, for a population of S2 neurons. The mean strength of rate modulations in S2 was comparable to that measured in S1: the average I_RATE in S2 was lower (0.14 ± 0.18 bits), but the maximum values were still around 1 bit, as shown in Figure 2i, and ∼20% of all values (139 of 689) were significant (a calculation similar to the one around Equation 5 in this case gave a typical I_RATE of ∼0.2 bits, assuming Poisson statistics). Thus, considerable rate modulation was also present in S2. However, comparison between S1 and S2 responses revealed four major differences.

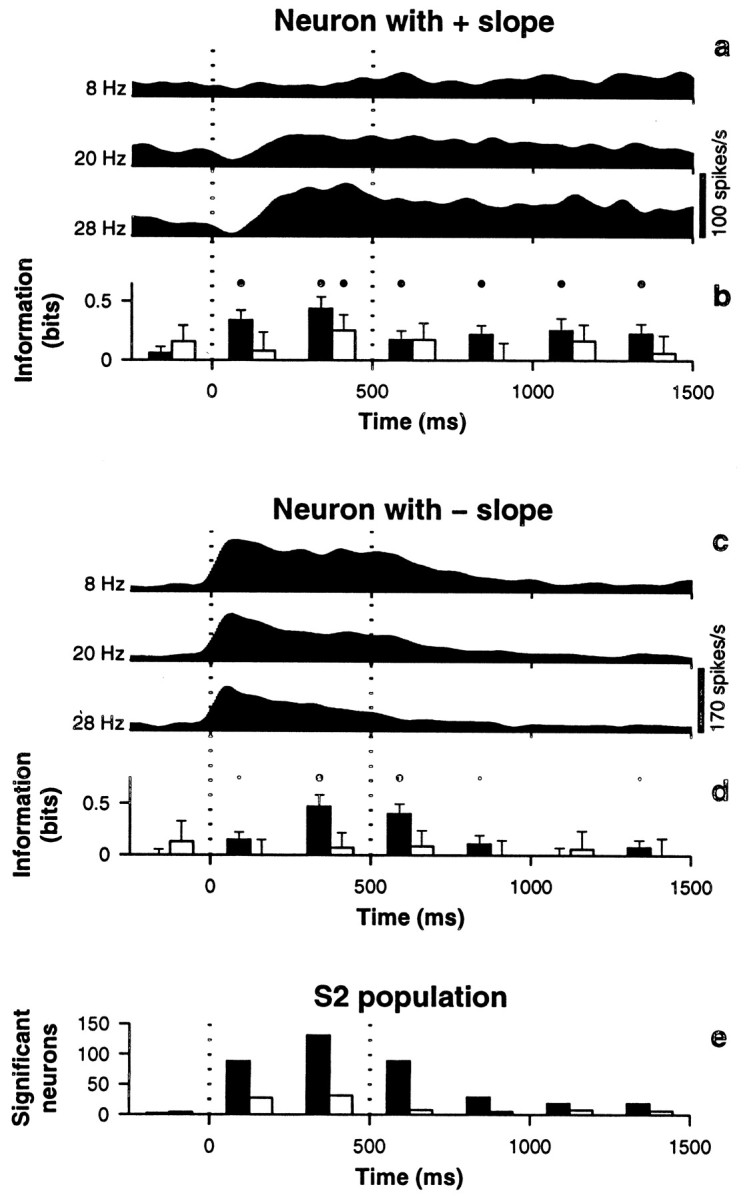
First, a lack of periodicity in S2 was revealed. This can be seen in the spike rasters of Figure 3, a and c, and in the pulse-triggered responses of Figure 3h. For the latter, the responses of neurons with positive and negative slopes were averaged, which is why the mean firing rates are so similar at the three frequencies shown. Note that phase-locking is hardly noticeable, especially at higher frequencies. Consistent with this, the mean PSFP in this case is practically independent of stimulus frequency, as illustrated in the examples of Figure 3f. In quantitative terms, the mean I_PSFP in S2, computed for the spikes evoked during the base stimulus, was an order of magnitude smaller than in S1 (0.17 ± 0.34 bits), and only 52 of the 689 neurons had values that were significantly different from zero.

Second, S2 contained a larger proportion of neurons that fired most strongly at low stimulation frequencies. The middle column of Figure 3illustrates such a unit, and e shows that its rate decreases as a function of frequency. As mentioned above, in S1 stronger activity typically occurred at higher frequencies, as shown in Figure2e. When firing rates were fitted (Press et al., 1992) as linear functions of frequency, in S1 only 8% (10/129) of the resulting slopes were negative, whereas in S2 42% (287/689) of the slopes were negative. This difference can be seen by comparing Figures2g and 3g. Interestingly, a similar transformation between S1 and S2 representations has been reported for textured surfaces (Sinclair and Burton, 1993). Here we should also mention that, in both areas, most response curves were approximately monotonic. First, the linear fits were acceptable [Q > 0.001; see Press et al., (1992)] in 53% (68/129) and 87% (602/689) of the neurons in S1 and S2, respectively. When Gaussian tuning curves were fitted to the same data, 98% of the fits were acceptable in both areas (126/129 in S1, 673/689 in S2). This is not surprising, because Gaussian tuning curves had four parameters: baseline, amplitude, center frequency, and width (see Eq. 1). Still, many of the resulting curves were monotonic, because the centers of the best fitting Gaussians were either outside or at the edges of the frequency interval that contained the data. For instance, the area 1 neuron in Figure 2e (right) had a center frequency C = 31 Hz, beyond the highest frequency tested, and a width ς_G = 18 Hz. For other neurons, the Gaussian curves fitted better the saturation effects often seen at lowest or highest firing rates. For example, the firing rate of the area 3b neuron in Figure 2e (left) is lower for 36 than for 28 Hz, although it has a positive slope. The Gaussian fit for this neuron had center frequency C = 29 Hz and width ς_G = 18 Hz. We considered a neuron as tuned if the limits C ± ς_G were both inside the interval of tested frequencies and if the neuron also had a significant I_RATE. The first condition assures that small saturation effects, like that of the area 3b neuron in Figure2e (left), are not counted as actual tuning, and the second one guarantees that the Gaussian curve is significantly different from flat. Few neurons were found that satisfied these criteria: 12% (15/129) in S1 and 1% (8/689) in S2. In conclusion, most S1 and S2 rate-versus-frequency curves were reasonably monotonic, with negative slopes being more common in S2.

The third difference was that “flat” neurons were more abundant in S2 (62%, 428/689) than in S1 (31%, 40/129). Flat neurons had firing rates that did increase or decrease significantly during stimulation, compared with the baseline activity preceding the base stimulus, but were not affected by stimulus frequency, i.e., I_RATE was not significant (here we used p > 0.05 as a criterion). This was also reflected in the distribution of slopes: a larger fraction of S2 neurons had slopes that were close to zero, as can be seen by comparing Figures2g and 3g. This difference in the proportion of flat neurons could be caused partly by suboptimal stimulation of S2; we have observed that S2 receptive fields have essentially no preference for one or another fingertip (Fitzgerald et al., 1999), but sometimes they do extend beyond the hand (Pons et al., 1987, 1992; Sinclair and Burton, 1993).

Fourth, many neurons in S2 either sustained their frequency-specific responses beyond the base stimulus or displayed them only after stimulus offset, during the interstimulus interval. Figure4a illustrates this for a neuron with positive slope that maintained significant rate modulation even 1 sec after stimulus offset. Figure 4c shows the activity of another, more typical neuron that had a negative slope and prolonged its response for a few hundred milliseconds. The histograms in Figure 4, b and d, indicate the amount and significance of I_RATE and I_PSFP for these neurons as a function of time, and the plot in Figure 4e presents the numbers of S2 neurons with significant information (I_RATE and I_PSFP) also as a function of time. Notice that ∼13% (89/689) of the neurons displayed significant rate modulations in the 250 msec window after stimulus offset. Figure 4e also shows that during this same period, 10 neurons also had significant I_PSFP; however, the number expected just by chance was seven. This means that the sustained activity lacked a significant oscillatory component. Significant rate modulations after the stimulus were not observed in S1: four neurons had significant I_RATE during the interstimulus interval, but three were expected just by chance. Therefore, sustained activity was absent in the primary sensory area [compare with Zhou and Fuster (1996, 1997)]. The significance of maintained S2 activity is hard to pinpoint. To perform the task correctly, the monkeys had to store the frequency of the base stimulus in short-term memory (Hernández et al., 1997; Romo et al., 1999). Some prefrontal neurons are also active in this task, throughout or at different points of the interstimulus interval, and their mean firing rates also increase or decrease quasilinearly as functions of stimulus frequency (Romo et al., 1999). Additionally, we found that the sustained modulation in S2 was greatly reduced during passive stimulation, when the stimuli were applied but did not have to be remembered (data not shown). Hence, it is tempting to think that such sustained activity may be related to the working memory requirements of the task, but this is speculative.

Fig. 4.

Sustained neuronal responses in S2. The base stimulus turned on at time zero, lasting 500 msec; stimulus onset and offset are indicated by dotted vertical lines. Interstimulus interval duration was 1–3 sec. a, Spike density histograms of a neuron that fired most strongly at high frequencies (positive slope). For the shown traces, stimulus frequencies were 8, 20, and 28 Hz, as indicated. b, Information (+1 SD) carried by the neuron illustrated in a as a function of time. I_RATE (black bars) and I_PSFP (white bars) were computed every 250 msec using the spikes contained in a 250 msec time window centered at the midpoint (x coordinate) between bars.Large and small dots indicate significance levels of p < 0.01 and p < 0.05, respectively. c, Spike density histograms of a neuron that fired most strongly at low frequencies (negative slope); same stimulus frequencies as in a. d, Information carried by the neuron illustrated in c as a function of time. e, Number of neurons with significant (p < 0.01) information about stimulus frequency as a function of time. Black barscorrespond to I_RATE and white bars to I_PSFP, as in b and d. All spike densities were obtained by convolving the spike trains with a Gaussian kernel of SD equal to 30 msec and averaging over trials of equal frequency.

A simple compromise between firing rate and timing

The above results show that, on the basis of single-cell comparisons, firing rate modulations in S2 were somewhat weaker than those in S1 in terms of information content; on average, I_RATE differed by a factor of 2. However, the difference in terms of periodicity was a factor of 10. Although in S2 the actual average values of I_RATE and I_PSFP were similar, two points should be stressed: first, that the fraction of neurons with significant I_RATE was twice as high as the fraction of neurons with significant I_PSFP, and second, that the I_PSFP values represent upper bounds.

We also checked whether distinctions between frequencies could be made based on the AIBI in each trial. A burst is simply a group of spikes close together in time, like those shown in Figure 2a(left). We defined a burst through a time window τ such that any two spikes within τ milliseconds of each other belonged to the same burst. Notice that the rate of bursts and the rate of spikes are correlated—indeed, if τ is very small each spike equals a burst and the two rates become equal—but grouping by bursts with more than one spike may produce more accurate results than simply counting spikes, especially when long interspike intervals correspond to intervals between consecutive stimulation pulses. The AIBI represents a plausible middle ground between counting the total number of spikes, ignoring their temporal distribution, and taking into account all individual interspike intervals.

For each neuron, the AIBI was obtained in each trial, and the information that the AIBI provided about stimulus frequency, I_AIBI, was computed (see Materials and Methods). Parameter τ was set to optimize the average I_AIBI in S1. It should be borne in mind that, having optimized τ, I_AIBI is expected to be at least equal to I_RATE, because one may always choose τ close to zero and count each spike as a burst. A positive value of I_AIBI − I_RATE means that additional information is extracted from the timing of spikes, in excess of the information provided by the rate. With an optimal τ of 20 msec, the average I_AIBI in S1 was 0.58 ± 0.49 bits (n = 129). Thus, although the PSFP was more efficient, the AIBI did capture some of the periodic structure of the spike trains, providing twice as much information as the firing rate alone (McLurkin et al., 1991). This was also true for the maximum values, which were 1.16 ± 0.09 bits for I_RATE and 2.29 ± 0.07 for I_AIBI. In contrast, in S2 I_AIBI was indistinguishable from I_RATE (p > 0.49, n = 689), and the maximum value was 0.65 ± 0.12 bits, quite below the maximum I_RATE, which was 1.04 ± 0.07 bits. Other values of τ were also tested for S2, but the results were similar: the mean I_AIBI always decreased with increasing τ. Hence, grouping spikes by bursts, which effectively doubled the information about stimulus frequency reported by the firing rate in S1, was entirely ineffective in S2. This confirms, with a different method, that phase-locking is strong in S1 and extremely weak in S2.

According to these results, neurons immediately downstream from S1 may read out stimulus frequency in at least two ways: either from S1 firing rate modulations or from the periodic structure of S1 spike trains. In contrast, for neurons downstream from S2, the second possibility may not be available. Hence, two areas involved in somatosensory processing could potentially use fundamentally different codes to represent the same quantity. S1 is extremely important for somatosensory processing: lesions in this area cause severe impairments in discrimination and categorization tasks (LaMotte and Mountcastle, 1979; Zainos et al., 1997), and activity driven by direct microinjection of electrical current into S1 may trigger sensory percepts that probably resemble natural sensations quite closely (Romo et al., 1998; Wickersham and Groh, 1998). Therefore, the crucial question is whether neurons downstream from S1 read out its periodicity and are affected by it. We performed other experiments to try to address this issue.

Context-dependent modulations of activity

In general, the attentional state of a subject performing a task may have a strong influence on the neurons involved in it; neuronal responses are often enhanced when attention is focused on a sensory feature that the neurons react to (Hsiao et al., 1993; McAdams and Maunsell, 1999; Treue and Martínez-Trujillo, 1999). We wondered whether spike periodicity or firing rate would be subject to similar modulatory effects. The same sets of stimuli used for discrimination—the active condition—were also delivered passively to the monkeys. During passive stimulation the responding arm was restrained, no behavioral reaction was required, and no reward was delivered.

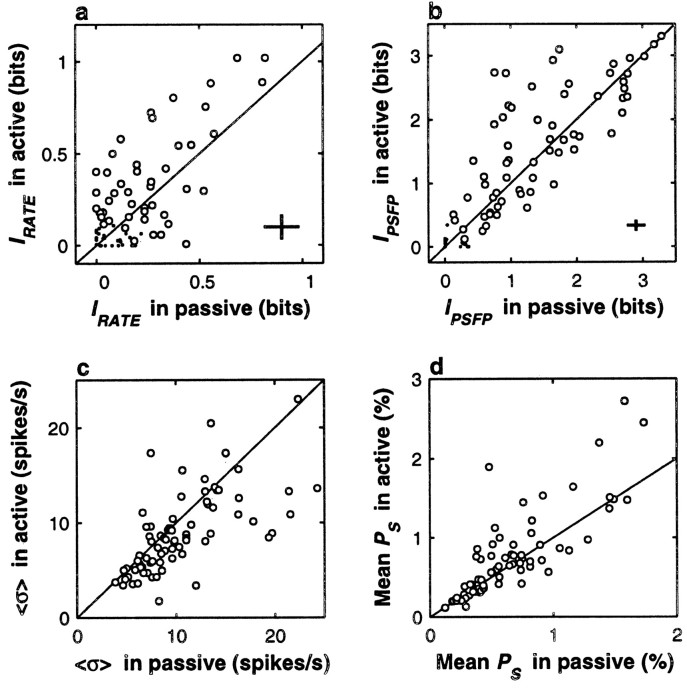
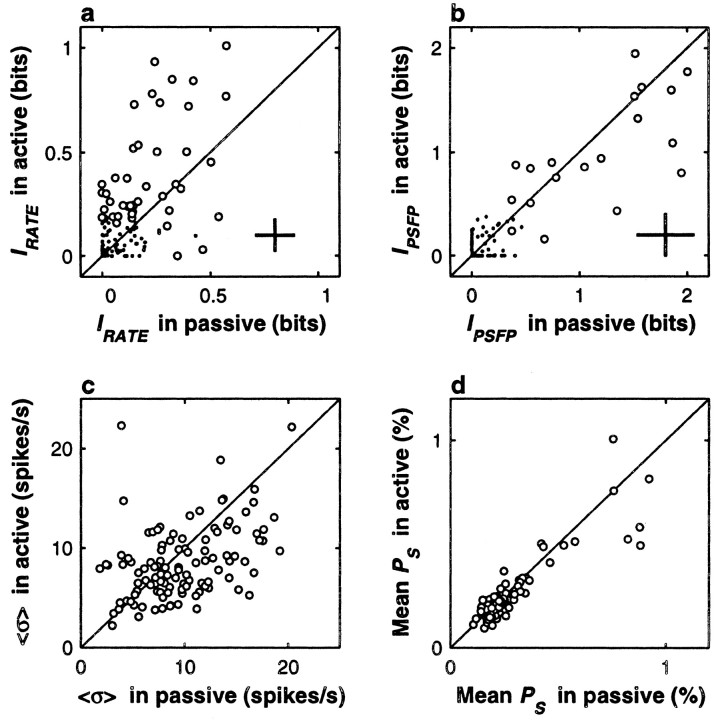
Figure 5 compares S1 activity evoked during the comparison stimulus in active and passive conditions. Figure5a shows that the mean I_RATE was significantly higher in the active condition (0.42 ± 0.35 bits in active, 0.27 ± 0.23 bits in passive; n = 50 neurons with significant information in at least one of the conditions; p < 0.0004); indeed, most points fall above the equality line. Other measures of neuronal activity also showed significant variations across conditions. Figure 5c shows the average variability in firing rate across trials, 〈ς〉, in the two conditions. In this case most points fall below the diagonal line, indicating that variability in firing rate was significantly smaller during active discrimination (〈ς〉 was 8.9 ± 4.2 spikes/sec in active, vs 10.5 ± 4.6 spikes/sec in passive; n = 77 neurons tested in the two conditions; p < 0.0002). Across conditions, changes in the signal-to-noise ratio (Eq. 2), which is a simple function of the firing rates, were strongly correlated with changes in I_RATE (linear correlation coefficient was 0.98, p < 0.0002). Thus, with all the measures tested we arrived at the same conclusion: the firing rate in S1 is a more reliable signal during discrimination than during passive stimulation.

We were concerned about this result, however, because we had not taken into account the correlations among neurons, i.e., the stimulus-independent co-fluctuations in numbers of spikes fired. For certain changes in the correlations, the information about stimulus frequency transmitted jointly by the rates of multiple neurons might have actually decreased, despite an increase in the information conveyed by individual neurons (Shadlen and Newsome, 1998; Zohary et al., 1994; Abbott and Dayan, 1999). Two additional results indicated that this was not the case. First, we measured ρ, the linear correlation coefficient between pairs of simultaneously recorded neurons averaged over all pairs. For each pair, the coefficient was calculated using Equation 3, and a mean over all pairs was computed. We found that ρ was actually smaller in the active condition, although the difference was not significant (0.10 ± 0.18 in active, 0.16 ± 0.21 in passive; n = 84 pairs tested in S1; p > 0.037). Second, we also computed the information provided jointly by the firing rates of pairs of neurons recorded simultaneously, which takes into account their pairwise correlation, and again we observed, on average, a significant increase in information about stimulus frequency in the active condition with respect to the passive (p < 0.0002).

Very similar differences between rate modulation in active and passive conditions were obtained in S2. Figure6a and c, illustrates this for I_RATE and 〈ς〉, but the same was also true for the signal-to-noise ratio and other measures of activity (Fig. 6, see legend). Interestingly, the sustained responses after the offset of the base stimulus exhibited similar but larger effects (data not shown). Regarding the correlation coefficients in S2, again, no difference was found between active and passive conditions (ρ was 0.07 ± 0.20 in active and 0.08 ± 0.21 in passive; n = 126 pairs tested in S2; p > 0.7), and the information carried jointly by the firing rates of pairs of neurons was also significantly higher during active discrimination (p < 0.0002). Therefore, the behavioral context of the task definitely had an impact on the evoked firing rates of S1 and S2 neurons: the numbers of spikes produced were significantly more regular across trials during active discrimination.

Fig. 6.

Behavioral context modulates neuronal activity in S2. In all plots, responses during active discrimination (y axes) are compared with responses during passive stimulation (x axes). Diagonal lines indicate equality between x and y axes. All comparisons are based on the responses of 108 S2 neurons tested in both situations. Format is the same as in Figure 5, except that all quantities were computed from the responses to the base stimulus. a, The mean I_RATE was significantly higher during active discrimination (p < 0.0002); note that higher values tend to fall above the x = y line. Circlescorrespond to 43 neurons with I_RATEsignificantly different from zero in at least one of the two conditions, and dots indicate nonsignificant neurons.Crosses indicate the mean uncertainty in the information values; they correspond to ±1 average SD in each direction. b, Circles correspond to 19 neurons with I_PSFPsignificantly different from zero in at least one of the two conditions, and dots indicate nonsignificant neurons. The mean I_PSFP was not significantly different in the two conditions (p > 0.11). Crossescorrespond to ±1 average SD in each direction. c, Trial-to-trial variability in the firing rate, quantified by 〈ς〉, was significantly smaller during active discrimination (p < 0.0062); note that small values, which correspond to higher reliability, tend to fall below the x = y line. d, The mean amplitude of the Fourier spectrum at the stimulus frequency (mean P_S) did not change across conditions (p > 0.06).

The periodicity of evoked spikes in S1 was also different in active and passive tests, although the changes seemed more subtle than for rate. This is shown in Figure 5b. Here a disproportionate number of data points seem to fall above the equality line, in agreement with the finding that the mean I_PSFP was larger in the active condition (1.62 ± 0.90 in active, 1.45 ± 0.85 in passive; n = 63 S1 neurons with significant I_PSFP in at least one condition), but the effect did not reach the significance criterion of 0.01 (p > 0.025). However, we also compared the mean power at stimulus frequency (mean P_S) across conditions. This quantity is just the percentage of power at the frequency bin that includes the stimulus frequency, averaged over all trials (see Materials and Methods). The data are shown in Figure 5d. The mean P_S was also larger during active discrimination (0.72 ± 0.53% in active, 0.62 ± 0.38% in passive; n = 77 S1 neurons), and in this case the effect was significant (p < 0.005). Thus, the timing of evoked S1 spikes relative to the stimulation pulses was more regular during active discrimination; tighter phase-locking occurred in this condition.

Figure 6, b and d, shows that in contrast to S1, no changes in periodicity were detected in S2 in terms of I_PSFP and mean P_S (Fig.6, see legend). The same happened for the mean power at the PSFP and for the mean power at twice the stimulus frequency.

Runs of passive tests were applied in blocks, typically after a block of active discrimination trials. Thus, we considered the possibility that the results of this section might have been corrupted by some sort of systematic drift in the recordings, such that later tests tended to be, for instance, more noisy. However, each neuron was typically tested in more than two conditions, so we were able to run the same battery of statistical comparisons on experiments of the same type, active or passive, testing for differences between early and late experimental runs. For example, if three runs (complete blocks of trials) were collected with the sequence active, passive, active, statistical tests were performed between the passive run and the first active run, and the same tests were repeated for the second and first active runs, as a control. Across the neural population, no significant effects were obtained in any of the control comparisons, showing that the described differences between active and passive conditions were not caused by drift artifacts.

In summary, these experiments showed an attentional or a contextual enhancement of neural activity. In both S1 and S2, the firing rate encoded stimulus frequency better when the stimulus guided the animal's behavior, in the sense that rate provided more information about the relevant stimulus feature. The periodicity of the evoked spikes did not change with behavioral context in S2, but it did so in S1. This was surprising and indicates that spike timing may be influenced by attention or behavioral context (Steinmetz et al., 2000). However, at the level of S1, these results do not favor one neural code over the other.

Responses to aperiodic stimuli

Two of the monkeys also discriminated the average frequencies of aperiodic stimuli (Romo et al., 1998) (see Materials and Methods). In this situation, the same numbers of pulses corresponding to each stimulus frequency were delivered in the 500 msec stimulation period, but the times between pulses were random and varied from trial to trial. To obtain a reward, the monkeys had to compare correctly the average frequencies of the base and comparison stimuli, just as with periodic vibrations. These animals did not go through a retraining period; they were able to perform the task from the initial runs. Because S1 neurons emit spikes that are reliably phase-locked to individual stimulation pulses, aperiodic stimuli impose a timing between phase-locked spikes or bursts of spikes that, by design, varies randomly within the stimulation period and across trials. Similar random timing can also be imposed directly through intracortical microstimulation (Romo et al., 1998).

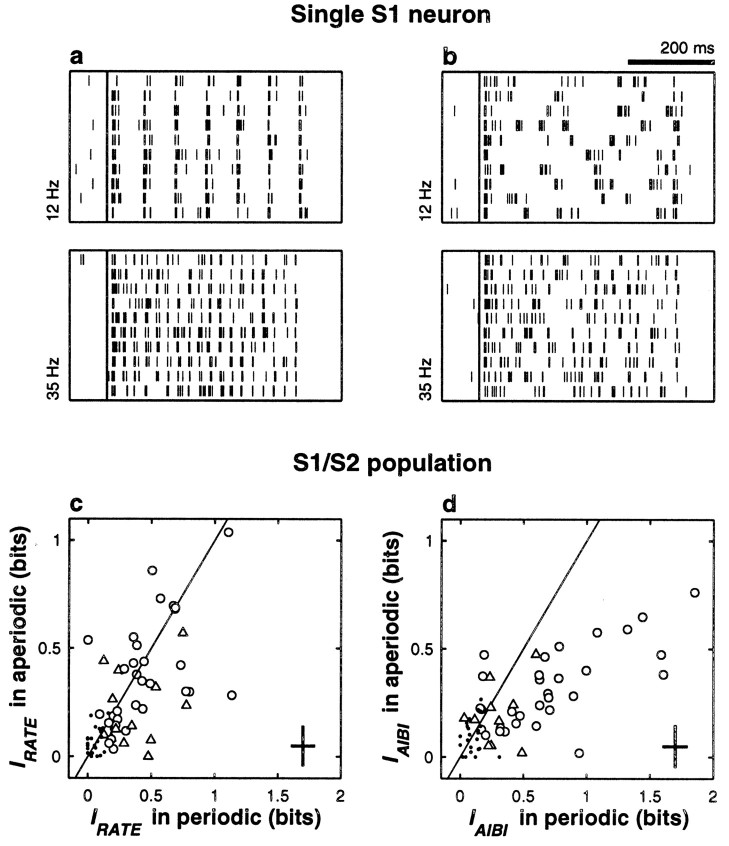
The monkeys' performance in this task only decreased slightly compared with discrimination of periodic stimuli: overall, 88 versus 80% correct (Romo et al., 1998). We investigated whether neuronal responses paralleled this similarity. Figure 7,a and b, shows the responses of an S1 neuron to periodic and aperiodic stimuli at two frequencies. This neuron responded quite faithfully to individual stimulation pulses. Notice the regular interspike intervals in the periodic condition, in Figure7a, and the much more variable spike trains elicited in the aperiodic condition, in Figure 7b. Figure 7cshows that for any given neuron, I_RATE could vary somewhat from the periodic to the aperiodic situation, but on average, firing rate modulations in S1 were indistinguishable across conditions (I_RATE = 0.44 ± 0.28 bits for periodic, 0.38 ± 0.25 bits for aperiodic; n = 31 S1 neurons tested in both conditions and with significant I_RATE in at least one of them; p > 0.19). Differences were slightly larger in S2 (I_RATE = 0.37 ± 0.22 bits for periodic, 0.22 ± 0.17 bits for aperiodic; n = 13; p > 0.055), but fewer samples were available. These results show that in the two areas, firing rate was, on average, similarly modulated by frequency in periodic and aperiodic conditions.

Fig. 7.

Neuronal responses to periodic and aperiodic stimuli. The four raster plots at the top show spike trains from an S1 neuron that was tested with periodic (a) and aperiodic (b) stimuli at frequencies of 12 and 35 Hz, as indicated. Each set of responses includes 10 trials collected during active discrimination. For a given stimulus frequency, the train of stimulation pulses was identical for all periodic trials but was different for all aperiodic trials. However, at a given mean frequency, the total number of pulses delivered was the same in both conditions.Long vertical lines indicate stimulus onset. In the periodic condition the neuron had I_RATE = 0.67 ± 0.10 and I_AIBI = 1.44 ± 0.10 bits; with aperiodic stimulation I_RATE = 0.70 ± 0.10 and I_AIBI = 0.65 ± 0.11 bits. I_RATE (c) and I_AIBI (d) were computed for 41 S1 and 30 S2 neurons tested with periodic and aperiodic stimuli. In both panels, circles and triangles correspond to S1 and S2 neurons, respectively, with significant information in at least one of the two conditions (periodic or aperiodic), and small dots indicate S1 and S2 neurons that had nonsignificant values in the two conditions. Diagonal lines indicate equal values in the two axes. Crosses on the bottom right cornersindicate ±1 average SD in each direction. I_RATEdid not change across conditions, in either area; data points in c are distributed symmetrically around the diagonal line. I_AIBI was significantly larger with periodic stimulation; data points in dtend to fall below the diagonal. With aperiodic pulses, I_AIBI was similar to I_RATE; the y -axis values inc and d are similar (see Results).

Not surprisingly, in these experiments I_PSFPpractically vanished: of 41 S1/S2 neurons with significant I_PSFP in the periodic condition, only one had a significant value in the aperiodic condition. The same thing happened with the mean power at the PSFP, at the mean stimulus frequency and at twice the mean stimulus frequency. This was expected and simply showed that no consistent modulations in periodicity are seen with aperiodic stimulation; the Fourier spectrum shows no regularity from one trial to the next.

What about bursts of spikes; could they provide a reliable measure of mean stimulus frequency for aperiodic stimuli? In the periodic condition, the AIBI of S1 neurons carried more information than the rate, as has been described. The AIBI of S1 neurons also provided significant information in the aperiodic condition but, as shown in Figure 7d, I_AIBI in this case was significantly smaller than with periodic stimulation (0.71 ± 0.47 in periodic, 0.32 ± 0.18 in aperiodic; n = 31 S1 neurons tested in both conditions and with significant I_AIBI in at least one of them; p < 0.0002); most data points fall below the equality line. The key observation here is that with aperiodic stimuli, I_AIBI was, on average, slightly smaller than I_RATE, and this was the case whether all neurons or only those with significant information were compared. This can be appreciated by comparing the y -axis values in Figure 7,c and d. Comparisons using bursts of other sizes were also made—we used τ = 20, 15, 10, and 5 msec—but the results were the same: collecting bursts rather than single spikes provided no additional information about stimulus frequency. Optimizing individually the τ of each neuron did not increase the information significantly either. Hence, for aperiodic stimuli, clustering the spikes into bursts was just as efficient as ignoring the interspike intervals altogether. For the few S2 neurons tested, there was no significant difference in the mean I_AIBI values across conditions (periodic versus aperiodic), and these values were similar to those of I_RATE (Fig. 7c, d, triangles).

Discrimination of periodic and aperiodic stimuli corresponds to slightly different tasks; in fact, the two types of stimuli can be distinguished easily by human subjects. This means that at least some information about the temporal structure of the stimuli is readily accessible perceptually. Therefore, these results cannot exclude the possibility that temporal information is used to construct the neural representation of stimulus frequency, even in the aperiodic condition. However, they provide two conclusions: first, that constructing a neural representation of stimulus frequency based on the temporal patterns of spikes evoked during aperiodic stimulation would require read-out mechanisms more powerful than simply identifying bursts of spikes in single cells, and second, that firing rate could provide a neural code for frequency common to the two tasks and the two areas.

Covariations between neuronal and behavioral responses

As mentioned in the introductory remarks, earlier studies pointed out a close match between the discriminability of flutter frequencies and the observed variance in the phase at which spikes are evoked by periodic stimuli (Mountcastle et al., 1969; Recanzone et al., 1992). This relationship was only a theoretical possibility, because the neurophysiological and psychophysical data that were compared had been collected in different experiments. However, a similar but direct comparison was possible using our data, because they were collected from behaving animals whose psychophysical performance was being monitored. If the periodicity of S1 spikes is important for frequency discrimination, then a subject should indeed be more likely to discriminate correctly when S1 neurons happen to fire spike trains with a highly periodic structure. This is the crux of the following analysis. We compared neuronal and behavioral responses on a trial-by-trial basis to try to detect any covariations between them. The results below apply to responses computed from neuronal activity evoked during the comparison stimulus. For the base stimulus, no significant effects were found for any quantity, which is not surprising considering the short-term memory component of the task.

The main idea was to compare neuronal responses during correct discriminations (hits) with responses during error trials. Because errors were much less frequent than hits, responses obtained for different conditions, i.e., for different combinations of base and comparison stimulus frequencies, had to be standardized and pooled, as described in Materials and Methods. In all data collection runs, two types of trials were considered separately. In trials of type 1, the frequency of the comparison stimulus was lower than the frequency of the base, and in trials of type 2, the frequency of the comparison was higher than the frequency of the base. Thus, for each run, two comparisons were made, one for each set of trials of the same type. In both cases the mean standardized response in error trials was compared with the mean standardized response in hit trials, and the significance of the difference was determined. Figure8, a and c, illustrates this procedure for a single S1 neuron, and Figure9, a and c, illustrates it for a single S2 neuron. Here H and E indicate hit and error categories, respectively, and the subscript indicates the type of trial. Each dot corresponds to a single trial, and the horizontal bars indicate the means for hits and errors in the corresponding categories. In both Figures, the difference between panels a and c lies in the quantity considered as the response.

To detect systematic variations in periodic spike timing, we computed standardized versions of the PSFP amplitude, of P_S, and of the amplitude of the power spectrum at twice the stimulus frequency. These three quantities tend to increase the closer a spike train is to a perfectly periodic arrangement, so high values should correspond to better likelihood for correct discrimination, if periodicity is related to performance. In most S1 and S2 cells, these quantities were the same in hit and error trials, as illustrated in Figures 8c and 9c. We did find four S1 neurons for which the mean standardized P_S was significantly different for hit and error trials, but this number of neurons was not significantly different (p > 0.21) from that expected by chance under the null hypothesis that hit and error responses come from the same distribution (among 238 S1 neurons, 2.38 significant tests at the 0.01 level were expected by chance). In other words, the result was not significant. The same was true for the three measures of periodicity, in both S1 and S2, and for type 1 and type 2 trials. The periodicity of spikes in single neurons showed no detectable covariations with behavior.

This negative result, however, was obtained by testing the neurons one at a time, but if higher periodicity tends to produce better performance, then across the population, standardized responses might show a tendency to be larger in hit trials than in error trials. Nevertheless, no such trend was observed. This is illustrated in Figures 8d and 9d. In these plots, each point corresponds to one neuron. Each x coordinate is the difference between the mean of all type 1 error trials and the mean of all type 1 hit trials, using the standardized P_Sas a response, and the y coordinate is the same quantity but for type 2 trials. Observe that the clouds of points are symmetric and centered at 0 in both directions. This is because, on average, differences between responses in hits and errors were not significantly different from zero and were not correlated across types of trials either: for the S1 population in Figure 8d, the correlation coefficient was practically zero (0.008, p < 0.9), and for the S2 population in Figure 9d, the correlation coefficient was −0.23, but it was not significantly different from zero (p > 0.025). Similar results were obtained when these tests were repeated using the standardized power at the PSFP or the standardized power at twice the stimulus frequency. No significant covariations between periodicity and behavior could be detected in either area.

In contrast, the numbers of evoked spikes did show significant covariations with behavioral performance. Figure 8a shows data from an S1 neuron with large differences between the means of the H and E categories. This neuron had a positive slope of 1.17 ± 0.12 spikes. The significant difference between H₁ and E₁ means that at any given comparison frequency lower than the base, on average, the chances of observing an error were higher when the neuron fired more spikes than usual for the given comparison frequency. This association was not a rare event. Among 231 runs that had at least five type 2 errors, we found 11 S1 neurons whose average standardized rates were significantly different in hit and error trials. This number may appear small, but with 231 samples the chances of finding at least 11 significant values when no real difference exists between two conditions is <3 in 10⁵ (binomial distribution with p = 0.01). Among the 219 runs with sufficient type 1 errors, only four neurons with significant differences were found, which was within the range expected by chance (p > 0.18), but there was additional evidence for the firing rate being related to behavior. In this case, a significant effect was observed across the population: the differences between standardized responses for hits and errors were significantly anticorrelated across trial types. This is shown in Figure 8b. In this plot the cloud of points is not symmetric; its correlation coefficient is −0.42 (n = 191, p < 0.0002). When a neuron fired, for instance, more spikes in incorrect versus correct discriminations in type 1 trials, it typically fired fewer spikes in incorrect versus correct discriminations of the opposite type. This result and the 11 neurons with significant differences in type 2 trials demonstrate a link between the firing rate of S1 neurons and psychophysical behavior.

In S2 the relationship between rate and behavior was even more evident. In type 1 trials, 28 of 321 neurons had significant differences between hits and errors, and in type 2 trials the numbers were 16 out of 206. The probability of finding these many by chance was, in both cases, <10⁻⁹. As can be seen in Figure 9b, differences across trial types were negatively correlated in this area too. These anticorrelation patterns would be expected if a comparison between the average rates of two neuronal populations underlaid the comparison between frequencies required by the discrimination process (Salinas and Romo, 1998), but this does not exclude other possibilities.

DISCUSSION

In these experiments, we examined the responses of S1 and S2 neurons to mechanical vibrations applied to the fingertips. Our aim was to determine, in our laboratory task where the only relevant stimulus feature is temporal frequency, what attributes of the evoked neuronal activity are important for behavior. In our simplified task this amounts to finding out what is the neural code for stimulus frequency. We specifically examined the hypothesis that such a code is constructed by some neural mechanism that reads out the periodic interspike intervals of the spike trains evoked in S1. As discovered in earlier work, the periodicity of spikes evoked by flutter vibrations was extremely prominent and reliable in this area. Unfortunately, however, we could not determine with certainty whether their precise timing plays a significant functional role in frequency discrimination. Previous studies contemplated a code for flutter frequency based exclusively on periodicity (Mountcastle et al., 1967, 1969, 1990;Talbot et al., 1968; Recanzone et al., 1992). What we did find, instead, is evidence that firing rate plays a significant role in encoding flutter frequency.

The evidence is as follows. First, rate modulations were widespread. We found that, contrary to earlier reports (Mountcastle et al., 1990;Recanzone et al., 1992), the firing rate of neurons in primary areas 3b and 1 varied significantly as a function of flutter frequency (Fig.2e,i). S2 neurons showed roughly similar rate modulations in terms of the information that rate provides about stimulus frequency (Fig. 3e,i), but interestingly, neurons firing most intensely at low frequencies were much more common in S2 than in S1 (compare Figs. 2g and 3g). In some S2 neurons, rate modulations also persisted beyond the end of the stimulus (Fig.4). The information conveyed by the rate was significant in ∼57 and 20% of the neurons in S1 and S2, respectively. The absolute amounts of information that we obtained were comparable to the numbers that have been reported by several groups working with visual cortical neurons (Richmond and Optican, 1990; Gawne and Richmond, 1993; Gochin et al., 1994; Tovee et al., 1995). These studies were based on various kinds of visual stimuli that were effective at driving the tested neural populations, just as flutter was in our case. The agreement between these information values and ours might be attributable to network properties that are common to widely different cortical areas. Second, rate modulations in S1 and S2 conveyed similar amounts of information in periodic and aperiodic conditions, which raises the possibility that the same code for mean stimulus frequency is used in the two tasks. Third, the firing rate in both areas was modulated by the behavioral relevance of the stimuli, and we estimated the net impact of this contextual modulation: the numbers of spikes fired at a given frequency were more reliable when the animals were actively discriminating than when the stimuli were applied passively and, presumably, were ignored (Figs. 4a,c, 5a,c). On average, then, the firing rate provided a clearer, more reliable signal encoding stimulus frequency when this quantity was relevant to behavior. Last, we also found that the fluctuations in firing rate of some neurons were significantly correlated with the animals' psychophysical performance on a single trial basis, suggesting that a few additional spikes fired by a single cell may have a detectable impact on discrimination performance, even in the case of a primary sensory neuron (Leopold and Logothetis, 1996).

Although not conclusive in terms of the specific question we pursued, the experiments with periodic stimuli revealed a number of interesting facts about the timing of evoked spikes in the somatosensory cortices. First, as found earlier, periodicity was extremely high in S1 (Fig.2f,h,i), and presumably it is even higher in primary afferents (Talbot et al., 1968; Vallbo, 1995), but periodicity diminished appreciably from area 3b to area 1 (Fig. 2i) and almost vanished in S2, suggesting that it is limited to early cortical representations. In view of this and of the presence of significant rate modulations already at the level of S1, the question that arises is whether the strikingly regular temporal structure of S1 spikes is somehow exploited independently from variations in mean firing rate to compute or encode stimulus frequency. The second finding regarding timing was that the degree of periodicity in S1 was also affected by the behavioral relevance of the stimuli: evoked spikes were more phase-locked to the stimulus during active discrimination than during passive stimulation (Fig. 4b,d). Not surprisingly, this effect was not seen in S2 (Fig. 5b,d), where periodicity was much less prominent, although other timing effects have recently been described in this area (Steinmetz et al., 2000). Last, we found no relationship between variations in periodicity and psychophysical performance in single trials. None of the measures of periodicity that we tested exhibited significant covariations with behavior (Figs.8c,d, and 9c,d). Clearly, analyses of this sort can only reveal subtle effects, especially when primary sensory neurons are concerned, but significant covariations between firing rate and performance were indeed found in S1 (Fig. 8a,b). This suggests that firing rate may have a larger weight in determining the neural code for stimulus frequency than the periodic alignment of spikes.

Coding mechanisms based exclusively on periodicity appear to be too rigid, as illustrated by the experiments with aperiodic stimulation: periodicity in S1 activity could not encode mean frequency during stimulation with aperiodic patterns, in the sense that mean frequency could not be read out from a Fourier decomposition of the evoked S1 responses, but temporal integration in a wider sense cannot be ruled out by these results. One key question in the discrimination task performed by our monkeys is how neurons postsynaptic to S1 integrate their incoming inputs: are they are able to read out some of the temporal features of the evoked activity? Neurons downstream from S1 must respond to certain features in the temporal structure of S1 activity, and they account for the ability of human subjects to distinguish without difficulty between periodic and aperiodic stimuli. From the comparisons between I_RATE and I_AIBI it appears that such features need to be more sophisticated than plain bursts of spikes from single neurons, but other schemes are possible. We also found that the precise timing of S1 spikes, in relation to the periodic stimulation pulses, was not appreciably correlated with psychophysical performance, but there might be particular time scales or temporally sensitive processes for which variations in S1 spike timing do have an impact in postsynaptic activity and in the code for flutter frequency, and the present experimental design or the analytic tools that we used may have been insensitive to those time scales. In the present task, the monkeys were not required to extract any features from the temporal structure of the stimuli other than the mean frequency, but the results—in particular the evoked activity in S2—might be different in tasks that do require such detailed temporal analysis.

Evidently, single cell recordings also have limitations; possible neural codes based on coordinated spike timing across multiple neurons have been reported (O'Keefe and Recce, 1993; DeCharms and Merzenich, 1995; Riehle et al., 1997; Dan et al., 1998). The following scenario, for instance, could apply to our task: the rate of synchronized spikes from two neurons might vary independently of the individual firing rates, providing additional information about the stimulus that cannot be extracted if synchronous and nonsynchronous spikes are considered equal and are lumped together to compute the firing rates (Dan et al., 1998). This is just one possible coding scheme based on temporal relationships between spikes. In general, these codes may be subtle, and testing whether they have a functional impact may be difficult. Even if they are present, neurons may or may not combine them with firing rate modulations to encode messages efficiently. To get a better understanding of neural coding in the cortex, what needs to be assessed is the effective contribution of all of these mechanisms to behavior.