Interplay between Facilitation, Depression, and Residual Calcium at Three Presynaptic Terminals

Abstract

Synapses display remarkable alterations in strength during repetitive use. Different types of synapses exhibit distinctive synaptic plasticity, but the factors giving rise to such diversity are not fully understood. To provide the experimental basis for a general model of short-term plasticity, we studied three synapses in rat brain slices at 34°C: the climbing fiber to Purkinje cell synapse, the parallel fiber to Purkinje cell synapse, and the Schaffer collateral to CA1 pyramidal cell synapse. These synapses exhibited a broad range of responses to regular and Poisson stimulus trains. Depression dominated at the climbing fiber synapse, facilitation was prominent at the parallel fiber synapse, and both depression and facilitation were apparent in the Schaffer collateral synapse. These synapses were modeled by incorporating mechanisms of short-term plasticity that are known to be driven by residual presynaptic calcium (Ca_res). In our model, release is the product of two factors: facilitation and refractory depression. Facilitation is caused by a calcium-dependent increase in the probability of release. Refractory depression is a consequence of release sites becoming transiently ineffective after release. These sites recover with a time course that is accelerated by elevations of Ca_res. Facilitation and refractory depression are coupled by their common dependence on Ca_res and because increased transmitter release leads to greater synaptic depression. This model captures the behavior of three different synapses for various stimulus conditions. The interplay of facilitation and depression dictates synaptic strength and variability during repetitive activation. The resulting synaptic plasticity transforms the timing of presynaptic spikes into varying postsynaptic response amplitudes.

Fast, chemical synaptic transmission provides the dominant means of information transfer between neurons, but presynaptic action potentials do not all give rise to identical postsynaptic responses. It has long been known that the history of recent activity dynamically regulates the strength of most synapses (Eccles et al., 1941; Feng, 1941; Magleby, 1987; Zucker, 1989). By converting trains of action potentials into varying amplitudes of postsynaptic responses, synapses perform a type of temporal filtering (Lisman, 1997; Zador and Dobrunz, 1997). This synaptic plasticity results from presynaptic changes in neurotransmitter release (Varela et al., 1997) and alterations in the responses of postsynaptic neurons to a given amount of transmitter (Trussell and Fischbach, 1989; Magee et al., 1998). In this study, we focus on how the temporal pattern of activity influences neurotransmitter release on the time scale of milliseconds to seconds.

Synapses show a wide range of responses to high-frequency stimulation such as enhancement, depression, and more complex behaviors (Feng, 1941; Eccles et al., 1964; von Gersdorff et al., 1997; Selig et al., 1999; Kreitzer and Regehr, 2000). This diversity has important implications for the transmission of information in the CNS. To demonstrate the effects of use-dependent plasticity on synaptic transmission, we considered some possible responses to a typical spike train recorded in vivo (Fig. 1A). We simulated responses to this spike train for two synapses with different presynaptic properties but identical postsynaptic properties (Fig.1B,C). The temporal pattern of postsynaptic depolarization in each example reflected the amount of facilitation and depression present during periods of high- and low-frequency activity. At one synapse, bursts of activity transiently boosted synaptic strength (Fig. 1B). In contrast, the other synapse conveyed the average rate of activity through EPSPs of relatively constant amplitude (Fig. 1C). These simulations highlight the importance of understanding presynaptic properties that determine the influence of a neuron on the firing of its targets.

To understand the mechanisms underlying presynaptic plasticity, it is necessary to consider presynaptic residual calcium (Ca_res) (Zucker, 1999). In contrast to the high calcium levels that trigger transmitter release after presynaptic depolarization (>10 μm for ∼1 msec), Ca_resis the modest elevation in calcium levels (hundreds of nanomolar) lasting for hundreds of milliseconds. During periods of high-frequency presynaptic activity, Ca_res accumulates and is involved in various short-term plasticities such as facilitation (Katz and Miledi, 1968; Zucker and Stockbridge, 1983; Kamiya and Zucker, 1994; Atluri and Regehr, 1996), augmentation (Zengel et al., 1980; Swandulla et al., 1991; Delaney and Tank, 1994), post-tetanic potentiation (Delaney et al., 1989), and recovery from presynaptic depression (Dittman and Regehr, 1998; Stevens and Wesseling, 1998; Wang and Kaczmarek, 1998). It is likely that differences in the contribution of various calcium-dependent mechanisms to synaptic strength will add to the diversity of synaptic behavior during repetitive activation.

Here, we present a simple framework for understanding synaptic dynamics in terms of underlying plasticities and Ca_res. We build on different aspects of models that were developed previously (Magleby, 1987; Abbott et al., 1997; Markram et al., 1998) and take advantage of recent clarification of the role of Ca_res in facilitation and recovery from depression. We develop an analytical expression for the use-dependent enhancement and depression of transmitter release driven by Ca_res and apply the scheme to three synapses with very different properties. This highly simplified model of presynaptic plasticity captures much of the apparent complexity observed during realistic Poisson train stimuli at all three synapses.

MATERIALS AND METHODS

Synaptic physiology. For cerebellar recordings, 300-μm-thick transverse slices were cut from the cerebellar vermis of 9- to 14-d-old Sprague Dawley rats (Llano et al., 1991). For hippocampal recordings, 300-μm-thick slices were cut from the hippocampus of 16- to 19-d-old Sprague Dawley rats, and the CA3 region was removed. Cerebellar slices were superfused with an external solution containing (in mm): 125 NaCl, 2.5 KCl, 1.5 CaCl₂, 1 MgCl₂, 26 NaHCO₃, 1.25 NaH₂PO₄, and 25 glucose, bubbled with 95% O₂/5% CO₂. For hippocampal slices, the external divalents were 2 CaCl₂ and 3 MgCl₂ to minimize multisynaptic activity and CA1 population spikes during repetitive stimulation. Flow rates were 4–6 ml/min at 34°C. Bicuculline (20 μm) was added to the external solution to suppress synaptic currents mediated by GABA_A receptors. During parallel fiber trains, the GABA_B receptor antagonist CGP55845a (2 μm), the adenosine A₁ receptor antagonist DPCPX (5 μm), and the mGluRIII antagonist CPPG (30 μm) were included in the external saline. During studies of the hippocampal Schaffer collateral synapse, (R)-CPP (5 μm) was present to suppress NMDA receptor-mediated currents.

Whole-cell recordings of Purkinje cells and CA1 pyramidal cells were obtained as described previously (Mintz et al. 1995) with an internal solution of (in mm): 35 CsF, 100 CsCl, 10 EGTA, 10 HEPES, and 0.2 D600, adjusted to pH 7.2 with CsOH. Synaptic currents were monitored at a holding potential of −40 mV to inactivate voltage-gated Na channels, and D600 was included to block voltage-gated calcium channels. In some CA1 recordings, QX-314 (5 mm) was also included in the internal solution. The access resistance and leak current (−20 to −200 pA holding at −40 mV) were monitored continuously. Experiments were rejected if either access resistance or leak current increased significantly during recording. Presynaptic fibers were stimulated with two glass electrodes (tip diameter, 10–12 μm) filled with external saline solution placed in the molecular layer. Brief pulses (200 μsec) of current (5–15 μA) were passed between the two stimulating electrodes. This configuration greatly reduced the size of the stimulus artifact. The inter-stimulus interval was 2 min for trains of ≤10 stimuli and 3 min for trains of >10 stimuli. Low stimulus intensities were used to keep initial synaptic currents small (−50 to −150 pA) thereby minimizing series resistance errors during the train.

Detecting presynaptic calcium transients. Parallel fibers, made up of granule cell axons and presynaptic terminals, were labeled with a high-pressure stream of the low-affinity calcium indicator magnesium green-AM (Molecular Probes, Eugene, OR) (Zhao et al., 1996) using techniques developed previously (Regehr and Atluri, 1995). Parallel fiber tracts were stimulated extracellularly, and epifluorescence was measured with a photodiode from a spot several hundred micrometers from the loading site, where the vast majority of the fluorescence signal arises from parallel fiber presynaptic boutons that synapse onto Purkinje cells. The peak ΔF/F change produced by a single stimulus was used as a linear measure of presynaptic calcium influx, as established previously (Regehr and Atluri, 1995).

Data acquisition and analysis. Outputs of the Axopatch 200A were filtered at 1 kHz and digitized at 20 kHz with a 16-bit D/A converter (Instrutech, Great Neck, NY) using Pulse Control software (Herrington and Bookman, 1995). Random train stimuli were generated off-line and sent through the DAC to the stimulus isolation unit. Both on- and off-line analysis as well as computer simulations were performed using Igor Pro software (Wavemetrics, Lake Oswego, OR).

Model of use-dependent plasticity driven by presynaptic calcium. We modeled the experimentally determined EPSC size as the product of the number of physical release sites(N_T) and the fraction of sites that undergo release on arrival of an action potential. This fraction was divided into two parts: a facilitation component (F) and a depression component (D), both of which could range between 0 and 1:

$$EPSC=\alpha ·N_T·F·D.$$ Equation 1

Note that release is scaled by the average mEPSC amplitude (α) to produce the final EPSC amplitude. The depression variable was set to unity at rest, reflecting the assumption that all potential release sites are available for release when no release activity has occurred for some time. Therefore, the resting probability of release is equivalent to the initial value of F(F₁).

Facilitation

Enhancement of release was assumed to be directly related to the equilibrium occupancy of the release site by a calcium-bound moleculeCaX_F with dissociation constant,K_F (see Fig. 3A for reaction scheme):

$$F(t)=\frac{1}{1+K_F/{\text{CaX}}_F(t)},$$ Equation 2

where CaX_F decays exponentially with time constant τ_F after a jump of size Δ_F after an action potential at time t_o:

$$\frac{{\text{dCaX}}_F}{\text{dt}}=-{\text{CaX}}_F(t)/{\tau }_F+{\mathrm{\Delta }}_F·\delta (t-t_{\text{o}}),$$ Equation 3

where δ(t) is the Dirac delta function and is defined to have units of sec⁻¹. Note that the notation here differs from a previous publication in which we definedδ(t) to be unitless (Dittman and Regehr, 1998). The treatment of CaX_F does not take into account the underlying decay time course of free calcium, but instead serves as an approximate description based on experimental evidence that the decay of paired-pulse facilitation is roughly exponential in nature (Atluri and Regehr, 1996). τ_F represents the decay time constant, which was measured to be ∼100 msec at the granule cell to Purkinje cell synapse at 34°C (Atluri and Regehr, 1996). We explored variations of Equation 2 with a power law relationship between facilitation and CaX_F, but the performance of the model was not improved with these modifications. We therefore chose the linear relationship for the sake of simplicity. To create an analytical expression for Equations 2 and 3 whereCaX_F is allowed to decay to 0, Equation 2 was modified with the addition of a baseline release probabilityF₁ in the absence ofCaX_F:

$$F(t)=F_1+\frac{1-F_1}{1+K_F/{\text{CaX}}_F(t)}.$$ Equation 2a

With this change, F(t) ranges fromF₁ to 1 as CaX_F increases from 0. Given a quiescent presynaptic terminal withCaX_F = 0 and F = F₁, then immediately after stimulation with a single action potential, CaX_F increases to Δ_F and F increases to:

$$F_2=F_1+\frac{1-F_1}{1+K_F/{\mathrm{\Delta }}_F}.$$ Equation 4

N_TD₁F₁sites have undergone release and entered a refractory state while N_T(1 − D₁F₁) sites remain available. If a second stimulus occurs just after the first stimulus such that no recovery from the refractory state has occurred, then the second EPSC will be determined by the increased release probabilityF₂ and the remaining number of release sites as follows:

$${EPSC}_2=\alpha ·N_T·(1-D_1·F_1)·F_2.$$ Equation 5

Therefore, the facilitation ratio (ρ) can be expressed as:

$$\rho =\frac{{EPSC}_2}{{EPSC}_1}=\frac{\alpha ·N_T·(1-D_1·F_1)·F_2}{\alpha ·N_T·D_1·F_1}=\frac{(1-F_1)·F_2}{F_1},$$ Equation 6

if D₁ = 1 (i.e., all release sites are initially available). Because F₂ cannot exceed unity, one can establish an upper bound on the initial probability of release: F₁ ≤ 1/(1 + ρ). By substituting Equation 4 into 6 forF₂ and solving for the constantK_F/Δ_F, one arrives at:

$$K_F/{\mathrm{\Delta }}_F=\frac{1-F_1}{(F_1/(1-F_1))·\rho -F_1}-1,$$ Equation 7

so the value of K_F/Δ_F is entirely determined by the experimentally observed value of facilitation and the initial release probability.

During regular stimulus trains at rate r, the amplitude ofCaX_F just before the ith stimulus is given by:

$${\text{CaX}}_{F_{\text{i}}}(r)={\text{CaX}}_{F_{\infty }}(r)·[1-exp(-(i-1)/r{\tau }_F)],$$ Equation 8

where:

$${\text{CaX}}_{F_{\infty }}(r)={\mathrm{\Delta }}_F·[exp(1/r{\tau }_F)-1{]}^{-1}.$$ Equation 9

The value of release probability just before the ith stimulus can be expressed as:

$$F_{\text{i}}(r)=F_1+\frac{1-F_1}{1+K_F/{\text{CaX}}_{F_{\text{i}}}(r)},$$ Equation 10

using Equation 2a. Release probability approaches a steady-state value of:

$$F_{\infty }(r)=F_1+\frac{1-F_1}{1+K_F/{\text{CaX}}_{F_{\infty }}(r)}.$$ Equation 11

Calcium dependence and kinetics of recovery from depression

Our model of recovery from depression has been previously described for the climbing fiber [see Scheme II in Dittman and Regehr (1998)]. Here, we have adopted different symbols for some of the parameters for clarity. We use CaX_D in place of Ca to refer to the calcium-bound site and τ_D instead of τ_c for the decay time constant of this species. The model assumes three possible states of the release apparatus (R, T, and N), whereR sites are in a refractory state, T are in a transitional state, qj N sites are release-ready, and there are a total of N_T release sites (R + T + N = N_T).

Calcium dependence of the recovery rate (R → N) was captured by the equilibrium binding occupancy of a calcium-bound molecule CaX_D, which instantaneously rises by Δ_D after an action potential at timet_o and decays to 0 exponentially with time constant τ_D:

$$\frac{{\text{dCaX}}_D}{\text{dt}}=-{\text{CaX}}_D(t)/{\tau }_D+{\mathrm{\Delta }}_D·\delta (t-t_{\text{o}}).$$ Equation 12

This treatment approximates the underlying kinetics of a reaction between Ca_res and some siteX_D in a manner similar to the facilitation scheme described above. Experimentally, the value of τ_Dwas estimated from the amplitude and duration of the rapid phase of recovery from paired-pulse depression at the climbing fiber synapse at 34°C [see Dittman and Regehr (1998) for a similar approach at 24°C]. Because τ_F and τ_D reflect distinct binding reactions, there is no a priori reason to assume that they will have equal values. As explained in Results, we found that the experimental data could be better fit using a value of τ_D that was about half the value of τ_F, perhaps reflecting different underlying calcium-binding kinetics.

The probability that a release site is release-competent is then given by the depression variable D = N/N_T, governed by the equation:

$$\frac{\text{dD}}{\text{dt}}=(1-D(t))·k_{\text{recov}}({\text{CaX}}_D)-D(t)·F(t)·\delta (t-t_{\text{o}}),$$ Equation 13

where

$$k_{\text{recov}}({\text{CaX}}_D)=\frac{k_{max}-k_{\text{o}}}{1+K_D/{\text{CaX}}_D(t)}+k_{\text{o}}.$$ Equation 14

For Equations 12 and 13, rapid equilibration withCaX_D and the steady-state approximationdT/dt ≈ 0 are assumed as described previously (Dittman and Regehr, 1998). For CaX_D = 0,k_recov = k_o, andD recovers exponentially with time constant τ_recov = 1/k_o. For values ofCaX_D ≫ K_D,k_recov = k_max, soD recovers exponentially at a faster rate with τ_recov ≈ 1/k_max. For intermediate, time-varying values of CaX_D,D recovers with both fast and slow kinetic components. The form of Equation 14 was chosen for mathematical convenience as in Equation 2a. With this form of rate dependence,CaX_D is allowed to decay to 0 while the rate of recovery slows to a fixed, calcium-independent rate.

For regular stimulus trains given at frequency r, Equations12, 13, and 14 can be used to generate an analytical expression for the fraction of available release sites during the ith stimulus:

$$D_{\text{i}}(r)=1-(1-(1-F_{\text{i}-1}(r))·D_{\text{i}-1}(r))e^{-k_{\text{o}}/r}·{\xi }_{\text{i}}(r),$$ Equation 15

where

$${\xi }_{\text{i}}(r)={\left(\frac{K_D/{\text{CaX}}_{D_{\text{i}-1}}+1}{K_D/{\text{CaX}}_{D_{\text{i}-1}}+exp(-1/r{\tau }_D)}\right)}^{-(k_{max}-k_{\text{o}}){\tau }_D}.$$ Equation 16

CaX_Di−1 is the level of calcium-bound X_D just after the (i − 1) th stimulus and is given by:

$${\text{CaX}}_{D_{\text{i}-1}}(r)={\text{CaX}}_{D_{\infty }}(r)·[1-exp(-(i-1)/r{\tau }_D)],$$ Equation 17

where:

$${\text{CaX}}_{D_{\infty }}(r)={\mathrm{\Delta }}_D·[1-exp(-1/r{\tau }_D){]}^{-1}.$$ Equation 18

For the i th stimulus in a regular train of rate r, the normalized EPSC_i can be expressed analytically:

$$\frac{{EPSC}_{\text{i}}(r)}{{EPSC}_1}=\frac{\alpha ·N_T·D_{\text{i}}(r)·F_{\text{i}}(r)}{\alpha ·N_T·D_1·F_1}=D_{\text{i}}(r)·(F_{\text{i}}(r)/F_1).$$ Equation 19

During a prolonged stimulus train, the number of available sites reaches a steady-state value that can be expressed analytically using Equations 9, 11, 15, 16, and 18:

$$D_{\infty }(r)=\frac{1-exp(-k_{\text{o}}/r)·{\xi }_{\infty }(r)}{1-(1-F_{\infty }(r))exp(-k_{\text{o}}/r)·{\xi }_{\infty }(r)}.$$ Equation 20

Combining this equation with Equation 11, one can then generate an analytical expression for the steady-state EPSC size normalized to the initial EPSC:

$$\frac{{EPSC}_{\infty }(r)}{{EPSC}_1}=D_{\infty }(r)·(F_{\infty }(r)/F_1).$$ Equation 21

Equations 19 and 21 were used to generate the simulations in Figures 3-6. Simulated EPSC waveforms were produced using the normalized alpha function, (t*e/τ_E)* exp(−t/τ_E) where τ_E was the decay time constant of the simulated EPSC. The alpha function was then scaled in amplitude to the value EPSC_i for the i th EPSC in a train:

$${EPSC}_{\text{i}}(t)=\alpha ·N_T·D_{\text{i}}·F_{\text{i}}·(t·e/{\tau }_E)·exp(-t/{\tau }_E).$$ Equation 22

For the synapses modeled in this study, τ_E was set equal to 2 msec. For the Poisson train simulations in Figure 7, Equations 10 and 15 were used with CaX_Fi and CaX_Di generated by the recursive equations:

$${\text{CaX}}_{F_{\text{i}}}={\text{CaX}}_{F_{\text{i}-1}}·exp[-(\mathrm{\Delta }{t}_{\text{i}})/{\tau }_F],$$ Equation 23

$${\text{CaX}}_{D_{\text{i}}}={\text{CaX}}_{D_{\text{i}-1}}·exp[-(\mathrm{\Delta }{t}_{\text{i}})/{\tau }_D],$$ Equation 24

where Δt_i is the ith inter-stimulus interval in a Poisson train. A summary of the model parameters is given in Table 1.

Fig. 3.

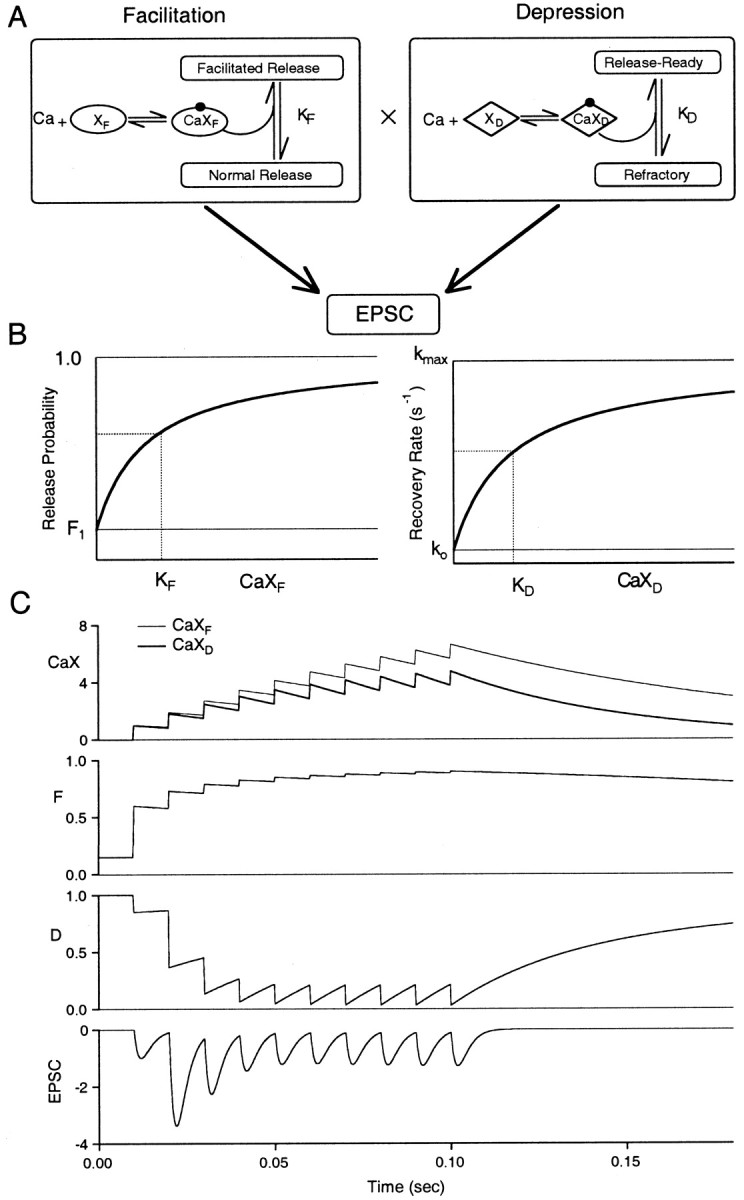
FD model for Ca-dependence of short-term plasticity. A, Left, Residual presynaptic calcium binds to site X_F, and the complex CaX_F then binds to the release site causing an enhancement of release probability. Right, Schematic of residual presynaptic calcium binding to site X_D, which then binds with the refractory release site driving a transition back to the release-ready state. B, Left, F plotted as a function of CaX_F ranging from a minimal probability of F₁ (no residual calcium) to a maximum of 1. The dissociation constant for CaX_F is K_F.Right, the recovery rate for depression is plotted as a function of CaX_D with a minimum rate of k_o, a maximum rate of k_max, and CaX_Ddissociation constant K_D. C, Presynaptic levels of CaX_F (thin line) and CaX_D (thick line), fraction of available synapses that undergo release (F), fraction of release-ready synapses (D), and normalized EPSC during a train of 10 stimuli at 100 Hz. Model parameters for this simulation were ρ = 3.4, F₁ = 0.15, τ_F = 100 msec, τ_D = 50 msec, k_max = 30 sec⁻¹, k_o = 2 sec⁻¹, K_D = 2. Note that CaX_F and CaX_D were normalized to their respective dissociation constants.

Fig. 4.

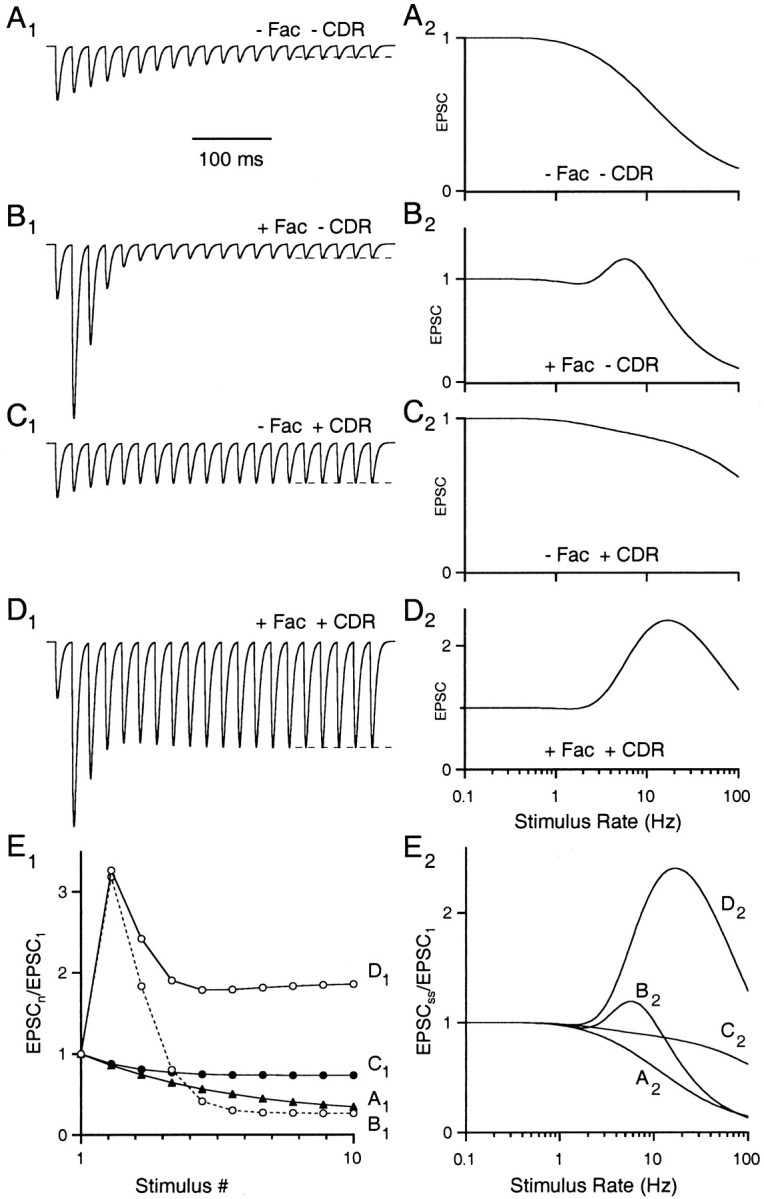
Effects of facilitation and CDR on presynaptic dynamics. A₁, Simulation of 20 EPSCs generated at 50 Hz in a reduced FD model with no facilitation or CDR.Dashed line represents the steady-state EPSC size. A₂, Steady-state EPSC magnitude (normalized to the first EPSC) as a function of stimulus frequency. B, Same as A for a simulation with facilitation only. C, Same as A for a simulation model with CDR only. D, Same as A for a simulation with both facilitation and CDR. Equations 19 and 21 were used with model parameters from Figure 3. E₁, EPSC peak amplitudes versus stimulus number for the four model synapses. E₂, Steady-state EPSC versus frequency curves from A₂ to D₂ are superimposed. For A and C, F was held constant at F₁. For A and B, the recovery rate was held constant at k_o.

Fig. 5.

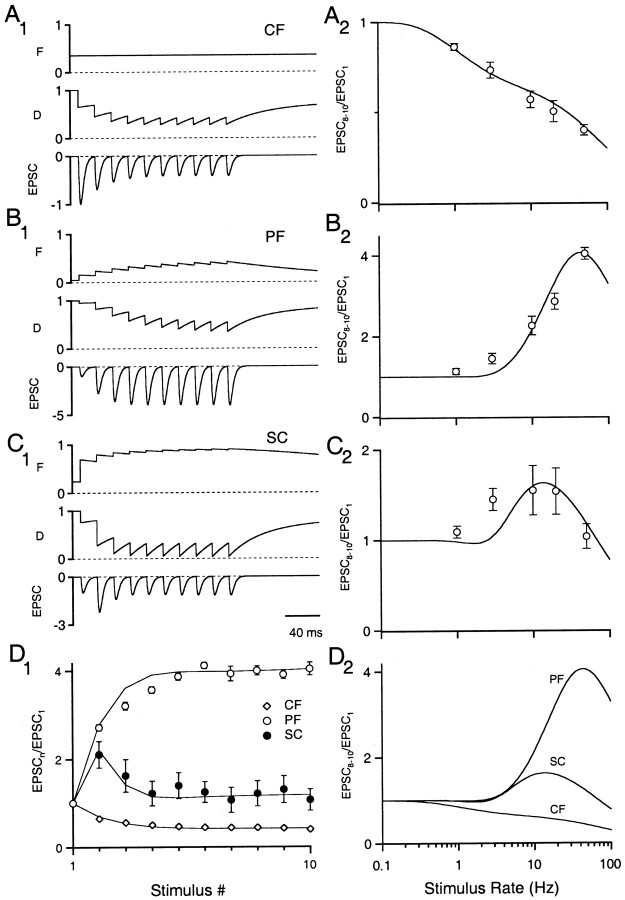
Application of the FD model to real synapses. A₁, F, D, and EPSC size during a 10 pulse 50 Hz stimulus train for a model climbing fiber to Purkinje cell synapse. A₂, Amplitude of the 8th–10th EPSC (taken from Fig. 2B) plotted against stimulus frequency. Solid line is the analytical solution given in Equation 21. Model parameters were F₁ = 0.35 for A₁, τ_D = 50 msec, k_max = 20 sec⁻¹, k_o = 0.7 sec⁻¹, K_D = 2. B₁, B₂, Same as A for the parallel fiber to Purkinje cell synapse. Model parameters for both B₁ and B₂ were ρ = 3.1, F₁ = 0.05, τ_F = 100 msec, τ_D = 50 msec, k_max= 30 sec⁻¹, k_o = 2 sec⁻¹, K_D = 2. C₁, C₂, Same as A for the CA3 to CA1 Schaffer collateral synapse. Model parameters were ρ = 2.2, F₁ = 0.24 for C, τ_F = 100 msec, τ_D = 50 msec, k_max = 30 sec⁻¹, k_o = 2 sec⁻¹, K_D = 2. D₁, Normalized average EPSC magnitude during a 50 Hz stimulus versus stimulus number. Open circlesrepresent mean EPSC amplitudes during 50 Hz trains plotted against stimulus number for the climbing fiber (CF), parallel fiber (PF), and Schaffer collateral (SC) synapses. Data are mean ± SEM with n = 5–7. D₂, FD model fits to the steady-state data in A₂–C₂ superimposed for comparison.

Fig. 6.

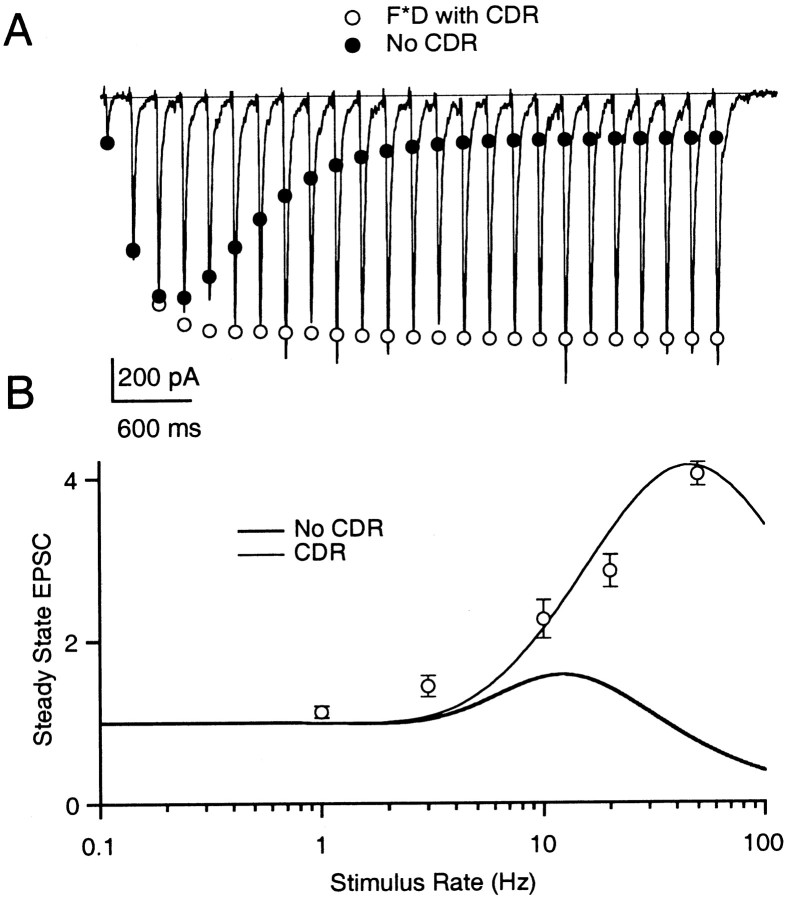
Importance of CDR at “low P” synapses. A, Parallel fiber to Purkinje cell EPSCs recorded during 25 stimuli at 50 Hz. Trace represents a single trial. Open circles are the predicted FD model EPSC magnitudes using Equation19. Filled circles represent the same FD model without CDR (CaX_D = 0). B, Steady-state EPSC size plotted against stimulus frequency for the parallel fiber synapse with (thin line) and without (thick line) CDR.Open circles are parallel fiber data from Figure 2B. Model parameters were ρ = 3.8, F₁ = 0.038, τ_F = 100 msec, τ_D = 50 msec, k_max= 30 sec⁻¹, k_o = 2 sec⁻¹, K_D = 2.

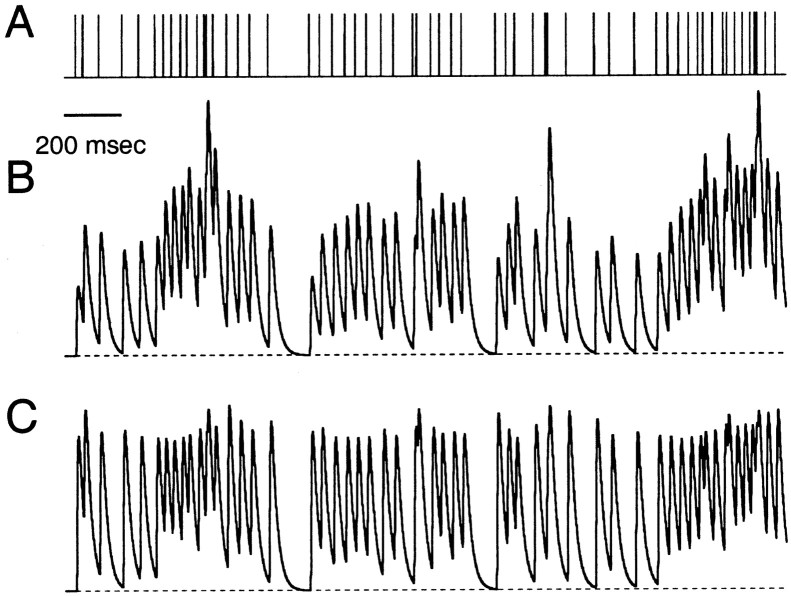
Fig. 7.

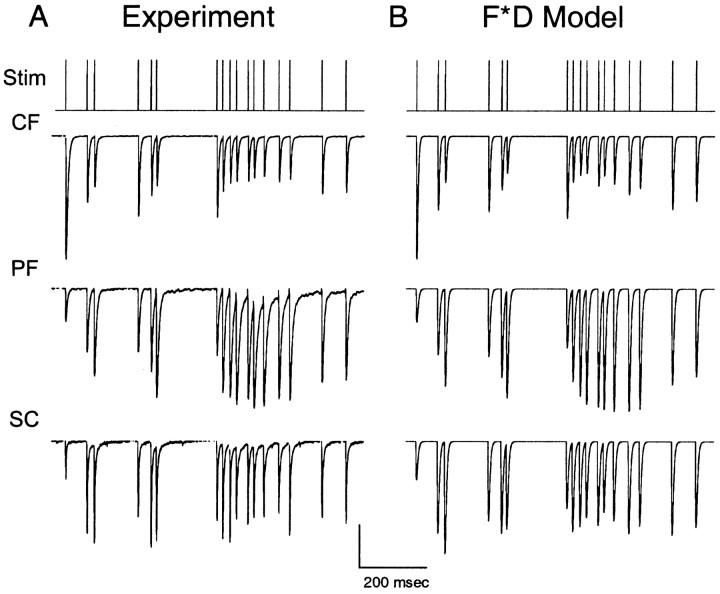
Presynaptic dynamics during Poisson stimulus trains. A, Examples of EPSCs recorded in response to an irregular stimulus train with average rate 20 Hz at the climbing fiber (CF), parallel fiber (PF), and Schaffer collateral (SC) synapases. Stimulus artifacts were suppressed for clarity. B, FD model simulations for the three synapses. Vertical scale bar is 1, 400, and 200 pA for the CF, PF, and SC synapses, respectively. Model parameters for CF wereF₁ = 0.57, τ_D = 50 msec,k_max = 30 sec⁻¹,k_o = 2 sec⁻¹,K_D = 3.6. Model parameters for PF were ρ = 2.7, F₁ = 0.05, τ_F = 100 msec, τ_D = 50 msec,k_max = 30 sec⁻¹,k_o = 2 sec⁻¹,K_D = 2. Model parameters for SC were ρ = 3.2, F₁ = 0.1, τ_F = 100 msec, τ_D = 50 msec,k_max = 18 sec⁻¹,k_o = 2 sec⁻¹,K_D = 1.8. Parallel fiber data adapted fromKreitzer and Regehr (2000).

Table 1.

Definitions of parameters used in the FD model

Symbol	Definition
CaXF	Concentration of calcium-bound site XF
CaXD	Concentration of calcium-bound siteXD
F	Facilitation variable; fraction of available sites activated by a stimulus
D	Depression variable; fraction of sites that are release-ready
pR	Probability of release; product of the probabilities F and D
F1	Initial probability of release
KF	Affinity ofCaXF for the release site
KD	Affinity ofCaXD for the release site
τF	Decay time constant ofCaXF after an action potential
τD	Decay time constant ofCaXD after an action potential
ΔF	Incremental increase inCaXF after a stimulus
ΔD	Incremental increase inCaXD after a stimulus
ko	Baseline rate of recovery from the refractory state
kmax	Maximal recovery rate from the refractory state
ρ	Facilitation ratio EPSC2/EPSC1 for closely spaced EPSCs
NT	Total number of release sites
α	Average mEPSC size

Simulated integrate-and-fire neuron. For Figure 8, we implemented a single compartment model neuron with membrane time constant τ_m = 20 msec, input resistance R_N = 100 MΩ, and resting potential V_rest = −70 mV. The EPSC waveforms generated with Equation 22 were then scaled to conductance values, G_syn(t), chosen to produce a particular EPSP magnitude (see Fig. 8) with synaptic reversal potential V_syn set equal to 0 mV. Membrane voltage (V_m) was determined by solving the first-order differential equation:

$${\tau }_{\text{m}} \frac{{\text{dV}}_{\text{m}}}{\text{dt}}=G_{\text{syn}}(t)·R_N·(V_{\text{syn}}-V_{\text{m}})+(V_{\text{rest}}-V_{\text{m}}),$$ Equation 25

where if the voltage exceeded threshold (V_thresh = −55 mV), its value was then jumped to +40 for 1 msec and then hyperpolarized to −75 mV using an idealized action potential waveform template. For Figure 8, Equation 25was numerically integrated with a first-order Euler routine.

Fig. 8.

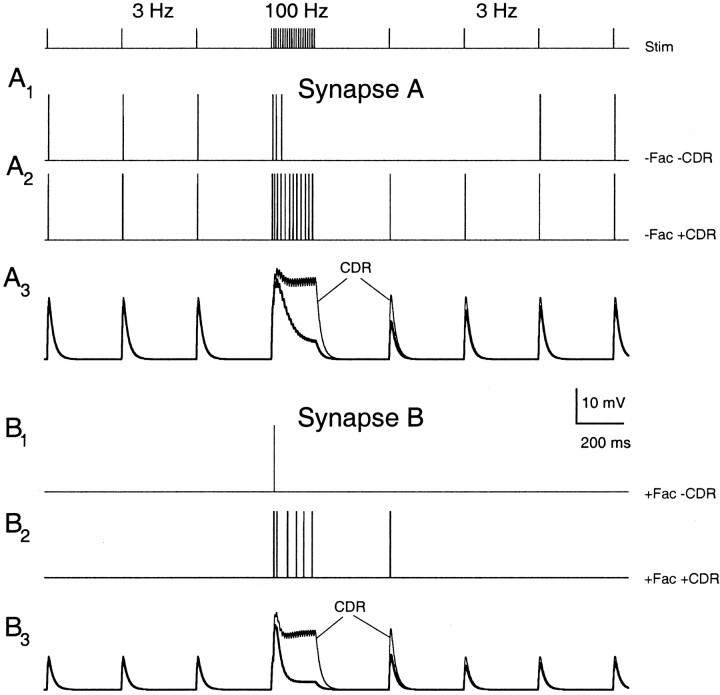
Potential postsynaptic effects of facilitation and CDR. A₁, A₂, Postsynaptic responses of a model integrate-and-fire neuron using a single nonfacilitating presynaptic input stimulated at 3 Hz with a 100 Hz burst. CDR is absent in A₁ (−Fac, −CDR) and present in A₂ (−Fac, +CDR). Synapse A had an initial peak conductance of 15 nS (suprathreshold). A₃, Postsynaptic potentials for synapse A with (thin lines) and without CDR (thick lines). B₁, B₂, Postsynaptic responses given the same presynaptic stimulus but facilitation was included. Synapse B had an initial conductance of 6 nS (subthreshold). CDR was absent in B₁ (+Fac, −CDR) and present in B₂ (+Fac, +CDR). B₃, Postsynaptic potentials for synapse B with (thin lines) and without CDR (thick lines). Model parameters for synapse A were F₁ = 0.24, τ_D = 50 msec, k_max = 30 sec⁻¹, k_o = 2 sec⁻¹, K_D = 2. Model parameters for synapse B were ρ = 2.5, F₁ = 0.24, τ_F = 100 msec, τ_D = 50 msec, k_max = 30 sec⁻¹, k_o = 2 sec⁻¹, K_D = 2. Postsynaptic integrate-and-fire neuron parameters: V_rest = −70 mV, V_thresh = −55 mV, τ_m = 20 msec, R_N = 100 MΩ.

RESULTS

We recorded synaptic currents during various stimulus conditions at three CNS synapses in rat brain slices. In addition, presynaptic calcium influx was measured in cerebellar granule cell presynaptic terminals for the same stimulus conditions. These experimental studies formed the basis of a model of synaptic plasticity that was then applied to each type of synapse.

Diversity of short-term synaptic plasticity in the CNS

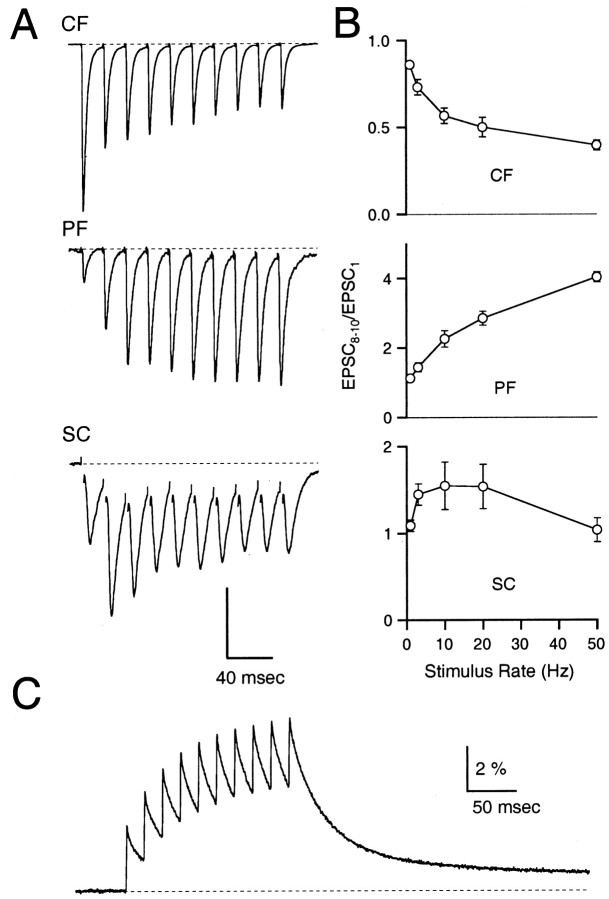
The responses of three types of synapses to 50 Hz stimulation were measured using whole-cell voltage clamp at 34°C (Fig. 2A). The inferior olive climbing fiber to Purkinje cell synapse (CF) depressed during stimulus trains as reported previously (Fig. 2A, top trace) (Eccles et al., 1966). The cerebellar granule cell parallel fiber to Purkinje cell synapse (PF) was activated under stimulus conditions identical to those of the climbing fiber synapse (Fig. 2A, middle trace) but synaptic strength enhanced markedly during the stimulation. In contrast to the previous examples, the hippocampal CA3 to CA1 Schaffer collateral synapse (SC) briefly facilitated and then depressed during the stimulus train. These three synapses demonstrate the wide spectrum of short-term transmitter release properties expressed during high-frequency stimulation.

Fig. 2.

Diversity of short-term plasticity in the CNS. A, Top, Climbing fiber to Purkinje cell EPSCs (CF); middle, parallel fiber to Purkinje cell EPSCs (PF); bottom, CA3 to CA1 Schaffer collateral EPSCs (SC) recorded while stimulating afferents at 50 Hz for 10 stimuli at 34°C. Traces are averages of four to six trials each. Stimulus artifacts were suppressed for clarity. Vertical scale bar is 2, 400, and 60 pA for the CF, PF, and SC synapses, respectively. B, Average magnitude of the 8th–10th EPSC normalized by the first EPSC plotted as a function of stimulus frequency for the climbing fiber (top), the parallel fiber (middle), and the Schaffer collateral (bottom) synapses. Data are shown as mean ± SEM (n = 4–5). C, Measurement of parallel fiber Ca_res during a 10 pulse, 50 Hz stimulus train using the calcium-sensitive indicator magnesium green. Vertical scale bar is percentage ΔF/F. Parallel fiber data were adapted fromKreitzer and Regehr (2000).

For all three synapses, the immediate effects of short-term plasticity began to plateau by the eighth stimulus. Therefore, the normalized average of EPSCs 8 through 10 (EPSC_8–10/EPSC₁) provided a useful measure of steady-state behavior. The frequency-dependence of steady-state transmitter release clearly differed at each type of synaptic connection (Fig. 2B). The climbing fiber depressed and the parallel fiber facilitated at all frequencies. The Schaffer collateral synapse facilitated at low rates but depressed during higher-frequency stimulation. During prolonged stimuli, processes acting on the tens of seconds to minutes time scale, such as post-tetanic potentiation and a slower form of presynaptic depression (Galarreta and Hestrin, 1998), could potentially affect release. Thus, stimulus trains were kept relatively short to isolate facilitation and shorter-lived forms of depression.

In addition to quantifying transmitter release, we recorded the behavior of Ca_res during high-frequency stimulation (see Materials and Methods). A representative measurement of granule cell Ca_res during a 10 stimulus 50 Hz train using the calcium-sensitive indicator magnesium green is shown in Figure 2C. Ca_res increased rapidly after each stimulus and then decayed over hundreds of milliseconds with a time course that is similar in many synapses in the CNS (Feller et al., 1996; Helmchen et al., 1997; Sinha et al., 1997).

A model of presynaptic plasticity

We developed a model to account for the behavior of these synapses during repetitive stimulation. Our aim was to keep the model as simple as possible while including a level of detail matched to the constraints provided by our experiments. A number of simplifying assumptions allowed us to obtain an analytical solution while retaining important aspects of facilitation and recovery from depression. According to our scheme, sustained presynaptic activity depletes the number of functional sites but also elevates Ca_res, thereby facilitating release and accelerating recovery from depression (Fig. 3A). The model is based on the following principles:

Assumption I

Release = N_T· p_R where N_T is the number of physical release sites and p_R is the probability of transmitter release (Del Castillo and Katz, 1954a).

Assumption II

Release probability is composed of two independent variables (probabilities): p_R = F·D where F and D both range between 0 and 1. Therefore, the average EPSC is given by α·N_T· F·D where α is the average mEPSC amplitude (Eq. 1). The values of F and D determine the state of the presynaptic terminal. Although F and D are thought to be stochastic variables at individual release sites, we treated them as deterministic averages in this study for the purpose of simplicity (Del Castillo and Katz, 1954b;Stevens and Wang, 1995). In this way, “release” represents the average of many trials at a particular synaptic connection, or equivalently the summation of many simultaneously activated synapses.

Assumption III

Facilitation is attributable to the calcium-dependent increase in the value of F from an initial value F₁ according to the fractional occupancy of some calcium-bound molecule CaX_F at the release site (Fig. 3A, B, left). CaX_Fincreases by a constant amount (Δ_F) with each action potential and decays exponentially toward 0 with time constant τ_F (Eqs. 2, 2a, and 3). A constant increment in CaX_F is equivalent to assuming that X_F remains unsaturated during a stimulus train.

Assumption IV

Depression is determined by the fraction of sites that undergoes transmitter release in such a way that D = (number of available sites)/(total number of sites). According to Assumptions I and II, N_T* F₁*D₁sites have undergone transmitter release and enter a refractory state, leaving N_T* (1 − F₁*D₁) sites available to release immediately afterward. Therefore D₂ = 1 − F₁*D₁ just after an action potential and recovers back to D₁ at a specified rate (see assumption V). For maximal simplicity in the model we explore here, it was assumed that D₁ = 1 (i.e., after long quiescent intervals, all sites are available to undergo release; see Eqs. 5 and 6). We refer to this form of depression as refractory depression [see also Dittman and Regehr (1998)].

Assumption V

Recovery from refractory depression is dependent on Ca_res in the following manner. In the absence of Ca_res, recovery proceeds at some minimal rate k_o. After a stimulus, the rate is accelerated by the interaction of a calcium-bound molecule CaX_Dwith the release site (Fig. 3A, right, and Eqs. 12,13, and 14). CaX_D increases by a constant amount Δ_D and decays exponentially to 0 with a time constant τ_D. We refer to this calcium-dependent acceleration of recovery from refractory depression as CDR. This treatment is based on our studies at the climbing fiber synapse (Dittman and Regehr, 1998). As in the case of X_F, we assume that X_D is not saturated during stimulus trains (see assumption III).

Assumption VI

Facilitation and depression are inherently coupled through assumptions I, II, and III. As facilitation increases the number of sites that undergo release, a larger fraction of the total number of sites enters the refractory state, thereby increasing depression. τ_F was estimated by the decay of paired-pulse facilitation at the parallel fiber to Purkinje cell synapse (Fig. 3B) (Atluri and Regehr, 1996). τ_D was estimated as in Dittman and Regehr (1998). The values of τ_F and τ_D are set in part by the decay of Ca_res, so changes in Ca_res will perturb the recovery kinetics of both facilitation and depression (Eqs. 15 and16).

An example of the proposed model is shown in Figure 3C during a 10 pulse 100 Hz stimulus train. The details of the model are described in Materials and Methods. During the train, Ca_resand the calcium-bound species CaX_F and CaX_D build up and then decay with their characteristic time constants. F is initially 0.15 and increases approximately fivefold during the train. Because the CaX_F binding sites are nearly saturated after 10 stimuli, F increases toward unity and remains elevated after free CaX_F decays toward 0. D quickly declines during the train, but recovery from the refractory state accelerates as CaX_D reaches a high concentration. As a result of the increase in F and the decrease in D, transmitter release first enhances and then declines during the stimulus train. The EPSCs shown in Figure 3C are scaled to reflect the product F·D normalized to the initial value F₁ (see Materials and Methods).

Categories of synaptic behavior arising from the facilitation–depression model

We next explored the contributions of calcium-dependent processes to synaptic behavior simulated by the facilitation–depression (FD) model (Fig. 4). The four simulations shown here describe the same synapse in the presence or absence of either facilitation (±Fac) or calcium-dependent recovery (±CDR) during a 50 Hz stimulus train. In the absence of facilitation and CDR, sustained activity gradually depressed synaptic strength (Fig. 4A₁). The steady-state level of depression was more pronounced at higher stimulus frequencies (Fig. 4A₂). Thus, the synapse behaves as a low-pass filter during regular stimulus trains with little attenuation at frequencies below 1 Hz, a frequency that corresponds to the slow recovery rate (k_o). Stimulation at higher frequencies eventually depletes a large fraction of available release sites because there is not sufficient time for recovery between stimuli.

When facilitation was added to this model synapse (+Fac, −CDR), a strikingly different behavior emerged during the first few stimuli (Fig. 4B₁). The EPSC amplitude transiently increased, reflecting an increase in F. However, the increasingly larger fraction of sites undergoing release rapidly depleted the number of available sites (decrease in D). After only five stimuli, transmitter release fell to similar levels as in the previous example, despite the presence of facilitation (Fig. 4E₁, traces A and B). In the absence of facilitation, steady-state levels of transmitter release were reached after more than 10 stimuli. Thus, facilitation reduces the time to reach steady state according to the FD model. The similarity in steady-state behavior between these two cases can be seen more explicitly by comparing the superimposed frequency response curves (Fig. 4E₂, traces A and B). The only difference between these two synapses at steady state is a boosting at intermediate frequencies (∼3–10 Hz).

For a nonfacilitating synapse, the inclusion of CDR (−Fac, +CDR) allows the synapse to remain much more effective over a wide range of stimulus frequencies (Fig. 4C). As the stimulus frequency increases, Ca_res increases proportionally, boosting the recovery rate at high frequencies and maintaining synaptic efficacy even during prolonged trains (Fig. 4E₂, traces A and C).

When facilitation and CDR are both present (+Fac, +CDR), two features become apparent (Fig. 4D). First, a transient increase in release is observed during the first few stimuli because of increases in F, similar to the (+Fac, −CDR) synapse. Second, steady-state release was maximal at a stimulus frequency of ∼12 Hz. This tuning curve arises from an interplay between facilitation and depression. At low frequencies (<1 Hz), there is little Ca_res accumulation, and neither facilitation nor refractory depression influences transmitter release. At intermediate frequencies (5–20 Hz), release probability begins to increase, and the recovery rate from depression accelerates in concert leading to a net enhancement. Finally, at high stimulus frequencies (>50 Hz), release probability and recovery rate have saturated at their maximal values but the inter-stimulus interval is too short for a significant amount of recovery to occur, so synaptic strength falls off precipitously.

The transient and steady-state responses of all four simulated synapses are superimposed in Figure 4E. Steady-state synaptic strength is identical for these synapses at stimulus rates <1 Hz because little if any Ca_res accumulates for long inter-stimulus intervals (>1 sec). The divergence in steady-state behavior observed at higher frequencies arises from recruitment of the calcium-dependent processes described above. Thus, the decay kinetics of Ca_res determine a frequency threshold, below which facilitation and CDR do not influence synaptic strength.

Fitting the FD model to three synapses

After characterizing some of the basic features of the FD model, we determined whether it could account for the observed behavior of the climbing fiber, parallel fiber, and Schaffer collateral synapses studied above. We began by establishing experimentally based values for many of the FD model parameters (Table2). At the climbing fiber synapse, F₁ was set by the amount of paired-pulse depression (35%) for two closely spaced stimuli. k_o was estimated from the recovery time course at long inter-stimulus intervals (Dittman and Regehr, 1998). For the parallel fiber synapse, the decay of CaX_F(τ_F) was constrained to match the decay of paired-pulse facilitation, and the amplitude of facilitation determined the value of ρ (Atluri and Regehr, 1996). For the Schaffer collateral synapse, only the amount of facilitation (ρ) was experimentally determined. To constrain the SC model further, we assigned all parameters (τ_F, τ_D, k_o, k_max, and K_D) to the values used in the parallel fiber simulations except for the initial release probability, F₁. Table 2 summarizes the FD model parameter values used to characterize all three synapses. The values in bold were determined by experiments at 34°C. Note that the parameter values differ from those reported in a previous study conducted at 24°C (Dittman and Regehr, 1998). The other values were chosen both “by eye” and with a least-squares minimization procedure. The predicted EPSC peaks and steady-state frequency curves shown in Figure5 were generated by analytical solutions to approximations of Equations 3, 13, and 14 (see Materials and Methods, Eqs. 15-21 for analytical solutions).

Table 2.

Model parameters for the three synapses

	Climbing fiber	Parallel fiber	Schaffer collateral
ρ	—	3.1	2.2
F1	0.35	0.05	0.24
τF	—	100 msec	100 msec2-a
τD	50 msec	50 msec	50 msec2-a
ko	0.7 sec−1	2 sec−1	2 sec−12-a
kmax	20 sec−1	30 sec−1	30 sec−12-a
KD	2	2	22-a

Parameter values in bold type were constrained from experimental values (see Results). Others are free parameters determined by fits to the data in Figure 5. ρ and τ_F were not included in the climbing fiber model.

^F2-aParameters taken from fits to parallel fiber data.

At the climbing fiber synapse, this model provided a reasonably good description of both the time course and frequency-dependence of depression (Fig. 5A₂, D₁). Because no facilitation was observed at this synapse, F was held constant for these simulations at ∼0.35. This fixed value of F implies that 35% of available sites release neurotransmitter when stimulated. The data were well approximated with only three free parameters (Table 2).

The model also captured the basic features of synaptic plasticity at the parallel fiber synapse (Fig. 5B₂, D₁). According to this simulation, the enhancement reflected a large increase in F from an initial value of ∼0.05 that was partially countered by a decrease in D. By the end of the train, the fourfold enhancement in release was the result of an eightfold increase in F and a twofold reduction in D. Simulations of the hippocampal Schaffer collateral synapse were similar to the parallel fiber synapse (Fig. 5C₂, D₁), but the initial release probability was about five times as large (0.24). During the train, F was close to unity (saturation of CaX_F binding sites), leading to a large reduction in D. The model could not account entirely for the enhancement of release observed at 3 Hz at either the parallel fiber or Schaffer collateral synapses (see Discussion). The model fits to steady-state release are superimposed in Figure 5D₂ for comparison. Despite the many simplifying assumptions that we made, the model accounts for synaptic dynamics during high-frequency stimulation fairly well at these three synapses.

Possible role for CDR at “low P” synapses

Calcium-dependent recovery from depression can play an important role in sustaining transmitter release during high rates of presynaptic activity. The importance of CDR has been demonstrated for synapses with high release probabilities where depression is prominent (Dittman and Regehr, 1998; Wang and Kaczmarek, 1998). However, CDR is more difficult to assess at low probability synapses such as the parallel fiber synapse, where facilitation tends to obscure any underlying depression. We used the FD model to explore a possible role of CDR in transmission at parallel fiber synapses (Fig. 6). During 50 Hz 25-pulse stimulation, the parallel fiber synapse reaches a steady-state level of facilitation with no sign of depression. In the absence of CDR with only slow calcium-independent recovery from depression present, the FD model did not predict a significant amount of steady-state facilitation (Fig. 6A, •).

We investigated several possible explanations for the sustained enhancement observed in Figure 6. One possibility is that an extremely low initial release probability (F₁) can account for the apparent lack of depression during a train. However, we were unable to fit the data in Figure 5 with values of F₁ smaller than ∼0.05 (data not shown), suggesting that simply lowering F₁ cannot explain the enhancement. Alternatively, recovery from depression could be fast enough to prevent most of the release sites from accumulating in the refractory state. This may reflect a fast basal rate of recovery (k_o) at the parallel fiber synapse (fit not shown) or a calcium-dependent acceleration of recovery from depression, as observed at the climbing fiber synapse. The FD model provided a good approximation to synaptic strength when the properties of recovery from depression were similar to those observed at the climbing fiber synapse, in that a slow component of recovery from depression and CDR were both present (Fig. 6A, ○).

These simulations emphasize that rapid recovery from depression may be important even at synapses with low initial release probabilities where depression is not apparent. The model suggests that fast recovery from depression is required to preserve synaptic strength during periods of prolonged activity. Without rapid recovery from depression, facilitating synapses cannot maintain significant enhancement at steady state. As shown in Figure 6, inclusion of CDR can account for the behavior of parallel fibers during long stimulus trains. However, further experiments are required to determine whether CDR is the mechanism responsible for fast recovery from depression at these synapses. This will be difficult to establish until the underlying molecular correlates of facilitation and CDR can be identified and independently manipulated.

Synaptic plasticity during irregular stimulus trains

As a further test of the FD model, synaptic currents were recorded at the climbing fiber, parallel fiber, and Schaffer collateral synapses during stimulation with irregular stimulus trains (Fig.7). The climbing fiber synapse showed sustained depression during the train, with significant recovery after inter-spike intervals greater than a few hundred milliseconds (Fig. 7A, top). In contrast, the parallel fiber synapse facilitated during periods of high-frequency activity (Fig. 7A,middle). The Schaffer collateral synapse enhanced to a similar degree but the temporal pattern of EPSC peaks differed from the parallel fiber synapse (Fig. 7A, bottom). At all three synapses, there was a high degree of peak-to-peak variability attributable in large part to the short-term plasticities described above.

The analytical FD model used in Figure 5 accounted for features of this EPSC variability as shown in Figure 7B. The significant peak-to-peak variation in EPSC magnitude arose from the interplay between facilitation and depression. As facilitation increased the fraction of activated sites, there were fewer available sites for the next stimulus. During periods of low-frequency activation, CDR boosted synaptic strength by increasing the number of available sites. Thus, the variation in synaptic strength directly reflects the temporal intervals of preceding stimuli according to the FD model. We noted some systematic deviations between the FD model and the data at all three synapses (for example, see the second to last EPSC in the burst of stimuli in Fig. 7). A few possible explanations for the limitations of the FD model are discussed below.

Simulated postsynaptic responses to the FD model

How does short-term synaptic plasticity contribute to a neuron's ability to influence the firing of its targets? We examined this question using the FD model for presynaptic transmitter release and a single-compartment integrate-and-fire model for spike initiation in the postsynaptic neuron (Fig. 8). The initial EPSP amplitude was adjusted to a range in which individual synapses could fire the postsynaptic cell. This is a greatly simplified situation in that single synaptic inputs do not usually have such a large impact on the postsynaptic neuron, although this situation is akin to “all-or-none” synapses such as brainstem auditory synapses (von Gersdorff et al., 1997), cerebellar climbing fiber synapses (Eccles et al., 1966), and the neuromuscular junction (Betz, 1970). Furthermore, the model for spike initiation did not take into account many features of action potential threshold found in realistic neurons (Llinas, 1988; McCormick, 1990). Despite its obvious limitations, this approach allowed us to explore the manner in which facilitation and CDR might contribute to neuronal firing.

We examined the contribution of CDR and facilitation for two types of presynaptic terminals during a burst stimulus pattern (Fig. 8) in which the synapse was stimulated at 3, 100, and then 3 Hz. For synapse A, the postsynaptic conductance change was chosen to be large enough to fire the postsynaptic neuron with a single presynaptic action potential (Fig. 8A₁, A₂). Facilitation was not included in synapse A. In the absence of CDR, the postsynaptic cell was unable to follow the frequency jump from 3 to 100 Hz. After the burst, the postsynaptic cell was unresponsive to low-frequency stimulation until significant recovery from presynaptic depression had occurred (Fig. 8A₁). In contrast, when CDR was included in an otherwise identical synapse, the postsynaptic neuron followed bursts reliably while maintaining low-frequency responsiveness immediately after the burst (Fig. 8A₂). This increased synaptic fidelity was attributable to the boosting of EPSP amplitudes during and after the burst by CDR (Fig. 8A₃).

Synapse B included facilitation, and synaptic strength was adjusted so that at 3 Hz, a single EPSP was well below threshold. In the absence of CDR, synaptic strength transiently increased to suprathreshold levels, and the postsynaptic cell fired once at the onset of high-frequency stimulation. Refractory depression rapidly overcame facilitation and subsequent EPSPs were greatly diminished (Fig. 8B₃). Thus, this type of synapse served as a burst detector: the postsynaptic target fired only when there was a large increase in presynaptic activity. The inclusion of CDR in this synapse resulted in two new postsynaptic behaviors (Fig. 8B₂). First, the postsynaptic neuron fired through the burst, although the rate of firing slowed. Second, the neuron fired again at the onset of lower frequency activity that had previously been subthreshold (Fig. 8B₂). Thus, the synaptic connection demonstrated in Figure 8B₂ responded to changes in input with increased efficacy for both increases and decreases in stimulation rate. This response requires that the synapse contain both facilitation and CDR, and that recovery from depression occurs more rapidly than does the decay of facilitation.

Although these simulations are based on a number of simplifications, they illustrate some of ways in which facilitation and CDR can influence postsynaptic firing. The postsynaptic behaviors demonstrated in Figure 8 hold true with multiple simulated presynaptic inputs undergoing relatively synchronous changes in firing frequency (data not shown). It will be interesting to examine the interplay between presynaptic properties and more realistic treatments of spike initiation in the postsynaptic cell.

DISCUSSION

In this study, we developed a model to account for the use-dependent changes in transmitter release that were observed during trains at three central synapses. We obtained an analytical expression for synaptic dynamics, which greatly simplify computations of synaptic strength. Although highly reduced, the model captured many of the essential features of use-dependent synaptic dynamics while providing insight into the means by which synapses filter temporal information.

Interpreting F and D in terms of presynaptic function

Despite large differences in behavior at the three synapses reported here, a single scheme provided reasonable descriptions for the underlying plasticities acting at each synapse. Central to our model is the concept that release is proportional to the product of two factors, F and D. A calcium-driven reaction enhances release (increases F), and entry of release sites into refractory states depresses release (decreases D). Residual calcium influences both the magnitude of enhancement and the extent of depression. F and D are also coupled by the fact that as F increases, more sites enter refractory states and thus D decreases. The synaptic behavior reported here can be understood in terms of differences in initial probabilities of release as well as the relative contributions of F and D. At the climbing fiber synapse, the initial probability of release was high (∼0.35), and all of the changes in synaptic strength were attributed to decreases in D. F was kept constant, because there is little if any facilitation at this synapse over a wide range of conditions (Dittman and Regehr, 1998). In models of parallel fiber and Schaffer collateral synapses, however, use-dependent changes in both F and D needed to be considered. According to our model, the pronounced differences in the behavior of parallel fiber and Schaffer collateral synapses during repetitive stimulation, which were estimated to be ∼0.05 and 0.25, respectively, are primarily a reflection of the initial release probability and subsequent changes arising from the coupling between facilitation and depression.

Comparisons with other models

The approach we take here to model short-term plasticity draws on many studies developed over the past 30 years (Elmqvist and Quastel, 1965; Gingrich and Byrne, 1985; Magleby, 1987; O'Donovan and Rinzel, 1997; Varela et al., 1997). Previous modeling efforts have focused on individual processes such as facilitation (Yamada and Zucker, 1992;Winslow et al., 1994; Bertram et al., 1996) and depression (Takeuchi, 1958; Elmqvist and Quastel, 1965; Betz, 1970; Wu and Borst, 1999), although some have considered the manner in which multiple processes combine to control release (Magleby, 1987; Markram et al., 1998). Some models attempt to be closely tied to an underlying mechanism responsible for synaptic plasticity, whereas others stress mathematical simplicity and general applicability to arbitrary data sets, without explicit reference to particular mechanisms (Abbott et al., 1997).

In this study, we incorporated specific properties of the underlying mechanisms that contribute to synaptic plasticity, while striving to retain computational simplicity. The approach chosen here is based in large part on a Ca_res model originally put forward byMagleby (1987) for enhancement and depression at the frog neuromuscular junction. The coupling between depression and facilitation here is similar to a recent model of synaptic efficacy, although that study did not distinguish between presynaptic and postsynaptic mechanisms (Markram et al., 1998). However, many aspects of our proposed scheme for plasticity differ from previous descriptions and are based on three recent experimental findings. First, Ca_res measurements from parallel fibers provided us with information about presynaptic calcium regulation during trains (Regehr and Atluri, 1995). Second, studies of the parallel fibers indicate that facilitation is a slow process driven by Ca_res (Atluri and Regehr, 1996). Third, the treatment of refractory depression and CDR is derived from our study of the climbing fiber synapse (Dittman and Regehr, 1998). The role of calcium in accelerating recovery from depression has only recently been demonstrated and has rarely been incorporated into models of synaptic plasticity (Gingrich and Byrne, 1985). According to our model, CDR is crucial for maintaining release at synapses during sustained periods of activity, regardless of the initial release probability (Fig. 6).

Limitations of the model

We made a number of assumptions to achieve computational simplicity (see Results). It is worth elaborating on some of these underlying approximations and limitations of the model so that we can understand how to better describe synaptic transmission for an extended range of stimulus conditions.

The present treatment of Ca_res is highly idealized in that the decay of Ca_res is assumed to occur with a single exponential component. However, slower components of Ca_resdecay have been observed, particularly after high-frequency stimulation (Regehr, 1997). Inclusion of a slowly decaying component of Ca_res in the FD model may account for the facilitation observed in the 1–5 Hz frequency range at both parallel fiber and Schaffer collateral synapses (Fig. 5B₂, C₂). Moreover, resting calcium is not considered in this model, although it may contribute to initial release probability and recovery from depression.

Calcium-dependent forms of plasticity are also modeled in an overly simplified manner. The model assumes that facilitation and recovery from depression are driven by chemical reactions with unsaturable sites that respond instantly to changes in Ca_res. As we learn more about calcium cooperativity and kinetics of facilitation and recovery from depression, the accuracy of our model will undoubtedly improve, although at the expense of its simplicity. Additional calcium-dependent mechanisms such as post-tetanic potentiation and delayed release of neurotransmitter may also need to be considered, particularly if we want to model the behavior of synapses for higher-frequency (>50 Hz) or longer-duration (>5 sec) stimulus trains.

Synaptic depression is restricted to a single mechanism in this study. However, other forms of depression related to changes in the size of the readily releasable pool or the buildup of inhibitory factors may play an important role at these and other synapses (Dobrunz et al., 1997; Stevens and Wesseling, 1998). During prolonged periods of presynaptic activity, additional forms of depression that are independent of residual calcium may be needed (Dittman and Regehr, 1998; Galarreta and Hestrin, 1998; Silver et al., 1998). For example, depletion of the readily releasable transmitter pool may dominate synaptic depression after large numbers of stimuli (Stevens and Wesseling, 1998; Schneggenburger et al., 1999), after sustained depolarization of the presynaptic terminal (Wu and Borst, 1999), or during osmotic shock (Rosenmund and Stevens, 1996). This type of depression would likely act in parallel with the refractory-site model proposed here, although further experiments are needed to determine the relationship between these two models of depression. Finally, decreased postsynaptic transmitter sensitivity caused by receptor desensitization was also not incorporated into our model but will need to be considered in a general treatment of short-term synaptic plasticity (Trussell et al., 1993).

In this study, we consider only the average plasticity of synapses with similar behavior, suppressing both the stochastic nature of release and variability in the initial release probability. Our model may not adequately characterize the postsynaptic response in situations where random fluctuations in release predominate over spike-to-spike changes in release probability. Furthermore, nonuniformities in release probability may be important when activating a small number of release sites with widely disparate release probabilities (Dobrunz and Stevens, 1997). More comprehensive modeling efforts will be needed to evaluate the significance of these properties.

Despite these simplifications, the model describes the behavior of three very different types of synapses remarkably well for various stimulus conditions. It is likely that refining the model as described above would improve its performance at lower frequencies and expand its dynamic range.

Implications for information transfer

In studying the influence of synaptic activity on the firing pattern of a neuron, it is necessary to consider how the plasticity of neurotransmitter release interacts with the properties of the postsynaptic cell. Using a greatly simplified model of postsynaptic spike initiation, we gained insight into some of the ways in which the facilitation and CDR shape the firing pattern of a synaptically driven cell (Fig. 8). Through these highly reduced simulations, multiple patterns of spiking that are usually ascribed to postsynaptic nonlinearities arose naturally from the use-dependence of transmitter release. Behaviors such as accommodation and rebound excitation could be observed depending on the presence or absence of facilitation and CDR. Temporal filtering features such as burst detection could be demonstrated explicitly (Fig. 8C). It will be interesting to elaborate on the interplay between presynaptic and postsynaptic dynamics using more realistic postsynaptic neurons.

The temporal patterning of spikes has been suggested to carry information from one neuron to the next at numerous vertebrate and invertebrate circuits (Softky and Koch, 1993; Rieke et al., 1997; Usrey and Reid, 1998). During irregular trains, synaptic strength can vary from pulse to pulse and yet maintain high reproducibility for a given stimulus pattern (Zador and Dobrunz, 1997; Dobrunz and Stevens, 1999). In this manner, short-term plasticity allows for the timing of presynaptic spikes to be reflected in the amplitude of the postsynaptic voltage changes (Fig. 1) (Segundo et al., 1963). Thus, the properties of presynaptic terminals may play a critical role in transmitting temporal information to their postsynaptic targets.

Fig. 1.

Effects of presynaptic plasticity on synaptic transmission. A, Representative spike train recorded from the basal ganglia of an awake, behaving macaque. B, C, Simulated EPSPs resulting from the stimulus in A (see Materials and Methods). The mean peak EPSPs were the same in both examples (i.e., synaptic currents were normalized to give the same average depolarization). The only difference between the presynaptic terminals in B and C is the amount of facilitation and initial release probability (F₁). Comparison of the traces reveals the different temporal patterns of depolarization associated with each type of presynaptic plasticity. The postsynaptic cell was simulated using a passive single compartment model with parameters τ_m = 20 msec, V_rest = −70 mV, R_N = 100 MΩ. The FD model parameters for B were ρ = 3.1, F₁ = 0.05, τ_F = 100 msec, τ_D = 50 msec, k_max= 30 sec⁻¹, k_o = 2 sec⁻¹, K_D = 2. Model parameters for C were ρ = 2.2, F₁ = 0.24, τ_F = 100 msec, τ_D = 50 msec, k_max= 30 sec⁻¹, k_o = 2 sec⁻¹, K_D = 2. The spike train in A was kindly provided by John Assad and Irwin Lee.