Switching Off and On of Synaptic Sites atAplysia Sensorimotor Synapses

Abstract

Using the highly plastic synapses between mechanoreceptor sensory neurons and siphon motor neurons of Aplysia as a model, we have investigated whether switching off and on of individual synaptic release sites is a strategy that is used by neurons in forms of short-term synaptic modulation with a time course of minutes to hours. We have modified some of the techniques of classical quantal analysis and examined the kinetics of synaptic depression under different stimulation protocols to answer this question. Our analysis shows that both synaptic depression caused by homosynaptic activity and synaptic facilitation induced by an endogenous facilitatory transmitter occur by means of the shutting off and turning on, respectively, of synaptic sites, without intermediate changes in the probability of release. Our findings imply that other forms of plasticity at these synapses, such as post-tetanic potentiation, long-term facilitation, and long-term potentiation, are also expressed by all-or-none changes in activity at individual sites. We thus show that in addition to the mechanisms of synaptic integration that are known to operate in single cells and networks, neurons can exercise a further layer of fine control, at the level of individual release sites.

Synaptic phenomena such as long-term potentiation and depression represent cellular mechanisms that may contribute to learning (McKernan and Shinnick-Gallagher, 1997; Murphy and Glanzman, 1997; Rogan et al., 1997), as do short-term processes such as homosynaptic depression and heterosynaptic facilitation (Zucker, 1972; Byrne et al., 1993; Cohen et al., 1997). Although detailed mechanistic explanations for these phenomena are lacking, evidence has been marshalled for such general possibilities as changes in the probability of neurotransmitter release (Bolshakov and Siegelbaum, 1994; Stevens and Wang, 1994) or the insertion or activation of postsynaptic receptors (Isaac et al., 1995; Liao et al., 1995). Other studies have reported that some synapses release no neurotransmitter initially but can be recruited by various treatments (Wojtowicz et al., 1991; Charpier et al., 1995; Wang et al., 1996). We have taken advantage of the favorable properties of sensorimotor synapses of Aplysia to examine whether shifting of synapses into and out of the active pool occurs in short-term synaptic plasticity.

Modulation of sensorimotor transmission in Aplysiacontributes to changes in its responsiveness to tactile stimulation (Carew et al., 1983; Walters and Byrne, 1983; Byrne et al., 1993;Stopfer and Carew, 1996; Cohen et al., 1997). Homosynaptic depression is a progressive decline in transmitter release that occurs even at low stimulation frequency (Castellucci and Kandel, 1974). Heterosynaptic facilitation is the increase in transmitter release, mediated by facilitatory transmitters such as serotonin (5HT), that follows a noxious stimulus (Brunelli et al., 1976; Castellucci and Kandel, 1976; Abrams et al., 1984). These and other forms of synaptic modulation in the intact nervous system can be reconstituted in cultures with a single sensory neuron contacting a single motor neuron (Schacher et al., 1990; Klein, 1993, 1994; Lin and Glanzman, 1994). Reconstitution in culture facilitates quantal analysis by permitting unequivocal identification of the source of synaptic input (Dale and Kandel, 1990; Eliot et al., 1994). We present here an analysis of homosynaptic depression and 5HT-induced facilitation beginning with synapses in cell culture and then extending the analysis to intact ganglia.

Our analysis consists of two parts. In the first part, we use a modified quantal analysis to distinguish between graded changes at synapses and selective, all-or-none switching between release states. In the second part, we support our conclusion of all-or-none switching by examining the kinetics of synaptic depression and recovery with various stimulation protocols.

Our results show that the connection between a sensory neuron and a motor neuron comprises more than one subpopulation of synapses. One group of synapses undergoes rapid depression and facilitation. These synapses respond once or a few times to a presynaptic impulse and fully recover the ability to transmit only after several hours of rest; they can, however, be rapidly reactivated by tetanization or the introduction of facilitatory neurotransmitters. A second subpopulation transmits stably and is less affected by modulatory treatments. The third subpopulation is silent until recruited by facilitatory treatments. We conclude that short-term plasticity in this system is achieved through all-or-none switching off and on of individual sites of synaptic transmission.

MATERIALS AND METHODS

Preparation. Adult Aplysia californica(75−150 gm; Marine Specimens Unlimited, Pacific Palisades, CA, and Alacrity Marine Biological Services, Redondo Beach, CA) were anesthetized by injection of 50−100 ml of 385 mm(isotonic) MgCl₂. For recordings in ganglia, abdominal ganglia were extracted, pinned to the bottom of dishes coated with Sylgard, and desheathed in a high magnesium solution [1:1 isotonic MgCl₂ to artificial seawater (ASW), composition given below]. For cultures, tail sensory neurons (Walters et al., 1983) and siphon motor neurons [LFS neurons (Frost and Kandel, 1995] were isolated and maintained as previously described (Klein, 1994; Coulson and Klein, 1997). Sensory and motor neurons were maintained in separate Petri dishes at room temperature (21−24°C) in 10% Aplysia hemolymph in Leibovitz L15 culture medium (Life Technologies, Grand Island, NY) supplemented with salts (Schacher and Proshansky, 1983). Under these conditions, the neurons retract their processes and become spherical in shape after 1−3 d. A single sensory neuron was then manipulated into contact with each motor neuron, and the pairs were left to incubate at least 1 d, by which time the EPSP amplitude has reached a plateau (Coulson and Klein, 1997).

Electrophysiological recording. An Axoclamp 2A amplifier (Axon Instruments) and borosilicate glass micropipettes (tip resistance 10−20 MΩ) filled with 2 m potassium acetate, pH 7.5, were used for intracellular recordings. In some experiments on cultured synapses, the presynaptic electrode was filled with 2 mpotassium chloride. Recordings were performed in ASW [(in mm): 460 NaCl, 10 KCl, 11 CaCl₂, 55 MgCl₂, and 10 HEPES, pH 7.5] or in high calcium solution [in mm) 368 NaCl, 8 KCl, 80 CaCl₂, 48 MgCl₂, and 10 HEPES, pH 7.5] in experiments on cultured synapses and in high divalent cation solution [(in mm): 368 NaCl, 8 KCl, 14 CaCl₂, 114 MgCl₂, and 10 HEPES, pH 7.5] (Trudeau and Castellucci, 1992) in most of the experiments on intact ganglia. Postsynaptic neurons were LFS siphon motor neurons in all experiments both in ganglia and in cultures.

In experiments examining the kinetics of synaptic depression and recovery, impalements were performed in zero calcium solution (identical to ASW except for substitution of MgCl₂ for CaCl₂) to avoid transmitter release on impalement of the presynaptic neuron, and then ASW or high calcium solution was perfused into the experimental chamber. In some of the experiments examining the kinetics of depression and recovery from depression, CNQX (6−20 μm) was added to reduce the EPSP amplitudes and thereby avoid activation of voltage-dependent currents. CNQX was used in the kinetic experiments because the complete time course of depression had to include the very first EPSPs in the experiment, and these could be as large as 50 or 60 mV without the blocker. In the quantal analysis experiments, in contrast, the analysis was begun only after the initial rapid phase of synaptic depression had already taken place, and CNQX was therefore not necessary.

Neuron type was confirmed by the response to release of hyperpolarizing current (Eliot et al., 1994). Throughout the experiments, the sensory neuron was held at −50 mV, and the LFS motor neuron was hyperpolarized to −80 mV in current clamp mode. Slow perfusion (∼1 ml/min) was maintained during the whole experiment for recordings in ganglia and was turned on during rests in experiments on cultures. Serotonin [(10 μm) creatinine sulfate, 5HT; Sigma, St. Louis, MO) was perfused into the chamber during rests from stimulation.

Data acquisition and analysis. Experiments were recorded on a MacIntosh IIVX computer using the Axodata program (Axon Instruments), and EPSP amplitudes were measured with the Axograph program (Axon Instruments). EPSP amplitudes were measured by subtracting the average of a 3 msec period at the base of the EPSP from the average of a 3 msec period centered on the peak of the EPSP (Redman, 1990). The variance of the noise was determined by taking the difference between the averages of two 3 msec periods separated by the same interval as that between the baseline and the peak EPSP periods. In two experiments, an electrical component (<0.5 mV) that persisted in the presence of cadmium was observed and subtracted from the postsynaptic potential.

Data files were transferred to Microsoft Excel (version 7) and GraphPad Prism (version 2) for analysis and plotting.

Quantal analysis and estimation of p and n. The quantal amplitude, q, was determined from the asynchronous release elicited by application of a hypertonic sucrose solution (250 or 500 mm sucrose in ASW) to the cultures. The distribution of miniature amplitudes was skewed to the right, as has been reported for other synapses (Bekkers et al., 1990; Frerking and Wilson, 1996) and could be well fit by an equation based on a Gaussian distribution of synaptic vesicle diameters (Bekkers et al., 1990). The mean mini amplitude in 20 cultures ranged from 0.35 to 1.42 mV (mean 0.717 ± 0.272 SD), with a coefficient of variation (cv) that ranged from 0.52 to 0.99 (mean 0.699 ± 0.125 SD).

To fit the amplitude distributions of the evoked PSPs, the mini distribution was convolved against itself n-1 times and against the noise to obtain distributions resulting from the simultaneous release of n quanta. The height of each of then components was then scaled so that the ensemble of the respective areas was appropriate for any given value of p, and the derived distribution that gave the best fit to the distribution of the evoked PSPs (determined by minimizing the χ²) was used to estimate the experimental p and n. The goodness of fit was determined from calculation of the χ²with the number of degrees of freedom equal to the number of bins minus 3. This method of fitting histograms of experimental data does not depend on the presence of discrete peaks in the evoked amplitude distribution.

The second method we used for estimating p involves calculation of p from the ratio of the variance to the mean of the PSP with corrections for the noise and the quantal variance (see next paragraph).

Quantal variance can arise from two sources: variability of the quantal amplitude at each site (intrasite variability) as well as variability between sites (intersite variability). The general expression relatingp to the mean and variance of the PSP includes terms for the quantal cv that take into account the source of the quantal variability:

$$p=1-[(V/\text{qM}-W*{\text{cv}}^2)/(1+(1-W)*{\text{cv}}^2)]$$ Equation 1

[from Eq. 18 of Frerking and Wilson (1996), modified by dividing the numerator and denominator of their left-hand term by μ_m², the square of the quantal amplitude in their notation] where V andM are the variance and the mean of the PSP, q is the quantal amplitude, cv is the coefficient of variation of the quantal amplitude, and W is the fraction (which can range from 0 to 1) of the quantal variance that originates from intrasite variability. The two extreme cases occur when all of the variability is either intrasite or intersite. When all of the variability is within-site (W = 1), the expression forp is:

$$p=1-V/\text{qM}+{\text{cv}}^2,$$ Equation 2

and when all the variability is between-site (W= 0) the expression is:

$$p=1-[(V/\text{qM})/(1+{\text{cv}}^2)].$$ Equation 3

For experiments in which we used mini amplitudes to estimate the quantal parameters, we expressed the EPSP in terms of the quantal content, m, where m = M/q.

Because the EPSP decreases with repeated stimulation as a result of homosynaptic depression, we also devised a method for estimatingp for a progressively changing EPSP that we have called “sliding p.” In this method, p is calculated from the mean and the variance of the EPSP for successive groups of five evoked responses, moving one response at a time, using the above expressions (for an example see Fig. 5A,B). Although the use of such small sample sizes would be expected to give rise to a large scatter in successive estimates of p, any overall trend in p in a given experiment should still be detectable.

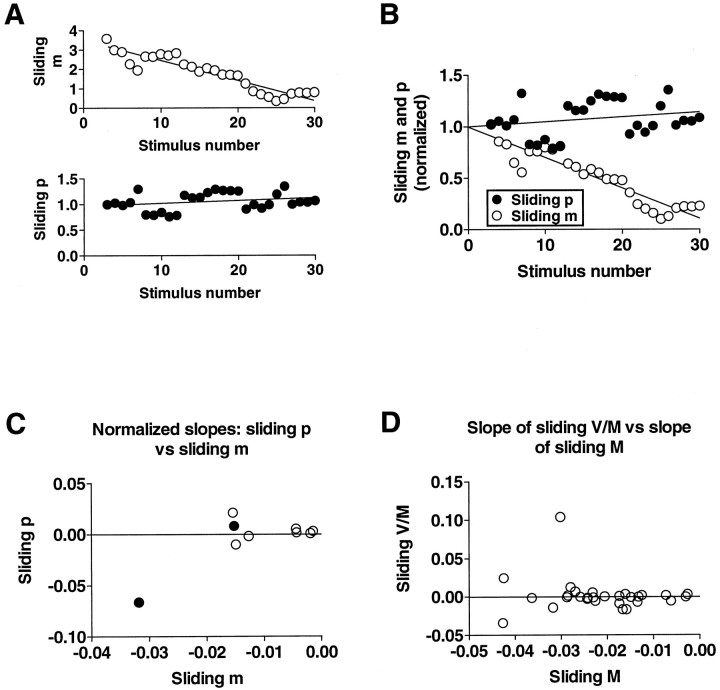
Fig. 5.

Absence of change in sliding estimate ofp during homosynaptic depression. Plots inA and B are from one experiment and illustrate how the slopes of sliding m andp were derived and normalized. Sliding p(calculated from Eq. 1, with W = 0.65) andm were determined for groups of five responses, moving one response at a time. In A, the approximately linear decline in sliding m was fit by linear regression, as was the corresponding portion of the plot of sliding p.B illustrates normalization of the slopes of slidingm and p to permit direct comparison of the slopes; the slopes were normalized by setting the respectivey-intercepts equal to 1. C is a plot of the normalized slope of sliding p against the normalized slope of sliding m in nine experiments on cultures in normal ASW medium. The two filled circles represent experiments in which the average p was ∼0.3;p in all of the other experiments was >0.6. Theline represents a slope of zero for slidingp. D, For experiments without an independent estimate of the quantal amplitude and variance, the variance (V) and mean (M) of the EPSP amplitude were used to test for changes in p; no change in the ratioV/M implies no change in p(see Results). The line represents a slope of zero for sliding V/M.

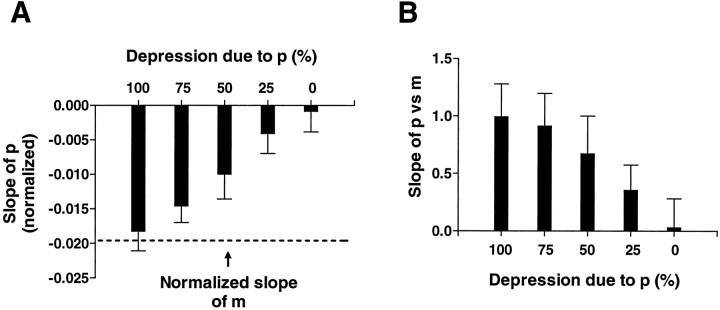
To test the reliability of this method of estimating p, we applied this analysis to 15 sets of simulated EPSP amplitudes for which the slope of synaptic depression was similar to that observed in our experiments (see Fig. 6A, broken line). We then generated sets of parameters n and p such that the monotonic decline in the simulated EPSP was attributable to changes in n or p, or both. We generated 10 sets of 15 simulated experiments for each of five combinations of changes inn and p, where the rate of change of pranged from 0 to 100% of the rate of change of the quantal content,m. Specifically, we simulated homosynaptic depression which was caused by changes only in p, only in n, equally in p and n, or a combination of changes in p and n such that one changed three times more than the other. We then plotted the estimates of the changes inp from the sliding p calculations against the relative proportion of the simulated depression attributable to a change in p (see Fig. 6A). In addition, we examined the relation between p and m across all the simulated experiments for each of the different conditions (see Fig. 6B). The results indicate that this method yields estimates of p that are in excellent agreement with the values given in the simulations. This method of estimatingp is very sensitive to changes in p, so that an overall change in p in a simulation could be detected even when as little as 25% of the change in the simulated response was caused by a change in p.

Fig. 6.

Test of sliding p technique by application to simulations with different contributions of decliningp to depression. A, Slope of calculated sliding p as a function of different rates of decline inp in simulations (n = 10 for each condition). B, Slope of the relation betweenp and m in simulations. The slope of this relation varies with the contribution of declining p to homosynaptic depression, ranging from close to 1 when all of the depression is caused by a drop in p, to near 0 when depression is attributable exclusively to a decline inn. See Materials and Methods for details.

To compare the change in the EPSP amplitude with the change inp in our experiments, we normalized the slopes of the respective regression lines by dividing by the y-intercept (see Fig. 5B) and plotted the normalized slope of slidingp against the normalized slope of sliding m (see Fig. 5C).

In experiments for which we had no direct measurements of the quantal amplitude and variance, we used the sliding value ofV/M as an indication of whether p was changing with synaptic depression and facilitation. This procedure is justified by the fact that as long as the quantal amplitude and variance remain constant, changes in the ratio of V toM reflect changes in p according to the above equations, independent of the source of the quantal variability. We verified that the quantal parameters were unchanged by applying hypertonic sucrose twice and comparing the mean amplitude andcv of the miniature potentials elicited with each application (see Results).

Except where noted otherwise, statistical comparisons were performed using Student's t test. All the analysis programs were run using Microsoft Excel.

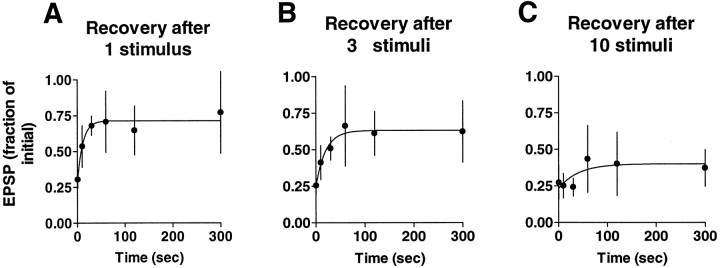
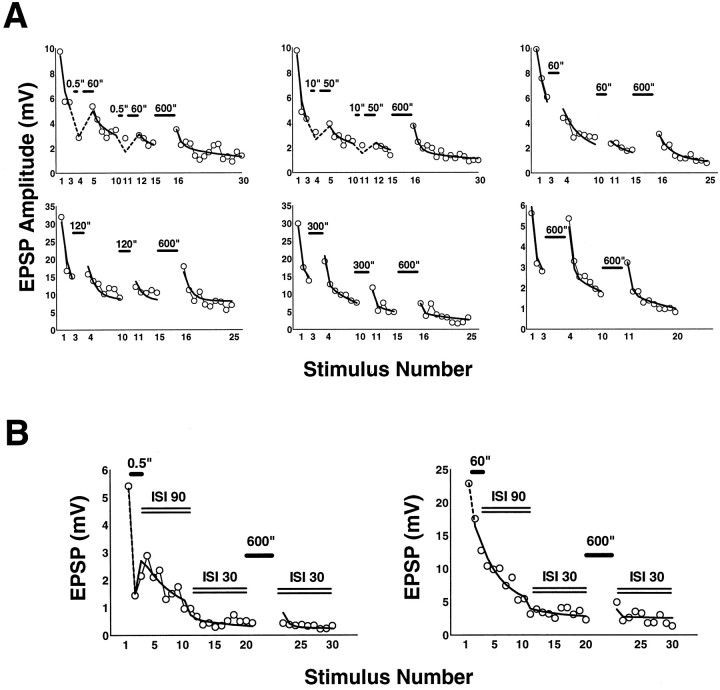
Analysis of recovery from synaptic depression. Recovery from depression was measured after 1, 3, or 10 stimuli. Ratios of the EPSPs after rest to the first EPSPs of the experiments were plotted against their respective rest intervals (0.5, 10, 30, 60, 120, and 300 sec) and then fitted with a single exponential using Prism software (see Fig.7). Cells were impaled in calcium-free medium to avoid transmitter release during impalement. After introducing normal ASW medium, the sensory neuron was stimulated 1, 3, or 10 times with an interstimulus interval of 30 sec, and the test measurement to a single stimulus was made after one of the rest intervals listed above. Each pair of cells was used for only one measurement.

Fig. 7.

Decline in recovery from depression with progressive stimulation. Stimulation was stopped after 1, 3, or 10 stimuli in different experiments (each experiment was on a different pair of cells), and recovery was examined by presenting a single stimulus after 0.5, 10, 30, 60, 120, or 300 sec. Recovery relative to the first EPSP of the experiment proceeds with an exponential time course to a plateau that is below the level of the initial EPSP. The plateau decreases with increasing number of stimuli, suggesting that an increasing proportion of the sites is progressively switched off. Each point is the average of four to seven separate experiments (error bars indicate SD). The time constants of recovery based on the exponential fits are 11.63, 20.11, and 40.03 sec after 1, 3, and 10 stimuli, respectively. Each of these values is within the 99% confidence intervals of the other two.

Modeling of kinetics of synaptic depression and recovery. A given pair of neurons was used for only one experiment; averages therefore represent data taken from several pairs of neurons.

Homosynaptic depression was modeled assuming that each site releases one quantum of neurotransmitter with a constant probabilityp and then recovers the ability to transmit with a time constant τ. An expression for the EPSP amplitude was derived that takes into account sites that have released and have not yet recovered, sites that have released and recovered, and sites that have not released at all to previous stimuli. The expression was derived as follows.

The amplitude of the first EPSP of an experiment,A₁, is equal to the product of the probability of release, p, and a maximal amplitude,A₀, proportional to the total number of sites initially available for release:

$$A_1=p(A_0).$$

At the time of the second stimulus, the EPSP consists of two components: (1) a component contributed by sites that had not released with the first stimulus, equal top(A₀)(1 −p) orp(A₁/p)(1 − p), and (2) a component contributed by sites that had released with the first stimulus and have recovered the ability to release by the time of the second stimulus:

$${\text{pA}}_1(1-e^{-\mathrm{\Delta }\text{t}/\tau }),$$

where Δt is the interstimulus interval and τ is the time constant of recovery.

The amplitude of the second EPSP will then be:

$$A_2=p[(A_1/p)(1-p)+A_1(1-e^{-\mathrm{\Delta }\text{t}/\tau })].$$

At the third stimulus, the amplitude contributed by sites that had not released with the second stimulus is:

$$p(A_2/p)(1-p).$$

The sites that have recovered the ability to release by time of the third stimulus will include some sites that had released with the second stimulus as well as some that had released with the first stimulus but had not recovered by the time of the second stimulus, resulting in a contribution of:

$$p(1-e^{-\mathrm{\Delta }\text{t}/\tau })[(A_2+A_1(e^{-\mathrm{\Delta }\text{t}/\tau })].$$

The amplitude of the third EPSP will then be:

$$A_3=p[(A_2/p)(1-p)+(1-e^{-\mathrm{\Delta }\text{t}/\tau })[(A_2+A_1(e^{-\mathrm{\Delta }\text{t}/\tau })]].$$

The general expression for the EPSP is:

$$A_{\text{m}+1}=p[(A_{\text{m}}/p)(1-p)+(1-e^{-\mathrm{\Delta }\text{t}/\tau })({\sum }_{\text{i}=1 \text{to m}}{A}_{\text{i}}{e}^{-(\text{m}-\text{i})\mathrm{\Delta }\text{t}/\tau })],$$ Equation 4

where A_m is the amplitude of the EPSP at the mth stimulus and Δt is the interstimulus interval.

We modified this expression to take into account the fact that each stimulus also results in the shutting off of a fraction of the sites that have released, as we demonstrate in Results. To account for our data (see discussion of Figs. 7-9 in Results), we posited that the fraction of sites that drops out with each stimulus declines exponentially from an initial value α with a time constantZ (expressed in terms of the number of stimuli), until a steady state is reached in which a portion of the total number of sites continues to release according to Equation 4.

Fig. 8.

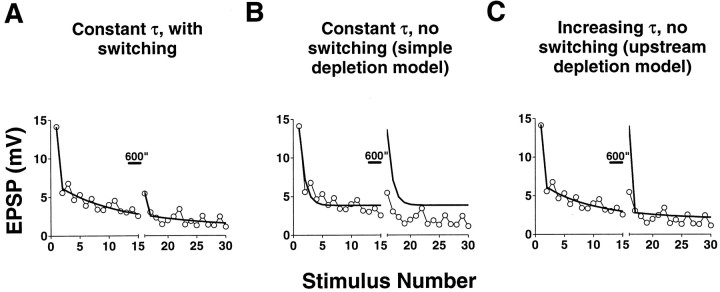
Fits of homosynaptic depression and recovery with a model incorporating switching off of release sites. Shown are fits of a sample experiment with three different models of depression; only the switching model fits both the kinetics of depression and recovery after rest. Experiments were performed with interstimulus intervals of 30 sec, with rests indicated by bars. For the same experiment, EPSPs 1 to 15 were fit with three different models (see Results for details). The solid curves for stimuli 16 to 30 are predictions based on the parameters obtained from best fits of stimuli 1 to 15 (Table 2). Only the model incorporating switching off of synaptic sites is able both to fit the initial depression and to predict the recovery and depression after rest.

Fig. 9.

A, Fits of depression and of recovery after varying periods of rest with the switching model. Experiments (circles) with 30 sec interstimulus intervals and interspersed periods of rest of various durations were fit with the switching model (solid and dashed lines; see Table 2 for parameter values). Stimuli after 0.5 and 10 sec rests were followed by 60 and 50 sec rests, respectively, to keep the average interstimulus interval constant. B, Fits of experiments with changing interstimulus intervals. Eachplot represents a single experiment. The interstimulus interval, initially 90 sec, was changed to 30 sec after 10 stimuli, as indicated by the double lines. Rests after the first EPSPs were 0.5 and 60 sec, respectively, and a second rest of 5 min was introduced after EPSP 20 or 21. Fits are solid anddashed lines. See Table 2 for parameter values that gave the best fit.

Thus, the expression for the EPSP when switching off of sites is taken into consideration is:

$$A_{\text{m}+1}=p[(A_{\text{m}}/p)(1-p)+(1-e^{-\mathrm{\Delta }\text{t}/\tau })({\sum }_{\text{i}=1 \text{to m}}{A}_{\text{i}}{e}^{-(\text{m}-\text{i})\mathrm{\Delta }\text{t}/\tau }(1-$$ Equation 5

$$\alpha e^{-\text{i}/Z}))].$$

Starting with this expression, different models were implemented by varying some of the parameters, as described in the text.

Minimization of the sum of the squared differences was used to fit the different models to experimental data using Microsoft Excel.

RESULTS

In a series of experiments aimed at examining the time course of the development of synaptic transmission and the potential for synaptic regulation at Aplysia sensorimotor synapses in cell culture (Coulson and Klein, 1997), we observed a number of synaptic pairs that showed extremely little variation in the evoked EPSP after the initial homosynaptic depression (Fig. 1). In 14 of 50 experiments, the coefficient of variation of the depressed EPSP (estimated quantal content 2.37 ± 1.49 SD) was <0.35, and in five of these it was <0.25. The small variability of the EPSP in combination with the low quantal content suggests that release in the steady state reflected the activity of a small number of sites transmitting with a high probability. This observation is not consistent with the idea that homosynaptic depression proceeds by a gradual decrease in the probability of release at all release sites equally, but suggests rather that individual sites are turned off while other sites remain active.

Fig. 1.

Small variability of depressed EPSPs and large facilitation by 5HT. Records of successive groups of monosynaptic potentials from a sensorimotor pair in culture (A) and plot of the whole experiment (B). C, Magnified view of EPSPs 4–15 showing the small variation in amplitude. Stimulation was interrupted for 5 min after EPSP 15, and two more EPSPs (data not shown) were elicited before addition of 5HT. The interstimulus interval was 30 sec. Calibration bars: A, 2 mV, 10 msec; C, 1 mV, 10 msec.

The possibility that release at individual sites is controlled in an all-or-none manner is supported by the facilitation of transmission. In the same study, we reported some pairs that showed no evoked release before addition of the endogenous facilitatory transmitter 5HT, with clearly detectable responses afterward, indicating the presence of inactive synapses that were recruited in synaptic facilitation. In addition, in experiments like that of Figure 1, the EPSP increased many-fold in amplitude on application of 5HT, despite the small amount of variability in the EPSP before facilitation. This observation too suggests the presence of a population of synaptic release sites that contributes little or nothing to the depressed EPSP and is then recruited on application of 5HT. The results collectively suggest that homosynaptic depression as well as 5HT-induced facilitation proceed by means of a switching off and on of individual release sites rather than by a graded change in their release properties. The purpose of the following analysis is to test this hypothesis in a quantitative manner.

Amplitude and amplitude distribution of quantal synaptic potentials

We have modified the techniques of cell culture inAplysia to enable us to form soma-to-soma synapses (Klein, 1994) (see Materials and Methods), which have two further important advantages for quantal analysis. First, the electrical distance from the recording site to the site of synaptic action is short, thus reducing problems associated with electrotonic distortion of the shapes of synaptic potentials, as well as the likelihood of conduc- tion block at branch points of presynaptic neurites. Second, such cultures form physiological synapses progressively during the 12–15 hr after pairing and therefore permit the examination of the properties of small numbers of synaptic sites in early cultures. We have shown (Coulson and Klein, 1997) that short-term synaptic modulation is present at the earliest times after synapse formation and that, with the exception of the amplitude of the synaptic potentials, the early synapses do not differ significantly in their properties from later synapses or from synapses formed using the conventional culture configuration. Finally, further facilitating quantal analysis, we use as the postsynaptic elements at these synapses small siphon motor neurons [LFS neurons (Frost and Kandel, 1995)] in which the quantal synaptic potential is often large relative to the recording noise, sometimes reaching an amplitude of 2 or 3 mV or more.

We determined the quantal amplitude by eliciting asynchronous release with hypertonic sucrose (Materials and Methods). Because it has been proposed that the transmitter release caused by exposure to hypertonic solutions is independent of calcium (Dale and Kandel, 1990; Rosenmund and Stevens, 1996), the possibility arises that different pools of transmitter might be mobilized by depolarization-induced calcium entry and by hypertonic sucrose. If this were the case, it would not be appropriate to use the quantal parameters derived from sucrose applications to analyze release evoked with action potentials. To address the possibility that the quantal amplitude q as determined from application of sucrose might differ from that elicited by depolarization and calcium entry, we compared the amplitude and variance of minis elicited with sucrose with those of the minis elicited with a weak depolarization of the presynaptic neuron in the same pair of neurons. There was no difference between the mean values of the miniature amplitude using these two methods of eliciting asynchronous release (Table 1). Although the coefficients of variation of the miniature distributions were not identical, the cv of the minis elicited with sucrose differed from that of the minis elicited with depolarization by <7% on average (Table 1).

Table 1.

Comparison of miniature postsynaptic potentials elicited by application of hypertonic sucrose and by weak depolarization of the presynaptic neuron

	Number	Mean	SD	cv	t	p
Sucrose	33	0.658	0.294	0.447
Depolarization	144	0.690	0.302	0.437	0.557	0.578
Sucrose	101	0.538	0.332	0.618
Depolarization	53	0.542	0.255	0.470	0.093	0.926
Sucrose	129	0.718	0.507	0.707
Depolarization	80	0.863	0.711	0.823	1.597	0.113

Each pair of values is from a single sensory neuron–motor neuron pair. In the first pair, sucrose was applied between two periods of imposed depolarization; the values used for the minis elicited with depolarization are the averages of the values obtained with the two depolarizations (which were not different from one another). In the second pair, sucrose was applied before a single depolarizing period, and in the last pair, the depolarization was imposed before the sucrose application. Means were compared using Student's t test for the first pair and Welch's alternate t test for the second two pairs, for which the variances differed between the minis elicited with sucrose and with depolarization.

The amplitude distribution of EPSPs evoked with action potentials at sensorimotor synapses is consistent with a binomial model of transmitter release

If switching between release states occurs, and if release behaves as a binomial process, then quantal analysis should reveal that both synaptic depression and facilitation are accompanied by changes in the apparent number of release sites, or the binomial parametern, rather than by a change in the apparent probability of release, or binomial p.

Quantal analysis requires that a sufficient number of synaptic responses be recorded under steady-state conditions. Because the synaptic processes that we were interested in analyzing involve changes in the average amplitude of the synaptic response over time, it is generally not possible to perform this kind of analysis on whole experiments. We therefore limit the first part of our analysis to periods during which the response remains fairly stationary, after the major part of homosynaptic depression has already taken place. In all of these experiments we used the distribution of miniature EPSPs evoked with hypertonic sucrose to estimate the mean and variance of the quantal unit, and we constructed the theoretical curves of the evoked responses by convolving the mini distribution against itself and against the noise (see Materials and Methods). Figure2A shows examples of experiments with stationary stretches in which amplitude histograms could be fit adequately using binomial parameters. In 13 of 15 experiments, the binomial model gave a satisfactory fit (p > 0.05). We have also reanalyzed previously published amplitude histograms that were originally fit using Poisson statistics (Castellucci and Kandel, 1974) and found that some of them were fit significantly better by binomial statistics (data not shown).

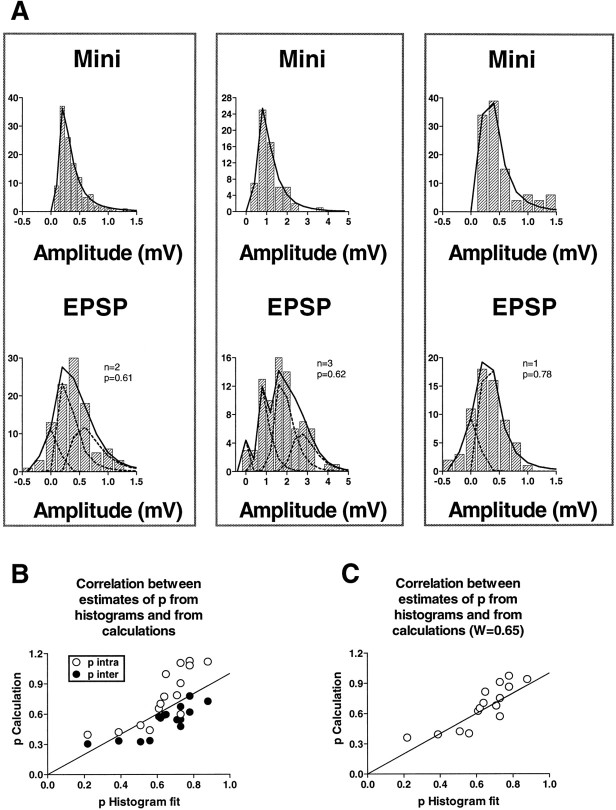
Fig. 2.

Binomial fits of amplitude distributions of sensorimotor EPSPs. A, Examples of amplitude histograms and fits. In each column the top andbottom amplitude histograms represent miniature synaptic potentials evoked with hypertonic sucrose and evoked EPSPs from the same pair of cells, respectively. Fits (solid lines) to the mini distributions were performed using Equation 1 of Bekkers et al. (1990); fits to the EPSP distributions were performed on the assumption that evoked release follows a binomial distribution based on the quantal parameters derived from the mini distribution in the same pair of cells. The broken lines represent the underlying distributions of noise (peak at zero) and convolutions of the uniquantal distribution that resulted in the best fits, characterized by the binomial parameters n and p shown to the right of each graph. B,C, Correlation between estimates of pfrom histogram fits and from calculations. B, Estimates of p derived from Equations 2 (all quantal variability intrasite) and 3 (all quantal variability intersite) are plotted against estimates of p from the best fits to histograms. The line through the origin has a slope of 1, representing perfect agreement. C, Estimates ofp derived from Equation 1 (quantal variability from both intrasite and intersite sources), with the fraction of the total variability from intrasite variance equal to 0.65.

Although best fits to the amplitude histograms could be determined on the basis of the χ² test (Materials and Methods), other values of p and n could generally not be excluded because of the small number of events. Nevertheless, the fact that the fits were satisfactory indicates that these synapses can be analyzed using a binomial model. To circumvent the problem posed by the small number of responses available for amplitude histograms, we took advantage of the fact that the binomial parameters pand n can be calculated on the basis of the mean and the variance of stretches of responses, as outlined in Materials and Methods. Specifically, p can be calculated from the mean and the variance of the EPSP, together with the coefficient of variation of the quantal unit (obtained from the distribution of the miniature amplitudes). As discussed in Materials and Methods, the source of the variability in the quantal unit must be taken into account to make these calculations. We initially calculated p based on the two extreme cases, assuming that the quantal variability arises either exclusively from within each release site (Eq. 2) or, alternatively, exclusively from between release sites (Eq. 3).

Before relying on calculated values of p, it is important first to ensure that the parameters derived by calculation are consistent with the amplitude distribution of the synaptic responses. We therefore compared the calculated values with the p that gave the best fit to the amplitude histogram in each case. As shown in Figure 2B, the two ways of arriving at estimates ofp are in fair agreement.

The values of p calculated on the assumption that all of the quantal variance is within-site are generally greater than the values obtained from the histogram fits, whereas the p calculated on the assumption that all of the variance is between-site is generally lower (Fig. 2B). This is to be expected if the variance of the quantal amplitude is actually a composite of both intrasite and intersite variability. We therefore looked for a combination of the relative weights of the two kinds of variability that would give a better match to the values obtained from the fits. Using Equation 1, we found that a ratio in the weights of the intrasite to the intersite variability of ∼0.65:0.35 gave a slope of 1 for the line relating the calculated p to the p from the fits, with an intercept close to zero (Fig. 2C) (correlation coefficient 0.82, p < 0.0001). The values ofp obtained in this way were not different from those obtained from the histogram fits (n = 15,t = 0.773, p = 0.452, pairedt test). The agreement between the two different ways of estimating p supports the idea that transmission at these synapses behaves according to a binomial model and justifies the use of parameters derived from the calculations in examining the underlying mechanisms of depression and facilitation.

It is not possible to determine from this kind of analysis whether the parameter p represents a probability of release that is the same for all release sites or a weighted average of different probabilities at different sites, with the higher probability sites predominating. In the interests of simplicity, we will begin the analysis assuming uniform p; nonetheless, as we will discuss below and at greater length in Discussion, our conclusions do not depend on the assumption of uniformity in p across sites.

Estimation of p and n in stationary experiments with known quantal parameters: synaptic depression cannot be accounted for by a change in p

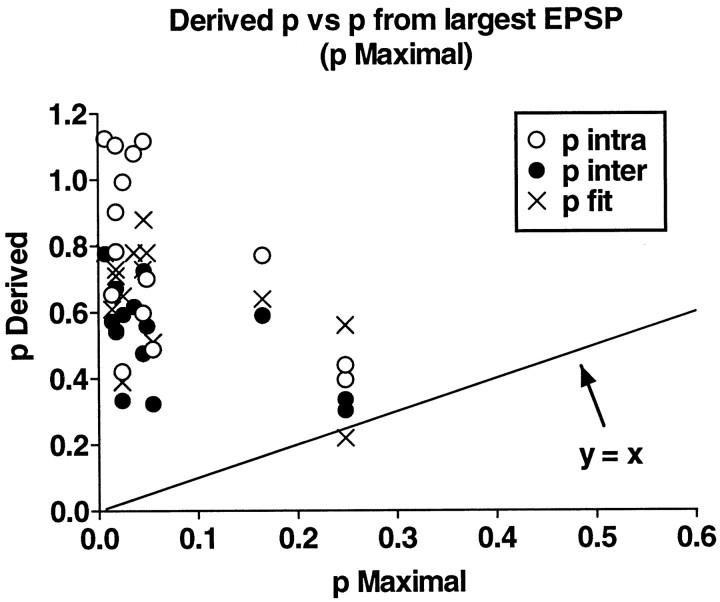
For the analysis of experiments with substantial stationary periods, we took the estimates of p from the best fits and from calculation using Equations 2 and 3 and compared these with thep that would be predicted if synaptic depression depended on a change in p alone. For example, if the steady-state depressed response was 20% of the first, undepressed EPSP of the experiment, and if all the synapses contributed equally (uniformp), then the p in the steady state would have to be ≤0.2. We call this value “maximal p.” Ifp estimated from the binomial model was significantly higher, this would indicate that the probability of release was nonuniform, i.e., that a few high probability synapses were contributing disproportionately to the overall response whereas other synapses were releasing with a low probability. Depending on the estimated value of p, it is possible to estimate how many of the synapses are contributing significantly to the overall release and whether others are effectively silent. In this way it is possible to determine whether a uniform change in the probability of release can account for synaptic depression and facilitation.

A summary of the estimated and the maximal p for all experiments is shown in Figure 3. The values of p obtained by fits or by calculation from the mean and variance are much greater than the predicted maximal pin practically all cases. This result implies that a change in a uniform probability of release cannot account for synaptic depression.

Fig. 3.

Comparison of derived p with “maximal” p predicted from uniform decline inp during homosynaptic depression. Binomialp estimated from the best fit to amplitude histograms of EPSPs (pfit) or from calculation by Equations 2 (p intra) and 3 (p inter) is generally much greater than that predicted if homosynaptic depression were caused by a uniform decrease inp at all release sites (maximal p).Line has a slope of 1. See Results for definition of maximal p.

Examination of synaptic plasticity in stationary experiments without known quantal parameters: synaptic depression and facilitation are not associated with changes in p

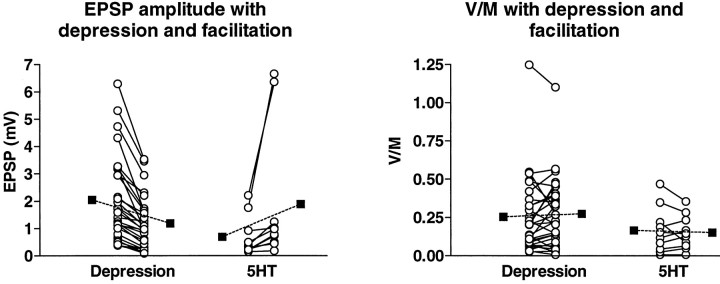
In the next part of the analysis, we looked for changes inp that might accompany synaptic plasticity in cases in which we had no independent measures of the quantal amplitude and variance and there were two stationary periods between which the EPSP either depressed further as a result of continued stimulation or else facilitated as a result of application of 5HT. As can be seen from Equation 1, the variance of the EPSP amplitude, V, divided by the mean, M, is linearly related to 1 −p. As long as the quantal amplitude and cv and the sources of quantal variability do not change between successive episodes within an experiment (see below for evidence that the quantal parameters are stable), any change in p will be reflected in a change of the opposite sign in V/M, whereas ifp remains unchanged there will also be no change inV/M.

We observed no change in the ratio of the variance to the mean—and therefore in p—on average, either with synaptic depression or with facilitation by 5HT (Fig. 4). In 29 experiments, the EPSP declined to 56 ± 18% of its earlier amplitude with further depression (p < 0.001, paired t test), whereas the values ofV/M were 0.255 ± 0.249 with the initial depression and 0.275 ± 0.231 after further depression (p = 0.331, Wilcoxon signed rank test). On application of 5HT in 10 experiments, the EPSP increased to 244 ± 101% of the pre-5HT amplitude (p < 0.001, paired t test), whereas V/M was 0.166 ± 148 before application of 5HT and 0.151 ± 0.110 afterward (p = 0.855, Wilcoxon signed rank test). Thus, in neither synaptic depression nor facilitation is there a change in p as calculated from the equations.

Fig. 4.

Absence of change inp with synaptic depression or 5HT-induced facilitation. EPSP amplitude (left) and ratio of the variance to the mean (right) for stationary periods in individual experiments (open circles) at earlier and later times during progressive synaptic depression (29 experiments) and before and after application of 5HT (10 experiments); filled squares are means. Experiments on depression included 8 in intact ganglia, 12 in cultures in normal ASW medium, and 9 in cultures with high calcium medium. Because there was no difference among the three groups, the results were pooled. Experiments with 5HT included five in intact ganglia, three with normal ASW in culture, and two with high calcium medium in culture. The absence of a change in the average ratio of the variance to the mean in both homosynaptic depression and 5HT-induced facilitation implies no change in p.

These conclusions hold only if the quantal amplitude and cvdo not change during an experiment. In agreement with reports by others (Castellucci and Kandel, 1974, 1976; Dale and Kandel,1990; Eliot et al., 1994), we found no change in the quantal parameters associated with synaptic plasticity at these synapses. We examined the quantal parameters derived from responses elicited by hypertonic sucrose both before and after synaptic depression in four experiments and found no change in either the quantal amplitude or the quantal cv(before depression q = 0.748 ± 0.414 mV andcv = 0.667 ± 0.140; after depressionq = 0.697 ± 0.418 mV and cv = 0.691 ± 0.124 afterward; p = 0.42 and 0.80 for comparisons of amplitude and cv, respectively; pairedt test). We compared the mean and cv of the miniatures in three experiments before and after application of 5HT and found no significant differences (p = 0.69 and 0.44 for q and cv, respectively).

To test whether we could detect a change in V/Mwhen a change in p would be expected, we computedV/M in experiments in culture in which we changed the extracellular calcium concentration from the normal 11 mm to either 55 or 80 mm. The mean V/M decreased (indicating an increase inp) from 0.606 ± 0.565 in normal ASW to 0.276 ± 0.271 in high calcium (p = 0.016, Wilcoxon signed rank test).

The apparent p obtained from calculations and histogram fits could represent the combined contributions of different probabilities at different release sites, with the distribution of individual probabilities unknown. The apparent p in any one measurement, therefore, may be a poor indication of the individual probabilities. However, the only obvious way for the apparentp to consistently remain unchanged in two measurements at the same synapses in the face of a change in the quantal content is for the contributions of the individual sites to increase or decrease to the same extent at all sites, while the overall distribution of the individual probabilities remains the same. It is possible in some cases to find ad hoc combinations of p values for individual sites that could yield the same apparent overall p for differentm, but there is no reason to suppose that these ad hoc combinations of values for individual sites would be able to account for a general and consistent finding of constant p despite changing m. (This issue will be elaborated in Discussion). There are two possibilities. Either apparent p reflects a uniform probability of release at all contributing sites, and the number of these sites changes, or else apparent p is the result of a nonuniform distribution of individual probabilities that does not change. The latter possibility implies that the number of contributing sites goes up or down to the same extent for all sites, independently of their respective individual probabilities. Both possibilities necessitate the dropping out or recruitment of release sites to account for synaptic depression and facilitation, respectively.

Analysis of nonstationary experiments: synaptic depression and facilitation can be accounted for by changes in nalone

Our observations in experiments with stationary periods in culture led us to analyze experiments with larger numbers of responses both in cultures and in intact ganglia to determine whether switching between release states accounts for synaptic depression and facilitation generally. In most experiments on intact ganglia we used an extracellular solution containing elevated concentrations of calcium and magnesium ions to raise spike thresholds and thus to reduce or eliminate any polysynaptic contribution to the EPSP. (We were also able to obtain apparent monosynaptic responses using normal seawater medium in two cases.) This high divalent cation solution changes neither the amplitude of the monosynaptic EPSPs from the sensory neurons nor the kinetics of homosynaptic depression at the sensorimotor synapses (Trudeau and Castellucci, 1992). For synapses in culture, we used artificial seawater with a high concentration of calcium in some of the experiments (to increase the overall probability of release) and normal seawater in the others.

To circumvent the problem of nonstationarity we used Equation 1 for the analysis, as follows. For experiments in which we had estimates of the quantal amplitude and cv based on asynchronous release elicited with hypertonic sucrose, we computed sliding m and sliding p as described in Materials and Methods. To compute sliding p, we assumed a ratio of 0.65:0.35 (Fig.2C) in intrasite to intersite variability in the quantal response. We then asked whether a decrease in p accompanied synaptic depression.

After the initial rapid decline during the first few stimuli, further synaptic depression is approximately linear (Fig.5A). We compared the normalized slopes of sliding m and sliding p for the linear portion of synaptic depression (ranging from 20 to 110 stimuli in different experiments) (Fig.5A,B). There was no relation between the normalized slopes of sliding m and of slidingp in individual experiments (Fig. 5C). Moreover, the average slope of sliding p taken across all the experiments was not significantly different from zero (−0.0044 ± 0.0247), whereas sliding m showed a consistent decline (average slope −0.0113 ± 0.0097). Because experiments with a low average p would have greater errors in calculation of p—which might obscure any underlying trend in p—we also examined separately those experiments in which the average p was >0.6 (seven of nine experiments) (Fig.5C, open circles). The average slope of slidingp was still not different from 0 (average slope positive, 0.0027 ± 0.0094). Finally, when we examined the slopes of slidingp in individual experiments, it was either positive or not significantly different from zero in eight of the nine cases. Thus, because p does not change during synaptic depression, the decline in the synaptic response is attributable to a reduction inn. Once again, as noted in the previous section and in Discussion, the possibility that the apparent p may reflect a nonuniform population of individual release probabilities does not affect our conclusion that sites must be dropping out during depression.

For experiments in which we had no independent measure of the quantal amplitude and cv, we performed a similar calculation, but instead of computing sliding m and p, we used a sliding estimate of M and V/M. We compared the overall change in sliding V/M with the change in sliding M to determine whether the decrease in the amplitude of the EPSP with synaptic depression was mirrored by an increase in V/M, which would reflect a decrease in p (Eq. 1). Because there was no obvious difference in the rates of synaptic depression or in the slopes of sliding pbetween synapses in intact ganglia and in soma-to-soma cultures, all the results are presented together. Again, we saw no relation between the decline in the EPSP amplitude and the normalized slope ofV/M (Fig. 5D). In 30 measurements (14–66 stimuli), the average slope of slidingV/M was 0.0016 ± 0.0217 (not different from zero; t = 0.4, p > 0.6), whereas the average slope of sliding M was −0.0222 ± 0.0116 (t = 10.48, p < 0.0001). In 24 of the 30 cases, the slope of sliding V/M was either negative (indicating an increase in p) or not different from zero.

We used the same technique to determine whether facilitation by 5HT is accompanied by an increase in p. In eight experiments, the average values of sliding V/M before and after 5HT application were 0.115 ± 0.063 and 0.142 ± 0.077, respectively (p = 0.461, Wilcoxon signed rank test), whereas the EPSP more than tripled in amplitude on average. Thus, synaptic facilitation induced by 5HT, like synaptic depression, is not accompanied by a change in p but can be accounted for by an increase in the number of active synaptic sites.

As described in Materials and Methods, we tested the accuracy of the method of sliding p by applying it to simulated data sets with known n and p and found that the technique could in fact detect changes in sliding p if they occurred (Fig. 6). These simulations, together with the decrease in sliding V/M that was associated with an increase in the extracellular calcium (above), indicate that our methods are capable of detecting both increases and decreases in p.

A further conclusion from these experiments is that some release sites are effectively silent even before undergoing synaptic depression. If the probability of release remains constant during synaptic depression and facilitation (see the next section for evidence that pdoes not change even during the initial rapid phase of depression), then a significant increase in the facilitated EPSP over the initial EPSP implies the presence of inactive sites even before the induction of homosynaptic depression (see Fig. 1 for example). Although we did not perform experiments to examine directly other forms of plasticity, our observation that p was high in many of the experiments implies that other forms of synaptic facilitation at these synapses—including frequency facilitation, post-tetanic potentiation, and long-term potentiation—must also result primarily from increases in the number of sites contributing to the overall synaptic response.

Kinetics of homosynaptic depression and recovery from depression: synaptic sites switch between on and off states in an all-or-none manner

A completely independent kind of analysis supports the idea that homosynaptic depression is an all-or-none switching process. This analysis involves examining the time course of recovery from depression. Recovery after a single stimulus takes place with a time course consisting of a relatively rapid and an extremely slow phase. The time constant of the rapid phase of recovery is on the order of 10–100 sec, whereas the slow recovery process is so slow as to be unmeasurable out to at least 10 min. As the response depresses further with additional stimulation, a progressively smaller fraction of the initial response recovers with the fast time constant, and a progressively larger fraction fails to recover (Fig.7). This partial recovery is consistent with the idea that only a portion of the synaptic sites recovers after stimulation, with the rest remaining essentially inactive. In the steady state, the active synaptic sites recover rapidly between stimuli to the steady-state level, whereas the rest of the sites remain in the inactive state. Although the proportion of rapidly recovering sites decreases with depression, the time constant of recovery does not change significantly. This suggests the presence of only two pools of synaptic sites, an “on” and an “off” pool, rather than a continuously varying population.

The graphs of Figure 7 also suggest that the proportion of sites that drop out with each successive stimulus is not constant but rather declines progressively. Thus, after one stimulus the EPSP has depressed by ∼29% (Fig. 7A). If the same amount of depression occurred with the second and third stimulus, then the recovery after the third stimulus should be to only ∼35% of the initial amplitude rather than the 63% measured in Figure 7B, and recovery after the tenth stimulus (Fig. 7C) should be to ∼3% of the initial value. These calculations are conservative in that they assume that all synaptic sites are subject to depression. If it is assumed that some sites are not subject to depression, then the discrepancy between the observed and the predicted depression is even greater.

A further indication that this switching model can account for synaptic depression and facilitation comes from experiments in which the depression run was interrupted by rests of varying duration, after which stimulation was continued at either the same or a different stimulation frequency. In these experiments we found that virtually all aspects of the behavior of the responses were accurately predicted by a model in which synapses do not undergo a graded change in their properties but rather are subject to all-or-none switching off with progressive stimulation (Eq. 4 and 5 in Materials and Methods).

The model was constructed as follows (see Materials and Methods for more details). The first stimulus of an experiment causes release from a fraction, equal to p, of the available release sites. Of the sites that have released transmitter, some recover the ability to release with a time constant τ, whereas some switch into the off state. The second stimulus then causes release from a fraction (again equal to p) of the sites that had not released with the first stimulus, as well as from the same fraction of sites that had released to the first stimulus and had recovered by the time of the second stimulus. The second stimulus also results in the switching off of an additional fraction of sites. Release to subsequent stimuli is treated analogously, with the provision that the fraction of sites that switches into the off state decreases exponentially to zero. We allowed both p and τ, as well as the switching parameters α andZ (Eq. 4 and 5 in Materials and Methods), to vary freely, and, in addition, allowed p and τ to change their values during the course of a single experiment. The best fit of the predicted values to the data was determined by minimizing the sum of the squared errors (Table 2).

Table 2.

Parameters for best fits to data of Figures 8 and 9

Figure	p	τ (msec)	α	Z
8A	1.00	46.95	0.076	29.93
9A
Top left	0.41	57.00	0.087	5.88
Top center	0.47	90.20	0.080	23.76
Top right	0.23	159.48	0.092	35.37
Bottom left	0.36	96.70	0.166	4.19
Bottom center	0.86	32.29	0.115	26.14
Bottom right	0.65	53.85	0.059	>106
9B
Left	0.67	84.19	0.161	15.52
Right	1.00	23.57	0.255	7.46

Using this model, we found that all of the responses of a given experiment were best fit with constant values for p and τ (Figs. 8A, 9) and that values of τ were in the same range as those measured in the recovery experiments (i.e., on the order of tens of seconds). Synaptic depression and recovery could not both be fit without introducing switching into the model, whether τ was kept constant, as would be the case for a simple depletion model (Zucker and Bruner, 1977; Liu and Tsien, 1995) (Fig. 8B), or allowed to increase progressively, as might be the case if there were progressive depletion of an upstream feeding pool of transmitter (von Gersdorff and Matthews, 1997) (Fig. 8C). Not only was the initial decline well fit with constant values for p and τ, but the recovery after rest and the time course of the subsequent decline were also accurately predicted, whether the stimulation frequency was kept constant (Figs.8A, 9A) or changed (Fig. 9B). The only failure of the model to closely fit the observed responses occurred when the rest was 10 sec or less (Fig. 9A), presumably because frequency facilitation was recruited at the short interstimulus intervals (Byrne, 1982; Eliot et al., 1994).

Of particular significance is the fact that both the initial rapid phase of depression and the subsequent slow phase were well fit using this model, indicating that the combination of recovery between stimuli at some sites and the putative switching process can account for all aspects of synaptic depression and that it is not necessary to invoke two separate depression processes to account for the dual time course of depression.

Another characteristic property of these synapses is that the EPSP undergoes partial recovery with rest, but then declines back to the previous steady-state level after only one or two stimuli. This behavior too is accurately predicted by our model, simply as a consequence of the fact that the rapidly recovering sites have enough time to recover fully during the pause in the stimulation and then revert to the steady-state level when stimulation is resumed at the initial frequency. The synapses that had been switched into the inactive state, on the other hand, do not recover appreciably if the rest from stimulation is brief compared with the slow time constant of recovery, which is on the order of hours.

Parameters τ and α that gave the best fits (Table 2) were in general agreement with those that could be independently estimated from the experiments of Figure 7. Nonetheless, α, the fraction of sites that drops out with each stimulus, tended to be smaller than the depression to a single stimulus (Fig. 7A). Attempting to fit the data without incorporating a progressive decline in α (i.e., without parameter Z; see Materials and Methods), consistently yielded values for τ and α that were greater and smaller, respectively, than those used for the fits shown, and were thus further from the values estimated from the experiments of Figure7. Overall, the median τ and α in 29 fits incorporatingZ were 82 msec and 0.13, respectively, whereas the median values without Z were 124 msec and 0.07. In addition, omitting Z led to a predicted depression that was consistently greater than that observed (data not shown). We therefore conclude that the fraction of sites that drops out with each stimulus undergoes a progressive decline.

DISCUSSION

Our analysis indicates that synaptic depression and facilitation involve switching of release sites between active and inactive states. Entry into the inactive state is functionally equivalent to turning off synaptic transmission, although it is difficult to distinguish between a release probability of zero and very low, but non-zero, release probabilities. Switching to the off state can occur with even a single stimulus, and some sites are in the off state without previous stimulation. Facilitation results from the switching on of synapses that had been in the off state previously, whether they entered that state as a result of homosynaptic depression or not. Interestingly, on the basis of a completely different kind of analysis, it has been proposed that 5HT increases synaptic transmission at neuromuscular junctions of the crayfish by recruiting silent synapses (Wang and Zucker, 1998).

Synaptic facilitation by 5HT is mediated through two second-messenger systems, those involving protein kinases A and C (Braha et al., 1990;Sacktor and Schwartz, 1990; Ghirardi et al., 1992; Sugita et al., 1992;Byrne et al., 1993; Klein, 1993). The biochemical cascades involving these kinases act in different ways: PKA facilitates only synapses that have not been severely depressed by previous stimulation, whereas PKC enhances release even at depressed synapses (Braha et al., 1990;Ghirardi et al., 1992; Klein, 1993). Our analysis suggests that the two kinases might differ in their ability to cause switching from the off to the on release state, with PKC capable of inducing switching and PKA able to increase release at active release sites but unable to cause switching. This hypothesis implies that facilitation by PKA results from an increase in p, which we did not observe with facilitation by 5HT. However, in all of our experiments, 5HT was applied to depressed synapses, where the contribution of PKA would be minimal (Klein, 1993). This hypothesis predicts that PKA would be relatively ineffective at synapses with high p, a prediction that could be tested by changing the extracellular calcium concentration, for example.

Nonuniformity of p

One problem in attempting quantal analysis is the possibility thatp differs at different release sites (Hessler et al., 1993;Rosenmund et al., 1993). If the variance of p is significant, the estimated p will be higher than the (unweighted) average probability of release, and the estimatedn will be lower than the actual number of sites (Del Castillo and Katz, 1954). It is therefore possible that an apparent change in n with no change in p could result from changes in the probability of release at some sites, without sites dropping out completely or being recruited. Two considerations argue against our results being attributable to this possibility. First, we observe no overall change in p despite large decreases inm during homosynaptic depression (Figs. 4, 5). Although any single pair of values of m and p can be accounted for on the basis of a nonuniform p with the consequent underestimate of n, there is no obvious way of accounting for a constant p in the face of changing m by altering the distribution of p across release sites. Because sliding p was computed on the basis of its linear relation with V/M (Eq. 1–3), constant pnecessitates that V/M remains constant. Another way of expressing this condition is:

$$\sum (p_{\text{i}}{)}^2/\sum p_{\text{i}}=\text{constant},$$

where p_i is the probability of release at the ith site. The only general way this condition is met is if the relative distribution of pat all sites remains the same, i.e., if the same proportion of sites drops out for all values of p. If p is nonuniform, this leads to the interesting conclusion that the shutting off of a site is independent of release. This conclusion excludes all depletion models. On the other hand, if p is uniform, dropping out of sites may or may not depend on release.

A less general argument against the possibility that the apparent change in n is the result of changes in nonuniformp applies in a subset of our experiments. If the minimal number of release sites is much greater than the estimated nafter synaptic depression, and, in addition, the estimated pis high, the probability of release at a large proportion of the sites must be close to zero (McLachlan, 1978).

Studies of depression and facilitation at Aplysiasensorimotor synapses

We find that the sensorimotor synapses undergo only partial recovery with rest after as little as a single stimulus (Figs.7-9). The amount of recovery in our experiments is comparable to that reported by others both in intact ganglia (Walters and Byrne, 1985;Trudeau and Castellucci, 1992; Nakanishi et al., 1997) and in conventional cultures using extracellular stimulation (Lin and Glanzman, 1994; Bao et al., 1997). Five to 10 minutes after one stimulus, the EPSP in the cultures averaged 0.78 of the initial EPSP, after three stimuli it was 0.63, and after 8–10 stimuli it was 0.47. In intact ganglia, the EPSP averaged 0.80 after one stimulus, 0.64 after three stimuli, and 0.32 after 7–10 stimuli (only two of the three studies in intact ganglia included more than six stimuli). Our values (Fig. 7) were 0.72, 0.63, and 0.40, respectively.

All the analyses of depression and facilitation at Aplysiasensorimotor synapses find that the quantal amplitude does not change (Castellucci and Kandel, 1974, 1976; Dale and Kandel, 1990; Eliot et al., 1994), a result that is commonly interpreted as indicating that the changes in transmission result from changes in transmitter release. Although it is theoretically possible for all of the postsynaptic receptors at individual sites to be switched off and on as a unit, we believe that the rapidity and reversibility of switching favors a presynaptic locus of plasticity, as proposed in the earlier studies.

Other studies have examined the possible basis of homosynaptic depression at these synapses. One report suggested that a progressive decrease in the amount of calcium entering the presynaptic terminals with each action potential might contribute to the depression of release (Klein et al., 1980). Because we find that changing external calcium changes the probability of release, and repeated stimulation does not, this mechanism appears unlikely.

Gingrich and Byrne (1985) attempted to account for homosynaptic depression as the depletion of a pool of transmitter whose refilling is dependent on intracellular calcium. Their model could account for the kinetics of depression as well as the effect of tetanization in increasing transmission. However, this model could simulate the recovery from a single depression run to only a limited extent (Gingrich and Byrne, 1985, their Fig. 3), and no attempt was made to simulate subsequent bouts of homosynaptic depression.

In an ultrastructural study, Bailey and Chen (1988) reported that depletion of synaptic vesicles from the active zones accompanies homosynaptic depression, suggesting depletion of a releasable pool of transmitter. In contrast, Eliot et al. (1994) found that depression of evoked transmission was not accompanied by a decrease in the frequency of spontaneous release, suggesting to them that simple depletion of vesicles from the active zones was not responsible for the depression of the evoked responses.

We constructed our model on the assumption that switching off of synapses occurs only after release, as would be the case for a depletion model. However, as discussed earlier, our model does not depend on this assumption. Our inference that some synapses are inactive even in the absence of previous stimulation entails a mechanism for the silencing of synapses that does not depend on release. Furthermore, as discussed earlier, if p is not uniform across release sites, our failure to observe a decrease inp with synaptic depression implies that switching is independent of release.

Distinct pools of synaptic sites

Although some synapses switch from an active to an inactive state with repeated stimulation, a residual pool of synapses remains active even after many stimuli. This difference among synapses suggests that a single sensory neuron could express preferentially one or another type of synapse with different targets. Synapses with different targets could then show intrinsic quantitative or even qualitative differences in synaptic transmission and plasticity, depending presumably on interactions with the postsynaptic neuron (Davis and Murphey, 1994).

Our findings indicate that the population of effectively transmitting synapses is subject to rapid change and imply that changes in the synaptic population are expressed in short-term learning processes. We can suggest some possible advantages in being able to control subpopulations of synapses in this manner. First, groups of synapses, together with the behaviors they control, could be kept silent until the appropriate circumstances call for their recruitment. In addition, the switching of groups of release sites by a particular stimulus would allow the nervous system to shape complex responses into the most appropriate configurations for a given situation without the need for the continued activation of dedicated modulatory pathways for small groups of release sites. Switching of individual release sites thus adds a layer of fine control to the mechanisms of integration known to operate at the level of individual neurons and of neuronal assemblies.