Modeling LGN Responses during Free-Viewing: A Possible Role of Microscopic Eye Movements in the Refinement of Cortical Orientation Selectivity

Abstract

Neural activity appears to be essential for the normal development of the orientation-selective responses of cortical cells. It has been proposed that the correlated activity of LGN cells is a crucial component for shaping the receptive fields of cortical simple cells into adjacent, oriented subregions alternately receiving ON- and OFF-center excitatory geniculate inputs. After eye opening, the spatiotemporal structure of neural activity in the early stages of the visual pathway depends not only on the characteristics of the environment, but also on the way the environment is scanned. In this study, we use computational modeling to investigate how eye movements might affect the refinement of orientation tuning in the presence of a Hebbian scheme of synaptic plasticity. Visual input consisting of natural scenes scanned by varying types of eye movements was used to activate a spatiotemporal model of LGN cells. In the presence of different types of movement, significantly different patterns of activity were found in the LGN. Specific patterns of correlation required for the development of segregated cortical receptive field subregions were observed in the case of micromovements, but were not seen in the case of saccades or static presentation of natural visual input. These results suggest an important role for the eye movements occurring during fixation in the refinement of orientation selectivity.

Since the discovery that high percentages of cells in the primary visual cortex of different mammal species respond preferentially to luminance edges with specific orientations (Hubel and Wiesel, 1962), the developmental origin of cortical orientation selectivity has been studied intensively. Substantial experimental evidence (Zahs and Stryker, 1988; Chapman et al., 1991; Reid and Alonso, 1995; Ferster et al., 1996; Chung and Ferster, 1998) supports the proposal that the adjacent oriented excitatory and inhibitory subregions present in the receptive fields of simple cells receive selective input from geniculate ON- and OFF-center cells in the same retinotopic positions (Hubel and Wiesel, 1962). However, the mechanisms underlying the emergence of such segregation of thalamic afferents are still unclear.

The essential elements of cortical orientation selectivity seem to develop before the exposure to patterned visual input (Wiesel and Hubel, 1974; Blakemore and Van Sluyters, 1975; Sherk and Stryker, 1976;Fregnac and Imbert, 1978; Albus and Wolf, 1984; Chapman and Stryker, 1993; Chapman et al., 1996; Crair et al., 1998). Nevertheless, visual experience appears essential for both refining orientation selectivity and maintaining the normal response properties of cortical neurons (Pettigrew, 1974; Blakemore and Van Sluyters, 1975; Buisseret and Imbert, 1976; Fregnac and Imbert, 1978; Hirsch, 1985; Chapman and Stryker, 1993; Crair et al., 1998). A number of experimental findings (Stryker and Harris, 1986; Fregnac et al., 1992; Chapman and Stryker, 1993; Weliki and Katz, 1997) support the hypothesis that the development of orientation-selective responses relies on Hebbian/covariance mechanisms of plasticity, which transform the temporal contiguity of firing patterns into spatial proximity of synaptic contacts (Stent, 1973; Changeux and Danchin, 1976). According to this hypothesis, the clustering and/or segregation of neural inputs emerges from the stabilization of synchronously firing afferents onto common postsynaptic neurons and the destabilization of nonsynchronous ones. A necessary requirement of the Hebbian hypothesis is a consistency between the correlated activity of thalamic afferents and the organization of simple-cell receptive fields. Synchronous activation is required among geniculate cells of the same type (ON- or OFF-center) with receptive fields located at distances smaller than the width of a simple-cell subregion, and among cells of opposite polarity with receptive fields at distances comparable to the separation between adjacent subregions. Modeling studies (Linsker, 1986; Miyashita and Tanaka, 1992; Miller, 1994) have shown the feasibility of this proposal assuming similar spatiotemporal patterns of spontaneous activity in the LGN before eye opening.

After eye opening, the spatiotemporal structure of LGN activity depends not only on the characteristics of the visual input, but also on the movements performed by the animal while exploring its environment. It may be expected that changes in the visual input induced by these movements play an important role in shaping the responses of neurons in the visual system. Experiments in which kittens were raised with their eyes paralyzed have shown basic deficiencies in the development of visually guided behavior (Hein et al., 1979), as well as impairments in ocular dominance plasticity (Freeman and Bonds, 1979; Singer and Raushecker, 1982). In addition, it has been shown that eye movements are necessary for the reestablishment of cortical orientation selectivity in dark-reared kittens exposed to visual experience within the critical period (Buisseret et al., 1978; Gary-Bobo et al., 1986). This indicates that simultaneous experience of visual input and eye movements (and/or eye movement proprioception) may be necessary for the refinement of orientation selectivity (Buisseret, 1995).

The focus of this paper is on how visual experience and eye movements might jointly influence the refinement of orientation selectivity under the assumption of a Hebbian mechanism of synaptic plasticity. We have analyzed the second order statistical structure of neural activity in a model of cat LGN. In the absence of eye movements, when a natural visual environment was observed statically, similar to the way it is examined by animals with their eyes paralyzed, we found that the simulated responses of geniculate cells of the same type at any separation smaller than the receptive field of a simple cell were strongly correlated. These spatial patterns of covarying geniculate activity did not match the structure of simple-cell receptive fields. A similar result was obtained when natural scenes were scanned through saccades. Conversely, in the case of micromovements, including both microsaccades and the combination of ocular drift and tremor, strong correlations were measured among cells of the same type located nearby and among cells of opposite types at distances compatible with the separation between different subregions in the receptive fields of simple cells. In this case, the covarying activity of LGN units closely matched the spatial structure of simple-cell receptive fields. These findings support a role for micromovements in the refinement of orientation-selective cortical responses.

MATERIALS AND METHODS

In the experiments described in this paper we simulated the activity of geniculate cells with receptive fields in different positions of the visual field, while receiving visual input in the presence of different types of eye movements. The following describes each element of the model in detail.

Modeling the activity of LGN cells

LGN cells were modeled as linear elements with quasi-separable spatial and temporal components as proposed by Cai et al. (1997). This model, derived using the reverse-correlation technique, has been shown to produce accurate estimates of the activity of different types of LGN cells. Changes in the instantaneous firing rates with respect to the level of spontaneous activity l_xy(t), were generated by evaluating the spatiotemporal convolution of the input image I with the receptive field kernel K:

$$l_{\text{xy}}(t)=[K(x,y,t)★I(x,y,t){]}_{\theta }=\left[\underset{0}{\overset{\text{t}}{\int }} \underset{-\infty }{\overset{\infty }{\int }} \underset{-\infty }{\overset{\infty }{\int }} K(x^{\prime },y^{\prime },t^{\prime })I(x-x^{\prime },\right.$$ Equation 1

$$y-y^{\prime },t-t^{\prime }){\text{dx}}^{\prime } {\text{dy}}^{\prime } {\text{dt}}^{\prime }\left]{}_{\theta },\right.$$

where ★ is the symbol for convolution, (x, y) and t are the spatial and temporal variables, and the operator [.]_θ indicates rectification ([x]_θ = x − θ if x > θ,0 otherwise). For each cell, the kernel K consisted of two additive components, representing the center (c) and the periphery (s) of the receptive field, respectively. Each of these two contributions was separable in its spatial (F) and temporal (G) elements:

$$K(x,y,t)=F_{\text{c}}(x,y)G_{\text{c}}(t)-F_{\text{s}}(x,y)G_{\text{s}}(t).$$

The spatial receptive fields of both center and surround were modeled as two-dimensional (2D) Gaussians, with a common space constant for both dimensions:

$$F(x,y)=(A/2\pi {\varsigma }^2)exp(-(x^2+y^2)/2{\varsigma }^2).$$

As is the case for their biological counterparts, ON-center units were characterized by an increase in their activation when a spot of light was flashed at the center of their receptive field and were inhibited when stimulated in the periphery. The opposite was true for OFF-center units, which were equivalent to ON units with reversed sign in the spatial receptive fields. F was set to zero for distances larger than 3ς. The spatial parameters, A_c, A_s, ς_c, ς_s, varied with eccentricity following measurements performed by Linsenmeier et al. (1982). Linear interpolation as described in Linsenmeier et al. (1982)was used to estimate the sizes of the 2D Gaussians on the basis of eccentricity, and the amplitudes of excitatory and inhibitory zones on the basis of their respective sizes. The specific values of the parameters used in the simulations are given in Results.

Following Cai et al. (1997), the temporal profile of the response was given by:

$$G_{\text{c}}(t)=k_1\frac{[c_1(t-t_1){]}^{{\text{n}}_1}exp(-c_1(t-t_1))}{n_1^{{\text{n}}_1}{e}^{-{\text{n}}_1}}-k_2\frac{[c_2(t-t_2){]}^{{\text{n}}_2}exp(-c_2(t-t_2))}{n_2^{{\text{n}}_2}{e}^{-{\text{n}}_2}}$$

and

$$G_{\text{s}}(t)=G_{\text{s}}(t-t_{\text{d}}),$$

i.e., the temporal function for the periphery was the same as that for the center, except for the time delay t_d. To reduce the intense computational load of the simulations, only nonlagged, ON- and OFF-center X cells were considered, with temporal parameters k₁ = 1, c₁ = 60 s⁻¹, t₁ = 0 sec, n₁ = 2, k₂ = 0.6, c₂ = 40 s⁻¹, t₂ = 0 sec, n₂ = 2. For all units, a time delay t_d = 3 msec was used.

In the simulations described in this paper, unless explicitly stated otherwise, geniculate cells were assumed to operate in their linear range, and rectification was not considered (i.e., θ = −∞ in Eq. 1). When rectification was present, different thresholds were used for cells with opposite polarities. Rectification thresholds for each image and for cells with different polarities were defined as a fraction c of the negative peaks of steady-state activity (the mean value of steady-state activity was assumed to be zero), and rectification levels as their complementary values (1 − c). Thus, a rectification of 50% indicates that half of the range of steady-state negative responses has been eliminated, whereas only positive responses are present with a rectification of 100%.

Modeling eye movements

Modeled eye movements included saccades (both large-scale saccades and microsaccades), ocular drift, and tremor.

Saccades. Voluntary saccadic eye movements, the fast shifts of gaze among fixation points, were modeled by assuming a generalized exponential distribution of fixation times (Harris et al., 1988). According to this model, the probability of two saccades following each other by an interval of t msec was given by:

$$f(t)=\left\{\begin{array}{cc}(1/\beta )e^{-(\text{t}-\alpha )/\beta }& t>\alpha \\ 0& t\le \alpha \end{array}\right.,$$

where α is a refractory period that prevented the occurrence of new saccadic movements immediately after each saccade. Although this model was originally proposed to describe fixation times in humans, a similar skewed distribution of intersaccadic intervals during free-viewing has also been observed in other species, such as cats and birds (Harris et al., 1988). In the experiments, we set α = 150 msec and β = 300 msec, to produce an average of roughly two saccades per second. The amplitude and direction of a saccade were randomly selected among all possible saccades that would keep the point of fixation on the image. All possible saccades had an equal probability of being selected. This assumption neglects the fact that saccades may occur toward preferred points in the scene and that the properties of the visual input around these points may bias the measured patterns of correlation. Following data described in the literature (Ditchburn, 1973), the duration D_s of each saccade was proportional to its amplitude M_s:

$$D_{\text{s}}=v_s^{-1}(M_{\text{s}}-m_{\text{s}})+d_{\text{s}},$$

where the velocity v_s was a random variable uniformly distributed between 0.4 and 0.6 °/msec, m_s = 10° and d_s = 40 msec. A modulation of geniculate activity was present in correspondence of each saccade. Neu-ral activity around the time of a saccade was multiplied by the modulatory function:

$$G(t)=\left\{\begin{array}{cc}1+A_{\text{pre}}(t-T_{\text{e}}{)}^2{e}^{(-0.02(T_{\text{e}}-\text{t}))}& t<T_{\text{e}}\\ 1+A_{\text{post}}(t-T_{\text{e}}{)}^2{e}^{(-0.02(\text{t}-T_{\text{e}}))}& t\ge T_{\text{e},}\end{array}\right.$$

where T_e is the time at which the saccade ends, A_pre = −7.4 × 10⁻⁵ and A_post = 1.5 × 10⁻⁴. In this way the initial suppression of activity with a peak of 10%, gradually reversed to a 20% facilitation with peak occurring 100 msec after the end of the saccade (Lee and Malpeli (1998)).

Micromovements. Micromovements included microsaccades, ocular drift, and tremor. Microsaccades were modeled in a similar way to voluntary saccades, with amplitude randomly selected from a uniform distribution between 1 and 10 min of arc [the frequency characteristics of microsaccades can be found in Ditchburn (1973)]. No modulation of LGN activity was present in the case of microsaccades.

Ocular drift and tremor were modeled together following a method similar to the one proposed by Eizenman et al. (1985). According to this model, the power spectrum of ocular drift and tremor can be approximated by two processes: a Poisson process filtered by a second-order eye plant transfer function over the frequency range 0–40 Hz where the power declines as 1/f², and a cyclo-stationary process that produces a broad spectral peak in the range of 40–100 Hz. The two terms represent the irregular discharge rate of motor units for frequency <40 Hz and their more regular firing pattern for higher frequencies, respectively (Kuboki, 1957; Sindermann et al., 1978). For simplicity, given its predominant contribution, only the first term with power spectrum proportional to 1/f² was considered. Parameters were adjusted to give a mean amplitude of 1.21° and a mean velocity equal to 14.9°/sec, which are the values measured in the cat (Olivier et al., 1993).

Data collection and analysis

The activity of 10 simulated LGN units was analyzed when input images were scanned through sequences of eye movements. Unit receptive fields were equispaced along a chosen axis, and the orientation of this axis was changed systematically to sample the full spectrum of possible directions. The results shown in this paper are averages over all examined directions. This allowed a direct comparison between the results of the simulations and neurophysiological data from cortical simple cells (Wilson and Sherman, 1976; Jones and Palmer, 1987b). For most of the experiments described in this paper, the distance between the receptive fields of two adjacent simulated units was equal to 8 arcmin. Thirty images extracted from a database of natural scenes (van Hateren and van der Schaaf, 1998) were used. These images consisted of 1024 × 1024 pixels, spanning 24° of visual angle. The degree of correlation between unit activity was evaluated in the presence of different types of eye movements. In most of the experiments, each image was examined for a period of 250 sec, during which eye movements occurred.

Levels of correlations in the activity of LGN units were measured by means of correlation coefficients. Given a unit of type a (ON- or OFF-center) at position i, and one of type b at position j, with activation u_i and u_j, the correlation of activity was evaluated as:

$$C_{\text{ij}}^{\text{ab}}=\frac{\langle (u_{\text{i}}(t)-{\overline{u}}_{\text{i}})(u_{\text{j}}(t)-{\overline{u}}_{\text{j}})\rangle }{{\varsigma }_{\text{i}}{\varsigma }_{\text{j}}}=\frac{c_{\text{ij}}^{\text{ab}}(0)}{\sqrt{c_{\text{ij}}^{\text{aa}}(0)c_{\text{ij}}^{\text{bb}}(0)}},$$ Equation 2

where c_ij^ab is the cross-covariance of units activity, c_ij^ab and c_ij^bb are their autocovariances, $\overline{u}$_i and ς_i are the mean and variance of the response of the i -th LGN cell. The mean values of activity ( $\overline{u}$_i, $\overline{u}$_j) were evaluated over a time window of length T. This window must not be confused with the duration length of the simulated recordings (usually 5 sec, selected on the basis of the available computational power) over which the external average 〈.〉 was estimated. In most of the experiments described in this paper, $\overline{u}$_i and $\overline{u}$_j were running averages of neural activity. The alternative possibility of evaluating the actual “covariance” over a window T (in which the duration of the experiment is also set to T) produced results that were practically indistinguishable from the ones presented in this paper. As expressed by Equation 1, the deviations in the activity of OFF cells with respect to their resting levels were equal in magnitude and opposite in direction to the deviations of the activity of ON cells. As a result, in the linear range of geniculate responses, C^ONON was equal to C^OFFOFF. The relative level of correlation between units of the same and different types at positions i and j in the LGN was measured by means of the correlation difference, C_ij^D = C_ij^ONON − C_ij^ONOFF, where the two terms are the correlation coefficients evaluated between the two ON units at positions i and j, and between the ON unit at position i and the OFF unit at position j, respectively. C_ij^D is positive when the activity of units of the same type covaries more strongly than that of units of different types and is negative when the opposite occurs. The average relative levels of correlation between units with receptive fields at different distances in the visual field were examined by means of the function C^D(d) = <C_ij^D >_{‖i−j‖=d}, which evaluates the average correlation difference C_ij^D among all pairs of cells at positions i and j at distance d from each other. For simplicity, in the following we refer to C^D(d) as the correlation difference, implicitly assuming that a spatial averaging has taken place. The correlation difference is a useful tool for predicting the emerging patterns of connectivity in the presence of a Hebbian mechanism of synaptic plasticity (Miller (1994). The average separation at which C^D(d) changes sign is a key element in determining the spatial extent of the different subfields within the receptive fields of simple cells.

In some cases a first-order approximation of the correlation difference was evaluated by considering the LGN as a linear filter. This approximation neglects any effects of rectification. The correlation difference was evaluated by using the spatiotemporal correlation r(d, t) of the input (the correlation function evaluated at time lag t of the luminance of pixels located at a spatial lag d), or equivalently the input power spectrum R(w, f), where w and f indicate spatial and temporal frequencies. Under the assumption of linearity, the correlation among geniculate cells of the same type l(d, t) can be evaluated by the inverse Fourier transform of the power spectrum of LGN activity l(d, t) = ℱ⁻¹(‖H(w, f)‖²R(w, f)), where H is the spatiotemporal Fourier transform of the LGN kernel [see, for example, Bendat and Piersol (1986)]. With the simplifying assumption that all cells are characterized by equal values of mean activity η and standard deviation ς, the correlation difference was estimated as:

$$C^D(d)=\frac{2}{{\varsigma }^2} (l(d,0)-{\eta }^2).$$ Equation 3

The results of the simulations were compared with the typical profile of a simple-cell receptive field as estimated by Jones and Palmer (1987b). According to the 2D Gabor filter model proposed byJones and Palmer (1987a,b), the typical receptive field profile in the preferred direction θ is given by:

$$w(r)=〈exp\left(r^2\frac{b^2{cos}^2(\theta )+a^2{sin}^2(\theta )}{2a^2{b}^2}\right)cos(-2\pi F_{\text{o}}r)〉,$$

where r indicates the distance from the center of the receptive field, and the averaging operation is over a number of cells with parameters shown in Table 1 of Jones and Palmer (1987b). The parameters a and b are the amplitudes of the Gaussian term along the two axes, θ gives the relative orientation of the Gaussian and wave modulations in the model, and F_o is the wave frequency.

RESULTS

LGN activity with static input presentation

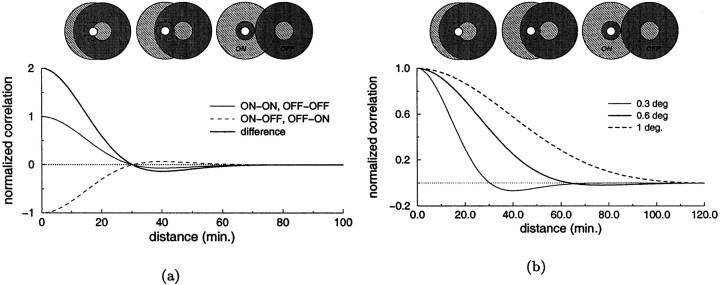
We first focus on the spatial characteristics of geniculate responses and consider the average activity of LGN cells in different situations. Figure 1 illustrates schematically some spatial factors that contribute to the emergence of correlated activity in the LGN and introduces the tools that we use to quantify such correlations. In this example we have measured the level of correlation between pairs of cells with receptive fields at different separations when a spot of light was presented as input. An important element in the resulting level of correlation is the polarity of the two cells (i.e., whether they are ON- or OFF-center). As shown in Figure 1a, because geniculate cells tend to be coactive when the ON and OFF subregions of their receptive fields overlap, the correlation between pairs of cells of the same type decreases when the separation between their receptive fields is increased, whereas pairs of cells of opposite types tend to become more correlated. As a consequence, the correlation difference function, C^D(d), is positive at small separations and negative at large ones. Fig. 1b illustrates an example of the dependence of the levels of correlation on the spatial structure of the visual input. The correlation difference function changes significantly when the spot of light used for the stimulation is enlarged. In particular, C^D(d) becomes positive for d in the range 30–70′ for a sufficiently large beam of light, indicating that when a large spot of light is present, pairs of cells with receptive fields at such separations possess stronger correlation if they have the same polarity, whereas the correlation between cells of opposite types predominates in the presence of a smaller spot.

Fig. 1.

Analysis of some spatial factors affecting the correlation between the responses of two geniculate cells. Both graphs show the correlation coefficients or the correlation difference function, C^D(d), for pairs of cells with receptive fields at different separations. Theicons on the top of each graph represent the positions of the receptive fields of the two cells at the corresponding separations along the x axis. The bright dotmarks the center of the spot of light. a, Effect of the polarity of the cells. The three curves represent the correlation coefficients for pairs of units of the same type C^s(d) (continuous thin line), units of opposite types C^o(d) (dashed line), and the correlation difference function C^D(d) = C^s(d) − C^o(d) (bold line). b, Effect of the spatial structure of the visual input. Correlation difference functions measured in the presence of spots of light with three different sizes (0.3, 0.6, and 1°). Positive (negative) values of C^D(d) indicate that the activity of LGN cells of the same (opposite) type covary more closely than the activity of cells of opposite (same) types.

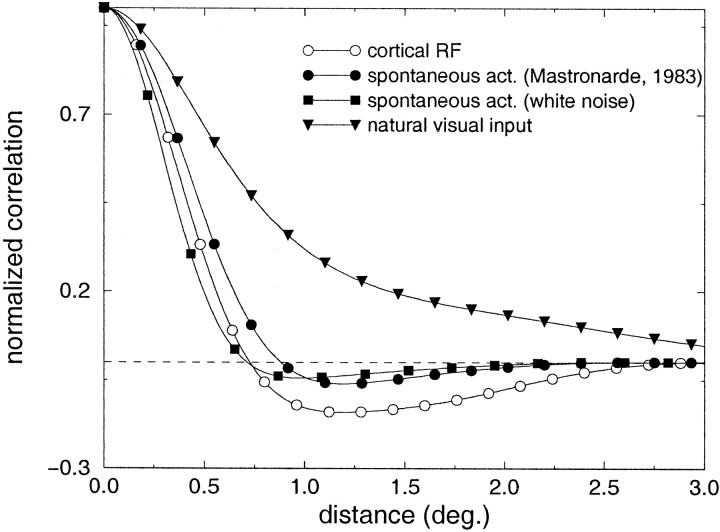
In Figures 2 and3, a similar analysis is presented for two richer types of visual input: retinal spontaneous activity and natural visual stimulation. Again, the data refer to the steady-state responses. Because little is known regarding the patterns of correlation in cat LGN during spontaneous activity, we have evaluated a first-order approximation on the basis of retinal inputs. Following the theory of linear filtering [see, for example, Bendat and Piersol (1986)], the autocovariance of LGN activity is given by the inverse Fourier transform of the output power spectrum l_e(x, y) = ℱ⁻¹(‖H_e(w_x, w_y)‖²R_e(w_x, w_y)), where R_e(w_x, w_y) and H_e(w_x, w_y) are the Fourier transforms of the pattern of autocovariance of the inputs r_e(x, y) and the spatial geniculate kernel h_e(x, y) (see Materials and Methods). l_e(x, y) and r_e(x, y) are measures of the covariances among same-type geniculate and ganglion units with receptive fields located around eccentricity e and spaced by x and y in the horizontal and vertical dimensions. As shown in Materials and Methods (Eq. 3), given l_e it is possible to estimate the correlation difference function. In Figure 2 we show the results for a typical LGN cell at 17° of eccentricity [ς_c = 18′, ς_s = 1.3° (Linsenmeier et al., 1982)]. As a first approximation, the activity of retinal receptors was modeled as a white noise process; that is, the activation of each receptor was assumed to be independent from all the others. This approximation (data marked byfilled squares in Fig. 2) is likely to underestimate the correlation difference of LGN cells in the cat, because it neglects any source of correlation other than the spatial organization of geniculate receptive fields. For example, positive correlations may already be present in the activity of neighboring retinal receptors, possibly originating from intrinsic connectivity (Vardi and Smith, 1996). In a second approximation, r_e(x, y) was evaluated on the basis of Mastronarde's data on the correlated firing of ganglion cells in the cat retina (Mastronarde, 1983). Mastronarde's estimate of the correlation between the activity of two X cells at a relative distance d [Mastronarde (1983), his Fig. 10] was approximated by the function c_e = 15 − 3.75s_e(d), where e is the visual eccentricity and s_e(d) indicates the distance expressed in spacings [s_e(d) = 0.186d $\sqrt{N_{\text{e}}}$; N_eis the cell density at eccentricity e as given by Hughes (1975)]. This second measurement (curve marked byfilled circles in Fig. 2) is likely to provide an overestimate of the LGN autocovariance, because the spatial extent of positive correlations among the activity of ganglion cells is presumably larger than at the level of retinal receptors. For comparison, the average receptive field profile of a simple cell within the central 5–25° of the visual field is also shown. This prototypical cortical receptive field was taken from the measurements by Jones and Palmer (1987a,b). As illustrated by the graph, despite the fact that our method provides only a rough estimate of the correlation difference for the case of spontaneous activity, a close correspondence is present between these curves and the response profile of an average cortical simple cell, indicating that a Hebbian mechanism of synaptic plasticity can well account for the structure of simple-cell receptive fields before eye opening.

Fig. 2.

Predicted correlation difference functions of steady-state LGN activity evaluated around 17° of visual eccentricity. ■, Case of spontaneous activity (white noise approximation). ●, Case of spontaneous activity (approximation with Mastronarde's data). ▾, Natural visual input. The curvemarked by open circles is the average receptive field of a simple cell, as measured by Jones and Palmer (1987) shown here for comparison.

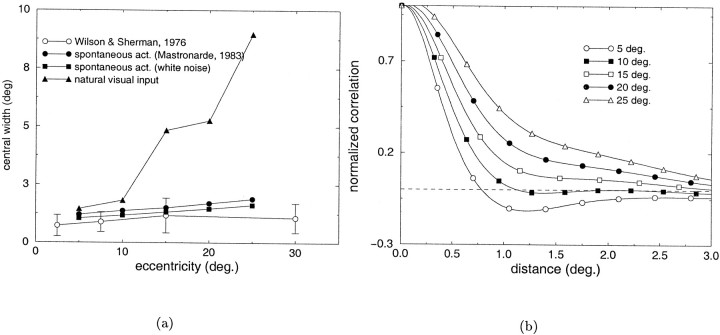
Fig. 3.

Analysis of the covariance patterns of steady-state LGN activity at different visual eccentricities. a, Comparison between the width of the larger subfield in the receptive field of simple cells at different eccentricities as measured by Wilson and Sherman (1976) (open circles) and the width of the central lobe of the correlation difference functions measured in the cases of spontaneous activity and natural visual input. Symbols as in Figure 2. b, Correlation difference functions measured in the presence of natural visual input at different eccentricities.

What happens in the presence of natural visual input? A linear analysis similar to the case of spontaneous activity was performed using a database of 30 snapshot images of natural scenes. The mean power spectrum of our database was best approximated by S(k) = Aw^−2.04, which is consistent with the results of several studies investigating the power spectrum of natural images (Field, 1994; Ruderman and Bialek, 1994; van der Schaaf and van Hateren, 1996). The mean correlation difference function measured when the input images were filtered by the spatial kernel of a LGN cell at 17° of visual eccentricity is marked by filled trianglesin Figure 2. This function was obtained from the mean autocovariance of LGN activity averaged along all possible orientations. Because of the wide spatial correlations of natural visual input, the estimated correlation difference did not change sign within the receptive field of a typical simple cell. That is, LGN cells of the same type were found to covary more closely than cells of opposite types at all separations within the receptive field of a simple cell. This result is not consistent with the putative role of a direct Hebbian/covariance model in the refinement of orientation selectivity after eye opening.

Figure 3 shows the results of the previous analysis for LGN cells at different visual eccentricities. Theopen circles in Figure 3a represent the width of the largest subfield in the receptive field of cortical simple cells as measured by Wilson and Sherman (1976). The other curves represent the widths of the central lobe of the correlation difference functions (the spatial separation over which cells of the same type possess correlated activity, measured as the double of the point at which the correlation difference function intersects the zero axis) in the cases of spontaneous activity and natural visual input. As in Figure 2, a close correspondence was present between the experimental data and the subregion widths predicted by the correlation difference function in the case of spontaneous activity [in Fig. 3a, filled squares indicate white noise estimate, and filled circles indicate estimate on the basis of Mastronarde's data (Mastronarde, 1983)]. Conversely, a significant deviation between the two measurements was present in the case of natural visual input (Fig.3a, filled triangles). The measured correlation differences at different visual eccentricities in the case of natural visual stimulation are shown in Figure 3b.

So far we have neglected the temporal evolution of neural responses. However, the activity of geniculate cells exhibits a large temporal variability, and several categories of geniculate cells have been identified on the basis of their dynamics. Depending on its own intrinsic dynamics, each LGN cell responds differently to changes in the visual input as a result of both the modifications of the surrounding environment and the motor behavior of the organism. In Figure 4 we analyze the levels of covariance in the activity of nonlagged X geniculate cells in the presence of natural time-varying input. Similar to the previous analysis, the correlation difference function was derived from the covariance of the activity of same-type cells, estimated by filtering the power spectrum of natural time-varying images with a typical spatiotemporal geniculate kernel. The results shown in Figure 4 refer to cells located around 17° of visual eccentricity. Thecurve marked by filled circles in Figure 4represents the correlation difference function evaluated when the power spectrum of time-varying natural images was approximated by considering visual scenes as collections of objects moving with a power-law distribution of velocities, as suggested by Dong and Atick (1995). An example in which the input power spectrum was experimentally evaluated on a sequence of images is also shown in Figure 4 (filled squares). In both cases, the positive values of the correlation difference functions indicate that cells of the same type tend to covary more strongly than cells of opposite polarity at all separations within the receptive field of a typical simple cell.

Fig. 4.

Correlation difference functions estimated in the presence of time-varying natural visual input. The curveswith filled squares and circles are the results of two different approximations of the power spectrum of time-varying natural scenes (see Results for details). The curvemarked by white circles is the average receptive field of a simple cell as measured by Jones and Palmer (1987) shown here for comparison.

These results show that after eye opening the correlated activity of LGN cells derived from the static presentation of natural visual input does not match the structure of simple-cell receptive fields.

LGN activity in the presence of eye movements

In the remainder of this paper we focus on how changes in the visual input attributable to eye movements affect the correlated activity of geniculate cells. As described in Materials and Methods, both macroscopic (voluntary) and microscopic (involuntary) eye movements were modeled following the data available in the literature.

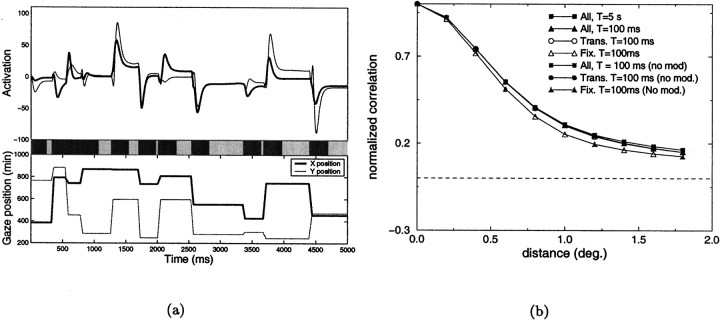
Figure 5 illustrates the results obtained when the images of the database were examined through random sequences of saccades. An example of the activation of two ON-center units with receptive fields separated by 0.8° is shown in Figure 5a. Deviations of neural activity from their resting levels are shown in the top portion of the figure, and the x and y coordinates of the direction of gaze during the considered 5 sec are plotted in the bottom part. The bar in the middle of the figure illustrates two different phases of the neural responses. The light portions of the bar correspond to fixation periods, defined as the time intervals starting 200 msec after the acquisition of a fixation point and ending with the occurrence of a new saccade. Dark segments correspond to the transitory periods occurring between fixations. The measured correlation difference functions are shown in Figure 5b. The curves marked by filled symbols in Figure 5b show the correlation differences obtained when the mean activity of LGN cells ( $\overline{u}$_i and $\overline{u}$_j in Eq. 2) were evaluated over different periods of observation T. Results presented later in the paper will illustrate the potential importance of this parameter. C^D did not change significantly when T was reduced by two orders of magnitude (from 5 sec to 100 msec), despite the fact that the averages of cell activity were estimated over several fixation points with T = 5 sec, and within a single fixation with T = 100 msec. Similar results were obtained when different phases of the neural responses were analyzed separately. The curves marked by open symbols in Figure 5b are the correlation differences estimated with T = 100 msec for the fixation (open triangles) and transitory phases (open circles). No significant differences were found in the case in which no modulation of cell activity was present at the time of saccades (gray symbols in Figure 5b). In all cases studied, the correlation difference function was positive at all of the separations that were considered.

Fig. 5.

Analysis of the correlated activity of LGN cells in the case of saccades. a, Example of the response of two geniculate cells during a sequence of saccades. Neural activity is shown on the top. The curves on thebottom are the x and y coordinates of the direction of gaze. The bar in the middleindicates the two different phases of neural responses: fixation periods are marked by the light segments, transitory periods by dark segments. The receptive fields of the two cells were 0.8° apart. b, Correlation difference functions obtained in the presence of saccades. The results obtained over different time windows and for different phases of the responses are shown in the presence and absence of saccadic modulation of neural activity.

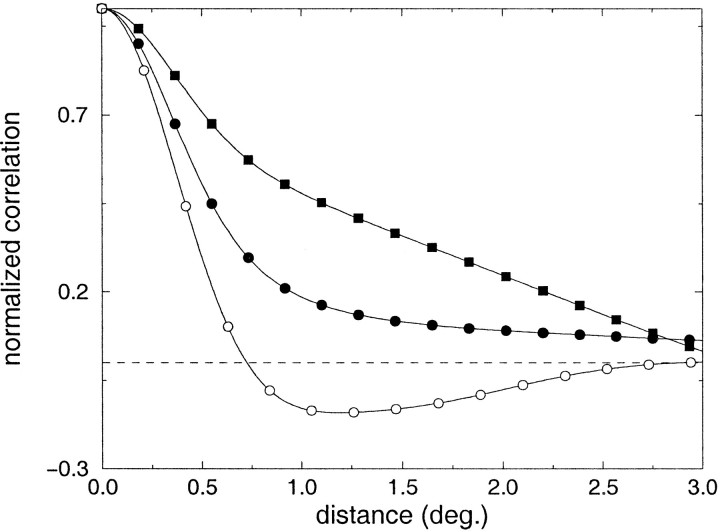
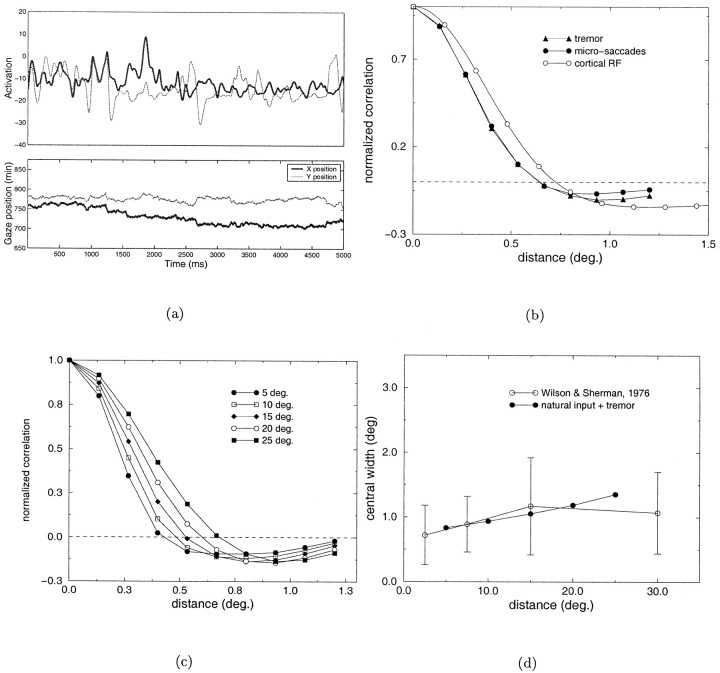
A similar statistical analysis on the joint activity of pairs of geniculate cells for the case of microscopic eye movements is shown in Figure 6. In this experiment, 50 fixation points were randomly selected for each image. Each fixation lasted for a period of 5.5 sec, during which micromovements occurred and cell activity was evaluated. To isolate the contribution of micromovements with respect to that of saccades, correlation functions were evaluated starting 500 msec after the onset of each fixation. Figure6a illustrates an example of the activity of two cells with receptive fields separated by 0.8° during a sequence of micromovements. As before, the spatial parameters of the LGN kernel were chosen so as to model a cat geniculate cell at 17° of visual eccentricity. The two curves marked by filled symbols in Figure 6b illustrate the correlation difference functions obtained for the case of microsaccades (filled circles), and for the joint presence of ocular drift and tremor (filled triangles). Because in these experiments each fixation was maintained for a long period of time, the time window of observation, T, over which the averages of neural activity were evaluated was not an important parameter. For the curves in Figure 6b, T = 5 sec was used. Interestingly, the correlation difference functions measured with the two types of micromovements were very similar. In both cases, strong correlations were found between the activity of LGN cells of opposite polarity with receptive fields located at separations larger than 0.6°, which is similar to the receptive field profile of a typical simple cell. Figure 6c shows the correlation difference functions obtained at different visual eccentricities in the presence of tremor and ocular drift. The minimum separation between receptive fields necessary for observing strong levels of covariance between cells with opposite polarity increased with eccentricity, as illustrated by the points of zero-crossing of the different curves. Figure 6d compares the widths of the central lobe of the estimated correlation functions at the different visual eccentricities with the size of the larger subfield in the receptive field of simple cells as measured by Wilson and Sherman (1976). In contrast to the results of Figure 3a, a close correspondence is now present between the spatiotemporal characteristics of LGN activity and the organization of simple-cell receptive fields.

Fig. 6.

Analysis of the correlated activity of LGN units in the presence of different types of microscopic eye movements. a, Example of the activation of two cells (top graph) during a sequence of microsaccades and tremor (bottom graph). b, Correlation differences in the case of microsaccades (●) and ocular drift and tremor (▴). c, Correlation differences evaluated at different visual eccentricities. d, Comparison between the width of the central lobe of the correlation difference function and the width of the larger subfield in the receptive fields of simple cells at different eccentricities (Wilson and Sherman, 1976).

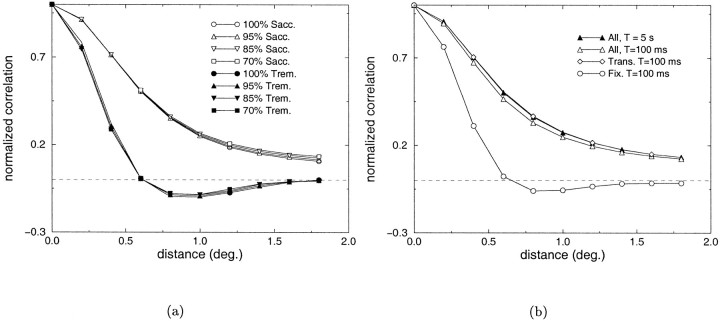
Because the variation of retinal inputs is higher in the presence of saccades than with micromovements (in the simulations, the ratio between the SDs of the input signals in the two conditions was close to 2), it is to be expected that the correlations originating from macroscopic shifts of gaze will prevail when all movements are considered simultaneously. Figure 7 shows the results obtained when the images of the database were examined in the presence of both saccades and micromovements. Sequences of saccades were generated similarly to the experiments of Figure 5, and micromovements were overlapped during fixation periods. Figure7a shows an example of neural activity during a sequence of such movements. In this case, the time window over which the mean activation values are calculated becomes crucial, as illustrated in Figure 7b. In addition to considering the whole sequence of neural activity, geniculate responses in the fixation and transitory phases were also analyzed separately. When the whole response was considered without differentiating between the two phases, the correlation difference was positive at all of the separations considered, independent of the length of the time window of observation. A similar result was also found for the transitory phase. Conversely, strong correlations between the activity of LGN cells of opposite polarity were found during fixation periods, when the covariances were evaluated over a time window of 100 msec. No significant differences were found when neural activity was not modulated during saccades. These results indicate that in the presence of eye movements, a Hebbian scheme of plasticity can account for the organization of simple-cell receptive fields, if synaptic changes are prevented during saccades and the induction of plasticity is sensitive to the covariance of neural activity occurring within a time window smaller than the average fixation.

Fig. 7.

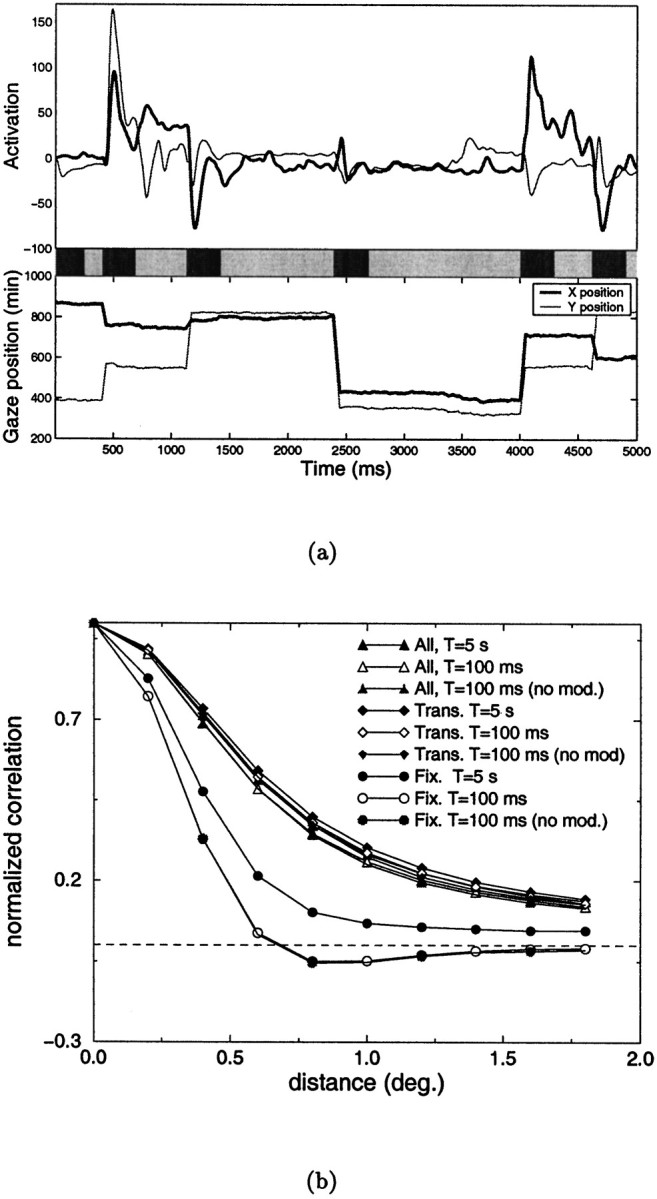
Analysis of the correlated activity of LGN units when both macroscopic and microscopic eye movements are simultaneously present. a, Example of the response of two geniculate units with receptive fields 0.8° apart (top) during a sequence of eye movements including macrosaccades and micromovements (bottom). The bar in the middleindicates the two phases in which responses have been subdivided: fixation periods are marked by the light segments, transitory periods by dark segments. b, Correlation difference functions obtained when the different phases of the response were analyzed separately. Data obtained in the absence of modulation of activity during saccades are also shown.

What factors are responsible for the differences in C^D measured in the presence of saccades and micromovements? Because the kernels used to model LGN cells were identical in the two conditions, corresponding statistical differences should be present in the input visual patterns. An obvious difference between saccades and microscopic eye movements is the spatial scale of the visual analysis involved. When saccades of random amplitude covering the whole input image are performed, retinal inputs depend on the global statistical properties of the visual scene. The amplitude of saccades is on average significantly larger than the separations among receptive fields considered in this paper. Because the broad correlations within natural visual scenes, when areas with different brightness in the input image are swept across receptive fields, visual inputs to nearby retinal receptors tend to vary in a similar way. Given the high speed of saccades, the mean value of such inputs is close to the average brightness of the image even when evaluated over relatively short time windows. As a result, the covariance of the inputs to retinal receptors at different separations evaluated on a time window T is largely determined by the correlation structure of static natural images for a wide range of T. The situation is significantly different in the presence of micromovements, both microsaccades and the combination of ocular drift and tremor. In this case, if a time window shorter than the average fixation is chosen, the broad correlations of luminance typical of natural visual images tend to be discounted by the operation of covariance, because they are largely reflected by the mean levels of cell activity over the considered window. In the presence of a short window of observation, the remaining temporal covariances of input activity depend on the local statistical characteristics of the images around each point, i.e., the covariances in pixel intensities at a spatial scale determined by the extent of micromovements. Because broad luminance covariances are subtracted out by using short time windows, the correlation difference function of geniculate activity tends to be determined by the spatial structure of geniculate cell receptive fields.

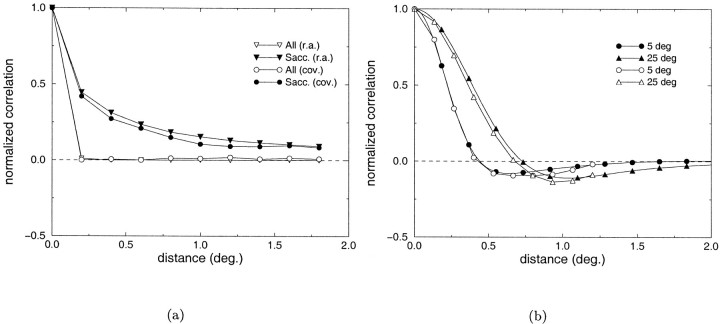
In Figure 8a the correlation coefficients evaluated over 100 msec between inputs to pairs of retinal receptors at different separations are plotted for the two situations of all movements (filled circles) and saccades only (open circles). These data were calculated on a set of 6000 observations, each composed of a time period of 5.5 sec in which the different types of eye movements occurred. The simulated trains of retinal inputs were divided into chunks of 100 msec over which covariances were evaluated. In the presence of ocular drift and tremor, retinal inputs were independent for separations >0.25°, whereas during saccades, retinal inputs remained correlated over large separations. As a result of the reduction in the extent of spatial correlations, in the presence of micromovements the correlation difference evaluated over a similar time window was largely determined by the characteristics of the geniculate kernel. This is shown in Figure 8b, where the correlation difference functions measured at two different visual eccentricities are compared with the autocovariances of the geniculate filters in the two positions. Figure8a also shows the patterns of covariance measured using running averages (filled and open triangles for the two experimental conditions) as in the experiments in Figure 7. These curves are almost identical to those derived on the basis of the covariance on the same time interval. It is important to notice that the data in Figure 8a do not depend on the duration of the experiment, but they are exclusively a function of the window T on which covariances are evaluated or running averages are performed.

Fig. 8.

a, Second-order statistics of the visual input measured in the presence of all movements (open symbols) or saccades only (filled symbols). See Results for details. b, Comparison between the autocovariances of typical LGN receptive fields (filled symbols) and the correlation difference functions (open symbols) obtained at 5 and 25° of visual eccentricity in the presence of micromovements.

In the simulations described so far we have made the assumption that variations in geniculate activity occurred within the linear range. However, in reality LGN responses often deviate from these linear approximations. The main source of nonlinearity is known to originate from the rectification of activity, an operation that eliminates negative firing rates ([.]_θ in Eq. 1). Because neural responses can be significantly different after rectification, it is important to study the patterns of covarying activity in the presence of such operation. Figure 9a shows the effects of different levels of rectification when saccades (open symbols) and tremor (filled symbols) were selectively present. No significant changes were measured in the correlation difference even in the case of a 100% rectification, when the range of negative responses was completely eliminated. Figure9b shows the correlation difference functions obtained for a 100% rectification when both saccades and micromovements were simultaneously present. As shown by the graphs, the patterns of covariance were similar to those of Figure 7b obtained in the absence of rectification.

Fig. 9.

Analysis of the correlated activity of LGN units in the presence of different levels of rectification. a, Correlation difference functions obtained in the cases of saccades and tremor. b, Correlation difference functions obtained with a 100% rectification when both saccades and micromovements were present.

DISCUSSION

In this paper we have used computer modeling to study the correlated activity of LGN cells when images of natural scenes were scanned to replicate cat eye movements. In our simulations, the measured patterns of covarying activity matched simple-cell receptive fields as required by a direct Hebbian/covariance mechanism of synaptic plasticity in the presence of micromovements, but not when natural scenes were statically presented or scanned through sequences of saccades. These results suggest a developmental role for the microscopic eye movements that occur during visual fixations.

Eye movements and the development of cortical orientation selectivity

Although the role of visual experience in the development of orientation selectivity has been extensively investigated, relatively few studies have focused on whether eye movements contribute to the development of the responses of cortical cells. Our finding that the patterns of LGN activity with static presentation of natural images did not match the spatial structure of the receptive fields of simple cells is in agreement with the hypothesis that exposure to pattern vision per se is not sufficient to account for a normal visual development (Buisseret et al., 1978; Freeman and Bonds, 1979; Gary-Bobo et al., 1986; Buisseret, 1995).

A main assumption of this study is that the refinement and maintenance of orientation selectivity after eye opening is mediated by a Hebbian/covariance process of synaptic plasticity (Stent, 1973;Changeux and Danchin, 1976). The term Hebbian is used here with a generalized meaning to indicate the family of algorithms in which modifications of synaptic efficacies occur on the basis of the patterns of input covariances (Sejnowski, 1977; Montague et al., 1991;Cruikshank and Weinberger, 1996). Although no previous theoretical study has investigated the influence of eye movements on the development of orientation selectivity, some models have shown that schemes of synaptic modifications based on the correlated activity of thalamic afferents can account well for the segregation of ON- and OFF-center inputs before eye opening in the presence of suitable patterns of spontaneous activity (Linsker, 1986; Miyashita and Tanaka, 1992; Miller, 1994). By showing that, during fixation, the spatiotemporal structure of visually driven geniculate activity is compatible with the structure of simple-cell receptive fields, the results of the present study extend the plausibility of such schemes to the period after eye opening in which exposure to pattern vision occurs.

The results of our simulations appear to contrast with those of some modeling studies showing that Hebbian mechanisms of plasticity lead to the development of oriented receptive fields when natural images are statically presented (Barrow et al., 1996; Shouval et al., 1997). Although these simulations produced receptive fields that qualitatively resembled those of cortical simple cells, a quantitative comparison like the one in this paper was not performed. It should also be noted that computational studies have shown that the segregation and/or clustering of synaptic inputs may depend on factors other than the patterns of input correlations (Goodhill, 1993; Miller and MacKay, 1994). In particular, a segregation of afferents could occur even in the presence of predominant correlations among cells of the same type, if a rule of synaptic modification based on subtractive normalization is adopted (Miller and MacKay, 1994). However, subtractive normalization has been questioned on the grounds of biological plausibility (Elliott and Shadbolt, 1998). Moreover, our finding of strong covarying activity among cells of opposite polarity during fixation eliminates the need to postulate a specific type of normalization.

As in any modeling study, our results depend on the degree of accuracy with which biological signals are replicated. A number of factors were not present in the model, including sources of correlated activity in the LGN other than shared visual stimulation (Sillito et al., 1994;Alonso et al., 1996; Neuenschwander and Singer, 1996; Dan et al., 1998), and changes in the spatiotemporal characteristics of geniculate responses during growth (Braastad and Heggelund, 1985; Cai et al., 1997). Considerations of this sort emphasize the need to validate the predictions of our study with in vivo experiments. In any case, the results presented in this paper were robust with respect to a number of factors. When the spatial characteristics of simulated geniculate units were changed to replicate the properties of cells in different regions of the visual field, results consistent with physiological data were obtained. Measured patterns of correlation were found to be tolerant with respect to the fine characteristics of simulated eye movements, modulation of activity, and degree of rectification.

Predictions

A first prediction of this study is that the experience of pattern vision in the absence of microscopic eye movements may lead to an impairment in the development of orientation selectivity. Microscopic eye movements occurring during fixation have been studied mainly in humans (Ditchburn, 1973; Steinman et al., 1973), but they are known to occur also in monkey (Skavenski et al., 1975; Leopold and Logothetis, 1998) and cat (Conway et al., 1981; Gomez et al., 1986). Although experiments aimed at selectively analyzing the developmental role of different types of eye movements have not been performed, it is interesting to note that a reduction in the percentage of orientation-selective cells and an increase in the size of simple-cell receptive fields have been found in cats reared under low-frequency stroboscopic illumination (Cynader et al., 1973; Olson and Pettigrew, 1974; Cremieux et al., 1987), a condition that alters the sampling of the visual environment similar to that occurring during an oculomotor manipulation. It has been suggested that such impairment in the development of orientation selectivity could be caused by the prolonged intervals of darkness that make this condition similar to dark rearing. The results described in this paper suggest the possible alternative interpretation that low-frequency stroboscopic illumination could operate by eliminating the effect of micromovements and constraining the spatiotemporal structure of the visual input to be similar to that recorded during sequences of saccades. In the oculomotor behavior of strobe-reared kittens, profound changes selectively affecting fixation eye movements have been reported (Conway et al., 1981).

Additional predictions of this study concern the developmental mechanisms of plasticity. A first observation is that synaptic changes should be affected by the covarying activity of presynapticafferents evaluated over time windows smaller than the average fixation period. Indeed, suitable patterns of covariance were not present in the model when evaluated over longer windows. Although little is known about the length of such intervals, they should not be confused with the longer period of time over which previous postsynapticactivity may influence synaptic plasticity (Huang et al., 1992;Kirkwood et al., 1996). A second observation is that a gating of synaptic plasticity should be present during macroscopic redirection of gaze to prevent a degradation in the segregated structure of geniculate afferents. It has been proposed that experience-dependent modifications of simple-cell receptive fields may be gated by proprioceptive inputs (Buisseret and Singer, 1983). This proposal is consistent with the impairment found in the reestablishment of orientation selectivity in dark-reared kittens exposed to a few hours of visual experience when proprioceptive inputs from extraocular eye muscles were eliminated (Buisseret and Gary-Bobo, 1979; Trotter et al., 1981). There are several plausible ways in which such gating of plasticity could be accomplished. One possibility is that synaptic modifications are minimized during saccades after a reduction of the correlated activity of presynaptic and postsynaptic elements. Given the multiplication of presynaptic and postsynaptic activity postulated by the Hebbian/covariance rules, even a 10% reduction in geniculate activity (Lee and Malpeli, 1998) could be sufficient to preserve segregation if a depression of cortical activity is simultaneously present. A transient depression of neural activity in the striate cortex in conjunction with saccades has been reported (Duffy and Burchfiel, 1975;Toyama et al., 1984). Alternatively, a gating of synaptic plasticity could be achieved by affecting the chain of cellular events after a change in the level of correlation, independent of any direct effect on the correlation itself.

A stimulating hypothesis is that proprioceptive gating of plasticity is mediated by the activity of diffuse-projecting neuromodulatory systems, such as the monoaminergic and cholinergic systems (Singer, 1982). A large body of evidence indicates that the neuromodulators released by these systems play a role in long-term plasticity (Kasamatsu et al., 1979; McGaugh, 1989; Artola and Singer, 1993; Bear and Kirkwood, 1993;Gu and Singer, 1993, 1995), and it is also well established that the activity of these systems is higher in the presence of salient sensory events and in states of arousal (Foote and Morrison, 1987; Aston-Jones et al., 1991; Marrocco et al., 1994; Robbins and Everitt, 1995), conditions likely to occur in conjunction with saccades. In this view, the activation of diffuse-projecting modulatory systems in correspondence with a shift of gaze (Steinfels et al., 1983;Aston-Jones et al., 1991) would enable the occurrence of long-term synaptic changes during the fixation periods after each saccade. We have recently proposed a similar scheme of plasticity, in which synaptic changes are gated by the activity of diffuse-projecting neuromodulatory systems so as to occur after a redirection of gaze, to account for the registration of multimodal maps of space in the optic tectum of the barn owl (Rucci et al., 1997).

Extensions and future directions

The simulations described in this paper were designed to replicate the changes in the visual input that occur during eye movements in the cat. It remains to be studied whether the visual changes induced by other behaviors (for example, head movements and navigation) could have a similar developmental role. It should also be noted that smooth pursuit eye movements were not considered in this study. Smooth pursuit has been observed in naive cats only in complete darkness and for low target velocities (∼2°/sec) (Missal et al., 1995). In the light, cats appear to pursue moving targets with saccades triggered every time the target moves too far from the area centralis. It is conceivable that smooth pursuit may play an important role in the visual development of different species possessing such eye movements.

Although in this paper we have focused on the development of thalamocortical projections, oculomotor activity could also directly influence the development of intracortical connectivity. During fixation, micromovements could foster the development of long-range patchy connectivity by correlating the activity of cells with similar response characteristics. Hebbian mechanisms of plasticity have been proposed to be responsible for the development of the patchy organization of horizontal cortical connections (Katz and Callaway, 1992; Löwel and Singer, 1992; Ruthazer and Stryker, 1996; Troyer et al., 1998). In addition, in monkey striate cortex both depression and facilitation of neural responses have been observed after microsaccades (Leopold and Logothetis, 1998).

Ocular movements are a common feature of the visual system of different species. It should not come as a surprise that a trace of their existence can be found even in some of the most basic properties of neurons in the early stages of the visual system, such as orientation selectivity. Further studies are needed to investigate whether similar traces can be found in other features of visual neural responses.