Occlusion and the Interpretation of Visual Motion: Perceptual and Neuronal Effects of Context

Abstract

Visual motion can be represented in terms of the dynamic visual features in the retinal image or in terms of the moving surfaces in the environment that give rise to these features. For natural images, the two types of representation are necessarily quite different because many moving features are only spuriously related to the motion of surfaces in the visual scene. Such “extrinsic” features arise at occlusion boundaries and may be detected by virtue of the depth-ordering cues that exist at those boundaries. Although a number of studies have provided evidence of the impact of depth ordering on the perception of visual motion, few attempts have been made to identify the neuronal substrate of this interaction. To address this issue, we devised a simple contextual manipulation that decouples surface motion from the motions of visual image features. By altering the depth ordering between a moving pattern and abutting static regions, the perceived direction of motion changes dramatically while image motion remains constant. When stimulated with these displays, many neurons in the primate middle temporal visual area (area MT) represent the implied surface motion rather than the motion of retinal image features. These neurons thus use contextual depth-ordering information to achieve a representation of the visual scene consistent with perceptual experience.

The locally measured motion of a one-dimensional visual image feature, such as an edge, is ambiguous (Wohlgemuth, 1911; Wallach, 1935; Marr and Ullman, 1981). This is known as the “aperture problem.” This ambiguity can, in principle, be overcome by measuring the unambiguous motion of a two-dimensional visual image feature, such as where two edges of a surface meet to form a corner. Many two-dimensional visual image features, however, occur where edges from two different but overlapping surfaces meet. Such compound features are “intrinsic” to neither surface and have been termed “extrinsic” (Nakayama et al., 1989).Shimojo et al. (1989) demonstrated that human observers differentiate intrinsic and extrinsic features on the basis of depth-ordering cues that exist at occlusion boundaries. Furthermore, these investigators discovered that intrinsic features are used to overcome the aperture problem, whereas extrinsic features have relatively little influence. By allowing classification of image features as either intrinsic or extrinsic to a moving surface, depth-ordering cues thus provide a context for the correct interpretation of ambiguous motion information.

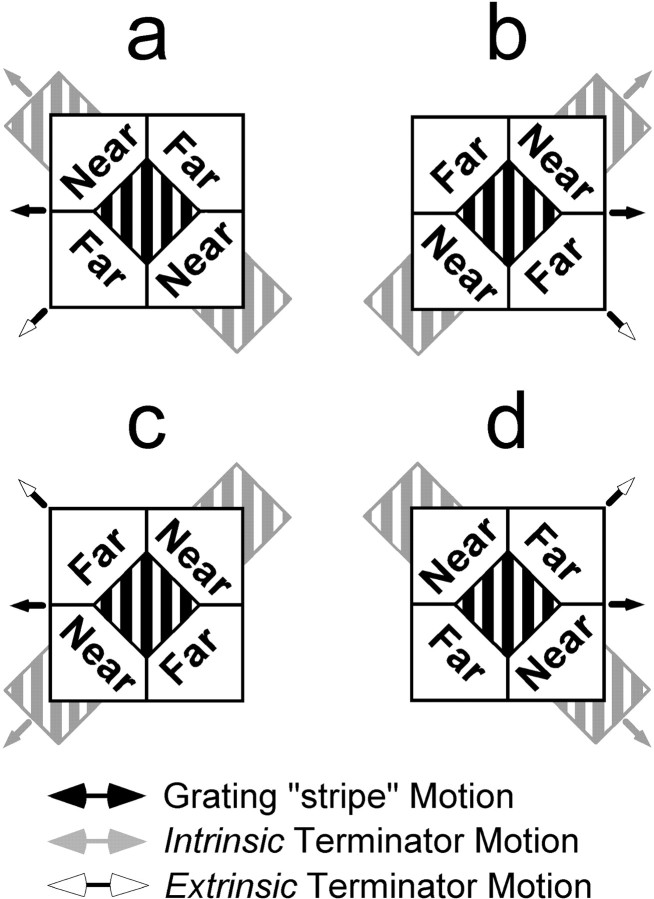
To explore this contextual motion–depth interaction, we developed a variation of the classic barber-pole illusion (Wallach, 1935). Our “barber-diamond” stimuli (see Fig. 1) consist of a moving grating framed by a static, diamond-shaped aperture. Two of the four textured panels that define the aperture are placed in front of the grating via stereoscopic depth cues, and the other two are placed behind. These depth manipulations simulate partial occlusion of the grating, such that features formed by termination of the individual grating stripes at the “far” panels are commonly seen as intrinsic to the grating. In contrast, the features defined by the stripe terminations at the “near” panels generally appear as an accident of occlusion and thus extrinsic to the grating.

Fig. 1.

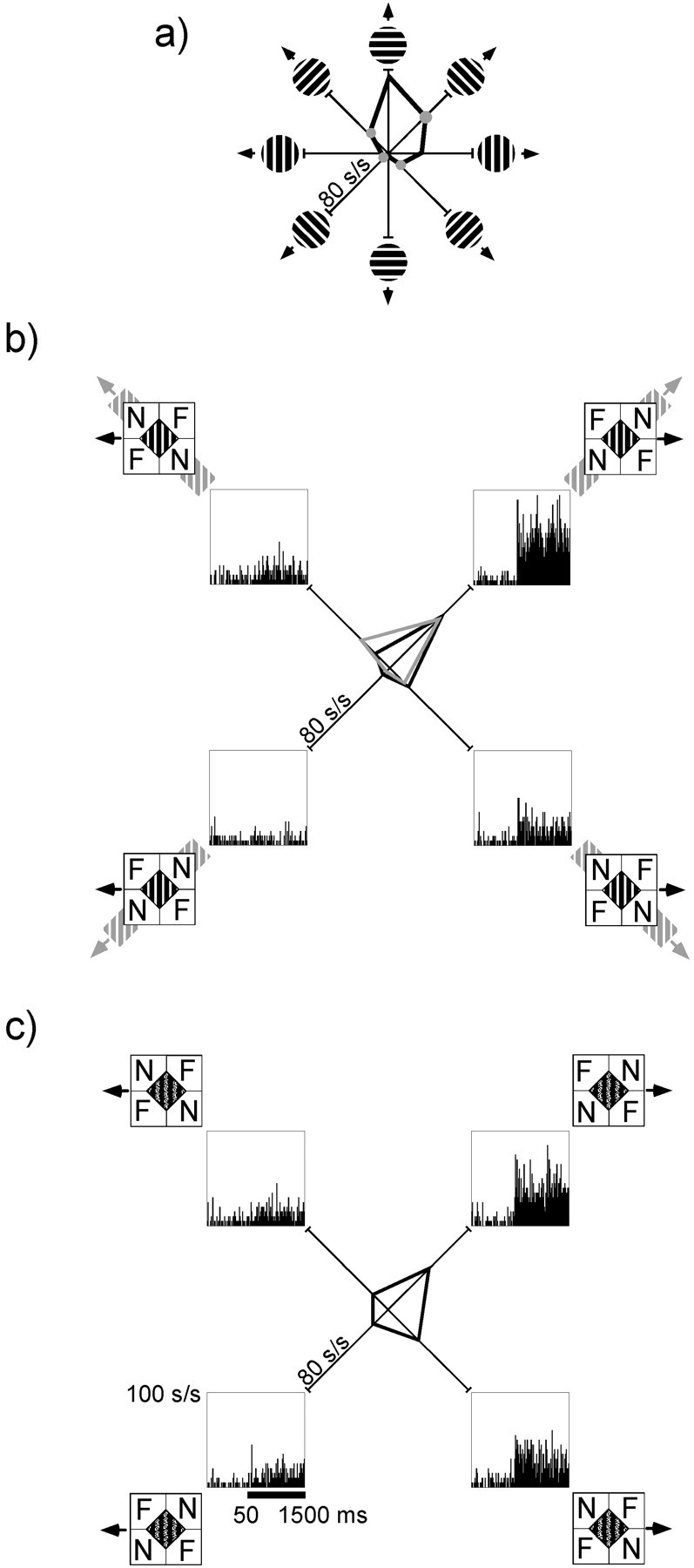
Barber-diamond stimuli were used to study the influence of context on perceived motion and its neuronal correlates (a demonstration can be seen at http://www.cnl.salk.edu/∼gene/). These stimuli consisted of a moving square-wave grating framed by a static, diamond-shaped aperture. The grating itself was placed in the plane of ocular fixation while four textured panels that defined the aperture were independently positioned in depth using binocular disparity cues.Near and Far identify the depth ordering of the textured panels relative to the plane of the grating. Direction of grating motion is indicated by a black arrow. Four stimulus conditions were used (a, b,c, and d). The stimulus conditions were created by the conjunction of two directions of grating motion (leftward, a and c; rightward,b and d) and two depth-ordering configurations (1, a and d; 2,b and c). The line terminators between the perceptually near surface and the grating are classified as extrinsic features resulting from occlusion, and the grating appears to lie occluded behind the near surface (gray). (Note that gray stripes are not part of the stimulus and are used solely to illustrate perceptual completion of the partially occluded grating. Additionally, amodal completion is only one of several ways that depth-ordering cues could affect motion interpretation. See Discussion.) As a result of this manipulation, observers typically perceive the grating as belonging to a surface sliding behind the near regions and across the far regions (direction indicated by gray arrows). This direction is identified with motions of intrinsic terminators. White arrows, on the other hand, indicate the motions of extrinsic terminators.

We hypothesized that movement of the grating would elicit a motion percept that follows the path of intrinsic, but not extrinsic, terminators. In particular, we predicted that a grating with leftward physical motion would be perceived as moving either up-left (see Fig.1a) or down-left (see Fig. 1c), depending on the depth-ordering configuration. Similar predictions were made for gratings that moved rightward (see Fig. 1b,d). Our psychophysical experiments confirmed this hypothesis (a demonstration can be seen at http://www.cnl.salk.edu/∼gene/).

These perceptual effects imply a sophisticated interaction between depth and motion information. The middle temporal area (area MT) of primate visual cortex is a plausible site for this interaction to occur because information about direction of motion and binocular disparity is known to converge within this area (Maunsell and Van Essen, 1983;Bradley et al., 1995; Bradley and Andersen, 1998; DeAngelis et al., 1998; DeAngelis and Newsome, 1999). Accordingly, we examined the sensitivity of MT neurons to the contextual manipulations demonstrated to influence perception. A subset of MT neurons exhibited directional selectivity consistent with perceived surface motion rather than with the motion of the image features present in their receptive field. These cells properly distinguished between the motions of intrinsic and extrinsic terminators on the basis of depth-ordering information. Moreover, we found that depth discontinuities limited to the receptive field surround are sufficient to elicit the observed effects, suggesting that depth-ordering information outside the classical receptive field (CRF) can be used to resolve ambiguous motion information found within.

MATERIALS AND METHODS

General

We conducted psychophysical experiments using human subjects and neurophysiological experiments on monkeys. Visual stimuli, apparatus, and behavioral paradigms were identical for both sets of experiments, except where noted.

Apparatus

All studies took place in a quiet, light-controlled room (ambient light ∼2 cd/m²). Stimuli were generated using a graphics display controller (Pepper SGT+, 640 × 480 pixels, 8 bits/pixel; Number Nine Computer Corp., Cambridge, MA) and displayed on a 17 inch analog red–green–blue video monitor (Superscan Elite 17; Hitachi, Westwood, MA). Each pixel subtended 0.05° of visual angle when viewed from 60 cm. The voltage–luminance relationship of the monitor was measured and used to create linear lookup tables. Stimulus presentation, behavioral control, and data acquisition were controlled by a computer with a Pentium II microprocessor (Gateway, San Diego, CA) using specialized software developed at the Laboratory of Neuropsychology, National Institute of Mental Health (Cortex, version 5.3).

We used stereo goggles with liquid crystal shutters (CrystalEyes PC; Stereographics Corp., San Rafael, CA) to alternately transmit left- and right-eye views of the display monitor at a monocular frequency of 60 Hz. When closed, each lens attenuated all but 6% of the luminance from the image intended for the other eye.

Visual stimuli

Barber diamonds. The methods provided in this section describe the main barber-diamond stimulus used for psychophysical and neurophysiological experiments. Variants of this stimulus were also used for psychophysical experiments and (or) as control stimuli in neurophysiological experiments. Details of these stimuli are described below where appropriate.

The barber-diamond stimulus is illustrated in Figure1. Stimulus conditions, randomly interleaved from trial to trial, consisted of the four possible combinations of two directions of horizontal grating motion (i.e., leftward or rightward) and two depth-ordering configurations. Direction of grating motion and depth-ordering configuration were thus the two independent variables of the main experiment. The dependent variable was either perceived direction of motion (for psychophysical experiments) or neuronal response preference (for neurophysiological experiments).

Barber-diamond stimuli had three distinct sets of moving features: (1) the individual stripes of the grating, which translated either leftward or rightward, (2) the stripe terminators that moved upward 45° relative to the horizontal, and (3) stripe terminators that moved downward 45° relative to the horizontal. We predicted that the depth-ordering cues present in the barber-diamond stimuli would lead to one set of terminators being classified as intrinsic to the grating and the other set as extrinsic. As a consequence, we anticipated that both perceptual and neuronal responses would reflect the direction of surface motion implied by the intrinsic terminators. This direction is determined by the conjunction of the two independent variables and is indicated by the gray arrows in Figure 1. Reversing the depth ordering of the regions surrounding the grating (e.g., changing from the configuration in a of Fig. 1 to that inc) changes the set of grating terminators that should be seen as intrinsic (rather than extrinsic) and hence changes the predicted motion interpretation.

The vertically oriented, square-wave grating of the barber diamond was framed by an equilateral, diamond-shaped aperture spanning 11° from corner to corner. The grating was always at zero disparity relative to the fixation plane and had a spatial frequency of 0.59 cycle/°. Grating contrast was 94%; the mean luminance of the bright bars of the grating was 18 cd/m², and the mean luminance of the dark bars was 0.56 cd/m²(measured with photometer model PR-650; Photo Research, Chatsworth, CA). For a given trial, the grating moved leftward (Fig.1a,c) or rightward (Fig.1b,d) at 6 °/sec. Black arrows in Figure 1 indicate the horizontal motions of the grating.

Binocular disparity was used to position the four surrounding textured regions in near or far depth planes relative to that of the grating. Depth ordering for one condition consisted of a pair of diagonally opposed textured regions with 0.2° crossed disparity and two complementary regions with 0.2° uncrossed disparity (Fig.1a,d). The sign of disparity for each textured region was reversed to create a different depth ordering for the second condition (Fig. 1b,c). Our depth manipulations also included monocular half-occlusions; features of the background surface that lay immediately adjacent to the occlusion boundary were visible to one eye but not to the other (Andersen, 1999; Castet et al., 1999). The relevance of these monocular features to the results reported herein will be addressed in Discussion. A stereogram rendition of a barber-diamond stimulus is shown in Figure2.

Fig. 2.

Barber-diamond stereogram. A stereo pair for one of the depth-ordering conditions in our main experiment (depicted schematically in Fig. 1b,c) is presented. Cross-fusing the two images promotes an illusion of depth ordering between the square-wave grating and the surrounding textured regions. The regions located up-right and down-left relative to the grating should be perceived as foreground surfaces. Conversely, the regions located down-right and up-left relative to the grating should be seen as background surfaces. The zero-disparity grating should be perceived to lie in the middle depth plane.

The random dot textures (50% density) filling the near and far regions had element sizes of 0.05° of visual angle. The space-averaged luminance of these surrounding textured regions was 18 cd/m², which was identical to the mean luminance of the bright bars of the grating. The overall stimulus dimensions, including the surrounding textured regions, were 32° wide × 24° high.

Gratings within a circular aperture. Responses to gratings framed by a circular aperture were used as a benchmark by which to evaluate perceptual and neuronal responses to barber-diamond stimuli. Apart from the circular aperture (11° diameter), these gratings were identical to those of the barber diamonds with respect to spatial frequency, contrast, and speed. These stimuli are hereafter referred to as “circular gratings” to distinguish them from the gratings used to construct barber diamonds. A zero-disparity textured field, otherwise identical to that used for the barber-diamond stimuli, surrounded the circular gratings. Circular gratings moved in each of eight directions: left (180°), right (0°), up (90°), down (270°), up-left (135°), up-right (45°), down-left (225°), and down-right (315°). All of these directions except “up” and “down” correspond to the family of motions in which the barber-diamond grating and its terminators moved.

Monocular control and textured barber diamonds. Both human and monkey subjects observed the barber-diamond stimulus monocularly on a separate set of trials to verify that any perceptual or neuronal effects observed were attributable to stereoscopic depth ordering. In addition, to confirm that neuronal responses to barber diamonds were based on the ability of depth-ordering cues to alter motion interpretation, we included a condition in which the white bars of the grating were replaced with the same texture used for the flanking regions. This textured grating was presented at zero disparity, and the space-averaged luminance of the textured bars (18 cd/m²) matched the space-averaged luminance of the flanking regions, as well as that of the bright bars of the untextured grating. The mean luminance of the dark bars was 0.56 cd/m², which matched the value used for the untextured barber diamonds. The textured grating moved horizontally leftward or rightward. The texture disambiguated the motion of the grating, which we predicted would override the ability of the depth-ordering cues to alter motion interpretation.

Human psychophysical experiments

Subjects. Six naïve psychophysical observers (RD, CL, KS, DE, BG, AV) and one author (ROD), all with normal acuity and stereo vision, participated in our psychophysical experiments.

Apparatus. Each subject's head was stabilized with a chin rest assembly and a bite bar. A noninvasive video pupilometer sampling at 60 Hz (model RK-426; ISCAN, Cambridge, MA) was used to monitor eye position. When monocular viewing was required, we secured a cardboard occluder to the stereo-goggle lens covering the eye that was not monitored by the eye tracker.

Stimuli. We examined the effect of varying aperture size and viewing eccentricity on perceived direction of motion of barber diamonds to assess the robustness of the barber-diamond illusion and to select stimulus parameters compatible with the constraints imposed by neurophysiological experimentation. The first set of experiments used the standard barber-diamond stimulus configuration described above, which was identical to that used for the neurophysiological experiments. Stimuli were positioned at either the center of gaze or a point 10° directly to the right of the point of fixation. Barber-diamond stimuli were always presented at the same central region of the video monitor, and the fixation spot was moved to achieve eccentric viewing. In another experiment, the aperture size was reduced to 5.5° along the diagonal. Viewing for this condition was always foveal.

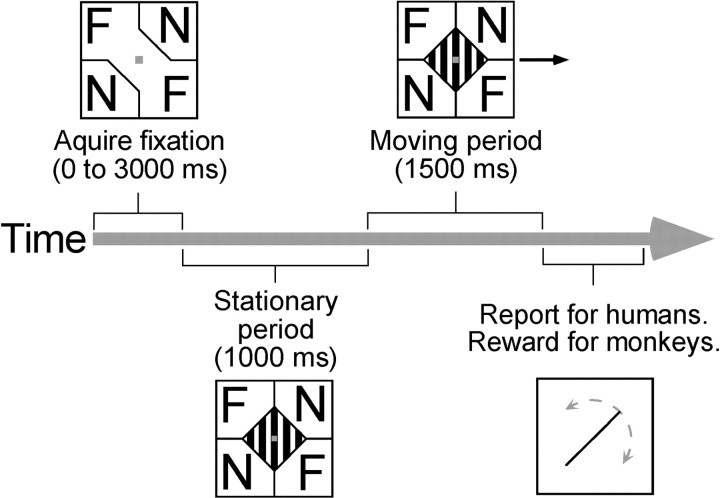
Procedure. Each experiment lasted ∼15 min, and subjects took breaks between experiments to avoid fatigue. The time course of stimulus presentation is depicted schematically in Figure3. For psychophysical experiments using binocular barber-diamond stimuli, trials began with a stereoscopically defined (zero disparity) square (1 × 1°) presented at the center of gaze. After fixation was achieved, this textured square was replaced by a smaller (0.4 × 0.4°) red square, and a stationary version of the barber diamond appeared. [A chromatically defined fixation target was used once the barber-diamond stimulus appeared because the zero-disparity target could not be defined by stereoscopic cues when it was placed within the zero-disparity grating (as was true for all noneccentric viewing conditions; Fig. 1).] For circular gratings and monocular barber-diamond stimuli, the fixation target began as a chromatically defined red square (1 × 1°), which was then replaced by the smaller 0.4 × 0.4° red square. After 1000 msec of static stimulus presentation, the grating (either viewed through the diamond-shaped or circular aperture) moved for 1500 msec. Subjects were instructed to maintain fixation for the duration of each stimulus presentation. Trials were aborted if eye position deviated >0.5° from the fixation target.

Fig. 3.

Time course of stimulus presentation. Barber-diamond trials began with onset of stereoscopically defined 1 × 1° square (zero disparity relative to fixation plane). After fixation of this stereoscopic target was achieved, it was replaced by a 0.4 × 0.4° chromatically defined red target, and a stationary version of the stimulus appeared. After 1000 msec of static stimulus presentation, the grating was moved for 1500 msec. Trials were aborted if fixation deviated >0.5° from the fixation target. Upon successful completion of a trial, human subjects reported the direction of perceived motion by adjusting the orientation of a line (0.05 × 5°) using key presses. Perceived direction of motion was sampled at 15° intervals by this means. Monkeys were not required to make a report but, instead, were given a juice reward at the end of trials during which fixation was adequately maintained. Trial events and procedures were identical for other stimuli used with one exception; for circular gratings and monocular viewing conditions, the fixation target was always chromatically defined.

Each completed trial concluded with a report by the subject of the perceived direction of motion. Subjects made these reports by adjusting the orientation of an elongated bar (0.05 × 5°) using a standard computer keyboard. These reports were sampled with a resolution of 15°. Subjects were instructed to base their judgments on perceived direction during the final epoch of stimulus motion. An interval of 2000 msec was inserted between trials, during which the barber-diamond stimulus was replaced by a randomly textured field at zero disparity.

Analysis. As outlined above, barber-diamond stimuli had three sets of distinctly moving features: (1) horizontally translating stripes, (2) terminators moving 45° upward from the horizontal axis, and (3) terminators moving 45° downward from the horizontal axis. We predicted that our depth-ordering manipulations would lead to one set of terminators being classified as intrinsic and that directional reports in the direction of these terminators (“intrinsic reports”) would outnumber those in the direction of the extrinsic terminators (“extrinsic reports”). Importantly, these predictions were not based on any expectations regarding the frequency of horizontal reports. If intrinsic directional reports were to outnumber extrinsic reports, we would take that as evidence of depth ordering having had the predicted effect on motion interpretation, even if intrinsic reports were exceeded in number by horizontal reports (as reported below, however, this was not found to be the case). To evaluate our hypothesis, we classified reports of perceived direction as horizontal (0°) or oblique. Oblique directional reports were, in turn, classified as having an upward or downward component consistent with either the motion of the intrinsic terminators (intrinsic reports) or with the extrinsic terminators (extrinsic reports). Intrinsic reports were broadly considered to be any direction ±30° from the direction in which the intrinsic terminators actually moved. Extrinsic reports were, conversely, any direction ±30° from the direction in which the extrinsic terminators moved. We evaluated the relative frequencies of intrinsic, extrinsic, and horizontal reports using χ² statistics (Batschelet, 1981).

Neurophysiological experiments

Subjects. One adult male and one adult female rhesus macaque (Macaca mulatta) served as subjects in our neurophysiological studies. Monkeys were screened for refractive error using standard optometric procedures. Protocols used for these experiments were approved by the Salk Institute Animal Care and Use Committee and conform to both United States Drug Administration regulations and National Institutes of Health guidelines for care and use of laboratory animals.

Surgical preparation and training of the animals. Surgical preparation, animal training, and electrophysiological recording procedures were routine and have been described previously (Dobkins et al., 1998; Croner and Albright, 1999; Thiele et al., 1999). Surgical procedures were conducted under aseptic conditions using isoflurane anesthesia. Before training, a stainless steel post was fixed to the skull for the purpose of restraint. Monkeys were secured by the head post in standard primate chairs (Christ Instruments, Damascus, MD) for positioning and to prevent movement. A scleral search coil for measuring eye position was implanted under the conjunctiva of one eye (Robinson, 1963; Judge et al., 1980). Monkeys were trained to fixate a stereo-defined square until they could successfully complete >1000 trials in 2 hr. After the animals reached this behavioral criterion, a stainless steel recording chamber was implanted over the dorsolateral cortex to allow microelectrode access to area MT. The positioning of the chamber was guided by magnetic resonance imaging scans obtained at the University of California, San Diego Center for Magnetic Resonance Imaging.

Apparatus. The liquid crystal shutter goggles used to produce stereoscopic images were identical to those used for human subjects, except for a modification to accommodate the smaller interpupilary distance of monkeys.

Electrophysiological recording. Extracellular potentials from isolated neurons were recorded using microelectrodes (Frederick Haer Co., Bowdoinham, ME). The recorded signal was filtered, amplified, and directed to either an electronic window discriminator (Bak Electronics) or an off-line spike-sorting system (DataWave Technologies, Longmont, CO). Several criteria were used to determine whether the electrode was positioned in MT. First, recording sites had large proportions of directionally selective cells. Second, the size and location of the recorded receptive fields relative to their eccentricity were consistent with known topography (Gattass and Gross, 1981; Van Essen et al., 1981; Desimone and Ungerleider, 1986). Third, the position of the electrode relative to the superior temporal sulcus was determined using previously obtained structural magnetic resonance images.

Initial characterization of response properties. After each neuron was isolated, the receptive field properties were assessed. These measurements were made while the animal fixated on a 0.4° red square on a black background (∼0.1 cd/m²). Receptive field boundaries and preferred direction of motion were determined using a white bar (32 cd/m²) moved under manual control and an audio monitor of neuronal activity. The size, orientation, speed, and position of the bar were adjusted on-line by the experimenter.

Subsequently, the directional selectivity of the neuron was assessed quantitatively using circular gratings. Parameters of these stimuli were as described in General Methods. Circular gratings were centered on the receptive field, and the fixation target was placed so that the receptive field of the neuron was centered on the video screen. These stimuli remained static for the first 1000 msec and then moved within the aperture for an additional 1500 msec. Motion was in one of eight directions, along the cardinal axes and two 45° diagonals. Directions of motion were randomly interleaved across trials.

Barber-diamond stimuli. Barber-diamond stimulus parameters were as described in General Methods and were chosen to generate a robust perceptual illusion while fulfilling our neurophysiological objectives. Aperture size (11°) was thus selected with the goal of confining the textured panels of the barber diamonds to the region outside of the classical receptive field. The spatial frequency of the grating used for these stimuli (0.59 cycles/°) was selected because it is known to elicit vigorous responses from MT neurons (Movshon and Newsome, 1996; Thiele et al., 1999). Our psychophysical studies verified that this set of stimulus parameters, even for peripheral viewing up to 10°, was effective in generating the illusion of perceived motion in the direction of the intrinsic terminators.

Procedure. All visual stimuli, apparatus, and procedures for the neurophysiological experiments were identical to those used for the human psychophysical experiments described above, with the following exceptions. (1) Eye position was recorded using a magnetic scleral search coil system (CNC Engineering, Seattle, WA). (2) Although the time course of stimulus presentation (Fig. 3) was identical to that for humans, monkeys were not required to report perceived direction of motion. (3) Upon successful completion of each trial, monkeys were given a small juice reward (∼0.15 ml). (4) The fixation target was positioned so that the stimulus was centered over the receptive field.

Data analysis. Neuronal responses were measured as the number of action potentials that occurred from 50 to 1500 msec after the onset of stimulus motion. For barber-diamond stimuli, responses were averaged across 10 trials. For circular gratings, responses were averaged across five trials to determine the direction evoking the maximal response (the “preferred” direction).

As discussed in General Methods, the direction of grating motion and the depth ordering of surrounding textured regions were the two principal independent variables in the main neurophysiological experiments; the dependent variable was neuronal response. Responses could be influenced potentially by one or both of these two independent variables and (or) an interaction between them. The proposal that MT neurons encode the motion implied by depth-ordering manipulations leads to two related predictions: (1) the pattern of neuronal responses should reflect an interaction between the two independent variables of these experiments, and (2) neuronal response preference should coincide with the direction of intrinsic terminator motion.

To test the first prediction, we subjected our neuronal data to a two-way ANOVA in which the factors for analysis were depth-ordering configuration and direction of grating motion. This analysis allowed us to identify neurons selective for either of the two primary stimulus variables and for the hypothesized interaction. Significant interaction terms would indicate that responses cannot be accounted for by a simple linear combination of selectivity for horizontal motion and selectivity for depth ordering. Neurons that use depth-ordering information to construct a representation of a moving surface should exhibit this type of interaction. There are, however, two complementary forms of motion–depth interactions possible, only one of which is readily consistent with the recovery of surface motion. A second method of analysis was needed to distinguish between these two possible types of interactions.

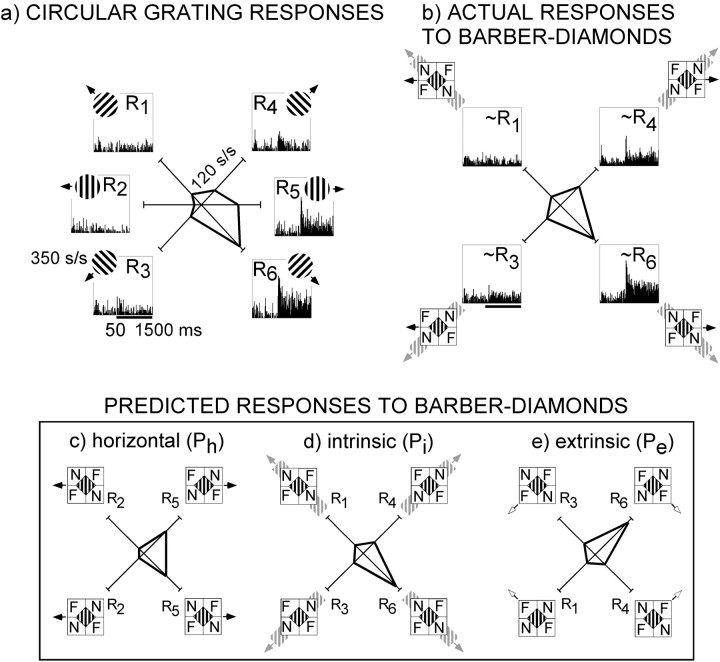
The method we adopted for this purpose involved creation of a unique response prediction for each of the three distinct directions of motion present in our barber-diamond stimuli. These predictions were based on the responses to drifting circular gratings. The procedure we used to create these predictions and to compare them with neuronal responses to barber diamonds is illustrated in Figure4. The responses shown are from a single MT neuron that exhibited a significant motion–depth interaction (ANOVA; p < 0.0001). Figure 4a shows the responses of this neuron to circular gratings, and Figure 4bshows the responses of this neuron to barber diamonds. The “horizontal motion prediction” (P_h) (Fig.4c) corresponds to the barber-diamond responses expected if this neuron were simply encoding the leftward versus rightward motion of the grating. This prediction is based on the observed neuronal responses to leftward (R₂) and rightward (R₅) motions of circular gratings. Because the magnitude of P_h is related to only one of the two independent variables (i.e., the direction of grating motion), its value alone reveals nothing about motion–depth interactions. We accordingly computed two additional predictions that allow characterization of any such interaction as being either consistent or inconsistent with the recovery of surface motion. The “intrinsic motion prediction” (P_i) depicted in Figure4d anticipates that the pattern of responses to the four barber-diamond directions will be similar to that elicited by the four circular gratings moved in the direction of the intrinsic terminators (R₁, R₃, R₄, R₆). P_e, the “extrinsic motion prediction” (Fig.4e), is simply P_i inverted about the horizontal axis and is generated by switching R₁with R₃ and R₄ with R₆. For the neuron illustrated in Figure 4, the pattern of responses elicited by the barber diamond (Fig.4b) appears to match the intrinsic motion prediction better than either the extrinsic or horizontal motion predictions.

Fig. 4.

Influence of depth ordering on direction selectivity of an MT neuron. The receptive field of this neuron was located 4° eccentric to the center of gaze and was 4.5° in diameter. a, Peristimulus time histograms (PSTHs) illustrate neuronal responses to circular gratings moved in each of six directions. Mean responses are indicated on the polar plot atcenter in which polar angle corresponds to direction of stimulus motion and radius corresponds to response amplitude in spikes per second. These responses (R₁–R₆) were used to form three different predictions for barber-diamond stimuli (c–e). b, Actual responses to barber-diamond stimuli. PSTHs for each of the four barber-diamond conditions are presented. The mean responses to moving barber diamonds are plotted in polar coordinates at center. Thebars under the bottom left histograms ina and b indicate the period of stimulus movement. c, Horizontal motion prediction (P_h). Icons illustrate the stimulus configuration for each of four experimental conditions. Predicted neuronal responses to each condition are shown on the polar plot atcenter. This prediction holds that neuronal responses will be influenced solely by the direction of grating motion (black arrows) and, hence, be of the same relative magnitude as responses to circular gratings moved leftward (R₂) and rightward (R₅), regardless of depth-ordering configuration. d, Intrinsic motion prediction (P_i). This prediction holds that responses will be associated with the direction of intrinsic terminator motion (gray arrows) and hence be of the same relative magnitude as responses to circular grating moving in the corresponding oblique directions (R₁, R₃, R₄, and R₆). e, Extrinsic motion prediction (P_e). This prediction holds that responses will be associated with the direction of extrinsic terminator motion (white arrows) and hence be of the same relative magnitude as the intrinsic motion prediction but flipped about the horizontal axis. Observed responses (b) of this neuron to barber-diamond stimuli (R_i‖h = 0.85) were more closely correlated with the intrinsic motion prediction than with either the horizontal or extrinsic motion prediction.

We wished to quantify the correspondence between neuronal responses and the three predictors. This process was complicated by the naturally existing correlations between the three predictions themselves. As exemplified by the data in Figure 4, the two terminator motion predictions, P_i and P_e,typically include biases for leftward versus rightward motion in addition to their upward versus downward motion biases. For this example, all three predictors favor rightward over leftward motion, i.e., they are correlated. To identify the portion of the neuronal response uniquely associated with each prediction, we computed a partial correlation between P_i and the observed neuronal responses, with P_h partialed out. This partial correlation is expressed as

$$R_{\text{i}\Vert \text{h}}=({\text{r}}_{\text{i}}-{\text{r}}_{\text{h}}{\text{r}}_{\text{ih}})/((1-{\text{r}}_{\text{h}}^2)(1-{\text{r}}_{\text{ih}}^2){)}^{0.5}$$

where R_i‖h, the “intrinsic correlation coefficient,” is the partial correlation between P_i and the data with the contribution of P_h removed, r_i is the correlation between P_i and the data, and r_h is the correlation between P_h and the data, and r_ih is the correlation between P_i and P_h. R_e‖h, the partial correlation between P_e and the data with the contribution of P_h factored out can likewise be computed by exchanging P_i and P_e. Because P_i and P_e are mirror images of each other about the horizontal axis, however, this turns out to be unnecessary; R_i‖h and R_e‖h always have the same magnitude but opposite sign. Consequently R_i‖h has the advantageous property that a positive coefficient suggests selectivity for motion in the direction of the intrinsic terminators, a negative coefficient suggests selectivity for motion in the direction of the extrinsic terminators, and a coefficient of zero indicates neuronal selectivity for left–right motion exclusively. R_i‖h thus captures, in a single measure, the correspondence between neuronal response and each of our three direction of motion response predictions. The partial correlation for the example shown in Figure 4is 0.85, which confirms that the form of motion–depth interaction exhibited by this neuron is consistent with a representation of intrinsic feature motion.

It should be stressed that it is the sign rather than the magnitude of the partial correlation coefficients that chiefly concerns us. This is because we expect imperfect correlation simply as a result of the trial-by-trial variation in neuronal response magnitudes. Thus, even if all area MT neurons were exclusively selective for intrinsic terminator motion, we should expect the average coefficient to be <1.0. How much less is difficult to determine (and obviously depends on the number of trials collected). For that reason, we have refrained from imposing any interpretation upon the magnitude of these coefficients.

Neuronal database

Detecting neuronal selectivity for the implied direction of surface motion in our paradigm obviously requires that a neuron be directionally selective. Another requirement is that the neuron not be exclusively selective for motion along the horizontal axis. Another way of expressing these two constraints is that P_iand P_h must be sufficiently different from one another. We screened neurons for this difference by comparing, via two-way ANOVA, the grating responses used to generate the two predictors. The first factor compares the P_i and P_h predictions. The second factor includes the four barber-diamond conditions that represent the conjunction of the two directions of grating motion and the two depth configurations. A significant ANOVA interaction implies that the terminator and horizontal predictions are neither identical nor simply scaled versions of one another. Graphically, this interaction can be revealed by plotting the two response predictions (the first factor) as a function of the four barber-diamond conditions (the second factor). To the extent that the two curves intersect or diverge, the two factors have some degree of interaction. Neurons with an interaction were selected for further study. As expected, rejected neurons (37%) were either poorly directionally tuned or primarily selective for motion along the horizontal axis.

RESULTS

Human psychophysical experiments

We wished to assay the ability of depth-ordering manipulations to alter perceived direction of motion. In addition, we sought to determine the range of stimulus parameters over which this ability extended. We predicted that these contextual manipulations would disambiguate the direction of motion of the barber-diamond grating such that it would be seen to move in the direction of its intrinsic terminators.

Responses to circular gratings

Directional judgments for circular gratings were recorded to obtain a yardstick by which responses to barber-diamond stimuli could be compared and to train subjects to make such reports. Each of the seven subjects reported motion perpendicular to the orientation of the grating on over 98% of the trials. The few remaining reports were within 30° of this direction.

Responses to barber diamonds

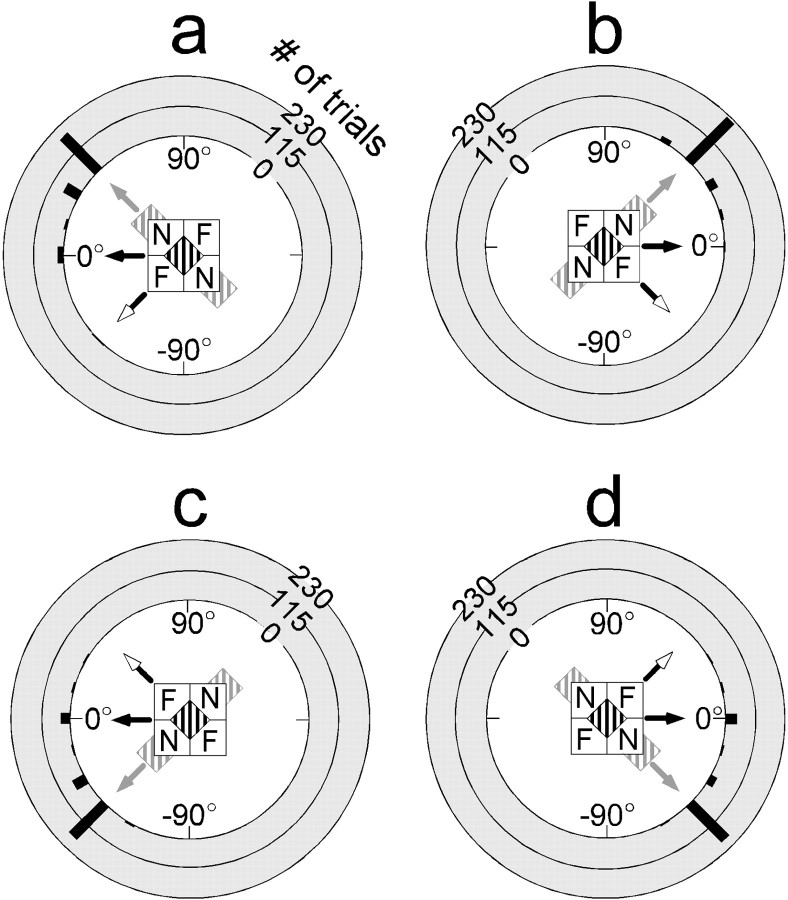
The perceptual effect elicited by the barber-diamond stimuli was striking. Figure 5 illustrates the cumulative responses for all seven subjects who observed foveally presented barber diamonds with apertures spanning 11° across their diagonal. Each of the four stimulus conditions represents the conjunction of one of two directions of grating motion and one of two depth-ordering configurations. Each panel of Figure 5contains a polar frequency distribution of directional judgments for one of the four barber-diamond stimuli in which the polar axis represents perceived direction of motion and the radial axis represents number of trials. Approximately 89% of the responses were classified as intrinsic reports (i.e., ±30° from the direction in which the intrinsic terminators moved; see Materials and Methods). The majority of these responses (69%) were within 15° of the direction of intrinsic terminator motion. Nine percent of the reported directions were along the horizontal axis. Only 1% of 640 total responses were extrinsic reports (i.e., ±30° from the direction consistent with the motion of the extrinsic terminators). The difference between the number of intrinsic versus extrinsic reports was highly significant (χ²; p < 0.0001).

Fig. 5.

Perceptual responses to centrally presented barber diamonds. Stimuli possessed 11° apertures and gratings of 0.59 cycles/°. Data were obtained from seven human subjects (RD, CL, KS, DE, BG, AV, and ROD). a–d depict responses to a particular barber-diamond condition as indicated byicons. Black arrows indicate direction of grating motion for each condition. N andF indicate crossed- and uncrossed-disparity regions that make up each depth-ordering configuration. Each barber-diamond condition consisted of a different combination of grating motion (left,a and c; right, b andd) and depth-ordering configuration (aand d, or b and c). The implied direction of surface motion (intrinsic terminator motion) that results from these combinations is indicated by gray arrows. White arrows indicate the direction of extrinsic terminator motion. For each graph, the direction of motion reported is plotted on the polar axis, and the frequency of responses for each direction is plotted on the radial axis (black bars). Left–right perceived motion is indicated on the horizontal axis, and up–down motion is represented on the vertical axis. Each subject participated in 40 trials per condition (n = 1120). Most of the reports for each condition were biased in the direction of the intrinsic terminators (89% overall). Sixty-nine percent of these reports were 45° away from the horizontal axis in the predicted direction. Each condition elicited a lesser but notable portion of reports for motion consistent with horizontal motion of the grating stripes (9% overall).

Responses made by four subjects (KS, CL, RD, ROD) who viewed barber diamonds at 10° eccentricity were very similar to those found for foveal viewing (Fig. 6). To facilitate visual comparison, the psychophysical responses to the four barber diamonds presented at the center of gaze are plotted again (Fig.6a) as a single summary histogram. The histogram represents the combined responses to all four conditions for all seven subjects. Responses were aligned with respect to the three responses predictions (i.e., intrinsic, horizontal, and extrinsic). The responses to barber diamonds presented at 10° eccentricity are presented in Figure6b using the same plotting convention. For the later condition, 82% of the reports of perceived motion followed the path of the intrinsic terminators (±30°), and 47% of these reports were within 15° of the prediction. In contrast, 16% were in the horizontal direction, and only 2% were in the extrinsic direction (±30°). The difference between the numbers of intrinsic versus extrinsic reports was highly significant (χ²; p < 0.0001). Because viewing eccentricity never exceeded 10° in our neurophysiological experiments, these psychophysical data demonstrate that the barber-diamond illusion is robust over the conditions used to evaluate neuronal selectivity.

Fig. 6.

Perceptual responses to barber diamonds presented centrally and in the periphery. Each panel contains a summary response histogram in polar coordinates for two psychophysical experiments: a, foveally presented barber-diamonds;b, peripherally presented barber diamonds. For each viewing condition, responses were collapsed across all four barber-diamond conditions (i.e., up-left, down-left, up-right, down-right) and aligned with respects to three predictions (i.e., P_i, P_e, and P_h). a, Foveally presented barber diamonds. Responses for seven subjects to foveally presented barber diamonds are aligned and replotted from Figure 5 as a summary histogram. All other plotting conventions remain the same.b, Peripherally presented barber diamonds. Summary histogram presents data from four human subjects (RD, CL, KS, and ROD). The proportions of responses for intrinsic motion (82%), extrinsic motion (2%), and horizontal motion (16%) are visually similar to those for foveally viewed barber diamonds (a). The number of intrinsic reports similarly exceeds that of extrinsic reports (χ²; p < 0.0001).

Responses made by the same four subjects to barber diamonds with 5.5° apertures were similar to those for larger (11°) apertures; 79% of the reports of perceived motion followed the path of the intrinsic terminators (±30°). Only 18% were in the horizontal direction. The difference between the numbers of intrinsic versus extrinsic reports was highly significant (χ²;p < 0.0001).

Textured barber-diamond control

In our neurophysiological experiments, we wished to be certain that apparent neuronal selectivity for the implied surface motion of the barber diamond did not reflect a motion–depth interaction unrelated to motion interpretation. To achieve this goal, we superimposed a random texture on the moving grating of the barber diamond. As expected, this unambiguously moving texture captured the perceived motion of the grating for the four subjects tested (DE, BG, AV, ROD), completely eliminating the influence of the depth-ordered surround; 99% of the reports were for either leftward or rightward motion. This psychophysical finding validates the use of the textured barber diamond as a control in our neurophysiological experiments.

Monocular viewing of the barber diamond

To confirm that perceived direction of barber-diamond motion was dependent on binocular depth cues, we examined direction judgments of four human observers (DE, BG, AV, ROD) under monocular viewing conditions. Eighty-eight percent of the reports were for horizontal motion, 5% of the reports were for intrinsic motion, and 7% of the reports were for extrinsic motion. The marked reduction in reports of intrinsic motion under monocular viewing conditions led us to conclude that the perceived direction of motion for binocular barber diamonds depends on depth cues.

Neurophysiological experiments

We asked whether MT neurons simply encoded the horizontal motion of the grating or (more interestingly) were selective for either the motion of the intrinsic or extrinsic terminators of that grating.

Neuronal responses to barber diamonds

We analyzed data from 265 MT recording sites, in two alert, fixating rhesus monkeys. The majority (63%) of these recordings were from isolated single units. The remaining recordings were judged to be from small clusters of two or more neurons (multi-units). No obvious difference in response to our manipulations was seen for single versus multi-unit recordings, and the data have therefore been pooled.

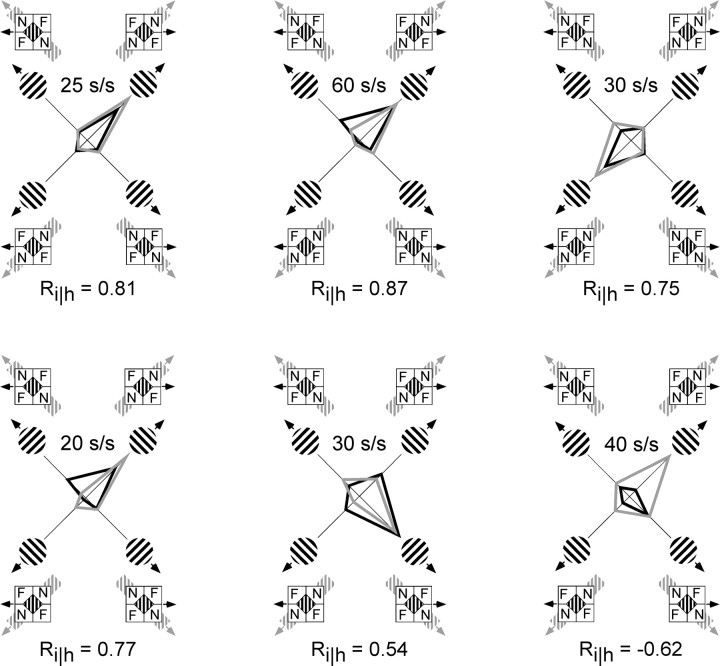
Data from one neuron are illustrated in Figure 4. This neuron, which was discussed above (see Materials and Methods) to introduce our method of analysis, showed a significant motion–depth interaction (two-way ANOVA; p < 0.0001) consistent with the intrinsic motion prediction. The responses of six additional representative MT neurons are depicted in Figure 7.Black lines connect the neuronal responses predicted by P_i. Actual responses to barber-diamond stimuli are connected by gray lines. Each of these neurons had significant motion–depth interactions (two-way ANOVA; allp < 0.0004), indicating that responses could not be accounted for by a simple linear combination of selectivity to leftward versus rightward motion and selectivity for one of the two depth-ordering configurations. Five of the neurons illustrated exhibited a positive R_i‖h and hence behaved in a manner consistent with the intrinsic motion prediction. The cell in the bottom right is an example of a cell with a negative correlation coefficient; the responses of this neuron were consistent with selectivity for the motion of the extrinsic terminators (P_e is not shown but is simply P_i reflected about the horizontal axis).

Fig. 7.

Barber-diamond responses from six MT neurons, each of which demonstrated significant motion–depth interactions. Five of these neurons had positive intrinsic correlation coefficients, and one neuron had a negative coefficient (bottom right). Responses to circular gratings were averaged across five trials and plotted in polar coordinates (black lines). The direction of motion for each grating condition is indicated by theicons along the polar axis, and the mean response to each condition is plotted along the radial axis. Responses to each barber-diamond condition were averaged across 10 trials and were plotted along with corresponding icons on the same graphs (gray lines). Each of these neurons demonstrated individually significant responses to barber diamonds that were configured to elicit upward versus downward motion (ANOVA; allp < 0.0004). Neurons with positive coefficients (R_i‖h) have directionally selective responses consistent with the direction of motion of the intrinsic terminators. See also legend to Figure 4.

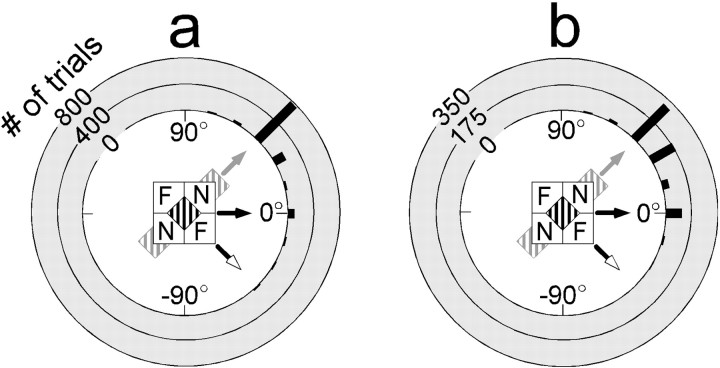
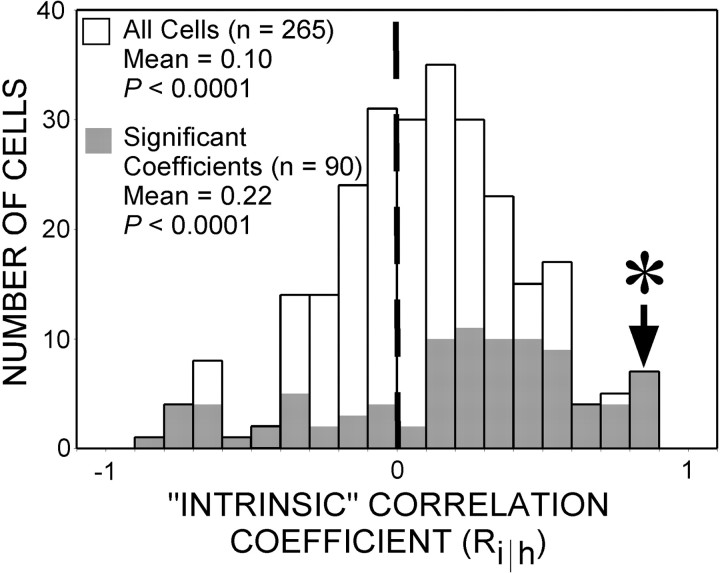
Thirty-four percent (90 of 265) of the sampled units had significant motion–depth interactions (two-way ANOVA; all p < 0.05). The distribution of correlation coefficients for these units is plotted in Figure 8 (gray bars). This subset of neurons exhibited a very strong bias in favor of positive correlation coefficients; 74% (67 of 90) exhibited positive correlation coefficients (median of 0.4), and the remaining coefficients were negative (i.e., anti-correlated with P_i and thus positively correlated with P_e). This bias in the number of positively versus negatively correlated responses was highly significant (χ²; p < 0.0001), which suggests MT neurons, or a portion thereof, encode the direction of motion implied by our contextual manipulations and is consistent with perceptual experience.

Fig. 8.

Population data. Distribution of intrinsic correlation coefficients for the sample of 265 MT neurons studied (white bars). The subset of cells for which coefficients reached statistical significance (ANOVA; all p < 0.05) is indicated by the gray bars. Positive coefficients (R_i‖h) reflect a positive correlation with the motion of intrinsic terminators. The population as a whole displays a significantly positive shift in the mean (0.10) for intrinsic correlation coefficients (t test; p< 0.0001). The population of individually significant cells displays a larger number of positive coefficients (n = 67) relative to negative ones (n = 23).Asterisk denotes coefficient for neuron illustrated in Figure 4. For the entire sample of 265 neurons, mean eccentricity of receptive field centers was 5.5°, and mean receptive field diameter was 5.4°.

An interesting question is whether neurons with significant motion–depth interactions constitute a distinct subpopulation. In an attempt to address this question, we applied our correlational analysis to the entire population of 265 neurons. The resultant distribution was normal without any obvious modes that might suggest distinct subpopulations (Fig. 8, white bars). Moreover, the distribution of correlation coefficients for the population of neurons that did not exhibit individually significant motion–depth interactions had a significant shift (t test;p = 0.02) in favor of positive correlation coefficients (although much reduced relative to neurons with positive significant motion–depth interactions; median of 0.04). Based on these analyses, we cannot draw any conclusions as to whether a distinct set of MT neurons exists that use depth-ordering cues to reconstruct visual motion (see Discussion).

We next addressed the question of whether some of the observed motion–depth interactions might reflect visual processes unrelated to the implied motion of the grating. This has special significance with regard to the interpretation of negative coefficients.

Neuronal responses to textured barber diamonds

Previous experiments have shown that many MT neurons are modulated by differential disparity between the CRF and the non-CRF (Bradley and Andersen, 1998). The barber-diamond stimuli used in the present experiments possess such differential disparity and, indeed, we found evidence for this type of modulation; 40% of our neurons were significantly selective for one of the two depth-ordering configurations (two-way ANOVA; p < 0.05). Bradley and Andersen (1998) also found that a small percentage of area MT neurons show motion–depth interactions unrelated to the perceived direction of motion. To assay the contribution of such motion–depth interactions in our experiment, we superimposed a random texture on the moving grating of the barber diamond. As reported above, this unambiguously moving texture captured perceived motion for human observers, thereby eliminating the impact of the depth-ordered surround on motion interpretation.

The responses of a single MT neuron that was presented with both textured and untextured barber diamonds are illustrated in Figure9. Similar to our previous examples (Figs. 4, 7), this neuron exhibited a pattern of responses to untextured barber diamonds with a significant motion–depth interaction (two-way ANOVA; p < 0.0001) that agreed with the intrinsic motion prediction (R_i‖h = 0.87) (Fig.9b). In contrast, addition of texture eliminated the motion–depth interaction (two-way ANOVA; p = 0.56); responses were not significantly correlated with the intrinsic motion predictor (R_i‖h = 0.46) (Fig.9c).

Fig. 9.

Responses of an MT neuron to textured barber diamonds. a, Neuronal responses to circular gratings moved in each of eight directions. Gray dots indicate responses used to form intrinsic motion prediction. b, Responses to untextured barber diamonds. Mean responses corresponding to intrinsic motion prediction are replotted in gray. Mean responses to untextured barber diamonds are plotted inblack. Peristimulus time histograms illustrate observed responses to each of four barber-diamond conditions. As predicted, this cell responds significantly more (ANOVA; p < 0.0001) to conditions in which barber diamonds were configured to elicit a percept of upward motion rather than downward motion (R_i‖h = 0.87). c, Responses to textured barber diamonds. Arrows indicate typical perceived motion for humans when the same four barber-diamond conditions are superimposed with unambiguously moving texture. Responses of this cell no longer exhibited a significant (ANOVA;p = 0.56) motion–depth interaction, and the intrinsic motion prediction (R_i‖h) was 0.46. See also legend to Figure 4.

Sixty-seven neurons were studied using both the standard and textured barber diamonds; the distribution of intrinsic correlation coefficients (R_i‖h) is plotted in Figure10 for both stimulus types. For this sample, the number of significant motion–depth interactions found in response to the textured barber diamonds was significantly reduced (χ²; p = 0.0003) relative to standard barber diamonds (10 vs 37%). Neuronal motion–depth interactions were thus detected mainly under those conditions in which depth ordering was capable of altering perceived motion for human observers. This finding stands in sharp contrast to the number of neurons that were found to be selective for depth configuration alone. This number was essentially the same (χ²; p = 0.72) for both stimulus conditions (33% for textured barber diamonds and 36% for untextured barber diamonds). Therefore, unlike selectivity for particular conjunctions of depth and motion, selectivity for depth configuration appears to be unrelated to motion interpretation. Furthermore, positive correlation coefficients (n = 43) outnumbered negative coefficients (n = 24) when neurons were shown the standard barber diamond (χ²; p = 0.02) but not when neurons were shown the textured barber diamond (n = 33 vs 34;χ²; p = 0.9). We conclude therefore that the number of significant motion–depth interactions and the dominance of positive over negative intrinsic correlation coefficients observed in the main experiment reflect the neuronal recovery of surface motion.

Fig. 10.

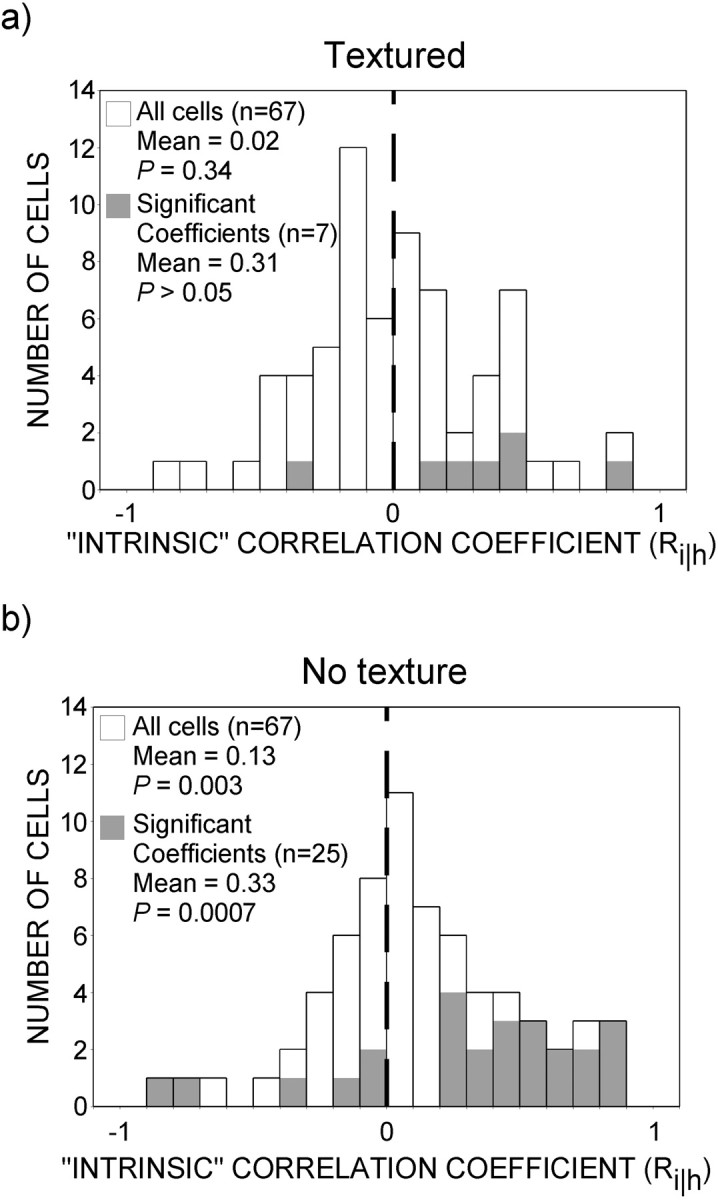
Responses to textured versus untextured barber diamonds for a subpopulation of neurons. Distribution of intrinsic correlation coefficients for the sample of 67 MT neurons that were studied using textured and untextured barber diamonds (outlined bars). The subset of cells for which coefficients reached statistical significance (ANOVA; all p < 0.05) is indicated by gray bars. Positive coefficients (R_i‖h) reflect a positive correlation with the motion of intrinsic terminators. a, Population responses to textured barber diamonds. The mean (0.02) for the distribution of coefficients for cells when textured barber diamonds were presented was not significantly different from zero (t test;p = 0.34). The number of positive (n = 33) and negative (n = 34) coefficients was not significantly different (χ²;p = 0.9). The mean (0.31) of the distribution of coefficients for individually significant cells was not significantly different from zero (t test; p > 0.05). b, Population responses to untextured barber diamonds. The population as a whole displayed a significantly positive shift in the mean (0.13) for intrinsic correlation coefficients (t test; p = 0.003). Additionally, there were more positive coefficients (n = 43) compared with negative ones (n = 24) (χ²; p = 0.02). The mean (0.33) for the population of individually significant cells was significantly positive (t test;p = 0.0007), and the distribution displayed a larger number of positive (n = 19) coefficients than negative (n = 6) ones (χ²;p = 0.009). The mean for the distribution of coefficients for the untextured condition was significantly greater than the mean for the distribution for the textured condition (t test; p = 0.0002). Moreover, the number of individually significant responses to textured barber diamonds was significantly reduced relative to that for untextured barber diamonds (χ²; p = 0.0003).

In the main experiment, we found that the percentage (8.7%) of the neuronal population that exhibited significant motion–depth interactions with negative intrinsic correlation coefficients was greater than that expected by chance (based on a 0.05 criterion, we expected 2.5% for positive and 2.5% for negative coefficients). An interesting question is whether these negative coefficients truly reflect selectivity for motion of the extrinsic features or, alternatively, indicate a motion–depth interaction unrelated to motion interpretation (such as detecting image discontinuities, see Discussion). Evidence bearing on this question comes from the textured barber diamond control. Because the addition of texture eliminated the ability of depth ordering cues to influence motion perception in human observers, the significant neuronal motion–depth interactions associated with the textured barber diamond presumably reflect processes unrelated to the recovery of surface motion. The number of these interactions (of both types) found for the textured barber diamonds is slightly more than expected by chance (10% vs the 5% expected based on the 0.05 criterion). Negative coefficients were, however, slightly more prevalent in our main experiment than for the textured control. We are thus left with the possibility that some of the negative coefficients found in the main experiment may reflect selectivity for motion of the extrinsic terminators. This intriguing notion requires further experimentation to resolve.

Neuronal responses to monocular components of barber-diamond stimuli

To confirm that our results depended on binocular depth cues, we examined the responses of neurons under monocular viewing conditions. Monocular viewing, for human observers, resulted in directional reports predominately along the horizontal axis and completely eliminated the intrinsic versus extrinsic bias found with binocular viewing. Sixty-two neurons were studied using both the standard and monocular barber diamonds. The number of cells with significant motion–depth interactions for standard barber diamonds (39%) was significantly greater (χ²;p < 0.0001) relative to monocular (for which “depth” refers to that of the corresponding binocularly viewed stimuli) barber diamonds (8%). As expected, the number of positive (n = 17) coefficients for the individually significant responses to the barber-diamond stimuli was greater than the number of negative (n = 7) coefficients (χ²; p = 0.04). In contrast, there were not enough cells (n = 5) with individually significant responses to the monocularly viewed barber diamonds to conduct a χ² test. It is also important to note that the mean (0.04) for the distribution of coefficients corresponding to monocular viewing conditions was not significantly different from zero (t test; p= 0.08), whereas the mean (0.11) for the binocularly viewed barber diamonds was significantly shifted (t test;p = 0.01). We conclude that both the contextual influence on perceived surface motion and the presumed neuronal correlates of this phenomenon are attributable to the binocular depth cues present in our stimuli.

Possible effects of vergence angle

The diamond-shaped aperture of our barber-diamond stimuli spanned 11° between opposing corners. As a consequence, for neurons with CRF centers further than ∼5° eccentric to the center of gaze, the zero-disparity fixation target was unavoidably positioned within one of the flanking regions that was not at zero disparity (i.e., either a near or a far region, depending on which depth-ordering configuration was present). It is possible that vergence angle was influenced by this non-zero disparity. If that were the case, retinal disparity within the CRF could vary as a function of depth-ordering configuration. It follows that an MT neuron selective for binocular disparity might therefore give different responses to our two depth-ordering configurations, not because of disparity differences between the CRF and the surround per se, but because of unintended differences in CRF disparity alone. It is furthermore conceivable that significant neuronal interactions between motion and CRF disparity might exist.

Because we only monitored the position of one eye of each monkey, we cannot rule out the possibility that the different barber-diamond stimulus conditions elicited different vergence angles. Several lines of evidence argue against this possibility, however. First, although differential vergence angles might render neuronal selectivity for one of our two depth-ordering configurations, it is difficult for this potential confound to account for the observed interaction between direction of motion and depth-ordering selectivity. Second, even if differential vergence did lead to such an interaction, there is no principled means by which it could consistently yield neuronal selectivity coincident with our intrinsic motion prediction. Third, textured barber diamonds produced far fewer significant motion–depth interactions than did the standard barber diamonds despite the fact that the potential for differential vergence was the same for both stimulus types. Finally, unlike the case for standard barber diamonds, no bias in positive versus negative coefficients was found in the texture control experiment. Thus, we believe that differential vergence angles, if they did exist, are unlikely to account for the finding of motion–depth interactions and neuronal selectivity consistent with the motion of the intrinsic terminators.

Nevertheless, to explore further the potential impact of vergence angle, we separately analyzed data from 93 cells whose receptive fields were close to the fovea. For these neurons, the region immediately surrounding the zero-disparity fixation spot (1.5–4° depending on the distance between the CRF center and the barber diamond aperture) was at zero disparity for all stimulus conditions. The state of vergence, if it varied at all, was expected to vary much less under these conditions than for the cases in which the fixation spot was surrounded by a region of non-zero disparity. Thirty percent of the neurons in this population (n = 28) demonstrated significant motion–depth interactions (Fig.11a) compared with 36% of the neurons (n = 62) with more peripheral receptive fields (Fig. 11b). The mean (0.09) of the distribution of correlation coefficients for cells under foveal viewing conditions was significantly positive (t test; p = 0.002), and the number of positive coefficients (n = 58) was greater than the negative (n = 35) (χ²; p = 0.02). A comparison between the distribution of correlation coefficients for foveal neurons and those in which the fixation spot was beyond the stimulus aperture (mean of 0.11) revealed no difference (t test; p = 0.72). Thus, we see no evidence that differential vergence angle can account for the finding that neuronal responses are consistent with the intrinsic motion prediction.

Fig. 11.

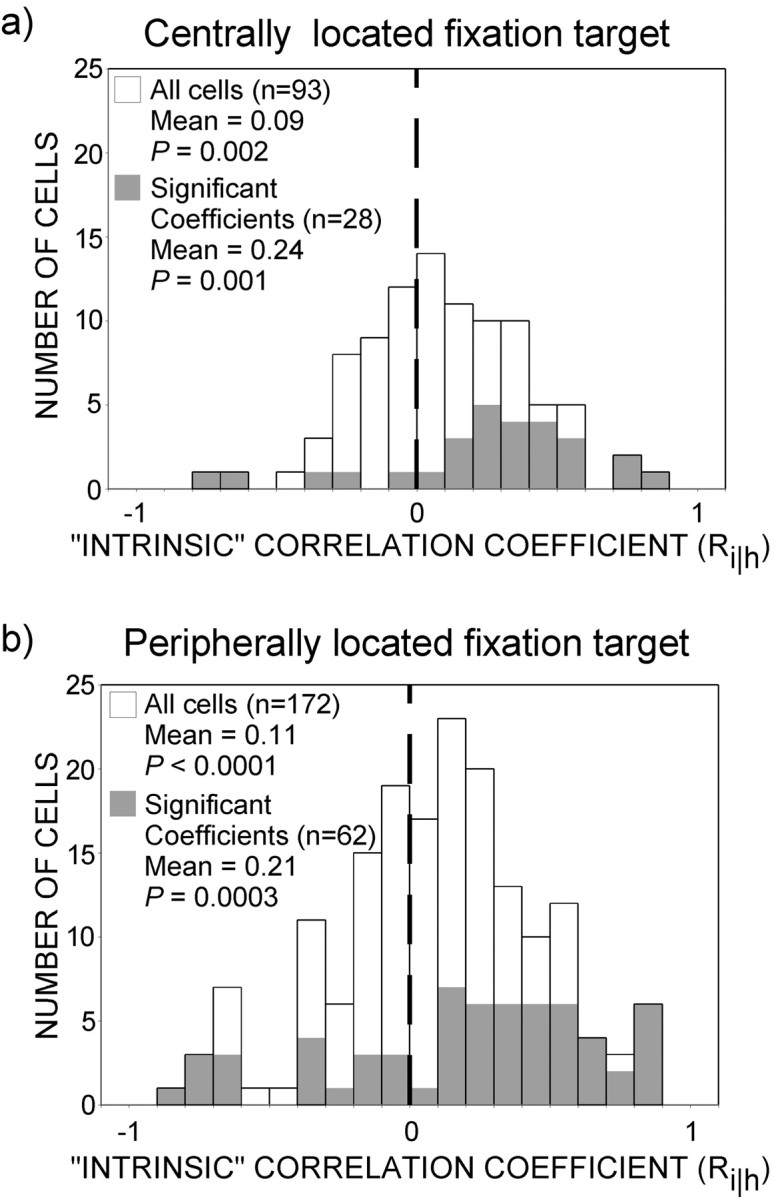
Possible effects of vergence eye movements on neuronal responses to barber diamonds. To explore the potential impact of vergence, we compared the responses of cells under foveal and peripheral viewing conditions. Plotting conventions for eachpanel are same as for Figure 8. a, Under foveal viewing conditions, the fixation target is close to the center of the barber-diamond grating, and the region immediately surrounding (1.5–4°) the zero-disparity fixation spot was also at zero disparity. State of vergence was thus not expected to vary between stimulus conditions. The mean (0.09) of the distribution of correlation coefficients for cells studied under these foveal viewing conditions was significantly positive (t test;p = 0.002), and the number of positive coefficients (n = 58) was greater than the number of negative (n = 35) (χ²;p = 0.02). Thirty percent (28 of 93) of cells exhibited significant motion–depth interactions (gray). The mean (0.24) for the distribution of significant cells was also positive (t test;p = 0.001), and there were more positive than negative coefficients (χ²;p = 0.0007). b, Distribution of coefficients for the cases in which the fixation spot was surrounded by a region of non-zero disparity. The means for the population (0.11) and the subpopulation of individually significant cells (0.21) were greater than zero (t test; p < 0.0001 andp = 0.0003, respectively). The number of positive coefficients was greater than the number of negative coefficients for both groups as well (χ²; allp < 0.001). A comparison between the means for the foveal conditions (0.09) and peripheral conditions (0.11) revealed no difference (t test; p = 0.72). There was also no difference between the means for the distribution of significant cells (t test; p = 0.73). These results suggest that differential vergence angles, had they existed, made no significant contribution to neuronal responses consistent with the intrinsic motion prediction.

Contextual effects mediated by nonclassical surround

Barber-diamond stimuli were positioned with the intention that the textured panels should lie outside the CRF. Because of the imprecision of CRF boundaries and the techniques used to determine them, however, one or more of the panels may have intruded slightly upon the CRF for some neurons. We wondered whether the observed effects on motion processing were supported when the contextual information was present only in the surround. To address this question, we separately analyzed data from 90 cells for which we had the strongest evidence that the CRFs lay within the diamond-shaped aperture of the stimulus. Our confidence was derived from the fact that these “CRF-only” cells had relatively small CRFs, ensuring that the diamond-shaped aperture extended well beyond the CRF in every direction. The distributions of intrinsic correlation coefficients (R_i‖h) for CRF-only neurons and for the remaining group of cells are plotted in Figure 12. Thirty-three percent of CRF-only cells exhibited significant correlation coefficients compared with 34% for the remaining neurons. For CRF-only neurons that exhibited significant motion–depth interactions, positive coefficients outnumbered negative ones 3.3:1 (χ²; p = 0.003) compared with 3:1 for the remaining neurons (χ²; p = 0.0003). Moreover, the mean (0.08) for the distribution of coefficients was significantly positive for the CRF-only neurons (t test;p = 0.03) and did not differ (t test;p = 0.20) from that of the remaining neurons (mean of 0.12). The means for the cells with significant responses (CRF-only, 0.20; other, 0.23) also did not differ between the two groups (t test; p = 0.75). We conclude that depth ordering restricted to the CRF surround can alter directional responses to moving features within the CRF.

Fig. 12.

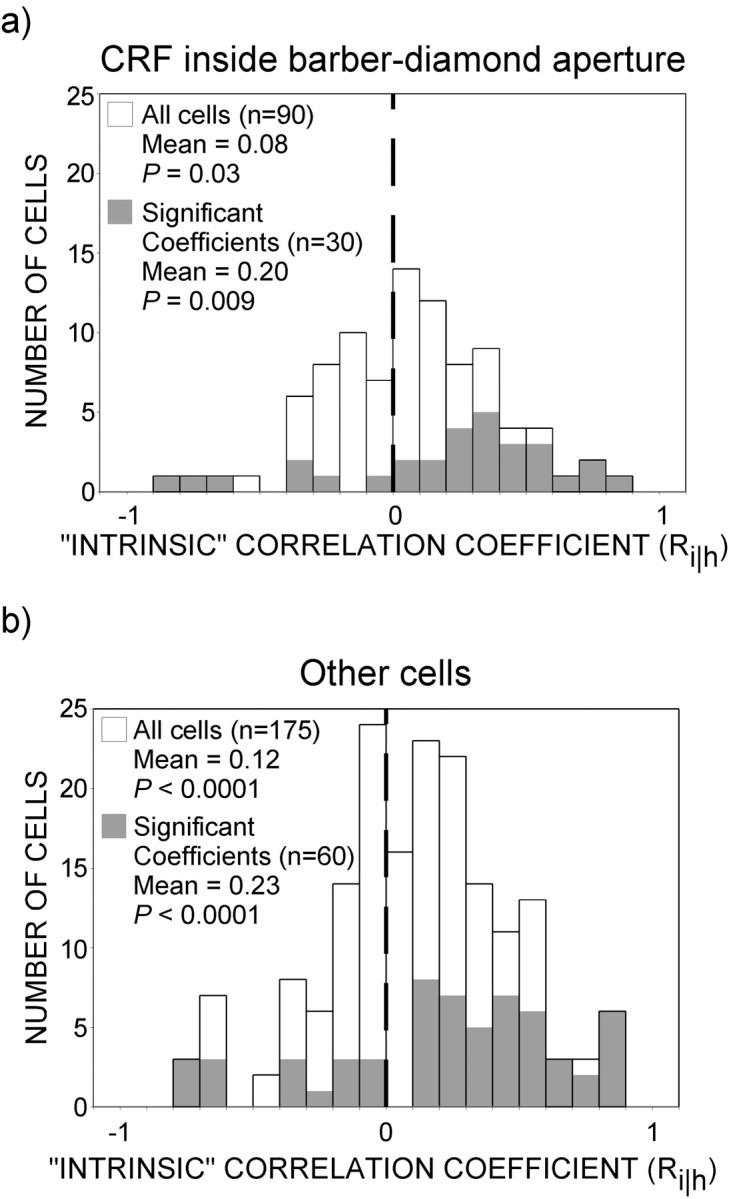
The nonclassical receptive field mediates contextual effects. We sought to determine whether the influence of depth ordering on the responses of MT neurons could be governed solely by the nonclassical receptive field. The responses of cells whose CRFs lay within the diamond-shaped aperture of the stimulus were compared with cells whose CRFs may have extended beyond the stimulus aperture. Plotting conventions are the same as for Figure 8.a, CRF inside barber-diamond aperture. Mean coefficient (R_i‖h) for the population of 90 cells (0.08) was significantly greater than zero (t test;p = 0.03), and the number of positive (n = 55) coefficients was greater than the number of negative (n = 35) coefficients (χ²; p = 0.04). The mean (R_i‖h) for the distribution of individually significant coefficients (0.20) was also greater than zero (t test;p = 0.009), and there were more positive (n = 23) than negative coefficients (n = 7) as well (χ²;p = 0.003). b, Other cells. Mean of the distribution of coefficients for these 175 cells was positive (0.12; t test; p < 0.0001), and positive coefficients (n = 111) outnumbered negative (n = 64) ones (t test;p = 0.004). Mean for the distribution for significant cells was also positive (0.23; t test;p < 0.0001), and positive coefficients (n = 44) outnumbered negative (n = 16) coefficients (t test;p = 0.0003). More importantly, there was no difference between the populations of coefficients when the CRF was inside versus outside the barber-diamond aperture (ttest; p = 0.20). There was also no difference between the distributions of significant cells when the CRF was inside or beyond the aperture (t test; p = 0.75). Hence, depth-ordering information restricted to the nonclassical receptive field can alter directional responses to moving features within the CRF.

DISCUSSION

Our results demonstrate that depth-ordering cues play a decisive role in the interpretation of moving stimuli, not only perceptually, but also in the directional responses of individual area MT neurons. At least a subset of MT neurons distinguish between the motions of intrinsic and extrinsic image features on the basis of depth-ordering cues that simulate occlusion boundaries. These cells thereby build a representation of visual scene motion consistent with perceptual experience. In this discussion, we briefly review related psychophysical experiments exploring the role of depth-ordering cues in the interpretation of ambiguous visual motion input. Second, we discuss what neurophysiological experiments using plaid patterns tell us about the neuronal interpretation of visual motion and how those results relate to those presented here. Third, we discuss the implications of our work with regard to motion–depth interactions within area MT and, in particular, the role of the nonclassical receptive field in contextual sensory interactions. Finally, we speculate about the mechanism underlying the interaction between depth and motion information in the interpretation of visual motion.

Occlusion and the solution to the aperture problem: psychophysical studies

Whatever its true motion, a moving grating viewed through a circular aperture appears to move orthogonal to its orientation. This is a perceptual consequence of the “aperture problem,” which states that local measurements of the motion of oriented image features provide insufficient information to determine the true trajectory. If that same moving grating is viewed through a rectangular rather than a circular aperture, the dominant perception is of motion along the long axis of the rectangle. This is the barber-pole illusion (Wallach, 1935). Early computational approaches to understanding the barber-pole illusion are primarily characterized by “smoothing” operations, through which motion signals arising from the grating terminators (i.e., where the grating meets the aperture) are pooled with the ambiguous signals arising from the interior of the aperture (Bulthoff et al., 1989; Wang et al., 1989). An indiscriminate pooling of velocity measurements, however, is incapable of accounting for the fact that placing the rectangular aperture stereoscopically in front of the moving grating (thereby simulating occlusion of the grating by the aperture) destroys the illusion (Shimojo et al., 1989). Shimojo et al. argued that “release” from the barber-pole illusion was a result of the classification of the grating terminators as extrinsic to the grating. Specifically, because the terminators are not intrinsic to (i.e., not part of) the grating, their motions should not be attributed to (and pooled with) that of the grating.

Another important stimulus that has been used to investigate how the visual system solves the aperture problem is the moving “plaid pattern.” “Plaids,” as they are oftentimes called, are created by superimposing two differently oriented moving component gratings. Plaids can be seen to move as a single coherently moving surface (“coherent” motion) or as two independently moving gratings (“noncoherent” motion). Stoner et al. (1990) observed that plaid motions tend to be seen as noncoherent if they are made to resemble one transparent grating overlying another. This effect was interpreted as evidence of the following: (1) that the visual system attempts to interpret these stimuli in terms of overlapping real-world surfaces, and (2) that classification of regions of grating overlap as intrinsic or extrinsic to the moving surfaces plays a major role in motion coherence (Stoner and Albright, 1994). Several studies have provided additional support for this hypothesis (Trueswell and Hayhoe, 1993;Stoner and Albright, 1996; Dobkins et al., 1998).

Occlusion and the solution to the aperture problem: neurophysiological studies

Perceptually coherent plaid patterns have been used to distinguish neurons that are selective for the motions of individual oriented (one-dimensional) components (“component neurons”) from those that are selective for the motions of two-dimensional patterns (“pattern neurons”) (Movshon et al., 1985; Rodman and Albright, 1989). Whereas component neurons are subject to the aperture problem (i.e., they only signal the direction of motion orthogonal to each grating), pattern neurons appear to have “solved” the aperture problem (i.e., they signal the motion consistent with a single moving surface). [For a somewhat different characterization of pattern neurons, see Grzywacz and Yuille (1991).] Based on theoretical arguments and the finding that component neurons are more common in the input layers whereas pattern neurons are found in the output layers (Movshon et al., 1985), it is strongly suspected that pattern neurons achieve their response properties by virtue of converging input from component neurons.

At what processing stage(s) within area MT (component or pattern) do depth-ordering cues exert their influence on motion interpretation? The results presented here do not allow us to answer this question with any confidence. Nevertheless, a previous study of the neuronal correlates of perceptual motion coherence–noncoherence (Stoner and Albright, 1992) sheds some light on this issue. Using monocular depth-ordering cues (i.e., luminance and figural cues for transparent surface overlap) to manipulate motion coherence (see above discussion), Stoner and Albright found that both component and pattern neurons responded comparatively less to plaids moved in the preferred direction of the cell when the plaid intersections were configured to be perceived as extrinsic rather than intrinsic. Those results suggest that depth influences motion interpretation before the level at which component neuron motion signals are integrated by pattern neurons. Whether depth ordering and motion mechanisms interact at a site earlier in the visual motion pathway than area MT will surely be a subject of future experiments.

Integration of depth and motion information within area MT: neuronal basis for contextual interactions

That area MT has neurons selective for horizontal binocular disparity as well for direction of motion is well known (Maunsell and Van Essen, 1983, DeAngelis et al., 1998), and various proposals have been offered for the functional significance of this convergence of visual cues. One relevant proposal concerns the role of antagonistic “surrounds” that lie outside the CRF. A major revision of how we think about receptive field structure came with the discovery that responses within the CRF could be dramatically modulated by stimulation of the non-CRF or surround (Frost and Nakayama, 1983; Allman et al., 1985). Within area MT, these contextual effects have been reported to be primarily antagonistic such that response magnitude increases when features placed in the non-CRF move in a different direction of motion from those in the CRF. Recently, a similar antagonism was reported for binocular disparity (Bradley and Andersen, 1998). These two types of antagonistic interactions might be termed “intra-modal” (i.e., motion–motion and depth–depth). The convergence of motion and depth information within these neurons may be important for signaling image discontinuities (Bradley and Andersen, 1998) defined by either visual cue. Another related possibility is that these antagonistic surrounds extract depth variation based on either motion parallax or binocular disparity (Buracas and Albright, 1996; Liu and Kersten, 1998).

The neurophysiological effects reported here constitute an “inter-modal” surround effect whereby image discontinuities within the non-CRF defined by one modality (depth) alter the response selectivity to another modality (motion) within the CRF. Using experimental manipulations of depth that had no effect on perceived direction of motion, Bradley and Andersen (1998) previously found that motion–depth interactions were relatively rare (11%) in area MT. Their result is mirrored by those of our texture control experiment in which influence of depth on motion perception was similarly absent, and the proportion of cells demonstrating motion–depth interactions was infrequent (10%; see Results). Our study reveals that the predominance of simple intra-modal antagonism over inter-modal interactions extends only to a limited stimulus set. Detection of the sophisticated inter-modal surround effects reported herein required using visual stimuli for which depth cues disambiguated direction of motion, a situation arguably common for natural scenes.

The barber-diamond stimuli used in these experiments have, in addition to horizontal disparity, a second type of depth cue: monocular half-occlusions (see Materials and Methods). Evidence has been provided recently that monocular half-occlusions, not horizontal disparity, may be the critical variable in the ability of binocular depth manipulations to affect terminator classification and motion perception in barber-pole type displays (Andersen, 1999; Castet et al., 1999). Determining the relative importance of monocular half-occlusion and horizontal disparity in the neurophysiological effects reported here awaits further experimentation. We next consider the type of mechanisms that might be involved.

How does depth-ordering information affect motion interpretation?

Where in the visual processing hierarchy is depth-ordering information represented? Evidence suggests that this may occur as early as area V2. Peterhans and von der Heydt (1991) have found indications that V2 neurons signal depth ordering at occlusion boundaries signaled by T junctions. Using stimuli that simulate dynamic occlusion (also commonly referred to as accretion–deletion) boundaries, one study found preliminary evidence that some area MT neurons may themselves encode depth ordering (Stoner et al., 1998).

In addition to the binocular disparity and monocular half-occlusion cues examined in our study, a variety of other depth-ordering cues have been shown to be important in resolving the aperture problem; T junctions (Liden and Mingolla, 1998), X junctions (Stoner and Albright, 1994), and even shadows (G. R. Stoner, unpublished observations) have been shown to exert a profound effect on perceived direction of motion in barber-pole type displays. From these observations, we conclude that the neural mechanisms underlying classification of features at occlusion boundaries generalize across different depth cues and hence are, to some extent, “form-cue invariant” (Albright, 1992). Whether individual neurons that encode depth ordering do so in a form-cue invariant manner is an exciting question awaiting future experimentation.

Given this tentative identification of where in the visual pathway depth ordering is detected and where it influences motion processing, a second-order question concerns how depth-ordering mechanisms influence the behavior of directionally selective neurons. One possibility is based on the “amodal” completion of occluded surface regions. This amodal representation may introduce additional motion signals that, when pooled with the motion signals arising from visible parts of the surface, alter motion interpretation. For the case of the barber diamond, amodal completion behind the near panels (Fig. 1, gray stripes) would produce additional motion signals favoring an interpretation of motion along the “long axis” of the barber-diamond stimulus (Fig. 1, gray arrows).

A second possibility for the recovery of surface velocity involves selective pooling of one-dimensional motion measurements. According to this notion (Stoner and Albright, 1994), the motion signals arising from the oriented features that define a surface are pooled if those features are classified as intrinsic but not if they are classified as extrinsic. It is important to realize that the selective-pooling solution is not necessarily restricted to the linking of two moving image features; an apparently stationary oriented feature is, in fact, consistent with motion parallel to its orientation and can potentially affect the perceived motion of another superimposed moving feature. Accordingly, barber-diamond stimuli possess three distinct sets of oriented features that could conceivably be pooled: (1) the horizontally moving grating stripes, (2) the edge at the junction of the grating stripes and the far panels, and (3) the edge at the junction of the grating stripes and the near panels. The intrinsic–extrinsic classification of these features is enabled by the depth-ordering cues present in the barber diamonds. Only the first two of these three features are classified as intrinsic to the grating surface. Thus, the perceived motion of our barber-diamond stimuli might be accounted for by selective integration of the motion information provided by the moving grating stripes and the diagonal motion implied by the intrinsic edges.

A third mechanism consistent with our findings involves the direct suppression of motion signals arising from extrinsic features (Liden and Pack, 1999). According to this hypothesis, motion signals arising from extrinsic features would be actively inhibited and would not influence the recovery of surface velocity. For the case of the barber diamond, the motion signals corresponding to extrinsic terminators would be suppressed and the remaining intrinsic motion signals would, as a result, dominate motion interpretation.

It is important to recognize that the three mechanisms described above (amodal completion, selective linking of intrinsic motion signals, and selective suppression of extrinsic motion signals) are not mutually exclusive. Because the evidence reported here does not allow us to differentiate between them, we must await the results of future experiments to precisely determine the mechanisms underlying the ability of depth cues to disambiguate motion information.

In summary, we have devised stimuli that, via the incorporation of appropriate depth-ordering cues, simulate a partially occluded moving surface. Our psychophysical experiments demonstrated that this simulated surface is seen to move in the direction of visual image features that are perceptually classified as intrinsic to that surface rather than part of another occluding surface. We have also shown that many MT neurons exploit contextual cues for surface depth ordering. In doing so, they resolve the ambiguity of the motion information present in their CRF and thereby build a representation of visual scene motion consistent with perceptual experience. Because existing theoretical accounts of the behavior of MT neurons (Wilson and Kim, 1994;Simoncelli and Heeger, 1998) fail to provide for these and related neuronal phenomena (Stoner and Albright, 1992), our findings emphasize the need to develop realistic models that do (Stoner and Albright, 1994).