Postsynaptic Variability of Firing in Rat Cortical Neurons: The Roles of Input Synchronization and Synaptic NMDA Receptor Conductance

Abstract

Neurons in the functioning cortex fire erratically, with highly variable intervals between spikes. How much irregularity comes from the process of postsynaptic integration and how much from fluctuations in synaptic input? We have addressed these questions by recording the firing of neurons in slices of rat visual cortex in which synaptic receptors are blocked pharmacologically, while injecting controlled trains of unitary conductance transients, to electrically mimic natural synaptic input.

Stimulation with a Poisson train of fast excitatory (AMPA-type) conductance transients, to simulate independent inputs, produced much less variability than encountered in vivo. Addition of NMDA-type conductance to each unitary event regularized the firing but lowered the precision and reliability of spikes in repeated responses. Independent Poisson trains of GABA-type conductance transients (reversing at the resting potential), which simulated independent activity in a population of presynaptic inhibitory neurons, failed to increase timing variability substantially but increased the precision of responses. However, introduction of synchrony, or correlations, in the excitatory input, according to a nonstationary Poisson model, dramatically raised timing variability to in vivo levels. The NMDA phase of compound AMPA–NMDA events conferred a time-dependent postsynaptic variability, whereby the reliability and precision of spikes degraded rapidly over the 100 msec after the start of a synchronous input burst. We conclude that postsynaptic mechanisms add significant variability to cortical responses but that substantial synchrony of inputs is necessary to explain in vivovariability. We suggest that NMDA receptors help to implement a switch from precise firing to random firing during responses to concerted inputs.

Neurons in the mammalian cortex fire action potentials at apparently random intervals, like a Poisson process (Tomko and Crapper, 1974; Burns and Webb, 1976; Tolhurst et al., 1983; Snowden et al., 1992; Britten et al., 1993). A high convergence (Douglas and Martin, 1998), and integration of tens or hundreds of excitatory synaptic events per postsynaptic spike (Mason et al., 1991) make it hard to establish precisely the input that drives any particular cortical spike train. It is therefore difficult to distinguish between input variability and variability attributable to synaptic transmission and noise in the postsynaptic neuron. This distinction is central to debate about the significance of action potentials in central neurons: is there meaningful information in the precise timing of individual action potentials or only in their average rate (Abeles, 1990; König et al., 1996;Rieke et al., 1997)? Can noise have a positive role in the cortex, for example stochastic resonance (Gammaitoni et al., 1998)?

There are several well recognized sources of noise in cortical neurons that could contribute to spike train variability, for example, probabilistic release of transmitter, stochastic gating of ion channels, and fluctuations in metabolic rate. Intrinsic noise could be amplified by the nonlinearity of spike generation (Aihara and Matsumoto, 1986) or smoothed by integrating over time. Spike train variability could also arise from complex patterns of network presynaptic activity. Modeling has suggested that correlation of inputs in time (Softky and Koch, 1993) or independent inhibition (Shadlen and Newsome, 1998) could explain the high variability of firing observed in vivo.

To understand the nature of variable firing in the cortex, it will be necessary to characterize how cells integrate known complex inputs and how reliable this process is. Recently, a useful approach has been to inject complex current waveforms based on features of actual synaptic input and to examine the variability of spiking responses.Mainen and Sejnowski (1995) and Nowak et al. (1997) showed that quickly varying current produces quite reliable spike output, suggesting that synaptic input timing is responsible for high variability. Stevens and Zador (1998) found that stimulus current pulses resembling synaptic currents must be clustered in irregular bursts to obtain natural levels of variability.

Here, using slices of rat visual cortex, we extend this approach in several important ways. Instead of applying fixed current stimuli, we inject complex patterns of conductance (Robinson, 1991;Robinson and Kawai, 1993; Sharp et al., 1993) modeled on natural synaptic events. We reproduce the long-lasting NMDA receptor-mediated phase of synaptic conductance, including its steep voltage dependence (Nowak et al., 1984), and we add inhibition by shunting conductance transients resembling those at GABAergic synaptic terminals. Our results support previous suggestions that input synchrony is necessary to explain natural firing variability but also show that NMDA-type conductance introduces a large additional postsynaptic variability and that it gives rise to two phases of response to clustered bursts of inputs: an early phase in which spike timing is precise and a late phase (>20 msec) in which spike timing becomes highly unreliable.

MATERIALS AND METHODS

Slice preparation and recording

Transverse slices were prepared from occipital cortex of 4- to 19-d-old Wistar rats using standard techniques (Sakmann and Stuart, 1995). During slicing, tissue was kept in sodium-free solution that had the following composition (in mm): 254 sucrose, 2.5 KCl, 26 NaHCO₃, 10 glucose, 1.25 NaH₂PO₄, 2 CaCl₂, and 1 MgCl₂. Slices of 400 μm thickness were cut on a vibrating slicer (Campden Instruments, Leicester, UK) and kept in Ringer's solution at 30°C for 10 min and then at room temperature for at least 2 hr before recording. The Ringer's solution contained (in mm): 125 NaCl, 2.5 KCl, 25 NaHCO₃, 25 glucose, 1.25 NaH₂PO₄, 2 CaCl₂, and 1 MgCl₂. Both slicing and recording solutions were equilibrated with 95% O₂, 5% CO₂ gas to a final pH of 7.4.

Slices were viewed with an upright microscope (Olympus BW50WI, Olympus UK, London) using infrared differential interference contrast optics. All experiments were performed at 33 ± 1°C. Whole-cell patch-clamp recordings were made from the somas of neurons in layers II, III, and V using pipettes with resistances of 4–6 MΩ. During recording, the slices were perfused continuously with Ringer's solution in which 10 μm bicuculline, 10 μmCNQX, and 10 μm APV (Tocris Cookson, Bristol, UK) were included to block intrinsic synaptic conductances. The pipette solution contained 20 mm phosphocreatine Na₂, 5 U/ml creatine phosphokinase, 4 mm MgCl₂, 0.3 mm GTP, 4 mm ATP, 100 mmpotassium gluconate, 20 mm KCl, and 10 mmHEPES, balanced to pH 7.3 with NaOH. Somatic patch-pipette recordings were made with an Axoclamp 2B or Axopatch 200A amplifier (Axon Instruments, Foster City, CA) in current-clamp mode. Membrane potentials were corrected for prenulled liquid junction potential. Signals were filtered at 5 kHz (−3 dB, four-pole Bessel) and sampled with 12-bit resolution at 20 kHz.

Conductance injection

Cells were stimulated using the conductance injection technique (Robinson and Kawai, 1993). The opening of a population of receptor channels at the synapse is modeled by a conductance g(t), injecting a current I(t) that depends on the changing membrane potential V(t):

$$I(t)=g(t)[V(t)-E_{\text{rev}}],$$ Equation 1

where E_rev is the reversal potential of the conductance. To model AMPA and GABA receptor synaptic conductances, a custom analog circuit (Robinson, 1999) was used to implement Equation 1, producing a current command signal from the instantaneous membrane potential signal and a computer-generated conductance command waveform. The multiplication in Equation 1 was performed using an analog multiplier (AD738, Farnell, Leeds, UK). The 10–90% settling time of the circuit was 290 nsec.

The voltage-dependent block of open NMDA receptors by extracellular magnesium ions was reproduced by a further multiplication of Equation 1by a Boltzmann-type nonlinearity:

$$I(t)=\frac{g(t)[V(t)-E_{\text{rev}}]}{1+K_{1}exp(-K_{2}V(t))},$$ Equation 2

where K₁ and K₂were constants determining the voltage dependence of block (Ascher and Nowak, 1988; Jahr and Stevens, 1990; Koch, 1999). The additional exponentiation and division operations in this equation were implemented with high-precision analog computation amplifiers (AD538, Farnell), and the settling time of this circuit was 2.5 μsec (Robinson, 1999). When two conductances were injected simultaneously, the contributions of each conductance were summed electronically to create the total current command signal. Noise from the conductance-computing circuitry contributed <0.6 pS rms (DC to 20 kHz bandwidth).

Stimulus definition

Unitary events. All conductance stimuli were constructed by summing unitary conductance transients, representing the waveform of conductance activated by a single synaptic input. For each type of receptor conductance, the waveform was specified by a difference of two exponentials function:

$$g(t)=\left\{\begin{array}{c}\overline{g}[exp(-(t-t_0)/{\tau }_{\text{d}})-exp(-(t-t_0)/{\tau }_{\text{r}})],\text{for} t\ge t_0\hfill \\ 0,\text{for} t<t_0\hfill \end{array}\right.,$$ Equation 3

where τ_r is the activation time constant, τ_d is the decay time constant, t₀is the initiation time for the transient, and $\overline{g}$ is a scaling factor (Johnston and Wu, 1995; Sacchi et al., 1998; Kleppe and Robinson, 1999;Koch, 1999). The time constants were based on voltage-clamp measurements in the literature, adjusting for temperature differences, if appropriate, using a Q₁₀ of 3. τ_r and τ_d had respective values of (in msec): AMPA, 0.5 and 2 (Häusser and Roth, 1997;Kleppe and Robinson, 1999); NMDA, 5 and 150 (Hestrin et al., 1990; Lester et al., 1990; Stern et al., 1992). τ_dcorresponds to the longer-lasting phase of the two reported in biexponential fits of the decay (Konnerth et al., 1990): GABA, 0.5 and 7 msec (Pearce, 1993; Kapur et al., 1997; Ling and Benardo, 1999). E_rev was set to −10 mV (AMPA and NMDA) and the resting potential (GABA). $\overline{g}$ values were as follows (pS): AMPA, 1000 [equivalent to a peak amplitude of 30 pA at −65 mV (Stern et al., 1992; Hestrin, 1993;Stevens and Zador, 1998); NMDA, 100 [resulting in approximately one-fourth of the amplitude of the AMPA component at peak if fully unblocked, consistent with Lester et al. (1990); Robinson et al. (1991); Stern et al. (1992); Silver et al. (1995);Kleppe and Robinson (1999)]; GABA, 300 [consistent with the size of miniature events in Edwards et al. (1990); Salin and Prince (1996); Ling and Benardo (1999)]. When NMDA-type conductance was used, unitary AMPA and NMDA transients were activated simultaneously, giving a compound unitary AMPA–NMDA conductance transient (Bekkers and Stevens, 1989; Robinson et al., 1991), with a brief early AMPA phase and a much longer NMDA phase (see Fig.1A). Conductance of the NMDA phase was voltage dependent, as described by Equation 2, with g(t) having the form given in Equation 3, and with K₁ set to 0.6 and K₂ to 0.06/mV. The fraction of unblocked NMDA conductance as a function of voltage (given by the denominator of Eq.2) is shown in Figure 1B. Fluctuations caused by gating of single synaptic NMDA receptors, which would have added a small additional current variance at physiologically relevant frequencies (Robinson et al., 1991), were not included.

Fig. 1.

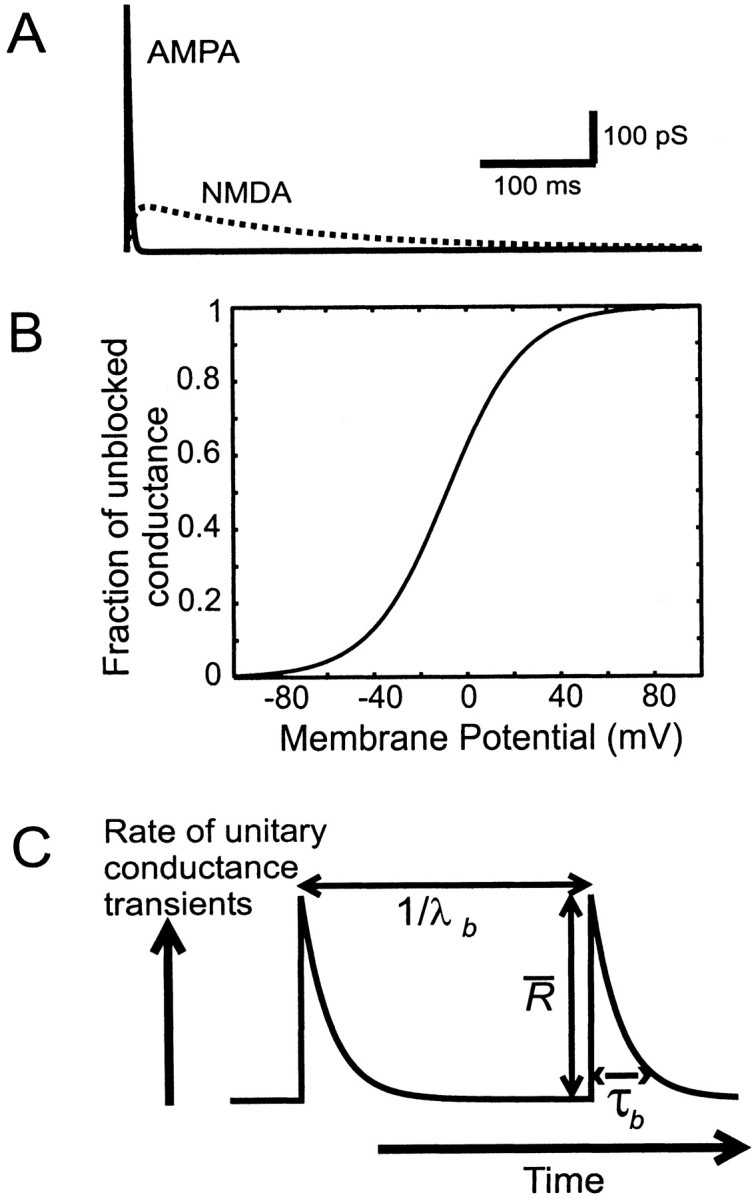
Stimulus definition. A, The unitary excitatory conductance transient with a fast AMPA phase, injected according to Equation 1, and a much slower NMDA phase, injected with the voltage dependence described by Equation 2. B, The fraction of commanded NMDA conductance, which is unblocked, as a function of membrane potential F(V) = 1/[1 + K₁exp (−K₂V)] (see Eq. 2 and Materials and Methods). C, Diagrammatic representation of the model used to simulate concerted or synchronized inputs. See Materials and Methods for details.

Poisson trains of synaptic events. Poisson stimulus trains were constructed by summing unitary events—AMPA, compound AMPA–NMDA, or GABA type—at intervals given by a random variable t_i, with the probability density:

$$p(t_{\text{i}})=\lambda exp(-\lambda t_{\text{i}}),$$ Equation 4

characteristic of a Poisson process. The strength of stimulation was varied by changing the rate λ.

Synchronous trains of synaptic events. To simulate correlated or synchronous firing of synaptic inputs, we used the following doubly stochastic model. Events were produced by a nonstationary Poisson process, whose rate was modulated in exponentially decaying transients (see Fig. 1C). The burst times T were determined by a stationary Poisson process with a rate λ_b, such that the rate of synaptic events was given by:

$$\lambda (t)=\overline{R} \sum _{\text{i},\text{t}>T_{\text{i}}}exp(-(t-T_{\text{i}})/{\tau }_{\text{b}}),$$ Equation 5

where τ_b is the time constant of decay of the rate during a burst, and $\overline{R}$ is the initial peak rate of each exponential transient. The mean rate of synaptic events is then given by $\overline{\lambda }$ = $\overline{R}$τ_bλ_b. For any given $\overline{\lambda }$, synaptic input could be varied from independent, approaching a stationary Poisson process (high τ_b) to highly clustered or synchronized input (τ_b ≪ 1/λ_b). Thus, the intervals between synchronous bursts are random and exponentially distributed, and the aggregate spike rate during a population burst decays exponentially. A different but related model has been used byTurcott et al. (1994) to fit responses to auditory stimuli in lateral superior olive neurons.

All test stimuli lasted for 2 sec, and at least 20 sec of recovery time at the resting potential were allowed between sweeps.

Data analysis

Measuring spike times. Action potentials were detected by threshold crossings of the derivative of the membrane potential signal. The time of each detected spike was measured as the time of the maximal derivative in the rising phase to a precision of 50 μsec (the sample interval).

Variability and reproducibility measures. Two different statistical measures of overall response variability were used. The first measure was the coefficient of variation (CV) of the interspike intervals, the ratio of the SD of the intervals to their mean, with a value of 1 expected for a stationary Poisson process (Koch, 1999). The second measure was the Fano factor of the spike counts (Fano, 1947; Teich et al., 1996), the ratio of the variance of the spike count to the mean spike count over fixed time intervals; in our case the sweep duration was 2 sec. When measuring CV and Fano factor, 15–30 sweeps were used, and the stimulus was resynthesized with fresh random numbers for each sweep.

We used two measures of the reproducibility of responses, termed the “precision” and “reliability” of repeatable spikes. To determine these quantities, an identical stimulus pattern was applied in 10–30 consecutive sweeps, and a peristimulus time histogram was constructed with a bin width of 5 msec. The first 200 msec of the responses were excluded to avoid the influence of adaptation. Repeatable spikes were defined by events in which firing occurred in the same time bin for at least 30% of trials and included spikes in these and the immediately adjacent time bins. Reliability was defined as the proportion of all spikes that were repeatable. Precision, or jitter, was defined as the average value of the SD of spike times within each repeatable event. These measures of reproducibility are similar to those used by Mainen and Sejnowski (1995) andNowak et al. (1997), allowing comparison.

RESULTS

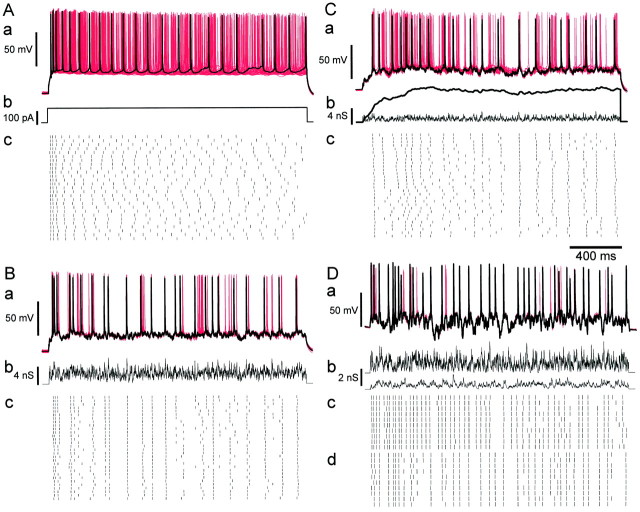
To examine how the reliability and regularity of firing in cortical neurons is determined by their electrical input, we carried out whole-cell recordings in 50 regularly spiking and intrinsic-bursting neurons in slices of developing rat occipital cortex. Unless stated otherwise, the analysis is based on results from 13 regularly spiking neurons. To allow precise control of the input, we blocked intrinsic synaptic conductances pharmacologically and stimulated the neurons using current and conductance injection through the recording pipette, in current-clamp mode (see Materials and Methods). Any variability of response, therefore, arises essentially from postsynaptic mechanisms. Example responses of neurons to the different stimulus conditions used in this study are collected in Figure 3.

Fig. 3.

Responses of cortical neurons to conductance inputs. A, Constant current injection in a regular-spiking neuron. a, Superimposed membrane potential trajectories for ensemble of presentations of the same stimulus. Black tracecorresponds to top spike train in c; the remaining 29 traces are plotted in red. b, The stimulus, consisting of a 2 sec current step of 150 pA, applied at 30 sec intervals. c, Raster plot of spike times during 30 successive presentations of the stimulus. B, Responses to fluctuating Poisson AMPA conductance excitation. Same neuron as in A. a, Superimposed membrane potential trajectories, plotted as in A. b, The stimulus, constructed by summing a Poisson train (rate 1600 Hz) of unitary AMPA conductance transients. c, Raster plot of spike times in 30 successive trials. C, Responses to Poisson trains of compound AMPA–NMDA conductance transients. Same neuron as in A and B. a, Superimposed membrane potential trajectories, plotted as in A. b, The stimulus, constructed by summing a Poisson train (rate 800 Hz) of compound AMPA–NMDA transients. Thin trace indicates the AMPA component of the conductance command;thick trace indicates the activation of the NMDA conductance command. The injected level of NMDA conductance is a function of the membrane potential according to Equation 2 and is not shown. c, Raster plot of spike times in 30 successive trials. D, Effect of inhibition in a different regular-spiking neuron. a, Superimposed membrane potential trajectories, plotted as in A. b, Stimulus: AMPA-receptor mediated (top trace, 800 Hz) and GABA receptor-mediated (bottom trace, 300 Hz) conductances. c, Raster plot of spike times of the response to only the AMPA component of the stimulus (10 trials). d, Raster plot of the responses of the same neuron to both conductance components—the same ensemble as in a . Firing frequency is reduced by inhibition, and spikes are often increased in precision and delayed.

Injecting steady currents

Figure 3A shows the response of a neuron to steady current injection in repeated identical trials. Responses show a slight adaptation, especially at the beginning of the sweep, characteristic of regular-spiking neurons (McCormick et al., 1985). When the timing of spikes between trials is compared, firing is seen to be most reproducible at the beginning of each trial, but this settles quickly into much less reproducibly timed spiking. In the superimposed membrane potential traces (see Fig. 3Aa), only the first two or three spikes are clearly repeated throughout the ensemble: the phase of subsequent spikes becomes independent, and the superimposed spikes are dense over the period of stimulation. As seen in the raster plot (see Fig. 3Ac), the response within individual trials appears quite regular, apart from the initial adaptation—much more regular than a Poisson process. These observations agree with those ofStevens and Zador (1998), who performed essentially the same experiment. As noted by Softky and Koch (1993), who found the same phenomenon in simulations, this regularity is far greater than observed during spontaneous or stimulus-induced firing at similar frequencies in vivo: a steady current stimulus is a poor model of natural excitatory synaptic drive.

Conductance injection

To provide a more realistic representation of synaptic input, we used fluctuating patterns of conductance. Excitatory stimuli were constructed by summing unitary conductance transients, with size, kinetics, and reversal potential similar to those at excitatory glutamatergic synapses. Unitary events consisted either of a fast transient of conductance lasting a few milliseconds, to represent synaptic conductance mediated by AMPA receptors, or of a compound event with a fast AMPA phase and a much longer-lasting phase representing activation of synaptic NMDA receptors (Fig.1A), which had a nonlinear instantaneous current–voltage relationship corresponding to the open-channel block of NMDA receptors by external magnesium (Mayer and Westbrook, 1984; Nowak et al., 1984), as described in Materials and Methods. Figure2 shows an example of a response to a periodic train of compound unitary events. AMPA and NMDA components of the conductance command are displayed separately, showing the different time scales at which each acts. The resultant current command signal is shown in Figure 2C and illustrates that the current produced by a conductance stimulus can be very far from linearly proportional to the conductance. In response to the stimulus, the cell fires an adapting burst of four action potentials. Two features are noteworthy. First, the size of current transients associated with AMPA phases is reduced with depolarization (Fig. 2C). This is one reason why the corresponding membrane potential transients are reduced in size (Fig. 2A); another reason is an increase in overall membrane conductance. Second, the voltage-dependent unblock of the NMDA receptor conductance cancels out much of the effect of the reduction in the driving force (unlike for AMPA phases), maintaining an approximately linear relationship between the conductance and inward current, despite approaching the reversal potential. Third, the shape of the current signal is dramatically distorted in the critical period leading into spikes. Several effects contribute to this: a rapid unblock of the NMDA-type conductance causes inward current notches or deflections just before spikes, the current actually reverses during spikes, as the membrane potential crosses the reversal potential, and the shape of the current between spikes, which will determine the interspike interval, is distorted by reblock of the NMDA conductance. Thus, using AMPA- and NMDA-type conductance for excitatory stimulation gives rise to major dynamic effects resulting from the interaction of stimulus and spike generation, which are lacking with predetermined current stimuli.

Fig. 2.

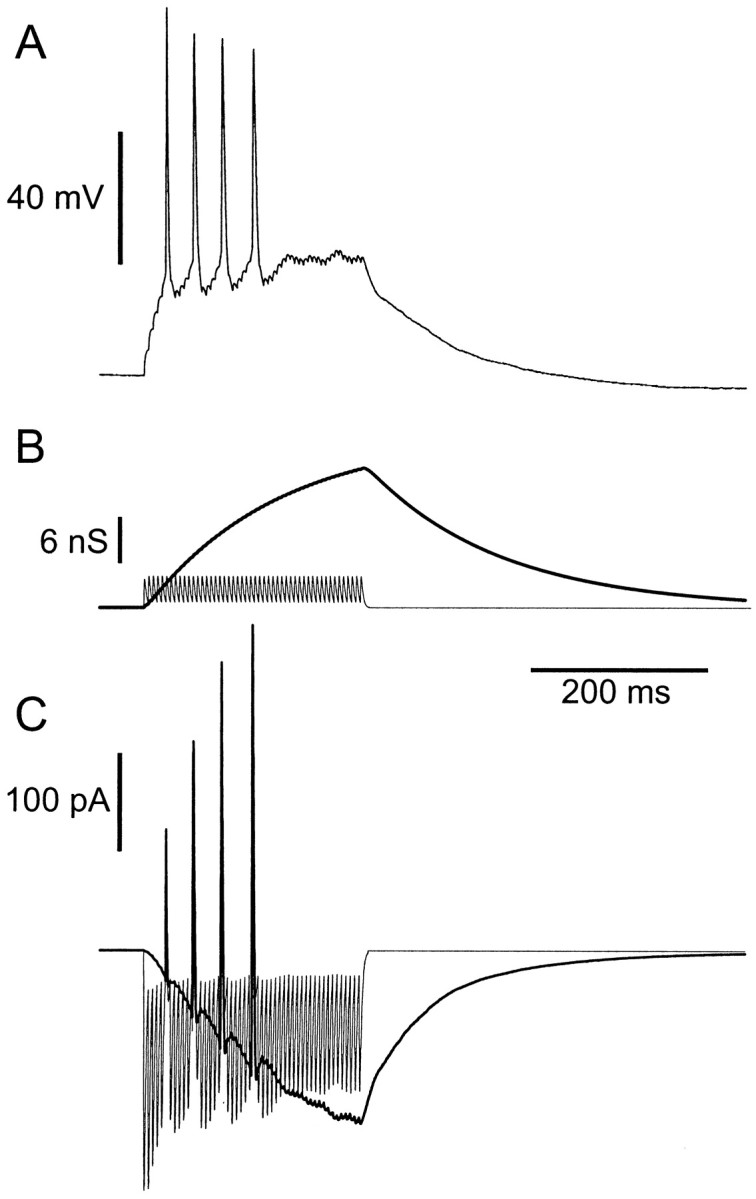
Response to a periodic train of compound unitary conductance events. A, Membrane potential, showing an adapting response with four action potentials. B, Conductance stimulus, comprising a train of 50 unitary compound AMPA–NMDA events (see Fig. 1A) at 5 msec intervals. AMPA (thin lines) and NMDA (thick lines) components are shown separately. C, The total current command signal, produced according to Equation 1 for the AMPA component and Equation 2 for the NMDA component. Inward current is downward.

Injecting Poisson trains of AMPA conductance transients

We investigated several different structures of conductance excitation. The first consisted of trains of AMPA-type excitatory events, the times of which were determined by a stationary Poisson process (see Materials and Methods). An ensemble of responses to such a stimulus is shown in Figure 3B for the same neuron that was stimulated with a current step in Figure3A. Although the average firing rate was approximately the same during both stimuli (10.5 Hz for the current step, 9.0 Hz for the Poisson AMPA stimulus), the temporal structure of the spike pattern was strikingly different. As noted above, step current responses were quite regular over time, but the trial-to-trial jitter of any particular spike in the response is large, and information encoded in precise spike timing is lost. In contrast, with fluctuating AMPA conductance stimuli (Fig. 3B), spikes were irregular, with a large range of interspike intervals, but precisely timed from trial to trial, as seen in the superimposed membrane potential traces of Fig.3Ba and the raster plot of Fig. 3Bc. Increased irregularity and precision of spikes in response to fluctuating current stimuli have been described by Mainen and Sejnowski (1995). The present results demonstrate that the same phenomena occur during dynamic stimulation with Poisson trains of AMPA-type conductance events.

Poisson trains of compound AMPA–NMDA conductance transients

In addition to the fast-activated AMPA receptors, a large fraction of glutamatergic synapses in the cortex also possess NMDA receptors (Nicoll et al., 1992; Stern et al., 1992). The conductances produced by the two classes of receptor are quite different. Although NMDA receptors are colocalized with AMPA receptors at individual synaptic terminals and experience the same pulse of glutamate in the synaptic cleft, they are activated for hundreds of milliseconds after each presynaptic action potential. NMDA conductance is highly voltage dependent because of block by extracellular magnesium ions, which is relieved by depolarization. We therefore decided to examine the impact on firing variability of including a component of NMDA-type conductance in the stimulus. Compound unitary synaptic events were used, incorporating both a fast linear conductance AMPA phase and a slower, nonlinear voltage-dependent NMDA phase (see Materials and Methods).

An ensemble of responses to a Poisson train of compound AMPA–NMDA events is shown in Figure 3C, in the same cell as in Figure3, A and B. The rate of the stimulus (800 Hz) was chosen to produce a similar mean postsynaptic spike frequency (9.2 Hz). As seen in Figure 3Cb, the aggregate NMDA conductance command summates slowly to a fairly smooth plateau; the actual conductance injected depends instantaneously on the membrane potential according to Equation 2 and is not shown. Incorporating NMDA conductance led to responses that were markedly different from responses to pure AMPA trains or current steps. Spike trains were more clearly regular than Poisson AMPA responses but less regular than current step responses. Even late in responses, there were precise spikes, identifiable from trial to trial, as for pure AMPA stimuli. Note that during the phase of increasing NMDA activation (approximately the first 500 msec), repeatability of spikes is particularly fragile, and jitter is large (Fig. 3Cc).

Relationship between input and output rates

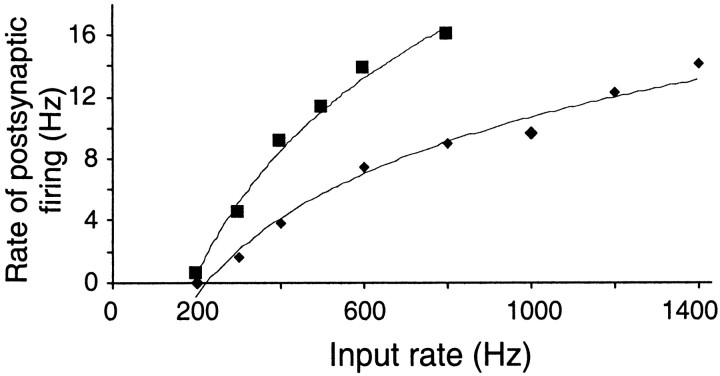
The relationship between the mean rate of postsynaptic firing and the rate of unitary conductance events for one cell is shown in Figure 4 for Poisson trains of AMPA events (diamonds) or compound AMPA–NMDA events (squares). In Poisson trains, the AMPA–NMDA events are about twice as efficient at eliciting action potentials as pure AMPA events: 45 events per spike (AMPA–NMDA) compared with 85 events per spike (AMPA only), with 600 Hz stimulation. A similar ratio was found in four other cells. The average charge injected per spike through the AMPA conductance (1.9 pC) is slightly less than that injected through the NMDA conductance (2.9 pC). The relationships between mean firing frequency and rate of input were concave and could be fitted reasonably well with a logarithmic function.

Fig. 4.

Input–output relationship of a regular-spiking pyramidal neuron. Average firing rate is plotted as a function of the rate of unitary AMPA conductance events (diamonds) or of compound AMPA–NMDA events (squares). Lines show fits to the equation R_out = k log_e R_in − A, with k = 7.2 and A = 40 (AMPA); k = 11.7 and A = 61 (AMPA–NMDA).

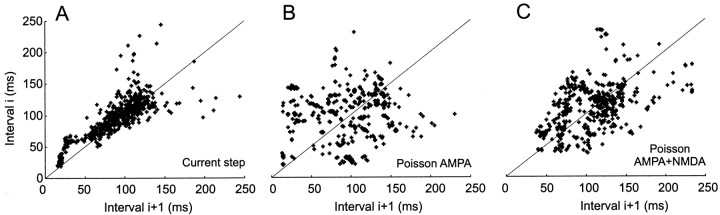
Sequential interval maps of spike times

The different dynamic characteristics of firing in response to these different conditions of steady excitation can be seen more clearly in return maps of successive interspike intervals T, in which T_i is plotted against T_i+1. Figure 5shows examples of these relationships for a single cell (the same as shown in Fig. 3A–C). During constant current stimulation (Fig. 5A), interspike intervals are regular, with a smooth adaptation over the course of the stimulus, so that points are concentrated along the diagonal. During a Poisson AMPA stimulus (Fig.5B), the distribution is spread over a much wider area and shows no attraction to the diagonal, reflecting irregularity. A large number of distinct clusters, corresponding to pairs of consecutive interspike intervals were repeated quite precisely in each trial. Figure 5C shows activation by trains of compound AMPA–NMDA unitary events. Regularity is increased and clusters are evident, indicating some precise spikes, but these are fewer and less compact than for AMPA only.

Fig. 5.

Sequential interval maps of firing in interspike intervals. Interval i is plotted against interval i + 1 for (A) constant current step as in Figure3A, (B) Poisson AMPA train as in Figure 3B, and (C) Poisson AMPA–NMDA train as in Figure3C.

Measures of spike time variability

To quantify the irregularity or variability of timing of postsynaptic spikes when activated by these trains of conductance stimuli, we used two standard statistical measures: CV of the interspike intervals and the Fano factor of the spike counts in each trial (see Materials and Methods). The strength of each type of stimulus was adjusted to produce a mean firing rate of 13–20 Hz. The results are summarized in Table 1. As expected, both measures of variability were low during current steps, dramatically higher during Poisson AMPA trains, and intermediate in value during Poisson compound AMPA–NMDA trains.

Table 1.

Coefficients of variation of interspike intervals (CV of ISI) and Fano factors of the spike counts in each trial, in regular-spiking neurons under different conditions of stimulation

Stimulus	n	Frequency (Hz)	CV of ISI	Fano factor
Current step	7  (3)	19.5  ± 2.6	0.12  ± 0.05	0.05  ± 0.07
Poisson AMPA	5  (4)	15.1  ± 5.3	0.51  ± 0.13	0.4  ± 0.36
Poisson	8  (3)	16.6  ± 5.3	0.37  ± 0.10	0.19  ± 0.16
AMPA + NMDA
Poisson	4  (3)	11.25  ± 2.4	0.53  ± 0.09	0.21  ± 0.12
AMPA + GABA
Synchronous	5  (2)	8.9  ± 2.8	1.28  ± 0.24	3.54  ± 1.33
AMPA + NMDA

For the synchronous compound AMPA–NMDA stimulus, τ_b was 0.1 sec and λ_b was 2 sec⁻¹. n = number of ensembles analyzed (number of cells in parentheses). For the Poisson AMPA + GABA stimulus, λ_GABA/λ_AMPAwas 0.75. Each value is average ± SD.

Precision and reliability of spikes

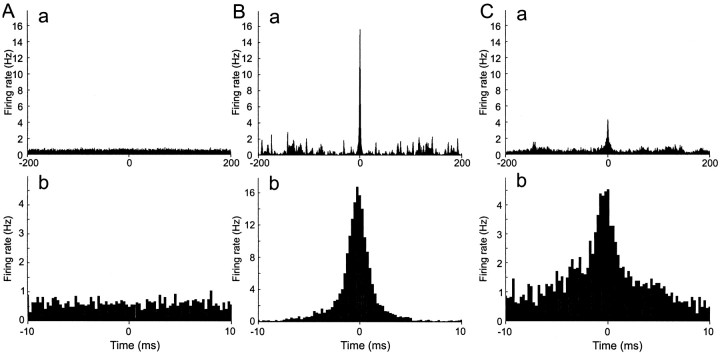
The Fano factor and CV characterize the overall statistics of spike timing, incorporating the variability of the input, but give no insight into the reproducibility of responses to the same input. We therefore examined spike timing in ensembles of responses to the same input. Repeatable spikes were those that were observed at nearly the same time in a large proportion of trials (see Materials and Methods for precise definition). Repeatable spikes were almost absent with step current stimulation, very common with Poisson AMPA stimulation, and present, in lower numbers, with Poisson AMPA–NMDA stimulation. We first characterized the prevalence and precision of repeatable spikes by calculating the average cross-correlation function of each spike train to all other spike trains in the ensemble. The first 200 msec of each trial are excluded, to remove correlations in spikes caused by the initial adaptation to the stimulus. An example set of results is shown in Figure 6. With a step current stimulus (Fig. 6A), only a flat background of uncorrelated firing is seen, reflecting a complete absence of repeatable spikes. In contrast, during Poisson AMPA stimulation, the central peak was large, reflecting a high incidence of repeatable spikes, and narrow (precise timing) (Fig. 6B). The presence of many sharp peaks at large time separations reflects the structure of the stimulus and implies that a repeatable spike resets the timing of spike generation, because if the jitters of successive repeatable spikes were additive, peaks would broaden at higher time separations. Adding NMDA conductance (Fig.6C) depresses and broadens the central peak, reflecting a drop in the number of repeatable spikes and an increase in jitter from trial to trial. However, the very central part of the peak is as sharp as for pure AMPA stimulation, suggesting that NMDA conductance might disperse the timing of some, but not all, repeatable spikes. Similar results were found in two other regular-spiking neurons.

Fig. 6.

Cross-correlation functions. Same cell as in Figures 3A–C and 5. The average one-way cross-correlation of each trace with all other traces in an ensemble was computed, excluding the first 200 msec of each spike train. A, Constant current stimulation. B, Poisson AMPA train stimulation. Fluctuating pattern of conductance input AMPA receptor conductance transients. C, Poisson compound AMPA–NMDA stimulation.

The reliability and precision of spikes were also measured using definitions similar to those used by Mainen and Sejnowski (1995) and Nowak et al. (1997) (see Materials and Methods). The results of this analysis for the three conditions of steady excitation are shown in Table 2. Reliability was low (17%) for current steps. The lack of any central peak in the cross-correlations for current steps indicates that spikes which satisfied the criteria for repeatability resulted simply from chance. The jitter was comparable to the upper limit of 2.81 msec, which we calculated by assuming that each trial is an independent Poisson process and taking into account the sampling bias of the detection procedure. Reliability is much higher for the Poisson AMPA stimulus condition (60%), and precision is most exact (1.75 msec). Adding NMDA conductance to each unitary event decreases reliability and increases jitter. These findings agree with the results of the cross-correlation analysis.

Table 2.

Reliability and precision of spikes during injection of steady excitatory stimuli

Stimulus	n	Reliability (%)	Precision (msec)
Current step	10  (5)	17  ± 11	2.87  ± 0.44
AMPA	12  (5)	60  ± 13	1.75  ± 0.52
AMPA + NMDA	18  (8)	49  ± 21	2.30  ± 0.39
Synchronous	5  (3)	76  ± 11	1.61  ± 0.49
AMPA + NMDA

Each analyzed ensemble comprises 10–20 trials. Mean firing frequency was between 5 and 25 Hz. n = number of ensembles analyzed (number of cells in parentheses). For the synchronous compound AMPA–NMDA stimulus, τ_b was 0.1 sec and λ_b was 2 sec⁻¹. The first 200 msec of each trial was excluded from analysis. Each value is average ± SD.

Interactions of steady excitatory and inhibitory conductance trains

The CV and Fano factor of firing during steady excitation by independent (Poisson) inputs, either AMPA or AMPA–NMDA events, is much lower than measured in vivo, where values of 1 or greater are typical for both measures (Softky and Koch, 1993;Gershon et al., 1998). One reason for this might be independently timed inhibitory synaptic events, which would add variance to the input (Shadlen and Newsome, 1998). We investigated this possibility by applying trains of shunting inhibitory conductance events during simultaneously applied Poisson AMPA stimulation. Inhibitory events had the size and kinetics of unitary GABAergic synaptic conductance transients (see Materials and Methods) and reversed at the resting potential. To attempt to achieve maximum irregularity, NMDA conductance was not added in these experiments. Timing of inhibitory events was determined by an independent Poisson process. A typical ensemble of responses is shown in Figure3D, which shows raster plots with (d) and without (c) inhibition, for the same train of AMPA excitation. Inhibition caused a number of spikes to drop out, as expected. Many of the remaining spikes show increased reliability and reduced jitter. Some spikes are delayed by inhibition, by up to 20 msec, as also observed by Häusser and Clark (1997). Spike-triggered averaging of the conductance stimulus (Fig.7) revealed that spikes are typically associated with a rise in AMPA conductance lasting 5–10 msec and peaking ∼5 msec before the spike. During simultaneous inhibition, a slower 10–15 msec depression of GABA conductance was also observed, also centered on 5 msec before the spike.

Fig. 7.

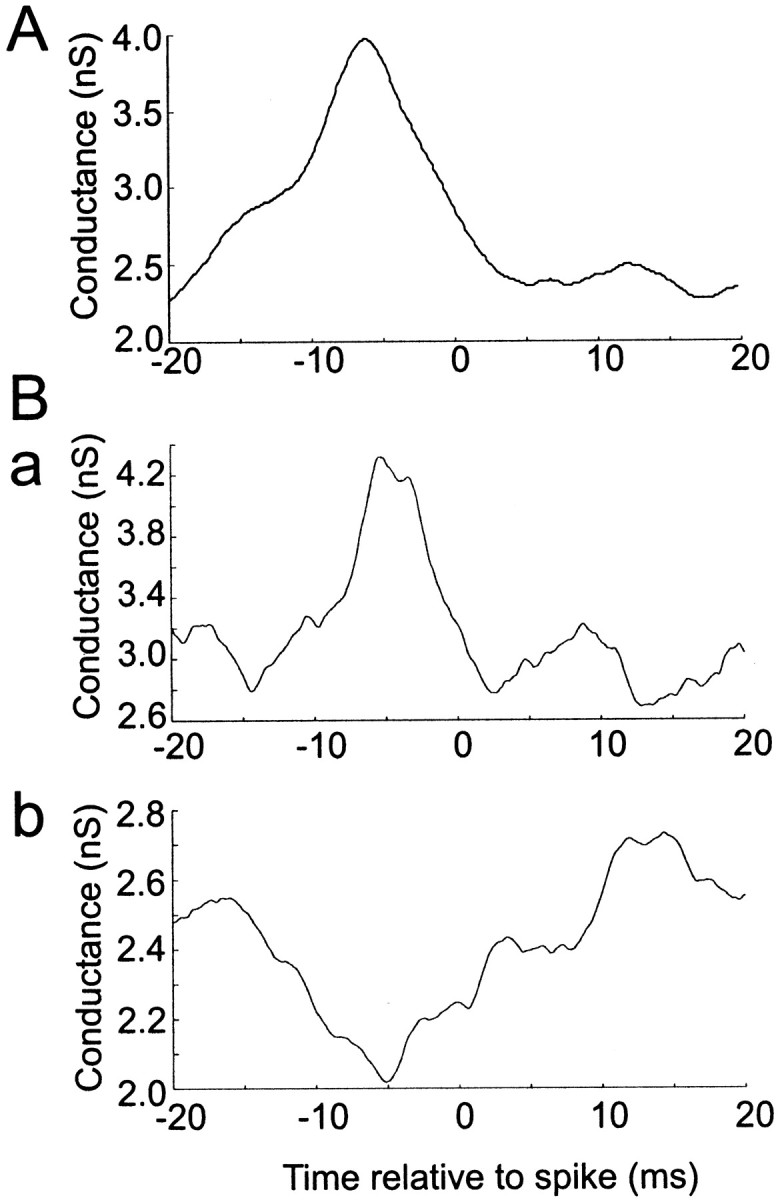
Average fast conductance changes associated with spikes. A, Spike-triggered average of AMPA conductance during Poisson AMPA stimulation, λ = 1600 Hz. B, Combined Poisson AMPA (2000 Hz) and GABA (1200 Hz) stimulation. Spike-triggered average of (a) AMPA conductance and (b) GABA conductance.

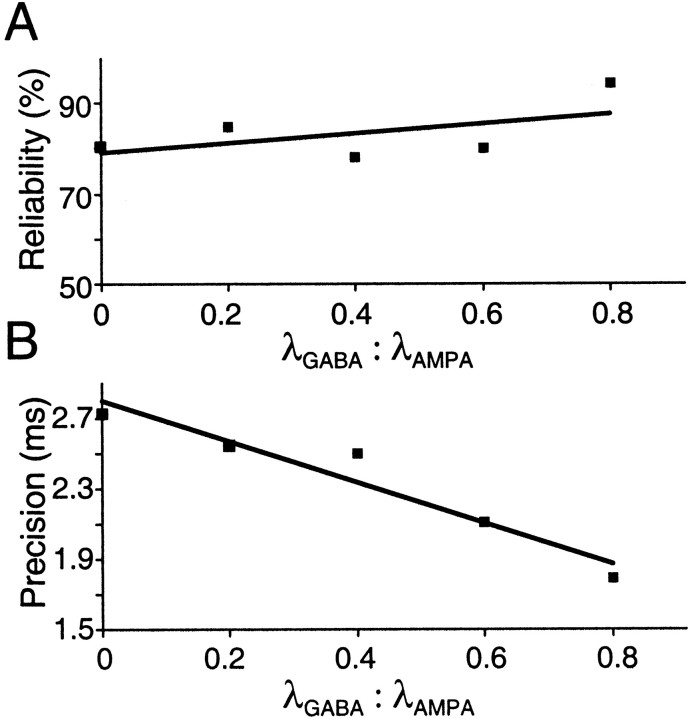
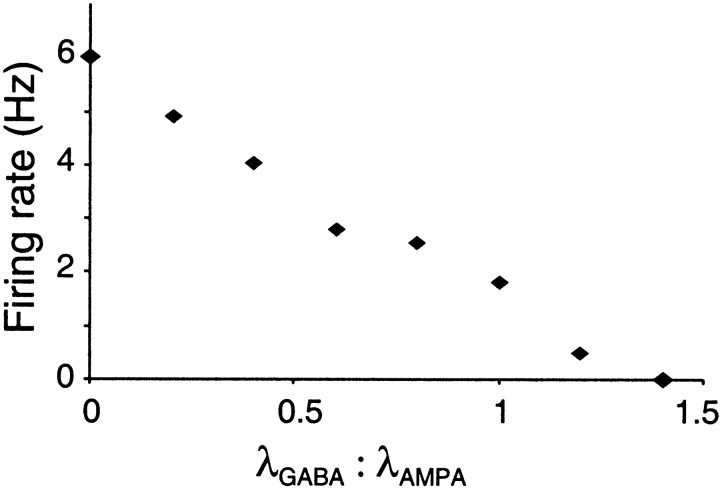
Figure 8 shows that reliability increases slightly as the proportion of inhibition is increased and jitter decreases. Increasing the λ_GABA/λ_AMPA ratio reduced firing frequency, in an approximately linear fashion (Fig.9), until firing was silenced at a ratio of 1.4:1 (for a fixed AMPA rate of 1000 Hz). A ratio of 0.8, blocking over half of the spikes, is likely to be higher than natural, considering the relative abundance of inhibitory and excitatory neurons. However, in three cells in which variability was measured using a long series of regenerated stimuli, increasing λ_GABA/λ_AMPA from 0 to 0.8 in one cell produced changes in CV and Fano factor from 0.45 to 0.52 and 0.06 to 0.12, respectively, whereas increasing λ_GABA/λ_AMPA from 0 to 0.5 in another cell changed CV and Fano factor from 0.3 to 0.4 and 0.4 to 0.29, respectively. This evidence suggests that independent shunting inhibition is unlikely to account for the high firing variability observed in vivo.

Fig. 8.

Effect of inhibition on reliability and precision. Points are averages from 10 trials, in one regular-spiking neuron.

Fig. 9.

Decrease in firing rate with increasing rate of GABA transients. λ_AMPA = 1000 Hz.

Synchronous excitation

Recently, there is increasing evidence that firing of cortical neurons is often correlated with concerted rises in activity in the surrounding network (Arieli et al., 1996; Azouz and Gray, 1999; Lampl et al., 1999;Tsodyks et al., 1999). We therefore examined how clustering of compound AMPA–NMDA conductance transients in time affected the measures of firing variability and the temporal fine structure of responses. To do this, we used a doubly stochastic model to determine the input event times, as described in detail in Materials and Methods and shown in Figure 1C, in which the rate of a nonstationary Poisson process is modulated in exponentially decaying transients (peak amplitude $\overline{R}$, decay time constant τ_b), at intervals specified by a stationary Poisson process (rate λ_b). This allowed the degree of synchrony to be varied, for any given $\overline{\lambda }$, from an effectively stationary Poisson process (high τ_b) to a highly clustered or synchronous input (τ_b ≪ 1/λ_b). This can be seen in Figure10, which shows examples of stimuli ranging from quite highly synchronous (τ_b = 0.1) to fairly evenly distributed (τ_b = 0.5), with the same mean rate of input (achieved by scaling $\overline{R}$).

Fig. 10.

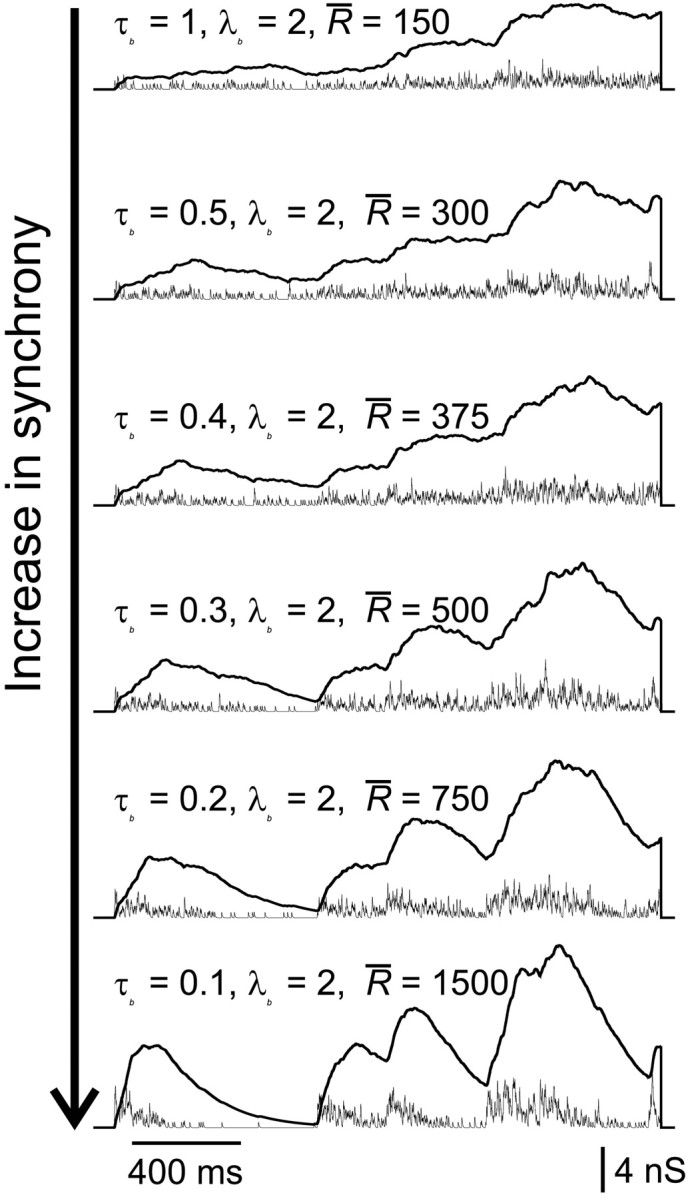
Examples of synchronous stimuli. Changing τ_b relative to λ_b (see Materials and Methods) smoothly increases the synchrony of unitary compound events (thin traces: AMPA; thick traces: NMDA). For clarity of presentation, the same burst times are used to compute each stimulus in this figure; in experiments, these were varied randomly in different stimuli.

A typical ensemble of responses to a synchronous AMPA–NMDA input is shown in Figure 11. The stimulus displays distinct clusters of events, and the cell fires in corresponding bursts. The NMDA conductance summates to high levels during a burst, and its decay phase long outlasts the period of AMPA conductance transients. Initial spikes of most bursts are fairly well aligned, whereas the precision and reliability of spikes appear to deteriorate at later stages in the burst. Alignment is particularly poor throughout the third burst, which occurs when depolarization and residual NMDA conductance is still elevated from the second burst.

Fig. 11.

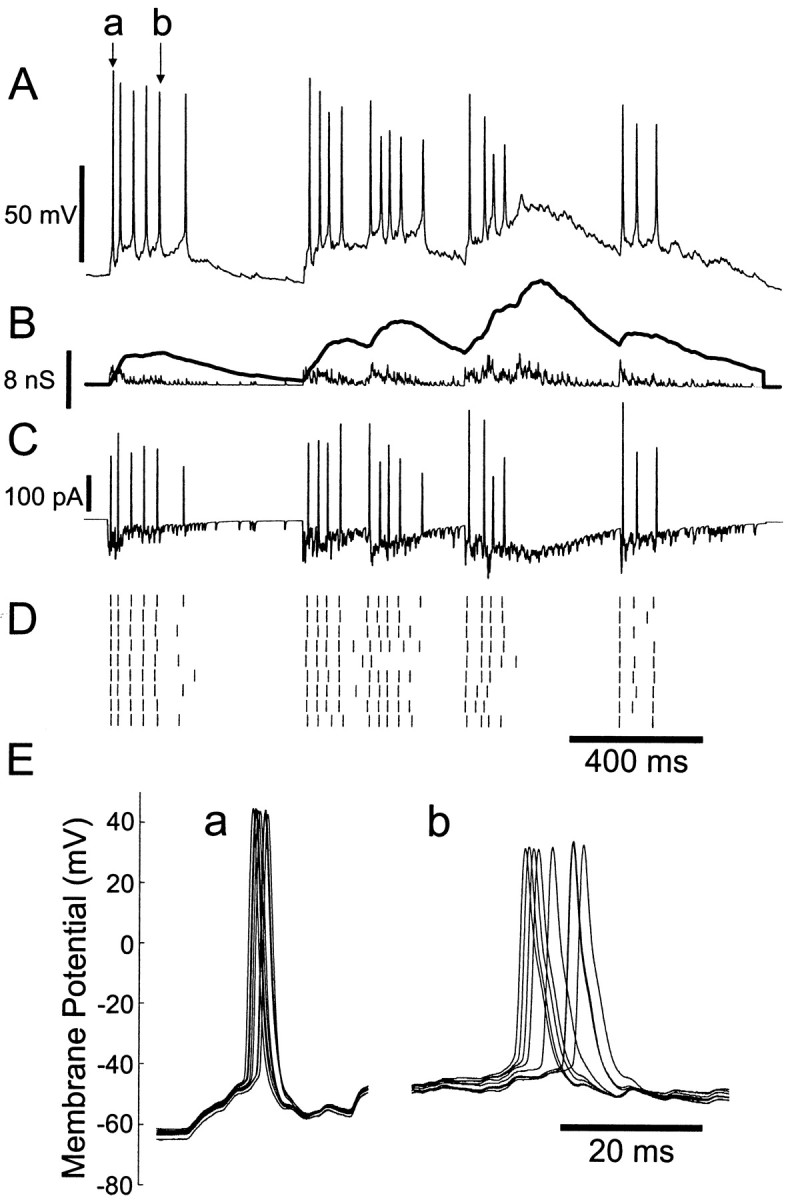
Responses to synchronous bursts of compound AMPA–NMDA conductance events, in a regular-spiking neuron. A, An example of membrane potential response (corresponding to top spike train in D). B, Conductance stimulus. Synchronized clusters of events were generated with parameters (see Materials and Methods) $\overline{R}$ = 1200 Hz, τ_b = 0.1 sec, and λ_b = 2.5 sec⁻¹. Thin line: AMPA conductance;thick line: NMDA conductance. C, Total command current resulting from interaction of conductance input and membrane potential trajectory. D, Raster plot. E, Superimposed membrane potential trajectories for precise spike a and imprecise spike b (as indicated in A).

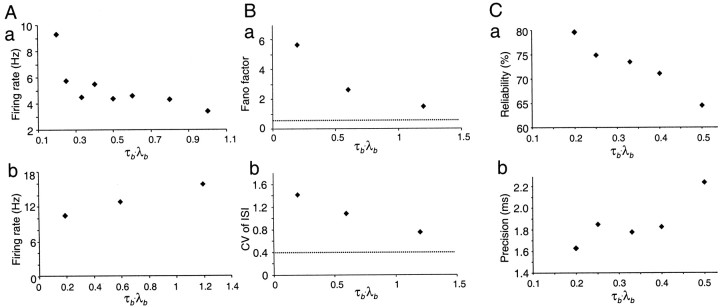
The effects of input synchrony on mean firing frequency, variability measures, and reliability and precision are shown in Figure12. Increasing synchrony had opposite effects on the mean firing rate of regular-spiking and intrinsic-bursting neurons, producing a fall in the mean firing rate of regular-spiking neurons (Fig. 12Ab), but a rise in the mean firing rate of intrinsic-bursting neurons (Fig.12Aa). This pattern was observed in three other regular-spiking neurons and three other bursting cells. This probably reflects refractoriness of the intrinsic-bursting neurons during the more maintained depolarizations in low-synchrony stimulation. In regular-spiking neurons, increasing input synchrony, by decreasing τ_b to 0.5 or below, raised the CV and Fano factor measures into the range of values observed in vivo (Fig.12B, Table 1). In ensembles of identical trials, both reliability and precision of spikes were increased by increasing synchrony (Fig. 12C).

Fig. 12.

Effect of synchrony on firing rate, spike variability, reliability, and precision. In all experiments shown, synchrony was increased by reducing the value of τ_b for a fixed value of λ_b (2 Hz), and scaling up $\overline{R}$ correspondingly to maintain the same mean rate of compound AMPA–NMDA excitatory conductance transients (300 Hz). A, Effect of synchrony on mean firing rate. a, In a fast-adapting neuron, firing rate increases with increasing synchrony. b, In a regular spiking neuron, the firing rate decreases with increasing synchrony. B, Effect of synchrony on spike timing variability in a regular-spiking neuron. Both Fano factor and CV of interspike intervals are increased by synchronous stimuli, to much higher values than for uncorrelated Poisson stimulus trains (indicated by dotted lines) and to values within the range of those commonly observed in vivo. Results are from 30 trials with resynthesized timings of unitary events in one cell. C, Increasing synchrony increases reliability (a) and reduces spike time jitter (b) in a regular-spiking cell (10 trials).

The action of NMDA conductance during synchronous input

The nonstationarity of synchronous stimuli means that the variability of spike trains changes with time. This is clearly seen in Figure 11: spikes are most reliable early in synchronous input bursts and become progressively more imprecise and unreliable with time after initiation of the burst. Because of its slow time course, the NMDA conductance plays a critical role in this phenomenon. With a burst of inputs, it produces a maintained inward current (which is also amplified nonlinearly with depolarization) (Fig. 11C). Spikes during the NMDA phase originate from a more elevated level of membrane potential and from smaller fast fluctuations of membrane potential and are smaller and slower (Fig. 11E). The effects of this are shown in Figure 13. Bursts of inputs were repeatedly applied to a regular-spiking neuron, and an ensemble of spike responses is recorded. In Figure 13A, compound AMPA–NMDA events are used, whereas in Figure 13B, pure AMPA events are used, with $\overline{R}$ increased to produce the same duration of spiking response. In Figure 13C, the precision of spikes is plotted as a function of time after the beginning of the input burst. The effect of incorporating NMDA conductance in unitary events is striking: at early times spike jitter is still fairly low, although already higher than without NMDA conductance, but there is a 2.5-fold more rapid rate of increase in jitter with time. Similar results were seen in four other cells. NMDA conductance thus modifies the dynamics of postsynaptic spiking during synchronous input, so that immediate responses to a cluster of synaptic events are precise, whereas the timing of later spikes is increasingly scattered by noise.

Fig. 13.

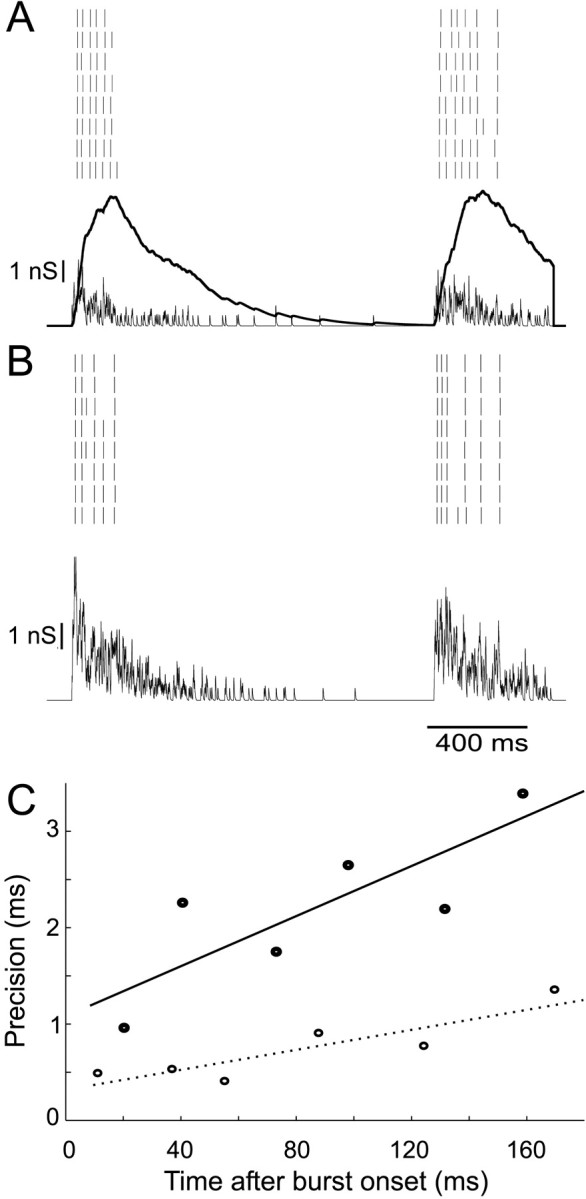
Loss of precision with time in response to synchronous bursts. A, Ensemble spike response to a synchronous stimulus (τ_b = 0.2, λ_b = 1, $\overline{R}$ = 800 Hz) of compound AMPA (thin line) and NMDA (thick line) conductances. B, Response of the same neuron to an AMPA-only conductance stimulus, in which $\overline{R}$ is increased to 2000 Hz to give the same duration of response. C, The jitter of identified spikes increases with time after onset of burst. With NMDA conductance (•), the rate of this increase is approximately three times faster than without (○).

DISCUSSION

In this work, we have demonstrated that cortical neurons can be stimulated to fire by precisely controlled but electrically natural conductance input and that postsynaptic mechanisms do add significant variability to cortical responses. We showed that substantial synchrony of conductance inputs is necessary to explain in vivovariability and ruled out a major role for independent random inhibition. Finally, we demonstrated that NMDA receptor conductance promotes a switch from early precise firing to late random firing during responses to concerted inputs.

Conductance inputs

In these experiments, in contrast to previous studies of integration in cortical neurons, the stimulus consisted of a controlled conductance rather than a predetermined pattern of current. The distinction is important because the current injected by a single conductance event depends dynamically on the membrane potential (Eq. 1). For AMPA conductance, current is almost halved by depolarization to the typical threshold for spikes during maintained activity and is reversed during spikes. For GABA conductance, whose reversal potential is near the resting potential, the fractional change in current is a steep function of membrane potential, and current changes sign frequently below threshold; shunting inhibition gives fundamentally different dynamic behavior from a fixed pattern of hyperpolarizing current. The voltage dependence of NMDA conductance suppresses current at rest but causes latent activation to be rapidly uncovered as the membrane is depolarized toward threshold.

Some important aspects of natural synaptic conductance are still not captured by these synthetic conductance stimuli. In this study, conductance was injected at the soma, not throughout the dendritic tree. However, this may have little effect on the statistical trends that we have measured. Spikes initiate consistently at the soma or proximal axon (Stuart and Sakmann, 1994), and simulations of cerebellar Purkinje cells have shown that the interval distributions of spikes produced by focal or distributed conductance inputs are little different (Jaeger and Bower, 1999). The greater voltage dependence of the current through GABA conductance (because of proximity to E_rev) and NMDA conductance may mean that the difference between somatic and distributed injection is greater for these components. This point needs to be examined in future studies, for example using conduction injection in the dendrite. Secondary effects of calcium influx through the NMDA receptors are also not reproduced, but influx through voltage-gated calcium channels, a far more significant source of calcium (Miyakawa et al., 1992), ought to occur normally.

Variability of firing during steady excitation

The statistical measures of spike variability used in this study average over many spikes arising from different trajectories of membrane potential to try to capture the overall behavior of cells in different stimulation conditions and to allow comparison with previous work. The variability of responses combines the variability of the presynaptic input and the unreliability of the postsynaptic neuron. The latter is clearly separated by measuring ensembles of responses to identical input, as in Figures 3 and 11. Mainen and Sejnowski (1995) reported that “stimuli with fluctuations resembling synaptic activity produced spike trains with timing reproducible to less than 1 millisecond.” However, at similar firing frequencies, we find less precision during stationary Poisson excitation, composed of either unitary AMPA or compound AMPA–NMDA conductance events. Although precisions of 1.75 msec (AMPA), 2.3 msec (AMPA–NMDA), or 1.6 msec (highly synchronous AMPA–NMDA events) were measured (Table 2), these are averages for those spikes that satisfied the strict criterion for repeatability. Inspection of spike trains (Fig. 3B,C) and cross-correlations (Fig. 6) shows that many reproducible spikes have much higher jitter (up to 30 msec) and often fail altogether. The postsynaptic cell can clearly produce a significant component of the overall variability of firing and contribute to the jitter in response to sensory stimuli (Bair and Koch, 1996; Oram et al., 1999). The principal source of this is likely to be stochastic gating of postsynaptic ion channels (White et al., 2000).

Nevertheless, in response to steady Poisson AMPA excitation, the total variability of spiking was far below that in vivo, where both CV and Fano factor exceed 1 at comparable firing rates (Buracas et al., 1998; Stevens and Zador, 1998). Adding NMDA conductance in Poisson excitation caused more regular firing, increasing this shortfall.

The effect of independent shunting inhibition on firing variability

Shadlen and Newsome (1998) suggested that the high variability of cortical neuron spiking might result from independent random inhibitory input, producing larger fluctuations for the same mean level of input. Häusser and Clark (1997)established clearly that spontaneous inhibitory input can greatly increase the variability of firing in cerebellar Purkinje cells and inhibitory interneurons. However, Stevens and Zador (1998) showed that in cortical neurons, independent Poisson trains of IPSCs failed to reproduce in vivovariability, although CV and Fano factor increased up to twofold, for an inhibitory/excitatory current ratio of 0.9. We performed a similar experiment (Fig. 3D), except that we used GABA-type conductance transients to oppose Poisson AMPA excitation with shunting inhibition. Even a very high level of inhibition (λ_GABA/λ_AMPA = 0.8) had a much smaller effect, producing only a slight increase in CV and an insignificant change in Fano factor. This difference appears to reflect the conductance nature of our inhibitory stimulus. The large variability caused by spontaneous inhibitory input demonstrated byHäusser and Clark (1997) could have resulted from synchrony in the presynaptic network of cerebellar inhibitory interneurons. We did not test the effect of synchronizing inhibitory conductance transients.

We also found, perhaps surprisingly, that a fluctuating background of inhibition markedly improved the postsynaptic precision and reliability of spikes (Fig. 8), a phenomenon that has not, to our knowledge, been highlighted previously. This effect may arise from suppression of subthreshold voltage fluctuations and a faster membrane time constant during activation of inhibitory conductance.

Synchronous input drive to cortical neurons

Leaky-integration behavior means that the most effective stimulus for causing a cell to spike is near-coincident activation of multiple synaptic inputs. It would be reasonable to suppose, therefore, that the dynamics of local network activity is attracted to synchronous firing. There is now evidence in vivo that spikes are driven by concerted surges in activity in multiple nearby cells (Azouz and Gray, 1999; Tsodyks et al., 1999). Networks of cultured cortical cells also fire spontaneous synchronized bursts at random intervals (Maeda et al., 1995). We therefore introduced correlations, or synchrony into the timing of excitatory stimuli, using a nonstationary Poisson process. The structure of the synchronous stimulus used by Stevens and Zador (1998) is not fully described but consisted of “the nearly synchronous (30–50 msec) arrival of on average about 100 to 200 EPSCs, yielding peak currents of 1 to 2 nA,” at a Poisson rate of 10 Hz. We found, in agreement with Stevens and Zador (1998), that synchronously structured excitation increases variability for the same mean input rate and makes it easy to increase variability to thein vivo levels. This general conclusion can be readily understood, because the variability of the input is greatly increased by the doubly stochastic input, and spike intervals exhibit two different time scales: within and between bursts.

By varying the duration of clusters relative to their rate, we could systematically vary the degree of synchrony in the input. A monotonic relationship was found between each variability measure and the degree of synchrony in single cells (Fig. 12B), indicating clearly that the variability is controlled by the level of synchrony. Increased synchrony also raised reliability and improved precision (Fig. 12) in this respect, offsetting the effect of including NMDA conductance in compound unitary events. We confirmed by spike-triggered averaging that during synchronous stimuli, the “average” spike is driven by a larger excitatory fluctuation of conductance (data not shown).

The effect of NMDA conductance in compound unitary events

To our knowledge, this is the first experimental study, in any system, to incorporate the slow decay and nonlinear voltage dependence of the NMDA receptor-mediated phase of excitatory postsynaptic events in a controlled electrical stimulus. This allowed us to characterize precisely its effect on firing variability. It regularized firing, yet in ensemble responses it increased jitter and reduced reliability. This inverse relationship between regularity and precision occurs because precise responses allow the cell to follow irregularity in the stimulus more accurately. Adding NMDA conductance shifts power in the stimulus current toward lower frequencies (Fig. 11C), which produces more regular, less dependable firing (Nowak et al., 1997). The size of fast fluctuations in membrane potential that are required for precise spike responses (Mainen and Sejnowski, 1995; Nowak et al., 1997) is reduced, because of the reduced proportion of excitation delivered by fast AMPA transients and the increased proportion delivered by maintained NMDA conductance. The basis for this effect may be that the more smoothly sustained depolarization will inactivate a greater fraction of voltage-gated sodium and low-threshold calcium channels near the threshold for spiking. The cell would then fail to fire in response to smaller surges in excitatory conductance, instead integrating the excitation over a longer period of time (increasing regularity, as observed), whereas the weaker membrane nonlinearity would allow the timing of individual spikes to be more easily scattered by postsynaptic noise.

A more complex effect of NMDA conductance emerges in the context of synchronous inputs. It leads to a sustained late phase of less precise firing after a cluster of inputs (Figs. 11, 13). This could have important functional consequences. For example, a population of identical neurons receiving the same complex burst input would respond initially with highly synchronized timing. The alignment of action potentials in different cells would then degrade progressively during the NMDA phase, yielding firing in the whole population that is much more evenly spread out in time. Thus information from the synchronous input would reside in precise spike timing during the early phase of the response but simply in the rate of firing in the population during the sustained phase. Functionally, this would allow initial rapid processing to be performed reliably but provide a stabler, longer-lasting “trace” of the activation in the network. Loss of information and reliability during the NMDA phase of population responses of cultured cortical networks to extracellular stimulation has recently been demonstrated by Pinato et al. (1999).