Mitochondrial Membrane Potential and Glutamate Excitotoxicity in Cultured Cerebellar Granule Cells

Abstract

The relationship between changes in mitochondrial membrane potential (Δψ_m) and the failure of cytoplasmic Ca²⁺ homeostasis, delayed Ca²⁺deregulation (DCD), is investigated for cultured rat cerebellar granule cells exposed to glutamate. To interpret the single-cell fluorescence response of cells loaded with tetramethylrhodamine methyl ester (TMRM⁺) or rhodamine-123, we devised and validated a mathematical simulation with well characterized effectors of Δψ_m and plasma membrane potential (Δψ_P). Glutamate usually caused an immediate decrease in Δψ_m of <10 mV, attributable to Ca²⁺ accumulation rather than enhanced ATP demand, and these cells continued to generate ATP by oxidative phosphorylation until DCD. Cells for which the mitochondria showed a larger initial depolarization deregulated more rapidly. The mitochondria in a subpopulation of glutamate-exposed cells that failed to extrude Ca²⁺ that was released from the matrix after protonophore addition were bioenergetically competent. The onset of DCD during continuous glutamate exposure in the presence or absence of oligomycin was associated with a slowly developing mitochondrial depolarization, but cause and effect could not be established readily. In contrast, the slowly developing mitochondrial depolarization after transient NMDA receptor activation occurs before cytoplasmic free Ca²⁺([Ca²⁺]_c) has risen to the set point at which mitochondria retain Ca²⁺. In the presence of oligomycin no increase in [Ca²⁺]_c occurs during this depolarization. We conclude that transient Ca²⁺loading of mitochondria as a consequence of NMDA receptor activation initiates oxidative damage to both plasma membrane Ca²⁺ extrusion pathways and the inhibition of mitochondrial respiration. Depending on experimental conditions, one of these factors becomes rate-limiting and precipitates DCD.

Pathological activation of NMDA receptors, with consequent disturbance in Na⁺ and Ca²⁺gradients across the plasma membrane, is a primary cause of delayed neuronal death after brain anoxia or ischemia (Rothman and Olney, 1986;Choi and Rothman, 1990; Yoshimura et al., 1998). Prolonged NMDA receptor activation in cultures of primary neurons from spine (Tymianski et al., 1993a), cerebellum (Kiedrowski et al., 1994;Kiedrowski and Costa, 1995; Budd and Nicholls, 1996a; Castilho et al., 1998), forebrain (Hoyt et al., 1992; Rajdev and Reynolds, 1994), striatum (Greene et al., 1998), or hippocampus (Dubinsky and Rothman, 1991; Randall and Thayer, 1992; Dubinsky, 1993; Keelan et al., 1999;Vergun et al., 1999) can result in a failure of the cell to maintain low, stable cytoplasmic free calcium ([Ca²⁺]_c). This delayed Ca²⁺ deregulation (DCD) precedes and reliably predicts the subsequent necrotic death of the cell (Tymianski et al., 1993b) and has been used extensively to model aspects of in vivo neuronal necrosis.

The potential across the inner mitochondrial membrane (Δψ_m) is the central parameter that controls mitochondrial respiration, ATP synthesis, and Ca²⁺ accumulation (for review, seeNicholls and Ferguson, 1992; Nicholls and Budd, 2000) as well as the generation of reactive oxygen species (Boveris et al., 1972; Van Belzen et al., 1997). Because each of these factors can influence the survival of the cell directly or indirectly, the monitoring of Δψ_m in glutamate-exposed neurons provides important information on the mechanism by which mitochondria influence the survival of glutamate-exposed neurons. The matrices of the in situ mitochondria load with Ca²⁺during glutamate exposure (White and Reynolds, 1995; Budd and Nicholls, 1996a; Wang and Thayer, 1996; White and Reynolds, 1997), and there is a general consensus that exposure of the neurons to glutamate results in a qualitative mitochondrial depolarization (Ankarcrona et al., 1995;Budd and Nicholls, 1996a; Isaev et al., 1996; Khodorov et al., 1996;Schinder et al., 1996; White and Reynolds, 1996; Kiedrowski, 1998;Prehn, 1998; Scanlon and Reynolds, 1998; Stout et al., 1998; Almeida et al., 1999; Keelan et al., 1999; Vergun et al., 1999). However, the cause, extent, and bioenergetic consequences of such depolarization remain unclear and need further clarification. Conversely, previous depolarization of mitochondria under conditions that prevent ATP depletion protects cultured neurons against DCD (Budd and Nicholls, 1996a; Castilho et al., 1998; Stout et al., 1998).

Fluorescent membrane-permeant cations are used widely to monitor Δψ_m in these circumstances (for review, seeNicholls and Ward, 2000), but interpretation of the complex signals obtained at single-cell resolution is far from trivial and has led to confusing and contradictory conclusions. To help resolve these issues, we have compared experimental traces with those obtained from a simple simulation of the whole-cell fluorescence in response to imposed changes in Δψ_m and plasma membrane potential (Δψ_p). Results are consistent with both mitochondrial depolarization and failed Ca²⁺ extrusion from the cell, the factor precipitating DCD depending on which first becomes rate-limiting under the experimental conditions.

MATERIALS AND METHODS

Materials. Fura-2 acetoxymethyl ester (fura-2 AM), rhodamine-123, and tetramethylrhodamine methyl ester (TMRM⁺) were obtained from Molecular Probes (Leiden, The Netherlands). Fetal calf serum and MEM were from Life Technologies (Paisley, Strathclyde, UK). Oligomycin, rotenone, and all other reagents were from Sigma (Poole, Dorset, UK).

Preparation of cerebellar granule cells. Granule cells were prepared as previously described (Courtney et al., 1990) from 6–7 d postnatal Wistar rats. Cells were plated on poly-d-lysine-coated glass coverslips (13 mm circular for nonperfusion experiments and 22 mm square for confocal microscopy) at a density of 280,000 cells per coverslip. Cells were cultured in MEM containing Earle's salts (Life Technologies) plus 10% (v/v) fetal calf serum, 25 mm KCl, 30 mm glucose, 2 mm glutamine, 100 μg/ml streptomycin, and 100 U/ml penicillin. After 24 hr 10 μm cytosine arabinoside was added to inhibit non-neuronal cell proliferation. Cells were maintained at 37°C in a humidified atmosphere of 5% CO₂/95% air and were used after 6–7 d in vitro (DIV).

Incubation conditions. Unless otherwise stated, incubations were performed at 37°C in medium containing (in mm) 120 NaCl, 3.1 KCl, 0.4 KH₂PO₄, 5 NaHCO₃, 1.2 Na₂SO₄, 1.3 CaCl₂, and 20 TES [N-tris(hydroxymethyl)methyl-2-aminoethane sulfonic acid] pH-adjusted to 7.4 at 37°C with NaOH. Unless otherwise stated, incubation media are Mg²⁺-free.

Epifluorescent imaging. Single-cell imaging was performed in a MiraCal Imaging facility (Life Science Resources, Cambridge, UK) with a Nikon DIAPHOT-TMD inverted epifluorescence microscope equipped with a 40× oil immersion objective and Sutter filter wheel. The imager was equipped with a Lambert intensifier 1187 (Life Science Resources) providing a 30× enhancement of the fluorescent signal, thus limiting photo toxicity. For imaging TMRM⁺, we equilibrated the cells with 50 nmTMRM⁺ (unless otherwise stated) for 30 min at 37°C before the experiment. In most experiments the dye, which was also present during the experiment, was excited via an Omega 485DF22 filter with peak transmission at 485 nm. The absorbance of TMRM⁺ is only 10% of maximum at this wavelength, but this has the advantage of limiting photodynamic damage to the cells at the concentrations of TMRM⁺ that are required to observe matrix quenching. Additionally, the use of this filter allows a dichroic/barrier filter transmitting at >520 nm to be used for both single dye and combined TMRM⁺ plus fura-2 imaging. However, experiments performed with 340/380/535 nm excitation and a Chroma fura-2/rhodamine dichroic gave essentially the same results (data not shown).

For dual loading the cells were loaded with 50 nmTMRM⁺ and 3 μm fura-2 AM for 25 min at 37°C in incubation medium containing additionally 30 μg/ml bovine serum albumin, 15 mm glucose, and 1.2 mm MgCl₂. After washing, the cells were incubated in the presence of 50 nmTMRM⁺ and were excited at 340/380/485 nm with emission >20 nm. Background subtraction and autofluorescence were corrected for, and controls were performed with cells loaded singly with either TMRM⁺ or fura-2, which established the absence of any significant crosstalk between the dyes at the wavelengths that were used. Fura-2 fluorescence is reported in terms of 340/380 nm excitation ratios to avoid potential errors because of any changes in the quenching of the >520 nm emission by cytoplasmic TMRM⁺.

For rhodamine-123 fluorescence a commonly used empirical loading protocol was applied (Khodorov et al., 1996; Hagen et al., 1997;Buckler and Vaughan-Jones, 1998; Schuchmann et al., 1998; Vergun et al., 1999). Cells were equilibrated with the probe (1 μg/ml, i.e., 2.6 μm) for 15 min at 22°C before the experiment; the probe was not added to the experimental medium. Then the cells were washed before the experiment (excitation 485 nm; emission >520 nm). It was found that an alternative loading paradigm [10 μg of rhodamine-123/ml (26 μm) for 15 min] sensitized the cells to photo-induced damage (data not shown).

TMRM⁺ fluorescence within the matrix of isolated mitochondria. TMRM⁺ (100 nm or 2 μm) was added to a medium containing (in mm) 100 NaCl, 25 TES (Na⁺salt), and 2 NaH₂PO₄ plus 16 μm albumin, pH 7.0, 37°C, in a thermostatted cuvette inserted in a Perkin-Elmer LS50B fluorometer. Fluorescence was recorded (excitation 543 nm, emission 580 nm) during the sequential additions of rat liver mitochondria (0.25 mg of protein/ml incubation), prepared as previously described (Nicholls, 1978), and 2 mm succinate. Fluorescent quenching after uptake of the probe was determined. The cuvette contents were centrifuged immediately for 30 sec in an Eppendorf microcentrifuge to pellet the mitochondria. The fluorescence of the supernatant was measured to determine the contribution of extramitochondrial TMRM⁺ to the total signal, and the mitochondrial pellet was resuspended in water to determine the fluorescence of the mitochondrial TMRM⁺ after release from the matrix. The assumption that the matrix fluorescence became invariant above the stacking concentration was tested by incubating isolated mitochondria in the presence of two widely differing concentrations of TMRM⁺, each sufficient to exceed the stacking concentration in the matrix, as confirmed by the decrease in cuvette fluorescence when the mitochondria were energized (Fig.1). The contribution of the quenched matrix TMRM⁺ to the total cuvette fluorescence was quantified by redetermining the fluorescence of the incubation after removing the mitochondria by centrifugation as described above. Figure 1 shows that the fluorescence of the matrix-located probe was similar for mitochondria equilibrated with both 100 nm and 2 μmTMRM⁺, although the actual concentration of TMRM⁺ in the matrix, confirmed by lysis of the mitochondria to release TMRM⁺, differed 12-fold.

Fig. 1.

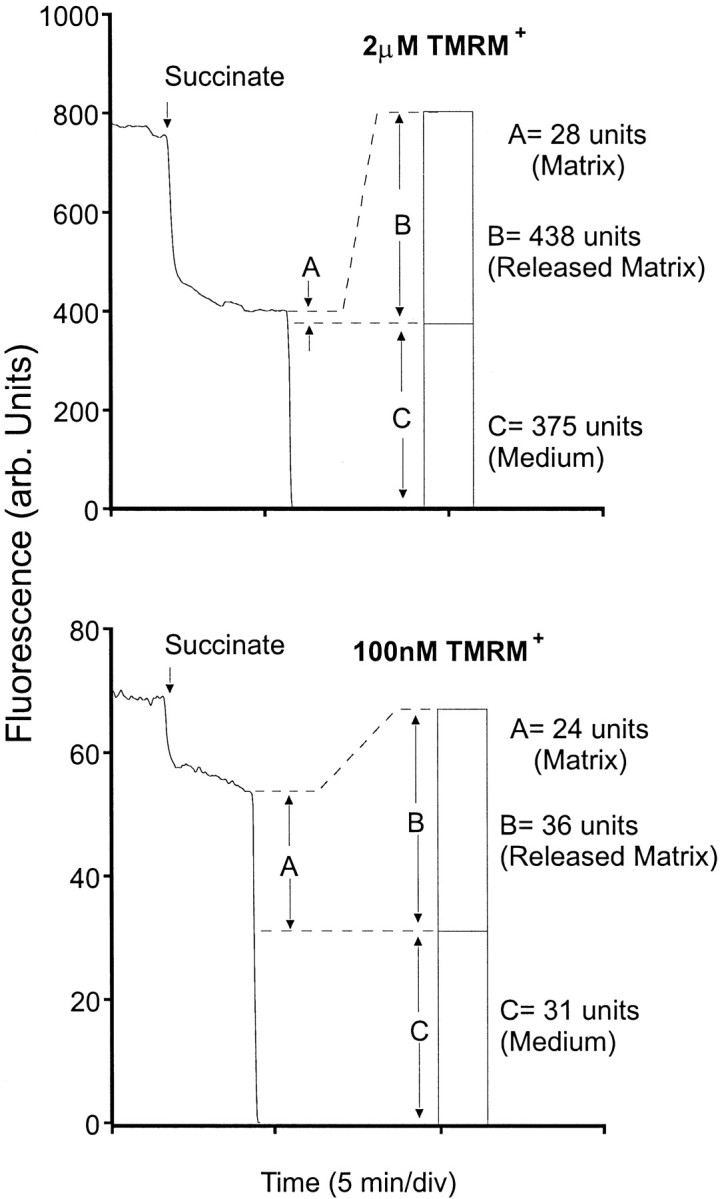
The fluorescence of TMRM⁺ in the mitochondrial matrix is concentration-independent above the quench threshold. A suspension of rat liver mitochondria was equilibrated with the indicated concentrations of TMRM⁺ in the absence of substrate, and the fluorescence was monitored. The addition of succinate as a substrate caused a decrease in fluorescence as the indicator was accumulated into the matrix. The contribution of the extramitochondrial probe to the total fluorescence (C) was determined after the removal of mitochondria by centrifugation. The difference (A) attributable to the fluorescence of matrix TMRM⁺ was similar at both concentrations although the total matrix TMRM⁺ (B), determined by resuspending the mitochondria in water, differed by 12-fold.

Simulating single-cell fluorescence of neurons loaded with membrane-potential probes. The simulation (see ) is based on the following premises. (1) Cationic lipophilic probes are nonselectively permeant across both plasma and mitochondrial membranes. (2) Probe distribution tends to a Nernst equilibrium across both membranes. (3) The rate at which the probe equilibrates across the small, highly invaginated inner mitochondrial membrane is much faster than across the plasma membrane because of the differing surface–volume relationships of the mitochondrial matrix and the cell soma. (4) The quantum yield of the probe is similar in both cytoplasm and matrix until a threshold concentration is reached in the latter, above which nonfluorescent H-aggregates form (Bunting, 1992) (Fig.1).

The initial Δψ_p was taken to be −60 mV (Becherer et al., 1997). The initial value of 150 mV for Δψ_m is in agreement with values determined by the distribution of the lipophilic cation TPP⁺ in synaptosomes after correction for the plasma membrane potential (Scott and Nicholls, 1980). The mitochondrial matrix within isolated nerve terminals accounts for 3% of terminal volume (Scott and Nicholls, 1980), whereas the lower value of 1% taken here for the soma reflects the relatively thin annulus of cytoplasm surrounding the nucleus.

The model is used to reproduce the behavior of two commonly used fluorescent probes, rhodamine-123 and TMRM⁺. The tetramethylrhodamine ester equilibrates more rapidly across membranes than the slowly permeant rhodamine-123 (Bunting, 1992), and empirical fits with experimental traces were obtained with a value for the permeability constantk for equilibration across the somatic plasma membrane in the presence of glutamate of 0.02/sec for TMRM⁺ and 0.001/sec for rhodamine-123. It should be emphasized that these values are for the somata of cultured cerebellar granule cells and would be lower for larger cells or conversely increased for thin neurites. In the absence of glutamate, probe equilibration was limited by constraints of charge neutralization across the plasma membrane (see Fig. 10), and lower values ofk were determined empirically.

Fig. 10.

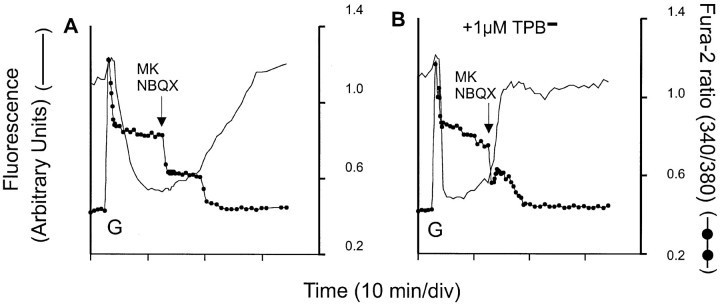
Tetraphenylboron accelerates plasma membrane equilibration of TMRM⁺. The 7 DIV cells were loaded with fura-2 and TMRM⁺ as in Figure 6 and exposed to 100 μm glutamate plus 10 μm glycine (G). Where indicated, 10 μm each of MK 801 and NBQX (MK/NBQX) was added. Tetraphenylboron (1 μm;TPB⁻) was additionally present inB.

The simulated “loading conditions” for the two probes followed the empirically determined optimal conditions that were used in this study. Because TMRM⁺ is rapidly lost from cells in the absence of external probe, the granule cells were equilibrated with probe, usually 50 nm, and this concentration was also present continuously in the “incubation” to allow continuous reequilibration across the plasma membrane. The less permeant rhodamine-123 is normally loaded by a brief exposure (insufficient for Nernstian equilibration across the plasma membrane) to a relatively high concentration of probe, typically 2–20 μm (Vergun et al., 1999). After this the cells are washed, and the subsequent experiments usually are performed in the absence of external probe. Where indicated, the simulation reflects this. In view of the lower permeability of this probe, loss across the plasma membrane is sufficiently slow to permit most (but not all; see Fig. 2) short-term experiments to be performed without excessive loss of probe from the cells.

Fig. 2.

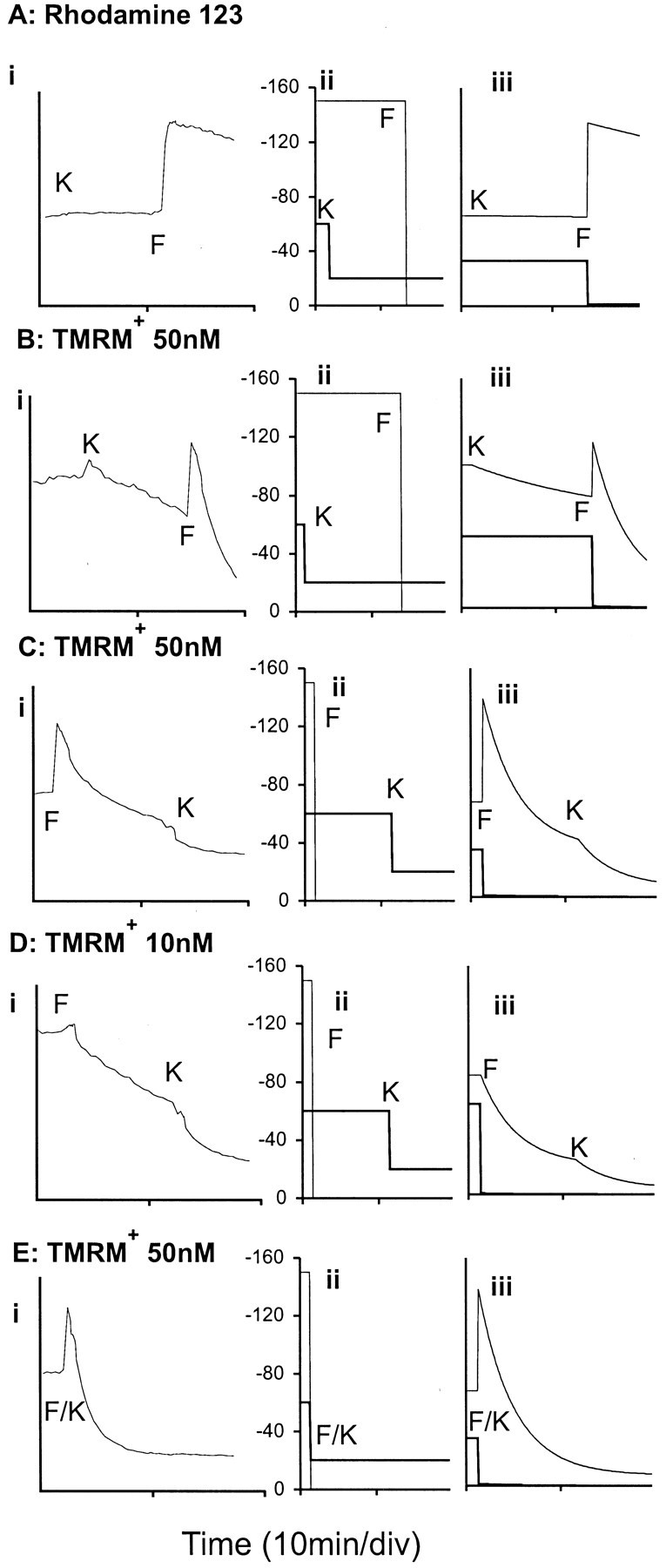
Fluorescence of individual granule cell somata loaded with rhodamine-123 or TMRM⁺ in response to selective plasma and mitochondrial membrane depolarization; curve fitting with the cell simulation. The incubation medium contained 1.2 mm MgCl₂. Ai–Ei, Granule cells were loaded with rhodamine-123 or TMRM⁺, as detailed in Materials and Methods. Where indicated, 50 mm KCl (K) or 5 μg/ml oligomycin plus 1 μm FCCP (F) was added, and the fluorescence was monitored. Each trace is from a single representative soma. Aii–Eii, Values for Δψ_m (thinline) and Δψ_p (thick line) used for the cell simulation. Aiii–Eiii, Cell simulation; total fluorescence (thin line) and mitochondrial component of fluorescence (thick line) are shown. The following parameters were used: matrix volume = 1% of cytoplasm; quench threshold = 50 μm; rate constant for plasma membrane equilibration = 0.0003/sec (rhodamine-123) or 0.003/sec (TMRM⁺).

Statistics. Each set of single-cell responses shown is representative of at least 60 individual cell somata that were monitored in at least three independent experiments from different cell preparations. Significance was assessed by unpaired variance Student'st test.

RESULTS

Validation of the simulation

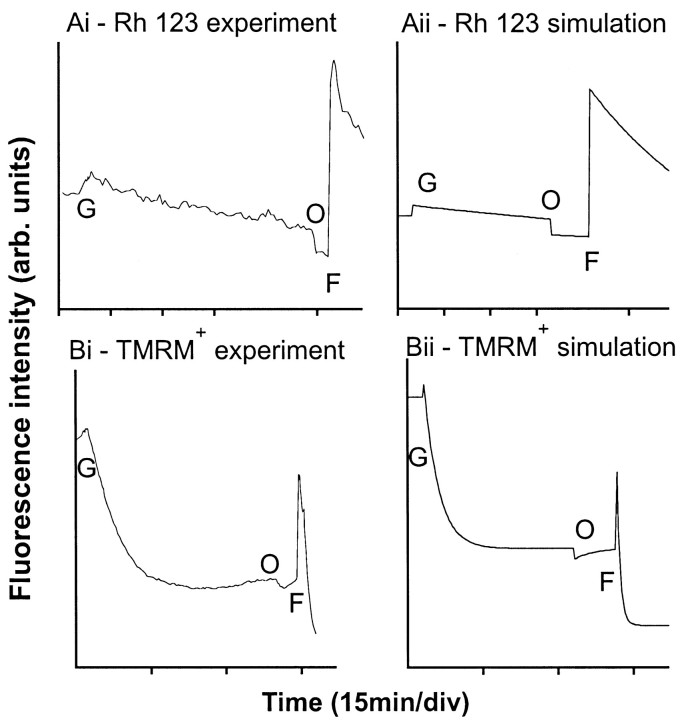
Figure 2 displays a gallery of fluorescence traces obtained by the addition of elevated KCl and FCCP/oligomycin to granule cells exposed to 2.6 μmrhodamine-123 for 15 min at 22°C before the experiment (Fig.2A) or equilibrated with either 50 nm(Fig. 2B,C,E) or 10 nmTMRM⁺ (Fig. 2D). Also shown are curves generated by the cell simulation for step changes in Δψ_p and Δψ_mthat would be induced by these agents. The simulated curves were fit to the experimental traces by varying the plasma membrane permeability coefficient, k, appropriate for TMRM⁺ and rhodamine-123 (see Eq. 9) until a satisfactory fit was obtained. Values of 0.003/sec (TMRM⁺) and 0.0003/sec (rhodamine-123) were adopted for these traces. A further empirically determined constant is the threshold concentration at which aggregation and quenching of the probe occur in the matrix. This was established by determining the loading concentration for TMRM⁺ at which protonophore-induced dequenching disappeared. Thus equilibration with 50 nm TMRM⁺ allows dequenching to be observed (Fig. 2C), but this vanishes when the loading concentration is reduced to 10 nm(Fig. 2D). With the initial conditions of a Δψ_p of −60 mV and a Δψ_m of 150 mV, this corresponds to a quench threshold (c⁺_[stacking]) (see Eq. 4) of ∼50 μm within the matrix, and this value was adopted for subsequent simulations.

Several features are revealed by these calibrating traces. When the cells are equilibrated with sufficient probe to exceed the matrix quench threshold, acute mitochondrial depolarization produces a spike followed by a decay in signal (Fig. 2A,B); when loading is subthreshold (Fig. 2D), only the decay phase is seen. This may reconcile some of the confusion in the literature as to the signal expected from a mitochondrial depolarization.

Because the total fluorescence of a single cell is the sum of that originating from the cytoplasm and matrix whereas the matrix fluorescence is invariant above the quench threshold, the changes in fluorescence mainly reflect changes in cytoplasmic probe concentration. The short-term insensitivity of rhodamine-123 to changes in Δψ_p (Fig. 2A) can be ascribed to the low permeability coefficient, although as will be seen later (see Fig. 8) there are important conditions for which this is not valid. In contrast, TMRM⁺ redistribution across the plasma membrane must be considered under all conditions, particularly with small somata such as those of granule cells. Equilibration of TMRM⁺ across the plasma membrane after KCl depolarization is slower than after protonophore (Fig. 2B), consistent with the increased buffering in the presence of the mitochondrial pool (see ). Finally, the decreased cell fluorescence after the decay of the FCCP/oligomycin “spike” (e.g., Fig. 2B) is attributable to the loss of the unquenched component of the mitochondrial TMRM⁺ fluorescence.

Fig. 8.

Temporal relationship between mitochondrial depolarization and DCD for granule cells exposed to glutamate/glycine. Cells were loaded with fura-2 and either 50 nmTMRM⁺ (A, B) or 2.6 μmrhodamine-123 (C). Where indicated, 100 μm glutamate plus 10 μm glycine was added to the incubation. D, Simulated depolarization time courses used to fit the experimental TMRM⁺ or rhodamine traces. The simulated plasma membrane potential changes from −60 to −20 mV on glutamate addition, whereas Δψ_m undergoes an initial 5 mV depolarization on glutamate addition, followed by an exponentially developing collapse in Δψ_m. Four increasing rates of mitochondrial depolarization are shown in the simulation. E, F, Simulated responses to glutamate of a cell loaded with TMRM⁺ (E) or rhodamine-123 (F) during the depolarization protocols shown inD. Smooth traces, TMRM⁺ or rhodamine-123 fluorescence; filled circle traces, fura-2 fluorescence ratio.

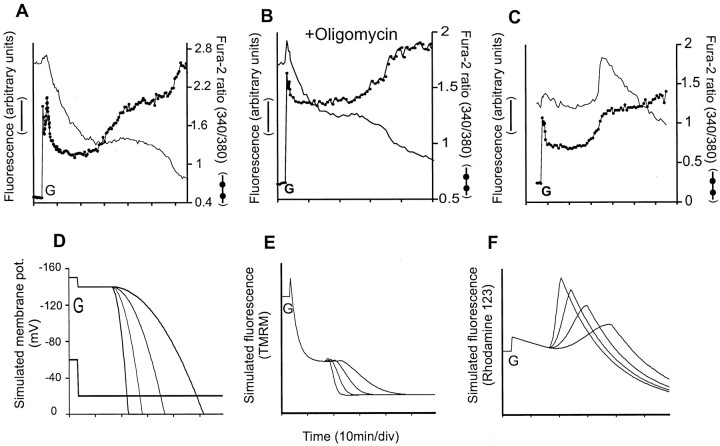
The cell simulation was devised to interpret the single-cell fluorescence responses during the complex, slow changes in Δψ_m associated with glutamate exposure and the delayed Ca²⁺ deregulation that occurs as a consequence of glutamate excitotoxicity (Tymianski et al., 1993b;Budd and Nicholls, 1996a). Figure 3investigates the effects of inhibitors of the respiratory chain and ATP synthase. Because the membrane potential of in situmitochondria in the presence of respiratory chain inhibitors is supported by ATP synthase reversal and hydrolysis of glycolytic ATP, respiratory chain inhibitors cause only a slight depolarization in cells with active glycolysis (Scott and Nicholls, 1980). However, the further addition of oligomycin to inhibit the ATP synthase will initiate a decay of Δψ_m, the kinetics of which will be limited by the inherent proton permeability properties of the inner mitochondrial membrane. Studies with isolated mitochondria indicate the presence of a non-ohmic inner membrane proton conductance, large at high potential and changing at lower potential to a decreased “ohmic” conductance (Nicholls, 1974; Nobes et al., 1990).

Fig. 3.

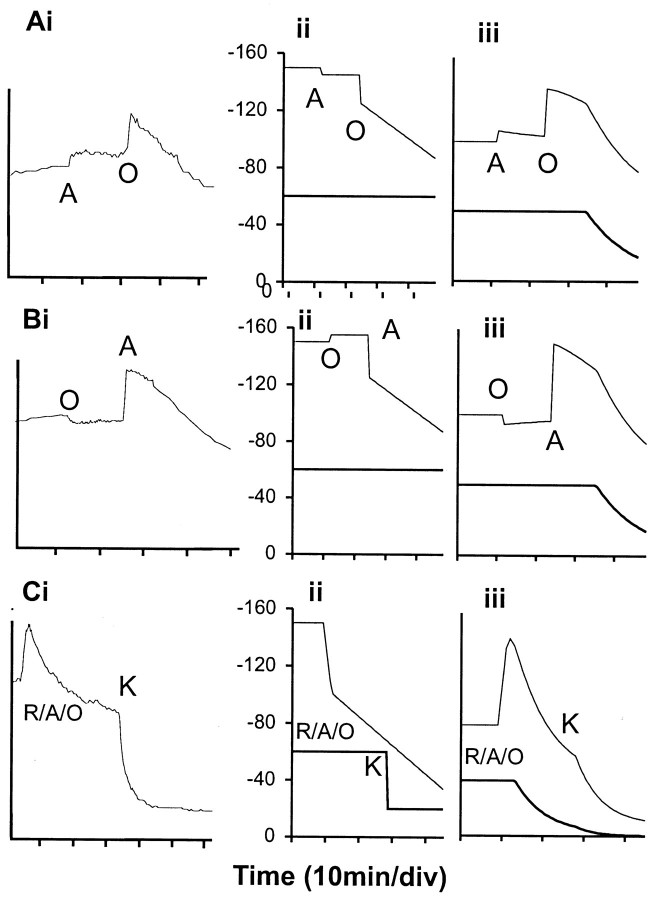
Fluorescence of individual granule cell somata equilibrated with 50 nm TMRM⁺ in response to mitochondrial inhibition; curve fitting with the cell simulation. Ai–Ci, Granule cells were equilibrated with 50 nm TMRM⁺. Where indicated, 3 μm antimycin A (A), 5 μg/ml oligomycin (O), 2 μm rotenone (R), or 50 mm KCl (K) was added. The incubation medium contained 1.2 mm MgCl₂. Each trace is from a single representative soma. Aii–Cii, Values for Δψ_m (thin line) and Δψ_p(thick line) were obtained by curve fitting for the cell simulation. Aiii–Ciii, Cell simulation; total fluorescence (thin line) and mitochondrial component of fluorescence (thick line) are shown. The following parameters were used: matrix volume = 1% of cytoplasm; quench threshold = 50 μm; rate constant for plasma membrane equilibration = 0.003/sec (TMRM⁺).

If this information is put into the cell simulation, the traces that are generated closely resemble the time course of the fluorescence response of granule cells exposed to these combinations of inhibitors. Thus Figure 3A suggests that antimycin A inhibition of mitochondrial complex III, which will inhibit respiration totally, causes only a 5–10 mV mitochondrial depolarization, consistent with the near-equilibrium bidirectional operation of the ATP synthase. The further addition of oligomycin to initiate decay of the proton gradient clearly reveals the biphasic decay consistent with the non-ohmic inherent proton conductance of the mitochondrion.

If the order of additions is reversed, the initial addition of oligomycin causes a slight mitochondrial hyperpolarization as use of the proton circuit for ATP generation is inhibited. This produces a decreased whole-cell signal (Fig. 3B). The addition of antimycin A now initiates the non-ohmic decay of potential. It should be noted in Figure 3Ci that the decay of fluorescence after the final KCl addition is faster than that simulated by even an instantaneous plasma membrane depolarization (Fig. 3Ciii). In the particular circumstances in which the efflux across the plasma membrane of TMRM⁺, which is electrogenic, can be charge-compensated by the entry of Ca²⁺ through voltage-activated Ca²⁺ channels, transiently activated by the depolarization, the reequilibration of TMRM⁺ is accelerated. It appears, therefore, that single-cell fluorescence can provide information on the kinetics of change in potential, as well as the approximate magnitude of any change.

The direction in which Δψ_m changes on the addition of oligomycin reveals whether the mitochondria within the cell are net generators or users of ATP (Fig. 3A,B), providing an independent in situ means to investigate the bioenergetic competence of the mitochondria, for example during glutamate exposure.

We previously have exploited the combination of rotenone plus oligomycin to depolarize mitochondria within cerebellar granule cells (Budd and Nicholls, 1996a,b; Castilho et al., 1998, 1999). However, rotenone is only ∼90% effective as an inhibitor of electron transfer through complex (Rottenberg and Wu, 1998), and it is evident from Figure 4A that a residual Δψ_m still can be detected in the presence of rotenone plus oligomycin, because the subsequent addition of FCCP causes a spike and decay of the TMRM⁺ signal consistent with a further collapse of potential. However, the residual proton current in the presence of rotenone plus oligomycin cannot maintain a detectable Δψ_m in the face of an increased load, for example Ca²⁺ uptake after KCl depolarization of the plasma membrane (Fig. 4B), because Δψ_m immediately collapses, as shown by the TMRM⁺ response synchronous with the spike in the fura-2 response indicating Ca²⁺ entry across the plasma membrane. As in Figure 3C, a rapid reequilibration of TMRM⁺ across the plasma membrane is seen as the probe efflux can be charge-balanced by Ca²⁺ entry.

Fig. 4.

Residual mitochondrial polarization in the presence of rotenone plus oligomycin. Granule cells (6–7 DIV) were loaded with fura-2 AM and 50 nm TMRM⁺. The medium contained 1.2 mm Mg²⁺. Where indicated, 2 μm rotenone (R), 5 μg/ml oligomycin (O) and 2.5 μmFCCP (F), or 50 mm KCl was added. Note that FCCP and KCl are each able to depolarize the mitochondria further (shown by the dequenching spike) in the presence of rotenone plus oligomycin. Smooth trace, TMRM⁺fluorescence; filled circles trace, fura-2 fluorescence ratio.

Acute changes in mitochondrial membrane potential in glutamate-exposed cerebellar granule cells

The consensus that glutamate addition depolarizes mitochondria within neurons (see introductory remarks) has been essentially qualitative so that the extent, mechanism, and bioenergetic consequences of the depolarization generally have not been addressed. Two phases of depolarization have been distinguished, an acute response on receptor activation and a second phase associated with DCD (Vergun et al., 1999). In cultured hippocampal neurons these phases generally follow closely on each other (Vergun et al., 1999), thereby preventing a clear separation of the two phases.

An experimental protocol was devised to monitor sequentially any acute mitochondrial depolarization on glutamate addition, the redistribution of TMRM⁺ across the plasma membrane in response to nondesensitizing NMDA receptor activation, the ability of the mitochondria to generate ATP during the glutamate exposure (by monitoring oligomycin-induced hyperpolarization), and the residual mitochondrial depolarization on the addition of protonophore.

Figure 5A shows representative traces for the subset of cells loaded with TMRM⁺ or rhodamine-123 that fail to undergo glutamate-induced delayed Ca²⁺deregulation within the time scale of the experiment (∼32% of the 7 DIV cells). It is apparent that equilibration of the probes across the plasma membrane is considerably more rapid in the presence of glutamate than in the presence of high KCl. Thus, comparing Figures2A and 5Ai shows that the final decay of the rhodamine-123 signal after FCCP is much more rapid in the glutamate-exposed cells than in the KCl-exposed cells. Similarly, the redistribution of TMRM⁺ because of plasma membrane depolarization is more rapid with glutamate (Fig.5Bi) than with KCl (see Fig. 2B). This difference can be explained plausibly as a glutamate-induced increase in the rate constant for equilibration across the plasma membrane. Increasing k for TMRM⁺ from 0.003 to 0.02 and for rhodamine-123 from 0.0003 to 0.001 allowed these signals, and subsequent glutamate traces, to be fit kinetically to the simulation with good precision (Fig. 5Bii,Cii). As discussed in the context of Ca²⁺ channel activation, it is likely that this increased rate of reequilibration is a consequence of the need for charge compensation during the net transport of the cationic probes across the plasma membrane (see also Fig. 10) and that this is facilitated by Na⁺ or Ca²⁺influx via the NMDA receptor.

Fig. 5.

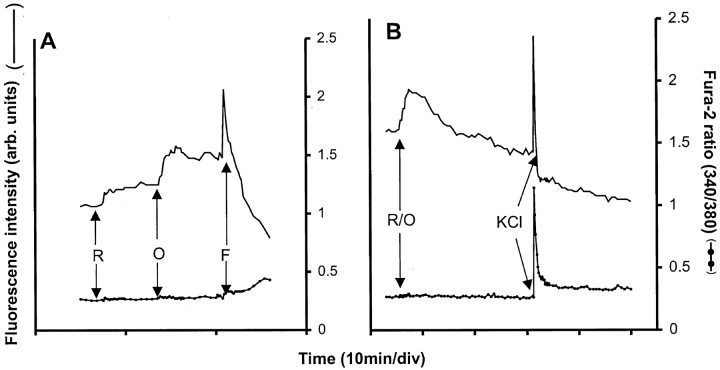
In situ membrane potential of granule cell mitochondria exposed to glutamate plus glycine: retained capacity to generate ATP. Shown is single soma fluorescence of granule cells loaded with rhodamine-123 (Ai) or 50 nm TMRM⁺ (Bi) exposed to 100 μm glutamate plus 10 μm glycine (G). Where indicated, 2 μg/ml oligomycin (O) and 1 μm FCCP (F) were added. Aii,Bii, Simulated traces were fit to the following potential changes: Δψ_p, depolarization from −60 to −20 mV on the addition of glutamate; Δψ_m, depolarization from 150 to 145 mV on the addition of glutamate and hyperpolarization to 155 mV on the addition of oligomycin (indicating retained capacity to generate ATP) and collapse of potential with FCCP.

We have reported previously (Castilho et al., 1999) that granule cells that maintain a stable [Ca²⁺]_c plateau in the presence of glutamate may fail to extrude the Ca²⁺ that is released from the mitochondrial matrix into the cytoplasm by oligomycin plus FCCP, and we have ascribed this to damaged plasma membrane Ca²⁺ efflux pathways. To establish whether this is associated with any sign of mitochondrial dysfunction, we monitored TMRM⁺ fluorescence in parallel with fura-2 (Fig. 6). The 20% of the 7 DIV cells that restore a low [Ca²⁺]_c after FCCP/oligomycin (Fig. 6A) maintain a stable fluorescence and show oligomycin-induced mitochondrial hyperpolarization, indicative of functional oxidative phosphorylation. The rapid recovery of a low [Ca²⁺]_c after FCCP indicates that plasma membrane Ca²⁺extrusion is still unimpaired in these cells.

Fig. 6.

Delayed Ca²⁺ deregulation induced in a subpopulation of cells by release of matrix Ca²⁺ into the cytoplasm occurs in the absence of previous mitochondrial dysfunction. The 7 DIV granule cells were loaded with fura-2 and equilibrated with 50 nmTMRM⁺. The cells were exposed to 100 μm glutamate/10 μm glycine (G); 2 μg/ml oligomycin (O) and 1 μm FCCP (F) were added where indicated. The traces represent the fura-2 (filled circles trace) and TMRM⁺ (smooth trace) responses from a single representative soma. A, Cell that regains cytoplasmic Ca²⁺ homeostasis after FCCP. The FCCP-induced fura-2 spike occurs during release of matrix Ca²⁺ and its subsequent removal from the cytoplasm. Note the oligomycin-induced fluorescent quenching diagnostic of mitochondrial ATP synthesis before the inhibitor addition.B, Cell that fails to restore a low [Ca²⁺]_c after FCCP. Note that the mitochondria in this cell also generated ATP before the oligomycin addition.

The subpopulation of cells that failed to restore a low [Ca²⁺]_c after FCCP/oligomycin (Fig. 6B) accounts for 32% of the total population of the 7 DIV cells. As previously reported (Castilho et al., 1999), these cells tend to display a slowly rising [Ca²⁺]_c during the plateau. The bioenergetic integrity of their mitochondria is unimpaired, because oligomycin-induced hyperpolarization and the FCCP spike are still apparent. This suggests that these cells have increasing difficulty extruding Ca²⁺ and that this occurs before any detectable mitochondrial dysfunction. However, it is also likely that the mitochondria in cells that deregulate on protonophore addition also have accumulated more Ca²⁺ (compare the magnitude of the Ca²⁺ elevations in Fig.6A,B).

Relation between initial mitochondrial depolarization and survival time before DCD

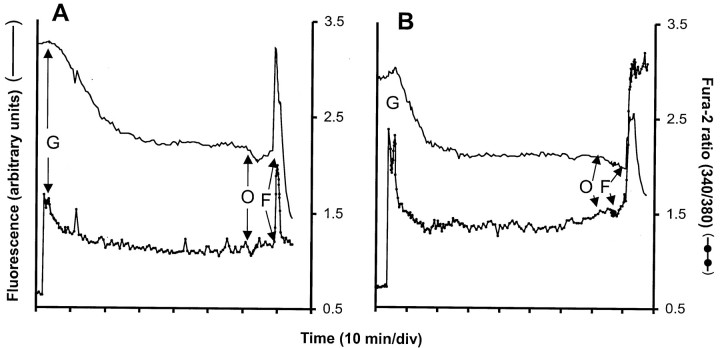
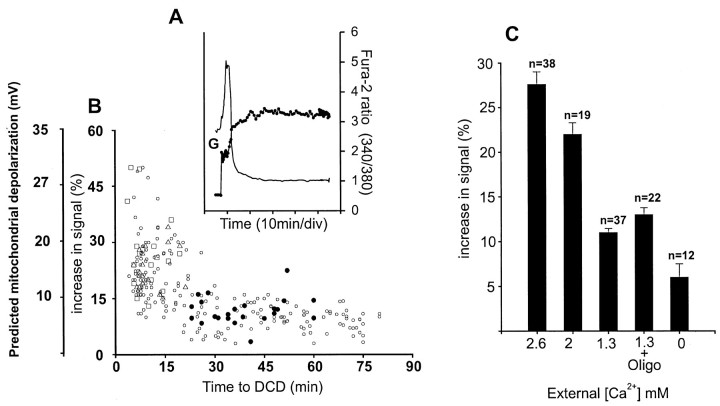
A minor population (14%) of the 7 DIV granule cells shows an extensive dequenching immediately on glutamate addition, accompanied by a rapid onset of DCD. This is the dominant response in published studies of hippocampal neurons cultured >11 DIV that are exposed to glutamate (Vergun et al., 1999). Figure7A shows an extreme example of a cerebellar granule neuron for which the mitochondria depolarize extensively with the addition of glutamate, followed by immediate Ca²⁺ deregulation. The relationship between the initial dequenching of TMRM⁺and the survival time before the onset of DCD was determined for 107 cells (Fig. 7B) that were incubated in varying external Ca²⁺ concentrations or in the presence of oligomycin. It is apparent that an inverse relationship exists between the extent of the initial dequenching and the time it takes cells to lose their Ca²⁺ homeostasis and deregulate.

Fig. 7.

Acute glutamate-induced mitochondrial depolarization: estimation of extent and consequences for DCD. The 7 DIV granule cells were loaded with fura-2, equilibrated with 50 nm TMRM⁺, and incubated in the presence of varying external Ca²⁺. A, Example of a cell showing massive initial depolarization and early DCD.Smooth trace, TMRM⁺ fluorescence;filled circles trace, fura-2 fluorescence ratio.B, Scatter plot relating the percentage of increase in TMRM⁺ fluorescence immediately after the addition of 100 μm glutamate/10 μm glycine to the time delay before DCD. The predicted mitochondrial depolarization was calculated as a function of fluorescence increase by running the simulation. Open circles, 1.3 mmCa²⁺; filled circles, 1.3 mm Ca²⁺ plus 2 μg/ml oligomycin;open triangles, 2 mmCa²⁺; open squares, 2.6 mm Ca²⁺. C, Mean increase in fluorescence as a function of external Ca²⁺ for the cells shown in B.

The cell simulation can be used to predict the extent of the initial depolarization corresponding to a given degree of dequenching. The alternative scale in Figure 7B suggests that an initial mitochondrial depolarization in excess of 10 mV is associated with a greatly decreased survival time. The acute mitochondrial depolarization is dependent on the extracellular concentration of Ca²⁺, persists in the initial presence of oligomycin, and is reduced in Ca²⁺-free medium (Fig. 7C). Thus the mitochondrial depolarization appears to be a direct consequence of calcium uptake rather than an associated enhancement in mitochondrial ATP demand, for example in response to increased Na⁺ pump activity.

Mitochondrial membrane potential during the plateau preceding DCD

Net⁴⁵Ca²⁺accumulation by granule cells after glutamate exposure is maximal immediately on agonist addition and then declines (Castilho et al., 1998). However, the partial mitochondrial depolarization induced by this uptake appears more permanent, as judged by the rhodamine-123 response (see Fig. 5A; see also Vergun et al., 1999). Ca²⁺-induced mitochondrial depolarization can be either dynamic, reflecting the use of the proton gradient during rapid net accumulation of the cation, or persistent, reflecting a limitation in the availability of cytoplasmic phosphate to accompany Ca²⁺ into the matrix (Nicholls, 1978). In the latter case ΔpH across the inner mitochondrial membrane will increase at the expense of Δψ_m, and this will be retained even after net Ca²⁺accumulation ceases. The present results suggest, therefore, that phosphate limitation rather than continuous net Ca²⁺ accumulation could be responsible for the initial depolarization.

Although the simulation is consistent with an initial mitochondrial depolarization of only 5–10 mV in cells that do not undergo DCD (Fig.7), it is perhaps more relevant in the present context simply to determine whether the protonmotive force (Δp) of the partially depolarized mitochondria is still sufficient for the generation of ATP. To this end, the ability to detect an oligomycin-induced mitochondrial hyperpolarization during the plateau phase was investigated. Sufficient time was allowed for the TMRM⁺ to reequilibrate across the plasma membrane in response to the NMDA receptor activation before oligomycin was added. In the majority of the 7 DIV neurons, oligomycin induced a significant step decrease in whole-cell fluorescence, indicating that the mitochondrial population in these individual cells was generating ATP before the addition of the inhibitor. Thus in these cells the calcium-induced decrease in mitochondrial membrane potential does not lower Δp below the threshold required for net ATP synthesis during the plateau phase before DCD. It should be noted that the oligomycin-induced hyperpolarization can be detected more readily with the slowly permeant rhodamine-123 (see Fig. 5A).

Kinetics of mitochondrial depolarization during delayed calcium deregulation

Delayed calcium deregulation is a stochastic event (Dubinsky et al., 1995) that is accompanied by a profound mitochondrial depolarization (Isaev et al., 1996; Khodorov et al., 1996; Schinder et al., 1996; White and Reynolds, 1996; Vergun et al., 1999). The majority of the 7 DIV granule cells undergoes DCD after 30–60 min of continuous exposure to glutamate and glycine (Budd and Nicholls, 1996a). Simultaneous monitoring of the fura-2 and TMRM⁺ signals allows the onset of DCD to be correlated with mitochondrial depolarization in individual cells. Granule cells loaded with fura-2 in Mg²⁺-free, low KCl medium exhibit responses to glutamate/glycine that vary from an almost immediate failure of cytoplasmic Ca²⁺ homeostasis to the maintenance of a low [Ca²⁺]_c throughout the duration of the experiment (Budd and Nicholls, 1996a).

The TMRM⁺ fluorescence decreases during DCD sometimes are preceded by a shallow hump (Fig.8A). The model can simulate this response as either a further plasma membrane depolarization or as a slowly developing mitochondrial depolarization. To distinguish between these possibilities, we used rhodamine-123 in parallel experiments (Fig. 8C). The rate of mitochondrial depolarization during DCD differs from cell to cell; however, the simulation can reproduce the experimental traces if the mitochondrial population within individual cell somata undergoes exponentially developing collapses of Δψ_m (Fig.8D). Figure 8, E and F, shows the families of simulated traces obtained for TMRM⁺ and rhodamine-123, respectively, in response to the depolarization protocols shown in Figure8C.

The time course of mitochondrial depolarization during DCD is clearly distinctive from that induced by protonophore plus oligomycin (see Fig.6), which results in an “instantaneous” collapse in Δψ_m, or by antimycin A plus oligomycin (see Fig. 3) in which a biphasic decay can be modeled. Depolarization is sufficiently slow to prevent a temporary accumulation of TMRM⁺ in the cytoplasm and hence a significant increase in whole-cell fluorescence (Fig.8A), and it is necessary to use the slowly permeant rhodamine-123 to show this transient increase in whole-cell signal (Fig. 8C). DCD and mitochondrial depolarization appear to be initiated at approximately the same time, although an extensive loss of Ca²⁺ homeostasis can be seen before mitochondrial depolarization has become extensive.

Mitochondrial depolarization will result in ATP synthase reversal and the depletion of cytoplasmic ATP, particularly if the proton conductance of the inner membrane is increased, for example by protonophore. In the presence of glutamate, protonophore or respiratory chain inhibition results in a failure of cytoplasmic Ca²⁺ homeostasis in these cells (Budd and Nicholls, 1996a; Castilho et al., 1998) that can be ascribed to ATP synthase reversal because it may be prevented or reversed by oligomycin. The close association of DCD with the collapse of Δψ_m therefore could be a bioenergetic consequence of such ATP depletion. To control for this possibility, we repeated the experiment in Figure 8A in the presence of oligomycin (Fig. 8B). A similar relationship between DCD and mitochondrial depolarization was observed in the presence of the inhibitor, eliminating ATP synthase reversal as a direct cause of the failed cytoplasmic Ca²⁺ homeostasis.

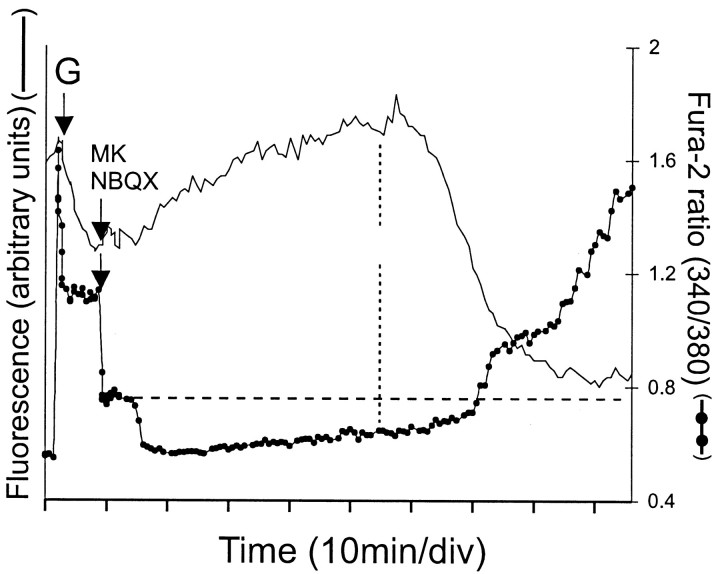
Mitochondrial membrane potential and DCD after transient glutamate receptor activation

Although transient NMDA receptor activation can be followed by a restoration of basal [Ca²⁺]_c, subsequent DCD can still occur (Tymianski et al., 1993b). In Figure9 the fura-2 and TMRM⁺ signals are monitored in granule cells that were exposed to glutamate followed by the addition, after 10 min, of MK 801 plus NBQX to inhibit NMDA and AMPA receptors. As has been reported by Thayer and Miller (1990), the recovery of the fura-2 signal to basal when Ca²⁺ loading is terminated is biphasic under conditions of mitochondrial Ca²⁺ accumulation. The shoulder after the first rapid recovery phase has been ascribed (Thayer and Miller, 1990) to the buffering effect on the cytoplasm of the efflux of Ca²⁺ from the mitochondrial matrix as [Ca²⁺]_c falls below the set point (Nicholls, 1978) at which the mitochondrial uptake and efflux pathways are in kinetic balance. Depletion of nonmitochondrial Ca²⁺ stores has little or no effect on the shape or duration of the shoulder (data not shown).

Fig. 9.

Delayed Ca²⁺ deregulation and mitochondrial depolarization in cells after transient exposure to glutamate/glycine. The 7 DIV cells were loaded with fura-2 and TMRM⁺ as in Figure 6 and exposed to 100 μm glutamate plus 10 μm glycine (G). Where indicated, 10 μm each of MK 801 and NBQX was added (MK/NBQX). Note that this is well before the fura-2 signal indicates that [Ca²⁺]_c has risen to the set point at which mitochondria become net accumulators of Ca²⁺(horizontal dashed line). Smooth trace, TMRM⁺ fluorescence; filled circles trace, fura-2 fluorescence ratio; vertical dotted line, time point at which mitochondrial depolarization starts.

The recovery of the TMRM⁺ signal appears to be delayed until this mitochondrial unloading is complete. The slowness of the recovery may reflect the problems of charge balance experienced in the absence of glutamate as discussed above, because plasma membrane repolarization presumably will be instantaneous after receptor inhibition. Support for this is found in the experiment in Figure 10B, in which a 1 μm concentration of the membrane-permeant anion tetraphenylboron is included in the incubation as a charge-compensating counter ion. Averaged over 30 cells, the time for the equilibration of TMRM⁺ after glutamate was reduced from 465 ± 17 to 192 ± 7 sec in the presence of TPB⁻ and that for recovery after receptor inhibition from 990 ± 30 to 290 ± 18 sec.

The spontaneous loss of signal that is initiated in Figure9A at ∼60 min reflects a slowly developing mitochondrial depolarization. Importantly, the depolarization is almost complete before [Ca²⁺]_c, as given by the fura-2 ratio, rises beyond the critical set point at which the mitochondria become net accumulators of Ca²⁺ (horizontal dashed line). Thus under these conditions mitochondrial depolarization can precede cytoplasmic Ca²⁺ deregulation. To establish whether this DCD is a consequence of cytoplasmic ATP depletion after ATP synthase reversal, we repeated the experiment in the presence of oligomycin that was added after recovery of the fura-2 signal (Fig.11A). The experimental trace can be fit to a slow delayed mitochondrial depolarization (Fig. 11B,C), but it is remarkable that cytoplasmic Ca²⁺ homeostasis is retained completely for the duration of the experiment. In particular, [Ca²⁺]_c remains at a stable baseline value far below the mitochondrial set point indicated by the shoulder after MK 801/NBQX addition. It is evident that no ATP depletion or plasma membrane depolarization occurs during the duration of this experiment, because this would result in an increase in [Ca²⁺]_c by failed Ca²⁺ extrusion or voltage-activated Ca²⁺ channel activation, respectively.

Fig. 11.

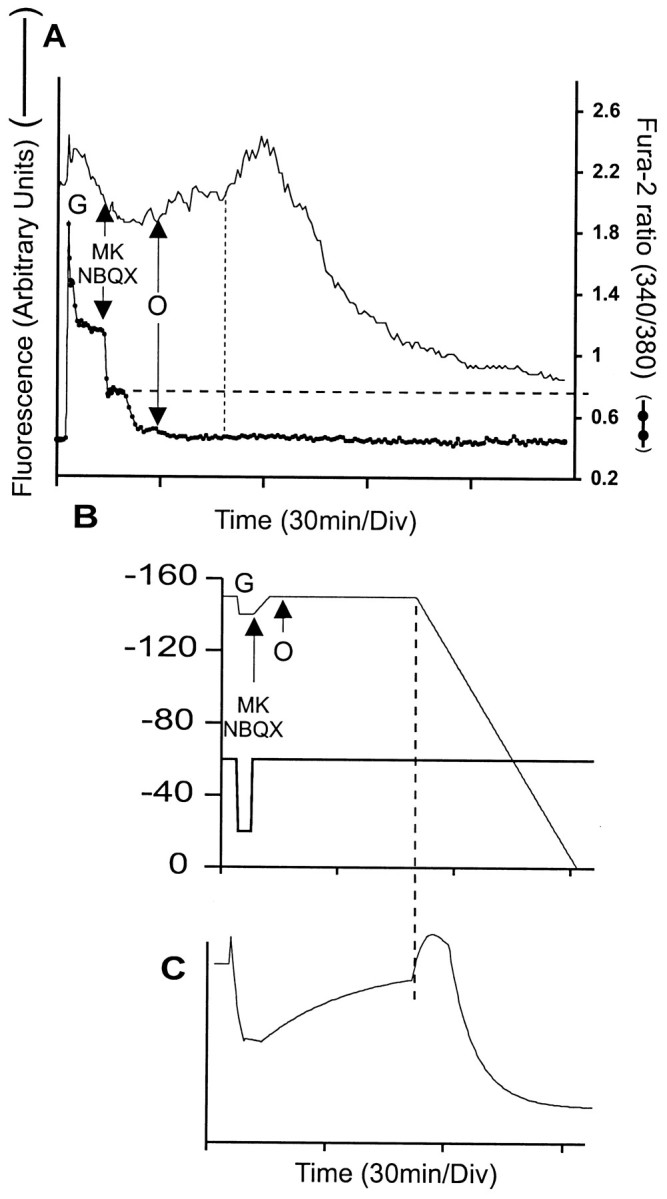
Oligomycin prevents DCD, but not mitochondrial depolarization, in cells after transient exposure to glutamate/glycine. The 7 DIV cells were loaded with fura-2 and TMRM⁺ as in Figure 6 and exposed to 100 μm glutamate plus 10 μm glycine (G). Where indicated, 10 μm each of MK 801 and NBQX (MK/NBQX) and 5 μg/ml oligomycin (O) were added. The vertical dotted line represents the time point at which mitochondrial depolarization can be detected. The horizontal dashed line shows the set point at which mitochondria become net accumulators of Ca²⁺. Smooth trace, TMRM⁺ fluorescence; filled circlestrace, fura-2 fluorescence ratio. B, Time course of Δψ_p and Δψ_m input into the simulation; note that the plasma membrane rate constant is taken to bek = 0.02/sec while NMDA receptors are active and 0.003/sec when the receptors are inhibited. C, Cell simulation. The vertical dashed line represents the time point at which mitochondrial depolarization starts.

DISCUSSION

Monitoring Δψ_m in intact neurons

The role of mitochondrial depolarization and/or dysfunction in glutamate excitotoxicity (Ankarcrona et al., 1995, 1996; Isaev et al., 1996; Khodorov et al., 1996; Schinder et al., 1996; White and Reynolds, 1996; Kiedrowski, 1998; Prehn, 1998; Keelan et al., 1999; Marks and Zhang, 1999; Vergun et al., 1999) may need reevaluation in the light of the present study. The technical complexity in the use of membrane potential probes at single-cell resolution has given rise to considerable confusion (for review, see Nicholls and Ward, 2000). The cell simulation may help to resolve some of these ambiguities. Although not precisely predicting the experimental trace, it allows for plasma membrane reequilibration, while differing patterns of mitochondrial depolarization can be distinguished, from the sharp spike and rapid recovery after the collapse of Δψ_m by protonophore (see, for example, Fig. 5) to the biphasic decay kinetics seen with antimycin A plus oligomycin (see Fig. 3), the exponentially developing depolarization during DCD (see Fig. 8), and the extremely slow, more linear, depolarization observed after NMDA receptor inactivation in the presence of oligomycin (see Fig. 11). In addition, approximate estimates can be obtained of the extents of the initial depolarization (see Fig. 7), oligomycin can be used to test for continued ATP synthesis (see Fig. 5), and finally the distinctive shape of rhodamine-123 and TMRM⁺ traces can be explained (see Fig. 5).

The relationship between mitochondrial depolarization and DCD

In the continued presence of glutamate, DCD and the final collapse in Δψ_m cannot be separated readily in time (see Fig. 8), which makes it difficult to establish whether mitochondrial depolarization causes DCD, DCD causes mitochondrial depolarization, or whether the two are independent effects. Certainly a mitochondrion cannot retain a high Δψ_m in an ambient free Ca²⁺ concentration that is maintained continuously above the set point, because, in the presence of sufficient phosphate, the matrix would load inexorably with Ca²⁺ until the mitochondria become damaged or the permeability transition is induced. A primary mitochondrial depolarization, on the other hand, could initiate DCD either by cytoplasmic ATP depletion or by dumping a massive matrix Ca²⁺ load into the cytoplasm.

Oxidative stress is a key component in acute glutamate excitotoxicity (for review, see Beal et al., 1997), and because the mitochondrial generation of superoxide is dependent on the maintenance of a high Δψ_m (Boveris et al., 1972; Skulachev, 1996;Braidot et al., 1999), reactive oxygen species generation by the calcium-loaded polarized mitochondria may be the key factor that depletes the antioxidant defenses of the cell, resulting in the ultimate failure of cytoplasmic calcium homeostasis.

Analysis of the extent of the initial mitochondrial depolarization on glutamate addition reveals that the larger the initial depolarization, the sooner the onset of DCD (see Fig. 7). This is similar to the correlation observed by Vergun et al. (1999) between the acute rhodamine-123 fluorescence increase with glutamate and the failure of hippocampal neurons to restore cytoplasmic Ca²⁺ homeostasis after glutamate removal. Because the TMRM⁺ spike is still seen in the presence of oligomycin, a depolarization associated with increased ATP demand can be ruled out, indicating that any depolarization is attributable to mitochondrial Ca²⁺ uptake. Indeed, a somewhat surprising feature of these cells is that survival in the continuous presence of glutamate is the same in control cells and cells preincubated with oligomycin (Budd and Nicholls, 1996a;Castilho et al., 1998). This suggests that the ATP demand of the glutamate-exposed cells is not greatly in excess of that of control cells.

Modes of mitochondrial depolarization

The following modes of mitochondrial depolarization in response to potentially excitotoxic NMDA receptor activation can be resolved in this and related studies.

(1) An acute depolarization on the addition of glutamate reflects accumulation by the mitochondria of Ca²⁺entering via the NMDA receptor. In most of the 7 DIV granule cells this depolarization only amounts to 5–10 mV (see Fig. 7). Mitochondria continue to generate ATP in the presence of glutamate for at least 30 min (see Figs. 5, 6), as judged by the oligomycin-induced hyperpolarization. This is consistent with the ability of granule cells supported by lactate or pyruvate in glucose-free media (cells dependent entirely on oxidative phosphorylation) to maintain a stable [Ca²⁺]_c in the presence of glutamate for as long as glucose maintained the cells (Castilho et al., 1998)

(2) As the initial depolarization increases above 20%, the survival time of the cells before DCD is shortened greatly (see Fig.7A), suggesting that Ca²⁺ entry via the NMDA receptors overwhelms the capacity of the mitochondrion plus plasma membrane to maintain cytoplasmic Ca²⁺ homeostasis in these neurons (see Fig. 7A).

(3) Immediate Ca²⁺ deregulation, ICD (Castilho and Nicholls, 1999), can be induced after glutamate by restricting respiratory chain capacity by rotenone (Budd and Nicholls, 1996a; Castilho et al., 1998) or antimycin A (Nicholls and Budd, 1998). Mitochondrial depolarization is limited by ATP synthase reversal (see Fig. 3) but at the cost of acute cytoplasmic ATP depletion by ATP synthase reversal (Budd and Nicholls, 1996a). ICD does not appear to be attributable to oxidative damage because it can be reversed by the inhibition of the NMDA receptor and ATP synthase (Castilho et al., 1998). The rapid loss of Ca²⁺ homeostasis observed in >11 DIV hippocampal neurons may relate to nitric oxide-mediated restriction of respiratory chain activity (Keelan et al., 1999).

(4) If mitochondria are depolarized without depleting cytoplasmic ATP by the combination of respiratory chain inhibitor plus oligomycin before the addition of glutamate, survival of the granule cells is enhanced greatly (Budd and Nicholls, 1996a). Cell-permeant antioxidants such as Mn-TBAP enhance granule cell survival, suggesting that the Ca²⁺-loaded polarized mitochondria are generating potentially toxic reactive oxygen species.

(5) If granule cells are exposed continuously to glutamate, the onset of DCD is associated with a slowly developing profound mitochondrial depolarization (see Fig. 8), which the simulation indicates may take between 10 and 15 min from inception to completion (see Fig.8C). As with hippocampal neurons (Vergun et al., 1999) it is not easy to resolve cause and effect when NMDA receptors are activated continuously. If the critical targets of oxidative damage are the plasma membrane Ca²⁺ extrusion pathways, this would increase [Ca²⁺]_c, leading to an inexorable mitochondrial Ca²⁺overload and ultimate depolarization. Alternatively, mitochondrial Ca²⁺ overload and depolarization could be the primary event initiating DCD, attributable possibly to induction of the permeability transition and the dumping of an irrecoverable Ca²⁺ load into the cytoplasm. However, brain mitochondria are highly resistant to the permeability transition (Murphy and Fiskum, 1999), and interpretation of the ability of cyclosporin derivatives to delay DCD in brain is controversial (Li et al., 1997; Nakai et al., 1997; Friberg et al., 1998, 1999).

(6) Transient exposure to glutamate is the classical paradigm in which to monitor in vitro neuronal necrosis (Choi et al., 1987;Tymianski et al., 1993b). When it is used in the present context, a clear dissociation between mitochondrial depolarization and DCD is evident. In the absence of oligomycin (see Fig. 9) mitochondrial depolarization is initiated well before [Ca²⁺]_c rises above the set point. That the subsequent DCD is a consequence of ATP synthase reversal and cytoplasmic ATP depletion is seen by comparison to Figure 11, in which the presence of oligomycin totally prevents DCD during the slow collapse of Δψ_m.

Because the cells will have only a slow basal Ca²⁺ influx after NMDA receptor inhibition by MK 801, the demands on the plasma membrane Ca²⁺ extrusion pathways are decreased relative to experiments in which the NMDA receptor is continuously active, first because Ca²⁺ influx is reduced to basal and second because the Na⁺/Ca²⁺exchanger should be competent to extrude Ca²⁺ from the cell. Thus the experiment does not preclude oxidative damage to the plasma membrane Ca²⁺-ATPase occurring during the glutamate exposure.

Because the mitochondria are Ca²⁺-depleted at the stage in which they depolarize, it is unclear whether the permeability transition is responsible. It is notable that mitochondria that are isolated from glutamate-exposed granule cells (Atlante et al., 1996) show no increase in State 4 respiration, which monitors the proton leakiness of the inner membrane (Nicholls and Ferguson, 1992), but they do show a greatly decreased State 3 respiration (NADH supply or respiratory chain capacity). A similar respiratory inhibition is observed in glutamate-exposed retinal neurons (Rego et al., 2000). This is also consistent with the high sensitivity of enzymes such as aconitase to oxidative damage (Melov et al., 1999).

Conclusion

Mitochondrial Ca²⁺ loading is the critical step in acute glutamate excitotoxicity (Budd and Nicholls, 1996a; Castilho et al., 1998; Stout et al., 1998). Even brief exposure to glutamate initiates DCD, and it is apparent that mitochondrial dysfunction is initiated in this period. The damage inflicted by transient Ca²⁺ loading may include cytochrome c release (Atlante et al., 1999), altering the redox poise of complex III and enhancing the generation of superoxide (Gonzalez Flecha and Boveris, 1995). The critical parameter that becomes rate-limiting to initiate DCD depends on the experimental design. Under the conditions of continued Ca²⁺ entry, plasma membrane Ca²⁺ extrusion may be the first to fail, whereas after inhibition of the receptor, mitochondrial dysfunction may precipitate DCD.

Modeling single-cell fluorescence of a cationic probe as a function of Δψ_p and Δψ_m

Nernstian equilibration of a generic membrane-permeant monovalent cation c⁺ among the extracellular, cytoplasmic, and mitochondrial matrix phases at 37°C results in the following relationships for the concentrations of the free cations at equilibrium:

$$c_{[\text{matrix}]}^{+}=c_{[\text{cytoplasm}]}^{+}·{10}^{\mathrm{\Delta }{\psi }_{\text{m}}/61.5},$$ Equation 1

$$c_{[\text{cytoplasm}]}^{+}=c_{[\text{medium}]}^{+}·{10}^{-\mathrm{\Delta }{\psi }_{\text{p}}/61.5},$$ Equation 2

$$\therefore c_{[\text{matrix}]}^{+}=c_{[\text{medium}]}^{+}·{10}^{(\mathrm{\Delta }{\psi }_{\text{m}}-\mathrm{\Delta }{\psi }_{\text{p}})/61.5},$$ Equation 3

where Δψ_p and Δψ_m are, respectively, the plasma and mitochondrial membrane potentials (using accepted sign conventions), and the divisor 61.5 is the value (in mV) for RT/F at 37°C.

For the continuous monitoring of changes in Δψ_m at single-cell resolution, loading conditions are designed such that the probe undergoes stacking and consequent fluorescent quenching within the matrix. For the purposes of the model (see Table 1) it is assumed that the quantum yield (q) of the probe remains constant until a critical threshold concentration (c⁺_[quench]) for the initiation of stacking is attained and that beyond this limit the matrix fluorescence (f_matrix) becomes independent of the probe concentration because of the formation of nonfluorescent H-aggregates (Cohen and Salzberg, 1978). This assumption was tested by incubating mitochondria in the presence of two differing concentrations of TMRM⁺ and determining the contribution of the quenched and unquenched matrix TMRM⁺ to the total cuvette fluorescence as described above. Figure 1 shows that the matrix fluorescence is the same in two mitochondrial incubations in which the total concentration of TMRM⁺ in the matrix differs 20-fold.

Therefore, if the volume of the matrix compartment isV_matrix:

$$\text{if} c_{[\text{matrix}]}^{+}>c_{[\text{quench}]}^{+} \text{then} f_{\text{matrix}}=q·c_{[\text{quench}]}^{+}·V_{\text{matrix}};$$ Equation 4

$$\text{if} c_{[\text{matrix}]}^{+}<c_{[\text{quench}]}^{+} \text{then} f_{\text{matrix}}=q·c_{[\text{matrix}]}^{+}·V_{\text{matrix}}.$$ Equation 5

The accumulation of probe in the cytoplasm (volume,V_cyto) is assumed always to be less thanc⁺_[quench]; thus under all equilibrium conditions the cytoplasmic fluorescencef_cyto will be:

$$f_{\text{cyto}}=q·c_{[\text{cytoplasm}]}^{+}·V_{\text{cyto}}.$$ Equation 6

The whole-cell fluorescence (f_cell) under the two conditions therefore will be the sum of the cytoplasmic and matrix signals:

$$\text{if} c_{[\text{matrix}]}^{+}>c_{[\text{quench}]}^{+} \text{then}$$ Equation 7

$$f_{\text{cell}}=q·c_{[\text{cytoplasm}]}^{+}·V_{\text{cyto}}+q·c_{[\text{quench}]}^{+}·V_{\text{matrix}};$$

$$\text{if} c_{[\text{matrix}]}^{+}<c_{[\text{quench}]}^{+} \text{then}$$ Equation 8

$$f_{\text{cell}}=q·c_{[\text{cytoplasm}]}^{+}·V_{\text{cyto}}+q·c_{[\text{matrix}]}^{+}·V_{\text{matrix}}.$$

Lipophilic compounds permeate nonselectively across the lipid bilayer regions of biological membranes. However, the much greater surface-to-volume ratio of the mitochondrial inner membrane-to-matrix relative to the plasma membrane-to-cytoplasm will mean that the half-time for equilibration between the mitochondrion and cytoplasm will be much more rapid than that between cytoplasm and medium. For the model it is assumed that after a step change in Δψ_m the probe reequilibrates across the mitochondrial membrane within the time frame of the sampling frequency (see, for example, Fig. 3). In contrast, the flux, J, of the probe across the plasma membrane is assumed to be first order with respect to the difference between the actual cytoplasmic concentration and that predicted by the Nernst equilibrium, such that:

$$J=k·(c_{[\text{cytoplasm},\text{actual}]}^{+}-c_{[\text{cytoplasm},\text{equilibrium}]}^{+}),$$ Equation 9

where k is a constant proportional to the permeability of the probe across the plasma membrane.

The effect of the rapidly equilibrating mitochondrial pool is to increase the total cellular pool of probe by a factor equal to:

$$1-((V_{\text{matrix}}/V_{\text{cyto}})·{10}^{\mathrm{\Delta }{\psi }_{\text{m}}/61.5}).$$ Equation 10

For the monitoring of changes in cytoplasmic concentration, this is interpreted most simply as an expansion of the “virtual” cytoplasmic volume by the same factor. Thus the rate of change of the cytoplasmic concentration, for example in response to a plasma membrane depolarization, will be slowed by the buffering afforded by probe release from the mitochondrial pool.

Program for the interpretation and modeling of single-cell resolution imaging of membrane-permeant cationic probes

The spreadsheet (Table 1) shows the calculation for a hypothetical cell in which the mitochondria occupy a fraction 0.01 (cell B2) of the soma volume. The cells are equilibrated initially with 50 nm (cell B3) of a cationic probe that equilibrates across the plasma membrane with a characteristic rate constant k/sec (cell B4; see Eq. 9). The probe displays fluorescence quenching when accumulated above the quench limit,c⁺_[quench](see Eqs. 4, 5). This value is entered into cell B5 and is taken to be 50 μm in this example. The sampling interval (sec) is entered into cell A6. Values for Δψ_p(column C) and Δψ_m (column D) are entered manually or are entered to fit an appropriate time course.

Table 1.

	B	C	D	E	F	G	H	I	J	K	L	M
2	0.010	Mitochondrial volume (fraction)
3	50	External probe conc. (nm)
4	0.020	Plasma membrane rate constant k (sec−1)
5	50	Quench limit (μm)
6	30	Interval (sec)

	Time (sec)	Δψp (mV)	Δψm(mV)	Equil [cyto] (nm)	Equil [matrix] (nm)	Virtual Cytoplasmic volume	Total probe	Actual [cyto] (nm)	Actual [matrix] (nm)	Invoking Quench limit	Matrix signal	Total signal
11	0	−60	−150	473	129899	3.7	1772	473	129899	50000	500	973
12	30	−20	−150	106	29053	3.7	1551	414	113755	50000	500	914
13	60	−20	−150	106	29053	3.7	1367	365	100196	50000	500	865
14	90	−20	−150	106	29053	3.7	1211	323	88807	50000	500	823
15	120	−20	0	106	106	1.0	1081	1070	1070	1070	11	1081
16	150	−20	0	106	106	1.0	502	497	497	497	5	502
17	180	−20	0	106	106	1.0	267	265	265	265	3	267

The program, using the programming conventions of Microsoft Excel, starts with an equilibrium distribution, governed by the Nernst equation.

Cell E11: Final equilibrium concentration of probe in the cytoplasm, calculated from Equation 1 above = + B$3 · POWER(10,(−C11/61.5)).

Cell F11: Final equilibrium concentration of probe in the matrix, calculated from Equation 2 above = + E11 · POWER (10,(−D11/61.5)).

Cell G11: The “virtual cytoplasmic volume” i.e., the volume of the cytoplasm expanded to account for the probe buffered by the mitochondrion (see Eq. 10) = 1 + (B$2 · POWER(10,(−D11/61.5))).

Cell H11: For the first time point only, the total accumulated probe at equilibrium = + G11 · E11.

Cell I11: The actual (as opposed to equilibrium) cytoplasmic concentration, obtained by dividing the total probe by the virtual cytoplasmic volume. For the first equilibrium time point this will be equal to the value in cell E11: = + H11/G11.

Cell J11: The actual mitochondrial concentration, obtained from the actual cytoplasmic concentration and the Nernst equation for the mitochondrion. For the first equilibrium time point this will be equal to the value in cell F11: = + I11 · POWER(10,(−D11/61.5)).

Cell K11: If the iterative mitochondrial concentration is less than the quench limit (cell B5), then the actual concentration is taken for the subsequent calculation of fluorescence; otherwise the quench limit is entered: = IF (J11 > 1000 · B$5, 1000 · B$5,J11).

Cell L11: The contribution of the matrix to the whole-cell fluorescence is equal to the matrix concentration of the probe (or quench limit if lower) multiplied by the fractional volume occupied by the mitochondria: = B$2 · K11.

Cell M11: The total cell fluorescence is the sum of the cytoplasmic fluorescence (equal to the cytoplasmic concentration, cell I11) plus the matrix fluorescence: = + I11 + L11.

Then the first row of formulae can be copied down the spreadsheet for as many data points as are required, with the exception of column H, in which the effects of the rate limitation in the equilibration across the plasma membrane have to be quantified. In the example shown in Table 1, Δψ_p is decreased to −20 mV after the first time point. The effect of this is to decrease the equilibrium cytoplasmic probe concentration from 473 to 106 nm. The simulation assumes that the probe redistributes across the plasma membrane as a first-order function of the difference between the actual (cell I11) and equilibrium (cell E12) cytoplasmic concentrations, taking into account the buffering effect of the mitochondrion in increasing the virtual cytoplasmic volume (see Eq. 9).

Cell H12 contains the equation for the calculation of the total probe: = + H11 + ((E12 − I11) · B$4 · B$6), which can be copied down to the remainder of column H.

In the example shown in Table 1, the matrix concentration remains above the quench limit and so the fluorescent contribution of the matrix does not change after plasma membrane depolarization. However, when Δψ_m is collapsed, simulating protonophore addition (row 15), probe floods into the matrix, raising its concentration from 323 to 1070 nm (cell I15), which more than compensates for the loss of signal from the quenched matrix (cell L15). As a result, there is the whole-cell signal increase (cell M15). The large disequilibrium across the plasma membrane (compare equilibrium value, cell E15, with actual value, cell H15), together with the lack of the buffering effect of the matrix (see cell G15), means that the cytoplasmic fluorescence (cells H16, H17) rapidly decays.