Spatial Generalization from Learning Dynamics of Reaching Movements

Abstract

When subjects practice reaching movements in a force field, they learn a new sensorimotor map that associates desired trajectories to motor commands. The map is formed in the brain with elements that allow for generalization beyond the region of training. We quantified spatial generalization properties of these elements by training in one extreme of the reachable space and testing near another. Training resulted in rotations in the preferred direction (PD) of activation of some arm muscles. We designed force fields that maintained a constant rotation in muscle PDs as the shoulder joint rotated in the horizontal plane. In such fields, training in a small region resulted in generalization to near and far work spaces (80 cm). In one such field, the forces on the hand reversed directions for a given hand velocity with respect to the location of original training. Despite this, there was generalization. However, if the field was such that the change in the muscle PDs reversed as the work spaces changed, then performance was worse than performance of naive subjects. We suggest that the sensorimotor map of arm dynamics is represented in the brain by elements that globally encode the position of the arm but locally encode its velocity. The elements have preferred directions of movement but are modulated globally by the position of the shoulder joint. We suggest that tuning properties of cells in the motor system influence behavior and that this influence is reflected in the way that we learn dynamics of reaching movements.

Motor commands that generate reaching movements are constructed by the brain by taking into account predicted force dynamics of the desired trajectory (Gottlieb, 1994;Shadmehr and Mussa-Ivaldi, 1994). When novel forces are imposed on the arm, the prediction will be incorrect, and the hand will not follow the desired trajectory (Lackner and Dizio, 1994; Goodbody and Wolpert, 1998; Flanagan et al., 1999; Krakauer et al., 1999). With practice, motor commands are modified, and the trajectory converges to the desired path. The computation being performed during this learning is analogous to forming a new sensorimotor map: an association between a desired hand trajectory and the corresponding motor commands. Tests of generalization have demonstrated that the alteration of the motor command is not limited to movements for which examples of the novel dynamics were provided (Conditt et al., 1997). For example, learning to compensate for novel forces along one direction of movement results in a generalization pattern to neighboring directions that decays with angular distance (Gandolfo et al., 1996; Sainberg et al., 1999; Ghez et al., 2000).

Using the computational framework of learning that was proposed byPoggio and Girosi (1990), we have hypothesized that these tests of generalization are essentially probes regarding the tuning properties of neurons that are taking part in representing the changing sensorimotor map. By quantifying how learning in one direction of movement affects other directions, we have inferred that the map is being formed with elements that encode hand velocity locally with nonlinear activation functions that have preferred directions of motion (Thoroughman and Shadmehr, 2000). We have argued that this property of the inferred computational elements is not unlike tuning properties of some cells in the cerebellum and the motor cortex.

Although these results have quantified how the formation of a new sensorimotor map generalizes in terms of velocity of the hand, considerably less is known about generalization patterns in position space. We had noted previously that after training in one region of the work space, subjects had aftereffects when movements were performed at a nearby work space (33 cm away) (Shadmehr and Mussa-Ivaldi, 1994). That is, subjects expected to experience specific forces at the new arm configuration. The patterns of aftereffects suggested that generalization was in intrinsic, joint-centered coordinates.

During learning of dynamics of arm movements, a muscle's activity (quantified as a function of movement direction) changes, and one way to quantify this change is via rotations in the preferred direction (PD) of activation of each muscle during the initiation of movement (Thoroughman and Shadmehr, 1999). With training, muscle PDs may gradually rotate from that observed in the null field (when no external forces are imposed). However, a muscle's PD may also depend on the configuration of the arm (Buneo et al., 1997). We thought that the patterns of spatial generalization of dynamics might be related to the relative change of muscle PDs that learning of a field induces. Specifically, learning a field in one work space might generalize to all other arm configurations if the field was such that it required a constant relative change in muscle PDs across work spaces. In these experiments we made such fields and tested this idea. From the results, we make further inferences regarding the mathematical properties of the elements that take part in representing the sensorimotor map for arm dynamics in the brain.

MATERIALS AND METHODS

Thirty-four healthy right-handed individuals (25 ± 5.7 years old) participated in this study. The study protocol was approved by the Johns Hopkins University Joint Committee on Clinical Investigation, and all subjects signed a consent form.

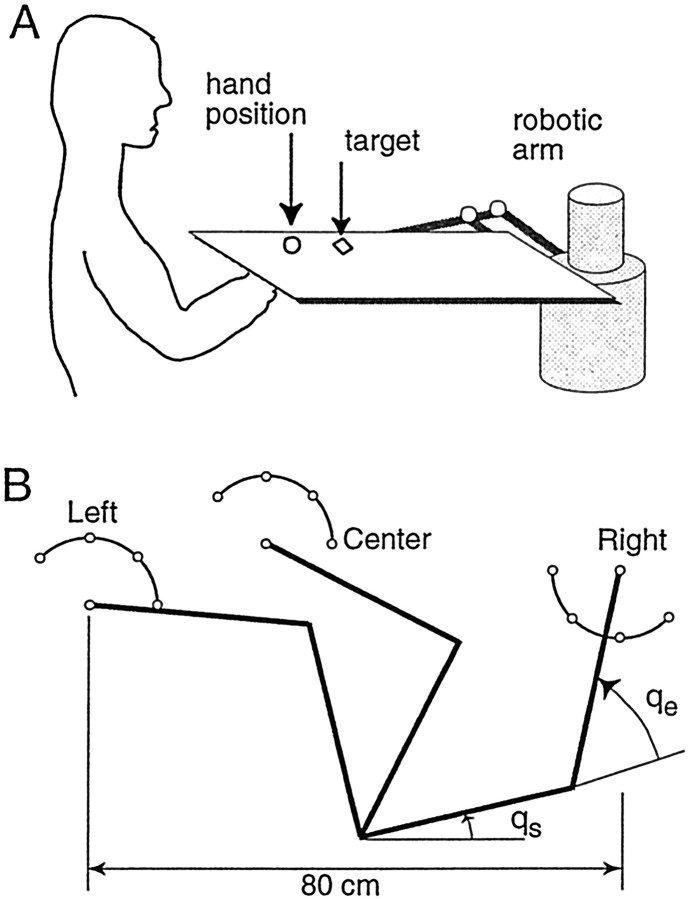
Experimental setup. The torque motors of a two-dimensional robotic manipulandum (Shadmehr and Brashers-Krug, 1997) were programmed to produce forces as a function of the position and velocity of the robot's handle. When the motors were turned off, the field was null. Subjects sat on a chair in front of the manipulandum and grasped its handle, with the right arm being supported by a sling. Figure1A shows the schematic of the apparatus. A projector was hung from the ceiling and displayed a cursor (2 × 2 mm²) representing hand position and boxes (8 × 8 mm²) representing targets of reaching movements on a 47 × 32 cm² horizontal screen positioned directly above the subject's hand (<1 cm above the robot's handle). To allow for a comfortable viewing angle, the subject was positioned so that his or her hand was 10 cm below the configuration in which the arm's motion is in the horizontal plane. Cursor location was tightly calibrated to coincide with the position of the handle. Arm link lengths for each subject were measured, and joint angles were computed from a simple three-dimensional kinematic model, represented in terms of the Z—Y–Z Euler angles (Craig, 1986). Because the arm's plane of action was only slightly outside the horizontal plane (by ∼10°), to compute two-dimensional force fields we projected the result onto the horizontal plane.

Fig. 1.

Experimental setup. A, Subjects reached to visual targets while holding the handle of a manipulandum. The location of their hand was displayed directly above their hand via a video projector on a horizontal screen that was mounted at <1 cm above the handle. B, Performance was measured in three small work spaces, each a semicircle of radius 10 cm. When the hand was in a given work space, it was initially positioned at the center target. For odd-numbered movements, targets were chosen randomly from the marked locations on the circumference of the work space. Targets for even-numbered targets were always at the center of the work space. The typical joint angle vector at the left work space (Left) was q_l = (104°,71°), that at the center work space (Center) was q_c = (63°,90°), and that at the right work space (Right) wasq_r = (13°,65°). A typical arm link length for the upper arm was l₁ = 33 cm, and that for the forearm wasl₂ = 34 cm.

The projection of the cursor on top of the hand, rather than on a computer monitor, allowed the subjects to maintain an angle of gaze similar to the one that they would use if they were looking directly at their hand. We found this to be a crucial factor in tests of spatial generalization in which the configuration of the arm was greatly changed from one position to another. If the subject did not look at the hand but looked at a vertical monitor, the angle of gaze at the right and left work spaces (Fig. 1B, Right, Left) was not the same as it would be when the subjects were looking at their hand. This discrepancy caused large errors in perception of target position with respect to the hand in the off-center locations, but not at the center location (Fig. 1B, Center). Therefore, it seemed that a test of spatial generalization that did not provide a tight coupling between the angle of gaze and the true position of the hand might introduce a confounding variable. The current setup was designed in view of this realization.

EMG signals were recorded from biceps, triceps, and anterior and posterior deltoids by pediatric cardiac electrodes in a bipolar mode. To reduce motion artifacts, EMG signals were preamplified differentially very near the electrodes (gain of 100) and then bandpass filtered (fourth-order Butterworth; 25–400 Hz), amplified (gain of 50), and RMS rectified (32 msec window). Hand position and velocity and the rectified EMG signals were digitized and sampled at 100 Hz.

Learning task. The task was to reach to a displayed target (displacement of 10 cm) within 500 ± 50 msec. If the target location was reached too slowly or too quickly, the target turned blue or red, respectively. The target “exploded” when the reach was in time. The hand was required to remain at the target until the next target was shown. A target set consisted of 192 targets. In some target sets, a target had a one-sixth probability of turning the force field off. These null field targets were catch trials in which we hoped to measure aftereffects of adaptation.

Movements took place in three arm configurations (Fig.1B), labeled left, center, and right work spaces (Left, Center, and Right). The work spaces were selected by moving the subject's chair while keeping the robot's arm configuration constant. Because the left and right arm configurations were near the limits of the reachable space, care was taken to choose target directions that could be comfortably reached. In the Center and Left work spaces, the initial target was chosen randomly from 0, 45, 90, or 135°. The next target was always at the center. In the Right work space, the initial target was chosen randomly from 180, 225, 270, and 315°. The next target was always at the center. A target set consisted of 192 targets. All subjects were familiarized with the task by performing one target set in the null field in each of the three work spaces at least 24 hr before the main experiment began.

Force field design. We had observed previously that learning a force field at a given work space resulted in changes in EMG patterns from those observed in the null field (Thoroughman and Shadmehr, 1999). These changes could be quantified as rotations in the PD of each muscle's spatial tuning function. A tuning function is defined as the average activity of a muscle during initiation of movement (−50 to 100 msec) as a function of movement direction. The preferred direction of this function is the vector sum of the individual activation vectors. Furthermore, a simple biomechanical model that parceled the joint torques into muscle forces via a moment arm matrix and assumed a mathematically reciprocal level of activation between antagonist muscles was able to predict accurately the magnitude of rotations that occurred during the learning of a given force field (Thoroughman and Shadmehr, 1999). The term “relative rotation of the PD vector” refers to the angular change that occurs at a given arm configuration to the PD vector between the null field and the learning of the force field. Our initial goal then was to use this model to design a field such that training at a given work space would result in muscle PD rotation that would be conserved across the work spaces; that is, the relative rotations should remain constant as a function of arm configuration. A good candidate was a field in which torques depended on joint angular velocity but were invariant to joint angular position.

One way to design such a field is to produce forces with the robot as a function of the subject's joint velocities. In practice, this is difficult because joint velocities of subjects are hard to estimate on-line. Another approach is to produce a field that depends on hand velocity and assume that the work space is small enough such that the relation between hand and joint velocities, called a Jacobian, remains constant. Although this can be accomplished by limiting training to only small-amplitude reaching movements (for example, 10 cm), the Jacobian would still need to be reestimated at each configuration to make the torques invariant to joint position.

It turns out, however, that there is a special class of force fields for which the reestimation of the Jacobian is not necessary. In these fields, the forces on the hand and the torques on the joints are simultaneously invariant to arm configuration. Because the torques are invariant, rotations in muscle PDs may remain nearly constant as a function of arm configuration.

We begin by deriving this class of fields. In our paradigm, the forces acting on a subject's hand are described by a matrix B and hand velocity {x˙}. Because we will be using a number of different force fields in this report, we index Bwith integer i:

$$f=B_i\dot{x},$$ Equation 1

where in our planar movementsB_i is a 2 × 2 matrix. The joint torques τ for the coordinate system shown in Figure1B can be written as:

$$\hspace{0.5em}\tau =J^T(q)B\dot{x}$$ Equation 2

$$J(q)\equiv \frac{\text{d}x}{\text{d}q}=\left[\begin{array}{cc}{l}_{1}sin(q_s)+l_{2}sin(q_s+q_e)\hfill & l_{2}sin(q_s+q_e)\hfill \\ -l_{1}cos(q_s)-l_{2}cos(q_s+q_e)\hfill & -l_{2}cos(q_s+q_e)\hfill \end{array}\right],$$

where q_s andq_e are shoulder and elbow joint angles, J(q) is the Jacobian matrix,l₁ andl₂ are lengths of upper arm and forearm, x is the hand position vector, and T is the transpose operator. Using the chain rule, we have {x˙} =J(q){q˙} and:

$$\tau =J^T(q)BJ(q)\dot{q}.$$ Equation 3

We observe that if B is skew symmetric, then matrix:

$$W(q)\equiv J^T(q)BJ(q),$$

where τ = W{q˙}, is independent of shoulder angle q_s. For example, when B = {0,1;−1,0} N.sec/m, we have:

$$W=\left[\begin{array}{cc}0& l_1{l}_{2}sin(q_e)\\ -l_1{l}_{2}sin(q_e)& 0\end{array}\right],$$ Equation 4

$$\tau =\left[\begin{array}{c}{l}_1{l}_{2}sin(q_e){\dot{q}}_e\hfill \\ -l_1{l}_{2}sin(q_e){\dot{q}}_s\hfill \end{array}\right].$$

Therefore, if B is skew symmetric, not only are the forces on the hand invariant to hand position, but the corresponding torques on the joints (in Eq. 3) are also invariant to the position of the shoulder. Furthermore, if we allow the elbow angle to change, its effect is merely to scale the W matrix. In other words, if one learns a field represented by a skew-symmetric matrix Bat an elbow angle of 90°, the field is the same at any other arm configuration but simply weaker depending on the position of the elbow angle. The word “same” in this case means that for this special field, the forces on the hand and the torques on the joints are approximately position invariant simultaneously.

Choice of joint coordinates. The representation of the Jacobian in Equation 2 assumed that the elbow angleq_e was measured relative to the upper arm (Fig. 1B). This is commonly called arelative joint coordinate system. Representation ofq_e in a different way will of course change the Jacobian. For example, if we choose to represent the elbow angle with respect to the x-axis (commonly called anabsolute coordinate system) and call this anglep_e, then with respect to our relative joint angle coordinates, p_e =q_s +q_e andp_s =q_s. The Jacobian in this absolute coordinate system becomes:

$$J(p)=\left[\begin{array}{cc}{l}_{1}sin(p_s)\hfill & l_{2}sin(p_e)\hfill \\ -l_{1}cos(p_s)\hfill & -l_{2}cos(p_e)\hfill \end{array}\right],$$

and the W matrix now becomes:

$$W=\left[\begin{array}{cc}0& -l_1{l}_{2}sin(p_s-p_e)\\ l_1{l}_{2}sin(p_s-p_e)& 0\end{array}\right]$$

Therefore, when the B matrix is skew symmetric, the corresponding torque field in relative or absolute joint coordinates maintains its characteristic weak dependence to arm configuration.

Pilot study: generalization to a near work space. We initially asked whether training at either Left or Right work spaces resulted in improved performance (as compared with that of naive subjects) at the Center work space. We recruited eight subjects. No EMG was recorded from this pilot group. These subjects were trained initially in the null field in each of the three work spaces. They then trained in field B₁ = {0,13;−13,0} N.sec/m at Right (two target sets; total of 384 targets). The force field was present in all movements. After a 5 min rest, subjects were tested in the same field at Center (a single target set). In Center we chose 33 random targets and turned off the field to record aftereffects of adaptation (Shadmehr and Mussa-Ivaldi, 1994). Subjects then returned on a second day. They were trained on a new force field B₂ = −B₁ at Left and then tested inB₂ at Center. The performance at Center was compared with the performance of naive subjects in the same field at Center. This naive group consisted of 21 subjects who only trained at Center; 14 learned B₁, whereas 7 learned field B₂. The data from this control group come from a previous experiment (Thoroughman and Shadmehr, 1999). The experiment with group 1 allowed us to ask whether generalization takes place when the arm's configuration is changed from the outside (Left or Right) to Center.

Experiment 1: generalization to a far work space. We next tested the hypothesis that generalization might occur over larger distances in hand position, i.e., from Left to Right and vice versa. We recruited six new subjects and trained them at Left inB₁ (three target sets) and tested them at Right in the same field (one target set). Performance at Right was compared with that of naive individuals (subjects in the pilot study). Subjects then returned on a subsequent day and trained inB₂ at Right (three target sets) and were then tested at Left (one target set).

Experiment 2: generalization in intrinsic coordinates. In Experiment 1 we expected generalization to occur because the field had torques that were essentially invariant to joint position, resulting in rotations in muscle PDs that remained constant across the work space. However, the force field was also invariant to hand position. Therefore, generalization might have occurred not because muscle PDs rotated by a constant amount but because forces on the hand were the same at the two locations. To differentiate between these two possibilities, we performed an experiment in which the torques were invariant to joint configuration but forces were not invariant to hand position. In this field, we expected muscle PDs to rotate by approximately the same amount at each of the two arm configurations (Left and Right) but the forces at the hand to be in opposite directions.

The field that we considered was B₃ = {−11,−11;−11,11} N.sec/m. This symmetric matrix produces joint torques that are highly dependent on the configuration of the arm. If subjects train in B₃ at the Left work space, our task is to find the field at the Right work space that would preserve the relative rotations in muscle PDs. We did this by translating B₃ from Left to Right so that the relation between joint torques and joint velocities was maintained. The procedure was as follows: In the Left work space where joint angles are described by vectorq_l, the forces imposed on the hand are F =B₃{x˙}, corresponding to joint torques:

$$\tau =J(q_l{)}^T{B}_{3}J(q_l)\dot{q}.$$

When this field is translated in joint coordinates to the Right work space where joint angles are described by vectorq_r, the forces on the hand are:

$$F=J(q_r{)}^{-T}J(q_l{)}^T{B}_{3}J(q_l)J(q_r{)}^{-1}\dot{x},$$

$$F=B_3^{*}\dot{x}.$$

Plugging in typical values forq_l = (104°,71°) andq_r = (13°,65°) provides the surprising result that:

$$B_3^{*}=\left[\begin{array}{cc}14& 10\\ 10& -12\end{array}\right]\approx -B_3.$$

This is intriguing because it predicts that the translation ofB₃ in joint space results in a fieldB₃^* that in terms of forces on the hand is very nearly opposite to the one that subjects originally trained in (correlation between force field generated byB₃^* and −B₃ is at r = 0.985). We had observed previously that if subjects trained in fieldA and then were presented with field −A in the same work space, performance was much worse than that with naive individuals (Brashers-Krug et al., 1996; Shadmehr and Brashers-Krug, 1997). The theory now predicted that if we train at Left inB₃ but then change the configuration of the arm to the Right work space and test in the fieldB₄ = −B₃, subjects would demonstrate generalization.

Five subjects were recruited for this experiment. All trained in null at Right and Left. They then trained inB₃ at Left (three target sets) and were then tested at Right in B₄ = {11,11;11,−11} N.sec/m (one target set). Performance at Right was compared with that of naive subjects (n = 4).

Experiment 3: generalization in extrinsic coordinates. It is possible that subjects generalized in the above experiments not because the coordinate systems matched their internal model but because they simply had become more familiar with the robot and regardless of the force field would do better than naive individuals would. We performed a control experiment to test for this possibility.

In this experiment, subjects were tested for generalization in a field that was translation invariant in hand space but not joint space. They trained in a field that resulted in the rotation of muscle PDs in one direction, but for the test of generalization at the new work space they were given a field that required muscle rotations in the opposite direction. Therefore, if the internal model generalized in terms of muscle PDs, then, after subjects trained in Left, performance at Right should be actually worse than those of naive individuals, despite the fact that forces remained invariant with respect to hand position.

For this last experiment, 11 new subjects were recruited. All subjects began by training in the null field in each of the two work spaces. Next, six subjects trained at Left inB₃ (three target sets) and then were tested at Right (one target set) inB₃. The remaining five subjects were trained at Right in B₃ and then tested at Left in B₃. The performance in the first set of training of each group of subjects was used as the control for the test of generalization of the other group.

Data analysis. The onset and termination of a movement were defined as when the tangential hand velocity crossed a threshold (0.03 m/sec) and remained above or below this level. In all fields, our measure of movement error was the maximum perpendicular displacement from a straight line to the target.

The method for calculating spatial tuning functions of recorded EMG signals has been described previously (Thoroughman and Shadmehr, 1999). Briefly, EMG traces were normalized, and the average value between 50 msec before and 100 msec after the onset of the movement was calculated for each movement and then averaged across movements for each direction. For each target set, there were eight scalar values representing the average EMG activity toward each of the eight directions. We multiplied each of the eight scalars by a unit vector in the direction of movement and formed a polar plot representing the function that mapped target direction into initial EMG activity. Summing the eight vectors resulted in a vector that represented the directional bias of the muscle activity, i.e., preferred direction of the tuning function for that muscle.

To determine whether a muscle's spatial tuning function had a significant directional bias, we used a nonparametric approach to estimate the distribution of the length and angle of the PD vector. By the use of a bootstrapping technique, the 192 vectors representing the 192 EMG values for a given muscle (one for each movement during a target set) were randomly sampled, with replacement, with uniform probability to generate 192 new vectors (Efron and Tibshirani, 1993). As described above, the PD vector was calculated from this resampled population. This procedure was repeated 200 times to produce a distribution of the PD vector for that muscle in that target set. From this distribution the confidence intervals (in terms of SDs) were estimated for the PD vector. We considered the tuning function to have a significant directional bias if the magnitude of the PD vector was >3 SDs larger than zero. Changes in the angle of the directional PD vector between two conditions were measured only if the tuning curves had a significant directional bias. Generally, the change in the PD vector was represented as rotation relative to the PD of that muscle in the null field.

RESULTS

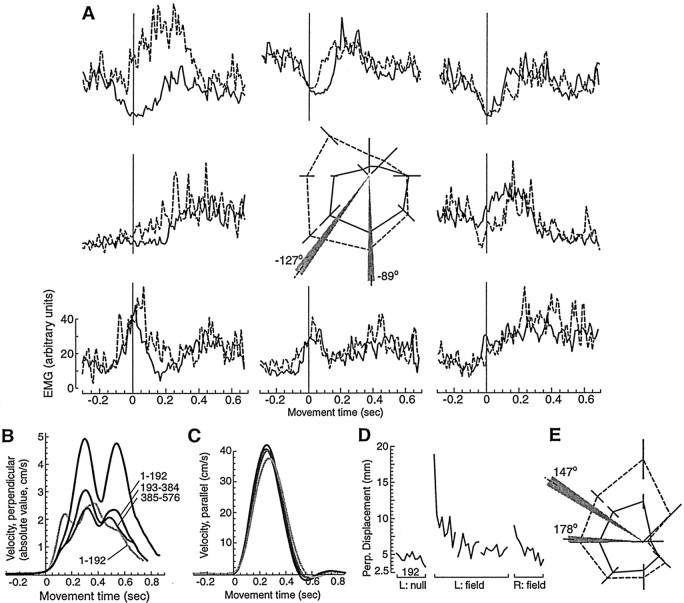
Our objective was to test the hypothesis that there is a link between how a sensorimotor map of arm dynamics generalizes from training in a small work space and the rotations that occur in muscle PDs. We imagined that learning a field in one work space might generalize to all other arm configurations if the field was such that it required a constant relative change in muscle PDs across work spaces. Data for a typical subject are shown in Figure2. In Figure 2A, the subject's arm is in the Left work space, and the EMG from biceps is illustrated for movements made to the eight directions in the null field and force field B₃ (a symmetric matrix in which joint torques are highly configuration dependent). The average EMG during initiation of movements (between −50 and 100 msec), averaged over all movements to that direction in the target set, is plotted as a function of movement direction in the center plot. In the null field condition, biceps has a PD vector that points toward −89 ± 1.9° (mean ± SD). With training in the field, the EMGs gradually change, resulting in a new PD at −127 ± 2.1°. The hypothesis predicts that when the arm is tested in another work space, the brain will expect the field to require the same amount of rotation in the PD of biceps. If this is the case, then performance will be better than that of naive individuals. If the field is such that it requires a rotation of biceps PD at the new configuration opposite that of the original training, then performance will be worse than that of naive individuals.

Fig. 2.

EMG and kinematic data from a typical subject who trained for three sets (each set, 192 movements) at Left in fieldB₃ and was then tested at Right in joint space translation of that field, named B₄.A, EMG data from biceps during movements in the null field (solid line) and in the force fieldB₃ (dashed line). Data are aligned to the initiation of movement. The arm is in the Left work space. Each subfigure indicates EMG activity for a movement toward a target at one of the eight directions. Thesolid line is for the null field, and the dashed line is for the last set of training in fieldB₃. The center figure is the spatial tuning function for this muscle in the null and force fields. The EMG from time −50 to 100 msec for each movement is averaged, and the mean ± SD over all movements toward each of eight directions is shown. The preferred direction vector is the sum of the eight vectors. The means ± SD of the vector's angle and the length are noted by the gray region. Training in the field is coincident with a −38° rotation in the preferred direction vector.B, Magnitude of the hand velocity vector perpendicular to the direction of the target, averaged for each target set. Theblack lines are for training inB₃ at Left (3 target sets). The gray line is for the test of generalization at Right inB₄ (1 target set). Movementnumbers are indicated. C, Magnitude of the parallel velocity vector toward targets. Little change is observed.D, Maximum displacement perpendicular (Perp.) to the direction of the target. The bin size is 16 movements. Connected lines indicate a target set (192 movements). E, Spatial EMG function for biceps in the Right work space. Field B₄ at Right required a rotation of −31° in the biceps' preferred direction, similar to the rotation that field B₃ required at Left. Coincident with this, performance measures indicated generalization.L, Left; R, Right.

Performance was measured by how far the force field displaced the hand from a straight-line path to the target. With training in the Left work space, the velocity of the hand in a direction perpendicular to that of the target was significantly reduced (Fig. 2B), resulting in the convergence of the hand's path to a straight line (Fig. 2D). The subject was then tested in the Right work space in field B₄. We had predicted that B₄ at Right would require approximately the same rotations in muscle PDs asB₃ at Left. It is worth noting that although the fields were completely opposed in hand coordinates, they were very similar in joint coordinates. Performance at Right demonstrated generalization (Fig. 2B,D). The EMG tuning function for biceps at the Right work space is shown in Figure2E; the PD for this muscle was at 178 ± 2.3° in the null field and rotated to 147 ± 2.8° in fieldB₄.

Fields that are position invariant in both hand and joint coordinates

A force field that produces torque on the arm in a way that is invariant to joint position may produce changes in muscle PDs that are also invariant to joint position. We began with a special class of such fields: a field that produced forces on the hand and torques on the joints that were simultaneously invariant to arm configuration. In this way we hoped to be able to ask whether there is generalization across arm configuration without having to specify the coordinate system in which the generalization might take place. When we found generalization, we performed further experiments to test between alternate coordinate systems of representation.

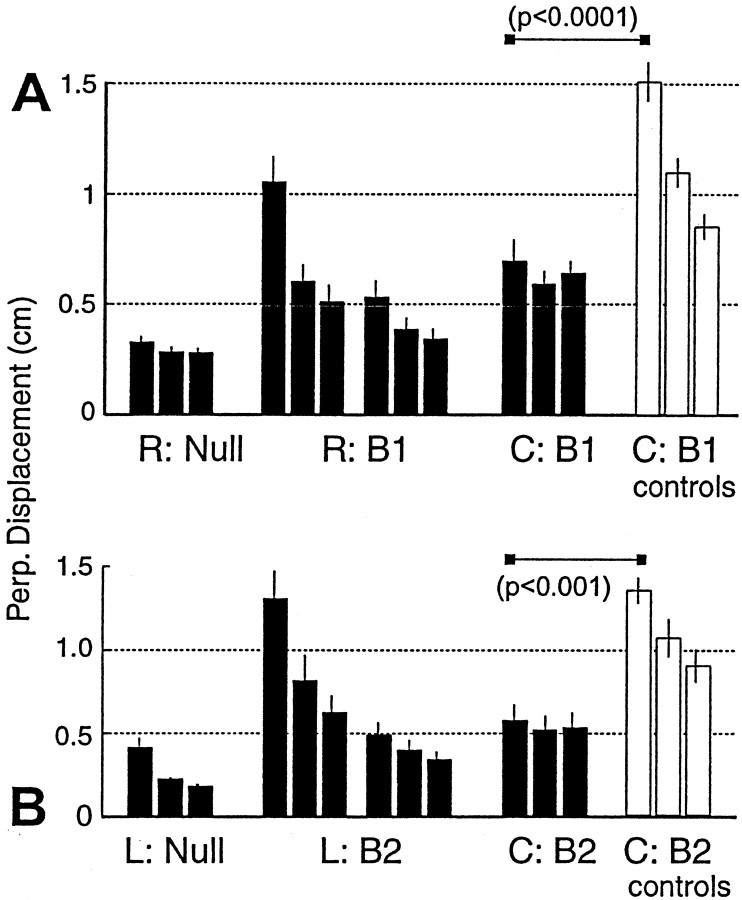
In the pilot study, subjects learned fieldB₁ (forces and torques invariant to hand or joint position) at the Right work space and then were tested at Center on B₁. On a separate day they learned B₂ at Left and were tested at Center on B₂. Two separate control groups learned either B₁ orB₂ only at Center. Subject performance is shown in Figure 3. Displacement significantly decreased as subjects learned the field at either Left or Right. When they were tested at Center, performance was significantly better than that of controls (p < 0.0001, Left to Center; p < 0.001, Right to Center), demonstrating generalization.

Fig. 3.

Generalization from Left or Right to Center. The fields are translation invariant in both hand and joint coordinates.A, Subjects practiced in the null field, then learned field B₁ at Right, and were then tested at Center (C) in field B₁(bin size = 64 movements; mean ± SEM). Performance at Center was significantly better than that of naive controls. B, Subjects learned field B₂ at Left and were tested at Center on B₂. Performance at Center was significantly better than that of naive controls.

Although control subjects at Center had to build gradually an internal model of the field and as a consequence gradually developed aftereffects, subjects that had trained in the field at Left or Right had significant aftereffects from the onset of testing at Center. On their very first catch trial (second movement in the field), trained subjects displayed an aftereffect of 1.59 ± 0.18 and 1.72 ± 0.20 cm for Left-to-Center and Right-to-Center groups, respectively. In contrast, during the same movements the control subjects had an average aftereffect size of 0.31 ± 0.2 cm. This suggested that the training in the small work space at Left (or Right) had resulted in an internal model that the brain could use to program movements at Center.

To test whether this generalization could be extended over larger changes in hand position, in Experiment 1 we trained subjects at Left in B₁ and then tested them at Right inB₁. On a separate day, the same subjects were trained at Right in B₂and then tested at Left in B₂. Despite the fact that work spaces were 80 cm apart, in the test of generalization there were significant aftereffects present from the very first catch trial: 1.49 ± 0.32 and 1.09 ± 0.18 cm from Left to Right and Right to Left, respectively. As predicted, performances during tests of generalization (Fig.4) were significantly better than that of controls (p < 0.05, Left to Right;p < 0.001, Right to Left).

Fig. 4.

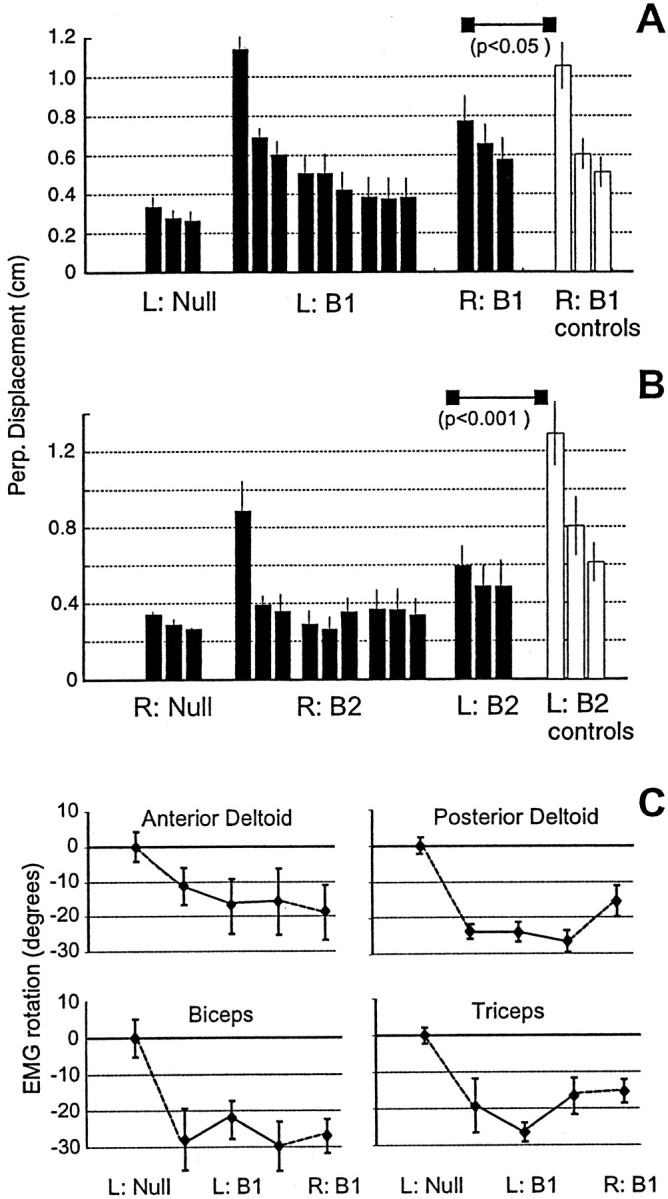
Generalization across the work space. The fields are translation invariant in both hand and joint coordinates.A, Subjects trained at Left inB₁ and were then tested at Right inB₁ (bin size = 64 movements). Performance at Right was significantly better than that in controls.B, Subjects trained at Right inB₂ and were tested at Left inB₂. Performance at Left was significantly better than that in controls. C, Rotations with respect to the null field in the preferred direction of EMG tuning functions during learning of field B₁ at Left (mean ± SE; bin size = 192 movements) and testing in fieldB₁ at Right are shown. At Right, the rotation of EMG was similar to the rotation that was recorded at Left. The field was nearly translation invariant in terms of muscle rotations (as well as hand forces), coincident with generalization of performance measures.

Because fields B₁ andB₂ are nearly translation invariant in joint space, we expected the rotation of muscle PDs to be invariant with respect to the location at which each field was learned. The EMG rotations are shown in Figure 4C. When subjects learnedB₁ at Left, the PDs rotated. When the same field was given at Right, the rotation remained essentially unchanged for the biceps, triceps, and anterior deltoid and reduced somewhat in the posterior deltoid. Therefore, generalization occurred across the work space in a force field that was nearly configuration independent, simultaneously, with respect to forces on the hand, torques on the joints, and muscle PDs.

We note, however, that performances during tests of generalization often declined when compared with the best performance in the original arm configuration. This may reflect the fact that for fieldB₂ in the two configurations tested in Figure 4, there is a small but nonzero dependence on the position of the elbow angle. The small difference in the angle of the elbow joint at these two configurations may have played a role in the lack of complete generalization.

Fields that are position invariant in joint but not hand coordinates

The next step was to remove the position invariance property of the field in terms of hand forces and to test whether generalization still took place. In Experiment 2, subjects learned fieldB₃ at Left and were then tested at Right in B₄. The fields were designed to produce similar rotations in muscle PDs at the left and right work spaces but to have opposite hand forces. Performance at Right as compared with that of naive controls (Fig.5A) was significantly better (p < 0.01). Because the fields were designed to produce similar torques as a function of arm velocity at the two work spaces, the EMG rotations remained invariant to the configuration of the arm (Fig. 5B).

Fig. 5.

Generalization across the work space. The field is translation invariant in joint coordinates but not hand coordinates.A, Subjects trained at Left inB₃ and were then tested at Right inB₄ (bin size = 64 movements). Performance at Right was significantly better than that in controls.B, Rotations with respect to the null field in the preferred direction of EMG tuning functions during learning of fieldB₃ at Left (bin size = 192 movements) and testing in field B₄ at Right are shown. EMG rotations remained invariant to changes in arm configuration. Such invariance is sufficient for generalization of training.

It is noteworthy that B₃ = −B₄ and that hand forces at Left and Right are reversed with respect to each other. If two fields with this property are presented in sequence in the same work space, subjects demonstrate negative interference, and performance in the second field is significantly worse than that of naive controls (Shadmehr and Brashers-Krug, 1997). However, with the change of the work spaces, the two very different force fields produce similar torque patterns in joint space, resulting in similar rotations in muscle PDs, and generalization of learning.

Fields that are position invariant in hand but not joint coordinates

It is possible that performance of the trained subjects in the above experiments was better than that of the naive control groups because they simply had more practice with the robot. A strong prediction of our hypothesis, however, is that if a field requires a rotation in muscle PDs at one configuration and that rotation is opposite that required for movement in a field in another arm configuration, then performance of the trained subjects should be worse than that of naive individuals. In other words, generalization would still occur, but it would impede performance.

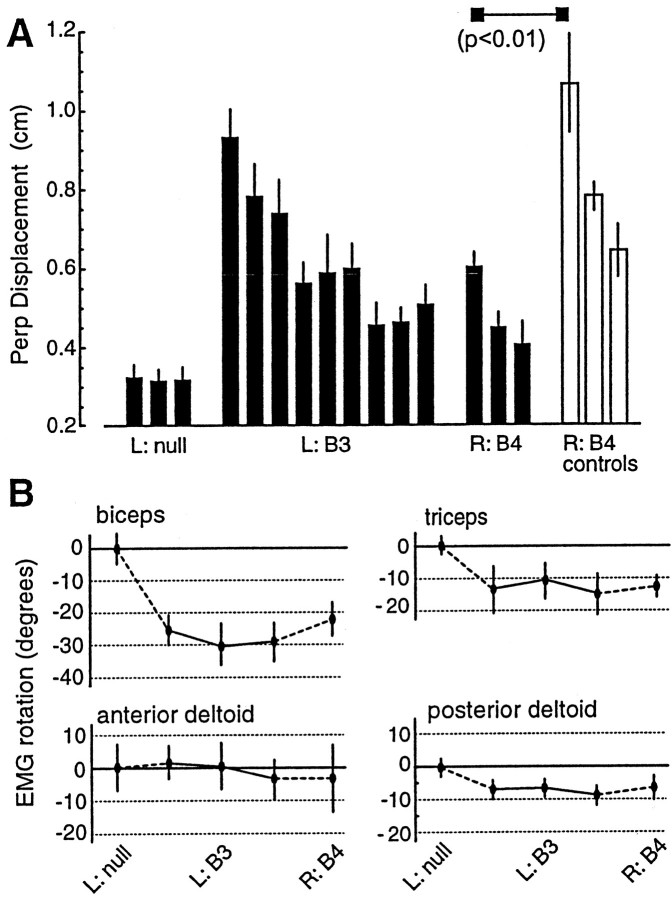
Some subjects in Experiment 3 trained in fieldB₃ at Left and then were tested at Right in B₃. Remaining subjects were trained in B₃ at Right and then were tested at Left in B₃. The fields at the two work spaces were identical in terms of forces on the hand but very different in terms of torques on the joints. Coincident with the learning of the field at Left was a negative rotation in PDs of some muscles (Fig.6B). However, when the subjects were tested at Right, the movements required a positive rotation in some muscle PDs. Predictably, performance at Right (Fig.6A) was now significantly worse than that of naive subjects (p < 0.01). Similarly, subjects that trained at Right and were then tested at Left (Fig. 6C) performed significantly worse than did naive subject (p < 0.01). The newly formed sensorimotor map continued to generalize, but now this generalization impeded performance because the torques in the field did not remain invariant to joint position.

Fig. 6.

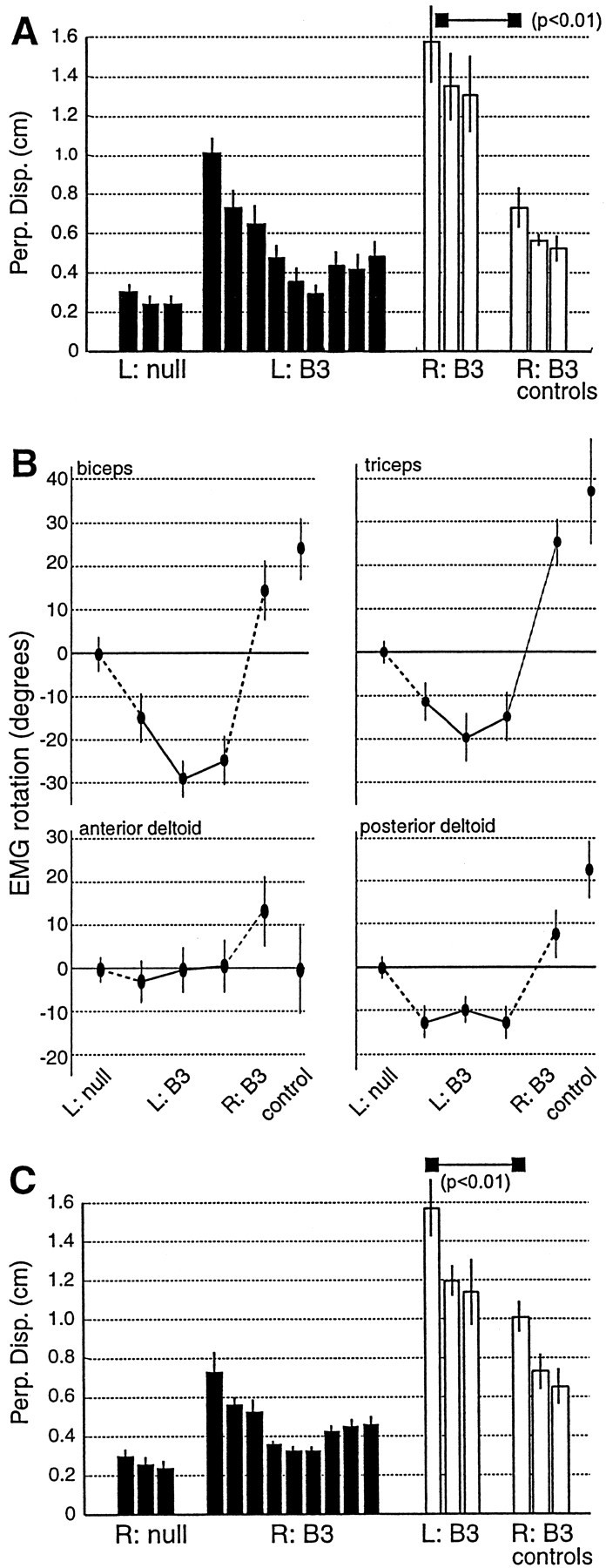
Generalization does not occur when the EMG rotations at one arm configuration do not match the rotations that are required for movements in another arm configuration. A, Performance of subjects that trained in B₃at Left and were tested in B₃ at Right (mean ± SE; bin size = 64 movements) is shown. The field was configuration independent in hand-centered coordinates but not joint coordinates. Subjects performed significantly worse than did naive controls. B, Rotations with respect to the null field in the preferred direction of EMG tuning functions during learning of B₃at Left and testing in field B₃ at Right are shown. The rotations at Left are opposite the rotations required to move in the same hand-centered field at Right. When the relative change in EMG PD angles rotates with arm configuration, training does not generalize. C, Subjects that learned fieldB₃ at Right were also significantly worse than control subjects in their test of generalization at Left.Disp., Displacement.

DISCUSSION

Learning to reach in a novel dynamical environment requires a change in the association between target directions and motor commands, i.e., formation of a new sensorimotor map. Previously we had observed that training in a force field at one arm configuration resulted in a sensorimotor map that allowed the subjects to generalize to a nearby arm configuration (Shadmehr and Mussa-Ivaldi, 1994). The generalization appeared to have a proximal coordinate system associated with it. When the force field was the same at the two work spaces in terms of a map that transformed hand velocities to hand forces, subjects performed poorly in the test of generalization. They performed much better, however, if the field was a map that transformed joint velocities into torques on the joints of the arm.

Practicing in a field at a given arm configuration results in a change in the pattern of muscle activations (or forces) as a function of movement direction (or desired motor state). The change may be quantified as a rotation in the spatial tuning curves, or preferred directions, of EMGs (Thoroughman and Shadmehr, 1999). In this work we hypothesized that although the PD of each muscle may depend on the configuration of the arm, learning might generalize as a constant relative change in muscle PDs across the arm's work space. This would be consistent with the coordinate system found in our previous study. To test this idea, we designed force fields such that their learning at a given work space would result in a constant relative change in muscle PDs across the work spaces. One of these fields was defined by a skew-symmetric transformation of hand velocity. This field had the desirable property that forces on the hand and torques on the joints were simultaneously invariant to the position of the shoulder joint. When subjects trained in a small work space in this field, their performance as compared with that of naive subjects was significantly better at a work space 80 cm away. Coincident with this was a constant relative change in the muscle PDs.

We next designed a force field that was dependent on arm configuration in a way that when the arm moved from one work space to another, the field nearly reversed directions. We had observed previously that subjects performed extremely poorly, significantly worse than naive controls, when they attempted to learn a field that was opposite the one in which they had just completed practice (Shadmehr and Brashers-Krug, 1997). In this case the hypothesis predicted that by changing the configuration of the arm, subjects would actually generalize to this opposite field. Our data were consistent with this prediction. Notably, the generalization was coincident with a constant relative change in muscle PDs. When the field was such that forces on the hand were invariant to hand position but not joint angles, coincident with a nonconstant relative change in muscle PDs, subjects performed worse than did naive controls in the test of generalization. Therefore, it seems that when the adapted sensorimotor map is asked to produce motor commands in arm configurations in which it has not been trained, it produces commands that are invariant to arm configuration when motor commands are expressed in terms of a relative change in muscle PDs.

Because the generalization was observed over very large portions of the shoulder's configuration space, we suggest that the map with which the brain represents dynamics of the arm is constructed with elements that do not have spatial tuning functions that locally encode arm configuration. If the map had such elements, then learning at one arm configuration would generalize to neighboring work spaces, but not globally. An example of such spatial locality is found among the cells in the early visual system of the cortex. If one was to learn a visual discrimination task with elements that have spatially localized response characteristics, then there will be little generalization beyond the region of training (Poggio et al., 1992)—a prediction that agrees with observation (Karni and Sagi, 1990; Ahissar and Hochstein, 1997). In contrast to the visual areas, cells in the primary motor cortex are generally not tuned to a specific arm configuration, but their firing is often modulated globally, and sometimes linearly, by arm configuration (Georgopoulos et al., 1984). Learning dynamics with elements that behave in this way should generalize globally, in agreement with what we have found in these experiments.

The spatial generalization observed here was associated with a specific coordinate system: that of joint torques and muscle PDs. This coordinate system is in agreement with results reported recently for learning of inertial fields but stands in sharp contrast to spatial generalization patterns for learning of kinematic transformations (which generalize in extrinsic coordinates) (Ghez et al., 2000). Are these observations potentially related to properties of cells in the motor areas of the brain? One such property is directional tuning during reaching movements (Caminiti and Johnson, 1992): when neuronal activity is expressed with respect to the direction of reach, the tuning function is broad and has a PD. When monkeys learn to reach in viscous force fields, PDs of some cells in the primary, premotor, and supplementary motor areas undergo rotations (Benda et al., 1997;Schioppa et al., 1999). These cells have been called “dynamic” cells to differentiate them from another group of cells that do not show changes in their PD (“kinematic” cells). The rotations in the former group are different among the cells, but as a population, the average rotation is not unlike the rotations in PDs of some muscles. However, unlike muscle PDs, many of these cells maintain the change in their PDs during the washout period after the field returns to null (Gandolfo et al., 2000). Therefore, these cells are not simply upper motoneurons but are likely involved in representing the memory of the novel arm dynamics.

We do not know how PDs of these “memory” cells change as a function of arm configuration, but other studies suggest that while making reaches in the null field, the active cells in one work space generally do not cease to fire in the new work space, and their PDs may rotate (Caminiti et al., 1990, 1991). The rotation is widely different among the cells, but as a population, the median change is similar to the change in the shoulder angle. This observation led Caminiti and colleagues (Burnod et al., 1992) to suggest that firing rates of some cells in the motor cortex simultaneously reflect two kinds of signals: a postural signal encoding the arm's configuration in joint space and a signal encoding aspects of dynamics of the reach. On the basis of the generalization patterns reported here, it seems reasonable that the memory cells reported by Bizzi and colleagues (Gandolfo et al., 2000) might have PDs that, as a population, rotate with the shoulder joint. This would be the contribution of a postural signal. The crucial prediction is that after training in a force field, when the arm returns to the null field, these memory cells as a population should maintain a constant relative change in their PD as the arm moves to various regions of the work space.

We are not implying, however, that the internal model is represented in the motor cortex. Clearly, tuning properties similar to those of the motor cortex have been found in the cerebellum (Fortier et al., 1993), and learning-related changes in the motor cortex may be caused by changing inputs from this region (Martin et al., 2000). Our suggestion is that tuning properties of cells in the motor system must influence behavior. Quantifying patterns of learning and generalization, as seen in adaptation to novel dynamics, is one way to visualize this influence. In further support of this conjecture, note that cells in the motor cortex and cerebellum are tuned with respect to direction of movement. This predicts a generalization in velocity space that will be distinctly different from generalization across arm configurations. Generalization in velocity space, for example, quantifies how learning in one direction will affect nearby directions of movement. When training is confined to a single arm configuration, learning a single direction of movement generalizes to other target directions as a function that decays with the angular distance of the targets (Ghez et al., 2000; Thoroughman and Shadmehr, 2000). The shape of this generalization function predicts that learning is with computational elements that have directional tuning characteristics not unlike those found in the cerebellum and the motor cortex (Thoroughman and Shadmehr, 2000). Taken together, current results from various laboratories on how humans learn dynamics of reaching movements point to a sensorimotor map that is composed by the brain with elements that encode arm configuration globally but arm velocity locally. The output of this map is force represented in joint- or muscle-based coordinates.

Nevertheless, the elements that are used by the brain to represent a particular sensorimotor map are likely to also depend on the degree of difficulty in the task. Studies in visual perceptual learning provide important clues: when a perceptual discrimination task is very difficult, learning is specific to the orientation and position of the stimulus and does not generalize (Karni and Sagi, 1990; Poggio et al., 1992). This suggests that the map is formed with elements that have the fine spatial retinotopy exhibited in the early stages of visual information processing (Poggio, 1990). However, when the perceptual task is easy, learning generalizes across orientations and retinal positions, matching the spatial generalization of higher visual-processing areas (Ahissar and Hochstein, 1997). Taken together, it seems that the perceptual-learning process in the brain begins by assembling elements at the highest levels of visual processing first, which in turn direct learning to their respective lower level inputs if the condition is hard enough to warrant it (Ahissar and Hochstein, 1997).

In the hierarchy of control in the motor cortical systems, the highest levels are often associated with pre-SMA, SMA, and the premotor regions, whereas the lowest level is occupied by the primary motor cortex. Approximately fitting into this framework is the result that stimulation generally produces complex multijoint bilateral movements in the SMA and single-joint unilateral twitch-like movements in the primary motor cortex. Therefore, the size of the “effective field” in the SMA is much larger than that of the localized field (in terms of region of influence in the configuration space of the entire body) that is evoked from the primary motor cortex stimulation. If one could learn a motor task with one hand and be able to generalize to another limb, then the theory predicts that learning had engaged elements in the higher levels of motor control in which effective fields are broad. An example of this is our ability to sign our name with our dominant hand and yet retain much of the stroke characteristics when the foot is used for the task. Interestingly, functional imaging shows that regions that are activated in both hand and foot signing are in the SMA and premotor cortex, and not in the primary motor cortex or the basal ganglia (Rijntjes et al., 1999).