Reciprocal Inhibitory Connections Regulate the Spatiotemporal Properties of Intrathalamic Oscillations

Abstract

Mice with an inactivated GABA_A receptor β₃ subunit gene have features of Angelman syndrome, including absence-like seizures. This suggests the occurrence of abnormal hypersynchrony in the thalamocortical system. Within the thalamus, the efficacy of inhibitory synapses between thalamic reticular (RE) neurons is selectively compromised, and thalamic oscillations in vitro are prolonged and lack spatial phase gradients (Huntsman et al., 1999). Here we used computational models to examine how intra-RE inhibition regulates intrathalamic oscillations. A major effect is an abbreviation of network responses, which is caused by long-lasting intra-RE inhibition that shunts recurrent excitatory input. In addition, differential activation of RE cells desynchronizes network activity. Near the slice center, where many cells are initially activated, there is a resultant high level of intra-RE inhibition. This leads to RE cell burst truncation in the central region and a gradient in the timing of thalamocortical cell activity similar to that observed in vitro. Although RE cell burst durations were shortened by this mechanism, there was very little effect on the times at which RE cells began to burst. The above results depended on widespread stimuli that activated RE cells in regions larger than the diameter of intra-RE connections. By contrast, more focal stimuli could elicit oscillations that lasted several cycles and remained confined to a small region. These results suggest that intra-RE inhibition restricts intrathalamic activity to particular spatiotemporal patterns to allow focal recurrent activity that may be relevant for normal thalamocortical function while preventing widespread synchronization as occurs in seizures.

The thalamus participates in a wide range of thalamocortical oscillations, including 7–14 Hz sleep spindles (Steriade et al., 1993). Spindle activity occurs in the thalamus of decorticated cats (Morison and Basset, 1945) and in thalamic slices (von Krosigk et al., 1993; Huguenard and Prince, 1994a;Bal et al., 1995a,b; Kim et al., 1995), but not in cortex that has been disconnected from thalamus (Burns, 1950), suggesting that the thalamus plays an important role in generating the spindle rhythm.

Several experimental observations suggest that reciprocal inhibitory connections between thalamic reticular (RE) neurons regulate thalamic spindle oscillations and prevent hypersynchrony characteristic of some epilepsies. The anti-absence drug clonazepam may function by enhancing GABA_A connections between RE cells, thereby reducing the output of RE cells to thalamocortical (TC) cells (Huguenard and Prince, 1994b). Additional evidence comes from mice lacking the β₃ subunit of the GABA_A receptor. Knock-out of the β₃ subunit reduces the strength and duration of GABA_A synapses between RE cells without affecting those from RE to TC cells (Huntsman et al., 1999). This highly selective change has important consequences for intrathalamic oscillations elicited by stimulation of internal capsule in vitro (Hunstman et al., 1999). First, oscillations last much longer in thalamic slices from knock-out (β₃^−/−) mice than in those from wild-type (β₃^+/+) animals. Second, phase differences between TC cell activity at different locations along knock-out slices are negligible. In wild-type slices by contrast, phase differences between TC cell activity at different locations grow with distance. The phase lags observed in wild-type slices are at least an order of magnitude larger than those in knock-out slices. These in vitro findings may help to explain why β₃^−/−knock-out mice have many features of Angelman syndrome, including seizures (Homanics et al., 1997; DeLorey et al., 1998).

Here we used computational models to evaluate mechanisms by which intact intra-RE inhibition could produce these differences between oscillations in wild-type and knock-out slices. We then studied how these mechanisms depend on the strength, kinetics, and spatial organization of intra-RE inhibition. Finally, we explore the functional consequences of these mechanisms for intrathalamic activity. Our findings suggest that particular properties of intra-RE inhibition, such as its slow decay, enable it to restrict intrathalamic activity to particular spatiotemporal patterns and thus prevent epileptiform activity.

MATERIALS AND METHODS

Model neurons. We studied a network model that included 400 TC and 400 RE neurons. Models for both types of neurons were presented in an earlier study (Sohal and Huguenard, 1998). Each neuron was modeled as a single compartment.V_T andV_R, the membrane potentials of TC and RE cells, respectively, evolved according to:

$$C_{\text{m}}{\dot{V}}_T=-g_L(V_T-E_L)-I_T-I_{\text{h}}-I_K-I_{\text{Na}}-I_{{GABA}_A(TC)},$$ Equation 1

$$\hspace{1em}{C}_{\text{m}}{\dot{V}}_R=-g_L(V_R-E_L)-I_{\text{Ts}}-I_K-I_{\text{Na}}-I_{AMPA}-I_{{GABA}_A(RE)},$$ Equation 2

where the specific capacitance of the membrane,C_m, equals 1 μF/cm²,g_L is the leak conductance,E_L is the reversal potential of the leak current, I_T andI_Ts are low-threshold calcium currents, I_h is the hyperpolarization-activated cation current,I_K andI_Na are the potassium and sodium currents underlying action potentials,I_GABA-A(TC) andI_GABA-A(RE) are the IPSCs mediated by GABA_A receptors on TC and RE cells, respectively, and I_AMPA is the EPSC mediated by AMPA receptors. We did not include intrathalamic GABA_B receptor-mediated currents, because they are extremely weak in mice (Warren et al., 1997), and GABA_A antagonists essentially abolish intrathalamic oscillations in mice (M. Huntsman and J. Huguenard, unpublished observations). Parameters and kinetics of intrinsic currents are described in Appendix . The total membrane area was 29,000 μm² for TC cells and 14,260 μm² for RE cells.

Synaptic currents. AMPA currents followed a first-order activation scheme, such that each presynaptic action potential activated half of the unoccupied postsynaptic receptors at that synapse. In simulations, AMPA currents rose with a time constant of 0.5 msec and decayed with a time constant of 5.6 msec. The reversal potential for AMPA currents was 0 mV.

GABA_A currents followed a similar first-order activation scheme. Based on intracellular recordings at 24°C in mouse RE cells (Huntsman et al., 1999), GABA_A currents always rose rapidly (τ_rise = 0.5 msec in all cells) but decayed at different rates in different cells (τ_decay = 75.8 msec in wild-type cells, τ_decay = 25.7 msec in knock-out cells, and τ_decay = 8.2 msec in all TC cells). Rise and decay times of GABA_A currents were temperature-corrected using a Q₁₀ of 2.2 (M. Huntsman and J. Huguenard, unpublished data). The reversal potential for GABA_A synapses was the same as the average RE cell rest potential, consistent with the mainly shunting function of GABA_A currents in RE cells (Sanchez-Vives et al., 1997; Ulrich and Huguenard, 1997).

Network architecture. As in earlier studies (Sohal and Huguenard, 1998), the network had a one-dimensional architecture with neurons distributed evenly along a straight line in two layers (one layer consists of RE cells, the other of TC cells). The network models a slice 1 mm in length, i.e., the distance between adjacent model cells corresponds to 5 μm along a thalamic slice. We used reflexive boundary conditions, so a neuron at position zero is at the center, not the edge, of the model slice.

Based on anatomical evidence that connections between RE and TC cells are topographic (Mitrofanis and Guillery, 1993; Agmon et al., 1995; but see Jones, 1985), earlier studies have defined connectivity using step functions, so that a TC cell located at position x contacts all RE cells within some radius of position x and vice versa (Destexhe et al., 1996a; Destexhe, 1998; Bazhenov et al., 1998a; Sohal and Huguenard, 1998). Many of these models defined their scaling laws by fixing the total postsynaptic conductance on each cell. Thus, as the number of model cells in the network increases, the relative influence of each presynaptic cell on a single postsynaptic cell decreases. This makes it difficult to reproduce the return excitation that occurs in an RE cell after that individual cell has been stimulated by intracellular current injection (Huguenard and Prince, 1994a; Bal et al., 1995b). To avoid this problem, we made the connections from RE to TC cells and those from TC to RE cells “sparse”, e.g., each RE cell received connections from a random subset of TC cells. A distance-dependent Gaussian distribution specified the probability of contact between a particular TC cell and a particular RE cell, and we insured that every presynaptic cell made the same number of connections and that every postsynaptic cell received the same number of connections. In this way, we both preserved the topography of connections between TC and RE cells and made individual connections between RE and TC cells relatively strong.

Connections from TC cells to RE cells. Retrograde labeling suggests that the axons of mouse TC cells from different barreloids remain well segregated in the thalamic reticular nucleus and that the axonal arborization from a single barreloid has a radius <50 μm in the thalamic reticular nucleus (Agmon et al., 1995). TC cells appear to make synaptic contacts on the somata of RE cells (Ide, 1982), but even if TC cells do contact the dendritic arbors of RE cells, these arbors typically have radii <100 μm (Scheibel and Scheibel, 1966; Spreafico et al., 1991; Lübke, 1993; Cox et al., 1996). Based on these observations, the five RE cells postsynaptic to a TC cell were drawn from a distance-dependent Gaussian distribution. This distribution had a SD of 50 μm and was centered at the location of the TC cell. The total postsynaptic AMPA conductance on each RE cell was$\overline{g}$_AMPA = 0.2 μS (however the fraction of activated AMPA receptors never exceeded 0.3, corresponding to an effective maximum conductance of 60 nS).

Connections from RE cells to TC cells. We followed the approach of earlier studies (Sohal and Huguenard, 1998) to account for heterogeneity in the anatomical (Cox et al., 1996) and physiological (Cox et al., 1997) properties of projections from RE to TC cells. We included two sets of connections from each RE cell to TC cells, to represent diffuse, “tickler” connections, and stronger “cluster” connections (Pinault and Deschenes, 1998). The conductance postsynaptic to each tickler connection was weaker than that postsynaptic to each cluster connection by a factor of 0.037, to account for the smaller postsynaptic currents elicited by and the greater failure rate of tickler synapses (Cox et al., 1997). However, a combination of anatomical (Cox et al., 1996) and physiological (Cox et al., 1997) evidence suggests that each TC cell receives many more tickler connections than cluster connections (for discussion, see Sohal and Huguenard, 1998). For this reason, each RE cell projected to 80 TC cells via tickler connections but only five TC cells via cluster connections. Postsynaptic TC cells were drawn from distance-dependent Gaussian distributions centered at the location of the RE cell. The SD of the distribution of TC cells postsynaptic to tickler connections was 200 μm, whereas TC cells postsynaptic to cluster connections were drawn from a distribution with a SD of 50 μm. In all the simulations we report, the total GABA_A conductance on a single TC cell, postsynaptic to both tickler and cluster connections, was 0.2 μS (however, in wild-type networks, the fraction of activated receptors never exceeded 0.2, corresponding to an effective maximum conductance of 40 nS). Significantly smaller conductances were insufficient to sustain network activity, and conductances that were twice as large produced results qualitatively similar to those reported here.

Connections between RE cells. Connections between RE cells are not required to simulate intrathalamic oscillations (Sohal and Huguenard, 1998), although they do modulate such activity. Thus, unlike individual synapses from RE to TC cells, individual synapses between RE cells do not need to be strong. For this reason, connections between RE cells were not sparse. Instead, each RE cell contacted other RE cells within a radius of 350 μm (Sanchez-Vives et al., 1997). The strengths of connections to one RE cell had a Gaussian spatial profile that was centered at the location of that RE cell and had a SD of 175 μm. The total postsynaptic GABA_A conductance on each RE cell was 2.25 μS in wild-type networks (however, in wild-type networks the fraction of activated receptors never exceeded 0.33, corresponding to an effective maximum conductance of 0.75 μS). The GABA_A conductance on each RE cell was reduced by a factor of 0.31 in knock-out networks, corresponding to the reduction in amplitude of evoked IPSCs in vitro (Huntsman et al., 1999). We verified that setting the total GABA_Aconductance on each wild-type RE cell to values between 1.5 and 2.5 μS produced results qualitatively similar to those reported here.

Initial conditions. Stimulation of corticothalamic fibers in internal capsule activates RE cells and evokes oscillations in vitro. We modeled the indirect activation of RE cells via stimulation of internal capsule two ways. Both schemes assumed stimulation was strongest near the center of the model slice. In the first scheme, a random set of RE cells were excited above their burst thresholds. The probability that a given RE cell was activated was a decreasing function of distance that had a Gaussian spatial profile. In this scheme, RE cells were either activated or received no initial input, and those RE cells that were activated began bursting at essentially the same time. To study how RE cells might begin to burst at different times, we sometimes used a second scheme in which the strength of excitatory input to RE cells decreased with increasing distance from the center of the model slice. To calculate the excitatory input to an RE cell distance (d) from the center, we assumed that it received excitatory synapses from 100 corticothalamic fibers. Each corticothalamic fiber was activated with a probability of

$${\text{e}}^{-\frac{1}{2\pi } (\text{d}/175 \mu \text{m}{)}^2}.$$

Computational methods. All simulations were run using Neuron (Hines and Carnevale, 1997) at a temperature of 32°C and with a time step of 0.1 msec.

RESULTS

Our results are organized as follows. First we deduce possible functions of intact intra-RE inhibition by comparing activity in wild-type and knock-out networks. Then we describe mechanisms by which intra-RE inhibition performs these functions. We study how these functions depend on the strength, kinetics, and spatial organization of intra-RE inhibition. Finally, we show that intra-RE inhibition restricts the types of intrathalamic activity that can sustain oscillations. Whenever possible, we compare our results to those obtained in vitro (Huntsman et al., 1999). We refer to thein vitro preparation using the term “slice” and to our simulations using the terms “network” or “model slice.”

Intra-RE inhibition shortens and desynchronizes intrathalamic oscillations

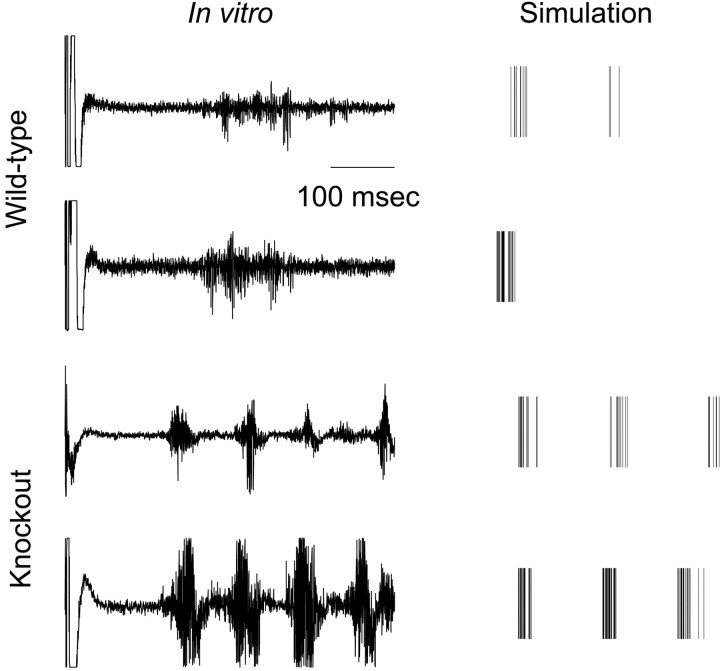
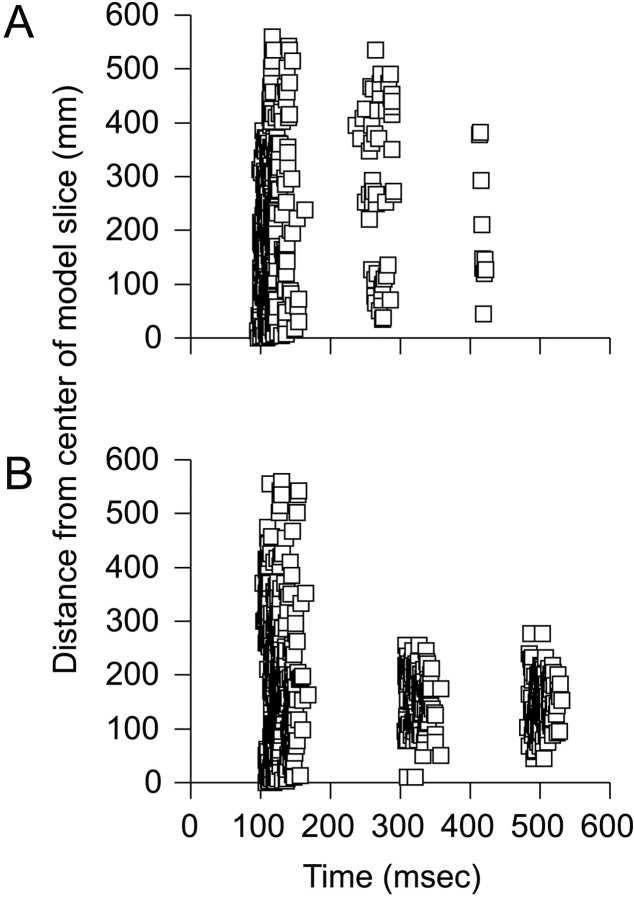
Figure 1 depicts the activity of TC cells at two locations, ∼500 μm apart, in a wild-type slice (top left), knock-out slice (bottom left), wild-type network (top right), and knock-out network (bottom right). Oscillations were elicited in slices by stimulating corticothalamic fibers in internal capsule, which then activate RE cells. To model this initial stimulus, we excited a random subset of RE cells above threshold at time 0. The probability of activation reaches a maximum of 0.5 for RE cells at position zero (because of the reflexive boundary conditions, position zero represents the center of the model slice). The probability that an RE cell is activated has a Gaussian spatial profile with a width of 125 μm. After activation of RE cells, the model reproduces two experimentally observed differences between activity after internal capsule stimulation in wild-type slices and that in knock-out slices (Huntsman et al., 1999). First, in the knock-out network, as in vitro, interactions between RE and TC cells sustain an intrathalamic oscillation for the duration of the simulation (600 msec) via a previously published cycle of events (von Krosigk et al., 1993;Huguenard and Prince, 1994; Bal et al., 1995a,b; Kim et al., 1995;Destexhe et al., 1996a; Golomb et al., 1996). In contrast, activity in the wild-type network had a much shorter duration.

Fig. 1.

Intrathalamic oscillations are shorter and less synchronized in wild-type slices and networks than in knock-out slices and networks. Each of the four panels shows activity of TC cells at two locations that are separated by ∼500 μm. Top left,Paired multiunit recordings of TC cell activity at two locations in a wild-type slice. In both recordings, activity is short-lived. Furthermore, activity in the top recording is phase-lagged relative to activity in the bottom recording. Top right, Times at which TC cells spike at analogous locations in a wild-type network. To simulate a multiunit recording, for each location, spike trains for 10 nearby TC cells are shown. As observed in vitro, activity is short-lived, and activity in the top train is phase-lagged relative to that in the bottom train. Bottom left,Paired multiunit recordings of TC cell activity at two locations in a knock-out slice. In both recordings, activity persists for several cycles. Furthermore, the initial bursts of activity in the two recordings are almost simultaneous, although subsequent cycles of activity become progressively less synchronized. Bottom right, Times at which TC cells spike in a knock-out network. As observed in vitro, the oscillation is relatively long-lasting, and the initial bursts of activity are highly synchronized.

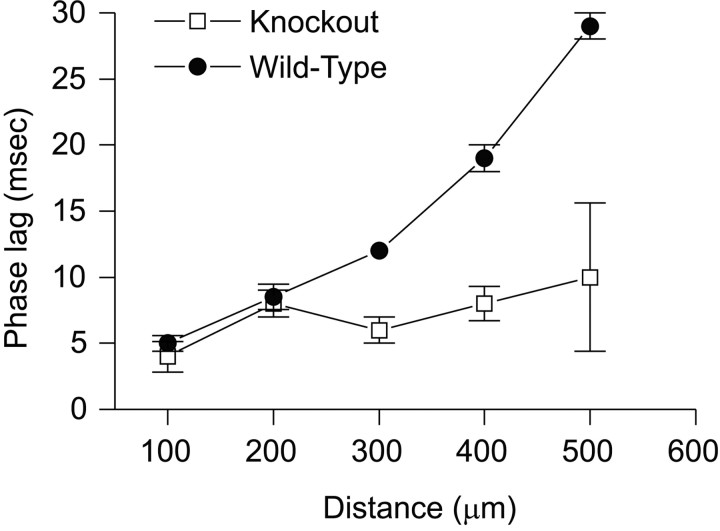
A second difference is that whereas the initial burst of TC cell activity in knock-out networks is relatively synchronous, even across large distances (Fig. 1, bottom right), in wild-type networks, TC cell activity becomes progressively phase-lagged with increasing distance from the center of the model slice (Fig. 1,top right). To make the latter observation precise, we found the phase lag of TC cell activity at various points along the model slice relative to activity at the center of the model slice using cross-correllograms. Cross-correllograms were computed using spike trains of TC cells, which had been averaged over ten neighboring neurons and several simulations with different random initial conditions. The resulting phase lags for wild-type and knock-out networks are plotted as functions of distance in Figure2. In wild-type networks, phase lags increase with distance, reaching 29 msec at 500 μm, whereas phase lags in knock-out networks remain under 8 msec over the same distances.

Fig. 2.

TC cell activity becomes progressively phase-lagged (relative to TC cell activity at the center of the slice) with increasing distance from the center of the model slice. These distance-dependent phase lags are much larger in wild-type networks than in knock-out networks. Phase lags were determined from cross-correllograms between spike trains of TC cells. Cross-correllograms were computed using a bin size of 2 msec. Spike trains had a duration of 600 msec and had been averaged over ten neighboring neurons and several simulations with different random initial conditions.

The small phase lag in knock-out networks, which becomes especially apparent on the third cycle, results from the fact that, although intra-RE inhibition is much weaker in knock-out networks than in wild-type networks, it is not negligible. The reduced amplitude of IPSCs (31% of wild-type) was based on the size of evoked IPSCs in RE cells. However, the low frequency of spontaneous IPSCs suggest that the actual ratio might be closer to 9% (Huntsman et al., 1999). When we simulated knock-out networks using the latter ratio, the emergent phase gradient was reduced but not abolished. In fact, there is a small emergent phase gradient even in the absence of any intra-RE inhibition (see Discussion).

Differences in the durations of the bursts of RE cells affect the timing of TC cell activity

To explain why initial TC cell activity is highly synchronized in knock-out networks but not in wild-type networks, we compared the initial bursts of RE cells in wild-type and knock-out networks. Figure3 plots the GABA_Aconductances and membrane potentials of two RE cells, one near the center, and the other toward the periphery, of a wild-type network. As Figure 3 shows, the bursts of RE cells are much shorter near the center of a wild-type network (Fig. 3B) than they are toward the periphery (Fig. 3C). In contrast, the bursts of RE cells are uniformly long across knock-out networks (data not shown). These observations can be explained as follows. Near the center of the model slice, the initial stimulus activates many RE cells. This results in a central level of intra-RE inhibition that is eventually strong enough to shunt T-current of RE cells and hasten the end of their bursts. Thus, the burst of the central RE cell ends early (Fig. 3B), when IPSC conductance is relatively large (Fig. 3A, solid line). In contrast, toward the periphery of wild-type slices, few RE cells are active, so intra-RE inhibition is weak (Fig. 3A, dashed line). As a result, the burst of the peripheral RE cell outlasts the burst of the central RE cell (Fig. 3C). Note that the onset of burst shunting (∼60 msec; Fig. 3B) occurs significantly later than the time when peak IPSP conductance is attained (∼15 msec; Fig. 3A). The shunt occurs because the GABA_A conductance persists while T channel conductance decays. Peak T conductance occurs at ∼10 msec and has decayed by ∼84% at 60 msec (data not shown), thus enabling the IPSP to outweigh the intrinsic Ca²⁺ conductance and thereby truncate the response.

Fig. 3.

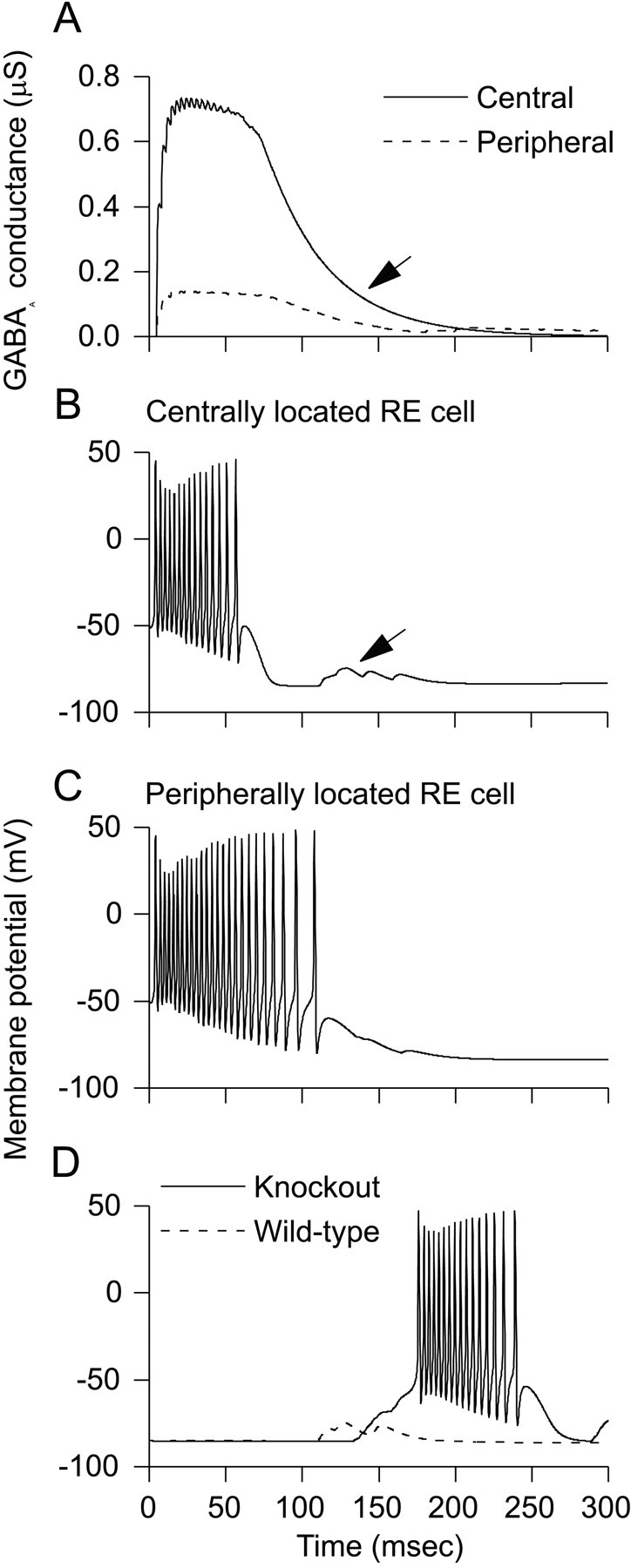
In wild-type networks, intra-RE inhibition shortens the duration of bursts in centrally located RE cells and shunts subsequent excitatory input to RE cells. A, Time courses of the total inhibitory synaptic currents plotted for RE cells at the center (solid line) and periphery (dashed line) of the model slice. Note that there is significant residual inhibition at the time when EPSPs recur in RE cells (arrow). B, Intra-RE inhibition shortens the burst in this centrally located RE cell and shunts subsequent EPSPs (arrow) in this cell. C, In the periphery, the level of intra-RE inhibition is low, so this RE cell bursts for an extended duration. D, Membrane potential of an RE cell in a knock-out network (solid line) and the same RE cell in a wild-type network (dashed line). In the wild-type network, intra-RE inhibition shunts EPSPs, preventing the RE cell from bursting.

These different RE cell burst durations explain the differences between phase lags in wild-type and knock-out slices. GABA_A currents in TC cells decay rapidly. As a result, there is a relatively short latency between the end of bursts in presynaptic RE cells and the beginning of the rebound burst in the corresponding postsynaptic TC cells. Thus, the progressive lengthening of bursts of the RE cells with increasing distance from the center of the model slice produces a corresponding phase gradient in the time of the rebound bursts of the TC cells. In contrast, nowhere within knock-out networks is intra-RE inhibition strong enough to significantly alter the duration of bursts of the RE cells. Thus, the duration of bursts of RE cells is relatively uniform across a knock-out network, and hence TC cell activity is synchronous across large distances.

Residual intra-RE inhibition shunts return excitation in RE cells

Figure 3 also helps to explain why activity has a much shorter duration in wild-type networks than in knock-out networks. Rebound bursts in TC cells elicit EPSPs in the centrally located RE cell, whose membrane potential is plotted in Figure 3B. However, comparing the synaptic currents with the membrane potential reveals that when the EPSPs arrive (Fig. 3B, arrow), many GABA_A channels are still open (Fig. 3A, arrow). As a result, the EPSPs are shunted. Figure 3Dshows how this shunting affects another centrally located RE cell (one that is not activated on the first cycle). In the knock-out network, the return EPSPs are sufficient to elicit a burst in this RE cell. However, in the wild-type network, the same RE cell fails to burst, because the EPSPs have been shunted. Note that in Figure 3D, EPSPs arrive earlier in the wild-type network than in the knock-out network. As discussed above, this reflects the relatively strong intra-RE inhibition in the wild-type network, which shortens the duration of bursts of the RE cells, thus hastening the onset of rebound bursts in TC cells.

Shunting inhibition does not significantly delay the beginning of the bursts of RE cells

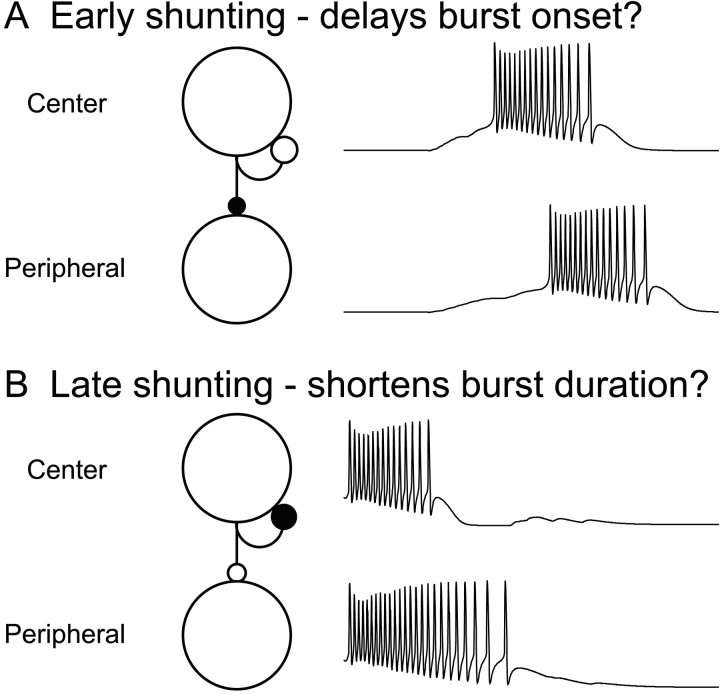
The preceding results elucidate one mechanism by which intra-RE inhibition could produce phase gradients in thalamic networks. Hereafter we will refer to this mechanism, in which GABA_A currents hasten the end of bursts of central RE cells, as “late shunting.” However, additional mechanisms might also contribute to intrathalamic phase differences. For example, suppose that the strength of excitatory input to RE cells decreases with increasing distance from the center of the model slice. Then centrally located RE cells will burst before their more peripherally located counterparts, because cells receiving stronger input burst before those receiving weaker input. Because this mechanism does not rely on intra-RE inhibition, we will refer to it as “shunting-independent.” Finally there is a mechanism through which intra-RE inhibition could amplify the shunting-independent phase delays resulting from spatially graded RE cell input. By this means, earlier-bursting, central RE cells inhibit later-bursting, peripheral RE cells. This inhibition could further delay the beginning of bursts in those peripheral RE cells. The resulting phase gradient would be greater than that produced by spatially graded input alone. We refer to this mechanism as “early shunting.” Figure4 contrasts the proposed mechanisms of early and late shunting.

Fig. 4.

Mechanisms by which early and late shunting might produce spatial phase gradients in RE cell activity. A,In early shunting, strong input activates centrally located RE cells before peripherally located RE cells. Shunting inhibition from the early bursting central RE cells might then delay the beginning of bursts in peripheral RE cells. The filled circlerepresents the active site of synaptic inhibition. For this mechanism, inhibitory synapses between central RE cells are unimportant.B, In late shunting, central and peripheral RE cells begin bursting at essentially the same time. However, near the center of the network, more RE cells are active, as a result the level of intra-RE inhibition is higher, and RE cell bursts are thus shorter than at the periphery. For this mechanism, inhibitory synapses from central RE cells to peripheral RE cells are unimportant.

In our previously described simulations, which showed that intra-RE inhibition can produce phase gradients through late shunting, RE neurons were excited above their burst thresholds at precisely the same time. As a result, they implicitly excluded phase differences that result from spatially graded input either directly (via the shunting-independent mechanism) or indirectly (via early shunting). Therefore, we performed additional simulations of wild-type networks in which the strength of excitatory input to RE cells decreased with increasing distance from the center of the model slice, as described in Materials and Methods. In these simulations all three of the mechanisms described above could contribute to phase gradients. We will refer to this kind of network, which includes wild-type intra-RE inhibition and spatially graded input to RE cells, as “normal.”

To determine whether early shunting was a contributing factor, we simulated two control networks. Each network had two properties that could be varied: the strength of intra-RE inhibition (i.e., it could be either wild-type or knock-out) and the initial condition (i.e., the pattern of RE cell activation). The first control network had wild-type intra-RE inhibition. To determine the initial condition for this network, we observed which RE cells burst in response to spatially graded RE cell input in the normal network. Then we activated that same population of RE cells, but insured that those RE cells began bursting at the same time. As a result, only late shunting (which hastens the end of bursts of central RE cells) should contribute to phase lags in this network. The second control network modeled a slice that lacked all intra-RE connections but had spatially graded input to RE neurons. Because this control network lacks intra-RE inhibition, neither late nor early shunting should contribute to phase lags. Thus, we can attribute phase gradients in the second control network to the shunting-independent mechanism (in which spatially graded RE cell input produces a gradient in the beginning of bursts of RE cells). We varied the total GABA_A conductance on each RE cell between 0.25 and 2.25 μS. We used the phase relationship per unit distance, obtained by linear regression, to compare phase gradients as a function of synaptic GABA_A conductance in different types of networks.

Because different mechanisms produce phase gradients in each of these three types of networks, we could determine whether early shunting contributes significantly to the gradients by comparing these networks. The phase gradient in normal networks was larger than the phase gradient in the late shunting only network (Fig.5, filled square vs open triangle). This suggests that one of the other two mechanisms, either early shunting and/or the shunting-independent mechanism augments the phase gradient in the normal network. Note that phase gradients were relatively large, even in the shunting-independent network, and that the gradient in normal networks was always less than the sum of the gradients in the two control networks (late shunting and shunting-independent, Fig. 5). Thus, late shunting and the shunting-independent mechanism can fully account for the phase gradient in the normal network. In contrast, if early shunting did contribute to the phase gradient, we would have expected the phase gradient in the normal network to be larger than the sum of the phase gradients in the two control networks. These results suggest that shunting during the initiation of RE cell bursts does not contribute significantly to phase gradients.

Fig. 5.

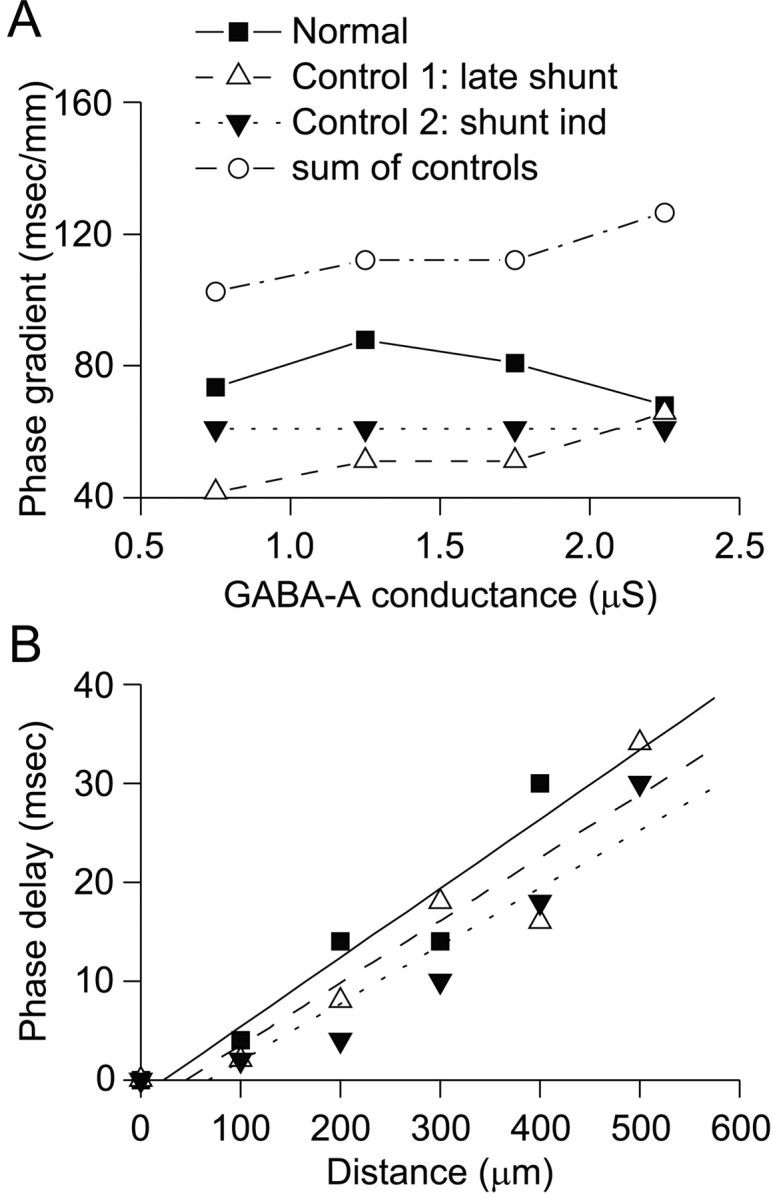
A, Phase delays in wild-type networks (normal, solid line) are larger than those in the either control network, but less than expected for combined effect of the two controls. Control 1: late shunting only,Open triangles and dashed line.Control 2: shunting-independent, Filled inverted triangles and dotted line. Sum of controls,Open circles and stippled line. B, We used linear regression to calculate phase gradients from the phase lag as a function of distance. Here, regression lines are shown for phase lags in one normal network, one control network with late-shunting only, and another control network with shunting-independent mechanisms only. For the normal network and first control network, g_GABA = 2.25 nS.

Intra-RE inhibition can prevent, but not delay, RE cell bursts

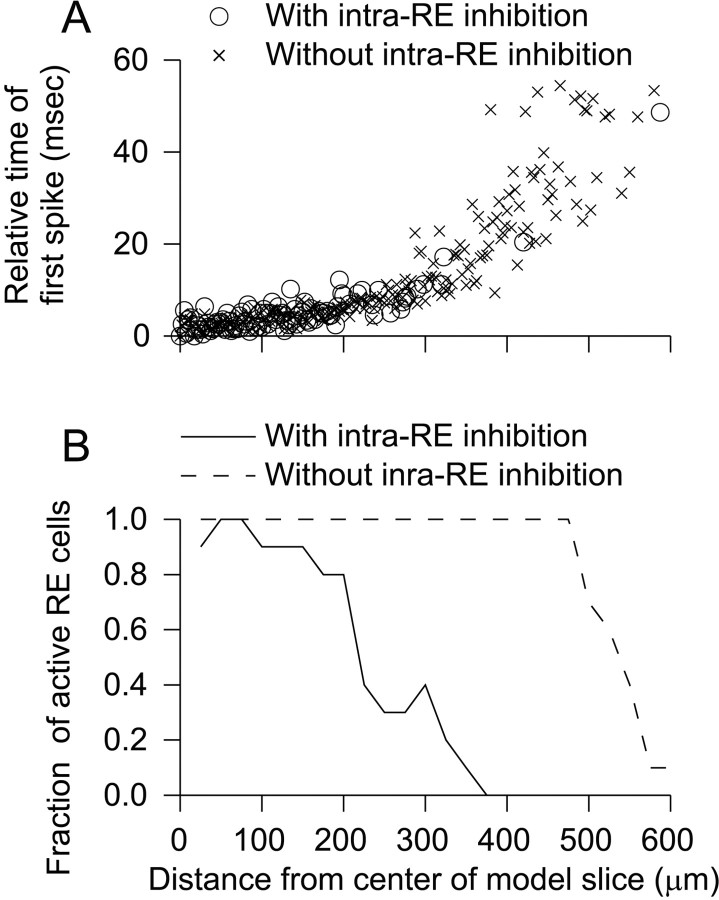
The observation that early shunting does not affect phase differences suggests that it does not significantly delay the beginning of bursts of RE cells. To test this hypothesis directly, we compared the times at which RE cells start bursting in a normal network to those in the knock-out network. The times at which RE cells first spike in two such networks are plotted in Figure 6(RE cells in the two networks receive the same spatially graded input). As Figure 6 shows, many more peripherally located RE cells burst in the knock-out network than in the normal network. However, RE cells that do burst in both networks begin to do so at essentially the same time. Thus, intra-RE inhibition can affect the population of RE cells that burst, but not the times of burst initiation. For example, as the GABA_A conductance on each RE cell increased from 0.4 μS (approximately equal to the conductance in knock-out networks) to 1.2 μS (approximately equal to the conductance in wild-type networks), the fraction of RE cells activated by the initial stimulus steadily declined from 36 to 28% of the total network. At the same time, relative burst times were unaffected by alterations in intra-RE GABA conductance (data not shown). These findings confirm that early shunting does not contribute significantly to spatial gradients in TC cell activity, as shown by Figure 5.

Fig. 6.

Intra-RE inhibition during the initiation of bursts of RE cells can affect which RE cells burst, but not the time at which bursting begins for RE cells that do burst. A, The relative times at which RE cells begin to burst are plotted for networks with (open circles) and without (crosses) intra-RE inhibition. Both networks have the same spatially graded initial input to RE cells. B, To show how intra-RE inhibition affects the population of RE cells that do burst, the fraction of RE cells bursting is plotted as a function of distance from the center of the model slice. In the network with intra-RE inhibition (solid line), the boundary between RE cells that do burst and those that do not is much closer to the center of the model slice than in the network without any intra-RE inhibition (dashed line).

Sufficiently strong and long-lasting IPSCs truncate intrathalamic oscillations

We studied whether both the large amplitude and slow decay of intra-RE inhibition in wild-type networks are required to shorten the duration of intrathalamic oscillations. Figure7A shows the duration of intrathalamic oscillations in a network as a function of the total GABA_A conductance on each RE cell and the time constant with which intra-RE inhibition decays. The duration of intrathalamic oscillations is shorter either when intra-RE synapses are stronger or when they decay more slowly.

Fig. 7.

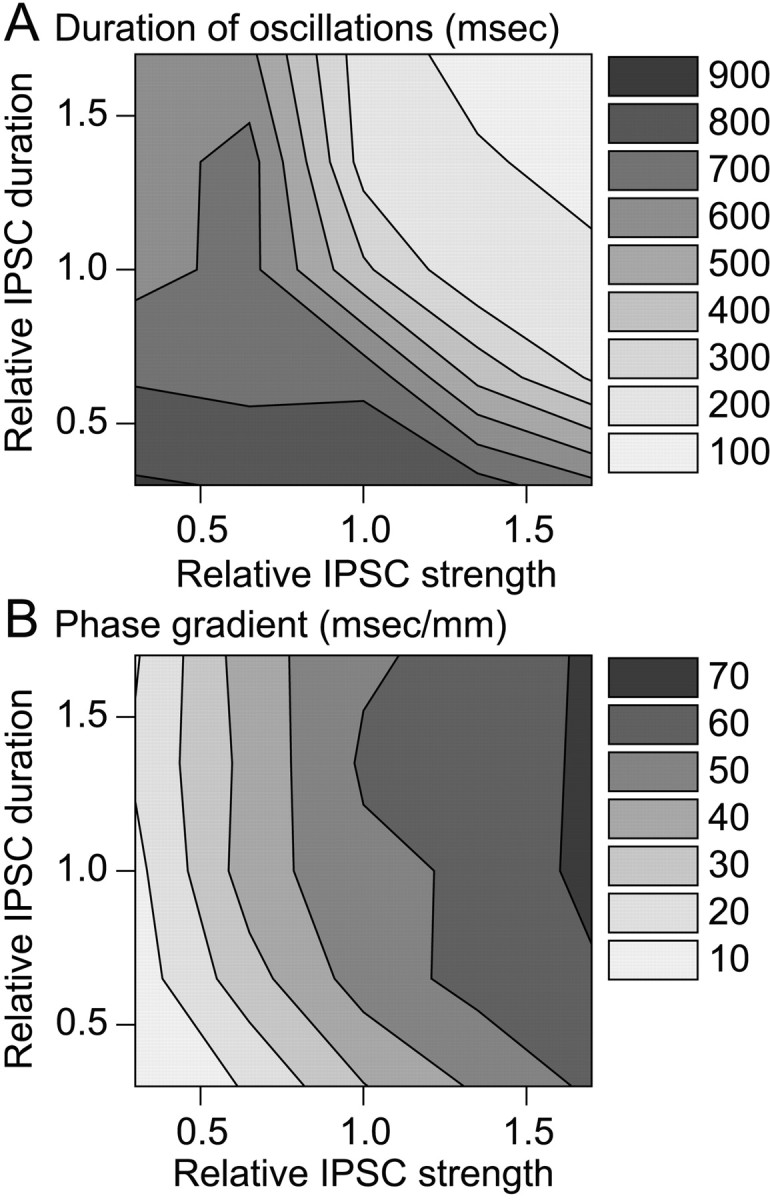
Strength and duration of intra-RE inhibition determine the duration and synchrony of intrathalamic oscillations.A, Contour plot of the duration of intrathalamic oscillation as a function of the strength and duration of IPSCs in RE cells. The duration was defined as the time of the last TC cell spike. Increases in either the strength or the duration of IPSCs in RE cells shorten the duration of intrathalamic oscillations. B,Contour plot of the phase gradient of intrathalamic oscillation as a function of the strength and duration of IPSCs in RE cells. The phase gradient increases with increasing IPSC strength, but is less sensitive to changes in IPSC duration. The minimum phase gradient occurs in thebottom left corner, where normalized IPSC duration and strength are both minimal. Maximal phase gradients occur in thetop right region, where normalized IPSC durations are 1 or larger, and normalized IPSC strength is maximal. In bothA and B, IPSC strength refers to the GABA_A conductance on each RE cell and is normalized so that 1 represents the conductance in wild-type networks. Similarly, IPSC duration, which refers to the time constant with which GABA_A IPSCs decay in RE cells, is normalized so that 1 represents the wild-type decay time constant. Each value plotted inA or B was averaged over eight simulations from different random initial conditions.

Phase gradients require sufficiently strong IPSCs

We also studied whether both the large amplitude and slow decay of intra-RE inhibition are required for the phase gradients observed in wild-type networks. Figure 7B shows the phase gradient of TC cell activity as a function of the total GABA_Aconductance on each RE cell and the time constant with which intra-RE inhibition decays. In this case, the phase gradient depends primarily on the strength of intra-RE inhibition and is largely independent of the rate at which that inhibition decays.

For example, when intra-RE synaptic currents have large amplitudes (similar to wild-type synapses) but decay rapidly (similar to knock-out synapses), phase lags are almost as large (48 msec/mm) as large as those in true wild-type networks. In contrast, when intra-RE synaptic currents have small amplitudes (similar to knock-out synapses) but decay slowly (similar to wild-type synapses), phase lags are very similar to those in true knock-out networks (16 msec/mm). In the former case, strong but short-lived intra-RE synaptic currents are powerful enough to hasten the end of bursts, but decay quickly and hence fail to shunt subsequent excitatory input. In the latter case, weak but long-lasting intra-RE synaptic currents are insufficient to either hasten the end the end of bursts of RE cells or shunt subsequent excitatory input. Thus, the relatively large amplitude of wild-type intra-RE IPSCs is important for both generating phase lags and abbreviating the oscillation, whereas the long durations of wild-type intra-RE IPSCs are primarily important for abbreviating the oscillation.

Only some spatial patterns of intra-RE connections truncate and desynchronize oscillations

So far, we have assumed that intra-RE connections are local and extend over a radius of a few hundred micrometers. By local, we mean that the strength of a synapse between two RE cells decreases monotonically as the distance between them increases. To study how the spatial organization of intra-RE connections influences the truncation and desynchronization of intrathalamic oscillations, we simulated networks with two alternative schemes of intra-RE connectivity. In the first scheme, strengths of connections from an RE cell had a Gaussian spatial profile that was centered at the location of that cell and had a SD of 10 μm, so that each RE cell only inhibited itself and its nearest neighbors. Figure8A plots the times at which TC cells spike in this network after the random initial activation of RE cells. As in other wild-type networks (Fig. 1,top right), oscillatory activity in this network does not last long, because RE cell activation produces intra-RE inhibition that prevents subsequent return excitation from eliciting RE cell bursts. However, in this network, unlike other wild-type networks, the activity of TC cells does not become strongly phase-lagged with increasing distance from the center of the model slice (16 mm/msec phase gradient). In this network, whenever any RE cell burst, it inhibited itself strongly, shortening the duration of its burst. As a result, the durations of bursts of RE cells at the center of the model slice were not significantly shorter than at the periphery.

Fig. 8.

Only certain patterns of intra-RE connectivity can shorten and desynchronize intrathalamic oscillations. A,The times at which TC cells spike after activation of RE cells in a network with very focal intra-RE inhibition. In this network, intra-RE inhibition does not produce a significant spatial gradient in the timing of TC cell activity. However, intra-RE inhibition is somewhat effective in shortening the duration of activity, because relatively few TC cells spike on the second and third cycles of activity.B, The times at which TC cells spike after activation of RE cells in a network with nonlocal intra-RE inhibition. Intra-RE inhibition fails to either shorten or desynchronize the intrathalamic oscillation in this network.

In the second scheme, only RE cells that were at least 87.5 μm apart were connected, and the strength of a connection between RE cells that were distance d apart was proportional toe^{−(d/350 μm)2}. As a result, there was a “hole” in the intranuclear arborization of each RE cell. Figure 8B plots the times at which TC cells spike in this network after the random initial activation of RE cells. Because intra-RE connections in this network are nonlocal, RE cells did not receive inhibition from themselves or their neighbors. Thus, there was no simple spatial gradient in either the duration of bursts of RE cells or in the timing of TC cell activity. In further contrast to activity in other wild-type networks (Fig. 1, top right), the hole in the intranuclear arborization allowed the network to sustain oscillations for several cycles in a small set of neighboring RE and TC cells. The spatial extent of this relatively long-lasting oscillation was similar to the diameter of the hole in intranuclear connectivity.

Comparison of Figures 1B, and 8, A andB, suggests that RE cells must inhibit their neighbors to shorten the duration of intrathalamic oscillations. Furthermore, spatial phase gradients were not obtained with either very localized intra-RE connections or with intra-RE connections that extend over large distances, but fail to contact nearby RE cells. This suggests that intra-RE connections that contact nearby RE cells and also extend over large distances are required to produce the phase differences observed in vitro.

Intra-RE inhibition allows particular spatial patterns of oscillatory intrathalamic activity

The preceding results raise the possibility that intra-RE inhibition simply prevents any sustained intrathalamic activity. However, activation of RE cells within a focal region can elicit multiple cycles of TC and RE cell activity even in wild-type networks. Figure 9A shows one such example. In this case, the probability of activation as a function of distance from the center of the model slice had a narrow Gaussian profile. The maximum probability was 0.5, and the width of the Gaussian was 12.5 μm. Unlike sustained oscillations in a knock-out network (Fig. 1, bottom right), sustained activity elicited by focal activation of RE cells in the wild-type network remained confined to the center of the model slice. And unlike activity that follows widespread activation of RE cells in wild-type networks (Fig. 1,top right), activity elicited by focal activation of RE cells is relatively synchronous. The activity shown in Figure9A resembles focal, sustained intrathalamic oscillations occasionally observed in some wild-type slices (Huntsman and Huguenard, unpublished data). Synchronous activation of a small fraction of RE cells across the entire network resulted in only a weak, abortive oscillation (data not shown).

Fig. 9.

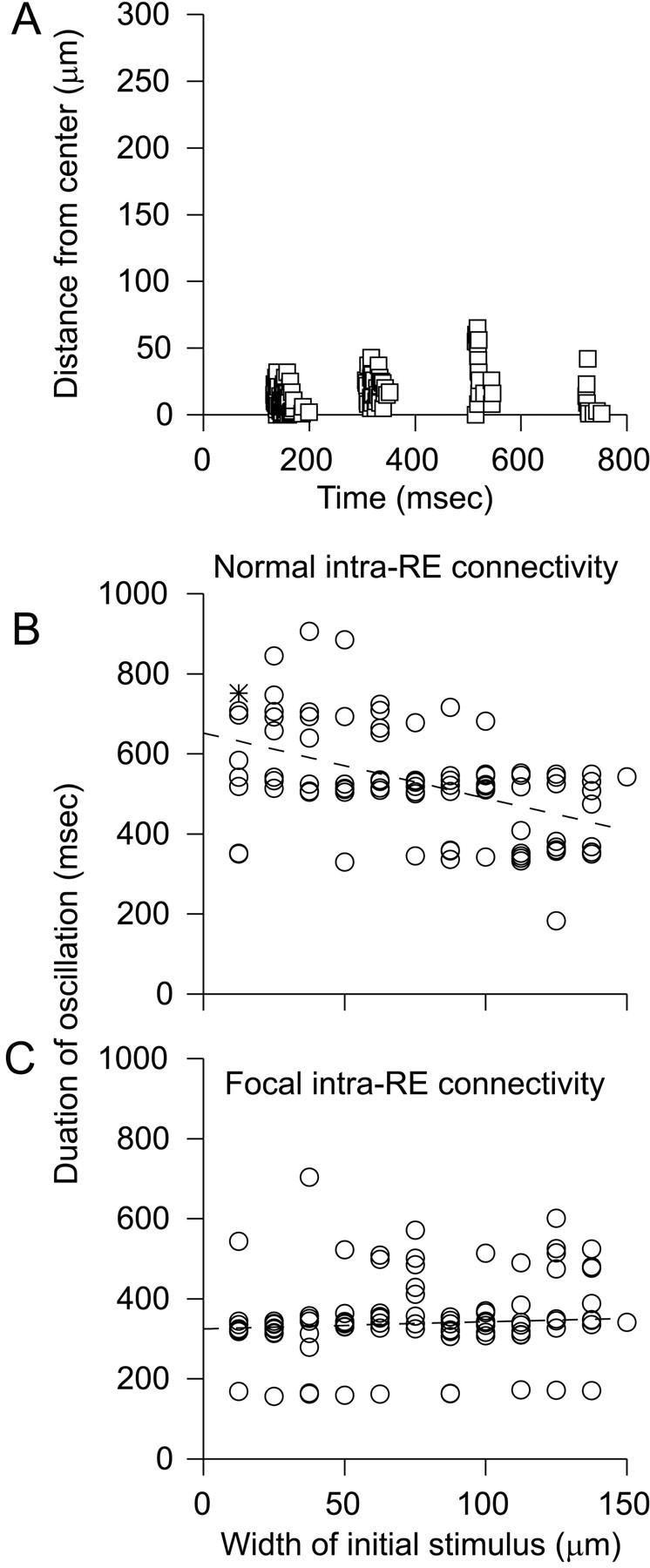
Wild-type thalamic networks can sustain focal patterns of activity. A, The times at which TC cells spike in a wild-type network are shown after activation of many RE cells within a relatively narrow region of the network. Note that this sustained activity remains confined to a relatively narrow region of the network and is nearly simultaneous across that region.B, More focal stimuli can elicit longer-lasting oscillations. The durations of oscillations are plotted versus the width of the initial stimulus. The asterisk represents the duration of the oscillation depicted in A. Eight simulations, each from different random initial conditions, were performed for each width. The dashed line, resulting from linear regression on these data, shows that the duration of oscillations tends to decrease as the width of the initial stimulus increases (r = −0.52; p < 0.0001). C, Durations of oscillations in a network with very focal intra-RE connectivity. In contrast to B, the duration of oscillations is not significantly related to the width of the initial stimulus (r = 0.15;p > 0.1).

We studied how the duration of intrathalamic oscillations depends on the spatial width of the initial stimulus. As described in the Materials and Methods, the probability that an RE cell was activated was a function of distance that was shaped like a Gaussian. Thus, the width of this Gaussian corresponds to the spatial extent of the initial stimulus. For each width, we simulated activity starting from eight random initial conditions. The duration of each resulting oscillation is plotted versus width in Figure 9B. For widths <50 μm, oscillations often lasted four or five cycles, whereas when the width was 125 μm, oscillations usually lasted only one or two cycles.

We hypothesized that activation of RE cells within a restricted region sometimes leads to multiple cycles of activity because only a fraction of inhibitory inputs of an RE cell are activated. For example, the peak GABA_A conductance activated in the RE cell at the center of the network depicted in Figure 9A is only 60% of the peak conductance in the RE cell at the center of the network depicted in Figure 3. To test this hypothesis, we again simulated activity elicited by initial stimuli of variable widths. These simulations were done for networks in which the strengths of intra-RE connections originating from one cell had a Gaussian spatial profile that was centered at that cell and had a width of just 50 μm. Thus, even the smallest initial stimuli activated a significant fraction of the inhibitory inputs to each active RE cell. Figure 9Cshows that as a result, oscillations in this network had a short duration regardless of the width of the initial stimulus. We conclude that when most of the RE cells that are presynaptic to an active RE cell are themselves active, then the duration of an intrathalamic oscillation is consistently abbreviated.

As noted above and shown in Figure 9A, oscillatory activity elicited by focal stimulation did not propagate along the model slice. This contrasts with earlier models of intrathalamic oscillations (Destexhe et al., 1996a; Golomb et al., 1996; Sohal and Huguenard, 1998). We hypothesized that the relatively strong intra-RE inhibition present in our simulations of wild-type slices prevented oscillatory activity from propagating. To test this hypothesis, we simulated activity in knock-out slices (i.e., with attenuated intra-RE inhibition) and model slices in which intra-RE inhibition was completely absent. In the former case, focal stimuli elicited oscillations that propagated outwards along the model slice for two to three cycles, before dying out. In the latter case, oscillations propagated across the full extent of the model slice. This shows that even relatively weak intra-RE inhibition can limit the propagation of intrathalamic oscillations.

Sensitivity to parameters

Figure 7 shows that intra-RE inhibition can shorten the duration of oscillations and produce phase gradients over a wide range of parameters. We also studied whether spatial gradients depended on a particular duration of RE cell bursts. To do this we reduced T-current permeability in RE cells by as much as 50%. We found that after such manipulations, the duration of and number of spikes per RE cell burst dropped significantly, and yet bursts of RE cells were still much longer at the periphery than near the center of wild-type networks. For example, when T-current permeability in RE cells was reduced by one-half, the maximum number of spikes per burst in peripheral RE cells dropped from 26 to 16, and yet TC cell activity 500 μm from the center of the network still lagged that at the center by 28 msec. Finally, we computed phase gradients using different spatial profiles of RE cell input in wild-type networks with spatially graded input, late-shunting-only networks, and shunting-independent-only networks. For each profile of RE cell input, we verified that early shunting does not contribute significantly to the phase gradient.

DISCUSSION

Using a computational model based on intracellular measurements of synaptic currents in thalamic slices from wild-type (β₃^+/+) and knock-out (β₃^−/−) mice (Huntsman et al., 1999), we evaluated one mechanism by which intra-RE inhibition shortens the duration of intrathalamic activity and two mechanisms by which intra-RE inhibition might desynchronize such activity. We examined how these mechanisms depend on the strength, kinetics, and spatial organization of intra-RE inhibition. Finally, we studied how these mechanisms are effective at restricting sustained intrathalamic oscillations in wild-type networks to particular spatial patterns. We found that: (1) Intra-RE inhibition produces a spatial gradient in the durations of bursts of RE cells through late shunting. After an initial condition that activates more RE cells at the center of the model slice than at its periphery, bursts of RE cells are shorter near the center, where the level of intra-RE inhibition is high, than at the periphery. As a result, TC cell activity is correspondingly phase-lagged. This mechanism, late shunting, requires that connections between RE cells be local and extensive and that GABA_A currents in RE cells be strong but not necessarily long-lasting. (2) Early shunting of input to RE cells by intra-RE inhibition does not significantly affect the time at which RE cells begin to burst. (3) Residual intra-RE inhibition after a cycle of activity can shunt subsequent EPSCs in RE cells, preventing large-scale sustained intrathalamic oscillations. Such shunting requires that RE cells inhibit their neighbors (i.e., that intra-RE connectivity is “local”) and that GABA_A currents in RE cells are sufficiently strong and long-lasting. (4) Stimuli that activate RE cells in a region that is small relative to the width of intra-RE connections can elicit sustained oscillations. Such activity remains localized and synchronous.

Relationship to experimental results

Observation 1 reproduces the in vitro finding that TC cell activity exhibits spatial phase gradients (Huntsman et al., 1999). Previous in vitro work also found gradients in TC cell activity (Kim et al., 1995). In that study, oscillations propagated along thalamic slices, and phase lags increased in the direction of propagation. This is consistent with our finding that phase lags increase with increasing distance from the center of stimulation. Furthermore, phase lags in vitro were largely abolished by the GABA_A antagonist bicuculline (Kim et al., 1995), consistent with the GABA_Acurrent-dependent mechanism we have described. The robust temporal interaction between the burst-inducing intrinsic mechanism (T-type calcium channels) and burst-terminating synaptic mechanism (intra-RE inhibition; Fig. 3) leads to dynamic regulation of thalamic and presumably thalamocortical network activity.

One difference between phase gradients in simulations and thosein vitro is that gradients in wild-type networks are somewhat smaller than those in wild-type slices. For example, activity at the center of the oscillation leads activity that is 500 μm away by 29 msec in simulations but by ∼70 msec in vitro. There are several explanations for this. First, the variability of in vitro phase differences is relatively large at 500 μm (Fig.3D; Huntsman et al., 1999). At smaller distances, e.g., 300 μm, in which the variability of in vitro phase differences is much smaller, simulation results are much closer to those in vitro. Second, simulations are based on spatial scales of connectivity measured in rats, whereas the in vitroexperiments were done in mice. Thus, phase differences measured at distances of 500 μm in simulations should perhaps be compared to phase differences measured at distances <500 μm in thalamic slices taken from mice.

Observation 3 reproduces and explains the in vitro finding that oscillatory activity lasts much longer in slices taken from knock-out mice than in those from wild-type mice. It might also help to explain why oscillations last longer in thalamic slices from ferrets (von Krosigk et al., 1993; Bal et al., 1995a,b) than in those from rats (Huguenard and Prince, 1994a) or wild-type mice (Huntsman et al., 1999). This difference might reflect the fact that, in ferrets, the mechanism described above for terminating oscillations, is attenuated. For example, in ferrets, GABA_A currents in RE cells might be weaker or decay more quickly.

Our findings might also may relate to the biophysical observation that postsynaptic GABA_A currents last much longer in RE cells than they do in TC cells (τ_decay = 75.8 msec in wild-type RE cells but only 8.2 msec in wild-type TC cells, Huntsman et al., 1999; see also Zhang et al., 1997). As Figure 7shows, in our simulations, long-lasting GABA_Acurrents in RE cells were required to shorten the duration of intrathalamic oscillations. Moreover, for any particular strength of intra-RE inhibition, slowing the decay time constant beyond 75.8 msec did not yield significant further shortening. Thus, the duration of GABA_A currents in RE cells may be in some sense “optimal” for preventing sustained, widespread intrathalamic activity.

Limitations of the model

In knock-out networks, TC cell activity at different locations eventually becomes desynchronized. As shown in Figure 1, similar phase differences can emerge in knock-out slices, but this is not always the case (Huntsman et al., 1999). As noted in Results, some phase differences persist even in the absence of any intra-RE inhibition. These residual differences result because on late cycles of activity, bursts of RE cells are shorter near the center of the network than toward the periphery. These spatial differences in burst durations presumably reflect differences in T-current inactivation, which in turn reflect the initial condition that activates more RE cells near the center of the network than toward the periphery. Further work may reveal whether this can be avoided using RE cell models that are more accurate than the single-compartment model used in this and other studies (Destexhe et al., 1996a,b; Bazhenov et al., 1998a; Destexhe, 1998; Sohal and Huguenard, 1998).

Implications for thalamocortical oscillations

These results suggest many functions for intra-RE inhibition during thalamocortical oscillations. First, intra-RE inhibition could prevent hypersynchronous oscillatory activity characteristic of some epilepsies. Earlier modeling studies have suggested a critical role for prolonged RE cell bursts during spike and wave seizures (Destexhe, 1998). We have shown that intra-RE inhibition could shorten bursts of RE cells (Fig. 2) and/or shunt subsequent excitatory input to RE cells, preventing them from bursting (Fig. 3). Phase gradients in TC cell activity caused by intra-RE inhibition might also prevent effective temporal summation of TC cell input to cortical pyramidal cells.

Second, intra-RE inhibition may restrict thalamocortical activity to particular spatiotemporal patterns. We found, somewhat surprisingly, that smaller stimuli elicited longer-lasting responses than did larger stimuli. In this way, intra-RE inhibition could prevent broad, synchronous patterns of activity while permitting patterns that are focal (i.e., have many active neurons within a narrow region). For example in Figure 9A, the region of activity is smaller than the radius of intra-RE inhibition, so that the resulting intra-RE inhibition is weak enough for activity to persist. As mentioned in Results, intra-RE inhibition also does not preclude diffuse oscillations. It is interesting to speculate that cortical feedback (Steriade and Contreras, 1998) might reinforce such activity, which is otherwise quite weak.

Restricting thalamocortical activity to particular spatiotemporal patterns may have important functional roles besides preventing broad, synchronous epileptiform activity. For example, activity patterns that activate all thalamic neurons encode no information. In contrast, selective activation of either small subpopulations of thalamic neurons or of a few, widely distributed thalamic neurons could allow the cortex to sample the space of possible thalamic inputs. In this manner, spindle oscillations could activate cortex as part of memory consolidation or refinement during sleep (Wilson and McNaughton, 1994).

Relationship to previous models

In previous simulations of intrathalamic (Bazhenov et al., 1998a) and corticothalamic (Bazhenov et al., 1998b; Destexhe, 1998) oscillations, most thalamic neurons fire in phase with each other. By contrast, Figures 1 and 3 show how broad RE cell activity produces intra-RE inhibition, which shunts subsequent excitatory input to RE cells. This suggests that during synchronized intrathalamic or corticothalamic oscillations, activity may be restricted to either focal regions or a small fraction of widely distributed neurons. This may not have been observed in previous simulations of intrathalamic activity (Destexhe et al., 1996b; Golomb et al., 1996; Bazhenov et al., 1998a) because intra-RE inhibition in those models was significantly weaker and more rapidly decaying than in our model.

Predictions

We predict that stimulation of internal capsule should activate many RE cells in one particular region of the thalamic slice (hereafter referred to as the “center” of the slice) and activate fewer RE cells with increasing distance from the center. Because of resulting differences in the amount of intra-RE inhibition, in the central region, stimulus-evoked RE cell bursts should be shorter than at the periphery. If RE cells receive excitatory input from TC cells to which they project (Huguenard and Prince, 1994a; Bal et al., 1995b), then these differences in burst duration should produce corresponding differences in the timing of subsequent activity. GABA_A antagonists should abolish these differences, producing uniformly long bursts across wild-type slices. In contrast, bursts of RE cells should be relatively long across the extent of β₃ knock-out slices.

PARAMETERS OF INTRINSIC CURRENTS

As in earlier studies (Hodgkin and Huxley, 1952; Huguenard and McCormick, 1992), we assumed that each intrinsic current was composed of many equivalent ion channels, each channel was comprised of at least one gate, and all of the gates comprising an individual channel must be open for the channel to conduct current. This leads to the same generic formalism for all voltage-dependent intrinsic currents:

$$\widehat{g}=m^M{h}^N,$$ Equation A1

where ĝ is the conductance or permeability of the current as a fraction of its maximum conductance or permeability.

We used Ohm's law to calculate non-Ca²⁺currents, i.e.:

$$I=g_{max} \widehat{g}(V_{\text{m}}-E_{\text{eq}}),$$ Equation A2

where V_m is the membrane potential and g_max andE_eq are the maximum conductance and equilibrium potential of the current, respectively. For the low-threshold Ca²⁺ currentsI_T andI_Ts we used the constant field equation:

$$I=\widehat{g}{\text{Pz}}^2\frac{V_{\text{m}} F^2}{RT}\frac{[{\text{Ca}}^{2+}{]}_{\text{i}}-[{\text{Ca}}^{2+}{]}_{\text{o}}{e}^{-{\text{zFV}}_{\text{m}}/RT}}{1-e^{-{\text{zFV}}_{\text{m}}/RT}},$$ Equation A3

where P is the maximum permeability, z is 2 (the valence of Ca²⁺), [Ca²⁺]_i = 240 nm and [Ca²⁺]_o = 2 mm are the concentration of Ca²⁺ inside and outside of the cell, respectively, F is Faraday's constant, and R is the universal gas constant.

The kinetics of I_Na andI_K were taken from Traub and Miles (1991), and the maximum conductances were adjusted to give action potentials of realistic height and duration.

To model I_T in TC cells, we used the two variable (m²h) kinetic scheme ofHuguenard and McCormick (1992), in which all rate constants were temperature-corrected using a Q₁₀ = 2.5. We set the maximum permeability of the T-current,P_T, to 40 × 10⁻⁹ cm³/sec (at 37°C). This permeability falls within the range of values observed in intact cells (McCormick and Huguenard, 1992).

We modeled I_h in TC cells using the single-variable (m) kinetic scheme of Huguenard and McCormick (1992), in which all rate constants were temperature-corrected using aQ₁₀ = 3. We set the maximum h-current conductance to 20 μS/cm². This was the same value used in a previous model (Destexhe et al., 1996a) and was sufficient to produce characteristic oscillations in isolated TC cells (data not shown; see McCormick and Huguenard, 1992). As in previous simulations (Huguenard and McCormick, 1992;McCormick and Huguenard, 1992; Destexhe et al., 1996a) the h-current equilibrium potential was −40 mV.

TC cells had a leak conductance of 24 μS/cm², corresponding to an input resistance of ∼140 MΩ, characteristic of TC cells in a deafferented slice. The E_leak of each TC cell was drawn from a normal distribution with a mean of −65 mV and SD of 2 mV. We used a distribution of E_leakvalues, to approximate the variation of cellular excitability in vitro and eliminate spurious results that might have been produced by nonphysiological symmetry in the network.

We modeled I_Ts in RE cells using a two-variable (m²h) kinetic scheme developed earlier (Destexhe et al., 1996b) and temperature-corrected all rate constants using Q₁₀ = 2.5. The maximum permeability of I_Ts, 1.0 × 10⁻⁷cm³/sec (at 37°C), was set so that the amount of T-current at rest was similar to that in previous studies (Destexhe et al., 1996b).

RE cells had a leak conductance of 25 μS/cm2. We found that a leak current equilibrium potential of −85 mV in an RE cell was sufficiently hyperpolarized that I_Ts would deinactivate between bursts, and the cell would not burst spontaneously. Therefore, the E_leak of each RE cell was drawn from a normal distribution with a mean of −85 mV and SD of 2 mV. Whereas these may be more hyperpolarized than the values observed in vitro (Destexhe et al., 1996b), they are similar those used in previous modeling studies (Destexhe et al., 1996a,b; Sohal and Huguenard, 1998).