Human Cortical Muscle Coherence Is Directly Related to Specific Motor Parameters

Abstract

Cortical oscillations have been the target of many recent investigations, because it has been proposed that they could function to solve the “binding” problem. In the motor cortex, oscillatory activity has been reported at a variety of frequencies between ∼4 and ∼60 Hz. Previous research has shown that 15–30 Hz oscillatory activity in the primary motor cortex is coherent or phase locked to activity in contralateral hand and forearm muscles during isometric contractions. However, the function of this oscillatory activity remains unclear. Is it simply an epiphenomenon or is it related to specific motor parameters? In this study, we investigated task-dependent modulation in coherence between motor cortex and hand muscles during precision grip tasks. Twelve right-handed subjects used index finger and thumb to grip two levers that were under robotic control. Each lever was fitted with a sensitive force gauge. Subjects received visual feedback of lever force levels and were instructed to keep them within target boxes throughout each trial. Surface EMGs were recorded from four hand and forearm muscles, and magnetoencephalography (MEG) was recorded using a 306 channel neuromagnetometer. All subjects showed significant levels of coherence (0.086–0.599) between MEG and muscle in the 15–30 Hz range. Coherence was significantly smaller when the task was performed under an isometric condition (levers fixed) compared with a compliant condition in which subjects moved the levers against a spring-like load. Furthermore, there was a positive, significant relationship between the level of coherence and the degree of lever compliance. These results argue in favor of coherence between cortex and muscle being related to specific parameters of hand motor function.

Oscillatory activity is a widespread feature of normal brain behavior. However, the functions of such activity remain unclear. In the visual system, oscillatory activity has been suggested to solve the “binding” problem, acting as a mechanism to link information related to the same function but processed in different neuronal populations (Singer and Gray, 1995). Such a mechanism could be important in any distributed network, and subsequent investigations of cortical oscillatory activity have interpreted synchrony between neuronal populations in an analogous manner (Kahana et al., 1999; Miltner et al., 1999; Rodriguez et al., 1999).

In monkey motor cortex, oscillatory 15–30 Hz activity has been observed in single cells and local field potentials (Murthy and Fetz, 1992, 1996; Baker et al., 1997; Donoghue et al., 1998; Lebedev and Wise, 2000). Similar oscillations have been observed in the human motor cortex by electroencephalography (EEG) (Stancak and Pfurtscheller, 1996; Halliday et al., 1998; Mima et al., 1999) (for review, see Hari and Salenius, 1999) and magnetoencephalography (MEG) (Conway et al., 1995; Salenius et al., 1997; Brown et al., 1998). The presence of oscillations in local field potential, EEG, and MEG recordings requires synchronous activity among large assemblies of neurons (Pfurtscheller and Lopes da Silva, 1999). Indeed, single-cell recordings from monkeys have demonstrated synchrony in the sensorimotor cortex over distances of up to 14 mm (Murthy and Fetz, 1996). The oscillatory neuronal network also includes the descending output neurons of the motor cortex (pyramidal tract neurons), and cortical oscillations have been shown to be coherent with oscillatory EMG activity in arm and hand muscles (Conway et al., 1995; Baker et al., 1997; Salenius et al., 1997; Hari and Salenius 1999; Kilner et al., 1999a).

The function of this oscillatory activity in the sensorimotor cortex remains controversial. Previous studies have demonstrated changes in the amplitude of the cortical oscillatory activity associated with a variety of tasks, with power in the 15–30 Hz range decreasing during movements of the contralateral hand and forearm and increasing during periods of maintained contractions (Salmelin and Hari, 1994;Pfurtscheller et al., 1996; Pfurtscheller and Lopes da Silva, 1999). These modulations were termed event-related synchronization and desynchronization, and these investigators interpreted the 15–30 Hz rhythm as an “idling rhythm;” the largest oscillations are seen at rest. However, in addition to these changes in the power of the cortical oscillations during movement, it has been shown that there are corresponding modulations in the extent of coherence between cortex and muscle and between muscles (Baker et al., 1997; Kilner et al., 1999a). Such modulations have lead to the interpretation that the oscillatory activity could link together motor commands in a manner analogous to that proposed for the binding of related visual information (Marsden et al., 2000).

However, if this oscillatory activity has a functional role in motor behavior, then it should show systematic variation with specific parameters of the motor task. The presence of coherent cortical and muscular oscillatory activity during the precision grip task opens up the possibility of exploring this important question. Our previous investigations showed that coherence was particularly marked during steady grip of a compliant, spring-like load (Baker et al., 1997,1999). Here we report changes in oscillatory synchronization in the 15–30 Hz bandwidth between human motor cortex and hand muscles that varies according to the time course of the task and the level of compliance of the gripped object. Interacting with such springy objects, which are a common feature of everyday life (spring clips, bottles of shampoo, etc.), requires precise coordination of both digit position and grip force. We suggest that synchronous oscillations could be important in recalibrating the sensorimotor network during changes in motor state that occur in the transition from movement to steady grip.

Parts of this work have been published previously in abstract form (Kilner et al., 1999b).

MATERIALS AND METHODS

Subjects

Experiments were performed on 12 healthy volunteers, aged 19–53 years old (eight males). The recordings had ethical committee approval, and all subjects gave informed consent and were right-handed by self report.

Behavioral task

Subjects gripped two short aluminum levers (20 × 40 × 1.5 mm) between the tips of the thumb and index finger of their right hand; the forearm was supported in the fully pronated position, and the other digits were flexed out of the way. Subjects were instructed to relax their left arm during task performance. The levers were mounted on a table in front of the subject and were attached to the shafts of two direct current motors by 2 m long brass shafts; the latter allowed the motors to be positioned outside the magnetically shielded room, which housed the neuromagnetometer, to avoid contamination of the MEG signal. Lever position was measured using optical encoders (resolution of ∼40 counts per millimeter movement of the lever tip). The force generated by the motors could be controlled continually as a function of position by a computer fitted with a robotic interface (Phantom Haptic Interface; SensAble Devices, Woburn, MA); this allowed simulation of a spring-like load in which force was proportional to displacement. Force on the levers was measured using pairs of sensitive foil strain gauges. Visual feedback of the forces exerted on the levers was given by square cursors displayed on a screen mounted at the subjects' eye level. Subjects were instructed to keep these cursors within two target boxes, also shown on the screen; the width of the targets required an accuracy of force control of 0.05 N. The screen was positioned 110 cm from the subject, and the maximum distance between target boxes displayed on it was 28 cm. Subjects performed the precision grip task under a number of different conditions so that task-related modulations of MEG–EMG coherence could be modulated.

First series of experiments. In the first series of experiments, the effect of lever compliance was investigated in nine subjects (five males). At the onset of each trial, the target boxes appeared on the screen, and the subject had to produce a rapid contraction to increase the force on each lever to 1.3 N in <300 msec. This force was maintained for 3 sec (Fig.1A, Hold 1). The subjects then tracked a linear increase of the force to 1.6 N over a 2 sec period (Ramp), followed by an additional hold at this force level for 3 sec (Hold 2). The target boxes then disappeared, and the subjects released the levers.

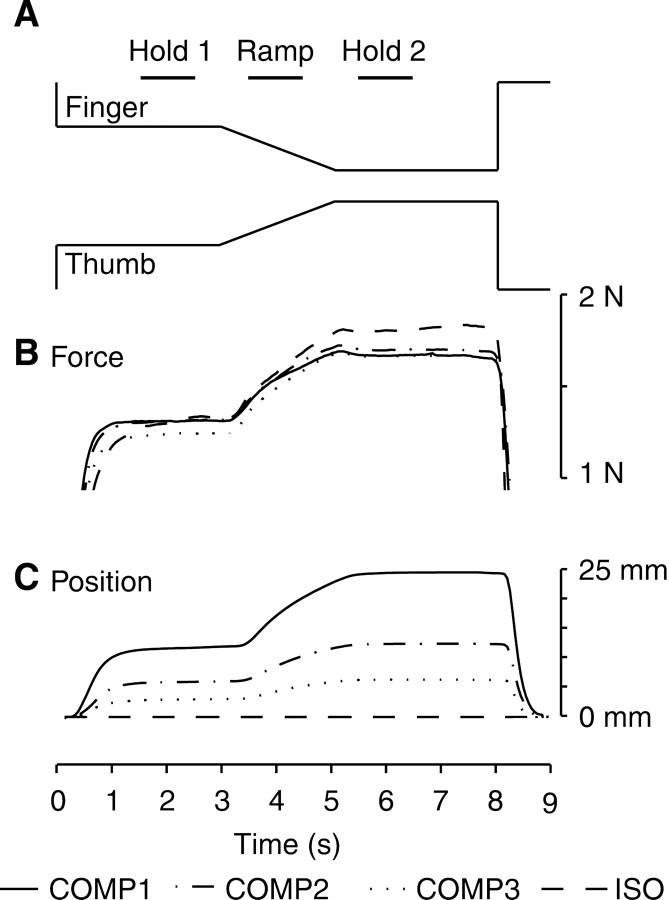
Fig. 1.

Averaged data for performance during the precision grip task. A, Schematic of the task showing the forces required to be exerted on the finger and the thumb levers by the subjects. The different phases of the task (Hold 1, Ramp, Hold 2) are indicated, and the ramp phase is highlighted by the pale gray box. B, The force profiles actually recorded from the strain gauge signals for the three conditions in which the levers carried a compliant load (COMP1, COMP2, COMP3) and for the condition in which they were fixed and forces exerted isometrically (ISO). C, The lever position traces calculated from the optical encoder signals for the COMP1, COMP2, COMP3, and ISO tasks. Data for each of these traces were averaged across trials, across subjects, and across levers.

We tested four different task conditions. In three of them, the motors opposed the subjects' movements with a compliant, or spring-like, load with different spring constants. To track the displayed target forces, subjects had to move the levers to different extents. When the levers were most compliant (COMP1 condition), a displacement of ∼12 mm was required to reach the 1.3 N target force in the Hold 1 phase; stiffer spring conditions (COMP2 and COMP3) required smaller displacements of ∼6 and ∼3 mm, respectively. In the Hold 2 phase, displacements of ∼24, ∼12, and ∼6 mm displacements were required to reach the 1.6 N force target. In these compliant conditions, an initial force of 1 N was required to move the levers from their rest position. In the fourth condition, the levers were rigidly locked in place. Subjects thus gripped the levers isometrically (ISO). The four task conditions therefore required the same force profiles to be produced (Fig. 1B) but with very different displacements (Fig. 1C). Each task condition was repeated >75 times. The order of presentation of the different task conditions was randomized for each subject.

For two of the four conditions, COMP1 and ISO, six of the nine subjects performed a variant of the standard task for the last trial in the series of 75. During this last trial, the target boxes did not disappear at the end of the trial but remained at the Hold 2 force level for a period of over 180 sec. Subjects were thus required to produce a long, steady contraction. We refer to these trials as Neverending.

Second series of experiments. In a second series of experiments (seven subjects) two variants of the precision grip task were investigated. These are illustrated schematically in Figure 5,I and J. One variant, termed RAMP (see Fig.5I), was identical to the COMP1 condition in the first series, with a low force (1.3 N) in Hold 1 and a higher force (1.6 N) in Hold 2. The other was a BALLISTIC task (see Fig.5J) in which the transition from low to high force was achieved by a rapid movement, produced as the subjects attempted to track a step jump in target position. Each task was repeated ∼75 times. The order was varied across subjects.

Fig. 5.

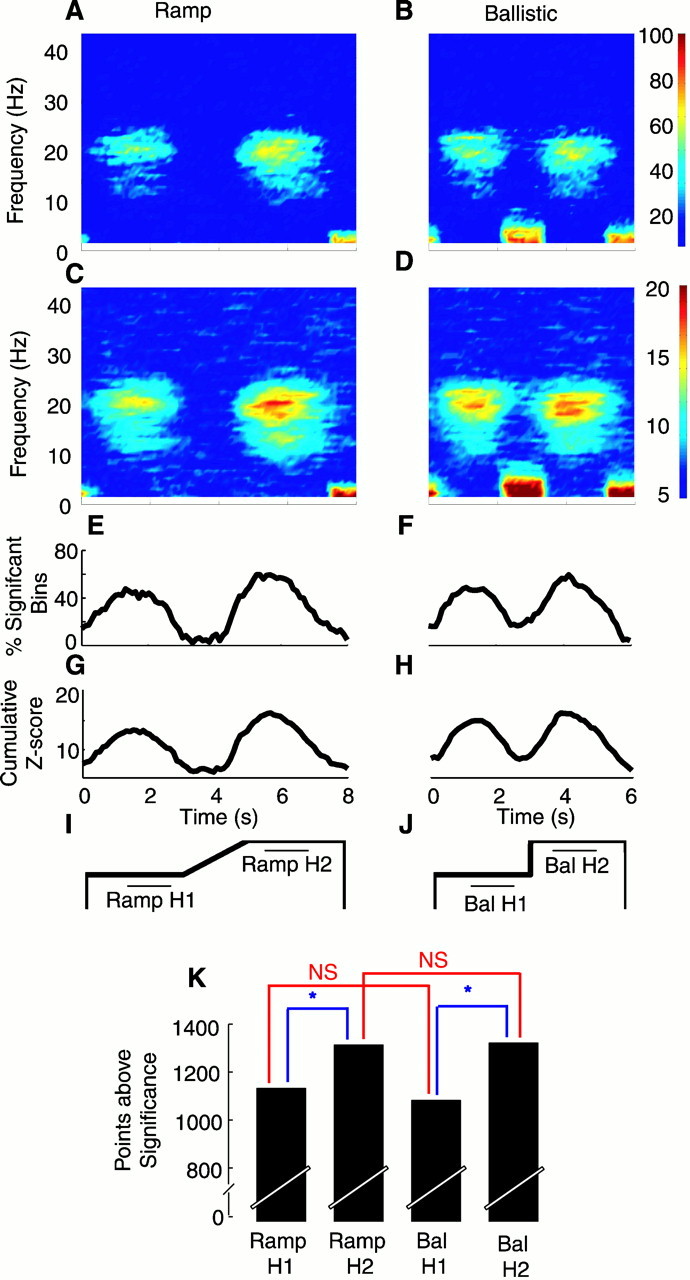
Effect of type of movement on MEG–EMG coherence.A, B, Coherence frequency versus time maps. The colors indicate the percentage of points above 95% significance pooled using the nonparametric method across all seven subjects and four muscles (color scale bar to right ofB applies to both maps; at any point, 100% would be equal to 28 of 28 points). A shows the data for the Ramp task, and B shows the data for the Ballistic task.E and F show the mean percentage of significant points in the 15–30 Hz range for Ramp (E) and Ballistic (F;Bal) tasks. Data for each of these traces were averaged across trials, across muscles, and across subjects.C, D, G, andH show the same data for the parametric pooling method.I and J show the schematic of the two tasks; the horizontal bars indicate the periods of the task from which data were used for statistical testing (see K;H1, Hold 1; H2, Hold 2). Kshows the number of points above 95% significance summed over the 15–30 Hz range and the periods marked in I andJ. Maximum number of points was 5040. NS, Not significant (p > 0.05, corrected); * indicates significance (p < 0.05, corrected).

Recordings

Bipolar surface EMGs were recorded from first dorsal interosseous (1DI), abductor pollicis brevis (AbPB), flexor digitorum superficialis (FDS), and extensor digitorum communis (EDC) of the right hand and forearm with a pass band of 1–330 Hz. Cortical signals were recorded with a 306-channel whole-scalp neuromagnetometer (bandpass, 0.1–330 Hz; Vectorview; Neuromag Ltd., Helsinki, Finland). These recordings, together with finger and thumb lever position and force and markers indicating task events were digitized at 1 kHz and stored on magneto-optical disks for off-line analysis. The exact position of the head with respect to the sensor array was determined at the start of each recording by measuring magnetic signals from four indicator coils placed on the scalp.

Analysis

Off-line, finger, and thumb lever position and force records were examined by eye; trials in which subjects did not perform the task correctly (<6%; 220 of 3078) were rejected before further analysis.

The EMG signals were high-pass filtered at 10 Hz and rectified. All the EMG, MEG, and strain gauge signals were then low-pass filtered at 100 Hz and down-sampled to an effective sampling rate of 200 Hz. Subsequent spectral analysis used these processed signals, permitting a maximum detectable frequency of 100 Hz (Nyquist theorem; Newland, 1993). In a first analysis, coherence spectra were calculated between all MEG sensors and 1DI EMG over the entire data set using an Fast Fourier Transform window of 256 points, permitting a frequency resolution of 0.77 Hz. Coherence is an estimate of the amplitude and phase correlation within a particular frequency band between two sources and is bounded between 0 and 1. The calculations for coherence are described by Rosenberg et al. (1989) and Baker et al. (1997). The MEG sensor over the left sensorimotor cortex with the greatest coherence was selected and subsequently used for the further analyses. This choice was well justified because the planar gradiometers of the neuromagnetometer pick up the largest signals just above a local cortical source.

Time–frequency analysis was then performed to determine the modulation of coherence with task performance. Any trends in the data associated with the ramp phases of the task were first removed using linear regression techniques (Kilner et al., 1999a). Power spectra and estimates of the coherence between all of the EMG signals and the selected MEG sensor were calculated over a sliding 1.28 sec time window with a 256 point Fast Fourier Transform (Rosenberg et al., 1989); estimates from windows with the same alignment to the task onset were averaged across trials. The time window was moved through the task in 0.1 sec steps to generate a time–frequency map.

Our study required estimates of coherence between MEG and different muscle EMGs, and from different subjects, to be combined into a single, more reliable estimate. This is a difficult statistical problem, with potential pitfalls (Baker, 2000). We therefore chose to use two distinct methods: one parametric, the other nonparametric. Their qualitative agreement provides confidence that the results are genuine and are not influenced by statistical artifacts (Halliday et al., 1999).

For the nonparametric analysis, all MEG–EMG coherence spectra were thresholded at the 95% confidence level (Rosenberg et al., 1989); any points above the level were given the value 1 and those below or equal were given 0. These binary spectra were summed across subjects and muscles in which coherence with MEG was estimated to allow a combined display.

In the parametric analysis, coherence values were transformed as follows:

$$Z=\text{arctan} h\left(\sqrt{C}\right)\times \sqrt{2L}$$

where C is the coherence value, and L is the number of disjoint sections; the dependence of C and Z on frequency, and time relative to task onset, are suppressed for simplicity of notation. Such a value can be considered as an estimate of the “true” Z-transformed coherence between the two signals, with a mean equal to this underlying value; it will be normally distributed with an SD of approximately one (Rosenberg et al., 1989). Such values were combined across all subjects and MEG–EMG pairs to produce a composite value according to

$$\xi =\frac{1}{\sqrt{N}} \sum _{i=1}^{i=N} Z_{\text{i}}$$

where N is the number of different MEG–EMG pairs that were combined.

Statistical differences between coherence spectra

Differences between conditions were tested using separate methods depending on the nature of the data tested.

Difference tested using the arctanh transform. Significant differences between the MEG–EMG coherence spectra obtained during the different compliant and isometric task conditions in the first experimental series were tested using the arctanh transform, which compares spectra calculated over the same number of disjoint sections (Rosenberg et al., 1989). Comparisons were made between COMP1 and one other condition. For each MEG–EMG pair, such a transform produced a time–frequency Z-score map; elements of this map should have a mean of zero and an SD of one on the null hypothesis that the two task conditions compared have equal coherence.

These Z-score spectra were combined using both parametric and nonparametric methods. In a nonparametric summation of these differences, each MEG–EMG spectrum comparison was thresholded at a significance level of p < 0.05; points with Z > 1.96 were given the value 1, points with Z < −1.96 were given the value −1, and all other points were set to 0. The thresholded scores were then summed across all subjects and MEG–EMG pairs within the 15–30 Hz frequency band for all positive and negative differences independently to produce two separate spectra. Bins above significance were analyzed for significant main effects of task type and MEG–muscle pair using ANOVA designs in SPSS 8.1 (SPSS, Chicago, IL). In a parametric summation of these differences, each Z-score spectrum was combined across subjects and MEG–muscle pairs, and the number of points in the 15–30 Hz range greater than the Bonferroni corrected significance level of p < 0.05 was calculated.

Difference tested using paired t tests. The arctanh method of comparison was used only when the tasks compared had exactly the same temporal profile (i.e., COMP1–ISO tasks). Differences within a task or between different parts of the same task were tested using Student's paired t tests on the Z-score-transformed coherence estimates in the 15–30 Hz range in discrete sections of the task. All significance levels were corrected in the event of any multiple comparisons.

Cortical source localization

Sources of oscillatory MEG signals were modeled in the time domain as equivalent current dipoles (ECDs) (Hämäläinen et al., 1993), found by a least-squares search based on the MEG signal distribution. The EMG was first converted to a series of events by detecting the times when it crossed a given voltage in the positive-going direction; the threshold level was set to obtain 10–15 triggers per second. The MEG signals were then averaged relative to these triggers. Source localization was restricted to the EMG-triggered averages from the 60 detectors centered over the rolandic area in each hemisphere, because signals from other detectors showed no consistent signals. The value of the mean field at a lag chosen to coincide with the peak deflection was used to produce a field map over the scalp, to which an ECD model was fitted. Only sources that accounted for >75% of the field variance were accepted. Sources were identified using the 1DI muscle for all task conditions. In the COMP1 condition, source locations were found for all four EMGs recorded to allow their comparison.

RESULTS

Effect of compliance on coherence between cortex and muscle

Figure 2 shows representative results for a single subject performing the hold–ramp–hold precision grip task under COMP1 (most compliant) conditions. Figure 2,A and B, shows, respectively, the power spectra of the MEG from the contralateral sensorimotor cortex and from the 1DI muscle EMG averaged over the entire task. Both spectra showed distinct peaks between 10–12 and 18–25 Hz. In the MEG power spectrum, the ∼10 Hz peak was much larger in amplitude than the ∼19 Hz peak, whereas for the EMG, the ∼12 and ∼24 Hz peaks were of approximately equal magnitude. The MEG power spectrum also showed a smaller but distinguishable peak at ∼31 Hz; no corresponding peak was observed in the EMG power spectrum. Figure 2C shows the coherence spectrum between MEG and 1DI muscle EMG, averaged across the entire task. There was a single, clear peak in the 15–30 Hz range centered around ∼22 Hz; this peak was statistically significant (p < 0.05).

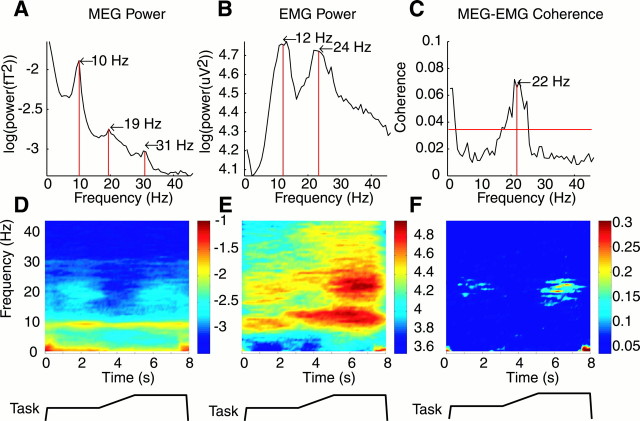
Fig. 2.

Single subject data for the COMP1 condition.A, B, Power spectra for MEG signal (A) recorded from a sensor overlying the sensorimotor cortex and the EMG recorded from the 1DI muscle (B), averaged over the whole task and for all trials (n = 75). C, The coherence spectra calculated between the two power spectra shown inA and B. The red lineindicates the 95% significance level. D,E, Frequency versus time power spectra maps for MEG and 1DI EMG activity calculated with respect to the task;below each trace is a schematic of the task.F, Maps of MEG–EMG coherence frequency calculated for the different periods of the precision grip task. The color bar indicates the level of coherence estimated; only values above the 95% significance level are shown. The frequency scale on the ordinate inD applies also to plots E andF.

Such averaged spectra tell us little about any functional modulations in the coherence during the task. For this purpose, time–frequency maps were calculated (Fig. 2D–F). Both MEG and EMG power changed in amplitude during the task (Fig.2D,E, respectively). Both MEG and EMG power in the 15–30 Hz range was greatest during the two hold periods of the task and for the EMG was reduced, but was not absent, during the ramp. The ∼10 Hz frequency signal in the MEG trace showed no obvious modulation during the task. The EMG signal showed power at ∼10 Hz throughout the task, with a slight increase in its peak frequency during the ramp and second hold period. Figure2F shows the time–frequency coherence map between the sensorimotor MEG recording and 1DI EMG. The color scale of this figure has been adjusted so that all points that failed to reach significance (p < 0.05) are black. Coherence was tightly confined to the 15–30 Hz range, despite the presence of power at neighboring higher and lower frequencies. Coherence was also seen at low (<4 Hz) frequencies; this is the frequency domain analog of a movement-related field.

As we have demonstrated previously for EMG–EMG coherence (Kilner et al., 1999a), the MEG–EMG 15–30 Hz coherence has a marked task relationship. It was significant during both hold periods but abolished during the ramp movement, and in the second hold period, the coherence reached higher levels than it did in the first. Across subjects, the level of 15–30 Hz MEG–EMG coherence during the COMP1 condition ranged from 0.086 to 0.599 and was significant at some point during the task in all subjects (p < 0.05) and for all MEG–EMG pairs in at least one condition. Across subjects, the frequency of peak coherence at 15–30 Hz ranged from 16.2 to 25.8 Hz (mean of 20.3 Hz).

Time–frequency coherence maps for each subject and each MEG–EMG pair were combined using the two different techniques described in Materials and Methods. They are shown in Figure 3, in the left column for the nonparametric analysis and in theright column for the parametric analysis. Both methods show that, as in the single subject data (Fig. 2), coherence was seen only at low frequencies (1–4 Hz) and in the 15–30 Hz frequency band during the hold phases. The coherence at the low frequencies (1–4 Hz) reflected the spectral components of the rapid movement of the levers and was only present during the fast ballistic movements at the beginning and end of each trial. Because such coherence could be artifacts of the movement, no further analysis was performed on coherence in this frequency range. The level of hold period coherence was clearly related to the conditions under which the task was performed. Both analysis methods showed that coherence was greatest for the most compliant condition (COMP1) (Fig.3A,F), in which subjects made the largest digit movements. Coherence declined with progressively smaller movements (Fig.3B,C,G,H) and was least for the isometric condition (Fig.3D,J), in which no digit movement occurred. For COMP1 (most compliant), COMP2, COMP3 (least compliant), and ISO, the mean maximum coherence levels were 0.140, 0.133, 0.125, and 0.061, respectively. A second feature was that, for the three compliant task conditions (Fig. 3A–C,F–H) but not for the isometric task (Fig.3D,J), the level of coherence was significantly greater during the second compared with the first hold period (comparing Z-score-transformed coherence estimates in the 15–30 Hz range during 1.0–2.5 sec in Hold 1 to the coherence from 5.5–7.0 sec in Hold 2 (Student's paired t test;p < 0.01). Figure 3, E and K, shows data combined across frequencies in the 15–30 Hz range for each of the four task conditions. There was a clear increase in the magnitude of coherence with the degree of lever compliance.

Fig. 3.

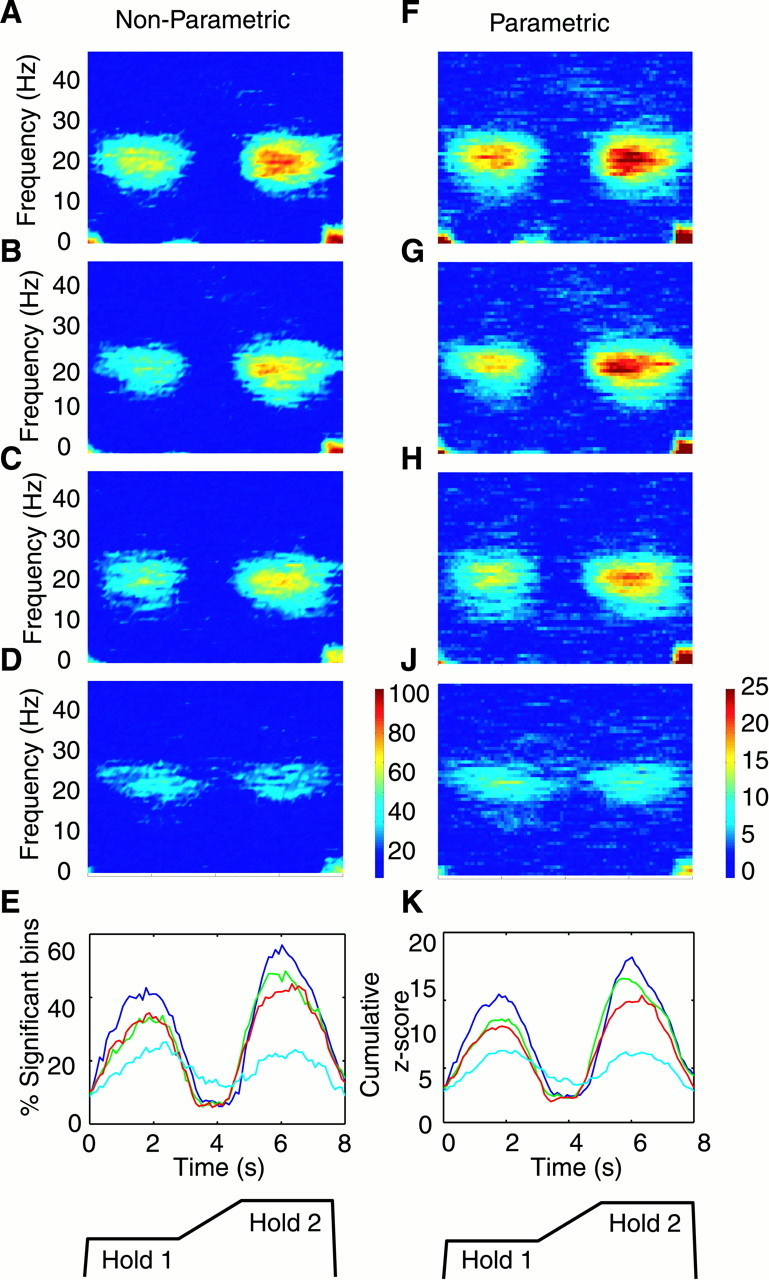
Effect of task condition on MEG–EMG coherence.A–D, Coherence frequency versus time maps. Thecolors indicate the percentage of points above significance pooled using the nonparametric method (see Materials and Methods) for data from all nine subjects and four muscles (see color scale bar to the right of D). At any point, 100% would be equal to 36 of 36 points. The levers were most compliant in A (greatest digit displacement required to exert the target force level), and compliance was reduced in the following direction: A, COMP1; B, COMP2;C, COMP3; and D, ISO (no lever movement).E shows the mean percentage of significant points in the 15–30 Hz range for each of the four task conditions with respect to the task (dark blue, COMP1; green, COMP2;red, COMP3; and light blue, ISO). Data for each of these traces were averaged across trials, across muscles, and across subjects. F–K show the same data combined using the parametric method. Below eachcolumn is a schematic of the task.

Figure 4 presents a detailed comparison of the relationship between task condition and MEG–EMG coherence. Coherence at 15–30 Hz was compared for task conditions COMP2, COMP3, and ISO relative to COMP1 by calculating arctanh-transformed coherence differences and thresholding them for significance as described in Materials and Methods. The comparison was performed for three discrete 1.5 sec sections of the task: Hold 1 (1–2.5 sec after task onset), Ramp (3.2–4.7 sec), and Hold 2 (5.5–7 sec); these sections are marked in Figure 1A. The bar charts of Figure4A–C show summed nonparametric coherence comparisons; the parametric comparisons are shown in Figure4D–F. In all cases, a positive difference indicates that coherence was higher during COMP1. During the ramp phase, when coherence was all but abolished, very few bins showed any difference across task condition (Fig. 4B,E). For both hold periods, the greatest difference in coherence was seen between the condition involving the largest movement (COMP1) and that with none (ISO) (Fig.4A,C,D,F,white bars). The difference in coherence was smaller for the COMP1–COMP3 comparison (gray bars) and smallest of all for COMP1–COMP2 (black bars), for which the difference in digit displacement was smallest. These effects only reached significance for the Hold 2 period (ANOVA; Hold 1 period (Fig. 4D),F_(2,16) = 3.458; p > 0.05; Hold 2 period (Fig. 4F),F_(2,16) = 7.704; p < 0.005).

Fig. 4.

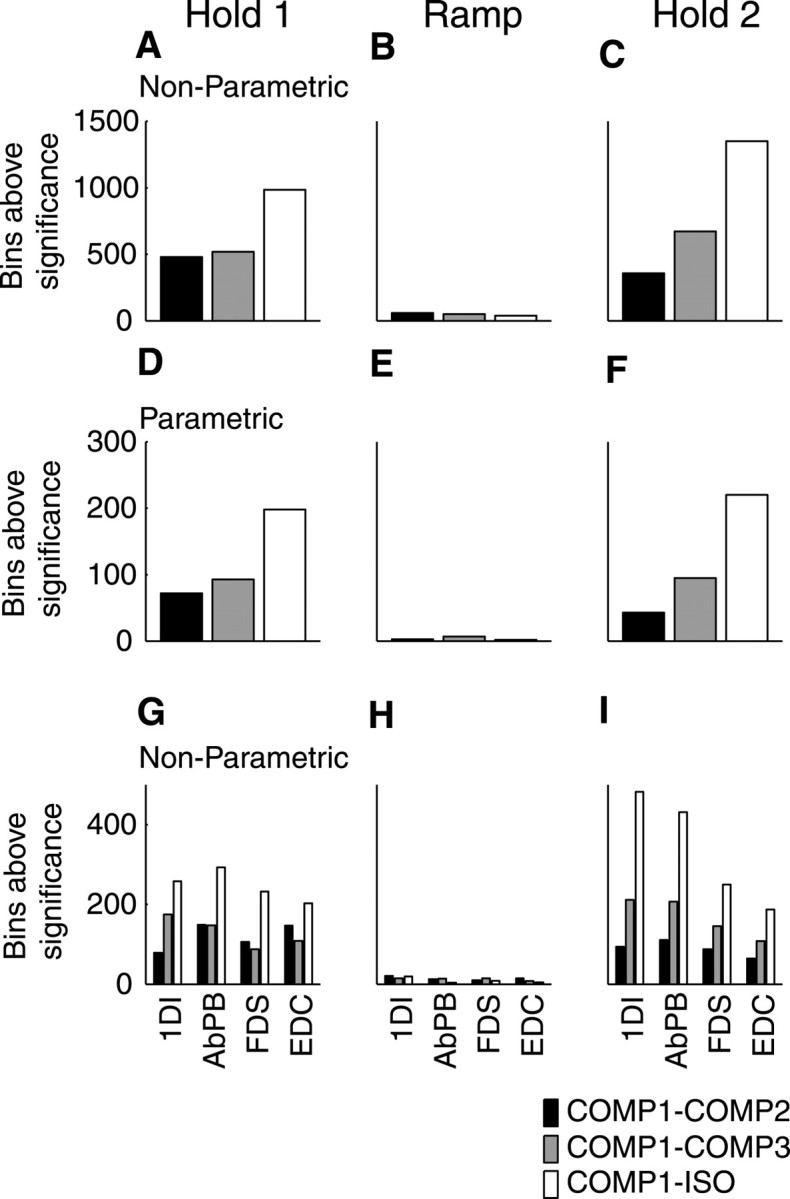
Quantitative estimate of the change in MEG–EMG coherence with task condition. Histograms showing differences in coherence in the 15–30 Hz range between task conditions, all expressed relative to the COMP1 condition and plotted for data recorded during the different phases of the task (see Fig. 1A).A, D, and G show the results for Hold 1; B, E, andH show results for Ramp; and C,F, and I show results for Hold 2.A–C show the positive changes summed across all subjects and muscles using the nonparametric method. For each of these plots, the maximum possible number of points greater than significance was 6480. D–F show the same data averaged using the parametric method. G–I show the data for each muscle summed across subjects using the nonparametric method. For each of these plots, the maximum possible number of points greater than significance was 1620.

The differences between the task conditions varied in strength according to the muscle whose EMG was used in the coherence analysis. Figure 4G–I shows greater differences for the intrinsic (1DI and AbPB) compared with the extrinsic (FDS and EDC) hand muscles. For the Hold 2 period, there was also a main effect of muscle (ANOVA;F_(3,24) = 3.228; p < 0.05) (Fig. 4G–J). There was no significant interaction between MEG coherence with different muscles and the task (p > 0.05).

We can conclude from this first series of experiments (Figs. 3, 4) that there is no simple relationship between the level of cortex–muscle coherence and grip force. Rather, coherence during the second hold period showed significant changes with task condition, although the grip force in the second hold period was identical for all four task conditions (Fig. 1B). The results show that coherence does covary with force/displacement relationship, i.e., with lever compliance.

Is the level of coherence affected by the pattern of grip force increase?

It is clear from Figure 3 that, after subjects increased the force exerted on the compliant levers that they were already gripping, there was an enhanced level of cortex–muscle coherence. In the second series of experiments, we tested whether the level of this coherence is affected by the pattern of grip force increase that subjects use to track the target between the first and hold periods. We compared coherence when subjects performed a slow ramp increase in grip force (compare Figs. 1, 5I) with that obtained when subjects made a ballistic force increase to track the target when it jumped from one position to another (Fig.5J).

Figure 5, A and B, shows the MEG–EMG coherence for both the tasks combined across subjects and different MEG–muscle pairs using the nonparametric method; data combined across frequencies in the 15–30 Hz range are shown in Figure 5, E andF. Results obtained with the parametric method are shown in Figure 5, C, D, G, and H. The RAMP task was identical to that performed in the first series and produced identical findings, with coherence significantly greater during the second compared with the first hold period. This is shown in Figure 5K, which compares coherence estimates in the 15–30 Hz range during 1.0–2.5 sec in Hold 1 with the coherence from 5.5–7.0 sec in Hold 2 (Student's paired t test; p< 0.05, corrected for multiple comparisons). The same pattern of modulation was obtained in the BALLISTIC task (Fig.5B,D). Figure 5K shows that the Hold 1–Hold 2 difference was significant. The modulation was consistent across all four muscles (Fig. 4G–J). Coherence during either the first or second hold period of the two tasks was not significantly different (p > 0.05, corrected for multiple comparisons) (Fig. 5K,red bars).

We can conclude from this second series that the change in coherence is not significantly dependent on the type or speed of force increase used between the two holds.

Does MEG–EMG coherence persist for longer hold periods?

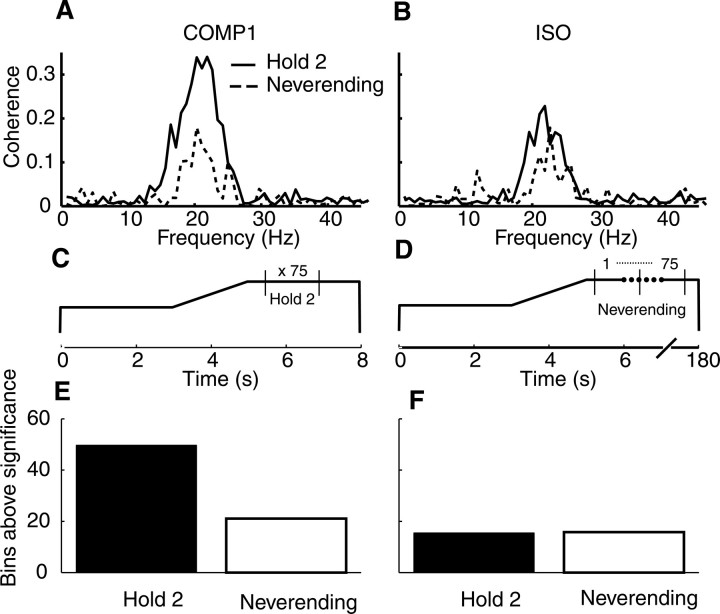
We investigated whether the enhanced level of coherence observed in the second hold period persisted throughout a maintained steady contraction. Figure 6 compares two coherence spectra. The first (Fig.6A,B, solid lines) shows coherence calculated using 1.28 sec windows beginning 5.5 sec after the task onset and averaged across 75 trials (calculation shown schematically in Fig. 6C). The second spectrum (Fig.6A,B, dotted lines) was calculated over 75 consecutive 1.28 sec windows during the Neverending task, when the subject continued to hold for ∼180 sec (Fig.6D). Figure 6A shows the comparison in a single subject for the MEG–1DI EMG coherence with the COMP1 conditions. Although there was a significant 15–30 Hz coherence peak in both cases, the peak was larger and broader when calculated across the second hold period than during the Neverending task. Interestingly, this difference was not seen when the task was performed under isometric (ISO) conditions (Fig. 6B).

Fig. 6.

Comparison of coherence during short versus long precision grips. A, Coherence spectra for MEG–1DI pair for a single subject during the second hold period (solid line) of the standard task, shown schematically inC and averaged from data recorded in 75 successive trials compared with coherence in data recorded during a single long hold period (dashed line) of the Neverending task, which lasted for up to 180 sec shown schematically in D (notebroken time scale). Both tasks were performed under most compliant (COMP1) conditions. B, Coherence spectra for MEG–1DI pair for a single subject during the second hold period averaged across trials (solid line) and during the long hold, Neverending task (dashed line), for the task performed under isometric (ISO) conditions. E, The percentage of points above 95% significance in the 15–30 Hz range for the Hold 2 (filled bar) and Neverending task (open bar) for COMP1 conditions. Fdisplays the same data as E for the ISO task. For bothE and F, 100% would be equal to 532 of 532 points.

Across subjects and muscles, the peak coherence value in the 15–30 Hz band had a mean of 0.14 for the second hold period compared with 0.082 for the Neverending task under COMP1 conditions. The means under ISO conditions were 0.09 and 0.07, respectively. Figure 6, E andF, shows the number of bins above significance in the 15–30 Hz range when pooled across subjects and MEG–EMG pairs. There was significantly more coherence in the second hold period compared with the Neverending task only for the COMP1 condition (p < 0.05; tested using arctanh comparisons of the coherence spectra for the Hold 2 and Neverending tasks). For COMP1, 88% of EMG–MEG pairs had significantly higher coherence during Hold 2 than during the Neverending compared with only 8% for the ISO task.

Where is the source of the coherence?

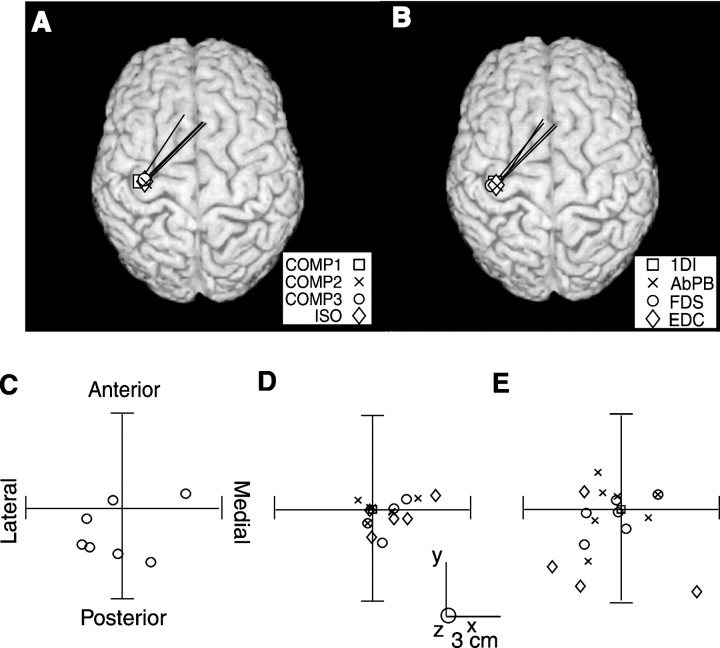
Figure 7 shows for a single subject the generation sites of MEG signals that displayed the strongest MEG–EMG coherences. The different symbols refer to each MEG–muscle pair during the second hold of the COMP1 task in Figure7B and to MEG–1DI coherence for the second hold of the COMP1, COMP2, COMP3, and ISO tasks in Figure 7A. For all tasks and MEG–EMG pairs, the generator site of the EMG signal agreed with the hand area of the primary motor cortex.

Fig. 7.

Cortical source analysis of coherent MEG activity.A, B, Single subject data showing the direction and strength of the current dipole on the subject's surface-rendered magnetic resonance image for MEG–1DI EMG coherence during the second hold period for the four task conditions COMP1, COMP2, COMP3, and ISO (A), and the MEG–EMG coherence for the four muscles recorded during the second hold period (B). C shows the distances of the cortical sources of the MEG–1DI coherence spectra during the first hold period relative to those during the second hold period of the task performed under COMP1 conditions. Each point represents a different subject. D, The distance of the sources of the MEG signal with the highest level of coherence signals for MEG–AbPB (×), MEG–FDS (○), and MEG–EDC (⋄) pairs relative to those for the MEG–1DI pair during the second hold period under COMP1 conditions. Each point represents a different subject.E, The distance of cortical sources for the MEG–1DI coherence spectra during Hold 2 under COMP2 (×), COMP3 (○), and ISO (⋄) conditions relative to those for the COMP1 condition. Eachpoint represents a different subject.

To compare MEG source sites across subjects, the source explaining the coherence between MEG and 1DI EMG during the second hold of the COMP1 task was used as a reference point, and the sources from other conditions were plotted relative to this point. Figure 7Cshows the source location for MEG–1DI coherence in the first hold of the COMP1 task plotted in this way. There was no significant difference (Student's paired t test; p < 0.05) between the coherence source location in the different hold periods.

Figure 7D plots the relative source localizations for different muscles; these locations did not differ significantly (Student's paired t test; p < 0.05) across muscles, in agreement with the known distributed representation of muscles within the motor cortex (Porter and Lemon, 1993). Figure7E shows the source locations for MEG–1DI coherence during the second hold during the COMP2, COMP3, and ISO tasks. Once again, no significant differences (Student's paired t test;p < 0.05) in these locations were found.

DISCUSSION

In this study, we have shown that the coherence between 15–30 Hz oscillatory activity in the sensorimotor cortex and in contralateral hand and forearm muscles during performance of the precision grip task is strongly and systematically modulated by the conditions under which the task is performed. Previous studies have established that both the magnitude of the cortical oscillations and the cortical–muscular coherence are most pronounced during the steady hold period of this task, being abolished during movements and greatest during steady hold periods just after movements (Salmelin et al., 1995; Pfurtscheller et al., 1996; Baker et al., 1997; Hari and Salenius, 1999; Kilner et al., 1999a). The results of the current study both support and extend these previous results, with the novel finding that the level of coherence covaries with the degree of compliance of the levers operated by the subject.

Modulations of cortex–muscle coherence during grasp of a compliant object

Figures 3 and 4 show that the degree of coupling between the sensorimotor cortex and the contralateral hand and forearm muscles is modulated by the task condition. The changes in coherence during the second hold period cannot be related to grip force, because this was constant in each condition (Fig. 1A), a finding that confirms results from previous studies performed using a similar range of low grip forces (Kilner et al., 1999a, their Fig. 4; Mima et al., 1999). Likewise, these results show that there is no simple relationship between coherence and digit displacement. For example, exactly the same displacement was required in Hold 2 of the COMP3 condition as in the Hold 1 of the COMP2 condition (Fig.1A), but the level of coherence during these two hold periods was quite different (Fig. 3, compare B,C). These differences between Hold 2 and Hold 1 periods cannot be attributable to the different type of movement into the respective holds, ballistic, or slow ramp, because there was no difference in the level of coherence during the second hold period after a slow ramp compared with that after a ballistic jump (Fig. 5). Instead, Figure 4 suggests that the key parameter is the force/displacement ratio i.e., the compliance of the levers.

These systematic changes in coherence in the 15–30 Hz frequency range were present in both parametric and nonparametric analyses of combining data from different muscle and subjects. Neither one of these methods is a perfect way of combining coherence spectra across subjects and across muscles, but the corroboration between the results increases the certainty that the results are real and not artifactual.

Time course of coherence after movement

We have suggested previously that synchronous motor cortex output to motoneurons may maintain grip force at lower firing rates of cortical neurons than would be needed otherwise (Baker et al., 1997,1999). In this case, coherence between muscle and cortex should be present during sustained periods of grasp. The results in Figure 6confirm that, when subjects had to maintain steady grasp for periods of up to 3 min, some significant coherence was present in the 15–30 Hz range. However, this coherence was significantly lower than just after movement. It is possible that this temporal modulation in coherence reflects two different functions of coherent oscillatory activity, one that is related to maintained contractions (for example, during the Neverending task) and another that is related to the changes in the motor state and that appears as a rebound. Interestingly, this difference between brief and protracted hold periods was not present for cortex–muscle coherence during grasp under isometric conditions, once again underlining the importance of coherent oscillations during grasp of compliant objects.

The results reported here are important in two ways. First, in a general sense, they demonstrate a systematic relationship between coherence in the 15–30 Hz range and a specific parameter of the motor task. This relationship was only observed in the degree of coherence between the cortex and the muscles and was not present in the corresponding power spectra from either the MEG or EMG recordings. It is clear that the cortical activity, which is coherent with the hand and forearm muscles, represents something much more than just an “idling rhythm” (Adrian and Matthews, 1934; Buser, 1987; Lopes da Silva, 1991). Second, our results suggest a specific function related to the grasp of compliant objects; in everyday life, this includes a large range of tools and many other objects (food, clothing, etc). Coherence was at a much lower level during isometric grip of the fixed levers compared with grasp under compliant conditions (Fig. 3).

Function of synchrony during grasp of compliant objects

Why should coherence during grasp be related to the compliance of the object? When the spring constant simulated by the manipulandum interface was steadily reduced (from COMP3 to COMP1), subjects had to produce larger displacements of their digits to achieve the force targets displayed. During such tasks, the length–tension relationships of the different hand muscles show complex changes (Joyce et al., 1969). Additionally, both central and peripheral signals concerned with force control would be markedly different under compliant and isometric conditions (Edin and Vallbo, 1990; Wilson et al., 1995; Kakuda et al., 1996). It is possible that the modulation of coherent oscillatory activity signals and scales these important changes in motor state. Control of both force and displacement is required for effective manipulation of a compliant object; information related to both parameters is represented in the primary motor cortex (Wannier et al., 1991; Picard and Smith, 1992; Hepp-Reymond et al., 1999; Kakei et al., 1999), and it is possible that coherent oscillatory activity reflects the appropriate combination of these two sources of information.

The hold–ramp–hold nature of the task we have studied requires a sequence of changes in the motor state of the hand and forearm. During the hold period, the dominant pattern of muscle activity is co-contraction compared with a more fractionated pattern of activation during the dynamic changes in force/displacement (Smith, 1981; Bennett and Lemon, 1996; Kilner et al., 1999a). The results also show that coherence is particularly marked during a steady hold that succeeded a period in which subjects closed their grip aperture and exerted a greater force on the object. Thus, the level of coherence may also reflect the resetting of the control system as it passes through an important change in state: from increased grip force to maintenance of a new level of grip force and digit position (Kilner et al., 1999a). Having parameterized this new motor state (Johansson, 1996), the level of synchrony may reflect a recalibration of both feedback (Edin and Vallbo, 1990; Wilson et al., 1995) and feedforward (Miall and Wolpert, 1996) control within the sensorimotor system suitable for effective grip. Such a mechanism would be of particular importance during manipulation of compliant objects, which entails successive periods of movement and steady grasp.