Quantifying the Independence of Human Finger Movements: Comparisons of Digits, Hands, and Movement Frequencies

Abstract

To determine whether other digits move when normal humans attempt to move just one digit, we asked 10 right-handed subjects to move one finger at a time while we recorded the motion of all five digits simultaneously with both a video motion analysis system and an instrumented glove. We quantified the independence of the digits to compare (1) the different digits, (2) the right versus the left hand, and (3) movements at a self-paced frequency versus externally paced movements at 3 Hz. We also quantified the degree to which motion occurred at the proximal, middle, or distal joint of each digit. Even when asked to move just one finger, normal human subjects produced motion in other digits. Movements of the thumb, index finger, and little finger typically were more highly individuated than were movements of the middle or ring fingers. Fingers of the dominant hand were not more independent than were those of the nondominant hand. Self-paced movements made at ∼2 Hz were more highly individuated than were externally paced movements at 3 Hz. Angular motion tended to be greatest at the middle joint of each digit, with increased angular motion at the proximal and distal joints during 3 Hz movements. Simultaneous motion of noninstructed digits may result in part from passive mechanical connections between the digits, in part from the organization of multitendoned finger muscles, and in part from distributed neural control of the hand.

The digits of the human hand often are assumed to move independently of one another, like the digits of a robotic hand. Casual observation suggests, however, that in performing functional tasks humans rarely move one finger alone. Recordings of finger movements during grasping, typing, or piano playing reveal that multiple digits actually are in motion simultaneously. The degree of simultaneous motion depends on the behavioral task performed, however. In grasping objects of various sizes and shapes, high degrees of covariation have been observed among the metacarpophalangeal (MCP) joint angles of the four fingers and among the four proximal interphalangeal (PIP) joint angles as well (Santello and Soechting, 1998; Santello et al., 1998). To a lesser extent, simultaneous motion of multiple digits also occurs even during the single keystrokes of typing or piano playing (Fish and Soechting, 1992; Soechting and Flanders, 1992; Engel et al., 1997), because subjects have no specific requirement to keep the other fingers still while one finger strikes a key, as long as the other digits do not strike other keys. We therefore evaluated the ability of normal human subjects to move each digit independently when specifically asked to move one digit at a time, while not moving any other digits.

We also investigated three additional aspects of finger independence. First, because the phenomenon of handedness might be related to the independence of finger movements in the dominant versus nondominant hand, we compared the finger independence of normal subjects' right and left hands. Second, because the primary motor cortex (M1) is crucial for the production of individuated finger movements (Schieber and Poliakov, 1998) and because functional activation of the M1 hand representation has been found recently to increase with movement frequency (Rao et al., 1996; Sadato et al., 1996; Schlaug et al., 1996;Kawashima et al., 1999), we investigated whether finger independence is affected by movement frequency. And third, because our subjects were free to move the proximal, middle, or distal joint of each digit, we examined how normal subjects chose to distribute angular motion proximodistally across the three joints of each digit.

Parts of this paper have been published previously (Hager-Ross and Schieber, 1999).

MATERIALS AND METHODS

Subjects

Subjects with hands measuring at least 18 cm from the distal crease of the wrist to the end of the middle fingertip and with no previous medical history of trauma or degenerative or neurological disease affecting the upper limbs were recruited from hospital staff. Ten right-handed subjects (four men; six women; mean age, 32.6 years; range, 24–45 years) participated after giving written informed consent according to the Declaration of Helsinki. When asked whether they had any particular finger skill (such as typing) as a result of work or leisure activity, all subjects answered no. The study protocol was approved by the Research Subjects Review Board of the University of Rochester Medical Center and the Institutional Review Board of the Unity Health System (Rochester, New York). Each subject completed the 10 point Edinburgh Inventory to quantify their handedness (Oldfield, 1971) on a +100 (maximally right-handed) to −100 (maximally left-handed) laterality quotient scale. The laterality quotient for these 10 subjects ranged from +75 to +100, with a mean of +89.

Experimental procedure

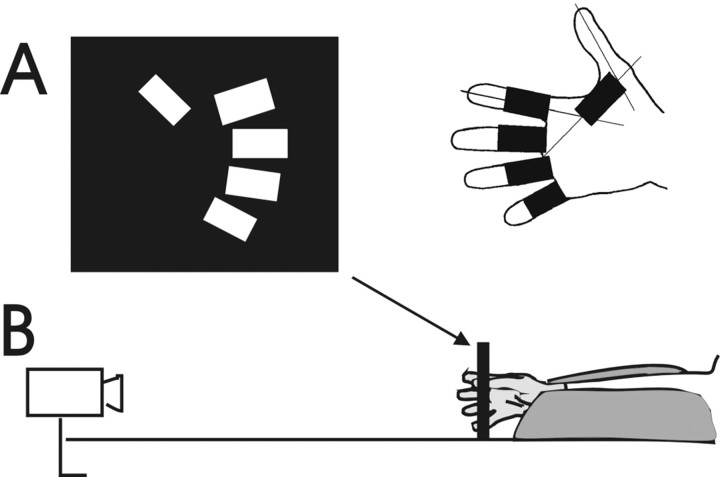
The size and shape of the hand vary among normal human subjects. To compare the finger movements of different subjects, we therefore attempted to standardize the movements performed by each subject to the features of that subject's hands. The subject placed his/her right hand palm down on a piece of paper and abducted the digits as far as comfortable. In this position, the subject's hand was traced, and the tracing was used to create a guide for that subject's finger movements (Fig. 1A) as follows. For each finger, a rectangle was drawn along the long axis of the traced finger, from the level of the MCP joint to the level of the distal interphalangeal (DIP) joint. For the thumb, a line was drawn from the thumb MCP joint to the web space between the middle and ring fingers, and a rectangle was drawn along this line from the long axis of the thumb to the long axis of the index finger. The pattern of these five rectangles was transferred to a piece of black cardboard, and corresponding rectangular slots were cut in the cardboard. The slotted cardboard was mounted in a fixed vertical frame to serve as a guide for that subject's finger movements (Fig. 1B). When the subject subsequently flexed and extended each finger within its individually prepared slot, the distance from the inner end (the point touched by flexing each digit) to the outer end (the point touched by extending each digit) was approximately equal to the distance from that finger's MCP joint to its DIP joint. The same slotted cardboard was flipped and reinserted in the frame to guide either the right-hand or left-hand fingers.

Fig. 1.

Schematic drawing of the experimental setup.A, Slots proportional to finger length (right) were cut in a piece of black cardboard (left) that then was placed in a vertical frame (arrow). When the subject placed each fingertip in the center of its own slot (as in B), these slots made the range of flexion–extension movements proportional to the size of each subject's fingers. B, Finger movements were recorded simultaneously with (1) a video camera mounted orthogonal to the plane of the cardboard frame (left) and (2) an instrumented glove worn by the subject (right).

The subject then donned an instrumented glove and sat comfortably with the shoulder abducted ∼30°, the elbow joint flexed to ∼120°, and the forearm extended anteriorly in intermediate pronation/supination. The fingertips of the gloved hand were inserted into the appropriate cardboard slots with the fingers resting semiflexed. The forearm was positioned with the wrist extended 10–20° to optimize the ability to perform finger movements (Hunter, 1990) and such that the tips of the fingers came to lie approximately in the center of the appropriate slots. The forearm and wrist were stabilized in a vacuum cast molded to the individual's forearm. Because pilot studies indicated no difference in performance depending on whether or not the hand was visible to the subject (Hayes and Schieber, 1996), the subject was allowed visual feedback of the hand to minimize inadvertent drifting of the fingers from the centers of the slots.

The subject was instructed to perform cyclical flexion–extension movements of one finger at a time, moving the instructed digit back and forth between the inner and outer edges of its slot. Movement of each digit was initiated when the subject was given a verbal instruction such as, “Now move your middle finger.” After the experimenter verified that the subject was moving the correct digit, a manual switch was thrown generating a signal that marked the beginning of a period for data analysis; 3.5 sec later a tone sounded signaling the end of the data analysis period. After hearing this tone the subject stopped cyclical movement of the instructed digit and awaited the next instruction. All subjects were naive to the task but performed one introductory series of movements of the different fingers before data collection. During data collection, instructed movements of the different fingers were performed in a pseudorandom order, with two epochs of instructed movement of each finger included in each recording. Two such recordings were made, providing in total four epochs of instructed movement of each finger. After completing these movements at the subject's self-paced frequency, the subject performed another four epochs of instructed movement of each digit, paced by a metronome at 3 Hz. The subject performed both self-paced and 3 Hz movements first with one hand and then with the other, the right or left order being varied between subjects.

Data acquisition

As the subject performed the above tasks, movements of the fingers were recorded simultaneously with two complementary systems. First, a video recording was made at 60 frames/sec with a camera (JVC TK-1280) mounted 111 cm from the plane of the slotted cardboard guide to view the motion of the fingertips end on. To optimize the video image for automated off-line tracking of fingertip position (Motus, version 3.1; Peak Performance, Englewood, CO), a hemispherical reflective marker (8 mm diameter) surrounded by a dark brown sheath of soft cotton was sewn onto each fingertip of the instrumented glove. The video system provided a veridical record of the flexion or extension motion of each fingertip projected orthogonally onto a two-dimensional plane.

A second system was used in parallel to record the motion of each finger joint. These recordings were made via an instrumented glove (medium-size Cyberglove; Virtual Technologies, Palo Alto, CA), which was equipped with 22 resistive bend sensors that transduced motion of the joints of the hand. Data from each glove sensor were sampled at 54 Hz and stored to disk on a personal computer. Our analyses (below) used data from only 15 of the 22 sensors: the MCP, PIP, and DIP sensors for each finger (12 sensors) and the MCP, PIP, and opposition (OPP) sensors for the thumb (3 sensors). Calibration of the MCP, PIP, and DIP sensors for each digit was obtained for each subject by having the subject hold six objects of different size and shape. While the subject held each object, data were sampled from the glove, and the corresponding MCP, PIP, and DIP joint angles of each digit were measured with a hand-held goniometer. Plots of sensor reading versus joint angle typically were linear, and therefore linear regression was used to estimate the relationship between sensor output and joint angle. Pilot studies demonstrated that the OPP sensor provided output linearly related to motion of the carpometacarpal (CMC) joint in the flexion or extension plane of the thumb's three phalanges, and we therefore used the output of this sensor as a measure of motion at the CMC joint. Because we were unable to calibrate this sensor for each subject, however, the default calibration provided by the manufacturer was used for all subjects. Selecting subjects with a minimum hand size of 18 cm (above) ensured that the glove fit snugly enough to transduce the motion of most joints accurately, although in some subjects transduction of DIP motion was suboptimal.

Data analysis

Video recordings. Tracking fingertip positions in the video recordings demonstrated that the motion of each fingertip in the two-dimensional plane of the video image was constrained by the slots in the cardboard guide to be approximately linear (Fig.2A). For each digit, we therefore calculated the best-fit line for its position throughout the recording, projected its position in each video frame onto that line, and normalized its position along the line from 1 at maximum flexion to 0 at maximum extension. This provided a one-dimensional measure of the normalized position of each digit within its own flexion–extension range. Plotting the normalized position of each digit as a function of time (Fig. 2B) then revealed that whereas instructed movements of some digits were accompanied by little if any movement of noninstructed digits, instructed movements of other digits were accompanied by considerable movement of noninstructed digits. For example, in the recording from subject 9 shown in Figure2B, instructed movements of the thumb were accompanied by no detectable motion in other digits, but instructed movements of the ring finger were accompanied by overt motion in the middle and little fingers.

Fig. 2.

A, Fingertip positions throughout one recording are shown as viewed by the video system in a plane parallel to the slotted cardboard. The motion of the fingertips in this plane was essentially linear, because abduction and adduction movements were restricted by the slots. Linear regression was used to compute a best-fit line for each fingertip's positions (thin white lines). Scales are in video pixels; small squares inside the axes represent centimeters (cm) at the fingertips. Data are from subject 9. B, The normalized position of each fingertip is shown as a function of time. All the data points for each fingertip in A were projected onto the best-fit line for that finger, normalized from 0 (maximum extension) to 1 (maximum flexion) for each digit, and plotted as a function of time.C, Relative motion slopes are shown. Primarily linear relationships were evident when the normalized position of each digit was plotted against the simultaneous normalized position of the instructed digit throughout flexion–extension cycles of a given instructed movement. We used the slopes of these relationships to quantify the relative motion of each digit during instructed movement of a given digit. Data shown represent the period of instructed ring finger movement indicated by thevertical rectangle in B.I, Index; L, little; M, middle; R, ring; T, thumb.

To quantify how much the other, noninstructed digits moved during a given instructed movement, we plotted the normalized position of each digit as a function of the simultaneous position of the instructed digit. Figure 2C shows an example of such a plot using the data from the second epoch of instructed movement of the ring finger in Figure 2B. Plots of the motion of a given digit as a function of the instructed digit's motion typically had a large linear component. We therefore computed the best-fit line for each such relationship and used the slope of that line as a measure of the relative motion of that noninstructed digit during that instructed movement. This relative motion slope will be close to 0 if the noninstructed digit did not move during the instructed movement and closer to 1 the more the instructed digit moved along with the instructed digit. In Figure 2C, for example, the plot of thumb position versus ring finger position has a slope close to 0, reflecting the fact that the thumb did not move during instructed movement of the ring finger. The plot of little finger position versus ring finger position, however, has a positive, nonzero slope of 0.3, reflecting the motion of the little finger during the same instructed movement.

We then used these relative motion slopes to derive two indexes, quantifying two aspects of the independence of each digit (Schieber, 1991). An ideally independent digit (1) would move when instructed with no accompanying movement of other digits and (2) would not move during instructed movement of other digits. To quantify how much the other, noninstructed digits moved during instructed movement of a given digit, we computed an individuation index (II) as 1 minus the average relative motion slopes of the noninstructed digits or:

$${II}_j=1-\left[\left(\sum _{i=1}^n\Vert S_{\text{ij}}\Vert \right)-1\right]/(n-1),$$

where II_j is the individuation index for instructed movement of the jth digit,S_ij is the slope of the relative motion of the ith digit during the jth instructed movement, and n is the number of digits (here n = 5). One is subtracted from the sum of the slopes in the numerator and fromn in the denominator to remove the slope of the instructed digit plotted against itself. The individuation index will be close to 1 for an ideally individuated movement in which the instructed digit moves with no movement of noninstructed digits and closer to 0 the more noninstructed digits move simultaneously with the instructed digit.

To quantify how much a given digit moves whenever it was a noninstructed digit, we computed a stationarity index (SI) as 1 minus the average relative motion slope of that digit whenever it was a noninstructed digit or:

$${SI}_i=1-\left[\left(\sum _{j=1}^m\Vert S_{\text{ij}}\Vert \right)-1\right]/(m-1),$$

where SI_i is the stationarity index for the ith digit during the m instructed movements (here m = 5). One is subtracted from the sum of the slopes in the numerator and from m in the denominator to remove the slope of the noninstructed digit plotted against itself as the instructed digit. The stationarity index will be close to 1 for a digit that remains stationary whenever it is a noninstructed digit and closer to 0 the more the digit moves when it is a noninstructed digit.

Joint angle recordings from the instrumented glove. The joint angle recordings from the instrumented glove enabled us to examine how motion was distributed among the three joints of each digit. These analyses were performed for the three joints of each digit using data recorded during instructed movement of that digit. We plotted the angular position of a given joint against the angular position of each of the three joints in the same digit. These plots typically were relatively linear, indicating that subjects used a relatively constant ratio of angular movement among the three joints of a given digit. We therefore computed the slope of the best-fit line for the relationships of a given joint plotted as the dependent variable against each of the three joints plotted as the independent variable, which we call the relative angular motion slope. For the given joint plotted against itself, this slope of course was 1. The relative angular motion slope approached 0 the less the given joint moved compared with another joint of the same digit, but the slope reached values much larger than 1 if the given joint moved much more than the other joint. For each joint, we then totaled the absolute values of the three relative angular motion slopes obtained when the angular position of that joint was used as the dependent variable. This total was close to 1 if the given joint moved very little during instructed movement of the digit and was larger the more the joint moved.

We then used the relative angular motion slopes to derive two indexes quantifying the proximodistal distribution of angular motion in the joints of each digit (cf. Fritz et al., 1992). Computation of these indexes is simplified by expressing the total relative angular motion slope of each joint as a fraction of the sum across the three joints. If T_i is the total relative angular motion slope of the ith joint, then the fractional totalτ_i is:

$${\tau }_i=T_i/\sum _{i=1}^n T_i,$$

where n is the number of joints (heren = 3). We then computed a proximodistal index (PDI) to quantify the proximodistal distribution of joint rotation from −1 to +1, with +1 representing all angular motion occurring at the most proximal joint, 0 representing angular motion distributed symmetrically about the middle joint, and −1 representing all angular motion occurring at the most distal joint. The PDI is calculated as:

$$PDI=\sum _{i=1}^n{\tau }_i*w_i,$$

where τ_i is the fractional total relative angular motion slope of the ith joint,n is the number of joints, andw_i is a constant that provides a rank-ordered weighting of the joints:

$$w_i=(2i-n-1)/(n-1).$$

We also computed a divergence index (DIV) to quantify the degree to which angular motion occurred at just one joint (DIV = 0) versus being spread evenly over the joints (DIV = 1). The DIV is calculated as:

$$DIV=s*\sum _{i=1}^n{\tau }_i^{*}(PDI-w_i{)}^2,$$

where s is a scaling factor that normalizes for the number of joints:

$$s=3*(n-1)/(n+1).$$

Statistical analyses. In addition to descriptive statistics, separate tests of ANOVA with a nested design were used to determine main effects of subject (1–10), hand (right or left), and finger (1–5) on the following dependent variables: (1) individuation index, (2) stationarity index, (3) proximodistal index, and (4) divergence index. To test for differences between the two conditions with different movement frequency (self-paced vs externally paced at 3 Hz), we used two-way ANOVA (frequency and finger as independent factors). For each test the level of probability chosen as statistically significant wasp < 0.05. Nonparametric correlation was done using the Spearmans' rank correlation test, and the Wilcoxon matched-pairs signed-ranks test was used to evaluate differences pairwise between fingers on the right and left hand. Bonferroni corrections on the significance level were implemented to compensate for the number of statistical tests. Group estimates are presented in the form of means ± SD values unless otherwise stated in the text.

RESULTS

Individuation of human finger movements

An ideally independent finger would move without any accompanying motion of the other fingers. As illustrated in Figure 2, however, when instructed to move only one finger, human subjects often move other fingers as well. The extent of motion in noninstructed digits varied from finger to finger and depended on which finger was instructed to move. We used an individuation index to quantify the degree to which noninstructed digits moved during instructed movement of a given digit. The individuation index varies from 1 if there is no motion of any noninstructed digit to 0 if the noninstructed digits all move as much as the instructed digit (see Materials and Methods).

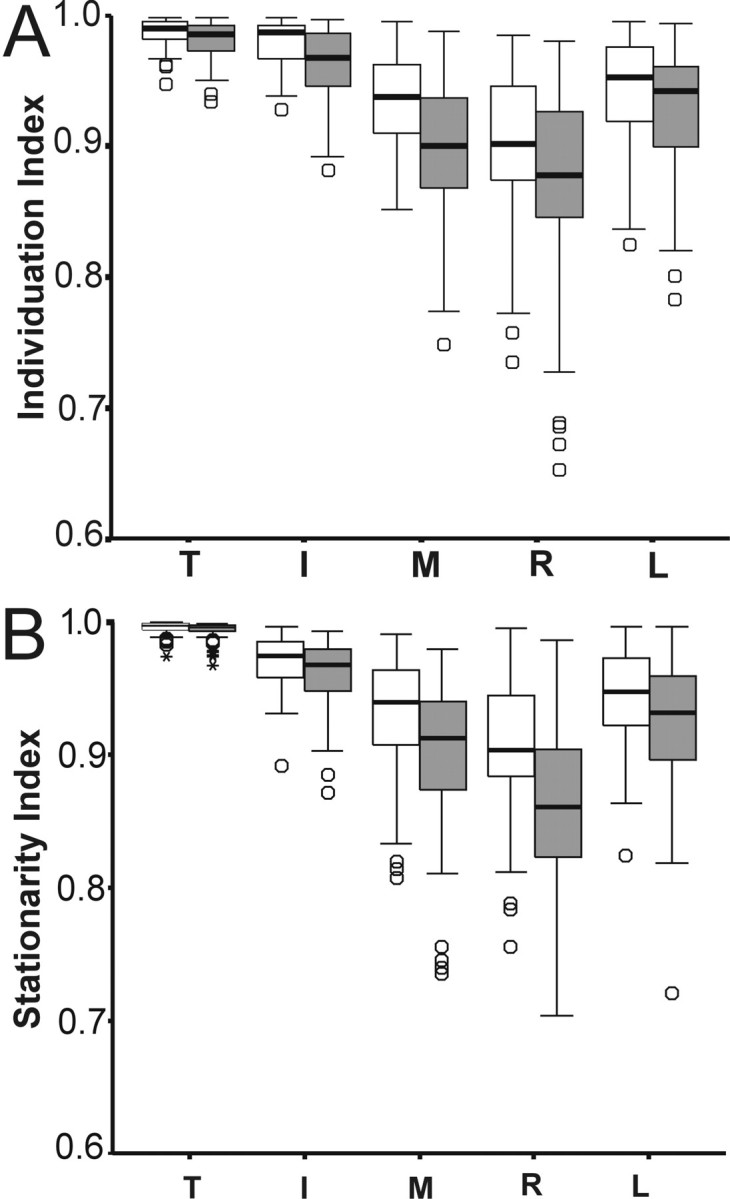
Table 1 presents the mean, SD, and range of the individuation indexes for self-paced movements of each finger, averaged across subjects. As might be expected, in both the right hand and left hand the thumb had the highest average individuation index. The index finger likewise had a high average individuation index, very close to that of the thumb. The little finger ranked third on average, whereas the middle finger and especially the ring finger tended to have the lowest individuation indexes. When the individuation indexes for the different digits of each hand of each subject were rank ordered from 1 (highest) to 5 (lowest), averaging across hands and subjects gave mean rankings for the thumb of 1.60, index finger of 1.60, middle finger of 3.63, ring finger of 4.65, and little finger of 3.50. These values are consistent with the common experience that the thumb and index finger are the most independent digits and the middle and ring fingers are the least independent.

Table 1.

Individuation indexes during self-paced movements

Digit	Individuation index of right hand		Individuation index of left hand
	Mean ± SD	Range	Mean ± SD	Range
Thumb	0.983  ± 0.013	0.947–0.999	0.991  ± 0.006	0.976–0.998
Index	0.982  ± 0.012	0.951–0.995	0.974  ± 0.022	0.928–0.999
Middle	0.937  ± 0.034	0.860–0.992	0.935  ± 0.039	0.851–0.995
Ring	0.907  ± 0.046	0.809–0.985	0.898  ± 0.060	0.735–0.985
Little	0.943  ± 0.042	0.825–0.994	0.945  ± 0.040	0.836–0.996

Such was not always the case for individual subjects, however. Figure3 shows the individuation indexes for instructed movement of each digit of the right hand of the 10 subjects (A) and of each digit of the left hand (B) and compares the medians and quartiles for the right and left hands (C). Each point in Figure 3,A and B, represents the mean of values computed from the four different epochs of a given movement performed by each subject. Although thumb movements often were the most highly individuated for a given subject, approximately half of the subjects showed a slightly higher individuation index on average for instructed movements of the index finger. Even the other fingers occasionally showed comparably high individuation indexes in particular subjects. Ring finger movements clearly tended to have the lowest individuation indexes. For all subjects except one (subject 10) the ring finger had the lowest individuation index in the right hand, and for all subjects except three (subjects 5, 8, and 10) the ring finger had the lowest individuation index in the left hand.

Fig. 3.

Individuation indexes during self-paced movements.A, B, Symbols connected by aline represent individuation indexes averaged over four epochs of instructed movements of the thumb (T), index (I), middle (M), ring (R), and little (L) finger of each subject's right (A) and left (B) hands.C, Box plots comparing the distributions across subjects display the median and quartiles of all values of the individuation indexes for the right (white boxes) and left (shaded boxes) hands. Each boxrepresents the 25th–75th percentile, and the horizontal line across the box is the median (50th percentile).Whisker lines extending above andbelow each box indicate the total range with the exception of small circles beyond thewhiskers that represent outliers >1.5 box lengths away from the bottom or top of thebox. Whereas the points shown inA and B each represent the average of values from four epochs of the same instructed movement, each of these four values contributed separately to the distributions shown inC. SUBJ, Subject.

Stationarity of human fingers

In addition to moving without any accompanying motion of the other fingers, an ideally independent finger would remain stationary during instructed movement of other digits. We used a stationarity index to quantify the degree to which a given digit remained still during instructed movements of the other digits (see Materials and Methods). The stationarity index for a given digit can vary from 1, if there is no motion of that digit during instructed movement of any other digit, to 0, if that digit moves as much as the instructed digit.

Table 2 presents the mean, SD, and range of the stationarity indexes for self-paced movements of each finger, averaged across subjects. These indexes indicate that, on average, the thumb remained most stationary during instructed movements of other fingers. The index finger and the little finger likewise remained relatively still when other fingers were moved, whereas the middle finger and particularly the ring finger tended to move the most and therefore had lower stationarity indexes. This rank order in the average stationarity index of the different digits did not apply consistently to the indexes for individual subjects, however. Figure4 shows that, as with the individuation index, the stationarity indexes of the middle and ring fingers showed the greatest variability among subjects.

Table 2.

Stationarity indexes during self-paced movements

Digit	Stationarity index of right hand		Stationarity index of left hand
	Mean ± SD	Range	Mean ± SD	Range
Thumb	0.994  ± 0.005	0.983–1.000	0.996  ± 0.005	0.974–0.999
Index	0.967  ± 0.021	0.891–0.997	0.973  ± 0.016	0.935–0.996
Middle	0.941  ± 0.031	0.864–0.991	0.925  ± 0.048	0.808–0.992
Ring	0.908  ± 0.054	0.755–0.982	0.905  ± 0.052	0.811–0.996
Little	0.943  ± 0.036	0.824–0.992	0.943  ± 0.035	0.864–0.996

Fig. 4.

Stationarity indexes during self-paced movements.A, B, Symbols connected by aline represent stationarity indexes averaged over four epochs of instructed movements of the thumb (T), index (I), middle (M), ring (R), and little (L) finger of each subject's right (A) and left (B) hands.C, Box plots comparing the distributions across subjects display the medians and quartiles of all values of the stationarity indexes for the right (white boxes) and left (shaded boxes) hands. Each boxrepresents the 25th–75th percentile, and the horizontal line across the box is the median (50th percentile).Whisker lines extending above andbelow each box indicate the total range with the exception of small circles beyond thewhiskers that represent outliers >1.5 box lengths away from the bottom or top of thebox. Whereas the points shown inA and B each represent the average of values from four epochs of the same instructed movement, each of these four values contributed separately to the distributions shown inC. SUBJ, Subject.

Nevertheless, digits with high individuation indexes tended to have high stationarity indexes as well. Indeed, within a hand, the different digit's individuation and stationarity indexes were significantly correlated (r_s = 0.74; p< 0.01; Spearmans' rank correlation; values pooled across hands and subjects). This suggests that similar factors both enable a specific finger to move without movement in the other fingers and enable that finger to remain still while other fingers move.

Are the fingers of the dominant hand more independent than those of the nondominant hand?

Introspection suggests that the fingers of one's dominant hand might be more independent than those of the nondominant hand. We used our data to test this hypothesis. Figure 3 shows that although some subjects had slightly higher individuation indexes for their dominant, right fingers (Fig. 3A) than for their nondominant, left fingers (Fig. 3B), the group median and quartiles for each digit of the right and left hands were quite similar (Fig.3C), as were their means and SDs (Table 1). An ANOVA-nested design (subject, hand, and finger), although confirming a clear main effect of finger (80, F = 19.4;p < 0.0001), showed no significant main effect of hand (10, F = 0.6; p > 0.80) on the individuation index. Performing a separate paired comparison of the individuation indexes for each digit of the right versus left hand revealed a significant difference only for the thumb, where the individuation index was higher for the left, nondominant thumb than for the right (p < 0.001 after Bonferroni correction for five tests, Wilcoxon matched pairs). Similarly, although some subjects had higher stationarity indexes for the dominant hand (Fig. 4, A vs B) and although for the group of 10 subjects the stationarity indexes varied significantly across the five digits (80, F = 18.3; p < 0.001, nested ANOVA), stationarity indexes were not significantly different in the right versus left hands (10, F = 0.6;p > 0.78). In the present task, the independence of the digits thus does not appear to differ systematically between the dominant and nondominant hands.

Effects of movement frequency

When asked to perform cyclical flexion–extension movements at a comfortable pace, our subjects chose frequencies of ∼2 Hz on average for each digit (Table 3). The measured movement frequencies of the middle and ring fingers were generally lower compared with that of the other digits. Moreover, self-paced frequencies of the middle and ring fingers of the dominant, right hand tended to be lower than were those of the middle and ring fingers of the left hand, although these differences were not significant after Bonferroni correction. When the same subjects performed movements externally paced at 3 Hz, the measured movement frequency was very close to 3 Hz for all digits of both hands (Table 3). Furthermore, the variability of movement frequency, as assessed by the group SDs, was reduced during externally paced movements at 3 Hz as compared with self-paced movements at 2 Hz, especially for the left hand. Metronome pacing at 3 Hz thus increased the frequency and decreased the variability of the cyclical flexion–extension movements performed by the subjects.

Table 3.

Measured movement frequencies

Digit	Self-paced		Externally paced at 3 Hz
	Right (mean ± SD), Hz	Left (mean ± SD), Hz	Right (mean ± SD), Hz	Left (mean ± SD), Hz
Thumb	2.10  ± 0.61	2.24  ± 0.63	2.99  ± 0.36	2.97  ± 0.20
Index	2.03  ± 0.65	2.20  ± 0.58	3.00  ± 0.37	2.97  ± 0.18
Middle	1.94  ± 0.64	2.19  ± 0.62	2.95  ± 0.38	2.94  ± 0.22
Ring	1.94  ± 0.56	2.17  ± 0.62	2.92  ± 0.39	3.00  ± 0.11
Little	2.17  ± 0.67	2.25  ± 0.66	3.02  ± 0.42	3.02  ± 0.12

Externally paced movements at 3 Hz were clearly less independent than were self-paced movements at 2 Hz. Reductions of the group individuation and stationarity indexes in the 3 Hz condition were evident for each digit of both the dominant hand and the nondominant hand (Fig. 5). As with the self-paced movements, there was no general effect by hand on the individuation or stationarity indexes during the 3 Hz condition (10, F = 0.8; p > 0.6; and 10, F = 0.7;p > 0.8, respectively, ANOVA-nested design in both cases). Therefore we pooled the data from the right and left hands to compare the independence of externally paced movements at 3 Hz versus self-paced movements. Two-way ANOVA (frequency and finger) on these pooled data confirmed that individuation indexes (1, F= 46.7; p < 0.001) and stationarity indexes (1,F = 49.9; p < 0.001) both were significantly lower during externally paced movements at 3 Hz.

Fig. 5.

Box plots comparing the independence of movements performed at a self-paced frequency (white boxes) versus movements paced by a metronome at 3 Hz (shaded boxes). A, Individuation indexes. B, Stationarity indexes. Box plots are described in Figure 3. Note the consistently lower indexes during the metronome-paced movements at 3 Hz. Data are pooled across both hands. I, Index; L, little;M, middle; R, ring; T, thumb.

The decrease in finger independence observed during externally paced movements at 3 Hz might have been related to the external pacing, the higher frequency, or both. To explore the effect of movement frequency on finger independence further, we examined the correlation between measured movement frequency and the individuation index during self-paced movements. Within- and between-subject variation provided a range of measured frequencies from ∼0.7 to 3.3 Hz for self-paced movements. Because of the effect of digit on individuation index, we tested the correlation between the individuation index and measured movement frequency separately for each digit, while pooling data values from each movement epoch across right and left hands and across subjects. Negative correlations—lower individuation indexes at higher movement frequencies—were found for all digits except the thumb. These correlations were significant (p < 0.05) for the four fingers, although the correlation for the middle finger was not significant after Bonferroni correction for five tests (uncorrectedp values, thumb p = 0.14; index fingerp < 0.001; middle finger p < 0.037; ring finger p < 0.001; little finger p< 0.001). These observations suggest that movement frequency per se has an effect on individuation: movements performed at higher frequencies tending to be less individuated than are those performed more slowly.

Interjoint coordination

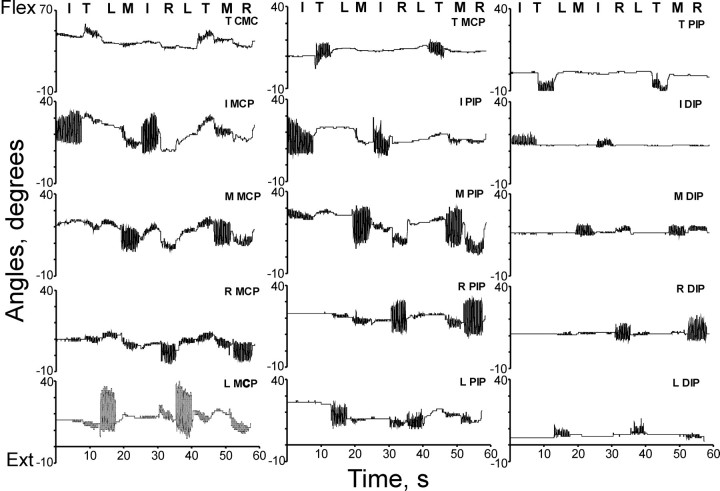
Data recorded with the instrumented glove enabled us to examine how the subjects moved the various finger joints. Figure6 shows glove sensor data on the simultaneous angular motion of 15 finger joints during the two 3.5 sec epochs of flexion–extension movements of each digit in a single recording from subject 5. Inspection of these data suggests that the distribution of angular motion across the three proximodistal joints varied from digit to digit. For the thumb, the least angular motion occurred at the CMC joint, the most at the MCP, and an intermediate amount at the PIP. For the middle finger, an intermediate amount of angular motion occurred at the MCP joint, the most at the PIP, and the least at the DIP. For the little finger, the most angular motion occurred at the MCP joint, an intermediate amount at the PIP, and the least at the DIP.

Fig. 6.

Data recorded simultaneously from 15 finger joint sensors of the instrumented glove for a single subject (number 5) during two 3.5 sec epochs of instructed flexion–extension movements for each digit. Although all data were recorded simultaneously,traces from different joints are shown in three columns representing the motion of the most proximal joints (left), the middle joints (center), and the most distal joints (right) of each digit, as indicated in the right corner above eachtrace. Rows of three traces thus represent the joints of each digit from the thumb at the top to the little finger at thebottom. The pseudorandom sequence of finger movements instructed to the subject is indicated above eachcolumn. CMC, Carpometacarpal;DIP, distal interphalangeal; I, index;L, little; M, middle; MCP, metacarpophalangeal; PIP, proximal interphalangeal;R, ring; T, thumb.

To permit comparison of the proximodistal distribution of angular motion in the different digits of the same subject, as well as across subjects, for the four epochs of each digit's movement recorded from each subject during self-paced movements, we calculated two complementary indexes. The PDI ranging from +1 to −1 summarizes the extent to which angular motion occurred at the digit's proximal, middle, or distal joint. The divergence index summarizes the degree to which motion occurred equally at all three joints (DIV = 1) versus only at a single joint (DIV = 0). Figure7 displays the average of these values for each digit of each subject's right (Fig. 7A) and left (Fig. 7B) hands. For all digits of both hands, the DIV index had midrange values, indicating that motion occurred at multiple joints (>0) but not equally at all joints (<1). At which joints the motion occurred is indicated by the corresponding PDI values. For example, the PDI of +0.5 for the little finger of subject 5's right hand (Fig.7A, Little, ▴) reflects that in this case the MCP joint moved more than did the PIP or DIP, as can be seen by inspection of Figure 6, bottom row. For the four fingers, considering the group of 10 subjects as a whole, PDI values skewed to the positive side of 0 indicate that the most angular motion occurred at the PIP joints followed by the MCP joints. For the thumb, the PDI values skewed to the negative side of 0 indicate that for the group as a whole the most angular motion occurred at the MCP (middle joint of the thumb), with less at the PIP (distal) and still less at the CMC joint (proximal). Thus for all five digits, the greatest angular motion occurred at the middle joint (PIP for the fingers and MCP for the thumb). The distribution of angular motion at the proximal and distal joints differed, however. The four fingers showed more motion at the proximal MCP than at the distal DIP (PDI > 0), whereas the thumb showed more motion at the distal PIP than at the proximal CMC joint (PDI < 0).

Fig. 7.

The DIV and PDI during self-paced movements. A, Right hand. B, Left hand. The DIV quantifies the extent to which the movements occurred in one joint versus being distributed across all three joints, whereas the PDI quantifies in which of the joints (MCP/CMC, PIP, or DIP) the motion mainly took place (see Materials and Methods). The figure displays mean data calculated over all four epochs of each instructed movement. The raw data from subject 5 (▴) for two of the four epochs of each instructed movement are shown in Figure 6.

Figure 7 also reveals considerable variability. That the proximodistal distribution of joint motion differed among subjects was confirmed by a main effect on the PDI and DIV by subject (9, F = 3.6;p < 0.03; and 9, F = 5.2; p < 0.008, respectively, nested ANOVA). The PDI and DIV were similar for right and left hands, however (10, F = 0.3;p > 0.98; and 10, F = 0.3;p > 0.97, respectively, nested ANOVA). Likewise, there was no effect on the PDI by the movement frequency (1,F = 2.6; p > 0.1, two-way ANOVA). The DIV, on the other hand, changed with movement frequency (1,F = 9.8; p < 0.002, two-way ANOVA): The DIV values were higher in the condition with externally paced movements at 3 Hz, indicating that the movements were more distributed across all three joints in this condition.

DISCUSSION

Independence of human finger movements

We found that even when asked specifically to move one digit without moving any other digits, normal human subjects produced low-amplitude motion in noninstructed digits simultaneous with the large-amplitude motion of the instructed digit. Consistent with common experience, instructed movements of the ring and middle fingers were associated with the greatest motion of noninstructed digits, whereas the thumb and index finger showed the highest degrees of individuation and stationarity, i.e., the greatest independence.

Our findings resemble those obtained in isometric paradigms involving much higher muscular forces. When subjects were asked to flex one finger so as to exert maximal isometric force at the fingertips, at the DIP joints or at the PIP joints, forces exerted by other fingers ranged from 2 to 52% of the force exerted by the instructed finger (Zatsiorsky et al., 1998). Without actively extending the other fingers away from contact at the flexor surface, subjects were unable to exert high forces in one finger without exerting substantial forces in the others. Our results suggest that the same is true in the low range of internal muscular forces needed to flex and extend the unloaded fingers. Normal subjects cannot generate the forces needed to move one finger isotonically through a substantial range without generating forces that simultaneously move adjacent noninstructed digits through a smaller range.

Most humans are right-handed, preferring to perform fine manipulations with the right hand. The preferred hand feels easier to control in complex movements. Such ease of control might result from a greater independence of finger movements in the preferred hand. In strongly right-handed subjects, however, we found no evidence of a systematic difference in finger movement independence between the right and left hands in terms of either individuation or stationarity. Our results are consistent with previous studies in which movements of single fingers were scored by visual observation (Kimura and Vanderwolf, 1970; Parlow, 1978). This suggests that handedness is not related simply to a greater independence of finger movements in the preferred hand. Indeed, tests of performance that are sensitive to handedness emphasize the speed of fine, accurate movements involving multiple digits simultaneously rather than finger independence alone (Annett, 1992; Jancke, 1996). Physiological differences in motor units and motor cortical activation on the dominant versus nondominant side (Schmied et al., 1994;Dassonville et al., 1997; Adam et al., 1998; Semmler and Nordstrom, 1998; Triggs et al., 1999) may not result in a difference in finger independence per se.

In contrast, we found a systematic decrease in the independence of finger movements externally paced at 3 Hz compared with self-paced movements at ∼2 Hz. Although we cannot exclude that the external pacing contributed to this difference, an effect of higher frequency seems most likely (Wessel et al., 1997). The greater motion of noninstructed digits during movements at higher frequency probably results in part from passive viscoelastic coupling between the digits; to cover the same distance at higher movement frequencies the instructed digit must be moved at higher velocity, increasing any velocity-dependent tendency to pull noninstructed digits along. To keep noninstructed movements as stationary as possible, however, the nervous system may generate additional muscle activity to counteract such viscoelastic forces, a function that in part may be mediated in the primary motor cortex (Humphrey and Reed, 1983). Greater functional activation of the M1 hand representation occurs during movements performed at higher frequencies (Rao et al., 1996; Sadato et al., 1996;Schlaug et al., 1996; Kawashima et al., 1999). Such frequency-dependent increases in M1 activity thus may result not only from the performance of more movement cycles per unit time and the production of higher muscular forces and rates of change of force to move through the same amplitude at higher velocities, but also from the additional muscular forces needed to stabilize noninstructed digits at higher movement frequencies (Schieber, 1990; Remy et al., 1994).

Factors affecting finger independence

The individuation and stationarity indexes measured in the present study varied considerably among our 10 normal human subjects. To some extent such intersubject variability may reflect differences in the long-term motor experiences of each subject. This variability also may result from intersubject differences in anatomic and physiological factors that affect the independence of the fingers, including biomechanical connections between the digits, functional organization of multitendoned finger muscles, and differences in the central inputs to spinal motoneuron pools.

Biomechanical interconnections between the digits come from many sources. The soft tissues of the web spaces couple adjacent fingers to some degree (von Schroeder and Botte, 1993). Better known are the juncturae tendinium of extensor digitorum communis (EDC) (Fahrer, 1981;von Schroeder et al., 1990). Just proximal to the MCP joints, these bands of connective tissue connect the EDC tendons running to adjacent fingers. In addition, the flexor digitorum profundus (FDP) tendons to the middle, ring, and little fingers typically are interconnected as they arise from the muscle belly and may also be interconnected within the palm by the bellies of the interosseous muscles that take origin from two adjacent FDP tendons (Fahrer, 1981). Furthermore, 20–30% of normal subjects may have “anomalous” interconnections, such as a tendinous band between flexor pollicis longus and the index finger portion of FDP (Linburg and Comstock, 1979; Austin et al., 1989;Gonzalez et al., 1997).

Finger movements also may be coupled by the organization of motor units in the multitendoned extrinsic finger muscles—FDP, flexor digitorum superficialis (FDS), and EDC. The extent to which these muscles contain a separate neuromuscular compartment acting on each finger versus compartments that act on multiple fingers simultaneously is an area of active investigation. In the extensor digitorum quarti et quinti of macaque monkeys (homolog of the human extensor digiti minimi), many single motor units have been found to act on both of the independent tendons to digits 4 and 5 (Schieber et al., 1997). In the human EDC, the tension of single motor units is distributed to multiple fingers more broadly than can be attributed to mechanical interconnections between the tendons (Keen and Fuglevand, 1999). In the present study, our subjects produced more motion at the PIP joint than at the MCP or DIP. We speculate that this may reflect a greater finger selectivity of motor units in FDS, which act across the MCP and PIP joints, compared with motor units in FDP, which act across the MCP, PIP, and DIP joints.

Finally, the motoneuron pools innervating different finger muscles receive considerable shared central input. As revealed by short-term synchronization between single motor units in different human muscles, intrinsic and extrinsic muscles acting on different fingers receive shared inputs (Bremner et al., 1991a,b). Shared central inputs have been shown in monkeys to come from spinal interneurons, rubrospinal neurons, and corticospinal neurons (Fetz and Cheney, 1980; Buys et al., 1986; Mewes and Cheney, 1991, 1994; Fetz et al., 1996; McKiernan et al., 1998; Perlmutter et al., 1998). Such shared inputs may account for the observation that as normal human subjects flex the tip of one finger, FDP motor units acting on adjacent fingers are recruited shortly after motor units acting on the finger being flexed (Kilbreath and Gandevia, 1994). Indeed, single neurons in the monkey M1 hand representation typically discharge during individuated movements of several different digits (Schieber and Hibbard, 1993; Poliakov and Schieber, 1999).

Human subjects demonstrated substantially higher individuation and stationarity indexes than those described previously in monkeys (Schieber, 1991). Species differences may shed additional light on finger independence. Pertinent differences may be found between the extrinsic multitendoned finger muscles of monkeys and humans (Serlin and Schieber, 1993). In macaques the mechanical interconnections among the tendons of FDP are more extensive than in humans, and the distal tendon to the thumb arises from FDP, with no separate flexor pollicis longus (FPL). Macaques also have two multitendoned finger muscles (extensor digitorum secundi et tertii and extensor digitorum quarti et quinti) that are homologous to monotendoned muscles in humans (extensor indicus proprius and extensor digiti quinti, respectively). These differences suggest that the greater independence of finger movements in humans arises in part from the splitting of a separate muscle belly and tendon in some instances (FPL) and from the loss of a tendon from multitendoned muscles in others (extensor indicis proprices and extensor digiti quinti), enhancing the independence of the thumb and index and little fingers in particular. Additional differences may exist in the M1 hand representation. Although humans and monkeys both show extensive overlap of the M1 territory activated during movements of different fingers (Schieber and Hibbard, 1993; Sanes et al., 1995), humans may have a somewhat more evident gradient of representation of the radial digits laterally in M1 and the ulnar digits medially (Grafton et al., 1993; Kleinschmidt et al., 1997; Schieber, 1999). The greater finger independence of humans compared with monkeys thus results in part from differences in the passive biomechanical connections among tendons, in the organization of motor units and muscle bellies, and in the M1 hand representation. Nevertheless, in agreement with the observation that in purposeful movements humans rarely if ever need to move each finger independent of the others, even human finger movements are not completely independent.