Four-Dimensional Neuronal Signaling by Nitric Oxide: A Computational Analysis

Abstract

Nitric oxide (NO) is now recognized as a transmitter of neurons that express the neuronal isoform of the enzyme nitric oxide synthase. NO, however, violates some of the key tenets of chemical transmission, which is classically regarded as occurring at points of close apposition between neurons. It is the ability of NO to diffuse isotropically in aqueous and lipid environments that has suggested a radically different form of signaling in which the transmitter acts four-dimensionally in space and time, affecting volumes of the brain containing many neurons and synapses. Although “volume signaling” clearly challenges simple connectionist models of neural processing, crucial to its understanding are the spatial and temporal dynamics of the spread of NO within the brain. Existing models of NO diffusion, however, have serious shortcomings because they represent solutions for “point-sources,” which have no physical dimensions. Methods for overcoming these difficulties are presented here, and results are described that show how NO spreads from realistic neural architectures with both simple symmetrical and irregular shapes. By highlighting the important influence of the geometry of NO sources, our results provide insights into the four-dimensional spread of a diffusing messenger. We show for example that reservoirs of NO that accumulate in volumes of the nervous system where NO is not synthesized contribute significantly to the temporal and spatial dynamics of NO spread.

A role for nitric oxide (NO) as an intercellular signaling molecule in the nervous system was first suggested by Garthwaite et al. (1988), and this has been confirmed by numerous subsequent studies, although NO remains an enigmatic neurotransmitter (for review, see Hölscher, 1997). Although NO is now a recognized neurotransmitter, it is the first in an entirely novel class with properties that have opened new dimensions in our thinking about how information is transmitted by neurons in both vertebrates and invertebrates (Gally et al., 1990; Edelman and Gally, 1992; Gelperin, 1994; O'Shea et al., 1998).

Traditionally neurotransmission is thought to be spatially and temporally restricted and from the presynaptic to the postsynaptic neuron. In other words, conventional synaptic transmission is essentially two-dimensional. However, because NO is a very small and nonpolar molecule, it will spread in three dimensions away from a site of synthesis regardless of intervening cellular or membrane structures (Lancaster, 1994; Wood and Garthwaite, 1994). Another feature of NO signaling is suggested by the fact that the neuronal isoform of nitric oxide synthase (nNOS) is a soluble enzyme and thus likely to be distributed throughout a neuron's cytoplasm. The whole surface of the neuron is therefore a potential release site for NO, in marked contrast to conventional transmitter release, which is restricted to the synaptic zone. These properties allow NO to act without the need for presynaptic specializations, and its action is not necessarily confined to the immediate postsynaptic neuron (Bredt and Snyder, 1992; Hartell, 1996; Park et al., 1998). This suggests a radically different form of signaling in the brain in which NO acts four-dimensionally in space and time, affecting volumes of the CNS perhaps containing many neurons. Thus the three-dimensional morphology of the NO source and the presence of structured NO sinks are likely to have a major influence on the shape and longevity of an NO “cloud” in the brain (O'Shea et al., 1998; Philippides et al., 1998). An accurate structure-based model of NO spread is for all these reasons essential in providing a realistic theoretical framework for evaluating the neuronal signaling capacity of NO.

In this paper we show that modeling continuous structures with realistic dimensions can provide insights into a number of salient functional questions that arise in the context of volume signaling. The most obvious of these is just how large a volume can be affected by a diffuse signal from a NO-generating neuron or group of neurons. Linked to this is the question of how long it will take for different parts of such a region to be affected. In short, how does the morphology of the source-neurons affect the dynamics of the spread? It is also important to consider how and to what extent the spread of NO is influenced by barriers to diffusion as might be represented by a blood vessel, for example. In addressing these issues we demonstrate how to model diffusion of NO from any arbitrary structure and in this way provide new insights into the spatial and temporal properties of the NO signaling system.

MATERIALS AND METHODS

Modeling NO diffusion from a point-source. The dynamics of diffusion are governed by the modified diffusion equation:

$$\frac{\partial C}{\partial t}-D{\nabla }^{2}C=-\lambda C$$ Equation 1

where C is concentration and D is the diffusion coefficient (Crank, 1980). The term on the right-hand side is an inactivation function, used to model the loss of NO through various oxidation reactions and binding to heme, for example. This has been taken to be exponential decay because there is no real data to suggest any other function, and the half-life of NO is therefore given by t_1/2 = ln(2/λ). To obtain the solution for an instantaneous burst of synthesis from a point-source positioned at the origin of some coordinate system, we envision an amount S_t = 0 of NO being deposited instantaneously at the origin at time t = 0. We then solve the diffusion equation under this initial condition, which gives us the following equation describing the evolution of the concentration of NO from a point (Crank, 1980):

$$C_{\text{inst}}(r,\theta ,\phi ,t)=\frac{S_{\text{t}=0}}{8(\pi \text{Dt}{)}^{3/2}}exp\left(\frac{-r^2}{4\text{Dt}}\right)e^{-\lambda \text{t}}$$ Equation 2

where C_inst(r, θ, φ, t) is the concentration of NO at time t at a point (r, θ, φ), defined in a spherical polar coordinate system (i.e., where r is the distance to the origin, θ is the azimuth, and φ is the angle of elevation).

The solution for a point-source that emits NO continuously is derived from the solution for an instantaneous source in the natural way, via the principle of superposition of linear solutions (Crank, 1980). First we define the “strength” of a source to be its rate of NO production. Next we define the concentration at time t′ and distance r from the origin, attributable to an instantaneous source of unit strength to be f(r, t′). Thus, if a source emits NO continuously at a rate governed by S(t), we have:

$$C_{\text{cont}}(r,t)=\underset{0}{\overset{t}{\int }}S(t-t^{\prime })f(r,t^{\prime }){\text{dt}}^{\prime }.$$ Equation 3

This can be understood by seeing that the contribution at time t′ ≤ t is attributable to an instantaneous pulse of NO t′ sec previously, with S(t − t′) the amount of NO per second produced at time t − t′ (i.e. t′ sec earlier). Thus, in Equation 3, the most recent pulses of NO are responsible for the lower limit of the integration, whereas the oldest pulses account for the upper limit. Similarly, we can derive the solution for times after a point-source that emitted NO continuously has stopped synthesizing. If the source synthesizes for T sec and, as before, the instantaneous solution is f(r, t′), then the concentration at a distance r from the source, t₁ sec after it has stopped synthesizing is:

$$C_{\text{burst}}(r,t_1+T)=\underset{t_1}{\overset{t_1+T}{\int }}S(t_1+T-t^{\prime })f(r,t^{\prime }){\text{dt}}^{\prime }.$$ Equation 4

This approach is valid because the diffusion equation is linear, and the principle of superposition of linear solutions therefore applies. The approach, however, relies on symmetry of the structure for tractability, and generally, radial symmetry is needed for this technique to be practical. If this is not the case other techniques must be used, as detailed below.

Modeling NO diffusion from a symmetrical three-dimensional structure. To model the spread of an amount of NO produced instantaneously throughout a continuous structure, we use techniques developed in the field of thermodynamics (Carslaw and Jaeger, 1959) that are readily applicable to modeling diffusion. The main technique used in this field is to build up solutions for complicated structures from summation of contributions from point-sources distributed throughout the structure. Of course, we are not implying that there is an infinite number of NO sources in the structure, but they are small enough that we are justified in imagining that they are uniformly distributed throughout the source with some density ρ. Hence for a spherical source of radius a, for instance, the method is to sum the contributions to the concentration at a point in space P, from all the points within the sphere. A step-by-step description of this process is given in the Appendix (see online version at http://www.jneurosci.org) with the following terms generated for the structures under consideration.

For a solid spherical source of radius a (see note in the Appendix) the concentration is given by:

$$C_{\text{SolidSphere}}(a,r^{\prime },t)=Q\rho e^{-\lambda \text{t}}\left[\frac{1}{2}\left(\text{erf}\left(\frac{a+r^{\prime }}{2\sqrt{\text{Dt}}}\right)+\text{erf}\left(\frac{a-r^{\prime }}{2\sqrt{\text{Dt}}}\right)\right)-\frac{1}{r^{\prime }}\sqrt{\frac{\text{Dt}}{\pi }}\left(exp\left(\frac{(a-r^{\prime }{)}^2}{4\text{Dt}}\right)-exp\left(\frac{(a+r^{\prime }{)}^2}{4\text{Dt}}\right)\right)\right].$$ Equation 5

For a hollow sphere of inner radius a and outer radius b:

$$C_{\text{HollowSphere}}(a,b,r^{\prime },t)=C_{\text{SolidSphere}}(b,r^{\prime },t)-C_{\text{SolidSphere}}(a,r^{\prime },t).$$ Equation 6

In the above equations, Q is the amount of NO produced per second from a single NO producing unit. Thus Qρ gives the concentration of NO produced per second (in units of moles per volume per second) and is a parameter that is independent of the particular shape of the structure being studied and so can be determined by empirical experiments and used throughout [as in Wood and Garthwaite (1994)].

These “instantaneous” solutions can then be integrated over the appropriate time intervals to get the solutions for the evolution of concentration of NO synthesized for a finite time interval, in the same way as for the point-source (as in Eq. 3 and 4). Here, however, because the volume term has already been implicitly factored into the integrals, we replace Qρ, the concentration/second at each instant, with S̃(t), a function that, for each time t, gives the value of Qρ t sec after the start of synthesis. Traditionally, instantaneous switch on and off of synthesis has been assumed, meaning that S̃(t) will be a square wave with maximum value of Qρ. This has the advantage of simplicity because S̃(t) is now constant and can be moved outside the integral in Equations 3 and 4. Obviously, such a mechanism of release is not strictly biologically plausible, but in the absence of experimental data on the kinetics of nNOS activationin vivo, it was thought that this was as good a first approximation as any other.

However, because we are using numerical integration throughout, it is no more work to use a more complicated strength function. For instance, if we were to assume that the amount of NO released were related closely to the amount of depolarization caused by an action potential, we could use a strength function with a sigmoidal rise to a peak synthesis rate of Qρ and exponential fall from the peak, with both rise and fall phases taking the same lengths of time. Such a function (Spike(t)) is described in the Appendix and used as S̃(t) in Results with the duration of the spike, i.e., the duration of the burst of synthesis (later referred to as the “burst-length”) set to 50 msec. When several spikes are generated, the function is simply made up of the requisite number of spikes, generated with the previous function, with a pause of 500 msec between each one.

Modeling diffusion of NO from an irregular three-dimensional structure. In cases in which the required symmetry does not exist, or when the amount of numerical integration needed is prohibitive, we can use difference equation techniques. One method recommended for use in diffusive problems is the Alternating Direction Implicit (ADI) method for two space dimensions with the Crank–Nicholson (CN) differencing scheme that, unlike simpler schemes, allows for examination of the solution at all time-steps (Press et al., 1971;Mascagni, 1989; Ames, 1992). This method is fast, second-order accurate in space and time, arbitrarily convergent, and thus unconditionally stable (Ames, 1992). This means that it is not subject to the stability limitation of explicit schemes where the maximum allowable time-step is roughly the diffusion time across a cell (for more detail see the online Appendix). We implemented this method with a cell size of 0.5 μm, on a square grid of size 1000 × 1000 and time step 1 msec with the boundary condition that the concentration gradient is flat (i.e., equal to 0) at the edge of the grid.

The equation to be approximated is:

$$\frac{\partial C}{\partial t}-D{\nabla }^{2}C=Source(\vec{x},t)-Sink(\vec{x})C-\lambda C$$ Equation 7

Here Source(x⃗, t) = Qρ for points inside the source during synthesis and is zero otherwise andSink(x⃗) = η for points inside sinks and λ for all other points where a sink is a local high concentration of an NO-binding moiety such as a heme-protein.

Parameter values. The value of D in an aqueous salt solution is given as 3300 μm²/sec (Malinski et al., 1993). It is reasonable to assume that it will not be significantly affected in a lipid or protein aqueous medium because of the very small molecular dimension and nonpolarity of NO. The value of the decay rate λ = 0.1386 sec⁻¹ gives a half-life of 5 sec, which is that recorded for dissolved NO perfused over living tissues in oxygenated saline solution (Moncada et al., 1989). Although other rate constants can be used, these are basically dependent on the oxidizing environment in which NO is diffusing. If this is anything other than a fairly simple environment, with a t_1/2 ≪ 5 sec, it should be treated separately, whereas anything longer has hardly any effect over the spatial and temporal scales examined here (Wood and Garthwaite, 1994). We have thus made the simplifying assumption that the background half-life is 5 sec. For strong NO sinks we used a decay rate η = 693.15 sec⁻¹ equivalent to a half-life of 1 msec, which was chosen as a conservative value based on the rate of NO uptake by a nearby hemoglobin-containing structure such as a blood vessel (Carlsen and Comroe, 1958).

The value of the synthesis rate Qρ is a more open question, with several values having been determined with the use of several different models. Before these are discussed, however, it should be noted that the effect of this parameter is purely one of scale because it is a constant that simply multiplies the concentrations. Thus, whatever the actual value of this parameter, the qualitative nature of the results is unchanged, and it is easy to see what effect a different value would have simply by rescaling. There are two determinations of Qρ that have underpinned NO diffusion modeling to date, both of which are based on the experimental findings of Malinski et al. (1993). Vaughn et al. (1998b) chose to use the in vivo determination, which is a more complicated situation to model. We, like Wood and Garthwaite (1994), base our model on the in vitro determination. Unlike Wood and Garthwaite (1994), however, we have used a true structure-based analysis. For this task, we used a hollow sphere of inner radius 6, outer radius 10, with the result that a value for Qρ of 1.32 × 10⁻⁴mol · μm⁻³ · sec⁻¹ is needed to generate a maximum concentration of 1 μm on the surface of the sphere. Significantly, this result is ∼300 times less than that used previously. Moreover, the peak concentration is attained after ∼14 sec, a result that agrees closely with the empirical data of Malinski et al. (1993) but was unexplained when the point-source model was utilized (Lancaster, 1997). This value of Qρ was used for all results apart from the first section.

Computational methods. The symmetrical solutions all required numerical integration [for an introduction, see Press et al. (1971)]. This was performed by the “quad8” function in Matlab, which uses an adaptive Newton Cotes 8 panel rule (Press et al., 1971) to a relative accuracy of 0.1%. Solutions were modified for cases when the lower limit of integration was <1 msec for the sphere and the point source. The reasons for this and a detailed description of the modifications are provided in the Appendix. The difference equation was written in C.

RESULTS

Point-source versus structure-based modeling

There are a number of problems associated with attempting to model the spread of NO that is assumed to be generated at a point-source. It is not difficult to see intuitively that problems might arise from the fact that a point-source is by definition singular. This means that it occupies zero volume, and the concentration of NO at the source during synthesis is therefore infinite. This represents a fundamental problem that is carried through to solutions of the equation outside the source after synthesis.

It could and has been argued that this problem might be avoided if we ignore solutions to the diffusion equation at or near the source, close to the time of synthesis. One could assume, for example, that the source was actually a “virtual sphere” of some volume that could be treated as if a point-source were located at its center. In this way, we would have a region inside of which the concentration could be deemed indeterminate, but we would have a volume for the source to occupy and thus a source density. This seems to be the style of reasoning taken by Wood and Garthwaite (1994) and Lancaster (1994) and may be justified because the solution for a sphere can be shown to reduce to the point-source solution for vanishingly small radii (Carslaw and Jaeger, 1959). Thus we may have a good approximation, provided that the sphere is small enough relative to the speed of diffusion and provided we do not need to know the concentration of NO in the interior of the virtual sphere. Such an approach, however, glosses over the problem because, as the diffusion equation is continuous in both space and time, we cannot expect its solution simply to jump from being implausible at the spatiotemporal origin to being well behaved somewhere else. Nevertheless, because others have used this type of approach, we present results for the virtual sphere around a point-source and make a direct comparison with a very different approach in which the diffusion equation is solved for a source with a “real” spherical structure.

For a correct and fair comparison, both sources must be equivalent in strength. Thus, the source strength (S_t = 0 in Eq. 2) has been set using:

$$S_{\text{t}=0}=Q\rho \times VolumeofVirtualSphere=Q\rho \frac{4}{3} \pi r^3,$$ Equation 8

with r being the radius of the virtual sphere under consideration. It should be noted, however, that there is a problem inherent with this approach because we have had to assign a volume to a dimensionless entity. Thus modeling two different bodies of equal volume in this manner, for instance a sphere and an ellipsoid, would yield identical results.

The results of this comparison are presented in Figure1. Examining Figure 1Awe see that the error in the solution is tolerable for the speed of diffusion of NO and the size of sphere (0.5 μm) used by Wood and Garthwaite (1994). As we compare the results for larger spheres, however, we can see that the two solutions look very different from each other, and radically different results are generated. Importantly, for larger spherical sources the distance at which the NO concentration is still potentially effective is much greater for the real spheres. For example, a real spherical source with radius 25 μm affects ∼3.5 times the volume affected by a virtual sphere.

Fig. 1.

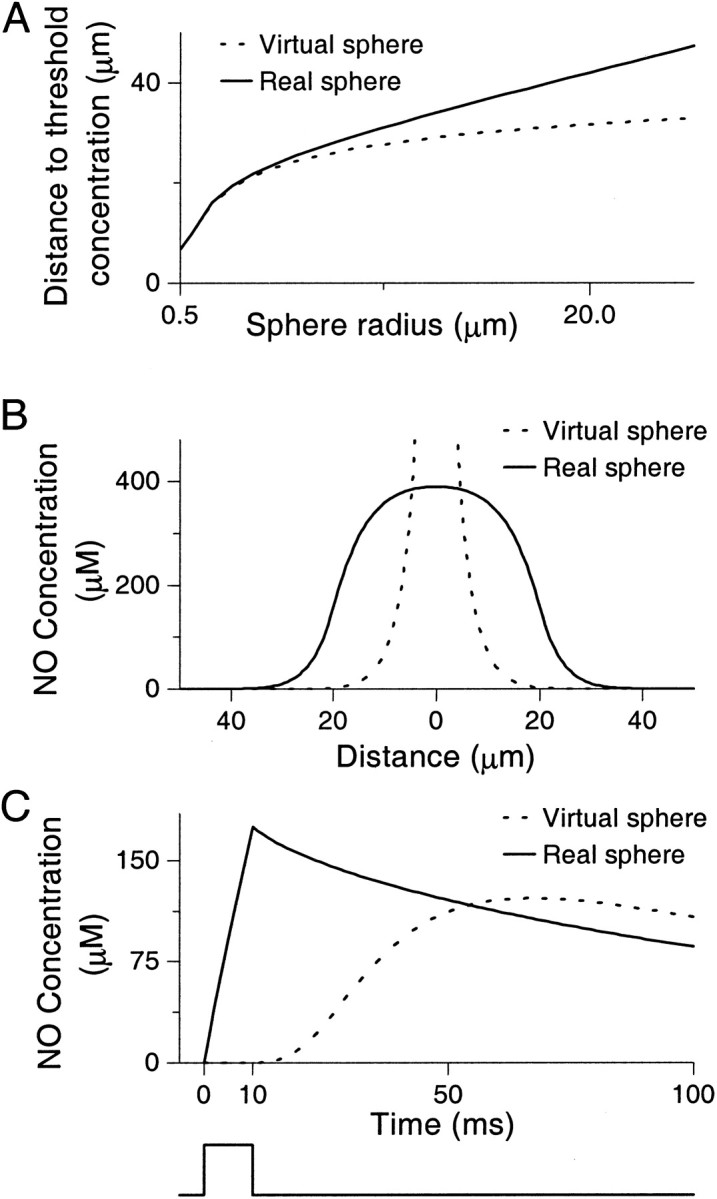
Comparison of real and virtual spheres.A, Plot of the distance at which the concentration of NO drops below 0.1 μm (the threshold concentration). This concentration is about the same as the equilibrium dissociation constant for soluble guanylyl cyclase (an NO receptor), 0.25 μm (Stone and Marletta, 1996). Thus, this distance defines the area within which NO can have a functional role (Vaughn et al., 1998a). Both virtual and real sources have been set to have the same source strength. The solutions give similar results for “spheres” of radii <5 μm but diverge for greater radii.B, Concentration of NO against distance from the center of virtual and real spheres of radius 20 μm measured at the end of a 10 msec burst of synthesis. Both sources have been set to have the same strength. Note the very different solutions both inside (where the point source has infinite concentration at the center) and outside the sphere. C, Concentration of NO measured at 35 μm from the center of virtual and real spheres of radius 35 μm for a 10 msec burst of synthesis. As in B, both sources have been set to have the same strength. The difference between the two solutions is clear, with the point-source producing its peak concentration around time t = 70 msec, well after synthesis has finished. The square wave shown beneath the figure represents the strength function.

Figure 1B highlights another issue associated with the point-source approach: namely, how can the concentration inside the sphere be determined? During synthesis the concentration is infinite at the spatial origin (i.e., at the center of the sphere). We cannot therefore use the concentration at the center, and to pick another point at which to measure the concentration is arbitrary. We could use the concentration at the surface of the sphere, but this can be seen to be lower than that of the interior and hardly answers the question of what the interior concentration is. We could use an average value over the interior of the sphere, but this would be infinite because of the singularity at the center. Thus we have to conclude that the concentration inside the sphere is indeterminate. Finally, Figure1C shows that the concentration at the surface of the neuron attains its maximum value significantly after synthesis has stopped rather than at or very near the end of synthesis as should be seen, and indeed is seen in the structure-based model (real sphere).

Diffusion from cell body cytoplasm

The method used in the previous section to generate results for the solid sphere can be generalized to obtain the solution for simple symmetrical structures of greater biological interest. For example, we can solve for structures such as a neuronal cell body in which NO is synthesized in the cytoplasm but not in the nucleus. We have therefore examined the solution for a hollow spherical source of inner radius 50 μm (the nucleus) and outer radius 100 μm (cell body). These dimensions, although large for many neurons especially in vertebrates, do correspond to the dimensions for some identified giant molluscan neurons whose cell bodies are known to synthesize NO. In fact our emphasis on these neurons stems from our empirical in vitro data showing that such neuronal cell bodies can mediate volume signaling (Park et al., 1998). Even allowing for the shortcomings of the point-source approach, obtaining a meaningful solution for such a structure using this method would be impossible.

Of course we are not suggesting that neurons are perfectly spherical but rather that hollow spheres are a useful approximation for neurons. They can tell us, for example, about the importance of morphological irregularities. For instance, if one had a cell that was mainly spherical but had a lot of small-scale variability in its outer structure, we could use two ideal models, one with the outer radius set to the minimum radius and the other with the outer radius set to the maximum. In this way analytical solutions can be used to determine whether the irregularity has a significant effect. In fact, we have seen that because of the speed of diffusion of NO, small-scale irregularities (±2.5% of source size) have a negligible effect. Using such an approach we can also investigate the sensitivity of the diffusional process to other parameters, such as boundary conditions whose complexity makes the analytical solution intractable. Thus, if we have to make simplifications to a model to render derivation of the analytical solution tractable, we can tell whether these simplifications generate gross inaccuracies.

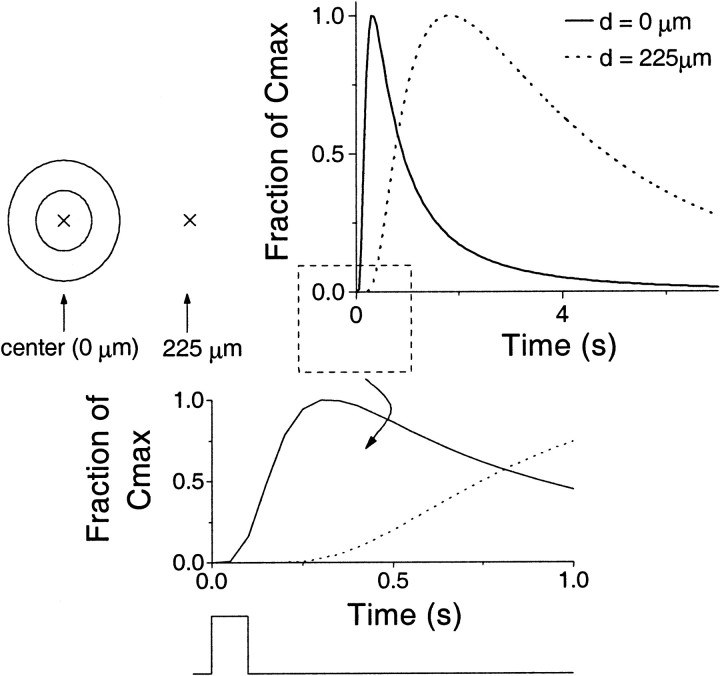
The solution for the hollow sphere was examined for a burst of synthesis of duration 100 msec, with results shown in Figures2 and 3. There are two new points of note to be brought out from these results, namely the length of time for which the concentration in the center of the sphere remains high and the significant delay between the start of synthesis and the rise of concentration for points distant from the source (Fig. 2).

Fig. 2.

Concentration of NO plotted against time after synthesis for a hollow spherical source of inner radius 50 μm and outer radius 100 μm for a 100 msec burst of synthesis. Here thesolid line depicts the concentration at the center of the cell (0 μm), whereas the dotted line shows the concentration at 225 μm from the center. Because the absolute values attained at the two positions differ from one another markedly, the concentration is given as a fraction of the peak concentration attained. These peak values are 7.25 μm(center) and 0.25 μm at 225 μm. The cell and the points at which the concentration is measured are depicted to theleft of the main figure. Note the high central concentration, which persists for a long time (above 1 μmfor ∼2 sec). Also, there is a significant delay to a rise in concentration at distant points, which is more clearly illustrated in the expanded inset. The square wave shown beneath theinset represents the strength function.

Fig. 3.

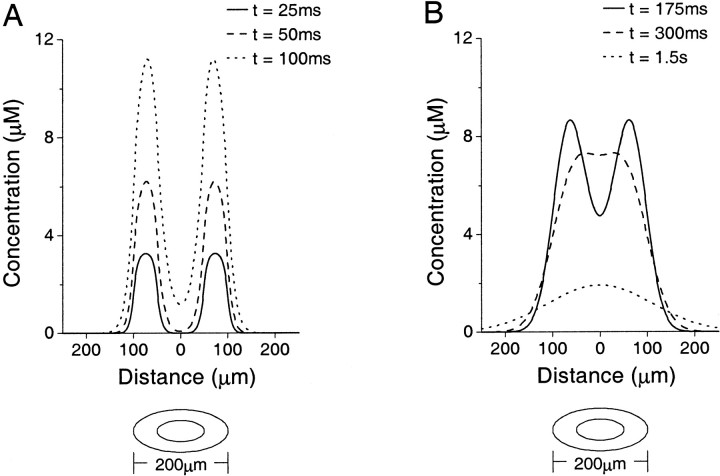
Concentration of NO plotted against distance from the center of a hollow spherical source of inner radius 50 μm and outer radius 100 μm for a 100 msec burst of synthesis starting at time t = 0. The graphics underneath each plot depict the structure. A, Concentration of NO at times t = 25, 50, and 100 msec, two time points during and one at the end of synthesis. B, Concentration of NO after synthesis at times t = 175, 300, and 1.5 sec. The reservoir effect after the end of synthesis is clearly seen as the centrally accumulated NO is trapped by the higher surrounding concentrations (see Diffusion from cell body cytoplasm in Results).

The cause of these phenomena can be seen if we examine Figure 3. During the synthesis phase, we see that the concentration outside the cell rises very slowly. In the nucleus, however, a “reservoir” of NO starts to build up (Fig. 3A), albeit relatively slowly when compared with the rise in the synthesizing area (the cytoplasm). After the end of synthesis, this reservoir continues to fill up for ∼200 msec as the NO in the cytoplasm diffuses away from its point of origin to points of lower concentration in the nucleus. However, the concentration outside the cell still rises slowly because of the vastly bigger volume. Later, the situation changes somewhat, because we are now in the position at which the concentration in the nucleus is roughly equal to the concentration in the cytoplasm, giving a wide flat peak to the concentration profile. Until this point, the NO that had diffused into the center was “trapped” and could not be dissipated because of the higher concentration present in the cytoplasm. Now though, we see this large reservoir spreading away from the cell in a wave of high concentration that finally starts to raise the distal concentrations to significant levels. However, the concentration at the center remains high and does not spread outward very quickly because here the concentration gradient is virtually flat, meaning that there is very little diffusive pressure on the NO in this area. It is this effect that produces the unexpected time delay at distant points.

Examination of the concentration at 225 μm from the center of the cell (Fig. 2) shows that it remains low until ∼400 msec after synthesis has stopped. It peaks shortly afterward and stays relatively high for a relatively long period. This has implications for the temporal dynamics of NO signaling in a neurobiological context. For example, suppose there was an NO-responsive neuron at a distance of 225 μm from the center of the source neuron. Assuming a threshold concentration of 0.1 μm (see legend to Fig.1A), this neuron would not be affected until 600 msec after the end of synthesis and would continue to be affected for a period of ∼4 sec. Such a process could be used to introduce a time delay in NO-mediated neural signaling. The high central concentration also has implications for neural signaling because the effect of the NO synthesizing event remains long after this event has passed.

There is another interesting factor seen in these results, namely the temporal dynamics of the solution in the cytoplasm during synthesis. Here it is enough to note that the concentration continues to rise for a very long time of continuous synthesis before a steady state is approached. Thus, although much of the work using point-source models has considered solutions at steady state, such considerations may be inappropriate in the context of real structures.

Effect of neuron size

The effects reported above are generated by the relatively large dimensions typical of some molluscan neurons. Questions therefore arise as to whether similar phenomena are present for smaller neurons such as those found in mammalian brains. To examine the effect of cell size we looked at the maximum region around a source that could be affected via the NO–cGMP signaling pathway during and after the generation of NO from hollow spherical sources of various sizes. The sources are directly comparable because they share the same ratio of inner (nucleus) and outer (cell) radii (Fig.4). The affected region is defined by the volume within which the concentration is above the equilibrium dissociation constant for the NO receptor soluble guanylyl cyclase (Stone and Marletta, 1996). For this analysis it is clear that the relative rather than the absolute affected region is critical. This is because the important comparator is the number of potential neuronal targets within the affected region, and this depends on their size. A similar argument applies when considering the effect of neuron size on delay. Clearly, the absolute delays to the threshold distance are different for each source. Thus the appropriate comparator for delay is delay relative to the time taken for NO traveling at some structure-independent constant speed to reach threshold distance, a variable that is directly proportional to the threshold distance.

Fig. 4.

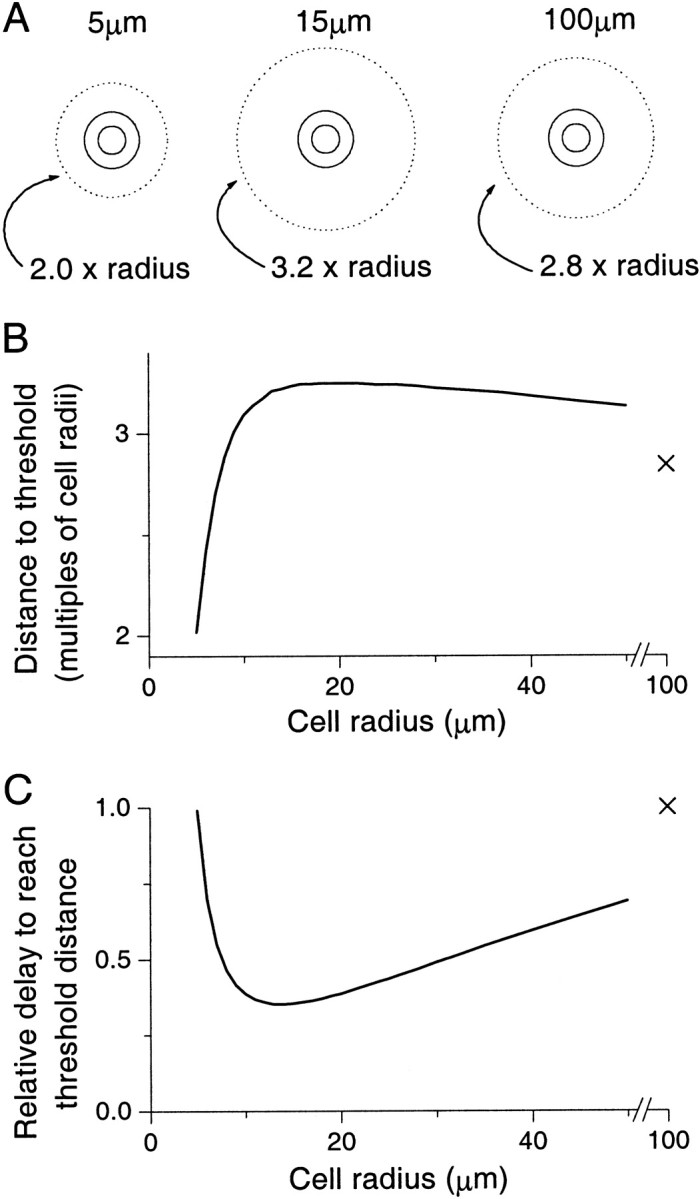
Maximum affected region after a 100 msec burst of synthesis from hollow spherical cells of varying outer radii. The affected region is defined as that which experiences a concentration of NO above 0.1 μm: the threshold concentration (see Fig.1A legend). This region defines a limit outside which the NO signal has no effect via the NO–cGMP signaling pathway. In all graphs the radius that is referred to is the outer cell radius, with the radius of the nucleus being half the cell radius. A, Maximum affected region for cells of outer radii 5, 15, and 100 μm. The dotted line denotes the extent of the affected area, whereas the solid lines show the inner and outer radii of the cells. For comparison, the cells have all been drawn the same size, with the affected regions shown in multiples of the source radius. Note that the 15 μm cell is the one that affects the greatest relative volume. B, Threshold distance in multiples of the outer radius plotted against the cell radius. The threshold distance is defined as the distance from the center of the cell at which the affected volume is maximized over time. The X shows the data point for a 100 μm cell. C, Relative delay until the affected region reaches its maximum extent against the cell radius. The X again denotes the data point for a 100 μm cell. The relative delay is defined as being proportional to the time after the start of synthesis at which the threshold distance (and thus the affected volume) is maximized relative to this distance. The relative delays are thus in arbitrary units and shown as a fraction of the maximum value, which is achieved for the 100 μm cell. Here we see that the shortest delay is generated by cells (15–20 μm) that have roughly maximal affected regions, whereas delays for the smallest and largest cells (5 and 100 μm) are the longest.

The relationship between neuron size and the volume affected at any one time was counter-intuitive (Fig.4A,B). Thus, surprisingly, the neurons that affect the largest volume are those with outer radii in the range 15–20 μm and not those with radii of giant molluscan neurons (∼100 μm). In fact, over the wide range of neuron radii from 5 to 100 μm, the relative affected region, in terms of multiples of the source radius, changes surprisingly little. Thus a 5 μm neuron affects 2 times its radius, a 15 μm neuron 3.2 times its radius, and a 100 μm neuron 2.8 times its radius (Fig.4A,B). For sources substantially smaller than 5 μm, the affected region approaches the source size. Nevertheless, even very small sources may affect larger regions if they act in concert. This is because small sources acting together in proximity behave as if they were a single larger source with the attendant temporal and spatial phenomena associated with a source of the combined shape and size. An example of this is provided by endothelial cells that act as a multicellular complex of many very small cells (Vaughn et al., 1998a).

The influence of the cell size on the temporal aspects of the NO spread is approximately the converse of the effect on the spatial dynamics (Fig. 4C). Here we see that those neurons that affected the greatest region (15–20 μm radius) generate the shortest relative delay, whereas the small (∼5 μm) and large ones (∼100 μm) that affected relatively smaller regions generate the longest. Indeed, the smallest delay is only ∼35% of the longest, and it is also somewhat surprising to see the similarity in the delays for the smallest and largest neurons. Thus the delay between initiation of synthesis and the maximum affected radius being reached is significant and is influenced by neuron size in quite a complex manner that is not intuitive.

Coupling NO synthesis to electrical activity in a neuron

In the preceding results on the concentration of NO within the source (Fig. 1C), it can be seen that there is a very sharp change between synthesis and nonsynthesis of NO that is physically implausible. This is a consequence of using a square wave to represent the synthesis of NO. To counteract this artifact, a smoother strength function (described in Materials and Methods) has been used. This has the effect of smoothing out the sharp corners of the previous results. However, if one compares the results with those for a square wave giving out the same amount of NO per second, one can see that the results are qualitatively very similar, the only differences being the slight smoothing at the beginning and end of synthesis, as expected. Thus, for reasons of simplicity, it can be concluded that use of a square wave rather than a smoothed square wave does not impair the performance of the model.

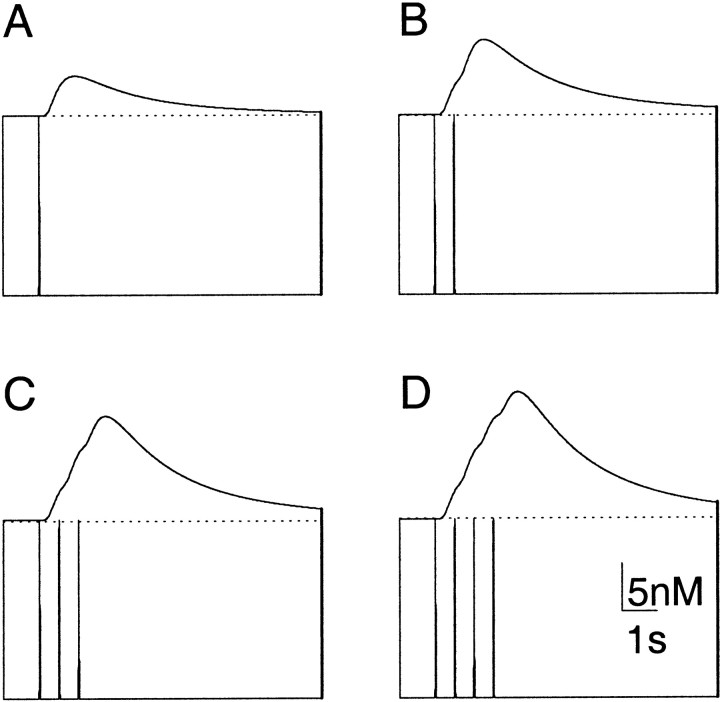
Despite its similarity to the square wave, the smoothed strength function was used again to generate a series of “spikes” of NO synthesis, the results of which are seen in Figure5. Here, it can be seen that the rise in NO concentration at points distant to the sphere is additive over each of the spikes. This additive rise mirrors recent experimental findingsin vitro in which summating depolarizations are induced in a distant NO-responsive neuron during a series of action potentials generated in a presynaptic NO-producing neuron (Park et al., 1998). In particular, if we imagine that there is some threshold above which the NO concentration must rise before the NO-responsive neuron is depolarized, the results are very similar indeed to these empirical data [compare our Fig. 5 with Fig. 7A in Park et al. (1998)].

Fig. 5.

Concentration of NO plotted against time after synthesis for a hollow spherical source of inner radius 15 μm and outer radius 30 μm measured at 150 μm from the center of the source. The results have been generated using a strength function that is a concatenation of different numbers of spike functions. Each spike lasts for 50 msec and is separated by a pause of 500 msec, as described in Materials and Methods. Both spatial and temporal dimensions have been chosen to model the in vitro electrophysiological experiments of Park et al. (1998). In each figure, the topmost line indicates the concentration, and the bottom line shows the strength function responsible for it on the same time scale. A, Effect of a single spike. B, Effect of two spikes. C, Effect of three spikes.D, Effect of four spikes. As in the empirical data, the effect of each new spike is additive and outlasts the causal signal [see Fig. 7A in Park et al. (1998)].

Irregular sources and sinks

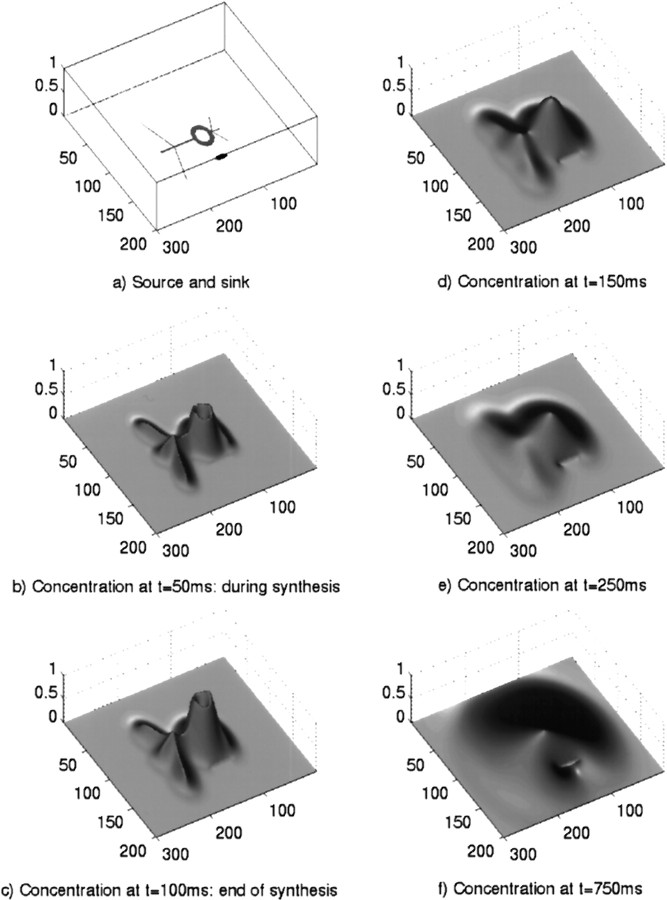
In this section of results, the effect of using an irregular structure is examined. Here we have used a neuron-like source that is in close proximity to an NO sink, as shown in Figure6A. It should be noted, however, that any structure can be modeled to arbitrary accuracy with this style of modeling. The rest of Figure 6B–Fshows the evolution of the concentration of NO, where the cloud of NO synthesized inside the neuron diffuses outward and is inactivated. It can be seen that the small-scale structure of the source (the “dendrites”) is soon obscured by the large amounts of NO coming from the main body of the cell. Here, the center effect discussed in the previous section is clearly visible, with a high concentration remaining long after synthesis has finished. It is also interesting to note the effect of the sink (a “blood vessel,” for example), which seems to have a basin of attraction around itself that forms a semipermeable barrier to the gas. Thus, there appears to be a “shadow” behind the sink into which NO is unable to diffuse. However, at later time steps the concentration in the “shadowed” areas begins to rise. This is mainly attributable to NO that diffused past the edges of the sink spreading into the area of low concentration behind it. There is also a small contribution from NO that manages to diffuse through it.

Fig. 6.

Diffusion of NO from a fictive neuron being influenced by an NO sink at several time steps after the initiation of a 100 msec burst of synthesis. a, Position of the neuron and sink. The neuron is the large, annular body with several processes. The sink is the smaller elliptical shape near the cell body. b, Concentration profile 50 msec after the start of synthesis, i.e., during synthesis. c, Concentration profile 100 msec after the start of synthesis, i.e., at the end of synthesis. d, Concentration profile 150 msec after the start of synthesis.e, Concentration profile 250 msec after the start of synthesis. f, Concentration profile 750 msec after the start of synthesis. The heights in b–f denote the concentration and are shown as the fraction of peak concentration attained (6.32 μm). The x- and y -axis scales are in micrometers. Note the reservoir effect at the center of the large cell body. The NO sink causes a “shadow” behind it where the concentration is relatively low (f).

As an illustrative example of the utility of this approach, we have included results showing contour plots of the limit of the region where NO may have an effect via the NO–cGMP signaling pathway, i.e., where the concentration drops below the threshold of 0.1 μm(Fig. 7). This region that evolves in space and time may be regarded as the effective NO “cloud.” The source is of the same shape as that used previously, but is 3.5 times smaller so that the cell body has a radius of 5 μm. The sink has maintained an elliptical shape and is intended to approximate a nearby capillary, for example. Here we can see the affected region (the effective NO cloud) starting to surround the sink as NO diffuses around it and even through it, with part of the front edge of the sink experiencing a concentration above threshold. In this case the area directly behind the sink is unaffected, but when other parameters such as a longer synthesis duration are used, this area can be included in the affected region. Sinks therefore should not be viewed as unsurmountable barriers to diffusion, as an alternative one-dimensional model predicts (Lancaster, 1997). Despite the smaller size of the neuron, the effect of the NO in the nucleus can still be seen, with the threshold contours being roughly centered on the main body. Unlike the previous instance (Fig. 6), however, we can see that this effect is deformed after the end of synthesis by the much greater action of the sink relative to the size of the neuron, which means that the affected area is displaced significantly off center from the source (Fig.7).

Fig. 7.

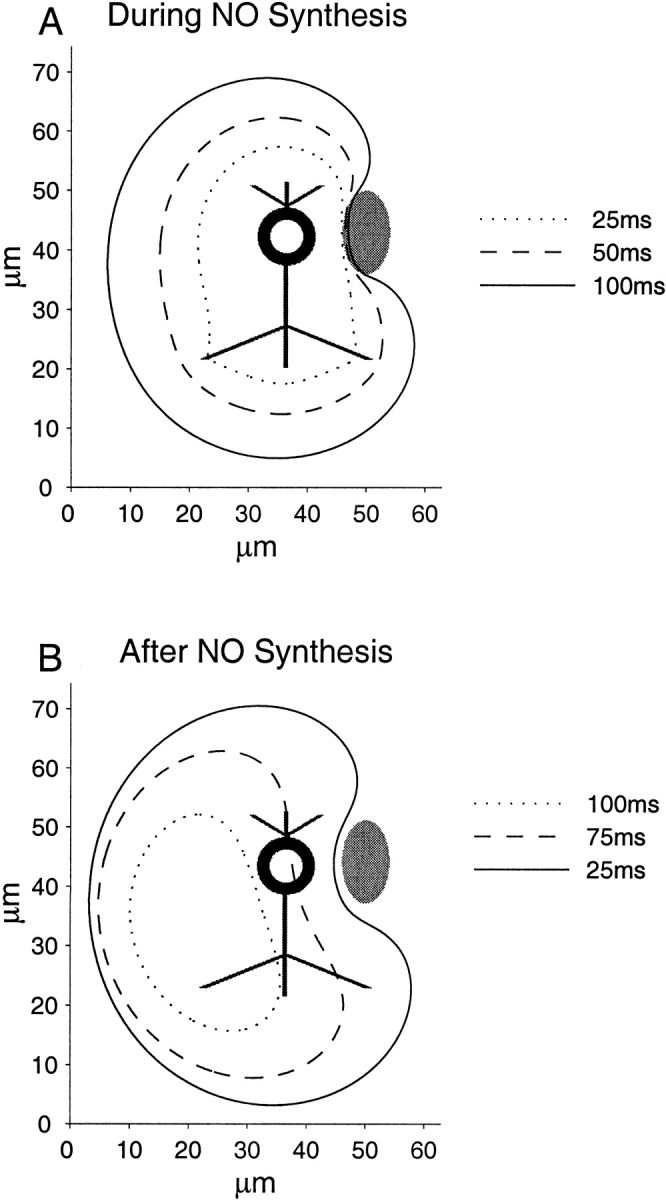
Contour plot of the threshold concentration for the NO–cGMP signaling pathway. Various time steps during and after a 100 msec burst of synthesis are illustrated together with source (black) and sink (gray). For each time step, the contour defines the region within which the NO signal can affect the NO receptor soluble guanylyl cyclase. A, Threshold concentrations contours at times 25 and 50 msec after initiation of synthesis and at the end of synthesis, 100 msec after the start. B, Threshold concentrations contours at times 25, 75, and 100 msec after the end of synthesis. In both graphs, the x - and y -axis scales are in micrometers. Note the affected area surrounding the sink during and just after synthesis and the leftward drift of the effective cloud attributable to the action of the sink in conjunction with the central reservoir formed during synthesis.

DISCUSSION

We have highlighted the importance of the morphology of NO-generating structures in determining the dynamics of the spread of NO in the nervous system. The diffusion of NO differs from the diffusion of other neurotransmitters or modulators in an important aspect. All transmitters will of course diffuse some distance away from their sites of release. Thus even in classical neurotransmission, generally regarded as point-to-point, there is an element of volume transmission allowing for the possibility of cross-talk to occur between distinct synapses (Barbour and Häusser, 1997). However, because most transmitters are relatively large and polar molecules, their spread will be slow and more importantly restricted to the extracellular space near their release site. The accurate modeling of this situation presents formidable problems, not least because details of the morphology of the extracellular space and the nature of local inhomogeneity will profoundly alter the extent and direction of migration. The diffusion of NO, however, presents a more tractable problem. Primarily because of its minute size and nonpolarity, it is able to diffuse freely through physiological barriers to affect target cells across an extensive volume. Also because the release of NO does not require presynaptic specialization, the whole surface of an NO generating neuron is a potential source. Thus in modeling NO diffusion the morphology of the whole source is crucial, whereas the surroundings can be regarded as homogeneous. In contrast, when modeling diffusion of conventional neurotransmitters and neuromodulators, the morphology of the extracellular space is of primary significance.

That incorporating the morphology of a source into the diffusional process for NO is important has been recognized by others, and a number of attempts to do so have been reported, with the majority using a compartmental model of the body under consideration (Gally et al., 1990; Lancaster, 1994, 1997). Such models do give valid insights into the overall role of a diffusing messenger but are hampered by the limit on the duration of the time step used (Mascagni, 1989). This limitation necessitates the use of relatively large compartments leading to rather gross approximations. In view of this, we believe a more sophisticated form of numerical approximation, such as the one presented here, should be used when the complexity of the morphology makes an analytical solution impractical. In adopting this approach we have avoided the shortcomings of point-source models and the degree of approximation associated with compartmental models.

The data presented reveal a number of morphology-driven properties of NO diffusion that would be difficult to predict using other methods. First, we identify the central reservoir effect and have quantified its consequences for the spatial and temporal dynamics of the NO signal (Figs. 2-4). For example, for a cell body of outer radius 30 μm (typical of many molluscan neurons) that synthesizes NO for 100 msec, our model predicts that the volume affected by an above-threshold concentration has a radius of 96 μm (Fig. 4). This is comparable to the experimental findings in vitro for the identified NO synthesizing B2 motoneuron in the mollusc Lymnaea stagnalis. The cell body of this neuron is ∼30 μm in radius and when stimulated affects a cocultured target neuron at least 70 μm away (Park et al., 1998). Although the two situations are not directly comparable, it is reassuring that the spatial prediction is in close agreement with the experimental findings. The affect of the central reservoir on the temporal aspects of the NO signal are summarized in Figure 2 where we see its contribution to the distance-dependent delay. For example, in the case of the 30 μm neuron described above, a cell on the very edge of the affected volume would not receive an above-threshold NO signal until 145 msec after synthesis had begun.

The reservoir effect is generated in the center of NO sources and is attributable to the inability of NO to diffuse radially while the concentration is high in the surrounding NO synthesizing region. Results are presented for an individual spherical cell, but the conclusions are equally valid for multicellular structures with glomerular, barrel-shaped, columnar, or tubular morphologies. As a consequence of the reservoir effect, relatively stable and high concentrations of NO can accumulate in the centers of such structures, even if NO is not synthesized there. An example of a multineuronal morphology suggesting that this feature of NO diffusion is of functional significance can be found in the mushroom bodies of an insect brain (O'Shea et al., 1998). The bilaterally paired mushroom bodies are specialized for associative learning (Davis, 1993), and in the locust they feature six tubular structures per side (O'Shea et al., 1998). Each consists of a central core of neurons surrounded by a region rich in NO synthesizing tissue forming a cylindrical surround. Our model as applied to tubular morphologies predicts that the central neurons will be exposed to high concentrations of NO for a significant period of time after NO synthesis is finished. Thus in the insect brain there are tubular compartments containing concentrations of NO representing a “memory” of past NO synthesis in surrounding regions. Similar effects are likely to be seen in barrel-shaped or glomerular structures in which a central core is surrounded by NO synthesizing cells. So as a consequence of source morphology and perhaps unexpectedly for a freely diffusing messenger, NO can have a spatially targeted and persistent influence in the nervous system.

Our model also shows how the size of a source has an unexpected influence on the dynamics of the diffusing NO cloud. In particular we have shown that the maximum relative affected volume is related to the absolute size of the source. Here neurons in the range of 15–20 μm radius that synthesize NO for 100 msec affect the largest relative volume. This result is nonintuitive and warrants some discussion. The explanation lies in the complex dynamical interactions of the spatial and temporal factors of the governing equations. For smaller neurons the concentration–time relations suggest that steady state will be reached before the end of a 100 msec burst of synthesis. Thus the rise in the NO concentration in a smaller neuron will be complete before the end of synthesis, leading to a lesser relative volume being affected than is affected by the 15–20 μm neurons. For the larger neurons, attributable to the greater volume into which the NO diffuses, the spatial concentration gradient will be lower, slowing the NO spread. At the end of synthesis, therefore, the spatial gradient resembles that of a smaller neuron before the end of synthesis, and we might envisage that in effect the burst of synthesis has been shortened. A second factor leading to a reduction in the relative affected volume that is easier to picture is the greater action of decay attributable to the increased time taken for the NO signal to reach its limit.

In our examination of the maximum volume affected by a branched morphology influenced by a nearby sink (Figs. 6, 7), we showed that even if the sink is a comparable size to the cell body it is not an insurmountable barrier to diffusion. Although very little NO can diffuse through it, diffusion occurs in a volume, and therefore NO can affect regions behind the sink by diffusing around it. Our analysis of a branched structure also shows that because of the speed of diffusion of NO, the small-scale branching is soon obscured by the diffusing cloud, although the aggregate shape can still be seen. It is important to note that in this example one would not know from which dendrite or part of a neuron the NO at a given location is emanating. This raises a significant conceptual point about NO signaling. Namely, in volume signaling, unlike conventional point-to-point neurotransmission, the signal has no address. In thinking about the information content of a volume signal, it is therefore important to recognize that the location or identity of the source cannot be determined unambiguously by the target.