Structured Long-Range Connections Can Provide a Scaffold for Orientation Maps

Abstract

In the visual cortex of the cat and ferret, it is established that maturation of orientation selectivity is shaped by experience-dependent plasticity. However, recent experiments indicate that orientation maps are remarkably stable and experience-independent. We present a model to account for these seemingly paradoxical results. In this model, a scaffold consisting of non-isotropic lateral connections is laid down in horizontal circuitry before visual experience. These lateral connections provide an experience-independent framework for the developing orientation maps by inducing a broad orientation tuning bias in the model neurons. Experience-dependent plasticity of the thalamocortical connections sharpens the tuning while the preferred orientation of the neurons remains unchanged. This model is verified by computer simulations in which the scaffolds are generated both artificially and inferred from experimental optical imaging data. The plasticity is modeled by the BCM synaptic plasticity rule, and the input environment consists of natural images. We use this model to provide a possible explanation of the recent observation in which two eyes without common visual experience develop similar orientation maps. Finally, we propose an experiment involving the disruption of lateral connections to distinguish this model from models proposed by others.

Rearing experiments have established that synaptic connections in the geniculocortical pathway are highly plastic during early postnatal development. A classical example of this plasticity is the binocular properties of neurons (Wiesel and Hubel, 1962, 1965; Mioche and Singer, 1989). Plasticity of orientation selectivity, however, is a more complex phenomenon. Although some orientation selectivity is present at birth, further development of orientation selectivity is guided by visual experience. It is clear that dark rearing prevents the normal development of orientation selectivity at eye opening in both cats (for review, see Frégnac and Imbert, 1984) and ferrets (Chapman and Stryker, 1993).

The effect of rearing animals in visual environments with a restricted set of orientations has been controversial. Most experiments have found that more cells become selective to the orientations prevalent in the environment (Hirsh and Spinelli, 1970; Pettigrew, 1974; Blakemore and Van-Sluyters, 1975; Rauschecker and Singer, 1981; Sengpiel et al., 1999) (but see Stryker and Sherk, 1975).

Recently, investigators have shown that orientation maps are present in binocularly deprived animals at eye opening (Chapman et al., 1996;Gödecke et al., 1997; Crair et al., 1998) and that orientation maps are stable throughout the critical period (Chapman et al., 1996;Gödecke et al., 1997). Furthermore, a dramatic optical-imaging/reverse suture experiment (Gödecke and Bonhoeffer, 1996) has shown that two eyes without common visual experience develop similar orientation maps.

The central question addressed in this paper is, how can we reconcile these two apparently contradictory findings about the plasticity of orientation selectivity in the visual cortex? On one hand, there are strong indications that orientation selectivity shows experience-dependent plasticity. On the other, orientation maps seem stable throughout development and are laid down independent of visual experience.

We have formulated a model that accounts for these seemingly paradoxically results. Our major hypothesis is that a network of lateral connections in the visual cortex forms a scaffoldthat sets the orientation map, produces broadly tuned cells, and biases the development of orientation selectivity. The orientation selectivity then develops through experience-dependent modifications of the feedforward synaptic connections.

The structure of lateral connectivity assumed in the model is based on several experimental observations. It has been established that long-range excitatory horizontal connections link together subsets of neurons that share similar orientation preference (Ts'o et al., 1986;Gilbert and Wiesel, 1989; Weliky and Katz, 1994; Ruthazer and Stryker, 1996). This is known as modular specificity. In addition, individual neurons receive input from other neurons whose receptive fields are displaced along an axis in visual space that corresponds to their preferred orientation (Bosking et al., 1997; Schmidt et al., 1997) (see Fig. 1a). This is known as axial specificity. In contrast, there is no indication that short-range connections (below ∼500 μm) have any specificity. In our model, two neurons must satisfy both the modular and axial conditions to be connected. Structured lateral connections have been shown to exist in layers II–III of visual cortex; we assume that these neurons interact with layer IV neurons and affect their responses as well.

To model thalamocortical plasticity, we use the BCM synaptic modification rule (Bienenstock et al., 1982; Intrator and Cooper, 1992). Because the development of orientation selectivity depends on the existence of a patterned visual environment, we have used a natural image environment (Law and Cooper, 1994).

The key elements of our model are as follows: (1) nonisotropic, long-range lateral connectivity, based on axial and modular specificity, provides an experience-independent scaffold that determines the orientation map organization; and (2) plastic feedforward connectivity provides the experience-dependent component of map development that determines the sharpness of the orientation tuning.

We show that this scaffold model can account for both the observed stability of an orientation map and the experience-dependent plasticity of single cells. To this end, we reproduce and explain the results of the reverse suture experiment of Gödecke and Bonhoeffer (1996). Finally, we propose an experiment that could serve to distinguish the scaffold model from models proposed by others.

MATERIALS AND METHODS

We simulated receptive field (RF) development in a binocular, single-layer striate cortex. The simulation consisted of a set of preprocessed input images and a two-dimensional array of cells. These cells were connected to the images through a set of modifiable synapses corresponding to geniculocortical synapses and to each other through a set of nonmodifiable synapses corresponding to intracortical lateral connectivity. For a single simulation iteration, a random location from a random image provided the input. The activity of each cell was calculated in two stages. First, the activity attributable to the geniculocortical feedforward component was calculated. Then, activity attributable to the lateral component was added. Synaptic strength was then modified on the basis of the total activity. At the conclusion of the simulation, sine-wave grating stimuli were used in place of natural images for calculating orientation maps, similar to those used in optical imaging experiments. The model we propose is not intended to be a complete model of experience-dependent plasticity in visual cortex. Rather, we have included those elements that seem essential to explain the set of results we wish to account for.

Input images. Our model of the visual environment consists of a set of 12 natural images of 256 × 256 pixels scanned at a resolution of 256 gray scales as in Shouval et al. (1996). To make the visual environment more orientation-invariant, we added 36 additional images that were generated by rotating the original 12 by 45, 90, and 135°. To approximate retinal and LGN processing (Linsenmeier et al., 1982), these images were preprocessed by a center-surround difference-of-Gaussians (DOG) filter with center radius of 1 pixel and surround radius of 3 pixels.

To simulate monocular deprivation experiments, preprocessed images for the deprived eye were replaced by random noise, uniformly distributed in the range [−0.5, 0.5].

Feedforward connectivity. Each cortical cell received input from a circular region of diameter 14 pixels. The RF center for each neuron was shifted with respect to its immediate neighbors in both the horizontal and vertical directions by ½ pixel. Initially, all feedforward synaptic weights were randomly distributed in the range [0.1, 0.2]. The activity of the k th neuron attributable to feedforward connectivity was:

$$c_k^0=\sum _l m_{\text{kl}}{d}_l,$$

where d_l represents the activity of the l th input neuron, m_klrepresents the synaptic weight connecting the l th input neuron to the k th cortical cell, and the sum is taken over the 14-pixel-diameter input neighborhood.

Lateral connectivity. Because we do not have explicit information about the complete lateral connectivity in the visual cortex, we inferred the connectivity using the following procedure. First, we created a map of the axes of the neurons in the network. For reasons explained below, this axial map can be thought of as a schematic representation of lateral connectivity of the network and has a strong influence over the final orientation map. We generated this map using the field analogy model (Wolf et al., 1994). This model assumes that the cortical map is an optimally smooth map with a predetermined set of singularities. A singularity is a point of a discontinuity in the orientations around, which the orientations change by 180°. We set the singularities on a square grid with alternating polarities. The singularity locations were then randomly shifted from the grid, and then the map was generated. We used a varying number of singularities, ranging from 49 to 81. The random shifts were chosen from a uniform distribution [−a, a] independently in the x and y directions. The values of a were between 2 and 3.

Next, we operated on the axial map to generate the lateral connectivity. Long-range lateral connectivity was determined by two conditions, both of which had to hold for two neurons to be connected (Fig. 1a). First, if two neurons, 1 and 2, had similar preferred orientation, they satisfied a comodularity condition. Specifically, if the preferred angles φ₁ and φ₂ of two neurons as set by the schematic differed by less than a critical angle φ_crit, then they were comodular. We used φ_crit = 28°. Second (see Fig. 1a and Results), if the line connecting the center of the RF of neuron 1 to neuron 2 was nearly parallel to the other neuron 2 preferred orientation, then the axial condition was satisfied for the connection from neuron 2 to neuron 1. Specifically, for each neuron, a straight band of half-width s_w and half-length s_l was extended along its axis. Any other neuron that falls in this band satisfied the axial condition. We used s_w = 3 neurons and s_l = 32 neurons. We also established a radially symmetric short-range connectivity. A neuron was connected to all other neurons with a radius less than r_short. We chose r_short = 4 neurons.

We then normalized the lateral weights by counting the number of connections each neuron received from other cortical neurons and setting each of the incoming weights to the reciprocal of this number. Thus, ∑_kL_ik = 1 for each i.

The activation of the i th neuron attributable to lateral connectivity was:

$$n=\sum _{\text{k}} L_{\text{ik}}\varsigma ({\text{c}}_{\text{k}}^0),$$

where c_k⁰ represents the feedforward activity of the k th cortical neuron, as above, ς is a sigmoidal activation function with a lower saturation limit of −1 and an upper saturation limit of 100, L_ik represents the synaptic weight connecting the k th cortical cell to the i th cortical cell, and the sum is taken over the set of lateral connections described above.

Therefore, the total activity of the i th cell in the network was:

$$c_i=\varsigma \left(\begin{array}{c} \\ \hfill \hfill \end{array}\sum _j m_{\text{ij}}{d}_j+\sum _k L_{\text{ik}}\varsigma (c_k^0)\right),$$ Equation 1

where the term on the left represents the activation attributable to feedforward input. d_j represents the activity of the j th input neuron, and m_ij are the synaptic weights connecting cortical neuron i to input neuron j. The sum is taken over the 14-pixel-diameter input neighborhood. The term on the right represents the combined influence of all the lateral connections. The output is bounded by the sigmoidal function ς.

We have made several simplifying assumptions about the structure of the cortical network. For example, thalamic projections terminate primarily in layer IV, whereas long-range lateral interactions are between layer II and III neurons. Our model has only one layer; thus a model neuron is assumed to represent a subnetwork of neurons spanning different layers.

Learning rule. We used BCM synaptic modification to simulate synaptic plasticity. This rule specifies that for postsynaptic activity (c) larger than a threshold (θ_m), synapses are potentiated [long-term potentiation (LTP)], whereas for values of c smaller than θ_m they are depressed [long-term depression (LTD)]. Furthermore, to stabilize synaptic weights, the threshold (θ_m) moves in time as a monotonically increasing function of the history of postsynaptic activity.

This rule has been shown to produce receptive fields similar to those found in the visual cortex (Law and Cooper, 1994; Shouval et al., 1997) and is in agreement with deprivation experiments (Blais et al., 1999;Rittenhouse et al., 1999). In addition, there is direct experimental evidence for BCM synaptic modification from LTP and LTD data on the cellular level in visual cortex as well as other cortical areas, in different species and for different ages (Kirkwood and Bear, 1994;Kirkwood et al., 1996). The synaptic modification rule chosen must be able to develop oriented receptive fields in a natural image environment as well as reproduce the results of monocular deprivation and reverse suture; otherwise it could not be used for the simulations carried out in this work.

A synaptic plasticity rule that depends only on the presynaptic activity would converge to the mean of the input, thus for a stationary environment the receptive fields produced would be uniform and nonoriented. Therefore, such a rule cannot be used. It is therefore necessary to use a rule that depends at least on the second-order statistics of the input. It should be noted that the choice of the BCM rule is not crucial to our results; it is likely that other synaptic modification rules, which can produce binocular orientation-selective receptive fields and replicate deprivation experiments, such as reverse suture for a reasonable visual environment, would produce similar results.

We used a modified version of the quadratic BCM learning rule (Bienenstock et al., 1982; Intrator and Cooper, 1992; Law and Cooper, 1994; Blais et al., 1998), with a variable learning rate of the form

$${\dot{m}}_{\text{ij}}=\frac{\eta }{{\theta }_i} c_i(c_i-{\theta }_m)d_j,$$

where, as above, d_j represents the activity of the j th input cell, c_irepresents the activity of the i th cortical neuron, andm˙_ij represents the rate of change of the synaptic weight from the j th input cell to the i th neuron. In addition to the input and output activities, the magnitude of this rate of change depends, in broad terms, on the difference between the output activity of the cell and a variable threshold θ_m. The scaling constant η represents a learning rate.

θ_i is expressed in the integral form as:

$${\theta }_i(t)=\tau \underset{\infty }{\overset{t}{\int }} e^{\frac{(t-t^{\prime })}{\tau }}(c_i(t^{\prime }){)}^2{\text{dt}}^{\prime },$$

where τ is the time constant for the temporal average. That is, the rate at which the threshold itself changes depends on the difference between the threshold and the square of the activity of the cell. In these simulations, we chose the value of η = 0.01/(RF size) and τ = 1000. The simulations are qualitatively robust to a range of parameters, and we chose these values to optimize run times.

This learning rule has stable fixed points as shown analytically for a single cell (Bienenstock et al., 1982; Intrator and Cooper, 1992) and networks (Castellani et al., 1999), as well as in simulations with natural images (Law and Cooper, 1994; Shouval et al., 1997).

Parallel processing. The simulation was implemented on a Paragon XPS/5 parallel computer (Intel, Beaverton, OR) with 128 processors. Most of the simulations were executed using 64 processors. The preprocessed image data were replicated on each processor. For each iteration, processors used a synchronized random number generator to select a subimage and without interprocessor communication calculated feedforward activity for a subset of the neurons. The vector representing this intermediate activity for all neurons was collected onto all processors using an all-to-all broadcast. Each processor then calculated, for its subset of neurons, the activity attributable to lateral connectivity and the total activity. Then the feedforward synaptic weights were modified. A sparse matrix representation of the lateral connectivity was used to speed processing. Periodically (typically every 100,000 iterations), the state of the simulation was archived in a checkpoint file.

Selectivity measure. We quantitatively evaluated the degree of orientation selectivity for each neuron. At the conclusion of the simulation, the final checkpoint file was transferred to a serial processor for evaluation. For each cell, a tuning curve at the optimal spatial frequency was generated as a 24-dimensional vectorTC. The tuning curve was Fourier-transformed to give the vector $\begin{array}{c}{}_{\mathbf{\sim }}\\ \hfill \mathbf{TC}\hfill \end{array}$. An orientation selectivity measure was defined as S = ‖ $\begin{array}{c}{}_{\sim }\\ \hfill TC\hfill \end{array}$(2)‖/ $\begin{array}{c}{}_{\sim }\\ \hfill TC\hfill \end{array}$(1). This is similar to a measure used experimentally (Chapman and Stryker, 1993).

Circular correlation. The circular correlation between two maps was calculated in the following manner. For each corresponding pair of neurons in the two maps the circular correlation for that pair of neurons was set as:

$$CC(i,j)=cos(2[\alpha (i,j)-{\alpha }^{\prime }(i,j)]),$$ Equation 2

where α(i, j) and α′(i, j) are the preferred orientations for pair of neurons with coordinates i, j in the two maps, respectively. We then create a circular correlation matrix with the same dimensions as that of the maps. The average over all pixels is the circular correlation between two different maps.

Optical maps. Optical maps were provided to us by A. K. Parshanth. The methods for extracting the maps are similar to those ofEverson et al. (1998). The maps were cropped to a square and represent 3.5 × 3.5 mm² of cortex. The map is displayed rotated such that the horizontal direction is approximately the horizontal in visual space.

RESULTS

Description of connectivity

Ideally, we would like to use a lateral connectivity pattern directly extracted from experimental observations; however, such data are not available. Instead, we qualitatively approximate the lateral connectivity in visual cortex in a manner that is consistent with experimental results.

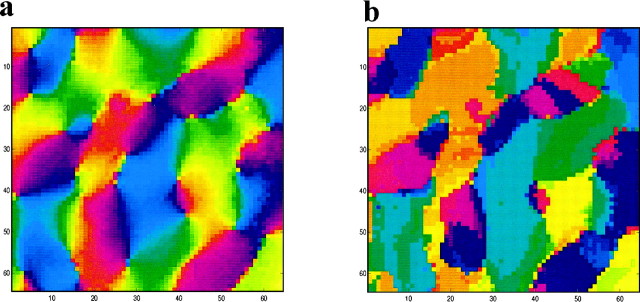
To generate the lateral connectivity pattern, we first created aschematic of an axial tuning map. By this, we mean a map that dictates the axis for each neuron. This axis, we will see below, also effects the preferred orientation of each neuron. The schematic map is set either by the theoretical field analogy model (FAM) (Wolf et al., 1994) or from optical imaging data. A typical schematic, created by the FAM model, which has 64 × 64 neurons and 64 singularities (pinwheels), is presented in Figure 1b. We can use the number of singularities per square millimeter to set the scale of the simulations in millimeters rather than pixels. In different simulations, the number of singularities ranged from 49 to 81. Experimental data for cats indicate that the singularity density is ∼1.2 singularity/mm² (Bonhoeffer and Grinvald, 1993). This implies that we simulate networks with physical dimensions in the range ∼6.5 × 6.5–8.5 × 8.5 mm². These schematics were then used as a basis for determining the modular–axial connectivity pattern used in the simulations. Figure 1a illustrates how the lateral connections for the network were determined. If two neurons have the same preferred orientation (comodular), but neuron 2 does not lie on the axis of neuron 1, they will not be connected (Fig. 1a, I). Two neurons that do not have similar orientations are not connected, even if neuron 1 lies on the axis of neuron 2 (Fig. 1a, II). Note that the axial component is nonsymmetric: neuron 1 lies on the axis of neuron 2 but neuron 2 does not lie on the axis of neuron 1. Neurons are connected only if they lie on the same axis and have a similar preferred orientation (Fig. 1a. III). When two neurons satisfy both the axial and modular requirements, they will both be connected to each other; thus the axial modular connectivity rule is symmetric.

Examples of the incoming lateral connections to two neurons in this network are shown in Figure 1c. The connectivity map used was binary; that is, for each possible neuron–neuron pair, a connection was either present or absent. These connectivity patterns were normalized such that the incoming connection strengths to a neuron were proportional to the reciprocal of the number of connections it received.

Fig. 1.

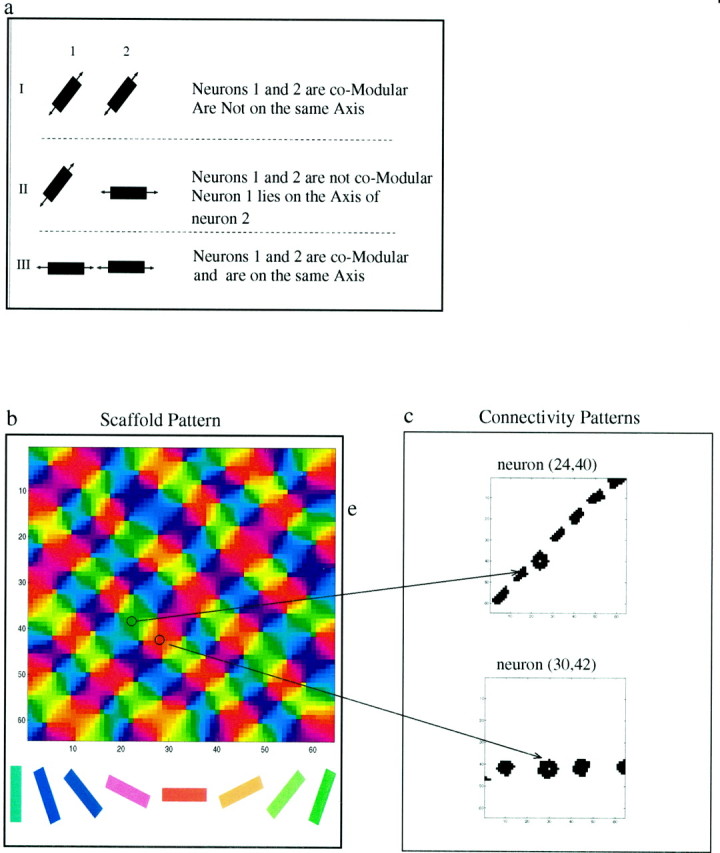
Modular–axial connectivity in visual cortex. a, I, Both neurons have a similarly oriented connectivity axis (comodular), but their axes are not aligned, so the two neurons will not be connected. II, Although neuron 1 lays on the axis of neuron 2 (axial), the connectivity axes of these two neurons have significantly different orientations and will not be connected. III, These two neurons are comodular and lie on each other's axis; they are therefore reciprocally connected. b, Map of the orientations of the connectivity axes for a 64 × 64 neuron network. Orientation is indicated by color. This map, along with the modular–axial connectivity rule, specifies long-range lateral connectivity within the cortex. c, Examples of lateral connectivity patterns for two representative neurons.

Naïve networks and normal rearing

Each of the neurons in our model was assumed to have a receptive field center that is shifted with respect to the receptive field of its neighbors. This shift creates a retinotopic map in the cortex. Because of nonisotropic lateral connections and the shift in receptive field centers, there is a component of orientation selectivity that is entirely of cortical origin, even if the thalamocortical projections are random or uniform.

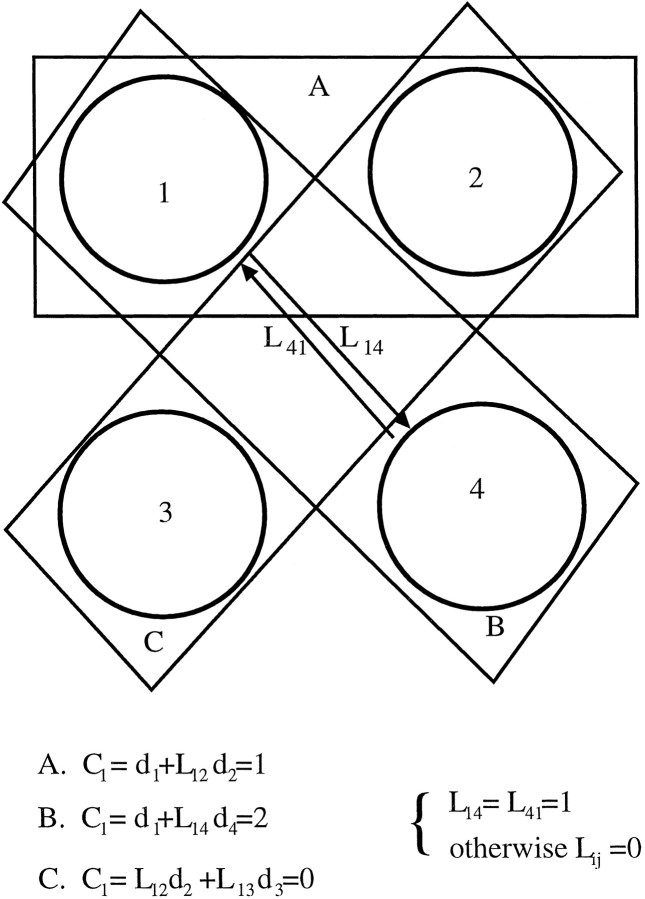
To show how nonisotropic lateral connectivity and shifted receptive fields create orientation selectivity, we give a simple numerical example with four neurons (Fig. 2). The activity of each neuron is the sum of its feedforward input and the inputs it receives from its neighbors (Eq. 1). In this example, we assume that neurons 1 and 4 are connected with a connection strength of 1 (L₁₄ = L₄₁ = 1). All other connections are assumed to be zero. The feedforward connections of each neuron are assumed to be uniform (m = 1). When a light bar overlaps the feedforward portion of the receptive field, the input value is 1 (d = 1). When it does not overlap, the value of the input is 0 (d = 0). Three distinct conditions A, B, and C are compared in this example, each representing a bar with a different orientation. We use Equation 1 to calculate the activity of neuron 1 for each of the different conditions. As shown in Figure 2, the bar with the same orientation as the connections produces the largest response in the cell. This would not occur if the receptive fields of the connected cells were completely overlapping.

Fig. 2.

Lateral connectivity can create an orientation bias. A simple example is shown with four neurons that have nonoverlapping receptive fields. We assume each neuron has a single feedforward weight of strength 1. A–C, Oriented bar stimuli with three different orientation. The text at thebottom indicates the activity in response to each of the bars.

The brightness of each pixel in the pseudocolor maps in Figure3 codes for the degree of orientation selectivity (The definition of S, the orientation selectivity measure, is given in Materials and Methods). Initially, in a naïve network (i.e., an untrained network), there is an orientation bias, which is highly correlated with the schematic map (Fig. 3a). The low intensity levels show that these neurons are very broadly tuned. This can be seen more clearly when we compare tuning curves before and after training (Fig. 3c) for two of the cells in the network. This holds for the whole network as shown in Figure 3d, where the bottom surface depicts the orientation selectivity across the naïve map and the top surface depicts that of the trained map. Initially, S has low values, typically less than 0.1. Optimal spatial frequency is also very low in the untrained map (Fig. 3e). For all cells, we found that the optimal spatial frequency had the lowest value for which we tested, SF = 0.2 radians per pixel. After 700,000 iterations (Fig. 3b), the network has preferred orientations, which are very similar to the predetermined axis in the schematic (Fig. 1b). To assess the similarity, we calculated a circular correlation measure (see Materials and Methods) between the mature map and the schematic. In this case we find a circular correlation of 0.82 between the schematic and mature maps. The network develops a high level of orientation selectivity. The receptive field structure does not keep changing, and the tuning curves do not get sharper, because the network, as a result of the stable learning rule, reaches a stable fixed point.

Fig. 3.

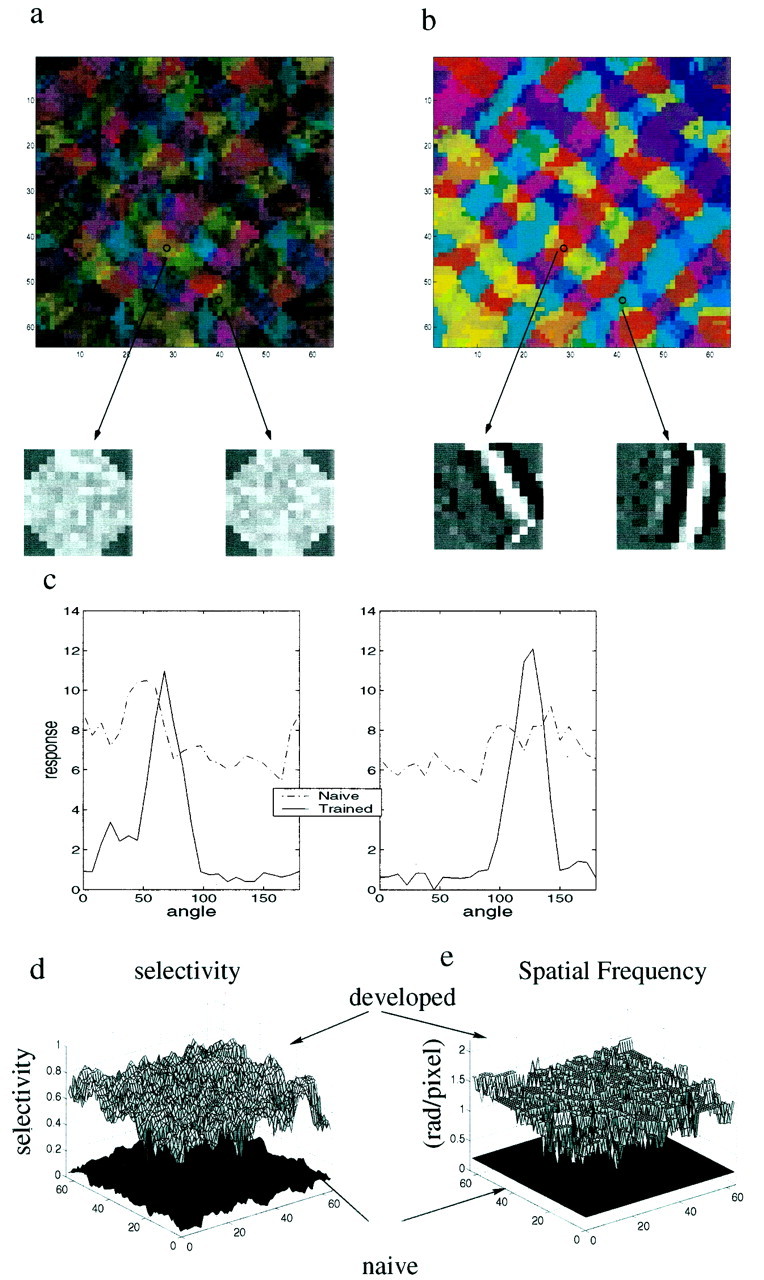
Effects of training on a network of neurons with modifiable geniculocortical synapses and static lateral synapses. Orientation preference for stimuli is indicated by color, as in Figure1. Brightness indicates degree of orientation selectivity: light colors indicate highly selective cells; dark colorsindicate weakly selective cells. a, Orientation selectivity in the naïve map, using the scaffold of Figure 1a. The generally dark colors indicate broadly tuned cells. There is a high level of correlation between this map and the scaffold. That this initial orientation selectivity is entirely of cortical origin is apparent from the two representative feedforward receptive fields displayed below, grayscale codes for the strength of thlamocortical connections: bright represents a strong connection, and dark represents a weak connection. Initially the thalamocortical weights are random. Arrows indicate the locations of these cells. b, The same network after 700,000 training iterations. Brighter colors indicate highly selective cells. The circular correlation between this map and the schematic displayed in Figure 1a is 0.82. Below we show the feedforward receptive fields of the same cells displayed in Figure 2a, after training. c, Orientation tuning of two cells, before (dashed line) and after (solid line) training. Cells have a slight orientation bias before training and are sharply tuned after training. These tuning curves are the basis for generating the selectivity index (see Materials and Methods). d, Orientation selectivity for the whole network before and after training. The bottom surface shows the naïve network, and the top surface shows the trained network. e, Spatial frequency before and after training. Thebottom surface shows optimal spatial frequency for the naïve network. All cells in the naïve network were found to have the lowest spatial frequency for which we tested (0.2 radians per pixel). After training (top surface) the optimal spatial frequency is greatly increased for all neurons.

The sharpening of the tuning curves and the increase in optimal spatial frequency are accounted for by the changes in thalamocortical connectivity. The small grayscale images in Figure 3,a and b, bottom, represent the thalamocortical connections. A bright color represents a strong connection, and adark color represents a weak connection. These images are similar but not identical to receptive fields as extracted by reverse correlation (Jones and Palmer, 1987). Before training (Fig. 3a), the thalamocortical connections are random. During training they evolve to highly organized structures that exhibit elongated subregions of alternating signs (Fig. 3b) reminiscent of simple cells in visual cortex.

Thus, the main effects of training are increased orientation selectivity, an increase in the preferred spatial frequency, and at most a modest change in orientation preference. Because the only modifiable synapses in our simulation are the geniculocortical synapses, these changes are mediated solely by this set of connections.

To obtain biasing of the network toward the direction of the scaffold, we have used a modular–axial connectivity scheme. The axial component of the connectivity pattern is essential for obtaining these results. We have previously shown, using simulations on a smaller scale, that an axial component alone can be sufficient (Goldberg et al., 1999).

Extension to real maps

The simulation in Figure 3 was performed for an artificial schematic map. We tested to see whether similar results could be obtained with lateral connectivity inferred from real optical imaging maps. We created a schematic from optical imaging maps (data provided by A. K. Prashanth in Udi Kaplan's laboratory; Everson et al., 1998). The imaged section of cortex (Fig. 4a) used to create the scaffold has dimensions of 3.5 × 3.5 mm². The parameters used are essentially identical to those used with the artificial schematic; however, because the map represents a smaller section of cortex, the connections here will have a nonsymmetric structure at a shorter range. The simulated network map after 700,000 iterations (Fig. 4b) was similar to the original with a circular correlation of 0.78 between the inferred schematic and the mature map. This is within the range of results obtained for artificial maps and significantly >0, which is the circular correlation between two random maps. We performed the same procedure for one other map obtained from optical imaging and obtained similar results. Thus, we have established that the effect of the scaffold is not an artifact of the artificiality of the maps. For the remainder of this paper we use the artificial maps, because they are bigger, depend on long-range lateral interactions, have parameters we can control, and are easier to generate.

Fig. 4.

Scaffold created from optical imaging maps. a, Section of an optical imaging map (data courtesy of A. K. Parshanth and U. Kaplan; Everson et al., 1998). This map was used as a schematic for a scaffold. b, The mature map obtained using the schematic in Figure 3a. The circular correlation between the maps in a and b is 0.78. Color code as in Figure 1.

Reverse suture

If the scaffold can bias the development of the map, it should in a similar fashion bias an orientation map that develops independently in both eyes. We performed simulations of the type of reverse suture experiments performed by Gödeke and Bonhoeffer (1996) (Fig.5). We initialized the thalamocortical connections for both left and right eye channels independently from a random distribution and then ran a monocular deprivation (MD) training phase in which one eye received a natural image environment and the other eye received noise. Orientation maps through both eyes, after this phase, are presented in Figure 5a, top. As expected, the thalamocortical connections for the eye receiving patterned input developed strong orientation selectivity, whereas the selectivity in the connections from the contralateral eye were substantially weaker.

Fig. 5.

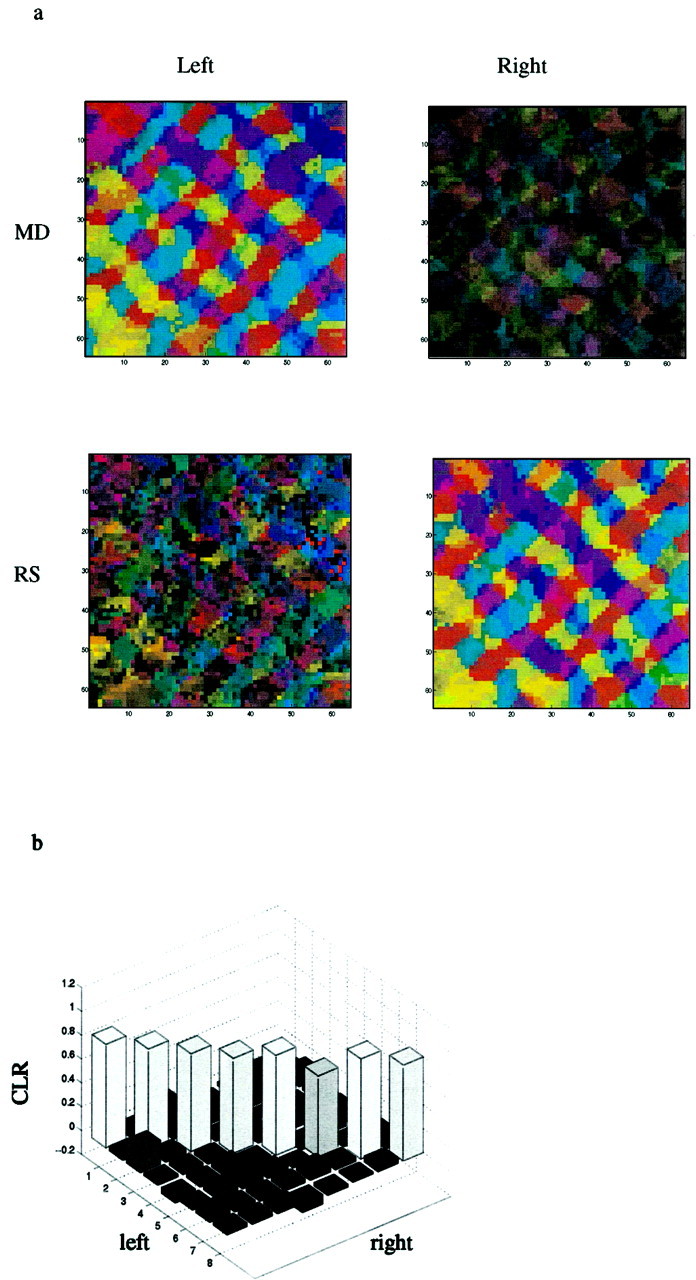
Simulation of reverse suture experiments performed on a binocular network. a Example of a reverse suture experiment. The schematic used in this example is the same as Figure 1a. The orientation maps obtained after the initial 700,000 iteration MD stage are illustrated above. On the left, a highly selective organized map is shown for the open eye. On the right, the map imaged from the closed eye is shown. Maps obtained after the 1 million iteration RS stage are illustrated below. The newly opened right eye shows a high degree of selectivity and an organization similar to the map imaged from the left eye after the MD phase. The circular correlation between these two maps is 0.87. b, Circular correlations between left eye after MD and right eye after RS. Simulations were run for eight different schematics that differed in the number of singularities (49–81) and their random displacement (see Materials and Methods). On the diagonalthe correlations between left eye after MD and right eye after RS for the same scaffold are displayed. In the off-diagonal the correlations between maps with different schematics are displayed.

We then ran a reverse suture (RS) phase in which the eye that previously received patterned input received noise, and the previously deprived eye received a patterned input. We ran the reverse suture phase for 1 million iterations. After training, the orientation selectivity in the newly deprived eye decayed, whereas the orientation selectivity in the formerly deprived eye increased (Fig. 5a,bottom). Despite the fact that the two eyes never experienced common visual input, the maps obtained from the left eye after monocular deprivation (Fig. 5a, top left) and from the right eye after the reverse suture phase (Fig. 5a,bottom right) are very similar. The circular correlation between these maps was 0.87. These results are agreement with the experimental results of Gödecke and Bonhoeffer (1996).

To verify that this is not a special case, we repeated this procedure for eight different artificial maps. To illustrate that this does not occur only for maps that have similar statistics, we chose maps with a varying number of singularities. We calculated the circular correlation (Eq. 2) between the left eye after MD and the right eye after RS among all of these maps (Fig. 5b). The diagonal values show the circular correlations for the same simulation, and the off-diagonals give the circular correlations between maps obtained in different simulations. The within-simulation correlation values are high (all >0.68 with a mean of 0.81 and SD of 0.05). In contrast, the off-diagonal elements are all close to zero (mean, 0.04; SD, 0.05), which is what we would expect for totally uncorrelated maps.

Disruptions

Other models could also account for these experimental results. For example, there could be an initial orientation bias in the thalamocortical connections that is similar for both eyes. We suggest an experiment to distinguish our model from this possibility. We propose to rear cats monocularly from birth and then perform reverse suture as in the Gödecke and Bonhoeffer (1996) experiment. At the end of the MD phase, the maps are imaged, and small, paired, parallel cuts are made in the cortex to disrupt the long-range horizontal connections. At the end of the reverse suture phase the orientation maps that developed in the contralateral eye are imaged.

We expect, if the scaffold model is correct, that orientation maps that develop in the contralateral eye will be disrupted in a particular manner. Specifically, we expect that the changes in the orientation maps will be correlated with the orientation of the cuts. If the paired cuts disrupt long-range connections along the line of axial specificity, orientation selectivity will be disrupted in the region between the cuts. However, if the paired cuts are made orthogonal to the line of axial specificity, orientation selectivity in the region between the cuts will not be disrupted at all. That is, in the latter case, we will observe that nearly identical orientation selectivity will develop in the maps for both eyes but not in the former case. Our expectations stand in sharp contrast to what one would expect if a built-in thalamocortical bias, similar in both eyes, determines final orientation preference. In this case, one would expect few changes in the MD or RS maps, regardless of the orientation of the cuts.

Figure 6 illustrates a simulation of this experiment. In Figure 6a, we display the map after the MD stage from the open eye. In Figure 6b, and c, we display the maps at the end of the RS phase. In Figure 6b cuts were made along the line of axial specificity for the central red region and have strongly disrupted the horizontal connections. Thus, after reverse suture, they alter the preferred orientation of the cells affected. To quantify the strength of this effect, we calculated the circular correlation for each pixel, between the region of interest in the maps in Figure 6a and b. The correlation map, within the region of interest, displayed in Figure 6a, right, shows that there is a large difference between these maps.

Fig. 6.

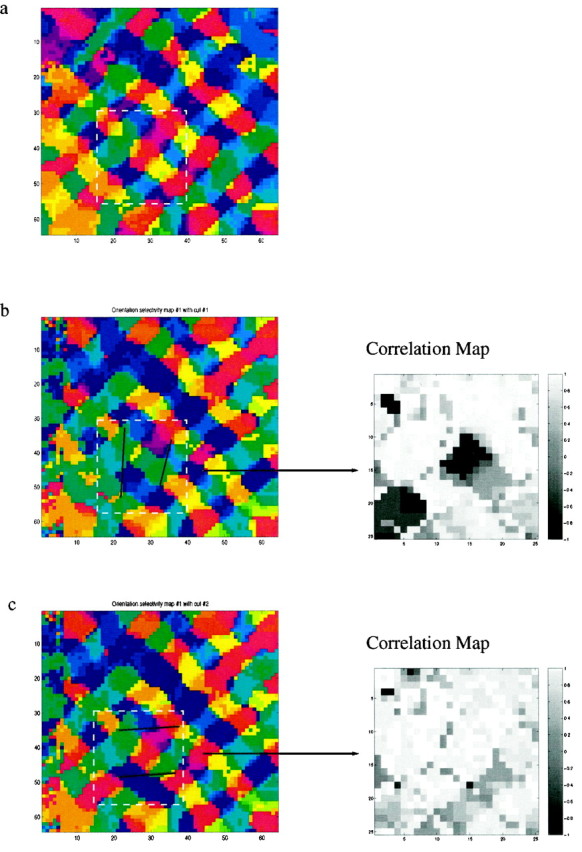
Proposed experimental test for the scaffold hypothesis. We expect that the location and orientation of small cuts would affect the layout of the orientation map that develops during the reverse suture phase. a, Trained map after MD, as in Figures 2b and 4a. Before RS, selective small cuts are made to the cortical surface, disrupting lateral connections. After RS, the maps are imaged. b, Black lines indicate two cuts designed to sever many of the horizontal lateral connections to a region preferring horizontal orientations (red). The cuts created a significant difference in the preferred orientation after RS. On the right a circular correlation map, in a region of interest, between the uncut map (Fig. 5a) and the cut map is shown. Small values are indicative of significantly different preferred orientations. c, Control experiment, in which two cuts do not disrupt the horizontal connections. In this case, we anticipate a much smaller change in the orientation map, indicated by the absence of small values in the correlation map.

Cuts made at a similar distance to the horizontally tuned cells after the MD phase orthogonal to the line of axial specificity have a very different effect. In this case, the orientation selectivity that develops in the RS eye (Fig. 6c) is nearly identical to the map that developed in the MD eye (Fig. 6a), and the correlation map (Fig. 6c, right) contains almost no large values.

A possible problem with the proposed experiment is that such cuts, despite their small size (∼1 mm), could damage blood vessels in the region of interest. Such reduction in the blood flow could reduce the intrinsic signals used in optical imaging, thus making the results harder to observe. It might therefore be necessary to find a less-invasive alternative to cuts that would similarly alter the lateral connectivity. Another possible problem is that by chance the new map may develop an orientation similar to the undisrupted map. This, however, should happen only in a small fraction of the experiments.

DISCUSSION

Experimental evidence concerning plasticity of orientation selectivity in visual cortex poses an apparent dilemma. There are strong indications that orientation selectivity of single cells in visual cortex is experience-dependent and dependent on synaptic plasticity. On the other hand, preferred orientation seems very stable. Moreover, preferred orientation is identical for both eyes, even if they never experience common visual input.

To account for this, we propose that a scaffold is embedded in the structure of the long-range lateral connectivity. Its structure determines the initial orientation preference observed in animals with no visual experience and accounts for the stability in the orientation maps that develop in eyes with no common visual experience. The scaffold model is consistent with the broadly tuned, low-spatial frequency orientation selectivity seen in very young animals (DeAngelis et al., 1993). It is also consistent with the observation that orientation selectivity increases with visual experience, without markedly changing orientation preference (Chapman et al., 1996;Gödecke et al., 1997). According to this view, plasticity operates primarily on the thalamocortical synapses. Thus, adult orientation selectivity is determined by the thalamocortical connections. This too is consistent with experimental results (Ferster et al., 1996; Chung and Ferster, 1998).

There is evidence that the development of clustered lateral connections, in ferret, starts before eye opening (Durack and Katz, 1996), although the refinement of these connections occurs synchronously with the maturation of receptive fields after eye opening. Furthermore, it has been shown that the early phase of development of long-range connections is not prevented by enucleation (Ruthazer and Stryker, 1996). These findings are consistent with our assumption that the structure of the lateral connectivity is laid out at eye opening and is the substrate of orientation selectivity at eye opening. We have not considered plasticity of the lateral connections in the present model; however, we do not exclude this possibility. It could indeed be the case that the structure we assumed for the lateral connectivity develops concurrently and interacts with the development of structure in the thalamocortical pathway. However, even if lateral connections are not entirely static, our present model can still account for the results of Gödecke and Bonhoeffer (1996), because the lateral connections developed during the initial MD phase would be in place during the RS phase to bias the development of the connections to the second eye.

Plasticity of orientation selectivity in visual cortex is quite controversial. There has been a long-standing dispute about the degree of orientation selectivity at eye opening. Hubel and Wiesel (1963)claimed that orientation selectivity right after eye opening is nearly identical to orientation selectivity in adults. In contrast, Barlow and Pettigrew (1971) claimed that there is almost no orientation selectivity immediately after eye opening. Other research supports the intermediate view that there is some degree of orientation selectivity at eye opening, although fewer cells are orientation-selective, and those that are more broadly tuned than in adults (Blakemore and Van-Sluyters, 1975; Buisseret and Imbert, 1976). An extensive reverse correlation study has recently shown that there is orientation selectivity after eye opening; however, both spatial and temporal properties of cells develop after eye opening (DeAngelis et al., 1993). Spatial tuning reaches adult levels at ∼4 weeks of age, whereas temporal properties keep developing beyond 8 weeks. The reverse correlation technique requires a large amount of data, therefore, weakly responsive cells had to be eliminated from the sample. Thus the sample they produce might be somewhat biased, and actual orientation selectivity might be lower than they report, especially in the younger animals.

Regardless of the degree of orientation selectivity at eye opening, it is well established that dark rearing or binocular deprivation prevents the normal development of orientation selectivity. This has been shown for both cats (Imbert and Buisseret, 1975; for review, seeFrégnac and Imbert, 1984) and ferrets using both electrophysiological (Chapman and Stryker, 1993) and optical imaging techniques (Chapman et al., 1996). Another striking example of plasticity of orientation selectivity was provided by Sur and coworkers (1988), who had shown that when visual thalamic projections are rerouted into auditory cortex of ferrets, cells in auditory cortex become orientation-selective.

In another set of experiments animals were raised in artificial visual environments in which they were exposed to only a restricted set of orientations. Most of these experiments found that those orientations to which the animals were exposed were overrepresented by cells in their cortex (Hirsh and Spinelli, 1970; Pettigrew, 1974, Blakemore and Van-Sluyters, 1975). However, an experiment by Stryker and Sherk (1975)found no difference between normal animals and those reared in restricted environments. A similar experiment performed by Stryker et al. (1978) with a different deprivation methodology did find a difference between control animals and those raised in a deprived environment, but the researchers found many “dead zones,” that is, zones in which no cells responded. This raises the possibility that cells with an orientation preference not found in the environment do not change their preferred orientation but instead become unresponsive. Such plasticity is often referred to as permissive plasticity. A recent optical imagining study (Sengpiel et al., 1999), which uses a deprivation methodology similar to that of Stryker and Sherk (1975), has shown a significant over-representation of those orientations that existed in the environment. Furthermore, this experiment did not observe any dead zones. These recent results do not lend support to the permissive plasticity hypothesis.

The modular component of the proposed lateral connectivity has ample experimental evidence (Ts'o et al., 1986; Gilbert and Wiesel, 1989;Weliky and Katz, 1994; Ruthazer and Stryker, 1996). In contrast, there is less evidence for an axial component; however, it was found both in tree shrew (Bosking et al., 1997) and in cat (Schmidt et al., 1997). The disruption experiment we propose (Fig. 6) could be used to indirectly test the pattern of the lateral connectivity. If such experiments produce the results we predict, it would show not only that the lateral connectivity is a plausible substrate to the scaffold, but also that is has a modular–axial form. Our work implies that the structure of visual cortex maps arises from the lateral connectivity. However, it is not clear what drives the development of the lateral connectivity and which types of mechanisms are required to organize such intricate maps of lateral connections. This set of questions, which could be addressed both experimentally and theoretically, would then become central to the question of visual map organization.

A model proposed by Erwin and Miller (1998) has also been used to account for the results of Gödeke and Bonhoeffer (1996). This model assumes that orientation selectivity of thalamocortical connections is developed before eye opening and is the same for both eyes. The pre-eye-opening thalamocortical structure is then the substrate of the orientation selectivity observed at eye opening. In our model we assume that orientation selectivity at eye opening is caused by structured lateral connections in layers II–III, which also influence responses of neurons in layer IV. Our model assumes that thalamocortical plasticity occurs primarily after eye opening; we therefore use natural images for training. The Erwin and Miller (1998)model, in contrast, assumes thalamocortical connections develop before eye opening and therefore uses correlated noise as input. The model ofErwin and Miller (1998) can account for the results of Gödeke and Bonhoeffer (1996) by assuming that during the MD phase the structure of the thalamocortical RF in the deprived eye is not completely degraded. This remnant structure then biases the development of the RF during the RS stage. It is reasonable to assume that if the MD phase would be run longer, this model would predict that the maps from both eyes will no longer be similar, because the bias to the thalamocortical RF in the deprived eye would be eliminated. Another test is the disruption experiment proposed above (Fig. 6). If disruptions of lateral connectivity affect the development of the map from the second eye, this model would be ruled out, because it relies on a bias in the thalamocortical projections. If disruptions do not influence the second eye map, this could either indicate that remnant thalamocortical bias exists, or that the scaffold is encoded in short-range lateral connections.

Wolf and coworkers (1996) have proposed that the stability of the orientation map and, in particular, the results of the Gödecke and Bonhoeffer (1996) experiment could be explained by the shape of area 18. They claim that the shape of area 18, in which these experiments were performed, breaks the symmetry of different orientations and determines the structure of the orientation map. They predict that these results would not generalize to area 17. Such an experiment is difficult to perform, because it is difficult to optically image area 17. However, there is anecdotal evidence from a single-electrode study (Mioche and Singer, 1989) that cells in area 17 also tend to develop the same orientation preference in these conditions.