Electron Vorticity Indicative of the Electron Diffusion Region of Magnetic Reconnection

Abstract

While vorticity defined as the curl of the velocity has been broadly used in fluid and plasma physics, this quantity has been underutilized in space physics due to low time resolution observations. We report Magnetospheric Multiscale (MMS) observations of enhanced electron vorticity in the vicinity of the electron diffusion region of magnetic reconnection. On 11 July 2017 MMS traversed the magnetotail current sheet, observing tailward‐to‐earthward outflow reversal, current‐carrying electron jets in the direction along the electron meandering motion or out‐of‐plane direction, agyrotropic electron distribution functions, and dissipative signatures. At the edge of the electron jets, the electron vorticity increased with magnitudes greater than the electron gyrofrequency. The out‐of‐plane velocity shear along distance from the current sheet leads to the enhanced vorticity. This, in turn, contributes to the magnetic field perturbations observed by MMS. These observations indicate that electron vorticity can act as a proxy for delineating the electron diffusion region of magnetic reconnection.

Key Points

• We report MMS observation of enhanced electron vorticity in the reconnection site

• The magnitude of electron vorticity greater than the electron gyrofrequency indicates the electron diffusion region of magnetic reconnection

• The enhanced electron vorticity contributes to magnetic field perturbations observed by MMS

1. Introduction

Magnetic reconnection, one of the most fundamental physical processes occurring throughout the universe, enables the rapid conversion of large amounts of magnetic energy into kinetic energy. The multiscale kinetic structures associated with reconnection have long been a focus in space plasma physics: The initiation of reconnection and reconfiguration of magnetic topologies are thought to arise in the electron diffusion region (EDR) where the magnetofluid description fails for electrons. This region is embedded within a much larger ion diffusion region (IDR) where Hall physics resulting from demagnetized ions governs magnetohydrodynamics for ions.

The identification of the IDR from in situ observations was facilitated by Hall magnetic and electric field geometry. The EDR had been difficult to identify mainly because of its small size in conjunction with the limited time resolution of plasma measurements until the launch of the Magnetospheric Multiscale (MMS) mission (Burch, Moore, et al., 2016) on 12 March 2015. Webster et al. (2018) reported 32 EDR events during the Phase 1 dayside passes. These EDR encounters exhibited electron agyrotropy, that is, crescent‐shaped electron distributions (Burch, Torbert, et al., 2016), outflow reversals, and dissipative feature (J▪E′ > 0, where J is the current density and E′ is the electric field, E in the electron frame of reference, E′ = E + V _e × B, where V _e is the electron velocity and B is the magnetic field). Torbert et al. (2018) presented MMS observation on 11 July 2017 of a magnetotail EDR, which is evidenced by electron agyrotropy caused by multiple layers of electrons accelerated by the reconnection electric field, super‐Alfvénic electron jets reaching 20,000 km/s, electron bulk motions decoupled from the magnetic field, and Ohmic heating. Another magnetotail EDR event reported by Zhou et al. (2019) also exhibited J▪E′ > 0, electron agyrotropy, and super‐Alfvénic electron jets.

Vorticity is defined as the curl of the velocity vector and is hence a measure of local rotation or parallel shear of the fluid motion. The rotation phenomenon for electrons was predicted to exist in the exhaust region (adjacent to the inner edge of the separatrix) of dayside reconnection by Pritchett and Mozer (2009). They used two‐dimensional (2‐D) particle‐in‐cell simulations of asymmetric reconnection in the presence of a guide field and showed that a series of electron vortices formed along the electron velocity shear layer that arose at the inside edges of the separatrices. These vortices, which have ~0.3 d _i width and ~1 d _i spacing between vortices, are likely to have been generated by the Kelvin‐Helmholtz instability. They are found to produce fluctuating J▪E′ structures and substantial reductions in the guide field magnitude, suggesting that they influence energy dissipation and the reconnection topology. Fermo et al. (2012) used particle‐in‐cell codes to show that electron Kelvin‐Helmholtz vortices forming near the separatrix wrap the magnetic field lines, seeding secondary islands. This scenario has been supported by in situ observations from MMS (Zhong et al., 2018). Gurgiolo et al. (2011) reported electron vorticity burst regions that enclose the IDR using the data from the Cluster spacecraft with spacecraft separations of 230–4,500 km. Phan et al. (2016) showed enhanced electron vorticity observed within the reconnection exhaust region and the exhaust boundaries downstream of the X‐line. Reduction of electron vorticity toward the inflow region indicated that the enhancements resulted from reconnection processes.

Although vorticity has been widely used in fluid and plasma physics, it has not been frequently used in space physics, in particular, reconnection physics. The general lack of multipoint measurements and/or the usual relatively low time resolution of particle data have hindered addressing vorticity around reconnecting current sheets. The cause of the enhancement of electron vorticity, what information can be deduced from the direction and magnitude of vorticity to help to delineate the multiscale reconnection boundaries, and the role of vorticity in modifying magnetic field topology during reconnection have not been tackled experimentally. In this paper, we present the 11 July 2017 magnetotail reconnection event, during which the magnitude of electron vorticity exceeds the electron gyrofrequency and the components show good anticorrelations with the magnetic field perturbations.

The following section briefly describes the MMS instruments used for the present study. An overview of the event including the behavior of the electron vorticity in section 3 is followed by a description of the EDR signatures in section 4 and the first in situ observation of the magnitude of electron vorticity greater than electron gyrofrequency in section 5. We then investigate what causes the large electron vorticity and how the enhancement affects the reconnection geometry in sections 6 and 7. Discussion and conclusions follow in section 8.

2. Instrumentation

The MMS spacecraft (Burch, Moore, et al., 2016) fly in low‐inclination and highly elliptical orbits. The four MMS spacecraft are identically equipped with instruments including plasma instruments (Fast Plasma Instrument, FPI; Pollock et al., 2016), magnetometers (fluxgate magnetometer consisting of the digital fluxgate magnetometer and the analogue magnetometer‐AFG) (Russell et al., 2014), and electric field instruments (EDP) consisting of the spin‐plane double probe (Lindqvist et al., 2016) and the axial double probe (Ergun et al., 2014). We used the magnetic field data from the digital fluxgate magnetometers with a time resolution of 10 ms in burst mode, the DC electric field data calibrated from spin‐plane double probe and axial double probe (with a 0.122‐ms time resolution in burst mode), and particle data in burst mode from the FPI/dual ion spectrometers (DIS) for ions and FPI/dual electron spectrometers (DES) for electrons with a 150‐ and 30‐ms time resolution, respectively, a 11.25° angular resolution, and an energy range of ~10 eV to 26 keV.

3. Overview of the Event

At 2234:00 UT on 11 July 2017, the barycenter of the MMS quartet, encountering the magnetotail current sheet from south to north, was at [−18.1, 7.30, 0.66] Earth radii (R _E) in geocentric solar magnetospheric (GSM) coordinates. The four spacecraft were in a tetrahedron with an average separation of 21.2 km, less than an electron inertial length (d _e ~ 30 km) and electron gyroradius (ρ _e ~ 25 km). Figure 1a shows the detailed field and plasma signatures from 2233:55 to 2234:11 UT, observed by MMS3 (Figure 1a, A–K) and the current density, J · E′, and vorticities derived from the four spacecraft (Figure 1a, L–R).

Figure 1.

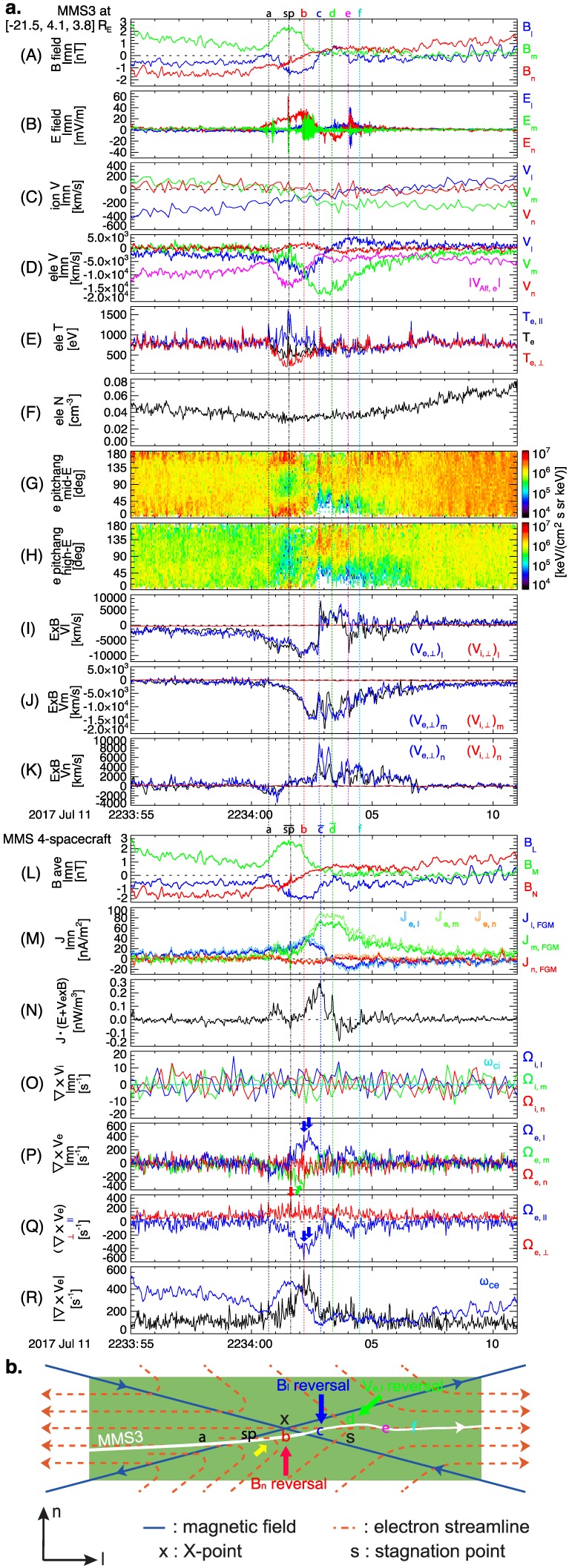
(a) The magnetotail current sheet crossing by MMS3): (A) the l (blue), m (green), and n (red) components of the magnetic field (B) in the LMN coordinates; (B) the electric field; (C) the ion velocity; (D) the electron velocity with the local electron Alfvén speed shown in magenta; (E) the total electron temperature (black in Figure 1E) together with the parallel (blue) and perpendicular (red) electron temperature; (F) the electron density; (G, H) the pitch angle distributions of the middle‐energy (100 eV < energy <1 keV; G), and high‐energy (>1 keV; H) electrons; (I–K) the l, m, and n components of the E × B drift (black) together with the ion (red) and electron (blue) velocities perpendicular to B; (L) the four‐spacecraft tetrahedral‐averaged magnetic field components, B _l, B _m, and B _n (blue, green, and red profiles); (M) the current density calculated from the curlometer technique; (N) Joule dissipation in the electron frame, J▪E′; (O) the ion vorticity (Ω _i = ∇  × V_i); (P) the electron vorticity (Ω _e = ∇  × V_e); (Q) Ω _e decomposed into parallel and perpendicular components to B (blue and red profiles); and (R) the magnitude of Ω _e. (b) A simplified sketch (adopted from Figure 6 of Hasegawa et al., 2019) illustrating possible magnetic field geometries in the l‐n plane seen in blue lines with electron streamlines as dashed red arrows. The white curve represents a possible MMS3 trajectory. Red, blue, and green arrows marks where B _n, B _l, and V _e,l reverses sign along the trajectory, corresponding to B–D in Figure 1a. MMS = Magnetospheric Multiscale.

The top panel (Figure 1a, A) shows the l (blue), m (green), and n (red) components of the magnetic field (B) in the boundary normal (LMN) coordinate system used by Torbert et al. (2018), that is, n in the direction of the maximum directional derivative in B at 22:34:02 UT, m perpendicular to n and maximizing the magnitude of the reconnecting current, and l given by n × m): l = [0.97, 0.22, −0.10], m = [−0.24, 0.94, −0.25], and n = [0.05, 0.27, 0.96] in GSM. The next three panels show the electric field (E, Figure 1a, B), and the ion (V _i, Figure 1a, C) and electron (V _e, Figure 1a, D) velocity. The total electron temperature (black in Figure 1a, E) is presented together with the parallel (blue) and perpendicular (red) electron temperature. Figure 1a (F) shows the electron density. Color coded are the pitch angle distributions of the middle‐energy (100 eV < energy < 1 keV; Figure 1a, G), and high‐energy (>1 keV; Figure 1a, H) electrons. The next three panels (Figure 1a, I–K) show the l, m, and n components of the E × B drift (black) together with the ion (red) and electron (blue) velocities perpendicular to the magnetic field.

At ~2234:02.2 UT (marked by the vertical dashed red line, “b”), B _n changes sign from negative to positive, indicating that the spacecraft were located first tailward, and then, earthward of an X‐line. A negative‐to‐positive change in B _l follows at ~2234:02.8 UT (the vertical dashed blue line, “c”). Coincident E _n (the Hall electric field) changes from positive to negative (Figure 1a, B) indicating an MMS crossing of the current sheet from the southern to northern hemisphere. At ~2234:03.3 UT (the vertical dashed green line, “d”), V _e,l changes from negative to positive, representing tailward‐to‐earthward outflow jets. The slight offset between the reversals of B _n and V _e,l suggests the displacement of the stagnant point from the X‐line along the l direction, as reconstructed by Hasegawa et al. (2019). Figure 1b, adopted from Figure 6 of Hasegawa et al. (2019), illustrates possible magnetic field geometries in the l‐n plane shown by blue lines with electron streamlines as dashed red arrows. The white curve represents a possible MMS3 trajectory. Red, blue, and green arrows mark where B _n, B _l, and V _e,l reverse sign along the trajectory, corresponding to “b,” “c,” and “d” in Figure 1.

Between “b” and “c,” the enhancements of middle‐ and high‐energy electron fluxes with ~90° pitch angles and reductions in 0° and 180° pitch angle components appear (Figure 1a, G and h), indicating a proximity to the X‐line in associated with electrons accelerated by the reconnection electric field, E _m ≈ 1–2 mV/m on average (Figure 1a, B; Torbert et al., 2018). A prior interval (between the vertical dashed black line, “a” on 2234:00.7 UT and B in Figure 1a) exhibits mainly bidirectional (parallel/antiparallel) populations and resulting electron temperature anisotropy (Figure 1, G, H, and E), consistent with typical signatures of the inflow and/or separatrix region (Egedal et al., 2005). The prominent B _m (Figure 1a, A) and E _n (Figure 1a, B) profiles coincide with strong decoupling between ions and electrons (red and blue profiles in Figure 1a, I and J). A singular feature between a and b, marked by the vertical dot‐dashed line “sp” at ~2234:01.5 UT (abrupt B change, large E, reduction in|V _e,m|, intense electron temperature anisotropy, and bidirectional high‐energy electrons, in particular, flowing away from the X‐line in Figure 1a, A, B, D, E, and H), might correspond to the separatrix crossing. (Note that Nakamura et al. (2018, 2019) identified the separatrix crossing as the edge of the EDR at ~2234:02.13 UT, around which the B _n reversal occurred in our LMN coordinates. We defer resolving the ambiguity in pinpointing the time of the separatrix crossing to a future study.) These observations suggest the spacecraft passage through the separatrix region toward the inflow region close to the X‐line (“a” and “b” in Figure 1b).

During a grazing encounter to the Northern Hemisphere (+B _l; between “c” and “e” on ~2234:04.0 UT, the vertical dashed magenta line in Figure 1a, A) including the V _e,l reversal (“d”), complex pitch angle variations appear in association with the stagnant point displaced from X. At ~“e,” MMS3 observed the fastest earthward electron jet (Figure 1ad) when it crossed the near‐X‐line exhaust region current sheet, returning to the Southern Hemisphere. After ~“e,” B _l fluctuating around 0 (Figure 1a, A) shows the spacecraft location near the current sheet until the end of the period shown in Figure 1a.

The overall features indicate that MMS traversed the near‐X‐line reconnection site from the southern hemisphere tailward‐then‐earthward of the X‐line to the Northern Hemisphere earthward of X, as illustrated in Figure 1b. In the following section, we detail the electron physics representing the EDR crossing.

4. Signatures of EDR Crossing

Ion velocities perpendicular to B (almost flat profiles shown in red; Figure 1a, I–K) deviate from the Ε × Β drift (black) over the entire period shown in Figure 1a, demonstrating the spacecraft location within the IDR. Electron velocities perpendicular to B (blue) approximately agree with the Ε × Β motion, but, starting at “c” significantly deviate from Ε × Β until “f” (a vertical dashed cyan line at ~2234:04.5 UT). The mismatch between the electron perpendicular velocity and Ε × Β maximizes at “c,” ~”d,” and “e,” supporting an interpretation that MMS' crossed the EDR. The deviation continues until ~2234:07 UT, as MMS3 stayed near the current sheet (B _l ≈ 0; Figure 1a, A).

Near the V _e,l reversal around “d,” the out‐of‐plane electron velocity (V _e,m; a green profile in Figure 1ad) notably increases along the −m direction. At “c” and “d,”|V _e,m|reaches ~17,500 km/s, greater than the upstream electron Alfvén speed between ~“sp” and ~“b” (magenta in Figure 1a, D; Torbert et al., 2018). Correspondingly, the current density calculated from the curlometer technique (Dunlop et al., 2002; J, solid curves in Figure 1a, M) peaks at ~75 nA/m². During the period of the current enhancement from ~2234:01 to ~2234:07 UT, the electron density is relatively constant and small (Figure 1a, F). Almost identical profiles between J _m and J _{e, m} (the m‐directional current carried by electrons; the dotted green curve in Figure 1a, M) thus indicates that the fast‐moving electrons mostly carry the current of the neutral sheet.

The −m‐directional velocity of these fast‐moving electrons are consistent with the −m‐directional drift of electrons meandering back and forth across the current sheet (Speiser, 1965), being repeatedly accelerated by the reconnection electric field (E _m ranging between 1 and 4 mV/m from Genestreti et al., 2018) when they cross the reconnecting current sheet. Those meandering populations are exhibited by multiple striated distributions in the electron distribution function. The right panels in Figures 2c–2f display reduced electron distributions at ~2234:02.2 UT (“b” in Figure 1a) onto two perpendicular directions in 3‐D velocity space: along the perpendicular component of the ion bulk velocity (V _i), V_⊥1 = Β × (V_i × Β) and V_⊥2 = Β × V_i. At MMS3 (Figure 2c), roughly three populations coexist: a core population in its Ε × Β drift (marked by a red arrow) and crescent‐shaped layers (magenta arrows). The latter are likely to be electrons doing the Speiser motion across the current sheet. The number of current sheet crossing during the Speiser motion or a residence time of the meandering electrons near the X‐line result in the phase density discreteness (magenta arrows) in velocity (energy; Ng et al., 2012; Bessho et al., 2014). Nakamura et al. (2019) confirmed that the observed distributions are in good agreements with the theory presented by Bessho et al. (2014). Although the crescent feature appear over 7 s from ~2234:00 to ~2234:07 UT, the multiple crescents are most distinctly found between ~“b” and ~“d.”

Figure 2.

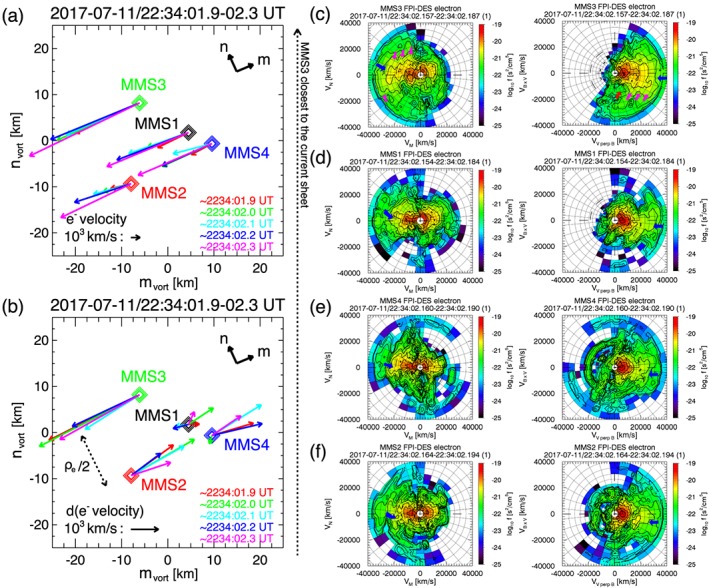
(a) The electron velocity vectors (V _e) observed by the four spacecraft projected onto the plane perpendicular to <Ω _e> that points to [0.99, −0.08, −0.13] in LMN at ~2234:01.9, 2.0, 2.1, 2.2, and 2.3 UT (red, green, cyan, blue, and magenta arrows), respectively; (b) d V _e = V _e $-\overline{{\mathbf{V}}_{\mathrm{e}}}$, where $\overline{{\mathbf{V}}_{\mathrm{e}}}$ is the four‐spacecraft tetrahedral‐averaged electron velocity at each of the five times; (c–f) the reduced electron distribution functions onto the (V_m, V_n) plane (left column) and (V⊥ ₁, V⊥ ₂) plane (right column) at ~2234:02.2 UT from top to bottom in the order of the distance of the spacecraft location from the current sheet (or along −n). Blue arrows point the meandering electrons that drift along −m or V⊥ ₂. Magenta arrows denote multilayered meandering populations that are most clearly observed at MMS3. FPI = Fast Plasma Instrument; MMS = Magnetospheric Multiscale.

Figure 1a (L) shows the four‐spacecraft tetrahedral‐averaged magnetic field components, B _l, B _m, and B _n (blue, green, and red profiles). The reversals of B _n (Figure 1a, L) and V _e,l (Figure 1a, M; indicated by J _{e, m}) still occur at “b” and ~“d” (“ $\overline{\mathrm{d}}$” on 2234:03.35 UT), respectively. The positive B _l signature (“c” to “e” in the upper panels) is absent as MMS3 was located north of the other spacecraft. Ohmic heating in the electron frame, J▪E′ (Figure 1a, N) is mostly positive during the period of interest, indicating magnetic energy dissipation and conversion into particle energy. The dissipation peaks between “a” and “ $\overline{\mathrm{sp}}$” (~2234:01.6 UT), at “ $\overline{\mathrm{c}}$” (~2234:02.9 UT) when the first peak in J _m (Figure 1a, M) is found, and at “ $\overline{\mathrm{d}}$” when V _e,l reverses. During ~2234:03.5–04.5 UT (after “d” to “f”), J▪E′ is mainly negative. The negative J▪E′ and electron jets that outrun the magnetic field (see Figure 1a, I; V _e,l > (Ε × Β)_l) characterize the outer region of the EDR as the electron bulk flow slows in the outer EDR, converting the bulk kinetic energy to thermal energy (Hwang et al., 2017; Karimabadi et al., 2007; Nakamura et al., 2018).

5. Electron Vorticity

Figure 1a (O and P) shows ion vorticity (Ω _i $=\mathbf{\nabla }\mathsf{\times }{\mathsf{V}}_{\mathrm{i}}$) and electron vorticity (Ω _e $=\mathbf{\nabla }\mathsf{\times }{\mathsf{V}}_{\mathrm{e}})$ in LMN. Ω _i displays no evident structures to be identified along with the multiple kinetic boundaries denoted by “a” to “f.” The l component is, however, positive between “b” and ~“f,” and its mean value (~47 rad/s) is much larger than the ion gyrofrequency (ω _ci, the cyan profile in Figure 1a, O).

Ω _e distinctly increases during “a”–“f.” The dominant component is +Ω _e,l, that is, Ω _e primarily points to Earth in the Southern Hemisphere in the vicinity of the magnetotail current sheet. The most intense peaks (blue arrows in Figure 1a, P) coincide with the B _n reversal at ~“b.” Weaker localized peaks in Ω _e,l are observed during ~2234:03–05 UT. At/prior to “b,” −Ω _e,m becomes significant (the green arrow in Figure 1a, P), which corresponds well to the sharply curved electron streamlines illustrated in Figure 1b (the yellow arrow in Figure 1b). Figure 1a (Q) shows Ω _e decomposed into two components parallel and perpendicular to B (blue and red profiles). In relation to +Ω _e,l the antiparallel component to B (−Ω _e,||) exhibits the prominent variations including its maxima at ~“b” (blue arrows in Figure 1a, Q). While the perpendicular component slightly increases during “a”–“f,” a localized peak is found at “ $\overline{\mathrm{sp}}$” (the red arrow between Figure 1a, P and Q), mostly due to large deviations in V _e,m along l (not shown), causing a sharp dip in Ω _e,n (Figure 1a, P).

Figure 1a (R) compares the magnitude of Ω _e (Ω _e) to the electron gyrofrequency (ω _ce, the blue profile in Figure 1a, O). Ω _e is much smaller than ω _ce at the beginning of the plotted interval shown in Figure 1a. It becomes comparable to ω _ce at/around “a,” notably larger than ω _ce from ~“b” to ~“ $\overline{\mathsf{d}}$” and, then, remains comparable to ω _ce until ~2234:07 UT. When Ω _e dominates over ω _ce (~“b” to ~“ $\overline{\mathsf{d}}$”), the positive J▪E′ enhances (Figure 1a, N), electron velocities perpendicular to B significantly disagree with $\mathsf{{\rm E}}\mathit{\times }\mathbf{{\rm B}}$ (Figure 1a, I–K), and the multilayered electron distributions emerges (Figure 2c).

Assuming that ω _system defines a characteristic frequency of a certain plasma region, when ω _system ≪ ω _ci, the plasma system can be described by magnetohydrodynamics; when ω _ci < ω _system < ω _ce, Hall (IDR) physics governs the magnetofluid description; when ω _system > ω _ce, the system enters into the EDR regime. Our first in situ observation of Ω _e greater than ω _ce well corresponds to other EDR signatures. This correspondence indicates that the electron vorticity can act as another proxy of EDR in the reconnection region.

A large velocity shear is also expected to occur across a thin boundary layer even without reconnection. The same is true for electron meandering motion and the resulting crescent‐shaped distributions. Indeed, when the spacecraft stayed around the neutral sheet from ~“f” to ~2234:07 UT (Figure 1a), the electron crescent continues to be observed and Ω _e remains comparable to ω _ce (Figure 1a, R). Therefore, the identification of a reconnection EDR requires simultaneous observations of subelements of the EDR, including nonzero J▪E′, decoupling from Ε × Β, electron crescents, and Ω _e > ω _ce.

6. Origin of the Enhanced Electron Vorticity

To investigate what causes the enhanced Ω _e, we plot the electron velocity vectors observed by the four spacecraft projected onto the plane perpendicular to <Ω _e> (Figure 2a). <Ω _e> represents the direction of Ω _e averaged over the interval including the times when Ω _e peaks (the blue arrows in Figure 1a, P and Q). Instead of a simple average, which gives the result that is very sensitive to the period selection of averaging, we performed a minimum variance analysis (Paschmann & Daly, 1998) using Ω _e during 2234:00–2234:03 UT: l _vort = [0.99, −0.08, −0.13], m _vort = [−0.03, 0.75, −0.67], and n _vort = [0.15, 0.66, 0.73] in GSM. The maximum variance eigenvector (l _vort used for <Ω _e>) is along ~x or ~l. The medium and minimum eigenvectors (m _vort and n _vort) are almost in the mn plane (see upper right corner of Figure 2a).

Red, green, cyan, blue, and magenta arrows present m _vort n _vort‐plane projected electron velocity vectors at ~2234:01.9, 2.0, 2.1, 2.2, and 2.3 UT, respectively. They predominantly points to −m at all four‐spacecraft locations. Note that there is a significant difference in the magnitude of V _{e m} between at MMS3 and MMS2/4. To emphasize this difference, Figure 2b shows d V _e = V _e $-\overline{{\mathbf{V}}_{\mathrm{e}}}$, where $\overline{{\mathbf{V}}_{\mathrm{e}}}$ is the four‐spacecraft tetrahedral‐averaged electron velocity at each of the five times. A parallel velocity shear, rather than a vortical motion, occurs with a maximum of ~6,300 km/s within about half an electron gyroradius (ρ _e ~ 25 km) along ~n (see a dashed black arrow in Figure 2b).

Figures 2c–2f show the reduced electron distribution functions onto the (V_m, V_n) plane (left column) and (V⊥ ₁, V⊥ ₂) plane (right column) at ~2234:02.2 UT from top to bottom in order of spacecraft distance from the current sheet (or along −n). All the four spacecraft observed the meandering electrons that drift along −m or V⊥ ₂, as denoted by blue arrows. MMS3, closest to the current sheet (Figure 2c) most clearly detected multilayered meandering populations (magenta arrows). Blue arrows point out that these populations most broadly spread along −V_m or V⊥ ₂ at MMS3, and shrink toward the core population away from the current sheet.

Figure 2 demonstrates that the enhanced electron vorticity results from the intense parallel velocity shear mostly along −m that originates from the rapid variation in the meandering electrons' velocity (within ~half the electron gyroradius) along the distance away from the current sheet. Since the meandering electrons carry the out‐of‐plane current (J _m in Figure 1a, M), one can expect that at the strong gradient of the current density the electron vorticity enhances. Indeed, Ω _e peaks (blue arrows in Figure 1a, P and Q) are embedded within the ridge of the current density (J _m) profile (Figure 1a, M).

Under these observations, the largest component of electron vorticity, that is, Ω _e,l (Figure 1a, P) can be approximately written: ${\Omega }_{e,l}~\frac{\partial V_{e,m}}{\partial n}~\frac{1}{e{n}_e}\frac{\partial J_m}{\partial n}~\frac{1}{e{n}_e{\mu }_0}\frac{{\partial }^2{B}_l}{{\partial n}^2}$. If B _l changes from 0 at the neutral sheet to B _edge at the southern/northern edge of an EDR with a thickness of d _e, ${\Omega }_{e,l}~\frac{1}{e{n}_e{\mu }_0}\frac{B_{\text{edge}}}{{d_e}^2}~{\omega }_{\mathit{ce}}$. Thus, the peak of Ω _e,l (blue arrows in Figure 1a, P and Q) that is comparable to or larger than ω _ce (Figure 1a, R) delineates the n‐directional edge of the EDR of reconnecting current sheets on d _e scales. This demonstrates why Ω _e compared with ω _ce can be a physical measure to identify EDRs.

7. Effect of the Enhanced Electron Vorticity

Figure 3a presents the four‐spacecraft averaged magnetic field (B) components together with the background magnetic field by fitting each component to a hyperbolic tangent function (B ₀) as shown in cyan. Figure 3b shows Ω _e (the same as Figure 1a, P). We note that B and Ω _e show an anticorrelation. In particular, local peaks of B _l and Ω _e,l relatively coincide (see vertical dashed magenta lines in Figures 4a and 4b).

Figure 3.

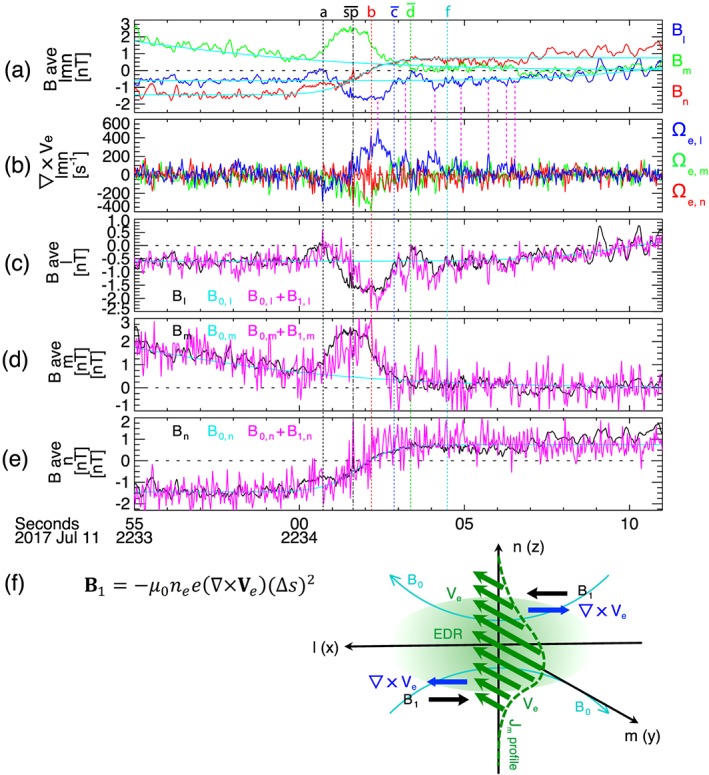
(a) The four‐spacecraft averaged magnetic field (b) components together with the background magnetic field by fitting each component to a hyperbolic tangent function (B ₀) as shown in cyan; (b) Ω _e; (c–e) the l, m, and n component of the measured magnetic field (B, black profiles), the fitted background magnetic field (B ₀, cyan), and B ₀ + B ₁ (magenta), where B₁ ≈  − μ₀n_ee(∇ × V_e)(∆s)² is the magnetic field perturbation induced by the large electron vorticity; (f) an illustration of the rapid variation in the meandering electrons' velocity forming the velocity shear layer, which induces the perturbed magnetic field B ₁, below and above the current sheet under reconnection.

Ampere's law predicts that the electron vorticity generates perturbations in the magnetic field, B₁ ≈  − μ₀n_ee(∇ × V_e)(∆s)², where μ₀ is the magnetic permeability of free space, n _e is the electron density, and ∆s represents the scale size of the electron vortex or velocity shear. We estimate ∆s by calculating V_e/∇V_e, for example, B_1,l ≈  − μ₀n_ee(∇ × V_e)_l(∆s_mn)², where ${∆s}_{\mathit{mn}}=\sqrt{{\left(V_{e,m}/{\nabla }_n{V}_{e,m}\right)}^2+{\left(V_{e,n}/{\nabla }_m{V}_{e,n}\right)}^2}$.

Figures 3c–3d compare the l, m, and n component of the measured magnetic field (B, black profiles), the fitted background magnetic field (B ₀, cyan), and B ₀ + B ₁ (magenta). The black and magenta profiles show relatively good correspondence throughout the period of interest. B _1,l induced by the large electron vorticity along l (Ω _e,l) significantly contribute to the measured B _l depression (Figure 3c) observed between “ $\overline{\mathrm{sp}}$” and “ $\overline{\mathrm{c}}$.” B _1,m also mostly explains the B _m hump (Figure 4d) seen between “ $\overline{\mathrm{sp}}$” and “ $\overline{\mathrm{b}}$.” The disagreement is relatively significant between “a” and “ $\overline{\mathrm{sp}}$,” where the Hall field due to ion‐electron decoupling increases (Figures 1b and 1a, I–K). This indicates that both ion‐electron decoupling occurring on the ion scale size and the electron vorticity occurring at the electron scales result in the variation of B _m in the proximity of the EDR, while the enhanced electron vorticity predominantly leads to B _m variations in the EDR.

8. Discussion and Conclusions

In this letter, we report the first in situ observation of the enhanced electron vorticity (Ω _e) in the EDR of the magnetotail current sheet under reconnection. The magnitude of Ω _e reaches about twice the electron gyrofrequency (ω _ce), suggesting the EDR of the d _e‐scale current sheet. The large electron vorticity originates from the large electron velocity shear (several 10³ km/s) occurring on a scale less than the electron gyroradius and inertial length. The meandering electrons' −m‐directional drift rapidly changes in distance away from the current sheet, resulting in the parallel velocity shear, which induces B ₁, modifying reconnection topology.

Figure 3f illustrates how the rapid variation in the meandering electrons' velocity forms the velocity shear layer below and above the current sheet, assuming a profile of J _m that is carried by the meandering electrons along n (green dashed curve). As indicated by the Ω _e peaks (Figure 1a, P and Q) located at the strong gradient of J _m (Figure 1a, M) and displaced from the J▪E′ peak (Figure 1a, N), the Ω _e peak most likely delineates the outer edge of the EDR along the n direction. Figure 3f predicts the opposite Ω _e and B ₁ in the northern EDR edge of the reconnection current sheet. Indeed, on 17 July 2017, MMS crossed the northern EDR during magnetotail reconnection and observed mostly negative l‐directional Ω _e enhancements and positive B _1,l, correspondingly (Hwang et al., 2018; to be detailed in the follow‐up study). These observations strongly indicate that the electron vorticity can act as a proxy of EDRs in the reconnection site, together with other EDR signatures including nonzero J▪E′, decoupling from Ε × Β, and electron crescents. The advantage of the electron vorticity as a new indicator of the EDR comes from the fact that Ω _e to be compared with ω _ce, which provides a quantitative criterion to identify EDR, is scalar, therefore, independent of a reference frame. The vorticity would be most useful to identify the edges of the EDR, in particular, along the current sheet normal direction. However, it would be locally depressed at the very center of the neutral sheet at/around the X‐line.

Hwang, K.‐J. , Choi, E. , Dokgo, K. , Burch, J. L. , Sibeck, D. G. , Giles, B. L. , et al. (2019). Electron vorticity indicative of the electron diffusion region of magnetic reconnection. Geophysical Research Letters, 46, 6287–6296. 10.1029/2019GL082710