Skip to main content
PMC home page
Wiley Open Access Collection logoLink to Wiley Open Access Collection
. 2019 Jul 22;46(14):7873–7882. doi: 10.1029/2019GL083361

High‐Frequency Wave Generation in Magnetotail Reconnection: Nonlinear Harmonics of Upper Hybrid Waves

Kyunghwan Dokgo 1,✉, Kyoung‐Joo Hwang 1, James L Burch 1, Eunjin Choi 1, Peter H Yoon 2,3,4, David G Sibeck 5, Daniel B Graham 6
PMCID: PMC6774311  PMID: 31598022

Abstract

MMS3 spacecraft passed the vicinity of the electron diffusion region of magnetotail reconnection on 3 July 2017, observing discrepancies between perpendicular electron bulk velocities and E→×B→ drift, and agyrotropic electron crescent distributions. Analyzing linear wave dispersions, Burch et al. (2019, https://doi.org/10.1029/2019GL082471) showed the electron crescent generates high‐frequency waves. We investigate harmonics of upper‐hybrid (UH) waves using both observation and particle‐in‐cell (PIC) simulation, and the generation of electromagnetic radiation from PIC simulation. Harmonics of UH are linearly polarized and propagate along the perpendicular direction to the ambient magnetic field. Compared with two‐dimensional PIC simulation and nonlinear kinetic theory, we show that the nonlinear beam‐plasma interaction between the agyrotropic electrons and the core electrons generates harmonics of UH. Moreover, PIC simulation shows that agyrotropic electron beam can lead to electromagnetic (EM) radiation at the plasma frequency and harmonics.

Keywords: magnetic reconnection, nonlinear plasma waves, PIC simulation

Key Points

  • Harmonics of upper‐hybrid waves are observed near an electron diffusion region of tail reconnection

  • Nonlinear beam‐plasma interaction between the core and crescent electrons is responsible for harmonics generation

  • Particle‐in‐cell simulation result suggests that radio emission is a result of the beam‐plasma interaction

1. Introduction

Magnetic reconnection is a fundamental plasma process that occurs ubiquitously in space, astrophysical, and laboratory plasmas. It converts magnetic field energy to kinetic energy of charged particles by dissipative electric fields. The electron diffusion region (EDR) is a key region of the magnetic reconnection process in which dissipative electric fields exist. In this region, electrons are demagnetized, so they do not follow the convection of the magnetic field line. The kinetic physics of electrons plays crucial roles in the EDR (Birn et al., 2001; Vasyliunas, 1975), and waves and electron structures are strongly associated with the reconnection process (Fujimoto et al., 2011; Hesse et al., 2011).

Investigations about electron‐scale phenomena of the EDR require high‐resolution data. The National Aeronautics and Space Administration's Magnetospheric Multiscale (MMS) mission enables observations of multiscale phenomena in the reconnection site (Burch, Moore, et al., 2016), and the four MMS spacecraft with small separations and high data rate provide detailed information about electron‐scale phenomena in or near the EDR. Various waves are observed in the vicinity of the EDR, such as upper‐hybrid (UH) or Langmuir like waves (Burch, Webster, et al., 2018; Graham et al., 2017), whistler waves (Burch, Webster, et al., 2018; Cao et al., 2017; Graham et al., 2016; Huang et al., 2017; Yoo et al., 2018), their nonlinear activities (Wilder et al., 2016, 2017), and highly localized standing whistler waves (Burch, Ergun, et al., 2018). The agyrotropic electron distribution or the crescent‐shaped electron distribution identified by Burch, Torbert, et al. (2016) is one of the most important characteristics of the EDR. Their presence was expected by previous studies (Aunai et al., 2013; Hesse et al., 2014; Scudder & Daughton, 2008), and they can generate reconnection electric field via off‐diagonal electron pressure tensor terms (Hesse et al., 2014; Hesse & Winske, 1994; Lyons & Pridmore‐Brown, 1990). Comparing spacecraft observations and analytic theory, it is known that exclusions by the cutoff energy affects the electron crescent distribution (Egedal et al., 2016; Rager et al., 2018). Moreover, it is shown that the agyrotropic electrons can be the source of free energy for beam‐plasma interactions near the EDR (Burch et al., 2019; Graham et al., 2017). Interacting with the core population, the agyrotropic electrons generate electrostatic UH waves propagating in a perpendicular direction with respect to the ambient magnetic field.

In this letter, we investigate the generation of nonlinear harmonics of UH waves by crescent electrons (agyrotropic electron beam) near an EDR of a tail reconnection event on 3 July 2017, when MMS3 spacecraft was located at [−17.6, 3.1, 2.2] in units of Earth radius (Re) in the geocentric solar ecliptic (GSE) coordinates. We use burst mode data from the fluxgate magnetometer (Russell et al., 2016), the electric field double probes (Ergun et al., 2016; Lindqvist et al., 2016), the fast plasma investigation (Pollock et al., 2016), and the search‐coil magnetometer (SCM; Le Contel et al., 2016). We compare the observation data with a two‐dimensional electromagnetic particle‐in‐cell (PIC) simulation and nonlinear theory of beam‐plasma interactions.

2. MMS Observation

Figure 1 presents data observed by MMS3 in the GSE coordinate. The total magnetic field is minimum at 05:26:50:730 UT and the Bx field reverses from negative to positive (Figure 1a). The electron density slowly increases from 0.25 to 0.36 cm−3, so the plasma frequency Fpe = ωpe/2π increases from 4.5 to 5.5 kHz (Figure 1b). Near the minimum of the magnetic field, the electron perpendicular temperature increases up to 400 eV (Figure 1c), and there are deviations between perpendicular electron bulk velocities and E⃑×B⃑ drift speeds (Figures 1d–1f). Perturbations of electric field are observed before the X‐line crossing as shown in Figure 1g not the X‐line. As will be shown in this letter, they are linked to the perpendicular drift to y direction much faster than E⃑×B⃑ drift speeds. Fast plasma investigation observed cigar‐shaped electron distribution in the parallel direction and crescent‐shaped electron distributions in the perpendicular V⃑⊥×B⃑ versus B⃑×V⃑ plane as shown in Figures 1l–1n.

Figure 1.

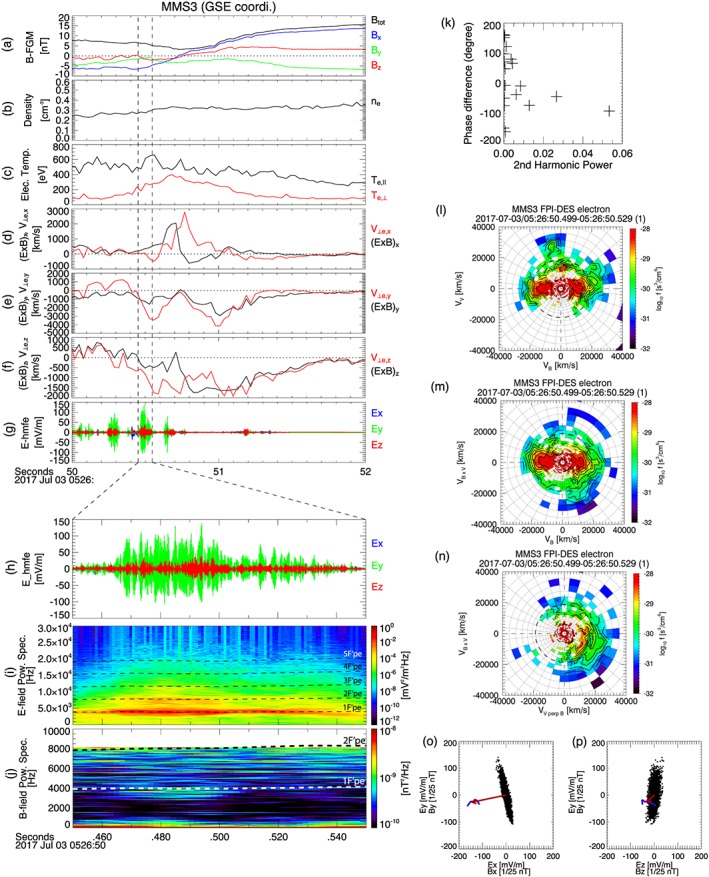
Figure 1

Open in a new tab

The electron diffusion region crossing observed by MMS3. (a) Magnetic fields; (b) electron density; (c) electron temperatures; E⃑×B⃑ drift speeds and perpendicular electron bulk velocities in (d) x, (e) y, and (f) z direction; and (g) electric field during 05:26:50–52. The most intense waves with nonlinear harmonics are observed during 05:26:50:450–550. In this period, (h) electric fields, (i) spectrogram of the electric field, and (j) magnetic field. Dashed lines in (i) and (j) are harmonics of Fpe′ (the frequency of maximum intensity of the fundamental mode). (k) Phase difference between the fundamental mode and the second harmonic versus the power of second harmonic. Electron distributions in (l) B versus V, (m) B versus B⃑×V⃑, and (n) V⃑⊥×B⃑ versus B⃑×V⃑ plane when the harmonics are observed. Hodograms in (o) the x‐y and (p) the z‐y plane where black and blue dots are electric and magnetic field data, respectively. The red arrow indicates averaged magnetic field direction. MMS = Magnetospheric Multiscale; GSE = geocentric solar ecliptic; FPI = fast plasma investigation; DES = dual electron spectrometers.

We focus on the period of 05:26:50:450–550 when the most intense electric field perturbations are shown. The maximum amplitude reaches up to ~140 mV/m as seen in Figure 1h, and the Ey oscillation is dominant. The Ez oscillation is finite but small compared to Ey, while Ex is negligible. Figures 1o and 1p present hodograms in x‐y plane and z‐y plane. Black dots are electric field data, blue dots are magnetic field data, and the red arrow indicates the averaged magnetic field direction. The magnetic field is amplified by 25 times in these hodograms. They show that electric field oscillations are in the perpendicular plane with respect to the ambient magnetic field and that the waveform is linearly polarized, which is consistent with an UH wave as reported by Graham et al. (2017). In the spectrogram of the electric field, discrete harmonic structures are observed as shown in Figure 1i. Up to the fifth mode is identified in this figure. The lowest frequency mode (the fundamental mode) is spread over the frequency range between 0.6Fpe and 1Fpe, and the maximum power is at 0.88Fpe ( ≡Fpe′). We note that the UH frequency Fuh can be replaced with the plasma frequency Fpe since the ratio between the electron plasma frequency and the electron gyrofrequency is very large (ωpe/ωce ≈ 27); thus, they are almost the same. Harmonics of Fpe′ are plotted by horizontal dashed lines in Figure 1i, and it seems that higher nth harmonics are located near nFpe′. The power of second harmonic is on average −15dB of the fundamental, and the second harmonic electric field is aligned with the fundamental within ~1° difference. The phase difference between the fundamental mode and the second harmonics is calculated using their Fourier coefficients for each 3‐ms time window, and they clearly converge to −90° as the power of the second harmonic increases as shown in Figure 1k. Therefore, we conclude that these harmonics are real and not instrumental (Graham et al., 2014). Figure 1k presents the spectrogram of the magnetic field. Because of the SCM noise floor above 1Fpe and that the SCM Nyquist frequency does not cover harmonics, only one mode consistent with the fundamental mode of the electric field is identified.

3. Simulation

3.1. Simulation Conditions

To investigate the generation of the wave and its harmonics, we use a two‐dimensional electromagnetic PIC code (Matsumoto & Omura, 1993) with a periodic simulation domain located in X‐Y plane. We assume homogeneous system because we are interested in local wave generation of high frequency and short wavelength compared to entire reconnection geometry. An ambient magnetic field lies on the X axis, and the agyrotropic beam propagates to the Y axis. Therefore, (X, Y, Z) axes in simulation correspond the GSE (X, Y, Z) axes, respectively. The grid sizes Dx and Dy both are 0.01/ωpe, and the time step Dt is 0.005 ωpe, where ωpe is the electron plasma frequency and c is the speed of light in vacuum. The numbers of grids are 1,024 × 1,024, and the number of time steps is 65,536. The proton‐to‐electron mass mi/me is set to the real value 1,836. On average, we use 1,080 particles of the second‐order shape per unit cell, so the total particle number is ~1.1 billion. Plasma parameters are based on the observed values, so they are chosen as follows: densities of the core electron nco = 0.915n0 and the crescent electron ncr = 0.085n0, where n0 is total electron density, a thermal speed of the core electrons vth,co = 0.011667c, the ion temperature is five times the electron temperature Ti = 5Te, the total electron plasma frequency ωpe = 20ωce, where ωce is the electron gyrofrequency, a drift speed of the crescent electron vd,cr≡vy,cr2+vz,cr2=0.043333c, a thermal speed of the crescent electron vth,cr = 0.011667c, and the range of gyro‐angle of the crescent electron Δ = 70°.

As an initial condition, we uniformly allocate isotropic Maxwellian core electrons and ions and crescent‐shaped electrons. An initial velocity distribution of the crescent electrons is given by a beam speed vd,cr, a thermal speed of the beam vth,cr, and the gyro‐angle range Δ. The gyro‐phase angle ϕ of each crescent electron is defined in the vy‐vz plane while the vy axis is set as ϕ = 0, and ϕ of each crescent electron is limited in the range of −Δ < ϕ < Δ. In addition, we consider that all particles are transient in order to model the particle motion near the EDR. Core electrons reside in the simulation domain during residence times tres,c, which are uniform randomly determined within a range of 0 < tres,c < 0.5 × 2π/ωce for each particle. A core particle escapes after its own tres,c, and a new particle is introduced into the system with new tres,c and new velocities. For a crescent electron, before the particle enters into the system, ϕenter and ϕesc are uniform randomly determined in the range of −Δ < ϕenter < Δ and ϕenter < ϕesc < Δ, respectively. Then, the electron enters with ϕ = ϕenter and escape when ϕ reaches ϕesc. However, this particle distribution is not stationary. Gyration motions and replacements of particles change the distribution even if there is no effect of δE→ and δB→ field. To make a stationary distribution, we carry out a presimulation from t =  − 2π/ωce to t = 0 using only the ambient magnetic field (without δE→ and δB→ field calculations). Then, as shown in Figure 2, we obtain a stationary electron distribution with the core and the crescent while all particles are transient.

Figure 2.

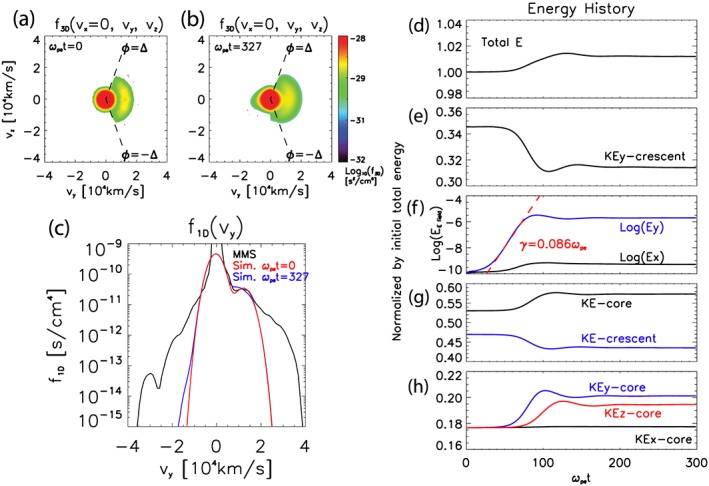
Figure 2

Open in a new tab

Electron distribution in the velocity phase space. f3D in the vy‐vz space where vx = 0 (a) at the beginning (ωpet = 0) and (b) the end (ωpet = 327). The crescent angle ϕ is limited by ±Δ, which are denoted by black dashed lines. (c) f1D as a function of vy. Black solid line is the observation data. Red and blue solid lines are electron distribution of the simulation at the beginning and the end.Time history of (d) total energy; (e) kinetic energies of core and crescent electrons; (f) components of core kinetic energy in x, y, and z direction; (g) y‐directional kinetic energy of the crescent electrons; and (h) electric field energy of x and y direction in a log scale. They are normalized by initial total energy and ωpe.

Figures 2a and 2b represent electron distributions in the velocity phase space at ωpet = 0 and ωpet = 327. They are 2‐D slices of the 3‐D distribution in vy‐vz plane where vx = 0, namely, f3D(vx = 0, vy, vz). The core is Maxwellian, and the crescent electrons are limited by ϕ =  ± Δ (black dashed line). Not including entire reconnection geometry to focus on the local wave generation, the truncation by the cutoff energy is not implemented. But this initial crescent distribution could correspond to a local observation of drifting Maxwellian truncated by the cutoff energy, as studied by Egedal et al. (2016) and Rager et al. (2018). Figure 2c is a reduced 1‐D distribution in which the vx and vz coordinates are integrated. The black line is the MMS observation, and the red and blue lines are simulation data at the beginning ωpet = 0 and the end ωpet = 327. To focus on the beam‐plasma interaction, we ignore the broadened high‐energy part of electron distribution for the initial electron distribution in this study. Thus, we use the same temperature for the core and the crescent beam, as mentioned above. If we consider meandering electrons without any other energization mechanisms, especially an effect of reconnection electric field, the temperature of the inflow core and the crescent would be the same. Therefore, by setting the same temperature, we can analyze the energization of electrons by the beam‐plasma interaction, separately. Details of the simulation will be discussed subsequently. We also carried out another simulation using a beam with higher thermal speed vth,cr = 0.025c. This choice was made in order to better fit the higher velocity portion of the distribution. However, it did not produce a good agreement in the vicinity of the crescent beam speed vd,cr. In this case, the beam‐plasma interaction was very weak, and so we do not present the results.

3.2. Simulation Results

In Figures 2d–2h, we present an energy history of particles and the electric fields normalized by initial total energy. As shown in Figure 2d, the total energy increases by 1.12% at the end of the simulation, and this energy comes from newly replaced particles. (We checked that the total energy changed by up to 0.1% without particle replacements.) In Figures 2e and 2f, the y‐directional kinetic energy of the crescent decreases, and the electric field energies increase after ωpet ≈ 40. They reach the minimum/maximum around ωpet ≈ 100 then saturate undergoing a mild undulation. In the simulation, the linear growth rate γ of the Ey field is 0.086ωpe, which matches very well during 40~70ωpe−1. Consequently, linear and nonlinear regimes can be separated by ωpet = 70.

The kinetic energy of the core electrons (KE‐core) increases from 0.531 to 0.573 during the instability as shown in Figures 2g and 2h. This amount of energy increase is ~7.9% in units of the initial kinetic energy of core electrons. The core energy peaks when the crescent energy (KE‐crescent) is at its minimum. The increase of core energy is larger than the decrease of the crescent energy, which leads to the total energy increasing. The y‐directional core energy (KEy‐core) changes similarly to KE‐core while the z‐directional energy (KEz‐core) is delayed by approximately 20ωpe−1=1ωce−1. Therefore, we could deduce that free energy supplied by crescent electrons is transferred to the core by a wave‐particle interaction mostly in the y direction. Then, due to the gyration, a portion of the KEy‐core changes to the KEz‐core.

Figure 3 shows ω − ky and kx − ky power spectra of Ey (Figures 3a–3d) and Bz (Figure 3e and 3f) fields as well as comparisons between the simulation and MMS observation (Figure 3g and 3h) obtained by a fast Fourier transform. The frequency and the wave number axes are normalized by ωpe and the electron skin depth c/ωpe, respectively, and the simulation unit is used for the power spectra. In the linear regime between ωpet = 0 and ωpet = 70, as shown in Figure 3a, the beam‐mode grows along the y direction as a result of beam‐plasma interaction. Even though the energy increase is almost linear, the second harmonic grows due to the high amplitude of the fundamental mode. In the nonlinear regime between ωpet = 70 and ωpet = 140, more harmonics are observed up to the fourth as shown in Figure 3b.

Figure 3.

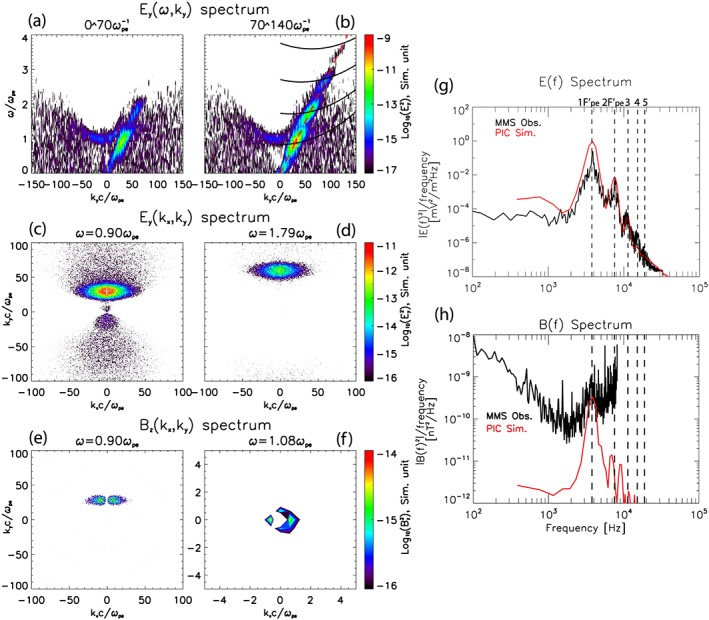
Figure 3

Open in a new tab

Power spectra of Ey and Bz fields. (a) Ey(ky, ω) in the linear regime ωpet = 0~70 and (b) the nonlinear regime ωpet = 70~140. Black solid lines are theoretical dispersion curves of harmonics, and the red dashed line is the effective beam speed. (c) Ey(kx, ky) at fundamental (ω = 0.90ωpe) and (d) second harmonics (ω = 1.79ωpe). (e) Bz(kx, ky) at ω = 0.90ωpe and (f) at ω = 1.08ωpe where the radiation is observed. Comparisons of power spectrum of (g) electric field and (h) magnetic. A black line is the Magnetospheric Multisc (MMS) data, and a red line is the simulation result. Dashed vertical lines indicate harmonics of Fpe′.

To analyze the beam‐plasma interaction, we employ nonlinear theory derived from the nonlinear spectral balance equation (Yoon, 2000; Yoon et al., 2003). Even though the theory explains the 1‐D nonlinear beam‐plasma interaction by a parallel beam or in unmagnetized plasma, it could be applicable to a perpendicular (agyrotropic) beam‐plasma interaction if the plasma is weakly magnetized. The full effect of the magnetic field will be briefly discussed in the subsequent section.

The nonlinear dispersion relation for nth harmonic mode, according to the theory by Yoon et al. (2003), is given by

ωknωpe′=n+23k~2vth,co2c2−3n−12k~vd,cr′c−n2vth,co2vd,cr′2.

Here k~ is a normalized wave number defined by k~=kc/ωpe, which is used in Figure 3. The third term on the right‐hand side in the equation is the nonlinear shift term estimated from weak turbulence theory. We note that we replace vd,cr and ωpe in the equation with an effective beam speed vd,cr′ and an effective plasma frequency ωpe′. Electrons with high∣ϕ∣have the effect of lowering the beam speed in the y direction so the effective beam speed vd,cr′ is smaller than vd,cr. The quantity vd,cr′ in the simulation is 0.03c, and we plot this in Figure 3b by a red dashed line.

We note that the theory of Yoon et al. (2003) focuses on the harmonics generation near nωpe where n is integer number and near higher‐k region, so they used the Bohm‐Gross dispersion for the fundamental mode. In our case, the fundamental beam mode is generated over a wide frequency range ω = 0.5~1.2ωpe and lower‐k region because of high beam density and relatively slow beam speed in comparison to previous studies (Rhee, Woo, & Ryu, 2009; Umeda et al., 2003). However, our fundamental mode locates in the same dispersion curve with the previous studies, because the beam dispersion and the Bohm‐Gross dispersion in higher‐k region make a single dispersion curve based on the linear theory of beam‐plasma instabilities. Consequently, we use ωpe′=0.88ωpe where the maximum power exists. The theoretical dispersion curves are plotted in Figure 3b by black solid lines. According to Rhee, Woo, and Ryu (2009), discrepancies between the dispersion curves and the spectral peaks arising in higher frequency and wave number might be attributed to the two‐dimensional effect of the simulation. As a consequence, we conclude that the power spectra of harmonics from the simulation are in good agreement with the theory, which predicts that the growth of harmonic modes should take place around the intersections between the beam mode line and the dispersion curves.

Figures 3c and 3d present power spectra associated with the fundamental mode at ω=0.90ωpe≅ωpe′ and the second harmonic at ω=1.79ωpe≅2ωpe′ in kx − ky space. The maxima of wave power are located in the (perpendicular) y direction while oblique propagations with respect to y direction have a certain amount of power. The kx spectrum is much broader than ky so that an ellipse‐shaped spectrum appears. When a drifting Maxwellian beam is used, the power spectrum can be modeled by an arc shape, which is proportional to Exp(cosϕ) (Willes et al., 1996; Ziebell et al., 2012); therefore, this ellipse‐shaped spectrum might originate from the crescent‐shaped beam.

Figure 3e shows the power spectra of Bz field at ω = 0.90ωpe. This magnetic field spectrum derives from oblique components of the fundamental beam mode in Figure 3c. We note the Bx (parallel B) component is dominant that agrees with the UH‐like properties. But we plot the Bz spectrum because it can show the whole spectrum structure. The fundamental long‐wavelength radiation is observed at ω = 1.08ωpe as shown in Figure 3f in which Bz spectra in the low‐k region is plotted. There are four intensity peaks, which indicate radiations propagating in the ±x and ±y directions. The most intense peaks are along the ±x propagation directions, and their powers are almost the same. These radiations propagating along ±x (normal directions with respect to the beam direction) can be explained by the electromagnetic decay process of the Langmuir waves (Edney & Robinson, 1999; Lee et al., 2018; Ziebell et al., 2015). The powers of radiations propagating to ±y directions are weaker than ±x propagations, and the generation mechanism of ±y propagations is not clearly understood at this stage, but somewhat similar pattern is observed in fully numerical solution of the equations of EM weak turbulence theory (Ziebell et al., 2015). We note that higher harmonics of magnetic field spectrum from oblique beam‐mode components and from radio emissions are also observed (not shown here). Magnetic field harmonics of oblique beam‐mode components are observed at the same frequency with electric field beam mode, integer multiples of 0.90ωpe, and radio emission harmonics are observed near integer multiples of 1.08ωpe.

Figures 3g and 3h show a comparison of electric field and magnetic field spectra between PIC simulation and MMS observation. We obtain the MMS3 spectrum data, which is an averaged power spectral density between 05:26:50.486 and 05:25:50.490 UTC when the powers of fundamental and harmonic modes are at maximum, and we transform the simulation data to real data units. The black line is MMS3 observation, and the red line is PIC simulation, respectively, and vertical dashed lines indicate nth harmonics of Fpe′. We could barely identify the fifth harmonic, which is too weak to be observable in Figures 1 and 3b. As can be seen in Figure 3g, each peak of the electric field spectrum locates slightly lower than nωpe, and the power decreases as the harmonic number n increases. The wave powers and frequencies of electric field peaks obtained from the simulation agree remarkably well with the observational counterparts.

Figure 3h plots the magnetic field data obtained from the simulation (red line) and MMS observation (black line). In the simulation data, the lower peak below nFpe comes from obliquely propagating components of nth harmonic beam modes, while the other peak slightly higher than nFpe is associated with the radio emission generated by a series of wave‐wave interactions (Rhee, Woo, & Ryu, 2009). The fundamental beam mode agrees between the simulation and the observation; however, other higher beam modes and radio emissions predicted from the simulation are not clearly seen in the MMS observation. Considering that the nominal frequency range of SCM (1 Hz to 6 kHz; Le Contel et al., 2016) does not cover harmonics (>8 kHz), this may come from the instrument limitation of the high‐frequency data.

4. Conclusion and Discussion

This letter shows the generation of harmonics near an EDR by agyrotropic crescent electrons. Comparing MMS observation, PIC simulation, and theoretical dispersion relation of wave modes, we identify harmonic modes generated by the nonlinear beam‐plasma interaction. Nonlinear beam‐plasma theory explains our study very well, which is applicable to zero guide‐field or weak guide‐field reconnection cases.

Since the theory employed in the present investigation assumes nonmagnetized or weakly magnetized plasmas, our findings may have a limited applicability for highly magnetized cases, however. When the ambient magnetic field is intense, then we could envision a situation where the correlation between the growing ES waves and particles interacting with the mode may be influenced by the gyration motion of electrons before a wave has a chance to grow substantially. Thus, when the growth rate is not high enough, for example, when the beam speed or the density is low, or when the distribution is broadened along the gyro‐phase angle, then for such a situation, the wave growth might be impeded even in the linear regime. We might make a conjecture that the ratio between the growth rate of the beam mode and the gyrofrequency would be a crucial factor for wave evolutions in the strongly magnetized situation, for example, as in the guide field reconnection. As such, even for a highly magnetized case, the present nonlinear beam‐plasma theory might still be applicable if the growth rate of the beam mode is sufficiently higher than the gyrofrequency.

The observation of nonlinear harmonics of beam mode implies that long wavelength electromagnetic radio emissions could be generated as a result of nonlinear processes based on previous beam‐plasma simulations. As shown in the PIC simulation, one probable scenario involves the harmonics of radio emissions near ω = nωpe, which is explained by a series of wave‐wave interactions (Lee et al., 2018; Rhee, Ryu, et al., 2009; Ziebell et al., 2015). The fundamental radiation is generated by the electromagnetic decay process [L→S+1H] or induced scattering that involves the eletrons [L→e+1H], while the electrostatic decay process [L→S+L′] leads to a backscattered L′ mode, where L stands for Langmuir waves, S for ion acoustic waves, 1H for fundamental radiations, e denotes electrons, and L′ for backscattered modes. The second harmonics radiation is produced by a wave coalescence process between the Langmuir wave and the backscattered mode [L+L′→2H] (Willes et al., 1996), and, finally, higher harmonics nH are generated by the Zlotnik‐Cairns process between the Langmuir wave and one lower harmonics [L+(n‐1)H→nH] (Cairns, 1988; Zlotnik, 1978). All of these processes are recently confirmed with numerical analysis, which is compared against the simulation (Lee et al., 2018; Ziebell et al., 2015). Another possibility is the mode conversion of Langmuir waves (Hinkel‐Lipsker et al., 1989; Willes & Cairns, 2001) due to the highly inhomogeneous plasma near EDR.

Large amplitude electrostatic waves can in principle efficiently accelerate the particles via wave‐particle interaction. As shown in Figure 2f, the core electrons gain ~7.9% of their initial kinetic energy as a result of the beam‐plasma interaction; hence, UH waves could play a role in energization, diffusion, or scattering of core and crescent electrons near the EDR and affect the reconnection process. However, this process is apparently not sufficient to explain the accelerated electrons in the higher speed range of the MMS3 distribution as presented in Figure 2b. We speculate that these higher‐speed electrons may result from acceleration by the reconnection electric field near the EDR, but more detailed analyses are obviously called for. Gathering from the fact that the beam‐plasma interaction was found to be inefficient in the simulation run with higher thermal speed—which we have carried out but not shown—we conclude that more precise modeling of electron distributions including double Gaussian for the core population, acceleration by the reconnection E‐field, reentering of gyrating electrons, and multiple crescents is called for. Moreover, investigations of kinetic equilibrium in the EDR or in the current sheet geometry could provide where the wave generation and the accelerations via wave‐particle interaction are feasible. In this regard, it is pertinent to note the basis of previous studies of electron acceleration near the EDR (Bessho et al., 2017; Shuster et al., 2015) that modeling double or multiple crescents may be important for the higher speed portion of the observed distribution.

In summary, we have shown that nonlinear harmonics of UH wave occurs near the EDR in the 3 July 2017 event. They are linearly polarized and propagate in the perpendicular direction with respect to the ambient magnetic field. The results of the PIC simulation with transient electrons are consistent with MMS observation. They show that the nonlinear beam‐plasma interaction between the core and the crescent beam generates perpendicular modes at the integer multiple harmonics of the fundamental beam mode. Moreover, PIC simulation results show that agyrotropic electron beams near the EDR can lead to radio emission at the plasma frequency and harmonics.

Acknowledgments

This study was supported, in part, by NASA Guest Investigator Grant 80NSSC18K1337. We acknowledge the use of Pleiades in NASA High‐End Computing Program. K. J. H. was supported, in part, by NSF AGS‐1834451 and NASA 80NSSC18K1534 and 80NSSC18K0570. K. D., K.‐J. H. and E. C. were partly supported by NASA 80NSSC18K0693 and ISSI program: MMS and Cluster observations of magnetic reconnection. P. H. Y. acknowledges Grant BK21 Plus to Kyung Hee University, Korea, from National Research Foundation of the Republic of Korea, and grant from the GFT Charity, Inc., to the University of Maryland. MMS data sets were provided by the MMS science working group teams (through the link http//lasp.colorado.edu/mms/sdc/public/).

Dokgo, K. , Hwang, K.‐J. , Burch, J. L. , Choi, E. , Yoon, P. H. , Sibeck, D. G. , & Graham, D. B. (2019). High‐frequency wave generation in magnetotail reconnection: Nonlinear harmonics of upper hybrid waves. Geophysical Research Letters, 46, 7873–7882. 10.1029/2019GL083361

References

  1. Aunai, N. , Hesse, M. , & Kuznetsova, M. (2013). Electron nongyrotropy in the context of collisionless magnetic reconnection. Physics of Plasmas, 20(9). 10.1063/1.4820953 [DOI] [Google Scholar]
  2. Bessho, N. , Chen, L.‐J. , Hesse, M. , & Wang, S. (2017). The effect of reconnection electric field on crescent and U‐shaped distribution functions in asymmetric reconnection with no guide field. Physics of Plasmas, 24(7), 072903 10.1063/1.4989737 [DOI] [Google Scholar]
  3. Birn, J. , Drake, J. F. , Shay, M. A. , Rogers, B. N. , Denton, R. E. , Hesse, M. , Kuznetsova, M. , Ma, Z. W. , Bhattacharjee, A. , Otto, A. , & Pritchett, P. L. (2001). Geospace Environmental Modeling (GEM) Magnetic Reconnection Challenge. Journal of Geophysical Research, 106(A3), 3715–3719. 10.1029/1999JA900449 [DOI] [Google Scholar]
  4. Burch, J. L. , Dokgo, K. , Hwang, K.‐J. , Torbert, R. B. , Graham, D. B. , Webster, J. M. , Ergun, R. E. , Giles, B. L. , Allen, R. C. , Chen, L.‐J. , Wang, S. , Genestreti, K. J. , Russell, C. T. , Strangeway, R. J. , & Le Contel, O. (2019). High‐frequency wave generation in magnetotail reconnection: Linear dispersion analysis. Geophysical Research Letters, 46, 4089–4097. 10.1029/2019GL082471 [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Burch, J. L. , Ergun, R. E. , Cassak, P. A. , Webster, J. M. , Torbert, R. B. , Giles, B. L. , Dorelli, J. C. , Rager, A. C. , Hwang, K. ‐J. , Phan, T. D. , Genestreti, K. J. , Allen, R. C. , Chen, L. ‐J. , Wang, S. , Gershman, D. , Le Contel, O. , Russell, C. T. , Strangeway, R. J. , Wilder, F. D. , Graham, D. B. , Hesse, M. , Drake, J. F. , Swisdak, M. , Price, L. M. , Shay, M. A. , Lindqvist, P. ‐A. , Pollock, C. J. , Denton, R. E. , & Newman, D. L. (2018). Localized oscillatory energy conversion in magnetopause reconnection. Geophysical Research Letters, 45, 1237–1245. 10.1002/2017GL076809 [DOI] [Google Scholar]
  6. Burch, J. L. , Moore, T. E. , Torbert, R. B. , & Giles, B. L. (2016). Magnetospheric Multiscale overview and science objectives. Space Science Reviews, 199(1–4), 5–21. 10.1007/s11214-015-0164-9 [DOI] [Google Scholar]
  7. Burch, J. L. , Torbert, R. B. , Phan, T. D. , Chen, L. J. , Moore, T. E. , Ergun, R. E. , Eastwood, J. P. , Gershman, D. J. , Cassak, P. A. , Argall, M. R. , Wang, S. , Hesse, M. , Pollock, C. J. , Giles, B. L. , Nakamura, R. , Mauk, B. H. , Fuselier, S. A. , Russell, C. T. , Strangeway, R. J. , Drake, J. F. , Shay, M. A. , Khotyaintsev, Y. V. , Lindqvist, P. A. , Marklund, G. , Wilder, F. D. , Young, D. T. , Torkar, K. , Goldstein, J. , Dorelli, J. C. , Avanov, L. A. , Oka, M. , Baker, D. N. , Jaynes, A. N. , Goodrich, K. A. , Cohen, I. J. , Turner, D. L. , Fennell, J. F. , Blake, J. B. , Clemmons, J. , Goldman, M. , Newman, D. , Petrinec, S. M. , Trattner, K. J. , Lavraud, B. , Reiff, P. H. , Baumjohann, W. , Magnes, W. , Steller, M. , Lewis, W. , Saito, Y. , Coffey, V. , & Chandler, M. (2016). Electron‐scale measurements of magnetic reconnection in space. Science, 352(6290), aaf2939 10.1126/science.aaf2939 [DOI] [PubMed] [Google Scholar]
  8. Burch, J. L. , Webster, J. M. , Genestreti, K. J. , Torbert, R. B. , Giles, B. L. , Fuselier, S. A. , Dorelli, J. C. , Rager, A. C. , Phan, T. D. , Allen, R. C. , Chen, L. J. , Wang, S. , Le Contel, O. , Russell, C. T. , Strangeway, R. J. , Ergun, R. E. , Jaynes, A. N. , Lindqvist, P. A. , Graham, D. B. , Wilder, F. D. , Hwang, K. J. , & Goldstein, J. (2018). Wave phenomena and beam‐plasma interactions at the magnetopause reconnection region. Journal of Geophysical Research: Space Physics, 123, 1118–1133. 10.1002/2017JA024789 [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Cairns, I. H. (1988). A theory for the radiation at the third to fifth harmonics of the plasma frequency upstream from the Earth's bow shock. Journal of Geophysical Research, 93(A2), 858 10.1029/JA093iA02p00858 [DOI] [Google Scholar]
  10. Cao, D. , Fu, H. S. , Cao, J. B. , Wang, T. Y. , Graham, D. B. , Chen, Z. Z. , Peng, F. Z. , Huang, S. Y. , Khotyaintsev, Y. V. , André, M. , Russell, C. T. , Giles, B. L. , Lindqvist, P.‐A. , Torbert, R. B. , Ergun, R. E. , Le Contel, O. , & Burch, J. L. (2017). MMS observations of whistler waves in electron diffusion region. Geophysical Research Letters, 44, 3954–3962. 10.1002/2017GL072703 [DOI] [Google Scholar]
  11. Edney, S. D. , & Robinson, P. A. (1999). Analytic treatment of electromagnetic emission near the plasma frequency via Langmuir wave decay. Physics of Plasmas, 6(10), 3799–3807. 10.1063/1.873644 [DOI] [Google Scholar]
  12. Egedal, J. , Le, A. , Daughton, W. , Wetherton, B. , Cassak, P. A. , Chen, L. J. , Lavraud, B. , Torbert, R. B. , Dorelli, J. , Gershman, D. J. , & Avanov, L. A. (2016). Spacecraft observations and analytic theory of crescent‐shaped electron distributions in asymmetric magnetic reconnection. Physical Review Letters, 117(18), 1–5. 10.1103/PhysRevLett.117.185101 [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Ergun, R. E. , Tucker, S. , Westfall, J. , Goodrich, K. A. , Malaspina, D. M. , Summers, D. , Wallace, J. , Karlsson, M. , Mack, J. , Brennan, N. , Pyke, B. , Withnell, P. , Torbert, R. , Macri, J. , Rau, D. , Dors, I. , Needell, J. , Lindqvist, P. A. , Olsson, G. , & Cully, C. M. (2016). The axial double probe and fields signal processing for the MMS mission. Space Science Reviews, 199(1–4), 167–188. 10.1007/s11214-014-0115-x [DOI] [Google Scholar]
  14. Fujimoto, M. , Shinohara, I. , & Kojima, H. (2011). Reconnection and waves: A review with a perspective. Space Science Reviews, 160(1–4), 123–143. 10.1007/s11214-011-9807-7 [DOI] [Google Scholar]
  15. Graham, D. B. , Cairns, I. H. , & Malaspina, D. M. (2014). Harmonic waves and sheath rectification in type III solar radio bursts. Journal of Geophysical Research: Space Physics, 119, 723–741. 10.1002/2013JA019317 [DOI] [Google Scholar]
  16. Graham, D. B. , Khotyaintsev, Y. V. , Vaivads, A. , Norgren, C. , André, M. , Webster, J. M. , Burch, J. L. , Lindqvist, P. A. , Ergun, R. E. , Torbert, R. B. , Paterson, W. R. , Gershman, D. J. , Giles, B. L. , Magnes, W. , & Russell, C. T. (2017). Instability of Agyrotropic Electron Beams near the Electron Diffusion Region. Physical Review Letters, 119(2), 1–6. 10.1103/PhysRevLett.119.025101 [DOI] [PubMed] [Google Scholar]
  17. Graham, D. B. , Vaivads, A. , Khotyaintsev, Y. V. , & André, M. (2016). Whistler emission in the separatrix regions of asymmetric magnetic reconnection. Journal of Geophysical Research: Space Physics, 121, 1934–1954. 10.1002/2015JA021239 [DOI] [Google Scholar]
  18. Hesse, M. , Aunai, N. , Sibeck, D. , & Birn, J. (2014). On the electron diffusion region in planar, asymmetric, systems. Geophysical Research Letters, 41, 8673–8680. 10.1002/2014GL061586 [DOI] [Google Scholar]
  19. Hesse, M. , Neukirch, T. , Schindler, K. , Kuznetsova, M. , & Zenitani, S. (2011). The diffusion region in collisionless magnetic reconnection. Space Science Reviews, 160(1–4), 3–23. 10.1007/s11214-010-9740-1 [DOI] [Google Scholar]
  20. Hesse, M. , & Winske, D. (1994). Hybrid simulations of collisionless reconnection in current sheets. Journal of Geophysical Research, 99(A6), 11177 10.1029/94JA00676 [DOI] [Google Scholar]
  21. Hinkel‐Lipsker, D. E. , Fried, B. D. , & Morales, G. J. (1989). Analytic expression for mode conversion of Langmuir and electromagnetic waves. Physical Review Letters, 62(23), 2680–2682. 10.1103/PhysRevLett.62.2680 [DOI] [PubMed] [Google Scholar]
  22. Huang, S. Y. , Yuan, Z. G. , Sahraoui, F. , Fu, H. S. , Pang, Y. , Zhou, M. , Fujimoto, K. , Deng, X. H. , Retinò, A. , Wang, D. D. , Yu, X. D. , & Li, H. M. (2017). Occurrence rate of whistler waves in the magnetotail reconnection region. Journal of Geophysical Research: Space Physics, 122, 7188–7196. 10.1002/2016JA023670 [DOI] [Google Scholar]
  23. Le Contel, O. , Leroy, P. , Roux, A. , Coillot, C. , Alison, D. , Bouabdellah, A. , Mirioni, L. , Meslier, L. , Galic, A. , Vassal, M. C. , Torbert, R. B. , Needell, J. , Rau, D. , Dors, I. , Ergun, R. E. , Westfall, J. , Summers, D. , Wallace, J. , Magnes, W. , Valavanoglou, A. , Olsson, G. , Chutter, M. , Macri, J. , Myers, S. , Turco, S. , Nolin, J. , Bodet, D. , Rowe, K. , Tanguy, M. , & de la Porte, B. (2016). The search‐coil magnetometer for MMS. Space Science Reviews, 199(1–4), 257–282. 10.1007/s11214-014-0096-9 [DOI] [Google Scholar]
  24. Lee, S.‐Y. , Ziebell, L. F. , Yoon, P. H. , Gaelzer, R. , & Lee, E. S. (2018). Particle‐in‐cell and weak turbulence simulations of plasma emission. The Astrophysical Journal, 871(1), 74 10.3847/1538-4357/aaf476 [DOI] [Google Scholar]
  25. Lindqvist, P. A. , Olsson, G. , Torbert, R. B. , King, B. , Granoff, M. , Rau, D. , Needell, G. , Turco, S. , Dors, I. , Beckman, P. , Macri, J. , Frost, C. , Salwen, J. , Eriksson, A. , Åhlén, L. , Khotyaintsev, Y. V. , Porter, J. , Lappalainen, K. , Ergun, R. E. , Wermeer, W. , & Tucker, S. (2016). The spin‐plane double probe electric field instrument for MMS. Space Science Reviews, 199(1–4), 137–165. 10.1007/s11214-014-0116-9 [DOI] [Google Scholar]
  26. Lyons, L. R. , & Pridmore‐Brown, D. C. (1990). Force balance near an X line in a collisionless plasma. Journal of Geophysical Research, 95(A12), 20903 10.1029/JA095iA12p20903 [DOI] [Google Scholar]
  27. Matsumoto, H. , & Omura, Y. (1993). Computer space plasma physics: Simulation techniques and software. Tokyo: Terra Scientific Publishing Company. [Google Scholar]
  28. Pollock, C. , Moore, T. , Jacques, A. , Burch, J. , Gliese, U. , Saito, Y. , Omoto, T. , Avanov, L. , Barrie, A. , Coffey, V. , Dorelli, J. , Gershman, D. , Giles, B. , Rosnack, T. , Salo, C. , Yokota, S. , Adrian, M. , Aoustin, C. , Auletti, C. , Aung, S. , Bigio, V. , Cao, N. , Chandler, M. , Chornay, D. , Christian, K. , Clark, G. , Collinson, G. , Corris, T. , de Los Santos, A. , Devlin, R. , Diaz, T. , Dickerson, T. , Dickson, C. , Diekmann, A. , Diggs, F. , Duncan, C. , Figueroa‐Vinas, A. , Firman, C. , Freeman, M. , Galassi, N. , Garcia, K. , Goodhart, G. , Guererro, D. , Hageman, J. , Hanley, J. , Hemminger, E. , Holland, M. , Hutchins, M. , James, T. , Jones, W. , Kreisler, S. , Kujawski, J. , Lavu, V. , Lobell, J. , LeCompte, E. , Lukemire, A. , MacDonald, E. , Mariano, A. , Mukai, T. , Narayanan, K. , Nguyan, Q. , Onizuka, M. , Paterson, W. , Persyn, S. , Piepgrass, B. , Cheney, F. , Rager, A. , Raghuram, T. , Ramil, A. , Reichenthal, L. , Rodriguez, H. , Rouzaud, J. , Rucker, A. , Saito, Y. , Samara, M. , Sauvaud, J. A. , Schuster, D. , Shappirio, M. , Shelton, K. , Sher, D. , Smith, D. , Smith, K. , Smith, S. , Steinfeld, D. , Szymkiewicz, R. , Tanimoto, K. , Taylor, J. , Tucker, C. , Tull, K. , Uhl, A. , Vloet, J. , Walpole, P. , Weidner, S. , White, D. , Winkert, G. , Yeh, P. S. , & Zeuch, M. (2016). Fast plasma investigation for magnetospheric multiscale. Space Science Reviews, 199(1–4), 331–406. 10.1007/s11214-016-0245-4 [DOI] [Google Scholar]
  29. Rager, A. C. , Dorelli, J. C. , Gershman, D. J. , Uritsky, V. , Avanov, L. A. , Torbert, R. B. , Burch, J. L. , Ergun, R. E. , Egedal, J. , Schiff, C. , Shuster, J. R. , Giles, B. L. , Paterson, W. R. , Pollock, C. J. , Strangeway, R. J. , Russell, C. T. , Lavraud, B. , Coffey, V. N. , & Saito, Y. (2018). Electron crescent distributions as a manifestation of diamagnetic drift in an electron‐scale current sheet: Magnetospheric multiscale observations using new 7.5 ms fast plasma investigation moments. Geophysical Research Letters, 45, 578–584. 10.1002/2017GL076260 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Rhee, T. , Ryu, C.‐M. , Woo, M. , Kaang, H. H. , Yi, S. , & Yoon, P. H. (2009). Multiple harmonic plasma emission. The Astrophysical Journal, 694(1), 618–625. 10.1088/0004-637X/694/1/618 [DOI] [Google Scholar]
  31. Rhee, T. , Woo, M. , & Ryu, C. (2009). Simulation study of plasma emission in beam‐plasma interactions. Journal of the Korean Physical Society, 54(9(5)), 313–316. 10.3938/jkps.54.313 [DOI] [Google Scholar]
  32. Russell, C. T. , Anderson, B. J. , Baumjohann, W. , Bromund, K. R. , Dearborn, D. , Fischer, D. , Le, G. , Leinweber, H. K. , Leneman, D. , Magnes, W. , Means, J. D. , Moldwin, M. B. , Nakamura, R. , Pierce, D. , Plaschke, F. , Rowe, K. M. , Slavin, J. a. , Strangeway, R. J. , Torbert, R. , Hagen, C. , Jernej, I. , Valavanoglou, A. , & Richter, I. (2016). The magnetospheric multiscale magnetometers. Space Science Reviews, 199(1–4), 189–256. 10.1007/s11214-014-0057-3 [DOI] [Google Scholar]
  33. Scudder, J. , & Daughton, W. (2008). Illuminating electron diffusion regions of collisionless magnetic reconnection using electron agyrotropy. Journal of Geophysical Research, 113, A06222 10.1029/2008JA013035 [DOI] [Google Scholar]
  34. Shuster, J. R. , Shuster, J. R. , Chen, L. J. , Hesse, M. , Argall, M. R. , Argall, M. R. , Daughton, W. , Torbert, R. B. , Bessho, N. , & Bessho, N. (2015). Spatiotemporal evolution of electron characteristics in the electron diffusion region of magnetic reconnection: Implications for acceleration and heating. Geophysical Research Letters, 42, 2586–2593. 10.1002/2015GL063601.1 [DOI] [Google Scholar]
  35. Umeda, T. , Omura, Y. , Yoon, P. H. , Gaelzer, R. , & Matsumoto, H. (2003). Harmonic Langmuir waves. III. Viasov simulation. Physics of Plasmas, 10(2), 382–391. 10.1063/1.1537240 [DOI] [Google Scholar]
  36. Vasyliunas, V. M. (1975). Theoretical models of magnetic field line merging. Reviews of Geophysics, 13(1), 303–336. 10.1029/RG013i001p00303 [DOI] [Google Scholar]
  37. Wilder, F. D. , Ergun, R. E. , Goodrich, K. A. , Goldman, M. V. , Newman, D. L. , Malaspina, D. M. , Jaynes, A. N. , Schwartz, S. J. , Trattner, K. J. , Burch, J. L. , Argall, M. R. , Torbert, R. B. , Lindqvist, P. A. , Marklund, G. , Le Contel, O. , Mirioni, L. , Khotyaintsev, Y. V. , Strangeway, R. J. , Russell, C. T. , Pollock, C. J. , Giles, B. L. , Plaschke, F. , Magnes, W. , Eriksson, S. , Stawarz, J. E. , Sturner, A. P. , & Holmes, J. C. (2016). Observations of whistler mode waves with nonlinear parallel electric fields near the dayside magnetic reconnection separatrix by the Magnetospheric Multiscale mission. Geophysical Research Letters, 43, 5909–5917. 10.1002/2016GL069473 [DOI] [Google Scholar]
  38. Wilder, F. D. , Ergun, R. E. , Newman, D. L. , Goodrich, K. A. , Trattner, K. J. , Goldman, M. V. , Eriksson, S. , Jaynes, A. N. , Leonard, T. , Malaspina, D. M. , Ahmadi, N. , Schwartz, S. J. , Burch, J. L. , Torbert, R. B. , Argall, M. R. , Giles, B. L. , Phan, T. D. , Le Contel, O. , Graham, D. B. , Khotyaintsev, Y. V. , Strangeway, R. J. , Russell, C. T. , Magnes, W. , Plaschke, F. , & Lindqvist, P. A. (2017). The nonlinear behavior of whistler waves at the reconnecting dayside magnetopause as observed by the Magnetospheric Multiscale mission: A case study. Journal of Geophysical Research: Space Physics, 122, 5487–5501. 10.1002/2017JA024062 [DOI] [Google Scholar]
  39. Willes, A. J. , & Cairns, I. H. (2001). Mode conversion and reflection of Langmuir waves in an inhomogeneous solar wind. Publications of the Astronomical Society of Australia, 18(4), 355–360. 10.1071/AS01051 [DOI] [Google Scholar]
  40. Willes, A. J. , Robinson, P. A. , & Melrose, D. B. (1996). Second harmonic electromagnetic emission via Langmuir wave coalescence. Physics of Plasmas, 3(1), 149–159. 10.1063/1.871841 [DOI] [Google Scholar]
  41. Yoo, J. , Jara‐Almonte, J. , Yerger, E. , Wang, S. , Qian, T. , Le, A. , Ji, H. , Yamada, M. , Fox, W. , Kim, E. H. , Chen, L. J. , & Gershman, D. J. (2018). Whistler wave generation by anisotropic tail electrons during asymmetric magnetic reconnection in space and laboratory. Geophysical Research Letters, 45, 8054–8061. 10.1029/2018GL079278 [DOI] [Google Scholar]
  42. Yoon, P. H. (2000). Generalized weak turbulence theory. Physics of Plasmas, 7(12), 4858–4871. 10.1063/1.1318358 [DOI] [Google Scholar]
  43. Yoon, P. H. , Gaelzer, R. , Umeda, T. , Omura, Y. , & Matsumoto, H. (2003). Harmonic Langmuir waves. I. Nonlinear dispersion relation. Physics of Plasmas, 10(2), 364–372. 10.1063/1.1537238 [DOI] [Google Scholar]
  44. Ziebell, L. F. , Yoon, P. H. , Gaelzer, R. , & Pavan, J. (2012). Langmuir condensation by spontaneous scattering off electrons in two dimensions. Plasma Physics and Controlled Fusion, 54(5). 10.1088/0741-3335/54/5/055012 [DOI] [Google Scholar]
  45. Ziebell, L. F. , Yoon, P. H. , Petruzzellis, L. T. , Gaelzer, R. , & Pavan, J. (2015). Plasma emission by nonlinear electromagnetic processes. Astrophysical Journal, 806(2), 237 10.1088/0004-637X/806/2/237 [DOI] [Google Scholar]
  46. Zlotnik, E. Y. (1978). Intensity ratio of second and third harmonics in type III solar radio bursts. Soviet Astronomy, 22(1), 228–230. [Google Scholar]

Articles from Geophysical Research Letters are provided here courtesy of Wiley

RESOURCES