Observing and Modeling Ice Sheet Surface Mass Balance

Abstract

Surface mass balance (SMB) provides mass input to the surface of the Antarctic and Greenland Ice Sheets and therefore comprises an important control on ice sheet mass balance and resulting contribution to global sea level change. As ice sheet SMB varies highly across multiple scales of space (meters to hundreds of kilometers) and time (hourly to decadal), it is notoriously challenging to observe and represent in models. In addition, SMB consists of multiple components, all of which depend on complex interactions between the atmosphere and the snow/ice surface, large‐scale atmospheric circulation and ocean conditions, and ice sheet topography. In this review, we present the state‐of‐the‐art knowledge and recent advances in ice sheet SMB observations and models, highlight current shortcomings, and propose future directions. Novel observational methods allow mapping SMB across larger areas, longer time periods, and/or at very high (subdaily) temporal frequency. As a recent observational breakthrough, cosmic ray counters provide direct estimates of SMB, circumventing the need for accurate snow density observations upon which many other techniques rely. Regional atmospheric climate models have drastically improved their simulation of ice sheet SMB in the last decade, thanks to the inclusion or improved representation of essential processes (e.g., clouds, blowing snow, and snow albedo), and by enhancing horizontal resolution (5–30 km). Future modeling efforts are required in improving Earth system models to match regional atmospheric climate model performance in simulating ice sheet SMB, and in reinforcing the efforts in developing statistical and dynamic downscaling to represent smaller‐scale SMB processes.

Key Points

• Emerging (remote) observational techniques provide enhanced insights in spatial and temporal variability of ice sheet surface mass balance (SMB)

• Regional climate models can be used to assess ice sheet SMB, although deficiencies remain in representing subgrid processes

• In the near future, Earth System Models can be used to assess internal variability, forced change, and positive feedbacks on ice sheet SMB

1. Introduction

Earth's ice sheets—the Greenland Ice Sheet (GrIS) in the Arctic and the Antarctic Ice Sheet (AIS) roughly centered around the South Pole—collectively contain more than two thirds of the planet's freshwater (Church et al., 2013). If melted completely, global mean sea level would be about 65 m higher than today (Alley et al., 2005). Observations show that both ice sheets are currently losing mass at accelerating rates (E. Rignot et al., 2011; Shepherd et al., 2012, 2018), in spite of large natural interannual variability. Even in a scenario of strong climate change mitigation, in which global mean temperature rise is limited to less than 2 °C relative to preindustrial values, ice sheets will continue to lose mass but are not likely to pass tipping points, in which case mass loss would become irreversible (Pattyn et al., 2018). In high‐emission scenarios, however, projected mass loss from the ice sheets becomes highly uncertain, especially for the AIS; some models predict AIS mass losses in excess of one meter of global sea level equivalent at the end of the 21st century, with multiple meters of potential additional sea level rise in the centuries thereafter (DeConto & Pollard, 2016).

1.1. Ice Sheet Mass Balance and Surface Mass Balance

Ice sheet mass loss/gain is commonly expressed as a negative/positive ice sheet mass balance (MB; Cogley et al., 2011). Ice sheet MB is determined by two main classes of processes: (1) surface mass fluxes (referred to as the surface mass balance, SMB) and (2) the flux of ice across the grounding line (referred to as ice discharge, D). The MB of the grounded ice sheet is defined as MB = SMB − D, which implies that both SMB and D have units of mass change with time (usually expressed in Gt per year, where 1 Gt = 10¹² kg is equivalent to the mass of 1 km³ of water). SMB generally is a positive term (as D is positive) but may also be negative, in which case MB becomes negative, a situation that is sometimes referred to as a tipping point for ice sheet mass loss (Robinson et al., 2012). Once it has crossed the grounding line, ice becomes afloat and forms ice shelves, which are prevalent on the AIS but rare on the GrIS. The MB of these ice shelves comprises of the difference of D + SMB (the incoming mass fluxes), and the two outgoing mass fluxes, (1) melting of the ice shelf base that is in contact with the ocean (basal melting), and (2) iceberg calving at the ice shelf front (Depoorter et al., 2013).

SMB components and relevant processes are visualized in Figure 1. During precipitation and condensation (dew formation) and deposition (riming), mass accumulates at the surface. Mass is lost when meltwater is not retained in the firn by refreezing and/or capillary forces and leaves the ice sheet as runoff; snow can also be redistributed by the wind (erosion/deposition) and/or sublimate, either from the surface or from drifting snow particles. Once accumulated, snow slowly changes into ice via the intermediate product firn, representing a layer of old (i.e., multiyear), compressed snow. The firn layer can be anything between 0 and 130 m thick, depending on the local climate (Ligtenberg et al., 2011). Because the firn layer plays such an important role in the ice sheet MB, in this paper we consider firn processes (meltwater percolation, retention, and refreezing) to be part of the SMB, although formally this use is referred to as “climatic mass balance” (Cogley et al., 2011). Mass is also lost by the movement of glacier ice from the interior ice sheet to the margins, driven by basal sliding and internal deformation, followed by solid ice discharge (D) when the ice crosses the grounding line and starts to float on the ocean.

Figure 1.

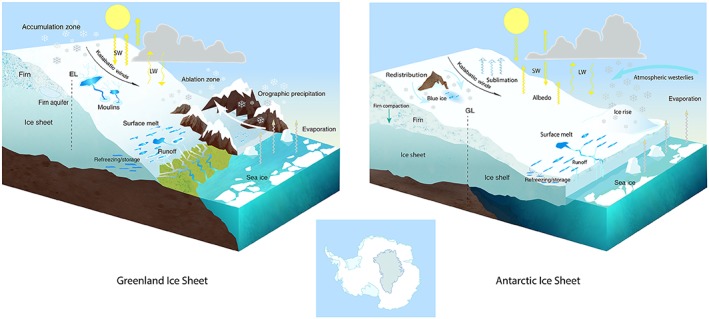
Illustration of all relevant surface mass balance processes on the Greenland (left) and Antarctic (right) ice sheets. Some processes are only indicated on the left or right, depending on where they are most important. The inset below shows a size comparison of the ice sheets, with the Antarctic ice sheet in white and the Greenland ice sheet in grey (Credit: Marlo Garnsworthy, Wordy Bird Studio).

The GrIS and AIS are remarkably different in many of their global characteristics (Figure 1). The AIS (12.9 million km²) is about 7.5 times larger in area than the GrIS (1.7 million km²), contains about eight times more ice (58.2 vs. 7.3 m sea level equivalent; Church et al., 2013), and is characterized by a generally colder, windier, and drier surface climate. An exception to that is the Antarctic Peninsula, which operates in similar ways to the GrIS, with narrow outlet glaciers draining into fjords (Figure 1) and which experiences a much warmer and overall wetter climate than the remainder of the AIS. Moreover, although both ice sheets are currently losing mass (i.e., their MB is negative), they do so at different rates via different mechanisms. While currently increasing AIS mass loss is solely attributed to an increase in D owing to glacier acceleration in spatially limited regions (Mouginot et al., 2014; Rignot et al., 2011; Rignot et al., 2019; Shepherd et al., 2018), GrIS mass loss is dominated by a decrease in SMB that has occurred essentially along its entire margin since the early 1990s (van den Broeke et al., 2016). Temporal SMB trends and their impact on ice sheet MB are discussed in sections 4 and 5.

To understand fully the physical processes that determine ice sheet MB, four different balances must be explicitly solved, one of which is SMB (Figure 2). Ice sheet SMB comprises the sum of multiple components; it is intimately linked to the liquid water balance, which describes sources and sinks of liquid water at the surface (melt, rain, and condensation) and in the firn layer (i.e., percolation/refreezing/retention of liquid water) as well as the surface energy balance (SEB), which determines the energy available for melt, evaporation/condensation, or sublimation/deposition. These processes will be discussed in section 1.2.

Figure 2.

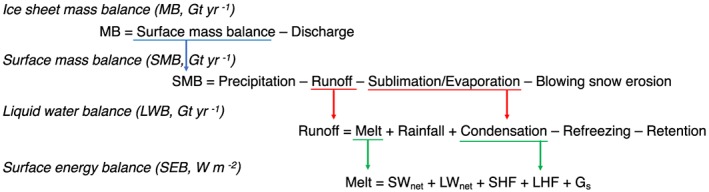
The four equations governing ice sheet MB and components. The colored vertical arrows show how the equations are linked. The SEB components are (all defined at the surface, and positive means that the flux is directed toward the surface): net shortwave radiation (SW_net), net longwave radiation (LW_net), sensible heat flux (SHF), latent heat flux (LHF), and ground/soil heat flux (G_s).

Thus far, we have defined SMB as an ice sheet‐integrated quantity. To evaluate changes at the process scale, we also study values of “local” SMB, expressed in millimeter water equivalent (w.e.) year^‐1 or kg m^‐2 year^‐1 (referred to as “specific SMB,” or “SSMB”). Following this definition, the ice sheet accumulation/ablation zones (Figure 1; see Glossary) comprise all locations where SSMB > 0/SSMB < 0, respectively.

1.2. Components of Surface Mass Balance

1.2.1. Precipitation

The dominant source of mass for ice sheets is precipitation, the transfer of ice particles (snow) or water droplets (rain) from the atmosphere to the ice sheet surface. Atmospheric ice and water can coexist in atmospheric clouds, depending on the thermodynamic characteristics of the atmosphere. Cloud droplets form by condensation onto atmospheric aerosols that act as cloud condensation nuclei. Over ice sheets, cloud condensation nuclei predominantly originate from in‐cloud ice particles, sea salt, and—to a lesser degree—biogenic nuclei, sulphates, dust, and black carbon from long‐range pollution sources or wildfires (Bromwich et al., 2012; Lathem et al., 2013). Clouds over ice sheets typically contain only ice particles (when temperatures less than ‐40 °C) or are mixed‐phase clouds (Bromwich et al., 2012; Shupe et al., 2013), which contain both (supercooled) liquid water droplets and ice. In mixed‐phase clouds, ice precipitation particles (snowflakes) predominantly grow through deposition of water molecules onto them, at the expense of supercooled liquid water droplets that evaporate (the Wegener‐Bergeron‐Findeisen, or simply Bergeron process). Besides this process, ice crystals can change by fragmentation (large ice particles break into smaller ones), accretion (supercooled liquid freezing onto an existing ice crystal), and aggregation (snowflakes merging). As the temperature in the atmosphere over ice sheets is usually below the freezing point, precipitation generally falls as snow. If temperatures in a sufficiently deep atmospheric layer exceed the melting point, however, snowflakes melt as they fall, and precipitation falls on the surface as rain. While other, convective‐weather precipitation types (hail, graupel, etc.) are considered rare over ice sheets (Serreze & Hurst, 2000), the cold and dry GrIS and AIS interior areas frequently experience “clear‐sky precipitation” (Bromwich, 1988). This type of precipitation falls from surface‐based clouds of ice crystals, often referred to as “diamond dust,” and typically occurs during cold and quiet conditions (Ricaud et al., 2017; Sato et al., 1981). Being frequently observed in the interiors of the AIS and GrIS, especially in winter (von Walden et al., 2003), locally diamond dust can contribute significantly (30–80%) to the total annual accumulation (Radok & Lile, 1977; Ricaud et al., 2017).

1.2.2. Surface Melt, Refreezing, Retention and Runoff

Melting (i.e., the phase change from solid to liquid state) of the surface snow and ice occurs when the surface temperature reaches the melting point (0 °C), while excess energy is available. Snow and ice can also melt at some small (<10 cm) depth below the surface (subsurface melt), caused by penetration of solar radiation (Brandt & Warren, 1993). The amount of energy available for melt is determined by the SEB, the sum of radiative, turbulent, and conductive subsurface heat fluxes, ignoring heat from rain (Figure 2; see Glossary). Meltwater generated at the surface can have five different pathways: (1) It collects at the surface in the form of supraglacial meltwater lakes (Koenig et al., 2015; Moussavi et al., 2016); (2) it runs off supraglacially (Bell et al., 2017; Smith et al., 2015); (3) it percolates into the snowpack or runs off englacially through vertical pathways in the ice (moulins) or is diverted laterally when it encounters an impermeable layer, such as ice or bedrock (Chandler et al., 2013); (4) it percolates into the snowpack and is stored in liquid form in weathered ice crusts (Cooper et al., 2018), firn aquifers (Forster et al., 2014), or subsurface lakes (Lenaerts et al., 2016); and (5) it percolates into the snowpack, refreezes, and is stored in the firn as ice (Harper et al., 2012). The pathway of surface meltwater thus strongly depends on surface and firn characteristics (section 1.3); in turn, meltwater pathways affect surface snow and firn characteristics (de la Peña et al., 2015; Machguth et al., 2016; Nienow et al., 2017).

1.2.3. Evaporation and Sublimation

Evaporation (i.e., the phase change from liquid to vapor state) can occur when liquid water is exposed at the ice sheet surface, that is, after melt, condensation, or rainfall. Over snow surfaces, liquid water will quickly penetrate the snowpack, preventing significant evaporation from occurring. However, standing water can be found on impermeable ice, mostly in the form of water collecting in topographic depressions of the ice sheet surface in the GrIS ablation zone (McMillan et al., 2007; Sundal et al., 2009), and on or near some Antarctic ice shelves (Kingslake et al., 2017; Langley et al., 2016; Lenaerts, Lhermitte, et al., 2017). Sublimation, the direct phase change between solid and vapor state, occurs more commonly on ice sheets (Bintanja, 1998; Box & Steffen, 2001; Lenaerts & van den Broeke, 2012; van den Broeke, 1997; van Lipzig et al., 2004). Sublimation represents a turbulent moisture flux and exists in two dominant forms. First, surface sublimation (SU_s) depends on the magnitude of the surface‐to‐air humidity gradient and the wind speed, which represents the wind shear required to generate turbulence (vertical mixing) in the stably stratified surface layer. Sublimation peaks when the sun heats the surface (i.e., typically in the summer season), the near‐surface air is dry, and wind speed is significant but not so high as to induce drifting snow (King et al., 2001). Second, sublimation is favored when snow particles become entrained in the near‐surface atmosphere (Liston & Sturm, 2002; Schmidt, 1982), referred to as drifting snow/blowing snow sublimation (SU_ds). Because the drifting particles are better ventilated than those at the surface, this type of sublimation is more efficient than surface sublimation (Bintanja, 2000, 2001; Déry et al., 1998). Drifting and blowing snow occurs in high‐wind conditions, which prevail in katabatic wind zones over much of the AIS (Lenaerts & van den Broeke, 2012; Palm et al., 2011) and large parts of the GrIS, particularly in winter (Lenaerts, van den Broeke, van Angelen, et al., 2012; Lenaerts, van den Broeke, van de Berg, et al., 2012; Lenaerts, van den Broeke, Déry, et al., 2012; Lenaerts, van den Broeke, Scarchilli, et al., 2012).

1.2.4. Snow Erosion

During drifting and blowing snow conditions, suspended snow particles are (partly) sublimated and/or deposited elsewhere (Essery et al., 1999; Palm et al., 2011). Depending on the surface characteristics and near‐surface wind field, this leads to snow redistribution (Lenaerts, van den Broeke, Déry, et al., 2012). In locations where the near‐surface air flow diverges and/or accelerates, snow will be eroded and—if not sublimated while entrained in the atmosphere—redeposited in areas where the flow convergences and/or decelerates. This implies net snow erosion (ER_ds positive, surface mass loss) in the former and net snow deposition (ER_ds negative, surface mass gain) in the latter regions (Das et al., 2013; Frezzotti et al., 2007; Scambos et al., 2012).

1.3. Factors Driving SMB and SMB Components

1.3.1. Large‐Scale Atmospheric Circulation—Greenland

GrIS SMB is strongly controlled by synoptic (100‐ to 1,000‐km scale) and large‐scale (>1,000 km) atmospheric dynamics. The transport of air masses with varying temperature and moisture content toward the GrIS affects all SMB components. Precipitation on the GrIS is mostly generated by advection of relatively mild, moist air by low‐pressure systems branching off the North Atlantic storm track, an elongated band of high cyclonic activity running southwest‐northeast across the North Atlantic Ocean basin, from the east coast of North America to Iceland and Scandinavia. When mild and moist air encounters the ice sheet, it is forced to rise, expand, and cool, leading to orographically induced precipitation. As a result, the depth and position of low‐pressure systems determine the spatial and temporal distribution of precipitation on the GrIS (Berdahl et al., 2018). In winter, when atmospheric baroclinicity resulting from horizontal temperature gradients peaks, cyclonic activity is focused around Iceland (generating the climatological “Iceland Low”), and weather systems regularly reach the south and southeastern coasts of Greenland. In this area and season, cyclonic activity can be enhanced by the presence of the ice sheet, generating so‐called “lee cyclogenesis” (Schuenemann et al., 2009). In summer, the storm track is less well developed, less symmetrical, and narrower (Chen et al., 1997; Ohmura & Reeh, 1991). In this season, the atmospheric flow is more frequently blocked by the GrIS and can become more north‐south oriented. Synoptic weather systems more frequently approach from the west or south and travel into Baffin Bay, where they become stagnant, bringing precipitation to the GrIS west coast for prolonged periods (Schuenemann et al., 2009). This seasonality in storm track behavior and resulting precipitation patterns explains the remarkable variation in seasonality between west Greenland, where precipitation peaks in summer, and south(‐east) Greenland, where precipitation peaks in winter (Berdahl et al., 2018).

The North Atlantic Oscillation (NAO; Hurrell et al., 2013) index is usually defined as the normalized sea level pressure difference between the Azores and Iceland. With generally low pressure around Iceland and high pressure around the Azores, the NAO index is usually positive, indicative of a well‐developed and zonally directed North Atlantic large‐scale atmospheric circulation. However, the NAO can become zero or negative when the pressure gradient is small or reversed, implying a weak and/or wavy jet stream and blocking conditions. Generally, such a small or negative NAO index is associated with dry conditions over the northern and western GrIS and wet conditions over the southern portion of the GrIS (Appenzeller et al., 1998; Bromwich et al., 1999; Lewis et al., 2017). As these two signals tend to compensate each other, the total GrIS precipitation does not correlate significantly with NAO (Hanna et al., 2011). More importantly, a weak NAO is associated with anomalously warm conditions and upper‐air ridging over Greenland in summer (Figure 3), which can be quantified by the Greenland Blocking Index (Hanna et al., 2016). A weak NAO and high Greenland Blocking Index in summer, such as predominantly observed between 2003 and 2012 (Fettweis et al., 2013; Hanna et al., 2018) in turn leads to anomalously high surface melt on the western GrIS, with 2012 as a peak anomaly. The summer NAO index has returned to positive values, and Greenland SMB has increased to average 1961–1990 values in recent years (2017 and 2018; see www.polarportal.org). Other climate indices that are commonly used to characterize atmospheric circulation variability in the middle to high northern latitudes include the Arctic Oscillation, which is similar to NAO in that it expresses the zonality of the midlatitude jet stream over the North Atlantic, and the Atlantic Multidecadal Oscillation, both of which can explain some degree of variability of GrIS SMB (Hanna et al., 2011; Lewis et al., 2017). Regarding links to tropical climate variability, it has been suggested that the recent weak NAO (and consequent high GrIS summer melt) is caused by anomalous Rossby wave activity originating in the tropical Pacific (Ding et al., 2014). However, on longer time scales, there is little evidence of significant correlations between GrIS SMB and various tropical climate variability indices (Hanna et al., 2006), such as the El Niño Southern Oscillation (ENSO) or the Pacific Decadal Oscillation.

Figure 3.

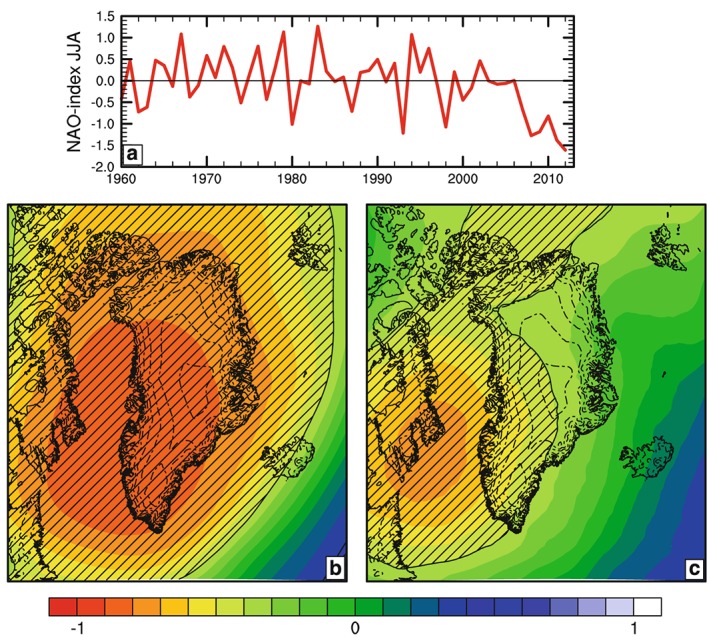
Averaged June–August (JJA) index for the North Atlantic Oscillation (NAO; data from the National Oceanic and Atmospheric Administration). Correlation fields between the JJA NAO index and the 500‐hPa geopotential height (b) and temperature (c) from RACMO2 for 1960–2012; hatched area indicates the 99% confidence level. Source: van Angelen et al. (2014).

1.3.2. Large‐Scale Atmospheric Circulation—Antarctica

Owing to its greater geographical symmetry relative to the large‐scale circulation and sheer size, the precipitation climate of the AIS is remarkably different to that of the GrIS. The circumpolar pressure trough (CPT), a band of low‐pressure systems in high southern latitudes, is deeper and more symmetrical than the storm track in the Northern Hemisphere, since fewer topographical barriers exist to disturb the large‐scale atmospheric flow, and fewer continents are nearby to generate high pressure during winter. Therefore, the CPT features prominently in zonally average pressure distribution, and the meridional transport of heat and moisture is less determined by topography, with the notable exception of the Antarctic Peninsula, a mountain range that extends northward between roughly 60°S to 75°S.

Three climatological low‐pressure systems are embedded in the CPT (Marshall, 2009), generating a zonal wave three atmospheric pattern in maps of average surface pressure (Raphael, 2004). The deepest climatological low‐pressure system is the Amundsen Sea Low (Turner et al., 2013, 2017), centered around 130°W, followed by the low‐pressure system off Wilkes Land in the South‐Central Pacific Ocean (around 100°E), and another system off Dronning Maud Land in the South Atlantic Ocean (around 20°E). The CPT around Antarctica and hence the position of these three climatological low‐pressure systems contract and expand twice a year—in austral spring and autumn—in response to peaks in the meridional temperature gradient and hence baroclinicity, known as the semiannual oscillation (Meehl, 1991; van Loon, 1967). This oscillation induces meridional circulation changes that profoundly affect seasonality in precipitation (Marshall, 2009) and temperature (van den Broeke, 1998), particularly in coastal regions. The largest intra‐annual and interannual variability in SMB is found on the east side of those low‐pressure systems, where southward moisture transport is most pronounced (Marshall, 2009). This is especially true around the Amundsen‐Bellingshausen region, which is sometimes termed the “pole of variability” (Lachlan‐Cope et al., 2001).

Antarctic precipitation is strongly controlled by the meridional (southward) transport of moisture from lower latitudes. The strength and zonality of the midlatitude westerlies are expressed by circulation indices such as the Antarctic Oscillation or Southern Annular Mode (SAM). The correlation between SAM and integrated Antarctic SMB is weak (Medley & Thomas, 2019), as the SAM‐forced precipitation signal predominantly reflects a spatial redistribution (van den Broeke & van Lipzig, 2004), where regional accumulation decreases are compensated for by increases elsewhere (Fyke et al., 2017). In particular, in response to a positive SAM, precipitation is lower in the western part of West Antarctica (around the Ross Ice Shelf), while it is higher on the eastern side on the Antarctic Peninsula (Medley & Thomas, 2019). There is a wide body of literature discussing the role of tropical variability in shaping Antarctic climate, in particular ENSO, but also the Atlantic Multidecadal Oscillation, the Madden‐Julian Oscillation, and Pacific Decadal Oscillation, as summarized by Yuan et al. (2018). Overall, the tropical‐high latitude connection is complex and manifests itself on subseasonal to multidecadal time scales. For example, the recent atmospheric warming on the Antarctic Peninsula in the 1990s (Vaughan et al., 2003) and subsequent cooling after 1998 (Oliva et al., 2017) are most likely linked to natural variations in the strength of the midlatitude westerlies (Turner et al., 2016). ENSO modulates heat and moisture transport onto the West AIS, affecting temperature and precipitation patterns. In response to ENSO, eastern West Antarctica experiences anomalously low sea surface temperatures (SSTs) and an atmospheric moisture flux directed away from the ice sheet, while western West Antarctica (the region around the Ross ice shelf) experiences higher than normal SSTs and anomalously high southward moisture fluxes (Marshall et al., 2017; Marshall & Thompson, 2016). Additionally, recent work suggests that stratospheric ozone depletion, apart from impacting Southern Ocean sea ice and atmospheric dynamics, has led to a spatial redistribution of Antarctic snowfall, and an increase in total snowfall (Lenaerts et al., 2018).

Source regions of precipitation vary strongly for both ice sheets, depending on the distance to the coast, seasonality, and large‐scale atmospheric circulation (Delaygue et al., 2000; Reijmer & van den Broeke, 2001; Sodemann et al., 2008). In general, coastal regions receive most of their precipitation from nearby ocean areas, while high‐elevation snowfall is sourced from remote, lower‐latitude regions, especially on the AIS (Delaygue et al., 2000; Sodemann & Stohl, 2009). The largest precipitation events are caused by “atmospheric rivers,” long‐fetched channels of high atmospheric moisture that protrude from the tropics or midlatitudes all the way to high latitudes (Gorodetskaya, Tsukernik, et al., 2014; Mattingly et al., 2018; Nash et al., 2018). In middle‐ and high‐elevation areas of the AIS, atmospheric rivers generate 30–100% of the annual precipitation (Gorodetskaya et al., 2013; Schlosser et al., 2010), depending on their strength, location, and frequency.

1.3.3. Topography and Winds

Ice sheets represent extensive and highly elevated (>3 km asl) surfaces with a relatively flat and homogeneous interior and steeper and more complex coastal topography, which have a profound impact on their climate and SMB. First, ice sheets interact with the prevalent atmospheric flow on multiple spatial scales. They generate planetary Rossby waves (James, 2006; Löfverström et al., 2014), which describe the large‐scale atmospheric circulation at midlatitudes. The topography of the ice sheet periphery is often relatively steep, rising vertically by ~1 km over a horizontal distance of 100 km or less, leading to orographic precipitation. This is the main driver of coastal precipitation on both ice sheets (Bromwich, 1988; Chen et al., 1997) and can result in high (multiple meters) annual snowfall amounts in areas where topography is steepest, that is, close to the ice sheet edge or in mountainous areas, and aligned perpendicular to the prevalent atmospheric flow, such as in southeast Greenland and the Antarctic Peninsula (van den Broeke et al., 2006; Ettema et al., 2009, section 3). Note that a positive feedback is active, as high precipitation amounts lead to a steeper ice sheet profile. Second, the ice sheet topography shapes the near‐surface wind field (Bromwich et al., 1996; Parish & Bromwich, 1987). Because net radiation is generally negative at the ice sheet surface, the near‐surface air is cooled, and the dominant ice sheet wind regime is katabatic (van den Broeke et al., 2002). If allowed enough time, this gravity‐driven flow of cold air from the ice sheet interior to the coast is turned along the ice sheet contours by the Coriolis force and maintains a downslope component near the surface owing to friction (van den Broeke et al., 2003). The katabatic wind field, and resulting snow redistribution, is subsequently altered by smaller‐scale topography: It is channeled and accelerated in narrow glacial valleys (Bromwich et al., 1990; Gallée et al., 1994; Lenaerts, van den Broeke, van Angelen, et al., 2012; Lenaerts, van den Broeke, van de Berg, et al., 2012; Lenaerts, van den Broeke, Déry, et al., 2012; Lenaerts, van den Broeke, Scarchilli, et al., 2012) and is slowed down and deflected by large obstacles, such as nunataks or topographic promontories. On ice shelves, in the absence of a significant surface slope, katabatic forcing is weak, and synoptic pressure gradients determine the wind field. In the escarpment zone, katabatic winds can be significantly enhanced by synoptic pressure gradients resulting from cyclonic activity over the Southern Ocean for the AIS (van den Broeke et al., 2002, 2003) or in Baffin Bay for the GrIS (van Angelen et al., 2011). Isolated mountain ranges, such as that in the AP, force upslope flow on their windward side, resulting in orographic precipitation, but also generate downslope flow on their leeward side. As it descends dry adiabatically (warming ~10 K/km), the downslope flowing air to the east of the AP mountain range is generally warm and dry and referred to as foehn winds (Elvidge et al., 2015), locally resulting in surface melt (Luckman et al., 2014), even in midwinter (Kuipers Munneke, Luckman, et al., 2018). Other local and regional wind phenomena include barrier winds, which result from the damming of cold air against a topographic barrier (Petersen et al., 2009; van den Broeke & Gallée, 1996), and tip jets, which are driven by orographic descent or flow distortion by an isolated topographic ridge and consequent flow acceleration (Doyle & Shapiro, 1999; Våge et al., 2009). Barrier winds are common on the east and west coasts of Greenland (Harden et al., 2011; van den Broeke & Gallée, 1996), east of the AP (Parish, 1983; Turner et al., 2002), and on the Ross Ice Shelf along the Transantarctic Mountains (Steinhoff et al., 2008). The existence of a tip jet is well documented for south Greenland (Doyle & Shapiro, 1999; Moore et al., 2005) but also occurs commonly in, for example, coastal West Antarctica (Lenaerts, Lhermitte, et al., 2017; Lenaerts, Ligtenberg, et al., 2017; Lenaerts, van Tricht, et al., 2017).

1.3.4. Clouds, Turbulence, Albedo, and Radiation

Ice sheet SMB, and each of its components, is tightly coupled to the exchange of momentum, heat, and moisture between the ice sheet surface and the turbulent near‐surface atmosphere, referred to as the atmospheric surface layer. Turbulent heat and moisture fluxes are part of the SEB, the sum of all the incoming and outgoing energy fluxes at the surface skin layer (Figure 2; see Glossary). Clouds play a pivotal role in determining the SEB through the competing effects of decreasing downwelling solar (shortwave) radiation while enhancing downward thermal (longwave) radiation. The net cloud radiative effect, defined as the difference in surface net all‐wave radiation between average conditions (including clouds) and clear skies, depends on cloud structure, height, and frequency of occurrence (Chen et al., 2000; Shupe et al., 2004; Wang et al., 2005). In polar regions, and over highly reflective snow and ice surfaces, the longwave cloud effect generally dominates the shortwave cloud effect, so that clouds generally result in a net warming of the surface (Curry et al., 1993; Zhang et al., 1996); that is, the net cloud radiative effect is positive. This warming effect by clouds is sometimes referred to as the radiation paradox (Bintanja & van den Broeke, 1995), as its sign is opposite to that of the typical midlatitude cloud effect. This also suggests that clouds over ice sheets can promote surface melting, as has been observed on Larsen C Ice Shelf (King et al., 2015), the GrIS (van Tricht et al., 2016), the grounded parts of the AIS (Hoffman et al., 2008), as well as Arctic sea ice (Kay & Gettelman, 2009).

Surface broadband albedo is the wavelength‐integrated shortwave reflectivity of the surface and determines which fraction of the incoming shortwave radiation is reflected and which part is absorbed by the surface. The spectral (wavelength‐dependent) albedo of clean, dry snow is high (0.8–0.9) in the near‐UV and visible wavelengths but decreases rapidly at larger wavelengths (Wiscombe & Warren, 1980). Snow albedo depends on a variety of atmospheric and surface factors, most prominently snow grain size, cloud cover, solar zenith angle, impurity content, and the presence of liquid water in the snow (Flanner & Zender, 2006; Kuipers Munneke et al., 2008; Wiscombe et al., 1980). Usually, freshly accumulated dry snow grains are relatively small (order 100 μm) and grow in time, driven by temperature and vapor gradients in the snowpack. This decreases snow albedo as larger grains predominantly scatter in the forward direction, that is, into the snowpack, enhancing the chances of absorption (Flanner & Zender, 2006). When surface snow melts, the liquid water will promote (wet) snow grain growth and quickly lower surface albedo (clean wet snow has an albedo of ~0.7, depending on liquid water content and other factors mentioned above). This highlights the powerful positive snowmelt‐albedo feedback, by which, in the absence of fresh snow accumulation, even a small amount of liquid water can decrease snow albedo, further promoting melt. Snow albedo increases with higher solar zenith angle, as the chances of forward scattering and absorption decrease at low sun angles (Wang & Zender, 2010). Lastly, snow albedo depends on the presence and concentration of impurities; at small wavelengths, even in very small quantities dust and black carbon are efficient absorbers of shortwave radiation (Dumont et al., 2014; Flanner & Zender, 2006; Warren & Wiscombe, 1980).

Locally, the firn layer can be fully removed by melt, runoff, and/or sublimation; glacier ice is then exposed at the surface, which has a much lower albedo than that of snow (0.55 for clean ice without impurities, down to 0.3 or lower for impurity‐rich ice). Exposed glacier ice is rare in Antarctica, as it requires ablation (i.e., a negative SSMB) at low temperatures: only approximately 0.8–1.6% of the surface of the AIS consists of bare or so‐called “blue” ice area (Winther et al., 2001), where clean (blue‐colored) glacier ice is (semi)continuously exposed at the surface. These blue‐ice areas appear to be self‐sustaining (Ligtenberg et al., 2014), as they promote surface sublimation, surface and subsurface melt (Liston et al., 2005), and/or blowing snow sublimation and erosion (Lenaerts, Lhermitte, et al., 2017), mechanisms by which any accumulated snow is efficiently removed. In Greenland, about 10% of the ice sheet consists of seasonally snow‐free ablation area (SSMB < 0). A portion of the ablation area in west Greenland is characterized by a relatively lower albedo (the so‐called dark zone), where algae (Stibal et al., 2017), dust (Wientjes et al., 2011), and/or black carbon (van Angelen et al., 2012) lower ice albedo to values of 0.3 or less. Even lower broadband albedo values are found in ice‐free regions, that is, rocks that are exposed above the ice sheet surface (nunataks), and seasonally snow‐free tundra adjacent to the ice sheet, both of which through convection can generate warm air in summer that enhances surface melting of the neighboring snow and ice (Kingslake et al., 2017).

Turbulent heat exchange between the ice sheet surface and the atmosphere can be either direct (sensible heat flux) or in the form of latent heat (through evaporation/sublimation or condensation/riming). The turbulent heat fluxes of sensible (SHF) and latent (LHF) heat are driven by wind shear and vertical gradients in potential temperature and specific humidity, respectively. When the radiation balance is negative (longwave cooling exceeds shortwave warming, i.e., during the polar winter or at night in summer), the surface temperature will sink below the air temperature, creating a surface‐based temperature inversion, a common phenomenon over ice sheets. The inversion can be as large as 30 K over interior East Antarctica (Phillpot & Zillman, 1970) and results in a downward directed SHF (cooling the air and heating the surface). When the surface melts, the surface temperature cannot exceed 0 °C, which means that when the air is warmer than 0 °C, a temperature inversion is again present and SHF is once more directed downward, further promoting melt. In both cases, under these statically stable conditions, wind (shear) is required to generate turbulence in the stably stratified surface layer. In the presence of a surface slope, this wind shear is “automatically” generated by katabatic winds (van den Broeke, van As, et al., 2005; van den Broeke, Smeets, et al., 2009). As a result, SHF can become an important energy source for surface melting in the marginal GrIS, especially when winds are strong over a rough ice surface, further enhancing turbulence intensity (Fausto et al., 2016). Under those conditions, and when the ambient atmosphere is sufficiently warm and moist, LHF can also become a heat source for the surface, in spite of the saturated surface. Under nonmelting conditions, sublimation (negative LHF) can become an important heat sink for the ice sheet snow surface, especially in summer when the sun heats the surface (Kuipers Munneke, Luckman, et al., 2018; Kuipers Munneke, Smeets, et al., 2018).

1.3.5. Firn Characteristics

Liquid water produced at the surface of the ice sheets seldomly runs off directly to the ocean. A thick (up to 130 m; Ligtenberg et al., 2011) layer of firn (compressed, multiyear snow with a density lower than 830 kg/m³) covers the accumulation zone of the ice sheet (~90% of the total area of the GrIS, ~99% of the AIS). The firn layer acts as a runoff buffer by retaining liquid water from melt and rain, as liquid water percolates into the cold firn column, it can be refrozen and stored. Current estimates indicate that almost half and virtually all of the meltwater produced on the GrIS and AIS, respectively, is refrozen and stored in the firn (van Angelen et al., 2013; Harper et al., 2012; Kuipers Munneke, Picard, et al., 2012; Pfeffer et al., 1990; Steger et al., 2017). Without this refreezing, all meltwater produced at the surface—even if temporarily stored in the firn as liquid water—would run off into the ocean unimpeded, enhancing the AIS and GrIS contribution to sea level rise (van Angelen et al., 2013). During the spring of 2014, before the onset of the melt season, liquid water was discovered at 5‐ to 20‐m depth in the firn layer of southeast GrIS (Forster et al., 2014). This body of perennial liquid water, aptly named the perennial firn aquifer, was later found to extend all the way along the southeastern coast to the southern tip of the ice sheet (Miège et al., 2016), with smaller aquifers being present along the southwestern and northwestern ice sheet margin. Formation of a firn aquifer requires high summer melt rates and high snowfall rates, to isolate the meltwater from the cold atmosphere so as to prevent refreezing during winter (Kuipers Munneke et al., 2014).

1.3.6. Sea Ice—Ocean Conditions

Oceanic conditions nearby the ice sheets, such as nearby sea‐surface temperatures (SST) and sea‐ice concentration, are able to modulate ice sheet SMB through various mechanisms. Sea‐ice‐free and/or warmer surface waters promote evaporation, increasing the moisture content of the atmosphere and enhancing precipitation in nearby areas, including the ice sheet coastal areas (van Lipzig et al., 2002). At the same time, open water also acts to warm the atmosphere through the exchange of sensible heat (Deser et al., 2010). Existing literature, focusing on the Arctic region and the GrIS, suggests a weak effect of Arctic sea ice decline on the recent increase in GrIS surface melting (Liu et al., 2016; Noël et al., 2014; Rennermalm et al., 2009; Stroeve et al., 2017). Alternatively, increasing SST and decreasing sea‐ice concentration might also enhance winter snowfall on the GrIS, potentially reducing summer melting through the resulting higher surface albedo (Day et al., 2013). Recent work indicates that similar interactions exist over Antarctica (Kittel et al., 2018; Krinner et al., 2014; Picard et al., 2012). On smaller scales, the generation of open water areas (polynyas) close to the ice sheet margins by strong offshore (katabatic) winds will increase heat and moisture fluxes to the atmosphere. For example, it has been suggested that the springtime opening of the North Water Polynya (in northern Baffin Bay) has triggered early GrIS melt (Stroeve et al., 2017). Large, ocean‐forced polynyas regularly develop in the Weddell Sea (Carsey, 1980), impacting regional atmospheric conditions (Weijer et al., 2017). As of yet, little is known about the possible effects of such large polynyas on AIS ice‐shelf and ice sheet climate and SMB. Lastly, changing oceanic conditions also indirectly affect ice sheet SMB by regulating large‐scale atmospheric circulation (Overland et al., 2012).

2. Methods to Estimate Ice Sheet SMB

Here, we very briefly summarize both traditional and newly emerging techniques for measuring ice sheet SMB. The review by Eisen et al. (2008) presents detailed descriptions of SMB observation methods used in Antarctica, which we briefly summarize.

2.1. Observations

Neglecting effects of horizontal ice flow that advects firn layers with it, at locations where accumulation exceeds ablation (SSMB > 0), a porous firn column is present (Ligtenberg et al., 2011) that is capable of storing meltwater as it percolates into the subsurface, either by refreezing or by capillary forces. If all meltwater is retained, runoff equals zero and SMB equals accumulation, providing the conceptual basis for traditional observations of SMB (e.g., snow stakes and GPR surveys, firn/ice cores); however, sampling must be deep enough to include the retained meltwater and the density of the accumulated material must be determined. In ice sheet ablation zones (SSMB < 0), measurements of surface ablation (using stakes or sonic height rangers) can be directly used to infer the SSMB, because the density of the ablated material (glacier ice) is reasonably well known (830–917 kg/m³); alternatively, if properly allowing for dynamic effects, repeat satellite and airborne altimetry can be used to assess ablation (Sutterley et al., 2018). The techniques described below use these principles to directly or indirectly measure SMB and/or its components. Because several of the techniques rely on the measurement of height (or volume) change for conversion to mass, we first discuss an important correction for firn density. Another correction, for longitudinal strain, is described in the Glossary.

The compaction of fresh snow into solid ice is a slow process that depends on the firn temperature and overburden pressure (Herron & Langway, 1980). In the accumulation zone, assessment of SSMB in water or ice equivalents requires knowledge of the depth‐varying density of the firn column. Density can be measured in situ by weighing a known volume of firn, either in bulk samples from a snow pit or segments of firn cores. These measurements are limited in vertical resolution by the sampling frequency and volume and are prone to measurement error; more recent techniques allow for finer‐scale sampling and improved accuracy (Hawley et al., 2008). Such methods include (1) dielectric profiling that links conductivity and permittivity to firn density (Wilhelms, 2005), (2) borehole optical stratigraphy (Hawley & Morris, 2006), (3) measurements of neutron‐scattering properties of the firn (Morris & Cooper, 2003), (4) gamma‐ray attenuation (Gerland et al., 1999), and (5) the Snow MicroPen snow penetration instrument (Proksch et al., 2015).

Numerous models of firn densification have been proposed, both steady state (Herron & Langway, 1980; Spencer et al., 2001) and time dependent (Arthern et al., 2010; Arthern & Wingham, 1998; Goujon et al., 2003; Li & Zwally, 2011; Ligtenberg et al., 2011; Simonsen et al., 2013). These models provide estimates of firn density with depth that are particularly useful when detailed in situ density measurements are lacking, for example, in the case of airborne and ground‐based radar profiling of isochrones. Next, when converting the surface height change to a fixed anchor point in the firn (e.g., stakes and Global Positioning System [GPS] Interferometric Reflectometry) into SMB, a correction for the firn compaction between the surface and the anchor point must be applied. Finally, the SMB observation needs to be corrected for longitudinal strain (see Glossary), which is based on simple (Dansgaard & Johnsen, 1969; Nye, 1963) to more sophisticated (Huybrechts et al., 2009) ice‐flow models.

2.1.1. Stakes

Perhaps the most traditional way to measure SMB is to a place a stake vertically in the firn or ice that protrudes above the surface (Black & Budd, 1964; Dibb & Fahnestock, 2004; Gow, 1965; McConnell et al., 1997). Immediately upon installation, an initial measurement of the distance between the top of the stake and the surface is made. Upon return, this measurement is repeated, and the difference between final and initial reading reflects the relative change in surface height relative to the level where the stake is anchored (units of meters). In the accumulation zone, the height change represents a seasonal snow depth change and requires multiplying with a bulk density (in units kg/m³) to yield SSMB (in units kg/m² or mm w.e. over time, i.e., the measurement interval). In the ablation zone, stakes are used to estimate ice ablation (Braithwaite, 1995; van de Wal et al., 2005), and the observed height decrease is converted to SMB using the density of glacier ice.

Given the high small‐scale spatial variability (SSV) of SSMB, especially in the interior dry snow zone, a single stake record does not necessarily represent the SMB of a larger area. For instance, interactions between the stake and the local wind field challenge interpretation of the record. To reduce associated uncertainties and quantify SSV, stakes can be combined into an array or farm (Frezzotti et al., 2005; Kameda et al., 2008) or along a transect (Frezzotti et al., 2007; Minghu et al., 2011). Because stakes require revisiting, these observations are typically limited in space and time, and to easily accessible regions. Stake measurements are not appropriate for SSMB measurements in the percolation zone, where surface meltwater can percolate down into the firn and be retained below the stake base.

2.1.2. Snow Pits

Seasonal differences in snow metamorphism allow for visual distinction of summer and winter snow as observed in snow pits (Benson, 1962). Specifically, the layering sequence of fine‐grained winter accumulation and coarse‐grained summer accumulation (depth hoar) is preserved within the firn (Alley et al., 1997). Although visual stratigraphic detection of annual layers is sometimes subjective, it is still a frequently used method for determining snow accumulation rates within snow pits and even with ice cores, mainly because it yields rapid results.

2.1.3. Firn/Ice Cores

Firn and ice cores provide SSMB estimates that vary in time span and resolution, depending on the length of the core, the accumulation rate, and the type of dating. The dating techniques rely on the fact that distinctive time markers are preserved within the firn and ice column. Several time markers or even annually resolved layers enable the construction of an SSMB time series.

2.1.3.1. Multidecadal Ice‐Core Records

The deposition of volcanic and/or radioactive material over polar ice sheets results in reference horizons that can be used as time markers. Long‐term, bulk accumulation rates can be determined by estimating the mass of snow, firn,and/or ice between well‐dated horizons, including the surface. The sequence of bomb tests during the mid‐1950s and early‐1960s left a unique signature of enhanced β‐activity that, when detected, provides a well‐known tie point for absolute dating of the ice (Picciotto & Wilgain, 1963). Similarly, deposition of volcanic sulfate aerosols provides well‐dated reference horizons, and their unique sequences are also well preserved in ice cores (Cole‐Dai et al., 2000; Zielinski et al., 1994). The use of reference horizons is most suitable in regions where snow accumulation rates are relatively low, challenging the detection of annual snow layers.

2.1.3.2. Annual Ice‐Core Records

Annually resolved SSMB records are useful, as they allow for assessment of the local and global drivers of change when analyzed in combination with atmospheric data (Thomas et al., 2015, 2017). Chemical detection of seasonally varying parameters, such as oxygen/hydrogen‐isotopic composition and concentrations of hydrogen peroxide, dust, and/or nonsummer sea salt sulfate, allows for objective determination of annual layers (Herron, 1982; McConnell et al., 2002). When combined with volcanic or radioactive time markers, uncertainty is largely reduced, yielding time series of annual snow accumulation. Several drilling programs have used a multiparameter approach for assessment of accumulation changes over Greenland (Mosley‐Thompson et al., 2001) and Antarctica (Kaspari et al., 2004; Oerter et al., 2000).

As with stake measurements, ice cores provide SSMB estimates for a single location, where local SSV due to wind redistribution (e.g., sastrugi) imparts additional noise on the record. If the accumulation rate is sufficiently low, this glaciological noise can overwhelm the large‐scale variability. Thus, the common interannual variability between measured and modeled accumulation rates in these low accumulation areas (e.g., East Antarctic Plateau) is often quite small, especially when compared to high accumulation regions (e.g., Antarctic Peninsula, Thomas et al., 2017). Regionally colocated cores are often stacked to minimize the impact of SSV (Banta et al., 2008; Fisher et al., 1985; Frezzotti et al., 2013; McConnell, Mosley‐Thompson, et al., 2000).

2.1.4. Ground‐Penetrating Radar

Ground‐ (or ice‐) penetrating radar (GPR) is a nondestructive method of mapping the internal stratigraphy of the firn and ice column along a transect. Because radar‐derived accumulation measurements capture the spatial variability better than widely spaced point measurements, they provide a more accurate representation of the spatial mean and thus are more appropriate for MB studies (Richardson et al., 1997). Moreover, they sometimes go back in time hundreds of years, enabling quantification of long‐term accumulation variability. Three‐dimensional mapping of the firn (i.e., in various horizontal directions) also allows us to quantify the impact of SSV on SMB estimation. As for ice cores, GPR analysis relies on the assumption that stratigraphic reference horizons can be dated in either an absolute or relative sense. It relies on the assumption that each radar horizon represents an isochrone, that is, is representative of a single deposition event. In the upper layers of the firn, where ice crystal fabric is relatively constant, and in absence of volcanic ash layers of melt layers that can impact conductivity, stratigraphic horizons in radargrams represent contrasts in dielectric permittivity, which are likely caused by seasonal variations in the physical and chemical properties of the firn (Arcone et al., 2005; Eisen et al., 2008).

Ground‐based radar imaging of both near‐surface (Anschutz et al., 2007, 2008; Eisen et al., 2005; Frezzotti et al., 2007; Rotschky et al., 2004; Sinisalo et al., 2004; Spikes et al., 2004; Urbini et al., 2008) and deep (Huybrechts et al., 2009; MacGregor et al., 2009; Nereson et al., 2000; Siegert & Payne, 2004; Waddington et al., 2007) internal horizons has provided the basis for calculating recent and historical spatiotemporal snow accumulation rates over Antarctica. In the last decade however, airborne‐based GPR has revolutionized observational ice sheet accumulation observations. The Center for Remote Sensing of Ice Sheets began development of several airborne radar systems, capable of surveying to different depths and at varying vertical resolutions, around the year 2000 (Kanagaratnam et al., 2004, 2007). Their continued improvement over the years accelerated in 2009 with the start of NASA Operation IceBridge (OIB) campaigns that are currently scheduled to run through 2019. The Center for Remote Sensing of Ice Sheets (CRESIS) “snow” and “accumulation” radars measure shallow (10 m) to intermediate (100 m) depths at respective vertical resolutions of ~3 and ~40 cm in firn, making them ideal candidates for measuring annual and multiannual accumulation rates (Rodriguez‐Morales et al., 2014). Using spatial extrapolation techniques, the relative (i.e., relative to a “background” large‐scale SMB value) or absolute SSMB derived from these OIB flight lines can be used to map drainage basin‐scale SMB, for instance over the Pine Island and Thwaites glacier catchments (see Glossary, Medley et al., 2013, 2014), and for the GrIS interior (Lewis et al., 2017; Overly et al., 2016) and Southeast (Koenig et al., 2016). Until late 2019, OIB flies annual campaigns over both ice sheets, including extensive portions of the GrIS, West Antarctica, and the Antarctic Peninsula; however, much of this vast archive of data has yet to be analyzed, leaving significant room for future analysis.

Estimation of SSMB from GPR begins with tracking the internal horizons, which is accomplished manually or in a semiautomated approach. Measured or modeled firn depth‐density profiles are used to convert the radar measurements of two‐way travel time τ (in seconds) to depth d (in meters) via a density‐dependent mixture model (Looyenga, 1965) of dielectric permittivity ε _d (d = cτ/2ε_d^1/2). The spatially varying depths are next converted to water or ice equivalents using the cumulative mass (depth‐integrated density) profiles (Medley et al., 2015). To estimate accumulation rates, the relative or absolute ages of the horizons of interest must be determined. Most studies rely on complementary firn or ice‐core depth‐age relationships along the radar profile to date the tracked horizons (Spikes et al., 2004). Where the vertical resolution of the radar system is sufficiently fine (5–10 cm) relative to the mean annual accumulation (>1 m), recent studies have avoided the need for ancillary ice core data by assuming that adjacent horizons are annually spaced (Medley et al., 2013; Scott et al., 2010). Once adjacent markers have been dated and their relative age difference assessed, accumulation rates are determined by dividing the water or ice‐equivalent thicknesses between markers by the age difference.

2.1.5. Automatic Weather Stations

Most automatic weather stations (AWSs) are equipped with an acoustic depth gauge (or sonic altimeter), which measures the vertical distance between the sensor (anchored in or placed on the snow surface at time of deployment) and the surface, which is displaced in time in response to accumulation and ablation. Knowing snow density, this measurement can be converted to an SSMB time series by taking the difference between the actual distance and the initial distance at each time of measurement. Although representing only a single location, and with data quality that can be poor at times during blowing snow or fog conditions, this technique can provide a semicontinuous SSMB record at high (typically hourly) temporal resolution (van den Broeke et al., 2004; Gorodetskaya et al., 2013; Qin et al., 2004).

In addition, in combination with an SEB model (van den Broeke, van As, et al., 2005; van den Broeke, Reijmer, et al., 2005), AWSs can provide in situ estimates of the SEB, which are urgently needed to improve models of the ice sheets and their projections (Trusel et al., 2015). This requires the operation of high‐quality instrumentation (Figure 2) (van den Broeke, van As, et al., 2005; van den Broeke, Reijmer, et al., 2005). An SEB model yields the turbulent latent heat flux to quantify sublimation, melt energy for the production rate of liquid water, and the subsurface heat flux, that is, the molecular conduction of heat into/away from the subsurface. The latter heat flux determines refreezing and hence runoff rates in the percolation zone. AWS data are indispensable for validating and calibrating, for example, satellite‐derived surface temperature (Reeves Eyre & Zeng, 2017) and melt (Trusel et al., 2012; Trusel et al., 2013). In contrast to Greenland, where melt is significant and even almost continuous during summer at lower elevations (Kuipers Munneke, Luckman, et al., 2018; Kuipers Munneke, Smeets, et al., 2018), melt in Antarctica is often a subtle and intermittent process, requiring accurate observations as melt energy represents the (small) difference of various large energy fluxes (van den Broeke, Bamber, et al., 2009; van den Broeke, König‐Langlo, et al., 2009; van den Broeke, Smeets, et al., 2009).

Recent investments have been made in developing a new generation of AWSs, for a multitude of reasons. First, the rapid expansion and high level of international collaboration in polar research implies that several teams of researchers and technicians from all countries and institutes must be capable of easily deploying, maintaining and checking AWSs on glaciers and ice sheets. Second, these activities must be performed as time efficiently as possible, while not compromising the personnel security and long‐term reliability of the AWS. And third, the number of batteries of any type involved in transport and AWS operation must be reduced as much as possible to enhance transportation safety, to protect the environment, and to reduce operational costs. An example of a new design AWS that considers these restrictions is the iWS (intelligent Weather Station for polar use; van den Broeke et al., 2013). The iWS unit is much smaller than the previous generation of AWSs but includes all meteorological sensors (except wind speed and radiation, which are installed externally), as well as an ultrasonic height ranger, an electronic compass and inclinometer and a GPS, data storage module, and satellite and Bluetooth connectivity. This new design uses ~95% less energy than AWS of the previous generation, using the latest sensor technology, a small solar panel, and efficient energy usage. The station has been successfully deployed on the GrIS and AIS (Figure 4).

Figure 4.

Examples of emerging measurement techniques. (a) iWS installed in high‐accumulation area in South‐East Greenland (installed in April 2014. Courtesy: Clément Miège, Rutgers University); (b) Using Global Positioning System (GPS; example on the left, courtesy: Matthew Siegfied) reflections to detect surface height changes (Dz_surf/Dt in sketch on the right). Right sketch taken from Shean et al. (2017); (c) ICESat‐2 laser altimeter, launched in September 2018 (source: icesat2‐gsfc.nasa.gov).

2.1.6. GPS Interferometric Reflectometry

A recent innovative technique uses the reflected signal recorded by GPS antennas to obtain surface height changes within an area surrounding the GPS antenna (Larson et al., 2015; Shean et al., 2017; Siegfried et al., 2017). This technique requires the continuous operation of dual‐frequency geodetic GPS receivers. The interference pattern of the combined direct and reflected signals can be directly related to the distance between the antenna phase center and the snow surface; thus, a continuous time series of surface height change (relative to the GPS antenna) can be derived in a fashion similar to sonic ranging (see section 2.1.3.2). Height changes can then be converted to SSMB if the density of the accumulated snow is known.

By adjusting the height of the antenna, the total area over which the reflected signal is returned to the GPS antenna is adjusted, allowing for precise tuning of the area‐integrated height change. The areal‐integration of the height change is unique to the GPS interferometry approach and minimizes the impact of local‐scale SSV, which makes for an ideal comparison of SSMB with atmospheric models (Siegfried et al., 2017). With an average accuracy of about 1 cm (Larson et al., 2015), the technique provides accumulated height change at daily resolution, a significant resolution improvement over the more traditional SSMB methods, potentially identifying snow accumulation at the event level.

2.1.7. Cosmic Ray Neutron‐Sensing Device

Cosmic ray neutron detection for snowpack monitoring has a long history within the field of snow science, yet until recently has been underutilized in ice sheet studies. Cosmic ray neutrons are formed through collision of the high‐energy radiation (cosmic rays) with the mass of our Earth's atmosphere, creating the secondary neutrons that then rain down toward the surface. Water attenuates the cosmic ray neutrons, prohibiting transmission to the sensing device. Therefore, the mass of snow that accumulates on top of the device directly determines the attenuation of cosmic‐ray neutrons reaching the device. This concept was already proven successful decades ago in alpine conditions (Kodama, 1980; Kodama et al., 1975; Kodama et al., 1979). Recently, Howat et al. (2018) investigated the applicability of a commercially available cosmic ray neutron‐sensing device for measuring SSMB on the GrIS. The device records hourly neutron counts; however, the surface flux of cosmic ray neutrons is not constant, and corrections are applied based on the variations in the incoming cosmic ray flux and barometric pressure (Howat et al., 2018). The former is assessed through placement of a secondary neutron‐sensing device above the surface.

Howat et al. (2018) summarize several advantages to using a neutron‐sensing device including the following: (1) It provides direct mass change measurements that integrate all the components of SSMB without the need for ancillary density measurements to convert from volume to mass; (2) measurements are integrated over a larger area (tens of square meters), reducing the impact of SSV in a similar fashion to the GPS‐Interferometric Reflectometry technique, although the spatial scale of integration is less quantifiable; (3) reduction of power constraints relative to comparable instruments, such as active radars, as the passive sensor has very low power consumption, which is critical in polar winter; (4) measurements are frequent (approximately hourly) and continuous, providing measurements at the event scale; and finally (5) the device is sensitive enough to survey the lowest accumulation areas, such as the interior of the ice sheets, where frequent redistribution and drifting making stratigraphic interpretation difficult.

Some limitations of the technique include (1) the precision of accumulated snow‐mass measurements decreases with burial as the neutron count decreases, suggesting that its use over long periods of time or in high‐accumulation areas might be limited; (2) its applicability in the percolation zone is unknown, as meltwater percolation and refreezing might impact the sensor; and (3) a better understanding between the relationship with drifting snow at the surface and observed mass change is required for proper validation with independent observations.

2.1.8. Airborne and Satellite Altimetry

Airborne and spaceborne observations of ice sheet height changes are comprised of several signals: short‐ and long‐term variability in (1) SSMB, (2) firn compaction rates, (3) ice dynamical imbalance, (4) solid earth deformation, and (5) basal melt rate and other oceanic signals such as tides and sea level change (over floating ice shelves only; Pritchard et al., 2012). They differ from traditional ground‐based height measurements in that they are relative to a reference ellipsoid (e.g., WGS‐84 for ICESat‐2) rather than an anchor point at or just below the surface. Thus, without ancillary information, it is impossible to isolate the contribution to integrated height change of these individual components, some of which are not even associated with a change in ice mass.

Altimetry‐based MB studies often utilize models of SMB and firn compaction to effectively remove the height change signal due to surface process in order to assess the ice dynamical change (Csatho et al., 2014; Shepherd et al., 2012, 2018; Zwally et al., 2005; Zwally et al., 2015). Progress toward measuring ablation from airborne altimetry, however, indicates that under specific circumstances SSMB can be estimated, providing excellent validation data for SMB models. For instance, Sutterley et al. (2018) suggested that the isolation of the height signal due to SSMB is possible by restricting focus to regions where (1) no firn column exists (i.e., the ablation zone) as defined by regional atmospheric climate model (RCM) output and (2) the underlying ice flow velocities fall under a reasonable threshold (<100 m/year), minimizing the impact of ice dynamics. After the rates of uplift due to Glacial Isostatic Adjustment (GIA) are removed, the remaining height change signal can be attributed to ice ablation (Sutterley et al., 2018).

Existence of long‐term records of both radar and laser altimetry combined with newly emerging models of SMB indicates that future altimetry studies can provide insight into modeled SMB. Although altimetry studies are limited in their ability to directly measure SMB, they have great potential to provide additional insight in distinguishing between the abilities of various SMB models to represent Greenland and Antarctic SMB, as evidenced by prior studies that related observed height change to precipitation (Davis et al., 2005; McConnell, Arthern, et al., 2000; McConnell, Mosley‐Thompson, et al., 2000), and ultimately to modeled height change due to surface processes (Kuipers Munneke et al., 2015; Ligtenberg et al., 2011). The latter studies indicate that height changes due to SMB can dominate the entire height‐change signal. Recent intercomparisons of ice sheet MB methodologies (Shepherd et al., 2012, 2018) indicate that there is common overlap in the results between altimetry and other independent techniques (i.e., gravimetry; see section 2.1.9).

The initial framework laid out by Sutterley et al. (2014) utilized IceBridge and ICESat data that provide only intermittent snapshots in time and space, yet due to the paucity of field observations, still provided several orders of magnitude more observations of height change. Further refinement of the spatial and temporal resolution is expected with NASA's ongoing ICESat‐2 laser altimetry mission (Figure 4), launched in September 2018, that provides complete ice sheet‐wide height change at the seasonal scale (91‐day repeat cycle; Markus et al., 2017).

Due to their large (several tens of kilometers) footprint, conventional radar altimeters struggled to generate precise height change measurements on the more steeply sloping regions of the ice sheet, including the ablation zone in Greenland (Brenner et al., 2007). CryoSat‐2, launched in 2010, overcomes this problem by operating in a synthetic aperture interferometric mode over the margins of the ice sheets. In this mode, Doppler processing is applied to a burst of short (17.8‐kHz frequency) radar pulses, which reduces the along‐track (i.e., along the line of flight) resolution to approximately 400 m. Since the satellite is equipped with two receiving antennas, the across‐track location of the echo can also be determined, based on phase difference of the received signal in the two antennas (Wingham et al., 2006). Unlike laser altimetry, radar altimetry is not affected by cloud cover, which allows continuous sampling of the ice sheets. The downside, however, is that at the Ku‐band (13.575‐GHz frequency) used by CryoSat‐2, the radar wave may penetrate several meters into the firn, challenging the interpretation of the reflected waveform, depending on vertically changing firn properties. An exemplar of this point was the extreme melt event during the 2012 summer in the interior of Greenland. Prior to the melt, part of the radar signal was reflected from within the top firn layer. The ice layer created by surface meltwater refreezing subsequently acted as an efficient reflector, resulting in an apparent jump of the surface of almost 50 cm in the CryoSat‐2 observations (Nilsson et al., 2015). Although this is an extreme case, slow changes in the structure of the firn layer may likewise bias altimetry‐derived surface height changes; reducing these effects is an active field of research. On the other hand, this limitation can also be exploited to estimate the firn structure by combining radar observations, firn models, and microwave radiative transfer models (e.g., Adodo et al., 2018). The CryoSat‐2 mission team is considering adjusting the satellite's orbit in the early 2020s so that its ground tracks will overlap once every ~2 days with those of ICESat‐2. Since the penetration depth of laser in firn is an order of magnitude smaller than that of radar waves (Rémy & Parouty, 2009), this is expected to provide a wealth of information on the firn structure and how it changes in time.

2.1.9. Gravity Recovery and Climate Experiment and GRACE‐Follow on

Since its launch in April 2002, the Gravity Recovery and Climate experiment (GRACE) has provided a novel tool for directly measuring mass variations of the ice sheets and other glaciated regions. The mission, which ended mid‐2017, consisted of two identical satellites, circling the Earth in the same near polar orbital plane, but separated by a distance of about 200 km. Because of this separation, local variations in the gravitational field of the Earth affected the orbits of the two satellites slightly differently, hence changing the intersatellite range. This range and its rate of change were measured continuously at micrometer accuracy using a microwave radar link between the two satellites. The Earth's gravitation field and its temporal variations could be mapped at monthly—or even shorter—time intervals, and at a spatial resolution of 300–400 km (see Wouters et al., 2014, for an extensive introduction to GRACE).

Atmospheric (and partly also oceanic) signals are removed during processing of the GRACE data, so that at annual to decadal time scales, variations in the gravitational field are largely related to redistribution of mass at the Earth's surface and at greater depth (Wahr et al., 1998). Whereas initial studies mainly focused on land hydrology applications, it soon became clear that the GRACE satellites could also provide invaluable information on the state of the ice sheets. Velicogna and Wahr (2005) provided a first estimate of the MB of the GrIS, revealing a mass loss of about 75 Gt/year for 2002–2004. Follow‐up studies confirmed this negative trend but reported numbers showed a substantial spread, roughly between 100 and 250 Gt/year (Luthcke et al., 2006; Velicogna & Wahr, 2006; Wouters et al., 2008). These estimates were based on short time spans and were therefore particularly sensitive to interannual variability in SMB, which can vary by several hundreds of Gt between years (Wouters et al., 2013, section 4). Similarly, early studies focusing on the AIS varied by a considerable amount, from −109 Gt/year for 2002–2007 (Sasgen et al., 2010) to −190 Gt/year for 2002–2008 (Chen et al., 2009). In this case, this was not only due to interannual variability in SMB but also because of differences in the correction for GIA, the ongoing redistribution of mantle material in response to past changes in ice loading. Such internal mass movement likewise induces a gravitational signal for which a correction must be applied, but early GIA models differed by several hundreds of Gt/year, depending on the Earth parameters used (Barletta et al., 2008). As longer data records became available and GIA estimates improved, trend estimates finally converged (See Figure 13 and section 4, which provide an update of Wouters et al., 2013).

Figure 13.

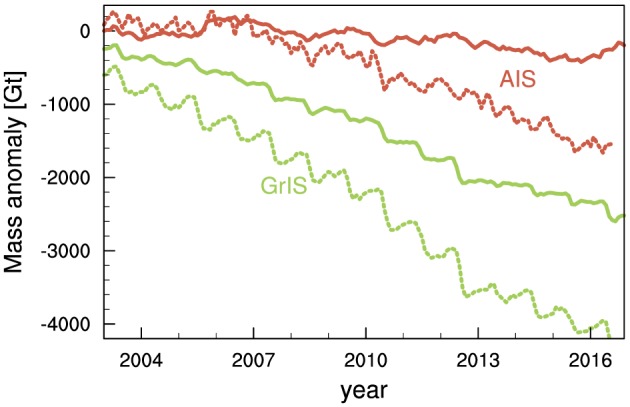
Surface mass balance anomalies over the period 2003–2016 (solid, taken to be the cumulative anomalies relative to a base period, that is, 1960–1990 for the Greenland ice sheet (GrIS), and 1979–2002 for the Antarctic ice sheet (AIS), as in van den Broeke, Bamber, et al. (2009), van den Broeke, König‐Langlo, et al. (2009), van den Broeke, Smeets, et al. (2009), and ice sheet mass anomalies derived from Gravity Recovery and Climate experiment (dashed, update from Wouters et al., 2013) for the GrIS (green) and AIS (red).

The drawback of the GRACE observations is that they represent the total mass change. Validation of SMB models by means of GRACE data therefore always requires auxiliary data to account for solid ice discharge. Van den Broeke, Bamber, et al. (2009) combined cumulative anomalies of SMB from the RACMO2 model and observed ice discharge (“input‐output” method), and found a close match between those and the GRACE‐derived GrIS MB record. This successful validation of the modeled SMB allowed for further partitioning of the 2000–2008 mass loss into SMB decrease and D increase, which was repeated and refined in follow‐up studies (Enderlin et al., 2014; van den Broeke et al., 2016). Similarly good agreement was found at regional scales (Sasgen et al., 2012; Velicogna et al., 2014), except for across the northwest and southeast of the GrIS, with the latter attributed to a bias in the (now superseded) RACMO2.0 climate model (Noël et al., 2018). Considering shorter time scales, Vizcaíno et al. (2013) compared the GRACE data to validate the mean seasonal cycle in SMB in the Community Earth System Model and demonstrated a good agreement in both the overall timing and amplitude. Schlegel et al. (2016) used GRACE data to validate a historical run of the Ice Sheet System Model forced with SMB anomalies from three different regional climate models. Again, a good agreement was found in the seasonal cycle, this time also on regional scales, although discrepancies remained in the northwest and southeast. The overall good agreement was largely attributed to the direct contribution of the SMB forcing. Long‐term trends, however, were significantly underestimated by the model, partly due to missing physical processes such as ice‐ocean interactions.

In Antarctica, similarly good agreement on seasonal time scales was found between GRACE observations and SMB data from the RACMO2 model (van Wessem et al., 2014). In regions with large interannual variability in SMB and a relatively constant ice flux, the combination of GRACE with regional climate model output has been shown to be instrumental in revealing large scale anomalous SMB signals, such as the 2009–2011 extreme snowfall episode in Dronning Maud Land and SMB‐driven mass loss events in Wilkes Land (see Glossary; Boening et al., 2012; Lenaerts et al., 2013; Mohajerani et al., 2018; Velicogna et al., 2014). Reconciling decadal mass loss, however, still remains challenging; in the latest Ice sheet Mass Balance Intercomparison Exercise 2 (Shepherd et al., 2018), budget closure between the input‐output method and GRACE estimates was not obtained for Antarctica, with the exception of West Antarctica where mass loss is dominated by dynamic discharge (Shepherd et al., 2018). Remaining uncertainties in the GIA correction for GRACE (Martín‐Español, King, et al., 2016; Martín‐Español, Zammit‐Mangion, et al., 2016), and in the estimates of ice discharge, to date limit the direct validation of secular SMB changes, in particular on regional scales. An interesting recent development, and the fusion of the use of altimetry and gravimetry, is the combination of several observational (altimetry, GRACE, GPS, and ice flow velocities) and model‐based (SMB and firn compaction) data sets in a Bayesian framework, which allows the simultaneous estimation of SMB anomalies, ice dynamics, and GIA (Martín‐Español, King, et al., 2016; Martín‐Español, Zammit‐Mangion, et al., 2016).

There are many factors that limit the application of GRACE to estimating or validating SMB fluctuations on shorter, monthly time scales. Shortcomings in the atmospheric and ocean models used in the processing of the GRACE data may cause significant errors in the GRACE derived time series. This is particularly true for Antarctica, where the models are rather poorly constrained and monthly errors can exceed 10 Gt (Hardy et al., 2017). Also, instrumental noise and the predominant sampling of the gravity field along the north‐south direction (defined by the satellites' orbit) introduces additional high‐frequency noise.

A follow‐on mission (GRACE‐FO) was launched on 22 May 2018. These satellites are a carbon copy of their predecessors but carry an experimental laser instrument in addition to the microwave ranging system to track the changes in distance between the satellites. This is expected to reduce the instrumental noise by some 20% (Flechtner et al., 2016). The spatial resolution of the observations will remain about the same (300–400 km) and hence will still not allow the isolation of local signals or the separation of signals occurring on the main ice sheet from those in its periphery (e.g., tundra or detached glaciers). To overcome these limitations requires a redesign of the mission concept, for example, with multiple satellite pairs flying in different orbits (Pail et al., 2015). Concept studies and funding negotiations are currently being carried out, and it is envisaged that such a mission will be launched in the mid‐2020s, allowing a second leap forward in our understanding of the state of the ice sheets.

2.1.10. Precipitation Radar (CloudSat, MRR)

Recently, spaceborne, and ground‐based precipitation radars have been used to estimate snowfall rates over the AIS (e.g., Boening et al., 2012; Palerme et al., 2014; Souverijns et al., 2018), where snowfall is by far the largest contributor to SMB. This technique is based on a relation between radar backscatter (Z) and snowfall rate (S), the Z/S relation, which is determined using a priori estimates of snow particle size distribution, microphysical and scattering properties, all of which are spatially and temporally variable over the ice sheet (Wood et al., 2014). Since the radar systems used are initially designed to measure rainfall, dedicated algorithms had to be developed to enable snow particle detection (e.g., Gorodetskaya, van Lipzig, et al., 2014; Gorodetskaya, Tsukernik, et al., 2014; Kneifel et al., 2011). Snowfall rates derived by spaceborne radar originate from a cloud profiling radar aboard NASA's CloudSat (part of the A‐Train constellation), and associated 2C‐SNOW‐PROFILE product (e.g., Palerme et al., 2014). This product shows a realistic snowfall climatology in comparison with ERA‐Interim reanalysis but is not able to detect individual snowfall events (Souverijns et al., 2018) because of its sparse spatial coverage (as it covers repeated tracks that are spaced tens of kilometers apart) and poor temporal sampling (revisit time of 2–4 days).

2.2. Modeling Tools

Eisen et al. (2008) showed that AIS SMB maps based on guided interpolation of in situ SMB observations fail to reproduce the high‐accumulation marginal zones of the ice sheet, as well as the coastal and inland blue ice areas, the only regions of the AIS (~1.7% coverage), where SMB is negative (Hui et al., 2014). For Greenland, the same is true for the wet southeastern ice sheet, which is almost devoid of observations yet home to the recently discovered perennial firn aquifers (Forster et al., 2014). That implies that we rely on modeling tools to reveal SMB in these areas. In this section we review traditional modeling techniques and discuss the recent developments in modeling SMB over ice sheets.

2.2.1. Statistical Downscaling

The lack of in situ observations in climatologically key areas in combination with insufficient resolution of SMB models has long hampered accurate ice sheet SMB estimates. Until the early 2000s, most estimates of ice sheet SMB were based either on idealized MB schemes or snowpack models using input from atmospheric general circulation models (GCMs; see Glossary) and/or atmospheric reanalysis (see Glossary) products, such as ERA‐40 and ERA‐Interim from the European Centre for Medium‐Range Weather Forecasts (ECMWF). Hanna and Valdes (2001) and Hanna et al. (2002) assessed the quality of ERA‐40 to determine the SMB of the GrIS. Bugnion and Stone (2002) used a snowpack model driven by ECMWF analyses to estimate GrIS SMB. Hanna et al. (2005) used ERA‐40 in combination with a meltwater retention model (Janssens & Huybrechts, 2000) to retrieve annual accumulation, runoff, and SMB on a 5 × 5 km grid for the GrIS for 1958–2003. Bougamont et al. (2005) presented a SMB model for the GrIS for use in GCMs and tested it using ERA‐40.

This statistical downscaling of the relatively coarse‐gridded GCM fields, employing a typical 100‐ to 150‐km resolution, to a scale that is required to the narrow GrIS ablation zone (tens of km) where most of the ablation occurs, or to narrow valleys in the AIS where precipitation gradients are largest, is a highly uncertain approach given the complex dynamics of the ice sheet atmospheric boundary layer (Denby et al., 2002) and the great variability in surface characteristics (albedo, roughness, etc.; Smeets & van den Broeke, 2008). Another shortcoming of many of the above methods is the simplified treatment of the SEB, using, for example, degree‐day factors (see Glossary).

2.2.2. Dynamical Downscaling (RCM)

An approach that circumvents these problems is dynamical downscaling, that is, to use a high‐resolution regional (atmospheric) climate model (RCM; see Glossary) forced at its boundaries with GCM or reanalysis data. This ensures a sufficiently high resolution over the ice sheet as well as an explicit, physically realistic calculation of all SMB components. A full interaction between the snow/ice surface and the atmosphere is achieved by coupling a realistic snow model to the atmosphere module. Almost two decades ago, regional climate models started to be used to hindcast the SMB of the AIS (Bromwich et al., 2004; van de Berg et al., 2006; Wacker et al., 2009) and GrIS (Box et al., 2004; Cassano et al., 2001; Dethloff et al., 2002; Fettweis et al., 2005). These studies have added significantly to our understanding of ice sheet SMB variability and the present‐day contribution of the AIS and GrIS to global sea level change (van den Broeke et al., 2011), as well as offering insights into the role of large‐scale circulation variability on the SMB of the GrIS (Fettweis et al., 2013) and the AIS (Marshall et al., 2017). The latest versions of these specialized RCMs show a high skill in simulating the contemporary SMB of the AIS (Agosta et al., 2018; van Wessem et al., 2018) and GrIS (Fettweis et al., 2017; Lucas‐Picher et al., 2012; Noël et al., 2018), although important regional discrepancies remain (Hermann et al., 2018). RCMs can also be used in forecasting mode (i.e., driven by atmospheric fields from a global weather forecasting model) for operational purposes, mainly for fieldwork planning. The Antarctic Mesoscale Prediction System (Bromwich et al., 2003; Bromwich et al., 2005; Powers et al., 2003, 2012) uses the Weather Research and Forecasting RCM with polar modification to provide a continuous 5‐day forecast of Antarctic weather conditions, while also providing an archive to study past weather phenomena (Nigro et al., 2012; Speirs et al., 2010; Steinhoff et al., 2008; Wille et al., 2014).

2.2.3. Improving Existing RCMs

Recently, several SMB processes not previously included have been added to address remaining RCM caveats in simulating the SMB of the AIS and GrIS. These include drifting snow physics (Gallée et al., 2013; Lenaerts, van den Broeke, van Angelen, et al., 2012; Lenaerts, van den Broeke, van de Berg, et al., 2012; Lenaerts, van den Broeke, Déry, et al., 2012; Lenaerts, van den Broeke, Scarchilli, et al., 2012), sublimation of falling snow (Grazioli et al., 2017), and resolving the all‐important albedo of snow and ice into multiple spectral bands (van Dalum et al., 2018). Further desired refinements have been identified, such as bio‐albedo paramaterizations for the GrIS (Stibal et al., 2017; van den Broeke et al., 2017), representation of low‐albedo/high‐melt areas such as nunataks and blue ice areas in Antarctica (Lenaerts, Lhermitte, et al., 2017; Lenaerts, Ligtenberg, et al., 2017; Lenaerts, van Tricht, et al., 2017), and the horizontal meltwater routing in snow and firn (Bell et al., 2017; Kingslake et al., 2017).

2.2.4. Earth System Models (ESMs)

The great advantage of using ESMs (see Glossary) to simulate ice sheet SMB is the use of consistent physics across the globe, the possibility of interactive coupling of the atmosphere to the ocean, sea ice and ice sheets, and the relative simplicity of performing ensemble runs for parameter uncertainty studies or assessing the uncertainty in future climate projections (e.g., Kay et al., 2014). Glimpsing into the future with further increases in available computing resources, it is safe to say that at some point in time, RCMs will become redundant and ESMs will be the modeling tools of choice to simulate contemporary and predict future ice sheet SMB. However, most state‐of‐the‐art ESMs suffer from two issues that currently preclude them from simulating a realistic ice sheet SMB. First, most ESMs do not include a sophisticated snow model that is required to represent snow processes and their interaction with the atmosphere. Second, typical ESM resolutions in the most recent Climate Model Intercomparison Project (Eyring et al., 2016; the results of which being released in 2019) of ~1 latitudinal degree are insufficient to resolve properly the SMB gradients along ice sheet margins. Recent work has focused on resolving both issues. To remedy the first issue, snow models in ESMs, typically designed to simulate seasonal snow (Krinner et al., 2018), have been progressively refined and tailored for application over the ice sheets (Cullather et al., 2014; van Kampenhout et al., 2017). To increase horizontal resolution, the pioneering study of Krinner and Genthon (1997) used a stretched‐grid GCM to study the Antarctic climate and MB, at the time resulting in a typical resolution of 100–150 km. More recently, attempts have been made to apply ESMs at resolutions typical for RCMs. In particular, the potential of using variable‐resolution in ESMs (Rhoades et al., 2015) to improve the representation of ice sheet SMB is currently being tested for the GrIS (van Kampenhout et al., 2018); using fixed, nested grids over the region of interest with resolutions up to 28 km, the regionalization added a factor 4 to the computational load. Additional ongoing ESM developments to improve ice sheet SMB, in line with those for RCMs, are focusing on remedying the high‐latitude atmospheric biases, such as precipitation (Noël et al., 2015), surface based temperature inversion strength and resulting stability (Vignon et al., 2018), and clouds and their radiative effects (van Wessem et al., 2018).

2.2.5. New Atmospheric Reanalysis Products

Until recently, atmospheric reanalyses (see Glossary) shared many disadvantages with ESMs, that is, the absence of a sophisticated snow/firn model and low resolution. Moreover, (1) the relative scarcity of meteorological observations over the polar regions in general, and over ice sheets in particular, to assimilate in the reanalyses, and (2) the optimization of atmospheric parameterizations to perform well in midlatitude conditions, led to substantial biases in, for example, ice sheet clouds and radiation (Lenaerts, Lhermitte, et al., 2017; Lenaerts, Ligtenberg, et al., 2017; Lenaerts, van Tricht, et al., 2017; Miller et al., 2018), precipitation (Bromwich et al., 1998, 2012; Chen et al., 2011; Medley et al., 2013; Nicolas & Bromwich, 2011), (near‐)surface temperature (Fréville et al., 2014; Jones & Lister, 2015; Lindsay et al., 2014; Screen & Simmonds, 2011), and turbulent heat exchange (Miller et al., 2018). Newly emerging reanalysis products will likely improve on many of these issues. For example, ECMWF's new reanalysis product ERA‐5 combines unparalleled horizontal resolution (0.25°) with refined atmospheric physics and a revised snow scheme (Dutra et al., 2010).

2.2.6. Further Downscaling

Despite the recent exciting developments of RCMs and ESMs, dedicated models will always be required to simulate processes at the smallest scales (5 km and smaller). Multiple studies have shown that increasing the horizontal model resolution, either by dynamical and/or statistical downscaling, can significantly improve the representation of ice sheet SMB. This can be applied to the full range of models, for example, ESMs (Vizcaino, 2014), RCMs, large eddy simulations, and direct numerical simulations. For the GrIS, it has been shown that further statistical downscaling, for example, using elevation dependency, from the current state‐of‐the‐art RCM resolution of ~5 to 1 km, remains necessary to properly resolve melt and runoff from low‐lying tongues of the narrow outlet glaciers (Noël et al., 2018). This technique also enables the construction of high‐resolution SMB fields over smaller ice masses, such as Greenland's peripheral ice caps (Noël et al., 2017). Another way to enhance RCM resolution is multiple nesting, in which one or more small spatial domains with higher horizontal grid resolution are embedded in a large spatial domain. For the AIS, double‐nesting has been successfully applied to RACMO2.3, effectively enhancing resolution from 27 to 5.5 km, for the Antarctic Peninsula (van Wessem et al., 2016), Adélie Land, where the use of a higher resolution revealed sublimation‐driven blue ice areas (Lenaerts, van den Broeke, van Angelen, et al., 2012; Lenaerts, van den Broeke, van de Berg, et al., 2012; Lenaerts, van den Broeke, Déry, et al., 2012; Lenaerts, van den Broeke, Scarchilli, et al., 2012, Figure 5), West Antarctica (Lenaerts, Ligtenberg, et al., 2017), and Dronning Maud Land (Lenaerts, Lhermitte, et al., 2017; Lenaerts et al., 2014). Further nesting is possible but requires computationally expensive, nonhydrostatic models (e.g., Mottram et al., 2017). An emerging approach for modeling interior ice sheet SMB at subkilometer resolution consists of employing sophisticated snow models that can resolve small‐scale redistribution patterns resulting from blowing snow. These models are typically forced by atmospheric forcing that is statistically downscaled to the snow model resolution (e.g., Groot Zwaaftink et al., 2013).

Figure 5.

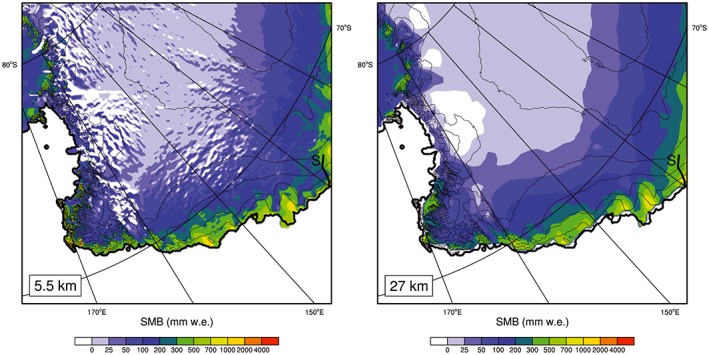
Surface mass balance in 2009 (mm w.e.) in RACMO2 at 5.5‐km resolution (left) and at 27 km (right). Source: Lenaerts, van den Broeke, Scarchilli, et al. (2012). Sublimation‐driven blue ice areas (in white, SMB < 0) are much more prevalent in the higher‐resolution product.

3. Spatial Variability of Ice Sheet SMB

3.1. Ice Sheet‐Wide Scale

Observational data sets are limited to a point‐scale to regional‐scale estimate of SMB, so we rely on RCMs to provide a continuous and gridded product of SMB for the full ice sheet. Here we use the output of the RACMO2.3p2 (RACMO2 hereafter) model (Noël et al., 2018; van Wessem et al., 2018) to present a side‐by‐side comparison of spatial distribution of SMB and its components on Greenland and Antarctica. In our analysis, we mostly focus on the period 1980–2015, which is covered by RACMO2 as well as all the reanalysis products that are discussed in sections 4 and 5.

Precipitation varies strongly on ice sheets (Figure 6a). The general pattern is for precipitation to increase from the ice sheet interior to the margins, with values <20 mm w.e./year observed in the East Antarctic ice sheet interior, to >2000 mm w.e./year in the Antarctic Peninsula and southeast Greenland (Koenig et al., 2016; Miège et al., 2013). Due to its higher elevation and colder climate, the interior of the AIS is drier than that of the GrIS, which in the driest part in the northeast still receives about 50 mm w.e./year of precipitation. We find regional precipitation maxima in southwest, west, and northwest Greenland, and in the Amundsen and Bellingshausen coasts in West Antarctica (see Glossary), and locally along the East Antarctic coast, for example, on the windward side of Law Dome (van Ommen et al., 2004, see Glossary). All these regions are characterized by close proximity to the coast at relatively low latitudes, ensuring sufficient moisture supply, and the presence of large‐scale, steep topography that is oriented perpendicular to the large‐scale atmospheric flow. Low precipitation areas are found not only further away from the coast on the elevated inland ice sheet but also in coastal regions leeward of topography, for example, in the eastern Antarctic Peninsula, or west of Law Dome; owing to the foehn effect, these areas receive an order of magnitude less precipitation than the windward sides. Precipitation on ice sheets mainly falls as snow, rainfall being limited to the northernmost Antarctic ice shelves and lowermost (<500 m above sea level [a.s.l.]) areas of the GrIS. Most of the rain (not shown) falls in coastal south Greenland, where it amounts to approximately 10–20% of the total annual precipitation.

Figure 6.

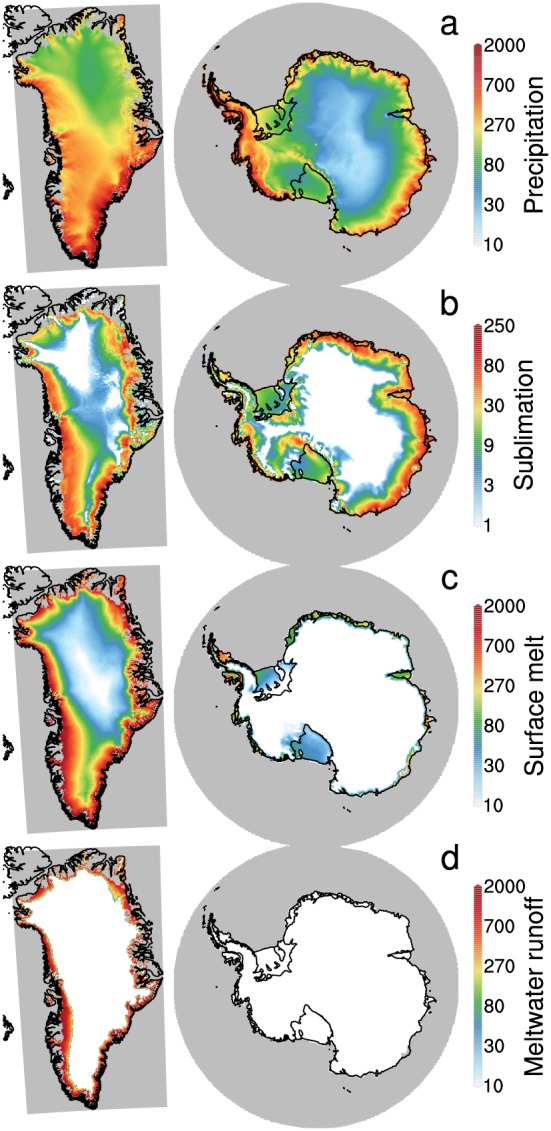
Annual mean (mm w.e./year, 1980–2015) surface mass balance (SMB) components from RACMO2 on the GrIS (left) and the AIS (right). (a) Precipitation; (b) sublimation (surface + drifting snow); (c) surface melt rate; (d) meltwater runoff.

Total sublimation, defined as the sum of surface sublimation and drifting snow sublimation, is small (or even negative—implying riming) over the ice sheet interiors (Figure 6b). The highest sublimation rates (>50 mm w.e./year) are found in the escarpment zones, where strong katabatic winds and low near‐surface relative humidity promote sublimation. Surface sublimation is most active in the GrIS ablation zone (outside of the melting season) and on low‐lying Antarctic blue ice areas and ice shelves in summer, where absorption of solar radiation results in relatively high surface temperatures, enhancing near‐surface vertical specific humidity gradients.

Surface melt rates over the GrIS are an order of magnitude greater than over the AIS (Figure 6c). Even the highest areas of Greenland (>3,000 m a.s.l.), experience surface melting in summer, for example in 2012, although that only occurs every few centuries (Nghiem et al., 2012). Melt rates exceed 2,000 mm w.e./year in the marginal ice sheet in the south and southwest and are between 1,000 and 2,000 mm w.e. in the northern ablation areas. In contrast, the vast majority of the grounded AIS does not experience any surface melting. The highest AIS melt rates (>400 mm w.e./year) are found on Antarctic Peninsula ice shelves (Larsen C, Wilkins, and George VI; see Glossary), while many of the smaller ice shelves fringing the coast of West and East Antarctica experience 50–200 mm w.e./year of melt. The large, southerly Ross and Ronne‐Filchner Ice Shelves typically have melt amounts less than 100 mm w.e./year.

Runoff from the GrIS is spatially constrained to a narrow zone along the margins of the ice sheet (Figure 6d). High runoff rates (500–2,000 mm w.e./year) are found in the ablation zones below 1,500–2,000 m a.s.l., where there is no firn layer (only the winter snow layer) in which melt water can refreeze locally (Figure 1). Other ways by which meltwater runoff to the ocean is delayed is by supraglacial (lakes) and englacial or subglacial storage (Chu, 2013; Palmer et al., 2013). Over Antarctica, nearly all the melt water that is produced at the surface refreezes in the firn, and runoff is deemed negligible as an ice sheet integrated mass loss term (Lenaerts, van den Broeke, van de Berg, et al., 2012). Nevertheless, runoff can be significant locally: Field and remote sensing studies indicate that extensive hydrological systems exist locally on Antarctic ice shelves (Bell et al., 2017) and that meltwater storage inside Antarctic ice shelves is more extensive than previously assumed (Lenaerts, Lhermitte, et al., 2017).

Snow divergence/convergence resulting from drifting snow transport leads to redistribution of accumulated snow through the interaction of surface topography and wind patterns. This leads to blowing snow erosion in exposed, windy areas and deposition in sheltered, calmer locations (Figure 5). Although a significant component on the local scale (see below), it is commonly believed that blowing snow redistribution does not significantly contribute to ice sheet‐integrated SMB (Lenaerts, van den Broeke, van de Berg, et al., 2012; Palm et al., 2011, 2017). The net effect of erosion and deposition largely cancels out if a large area is considered, and it is assumed that most of the blowing snow volume sublimates along the way (Palm et al., 2017).

The above analysis is based on output of an RCM (RACMO2), which provides well‐evaluated, high‐resolution, gridded, and temporally continuous estimates of each of the individual SMB components on both ice sheets (1979 onward for AIS and 1958 onward for GrIS). Potentially alternative products for mapping ice sheet SMB are atmospheric reanalyses. However, as discussed in section 2.2.1, these models often lack a dedicated snow model to properly represent the liquid water balance (Figure 2; see Glossary) and snow and ice albedo. The only two SMB components that can be compared amongst different reanalysis products are precipitation and evaporation (sublimation), the difference of which is commonly known as P−E (precipitation minus evaporation, or accumulation, assuming that sublimation equals evaporation). Figure 7 shows that the 1980–2015 mean P−E patterns (supplied as supplementary data sets to this paper) are broadly consistent among the different reanalyses (MERRA‐2, ERA‐Interim, and CFSR) and regional climate models (RACMO2, MARv3). However, a few differences stand out:

1. the higher spatial detail in regional climate models (RACMO2 and MARv3 at 1‐ to 35‐km resolution) relative to the lower resolution products (MERRA‐2 at 0.5° × 0.625° resolution, ERA‐Interim at 0.75° resolution, and CFSR at 0.5° resolution), which is especially evident on the GrIS in RACMO2.;

2. The generally lower P−E values in ERA‐Interim, and to a lesser degree CFSR, relative to the other products. This is especially evident in interior Antarctica (where ERA‐Interim P−E is <10 mm w.e./year in a very large region), but also over northern Greenland. Whereas ERA‐Interim is generally considered to be the best performing reanalysis product over high‐latitude regions, especially Antarctica (Nicolas & Bromwich, 2011), recent work has highlighted that the low P−E values in ERA‐Interim are unrealistic (van Wessem et al., 2014) and that MERRA‐2 shows improved agreement with a selection of Antarctic ice cores (Medley & Thomas, 2019).

Figure 7.

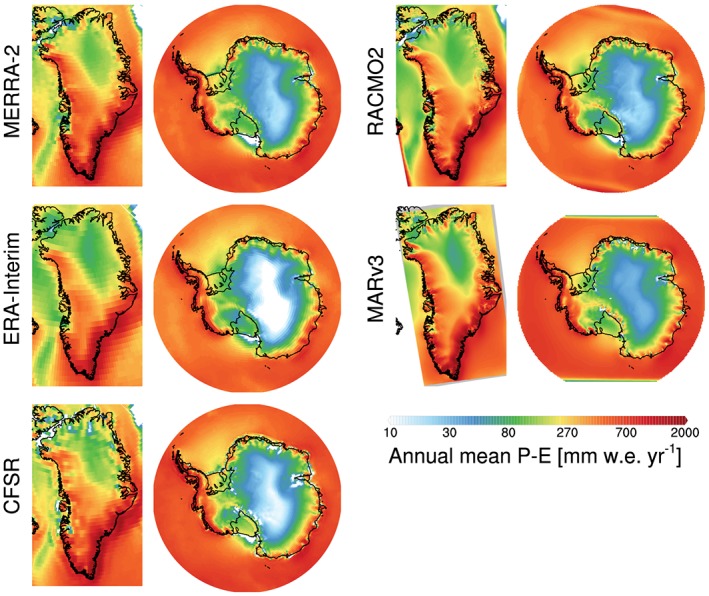
Annual mean P−E (mm w.e./year, 1980–2015) surface mass balance components from RACMO2 on the GrIS (left) and the AIS (right) according to atmospheric reanalyses (MERRA‐2, ERA‐Interim, CFSR), and regional atmospheric climate models (RACMO2 and MARv3).

3.2. Regional Variability (10–100 km)

The large spatial gradients in all SSMB components near the ice sheet periphery, in particular precipitation (AIS and GrIS) and runoff (GrIS only), lead to extreme SSMB gradients. In situ observations in these areas are therefore most useful if performed along transects. An example in Figure 8 shows a 20‐year semicontinuous record of SMB (derived from stakes) along the K‐transect in Southwest Greenland (which is currently still updated). The multiannual mean SSMB increases from −4 m w.e./year in the low ablation zone, near the glacier terminus at approximately 350 m a.s.l., to near zero (i.e., close to the equilibrium line) at around 1,500 m a.s.l., over a horizontal distance of only ~150 km. These large spatial SSMB gradients require the use of high horizontal resolution models and/or postprocessing of the model output using statistical downscaling methods (see section 2.2.6).

Figure 8.

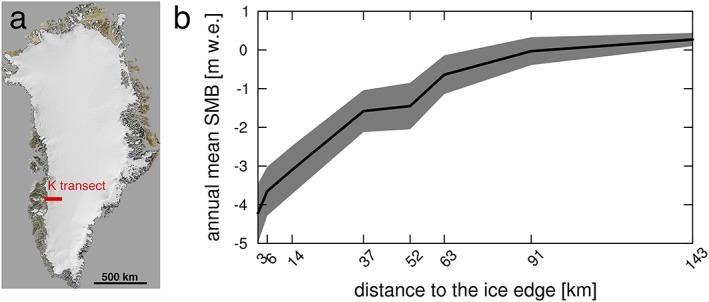
(b) Mean annual (1990–2011) surface mass balance along the K‐transect in Southwest Greenland). The location of the transect is shown in (a), which is a figure adapted from Kargel et al. (2012). Data source: van de Wal et al. (2012).

3.3. Subgrid Scale Variability (<10 km)

On the local scale (distance of meters to kilometers), spatial SSMB variability is largely governed by small‐scale variations in the local surface topography and the associated patterns of snow accumulation (during snowfall), blowing snow redistribution (during windy conditions), and heterogeneous snow and ice melting. Consequently, SSMB can vary by up to an order of magnitude over relatively short distances. Emerging SSMB measuring techniques, such as snow radar, and laser and SAR radar altimetry (see section 2.1) enable the mapping of these large gradients. An example is shown in Figure 9, which shows a snow radar transect on Pine Island Glacier (West Antarctica; see Figure 16) from the 2016 OIB airborne mission. The radar profile shows very large horizontal variability in the depth of the reflectors, indicative of large SSMB gradients. The alternating patterns between high and low SSMB are clearly linked to variations in slope. Near‐zero SSMB values are generally found over concave areas (near the peaks in slope in Figure 9b), where exposed terrain limits accumulation of fresh snow and enhances wind‐driven snow erosion. Highest SSMB values, in turn, are found in places where slopes are convex (close to the valleys in the slope shown in Figure 9b), providing wind sheltering and promoting snow accumulation and drifting snow deposition. Similarly alternating SMB patterns, driven by variations in surface topography, are found all over the AIS: around megadunes in interior East AIS (Fahnestock et al., 2000; Frezzotti et al., 2002, Figure 5), wind scour zones (Das et al., 2013, 2015; Scambos et al., 2012), on ice shelves, where the surface imprint of basal channels controls SMB patterns (Drews, 2015), and coastal ice rises (King et al., 2004; Lenaerts et al., 2014; Matsuoka et al., 2015).

Figure 9.

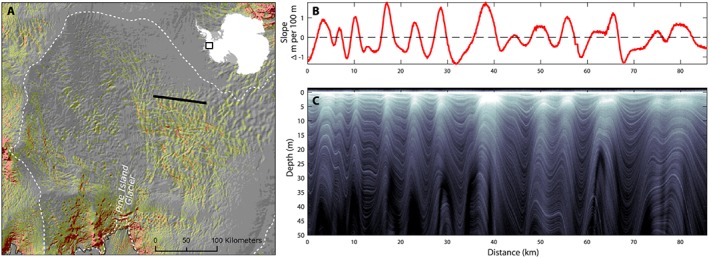
(b) Operation IceBridge surface slope (in units vertical meters per 100 horizontal meters, or %; derived from the Airborne Topographic Mapper) and (c) firn stratigraphy (as detected by Operation IceBridge's snow radar) along a transect on upper Pine Island Glacier (location shown in a), collected on 9 November 2016.

Figure 16.

Overview map of the Antarctic Ice Sheet with geographical names used throughout this paper highlighted.

4. Temporal Variability and Trends in Ice Sheet SMB

Driven by natural variability on time scales that range from subdaily (turbulence, daily cycle), interdaily (i.e., synoptic weather systems), subannual (seasonal cycle) to interannual (interannual to decadal), ice sheet SMB is highly variable across a spectrum of temporal scales. Precipitation over ice sheets is generated primarily by synoptic weather systems, whereas (surface) temperature variations on subdaily to seasonal time scales control sublimation, surface melt, and runoff. Moreover, ice sheet SMB exhibits long‐term changes (trends) that follow from external forcing, in particular human‐induced increase of atmospheric greenhouse gasses and subsequent atmospheric warming. Here we review the dominant modes of temporal variability in ice sheet SMB and present recent trends and potential drivers.

4.1. Interannual Variability

Ice sheet‐integrated SMB varies strongly on interannual time scales (Figure 10). During 1958–2017, modeled GrIS SMB varied from ~100 to ~700 Gt/year, with a standard deviation of ~120 Gt/year, that is, ~32% of the mean. This strong variability in GrIS SMB is a combined effect of variations in precipitation and runoff, which tend to be anticorrelated (fresh snow limits melt through high albedo), enhancing SMB variability. The marked post‐1995 decrease in GrIS SMB is driven mainly by increased meltwater runoff, an effect of increasing summer temperatures resulting from persistent anomalies in large‐scale atmospheric circulation (Delhasse et al., 2018; Fettweis et al., 2013). In the most recent years (2017 and 2018), the circulation pattern became more zonal and SMB returned to pre‐1995 values. Although the mean (grounded) AIS SMB is almost six times higher than the GrIS SMB (~2,150 vs. ~365 Gt/year), its absolute interannual variability is actually smaller (~100 Gt/year, or ~5% of the mean). This can be explained by (1) only precipitation variability contributing to AIS SMB variability, in the general absence of surface runoff, and sublimation being about ten times smaller and with low interannual variability, and (2) a larger surface area of the AIS, where negative precipitation anomalies in some regions are compensated by positive anomalies elsewhere (Fyke et al., 2017).

Figure 10.

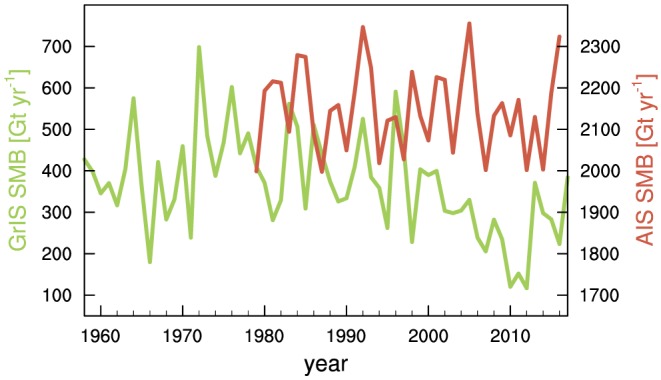
Annual ice sheet integrated surface mass balance (SMB) from RACMO2 for the Greenland ice sheet (GrIS; left, green axis, from 1958 to 2017) and for the Antarctic ice sheet (AIS; red, right axis, from 1979 to 2016). Note that the left and right axes differ, but the vertical extent is the same.

4.2. Seasonal Variability

Owing to their high‐latitude positions and consequent large seasonal fluctuations in insolation, the climates of the ice sheets are characterized by strong seasonal cycles, although this is partly offset by the high surface albedo, which reduces the absorption of solar radiation at the surface. Figure 11 shows that all (modeled) GrIS and AIS SMB components vary with the seasons. Precipitation shows a maximum in early fall (August–September) for the GrIS and early winter for AIS (March–May), and a minimum in summer. In contrast, melt, runoff, and sublimation peak in summer on both ice sheets, driven by higher insolation and ambient temperatures. While AIS melt is limited to the summer months (December and January), and runoff is negligible, the GrIS melt season starts already in May and usually does not end before early September. The onset of runoff is delayed with respect to melt, since the first batch of meltwater refreezes in the cold winter snow. Sublimation is active throughout the year on the AIS, indicative of an active drifting snow climate and the associated sublimation, and is comparable in magnitude to melt in summer, when surface sublimation dominates. The largest mass flux in all months of the year is AIS precipitation, exceeding peak GrIS surface meltwater production in July.

Figure 11.

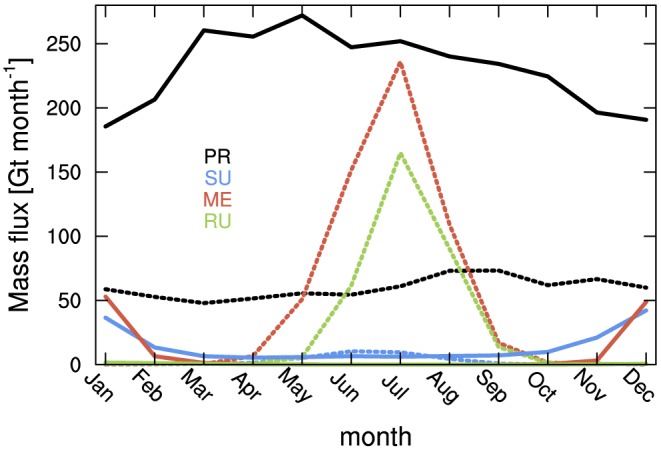
Seasonal cycle of surface mass balance components (in units Gt per month, including surface melt) according to RACMO2 for the Greenland ice sheet (dashed, 1958–2017 mean) and the Antarctic ice sheet (solid, 1979–2016 mean). PR = precipitation; SU = sublimation; ME = surface melt; RU = meltwater runoff.

4.3. Short‐Term Trends (1980–2015)

As mentioned in section 2.2.1, atmospheric reanalyses do not correctly represent ice sheet meltwater processes, which limits their use to analyze SMB trends to accumulation (P−E). Comparing trends in P−E (Figure 12) highlights significant differences in magnitude and even sign, in contrast with their comparable P−E climatology (Figure 7). For instance, MERRA‐2 shows a negative P−E trend over northern Greenland, which is not present in ERA‐Interim but appears in CFSR, although as part of a negative P−E trend over a much larger region. ERA‐Interim shows a significant P−E increase over central Greenland, which is not confirmed by MERRA‐2 or CFSR. Over Antarctica, the reanalyses show important differences but agree on negative P−E trends over Wilkes Land and the western Ross Ice Shelf. As both RACMO2 and MARv3 use ERA‐Interim for lateral boundary and surface ocean forcing, their trends broadly agree with those of ERA‐Interim (Figure 12). This result suggests that the choice of lateral forcing largely determines SMB trends in RCMs. The large disagreement among what are considered to be state‐of‐the‐art atmospheric reanalysis products indicates that modeled ice sheet P−E trends, especially those over the AIS, are associated with large uncertainties, and should be used with caution.

Figure 12.

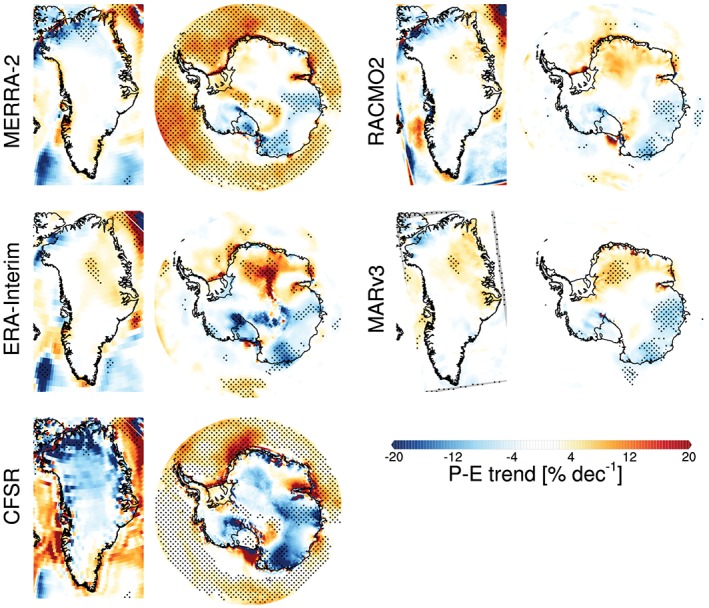
Relative linear P−E trend (in % per decade) over 1980–2015 on the Greenland ice sheet (left) and Antarctic ice sheet (right), according to atmospheric reanalysis products (MERRA‐2, ERA‐Interim, and CFSR), and regional climate models (RACMO2 and MARv3). Stippled areas indicate that the linear trend is significant at the 95% level.

RCM results show that AIS‐integrated SMB has not significantly changed over the period 1980–2015 (Figure 10), and that trends in other SMB components are negligible (not shown). Regional trends, in the absence of significant meltwater runoff, are driven by P−E changes (particularly snowfall). In contrast, the recent GrIS SMB decrease (Figure 10) is dominated by increased runoff (van Angelen et al., 2014; van den Broeke et al., 2016). We use SMB anomalies from RACMO2 and MB anomalies from GRACE (Figure 13) to quantify the contribution of SMB to ice sheet mass loss. From summer 2003 to summer 2016, the GrIS lost more than 4,000 Gt of mass (average MB = −290 ± 19 Gt/year; where the 2‐sigma uncertainty accounts for the formal error of the fit and uncertainties in the GIA correction). Most of this mass loss (~63%) can be attributed to a decrease in SMB over the same period (−182 ± 45 Gt/year; mean +/‐ 2‐sigma uncertainty of best linear trend of SMB anomaly in Figure 13). Note that the GrIS seasonal mass amplitude is higher in GRACE than in RACMO2, since the former includes the signal of seasonal snow buildup (fall‐winter) and melt (spring) on the tundra surrounding the GrIS, which GRACE cannot separate from ice sheet mass changes. In contrast, AIS mass loss over the same period (average MB = −147 ± 6 Gt/year) is only for a small part (~22%) explained by SMB (−32 ± 4 Gt/yr), confirming that recent AIS mass loss is predominantly driven by enhanced ice discharge (Shepherd et al., 2018). Higher‐frequency variability in AIS MB as measured by GRACE can be attributed to SMB (snowfall) anomalies; for instance, the increase in AIS mass during 2005 coincides with a positive SMB anomaly in that year. Similarly, the leveling off of AIS mass loss in 2008, and again in 2010–2011, coincide with periods of high AIS SMB. These snowfall anomalies are even more clearly detectable on a regional scale. In particular, recent high snowfall events in 2009 and 2011 in Dronning Maud Land, East Antarctica (Lenaerts et al., 2013), were detected by GRACE and CloudSat (Boening et al., 2012), as well as laser and radar altimetry (Shepherd et al., 2012).

4.4. Long‐Term Trends

Reanalyses and other model products that depend on them (such as RCMs) typically go back only to when satellite data were assimilated into the atmospheric products (around 1979). The recent release of a few century‐long reanalyses is promising for evaluation of long‐term changes. However, large spurious jumps in atmospheric pressure when additional data sets were assimilated, that is, around the International Geophysical Year (1957/1958) in the Arctic, and in 1979 around the AIS, suggest that they require further improvement before they are of sufficient quality for robust trend analysis (Schneider & Fogt, 2018). Therefore, ice core records are of immeasurable importance for contextualizing the satellite‐era time series in a historical sense for assessment of natural variability (Steig & Neff, 2018; Trusel et al., 2018).

Ice core records are typically synthesized in two manners: (1) by weighted or unweighted averaging by region (Frezzotti et al., 2013; Thomas et al., 2017) or (2) by spatiotemporal reconstruction (Medley & Thomas, 2019; Monaghan et al., 2006). The basis of the former is that there is a coherent regional signal that will emerge when enough records are averaged together, minimizing the impact of glaciological “noise.” The later uses the same principle, but derives the spatial coherence signal in SMB from atmospheric models instead from the ice core records themselves. A gridded reconstruction is next built by weighted averaging based on the model coherence patterns. In reality, the convolution of wind anomalies on the local topography controls the spatial pattern of precipitation, which means that nearby locations might not actual share a common signal. Thus, the additional coherence information provided by the atmospheric models improves the integrity of the reconstruction. Synthesis of several ice cores provides an invaluable tool for evaluation of trends within atmospheric reanalyses and RCMs.

Because there are large regions of Greenland where SSMB < 0, ice sheet‐wide reconstructions of accumulation are more challenging and are limited to the accumulation zone. The Program for Arctic Regional Climate Assessment produced several decadal records of accumulation change over the GrIS (Bales, McConnell, et al., 2001; Bales, Mosley‐Thompson, et al., 2001; Bales et al., 2009; Mosley‐Thompson et al., 2001)

While studies using Antarctic ice core compilations mutually agree that additional accumulation records from Antarctica are desperately needed, they also have a few commonalities. Specifically, several agree that recent (post‐1801) Antarctic‐wide accumulation has increased significantly, especially over the Antarctic Peninsula and portions of East Antarctica (Figure 14; Frezzotti et al., 2013; Medley & Thomas, 2018; Thomas et al., 2017). While Monaghan et al. (2006) found an insignificant negative trend since 1957, the combination of a short trend interval with use of ERA‐40 for the modern era makes trend detection challenging.

Figure 14.

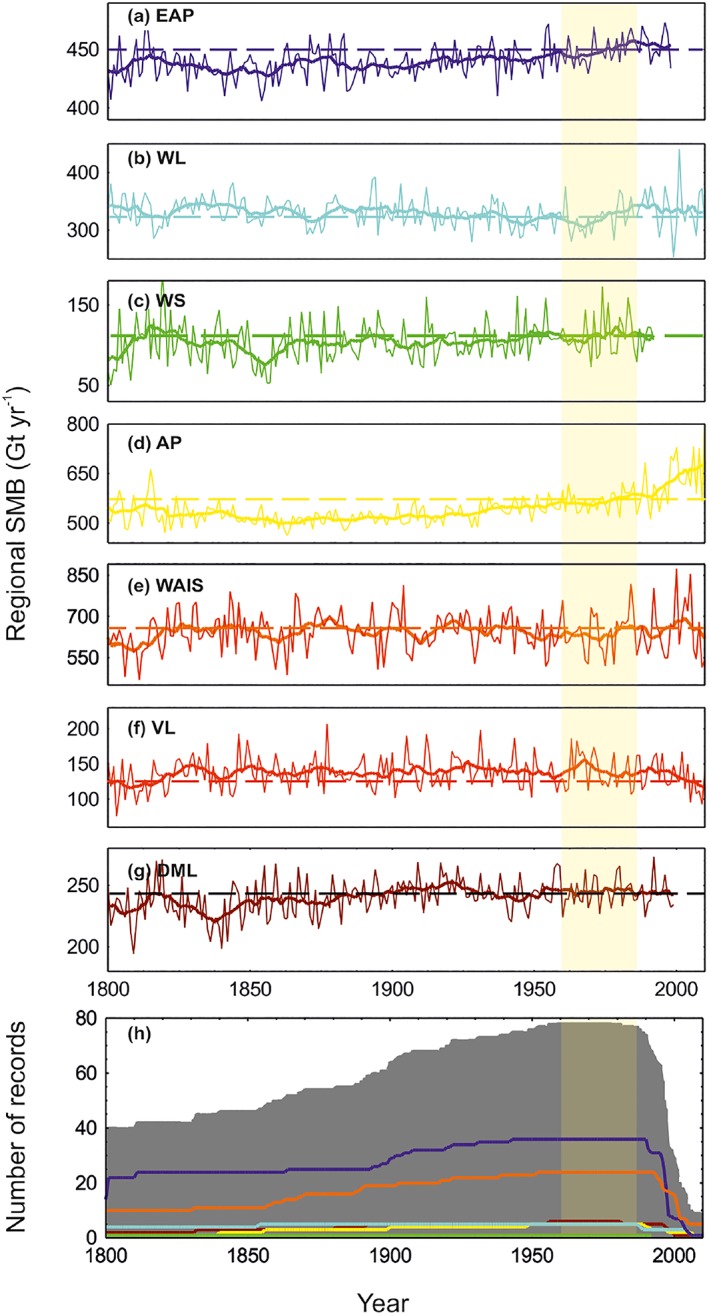
Regional surface mass balance composites (1800–2010) shown as annual averages (thin lines) and 10‐year running means (thick lines) for (a–g) the East Antarctic Plateau (EAP, dark blue); Wilkes Land coast (WL, cyan), Weddell Sea coast (WS, green), Antarctic Peninsula (AP, yellow), West Antarctic Ice Sheet (WAIS, orange), Victoria Land (VL, red), and Dronning Maud Land (DML, brown). Panel (h) represents the total number of records (solid grey) and the number of records by region. See Figure 16 for the location of the regions on the Antarctic ice sheet. Source: Thomas et al. (2017).

Medley and Thomas (2019) determined that the SAM plays a significant role in recent (post‐1957) accumulation trends; however, the positive trend in SAM index actually reduced net snow accumulation over Antarctica. Thus, the actual driver of the precipitation increase remains uncertain. Medley and Thomas (2019) suggest that the temperature trends required to generate the observed increases are similar to observations, indicating that thermodynamical forcing cannot be eliminated as a driver of recent precipitation increases. Additional work by Lenaerts et al. (2018) found that the signature of ozone depletion on Antarctic‐wide precipitation is remarkably similar to the Medley and Thomas (2019) reconstructed accumulation increase. While the ultimate mechanistic link between ozone depletion and increases in Antarctic precipitation has not been established as of yet, the work of Lenaerts et al. (2018) suggests that ozone depletion might have also played an important role in Antarctic‐wide SMB.

5. Future Ice Sheet SMB: Projections, Feedbacks, Uncertainties

With ongoing global warming and polar amplification, ice sheet SMB will inevitably continue to change. For the GrIS, despite large differences between models and scenarios, all future projections agree that increased runoff will dominate the future decrease of GrIS SMB (Figure 15), with the largest increases in runoff projected to occur in the strongest warming scenarios (Fettweis et al., 2008; Mottram et al., 2017; Rae et al., 2012; van Angelen et al., 2014), confirming the high sensitivity of GrIS SMB to atmospheric warming. An increase in snowfall can partly mitigate the higher runoff, but this signal is projected to be small (Rae et al., 2012). SMB changes will likely continue to dominate future GrIS mass loss, even more so when currently marine‐terminating glaciers, apart from those sitting on deeply incised channels (Morlighem et al., 2017), retreat onto land and GrIS solid ice discharge is reduced (Goelzer et al., 2013; Vizcaino et al., 2015). An important aspect of future GrIS SMB, especially beyond 2100, is the shrinking ice sheet geometry, in which the ice sheet lowers and retreats; to resolve these effects requires fully coupled dynamical ice sheet models (Vizcaino, 2014). GrIS SMB decrease is associated with multiple positive feedbacks that can further amplify GrIS mass loss: The increase of ice‐free land will enhance summer warming, favoring barrier wind effects (van den Broeke & Gallée, 1996), increasing the heat to melt the retreating ice sheet. The lowering ice sheet surface will experience higher ambient temperatures, further increasing melt. A retreating ice sheet increases its distance to sea, lowering precipitation, which decreases SMB. More precipitation will fall as rain, which saturates the firn layer and runs off when it falls on bare ice, reducing the negative snowfall‐albedo affect (Noël et al., 2015). Several of these processes are discussed in more detail below.

Figure 15.

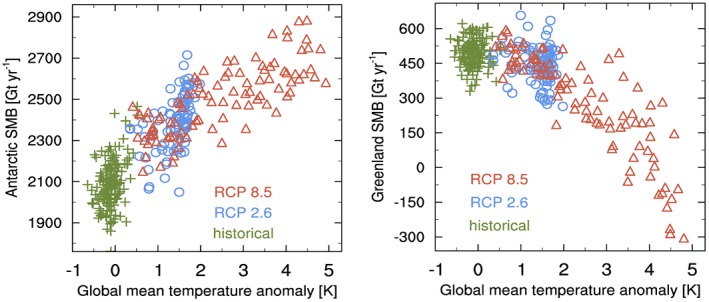
Antarctic ice sheet (left) and Greenland ice sheet (right) surface mass balance (SMB; each point in the plots represents an annual, ice sheet‐integrated SMB) in the CMIP5 ESM CESM1‐CAM5 (Lenaerts et al., 2015; Lenaerts et al., 2016) in the historical period (1850–2005, green), and two future climate change scenarios (2006–2099) from IPCC AR5: the strong mitigation scenario RCP2.6 (blue), and the high‐emission scenario RCP8.5 (red).

• Pore Space Loss in the Firn. Currently, almost half of the meltwater produced at the snow surface of the GrIS is refrozen and stored in the firn (Harper et al., 2012; Noël et al., 2017). However, as more liquid water enters the firn layer from melt and rain, this pore space is progressively lost while at the same time additional latent heat by refreezing warms up the firn, further enhancing densification and reducing pore space. As a result, the GrIS firn layer is expected to lose its buffering capacity, an effect that has been projected to become significant as early as the end of the 21st century (van Angelen et al., 2013) and that has already occurred in Greenland's smaller ice caps (Noël et al., 2017). Without this refreezing, all meltwater produced at the surface—even if temporarily stored in the firn by capillary forces—runs off into the ocean, enhancing the GrIS contribution to sea level rise.

• Melt‐Albedo Feedback. When snow melts, the powerful snowmelt‐albedo feedback kicks in. Melt water enters the snow and grains grow rapidly, reducing broadband surface albedo (from ~0.85 for clean fresh snow to ~0.7 for clean wet snow, i.e., essentially doubling net shortwave energy at the surface), which further promotes melting. If the entire winter snowpack is melted, ice is exposed with a surface albedo that is even lower, ranging from 0.55 for clean ice to much lower values determined by the presence of impurities. The “dark zone” in West Greenland, where dust outcropping and biological activity (Stibal et al., 2017) explain a very low (<0.3) ice albedo, will likely progress inward and upward as the ablation area grows, and the presence of impurities might increase, as the ice melts and warms and more water is available (Greuell, 2000).

• Melt‐Elevation Feedback. As surface ablation increases, surface elevation decreases, exposing the ice sheet to higher ambient temperatures, further enhancing ablation. Although this effect is typically assumed to be small on short temporal scales, and not considered in most projections, it is suggested to enhance GrIS SMB decrease with ~5% at the end of this century, becoming ever more important afterward (Edwards et al., 2014).

• Tundra‐Ice Sheet Interaction. As more dark tundra surface is exposed during summer through the retreat of peripheral glaciers and ice caps and a shortening of the snow‐covered season, more convection will occur, heating the tundra atmosphere; part of this heat may be transferred to the neighboring ice, enhancing melting.

The above feedbacks are typically not fully captured in low‐resolution model projections, enhancing the uncertainties associated with these projections. As discussed in section 2.2.5, even the latest generation of ESMs exhibits substantial biases in representing the Arctic atmosphere, ice sheet surface processes, and/or ocean and sea ice conditions. For now, RCMs will resolve these features better, but their results remain strongly dependent on the choice of the GCM/ESM forcing (Fettweis et al., 2013).

A tipping point in GrIS MB is sometimes defined as the moment at which GrIS SMB becomes negative, making MB definitively negative (Figure 2). Climate model predictions indicate that this threshold is reached at a global temperature increase of ~2 °C relative to the preindustrial climate (Robinson et al., 2012), although the above‐mentioned positive feedbacks might accelerate that (Pattyn et al., 2018). Depending on the scenario, this threshold might be reached as early as the 2030s (in high‐emission scenarios such as RCP8.5) or will not be reached at all (in low‐emission scenarios, which are the target of the 2015 Paris Agreement and which would limit global mean temperature rise to well below 2 °C above preindustrial levels).

In sharp contrast with the GrIS, future AIS SMB is expected to increase initially in response to atmospheric warming (Figure 15) as a result of enhanced snowfall, while runoff remains small. SMB is predicted to increase at a rate of ~100 Gt/year per degree of (near‐surface AIS) warming (Ligtenberg et al., 2013) by the mechanism of enhanced water vapor concentration in a warmer atmosphere. Additionally, changes in atmospheric dynamics, in turn driven by global warming, stratospheric ozone recovery, and/or natural variability, have recently been suggested to influence Antarctic SMB trends (Lenaerts et al., 2018; Medley & Thomas, 2019). Finally, changes in cloud phase and structure over Antarctica, sea ice decline, and ocean surface warming have been suggested to control AIS SMB into the future (Lenaerts et al., 2016). The projected Antarctic SMB increase is expected to mitigate some fraction of the currently ongoing dynamic mass loss in West Antarctica, which is about 200 Gt/year (Gardner et al., 2017; Shepherd et al., 2018). While the consensus is that dynamic losses will dominate future AIS MB, especially in marine sectors of the ice sheet in West Antarctica, the Antarctic Peninsula, and some portions of East Antarctica, some other parts of the AIS are likely to experience mass gain by enhanced snowfall, as long as surface runoff remains small (Winkelmann et al., 2012).

Other AIS SMB components, which are at least an order of magnitude smaller than snowfall, will likely continue to play a minor role in future SMB changes as long as the warming remains modest. A notable exception is the potential indirect role of increased rainfall and surface melt on controlling the stability of Antarctic ice shelves, and thereby the stability of the overall AIS. Similar to the GrIS, firn on AIS ice shelves can lose its meltwater buffering capacity through enhanced meltwater refreezing, latent heat release, and compaction. The water starts ponding on the surface and/or collects in crevasses. Eventually, the water finds its way down, as it exerts a downward or tensile pressure that exceeds that of ice, and ultimately reaches the ice shelf bottom, leading to rapid and catastrophic ice shelf disintegration (Banwell & Macayeal, 2015). This ice shelf hydrofracture mechanism has so far only been observed in the northernmost parts of the Antarctic Peninsula (Scambos et al., 2003 but might expand to other AIS regions in a warmer climate.

6. Conclusions and Recommendations

In this paper, we have reviewed the current state of knowledge of ice sheet SMB in Greenland and Antarctica. Traditional observational methods, which are convenient and cheap but carry relatively large uncertainties and often provide only a single‐point SMB measurement, are complemented by novel techniques, such as airborne and satellite radar and laser, and GPS. Although these new techniques provide more precise observations and give us insight in the spatial variability in SMB, they all measure snow depth or surface height changes, requiring knowledge of snow density (with the exception of cosmic ray neutron detection). Therefore, the development of instrumentation to measure snow density precisely over large areas is urgently needed. Cosmic ray counters, which measure snow water equivalent directly and thereby circumvent the need for density observations, have the potential to revolutionize the field of SMB observations into the future.

These new observational techniques have revealed previously unknown large spatial variability in ice sheet SMB, superimposed on the large‐scale gradients in SMB from the coast to the interior, both on the GrIS—transitioning from multiple‐meter ice ablation to net snow accumulation over less than 100‐km distance—and the AIS—where high‐precipitation regions coexist with blue ice areas along the coasts. On smaller scales (<1 km), SMB varies considerably as well, driven by surface topography undulations and consequent wind‐driven snow redistribution, which challenges the spatial representativeness of stake and firn/ice core records. This small‐scale variability is not represented by RCMs, which currently operate at horizontal resolutions of typically 5 km (full GrIS and local AIS) to 25 km (full AIS). Because small‐scale snow redistribution does not greatly impact the integrated SMB of a larger area, multiple RCMs now properly simulate SMB on scales of the entire ice sheet down to individual glacier drainage basins. Improved RCM performance was mainly achieved by (1) enhancing the horizontal resolution, including statistical downscaling; (2) including additional (snow) physical processes to represent all SMB components; and (3) the availability of observational datasets to enable detailed model evaluation, in particular GRACE and snow radar.

Further enhancement of horizontal resolution in RCMs will require using nonhydrostatic atmospheric models (e.g., Weather Research and Forecasting (WRF) model, HARMONIE) and/or continued development of statistical downscaling. In tandem, improved simulation of ice sheet SMB requires further development of (high‐resolution) atmospheric reanalyses and ESMs, with special emphasis on atmospheric processes (clouds, precipitation, radiation, and turbulence); snow‐atmosphere coupling; snow hydrology; snow and ice albedo; SMB downscaling; and, for ESMs in particular, coupling between SMB and ice sheet dynamics. In the not‐too‐distant future, rapidly increasing computational power will enable us to operate ESMs at horizontal resolutions similar to current RCMs, enabling a direct and fully coupled global framework to assess ice sheet SMB. This should not prevent continuation of model/observational efforts to understand and model small‐scale SMB variability (and its driving processes), such as refining statistical downscaling of SMB, developing models of heterogeneous water percolation in firn, and simulating wind‐driven processes.

Recent SMB trends strongly differ between the GrIS and the AIS. GrIS SMB has decreased significantly since the mid‐1990s, dominating GrIS mass loss since then although a return to pre‐1990 values occurred in 2017 and 2018. We expect melt and runoff from the GrIS to increase further under sustained global warming, the degree of which strongly depends on model formulations, climate change scenario, and the potential impact of positive feedbacks associated with GrIS SMB decline. In contrast, recent AIS SMB trends remain relatively poorly constrained, since atmospheric reanalyses differ substantially. Ice core records suggest that AIS SMB has been increasing since the start of the 20th century; however, it remains unclear whether the increase is driven by thermodynamics, atmospheric dynamics, or both, which suggests that our ability to assess future projections over the AIS is limited.

By dominating GrIS mass loss through increased runoff and partly mitigating dynamic AIS mass loss by increased snowfall, the future evolution of ice sheet SMB will continue to play a pivotal role in ice sheet mass changes and associated changes in sea level. Ice sheet SMB also influences past, present, and future ice sheet mass change by controlling ice sheet dynamical processes, such as basal hydrology, fjord circulation by basal runoff and determining meltwater input for Antarctic ice shelf hydrofracture and ice cliff instability (DeConto & Pollard, 2016; Edwards et al., 2019).

Glossary

Antarctic geographical names

Figure 16 shows an overview map of the Antarctic Ice Sheet, with names of regions, ice shelves, glaciers, and locations that are names in this review paper indicated on the map.

Mass balance (MB, Figure 2):

the rate of change of mass (M) of (in the context of this paper) an ice sheet with respect to time (t), or dM/dt. Mass balance is negative when an ice sheet loses mass in time and is positive when it gains mass in time. Units are [units mass] per [units time]; in the context of ice sheet mass balance typically expressed as Gt (=10¹² kg) per year.

Accumulation area or zone:

the group of locations where, over the course of one hydrological or calendar year (depending on the definition), SSMB is positive.

Ablation area or zone:

the group of locations where, over the course of one hydrological or calendar year (depending on the definition), SSMB is negative.

Equilibrium line:

the line of locations where, over the course of one hydrological or calendar year (depending on the definition), SSMB is zero. The equilibrium line constitutes the boundary between accumulation and ablation areas or zones.

Accumulation:

although sometimes used as a synonym for SMB, it is not the same. Accumulation is the difference between PR and SU (PR‐SU), that is, SMB without accounting for mass changes by meltwater runoff. Accumulation is identical to SMB at locations where there is no surface melt, or where all the surface meltwater locally refreezes in the snowpack.

Ablation:

a term used to refer to a negative SSMB over some amount of time.

Surface energy balance (SEB, Figure 2):

the balance of radiative (shortwave and longwave) fluxes (RAD), turbulent (sensible and latent) fluxes (TURB), and ground heat flux (GHF) at the ice sheet surface (units Watts per square meter (W m^‐2)

Liquid water balance (LWB, Figure 2):

the balance of processes adding to and removing liquid water from the ice sheet surface and firn (units (Gt/year)

Strain Correction:

Densification dominates the vertical strain experienced in the upper firn column. SMB measurements must account for layer thinning within the column as well as longitudinal stretching of the firn and ice due to variations in ice flow; this imparts an additional strain that accumulates with depth (i.e., over time). Therefore, in situ measurements of SMB must correct for the loss of mass via lateral stretching in regions experiencing high longitudinal strain rates or for longer‐term historical measurements (>10s/year). The SMB correction is typically used on firn/ice core or ground‐penetrating radar measurements.

Degree‐day factor:

a factor relating accumulated positive air temperatures (exceeding the melting point) to surface melt. Although this is an efficient method to calculate surface melt (and resulting runoff, if combined with a retention scheme) since it only requires (hourly) temperature data, it is prone to large uncertainties due to variations in surface characteristics (albedo, etc.).

Atmospheric reanalysis:

Atmospheric reanalysis products are essentially GCMs/ESMs assimilated with atmospheric observations to obtain a “reanalysis” of the global atmosphere, including that at the high latitudes.

Regional climate model (RCM):

an atmospheric model with a limited‐area domain (i.e., spanning a part of the globe, for example, the Greenland or Antarctic Ice Sheet and surrounding oceans), driven by vertical atmospheric profiles at its lateral boundaries and (commonly) the top of the troposphere, and sea‐ice extent and sea‐surface temperatures at its ocean surface boundary taken from a global data set (which is either an atmospheric reanalysis data set, or a GCM/ESM; see below for definition). Currently, RCMs are typically employed at horizontal resolutions of 5–35 km. For application on ice sheets, RCMs are coupled to a sophisticated snow model that uses the RCM atmospheric input to simulate snow and firn processes.

General circulation model (GCM):

a modeling framework that couples a global atmospheric, ocean/sea ice, and land model. A GCM only requires input of solar irradiance, concentrations of atmospheric greenhouse gases and aerosols, and land use and generates its internal climatology, which can also respond to changes in any of the above‐mentioned inputs (e.g., atmospheric CO₂ concentrations). Currently, GCMs are employed at horizontal resolutions of 1 to 2.5°.

Earth System Model (ESM):

a modeling framework that is an extension of that of a GCM, where ESMs also include models of the biogeochemistry of the ocean and land (carbon cycle, nutrient cycle, etc.), atmospheric chemistry, and dynamic ice sheets. With the additional processes included, ESMs are able to internally calculate atmospheric CO2 concentrations and aerosols and require only input of carbon into the natural system. Currently, ESMs are employed at horizontal resolutions of ~1°, but higher‐resolution ESM results (0.25°) will become available within the framework of the upcoming CMIP6 effort.

Supporting information

Supporting Information S1

Date Set S1

Date Set S2

Date Set S3

Lenaerts, J. T. M. , Medley, B. , van den Broeke, M. R. , & Wouters, B. (2019). Observing and modeling ice sheet surface mass balance. Reviews of Geophysics, 57, 376–420. 10.1029/2018RG000622