Abstract
Our understanding of the long‐term evolution of the Earth system is based on the assumption that terrestrial weathering rates should respond to, and hence help regulate, atmospheric CO2 and climate. Increased terrestrial weathering requires increased carbonate accumulation in marine sediments, which in turn is expected to result in a long‐term deepening of the carbonate compensation depth (CCD). Here, we critically assess this long‐term relationship between climate and carbon cycling. We generate a record of marine deep‐sea carbonate abundance from selected late Paleocene through early Eocene time slices to reconstruct the position of the CCD. Although our data set allows for a modest CCD deepening, we find no statistically significant change in the CCD despite >3 °C global warming, highlighting the need for additional deep‐sea constraints on carbonate accumulation. Using an Earth system model, we show that the impact of warming and increased weathering on the CCD can be obscured by the opposing influences of ocean circulation patterns and sedimentary respiration of organic matter. From our data synthesis and modeling, we suggest that observations of warming, declining δ13C and a relatively stable CCD can be broadly reproduced by mid‐Paleogene increases in volcanic CO2 outgassing and weathering. However, remaining data‐model discrepancies hint at missing processes in our model, most likely involving the preservation and burial of organic carbon. Our finding of a decoupling between the CCD and global marine carbonate burial rates means that considerable care is needed in attempting to use the CCD to directly gauge global carbonate burial rates and hence weathering rates.
Keywords: carbonate compensation depth, Earth system modeling, weathering feedback
Key Points
Compilation of deep‐sea carbonate preservation shows modest CCD deepening across the long‐term Late Paleocene to Early Eocene warming trend
Earth system modeling broadly reproduces mid‐Paleogene warming, δ13C and CCD trends via increases in volcanic CO2 outgassing and weathering
Earth system modeling suggests the long‐term position of the CCD is decoupled from global marine carbonate burial and weathering inputs
1. Introduction
On million year timescales, the partial pressure of atmospheric carbon dioxide (pCO2) and global temperature is widely assumed to be regulated primarily by global rates of silicate mineral weathering. If this were not the case, even relatively small changes in volcanic outgassing would give rise to repeated and unbounded approximately million year timescale swings in pCO2 and climate (Berner et al., 1983; Berner & Caldeira, 1997; Kump et al., 2000; Walker et al., 1981). These are not observed in the Cretaceous‐Recent geological record, for which we have relatively continuous and high‐resolution deep‐sea climate records. Yet silicate weathering is just one part of the system stabilizing our long‐term climate. The production, preservation, and burial of organic carbon (Kump & Arthur, 1999) and/or low‐temperature crustal alteration (Alt & Teagle, 1999) may exert additional important long‐term negative feedbacks on Earth's climate. In addition, direct evidence for the link between pCO2, climate, and silicate weathering rates (as estimated by variations in strontium (Palmer & Elderfield, 1985) and lithium isotopes (Misra & Froelich, 2012) in marine carbonates) is currently ambiguous, with multiple possible interpretations of weathering proxy data sets. For example, Large Igneous Province activity may dampen any potential weathering signal in Sr isotope records (Hodell et al., 2007), and flat Li isotope signals have been variably interpreted as tectonic limitation of weathering (Froelich & Misra, 2014; Misra & Froelich, 2012) or changes in the global denudation regime (Li & West, 2014). Thus, constraining the role of silicate weathering is central to a full understanding of Earth's climate history.
A conceptually simple approach to constraining global weathering is to consider the mass balance of the carbonate system and to utilize sedimentary indicators of changes in this balance, such as the carbonate compensation depth (CCD). The basis for understanding the CCD rests in the fact that the stability of calcium carbonate (CaCO3) decreases with increasing pressure (i.e., depth). Carbonate secreted by plankton near the ocean surface and transported to the seafloor will begin to dissolve once it exceeds the depth of the calcite saturation horizon (CSH)—the physical‐geochemical horizon of neutral CaCO3 stability. Somewhere below this depth, the sedimentary CaCO3 dissolution flux from the sediments will equal the supply of new CaCO3. This depth is termed the CCD (Farrell & Prell, 1991; Ridgwell & Zeebe, 2005; Zeebe & Wolf‐Gladrow, 2001); at depths greater than this, sediments become devoid of CaCO3 at steady state. Pore water organic carbon respiration can also influence sedimentary carbonate dissolution and sediments at depths shallower than the CCD may show carbonate dissolution fluxes due to respiration in sediment pore waters if there is a large supply of organic matter to the seafloor (Archer, 1996). The CCD can vary between ocean basins as a function of large‐scale patterns in ocean circulation and consequent water mass aging gradients. Prior to the proliferation of planktic calcifiers in the open ocean in the Mid‐Mesozoic (Bown et al., 2004; Hönisch et al., 2012) and the consequent oversupply of biogenic carbonate to the seafloor relative to global weathering (Ridgwell, 2005; Zeebe & Westbroek, 2003) deep‐sea carbonate compensation would not have occurred and hence no CCD can be defined.
The CCD is of particular interest in understanding past changes in global carbon cycling because it is a sedimentary feature that can be reconstructed from the geological record (e.g., Farrell & Prell, 1991; Van Andel, 1975). For instance, during the geologically rapid (several kiloyears; Kirtland Turner & Ridgwell, 2016; Zeebe et al., 2016), carbon release associated with the Paleocene‐Eocene Thermal Maximum (PETM, ~56 Ma), the CCD shoaled—evidence for neutralization of emitted CO2 by sedimentary CaCO3 dissolution and a carbonate system temporarily out of equilibrium (Hönisch et al., 2012). However, on longer timescales (hundreds of thousands to millions of years), the burial of CaCO3 in marine sediments depends on, and indeed must generally balance, the input of the terrestrial weathering products—predominantly Ca2+ (and Mg2+) HCO3 − (Ridgwell & Zeebe, 2005; Zeebe & Westbroek, 2003). The global marine CaCO3 budget is also influenced by CaCO3 burial on continental shelves (Berger & Winterer, 1974), but greater weathering flux can be counterbalanced by increased preservation of CaCO3 in deep‐sea sediments. Increased deep‐sea preservation would be expected to result in a deeper CCD, providing a potential proxy for global weathering rates and ocean carbonate saturation (Kump et al., 2009). In this way, the multimillion year CCD behavior fundamentally differs from short‐term CCD responses such as the PETM, when CO2 release outpaced weathering feedbacks (e.g., see Hönisch et al., 2012) and global carbonate burial rates were substantially suppressed compared to weathering inputs. In contrast, on multimillion year timescales, global carbonate burial should track weathering.
Its promise as a constraint on global weathering rates has led to extensive use of the position of the CCD in the reconstruction of Cenozoic changes in marine carbon cycling, ocean chemistry, and atmospheric pCO2 (e.g., Anagnostou et al., 2016; Komar et al., 2013; Roberts & Tripati, 2009; Stuecker & Zeebe, 2010; Tripati et al., 2009; Tyrrell & Zeebe, 2004). Here, we assess the interpretation of observed changes in the long‐term CCD and the strength of its link to climate change and global weathering rates, taking a multimillion year interval of progressive warming from the late Paleocene (~58 Ma) through early Eocene (~49 Ma; “LPEE”; Figure 1) as an illustration. Bottom water δ18O values in benthic foraminiferal carbonate across this interval decreased by nearly 0.8‰ (Cramer et al., 2009; Zachos et al., 2008), corresponding to a ~4 °C warming in the absence of any continental ice (Figure 1). This warming culminated in the Early Eocene Climatic Optimum (EECO; Zachos et al., 2001), characterized by peak Cenozoic bottom water temperatures (Cramer et al., 2009; Zachos et al., 2001, 2008). Multiple lines of evidence suggest that EECO warmth may be related to higher pCO2 as a consequence of elevated volcanic outgassing and/or a reduction in net organic carbon burial (Komar et al., 2013). Estimates of pCO2 roughly double (Beerling & Royer, 2011) between ~55 and ~49 Ma, and the δ13C values of benthic foraminifera trend toward more depleted values from ~58–53 Ma (Cramer et al., 2009; Figure 1). Concurrent with the early Eocene temperature rise was a trend toward depleted 87Sr/86Sr, which has been attributed to emplacement of the North Atlantic Igneous Province (Hodell et al., 2007)—a potential driver of increased volcanic outgassing rates (Eldholm & Thomas, 1993).
Figure 1.
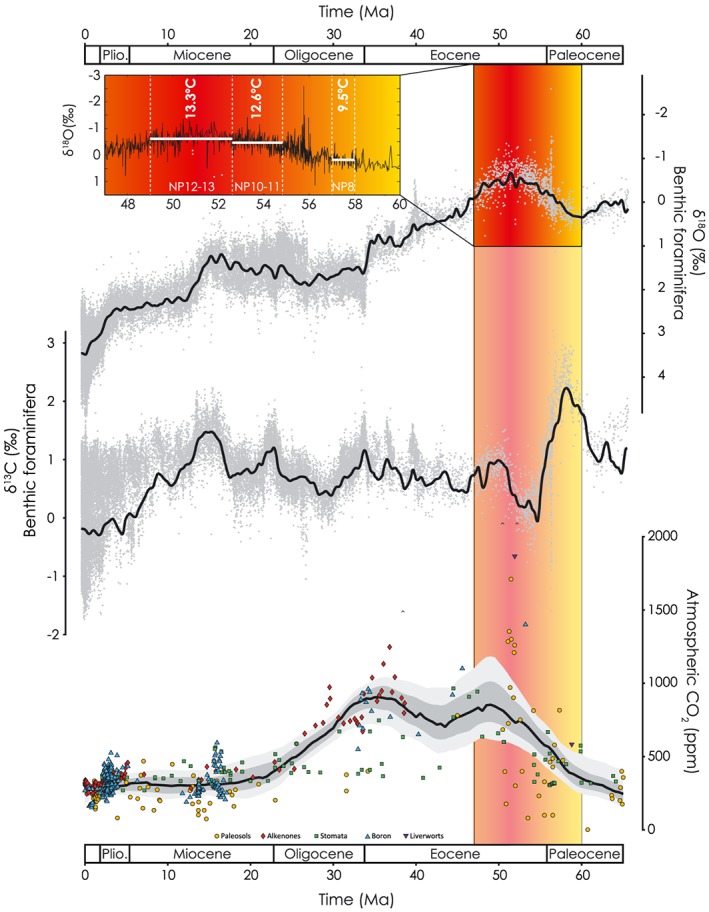
Climatic context for the LPEE. Cenozoic records of benthic foraminiferal δ18O (top), benthic foraminiferal δ13C (middle), and pCO2 (bottom). Isotope records are from Cramer et al. (2009). Inset shows the benthic foraminiferal oxygen isotope record across the LPEE. Three highlighted time slices are demarcated by their respective nannofossil zonations and mean temperature for each time slice is calculated via the Bemis et al. (1998) calibration. Cenozoic history of pCO2 is from Foster et al. (2017). Black line is most likely LOESS fit through the data; 68% and 95% confidence intervals shown as dark and light gray bands.
High global surface temperatures should have driven an increase in the rate of weathering, which would generally be expected to result in a deeper CCD. However, the only previous global reconstruction of CCD changes during the Paleocene and Eocene by Van Andel (1975; Figure 2) predated four decades of intense ocean drilling and thus relied on sparse data. Since this seminal paper, the position of the CCD across the LPEE has been reassessed regionally, based on clusters of sites (Hancock et al., 2007; Leon‐Rodriguez & Dickens, 2010) or depth transects (Pälike et al., 2012; Figure 2). These regional studies show discrepancies in the absolute position of the CCD. Specifically, the two studies based on different Equatorial Pacific sites disagree by over 500 m across the EECO (from ~53–51 Ma; Leon‐Rodriguez & Dickens, 2010; Pälike et al., 2012). These regional studies generally agree that the CCD was slightly shallower in the late Paleocene (~57 Ma) than at the onset of the EECO (55–53 Ma), but the trends diverge markedly, entering peak EECO warmth (52–50 Ma; Figure 2).
Figure 2.
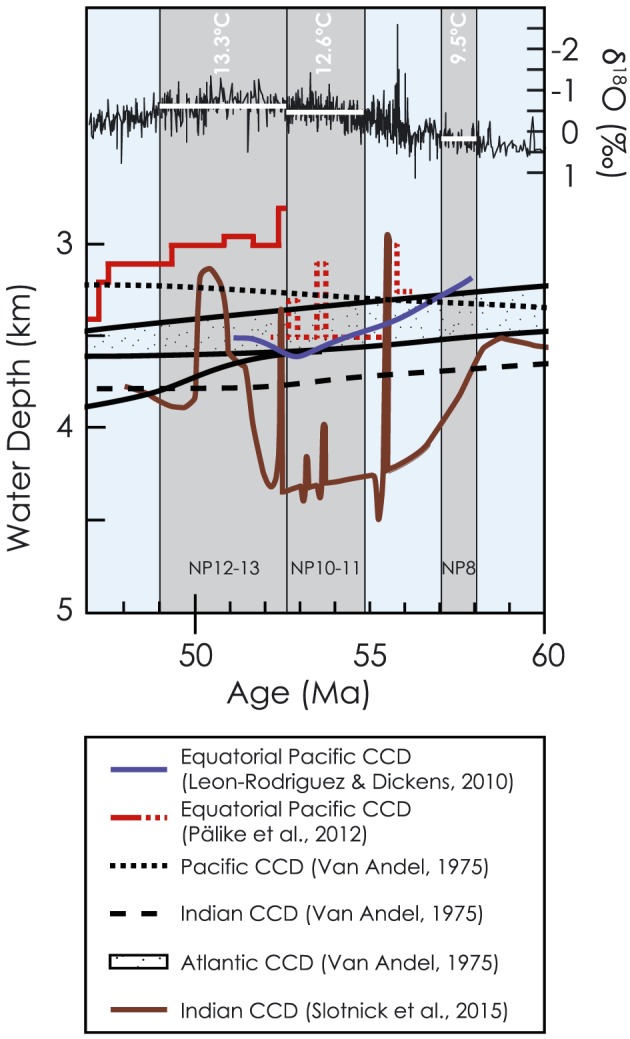
Previous CCD reconstructions across the LPEE. Black lines are from an early global compilation by Van Andel (1975), red line from the Pacific equatorial age transect of Pälike et al., 2012, blue line from the equatorial Pacific record of Leon‐Rodriguez and Dickens (2010), and brown line from the Indian Ocean record of Slotnick et al. (2015). CCD = carbonate compensation depth.
There are significant challenges in extrapolating from basin‐specific CCD reconstructions to a global CCD record. Changes in global ocean circulation patterns can drive regional changes in the CCD, even with little change globally. For example, the deep‐sea CaCO3 burial pattern from the Last Glacial Maximum to the present day (Catubig et al., 1998) shows profound CCD changes in the Atlantic, associated with local changes in ocean circulation (Chikamoto et al., 2008), yet no change in global burial rates between glacial and interglacial (Anderson & Archer, 2002). Circulation changes may also have regionally amplified the dramatic PETM CCD shoaling at Walvis Ridge in the South Atlantic via concurrent reductions in local deepwater formation (Zeebe & Zachos, 2007). In addition, changes in a site's latitude due to plate motion may correlate with differences in overlying productivity, biasing the CCD interpretation (Lyle, 2003).
Only an appropriately (area) weighted average CCD can reflect changes in global weathering rates. One could infer from (a) the dominance of the Pacific Ocean in the Paleogene in terms of area (Figure 3) and (b) existing estimates of either slightly deeper (Leon‐Rodriguez & Dickens, 2010) or slightly shallower (Pälike et al., 2012) Pacific CCD in the early Eocene than in the late Paleocene that relatively little CCD movement occurred across the LPEE globally (Figure 2). However, global carbon cycle box models predict a CCD deepening of >1 km (Komar et al., 2013) to explain observed long‐term warming and δ13C trends in terms of greater CO2 outgassing due to enhanced volcanism and consequently higher weathering rates. Such a large deepening is seen only in the northeastern Indian Ocean (Figure 2; Slotnick et al., 2015), for the interval 58 through 52 Ma. Here we assess the impact of LPEE climate change on the CCD by (a) reconstructing the CCD using time slices of deep‐sea sedimentary wt% CaCO3 and (b) modeling the position of the CCD in response to progressively increasing atmospheric CO2 with the Earth system model cGENIE.
Figure 3.
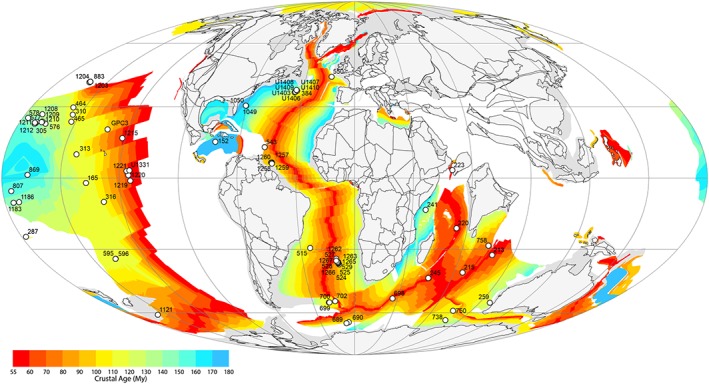
Paleogeography and deep‐sea drilling coverage. Paleogeography after Scotese (2010) showing locations of deep‐sea drilling sites, which appear in at least one of the three late Paleocene to early Eocene time slices presented.
2. Methods
2.1. Data Compilation
We compiled published wt% CaCO3 measurements and reconstructed paleodepths for Deep Sea Drilling Project (DSDP), Ocean Drilling Program (ODP), and Integrated Ocean Drilling Program (IODP) sites spanning the late Paleocene to early Eocene (Tables S1–S3 in the supporting infomation). Sites with upper Paleocene or lower Eocene sediments were included in our data set using the following criteria: (1) paleodepths deeper than 1,000 m, (2) no indication of reworking, and (3) existing wt% CaCO3 measurements. Our compilation thus includes 75 DSDP, ODP, and IODP sites. The data set includes three time slices: (1) the uppermost Paleocene (corresponding to nannofossil biozones NP7/8 or roughly coeval foraminiferal biozone P4c), (2) the lowermost Eocene (zones NP10/11 or foraminiferal zone P6a), and (3) the interval spanning peak warmth of the EECO (NP12/13 and if needed foraminiferal zone P7/P8). (The latter time slice is shown in the supporting information [SI] figures only). Zone NP9 (P5) hosts the PETM, which was deliberately excluded. Reported wt% CaCO3 values are averages of all measured values within a given time slice for each site. Biostratigraphy and wt% CaCO3 values are derived from DSDP/ODP/IODP volumes, primarily downloaded via the Janus web database (http://www‐odp.tamu.edu/database/) and the Ocean Drilling Stratigraphic Network database (http://www.odsn.de/) and supplemented by Hancock et al. (2007) for Site 259. For deep‐sea clay sites without wt% CaCO3 measurements but lacking CaCO3 in sedimentological descriptions, 0 wt% was assumed. Paleolatitude and paleolongitude for each site were computed for 55 Ma using the “Point Tracker (v. 7) for Windows” software package (www.scotese.com).
Paleodepths were derived via backtracking, which accounts for thermal subsidence and sediment unloading based on empirical approximations (from Stein & Stein, 1992), but ignoring possible effects due to dynamic topography (Campbell et al., 2018). We employ an empirically fitted curve with a free initial ridge height following Cramer et al. (2009), but using a simplified sediment unloading term that assumes linear sedimentation rates (see SI). Inputs are basement age, current water depth, and total sediment thickness. Basement ages are taken from Müller et al. (2008), with the exception of ODP Sites 689 and 690, for which a basement age of 83 Ma is taken from Barker et al. (1988). Present‐day water depths and sediment thicknesses are taken from the DSDP/ODP/IODP Initial Reports. For sites where basement was not identified or unclear from seismic data, the total drilled sediment thickness was taken as a minimum estimate. See SI for discussion of paleodepth error.
Contour plots of wt% CaCO3 against paleodepth assist in visualizing the CCD for each LPEE time slice. These plots (Figures 4 and 6) highlight the depth interval over which the preponderance of sites transition from high to low wt% CaCO3. We binned raw wt% CaCO3 into depth windows of 1,000 m, starting at 1,000 m, and moving deeper in increments of 100 m. For each depth window, the CaCO3 wt% bins span intervals of 10 wt%. Within each depth bin, wt% CaCO3 values are weighted using a triangular weighting function that assigns full weight to data at the center of the depth bin, with weight declining linearly to zero for data at the edges of the depth bin. The depth bin is then normalized to 1 and contoured, highlighting where the majority of the data within a depth falls in wt% CaCO3 space. We also overlay a vertical dotted line that delineates the median weight percent at any given depth, which indicates the depth over which our data transition from predominantly carbonate replete to predominantly carbonate poor.
2.2. Statistics
Having compiled wt% CaCO3 against paleodepth for each of the LPEE time slices, we next tested whether the position of the CCD differed between each time slice by determining whether wt% CaCO3 varied with paleodepth through time. To do this, we implemented a suite of Generalized Linear Mixed Models (GLMM) using the glmmAMDB package (version 7.2.12; Skaug et al., 2014) in Rstudio (version 0.97.336). Linear Mixed Models use regression analysis to parse how variation in a response, or dependent, variable relates to multiple explanatory, or independent variables, as well as random terms concurrently; that is, these statistical analyses take into account the potential effects of multiple factors on a particular response at the same time. GLMMs are an extension of linear mixed models that allow data to be modeled according to non‐normal distribution functions. In all models, each individual wt% CaCO3 measurement was entered as the response variable. Therefore, to account for sites with multiple samples within a time slice, we always included “site” as a random variable. Our percentage data most closely resembled the binomial distribution function; that is, this function was the best “fit” for our data, which we therefore applied in all models. In the first model, we included all paleodepths, and interacted paleodepth (continuous variable) with time slice (three categories: one, two, and three). Given that previous work (Hancock et al., 2007; Penman et al., 2016) and our data compilation indicated that Sites 259, 869, and 1403 were particularly significant because of paleodepths very close to the modern CCD, we reran this full model three additional times, removing one site from each model iteration. We additionally ran a similar suite of models, including only paleodepths below (a) 3,000 and (b) 3,500 m based on the assumption that data from these deeper sites would be particularly significant for constraining the CCD. In these models, time slice was entered as the only explanatory variable, but all other parameters were identical to above. We again removed each of the three sites (259, 869, and 1403) from these models to determine if the results were driven by site biases.
2.3. Modeling
2.3.1. Model Configuration
We utilize “cGENIE”—an Earth system model of intermediate complexity comprising: a 3‐D dynamic ocean circulation model with simplified “energy and moisture” balance atmosphere (and sea ice; Edwards & Marsh, 2005), a representation of the biogeochemical cycling of major nutrients, trace elements, and isotopes in the ocean (Ridgwell, 2007), plus components accounting for interactions between ocean and marine sediments (Ridgwell & Hargreaves, 2007) and terrestrial weathering (Colbourn et al., 2013), and hence closing the geological cycle of carbon.
cGENIE includes a full representation of the marine carbon cycle, which shapes water column carbonate saturation state (Ωcarb) and also includes a representation of marine sedimentary carbon cycling, namely, sedimentary aerobic respiration of organic carbon and CaCO3 dissolution (Ridgwell, 2007), which can influence pore water Ωcarb. The details of the ocean and sediment carbon cycle processes have been described elsewhere (e.g., Kirtland Turner & Ridgwell, 2013; Ridgwell, 2007; Ridgwell & Hargreaves, 2007; Ridgwell, Hargreaves, et al., 2007; Ridgwell, Zondervan, et al., 2007), so we focus on the specific configuration of the terrestrial rock weathering model. Here, the global fluxes of alkalinity (ALK) and dissolved inorganic carbon (DIC) resulting from carbonate and silicate rock weathering (plus associated Ca2+ and carbon isotopes) are estimated and routed to the coastal ocean in a pattern based on modern watersheds (Edwards & Marsh, 2005). In this study, we select parameterizations for these fluxes determined solely by, and in feedback with, mean global land surface temperature as in Colbourn et al. (2013). In this, temperature dependence of CaCO3 weathering follows Berner (1994; derived by correlating temperatures and bicarbonate concentrations of groundwater), whereas the relationship between silicate weathering and temperature is based on laboratory studies of the impact of temperature on the dissolution of Ca and Mg silicates (Brady, 1991). Note that we chose a zeroth order description (temperature dependence only) and omit potential additional modifiers accounting for the influence of, for example, runoff (Berner et al., 1983) or terrestrial productivity (Berner, 1991). Despite this, the specific combination of weathering feedback and marine sediment burial used gives rise to a millennial‐scale CO2 response comparable to that produced by other Earth system models (Archer et al., 2009). The dynamics and climate feedback sensitivity in cGENIE of these and alternative possible weathering parameterizations are described and assessed in detail by Colbourn et al. (2013, 2015).
We configure cGENIE using a late Paleocene/early Eocene bathymetry, continental configuration, and carbon cycle as in Kirtland Turner and Ridgwell (2016) and Gibbs et al. (2016). We use the following global carbon cycle conditions: major cations have initial mean oceanic concentrations of 18.2 mmol/kg [Ca2+], 29.9 mmol/kg [Mg2+], and 15.0 mmol/kg [SO4 2−] following Panchuk et al. (2008). The effect of elevated (compared to modern) Paleogene [Ca2+] and lower [Mg2+] in influencing ocean carbonate chemistry and global carbon cycling is included by assuming that deviations of [Mg2+] from modern modify K1, K2, while different [Mg2+]/[Ca2+] affects Ksp, as described in Panchuk et al. (2008). The marine biological CaCO3:POC export ratio is assumed globally uniform and set to a value of 0.200, a value determined to give rise to an optimal fit to global distributions of upper Paleocene wt% CaCO3 by Panchuk et al. (2008). Finally, the air‐sea gas transfer coefficient is increased from 0.31 to 0.52 to rescale (CO2) gas transfer to the inferred modern value of ~0.058 mol·m−2·year−1·μatm−1.
The model was initialized with a value of alkalinity (1,975 μmol·eq·kg−1) chosen to produce a mean sediment CaCO3 content (below 176‐m water depth) of ~47 wt% and a global deep‐sea sediment CaCO3 burial rate of 14.7 Tmol CaCO3/year to closely match the optimal upper Paleocene sediment distribution determined by Panchuk et al. (2008). Note that the calculation of fractional calcium carbonate preservation (Archer, 1991; Ridgwell, 2007) only allows for organic carbon to be respired aerobically and, moreover, requires that organic carbon reaching the seafloor is completely respired within the sediments (Archer, 1991). Note also that to provide consistency with the study of Panchuk et al. (2008), when necessary, we modified the seafloor depth (pressure) used to calculate carbonate stability in the sediment model at the specific model‐equivalent ocean drilling data locations identified. In an initial spin‐up phase, as described in Ridgwell and Hargreaves (2007), the ocean‐atmosphere carbon cycle is forced “closed” with global weathering fluxes tracking sedimentary burial of CaCO3 at all times and no bioturbation in the surface sediment layers. After 20 kyr of this closed system spin‐up with atmospheric CO2 kept at 834 ppm (~×3 preindustrial pCO2) and its δ13C at −4.9‰, DIC is constrained at 1,977 μmol/kg. The resulting equilibrium climatology is summarized in Ridgwell and Schmidt (2010). In a second follow‐on phase of spin‐up, the model was run for 200 kyr as an “open” system with temperature‐dependent silicate and carbonate weathering enabled (Archer et al., 2009; Colbourn et al., 2013) and atmospheric CO2 and δ13C free to evolve. The initial global Ca2+ weathering flux was diagnosed from the burial flux (14.7 Tmol Ca2+/year) at the end of the first spin‐up phase and split equally between silicate (7.35 Tmol Ca2+/year) and carbonate (7.35 Tmol Ca2+/year) weathering. An initial flux of volcanic CO2 of 7.35 Tmol C/year (δ13C of −6.0‰) was specified to balance consumption by silicate weathering. Bioturbation and hence mixing of the surface sediments was then enabled (following the procedure of Ridgwell & Hargreaves, 2007). The δ13C signature of carbonate weathering was set to balance the long‐term 13C budget, requiring an enriched signature of 13.58‰ because the model does not include organic carbon burial. Following the spin‐up to balance the geologic carbon cycle, a subsequent control experiment showed drift in atmospheric CO2 of less than 2 ppm over 2 Myr.
2.3.2. Extraction of Modeled CCD and CSH
For determining the simulated carbonate compensation depth in the cGENIE model, we adopted the methodology of Goodwin and Ridgwell (2010). Rather than identifying the model depth at which the sedimentary carbonate deposition and dissolution fluxes are equal, we instead assume that the CCD is coincident with the 20 wt% CaCO3 isoline following Van Andel (1975). (This alternative definition of the CCD is necessary for paleo‐applications as there is no possible way to reconstruct carbonate deposition and dissolution fluxes from a sediment core.) However, the chances of finding a location with almost exactly 20 wt% CaCO3 on a discretized grid of less than 1,000 ocean grid points (e.g., Figures S5 and S6) is relatively small, and even if one or a few such points existed, there would be a substantial risk that they would not be representative of the global CCD. We hence interpolated in depth to the 20 wt% boundary using the much larger number of pairs of locations that exhibit carbonate content either side of this value (i.e., one lower and one higher than 20 wt%). For grid points judged to lie below the CCD (i.e., >20 wt% CaCO3), immediately adjacent cells (including diagonal relationships) are tested as to whether they lie above the CCD (i.e., >20 wt% CaCO3). Grid points bordering land (i.e., continental slope) are excluded so as to avoid biasing by relatively few, but highly productive/upwelling continental margin locations. We also exclude pairs of adjacent grid points that are separated in depth by more than 2000 m to avoid excessive interpolation, but find that our results are virtually independent of the value of this cutoff. Setting a maximum depth separation of 1,000 versus 6,000 m leads to essentially the same answer for the global mean CCD in the model. Finally, CCD‐spanning pairs with the below‐CCD point having <1 wt% are excluded, together with pairs characterized by an above‐CCD point having >50 wt%. The purpose of imposing a maximum wt% CaCO3 in the above‐CCD point is to avoid distortions arising from averaging across the lysocline, above which the change in wt% CaCO3 with decreasing depth is much less steep. For each pair of CCD‐spanning adjacent model grid points, we then calculate the CCD depth as an average weighted by how close the carbonate content of the cell is to the 20 wt% boundary. In other words, in a grid point pair characterized by one point with 19 wt% CaCO3 and one with 50 wt%, the CCD depth will be much closer to the depth of the 19 wt% CaCO3 location. A typical distribution of CCD‐spanning grid point pairs is shown in Figure S6. The final estimate of the global mean CCD in the model is then simply the arithmetic mean of the interpolated CCD separating each grid point pair. For determining the depth of the carbonate saturation horizon (CSH) in the model, a quadratic regression is fit to the global distribution of Δ[CO3 2−] (the carbonate ion concentration relative to local saturation) versus depth in the model for depths greater than 1,000 m, and the intersection of this line with Δ[CO3 2−] = 0 (saturation) calculated.
2.3.3. Experimental Setup
Using the above configuration, we ran five ensembles of experiments designed to test controls on the position of the CCD in cGENIE. Ensemble 1 consists of a series of experiments with volcanic outgassing rate modified by factors ranging from 0.6 to 2.0 and run to a new steady state (2 Myr) as an open system. Ensemble 2 isolates the roles of [DIC] and [ALK] on the CCD by fixing radiative forcing so that global temperature is the same in each experiment and hence not a function of atmospheric CO2. Ensemble 2 was created by restarting each experiment from ensemble 1 and running for 20 kyr as a “closed system” with no further gains to or losses from the ocean‐atmosphere (Ridgwell & Hargreaves, 2007), thus preserving the [DIC] and [ALK] of the respective ensemble 1 experiments. We use radiative forcing of 3 times preindustrial (equivalent of 834 ppm) for all experiments, equivalent to our open‐system spin‐up. Fixing radiative forcing also eliminates differences in ocean overturning circulation between each experiment. In contrast, ensemble 3 isolates the role of temperature and ocean circulation on the CCD. All experiments in ensemble 3 were restarted from the 3 times preindustrial CO2 experiment from ensemble 1 with radiative forcing set to match the equivalent atmospheric CO2 from each ensemble 1 experiment. Each experiment was run for 20 kyr as a closed system so that [DIC] and [ALK] were relatively invariant. Ensemble 4 tests the impact of fixed global weathering rates on the CCD. All experiments in ensemble 4 were restarted from the 3 times preindustrial CO2 experiment from ensemble 1, but with atmospheric CO2 fixed equal to the CO2 value reached at the end of each equivalent ensemble #1 experiment. Ensemble 4 experiments were run for 20 kyr.
Finally, to test the potential influence of grid resolution on our modeled CCD, we ran one final ensemble (ensemble 5), duplicating ensemble 1 but replacing the bathymetry grid used for the calculation of pressure and carbonate stability in the sediment model (see Ridgwell, Hargreaves, et al., 2007, for an example). Compared to the standard sediment model grid derived by discretizing the underlying coupled GCM bathymetry (Tindall et al., 2010) according to the 16 depth layers of the ocean circulation model as used in Ridgwell and Schmidt (2010), we instead discretized at 64 levels and with a maximum 6,000 m (rather than 5,000 m) ocean depth. The alternative sediment model depth grid (Figure S8) is considerably smoother than the original (Figure S7).
3. Results
3.1. Reconstruction of the LPEE CCD
While we reconstructed three multi‐million year CCD time slices corresponding to nannofossil zones NP8, NP10‐11, and NP12‐13, most of the change in deep ocean temperature (as indicated by benthic foraminifera δ18O) occurs between the NP8 and NP10‐11 time slices, and these two time slices also show a larger difference in δ13C than comparing NP8 to NP12‐13. Hence, we focus most of our comparison and discussion on the NP8 versus NP10‐11 time slices, though results for NP12‐13 are provided in SI.
Paleodepth versus wt% CaCO3 for the NP8 and NP10‐11 time slices are plotted in Figures 4a and 4c (for NP12‐13, see Figure S1). Figures 4b and 4d show the same data in normalized contour plots. (The color shows the density of underlying data and sums to 1 across any given depth.) The dashed white lines indicate that a switch from a majority of high wt% sites to a majority of low weight percent sites occurs between ~4,000 and 4,500 m for both time slices. We hence interpret ~4,000 m as the upper limit for the global mean paleo‐CCD. We have confidence that the CCD was not shallower than 4,000m, as there are numerous records from shallower depths replete with carbonate. Below 4,000 m the sediments are predominantly carbonate‐free, but it is important to note that the data are sparser and almost entirely restricted to the Pacific basin. For these reasons, we have comparatively lower confidence about the maximum possible depth of the global mean CCD but consider it unlikely that it was much deeper than 4,000m in the Pacific basin. The most notable difference between our two time slices among deep sites occurs at Atlantic IODP Site U1403, where CaCO3 burial commenced in the earliest Eocene (NP10‐11 time slice; Expedition 342 Scientists, 2012; Figures 2 and 4). The temporal evolution of wt% CaCO3 within each time slice at each site is plotted in Figure S2. Importantly, there are no consistent trends toward increasing or decreasing wt% CaCO3 within any of our time slices.
Figure 4.
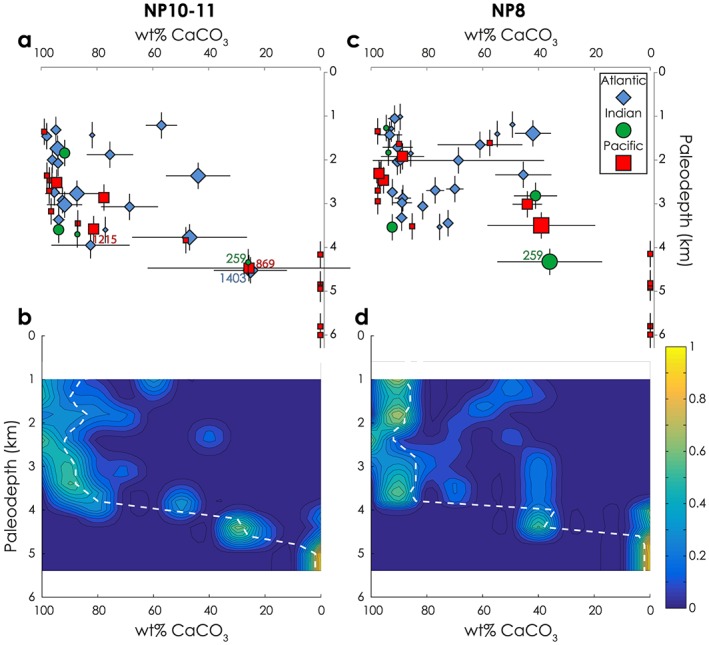
Reconstructed carbonate compensation depth across the LPEE. (a, c) Paleodepth versus wt% CaCO3 for two time slices spanning the LPEE (NP8 and NP10‐11). Symbol size denotes the number of wt% CaCO3 measurements averaged for each site (small: 1 measurement, medium: 2‐9 measurements, large: ≥10 measurements). Horizontal error bars represent 1σ from the mean wt% CaCO3 recorded at each site within the time slice. Vertical error bars represent ±300‐m paleodepth (an estimate derived by trebling the paleodepth error estimate for sites <25 Ma (Sclater et al., 1985) or doubling the ±150 m suggested by Van Andel, 1975 and Van Andel et al., 1975 for sites underlain by crust older than a few million years at the time of paleodepth reconstruction). (b, d) Same data set as above, but contoured and normalized to highlight where the data at any given depth fall in wt% CaCO3 space (see section 2.1). Color represents “density” of normalized weight and sums to 1 at any given depth. The white dashed lines denote the median weight percent value with 50% of the data at higher or lower weight percent values for any given depth.
Our statistical models indicate that time slice does not significantly correlate to wt% CaCO3. Specifically, when we included data from all paleodepths, there was no significant interaction between time slice and paleodepth (GLMM: p > 0.2 for all models), nor was there any overall effect of time slice (GLMM: p > 0.2 for all models). The interactions between paleodepth and time slice were identical or even more insignificant when any of the three deepest carbonate bearing sites (259, 869, or U1403) were removed (GLMM: p > 0.2; GLMM: p > 0.2; GLMM: p = 1.0, respectively). Likewise, when considering just data with paleodepths below 3,000 m, there was no detectable effect of time slice (GLMM: p > 0.9), nor was there when we removed Site 259 (GLMM: p > 0.9), Site 869 (GLMM: p > 0.9), Site U1403 (GLMM: p = 1.0), or all three sites together (GLMM: p = 1.0). The models revealed almost identical results when we considered data with paleodepths below 3,500 m. Thus, the comparatively high abundance of sites at shallower paleodepths does not mask statistical differences in the CCD between time slices. In sum, the three time slices are statistically indistinguishable.
Though statistically indistinguishable, visual comparison of the median wt% CaCO3 for any given paleodepth between the time slices (white dashed lines, Figure 4) shows they are not identical. The transition interval from a high median wt% CaCO3 to a low median wt% CaCO3 occurs at a slightly shallower paleodepth in NP8 than in NP10‐11. The transition to a majority of sites with carbonate content below 20 wt% occurs 160 m deeper for NP10‐11 than for NP8. However, we note that this degree of deepening is likely within the error of paleodepth estimates (see discussion in SI). Our results are thus generally consistent with a CCD deepening of a few hundred meters between 58 and 49 Ma in the equatorial Pacific as suggested by Leon‐Rodriguez and Dickens (2010). Our global‐scale analysis confirms that the CCD deepened, at most, very modestly during the LPEE. However, this modest deepening contrasts with the >1‐km CCD deepening suggested previously by models (Komar et al., 2013) seeking to explain LPEE climatic trends as a result of enhanced volcanism.
3.2. Interpreting the CCD as a Global Carbon Cycle Proxy
What explains the three main lines of marine geological observations across the LPEE: minor CCD deepening, global warming, and δ13C decline? Our CCD compilation lends itself to several possible interpretations: (1) The CCD was relatively unresponsive to increased weathering across the LPEE (Kato et al., 2011; Peucker‐Ehrenbrink & Ravizza, 2000); (2) the CCD is directly coupled to global weathering rates and the relatively minor difference in the CCD across time slices reflects only a minor increase in global weathering rates, despite the observed rise in temperatures (Froelich & Misra, 2014), or (3) increased weathering across the LPEE was accommodated by a commensurate increase in shelf CaCO3 burial, resulting in a relatively stable CCD. For the purposes of this study, we set aside one further possibility—(4) that the CCD deepened considerably (especially outside of the Pacific), but we missed this because of sparse data coverage below ~4,000 m in other ocean basins (Figure 4). This possibility can only be addressed by further drilling of open ocean sites at greater paleodepths. However, our data compilation excludes the possibility of kilometer‐scale deepening of the CCD in much of the Pacific. Given the areal dominance of the Pacific basin in the early Paleogene (Figure 3), this, in turn, excludes the possibility of a global mean kilometer‐scale CCD deepening.
Possibility (1), that progressive increases in atmospheric pCO2, surface temperature, and global weathering rates failed to result in any substantial deepening of the CCD, was first suggested by Pälike et al. (2012). Our results from ensemble 1 test this hypothesis by evaluating the position of the CCD as a function of changes in volcanic outgassing when including a temperature‐dependent weathering feedback (Tables S4–S18). From each experiment, we extract the CSH and CCD (Figure 5) following Goodwin and Ridgwell (2010). Our results are consistent with Pälike et al. (2012), in that the CCD changes little despite large changes in atmospheric CO2 and global temperature. Compared to the CCD in the ×3 pCO2 experiment, the CCD in ~×12 pCO2 experiment is just 300 m deeper. The change in deep ocean temperature of 3.1 °C between NP8 and NP10‐11 is best represented by comparing the ×3 pCO2 and ~×6 preindustrial pCO2 experiments. In the model, the CCD is 160 m deeper between these two experiments, consistent with our data compilation. The CSH, in contrast, is much more sensitive to changes in pCO2 and climate (Figure 5); at ~×6 preindustrial pCO2 the CSH is >425 m deeper than at ×3 pCO2.
Figure 5.
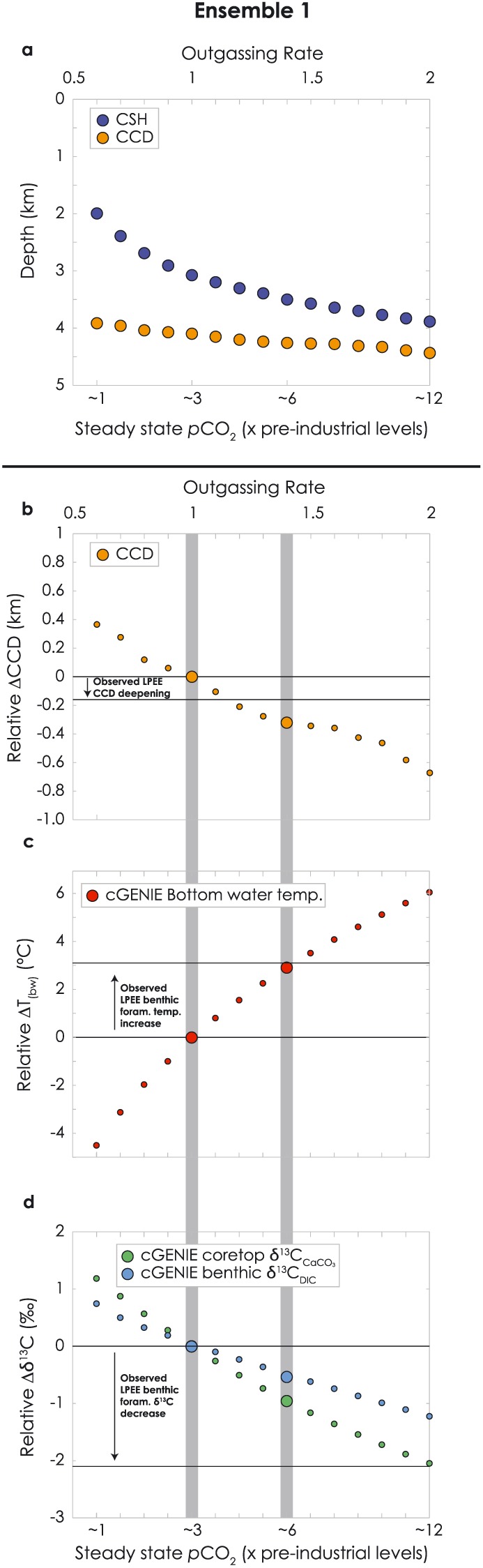
Relationship between CCD, CSH, bottom water temperature, δ13C, and climate in cGENIE relative to the “baseline” experiment at 3 times preindustrial pCO2. (a) Depth of CCD and CSH extracted from ensemble 1 experiments at various outgassing rates/atmospheric pCO2 levels; (b–d) CCD depth, mean bottom water temperatures, and mean core top δ13CCaCO3 from ensemble 1 experiments. Vertical gray bars highlight the best fit experiments for the pre‐EECO (NP8) bottom water temperatures (left) and EECO (NP10‐11) bottom water temperatures (right). CCD = carbonate compensation depth; CSH = calcite saturation horizon; EECO = Early Eocene Climatic Optimum.
These modest CCD changes occur despite the fact that we include temperature‐dependent weathering and simulate large increases in global temperatures. It is rather counterintuitive that a substantive increase in weathering rates and solute supply to the ocean should result in relatively little CCD deepening, because (1) any increase in weathering requires that additional carbonate burial occurs in order to eventually balance the system (Ridgwell & Zeebe, 2005) and (2) we ran all experiments in ensemble 1 to steady state with respect to the carbonate system. Closer inspection, however, reveals that our model accommodates the excess CaCO3 burial predominantly at depths above the CCD, rather than requiring the CCD to deepen. An increasingly bimodal distribution of wt% CaCO3 with depth develops at higher steady‐state atmospheric pCO2 (Figure 6a vs. 6b and 6c), with a sharp transition between high wt% and low wt% CaCO3 at around 4,000‐m water depth indicated by the white dashed lines. A similar pattern is perhaps detectable in the equivalent contour plots of our LPEE wt% CaCO3 data—particularly comparing NP8 to NP12‐13 (Figure S1)—although the data at these crucial depths are sparse.
Figure 6.
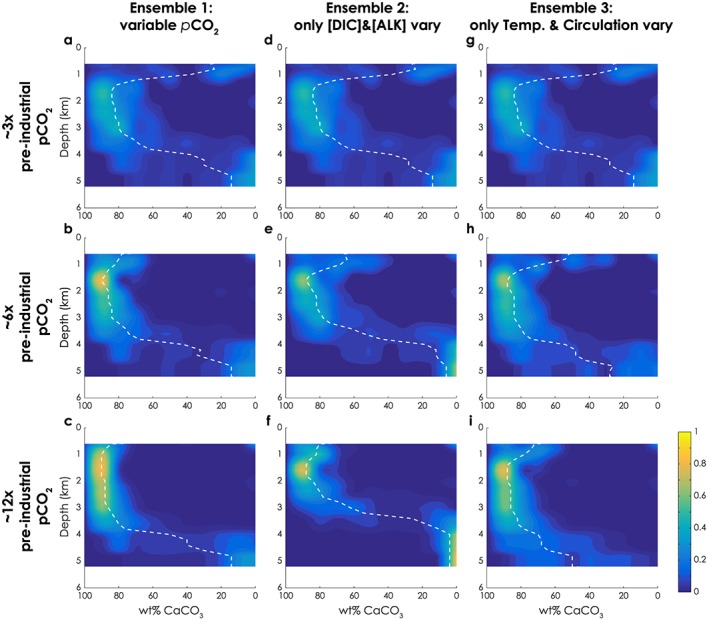
Competing climate influences on carbonate burial in cGENIE. Weight percent carbonate and depth data from model output contoured in the same manner as paleodata in Figure 1 (see section 2.1). (a–c) Three steady‐state experiments from ensemble 1 spanning a range of pCO2; (d–f) Three experiments from ensemble 2 with fixed temperature and circulation, but with variable total carbon inventory as in ensemble 1. (g–i) Three experiments from ensemble 3 with fixed total carbon inventory, but varying temperature and circulation as in ensemble 1. DIC = dissolved inorganic carbon.
The bimodal wt% CaCO3 pattern in the model occurs because sedimentary CaCO3 preservation is influenced by both the carbonate chemistry of the overlying ocean (Ridgwell, 2007; e.g., Figure S3) and geochemical reactions in pore waters. The dominant pore water reactions in a typical open ocean setting (and the only two pore water reactions in the cGENIE model) are aerobic respiration of organic carbon and CaCO3 dissolution (Archer, 1991; Ridgwell, 2007). Aerobic respiration decreases the pore water carbonate saturation state (Ωcarb) and reduces preservation of CaCO3; CaCO3 dissolution increases the pore water Ωcarb, buffering against further dissolution (Zeebe & Wolf‐Gladrow, 2001; Figure 7). Both reactions can occur in sediments at any water depth, but the relative importance of each reaction is depth dependent. At shallower depths (at or above the CSH) bottom waters are supersaturated (Ωcarb > 1), that is, not conducive to CaCO3 dissolution. However, at shallow depths there is still a notable flux of particulate organic matter to the sediments. (This flux decays exponentially with water depth; Ridgwell, Hargreaves, et al., 2007.) Combined with the requirement that all organic matter be remineralized aerobically, this means that aerobic respiration is the dominant reaction at depths shallower than ~2,000 m, driving pore water Ωcarb lower. Conversely, at greater depths below the CSH, CaCO3 dissolution in pore waters neutralizes the undersaturation inherited from bottom waters, elevating pore water Ωcarb until either (a) all carbonate is dissolved or (b) Ωcarb reaches 1, which inhibits further dissolution.
Figure 7.
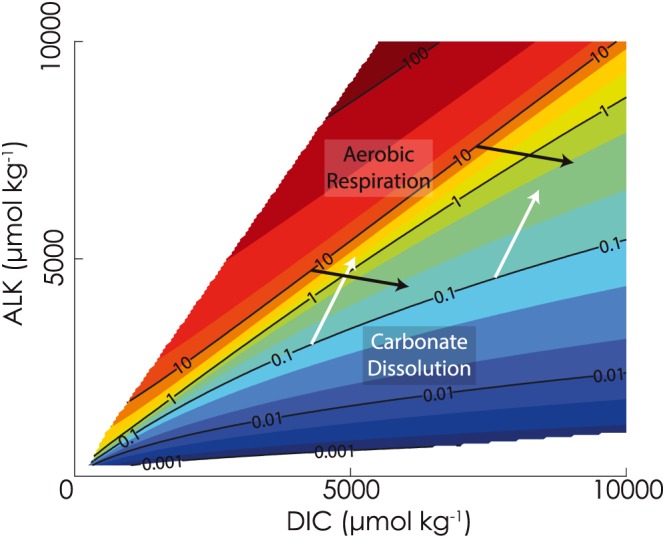
Pore water saturation state evolution in a carbon‐poor versus a carbon‐replete ocean. Lines of equal saturation state (Ω) of CaCO3 are plotted as a function of [ALK] and [DIC]. Two sets of vectors of equal length represent the trajectory of carbonate dissolution (white) and aerobic respiration of organic carbon (black) in saturation state space. The set of vectors that initiate at low [DIC] and [ALK] (left: a “carbon‐poor” ocean) depict larger changes in saturation state from arrow tail to arrow tip compared with the set of vectors that initiate at high [DIC] and [ALK] (right: a “carbon‐replete”) ocean. DIC = dissolved inorganic carbon.
However, the effects of respiration and carbonate dissolution on pore water Ωcarb differ as a function of the whole ocean concentrations of [DIC] and alkalinity [ALK] (illustrated in Figure 7). [DIC] and [ALK] are largely controlled by weathering rates. At higher steady‐state pCO2, thus higher weathering rates (leading to higher steady state [DIC] and [ALK]), aerobic respiration causes a smaller decrease in pore water Ωcarb in the model, driving less dissolution at shallower water depths. Thus, more CaCO3 burial occurs at depths above the CSH in a warmer world with higher weathering rates. Below the CSH, higher [DIC] and [ALK] mean that neutralizing undersaturated bottom waters requires more CaCO3 dissolution, reducing CaCO3 burial. The sum of these effects is to drive the CCD shallower in a warmer world with higher weathering rates. We illustrate these processes with experiments from ensemble 2 (listed in Table S20), in which we fixed global temperature and allowed only pCO2 [DIC] and [ALK] to vary as a function of changes in volcanic outgassing (Figures 6d–6f). In this ensemble the CCD lies shallower in the experiments with higher pCO2, [DIC] and [ALK].
Yet, the effect of higher ocean temperature as a consequence of higher pCO2 should work in the opposite direction, suppressing the solubility of both CaCO3 and CO2 (Zeebe & Wolf‐Gladrow, 2001), thus increasing the preservation of carbonate at depth. We illustrate this effect using experiments from ensemble 3 (listed in Table S21), in which we varied global temperature (and hence ocean circulation) but fixed the global ocean‐atmosphere carbon inventory. In these, the CCD deepens with temperature increase (Figures 6g–6i) by an amount that approximately offsets the effect shown in ensemble 2 (Figures 6d–6f). The combination of ensembles 2 and 3 thus explains the outcome from ensemble 1—higher volcanic outgassing leading to higher pCO2, warming, and enhanced weathering results in a relatively invariant CCD.
There is one additional observational constraint across the LPEE for which we can compare model and data: δ13C decline. Benthic foraminifera show a decrease of ~2‰ between NP8 and NP10‐11 (Cramer et al., 2009). At steady state in our model, the ~3 °C warming between NP8 and NP10‐11 (Figure 5c) requires a 1.4 times increase in CO2 outgassing rate (from ×3 to ~×6 preindustrial pCO2). The associated global mean change in bulk δ13CCaCO3 predicted by the model at steady state is ~−1‰ (Figure 5d and Table S19), only about half of the observed decrease (Figure S4). The changes in benthic δ13CDIC (Table S19) are somewhat more muted (−0.5‰), because the surface‐benthic δ13C gradient becomes more muted in experiments with higher outgassing rates, as the ocean becomes more carbon‐replete even at stable biological pump strength. These results show that increased volcanism and associated weathering can account for the observed LPEE trends in temperature and the CCD, but only partially explain the observed change in δ13C (Figures 5b–5d). However, our model experiments do not include representation of either marine or terrestrial organic matter burial. Decreased organic matter burial could drive additional decrease in benthic δ13C and could help explain this relatively poor fit between model and data. Eocene sediments are generally characterized by reduced burial rates of organic carbon relatively to today (Olivarez Lyle & Lyle, 2006), which may be a consequence of more intense recycling of organic matter in the water column (again, not represented in our model experiments; John et al., 2014). Yet, how organic carbon burial changed across the LPEE is not constrained by the data.
The alternative interpretations of our CCD reconstruction are that global weathering changed little across the LPEE (possibility 2), and/or that an increase in global weathering was accommodated by excess shelf carbonate burial (possibility 3). Proxy evidence for changes in weathering leading into the early Eocene hothouse is mixed. Lithium isotopes were relatively stable across the late Paleocene to early Eocene, interpreted as a tectonic limitation of weathering (Froelich & Misra, 2014; Misra & Froelich, 2012) or changes in the global denudation regime (Li & West, 2014). The Sr isotope trend through this interval likely reflects the emplacement of the North Atlantic Igneous Province (Hodell et al., 2007), which may have obscured the influence of continental weathering signals. If weathering did not appreciably increase in response to global temperature, it would suggest that our current parameterizations for a temperature‐dependent weathering feedback are incorrect. As this is a key process for returning long‐term CO2 to steady state, this possibility warrants further proxy investigation. Regarding possibility 3, we do not attempt to model changes in shelf burial in cGENIE. Rather, we deliberately restrict carbonate preservation and burial to ocean locations where the sediments lie deeper than 175 m to avoid environments where sediment porewaters at relatively shallow depths may become sulfidic and hence influence carbonate preservation via processes that are not currently represented in our sediment model. The global weathering flux in our model is therefore implicitly global weathering less an invariant (unspecified) carbonate removal term on continental shelves.
Experiments in ensemble 4 (Table S22), in which the global weathering rate is invariant, tested whether our data are consistent with (a) a progressively warming world without a weathering feedback or (b) increased weathering accommodated by increased burial on shelves. Higher pCO2 and temperature (without increased weathering flux) result in a noticeably shallower CCD (Table S22) at steady state. This is inconsistent with our global reconstruction and all previous regional studies (Hancock et al., 2007; Leon‐Rodriguez & Dickens, 2010; Slotnick et al., 2015) with the possible exception of Pälike et al. (2012), who interpreted that the CCD shallowed from late Paleocene to early Eocene. However, this interpretation compares late Paleocene off‐equatorial sites (Figure 2, dotted red line) to early Eocene equatorial sites (Figure 2, solid red line). Similarly, if excess weathering was accommodated by increased carbonate burial on shelves (a process not explicitly represented in our experiments), the CCD would shoal in response to higher pCO2 and temperature. We conclude that LPEE scenarios in which temperature and pCO2 are decoupled from global weathering, or in which a global weathering increase is entirely accommodated by increased shelf burial, are unlikely because of the lack of evidence for any substantial CCD shoaling.
One remaining question is whether in the simulation and subsequent calculation of the mean global CCD in cGENIE, the relatively coarse vertical discretization of ocean model grid (Figure S8) could lead to biases in our mean global CCD derivation and specifically, whether the CCD could get “pinned” in any way to a depth boundary between two different ocean grid levels, leading to an artificially low sensitivity of the CCD to changes in outgassing. Ensemble 5, with a smoother sediment model depth grid (Figure S9), explicitly tested for this possibility. We find that the smoother sediment model depth grid leads to a difference of no more than 30 m in the inferred CCD change between the extremes of outgassing rates (×0.6 and ×2.0) compared to the default (used in ensemble 1 experiments). In other words, we can rule out an artifact in our CCD‐identifying algorithm arising from the discretized‐in‐depth nature of the ocean circulation model grid. The modification of the seafloor depth at the data locations of Panchuk et al. (2008) did not affect the sensitivity of the steady‐state position of the CCD to changing rates of outgassing.
4. Conclusions
Our comprehensive data‐based CCD reconstruction from 75 DSDP/ODP/IODP deep‐sea drilling sites reveals a relatively stable CCD between the late Paleocene and the early Eocene (58 to 49 Ma) despite a warming of >3 °C (Cramer et al., 2009). Our modeling experiments demonstrate that significantly increased rates of global weathering are, counterintuitively, consistent with a relatively unresponsive CCD. The CCD can become decoupled not only from the background climate state, but also from total global carbonate burial fluxes, as burial of excess CaCO3 is accommodated at depths above the CCD. Driven only by changes in volcanic outgassing, the model is able to simultaneously reconcile observations of global ocean temperature and the CCD. However, the model underestimates the observed change in benthic δ13C across the LPEE. We attribute this model‐data mismatch to the lack of organic matter burial in our model. We suggest that Earth system changes across the LPEE were most likely driven by an increase in global volcanic outgassing rates, but models that include feedbacks in both inorganic and organic carbon burial will be necessary to simultaneously reproduce all the observed trends.
Our findings are not specific to the question of the drivers of LPEE climate, but create an unexpected challenge to the use of CCD reconstructions to constrain global carbon cycling over long timescales for any interval in Earth. First, further constraints about carbonate accumulation at shallower depths (e.g., large global compilations of carbonate abundance like this one and/or carbonate accumulation rates; Archer, 1996; Catubig et al., 1998; Pälike et al., 2012) in conjunction with numerical modeling are needed if CCD reconstructions are to be interpreted correctly. Second, we question whether numerical models that omit organic matter oxidation and the consequent release of CO2 to pore waters are fully appropriate for using CCD changes (or CCD stasis) as a proxy constraint.
Supporting information
Supporting Information S1
Supporting Information S2
Data Set S1
Data Set S2
Data Set S3
Acknowledgments
Sincere thanks to Sandra Arndt, Steve Barker, Tom Dunkley Jones, Cecily Pälike, and the attendees of our 2012 CCD workshop for helpful discussions, and to Jerry Dickens and several anonymous reviewers for their constructive feedback on previous versions of this manuscript. This work was funded by U.K. NERC Grants NE/H023852/1 and NE/P01903X/1, NSF grants NSF OCE 1657974, OCE 1536611 and NSF OCE 1658024, NERC Independent Research Fellowship NE/L011050/1 to S. E. G., Royal Society University Research Fellowship to D. N. S., an NSF International Research Fellowship to S. K. T., and a Leverhulme Visiting Professorship to E. T. A. R. was supported by a Heising‐Simons Foundation award, and by EU grant ERC 2013‐CoG‐617313. This research used data provided by the DSDP, ODP, and IODP. IODP is sponsored by the U.S. NSF and participating countries under the management of JOI, Inc. The supporting information data (Tables S1–S23 and MATLAB plotting scripts S1 and S2) are hosted on GitHub, can be obtained at https://github.com/carbonatefan/Greene_et_al_2019_PP/releases/tag/v1.0, and are assigned a DOI (https://doi.org/10.5281/zenodo.2656259). The code for the cGENIE.muffin model is also hosted on GitHub. The specific version used in this paper, tagged as release 0.9.4, can be obtained at https://github.com/derpycode/cgenie.muffin/releases/tag/v0.9.4 and is assigned a DOI (https://doi.org/10.5281/zenodo.2654971). A corresponding user manual detailing installation, configuration, and tutorials is available from https://github.com/derpycode/muffindoc website.
Greene, S. E. , Ridgwell, A. , Kirtland Turner, S. , Schmidt, D. N. , Pälike, H. , Thomas, E. , et al. (2019). Early Cenozoic decoupling of climate and carbonate compensation depth trends. Paleoceanography and Paleoclimatology, 34, 930–945. 10.1029/2019PA003601
References
- Alt, J. C. , & Teagle, D. A. H. (1999). The uptake of carbon during alteration of ocean crust. Geochimica et Cosmochimica Acta, 63(10), 1527–1535. 10.1016/S0016-7037(99)00123-4 [DOI] [Google Scholar]
- Anagnostou, E. , John, E. H. , Edgar, K. M. , Foster, G. L. , Ridgwell, A. , Inglis, G. N. , Pancost, R. D. , Lunt, D. J. , & Pearson, P. N. (2016). Changing atmospheric CO2 concentration was the primary driver of early Cenozoic climate. Nature, 533(7603), 380–384. 10.1038/nature17423 [DOI] [PubMed] [Google Scholar]
- Anderson, D. M. , & Archer, D. (2002). Glacial‐interglacial stability of ocean pH inferred from foraminifer dissolution rates. Nature, 416(6876), 70–73. 10.1038/416070a [DOI] [PubMed] [Google Scholar]
- Archer, D. (1991). Modeling the calcite lysocline. Journal of Geophysical Research, 96(C9), 17,037–17,050. 10.1029/91JC01812 [DOI] [Google Scholar]
- Archer, D. (1996). A data‐driven model of the global calcite lysocline. Global Biogeochemical Cycles, 10(3), 511–526. 10.1029/96GB01521 [DOI] [Google Scholar]
- Archer, D. , Eby, M. , Brovkin, V. , Ridgwell, A. , Cao, L. , Mikolajewicz, U. , Caldeira, K. , Matsumoto, K. , Munhoven, G. , Montenegro, A. , & Tokos, K. (2009). Atmospheric lifetime of fossil fuel carbon dioxide. Annual Review of Earth and Planetary Sciences, 37(1), 117–134. 10.1146/annurev.earth.031208.100206 [DOI] [Google Scholar]
- Barker, P. E. , Kennett, J. P. , & Shipboard Scientific Party (1988). Proc. ODP, Init. Repts (Vol. 113). College Station, TX: Ocean Drilling Program. [Google Scholar]
- Beerling, D. J. , & Royer, D. L. (2011). Convergent Cenozoic CO2 history. Nature Geoscience, 4(7), 418–420. 10.1038/ngeo1186 [DOI] [Google Scholar]
- Bemis, B. E. , Spero, H. J. , Bijma, J. , & Lea, D. W. (1998). Reevaluation of the oxygen isotopic composition of planktonic foraminifera: Experimental results and revised paleotemperature equations. Paleoceanography, 13(2), 150–160. 10.1029/98PA00070 [DOI] [Google Scholar]
- Berger, W. H. , & Winterer, E. L. (1974). Plate stratigraphy and the fluctuating carbonate line In Pelagic Sediments: On Land and under the Sea (pp. 11–48). Blackwell Publishing Ltd; 10.1002/9781444304855.ch2 [DOI] [Google Scholar]
- Berner, R. A. (1991). A model for atmospheric CO2 over phanerozoic time. American Journal of Science, 291(4), 339–376. [DOI] [PubMed] [Google Scholar]
- Berner, R. A. (1994). GEOCARB II: A revised model of atmospheric CO2 over phanerozoic time. American Journal of Science, 294(1). [DOI] [PubMed] [Google Scholar]
- Berner, R. A. , & Caldeira, K. (1997). The need for mass balance and feedback in the geochemical carbon cycle. Geology, 25(10), 955–956. [DOI] [Google Scholar]
- Berner, R. A. , Lasaga, A. C. , & Garrels, R. M. (1983). Carbonate‐silicate geochemical cycle and its effect on atmospheric carbon dioxide over the past 100 million years. American Journal of Science, 283(7), 641–683. [DOI] [PubMed] [Google Scholar]
- Bown, P. R. , Lees, J. A. , & Young, J. R. (2004). Calcareous nannoplankton evolution and diversity through time In Thierstein H. R. & Young J. R. (Eds.), From Molecular Processes to Global Impact (pp. 481–508). Berlin: Springer Verlag. [Google Scholar]
- Brady, P. V. (1991). The effect of silicate weathering on global temperature and atmospheric CO2. Journal of Geophysical Research, 96(B11), 18,101–18,106. 10.1029/91JB01898 [DOI] [Google Scholar]
- Campbell, S. M. , Moucha, R. , Derry, L. A. , & Raymo, M. E. (2018). Effect sof dynamic topography on the Cenozoic carbonate compensation depth. Geochemistry, Geophysics, Geosystems, 19, 1025–1034. 10.1002/2017GC007386 [DOI] [Google Scholar]
- Catubig, N. R. , Archer, D. E. , Francois, R. , deMenocal, P. , Howard, W. , & Yu, E.‐F. (1998). Global deep‐sea burial rate of calcium carbonate during the Last Glacial Maximum. Paleoceanography, 13(3), 298–310. 10.1029/98PA00609 [DOI] [Google Scholar]
- Chikamoto, M. O. , Matsumoto, K. , & Ridgwell, A. (2008). Response of deep‐sea CaCO3 sedimentation to Atlantic meridional overturning circulation shutdown. Journal of Geophysical Research, 113, G03017 10.1029/2007JG000669 [DOI] [Google Scholar]
- Colbourn, G. , Ridgwell, A. , & Lenton, T. M. (2013). The Rock Geochemical Model (RokGeM) v0.9. Geoscientific Model Development, 6(5), 1543–1573. [Google Scholar]
- Colbourn, G. , Ridgwell, A. , & Lenton, T. M. (2015). The time scale of the silicate weathering negative feedback on atmospheric CO2 . Global Biogeochemical Cycles, 29, 583–596. 10.1002/2014GB005054 [DOI] [Google Scholar]
- Cramer, B. S. , Toggweiler, J. R. , Wright, J. D. , Katz, M. E. , & Miller, K. G. (2009). Ocean overturning since the Late Cretaceous: Inferences from a new benthic foraminiferal isotope compilation. Paleoceanography, 24, PA4216 10.1029/2008PA001683 [DOI] [Google Scholar]
- Edwards, N. R. , & Marsh, R. (2005). Uncertainties due to transport‐parameter sensitivity in an efficient 3‐D ocean‐climate model. Climate Dynamics, 24(4), 415–433. 10.1007/s00382-004-0508-8 [DOI] [Google Scholar]
- Eldholm, O. , & Thomas, E. (1993). Environmental impact of volcanic margin formation. Earth and Planetary Science Letters, 117(3–4), 319–329. [Google Scholar]
- Expedition 342 Scientists (2012). Paleogene Newfoundland sediment drifts. IODP Preliminary Reports, 342. [Google Scholar]
- Farrell, J. W. , & Prell, W. L. (1991). Pacific CaCO3 Preservation and δ18O Since 4 Ma: Paleoceanic and Paleoclimatic Implications. Paleoceanography, 6(4), 485–498. 10.1029/91PA00877 [DOI] [Google Scholar]
- Foster, G. L. , Royer, D. L. , & Lunt, D. J. (2017). Future climate forcing potentially without precedent in the last 420 million years. Nature Communications, 8, 14845 10.1038/ncomms14845 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Froelich, F. , & Misra, S. (2014). Was the late Paleocene‐early Eocene hot because Earth was flat? An ocean lithium isotope view of mountain building, continental weathering, carbon dioxide, and Earth's Cenozoic climate. Oceanography, 27(1), 36–49. 10.5670/oceanog.2014.06 [DOI] [Google Scholar]
- Gibbs, S. J. , Bown, P. R. , Ridgwell, A. , Young, J. R. , Poulton, A. J. , & O'Dea, S. A. (2016). Ocean warming, not acidification, controlled coccolithophore response during past greenhouse climate change. Geology, 44(1), 59–62. 10.1130/G37273.1 [DOI] [Google Scholar]
- Goodwin, P. , & Ridgwell, A. (2010). Ocean‐atmosphere partitioning of anthropogenic carbon dioxide on multimillennial timescales. Global Biogeochemical Cycles, 24, GB2014 10.1029/2008GB003449 [DOI] [Google Scholar]
- Hancock, H. J. L. , Dickens, G. R. , Thomas, E. , & Blake, K. L. (2007). Reappraisal of early Paleogene CCD curves: foraminiferal assemblages and stable carbon isotopes across the carbonate facies of Perth Abyssal Plain. International Journal of Earth Sciences (Geol Rundsch), 96(5), 925–946. 10.1007/s00531-006-0144-0 [DOI] [Google Scholar]
- Hodell, D. A. , Kamenov, G. D. , Hathorne, E. C. , Zachos, J. C. , Röhl, U. , & Westerhold, T. (2007). Variations in the strontium isotope composition of seawater during the Paleocene and early Eocene from ODP Leg 208 (Walvis Ridge). Geochemistry, Geophysics, Geosystems, 8, Q09001 10.1029/2007GC001607 [DOI] [Google Scholar]
- Hönisch, B. , Ridgwell, A. , Schmidt, D. N. , Thomas, E. , Gibbs, S. J. , Sluijs, A. , Zeebe, R. , Kump, L. , Martindale, R. C. , Greene, S. E. , Kiessling, W. , Ries, J. , Zachos, J. C. , Royer, D. L. , Barker, S. , Marchitto, T. M. Jr. , Moyer, R. , Pelejero, C. , Ziveri, P. , Foster, G. L. , & Williams, B. (2012). The Geological Record of Ocean Acidification. Science, 335(6072), 1058–1063. 10.1126/science.1208277 [DOI] [PubMed] [Google Scholar]
- John, E. H. , Wilson, J. D. , Pearson, P. N. , & Ridgwell, A. (2014). Temperature‐dependent remineralization and carbon cycling in the warm Eocene oceans. Palaeogeography, Palaeoclimatology, Palaeoecology, 413, 158–166. 10.1016/j.palaeo.2014.05.019 [DOI] [Google Scholar]
- Kato, Y. , Fujinaga, K. , & Suzuki, K. (2011). Marine Os isotopic fluctuations in the early Eocene greenhouse interval as recorded by metalliferous umbers from a Tertiary ophiolite in Japan. Gondwana Research, 20(2–3), 594–607. 10.1016/j.gr.2010.12.007 [DOI] [Google Scholar]
- Kirtland Turner, S. , & Ridgwell, A. (2013). Recovering the true size of an Eocene hyperthermal from the marine sedimentary record. Paleoceanography, 28, 700–712. 10.1002/2013PA002541 [DOI] [Google Scholar]
- Kirtland Turner, S. , & Ridgwell, A. (2016). Development of a novel empirical framework for interpreting geological carbon isotope excursions, with implications for the rate of carbon injection across the PETM. Earth and Planetary Science Letters, 435, 1–13. 10.1016/j.epsl.2015.11.027 [DOI] [Google Scholar]
- Komar, N. , Zeebe, R. E. , & Dickens, G. R. (2013). Understanding long‐term carbon cycle trends: The late Paleocene through the early Eocene. Paleoceanography, 28, 650–662. 10.1002/palo.20060 [DOI] [Google Scholar]
- Kump, L. R. , & Arthur, M. A. (1999). Interpreting carbon‐isotope excursions: carbonates and organic matter. Chemical Geology, 161(1–3), 181–198. 10.1016/S0009-2541(99)00086-8 [DOI] [Google Scholar]
- Kump, L. R. , Bralower, T. J. , & Ridgwell, A. (2009). Ocean Acidification in Deep Time. Oceanography, 22(4), 94–107. 10.5670/oceanog.2009.100 [DOI] [Google Scholar]
- Kump, L. R. , Brantley, S. L. , & Arthur, M. A. (2000). Chemical Weathering, Atmospheric CO2, and Climate. Annual Review of Earth and Planetary Sciences, 28(1), 611–667. 10.1146/annurev.earth.28.1.611 [DOI] [Google Scholar]
- Leon‐Rodriguez, L. , & Dickens, G. R. (2010). Constraints on ocean acidification associated with rapid and massive carbon injections: The early Paleogene record at ocean drilling program site 1215, equatorial Pacific Ocean. Palaeogeography, Palaeoclimatology, Palaeoecology, 298(3‐4), 409–420. 10.1016/j.palaeo.2010.10.029 [DOI] [Google Scholar]
- Li, G. , & West, A. J. (2014). Evolution of Cenozoic seawater lithium isotopes: Coupling of global denudation regime and shifting seawater sinks. Earth and Planetary Science Letters, 401, 284–293. 10.1016/j.epsl.2014.06.011 [DOI] [Google Scholar]
- Lyle, M. (2003). Neogene carbonate burial in the Pacific Ocean. Paleoceanography, 18(3), 1059 10.1029/2002PA000777 [DOI] [Google Scholar]
- Misra, S. , & Froelich, P. N. (2012). Lithium Isotope History of Cenozoic Seawater: Changes in Silicate Weathering and Reverse Weathering. Science, 335(6070), 818–823. 10.1126/science.1214697 [DOI] [PubMed] [Google Scholar]
- Müller, R. D. , Sdrolias, M. , Gaina, C. , & Roest, W. R. (2008). Age, spreading rates, and spreading asymmetry of the world's ocean crust. Geochemistry, Geophysics, Geosystems, 9, Q04006 10.1029/2007GC001743 [DOI] [Google Scholar]
- Olivarez Lyle, A. , & Lyle, M. W. (2006). Missing organic carbon in Eocene marine sediments: Is metabolism the biological feedback that maintains end‐member climates? Paleoceanography, 21, PA2007 10.1029/2005PA001230 [DOI] [Google Scholar]
- Pälike, H. , Lyle, M. W. , Nishi, H. , Raffi, I. , Ridgwell, A. , Gamage, K. , Klaus, A. , Acton, G. , Anderson, L. , Backman, J. , Baldauf, J. , Beltran, C. , Bohaty, S. M. , Bown, P. , Busch, W. , Channell, J. E. T. , Chun, C. O. J. , Delaney, M. , Dewangan, P. , Dunkley Jones, T. , Edgar, K. M. , Evans, H. , Fitch, P. , Foster, G. L. , Gussone, N. , Hasegawa, H. , Hathorne, E. C. , Hayashi, H. , Herrle, J. O. , Holbourn, A. , Hovan, S. , Hyeong, K. , Iijima, K. , Ito, T. , Kamikuri, S. I. , Kimoto, K. , Kuroda, J. , Leon‐Rodriguez, L. , Malinverno, A. , Moore Jr, T. C. , Murphy, B. H. , Murphy, D. P. , Nakamura, H. , Ogane, K. , Ohneiser, C. , Richter, C. , Robinson, R. , Rohling, E. J. , Romero, O. , Sawada, K. , Scher, H. , Schneider, L. , Sluijs, A. , Takata, H. , Tian, J. , Tsujimoto, A. , Wade, B. S. , Westerhold, T. , Wilkens, R. , Williams, T. , Wilson, P. A. , Yamamoto, Y. , Yamamoto, S. , Yamazaki, T. , & Zeebe, R. E. (2012). A Cenozoic record of the equatorial Pacific carbonate compensation depth. Nature, 488(7413), 609–614. 10.1038/nature11360 [DOI] [PubMed] [Google Scholar]
- Palmer, M. R. , & Elderfield, H. (1985). Sr isotope composition of sea water over the past 75 Myr. Nature, 314(6011), 526–528. 10.1038/314526a0 [DOI] [Google Scholar]
- Panchuk, K. , Ridgwell, A. , & Kump, L. R. (2008). Sedimentary response to Paleocene‐Eocene Thermal Maximum carbon release: A model‐data comparison. Geology, 36(4), 315–318. 10.1130/G24474A.1 [DOI] [Google Scholar]
- Penman, D. E. , Turner, S. K. , Sexton, P. F. , Norris, R. D. , Dickson, A. J. , Boulila, S. , Ridgwell, A. , Zeebe, R. E. , Zachos, J. C. , & Cameron, A. (2016). An abyssal carbonate compensation depth overshoot in the aftermath of the Palaeocene‐Eocene Thermal Maximum. Nature Geoscience, 9(8), 575–580. 10.1038/ngeo2757 [DOI] [Google Scholar]
- Peucker‐Ehrenbrink, B. , & Ravizza, G. (2000). The marine osmium isotope record. Terra Nova, 12(5), 205–219. 10.1046/j.1365-3121.2000.00295.x [DOI] [Google Scholar]
- Ridgwell, A. (2005). A Mid Mesozoic Revolution in the regulation of ocean chemistry. Marine Geology, 217(3‐4), 339–357. 10.1016/j.margeo.2004.10.036 [DOI] [Google Scholar]
- Ridgwell, A. (2007). Interpreting transient carbonate compensation depth changes by marine sediment core modeling. Paleoceanography, 22, PA4102 10.1029/2006PA001372 [DOI] [Google Scholar]
- Ridgwell, A. , & Hargreaves, J. C. (2007). Regulation of atmospheric CO2 by deep‐sea sediments in an Earth system model. Global Biogeochemical Cycles, 21, GB2008 10.1029/2006GB002764 [DOI] [Google Scholar]
- Ridgwell, A. , Hargreaves, J. C. , Edwards, N. R. , Annan, J. D. , Lenton, T. M. , Marsh, R. , Yool, A. , & Watson, A. (2007). Marine geochemical data assimilation in an efficient Earth System Model of global biogeochemical cycling. Biogeosciences, 4(1), 87–104. 10.5194/bg-4-87-2007 [DOI] [Google Scholar]
- Ridgwell, A. , & Schmidt, D. N. (2010). Past constraints on the vulnerability of marine calcifiers to massive carbon dioxide release. Nature Geoscience, 3(3), 196–200. 10.1038/ngeo755 [DOI] [Google Scholar]
- Ridgwell, A. , & Zeebe, R. E. (2005). The role of the global carbonate cycle in the regulation and evolution of the Earth system. Earth and Planetary Science Letters, 234(3‐4), 299–315. 10.1016/j.epsl.2005.03.006 [DOI] [Google Scholar]
- Ridgwell, A. , Zondervan, I. , Hargreaves, J. C. , Bijma, J. , & Lenton, T. M. (2007). Assessing the potential long‐term increase of oceanic fossil fuel CO<sub>2</sub> uptake due to CO<sub>2</sub>‐calcification feedback. Biogeosciences, 4(4), 481–492. 10.5194/bg-4-481-2007 [DOI] [Google Scholar]
- Roberts, C. D. , & Tripati, A. K. (2009). Modeled reconstructions of the oceanic carbonate system for different histories of atmospheric carbon dioxide during the last 20 Ma. Global Biogeochemical Cycles, 23, GB1011 10.1029/2008GB003310 [DOI] [Google Scholar]
- Sclater, J. G. , Meinke, L. , Bennett, A. , & Murphy, C. (1985). The depth of the ocean through the Neogene. Geological Society of America Memoirs, 163, 1–20. 10.1130/MEM163-p1 [DOI] [Google Scholar]
- Scotese, C. R. (2010). The PALEOMAP Project Paleo Atlas for ArcGIS, vol. 1: Cenozoic Paleogeographic and Plate Tectonic Reconstructions. Arlington, TX: PALEOMAP Project. [Google Scholar]
- Skaug, H. , Fournier, D. , Nielsen, A. , Magnusson, A. , & Bolker, B. (2014). Generalized Linear Mixed Models using AD Model Builder. R package version 0.7.7.
- Slotnick, B. S. , Lauretano, V. , Backman, J. , Dickens, G. R. , Sluijs, A. , & Lourens, L. (2015). Early Paleogene variations in the calcite compensation depth: new constraints using old borehole sediments from across Ninetyeast Ridge, central Indian Ocean. Climate of the Past, 11(3), 473–493. 10.5194/cp-11-473-2015 [DOI] [Google Scholar]
- Stein, C. A. , & Stein, S. (1992). A model for the global variation in oceanic depth and heat flow with lithospheric age. Nature, 359(6391), 123–129. 10.1038/359123a0 [DOI] [Google Scholar]
- Stuecker, M. F. , & Zeebe, R. E. (2010). Ocean chemistry and atmospheric CO2 sensitivity to carbon perturbations throughout the Cenozoic. Geophysical Research Letters, 37, L03609 10.1029/2009GL041436 [DOI] [Google Scholar]
- Tindall, J. , Flecker, R. , Valdes, P. , Schmidt, D. N. , Markwick, P. , & Harris, J. (2010). Modelling the oxygen isotope distribution of ancient seawater using a coupled ocean–atmosphere GCM: Implications for reconstructing early Eocene climate. Earth and Planetary Science Letters, 292(3–4), 265–273. 10.1016/j.epsl.2009.12.049 [DOI] [Google Scholar]
- Tripati, A. K. , Roberts, C. D. , & Eagle, R. A. (2009). Coupling of CO2 and Ice Sheet Stability Over Major Climate Transitions of the Last 20 Million Years. Science, 326(5958), 1394–1397. 10.1126/science.1178296 [DOI] [PubMed] [Google Scholar]
- Tyrrell, T. , & Zeebe, R. E. (2004). History of carbonate ion concentration over the last 100 million years. Geochimica et Cosmochimica Acta, 68(17), 3521–3530. 10.1016/j.gca.2004.02.018 [DOI] [Google Scholar]
- Van Andel, T. H. (1975). Mesozoic/cenozoic calcite compensation depth and the global distribution of calcareous sediments. Earth and Planetary Science Letters, 26(2), 187–194. 10.1016/0012-821X(75)90086-2 [DOI] [Google Scholar]
- Van Andel, T. H. , Heath, G. R. , & Moore, T. C. (1975). Cenozoic History and Paleoceanography of the Central Equatorial Pacific Ocean: A Regional Synthesis of Deep Sea Drilling Project Data Geological Society of America Memoirs (Vol. 143, pp. 1–223). 10.1130/MEM143-p1 [DOI] [Google Scholar]
- Walker, J. C. G. , Hays, P. B. , & Kasting, J. F. (1981). A negative feedback mechanism for the long‐term stabilization of Earth's surface temperature. Journal of Geophysical Research, 86(C10), 9776–9782. 10.1029/JC086iC10p09776 [DOI] [Google Scholar]
- Zachos, J. , Pagani, M. , Sloan, L. , Thomas, E. , & Billups, K. (2001). Trends, Rhythms, and Aberrations in Global Climate 65 Ma to Present. Science, 292(5517), 686–693. 10.1126/science.1059412 [DOI] [PubMed] [Google Scholar]
- Zachos, J. C. , Dickens, G. R. , & Zeebe, R. E. (2008). An early Cenozoic perspective on greenhouse warming and carbon‐cycle dynamics. Nature, 451(7176), 279–283. 10.1038/nature06588 [DOI] [PubMed] [Google Scholar]
- Zeebe, R. E. , Ridgwell, A. , & Zachos, J. C. (2016). Anthropogenic carbon release rate unprecedented during the past 66 million years. Nature Geoscience, 9(4), 325–329. 10.1038/ngeo2681 [DOI] [Google Scholar]
- Zeebe, R. E. , & Westbroek, P. (2003). A simple model for the CaCO3 saturation state of the ocean: The “Strangelove”, the “Neritan”, and the “Cretan” Ocean. Geochemistry, Geophysics, Geosystems, 4(12), 1104 10.1029/2003GC000538 [DOI] [Google Scholar]
- Zeebe R. E., & Wolf‐Gladrow D. (Eds.) (2001). CO2 in Seawater: Equilibrium, Kinetics, Isotopes (p. 346). Amsterdam: Elsevier. [Google Scholar]
- Zeebe, R. E. , & Zachos, J. C. (2007). Reversed deep‐sea carbonate ion basin gradient during Paleocene‐Eocene thermal maximum. Paleoceanography, 22, PA3201 10.1029/2006PA001395 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information S1
Supporting Information S2
Data Set S1
Data Set S2
Data Set S3


