Complexity metrics for IMRT and VMAT plans: a review of current literature and applications

Abstract

Modulated radiotherapy with multileaf collimators is widely used to improve target conformity and normal tissue sparing. This introduced an additional degree of complexity, studied by multiple teams through different properties. Three categories of complexity metrics were considered in this review: fluence, deliverability and accuracy metrics. The first part of this review is dedicated to the inventory of these complexity metrics. Different applications of these metrics emerged. Influencing the optimizer by integrating complexity metrics into the cost function has been little explored and requires more investigations. In modern treatment planning system, it remains confined to MUs or treatment time limitation. A large majority of studies calculated metrics only for analysis, without plan modification. The main application was to streamline the patient specific quality assurance workload, investigating the capability of complexity metrics to predict patient specific quality assurance results. Additionally complexity metrics were used to analyze behaviour of TPS optimizer, compare TPS, operators and plan properties, and perform multicentre audit. Their potential was also explored in the context of adaptive radiotherapy and automation planning. The second part of the review gives an overview of these studies based on the complexity metrics.

Introduction

Compared to conformational radiotherapy (CRT), intensity modulated radiotherapy (IMRT) and volumetric modulated arc therapy (VMAT) improve target volume conformity and normal tissue sparing, resulting in reduced acute and late toxicities.^1–4 Considering conventional linear-accelerators (linacs), intensity modulation is achieved through different parameters, according to the technique used: multileaf collimator (MLC) position for step-and-shoot (or segmental) IMRT, MLC position and speed variation for sliding window (or dynamic) IMRT and additionally, gantry rotation speed and dose rate variation for VMAT. Due to the complexity of modulated plans, patient specific quality assurance (PSQA) is strongly recommended by various professional organizations.^5–11 The complexity level of a modulated plan is variable according to patient anatomy, dosimetric constraints, optimization algorithm and linac capabilities.

In order to quantify this level of complexity, a wide range of complexity metrics have been proposed but, up to date, without consensus. Plan complexity is generally defined from machine parameters and plan properties (fluence, MLC aperture, position and displacement, gantry speed and dose rate variations, MU) to study correlations with the agreement between delivered and calculated dose distributions. The main idea is that this agreement is more difficult to achieve for a plan with a high level of complexity. Complexity metrics are then based on identified sources of errors in IMRT/VMAT delivery (MLC leaf position, gantry rotation, beam stability) and treatment planning system (TPS) calculation (MLC modelling, off-axis and irregular field modelling, output factors for small field sizes).⁵ According to these considerations, Crowe et al¹² divided complexity metrics into three categories corresponding to different approaches:

• The fluence metrics exclusively consider the resulting fluence of a modulated plan or beam. They aim to quantify the complexity without identifying the sources (machine and/or TPS). They can be applied to both IMRT and VMAT plans. The hypothesis is that a highly heterogeneous fluence reflects a high level of complexity, comparing with CRT homogeneous beams. However, a limitation of fluence map-based metrics is their insensitivity to the degeneracy of fluence map.¹³ Indeed, the same fluence map could be generated either by a single large beam or by a combination of successive small beams, leading to a similar fluence-based metric.

• The deliverability metrics focus on machine capability of delivering the treatment as planned due to the variation of mechanical (gantry, MLC) and dosimetric (dose rate, MU) machine parameters. They are treated independently or combined. These metrics depends on the technique applied.

• The accuracy metrics aim to quantify the parameters identified as most likely to compromise accurate dose calculation due to the machine modelling and algorithm inaccuracy in the TPS. In particular, the small distance between opposite leaves, the off-axis leaf aperture, the leaf leakage dose and the aperture irregularities are pointed out. Accuracy metrics focus on MLC only and consequently can be applied to both IMRT and VMAT. Deliverability and accuracy metrics are intrinsically linked and some metrics could belong to both categories. As an example, the small distance between opposite leaves is a challenging situation for both the machine and the dose calculation as well. In ambiguous case, the intention of the authors describing the metric was considered.

The aim of this paper is to provide a wide review of existing complexity metrics and their applications. As complexity metrics depend on technical considerations, only conventional linacs were considered in this review. In early studies, complexity metrics were mainly developed with the purpose of predicting the PSQA outcome. Some strategies were then proposed to streamline PSQA process, reducing workload. Furthermore, in order to adapt the plan complexity to the dosimetric requirement, correlation between complexity metrics and plan quality was investigated. In the same way, complexity metrics were used to compare TPSs, optimization algorithms and plan properties. Some studies aimed to estimate their utility for multicentre external audit and in the context of adaptive radiotherapy and automation planning.

The literature was searched in “PubMed” and “google scholar” search engines, using the following keywords and logic statements: (“VMAT” OR “IMRT”) AND (“complexity” OR “modulation”) AND (“metric” OR “index” OR “level” OR “degree”). The term “complexity metric” was chosen in this review.

Complexity metrics

Table 1 lists the main complexity metrics grouped into the three categories defined by Crowe et al¹² and detailed in the introduction. Listed complexity metrics are described below.

Table 1. .

Main complexity metrics for IMRT and/or VMAT plans, divided into three categories¹²

Category	Complexity metrics	Main reference
Fluence complexity	FMC - Fluence map complexity	Llacer et al14
	MI - modulation index	Webb15
	2D MI - 2D modulation index	Nicolini et al16
	MIR - Maximum intensity ratio	Coselmon et al17
	PIMV - Plan intensity map variation
	Fractal dimension analysis methods: the variation, power spectrum and variogram methods	Nauta et al18
	Textural features: ASM, IDM, contrast, variance, correlation and entropy	Park et al19,20
Deliverability	MU, MU/Gy or PMU - Monitor Unit, monitor unit per Gy or plan normalized monitor unit	Du et al,13 Mohan et al,21 Masi et al22
	PI - Plan averaged beam irregularity	Du et al13
	PM - Plan averaged beam modulation
	AAV - Aperture area variability	McNiven et al23
	LSV - Leaf sequence variability
	MCS - Modulation complexity score (combination of LSV and AAV)
	DR - Variations of the nominal DR	Nicolini et al24
	GS - Variation of gantry speed
	Degree/MU - The gantry angle per MU	Miura et al22
	mm/MU - Leaf travel per MU
	MU/CP - Number of Monitor unit per Control Point and proportion of CP with MU <3 (%MU/CP <3)	Shen et al25
	Sl-h - The average proportion of leaf speeds from a given range	Park et al26
	Al-h - The average proportion of leaf accelerations from a given range
	MIs - Modulation index for speed of MLC	Park et al27
	MIa - Modulation index for speed and acceleration of MLC
	MIt - Modulation index for speed and acceleration of MLC, gantry acceleration and dose rate variation
	MCSv or MCSarc - Modulation complexity score for VMAT plans	Masi et al22
	LT - Leaf travel
	LTMCS - Combination of LT and MCSv
	MISPORT – Modulation index for station parameter optimized radiation therapy	Li and Xing28
Accuracy	Average leaf gap	Nauta et al18
	MFA - Mean field area	Kairn et al29 Crowe et al30
	SAS - Small aperture score and SAS(x)
	CLS - Closed leaf score
	CAS - Cross-axis score
	MAD - Mean asymmetry distance
	SA/CP - Segment area per CP	Shen et al25
	Modulation degree	Heijmen et al31
	PA - Plan averaged beam area	Du et al13
	Segment area/Perimeter or Circumference/area	Carlsson et al,32 Götstedt et al33
	EM - Edge metric	Younge et al34,35
	EAM - Edge area metric	Götstedt et al33
	CAM - Converted aperture metric
	LOIC - Leaf offset impact on calculation	Mathot et al,36 Dechambre et al37
Accuracy/Deliverability	MIc - Comprehensive modulation index	Park et al38

IMRT, intensity modulated radiotherapy; VMAT, volumetric modulated arc therapy.

Fluence metrics

IMRT/VMAT treatment planning with TPS generates fluence maps using optimizers. These fluence maps can be represented as two-dimensional (2D) matrices composed by beamlets (bixels) with different independent weights (intensities). The plan complexity can be assessed through metrics derived from these fluence maps, which serve as input to the leaf sequencer computing the time sequence of MLC settings.³⁹

This type of metrics was initially introduced for IMRT plans. Llacer et al¹⁴ defined the Fluence Map Complexity metric (FMC). The FMC likened to a smoothness measure is a normalized root sum over the local differences between bixel values and their two neighbours. It is sensitive to differences between adjacent beamlet weights and the existence of excessive large beamlet weights in the field periphery in an otherwise relatively uniform beam map. The FMC focuses on local differences without relating the local changes to the overall fluence standard deviation. In this context, Webb¹⁵ proposed the Modulation Index (MI) that better relates the local changes to the global ones. Indeed, the MI quantifies the variations of photon fluence along one direction between neighbouring pixels in the fluence map including a threshold defined as a fraction of the standard deviation in the beam. The definition of MI has been later generalized to changes along x, y and diagonal directions by Nicolini et al¹⁶ and called 2D MI.

Coselmon et al¹⁷ introduced the Plan Intensity Map Variation (PIMV) metric quite similar to MI and FMC. The PIMV is the sum of the intensity difference for each beamlet at the (j,k) position with its neighbours at (j,k + 1), (j + 1,k) and (j + 1,k + 1) positions. In addition, Coselmon et al¹⁷ defined a second metric called maximum intensity ratio (MIR) which considers the maximum intensity allowed for each beamlet during the optimization process.

Later, Nauta et al¹⁸ suggested that IMRT fluence map complexity could be assessed by means of fractal dimensions analysis. For this purpose, three types of fractal dimension have been evaluated: the Variation method, the Power Spectrum method and the Variogram method. The Variogram method based on the statistical Gaussian modelling of images was preferred to assess the complexity because of its good independency of image size, its strict increase with the theoretical dimension of the fractal and its precision.

The first fluence map metric dedicated to VMAT technique was published by Park et al.¹⁹ This work consisted in analysing six second-order statistical textural features of fluence map derived from its grey level co-occurrence matrix generated for three bixel displacement distances (d = 1, 5 and 10). Co-occurrence matrices allowed the characterization of pattern repetitions. In Park’s study, the following textural features were calculated: angular second moment (ASM) as a measure of homogeneity; inverse different moment (IDM) as a measure of local homogeneity; contrast as a measure of local variations; variance as a measure of inhomogeneity; correlation as a measure of linear dependency of grey levels; and entropy as a measure of randomness.

A limitation of fluence map-based metrics is that the same fluence map could be generated either by a single large beam or by a combination of successive small beams.¹³ In order to overcome this pitfall, Park et al²⁰ edge-enhanced fluence applying a feature analysis by doubling the pixel values representing MLC tips during the fluence map generation in order to prevent smearing out of small or irregular fields. Consequently, the edge-enhanced fluences showed a lot of short discrete lines perpendicular to the direction of MLC. Park et al²⁰ improved the performance of contrast (d = 1) as a complexity metric for VMAT.

Deliverability metrics

To overcome the limitations of fluence metrics, deliverability metrics were introduced, in regards to mechanical and dosimetric features of the machine. The observation made by several authors that the machine capability of delivering treatments as planned decreased with increasing MLC complexity^{16,21,40–42} led to the creation of different MLC-based deliverability metrics. The plan complexity in terms of delivery can be assessed by multiple comprehensive metrics¹³ or single metric summarizing different properties.²³ The advantage of these separated metrics is that they are easily interpreted due to their physical meaning.

Some machine parameters can be easily retrieved from a plan and used as deliverability metrics. One of them is the plan MUs, tending to increase with plan complexity.²¹ Du et al¹³ proposed to study the plan normalized MUs (PMU) defined as the plan MU normalized to a single fraction of 2 Gy, also used by Masi et al.²² Other authors introduced more complex metrics. For example, for each IMRT segment, Du et al¹³ calculated the aperture area (AA), the aperture perimeter (AP) and the aperture irregularity (AI) quantifying the non-circularity of the aperture. With these three metrics, they calculated the beam irregularity (BI) by weighting AA and AI with the MUs of each segment. The beam modulation (BM) is based on MU-weighted ratio between AA and the union area of all apertures. Corresponding plan metrics: plan averaged beam irregularity (PI) and plan averaged beam modulation (PM) were obtained by combining beam metrics weighted with the MUs per beam.

McNiven et al²³ defined the modulation complexity score (MCS), which combines two parameters: the leaf sequence variability (LSV) and the aperture area variability (AAV). LSV and AAV are close to PI and PM defined by Du et al,¹³ since they evaluate the field irregularity comparing adjacent leaf positions and the field area variation from a maximum area, respectively. MCS was initially described for step and shoot IMRT and designed as a simple score ranging from 0 to 1, with 1 referring to a plan without modulation.

VMAT plans combine MLC modulation with gantry rotation speed and dose rate variation. Gantry rotation is discretized into control points (CP) equivalent to IMRT segments. Among machine parameters easily retrieved, other parameters of interest for VMAT delivery than those previously described for IMRT were the variations of the nominal dose rate (DR) and gantry speed (GS), as investigated by Nicolini et al.²⁴ The gantry angle per MU (Degrees/MU) was proposed by Miura et al.⁴³ Shen et al²⁵ focused on the number of MU per CPs (MU/CP) since low MU/CP is potentially demanding in terms of MLC motion. They especially pointed out the proportion of CP with less than 3MU (%MU/CP <3).

Some studies^41,42 showed that leaf speed is correlated with MLC performance for dynamic and VMAT deliveries since a decrease of leaf speed improves positional accuracy of the MLC. In addition to mean MLC speed and acceleration, Park et al²⁶ proposed as complexity metric the average proportion of leaf speeds (S_l–h) and acceleration (A_l–h) within a given range. A particular metric, MI_SPORT, was used by Li et al²⁸ and represents the modulation of MLC around a given CP considering a certain range of adjacent CPs, weighted by the corresponding MU per gantry angle. Park et al²⁷ proposed to evaluate MLC speed and acceleration, gantry acceleration and variation of dose rate by adapting the MI initially proposed by Webb¹⁵ from IMRT to VMAT. MIs evaluates MLC speed, MIa adds MLC acceleration and MIt (or MItotal) combines the four parameters. Another metric was adapted from IMRT to VMAT by Masi et al,²² the MCS renamed MCSv for VMAT. Additionally, on the basis of the work of Chen et al⁴⁴ showing the dosimetric impact of leaf travel, they quantified the mean leaf travel (LT), considering leaf displacement of open leaf pairs. And they proposed a third metric named LTMCS combining LT and MCSv by multiplying MCSv with a normalized LT. Similarly, Miura et al⁴³ considered the leaf travel per MU (mm/MU).

Accuracy metrics

This third category was defined to deal with challenging MLC configurations. Some accuracy metrics focus on the small field feature. The average leaf gap was evaluated as a simple metric by Nauta et al.¹⁸ Other simple metrics were introduced by Kairn et al²⁹ and Crowe et al³⁰ such as the mean field area (MFA) and the small aperture score (SAS). The MFA considers segment areas without making distinction between single and split fields into a given segment and between line-like and circular-like fields. The SAS(x) counts for the proportion of open leaf pairs separated by less than a given distance x. Similarly, the segment area per CP (SA/CP) and the percentage of CPs with segment area < 5×5 cm² (%SA < 5×5 cm²) were used by Shen et al.²⁵ In the same way, Du et al¹³ calculated the plan averaged beam area (PA), by combining beam area (BA) weighted with the MUs per beam from aperture area (AA) of each segment. The Monaco TPS (Elekta AB, Stockholm, Sweden) calculates the modulation degree as the inverse of the sum over all segments of the segment area multiplied by the segment MU, weighted by the total beam MU and divided by the total beam area.³¹ This definition is very similar to MFA and, to our knowledge, Monaco is the only TPS providing an advanced complexity metric. The modulation degree is available during and after the optimization process.

Other metrics^29,30 focus on the beam aperture position relatively to the isocenter such as the closed leaf score (CLS), the cross-axis score (CAS) and the mean asymmetry distance or mean aperture displacement (MAD). The CLS, CAS and MAD consider the proportion of closed leaf pairs within the jaw field, the proportion of open leaf pairs with a leaf crossing the central axis and the mean distance between the centre of open leaf pairs and the central axis, respectively.

Carlsson et al³² presented a simple mean to quantify the aperture complexity: the perimeter–area ratio of the MLC aperture, also named circumference/area ratio (C/A) by Götstedt et al.³³ Younge et al^34,35 considered this metric in a more complex formula with the definition of the edge metric (M or EM). The EM quantifies the ratio between the MLC aperture perimeter and area, considering different weights between leaf side-and leaf end distances constituting the perimeter. Götstedt et al³³ also intended to improve the C/A by introducing the edge area metric (EAM). It is defined by the ratio between the area enclosing the field penumbra with 5 mm both sides of the MLC edge and the sum of this aforementioned area with the rest of MLC aperture area. Additionally, Göstedt et al³³ defined the converted aperture metric (CAM). This third metric combines complexity scores with regard to the mean MLC edge distances along and across the leaf displacement direction and the equivalent square field size. Those two parameters are converted by a non-linear function to increase the penalty for small fields.

The metric introduced by Mathot et al^36,37 aims to quantify the dosimetric impact of a MLC offset variation. Leaf offset impact on calculation (LOIC) was defined as the percentage variation of PTV mean dose with respect to a change in the leaf offset parameter of the machine model.

One of the complexity metric specifically designed to belong to both deliverability and accuracy metrics categories is the comprehensive modulation index MIc. Park et al³⁸ defined it from a previously suggested one, the MIt,²⁶ taking into account MLC speed and acceleration, gantry acceleration and dose rate variation as described in the deliverable metrics section. A weighting factor based on an aperture index (AI), WAI, was developed to account for dosimetric inaccuracies of some aperture sizes and geometries. This weighting factor is a monotonically increasing function depending on AI. AI determines the convergence speed of a function based on the line pixel quantification iteratively applied to binary images of MLC apertures after running a thinning algorithm well-known in image processing.

Among all the complexity metrics described above, some are highly correlated because they provide similar information and can therefore be considered equivalent.⁴⁵

Applications

Use of complexity metric during the optimization process

To our knowledge, Younge et al^34,35 and Li et al²⁸ presented the only studies in which the complexity metric is used to improve the optimization process. Using the EM complexity metric, Younge et al^34,35 introduced the penalization of the aperture complexity. Using the MI_SPORT complexity metric, Li et al²⁸ introduced the concept of “demand metric” to adapt the angular sampling of VMAT arc and thus its level of complexity. In 2007, during the worldwide spread of intensity modulation in clinical routine, Craft et al⁴⁶ demonstrated that the largely increased number of MUs observed in step-and-shoot IMRT was not mandatory in order to reach the expected plan quality. They included the number of MUs, as an objective in the optimization process and they showed that the number of MUs can sometimes be reduced more than twofold while maintaining a similar plan quality. In the same context Mohan et al²¹ demonstrated that complex anatomy and severe constraints lead to complex intensity patterns. They investigated the use of a filtration technique to reduce intensity map fluctuations and MUs in dynamic sliding window IMRT.

At the moment, most modern TPSs only offer the possibility to limit the treatment time and/or the number of MUs per beam/plan during VMAT optimization. This MU reduction correlates to an increase average size of MLC segments/CPs and thus might improve some metrics described in the previous section.

Optimization of the PSQA workload

A large majority of studies calculated metrics only for analysis, without plan modification. However, knowledge of the modulation level during or at the end of the optimization step allows to adapt the dosimetric objectives, to compare plans or TPS and to optimize the PSQA strategy. The primary focus reported in the literature is to predict PSQA results from complexity metrics, with the final purpose to reduce the QA workload.^36,37,47

PSQA consists in individualized measurements either before the first fraction (without patient) and/or during treatment (in vivo)^5–11 and is still considered as gold standard for treatment quality assessment, despite the workload. Assuming that agreement between calculations and measurements decreases as plan modulation increases, it should be possible to predict PSQA results from complexity metrics.

The first approach consists in finding correlation between PSQA results and complexity metrics. Table 2 lists the main published correlation studies which failed to reach a consensus. Correlation is strongly impacted by many parameters: (1) detector, (2) analysis method and criteria and (3) linac, treatment technique, TPS and beam modelling.⁵⁵ Such correlations are reduced by the spread out of PSQA results from highly modulated plans (Figure 1), which are more sensitive to the linac state at the time of measurement.

Table 2. .

Main correlations studies between complexity metrics and PSQA results.

Ref	Technique (localization)	QA system	Analysis	Evaluated metrics	Correlation coefficients
Crowe et al12	52 ss-IMRT plans (multisite)	EPID with Epiqa system (EPIdos)	γ 3%/3 mm and 2%/2 mm	MU, AAV, CAS, MAD, MCS, MI, SAS1, SAS5 and SAS10	Significant (F)
				MFA, CLS and FMC	Not significant (F)
Crowe et al12	70 VMAT plans (multisite)	EPID with Epiqa system (EPIdos)	γ 3%/3 mm and 2%/2 mm	MAD, MCS, MI and SAS1	Significant (F)
				MU, MFA, AAV, CLS, CAS, FMC, SAS5 and SAS10	Not significant (F)
Du et al13	65 ss-IMRT plans (prostate, head and neck, and spine) and 26 VMAT plans (prostate)	Ion chamber and radiographic films	Dose difference and γ 5%/3 mm	PA, PI, PM and PMU	None (s)
Park et al20	40 VMAT plans (20 prostate, 20 h&N)	MapCheck (Sun Nuclear)	γ local and global 2%/2 mm	Contrast1,5,10, ASM1, IDM1,5, Variance1,5, correlation5,10	Moderate (s)
				ADM5, IDM10, Variance10, correlation1, Entropy1,5,10	Weak (s)
				ASM10	None (s)
McNiven et al23	243 IMRT plans (multisite)	MapCheck (Sun Nuclear)	γ local 3%/3 mm and 2%/2 mm	MCS and MU	None (NA)
Masi et al22	142 VMAT plans (multisite)	Delta4 phantom (Scandidos)	γ local 3%/3 mm and 2%/2 mm	LT, MCSv and LTMCS	Moderate (p)
				PMU	Weak (p)
Shen et al25	71 VMAT (nasopharyngeal cancer)	ArcCheck (Sun Nuclear)	γ Individual volume-based 3D	MU/CP, SA/CP	Significant (c)
				%MU/CP < 3, %SA < 5×5, MCSv/arc and LT	Not significant (c)
Park et al26	40 VMAT plans (20 prostate, 20 h&N)	MapCheck (Sun Nuclear)	γ global and local 1%/2 mm	Mean MLC speeds and mean MLC accelerations	Weak and moderate (s)
Park et al27	40 VMAT plans (20 prostate, 20 h&N)	MapCheck (Sun Nuclear)	γ local 2%/2 mm	MIs, Mia and MIt	Moderate (s)
				MIsport	Weak (s)
				LTMCS	None (s)
Crowe et al30	122 ss-IMRT beams (prostate)	MapCheck (Sun Nuclear)	γ 3%/3 mm and 2%/2 mm	MI, MFA, SAS5 and SAS10	Significant (F)
				MCS, LSV, AAV, FMC, CLS, CAS, MAD, SAS2 and SAS20	Not significant (F)
Gödtstedt et al33	30 Artificial IMRT /VMAT beams	EPID	Dose difference pass rate (3 and 5%)	CAM, EAM, EM, Circumference/area and MU/Gy	Strong (p)
				Aperture area	Moderate (p)
				MCS and Aperture irregularity	Weak (p)
Gödtstedt et al33	30 Artificial IMRT /VMAT beams	Rradiochromic films	Dose difference pass rate (3 and 5%)	CAM, EAM, EM, Circumference/area and MU/Gy	Strong (p)
				MCS and Aperture irregularity	Moderate (p)
				Aperture area	Weak (p)
Dechambre et al37	93 VMAT plans (multisite)	ArcCheck (Sun Nuclear)	γ global 3%/3 mm and 2%/2 mm	LOIC, CAS and MCSv SAS and PMU MFA, MAD and CLS	Moderate (p) Weak (p) None (p)
Park et al38	52 VMAT plans (22 prostate, 30 h&N - two institutions)	MapCheck (Sun Nuclear)	γ local 2%/2 mm	MIt, MIc and MIsport MIc, LTMCS, variance, PI and PM MCSv, contrast, contrastedge and PA PMU	Strong (s) Moderate (s) Weak (s) None (s)
Agnew et al48	30 VMAT (prostate, prostate and pelvic node, H&N)	OCTAVIUS 4D and 729 array (PTW)	γ global 2%/2 mm	MCSv	Moderate (p)
				MU	None (p)
Glenn et al49	343 IMRT/ VMAT plans (H&N - 312 institutions)	TLD and Radiochromic films	Dose difference (5%) and γ 7%, 4 mm	MU, MCS, EM, PI, PM, MIs, MIa, MIt, LT, Mean DR variation, Mean GS var. Mean MLC speed var.	None (s)
Jurado-Bruggeman et al50	36 VMAT plans (2 prostate and 2 h&N done by nine institutions)	ArcCheck (Sun Nuclear)	γ global 3%/3 mm and 2%/2 mm	MU	Strong (p)
				PI, MCSv, MIt	None (p)
McGarry et al51	39 VMAT plans (virtual volumes - 34 institutions)	OCTAVIUS II and 729 array (PTW)	γ global and local 1%/2 mm	MCSv and MU	Weak (p) but Moderate (p) for Varian linacs
Park et al52	202 IMRT plans (multisite)	ArcCheck and MapCheck (Sun Nuclear)	γ global 2%/2 mm	PI and MCS	Moderate (s)
				MIs, PA and PM	None (s)
Wang et al53	20 IMRT plans (10 nasopharyngeal cancer and 10 prostate) with intentional MLC leaf errors	ArcCheck (Sun Nuclear)	γ 2%/2 mm	MCS	Strong (s)
Park et al54	240 VMAT plans (multisite)	ArcCheck (Sun Nuclear)	γ local 2%/2 mm	MIt, MIc, LTMCS, MIsport, PI and PM MCSv and PMU PA	Moderate (s) Weak (s) None (s)

IMRT, intensity modulated radiotherapy; MCS, modulation complexity score; MI, Modulation Index; PSQA, patient specific quality assurance; TPS, treatment planning system; VMAT, volumetric modulated arc therapy.

Statistical analysis methodologies used are Spearman (s), Pearson (p), Canonical (c) orF-test (F). Correlation for Spearman and Pearson coefficients were considered as strong r ≥ 0.7,moderate for 0.5 ≤ r<0.7,weak for 0.4 ≤ r<0.5 and none for r < 0.4. All presented data are associated with a p-value ≤0.05. According to these definitions, complexity metrics with a significant (Canonical and F-test) or a strong (Spearman and Pearson tests) correlation with PSQA results are in bold. If none is specified, only one institution is involved in the study.

Figure 1. .

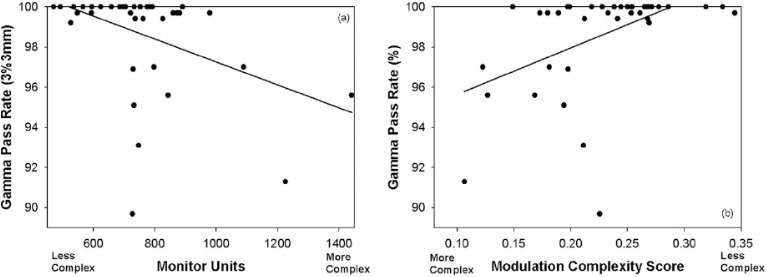
Typical aspect of correlation plots for two complexity metrics (MU and MCS) and PSQA results. An important spread out appears for plans with large MU (>700) and low MCS (<0.23) corresponding to high modulation level. Figure comes from McGarry et al.⁵¹ MCS, modulation complexity score; PSQA, patient specific quality assurance.

PSQA measurements are performed within phantoms with different geometry and material characteristics, using a wide variety of detectors which might be prone to calibration, response or setup errors.^5,55,56 Characteristics of detectors such as spatial resolution,⁵⁷ rotational dependence, water equivalency and uncertainties⁵⁸ affect PSQA measurements. In addition, authors used various analysis methods impacting PSQA outcome.^5,55,56,59 Most publications^{12,13,18,20,22,23,25–27,30,38,48–53,60,61} characterized measurements by means of γ index passing rates (GPR)⁶² but some used dose difference from point measurements^13,49 or dose difference pass rate.³³ Moreover, when GPR was used, options and criteria widely varied between studies. For example, Rajasekaran et al⁶¹ obtained very different correlation coefficient according to γ analysis option and criteria, preventing any conclusion. Furthermore, the γ index might be prone to misleading interpretation.^63–66 The well-known γ index remains the most widely used by the medical physics community.

In the same way, TPS configuration and beam modelling influence the agreement between calculated and measured doses. For example, Masi et al²² demonstrated the impact of CP spacing in TPS on PSQA results, and consequently on correlation with complexity metrics.

A second approach consists in evaluating the capability of complexity metrics to identify plans requiring no PSQA. This can be driven by means of receiver operating characteristic (ROC) analysis. ROC curves are generated for a specified complexity metric by varying the metric threshold and plotting the true positive rate (TPR, also known as “sensitivity”) vs the false positive rate (FPR, equal to “1 – specificity”). The purpose is to determine an appropriate complexity threshold above which a plan should be considered for either re-optimization (high specificity) or exemption from QA measurements (very high sensitivity, or even 100% sensitivity).^36,47 ROC area under the curve (AUC) quantifies the ability of the metric to distinguish between positive and negative cases, respectively. Nauta et al¹⁸ classified AUC ranging from 0.5 (chance accuracy) to 1.0 (perfect accuracy), with the following intermediate benchmarks: 0.6 (poor), 0.7 (fair), 0.8 (good), 0.9 (excellent), >0.95 (almost perfect). Park et al²⁷ performed ROC analysis with a 90% tolerance level for the GPR (local 2%/2 mm) and obtained the best performance in terms of sensitivity and specificity (AUC = 0.849) for the MIs (f = 2) metric, while the MCSv metric showed the poorest performance (AUC = 0.527). Using the edge metric (EM), Younge et al³⁵ obtained a 44% sensitivity (meaning only 44% of plans failing PSQA were correctly flagged) and 93% specificity (7% of plans passing PSQA incorrectly flagged). Enforcing no false positive (specificity 100%), Mc Niven et al²³ improved the sensitivity up to 36% using the MCS metric, as compared to 23% using the normalized number of MU.

The latest approach recently developed in the literature is the use of machine learning⁶⁷ to predict PSQA results. We can discern two strategies: technique designed by domain experts and deep neural networks without domain knowledge. The model developed by Valdes et al^60,68 belongs to the first category since input data were a large set of complexity metrics. Output data were local GPR 3%/3 mm measured with a 2D diode array. The resulting model predicted GPR with an error smaller than 3%. Moreover, a model analysis showed that metrics with major impact were MU/Gy,²² PI¹³ and SAS(10 mm).^29,30 The model was applied to a second institution that uses EPID measurements.⁶⁸ GPR were predicted within 3.5% for 120 out of 139 plans. Iterian et al⁶⁹ compared results obtained by Valdes et al^60,68 with a deep learning convolutional neural network (CNN) strategy. Fluence maps calculated for each plan were used as inputs to the CNN. Predictions from CNN were comparable to a system designed by physicist experts. Tomori et al⁷⁰ proposed for prostate plans, a CNN model based on following input data: the sagittal planar dose distribution calculated in a phantom, the volumes of the PTV, the rectum and their overlapping, and the MU for each beam. They found a moderate Spearman correlation between measured and predicted GPR values.

In the context of online adaptive radiotherapy, PSQA of adapted plans is not feasible. Complexity metrics can then be used as online and fast verification of the adapted plans. Crijns et al⁷¹ referred to five established plan metrics (number of MU, equivalent field size, MCS and the components of MCS, i.e. AAV et LSV) in order to validate adapted prostate VMAT plans in response to anatomical variations. They used a sophisticated forward planning approach correcting MLC apertures and MU for each CP, and compared the adapted plan to the original one by means of the abovementioned plan metrics. This method is much faster than replanning, allowing for online plan adaptation. In this context, MCS was not retained due to the contrasting behaviour of the AAV and LSV components. For the remaining four complexity metrics, a population model was built to derive tolerance tables. Adapted plans with complexity metrics within the tolerance were validated and delivered, without additional PSQA.

Correlation with plan quality

In parallel with correlations between plan complexity metrics and PSQA, the question arises whether these metrics are related to plan quality, i.e. the degree of achievement of planning objectives (mainly target coverage, dose homogeneity, dose conformity, dose fall-off and doses to organs at risk). In this context we should keep in mind that, on one hand, “a high degree of complexity is not necessarily a negative feature of a treatment plan, as it may be required due to the geometry and location of the target and organs at risk,”²³ on the other hand “more complex plans do not necessarily produce better dose distributions.”^45,46,72 In order to compare treatment plans, Jurado-Bruggeman et al⁵⁰ defined a plan quality index (PQI), which is a weighted sum of the score for a planning objective sets. They did not obtain a correlation between plan quality, plan complexity, and γ scores in a multicentre environment. In a multiinstitutional dosimetry audit for VMAT Mc Garry et al⁵¹ defined the plan quality metric (PQM) as a percentage of achievement for a specified planning constraint. They did not observe a correlation between PQMs and MCS, while PQM was significantly correlated with MU for planning systems independent of linac manufacturers. Using a multidimensional exploratory statistical method Shen et al²⁵ showed that some complexity parameters of 71 VMAT nasopharyngeal cancer patient plans (i.e. SurfaceArea/CP and percentage of CPs with SA < 5×5 cm2) were highly weighted in correlation with plan quality.

The results of these publications tend to show weak correlation (if not absent) between plan quality and plan complexity. This could be related to the established fact that complexity often results from unrealistic or conflicting optimization goals³⁵ and the increasing number of optimization iterations and/or successive optimizations during the inverse planning process,¹³ while similar plan quality might be achieved with less modulated or narrow beams. This highlights the need for dedicated complexity metrics to reach an acceptable trade-off between plan quality (with respect to the achievement of planning objectives) and plan complexity for a number of rival plans, as mentioned by Masi et al.²²

Comparison of TPSs, operators or plan properties

Complexity metrics can be used to compare the optimization results from different TPSs (differences in optimizers) or operators (use of the TPS). In a multicentre comparison, Jurado-Bruggeman et al⁵⁰ pointed out differences in value for three complexity metrics (BI, MCS and MIt) depending on the TPS manufacturer or the operator and demonstrated differences in terms of MLC, gantry speed and dose rate modulation management. Another comparison study⁵¹ based on complexity metrics divided TPS into two groups: those designed by the manufacturer for their own linac and those independently developed. This study recommended the use of a TPS and a linac from the same manufacturer. Llacer et al¹⁴ used the FMC, among other tools, to compare the behaviour of five different algorithms in inverse radiation therapy planning. The level of the FMC was linked to different complexity aspects on dose distribution such as the amount of very high beam weights in the periphery of some fluence maps. Hernandez et al⁴⁵ compared three different TPSs with the help of many complexity metrics (MCS, EM, LT, PI, PM, MIt). The range of complexity metrics for each TPS revealed significant differences between algorithms. Complexity metrics can also be used in the context of TPS change (or TPS version upgrade). Edouard et al⁷³ used the MCSv index in their evaluation of VMAT dosimetric practice changes when passing from Eclipse to RayStation. In the same way, complexity metrics were used in combination with plan quality metrics to evaluate a new optimizer and the impact of the optimization parameters.^74–76 The knowledge of the modulation level can be a valuable tool to improve plan properties. For example, based on MCSv and plan quality metrics, Li et al⁷⁷ found the optimal collimator angle (45°) for hypofractionated VMAT prostate treatment. Similar approach was used to compare different treatment techniques: classic vs HyperArc VMAT⁷⁸ or IMRT vs VMAT.⁷⁹ Additionally, Kantz et al⁷⁶ assessed the impact of various MLC type on the modulation degree. Russo et al⁸⁰ investigated if the cardiac-sparing benefit of the deep inspiration breath-hold (DIBH) technique for left breast VMAT treatment is achieved with lower plan complexity than free breathing (FB) technique. Based on various known complexity metrics (MUs, LT, EM, PI, MCSv and MIt), they obtained a slightly lower degree of plan complexity for DIBH-VMAT plans.

Within the last few years, automation algorithms were developed to streamline and standardize the treatment planning process.⁸¹ Among the large number of studies which compare manual and automated plans, some included complexity metrics.^31,82,83

Multicentre external audit

As described above, complexity metrics provide essential information on optimization process and plan properties and can be related to PSQA outcome. Consequently, they could play a role in external audits.⁵¹ Such audits aim to verify TPS modelling and treatment delivery, credentialing institution for accurate clinical implementation. Comparison is generally based on the same clinical data and dosimetric constraints. Among the studies listed in Table 2, three were carried out in the context of a multicentre external audit,^49–51 involving different linacs, treatment techniques, TPSs and beam modelling. These three studies attempted to detect correlations between complexity metrics and PSQA results and/or plan quality with variable success as discussed above. The study of Glenn et al,⁴⁹ which included 312 different institutions with various linacs, techniques and TPSs, provided no correlation. By comparison, the two other studies^50,51 involving a limited number of institutions obtained strong (considering 9 institutions) or moderate (considering 34 institutions) correlations. Furthermore, the correlation between the γ index passing rates and the complexity metrics might have been affected by the use of TLD presenting higher calibration and measurement uncertainties and thus requiring larger γ criteria (7% in dose and 4 mm distance-to-agreement). These higher γ tolerances had negative impact on correlations with complexity metrics since many highly modulated plans might have passed γ criteria, leading to an artificially high number of false positive plans and incidentally to weak correlations (low ROC AUC).

However, complexity metrics comparison between audited centres provided additional information. For example, in the audit of the Catalan Society of Medical Physicists,⁵⁰ complexity metrics underlined the different strategies of modulation employed by linacs and TPSs. On the basis of a UK national audit for VMAT,⁸⁴ McGarry et al⁵¹ highlighted the capability of complexity metrics, combined with plan quality metrics and TPS modelling parameters, to track excessive level of complexity. Thus, these strategies can lead to an improvement in planning methodologies and a full characterization of each TPS/linacs system.

Conclusion

A large number of complexity metrics is reported in the literature for IMRT and VMAT treatments. An informed choice has to be made between metrics enclosing the same source of complexity. Also studying correlations between complexity metrics is advised.

Correlation between complexity metrics and PSQA results is evaluated but strongly impacted by both dose measurement and dose calculation. For instance, measurement and modelling of small fields/segments are often inaccurate due to the need for dedicated measurement equipment and correction considerations and the chosen compromise during the TPS modelling. Consequently, both measurement and calculation of a plan with a lot of small segments could be affected. This is thus biasing the correlation analysis since the PSQA equipment is not supposed to add a complexity. Also machine state at the time of PSQA measurement has to be considered to be part of the analysis since it influences the PSQA results independently of the machine capabilities in a normal state. All of this explains the lack of consensus in the literature to highlight one particular metric among all the proposed definitions. Additionally, a given complexity metric is not showing the same correlation strength depending on studies, making any guidelines challenging. One of the most important guidelines is that the relationship between complexity metrics and PSQA results should be specifically established by each centre depending on PSQA process/material, machine settings and TPS modelling/optimizer. Moreover, ROC curve analysis is recommended for such studies as it can determine threshold values beyond which satisfying PSQA results are systematically achieved, although correlations are weakened by false negative. Automatically generated ROC curves based on centre specific PSQA results and well-chosen plan metrics might be an important step towards an experience-driven allocation of human and technical resources within medical physics departments.

PSQA workload optimization becomes crucial in a context of online adaptive radiotherapy since measurements are not possible. Complexity metrics, easily and almost instantly calculable, can be a way to overcome this issue.

Furthermore, complexity metrics allow interesting comparison between treatment technics, linacs, TPS and operators. In association with plan quality metric, they have demonstrated their usefulness to rationalize and standardize optimization process and their role in multicentre audits. With the recent development of automated planning approaches, such tools become essential for controlling the TPS. However, to our knowledge, only one TPS provides an advanced complexity metric. Moreover, the integration of complexity metrics into the cost function remains confined to MUs or treatment time limitations.

For future developments, one can imagine the wide implementation of complexity metrics into TPSs, their automated analysis and their use as a feedback to the system in an inverse optimization control loop.