Use of artificial neural network for pretreatment verification of intensity modulation radiation therapy fields

Abstract

Objective:

The accuracy of dose delivery for intensity modulated radiotherapy (IMRT) treatments should be determined by an accurate quality assurance procedure. In this work, we used artificial neural networks (ANNs) as an application for the pre-treatment dose verification of IMRT fields based two-dimensional-fluence maps acquired by an electronic portal imaging device (EPID).

Methods:

The ANN must be trained and validated before use for the pretreatment dose verification. Hence, 60 EPID fluence maps of the anteroposterior prostate and nasopharynx IMRT fields were used as an input for the ANN (feed forward type), and a dose map of those fluence maps that were acquired by two-dimensional Array Seven29^TM as an output for the ANN.

Results:

After the training and validation of the neural network, the analysis of 20 IMRT anteroposterior fields showed excellent agreement between the ANN output and the dose map predicted by the treatment planning system. The average overall global and local γ field pass rate was greater than 90% for the prostate and nasopharynx fields, with the 2 mm/3% criteria.

Conclusion:

The results indicated that the ANN can be used as a fast and powerful tool for pretreatment dose verification, based on an EPID fluence map.

Advances in knowledge:

In this study, ANN is proposed for EPID based dose validation of IMRT fields. The proposed method has good accuracy and high speed in response to problems. Neural network show to be low price and precise method for IMRT fields verification

introduction

Advanced radiotherapy techniques, such as intensity modulated radiotherapy (IMRT) or arc therapy, aim at the concentration of the dose inside the tumor while sparing the organs at risk. Hence, treatment plans often involve high gradient dose distributions, thus emphasizing the need for control of the beam delivery and patient positioning.^1,2 The accuracy of the dose delivery for IMRT treatments should be determined by an accurate quality assurance (QA) procedure.³ Linear accelerators (linacs) are equipped with an electronic portal imaging device (EPID), originally designed for patient positioning;⁴ however, because EPIDs have high sensitivity, spatial resolution, immediate digital format, and minimal setup requirements, they have also been utilized to determine the dose for the routine QA of linacs or dose verification of IMRT fields.^5–8 For pre-treatment dosimetric verification, different approaches can be used. In general, these approaches divided into two categories: EPID-based three-dimensional (3D) volumetric dosimetry and EPID-based two-dimensional (2D) planar dosimetry. For EPID-based 3D volumetric dosimetry, by use back-projection algorithms, 3D dose distribution reconstructs for pre-treatment dosimetric verification. For EPID-based 2D-planar dosimetry, EPID image converts into a 2D dose distribution and compare it with 2D dose predicted by TPS or independent engines, either analytical or based on Monte Carlo (MC).^6,9 These approaches must be validated in non-reference conditions—in particular, the accuracy and precision of these calibration models must be tested under various clinical situations. Another drawback of these methods is their requirement for a detailed model of the EPID. However, accurate technical details are not always available; moreover, these methods are time consuming and require very complex calculation algorithms.⁹ In several other studies, artificial neural networks (ANNs) and other knowledge-based applications have been widely used as a powerful tools in clinical and radiation therapy applications.^10–22 It was shown that patient-specific QA of IMRT based on EPID can be performed with neural networks algorithms.^23–26

One of the main tools used in machine learning is ANNs. ANNs are very similar to human neural network in term of learning and structural. Neural networks consist of input, hidden and output layers, the hidden layer is placed between the input and output layers and units (nodes) of hidden layer transform the input into something that the output layer can use. Hidden layer works like processor layer which find patterns that ANN must be work based that.²⁰ Learning is a fundamental component to an ANN, although a precise definition of learning is difficult to produce. In an ANN, learning typically occurs during a specific training phase. In the training phase, an ANN by using a teaching method and sample data can be trained to solve specific problems. After completing the network training, ANN learn function that based that, ANN capable to recognize similarities among different input patterns.^20–22 In this work, we used ANNs as an application for the pre-treatment dose verification of IMRT-fields-based 2D-fluence maps acquired by an EPID. The methodology generates a precise estimate of 2D-dose maps for IMRT fields. The fluence maps of IMRT treatment fields (without patient) in gantry zero position (GZP) obtained by an EPID were used as the inputs for the ANN and a dose map of those fluence maps, measured by the 2D Array Seven29^TM, as an output for the ANN in the training and validation phase.

methods and materials

ANN training

In the training phase of the ANN, for each IMRT field, a 2D-fluence map (image) acquired by an aSi1000 EPID and a 2D-dose map acquired by 2D Array Seven29^TM(PTW, Freiburg, Germany) are used as the input and output of the ANN, respectively.

After completing of the training phase, the ANN learned the function that the training was based on, and can convert 2D-fluence maps of the EPID to 2D-dose maps proportional to them. The next step was an accuracy test (validation phase) and the response evaluations of the ANN. To this end, the IMRT fields that were not shown earlier by the trained ANN was used and the 2D-dose was modeled by the ANN. Each 2D-dose modeled by the ANN were compared with the 2D-dose predicted by the Eclipse (v. 13.6) treatment planning system (Varian Medical Systems, Palo Alto, CA) via the γ evaluation algorithm.²⁷ The Eclipse treatment planning system was used to calculate the dose distributions of the IMRT fields. The IMRT 2D-dose map was calculated for the GZP treatment fields of different prostate and nasopharynx cases. Subsequently, the calculated 2D-dose maps were converted into a 5 cm depth of 30 cm-long cubic phantom, made of virtual water. The grid size for the dose maps in the training phase of the ANN was 1 cm, and an analytical anisotropic algorithm (AAA) was used for the dose calculation in the treatment planning system (TPS). Each plan was exposed twice, once for the delivery to the EPID and once for the delivery to the 2D array.

In this study, 30 dynamic IMRT GZP treatment fields (without patient) of the prostate and 30 dynamic IMRT GZP treatment fields (without patient) of the nasopharynx were used for the ANN training. The prescribed dose, dose calculation grid size, algorithm of plan optimization and dose constraint for structures were the same for all of the IMRT plans. Subsequently, 10 dynamic IMRT GZP treatment fields of the prostate and 10 dynamic IMRT GZP treatment fields of the nasopharynx (20 fields) were used for testing and evaluating the accuracy of the ANN performance. All the IMRT treatment fields were delivered to the linac treatment console via the ARIA record and verification system (Varian Medical Systems, Palo Alto, CA).

EPID setup and acquisition of fluence maps

Clinical IX, Varian linear accelerators (Varian Medical Systems, Palo Alto, CA) equipped with Millennium^™ 120 leaf multileaf collimator with two banks (left and right) each with 60 tungsten alloy rounded-end leaves mounted on a carriage, was used for irradiations. An amorphous silicon (a-Si)-based aSi1000 EPID (Portal vision; Varian Medical Systems, Palo Alto, CA) was used to acquire the images. The Portal Vision aSi1000 flat-panel EPID weigh about 7 kg. The active areas of the detector panels were 40 × 30 cm² containing 1024 × 768 pixels, which gives a spatial resolution of 0.39 × 0.39 mm². Each pixel consists of a light-sensitive photodiode and a thin-film transistor to enable the readouts. The aSi-1000 EPID consists of a 1 mm copper metal plate and a gadolinium oxysulphide phosphor screen. The array is overlaid with a copper plate (of 1 mm thickness) and a scintillating layer (gadolinium oxysulphide),^4,5 rendering the portal imager an indirect detection system. The total water-equivalent thickness of the construction materials in front of the photodiodes is 8 mm, as specified by the manufacturer. The thickness of the construction material (without the guard cover) in front of the photodiodes is 1.3 cm (water-equivalent thickness is 8 mm). The guard cover of the EPID removed, and all the IMRT EPID images (fluence map) were acquired at the source EPID distance (SED) of 98.7 cm with 4.2 cm water-equivalent additional build-up on the copper plate, in 5 cm water-equivalent depth (behind the build-up region of 6 Mv X-ray in water); the maximum frame acquisition rate was 9.574 frames/s. We used a set of RW3 polystyrene plates (PTW, Freiburg, Germany) for the additional build-up (Figure 1a). The RW3 slab phantom consists of 33 plates machined to 30 × 30 cm of various thicknesses. The mass density of RW3 is 1.045 g/cm³ and the electron density has a factor relative to water of 1.012.

Figure 1.

(a) Set-up of aSi1000 EPID for acquisition fluence maps of IMRT plan AP fields with 4.2 cm water equivalent additional build-up in SED = 97 cm(guard cover of EPID separated).(b) Set-up of 2D Array Seven29^TM for acquisition 2D-dose map of IMRT plan AP fields with 4.4 cm water equivalent additional build-up and 5.0 cm thick backscatter material (reference point of measurement was then located at 100 cm from the radiation source)$.$ 2D,two-dimensional; AP, anteroposterior; EPID, electronicportal imaging device; IMRT, intensity modulated radiotherapy; SED, source EPIDdistance.

When the EPID is used for dosimetry applications, such as the pretreatment verification of the intensity modulated beams, sufficient build-up must be applied to eliminate the contribution of scattered electrons to the dosimetric images.^5,9 An absence of build-up during the measurement will generate large deviations between the acquired and expected images, inhibiting both the relative and absolute evaluations of the dynamic delivery.⁹ Hence, we used sufficient build-up for the image acquisition.

The EPID was calibrated by the acquisition of dark field (DF) and flood field (FF) images. The DF image was acquired with no radiation and records the pixel offsets. The FF image was acquired by irradiating the EPID with an open field “uniform” irradiation covering the entire region of the imager (40 × 30 cm²) to determine difference in individual pixel sensitivity.⁵ The EPID images were acquired in the integrated mode and were saved in the dicom format.

2D array setup and acquisition of 2D-dose maps

The radiation detector used for the 2D-dose distribution acquisition in this study was the 2D Array Seven29^TM (T10024) model (PTW, Freiburg, Germany). This device is a 2D detector array with 729 vented ionization chambers arranged in a 27 × 27 matrix.

The ionization chambers are equally spaced, i.e. 1 cm center to center and they encompass an active area of 27 cm × 27 cm. Each chamber has a volume of 0.5 cm × 0.5 cm × 0.5 cm. The linear dimensions of the 2D Array Seven29 are 2.2 cm × 30.0 cm × 42.0 cm. The ionization chambers are enveloped with a 5-mm-thick PMMA front plate that is a part of the construction. The effective depth of measurement was found to be located at the back surface of the 5-mm-thick PMMA front plate, i.e. in the entrance plane of the air-filled chamber volumes. Therefore, the resulting water-equivalent depth is 6 mm. The 2D array measurement setup used throughout this work is shown in Figure 1b. For the build-up and the backscatter material, we used a set of RW3 polystyrene plates. The total thickness of the build-up was 5 cm water equivalent, and the backscatter material was 5.0 cm water equivalent.

The 2D Array Seven29 ^TM reference point of measurement was subsequently located at 100 cm from the radiation source. Before all the measurements were performed, for correct response of ionization chamber of detector, the 2D Array was calibrated using a cross-calibration procedure. In this procedure, a known dose was delivered and the response of the central detector was used to calculate a cross-calibration factor.

The architecture of the neural network

A feed-forward multilayer ANN was used to convert fluence map to dose map. The design, training, and testing of ANN, as well as data processing were performed using the software MATLAB (v. Work, USA).

The FF is a type of backpropagation NN that trained based a Levenberg–Marquardt algorithm in this study. The backpropagation NN is essentially a network of simple processing elements operating together to produce a complex output. These elements or nodes are arranged in different layers: input, hidden, and output. The input layer propagated a particular input vector’s components to the hidden layer. The hidden layer, which are neuron nodes stacked in between the inputs and outputs, allow NNs to learn more complicated features and compute output values, which subsequently become the inputs to the output layer. The output layer computes the network output for a particular input vector. In the training phase, ANN produces an output vector for a given input vector based on the current state of the network weights. The training set is repeatedly presented to the network and the weight values are adjusted in the training set.^17,26 Before use of 2D-dose map acquired by 2D Array Seven29TM as output of neural network in training phase a selected region of interest after applying a threshold of 5% of measured maximum dose, was considered. The created mask was applied for 2D-dose map.

Figure 2 shows the architecture of the neural network in this study. It consists of an input layer with nine nodes and a hidden layer with four nodes, and an output layer that leads to the terminal response. The choice of the proper input variables plays a crucial role on the performance of the ANN. The input layer has nine nodes (Figure 2) that consist of the pixel coordinates (i,j), pixel intensity X(i,j), row distance of target pixel from central pixel F(i), column distance of the target pixel from the central pixel F(j), and X(i-1,j), X(i + 1,j), X(i,j-1), X(I,j + 1), which are the neighboring pixel intensities of the target pixels. The accuracy of the network can be improved by introducing neighboring pixels.^20,23 Typically only one or two hidden layers based on the complexity of the pattern is enough. Adding one hidden layer increase both the complexity of the algorithm and the required time for convergence. In addition, using two hidden layers worsen the problem of local minima. Furthermore the number of hidden layers, by using hidden layers with a small number of nodes, it shown empirically that generalization to novel input patterns is improved. Use of small hidden nodes obliges the input patterns to be mapped through a low-dimensional space, enforcing proximities among hidden-layer representations that were not needfully present in the input-pattern representations. Nevertheless, we need to be reminded that there are also cases for which reduction of the number of hidden nodes did not improve generalization. In this investigation, we found that one hidden layer with four hidden nodes exhibited sufficient performance, and the regression of the network is beyond 0.96. Due to that, using more hidden nodes increase response time of ANN and results of regression are more than 0.95 so we refused to add more hidden node. The output layer of the ANN is the layer that yields a terminal response, which is a 2D-dose modeled by an ANN.

Figure 2.

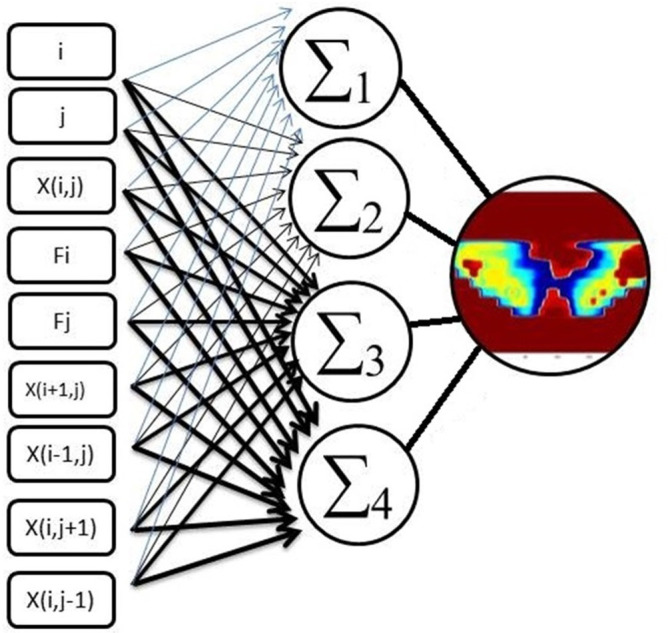
The schematic presentation of input variables of FF-ANN contains: Pixel coordinates (i,j), pixel intensity X(i,j), row distance of target pixel from central pixel F(i), and column distance of target pixel from central pixel F(j) and X(i-1,j), X(i + 1,j), X(i,j-1), X(i,j + 1), which are the neighboring pixel intensities of target pixels (∑1, ∑2, ∑three and ∑four are nodes of hidden layer). ANN, artificial neural network; FF, flood field

We noticed that the neural network training function continues to train the ANN until the improvement in the mean squared error (MSE) performance was minimal (< ${10}^{-3}$). After 70 epochs, the ANN performance did not change significantly, and sufficient convergence between the training and test was obtained. The best training performance (minimum mean square error) was shown at epoch six (Figure 3). An epoch is a single step in training a neural network; in other words when a neural network is trained on every training samples only in one pass we say that one epoch is finished. So, training process may consist more than one epochs.²⁰

Figure 3.

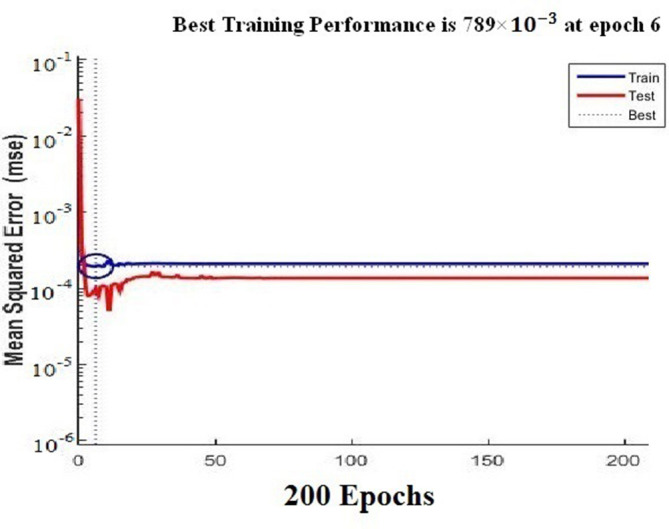
Performance of ANN architectures for the same set of training shows sufficient convergence between training and test data, best training performance (minimum mean squared error) seen at epoch 6. ANN, artificial neural network.

results

ANN 2D-dose maps

For the validation and response evaluations of the ANN, we used 20 dynamic IMRT GZP treatment fields of the prostate and nasopharynx. The pixel intensity of the 2D-dose map predicted by the TPS (target) and that of the 2D-dose map modeled by the ANN (output) were compared with using Bland–Altman plots. The 95% limits of the difference between the target and output intensity validated the ANN as ready for responses (Figure 4). Threshold of 5% of measured maximum dose, was considered for predicted dose by TPS as threshold used for measured dose by 2D Array Seven29^TM in training phase of ANN.

Figure 4.

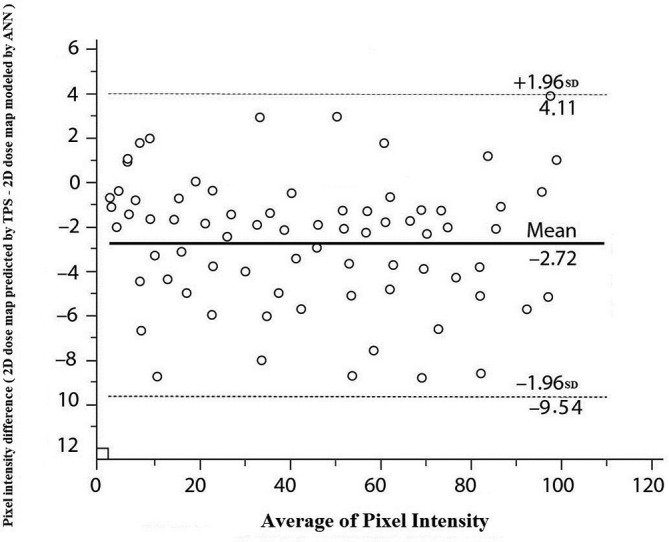
Bland–Altman plots of difference in pixel intensity between target (2D dose map predicted by TPS) and output (2D dose map modeled by ANN) data in validation phase of designed ANN. Solid horizontal lines is mean difference and dashed lines is the 95% limits of agreements (±1.96 SD of the difference). 2D,two-dimensional; ANN, artificial neural network; SD, standard deviation; TPS, treatmentplanning system.

After the training and validation, the ANN modeled the 2D-dose map of the fluence map from the EPID. A 2D-dose map modeled by the ANN is shown by Figure 5.

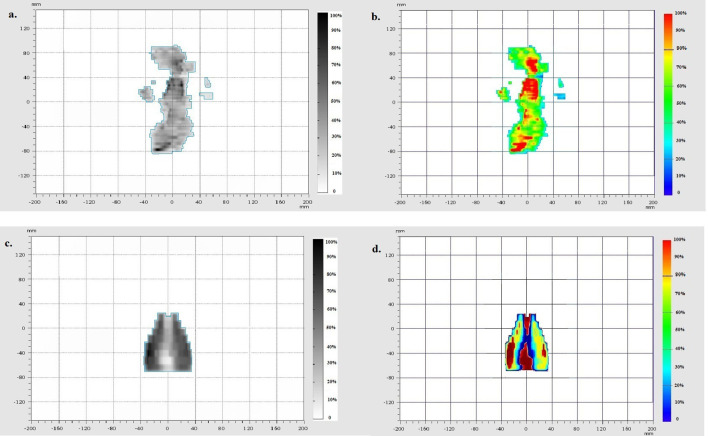
Figure 5.

The ANN modeled the 2D dose map of the fluence map from EPID. The fluence map EPID of nasopharynx case that was used as input for ANN (a), 2D-dose map modeled by ANN for nasopharynx case (b). The fluence map EPID of prostate case that was used as input for ANN (c), 2D-dose map modeled by ANN for prostate case (d). The blue line depicts the boundaries of the ANN replicated dose. 2D,two-dimensional; ANN, artificial neural network; EPID, electronic portalimaging device.

γ evaluation of neural network model

Usually two types of γ evaluation are available for compare two 2D-dose maps: global γ and local γ evaluation. In global γ evalution, to compare the ANN 2D-dose map with that from the TPS, we normalized the ANN dose map to its maximum dose. Similarly, the 2D-dose map from the TPS was normalized to the maximum dose. The γ evaluation of the 2D-dose prediction by the TPS and the 2D-dose modeled by the ANN indicate very similar results. The average overall field pass rate was beyond 96 and 95% for the prostate and nasopharynx fields, respectively, when the distance to agreement (DTA) of (less than or equal to symbol) 2 mm and a dose difference (DD) of (less than or equal to symbol) 3% were used. The pass rates of nasopharynx fields are 93.5±0.4% and 81.4±0.9% for the two sets of criteria: 2 mm/2% and 1 mm/1%, respectively. The pass rates of prostate fields are 94.4±0.4% and 86.4±0.9% for the two sets of criteria: 2 mm/2% and 1 mm/1%, respectively. This means that the average pass rates decrease when the criteria are made tighter, as expected.

To evaluate the robustness and accuracy of the trained ANN, we tested the trained ANN (as described in "ANN training") under stress conditions. Hence, we recalculated the 2D-dose of 10 prostate and 10 IMRT nasopharynx GZP fields as predicted by the TPS with different grid sizes: 0.8 cm, 0.6 cm, 0.4 cm, 0.2 cm, and 0.1 cm. A γ evaluation was used to compare the 2D-dose map predicted by the TPS with different grid sizes, with the 2D-dose map modeled by the trained ANN. For all grid sizes, the average γ value pass rates do not significantly change when the 2D-dose map grid sizes are lower (p-value < 0.05).

Local γ evaluation where percent dose difference is calculated relative to dose at each point. Local γ evaluation had more accuracy in compare global γ. Average global and local γ for prostate and nasopharyng summarized in Tables 1 and 2 respectively.

Table 1.

Local and global γ index evaluation between 2D-dose map modeled by trained ANN and 2D-dose map predicted by TPS for prostate fields with 1, 0.8, 0.6, 0.4, 0.2, and 0.1 cm grid sizes: pass rate with γ evaluation of 3%2 mm, 2%2 mm, and 1%,1 mm

2D-dose map grid size(cm)	γ criteria
	3%/2 mm		2%/2 mm		1%/1 mm
	Global	Local	Global	Local	Global	Local
1	96.2±0.2%	92.5% ± 0.2	94.4±0.3%	73.5±0.4%	86.4±1.4%	61.4±0.9%
0.8	95.7±0.1%	91.9% ± 0.1	94.0±0.3%	73.1±0.3%	86.1±1.1%	60.5±1.1%
0.6	95.5±0.1%	91.5% ± 0.3	93.3±0.5%	72.5±0.5%	85.9±1.3%	59.9±1.3%
0.4	95.2±0.2%	91.1% ± 0.2	93.0±0.1%	72.1±0.3%	85.8±1.4%	58.8±1.4%
0.2	95.0±0.1%	90.8% ± 0.1	92.5±0.4%	71.7±0.1%	85.4±0.9%	56.4±0.9%
0.1	94.6±0.3%	90.5% ± 0.0	92.1±0.2%	71.5±0.1%	85.0±0.2%	55.0±0.5%

ANN, artificial neural network; 2D, two-dimensional; TPS, treatment planning system.

Table 2.

Local and global γ index evaluation between 2D-dose map modeled by trained ANN and 2D-dose map predicted by TPS for nasopharynx fields with 1, 0.8, 0.6, 0.4, 0.2, and 0.1 cm grid sizes: pass rate with γ evaluation of 3%2 mm, 2%2 mm, and 1%,1 mm

2D-dose map grid size(cm)	γ criteria
	3%2 mm		2%2 mm		1%1 mm
	Global	Local	Global	Local	Global	Local
1	95.5% ± 0.2	91.5% ± 0.2	93.5±0.4%	72.5±0.4%	81.4±0.9%	60.4±0.9%
0.8	95.2% ± 0.1	91.2% ± 0.1	93.1±0.3%	72.1±0.3%	80.5±1.1%	59.5±1.1%
0.6	94.7% ± 0.3	90.7% ± 0.3	92.5±0.5%	71.5±0.5%	78.9±1.3%	58.9±1.3%
0.4	94.3% ± 0.2	90.3% ± 0.2	92.1±0.3%	71.1±0.3%	77.8±1.4%	57.8±1.4%
0.2	94.1% ± 0.1	90.1% ± 0.1	91.7±0.1%	70.7±0.1%	75.4±0.9%	55.4±0.9%
0.1	94.0% ± 0.0	90.0% ± 0.0	91.5±0.1%	70.5±0.1%	75.0±0.5%	54.0±0.5%

ANN, artificial neural network; 2D, two-dimensional; TPS, treatment planning system.

With 3%/2 mm γ criteria, overall passing rate with local γ was 4.2 and 4% smaller on the average than global γ rates for prostate and nasopharynx, respectively.

discussion

Previous studies have used ANN for modeling a 2D-dose distribution, percentage depth dose, and the dose profiles of different fields.^18–22 In this study, we used method for portal dosimetry, where an ANN facilitated the pretreatment verification of the IMRT treatment fields.

In this study, ANN used to model a 2D-dose map, based on a fluence map obtained by aSi1000 EPID. Thirty fluence maps of dynamic IMRT GZP treatment fields (without patient) of the prostate and thirty fluence maps of dynamic IMRT GZP treatment fields (without patient) of the nasopharynx obtained by the EPID were used as the inputs for the ANN (feedforward type), and a dose map of those fluence maps, measured by the 2D Array Seven29^TM as the output for the ANN in the training and validation phases. After the training and validation of the neural networks, the analysis of 10 IMRT prostate GZP field plans and 10 IMRT nasopharynx GZP field plans that were not shown earlier by the trained ANNs, showed excellent agreement between the ANN-modeled 2D-dose map and the dose map predicted by the TPS. The average overall global γ field pass rate was beyond 95% for both the prostate and nasopharynx IMRT fields when the 2 mm/3% criteria was used. Since the local γ evaluation is stricter than global γ evaluation, as expected average overall field pass rate for local γ in compare global γ evaluation, significantly decreased. Results of γ index analyze for 2D-dose modeled by ANN in this study well demonstrate that our portal dosimetry method has high accuracy, comparable with other complex portal dosimetry methods and commercial portal dosimetry softwares.¹⁵

In a similar study, Kalantzis et al²³ used 2D-dose predicted by TPS for training of ANN. The dose maps reconstructed by the ANN were evaluated and compared with the TPS, where the γ index was used. The most important limitations of the method proposed by Kalantzis²³ and our previous similar study²⁵ may be the absence of independence from the TPS calculation. The ANN has been trained with the dose distribution calculated by the TPS. This could be very dangerous because systematic errors would not be detected. In our study, the training of our designed ANN was independent from the TPS, as explained in the “Material and methods” section. All the fluence map measurements in the study of Kalantzis et al were performed without additional build-up that can be impressed by scattered electrons and a high-gradient dose region. These conditions are a source of uncertainty in the dose measurement and should ideally be avoided in the TPS prediction.^12,24 All the IMRT EPID images in our study (fluence map) were acquired with sufficient build-up materials (5 cm water-equivalent build-up). The suitable and optimized responses of our designed NN can be attributed to the precise introduction of input nodes and used enough data for training of ANN.

The good response and performance of the ANN trained by the 2D-dose map of 1 cm grid size in comparison to the 2D-dose predicted by the TPS with different grid sizes indicated the robustness and accuracy of the ANN in different and more stringent conditions. This phase of study increases our confidence about the performance of the trained ANN in different and stress conditions that were not shown earlier by the ANN.

The extension of our method would be to evaluate the ability of ANNs to predict the dose intensity for in vivo dosimetry in heterogeneous irradiation fields for different clinical situations. Another method to extend and evaluate the ANN ability for portal dosimetry is to use different NNs and compare their abilities for the task. Use of ANN for rapid arc pretreatment verification by true composite dose evaluation also can be another method that can think about it.

Conclusion

The results of this study showed that ANN can be used as efficient tool for patient-specific QA based on electronic portal imaging devices for IMRT fields. Further, the results indicate that ANN have lower price and higher speed in compare other commercial methods used for pre-treatment verification of IMRT treatments based EPID.