Defect induced, layer-modulated magnetism in ultrathin metallic PtSe₂

Abstract

Defects are ubiquitous in solids, often introducing new properties that are absent in pristine materials. One of the opportunities offered by these crystal imperfections is an extrinsically induced long-range magnetic ordering,¹ a long-time subject of theoretical investigations.^1–3 Intrinsic, two-dimensional (2D) magnetic materials^4–7 are attracting increasing attention for their unique properties including layer-dependent magnetism⁴ and electric field modulation⁶. Yet, inducing magnetism into otherwise non-magnetic 2D materials remains a challenge. Here, we investigate magneto-transport properties of ultrathin PtSe₂ crystals and demonstrate unexpected magnetism. Our electrical measurements show the existence of either ferromagnetic or anti-ferromagnetic ground state orderings depending on the number of layers in this ultra-thin material. The change in the device resistance upon application of a ~ 25 mT magnetic field is as high as 400 Ω with a magnetoresistance (MR) value of 5%. Our first-principles calculations suggest that surface magnetism induced by the presence of Pt vacancies and the Ruderman-Kittel-Kasuya-Yosida (RKKY) exchange couplings across ultra-thin films of PtSe₂ are responsible for the observed layer-dependent magnetism. Considering the existence of such unavoidable growth-related vacancies in 2D materials, ^8,9 these findings can expand the range of 2D ferromagnets into materials that would otherwise be overlooked.

While intrinsically magnetic materials are rare in nature, long-range magnetism can be introduced into non-magnetic 2D materials through adatom intercalation,¹⁰ proximity coupling,¹¹ and defect engineering¹² thanks to their large surface area to volume ratios. The latter strategy has been predicted for several 2D metallic materials including graphene,² but this has not been experimentally realized yet. Recently, PtSe₂ has been considered to be an ideal platform for investigating defect-induced magnetization.^13,14 First-principles calculations show that Se and especially Pt vacancies in monolayer PtSe₂ have a strong influence on its electronic properties; a large magnetic moment of up to 6 µ_B is expected for single or double Pt vacancies. Such defects in 2D materials can either form naturally during the growth/annealing processes⁸ or they can be intentionally created post-synthesis, e.g., under electron beam irradiation.¹⁵ Point defects including Pt vacancies are present at the topmost layers in chemical vapor transport-grown PtSe₂.⁹ Considering the existence of these unavoidable point defects in as-grown material⁹ and its metallic behavior above a critical thickness,^16,17 PtSe₂ holds a great promise for spintronic applications.

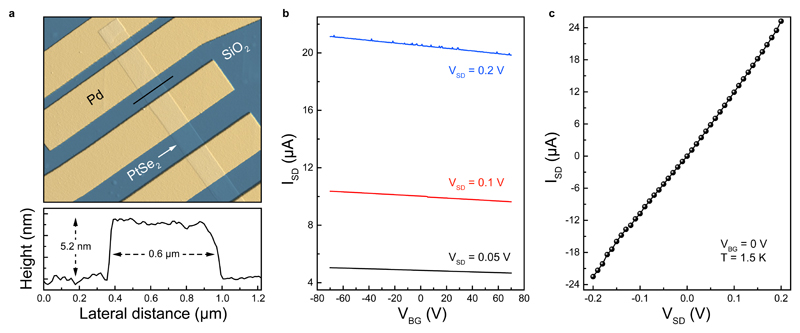
We obtain thin, ribbon-shaped PtSe₂ flakes by mechanical exfoliation from chemical vapor transport -grown bulk crystals (HQ Graphene) onto a Si/SiO₂ (270 nm) substrate. In total, ten devices were characterized with PtSe₂ thickness varying between ~ 4.15 nm to ~ 14 nm, as determined by atomic force microscopy (AFM), allowing us to study the thickness dependence of the magnetism. Non-magnetic metallic Palladium (Pd) contacts (80 nm thick) were formed using electron beam lithography and electron beam evaporation techniques. These non-magnetic Pd contacts were fabricated to exclude any influence of the contact on the magnetic response of the device. Due to the ribbon-like shape of our crystals, devices were fabricated in the two-terminal geometry. An AFM image of a completed device is shown in Figure 1a. Longitudinal device resistance was characterized as a function of back-gate voltage (V_BG), source-drain bias (V_SD), magnetic field and temperature.

Figure 1. Device structure and basic characterization.

a, An AFM image of the device A. Height scale bar is ± 40 nm. Following the black dashed line, we measure a height of 5.2 nm and a width of 0.6 µm for this device. b, V_BG dependence of I_SD measured at fixed V_SD = 0.05 V, 0.1 V and 0.2 V. c, Output characteristics of the device as a function of V_SD at fixed V_BG = 0 V. All charge transport measurements were performed at 1.5 K.

We first discuss the charge transport properties of a device based on a 5.2 nm thick PtSe₂ crystal (device A). Figure 1b shows the gate-voltage (V_BG) dependence of source-drain current I_SD at fixed bias-voltage (V_SD) values of 50, 100 and 200 mV where we observe nearly gate-independent transport characteristics. This indicates that 5.2 nm PtSe₂ is metallic, in good agreement with recent findings. This is also confirmed by the observation of nearly linear I_SD-V_SD relation even at low temperatures (Figure 1c) and by studying the temperature dependence of the device resistance (Supplementary Information 1). Since semiconducting behavior was observed in thinner samples (it is also challenging to electrically probe magnetism in such resistive samples (Supplementary Information 2-3)), we focus on crystals thicker than 4.15 nm for the remainder of this manuscript.

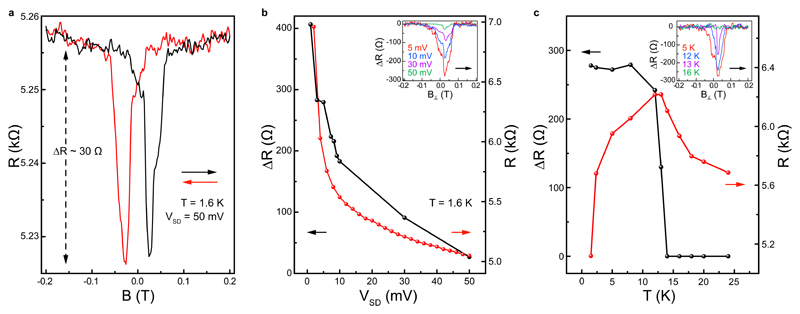
We utilize magnetoresistance measurements as a sensing tool to characterize the magnetism in PtSe₂. For this, we sweep an out-of-plane magnetic field (B) while recording the device resistance. As shown in Figure 2a, we observe a hysteresis loop with minima at ± 25 mT under backward and forward scans. Such hysteretic behavior and the presence of a minor loop (Supplementary Information 4) are the hallmarks of ferromagnetism and were previously observed in ferromagnetic metals such as Cobalt (Co) under the same measurement geometry.¹⁸ We extract a coercive field of ~ 25 mT which is also comparable to the one observed in Co wires.¹⁸ We observe a similar magnetoresistance response in five different samples with comparable coercive field values (Supplementary Information 5). We also note that, just like the total device resistance, the change in the device resistance under a magnetic field is almost insensitive to the V_BG (Supplementary Information 6).

Figure 2. Bias and temperature dependent magnetoresistance measurements in device A.

a, Magnetic field dependence of the device resistance measured at T = 1.6 K. The red (black) arrow represents sweep direction from 0.2 T (-0.2 T) to –0.2 T (0.2 T). b, Source-drain bias (V_SD) dependences of the change in the device resistance under the magnetic field (ΔR) and the longitudinal device resistance (R). Inset shows the resistance change under magnetic field acquired at fixed biases of V_SD = 1 mV, 3 mV and 50 mV. ΔR is calculated by subtracting a polynomial fitting from the device resistance (Supplementary Information 15). c, Temperature dependence of ΔR and R. Inset shows the magnetic field dependence of the resistance change measured at T = 1.5 K, 13 K and 16 K.

Next, we study the dependence of the change of device resistance (ΔR) on the bias voltage and the temperature. Figure 2b shows the V_SD dependence of ΔR measured at 1.6 K. The signal increases from ΔR = 30 Ω to 400 Ω as the bias is reduced from 50 mV to 1 mV. The extracted MR percental variation is 5% at low biases (Supplementary Information 7). As shown in Figure 2b, dependencies of both ΔR and device resistance on V_SD are similar and could be due to slightly non-linear charge injection at low biases. Its physical origin needs further investigation. Following, we present the temperature dependence of the magnetoresistance measured at a fixed bias of V_SD = 5 mV (Figure 2c). ΔR has a very weak temperature dependence in the 1.5 K < T < 13 K range. Raising the temperature just slightly over 13 K quickly suppresses the magnetic response of the device. The temperature dependence of device resistance also shows a similar sudden drop when T is raised above 13 K, which could be related to the suppression of spin-dependent scattering. The resistance keeps increasing as the temperature is further increased, due to the metallic nature of PtSe₂ (Supplementary Information 1).

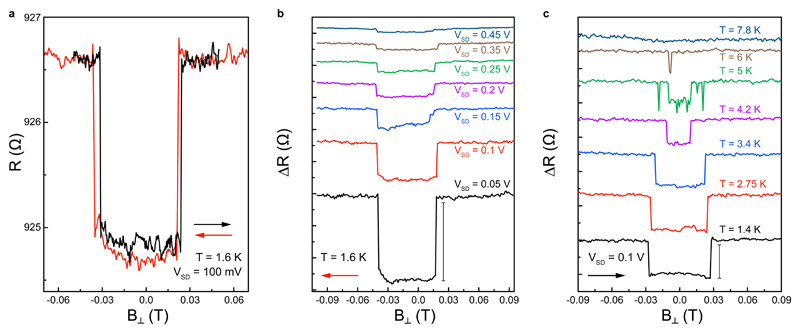
In contrast to this hysteretic magneto-transport response, another subset containing five out of ten characterized devices shows different characteristics (Supplementary Information 8-9). In Figure 3a, we show the magnetic field dependence (forward and backward sweep directions) of the device resistance for one of these devices (device B), which exhibits plateaus with two different values. Here, we observe the lower plateau at low fields in the -30 mT < B < 30 mT range, whereas a sharp jump to the high plateau is observed for fields above |30| mT. The height of the jump in this device is ΔR ~ 2 Ω and depends on the V_SD, as shown in Figure 3b. The width and height of this plateau are also strongly sensitive to the temperature, as the signal completely disappears above 5 K (Figure 3c). Here, we are confident that the transition between these plateaus is a result of the switching between antiferromagnetic ordering at low fields into a fully spin polarized state at higher fields due to the metamagnetic effect.¹⁹ Such magneto-transport response with two plateaus was previously observed in semiconducting bilayer CrI₃-based tunneling devices.^20,21 It was shown that each CrI₃ layer has initially opposite spin polarization at low fields and that the application of a field above the coercive field reverses the magnetization of one of CrI₃ layers causing both layers to have the same spin polarization. Additionally, the observation of very sharp switching between low and high plateaus indicates the out-of-plane direction magneto-crystalline anisotropy of PtSe₂, in good agreement with recent predictions.¹⁴ If the anisotropy had in-plane components, the switching would occur gradually with the field.

Figure 3. Bias and temperature dependent magnetoresistance measurements in device B (~ 9 nm thick).

a, Magnetic field dependence of the device resistance. The red (black) arrow represents the sweep direction from positive (negative) to negative (positive) values. b, V_SD dependence of the magneto-resistance change measured at T = 1.5 K. Scale bar is 5 Ω. Curves shown for sweeps at 0.1 V ≤ V_SD ≤ 0.45 V are offset for clarity. c, Temperature dependence of ΔR measured at fixed bias of V_SD = 0.1 V. Scale bar is 2 Ω. Curves shown for sweeps at 2.75 K ≤ T ≤ 7.8 K are offset for clarity.

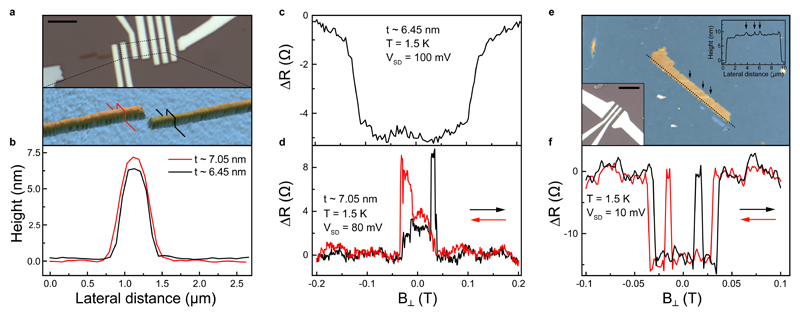
After presenting the existence of both ferromagnetic and antiferromagnetic ordering in metallic PtSe₂, we next check if there is a layer dependent magnetization. The natural way to investigate this dependence would be to compare magneto-transport response of mono and bilayer PtSe₂. PtSe₂ is however extremely resistive in this thickness range.¹⁶ Instead, we have characterized two adjacent devices prepared under identical conditions. As confirmed by the AFM scan, thickness of PtSe₂ crystals in these devices differs by only one layer, as shown in Figure 4a-b, which allows us to investigate layer-dependent magnetism. While the device with a 6.45 nm thick (10-11 layers-device C) PtSe₂ shows the characteristic response with two plateaus (Figure 4c), the device with an extra layer (device D) shows ferromagnetic response (Figure 4d). This observation indicates the layer-dependent magnetism in PtSe₂. To further investigate this effect, we prepared another PtSe₂ device (device E) containing additional one-layer thick fragments on the channel surface, as revealed by AFM imaging (Figure 4e). Magneto-transport response of this sample is very intriguing: both ferromagnetic and antiferromagnetic ordering coexist (Figure 4f). This measurement also allows us to directly conclude that the switching fields for these two contrasting magnetic orderings are different. Here, the strong layer-dependent relationship between different mechanisms could be stabilizing magnetic ordering differently and hence results in different switching fields. This observation is in good agreement with the different coercive fields probed by magneto-optic Kerr effect (MOKE) measurements for even and odd layers of insulating CrI₃ magnets.⁴ Existence of either ferromagnetic or antiferromagnetic ground state orderings depending on the number of layers is intriguing.

Figure 4. Layer-dependent magnetoresistance measurements.

a, Optical and AFM images of a completed PtSe₂ device and its crystal, respectively. Dashed area represents the scanned AFM region. b. Cross-sectional plots along the red and black lines in a. AFM scans show that crystals used in device C and device D has one-layer difference (~ 0.6 nm) in their heights. c, Magnetic field dependence of ΔR measured from the device C (6.45 nm thick). d, Magnetic field dependence of ΔR measured from device D (~ 7.05 nm thick). e, AFM image of a PtSe₂ crystal having multiple one-layer thick fragments on its surface. Top inset shows the cross-sectional plots along the black line in e. Black color arrows in e and top-inset e indicate the one-layer thick fragments. Bottom-inset e shows the optical image of the corresponding device. Black solid line represents the scale bar (5 µm) f, Magnetic field dependence of ΔR measured from the device E shown in e. We would like to note that the change in device resistance in these samples has opposite sign compared to the thinner devices shown in Fig. 2-a and Fig. S4-a. Such opposite switching signs were previously observed in Co and CoFe films.³⁵ To determine the origin of this behavior, the effect of the number of layers, distribution of defects and their effect on magnetism need to be extensively investigated.

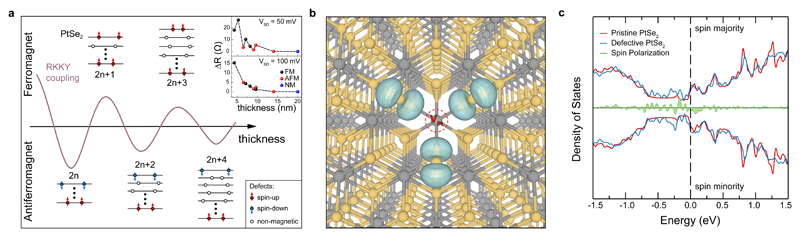
In the following, we propose a theoretical picture to interpret the observed effects. As pristine PtSe₂ does not present any intrinsic spin-polarization, neither in bulk nor in multilayer form, we suggest that the observed magnetism originates from lattice imperfections (Supplementary Information 10). The appropriate model describing the interaction between magnetic impurities mediated by conduction electrons is the well-established RKKY model.^22–24 According to this, the dependence of magnetic exchange coupling J on the distance R reads as J(R) ≈ cos(2k_FR)/R^α, with k_F being the Fermi wavevector of the metal hosting the magnetic impurities. The Fermi surface of PtSe₂ is composed of closed electron and hole pockets located at k_z = 0 and electron pockets at k_z = ±0.6 π/c.^25,26 The latter give rise to an oscillating and power-law decaying contribution to J(R) in the direction normal to the PtSe₂ layers with a period of approximately two layers, as schematically shown in Figure 5a. Hence, we see that adding or removing one layer from metallic PtSe₂ is sufficient to change the sign of the magnetic exchange coupling, thereby realizing a thickness-dependent ferro- or anti-ferromagnetic configuration. This observation is also in a good agreement with the summary of devices measured at fixed bias of V_SD = 50 mV and 100 mV. As shown in Fig. 5a-inset and Supplementary Information 12, we observe that MR decreases as crystal thickness increases, layer-dependent magnetism exist and magnetism is not detectable in thicker crystals.

Figure 5. Theoretical investigations of PtSe₂.

a, Schematic illustration showing the oscillating RKKY interaction across the PtSe₂ slab and the corresponding ground-state magnetic configurations. Inset plot shows the thickness dependence of MR curves for studied samples at fixed V_SD of 50 mV and 100 mV. b, Atomic structure and spin density (turquoise) around a surface V_Pt defect (red, dotted circle) in multilayer PtSe₂. Grey (orange) balls represent Pt (Se) atoms. Isosurfaces contour is set to 0.003 e Å^-3. c, Electronic density of states of multilayer PtSe₂ with (blue) and without (red) a surface Pt vacancy defect. In green, the difference between spin majority and spin minority states. Fermi level is set to zero (vertical dashed line).

Next, we step from model interactions to first-principles calculations performed on realistic models in order to suggest which type of defects may be responsible for the magnetic response observed in our samples. Earlier experimental investigations revealed the abundance of vacancy point defects in PtSe₂ films.⁹ Motivated by this, we assess the impact of such defects on the magnetic properties of PtSe₂ by introducing Se (V_Se) and Pt (V_Pt) vacancy in both metallic multilayer and bulk PtSe₂ models. In analogy with other transition metal dichalcogenides,²⁷ we find that the V_Se defect does not lead to magnetism (Supplementary Information 10). On the other hand, the introduction of the V_Pt defect at the surface of the multilayer model induces a local magnetic moment of ~1.2 μ_B per defect. We further observe that the spin density around the V_Pt defect mostly localizes on the neighboring selenium atoms within its first coordination shell, as shown in Figure 5b. Additionally, the investigation of the electronic density of states reported in Figure 5c indicates that the local magnetic moments stem from defect-induced spin-split states that emerge around the Fermi level. Remarkably, we find that the same defect does not lead to a local magnetic moment when forming in the bulk (Supplementary Information 10,¹²). Similarly, extrinsic adsorbents do not induce magnetism (Supplementary Information 11). It is worth noting in this context that PtSe₂ is more prone to hosting metal atom vacancies than conventional, group VI dichalcogenides (e.g. MoS₂) as a consequence of the substantially lower formation energy that this defect exhibits in the former material⁹ as compared to the latter.²⁷

In contrast to recently discovered intrinsic ferromagnets,^4–6 PtSe₂ has some key advantages for immediate research: it is stable in its pristine form (Supplementary Information 13) without the need for an encapsulation process,¹⁷ it can be easily grown with various scalable methods,²⁸ and readily isolated from its as-prepared substrate which makes it transferrable onto any arbitrary substrate.²⁸ Compared to these intrinsic metallic ferromagnets, the currently observed critical temperature in PtSe₂ is small. This could be in principle improved by control of the vacancy concentration (to increase the concentration and total magnitude of the resulting magnetic moment), control of crystal thickness (to control the sign of the coupling and the switching fields as discussed above) and Fermi level energy (to modulate the density of states at the Fermi level) in future experiments.

Contrary to the assumption that defects in 2D materials are detrimental for the overall crystal quality, defect engineering could be a key approach to enriching their functionality by inducing magnetism in air-stable materials. In the case of PtSe₂, combining the defect-induced magnetism with unique thickness-dependent properties could have several applications for realizing spintronic devices using atomically thin materials.^29–31 Thin semiconducting PtSe₂ could be utilized as a magnetic substrate for proximity studies.^32,33 On the other hand, thick metallic PtSe₂ could be integrated into lateral and vertical spin torque devices,³⁴ tunneling magneto-resistance devices,³⁵ and spin valve devices³⁶ for generating spin polarized charge carriers.

Methods

Device fabrication

PtSe₂ crystals were obtained by mechanical exfoliation from bulk crystals (HQ Graphene) onto a doped Si substrate with 270 nm of SiO₂. The substrate was imaged by using a color camera equipped optical microscope (Olympus BX51M). The thickness of selected crystals was determined by using AFM topography imaging (Asylum Research Cypher). Metallic contacts were prepared using e-beam lithography (Raith EBPG 5000+, 100 keV thermal field emission gun with a beam does of ~ 950 µC/cm²) and e-beam evaporation of Pd (Alliance-Concept EVA 760, 80 nm thick), without the use of any adhesion layers such as Cr or Ti.

Measurements

Cryogenic measurements were performed in an ICE Oxford liquid helium continuous flow cryo-magnetic system with a base temperature of ~ 1.5 K. Drain currents were measured using a Keithley Sourcemeter 2450, while a Keithley Sourcemeter 2400 was used for applying bias through the SiO₂ gate dielectric. The drain voltage was varying between 1 mV to 1 V, while the source was grounded. Electronic transport measurements were carried out in a two-terminal configuration.

First-principles calculations

First-principles calculations have been performed within the generalized gradient approximation to density functional theory devised by Perdew, Burke and Ernzerhof.³⁷ Geometry optimizations have been carried out with the VASP code,^38,39 using a kinetic energy cutoff of 400 eV and k-meshes equivalent to 18 k-points per unit cell along each periodic direction. During geometry optimizations, lattice constants and interlayer spacing were constrained to their experimental values of 3.73 Å and 5.08 Å, respectively, while the tolerance on atomic forces was set to 0.02 eV/Å. The electronic density of states has been calculated with the SIESTA code,⁴⁰ using a fine mesh equivalent to 120 k-points and a smearing of 0.02 eV. The adopted multilayer and bulk PtSe₂ models consist of a a 6-layer thick 3 × 3 supercell and a periodic 3 × 3 × 2 supercell, respectively. In the case of multilayer models, the defects are placed in the topmost layer and a vacuum region of 15 Å was introduced to separate periodic images.

Supplementary Material

Supplementary information is available for this paper at https://www.nature.com/nnano/.