A cell size threshold limits cell polarity and asymmetric division potential

Abstract

Reaction-diffusion networks underlie pattern formation in a range of biological contexts, from morphogenesis of organisms to the polarisation of individual cells. One requirement for such molecular networks is that output patterns be scaled to system size. At the same time, kinetic properties of constituent molecules constrain the ability of networks to adapt to size changes. Here we explore these constraints and the consequences thereof within the conserved PAR cell polarity network. Using the stem cell-like germ lineage of the C. elegans embryo as a model, we find that the behaviour of PAR proteins fails to scale with cell size. Theoretical analysis demonstrates that this lack of scaling results in a size threshold below which polarity is destabilized, yielding an unpolarized system. In empirically-constrained models, this threshold occurs near the size at which germ lineage cells normally switch between asymmetric and symmetric modes of division. Consistent with cell size limiting polarity and division asymmetry, genetic or physical reduction in germ lineage cell size is sufficient to trigger loss of polarity in normally polarizing cells at predicted size thresholds. Physical limits of polarity networks may be one mechanism by which cells read out geometrical features to inform cell fate decisions.

Specification of the germline in C. elegans begins with polarisation of the zygote, P0, which initiates the first of a series of four consecutive asymmetric divisions. At each division, beginning with P0 and continuing through its germline (P lineage) descendents P1, P2 and P3, germline determinants must be sequestered within the single P lineage daughter cell (Figure 3a). Because there is no cell growth between divisions and each cell division is unequal in both size and fate, each P lineage daughter is less than half the size of its parent. The final division of the P lineage, that of P4, is symmetric, giving rise to the two germline founder cells Z2/Z3 [1, 2]. How this switch between asymmetric and symmetric modes of division is regulated remains poorly understood.

polarisation of P0 depends on the PAR (par-titioning defective) proteins, which make up a self-organizing network that regulates cell polarity across metazoans [3, 4, 5]. Polarisation is initiated by a temporal program of PAR network activation coupled to deployment of two semi-redundant cues, resulting in the formation of two opposing PAR domains that define a single polarity axis [6, 7, 8, 9]. One domain is enriched in anterior or aPAR proteins (PAR-3, PAR-6, PKC-3, and CDC-42) and defines what will become the somatic daughter, while the other, enriched in posterior or pPAR proteins (LGL-1, PAR-2, PAR-1, and the CDC-42 GAP, CHIN-1), defines what will become the P lineage daughter that retains germline fate [10, 11, 12, 13, 14, 15, 16, 17, 18]. Each set of PAR proteins excludes the other from its respective domain through a set of mutually antagonistic feedback reactions. Due to diffusion of PAR proteins at the membrane, the interface between domains is characterized by opposing gradients. Such behaviour is consistent with predictions from theoretical reaction-diffusion models based on experimental measurements [7, 19, 20, 21, 22].

Theoretical models for cell polarity typically combine local activation or recruitment of factors at a polarity site in the cell with suppression of these factors elsewhere to ensure a single axis of polarity. Prototypical examples of such networks are so-called activator-inhibitor systems, in which a slowly diffusing ‘activator’ promotes its own production within a local peak while at the same time producing a fast moving ‘inhibitor,’ which suppresses formation of additional peaks elsewhere in the system [23, 24]. Several reaction-diffusion models have been proposed to underlie cell polarity in different contexts, including local excitation-global inhibition, wave pinning, and substrate depletion models [7, 25, 26, 27, 28, 29, 30]. Regardless of detailed mechanism, these models exhibit characteristic length scales that emerge from the kinetic parameters of their constituent molecules, which define characteristics such as the size, extent, or spacing of morphological features. For polarizing systems, these length scales must be tuned to the the size of the cell to ensure the formation of a single, delimited peak that marks the polarity axis.

Here we explore the link between the size of a cell and its ability to polarize, demonstrating that a general lack of scaling of the kinetic behaviours of polarity components results in a cell size-dependent polarity switch, which we propose limits asymmetric division potential in the C. elegans P lineage.

System-size-independent boundary gradients

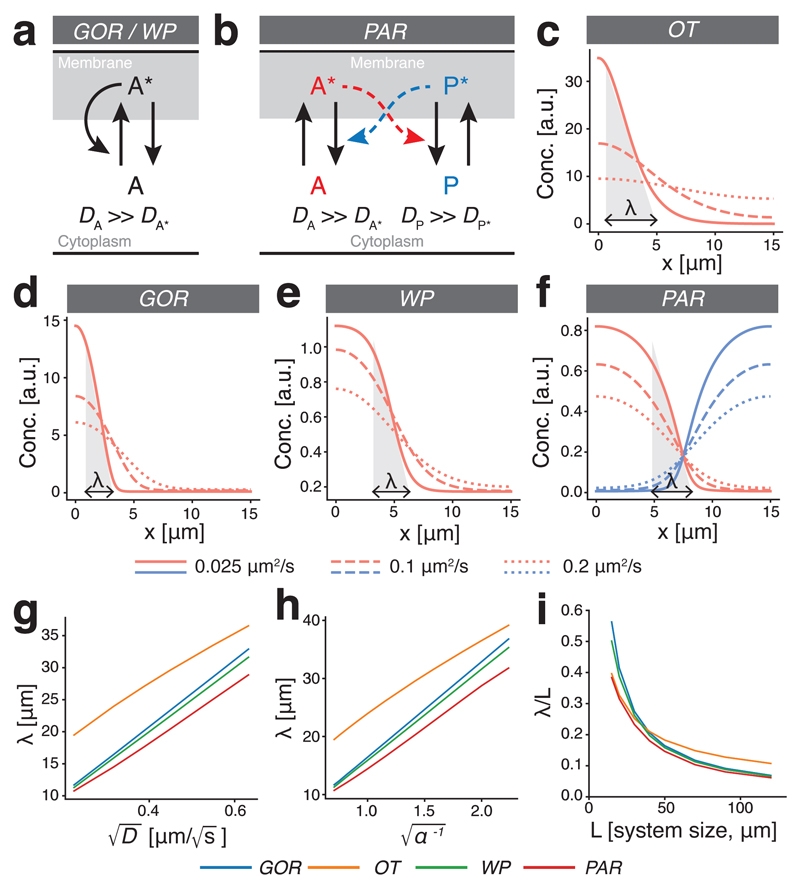
To explore how cell polarity networks respond to changes in cell size, we focused on several prototypical reaction-diffusion models. These included Turing-like systems as put forth by Goryachev and Pohkilko (GOR)[26] and Otsuji et al. (OT)[28], wave pinning (WP)[27], and a two-component reciprocal feedback model inspired by the PAR polarity network (PAR)[7, 31]. To simplify analysis for the PAR network, we assumed symmetric rates and dosages. These systems rely on mass conservation and limiting pools of components, interconversion between active membrane-associated and inactive cytoplasmic states, and auto-catalytic feedback loops, but differ in the precise form of feedback between species. For example, while GOR and WP rely on positive feedback, PAR relies on double negative feedback or mutual antagonism (Figure 1a,b).

Figure 1. Boundary interface in cell polarity models is defined by diffusive behaviour, not cell size.

(a) Reaction scheme for polarity models (OT, GOR, WP) based on a single species that interconverts between active (A*) and inactive states (A). Polarity relies on positive feedback in which A* locally recruits and activates A from a rapidly diffusing cytoplasmic pool. (b) Reaction scheme for a two-component polarity model based on two mutually antagonistic species that interconvert between active, membrane-bound (A* / P*) and rapidly diffusing inactive cytoplasmic states (A/P). (c-f) Sample steady-state distributions reached in various polarity models for varying diffusivities of the active species (D = 0.025, 0.1, 0.2 µm²/s). Shaded triangles illustrate λ for each model in the slowest diffusion case. (g) Linear dependence of λ on $\sqrt{D}$. (h) Linear dependence of λ on $1/\sqrt{\alpha }$ where α is a scaling factor applied to all reaction rates in the system. (i) When system size is reduced, λ occupies an increasing fraction of the system (λ/L), highlighting the general lack of scaling in these models.

Diffusion of active species on the membrane generally prevents sharp boundaries between polarity domains. Instead, boundaries take the form of spatially extended interfaces between domains, the length of which we define as λ. λ can intuitively be understood as the broadness of concentration peaks of active components in GOR and OT, and the width of the transitions that demarcate the boundaries of polarity domains in WP and PAR (Figure 1c-f). In a simple model involving a localized source with uniform degradation, one obtains $\lambda \propto \sqrt{D/k},$ where k is the degradation rate. For the models considered here, λ will be a function of both D and multiple rates. λ varied linearly with $\sqrt{D}$ of the active components, consistent with the length of these domain interfaces being directly related to the diffusion of components on the membrane (Figure 1c-g) matching expectations from prior experimental analysis of the PAR system in C. elegans [ 21]. When scaling all reaction rates by a common scaling factor α, λ varied linearly with $\sqrt{{\alpha }^{-1}}$ (Figure 1h), while varying individual reaction parameters yielded more complicated relationships due to changes in gradient shape (Supplementary Figure S2).

In contrast to this dependence on reaction and diffusion rates, λ failed to scale with system size. Consequently, as system size changed, the resulting distribution pattern of polarity components across the cell did not scale with cell size with λ occupying an increasing fraction of the cell as the cell became smaller (Figure 1i).

A cell-size threshold for cell polarity

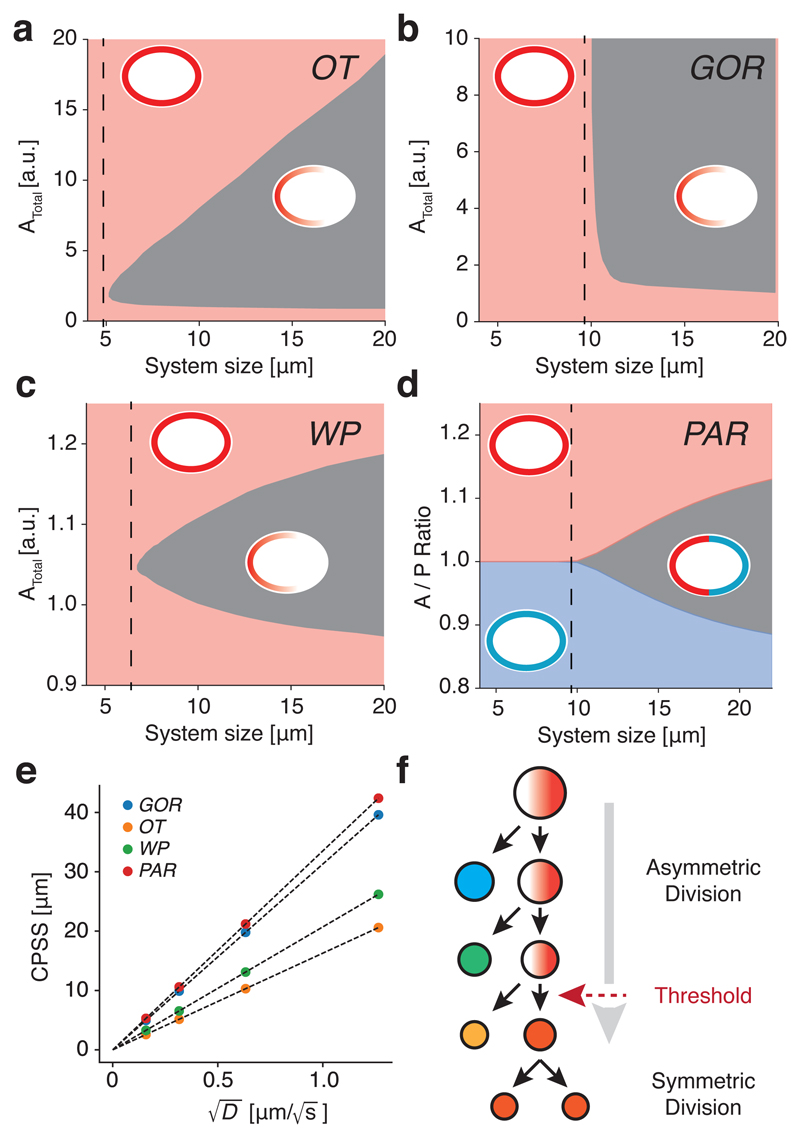
Due to lack of scaling, if the system becomes small enough, the dissipative effects of diffusion will dominate, the distributions of polarity components will become uniform, and a stable polarized state will no longer be possible. To identify a minimal system size in each model, we explored the parameter space defined by cell size and the pool(s) of available components. Through numerical solution of the underlying equations beginning with a polarized state, we found that a cell size threshold existed in all cases, below which the systems were unable to sustain polarity (Figure 2a-d and Movie S1). We termed this the critical polarizable system size (CPSS). CPSS was directly proportional to the square root of diffusion of active species on the membrane (Figure 2e). The precise relationship between CPSS and diffusion differs somewhat between models and becomes more complex for systems with multiple membrane-bound species with differing diffusivities such as the PAR model. In the PAR model, reducing the diffusion of a single membrane species modestly reduced CPSS even if diffusion of the other was held constant, but CPSS did not scale with the slower species, meaning that the kinetic behaviour of both species must be linked to cell size to achieve scaling of CPSS (Supplementary Figure S2).

Figure 2. Membrane diffusion imposes a minimum cell size threshold for stable polarisation.

(a-d) Polarity across parameter space defined by system size (L) and the pool (OT/GOR/WP) or ratio of pools (PAR) of available species. All exhibit a region of parameter space (grey) that permits maintenance of polarity, which is bounded by a CPSS (dashed lines). Insets show schematic representation of the steady-state (polarized or unpolarized). For the PAR system, whether A or P is the dominant membrane species in the unpolarized state is colour-coded. (e) CPSS varies linearly with $\sqrt{D}$ for all models. (f) Conceptual model for a cell-size-induced polarity switch in a stem cell-like lineage. A stem cell polarizes and divides asymmetrically to generate another stem cell and a differentiating cell. Absent cell growth, the stem cell becomes smaller at each division. If cell size limits polarisation, at some point the stem cell will fail to polarize leading to symmetric division.

Thus, consideration of the interplay between the effects of membrane diffusion of polarity components and system size suggests a simple mechanism by which cell size can induce size-dependent switching between a state that can maintain polarity and one that cannot, thereby limiting a cell’s capacity for asymmetric division at a defined size threshold (Figure 2f).

A lack of PAR gradient scaling in vivo

We next determined whether this behaviour could explain the division pattern in the P lineage. As in P0, asymmetric division of the remaining asymmetrically dividing P lineage cells (P1, P2, and P3) is associated with PAR protein asymmetry (Figure 3a). We confirmed that pPAR protein PAR-2 was localized to a single domain that defined what would become the germline daughter in the subsequent division[15], and this polarized distribution was sensitive to inhibition of the anterior kinase PKC-3 [12, 32](Supplementary Figure S1, Movie S2). Thus, P lineage cells up to and including P3 exhibit PAR protein-dependent polarity that follows the general paradigm defined for P0.

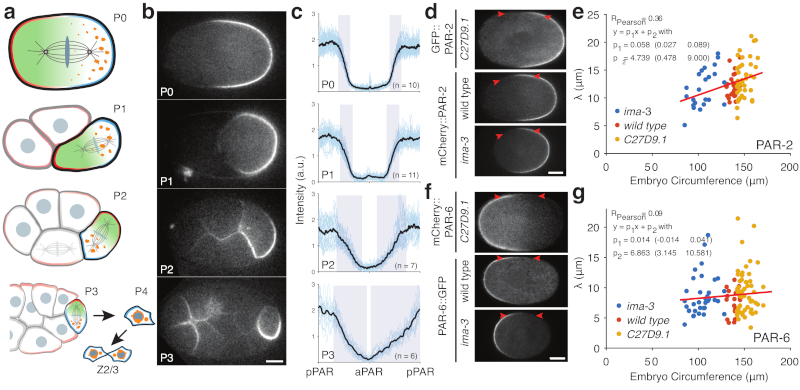
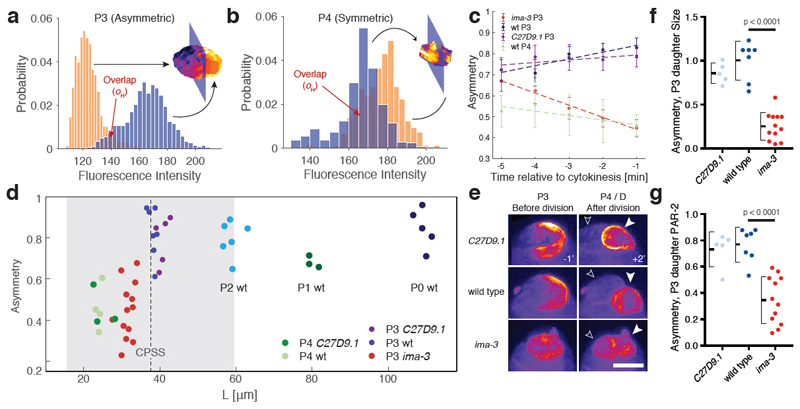
Figure 3. PAR boundary gradients fail to scale with cell size.

a) Schematic of PAR protein localisation in P lineage cells P0, P1, P2, and P3 (pPAR - cyan, aPAR - red). In each of these cells PAR proteins set up a cytoplasmic MEX gradient (green) that drives asymmetric segregation of germline fate determinants (orange) into a single P lineage daughter cell. The final P lineage cell, P4, divides symmetrically to yield the germline stem cells Z2/Z3. See Supplementary Movie S2. (b) Sample midplane images of PAR-2 in P0, P1 (dissected), P2, and P3 used for gradient measurements. (c) Individual and average plots of PAR-2 distributions in P0, P1 (dissected), P2 and P3 cells, showing that the domain boundary interface occupies a proportionally larger fraction of the circumference in smaller cells. Note full circumferential profiles around the entire cell are shown, normalized to cell circumference. Shaded regions highlight the interface regions between domains. Center of pPAR domain at x = 0, 1 and center of aPAR domain at x = 0.5. (d) Sample midplane images of PAR-2 at nuclear envelope breakdown in C27D9.1, wild-type, or ima-3 P0 embryos, with arrowheads highlighting the boundary region. (e) Plot of interface width vs embryo size for PAR-2 in C27D9.1 (yellow, n=41), wild-type (red, n=30), or ima-3 (blue, n=23) P0 embryos. (f,g) Same as (d,e) but for PAR-6. Note that the interface width is effectively constant across a twofold size range. Sample sizes: C27D9.1 (yellow) n = 56, wild-type (red) n=20, ima-3 (blue) n=36. Example fits shown in Supplementary Figure S3. Scale bars, 10 µm.

We next examined how the behaviour of the PAR network changed with system size. Despite polarity being qualitatively similar in different P lineage cells, the shape of PAR-2 concentration profiles across the cell varied (Figure 3b,c). In the larger P0 and P1 cells, anterior and posterior domains exhibited extended plateaus of low and high PAR-2 concentration at the anterior and posterior, respectively, separated by a clearly defined interface region. In the smaller P2 cell, plateaus were less clear and more of the cell was occupied by the interface. Finally, in the smallest polarized cell of the P lineage, P3, the interface occupied nearly the entire cell, with only a very small plateau visible. Thus, as cells become smaller, the PAR boundary interface separating anterior and posterior domains takes up an increasing fraction of the cell, consistent with the behaviour of theoretical models and a general lack of scaling.

We next sought to directly manipulate cell size in vivo by altering embryo size [33]. Mutation of C27D9.1 or its depletion by RNAi, hereafter C27D9.1, increases embryo size, while RNAi targeting ima-3 reduces size, which together yield an approximate two-fold range of cell sizes with circumferences spanning approximately 80-170 µm (wild type is approx. 140 µm).

To quantify the width of boundary interface, hereafter ’interface width’, as a function of cell size, we measured the distribution of PAR-2 and PAR-6 along the membrane in wild-type, C27D9.1 and ima-3 embryos (Figure 3d-g, see Methods and Supplementary Figure S3). Plotting embryo size vs. interface width, we observed a modest correlation between interface width and embryo size for PAR-2, and no effect of cell size on interface width for PAR-6 over the size range examined (Figure 3e,g). These data suggest that the PAR-2 concentration profile may sharpen somewhat in smaller cells; however, the interface width was not maintained at a fixed proportion to cell size. Consequently, for both PAR-2 and PAR-6, the interface occupied an ever larger fraction of cells as they became smaller, consistent with the lack of scaling of the PAR-2 interface observed in P lineage cells (Figure 3b-c).

Prior work reported that interface width of the PAR boundary is directly related to the diffusion and lifetime of PAR proteins on the membrane [21]. We therefore explicitly measured whether these kinetic behaviours of PAR proteins scaled with cell size, including both diffusivity D and off rate k_off.

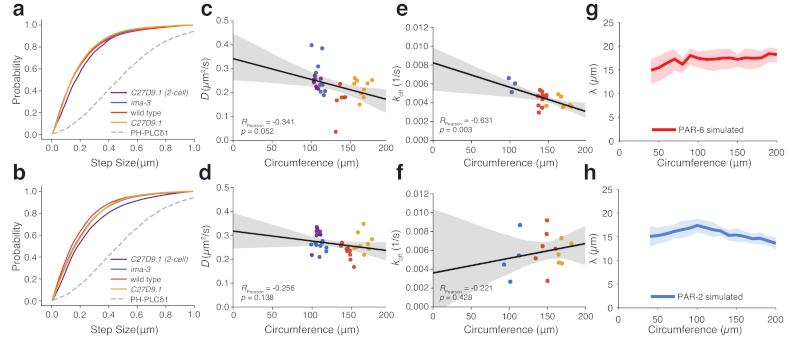
To measure diffusion of PAR-2 and PAR-6, we used single particle tracking to extract cumulative step size distributions, which matched well under all conditions, including C27D9.1 P1 cells (Figure 4a,b). We further estimated diffusion coefficients as a function of cell circumference based on fits of mean squared displacement for each cell examined. Again, this analysis failed to yield a significant trend for either protein (Figure 4c,d).

Figure 4. Reaction kinetics and diffusion rates of PAR proteins fail to scale with cell size.

(a-b) Cumulative step size distribution for PAR-6 (a) and PAR-2 (b) from all trajectories and embryos in (c-d) shown in comparison to a control membrane-associated molecule PH_PLCδ1. (c-d) Plots of mean D vs. cell size for PAR-6 (c) and PAR-2 (d) in wild-type (n=6 and n=9), ima-3 (n=11 and n=9) or C27D9.1 (n=9 and n=9) P0 embryos and C27D9.1 P1 embryos (n=7 and n=8). (e-f) Plots of mean k_off vs cell size for PAR-6 (e) and PAR-2 (f) in wild-type (n=11, n=6), ima-3 (n=3 and n=4) or C27D9.1 (n=6 and n=5) P0 embryos. For c-f, mean ± 95% confidence intervals shown as solid lines plus shaded region, respectively. (g-h) Predicted size dependence of interface width λ using observed cell-size dependence of D and k_off in a stochastic implementation of the PAR model. Mean ± STD shown as solid lines plus shaded region, respectively, n=20 simulations.

Off rates for varying cell sizes were measured using smPReSS (single-molecule Photobleaching Relaxation to Steady State) [34]. In neither case did k_off scale with cell size. PAR-6 exhibited a modest correlation with doubling of cell size leading to only a 50% decrease in k_off across the size range examined (Figure 4e) and no correlation was observed for PAR-2 (Figure 4f).

Reducing cell size disrupts polarity

We have so far shown that neither the patterns of PAR protein localisation across the cell nor the reaction-diffusion kinetics that are thought to underlie these patterns exhibit scaling with cell size. In the context of our theoretical analysis, this general lack of scaling predicts the existence of a minimum size threshold for PAR polarity in the C. elegans P lineage.

To estimate the relevant size threshold (CPSS), we fit a linear regression to experimental measurements of PAR protein kinetics and used this regression to specify D and k_off for PAR-2 and PAR-6 as a function of cell size (Figure 4c-f). These rates were fed into a stochastic implementation of the two-component PAR model, which is similar to the PAR model above, but allows distinct behaviours of A and P molecules and integrates noise levels similar to experiments, allowing better comparison with in vivo data. Fitting the anterior and posterior PAR domain boundaries produced by this model resulted in similar values for λ as observed in vivo (Figure 4g,h). Importantly, using the fit values for D and k_off, we found no correlation between λ and cell size. Using these empirical measures of PAR protein kinetics, we obtained a predicted CPSS corresponding to a circumference of approximately 41 µm (Figure 5d). Strikingly, this value roughly coincides with the size of P3 cells in wild type embryos (41.5±0.9 µm), which are the last of this lineage to divide asymmetrically. Thus, the diffusive behaviour of PAR proteins would be expected to impact the ability of cells to polarize at physiologically relevant length scales, potentially aiding the transition between asymmetric (P3) and symmetric (P4) modes of division.

Figure 5. Decreased P3 cell size in small embryos destabilizes polarity and induces premature loss of division asymmetry.

(a) Histogram of GFP::PAR-2 fluorescence values (yellow and blue bars) taken from the surface of the two cell halves bisected by the plane that maximizes asymmetry of the cell shown. Histogram overlap (o_H) is highlighted. (b) Same as (a), but for a wild-type P4 cell that divides symmetrically. (c) Plots of PAR-2 asymmetry (1 - o_H) by cell type or condition as a function of time before cytokinesis onset. Note loss of asymmetry in small ima-3 P3 cells as they approach division. Mean ± SEM shown. (d) Plot of asymmetry vs. cell size for P lineage cells taken from wild-type or genetically-induced large or small embryos. Vertical dashed line indicates predicted CPSS calculated from experimental parameters, with grey region denoting 95% CI estimate from parameter measurement variance. Measurements are taken 1 min before onset of cytokinesis. Sample sizes: P4 C27D09.1 n= 3, P4 wt n=4, P3 ima-3 n=13, P3 C27D9.1 n=5, P3 wt n=7, P2 wt n=6, P1 wt n=3, P0 wt n=5. (e) Z projections of GFP::PAR-2 in P3 cells 1 min prior to cytokinesis (-1) and the resulting daughter cells 2 min. after (+2’). Solid and outlined arrowheads denote P4 and its sister D. Note PAR-2 is inherited symmetrically between the presumptive D and P4 cells in ima-3 embryos. See Supplementary Figure S4, Movie S3 and Table S1. Scale bar, 5 µm. (f-g) ima-3 embryos exhibit reduced asymmetry in size (f) and GFP::PAR-2 fluorescence (g) between P3 daughter cells. Same samples as in (d), except one ima-3 cell could not be followed for sufficient time after division. Two sample t-test, two-tailed. Mean ± STD indicated.

To test these predictions, we turned to experimental reduction of embryo size. In this case, we examined polarity of P3 cells in small ima-3 embryos relative to wild type and C27D9.1. To quantify polarity in P lineage cells, we applied selective plane imaging (SPIM) to embryos expressing PAR-2::GFP along with a membrane marker (Movie S3). This allowed us to generate a 3D reconstruction of PAR-2 membrane distributions over time using image segmentation and identify the axis of maximal polarity. The axis of maximal polarity was defined as being perpendicular to a 2D plane through the cell center that maximizes PAR-2 intensity differences in the resulting two cell halves. Polarity was defined by $1-o_{\text{H}}$ where $o_{\text{H}}$ is the overlap in histograms of PAR-2::GFP membrane intensities for the two cell halves, with reduced $o_{\text{H}}$ reflecting increased asymmetry (Figure 5a,b and Supplementary Table S1).

Wild-type P3 cells were 41.5±0.9 µm in circumference, were distinctly polarized by five minutes prior to cytokinesis, and remained polarized throughout division (Figure 5a, c-e). Their polarity was similar to earlier P lineage cells (Figure 5d: P0, P1, P2, P3 wt). By contrast, P4 cells were 28±0.7 µm with a reduced maximal polarity, consistent with the fact that these cells do not polarize and undergo symmetric division (Figure 5b-d). P3 and P4 cells from C27D9.1 embryos were similar in both size and polarity or lack thereof compared to wild-type (Figure 5c-e).

P3 cells from ima-3 embryos showed significant reduction in size to 35.2±1.7 µm. At this size, P3 cells initially exhibited polarisation comparable to wild type (t = −5 min). However, as cells rounded up and approached cytokinesis, polarity declined, becoming indistinguishable from the polarity of P4 cells by one minute prior to cytokinesis (Figure 5c-e). To examine the consequences of this reduced PAR-2 polarity in P3 cells, we measured the resulting asymmetry of the P3 daughter cells - P4 and D. P3 daughter cells from ima-3 embryos showed reduced asymmetry in both cell size and PAR-2 levels (Figure 5f,g). This loss of functional polarity in small P3 cells suggests that there is an in vivo size threshold between approximately 30-40 µm, below which PAR polarity is destabilized, thereby compromising division asymmetry, consistent with model predictions.

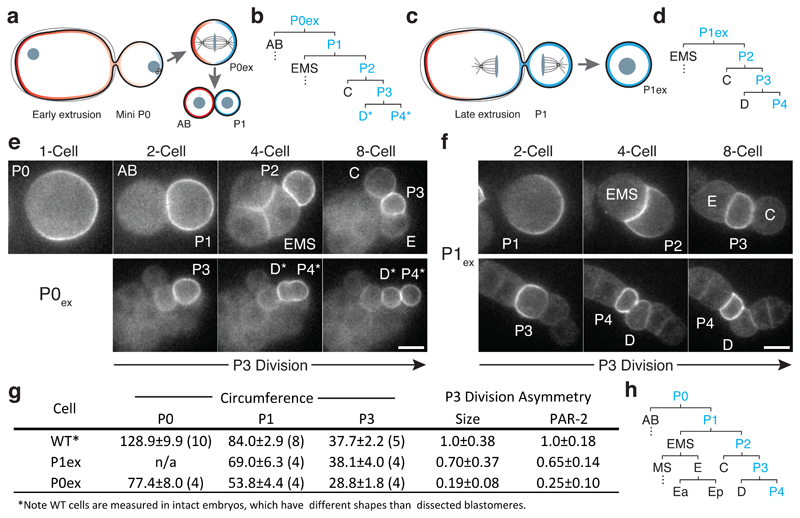
To provide further evidence that reduced size is the cause of symmetric P3 divisions in small embryos, we used laser-mediated extrusion to create mini embryos, or mini-P0 cells (P0_ex). Extrusion of posterior fragments of P0 early during polarity establishment yielded P0-like cell fragments that underwent a normal asymmetric P0-like division followed by an initially normal pattern of cell divisions [35] (Figure 6a,b, Movie S4). By contrast, P1-like cells (P1_ex), were obtained by extrusion during late anaphase after polarity of P0 was fully established (Figure 6c,d). Importantly, P0_ex cells were nearly as small as P1_ex cells (Figure 6g). Therefore, when P0_ex cells divided to yield AB and P1 daughter cells, the resulting P1 daughter was significantly smaller than P1_ex cells. Thus, by allowing extruded cells to divide in vitro, we could assess polarity and asymmetric division of the resulting differently-sized P3 cells generated in these two conditions.

Figure 6. Premature loss of polarity and division asymmetry in P lineage cells derived from cell fragments.

(a) Laser-mediated extrusion of a posterior fragment from early establishment phase embryos containing both centrosomes yields a mini-P0 cell (P0_ex) that undergoes normal asymmetric P0-like division to give rise to an AB:P1 cell pair. (b) Lineage derived from P0_ex. Division pattern is normal until P3 (see h for wild type), which undergoes a symmetric division to yield two symmetric daughters, denoted D*/P4*. Blue indicates inheritance of the P lineage marker PAR-2. See stills in (e). (c) Extrusion of a posterior fragment during P0 cytokinesis instead yields a P1-like cell (P1_ex). (d) Lineage derived from P1_ex. Division pattern is normal through division of P3, which undergoes an asymmetric division as in wild type. See stills in (f). (e) An extruded mini P0 cell undergoes normal asymmetric divisions through birth of P3, which then divides symmetrically. Stills show 1-, 2-, 4-, and 8-cell equivalent stages, followed by the symmetric division of P3. The resulting daughters (P4* and D*) are labeled according to their position relative to C and E descendants, but denoted by * to indicate symmetric division. (f) An extruded P1 cell (P1_ex) exhibits normal asymmetric divisions, including asymmetric division of P3. Stills show P1 and its descendants at the equivalent of the 2-, 4-, and 8-cell stages, followed by polarisation and asymmetric division of P3. Cell fragments in (e) and (f) were obtained from adjacent embryos mounted together on the same coverslip. Further examples in Supplementary Figure S5. Scale bars, 10 µm. For (e-f), see also Movie S4. (g) Table of extruded cell sizes and division asymmetries. Sample size indicated in parentheses. Mean ± STD shown. (h) Wild-type cell lineage showing division pattern of the 1- to 16-cell stage with cell identities indicated.

Extruded P0_ex cells underwent the expected pattern of asymmetric divisions until the birth of P3, including the relative positions and timings of divisions, and yielded P0_ex-derived P3 cells that were 28.8±1.8 µm in circumference (Figure 6b,e,g). However, these P3 cells exhibited symmetric divisions, showing reduced PAR-2 asymmetry prior to division and yielding two, similarly sized cells, with limited to no difference in PAR-2 inheritance. We denote these cells as P4* and D* based on their position. By contrast, P1_ex-derived P3 cells were larger (38.1±4.0 µm), exhibited polarized PAR-2 prior to division, and divided asymmetrically in all cases, with clearly asymmetric PAR-2 distributions and unequal cell size (Figure 6d,f,g). Thus, reducing P3 size through either genetic or physical means resulted in loss of polarity and a premature switch from asymmetric to symmetric modes of division.

We conclude that the reaction-diffusion kinetics of the PAR proteins impose a minimal cell size threshold for polarisation. In failing to scale with cell size, this threshold can serve as reference by which to facilitate cell size-dependent switching from asymmetric to symmetric modes of divisions. We anticipate that similar processes may underlie fate switches in other asymmetrically dividing lineages, such as embryonic neuroblasts in Drosophila and stomatal lineages in Arabidopsis, which undergo a limited number of self-renewing asymmetric divisions, with cell size decreasing with each division, ultimately culminating in a terminal symmetric division [36, 37]. The existence of a cell size threshold in asymmetrically dividing lineages could help explain the tight control over not only fate but size asymmetry at division, including in both the C. elegans P lineage and Drosophila and C. elegans neuroblasts[38, 39, 40]. Notably, loss of size asymmetry in Drosophila neuroblast divisions leads to premature decline in neuroblast size and reduced numbers of asymmetric neuroblast divisions[41], consistent with a size-dependent loss of stem cell potential.

Cells tend to have defined sizes, which may be intimately connected to function, with changes in cell size linked to changes in fate [42]. In many cases, fate choice affects cell size. Here we show the inverse in which cell size limits fate choice. In this alternative paradigm, function follows form[42, 43]: cells obtain information about their geometry through the impact of geometry on intracellular processes, which they can use to inform cell fate decisions, including when and how to divide.

Methods and Materials

Strains and reagents

Strain growth and media

C. elegans strains were maintained on nematode growth media (NGM) under standard conditions [44] at 16°C or 20°C unless otherwise indicated. Strains are listed in Table S2.

RNAi

RNAi was performed according to described methods [45]. Briefly, HT115(DE3) bacterial feeding clones were inoculated from LB agar plates to LB liquid cultures and grown overnight at 37°C in the presence of 10 µg/ml carbenicillin. 100 µl of bacterial cultures were spotted onto 60 mm agar RNAi plates (10 µg/ml carbenicillin, 1 mM IPTG). L4 larvae were added to RNAi feeding plates and incubated for 20-48 hr depending on gene and temperature. RNAi clones listed in Table S3.

Embryo dissection and mounting

For imaging, embryos were typically dissected in M9, egg buffer, or SGM [46] and mounted with 16-21 µm polystyrene beads (Polysciences) between a slide and coverslip or under a 2% agarose pad and sealed with VALAP [21]. 16-18 µm beads were used for single molecule imaging to maximize imaging surface. In most other cases, 21 µm beads were used to minimize compression effects on development. diSPIM imaging was performed in a water bath with the embryo mounted on a glass cover slip coated with a 2x2 mm patch of poly-L-lysine (Sigma).

Microscopy and image acquisition

Confocal Image Acquisition

Midplane imaging was performed on a Nikon TiE with 63x or 100x objectives, further equipped with a custom X-Light V1 spinning disk system (CrestOptics, S.p.A.) with 50 µm slits, 488 nm, 561 nm fiber-coupled diode lasers (Obis) and an Evolve Delta (Photometrics). Imaging systems were run using Metamorph (Molecular Devices) and configured by Cairn Research (Kent, UK). For imaging of P lineage gradients in P2 to P4 in Figure 3, 3D stacks were obtained and only embryos in which cells were near parallel to the imaging plane were used for profile analysis.

Single Molecule Image Acquisition

Single molecule imaging was performed as described in [34] on a Nikon TiE with 100x N.A. 1.49 objective, further equipped with an iLas TIRF unit (Roper), custom field stop, 488 nm, 561 nm fiber-coupled diode lasers (Obis) and an Evolve Delta (Photometrics). Imaging systems were run using Metamorph (Molecular Devices) and configured by Cairn Research (Kent, UK).

diSPIM Image Acquisition

SPIM images were acquired using a Marianas Light Sheet™ microscope (3i) with two 40x N.A 0.8 objectives. To minimize photobleaching, images were obtained with a single objective during extended timelapse. Image stacks were typically acquired once per minute. The microscope system was run using SlideBook™. To minimize potential pleiotropic effects on embryo development in small embryos, we standardized RNAi conditions to obtain small embryos that showed normal division patterns and cell arrangements, excluding excessively small embryos that had altered aspect ratios, which is known to affect development [47]. We also aimed, in so far as possible, to score relative timing and orientation of C, E and P lineage cells - see Supplementary Table S3. In all cases where divisions and cell identities could be reliably scored, E divided prior to both C and P in all cases, and C prior to P in all but 1 case, suggesting fate specification of P1 descendants is intact up to the P3 division.

Laser-mediated extrusion

For laser ablation and extrusion experiments, embryos were dissected and mounted in SGM. After inducing a hole in the eggshell using a 355 nm pulsed UV laser directed via an iLAS Pulse unit (Roper), modest pressure was applied to the coverslip to extrude the relevant cell fragment. P1 extrusions were performed as the cleavage furrow was completing. P0 extrusions were performed around the time of symmetry-breaking. Single image planes were captured at 1-2 min intervals to minimize phototoxicity.

Data Analysis

Interface width

Interface width was measured from fluorescence intensity profiles extracted from midplane images of PAR-2 and PAR-6 in dual labeled zygotes from nuclear envelope breakdown (NEBD) to the onset of cytokinesis, with two interface measurements obtained for each embryo (Supplementary Figure S3). We observed a general sharpening of the interface beginning 60-100 s prior to furrow ingression for PAR-2 (Supplementary Figure S3), which coincided with onset of cytokinetic ring assembly and a period of active alignment of PAR domain boundaries with the ingressing furrow [48]. No sharpening was observed for PAR-6 (Supplementary Figure S3).

The cortical profile was segmented for each timepoint using the available fluorescent channels and custom-built software in Matlab (Mathworks®), and subsequently straightened in Fiji [49], using a 20 pixel line thickness. Intensity profiles were obtained by averaging the brightest three pixels at each membrane position.

PAR-2 profiles were fit by

$$I\left(x\right)=(a+\frac{b}{2})+\frac{b}{2}\cdot \left(\text{erf}\left(\left(x-c\right)\cdot \sqrt{2}/\lambda \right)\right);$$

where erf is the error function as implemented in Matlab.

In a first round of fitting, the inflection point (interface center) of the curve was determined. A second round of fitting was performed on a region of ± 20 µm around the center to determine σ. Fitting accuracy was then determined by smoothing the data using a Savitzky-Golay filter and subtracting the data from the fitting curve within the gradient region. If the maximum of the absolute difference exceeded an empirically chosen value (between 6% and 8% of the amplitude of the fitting function, depending on the noise level) the data were discarded. We averaged PAR-2 distributions at three consecutive timepoints spaced 20 s apart at approximately 3 min prior to furrow ingression coinciding roughly with NEBD. Among the three considered timepoints at least two had to meet the threshold, otherwise the respective interface was not used for analysis.

PAR-6 profiles were initially fit by an error function to determine their center, top and ceiling. However, because the error function failed to capture the shape of the profile, the lower part of the curve was fit by an exponential

$$I\left(x\right)=A*e^{-x/\lambda }+c$$

using a 40% cutoff based on the top/bottom determined above to determine b. Varying the cutoff between 30% and 70% did not significantly alter the results, as expected for an exponential decay. Timepoints for analysis were defined as for PAR-2.

When tracing the entire circumference of cells to obtain profiles, two gradient regions were obtained. When fit individually, the two values of λ obtained for each embryo were not correlated (Supplementary Figure S3) and hence each gradient region was treated as an independent sample.

Polarity of P cells from SPIM images

Polarity of P cells was assessed by first creating a 3D membrane rendering of PAR-2 fluorescence intensity obtained by diSPIM imaging, using custom-built Matlab (Mathworks®) software. Subsequently, the center of mass is determined by averaging all positions of the membrane rendering. Next, a plane that cuts the center of mass is rotated in all directions in steps of 5°, at each step dividing the cell into two halves. At each step the histogram of surface fluorescence intensity is determined on either side of the plane and the overlap of these (normalized) histograms taken as a measure of polarity. High overlap indicates the two halves on either side of the bisecting plane are very similar, while no overlap indicates perfect polarity. The plane with minimal overlap (when the two sides are most different) is defined as the plane of maximum polarity. Asymmetry for these cells is defined as 1 – overlap and is what we report in Figure 5.

Cell Size

Cell size is typically reported as the circumference as measured directly from confocal images taken through the center of the cell of interest. The only exception to this was for cell size calculated from 3D stacks taken by diSPIM. An effective circumference was calculated as that of a spherical cell of the same volume.

Asymmetry quantification

For size asymmetry measures of P3 daughters in Figure 5f and 6g, cell size measurements were taken as above for the two P3 daughter cells and used to calculate an asymmetry index defined as:

$$ASI=\left|\frac{P4-D}{P4+D}\right|$$

with asymmetry reported relative to wild-type controls. For Figure 6g, PAR-2 intensity was measured along the membrane of the daughter cells in a single midplane section, excluding the cell interface, subtracting chip background, and averaged. These values were then used to calculate the ASI as above, again normalized to wild-type controls. For Figure 5g and Supplementary Table S1, membrane-associated GFP::PAR-2 was extracted as for SPIM analysis of P3 cell polarity above and histogram overlap (o_H) calculated to obtain a metric for asymmetry that was comparable to the Figure 5d.

Diffusion Analysis

Tracking was performed in Python, using the trackpy package [50], and custom code developed for our analysis (see code availability). Our analysis follows [34]. Briefly, MSD was calculated for each particle and the first ten lag times were fit to MSD = 4Dt^α. For every embryo, a mean value for D was obtained by averaging D for all particles between 0.9 < α < 1.2. Notably, we used 20 ms exposures and 60 ms intervals between frames, as opposed to continuous imaging every 33 ms in [34].

Off Rate Analysis - smPReSS

Dissociation rates were analyzed as described in [34] using the following fit equation for observed particle number N, assuming an infinite cytoplasmic pool:

$$\frac{dN}{dt}=k_{\text{app}}-\left(k_{\text{off}}+k_{ph}\right)N.$$

Here, k_app is the cytoplasmic on rate of unbleached particles, k_ph the bleaching rate induced by the imaging laser and k_off the dissociation rate of particles from the membrane.

Modeling

Simplified 2-component PAR System

The model used here was introduced in [7] and a similar symmetric version was used in [31]. Briefly, the governing equations are

$$\begin{array}{l}\frac{\partial A}{\partial t}=D\frac{{\partial }^{2}A}{\partial x^2}+k_{\text{on}}{A}_{cyto}-k_{\text{off}}A-k_{AP}{P}^{2}A\\ \frac{\partial P}{\partial t}=D\frac{{\partial }^{2}P}{\partial x^2}+k_{\text{on}}{P}_{cyto}-k_{\text{off}}P-k_{PA}{A}^{2}P\\ P_{cyto}={\rho }_P-\psi \overline{P}\\ A_{cyto}={\rho }_A-\psi \overline{A};,\end{array}$$ (1)

where A and P denote membrane concentrations, A_cyto and P_cyto are (uniform) cytoplasmic concentrations and ρ_A and ρ_P refer to the total amount of each protein species in the system. If not indicated otherwise, the following parameters were used: D = 0.1 µm² s⁻¹, k_on = 0.006 µm s⁻¹, k_off = 0.005 s⁻¹, k_AP = k_PA = 1 µm⁴s⁻¹, L = 30 µm (half circumference) and a dosage ratio between A and P of 1:1. Surface-area-to-volume ratios were adjusted depending on cell size assuming a constant prolate-spheroid geometry (aspect ratio 27:15). All other parameters relating cytoplasm and membrane were as described previously [7]. To simplify analysis, note that this system is symmetric with the same values for diffusion and reaction rates for both PAR species. This assumption is reasonable as empirical values for D and k_off, the most relevant rates for gradient length, are similar for the two species. However, for calculating a realistic CPSS for comparison to experiments, we used the measured values for both species, see Stochastic PAR System below.

To assess qualitative behaviour of the PAR network upon changing parameters, the governing system of partial differential equations was solved using an adaptive Runge-Kutta scheme [51], using custom-built Python code (see code availability).

Simulations were initialized with two opposing domains with a sharp boundary and run until t = 10000 s. A simulation was said to break down within the time limit if the concentration of one species was larger than the other across the entire domain.

Wave Pinning

The wave-pinning system was simulated using custom Matlab (Mathworks) code, using the pdepe function, with parameters similar to the ones described previously [27]. For Figures 1 and 2 parameters were changed as indicated in figure legends with the following base set: δ = 1/9 s⁻¹, γ = 1/9 s⁻¹, D_mem = 0.1 µm²s⁻¹, D_c = 100000 µm²s⁻¹, K = 1 and k₀ = 0.067/9 s⁻¹. Simulations were run until t = 10000 s. A simulation was said to have become unpolarized within the time limit if the difference between areas of high and low membrane concentration was less than 5%.

Mass-conserved Activator Substrate

The mass-conserved activator substrate model (Otsuji, OT) was implemented in Matlab similar to Wave Pinning above, using Model I, previously described[28], with the following parameters: D_v = 100000 µm²/s, a₁ = 1 s⁻¹, a₂ = 0.7 µM⁻¹ and s = 1, which approximates infinite diffusion. System size and membrane diffusion were chosen as indicated. Initial conditions were chosen as u(t = 0, x) = c_init · Θ(x − L/2) and v(t = 0, x) = c_init, where c_init is plotted as A_tot in Figure 2a. This sets the total amount of material due to mass conservation.

For the Goryachev model [26] the following reaction terms were used, which have already been described elsewhere [29]:

$$f\left(u,v\right)=a_1{u}^{2}v+a_{2}uv-a_{3}u$$

and the following parameters were used to create the phase space diagram: D_mem = 0.1 µm²s⁻¹, D_cyto = 10000000 µm²s⁻¹, a₁ = 0.0067 µm²s⁻¹, a₂ = 0.0033 µms⁻¹, a₃ = 0.01 s⁻¹. The shape of initial conditions was the same as used for the Otsuji model above. Simulations were run until t = 10000 s. Polarity was scored the same as above for wave pinning.

Stochastic PAR System

Stochastic simulations of the PAR system were performed using a Gillespie algorithm [52] implemented in Matlab. The governing equations are

$$\begin{array}{l}\frac{\partial A}{\partial t}=D_A\frac{{\partial }^{2}A}{\partial x^2}+k_{\text{on,A}}{A}_{cyto}-k_{\text{off,A}}A-k_{AP}PA\\ \frac{\partial P}{\partial t}=D_P\frac{{\partial }^{2}P}{\partial x^2}+k_{\text{on,P}}{P}_{cyto}-k_{\text{off,P}}P-k_{PA}{A}^{2}P\\ P_{cyto}={\rho }_P-\psi \overline{P}\\ A_{cyto}={\rho }_A-\psi \overline{A};,\end{array}$$ (2)

Note the different exponents conferring antagonism as well as different rate parameters for A and B compared to equation 1. Diffusion and dissociation rates were obtained from regressions in Figure 4. Surface-area-to-volume ratios were dependent on cell size, assuming a prolate-spheroidal geometry with aspect ratio 27:15. All other parameter values were as described above (Simplified 2-component PAR System) or as previously described[7]. Breakdown of simulations at a given cell size was scored as described above for the deterministic system for averages of at least eight individual simulations.

Determining λ as a function of cell size and diffusion/reaction rates

To examine the dependence of λ on reaction and diffusion rates we chose L = 100 µm to avoid strong boundary effects. All other rates were chosen as described in the respective figures and individual supplement sections. Note that for Supplementary Figure S2, because changing k_off alone alters membrane concentrations, to be able to vary $\sqrt{k_{\text{off}}^{-1}}$ across several orders of magnitude while still achieving a polarized state, k_on had to be increased tenfold.

To explore how λ depended on system size, we kept the overall protein concentrations (per cell volume) constant and initiated the system with the same initial conditions as above. System size was varied using parameters as described for individual models.

For deterministic simulations, we determined boundary length of simulated systems by measuring and inverting the maximum absolute slope of the concentration profile of membrane-associated species at steady-state. To account for concentration differences across models and conditions, we normalized profiles to the maximum membrane concentration. For the stochastic model, interface profiles were fit by an error function, using the same algorithm as for PAR-2 profiles, which facilitated direct comparison with experimental data.

Defining CPSS

To determine the CPSS for each system (Figure 2a-e), we simulated across a parameter space grid defined by either total component concentrations (OT, GOR, and WP) or relative component concentrations (PAR) and system size. Based on the criteria for each model stated above, this allowed us to define the polarized region of parameter space. CPSS was defined as the lowest simulated system size that permitted stable polarity domains. For the PAR model a bisection algorithm was used to refine the boundaries between regions, due to long simulation times.