Imputation techniques on missing values in breast cancer treatment and fertility data

Abstract

Clinical decision support using data mining techniques offers more intelligent way to reduce the decision error in the last few years. However, clinical datasets often suffer from high missingness, which adversely impacts the quality of modelling if handled improperly. Imputing missing values provides an opportunity to resolve the issue. Conventional imputation methods adopt simple statistical analysis, such as mean imputation or discarding missing cases, which have many limitations and thus degrade the performance of learning. This study examines a series of machine learning based imputation methods and suggests an efficient approach to in preparing a good quality breast cancer (BC) dataset, to find the relationship between BC treatment and chemotherapy-related amenorrhoea, where the performance is evaluated with the accuracy of the prediction. To this end, the reliability and robustness of six well-known imputation methods are evaluated. Our results show that imputation leads to a significant boost in the classification performance compared to the model prediction based on listwise deletion. Furthermore, the results reveal that most methods gain strong robustness and discriminant power even the dataset experiences high missing rate (> 50%).

Introduction

Clinical data with substantial missing information presents significant challenges for pattern classification and decision making. Machine learning and statistical analysis based clinical decision support systems associate the patient health status with the prediction for the disease or medical outcomes of interest, such as in-hospital mortality [11], breast cancer [7] and diabetes [20]. Data mining has been widely recognized as a crucial approach for many clinical prediction rules. In practice, collected clinical datasets are sometime incomplete, usually attributed to manual collection, erroneous measurements and equipment failures. The missing values dramatically degrade the performance if handled improperly. When the missing rate exceeds 15%, missing values should be carefully treated with a special consideration [1]. The simplest solution is the case deletion strategy, which discards all missing cases and works only when a few missing values exist. Another solution is substituting missing entries with the mean or mode values of a specific feature, which reduces the variability of the dataset and totally ignores the covariance among features [23]. Such techniques have many limitations and may not always benefit model construction. The motivations for innovative imputation are to develop efficient and beneficial algorithms to improve the classification performance. Many studies have demonstrated that machine learning based techniques are effective and useful in managing small to large missingness and data scales [13].

Over the last decade, there have been tremendous developments in clinical data analysis. BC is the most common type of cancer in women  [10, 12]. Among those who are of reproductive age (< 35 years) at diagnosed, 15% have not yet been pregnant or started a family yet [22]. According to [6], the 10-year survival rate of early BC is almost 85% and pregnancy does not negatively impact prognosis. However, one of the main side effects of cancer treatment is amenorrhoea (permanent cessation of menstruation), that can affect up to 98% of women in the reproductive age, and around 76% of survivors wish to conceive in the future pregnancy [19]. Therefore, infertility risk prediction after cancer treatment becomes a priority for young BC patients who wish to conceive after cancer. In this study, we are preparing datasets to describe factors related to fertility and breast cancer treatments to determine likely post-treatment amenorrhoea. The datasets are collected from six institutions over the world and originally archived in different formats, which are not fully aligned e.g. some essential features in one subset may be fully or partially absent in another. As a consequence, substantial missing values are introduced. We aim to evaluate the well-known imputation methods, i.e., mean/mode imputation, random imputation, multiple imputation using chained equation (MICE) [4], k-nearest neighbor (KNN) [3], random forest (RF) [24] and expectation maximization (EM) [15] imputation on missing values and find the potential relationship between cancer treatments and post-treatment amenorrhoea by constructing multiple classifiers. Use of the datasets are authorised by the FoRECAsT consortium of Psychosocial Health and Well-being Research (emPoWeR) Unit, University of Melbourne [17]. The quality of the imputation will be measured by the prediction accuracy of post-treatment amenorrhoea status. To this end, we undertake extensive experimental comparisons and simulations with some popular imputation algorithms. The main contributions of this paper are summarized as follows:

1. The work explores the impact of some notable imputation techniques using statistical and machine learning methods, and further evaluates the performance regarding the classification tasks on prediction of amenorrhoea after 12 months of breast cancer treatments.

2. We examine whether the imputation across different datasets achieves significant improvements, even if the data has a large amount of missing values.

The paper is structured as follows. Related work of imputation techniques and chemotherapy-related amenorrhoea are illustrated in “Related work”. “Experiments" reviews the clinical data and includes descriptions of experimental methodologies.  “Results and discussion” presents and discusses the results, and “Conclusion” concludes the paper.

Related work

Chemotherapy-related amenorrhoea (CRA) can be caused by breast cancer treatment, the involvements to maintain the fertility options should be accessed before the treatment regularly and young women should be informed of the possibility of amenorrhoea or recovery of menstruation and contraceptive choices [18]. Lee [10] reported that the incidence of CRA hinges on age at diagnosis and adjuvant endocrine therapy, for those who are older than 40 years, CRA is more likely to occur and be permanent, especially after adjuvant endocrine therapy. Also Liem [12] pointed out the age at diagnosis is the main factor associated with chemotherapy-related infertility. Apart from the age, post-cancer fertility will also depend on personal factors, Peate [18] found out that low knowledge can reduce the quality of decision making. To conclude, prediction of chemotherapy-related infertility involves consideration of complex factors such as age, lifestyle factors, knowledge, previous pregnancies, ovulation, history of previous medical and gynaecological diseases [8]. Decision support is critical in ensuring patients can make informed decisions about fertility preservation in a timely manner, but in practice women are making this decision without knowing their infertility risk, which has the potential for adverse effects. The key challenge with fertility prediction is that the data usually contains substantial missing elements which adversely impact the prediction results. Imputation methods can help to accommodate this issue.

Missing values

Missing values are common in datasets and these values have serious drawbacks in data analysis. The reasons for missing data may vary, some information cannot be obtained immediately, data might be lost due to unpredictable factors, or the cost for accessing the data is unaffordably high. There are four main types of approaches for dealing with missing data, these include deleting the incomplete data and only use complete data portion, treating missing values as a new category where standard routines can be applied, using statistical based procedures e.g. mean imputation and EM algorithms, and adopting machine learning methods, such as KNN, decision trees, and logic regression method.

Types of missing data are defined by Little and Rubin [14], who categorizes missing data into three types, which are missing completely at random (MCAR), missing at random (MAR) and missing not at random (MN-AR).

MCAR cases occur when the probability that an element missing is independent of the variable itself or any other related influences, simple examples of MCAR include accidental data lost, occasional omission collection of questionnaire, and manual recording errors in medical data. MAR is the case such that the missing value is independent of the missing attribute itself but can be predicted from the observed responses. A typical case is that young BC patients have more missing data in terms of fertility and productivity, compared with older patients, by leveraging the observed age information. MNAR situation occurs that the missingness is related to the missing feature itself and missing data can not be predicted only from the observed and missing entries from the database. For example, BC patients will be more inclined to conceal private information unrelated to the cancer such as education and salary levels, which are unlikely to be foreseen. Handing this category of missing data is problematic and there are no generalized methods that can resolve this issues properly.

In our cases, when the MNAR type is rare in this mixture of different missing data types [5], we may only consider that the missing values are under MCAR or MAR assumptions if a feature is not totally missing.

Imputation techniques

Imputation with statistical analysis

When missing data are MCAR or MAR, they are termed ’ignorable’ or ’learnable’, which implies that researchers can impute data with certain procedures, by statistical analysis or machine learning approaches. Some popular and well-known statistical imputation techniques will be presented in this section. The easiest way of filling missing value is imputing the average value of the observed data, known as ’mean imputation’. The method is elementary thus the drawbacks are obvious, e.g., it fails to deal with large amount of missing values, distorts the distribution of the dataset and totally ignores the covariance between different attributes as the expectation of the attribute $E[x_i]$ does not change in this case [23]. Another random imputation method, assigning a random selection of observed values for missing items [9], is also employed when missing features are quantitative. However this method neglects the latent potential relationship among present features. Another way to utilise the knowledge of whole dataset is the model-based approach. Expectation maximum (EM), is introduced to deal with missing data by constructing fitting models in incomplete data capitalizing of the knowledge from complete sets [16]. If the model is correct for the complete sample, the maximum likelihood estimation of the unknown parameters can be made by observing the marginal distribution of the data [14]. Expectation maximization is suitable and outperforms mean substitution and listwise deletion in cases where there is little or no interdependency between the input variables. The methods described above are single imputation and the statistical uncertainty of the missing values is not reflected. The multiple imputation (MI) procedure provides a solution to this issue [21], MI will replace all missing values with a set of conceivable attributes that can present the uncertainty of the plausible values which are generated by regression models. All missing data is filled in M times (M > 20) to generate M complete data sets. The M complete datasets are then analysed in certain standard tasks such as regression, classification and clustering. The results are pooled and averaged to produce a single estimate. MICE imputation is particularly flexible in a broad range of frameworks as it invents varied complete datasets and takes the uncertainty into account to yield accurate deviations. But as the prediction models are constructed successively, the computational cost is relatively high.

Imputation with machine learning methods

Machine learning achieves great success in many fields and the flexibility allows us to capture the high-order interactions in the data [7] and thus impute missing attributes. This section reviews several imputation routines characterized by machine learning concepts.

KNN approach is a type of hot deck supervised learning method, providing a path to find the most similar cases for the given instances, in which KNN is a useful algorithm that matches a case with its closest k neighbours in a multi-dimensional space. In missing data imputation, KNN aims to find the nearest neighbours to minimize the heterogeneous euclidean-overlap metric distance [26] between two samples, then missing items are further substituted with the values from k complete cases. The advantage is that the method is suitable for large amount of missing data, but the disadvantage is high imputation as it will compare all dataset and find the most similar cases. Moreover, Stekhoven [24] proposed a model-based iterative imputation meth-od based on random forest. The random forest is generated by decision trees from sampled subset of datasets, the proximity matrix from the random forest is learned and updated to approximate the missing values while a set of fitting models are constructed. The random forest imputation can deal well with non-parametric data with mixed types. In this study, we will compare six common imputation techniques, which are mean imputation, random imputation, multiple imputation using chain equations, expectation imputation, KNN imputation and random forest imputation, where the classification accuracy is measured in different datasets, compared with the outcome resulting in raw data by listwise deletion. Finally we examine whether the imputation works across different datasets.

Experiments

Experimental setup

Data description

The FoRECAsT dataset is split into six sub-datasets, and the basic information is summarized in Table 1, which contains 1565 records and 87 features. The six subsets are collected from different collaborators all over the world and combined in the regulated formats, e.g., all age data are grouped into a particular feature. As features of interest are not fully aligned, e.g., some features are observed in one track but totally absent in another, which will introduce large missingness in the whole dataset.

Table 1.

Data description for FoRECAsT dataset, the dataset is split into six subsets regarding the sources. Observed feature here implies that the feature has at least one observation within the dataset, and missingness hinges on the observed features

Data track	Instances	Observed features	Categorical	Numerical	Missingness (%)	Label
Track 1	725	19	19	0	8.6	‘Amen_ST12’
Track 2	280	36	36	0	9.1
Track 3	209	34	29	5	10.5
Track 4	154	20	20	0	22.2
Track 5	101	42	40	2	23.6
Track 6	96	47	43	4	18.3
Total	1565	87	76	11	72.5

Among all entries, 37,443 are observed and 98,712 are missing, presenting 72.5% missing of the whole dataset. The main features for mining include personal health status and some cancer-oriented features such as age category, smoking status, alcohol intake, body mass index (BMI) classes, and pregnancy-related status. The according outcome label of interest is the amenorrhoea status after the cancer treatment for 12 months, which are binary indicators, where 0 stands for negative status and 1 stands for positive. The outcome label is abbreviated as ‘Amen_ST12’ and it is totally complete (100% observation rate).

Method

The proposed method consists of two phases, imputation and prediction process. In the imputation procedures, we firstly test six common imputation methods on single data track separately to work out whether prediction can take advantage of filling missing items, and extended imputation experiments are conducted on the whole dataset by applying the different present features, namely ‘cross imputation’, the purpose of the simulation is to investigate the robustness of the imputation techniques and potentially find better correlation between cancer treatment and fertility, by intelligently utilising missing values across different datasets, rather than individual ones. Regarding the prediction procedures, a collection of common supervised learning classifiers are formed and the results of fivefold cross-validation predication accuracy are discussed.

Imputation and classification methods

To investigate the effectiveness of the imputation methods on infertility classification tasks, six notable approaches are adopted, which include mean imputation, random imputation, MICE, EM, KNN and RF imputation. All modules are implemented in Python 3.7 [25] in the operating system Mac OS 10.14.3.

The datasets are a mixture of types, including quantitative and qualitative data where RF imputation generally fits well. Specially for mean imputation, absent numerical data are substituted with mean while categorical cases are replaced with their mode. Random imputation and KNN imputation will fill missing values with possible selections from observed cases. Furthermore, two model-based algorithms, EM and MICE will learn series of classifiers and regressors for categorical data and numerical, respectively.

From the perspectives of prediction procedures, six common supervised learning classifiers are constructed to test the effectiveness of imputation. The classification model include support vector machine (SVM), decision tree (DT), multilayer perceptron (MLP), random forest (RF), logistic regression (LR), Gaussian Naive Bayesian (GNB), and KNN algorithms. We undertook a series of imputation approaches on the six sub-datasets as described, and our benchmarks are the prediction outcomes from the raw data by the listwise deletion. Extended simulations on the entire database (all instances included) using the cross imputation will also be reviewed.

Result and discussion

Imputation on single sub-dataset

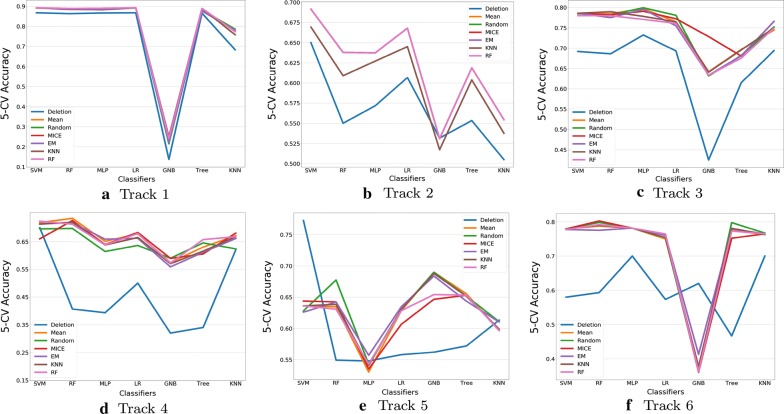
Figure 1 and Table 2 demonstrated the accuracy measured by 7 classifiers and 6 imputation techniques, for six data tracks respectively. The imputation is implemented within the single dataset and missingness of each set is relatively low, missing values are under the assumption of MCAR or MAR.

Fig. 1.

Resutls of prediction (Y axis) by seven classifiers (X axis) in terms of six sub-datasets, the imputation is performed on single sub-dataset

Table 2.

Classification accuracy and its standard deviation in different imputed datasets (upper) and classifiers (lower), the results are averaged by seven classifiers (upper) and six datasets (lower), respectively, using fivefold cross-validation

Accuracy averaged by the results from different classifiers (single dataset)
Data track	Deletion	Mean	Random	MICE	EM	KNN	RF
Track 1	$0.736\pm 0.253$	$\mathbf{0.781}\pm \mathbf{0.0223}$	$0.775\pm 0.224$	$0.781\pm 0.224$	$0.777\pm 0.230$	$0.779\pm 0.221$	$\mathbf{0.781}\pm \mathbf{0.223}$
Track 2	$0.567\pm 0.045$	$\mathbf{0.621}\pm \mathbf{0.055}$	$0.620\pm 0.055$	$0.620\pm 0.055$	$0.620\pm 0.055$	$0.601\pm 0.055$	$0.620\pm 0.055$
Track 3	$0.648\pm 0.095$	$0.745\pm 0.055$	$0.740\pm 0.063$	$0.686\pm 0.155$	$\mathbf{0.747}\pm \mathbf{0.055}$	$0.743\pm 0.054$	$0.741\pm 0.056$
Track 4	$0.469\pm 0.134$	$0.665\pm 0.045$	$0.656\pm 0.055$	$\mathbf{0.669}\pm \mathbf{0.053}$	$0.650\pm 0.045$	$0.655\pm 0.045$	$0.665\pm 0.045$
Track 5	$0.596\pm 0.077$	$0.624\pm 0.045$	$0.614\pm 0.045$	$0.615\pm 0.032$	$\mathbf{0.627}\pm \mathbf{0.045}$	$0.626\pm 0.045$	$0.616\pm 0.033$
Track 6	$0.605\pm 0.077$	$0.716\pm 0.141$	$\mathbf{0.719}\pm \mathbf{0.145}$	$0.714\pm 0.141$	$0.719\pm 0.145$	$0.718\pm 0.137$	$0.716\pm 0.146$

Accuracy averaged by the results from different datasets (single dataset)
Classifier	Deletion	Mean	Random	MICE	EM	KNN	RF
SVM	$0.710\pm 0.091$	$0.750\pm 0.081$	$0.745\pm 0.084$	$0.741\pm 0.087$	$0.745\pm 0.084$	$0.746\pm 0.084$	$\mathbf{0.751}\pm \mathbf{0.081}$
RF	$0.608\pm 0.141$	$0.745\pm 0.089$	$0.741\pm 0.092$	$\mathbf{0.747}\pm \mathbf{0.090}$	$0.738\pm 0.088$	$0.739\pm 0.095$	$0.742\pm 0.089$
MLP	$0.635\pm 0.151$	$\mathbf{0.714}\pm \mathbf{0.120}$	$0.708\pm 0.121$	$0.711\pm 0.117$	$0.701\pm 0.129$	$0.709\pm 0.117$	$0.711\pm 0.124$
LR	$0.633\pm 0.120$	$0.730\pm 0.087$	$0.727\pm 0.091$	$0.731\pm 0.089$	$0.726\pm 0.088$	$0.725\pm 0.091$	$\mathbf{0.731}\pm \mathbf{0.088}$
GNB	$0.433\pm 0.164$	$0.509\pm 0.155$	$0.497\pm 0.154$	$\mathbf{0.519}\pm \mathbf{0.169}$	$0.501\pm 0.155$	$0.507\pm 0.151$	$0.501\pm 0.152$
Tree	$0.569\pm 0.160$	$0.711\pm 0.095$	$0.705\pm 0.098$	$0.710\pm 0.095$	$0.709\pm 0.092$	$0.706\pm 0.100$	$\mathbf{0.712}\pm \mathbf{0.094}$
KNN	$0.636\pm 0.068$	$0.684\pm 0.084$	$0.687\pm 0.089$	$\mathbf{0.691}\pm \mathbf{0.085}$	$0.683\pm 0.093$	$0.679\pm 0.087$	$0.687\pm 0.086$

Highest accuracy and lowest standard deviation are highlighted in bold in each row

From the point view of classifiers, it can be seen that the SVM and RF prediction models achieve the highest accuracy, at approximately 74% in average and the number is almost 24% percentage higher than Naïve Bayesian method (50%). The low accuracy of GNB is due to that input space is categorical and as a result the distribution of most features is not Gaussian. On the other hand, by considering the imputation techniques, the results show a commonly observed pattern that most imputation methods help improve the classification performance, except a few conditions such as GNB result in track 6, MLP result in track 5. It is noticeable that even the elementary mean imputation can improve the performance to some extent and produce competitive results compared to other more complicated approaches, which emphasizes the importance of filling missing values and corresponds to the results from [2]. From the average results of the classifiers, RF and MICE achieved the best performance and RF showed more robustness in prediction.

In conclusion, when data are under MCAR or MAR cases and missingness is comparatively low, imputation is necessary as even the fundamental method can improve the prediction performance. The appropriate combination of imputation and classifier can lead to flexible and outstanding solutions for missing data.

Cross imputation across sub-datasets

In this section, we use a subset of dataset to impute missing values in other subsets and we call it as cross imputation.

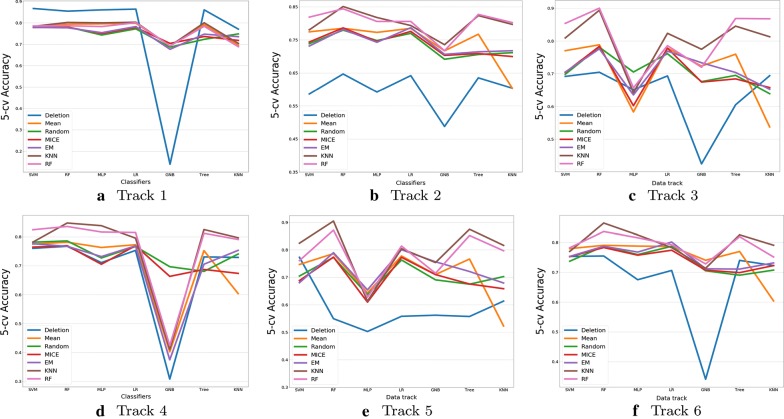
In cross imputation conditions, some present features in one subset may be completely missing in other subsets, the missing information is no longer under MAR or MCAR mechanism as the researcher did not have initials in collecting them. For example, track 1 has 725 records and 19 features are observed, but for the other tracks, features are not fully overlapped with track 1 and some of which may be entirely missing, then we learn a model with present features from track 1 to impute the missing features in the rest of the sub-datasets. As a consequence, this imputation will introduce more uncertainty. Cross imputation provides a possible solution for initialising the missing values under MNAR. We examine whether the imputation techniques can still perform well in the target dataset. The results are portrayed in Figure 2 and Table 3. The differences in deletion results between single and cross imputation are compared.

Fig. 2.

Resutls of prediction (Y axis) by seven classifiers (X axis) in terms of present features from various sub-datasets, the imputation is implemented by present features in different tracks using the entire database

Table 3.

Classification accuracy and its standard deviation in imputed whole dataset utilizing cross imputation with different sub-datasets (upper) and classifiers (lower), the results are averaged by seven classifiers (upper) and six datasets (lower), respectively, using fivefold cross-validation

Accuracy averaged by the results from different classifiers (whole dataset)
Data track	Deletion	Mean	Random	MICE	EM	KNN	RF	Missingness
Track 1	$0.745\pm 0.249$	$0.764\pm 0.045$	$0.748\pm 0.032$	$0.749\pm 0.029$	$0.750\pm 0.034$	$\mathbf{0.769}\pm \mathbf{0.045}$	$0.760\pm 0.044$	27.0
Track 2	$0.599\pm 0.051$	$0.744\pm 0.061$	$0.735\pm 0.031$	$0.738\pm 0.032$	$0.740\pm 0.03$	$0.8\pm 0.034$	$\mathbf{0.803}\pm \mathbf{0.038}$	46.5
Track 3	$0.638\pm 0.093$	$0.706\pm 0.095$	$0.708\pm 0.045$	$0.698\pm 0.06$	$0.711\pm 0.05$	$0.8\pm 0.073$	$\mathbf{0.807}\pm \mathbf{0.084}$	50.2
Track 4	$0.680\pm 0.153$	$0.693\pm 0.132$	$0.740\pm 0.038$	$0.719\pm 0.044$	$0.697\pm 0.133$	$0.757\pm 0.143$	$\mathbf{0.760}\pm \mathbf{0.138}$	46.1
Track 5	$0.588\pm 0.081$	$0.708\pm 0.088$	$0.707\pm 0.044$	$0.698\pm 0.055$	$0.726\pm 0.053$	$\mathbf{0.799}\pm \mathbf{0.088}$	$0.777\pm 0.078$	65.7
Track 6	$0.670\pm 0.137$	$0.751\pm 0.062$	$0.739\pm 0.037$	$0.742\pm 0.03$	$0.752\pm 0.033$	$\mathbf{0.796}\pm \mathbf{0.045}$	$0.789\pm 0.036$	48.2

Accuracy averaged by the results from different datasets (whole dataset)
Classifier	Deletion	Mean	Random	MICE	EM	KNN	RF
SVM	$0.739\pm 0.085$	$0.772\pm 0.012$	$0.740\pm 0.033$	$0.738\pm 0.032$	$0.738\pm 0.036$	$0.792\pm 0.019$	$\mathbf{0.804}\pm \mathbf{0.031}$
RF	$0.713\pm 0.097$	$0.788\pm 0.004$	$0.781\pm 0.005$	$0.779\pm 0.006$	$0.78\pm 0.007$	$\mathbf{0.861}\pm \mathbf{0.034}$	$0.846\pm 0.035$
MLP	$0.665\pm 0.110$	$0.724\pm 0.081$	$0.720\pm 0.041$	$0.695\pm 0.065$	$0.714\pm 0.051$	$\mathbf{0.756}\pm \mathbf{0.092}$	$0.751\pm 0.078$
LR	$0.703\pm 0.094$	$0.783\pm 0.008$	$0.770\pm 0.009$	$0.775\pm 0.003$	$0.785\pm 0.013$	$0.800\pm 0.012$	$\mathbf{0.802}\pm \mathbf{0.011}$
GNB	$0.377\pm 0.136$	$0.664\pm 0.118$	$0.691\pm 0.009$	$\mathbf{0.694}\pm \mathbf{0.018}$	$0.660\pm 0.130$	$0.680\pm 0.123$	$0.666\pm 0.109$
Tree	$0.688\pm 0.101$	$0.768\pm 0.012$	$0.695\pm 0.016$	$0.699\pm 0.02$	$0.717\pm 0.015$	$\mathbf{0.832}\pm \mathbf{0.023}$	$0.827\pm 0.027$
KNN	$0.689\pm 0.061$	$0.595\pm 0.056$	$0.708\pm 0.035$	$0.688\pm 0.027$	$0.712\pm 0.035$	$\mathbf{0.786}\pm \mathbf{0.038}$	$0.783\pm 0.054$

Highest accuracy and lowest standard deviation are highlighted in bold in each row

Similarly, imputation improves classification performance in most cases. In large scale imputation, missing mechanism is different and more data are absent, mean imputation is no longer as effective as some machine learning methods such as KNN and RF, which gained significant advantages and robustness in our experiments, as highlighted in Table 2. We also compared Table 2 with Table 3 and found out that cross imputation can even outperform single imputation, for example, in averaged results from different classifiers, cross imputation accuracy using RF (76–80.7%) is significantly higher than that of single imputation(62–78.1%). This also happens in KNN, mean, and random imputation techniques, indicating that though cross imputation introduces more uncertainty and complexity into analysis, utilization of full dataset with latent relationships between similar sub-datasets can have a better prediction performance. We can also conclude that for the datasets of mixed types, e.g., containing both numerical and categorical features, RF method can handle the missing values well in both single and cross imputation.

Conclusion

According to our analysis, results from various classifier with single imputation were similar, despite that results from Naïve Bayesian is much less precise. Compared with the listwise deletion, even simple mean imputation can achieve good results. The outcome also suggests that in general RF and MICE are likely to be the best approaches within a small scale database. When the scale enlarges and more uncertainty is introduced, the results indicate that mean imputation is no longer as efficient as machine learning based imputation such as RF and KNN, which are probably the best choices with the least standard deviation. Overall, most of the imputation techniques show strong robustness and high efficiency in cross-dataset imputation with regard to high missingness, even outperform than single imputation cases.

Funding

This work is fully funded by Melbourne Research Scholarships (MRS), Grant No. 385545 and partially supported by Fertility After Cancer Predictor (FoRECAsT) Study. Michelle Peate is currently supported by an MDHS Fellowship, University of Melbourne. The FoRECAsT study is supported by the FoRECAsT consortium and Victorian Government through a Victorian Cancer Agency (Early Career Seed Grant) awarded to Michelle Peate.