Skip to main content
NCBI home page
F1000Research logoLink to F1000Research
. 2019 May 9;8:646. [Version 1] doi: 10.12688/f1000research.19029.1

Network-based Observability and Controllability Analysis of Dynamical Systems: the NOCAD toolbox

Dániel Leitold 1,2, Ágnes Vathy-Fogarassy 1,2, János Abonyi 2,a
PMCID: PMC6777013  PMID: 31608146

Abstract

Network science has become increasingly important in life science over the last decade. The proposed Octave and MATLAB-compatible NOCAD toolbox provides a set of methods which enables the structural controllability and observability analysis of dynamical systems. In this paper, the functionality of the toolbox is presented, and the implemented functions demonstrated.

Keywords: Dynamical systems, Complex networks, Controllability and observability analysis, Robustness, MATLAB toolbox

Introduction

In the life sciences, the determination of driver nodes in networks that play a significant role in the emergence or treatment of diseases is an intensively researched field 1. In large-scale human liver metabolic networks (HLMN), the driver metabolites have essential functions, and the role of transport reactions and extracellular metabolites in terms of controlling HLMN has revealed the importance of the environment of human liver metabolism with regard to the health of the liver 2.

In terms of controlling the human signalling network, the role of different proteins was also systematically analysed with the toolset of network controlability in 3 to highlight the role of cancer-associated genes. Target control with objective-guided optimisation (TCO) was introduced to control a set of variables (or targets) of interest while the quantity of drivers and constrained nodes were minimised and maximised, respectively. This method is capable of determining the leading phenotype transitions in biological networks that can be identified as drug targets 4. Using statistical analysis, a subset of critical control nonprotein-coding RNAs (ncRNAs) enriched by human disease can also be determined 5. In intra-cellular networks, to understand the information flow, a natural control system was utilised and the robustness of such a control was analysed 6. The importance of determining the proper driver nodes in biological networks, or more generally in any dynamical system, is unequivocal, and the amount of research concerning network science has increased rapidly. A detailed study about the control principles in biological networks has already been published 7. The network science-based analysis of dynamical systems has spread rapidly as it provides simple and efficient tools to analyse the structural controllability of any linear or linearised system 1.

Although considerable research has utilised the method 8, a flexible software tool which may be used to support the research in this field has yet to be designed. Parallel research has resulted in a collection of applications, toolboxes, plug-ins and scripts that analyse and determine several structural properties of genes, protein-protein interaction or even social or urban networks. Most of these applications only analyse the structural properties of static networks and just a handful of them utilise these structural properties to draw conclusions concerning the dynamics of the system investigated. As our toolbox belongs to the second group, in the following section, the available applications and programs of this group are elaborated.

A brief summary of the available tools with expanded functionalities is given in Table 1. Applications or software packages implemented in Python and capable of analysing the controllability and observability of dynamical systems are: graph-control 9 and WDNfinder 10. The advantage of Python-based development lies in its widespread use and the countless methods and packages implemented in this language, including the tools developed for network analysis 11. Although in Python the focus is on developing a broad software package for complex system analysis, this has yet to be fulfilled and all of the available solutions have limitations. The graph-control toolbox only analyses the impact of network topology on the number of inputs and implements the fast matching algorithm 12. Even though WDNFinder only determines the minimum driver node set (MDS) and classifies nodes based on MDS, it is incapable of facilitating extended analysis.

Table 1. Toolboxes that implement some functions for dynamical analysis of complex systems based on their structural analysis.

Software Language Applied on GUI Ref. Last updated
netctrl C++ General networks No 16 January 8, 2015
CONTEST MATLAB General networks No 17 February, 2009
CytoCtrlAnalyser Java Biomolecular networks Yes 13 May 25, 2017
graph-control Python General networks No 9 December 16, 2015
WDNfinder Python Biological networks No 10 June 24, 2018
enaR R Ecological networks No 15 May 18, 2018
Open in a new tab

Additionally, the CytoCtrlAnalyser 13 plug-in for Cytoscape 14 has been developed, which was implemented in Java and offers graphical interfaces for users as well. It evaluates control centrality, control capacity and classifies nodes for biomolecular networks. Furthermore, the Ecological Network Analysis with R software package (enaR) provides some dynamical analysis functions and can generate models to analyse ecological networks in the R environment 15. As can be seen, both software packages deal with special kinds of networks. The netctrl program can determine the driver nodes and switchboard dynamics model for any complex network 16. CONTEST is a MATLAB toolbox which can analyse the dynamics of complex systems, but these dynamics do not cover the structural controllability and observability properties 17 of the analysed system. Although the presented software packages ensure the design of a controllable and observable system, they do not provide the opportunity to analyse the designed system exhaustively. These functions are helpful in terms of supporting the work of experts, but are insufficient for the sophisticated analysis of systems.

The contribution of this paper is to provide a novel toolbox, NOCAD 18, for the comprehensive analysis of linear or linearised dynamical systems based on the approach of network science. In the following section, the implemented functions and measurements are presented through examples of their application.

Methods

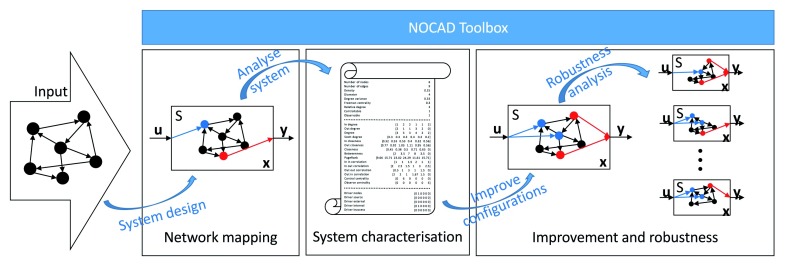
With the help of the presented Ocatave- and MATLAB-compatible toolbox, experts can create, analyse and improve any type of dynamical systems. As the structure of the dynamical systems is generally represented by their adjacency matrix and linear dynamical systems can be described by the state-space model that contains the state-transition, input, output and feedthrough matrices, the Octave/MATLAB programming language is a perfect environment to handle these matrices and provide comprehensive functionalities based on them. With the use of NOCAD 18, experts and researchers can effectively determine the input and output matrices of state-space models, calculate system-specific qualitative measurements (e.g. diameter, relative degree, control centrality and robustness of the system, etc.) and improve the system to satisfy the relative degree-based requirements. The workflow of the toolbox can be seen in Figure 1.

Figure 1. Workflow of the utilisation of the NOCAD toolbox.

Figure 1.

Open in a new tab

The network mapping module provides two methods to create a dynamical system based on the topology of the state variables. The system characterisation module generates more than 49 measures to analyse, classify and characterise the developed system. The improvement and robustness module offers five algorithms to improve the system with additional inputs (observers) as well as outputs (controllers), and can analyse the robustness of the designed system.

The functions of the toolbox can be performed step-by-step given its modular structure. Each module has a specific task and one function from each module calls the others. A system can be analysed by calling the main functions from the modules. The advantage of this structure is its modularity as each module can be expanded easily and further modules also implemented in a simple way. A list of their functions and dependencies on each other is presented in the manual.

Implementation

According to the aforementioned approach, the implemented functions of the toolbox were divided into three modules as follows: (1) network mapping module, (2) system characterisation module and (3) improvements and robustness module.

The network mapping module creates a dynamical system from a given network structure, i.e. the necessary matrices of the state-space model are generated for the topology in such a way, that the created system is structurally controllable and structurally observable. The determination of the input and output matrices can be achieved by the path finding and signal sharing methods 19, which modify the result of the maximum matching algorithm.

The system characterisation module performs the calculation of 49 numerical measures to qualify the dynamical system based on its structure. The implemented measures, on the one hand, are well-known static measures (e.g. the number of nodes and edges, closeness and betweenness centralities), and, on the other hand, measures that characterise the dynamics of the system (e.g. structural controllability, observability, control centrality and relative degree). This module can also be used for the purpose of simple network analysis.

The improvement and robustness module integrates two main functions. On the one hand, it enables the input and output configurations of the system to be extended in such a way that the relative degree of the modified system does not exceed the initially defined threshold. For this purpose, this module implements five methods, namely the set covering-based grassroot and retrofit methods 20, the centrality measures-based method 20, the modified Clustering Large Applications based on Simulated Annealing algorithm (mCLASA), and the Geodesic Distance-based Fuzzy c-Medoid Clustering with Simulated Annealing algorithm (GDFCMSA) 20, 21. On the other hand, this module allows users to examine the robustness of the extended configurations by removing nodes from the network representation and by checking the structural controllability and structural observability of the damaged system.

The implemented methods are introduced in detail in the cited articles and the manual of the NOCAD toolbox.

Operation

In order to use the NOCAD toolbox 18, installation of Octave or MATLAB is required. Then the directories of the toolbox must be copied into the working directory, or the directories of the toolbox must be added to the paths. The functions were implemented in Octave 5.1.0 and MATLAB R2016a on a Windows 64-bit system. On other operating systems, or with other Octave or MATLAB versions, proper operation is not guaranteed. Our toolbox is independent of other MathWorks toolboxes, it uses only the octave-networks-toolbox 22 and the greedy set covering implementation 23.

Use cases

In this section, the main functionalities of the NOCAD toolbox 18 presented through examples of use cases. Although many biological networks are available from public databases, due to their complex nature, they are unsuitable for such a simple illustration. Therefore, the services of the NOCAD toolbox are presented on simple artificial networks.

The first step in each workflow is to create a state-space model from the adjacency matrix that presents the structural description of the system. This can be achieved by the use of path finding and signal sharing methods implemented in the first module. Both methods are modified versions of the maximum matching algorithm. An example of the application of the path finding method for the creation of a state-space model from the adjacency matrix ( A) is shown in Figure 2. In this figure, B denotes the resulting input matrix, C the output matrix, while D stands for representing the direct feedthrough.

Figure 2. An example network with determined input (blue) and output (red) configurations according to the path finding method.

Figure 2.

Open in a new tab

The network represents the A state transition matrix. B denotes the input matrix in which the places of the nonzero elements are determined by the controller node allocation algorithm. Similarly, the C output matrix is defined with the observability analysis of the network of the state variables. The D matrix of the direct feedthrough contains only zeros.

As the configuration above is not complex enough to demonstrate the functions of the second module, a more complex configuration of the input and output nodes is used. The sample input and output configurations can be seen in Figure 3, where the input and the output nodes are denoted by blue and red, respectively.

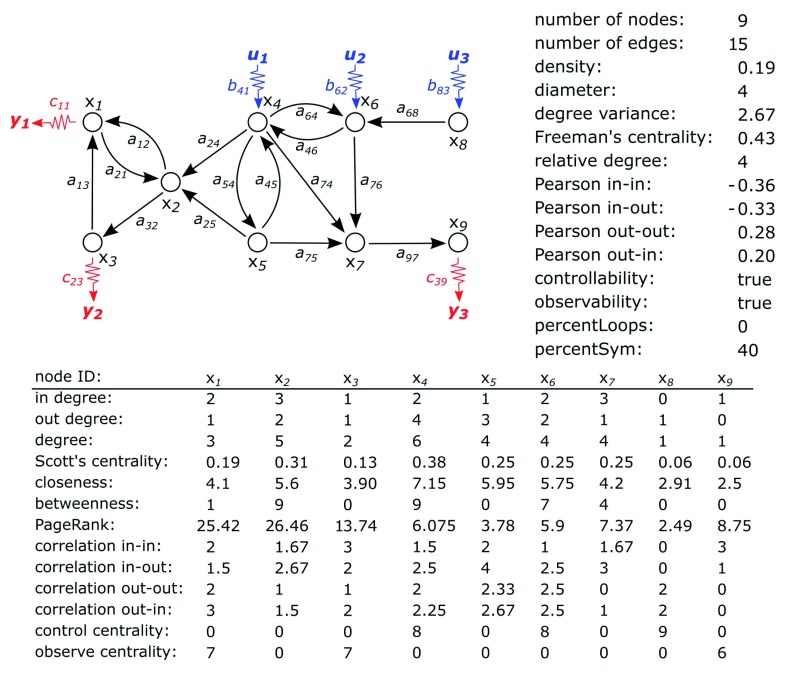
Figure 3. The complex configuration of the input and output nodes used for the demonstration of the system characterisation module of the NOCAD toolbox.

Figure 3.

Open in a new tab

The system presented in Figure 3 consists of 9 state variables and 15 directed connections between them. Quality measures calculated by the System characterisation module of the NOCAD toolbox can be seen in Figure 4, Figure 5, and Figure 6.

Figure 4. The example network with system and node centrality measures.

Figure 4.

Open in a new tab

Figure 5. Measures of node clustering and the representation of the topology of the network.

Figure 5.

Open in a new tab

Figure 6. Calculated edge centrality measures for the given topology.

Figure 6.

Open in a new tab

In Figure 4, measures qualifying the whole system with one value are presented. The density shows that the number of edges is almost a fifth of the possible maximum, and the diameter of the system (i.e. the longest shortest path in the network that presents its structure) is 4. The degree variance is 2.67, while the Freeman’s centrality is 0.43. The relative degree of the system is also 4. The Pearson coefficient shows that the in-in and in-out correlations are assortative in nature, while out-out and out-in correlations are likely to be disassortative. The system is controllable and observable. As no loop is present in the network, the percentage of loops relative to edges is 0%. As there are 6 edges that have symmetric edge pairs and the number of connections is 15, the percentage of the symmetric edge pairs relative to the edges is 40%.

Node centrality measures assigned to the state variables of the system are also presented in Figure 4. One of the most important values is the highest degree of the nodes, which belongs to state variable x 4. As Scott’s centrality is a normalised degree, the most important node is once again x 4. The closeness of node x i is calculated as the ratio of the number of nodes reachable from x i to the sum of their distances from x i. The higher value indicates the more central position of the node, and, once again, node x 4 is the most central element. The betweenness centrality shows how many shortest paths intercept the given node. If a node has a high value, then it is a critical node in the structure. The highest value belongs to nodes x 2 and x 4. The PageRank assigns a percentage value for each node, based on their centrality roles if Markov-chains are modelled. The measure referred to as correlation shows the proportion of the number of edges of neighbours’ and the number of neighbours. This information is useful when determining the assortativity of the system. The control centrality and observe centrality measures determine how many state variables can be influenced or observed by the nodes.

In Figure 5, the first vectors (referred to as driver and sensor nodes) show the driver and sensor nodes as logical vectors. The following four vectors classify these nodes as source, external, internal and inaccessible driver and sensor nodes. These types of nodes are introduced in 24 in detail. In the next section of the figure, the controlling and observing matrices are presented. Generally, these matrices are sparse matrices, as only the columns of drivers and sensors contain nonzero values. In Figure 5, we converted them into row vectors for their appropriate visualisation. The values show the number of derivations necessary to influence or observe a state variable in the system. Next, the similarity of the driver and sensor nodes is presented. The similarity of driver nodes x 4 and x 6 is 0.81. In this case, the reason why it is less than 1 is that although they control the same set of nodes, the numbers of derivations that influence them are different. In terms of sensor similarity, sensor nodes x 2 and x 3 observe the same set of nodes and they do this almost simultaneously, so their similarity is 0.91. R and R are the simple reachability matrices. They show which nodes can be controlled or observed by a given node. In R , the i th column shows which nodes can control node i. From the other viewpoint, elements in row i highlight those nodes which can be controlled by node i. In this example, node x 8 can influence every node, but it does not guarantee structural controllability. The R matrix can be interpreted analogously with regard to observability.

Finally, measures of edge centrality are seen in Figure 6. The betweenness has the same meaning as in the case of nodes, that is, it yields the number of shortest paths that intercept the edge 25. From this perspective, the most critical edge is the edge a 46 with a value of 10. The endpoint similarity shows how similar the influenced and observed sets of the state variables with regard to the endpoints of edges are. This metric has a high value if the edge is part of a cycle or creates a bridge in the network. As no bridges are present in this network, only cycles can be recognised by this measure. The edge similarity shows how similar the roles of edges are, and it allows redundancies, to be located. In the topology presented, nodes x 1, x 2 and x 3, or nodes x 4, x 5, x 6 and x 7 also create parts of the network that possess redundancy.

For the demonstration of the last module, configurations provided by the first module are used again ( Figure 2). Results provided by this module can be seen in Figure 7. In this case, five methods were applied to the system to extend the configuration as follows: the required relative degree was set at 2, while the alpha parameter of the cost function was set at 0.5 21. Results show that all the methods determine the same set of driver nodes for the system, that is, they are sufficient to influence state variables x 4 and x 8. The resultant cost is 1.5556, the relative degree is 2 which satisfies the requirements, and the mean of the relative degrees is 1.1111. In this configuration, six different nodes can be identified which can be damaged separately and the system remains controllable. This is expressed by the value of robustness (66.6%). The most important nodes in terms of controllability are x 2, x 4 and x 7. In the case of observability, methods yield different solutions with the exception of the centrality measures-based and mCLASA algorithms which provide the best configuration in this case. Although the cost as well as the maximum and mean of the relative degree were identical in the case of retrofit set covering-based and GDFCMSA methods as well, the robustness analysis of these configurations exhibits a higher degree of vulnerability.

Figure 7. Improvement and robustness analysis of the system.

Figure 7.

Open in a new tab

Conclusions

In this article the Octave- and MATLAB-compatible NOCAD toolbox 18 was proposed to support the network-based controllability and observability analysis of dynamical systems. The toolbox offers two methods to design a structurally controllable and observable system based on the state-transition matrix. The designed system can be analysed by 49 qualitative measures both from structural and dynamical points of view. The toolbox serves five methods to improve the designed system by adding new inputs and outputs to it, thus, its relative degree can be decreased. Then the robustness of the individual designs can also be evaluated. The modular structure of the toolbox supports the facile improvement of the modules by adding new functions and the toolbox can be extended by new modules as well. Even though the modules are built on each other, most of their functions can also be used independently from each other.

Although our goal in this paper is to draw the attention of researchers of life sciences to the services provided by the NOCAD toolbox, it can be utilised in practice in various fields of sciences as well, for example, it enables social networks to be controlled in the economy, transaction networks to be analysed in finance or dynamical systems to be designed in engineering.

Data availability

All data underlying the results are available as part of the article and no additional source data are required.

Software availability

Source code available from: https://github.com/abonyilab/NOCAD.

Archived source code at time of publication: https://doi.org/10.5281/zenodo.2656674 18

License: GNU General Public License v3.0

Author contributions

Dániel Leitold reviewed the literature on network science, developed the algorithms, implemented the Octave and MATLAB functions, designed as well as performed the experiments, and wrote the related sections. Ágnes Vathy-Fogarassy participated in the formalisation of the methodology. János Abonyi developed the algorithms, implemented the Octave and MATLAB functions and proofread the paper.

Funding Statement

This research was supported by the National Research, Development and Innovation Office NKFIH, through the project OTKA-116674 (Process mining and deep learning in the natural sciences and process development) and the EFOP-3.6.1- 16-2016- 00015 Smart Specialization Strategy (S3) Comprehensive Institutional Development Program. Dániel Leitold was supported by the ÚNKP-18-3 New National Excellence Program of the Ministry of Human Capacities.

The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

[version 1; peer review: 2 approved with reservations]

References

  • 1. Liu YY, Slotine JJ, Barabási AL: Controllability of complex networks. Nature. 2011;473(7346):167–73. 10.1038/nature10011 [DOI] [PubMed] [Google Scholar]
  • 2. Liu X, Pan L: Detection of driver metabolites in the human liver metabolic network using structural controllability analysis. BMC Syst Biol. 2014;8(1):51. 10.1186/1752-0509-8-51 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3. Liu X, Pan L: Identifying driver nodes in the human signaling network using structural controllability analysis. IEEE/ACM Trans Comput Biol Bioinform. 2015;12(2):467–72. 10.1109/TCBB.2014.2360396 [DOI] [PubMed] [Google Scholar]
  • 4. Guo WF, Zhang SW, Shi QQ, et al. : A novel algorithm for finding optimal driver nodes to target control complex networks and its applications for drug targets identification. BMC Genomics. 2018;19(Suppl 1):924. 10.1186/s12864-017-4332-z [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5. Nacher JC, Akutsu T: Controllability methods for identifying associations between critical control ncrnas and human diseases. Methods Mol Biol.In Computational Biology of Non-Coding RNA.2019;1912:289–300. 10.1007/978-1-4939-8982-9_11 [DOI] [PubMed] [Google Scholar]
  • 6. Ravindran V, Nacher JC, Akutsu T, et al. : Network controllability analysis of intracellular signalling reveals viruses are actively controlling molecular systems. Sci Rep. 2019;9(1): 2066. 10.1038/s41598-018-38224-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7. Li M, Gao H, Wang J, et al. : Control principles for complex biological networks. Brief Bioinform. 2018. 10.1093/bib/bby088 [DOI] [PubMed] [Google Scholar]
  • 8. Liu YY, Barabási AL: Control principles of complex systems. Rev Mod Phys. 2016;88(3): 035006. 10.1103/RevModPhys.88.035006 [DOI] [Google Scholar]
  • 9. Chaturvedi V: Controllability of networks. Reference Source [Google Scholar]
  • 10. Chu Y, Wang Z, Wang R, et al. : Wdnfinder: A method for minimum driver node set detection and analysis in directed and weighted biological network. J Bioinform Comput Biol. 2017;15(5):1750021. 10.1142/S0219720017500214 [DOI] [PubMed] [Google Scholar]
  • 11. Zinoviev D: Recognize-Construct-Visualize-Analyze-Interpret. Pragmatic Bookshelf.2018. Reference Source [Google Scholar]
  • 12. Faradonbeh MKS, Tewari A, Michailidis G: Optimality of fast-matching algorithms for random networks with applications to structural controllability. IEEE Trans Control Netw Syst. 2017;4(4):770–780. 10.1109/TCNS.2016.2553366 [DOI] [Google Scholar]
  • 13. Wu L, Li M, Wang J, et al. : Cytoctrlanalyser: a cytoscape app for biomolecular network controllability analysis. Bioinformatics. 2018;34(8):1428–1430. 10.1093/bioinformatics/btx764 [DOI] [PubMed] [Google Scholar]
  • 14. Shannon P, Markiel A, Ozier O, et al. : Cytoscape: a software environment for integrated models of biomolecular interaction networks. Genome Res. 2003;13(11):2498–504. 10.1101/gr.1239303 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15. Borrett SR, Lau MK: enaR: an R package for ecosystem network analysis. Methods Ecol Evol. 2014;5(11):1206–1213. 10.1111/2041-210X.12282 [DOI] [Google Scholar]
  • 16. Nepusz T, Vicsek T: Controlling edge dynamics in complex networks. Nat Phys. 2012;8(7):568–573. 10.1038/nphys2327 [DOI] [Google Scholar]
  • 17. Taylor A, Higham DJ: Contest: A controllable test matrix toolbox for matlab. ACM Trans Math Softw. 2009;35(4):26 10.1145/1462173.1462175 [DOI] [Google Scholar]
  • 18. Abonyi J: abonyilab/nocad v2.0.2019. 10.5281/zenodo.2656674 [DOI] [Google Scholar]
  • 19. Leitold D, Vathy-Fogarassy Á, Abonyi J: Controllability and observability in complex networks–the effect of connection types. Sci Rep. 2017;7(1): 151. 10.1038/s41598-017-00160-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20. Leitold D, Vathy-Fogarassy Á, Abonyi J: Evaluation of the complexity, controllability and observability of heat exchanger networks based on structural analysis of network representations. Energies. 2019;12(3):513 10.3390/en12030513 [DOI] [Google Scholar]
  • 21. Leitold D, Vathy-Fogarassy A, Abonyi J: Network distance-based simulated annealing and fuzzy clustering for sensor placement ensuring observability and minimal relative degree. Sensors (Basel). 2018;18(9): pii: E3096. 10.3390/s18093096 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22. Bounova G: Octave networks toolbox.2015. Reference Source [Google Scholar]
  • 23. Gori F, Folino G, Jetten MS, et al. : MTR: taxonomic annotation of short metagenomic reads using clustering at multiple taxonomic ranks. Bioinformatics. 2011;27(2):196–203. 10.1093/bioinformatics/btq649 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24. Ruths J, Ruths D: Control profiles of complex networks. Science. 2014;343(6177):1373–1376. 10.1126/science.1242063 [DOI] [PubMed] [Google Scholar]
  • 25. Freeman LC: A set of measures of centrality based on betweenness. Sociometry. 1977;40(1):35–41. 10.2307/3033543 [DOI] [Google Scholar]
F1000Res. 2019 Jun 25. doi: 10.5256/f1000research.20856.r48912

Reviewer response for version 1

Luis A Aguirre 2, Arthur Montanari 1, Ercílio Moreira 1

In this paper the authors describe the NOCAD toolbox developed for the analysis of some aspects of networks as, for instance, structural controllability and observability. The topic of the paper is not only very interesting but also timely as issues relating to controllability and observability of networks could be fundamental in a number of practical situations. Hence to have a nice set of tools to analyze dynamical networks is welcome.

The toolbox described is useful in a specific range of problems. Here we focus on the controllability and observability properties of networks, as prompted by the title. The tools presented focus on structural controllability and observability of linear systems. The assumption of linearity is not mentioned in the abstract. As a matter of fact, the opening phrase of the last paragraph in the introduction should be copied to the abstract.

The nonlinear case and other definitions of controllability and observability, such as, dynamical and symbolical are not mentioned in the paper nor are handled by the toolbox. This is an important remark as it is now known that some algorithms underestimate the cardinality of the set of sensor nodes when applied to nonlinear systems.

The paper

In the second paragraph of the Introduction, the authors mention the importance of “determining the proper driver nodes”. We wonder if the average reader would know what that is. In clarifying this point the authors would like to address first what is “a” proper set of driving nodes (e.g. one that will guarantee full controllability). However, in order to specify “the” proper set, possibly some more detailed measure of controllability should be employed. For instance, suppose two sets of driving nodes S1 and S2, both with the same cardinality, such that the network is fully controllable either from S1 or from S2. Hence S1 is “a” proper set of driving nodes (assuming that by proper the authors are referring to full controllability) and S2 is another one. Now, it could well be that using S1 less energy is required to drive the network from one state x(ti) to another x(tf) when compared to S2. In that case, S1 and S2 are not totally equivalent. Structural controllability and observability are unable on their own to provide this distinction. 

Following the same vein, we wonder if the average reader of F1000Research would know the distinction of static and dynamic networks. A word about this would be profitable, especially because the toolbox refers mainly to the second class.

In some parts of the paper the authors refer to matrix A as the “state transition” matrix. In continuous-time this is incorrect. In discrete-time this is only correct for a transition time of one sampling period. Matrix A is called the “dynamical matrix”. State transition matrix is something else.

Relevance to the journal

The MS introduction is written in such a way that it instigates interest from the target audience of this journal (mathematical biology). However, the techniques implemented in the toolboxes are usually found around the network science community, which includes several other fields that range from power systems to social networks. To show more coherence to this journal, the authors should provide some example of application on a “real-world network” under a biological context. This is also interesting to show how the results provided by the toolbox can be useful to draw conclusions under a practical context other than a “toy problem” as presented.

Background

The MS content is not sufficient to understand the techniques implemented in the toolbox. We know that the paper does not aim at providing extensive background, but some could be helpful. A reader coming from a control theory background might expect the toolbox to provide results based on Kalman’s definition of controllability and observability. However, the toolbox is based on Liu and coworker’s maximum matching algorithm which is based, in turn, on Lin’s structural definition (1974) (which is not even mentioned in the MS). Which definition of controllability and observability the toolbox is based on should be crystal clear in the main text and abstract. Moreover, the notions of structural controllability and observability should be presented to the reader and how they interplay with the more well-known notion in Kalman’s sense (e.g. Lin’s definition is only a necessary condition for Kalman’s definition).

Although we think that the definitions of controllability and observability should be mentioned on the main text, the authors provide some background on the implemented maximum matching algorithms in the toolbox. This, however, should be mentioned explicitly in the MS.

Examples

The paper furnishes examples to illustrate some of the features of the new toolbox. The network topology is the same in each example, which facilitates understanding and comparison. In some cases, more discussion would be welcome. For instance, in the last example (Figure 7) not all the indices are clearly defined to the user, for instance the critical nodes are given as x2, x4 and x7. From the context it seems that if any of these nodes is lost, the network would become uncontrollable, but this is not directly stated.

In referring to Figure 5 the authors speak in terms of Reachability matrices: Rc and Ro. It is clear from Figure 5 that Rc shows which nodes have a path to node i (the ith column). As for Ro, it seems that we should look row-wise instead of column-wise, is that right? Anyhow, we do not think it is adequate to say that Rc shows which nodes can be controlled from another one. The word “control” is perhaps too general. We would suggest just to say that Rc shows which nodes can be reached from another one.

Toolbox

The toolbox is subdivided in three modules. The first one, “network mapping module”, implements the maximum matching algorithm (and related modifications) to return a structurally controllable (observable) network with the smallest set of driver (sensor) nodes. This is a welcome feature, especially for a MATLAB environment, which we are unaware of any alternative.

The second module, “system characterization module”, provides several graph measures that are available on other MATLAB-based toolboxes, but are indeed useful to assess the network controllability and observability properties of a system. Thus, its presence is justifiable.

The third module, “improvements and robustness module”, is a set of functions which specifically implement previous results of the authors (e.g. Refs. 20 1, 21 2). It seems quite specific, but nevertheless the toolbox relevance is justifiable in great part for its module one.

The toolbox seems fast and no bugs were found in its implementations as far as the MATLAB environment is concerned. See further comments on some compatibility issues when using Octave.

The target audience of the toolbox

The toolbox is applicable to any kind of network (graph), be it directed or undirected, weighted or unweighted, and so on. However, although general, the authors should discuss in the MS what are the kinds of networks where a structural analysis of controllability and observability are more useful. For instance, a linearization of a power system model modelled by interconnected Kuramoto oscillators yield a dynamical matrix “A” whose corresponding adjacency graph is not only highly connected but also undirected. Consequently, the toolbox points out that only one driver node is needed to structurally control the network, independently of its size “n”(which is true in this case according to Lin’s definition). However, this does not give insight to the problem since basically any node can be chosen as a driver node, and only one node being sufficient seems quite unrealistic. The question is: For what kind of networks is the structural approach more interesting (and hence the toolbox)? It could be that the toolbox could be extra-helpful in the context of more sparse and directed networks (with higher hierarchy).

Some nitpicking:

Sometimes it is not clear whether the authors refer to the dynamical matrix “A” or the adjacency matrix “A^T”. We recommend that different nomenclatures be used, such as “A” for the dynamical matrix and “A_{Adj}” for the adjacency matrix. This should be changed in the MS and manual.

Regarding the installation of the NOCAD toolbox. We noticed that the NOCAD already comes with a “octave-network-toolbox” folder which does not have all the necessary functions to use Module 2. Thus, we had to download the “octave-network-toolbox-master” folder in Ref. 22 to have access to all needed functions. Is this necessary or is the NOCAD toolbox really missing some functions?

Some statements in Section “Use Cases”, Paragraph 5, are redundant with the information already present in Fig. 4. Instead of repeating the same information, it might be more interesting to make some comments on how useful some of these network measures can be to design better and more robust networks from a control and observation point-of-view.

There are some issues in the Octave version of this toolbox. For instance, function “heatmaps” has some bugs in Octave but works well in MATLAB. This happens because the function “colormap” from Octave accepts the argument “hot” but not “Hot”. The authors should do a careful review of the Octave toolbox and check for further compatibility issues.

We confirm that we have read this submission and believe that we have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however we have significant reservations, as outlined above.

References

  • 1. : Evaluation of the Complexity, Controllability and Observability of Heat Exchanger Networks Based on Structural Analysis of Network Representations. Energies.2019;12(3) : 10.3390/en12030513 10.3390/en12030513 [DOI] [Google Scholar]
  • 2. : Network Distance-Based Simulated Annealing and Fuzzy Clustering for Sensor Placement Ensuring Observability and Minimal Relative Degree. Sensors (Basel).2018;18(9) : 10.3390/s18093096 10.3390/s18093096 [DOI] [PMC free article] [PubMed] [Google Scholar]
F1000Res. 2019 May 28. doi: 10.5256/f1000research.20856.r48269

Reviewer response for version 1

Gilles Didier 1

This software tool article presents the Octave/MATLAB toolbox "NOCAD" for networks analysis. NOCAD implements various standard measures on networks and their nodes (density, betweenness, centrality...). Its main novelty stands in the ``dynamical-systems-based'' tools to analyse (static) networks that it provides. This article can be seen as a companion paper of the reference 19 1 from the same authors (It could be stated somewhere in the text).

The ideas implemented in the toolbox are interesting, but I feel that their presentation has to be improved. First, I suggest you get your text proof-read by a native speaker. Second, many concepts used in the manuscript should be at least briefly recalled. Third, the article lacks a detailed description of the input (in the general sense, including user interaction) of the toolbox. The basic input seems to be the incidence matrix of a directed network but, if I well understood, the toolbox allows to set input and output nodes and has network design capabilities.

Another major concern is that though one of the aims of the article is to draw attention of life science researchers, it does not present clearly how the toolbox can be used on biological networks and on which kind of biological networks it can be applied. Real biological examples should be actually more than welcome in the "Use cases" section, which contains only toy examples. Without such examples, I am afraid that the article fails to draw attention of its expected audience. In particular, I am wondering in what extent the toolbox can be used on standard biological datasets, e.g., PPI networks can have thousands vertices.

Please find below some detailed comments:

Abstract

The abstract has to be extended in order to give a better idea of the content of the article.

Introduction

The introduction does not reflect well what follows and the topic of the paper. You should start by briefly introducing the general ideas of dynamical analysis of networks, precise in what sense you use the term "driver node", which is sometimes used in a biological context etc. First mention of dynamical system comes at the end of the second paragraph and could be developed (e.g. by briefly recalling ideas of [7] 2) while biological examples may not need to be as much detailed.

The description of previous software sounds good. It may take place a dedicated section.

Method

The method section should recall the notions of controllability and observability and the general principles of ``dynamical analysis'' (it can be brief, something like the two first subsections of the section "Results" of [19] 1). In the current version, I don't think that this part can be understood without reading your reference [19] 1.

You should state explicitly which are the inputs of your toolbox, the accepted formats etc.

I found the paragraph about the modularity of the toolbox is not very useful. It could be shortened or even discarded.

Subsection "Operation" ("Installation"?) is OK.

Use cases

If I well understood, the input is the incidence matrix A from which are computed the matrices B, C and D as illustrated with the first example. It should be interesting to apply the approach on a biological network, for instance a protein-protein interaction network or a regulatory network, in order to illustrate the interest of the results obtained in this context.

In the second example (Figure 3), input and output nodes seem to be set arbitrarily in order to get a system complex-enough to show the function of the second module of the toolbox (incidence matrix is the same as that of the first example). Is it possible to illustrate the toolbox with an example in which the input and outputs are not fixed? I am actually concerned with the fact that the use cases do not really show how the toolbox can be used on a real dataset, which may not have natural input and outputs.

Figures 4, 5 and 6 displays the results of the toolbox on the second example. These results are briefly discussed in the text which also recalls the definitions of some of the measures. Applying the toolbox on a real dataset would make the discussion of the results of the toolbox much easier to interpret. Moreover, a real dataset could provide evidence of the relevance of the results obtained by relying on the nature of nodes distinguished by the toolbox.

The different types of nodes displayed in Figure 5 should be defined rather than just refer to [24] 3.

Could you please give an idea about what kind of biological networks can be studied by the means of your third module? This part is not very intuitive from a biological point of view.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

References

  • 1. : Controllability and observability in complex networks – the effect of connection types. Scientific Reports.2017;7(1) : 10.1038/s41598-017-00160-5 10.1038/s41598-017-00160-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2. : Control principles for complex biological networks. Brief Bioinform.2018; 10.1093/bib/bby088 10.1093/bib/bby088 [DOI] [PubMed] [Google Scholar]
  • 3. : Control profiles of complex networks. Science.2014;343(6177) : 10.1126/science.1242063 1373-6 10.1126/science.1242063 [DOI] [PubMed] [Google Scholar]

Associated Data

    This section collects any data citations, data availability statements, or supplementary materials included in this article.

    Data Availability Statement

    All data underlying the results are available as part of the article and no additional source data are required.

    Articles from F1000Research are provided here courtesy of F1000 Research Ltd

    RESOURCES