Milestone prediction for time-to-event endpoint monitoring in clinical trials

Abstract

Predicting the times of milestone events, ie, interim and final analyses in clinical trials, helps resource planning. This manuscript presents and compares several easily implemented methods for predicting when a milestone event is achieved. We show that it is beneficial to combine the predictions from different models to craft a better predictor through prediction synthesis. Furthermore, a Bayesian approach provides a better measure of the uncertainty involved in prediction of milestone events. We compare the methods through two simulations where the model has been correctly specified and where the models are a mixture of three incorrectly specified model classes. We then apply the methods on two real clinical trial data, North Central Cancer Treatment Group (NCCTG) N0147 and N9841. In summary, the Bayesian prediction synthesis methods automatically perform well even when the data collection is far from homogeneous. An R shiny app is under development to carry out the prediction in a user-friendly fashion.

1 |. INTRODUCTION

Randomized clinical trials involving failure-time endpoints are typically powered by the number of events. For safety and efficiency reasons, one or more planned interim analyses would be performed prior to the final data analysis. Since the statistical information of failure-time endpoints is in proportion to the number of events, the planned interim analyses are typically carried out after a pre-specified number of events have occurred, such as 50% of the total number of events. In this manuscript, we refer to pre-specified analysis times as “milestones.” From a management perspective, it is important to predict when the milestone events will be attained so that one can allocate statistical resources in a practical manner. On the other hand, these predictions may be carried out repeatedly in the lifetime of a trial so the prediction should be suitably accurate and easy to perform to enhance efficiency in trial monitoring.

Some methods have been developed previously for predicting the milestone time. Rubinstein et al¹ used the Poisson process and exponential survival model to predict milestone event times, and Bagiella and Heitjan² constructed predictive intervals for the milestone using the predictive distribution from simulation. These proposed methods require parametric assumptions and have the limitation that the predictions may be inaccurate if the assumptions were not met. To overcome this limitation, Ying et al³ developed a nonparametric prediction method utilizing Bayesian bootstrap resampling with a Kaplan-Meier curve. This method provides a better prediction when the parametric assumptions are invalid but is inefficient when the parametric assumptions are satisfied. More recent developments include Anisimov⁴ that took into account the variation in recruitment rate across different centers, and the cure rate model was used for prediction in Chen.⁵ Each of the aforementioned methods requires careful consideration and comparisons between various models, thus requiring statistical input for each prediction and can be difficult to be bundled into a more automated process. A nice adaptive method was developed in Lan and Heitjan,⁶ which uses Bayesian model selection to identify the best-fitting model and use the single best-fitting model to create prediction densities. However, the prediction interval coverage of Lan and Heitjan⁶ tends to be very poor.

In this manuscript, we propose to combine the predictions from several models to come up with a better prediction. As such, there is little concern whether the individual models actually fit the data particularly well. These methods are intended to be simple, easy to implement, and largely automated without need for extensive modeling. The intention is that the method could be created once and then used to provide reasonable estimates on a wide variety of survival experiments with very limited modeling and coding. This approach is intended solely for trial monitoring and not intended to make corrections for the actual number of events needed to attain a proper size and power for the study.

In clinical trial design, prior trial results are often used as the historic information for the control arm in sample size/power calculation. This prior knowledge suggests that a Bayesian approach could be used for the estimation of the time until a milestone is achieved. Hence, this manuscript will investigate milestone prediction from both frequentist and Bayesian perspectives. Specifically, we focus on prediction synthesis methods⁷ for combining individual model predictions for estimating the time until milestone events are reached for an ongoing clinical trial with time-to-event endpoint. Prediction synthesis is a novel method in that it finds the best combination of individual models that provide the best prediction accuracy rather than the combination that fits the observed data the best.

The general data structure and model building will be described in Section 2. Prediction synthesis under frequentist and Bayesian perspectives will be presented in Section 3. Section 4 contains two numerical simulations and is followed by an analysis of the data from two real clinical trials, N0147 and N9841, in Section 5. We conclude with a discussion describing alternative formulations, limitations, and extensions, which could prove helpful for future improvements.

2 |. DATA AND MODELS

Let the observed data at a given time point be (a_i, t_i, δ_i), where i indexes each patient. a_i is the time in which a subject enters the study, and we assume that a_i are in increasing order. δ_i is an indicator of whether the failure time has been observed, s_i is the failure time, and t_i is the minimum of the failure time and the time where the event prediction takes place (denoted by) T. At time T, the data will be summarized as X_T = {0 ≤ a_i ≤ T, t_i = min(s_i, T), δ_i = I(s_i ≤ T)}.

2.1 |. Models

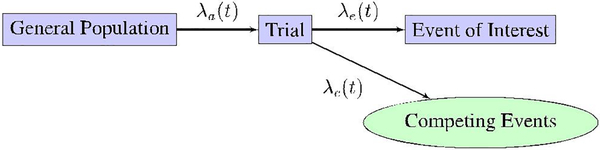
The system of interest behaves very much like a queue, with subjects entering the system over time t, with a rate λ_a(t).⁸ Once in the system, the subject immediately begins waiting until a terminal event occurs. The terminal event may be the event of interest or a competing event, such as a loss of follow-up. Figure 1 displays a graphical depiction of the general model dynamics over time.

FIGURE 1.

Schematic model for the event data collection

Modeling of the observed data will be broken into two independent parts. First is the modeling of the interarrival time b_i = a_i − a_{i − 1} for subjects entering the study, and the second is modeling the time from arrival until a stopping time, either the event or interest or the competing events, has been reached. The arrival and failure-time processes are assumed to be independent for our estimation purposes, which is a reasonable assumption in clinical trials.

2.1.1 |. Interarrival time

It is assumed that subjects come individually, and the number of subjects in each nonoverlapping interval is independent; hence, the arrival follows a Poisson process⁹ with rate function λ_a(t). In other words, the number of subjects joining the study between time t₁ and t₂(t₁ < t₂) would be a Poisson random variable with parameter

$$\mathrm{\Lambda }\left(t_1,t_2\right)={\int }_{t_1}^{t_2}{\lambda }_a(t)dt.$$

For simplicity, we suppose that the intensity function is homogeneous over time, ie, λ_a(t) = λ_a. Hence, interarrival times are distributed with an exponential distribution with rate λ_a. The likelihood function for the observed data would be

$$L\left({\lambda }_a|b,t\right)=e^{-{\lambda }_a\left(t-b_{N(t)}\right)}\prod _i{\lambda }_a{e}^{-{\lambda }_a{b}_i}={\lambda }_a^{N(t)}{e}^{-{\lambda }_{a}t},$$ (1)

where N(t) is the number of subjects that entered the study by time t.

2.1.2 |. Failure time

Once entering a study, a subject will transition to the event of interest or another terminal event. The transition to a terminal state differs from the arrival process in that the “countdown” begins once a subject enters the study, whereas the rate function for the arrival process does not restart after an arrival is observed. Supposing that F_θ is the distribution and f_θ is the density of the failure time, then the likelihood function for the observed failure-time data would be

$$L(\theta |x)=\prod _{i}f{\left(t_i-a_i\right)}^{{\delta }_i}F{\left(t_i-a_i\right)}^{1-{\delta }_i}.$$ (2)

It should be noted that F(t) is not necessarily a proper distribution function because not all subjects will terminate in the event of interest, meaning that F(t) may converge to a value less than 1 as t →∞. However, in this prediction synthesis scenario, proper distribution functions will be used. This may be remedied by assuming that subjects who reach other terminal states are right censored at the time the other terminal state was reached.

The model for the failure time does not take into account explanatory variables X (such as the treatment arms). In essence, the distribution function for the stopping time will be the marginal distribution after integrating over the explanatory variables. This supposes that the distribution of X does not change appreciably as a function of time. For other modeling purposes, it would be better to account for explanatory variables; however, it would lead to an increased number of parameters making sampling from the posterior distribution more computationally expensive. This also forgoes the need to adjust models when different randomization ratios are used. Furthermore, allowing for explanatory variables would lead to a larger class of models making the selection of appropriate models more labor intensive for the statistical analyst and more difficult to build into a reusable program.

Parametric models will be used for the stopping time as presented in Table 1. These four distributions were selected because they are commonly used and each has explicitly defined density and distribution functions. This is not meant to be an exhaustive list of useful distributions, and many more could be added. However, for the purposes of this manuscript, these four distributions are sufficient to demonstrate the benefits of prediction synthesis. In the remainder, the individual models will be referred to solely by the distribution used in the survival process, namely, the Weibull, lognormal, Gompertz and loglogistic.

TABLE 1.

Distributions

Model	Density	Distribution	Parameters
Weibull	$\frac{k}{\lambda }{\left(\frac{x}{\lambda }\right)}^{k-1}{e}^{-{\left(\frac{x}{\lambda }\right)}^k}$	$1-e^{{\left(\frac{x}{\lambda }\right)}^k}$	λ > 0; k > 0
Gompertz	$b\eta e^{bx+\eta -\eta e^{bx}}$	$1-e^{\eta -\eta e^{bx}}$	$\eta \in \mathcal{R}$; b > 0
Loglogistic	$\frac{(\beta /\alpha ){(x/\alpha )}^{\beta -1}}{{\left(1+{(x/\alpha )}^{\beta }\right)}^2}$	$\frac{1}{1+{(\alpha /x)}^{\beta }}$	α > 0; β > 0
Lognormal	$\frac{1}{x\sigma \sqrt{2\pi }}{e}^{-\frac{{(\text{ln}(x)-\mu )}^2}{2{\sigma }^2}}$	$\frac{1}{2}+\frac{1}{2}\mathrm{\Phi }\left(\frac{\text{ln}(x)-\mu }{\sqrt{2}\sigma }\right)$	$\mu \in \mathcal{R}$; σ > 0

3 |. METHODS

Given the aforementioned individual models, the predictors will be constructed using the following approaches:

1. Fit the individual parametric models with the maximum likelihood estimate of the available survival data, and then use the fit models to make predictions.

2. Use Bayesian posteriors of individual parametric model parameters to make predictions from the posterior.

3. Use prediction synthesis methods over the predicted distributions from individual frequentist model fits.

4. Use prediction synthesis methods over the individual posterior prediction densities (Bayesian).

For method A, once the parameter estimates are computed, the duration will be predicted as the average of simulated predictions. Method B will use a Metropolis-Hastings algorithm to create a Markov chain of parameter values from the posterior distribution of each individual model. Each parameter value in the chain will be used to simulate a single predicted future milestone time. The estimated time until completion will be based on the mean of Markov chain predictions over a stationary portion of the chain, ie, chain values after an acceptable burn-in has been observed. The mechanisms used for the prediction synthesis methods mentioned in C and D will be described in Section 3.2.

3.1 |. Prior distributions

To ease implementation and to automate the modeling, we have chosen the prior distribution for parameters in the following fashion. The prior distribution for the exponential distribution parameter of the interarrival times will be a constant noninformative prior. This means that the posterior for the rate parameter λ_a will be distributed as a gamma distribution with shape parameter N + 1 (N is the number of interarrivals observed) and scale parameter t (current time) as suggested by Equation 1. This is a variant of the Poisson-gamma model^10,11 applied to a single center.¹² The flat prior does have the drawback that accruals must be observed prior to being able to predict future accrual milestones. If one has a good idea about the mean and/or variance of the fixed rate parameters for an individual center, these could be adapted to a more informative prior gamma distribution.

The prior distributions for parameters taking values on the entire real line, such as η in the Gompertz distribution and μ in the lognormal distribution, will be normally distributed, and gamma prior distributions will be used for positive valued parameters. In a typical clinical trial design with time-to-event endpoints, very often, one assumes that the underlying failure time is exponentially distributed with rate parameter λ_e. Since the exponential distribution is a special case of the Weibull distribution when k is set to 1, the prior mean for k will be set to 1 and the prior rate parameter λ_w for the Weibull distribution will be set to λ_e. The remaining means for other parameters will be constructed by equating features of the exponential distribution with features of the respective distribution. The resulting relationships are presented in Table 2. The variance for each parameter should reflect the certainty one has in the parameter values. Without strong certainty, one should make the variance large so that the prior has limited influence on the predictors.

TABLE 2.

Mean for the prior parameters

Distribution	Prior Means
Weibull	${\mu }_{{\lambda }_w}$= λe	μk = 1
Gompertz	μη = 1	μb = λe1og(log(2) + l)/log(2)
Loglogistic	μα = 1/λe	μβ = 1
Lognormal	μμ = −log(λe)−log(2)/2	${\mu }_{\sigma }=\sqrt{\text{log}(2)}$

3.2 |. Prediction synthesis

In the preceding section, we described how we would construct prediction models from the observed data, ie, the data collected thus far within the current trial. Using these models, one could simulate future observations and find the times when the desired milestone is reached. After many simulations from a model, one could get an approximate predicted distribution for that model. As our goal is to find a good predictor, it is important to assess the performance of prediction densities rather than how well the likelihood fits the observed data. A good choice for a predictor would be to select the model that gives the best predictions; however, it has also been shown that combining individual model prediction densities can lead to a better predictor.¹³ Readers who are interested in more technical discussions of prediction synthesis should consider the following literature.^7,14–16

Prediction synthesis is a field that attempts to select and/or combine predictors from different models to create a better predictor based on the observed prediction performance. Consider J individual prediction models (either frequentist or Bayesian) that will be viewed as agents that use their best respective judgments to make a density for prediction, h_j(y). The predictions will be synthesized by a decision maker that combines the results from each agent to create a better decision. We will adopt the linear decision maker of Breiman¹⁷ that would generate predictive densities of the form

$$h(y)=\sum _{j=1}^J{\alpha }_j{h}_j(y),$$ (3)

with the constraints α_j ≥ 0 and ${\sum }_1^J{\alpha }_j=1$ added to guarantee that the composite prediction distribution will remain a valid probability distribution. The form of Equation 3 is a linear version of the best form presented in West.¹⁴ Prediction synthesis can be carried out in the same fashion regardless of whether h_j(y) is the density of predictions based on the maximum likelihood estimate (MLE) fit model or the predictions based on parameter values of the posterior densities. A more detailed presentation of (Bayesian) prediction synthesis is described in McAlinn and West⁷ and West.¹⁴

This method is similar to model averaging, except that the focus is on averaging over the prediction distributions rather than the likelihood functions of the observed data. Since our analysis methods will be based on simulations and α_j must be estimated, Equation 3 will be approximated by

$$\widehat{h}(y)=\sum _j{\widehat{\alpha }}_j\frac{1}{n_j}\sum _{i=1}^{n_j}{\delta }_{z_{j,i}}(y),$$ (4)

where δ_Z is a point mass at Z and Z_j,i is the ith simulated prediction from model j.

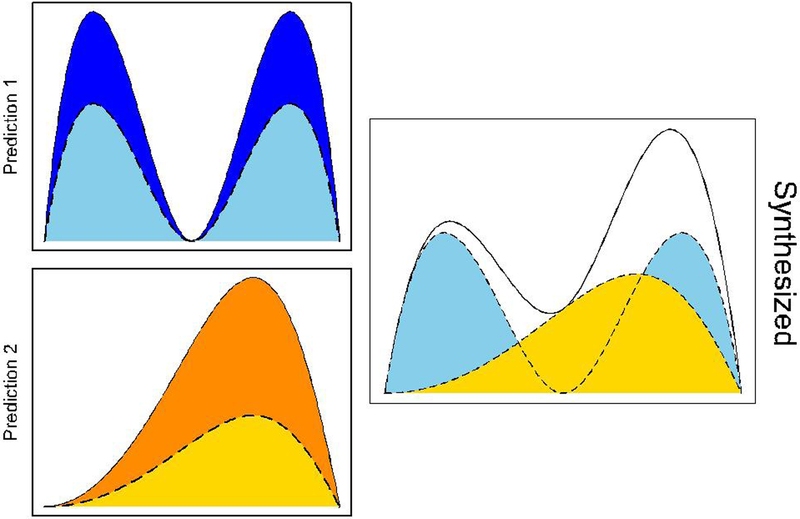
A graphical illustration of predictive synthesis is shown in Figure 2. Suppose that we have two prediction densities, h₁(·) and h₂(·) generated from two different models, denoted by the areas shaded with dark blue and dark orange, respectively. Suppose the prediction synthesis weights are 0.6 and 0.4 for α₁ and α₂, respectively. The weighted predictive densities, α₁h₁(·) and α₂h₂(·), are the areas shaded with light blue and light orange, respectively. The synthesized predictive density, h(·), is the area outlined by the solid line in the right hand-side panel.

FIGURE 2.

A graphical illustration of the concept behind predictive synthesis

The point estimate for the prediction will be the mean $\dot{y}$ of the distribution h(y) (or $\widehat{h}(y)$). The prediction point estimate is easily recovered from the individual model means ${\dot{y}}_j$ through $\dot{y}=\sum {}_j{\widehat{\alpha }}_j{\dot{y}}_j$. The constraint placed on α = {α₁, …, α_J : α_j ≥ 0, ∑ α_j = 1} assures that ${\text{min}}_j{\dot{y}}_j\le \dot{y}\le {\text{max}}_j{\dot{y}}_j$, where ${\dot{y}}_j$ is the mean prediction from agent j. The combined prediction $\dot{y}$ can be no more extreme than the most extreme individual model value ${\dot{y}}_j$. In other words, there is a built-in mechanism to hedge against drastic prediction choices.

It should be noted that this is different than if the prediction distribution was constructed from the weighted average of individual predictors, y = ∑_jα_jZ_j for draws Z_j drawn from the predictions of model j. The prediction synthesis method leads to a density of predictors with more spread than the density of weighted averages reflecting our greater uncertainty in model selection. The mixture of prediction densities is also more in line with a Bayesian treatment of the posterior prediction density where one would first select the model, then the parameter, followed by simulation of the predicted value. This is an ad hoc approach to a fully Bayesian treatment where a posterior density would be constructed over all of the individual densities and would likely require a reversible jump Monte Carlo Markov chain to approximate. Since the full Bayesian treatment would be assessing the fit of the likelihood functions rather than the prediction densities, the prediction synthesis technique should be advantageous.

3.2.1 |. Average weights

The simplest version of this prediction synthesis model is to set ${\alpha }_j={\widehat{\alpha }}_j=1/J$. This drastically eliminates computational issues by adopting a democratic approach to the decision-making procedure. A marked disadvantage of this approach is that the decision maker does not converge to the best possible predictor among the class of linear decision makers. Nonetheless, this method will be evaluated, because it is very easily implemented and should provide a pretty good solution. In the subsequent presentation, this method will be referred to as the “average” (prediction synthesis) model.

3.2.2 |. Estimating weights for prediction synthesis

Herein, we shall present two methods for estimating the weights of Equation 3 using the observed data, ie, the data collected thus far within the current trial. Specifically, we will estimate the values α_j by observing how well the respective models were able to predict previous milestones within the current trial. The overarching idea is the following:

• Use all observed data to determine the model parameters (either the parameter estimates from the frequentist approach, ${\widehat{\theta }}_j$, or a random draw from a posterior distribution from the Bayesian approach, π_j(θ_j|X_T)).

• From the observed data, randomly select K pairs of data (t_i, r_i) where t_i is an observed event time and r_i is an earlier event time, with i = 1, … ,K. Find the total number of events occurring up to and including time t_i. Label this Ñ_i.

• For each i, truncate the data at r_i, ie, events occurring after r_i would be censored at r_i and patients entering the study after r_i would be removed from the dataset.

• Using the data truncated at r_i, make M predictions for the Ñth event time. In other words, simulate additional patients after r_i following the homogeneous Poisson process as described in Section 2.1.1 and event times for the newly generated patients and event times that were censored at r_i. From this simulation, select the Ñth event time. Let $t_{j,i,k}^{\prime }$ denote the M values from the prediction density for model j, where k = 1, …, M is the index for prediction of t_i.

Unlike the average weighting method, estimating the weights through previous predictions requires observation of multiple accrual and failure events. In the subsequent data analysis, the weight estimation is seen to be of benefit even with only 25 observed events.

There are different ways to choose the “optimal” weights, and we considered the following two methods that favor computational efficiency with suitable accuracy. The first method to estimate the weights α_j will be through minimum squared prediction error (MSPE), which minimizes

$$\widehat{\alpha }=\underset{{\alpha }_j\ge 0;{\sum }_j{\alpha }_j=1}{\text{arg}\text{min}}\sum _j{\alpha }_j\sum _i{\left(t_i-{\overline{t}}_{j,i}^{\prime }\right)}^2,$$ (5)

where ${\overline{t}}_{j,i}^{\prime }=1/M\sum _k{t}_{j,i,k}^{\prime }$. This is in the form of a constrained quadratic optimization and can be implemented using standard software.

The second method is based on giving each prediction model a proportion based on how well they were able to predict previous milestones. The weights would be calculated as

$${\widehat{\alpha }}_j=\frac{1}{N}\sum _{i}I\left(j=\underset{q=1,\mathrm{\dots },J}{\text{min}}\left|t_i-{\overline{t}}_{q,i}^{\prime }\right|\right),$$ (6)

where I(A) is a binary variable indicating whether A is true or not. If it is possible to have ties in the deviances (typically of probability 0), the tied values should split the “vote” in equal amounts. The voting method differs from the MSPE method in that it does not require quadratic optimization making it easier (and more stable) to implement in R. Subsequent reference to this weighting method will be with the term “vote.”

3.3 |. Prediction intervals

In addition to the point predictions based on the mean of the respective prediction densities, prediction intervals will be created. They will use the quantiles of simulated predictions from the prediction density and take the form (t_α/2,t_1−α/2), where t_s is the sth quantile of the associated simulated predictions. It is possible to create many other prediction intervals, particularly by assuming that the prediction interval is roughly normally distributed, but the selected quantile method seems to be a much better choice.

4 |. NUMERICAL SIMULATIONS

Herein, we present two simulations. The first will use one of the individual models included in Table 1, and the second will use a range of models outside of Table 1. The interarrival times b_i will follow an exponential distribution with rate parameter λ_e = 0.5. For the Bayesian analysis, all priors will have a mean of 1 and a variance of 50 using either the normal or gamma distribution as explained in the preceding discussion. The simulations will be tested for prediction of the milestone target of 100 or 500 events after observation of 25%, 50%, or 75% of the milestone value. Each combination of target and partial observation window will be run 1000 times. The results concerning individual models will be referred to solely by the survival process model, namely, Weibull, lognormal, Gompertz, or loglogistic. The predictive synthesis model will combine the four individual models, and the results will be marked with PredSynth and either average, MSPE, or vote to denote weight estimation method. To evaluate predicted milestones, we calculated the percentage of prediction error as (predicted day — actual milestone day)/(actual milestone day). The median of the absolute value of percentage error (median absolute percentage error [MAPE]) was used to summarize the prediction performance. MAPE was used because the actual milestone day in each simulated dataset would be different; therefore, MAPE provides a good gauge of the error while taking into account the different actual milestone day.

4.1 |. Simulation 1: lognormal failure times

For the first simulation, the failure time will be distributed with a lognormal distribution with μ = 5 and σ = 0.25. This model was selected because it is one of the individual models used. The results of the ensuing analysis are presented in Table 3. The reported figures are MAPE. For reference, the mean time until 500 events were observed is 1152 days, so a MAPE of 3.37% would account for approximately 39 days at 25% of events observed. The mean time until 100 events were observed is 352 days, so a MAPE of 2.10% would account for approximately 7 days at 25% of events observed.

TABLE 3.

Median absolute percentage error for simulation 1

Model	% Event Observed	25%	50%	75%	25%	50%	75%
	Method	Nevent = 100			Nevent = 500
Weibull	Freq	1.98	1.59	1.37	3.34	1.92	0.91
	Bayes	2.00	1.56	1.37	3.34	1.93	0.90
Lognormal	Freq	2.06	1.55	1.38	3.36	1.91	0.90
	Bayes	2.14	1.62	1.40	3.29	1.94	0.90
Gompertz	Freq	2.01	1.56	1.43	3.34	1.91	0.90
	Bayes	2.02	1.74	1.54	3.32	1.90	0.91
Loglogistic	Freq	2.05	1.54	1.38	3.37	1.93	0.91
	Bayes	2.10	1.58	1.37	3.36	1.94	0.91
PredSynth	Freq	1.99	1.54	1.40	3.36	1.92	0.90
(Average)	Bayes	1.92	1.50	1.39	3.29	1.92	0.91
PredSynth	Freq	1.98	1.54	1.37	3.37	1.93	0.92
(MSPE)	Bayes	1.99	1.61	1.40	3.31	1.93	0.90
PredSynth	Freq	2.00	1.55	1.41	3.37	1.92	0.90
(Vote)	Bayes	1.97	1.54	1.43	3.29	1.92	0.91

Abbreviation: MSPE, minimum squared prediction error.

These results suggest that anyone of the applications would perform with nearly identical prediction results. It is surprising that the lognormal model does not have the best performance for either the Bayesian or frequentist prediction method for any of the partial milestone percentages. The prediction synthesis methods perform very well compared with the other predictions, even though they are not uniformly better than the others.

Table 4 gives the results of the 95% prediction interval study for simulation 1. The display gives the percentage of the prediction interval as a function of the target milestone value, ie, 100% × interval length/milestone. The frequentist intervals are considerably smaller than the Bayesian prediction intervals. For instance, at 25% of the target number of events (out of 500), the frequentist prediction interval lengths are approximately 11.5%, meaning that they have a length of about 132 days, compared with the Bayesian prediction intervals of 212 days (18.4%). However, the frequentist prediction interval coverages are far lower than the expected coverage values. With a target of 500 and observation of 25%, the maximum coverage of the frequentist prediction intervals is 76.1, whereas the worst Bayesian prediction interval coverage is 94.2%. While prediction intervals of 212 days may seem large, it is for an event that will occur about 2 years in the future; therefore, a wider confidence interval is expected while providing coverage probability close to 95%. In all scenarios, the Bayesian versions have coverage closer to the expected target of 95%. For the 100-event milestone predictions, even the Bayesian methods have poor coverage, particularly for the Gompertz model. However, all of the Bayesian prediction synthesis methods are within 2% of the 95% coverage target.

TABLE 4.

Prediction intervals for simulation 1 based on raw quantiles^a

Model	% Event Observed	25%	50%	75%	25%	50%	75%
	Method	Nevent = 100			Nevent = 500
Weibull	Freq	7.4	6.9	6.7	11.5	8.7	4.6
		77.1	85.8	89.5	74.9	86.8	90.6
	Bayes	10.5	8.7	7.7	18.4	11.0	5.0
		90.1	93.2	94.2	94.2	92.8	93.8
Lognormal	Freq	8.1	7.1	6.8	11.5	8.7	4.7
		80.3	86.5	90.3	75.4	86.9	90.6
	Bayes	11.1	8.7	7.5	18.4	11.0	5.0
		89.8	91.9	93.7	94.4	93.7	93.4
Gompertz	Freq	7.3	7.0	7.0	11.5	8.7	4.7
		76.1	86.0	89.7	75.9	85.8	91.1
	Bayes	7.9	8.4	7.9	18.4	11.0	5.0
		78.2	90.6	91.8	94.9	93.6	93.9
Loglogistic	Freq	8.2	7.1	6.8	11.5	8.7	4.7
		81.7	86.6	90.4	75.2	86.2	90.3
	Bayes	12.2	9.2	7.8	18.4	11.0	5.1
		94.6	94.7	94.8	95.0	93.7	93.4
PredSynth	Freq	8.2	7.2	7.1	11.7	8.9	4.8
		82.6	87.8	91.7	76.1	87.2	91.9
(Average)	Bayes	11.4	9.3	8.2	18.5	11.1	5.1
		94.0	95.7	95.9	95.1	93.5	94.4
PredSynth	Freq	7.9	7.1	6.9	11.5	8.7	4.7
		81.3	86.4	90.6	74.9	86.4	91.1
(MSPE)	Bayes	11.2	9.1	8.0	18.4	11.0	5.1
		93.0	94.8	95.0	95.1	93.7	93.7
PredSynth	Freq	8.1	7.1	7.0	11.5	8.7	4.7
		81.9	87.6	91.2	75.0	86.5	91.3
(Vote)	Bayes	11.4	9.2	8.1	18.4	11.0	5.1
		93.8	95.4	95.7	95.1	93.5	93.6

Abbreviation: MSPE, minimum squared prediction error.

^aThe top numbers are the mean interval length as a percentage of the target values. The bottom number is the coverage percentage.

4.2 |. Simulation 2: mixture of models for failure time

The second simulation will use identical priors for each model type as were used in the preceding simulation; ie, each prior parameter has a mean of 1 and a standard deviation of 50. The failure time S_i will be a random mixture of three different distribution functions. Model 1 will be a gamma distribution with shape 4 and scale 20. Model 2 will be a loglogistic distribution with shape 3 and scale 15. Model 3 will be a Fréchet distribution with location 12, scale 2, and shape 3. For each simulated dataset, two uniform (0,1) random variables will be selected then ordered, ie, 0 < u₁ < u₂ < 1. The model for the survival time of observation i will be from model 1 with probability u₁, model 2 with probability u₂ — u₁, and from model 3 with probability 1 − u₂. The random mixtures were used so that at different mixing values, different individual models would perform better. The models used for generating the data are very different from the models considered for the prediction synthesis because we wish to demonstrate the flexibility of the prediction synthesis methods; ie, the prediction synthesis methods will perform well even though the true underlying models were not used for prediction synthesis. The interarrival time will be distributed with an exponential distribution with rate of 0.5. The simulation will be run 1000 times with the intent of predicting the 100- and 500-event milestones after observing 25%, 50%, and 75% of the milestone value.

The MAPE results of simulation 2 are presented in Table 5. The mean time for the 500-event milestone of the simulations was 1055 days, so the maximum percentage error of 4.73% accounts for 50 days at the time when 25% of events were observed. The mean time for the 100-event milestone of the simulations was 240 days, so the maximum percentage error of 9.87% accounts for about 24 days at 25% of events observed. The Bayesian method has performance on par with the frequentist methods. As in the preceding simulation, the prediction synthesis methods provide predictions that are middle of the pack.

TABLE 5.

Median absolute percentage error for simulation 2

Model	% Event Observed	25%	50%	75%	25%	50%	75%
	Method	Nevent = 100			Nevent = 500
Weibull	Freq	7.65	4.69	2.71	4.39	2.52	1.46
	Bayes	7.78	4.64	2.77	4.51	2.57	1.41
Lognormal	Freq	9.87	5.68	3.33	4.69	2.87	1.62
	Bayes	8.30	4.94	3.04	4.61	2.82	1.58
Gompertz	Freq	8.32	5.64	3.56	4.47	2.53	1.53
	Bayes	7.50	4.73	2.78	4.48	2.58	1.49
Loglogistic	Freq	9.18	5.67	3.23	4.73	2.96	1.70
	Bayes	9.06	5.63	3.19	4.71	2.91	1.71
PredSynth	Freq	7.92	4.93	2.93	4.48	2.66	1.48
(Average)	Bayes	7.95	4.94	2.90	4.52	2.69	1.51
PredSynth	Freq	7.94	4.95	2.88	4.38	2.49	1.53
(MSPE)	Bayes	7.58	4.77	2.84	4.54	2.73	1.62
PredSynth	Freq	7.69	4.85	2.90	4.50	2.61	1.44
(Vote)	Bayes	7.78	4.87	2.85	4.49	2.74	1.50

Abbreviation: MSPE, minimum squared prediction error.

Table 6 gives the results of the prediction interval study for simulation 2. The results are similar to those shown in simulation 1. The frequentist intervals are smaller than the Bayesian prediction intervals, but the Bayesian versions provide coverage that is closer to the 95% value. While the frequentist prediction synthesis methods tend to generate larger prediction intervals than the individual frequentist model methods, the coverage is closer to the desired 95% coverage level. All of the Bayesian prediction synthesis methods are within 4% of the 95% coverage target. The worst Bayesian coverage is 90.9% for this scenario with a target of 100 events and observation of only 25 using the loglogistic model and the raw quantile method.

TABLE 6.

Prediction intervals for simulation 2 based on raw quantiles^a

Model	% Event Observed	25%	50%	75%	25%	50%	75%
	Method	Nevent = 100			Nevent = 500
Weibull	Freq	25.2	19.4	12.9	13.9	11.1	7.5
		72.1	83.2	88.6	70.4	83.4	91.2
	Bayes	43.0	25.6	14.6	26.2	15.5	8.6
		92.6	93.5	91.8	95.8	94.2	94.1
Lognormal	Freq	27.6	21.6	14.7	14.0	11.3	7.8
		64.9	77.5	87.3	68.5	81.6	88.7
	Bayes	48.2	28.4	16.3	26.7	15.7	9.0
		93.9	94.2	93.3	95.6	93.9	93.8
Gompertz	Freq	24.5	18.4	11.5	13.9	11.2	7.5
		69.3	75.1	71.3	70.7	82.0	88.9
	Bayes	42.1	24.8	14.2	26.2	15.4	8.6
		93.2	93.1	91.5	96.0	94.0	93.3
Loglogistic	Freq	27.2	21.3	14.4	14.0	11.3	7.8
		67.7	78.8	87.0	68.4	79.7	87.4
	Bayes	47.6	28.5	16.4	26.8	15.8	9.0
		90.9	92.1	91.4	95.2	92.5	92.3
PredSynth	Freq	32.3	24.0	15.8	15.0	12.0	8.3
		82.2	89.0	93.5	73.3	84.8	93.4
(Average)	Bayes	47.1	27.9	16.0	27.0	16.0	9.1
		94.6	94.8	93.8	96.6	94.8	95.0
PredSynth	Freq	29.2	21.6	14.1	14.2	11.4	7.8
		76.8	86.3	89.0	71.7	83.8	90.1
(MSPE)	Bayes	42.4	24.9	14.2	26.3	15.5	8.8
		93.3	93.0	91.5	96.0	93.4	92.1
PredSynth	Freq	31.8	23.6	15.5	14.7	11.8	8.1
		81.0	89.3	92.8	72.9	84.4	92.7
(Vote)	Bayes	45.4	26.7	15.3	26.7	15.8	9.0
		93.9	94.3	93.1	96.3	94.4	93.5

Abbreviation: MSPE, minimum squared prediction error.

^aThe top numbers are the mean interval length as a percentage of the target values. The bottom number is the coverage percentage.

4.3 |. Simulation conclusion

The results of these simulations demonstrate that nearly any of the individual or prediction synthesis models give very similar point estimates for the desired milestone. The real difference between the methods can be seen in the generated confidence intervals. There is a systematic undercoverage with the frequentist methods since they do not factor in the uncertainty of the model parameters. The coverage of the individual Bayesian models varies. However, the Bayesian prediction synthesis methods provide coverages very close to the desired 95% over all of the simulations.

5 |. CASE STUDIES

The event forecasting methods were tested on the North Central Cancer Treatment Group (NCCTG) N0147 (Alliance)¹⁸ and NCCTG N9841 (Alliance)¹⁹ studies, which are two completed colorectal cancer treatment studies conducted by the NCCTG now part of the Alliance for Clinical Trials in Oncology (Alliance). The predictions were performed after every 10% increase in the number of observed events as a percentage of the intended milestone number of events.

The N0147 study was designed to assess the potential benefit of cetuximab added to the modified sixth version of the FOLFOX regimen in patients with resected stage III wild-type KRAS colon cancer.¹⁸ A total of 515 disease-free survival (DFS) events would properly power the study, but N0147 was terminated for futility at the second interim analysis (50% event). At the time of termination, 1863 (of 2070 planned) patients were accrued. For demonstration purposes, the target milestone for N0147 is 258 events, which constitutes approximately 50% of the targeted number of events and occurred after 1681 days. N0147 was chosen to represent a study where the events occurred relatively slowly; ie, the median DFS is around 5.8 years.

The N9841 study was designed to determine whether overall survival (OS) of fluorouracil (FU)-refractory patients was noninferior when treated with second-line infusional FOLFOX4 versus irinotecan. The study accrued a total of 491 patients, and 405 OS events were needed to properly power the study. The target milestone for N9841 is 405 OS events, which occurred at 1689 days. N9841 was chosen to represent a study where the events occurred relatively quickly; ie, the median OS is around 10 months.

With each of the targeted milestones, the observed dataset was censored for events occurring after a proportion of the milestone was observed. For example, if we want to predict the 500th event after 250 events (50% of events) were observed, all events occurring after the 250th event will be censored. The predictions were made with each of the seven prediction models, ie, Weibull, lognormal, Gompertz, loglogistic, PredSynth(Avg), PredSynth(MSPE), and PredSynth(Vote), using the frequentist and Bayesian methods.

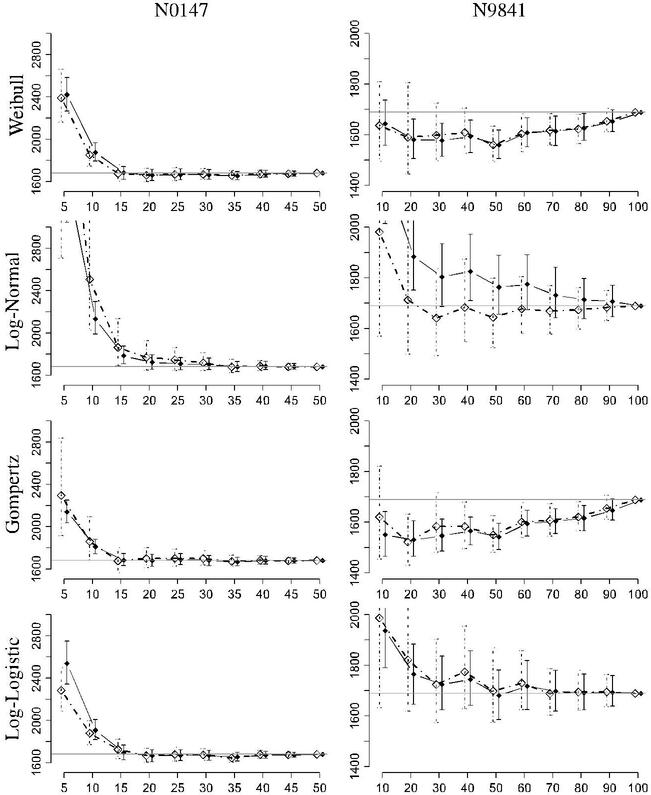
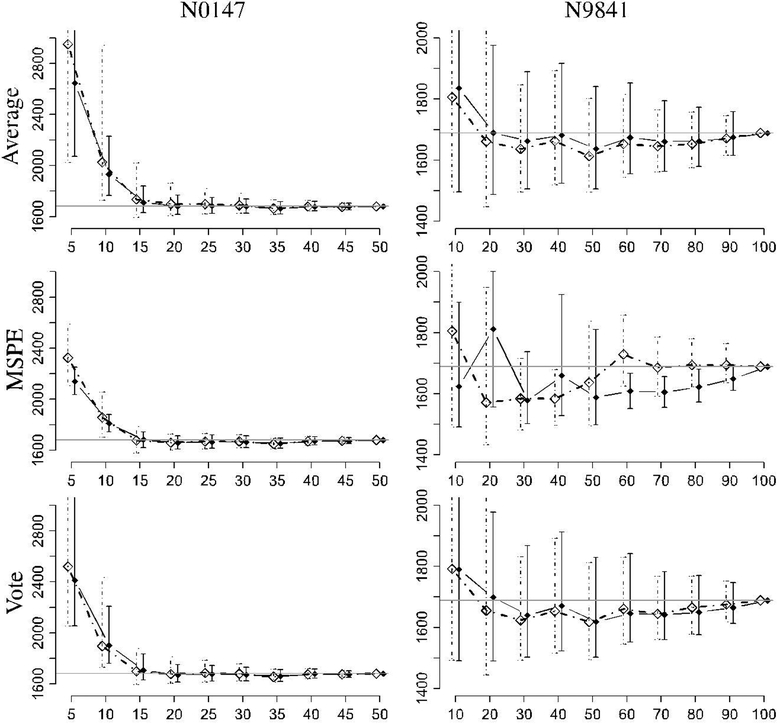
The results of this analysis are presented in Figures 3 and 4. The frequentist method predictions are shown using solid diamonds with solid lines for the prediction intervals, and the Bayesian method predictions are shown using empty diamonds with dotted lines for the prediction intervals.

FIGURE 3.

Predicted milestone vs percentage of observed events for the N0147 and N9841 studies. Bayesian results use an open diamond and dotted lines, and the frequentist results are solid. The target is indicated by the horizontal gray line. The targets are 1681 and 1689 days for N0147 and N9841, respectively

FIGURE 4.

Predicted milestone vs percentage of observed events for the N0147 and N9841 studies. Bayesian results use an open diamond and dotted lines, and the frequentist results are solid. The target is indicated by the horizontal gray line. The targets are 1681 and 1689 days for N0147 and N9841, respectively. MSPE, minimum squared prediction error

The two sets of simulations show fairly similar performance for the Bayesian and frequentist methods with a preference for the prediction synthesis methods. The behavior of the lognormal distributions for estimation of the N0147 milestone behaves very sporadically when less than 10% of the milestone is observed, and these values have been truncated from the figures to better observe the behavior of the remaining predictions. In view of the poor performance of the lognormal distribution, a key difference for the prediction synthesis methods can be seen. The Average method gives equal weight to the poor predictor making it perform poorly. On the other hand, the MSPE and Vote methods are able to determine that the lognormal model does not provide ideal predictions and places very little or no weight on the predictor, even after only observing around 25 events. For N0147, every single model with the exception of the lognormal model has a mean prediction within 20 days of the actual milestone completion, after 20% of the total number of events were observed (ie, 40% of the milestone events). The lognormal model predictions remain within 20 days after 30% of the milestone data number is observed for the frequentist version and 35% for the Bayesian method. All of the prediction intervals cover the milestone value after 15% except for the lognormal model, which covers after 20% of events are observed.

The results from the N9841 analysis show that the individual models have highly differing biases. The lognormal and loglogistic show large biases exceeding the actual value of 1689 days, while the Weibull and Gompertz models have much smaller biases for earlier predictions but have a tendency to under predict. Interestingly, the Bayesian version of the lognormal model is far better than the frequentist version with very little bias after 20% of the events are observed. All of the Bayesian PredSynth methods are within 40 days of the target by 60% of the target events. The frequentist PredSynth methods also attained the 40-day bias limit after 60% of the target number of events was reached, with the exception of the MSPE method. From 50% of events, the loglogistic model becomes the most accurate of the individual models in terms of mean squared prediction error. The Bayesian MSPE method picks up on this and is essentially identical to the loglogistic predictor when more than 60% of the target is reached. After 70% of the milestone events, both the loglogistic and Bayesian MSPE methods remained within 8 days of the target value.

In both of the case studies, when a sufficient number of events are observed (ie, around 60%−70% of milestone events), the bias of the prediction is in the range of 8 to 20 days.

6 |. CONCLUSION

It should be apparent that the prediction synthesis methods hedge losses over individual models and estimating weights for synthesis has the flexibility for improving estimates by using all information provided in a partial sample. The prediction interval coverage for the Bayesian prediction synthesis methods appears to be close to the desired coverage level even when some of the individual models do not have the proper coverage as seen in Table 4. Therefore, we recommend using prediction synthesis under the Bayesian paradigm. The three different weighting schemes all have comparable coverage, but the MSPE method is appealing since it has nice asymptotic convergence properties. Therefore, prediction synthesis under the Bayesian paradigm with the weights generated from minimizing MSPE is our recommendation. The amount of information available will affect the accuracy of the prediction; therefore, it is advised to predict the milestone when more than 50% of milestone is observed; for example, if the interim analysis is planned at 50% of events, then prediction can be carried out after 25% of events have been observed to facilitate resource planning. A practitioner should also keep in mind that the accuracy of prediction depends on the information available and the variability inherent in the process being predicted; therefore, care should be given to take into account the confidence interval in addition to the point prediction in resource planning.

The accrual model used herein assumes that a clinical trial enrolls patients from a fixed number of clinical centers and that the accrual phase will continue until a fixed predetermined number of patients are attained. A more realistic model would carefully account for the number and size of clinical centers accruing patients as a function of time.^10,11 One could further refine this model by incorporating nonhomogeneous arrival rates catering to each specific clinical center.²⁰ There are many more improvements for the interarrival rate model, and a thorough review is available in Heitjan et al²¹ and Anisimov.²² While the selected models have room for improvement, our goal is to demonstrate the utility of prediction synthesis in improving prediction results. If one started with more realistic model for the interarrival time, prediction synthesis is still expected to improve results.

In practice, one will not be able to compare the predicted milestone values against an actual milestone time and must make a decision a priori based solely on analysis applied to a partially observed dataset. One could fit the models to the observed data and then use the best fit model for predictions, but this may not yield the best results as can be seen from simulation 1 where the actual model class performed worse than some other individual model predictions. It is indeed very curious that the correct model does not have the best performance. This is because the model is fit to observable data rather than based on prediction accuracy.

There are foundational differences between the method proposed by Lan and Heitjan⁶ and our work. Specifically, the previous study⁶ selects one model that best “fits” the observed data from the individual models and then uses that single model to create predictions. The “cure model” was considered as one of the individual models to provide predictions, and the method allows different treatment arms. In contrast, prediction synthesis compares the prediction accuracy of individual models and then uses the results to combine all individual model predictions into a new prediction density. The “cure model” and different treatment arms can be incorporated into the prediction synthesis model, which may improve the prediction accuracy.

The most difficult problem expected in practice is prediction of the arrivals for future subjects. This feature cannot be predicted from a statistical analysis of the arrival history and is largely controlled by management of a trial. If one envisions a change in the incoming subjects due to a management decision, for example, protocol amendment, changing the set of clinical centers accruing patients, or halting accrual for interim analysis, one could encode these changes into the predictions. Also, if it is known that accrual practices have changed within the observed data chain, it would be wise to base future accrual on the most relevant portion of the accrual chain, typically the most recent. To do so, one could give heavier weight to the most recent accrual data to create a nonhomogeneous Poisson process that is better able to adapt to changing behavior. If one were to include more realistic models for the interarrival times, the predictions are very likely to improve. It is still expected that a prediction synthesis method could be used in conjunction with these improved models to create even better predictions.

There is a natural delay in the data entry for a real clinical trial. The prediction method proposed in this manuscript does not account for this delay. Statisticians who wish to use the proposed method should have a good idea about the natural delays for their specific trial and adjust the predictions accordingly.

We are in the process of creating an R shiny app to implement the aforementioned method. The R shiny app will be available at the following website, https://rtools.mayo.edu/home/.