Fibronectin fiber creep under constant force loading

Abstract

Viscoelasticity is a fundamental property of virtually all biological materials, and proteinaceous, fibrous materials that constitute the extracellular matrix (ECM) are no exception. Viscoelasticity may be particularly important in the ECM since cells can apply mechanical stress resulting from cell contractility over very long periods of time. However, measurements of ECM fiber response to long-term constant force loading are scarce, despite the increasing recognition that mechanical strain regulates the biological function of some ECM fibers. We developed a dual micropipette system that applies constant force to single fibers for up to 8 hours. We utilized this system to study the time dependent response of fibronectin (Fn) fibers to constant force, as Fn fibers exhibit tremendous extensibility before mechanical failure as well as strain dependent alterations in biological properties. These data demonstrate the Fn fibers continue to stretch under constant force loading for at least 8 hours and that this long-term creep results in plastic deformation of Fn fibers, in contrast to elastic deformation of Fn fibers under short-term, but fast loading rate extension. These data demonstrate that physiologically-relevant loading may impart mechanical features to Fn fibers by switching them into an extended state that may have altered biological functions.

1. Introduction

Mechanical stress is ubiquitous within living organisms, and the extracellular matrix (ECM) is routinely loaded by physiological processes such as breathing, fluid flow, and cell contractility. Many ECM structures are also known to be both relatively soft and highly extensible, with extensibilities of beyond 150% strain[1]. Fibronectin (Fn) fibers represent an important provisional component of the ECM that is needed for dynamic alterations in tissue structure during processes such as development, disease progression, and wound hemostasis[2, 3]. The response of Fn fibers to mechanical stretch is a fundamental part of their biological function since these fibers are mechanically stretched by cells in culture[4, 5] as well as in tissue in vivo[6–8]. In fact, most Fn matrix appears to exist in a strained state[5]. However, investigations of the mechanical properties of Fn fibers are limited to constant loading rate experiments[9–11], although investigation of creep under a constant load may more accurately replicate physiological loading.

The need for a detailed understanding of the mechanical properties of Fn fibers is motivated by two factors. First, stretched Fn fibers are a major component of the ECM in numerous physiological processes. It is now widely regarded that many cell types are sensitive to the mechanical properties of their surroundings[12]. This finding has been widely confirmed with the use of reductionist 2D substrates and 3D biomaterials that may have tunable stiffness, porosity, and fiber architecture. However, many cell types in vivo sense and respond to ECM fibers and fibrous mats or sheets. Translation of rigidity sensing work with reductionist model systems such as hydrogels to more native ECM structures requires a detailed understanding of these natural materials. Furthermore, cellular mechanotransduction systems are also sensitive to the viscoelasticity of their surroundings[13, 14], motivating a need to interrogate viscoelastic properties of Fn fibers.

Second, some ECM structures do more than simply resist mechanical loads; mechanical stress also alters the biological functions of some ECM components such as Fn fibers[15]. For example, collagen[16] and fibrin fibers[17] were demonstrated to have altered degradation rates by proteolytic enzymes when these fibers were mechanically loaded relative to their unstressed states. Fn fibers also have altered biological functions in strained versus relaxed states. Fn fiber strain is accommodated by changes in protein conformation including both quaternary and tertiary protein structural changes[18, 19]. Proteins that are known to bind Fn fibers when they are relaxed, but not highly stretched, include bacterial Fn-binding proteins[20], collagen’s R1R2 peptide[21], and integrin α₅β₁[7, 22]. Conversely, mechanical stretch increases the binding of some Fn binding partners through unmasking of cryptic sites in Fn, including interleukin 7[23] and Fn or Fn fragments[24]. It is also possible to image the strained state of Fn fibers by using monoclonal antibodies[18, 25, 26] or other binding partners such as bacteriophage[8] that are also sensitive to Fn molecular conformation. Fn fiber viscoelasticity could have an important impact on Fn fiber function since constant force loading could slowly tune Fn fibers through different biological functions due to creep-induced extension of fibers, which is not captured in the studies above that clamp Fn fibers in a specific strain state.

Although the in vivo loading condition of Fn fibers likely resembles a phase of low strain rate followed by constant or fluctuating force, previous studies of Fn have extended the fibers under variable strain rate conditions. Klotzsch et al. tested Fn fibers at ~10 μm/s[9], and strain rate decreased as strain increased due to the string plucking orientation of the fiber stretching approach. Likewise, Deravi et al. tested Fn fiber mechanics at a stretching rate of 1 μm/s so that strain rate also decreased temporally due to the constant velocity of the tip used for fiber deformation[10]. Thus, a need remains for a more controlled mechanism for Fn fiber extension.

The extensibility of Fn fibers must be accommodated through the breaking of bonds within the fiber. These bonds could stabilize the protein structure of the individual Fn molecules, and intermolecular bonds that stabilize the fiber could also rupture, likely leading to plastic deformation. Previously, we and others have shown that mechanical measurements of Fn fibers are in good agreement with models of Fn fibers based on entropic stretching and stochastic unfolding of FnIII domains[10, 19, 27, 28]. FnIII domains unfold and fold with transition rates proportional to the exponential of force, and thus domains will continue to unfold under constant force[29]. These unfolding events provide this model with inherent time dependence and suggest a hypothesis that time dependence in Fn fibers is due to stochastic unfolding and refolding of FnIII domains under force. Studies of viscoelasticity in single filaments of the ECM components fibrin[30] and collagen[31] have shown that the response of individual fibers of these ECM proteins to force is viscoelastic. Observations of Fn fibers have also suggested a viscoelastic response. Stretch then relaxation of Fn fibers shows fiber hysteresis[10]. In addition, length recovery after stretch then relaxation has been demonstrated to be a time dependent process with complete recovery taking ~8 min[9, 10].

Here, we developed a system to test the creep response of single Fn fibers to a constant force loading regime. This system uses a custom feedback system to maintain a constant force on the fiber even as it extends. This system allows for measurements up to 8 hours while fully immersed in fluid and with high resolution microscopic imaging. We demonstrate that Fn fibers creep under constant force for the full duration allowed with our instrument. In addition to confirming the viscoelastic nature of Fn fibers, these findings also have important implications for Fn mechanobiology since constant force creep leads to significant plastic deformation of these fibers. Thus, plastic deformation may impart a conformational memory to Fn fibers that permanently changes their molecular conformation and hence biological activity.

2. Methods

2.1. Microneedle force probe

Microneedle bending has long been used as a force probe in biological experiments[32–34] and is capable of exquisite sensitivity[35]. Experimental setups similar to the one used here have been used in previous studies of hagfish slime fibers[36] and, more recently, thin Fn mats under constant strain rate conditions[10].

Long term viscoelastic behavior of Fn fibers was tested on a custom built uniaxial tensile tester consisting of a motorized stage on which a single Fn fiber was stretched (see Fig. 1). The fiber was held taut between two glass microneedles of known stiffness. Displacement of the microneedles and hence Fn fiber was measured optically using an Olympus IX-81 inverted microscope (Olympus America, Melville, NY) with an Olympus UPLSAPO 10X 0.4NA lens. The fiber was attached to the ends of two glass microneedles drawn from borosilicate glass capillary tubing (Sutter #B100-75-10) using a Flaming/Brown micropipette puller (Sutter P-97). The fiber was attached to the two glass microneedles via nonspecific adhesion. The tips of the micropipettes were broken off leaving tips of ~7 μm in diameter to which a ~20 μm diameter bulb of soda-lime glass was added. The fixed microneedle was held in a custom fabricated clamp attached to 3-axis stage (Thorlabs DT-12). The second microneedle was held in an identical clamp mounted to another 3-axis stage (Thorlabs DT-12 and MT-1 for motorized axis). The Y-axis of the second micropipette was controlled by a motorized actuator (Thorlabs Z812B with TDC001 motor controller). The fiber was immersed in a fluid chamber formed by top and bottom coverslips separated by 1.3 mm. The fluid is held in the chamber by surface tension allowing the microneedles to penetrate the chamber through the open sides. Thus, all mechanical measurements were performed wet.

Figure 1.

Image of the fiber stretching apparatus attached to the microscope stage. The glass micropipettes were held in XYZ stages attached to the microscope stage by an adaptor plate. The Fn fiber is attached between the stationary sensor pipette and the actuated stretch pipette and immersed in buffer solution in an open sided sample chamber. The position of the stretch pipette is controlled by a proportional feedback loop to maintain a constant force on the Fn fiber.

2.2. Microneedle control system

The microneedle probes were controlled by a custom program written in the Visual Basic language that coordinates motion of the actuated stretching axis through the Thorlabs APT ActiveX modules and image acquisition through the Metamorph Visual Basic programming interface (Molecular Devices, LLC). The Fn fibers were held initially slack before the stage was moved at a maximum velocity of 2 mm/s with an acceleration of 1.5 mm/s². After the stage movement was completed, the fiber and displacement of the microneedle were imaged in brightfield every 1.5 to 2 seconds. A line scan through the end of the pipette (Fig. 2A, C) was saved for analysis in post-processing. The line scan was analyzed in real time to detect the edge of the pipette by detecting an above threshold intensity. The tracked position of the microneedle was used in a proportional feedback loop to keep the applied tension on the fiber constant over the course of the experiment. At each time point the line scan was recorded as well as the elapsed time and the motorized actuator position. We have found a limit to this system of about 8 hours. The open design requires that the water column around the fiber be supplemented with additional water during the experiment due to evaporation. Experiments with PBS require that it be flushed as it evaporates to ensure that salt concentration remains constant.

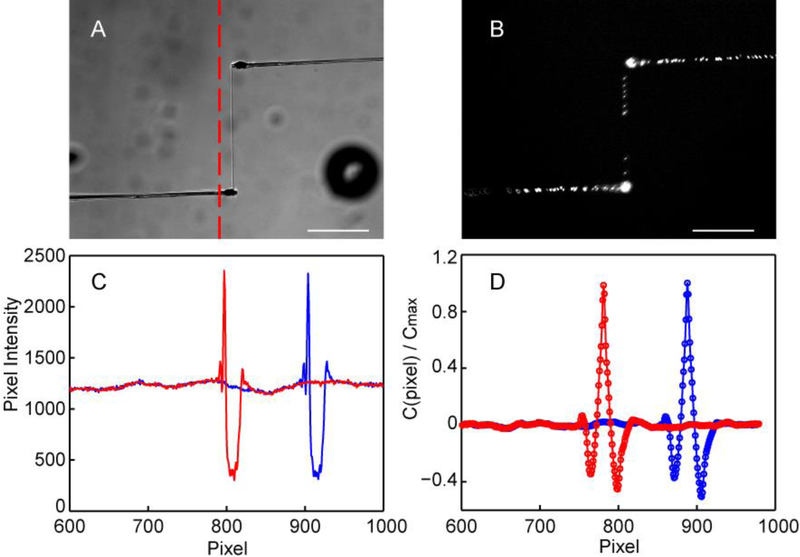
Figure 2.

Pipette tracking method. A) The fixed sensor pipette (bottom-left), Fn fiber, and puller pipette (top-right) are imaged in a brightfield microscope at each time point. A linescan (dashed red line) crossing the end of sensor pipette is processed to track its displacement. B) The Fn fiber contains sparsely distributed fluorescent beads as fiducial markers. C) Representative linescans for the region shown with a vertical dashed red line show the sensor pipette profile when relaxed (blue) or under tension (red). D) The sensor pipette is tracked by comparing the displacement of the pipette signature between the relaxed position (blue) and current position (red) using a cross correlation function C(n) defined in Eq. (1). Sub-pixel resolution was obtained by fitting a quadratic function to the peak of the cross-correlation function. Scale bars are 50 μm, and the length/pixel ratio is 0.64 μm/pixel.

2.3. Fn fiber stretching protocol

Fn fibers were created by dragging a drop of ~1 mg/ml Fn solution with the end of a pipette from one glass microneedle over a gap to the second glass microneedle. As the drop is removed from the first microneedle, a Fn fiber is drawn from the surface of the Fn solution forming a fiber[24]. As the drop is then rolled over the second glass microneedle, the fiber attaches to the needle. This technique is very similar to one we have previously used with the addition of attachment of the fiber to a glass micropipette[19, 24]. The tip must cross the air/water interface of the drop. Although a Fn fiber only results from breaking this interface about 50% of the time, the fibers themselves are highly reproducible as determined by their consistent diameters and their mechanical properties, which are previously published. In a small subset of experiments, a dilute solution of 0.2 μm, polystyrene latex fluorescent beads (Fluoresbrite YG, Polysciences, Inc.) was formed with the Fn solution to provide fiducial markers within the fiber. The fiber was then submerged in 1X phosphate buffered saline (PBS). Mechanical measurements were similar between Fn fibers that did or did not contain fluorescent beads (data not shown).

To extract the position of the needles from the linescan, a discrete cross correlation function was used to identify the displacement of the sensor microneedle from its position at time 0 (Fig. 2C, D). We used a cross correlation function to define the location of the microneedle according to:

$$C(n)={\sum }_m{P}_{needle}(m)P_{linescan}(m+n)$$ (1)

where C(n) is the discrete cross correlation function, P_linescan(m +n) represents the pixel intensities with indices m +n from a line of the image. P_needle are the pixel intensities of the needle signature in the first frame of the time lapse. Thus, the maximum of C(n) tracks the position of the needle. To obtain sub-pixel resolution, the peak in the cross-correlation function was fit with a quadratic function, the maximum of which represents the true pipette location.

The tension on the fiber, F, was calculated using sensor pipette displacement, y, and the effective sensor spring constant, K_sensor, as F(y) = K_sensory. The bending stiffness of the glass microneedles, K_sensor, was determined by comparison to a standard of known stiffness. The calibration standard was made from a single mode optical fiber (Thorlabs #SM800G80, outer diameter 80 μm) that was stripped of its polymeric cladding by soaking in dichloromethane, then secured into a short piece of capillary tubing with epoxy adhesive. The stiffness of the optical fiber, K_cal, was calculated as a cantilevered cylindrical thin beam, K_cal = (3π/4)Er⁴/L³, where E is the elastic modulus of 70 GPa [37], fiber length L was measured with calipers, and r is the fiber radius, 40 μm. The optical fiber modulus was confirmed experimentally by hanging weights on the ends of fibers and measuring the fiber displacement (Fig. 3A). The fiber stiffness, K, was found using the force-displacement linear least squares regression (Fig. 3B) and used to calculate the fiber modulus, which was in good agreement with literature values (Fig. 3C). To calibrate the microneedles, the optical fiber calibration standard was placed in the fixed pipette holder and the microneedle was placed in the pipette holder attached to the motor. The microneedle was brought into contact with the optical fiber and the displacement of the optical fiber by the microneedle was optically tracked to determine the microneedle stiffness (Fig. 3D, E). The microneedle sensor spring constant was defined according to:

$$K_{sensor}=\left(K_{cal}\left(y/Y_{motor}\right)\right)/\left(1-\left(y/Y_{motor}\right)\right)$$ (2)

where y is the calibration standard displacement and Y_motor is the motor displacement, which is the same as the displacement of the microneedle base. The quantity (y/Y_motor) was determined by a linear least squares regression of the tracked calibration standard position (Fig. 3F).

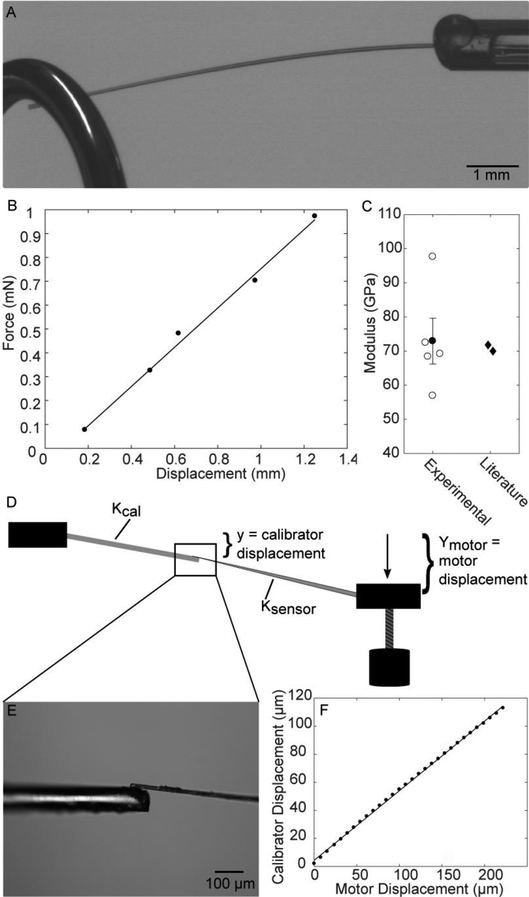
Figure 3.

Microneedle calibration method. A) A weight is hung from the optical fiber calibration standard. B) The displacement of the optical fiber and the force due to the weights are plotted to find the optical fiber stiffness. C) The stiffness is used to calculate the fiber modulus and compare to literature values. Open circles represent individual fiber modulus values, the filled circle is the mean. Error bars show standard error. D-E) Micropipette calibration setup. The displacement of the optical fiber by the microneedle is tracked. F) The linear regression of the calibration fiber displacement and the motor displacement is used to calculate the stiffness of the microneedle.

2.4. Power law curve fits

Fn fiber strain versus time data were fit to a power law of the form f(x) = ax^b±c using Matlab, where a is a fitting parameter, b is the power law scaling parameter, and ±c is the 95% confidence bound of b. Pearson correlation coefficients were also calculated in Matlab after taking the log of fiber strain and time.

2.5. Statistical Analysis

Standard error was calculated as the standard deviation divided by the square root of the number of samples. Pearson correlation coefficients were used to evaluate the strength of the power law relationships, and strong positive correlations were indicated by values close to 1. All calculations were performed in Matlab.

3. Results

3.1. Tracking fiber strain with fiducial markers

We developed a dual micropipette system to measure Fn mechanical properties under constant force extension (Fig. 1). Fn fibers drawn from a solution of purified plasma Fn were suspended between two flexible micropipettes with spring constants of ~4 pN/nm each and immersed in 1x PBS. A fast ramp to a predetermined position was applied to the ‘stretch’ pipette before the bending displacement of the fixed ‘sensor’ pipette was tracked every 1.5 to 2 seconds for times ranging up to 8 hours. The displacement of the sensor pipette was used in a proportional feedback loop to maintain the force at a constant level by moving the position of the stretch pipette. This initial position results in a force value that cannot be predicted. The tension to be applied to the fibers is not set directly but results from the fast extension phase of the experiment before the force is clamped. Typical values of tension on the fibers ranged from 100 nN to 1000 nN. In addition, the maintenance of the fiber force is determined optically using the feedback system. Given the resolution of our images and the sensitivity of the micropipettes used in this study, we could maintain fibers in a band of ±5 nN over the course of the experiment by the feedback mechanism. However, in some experiments this feedback is less optimal, and feedback control could be limited to bands as low as ±30 nN (see Suppl. Fig. 1). Although we cannot make direct comparisons with the force values on Fn fibers in vitro or in vivo, we do know from numerous previous studies that Fn fibers experience strain values of up to 400% strain and that Fn fibers are strained to failure[4, 5, 38]. Thus, we assume that the stress values applied to Fn fibers in this study are consistent with stresses applied to natural Fn matrix fibers.

First, four Fn fibers were tested to ensure that fiber strain was not the result of detachment from the pipettes (Fig. 2). To validate fiber strain, Fn fibers were generated (Fig. 2A) from a drop that also contained a small amount of 0.2 μm fluorescent beads so that Fn fibers pulled from the drop contained fluorescent beads inside the Fn fiber as shown in Fig. 2B. The fiber strain calculated by bead tracking is shown for segments of one fiber in Fig. 4 alongside the fiber strain calculated from the two beads nearest the two ends of the fiber as well as the fiber strain calculated from the inside to inside pipette dimension and the center to center pipette dimension. The bead tracking method determines the fiber strain independently of the pipette to fiber connection and motor position, thus demonstrating the accuracy of the pipette tracking method. The agreement between the two measurements validates that the Fn fibers are securely attached to the pipettes, and this also demonstrates that force values strictly result from fiber strain and not from fiber detachment from the pipettes. The difference between the pipette center to center strain and the inside edge to inside edge strain demonstrates the uncertainty in fiber strain due to the determination of initial fiber length. The initial length of the fiber cannot be determined with higher accuracy than demonstrated in Fig 4. This uncertainty will be reduced in proportion to the fiber initial length.

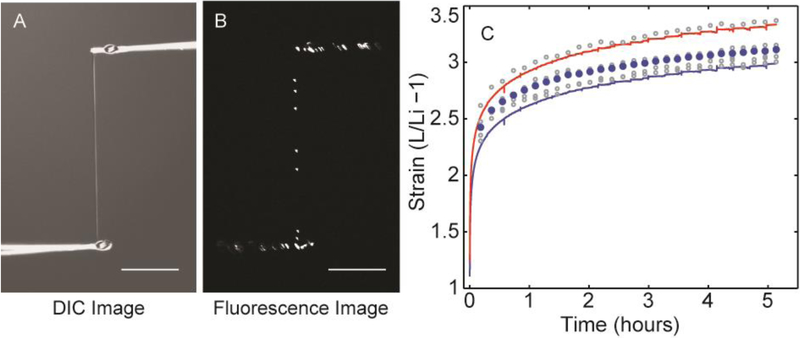
Figure 4.

Fn fiber strain was validated by tracking the positions of fluorescent microbeads embedded within the Fn fiber. These beads acted as fiducial marks along the length of the fiber allowing the fiber strain to be tracked optically independent of the pipette locations. The strain of individual fiber segments calculated by measuring the distance between different pairs of beads is shown as open circles. The total fiber strain determined by the positions of the first and last bead is shown as filled blue circles. These data are compared to the fiber strain determined by pipette displacement and motor position. The fiber initial length in this case was determined by initial pipette-center to pipette-center distance (blue line) or initial pipette-inside-edge to pipette-inside-edge distance (red line). This fiber was stretched with a constant force load of 175 nN.

We first stretched Fn fibers under constant force for up to 8 hours. The feedback system uses a vertical linescan through the image to track movement of the pipette due to stress relaxation (Fig. 2C, D). The feedback system then moves the pipette back to the set force point. A typical constant force extension plot is shown in Fig. 4. All tested Fn fibers showed a decaying, but continuous constant force creep for the duration of all experiments.

3.2. Permanent deformation of Fn fibers after creep testing

Whether Fn fiber stretch leads to plastic deformation of the Fn fiber is an important biological question since Fn fiber plastic deformation may lead to irreversible changes in Fn fiber biological functions. Although the first study on Fn fiber mechanical properties from Dr. Vogel’s group showed no plastic deformation at high rates of extension[9], a later study from Dr. Parker’s lab using slower extension was shown to cause plastic deformation[10]. To determine if constant force extension causes plastic deformation, we repeatedly extended fibers after a brief relaxation period between forced extension. Figure 5 shows a representative plot for a Fn fiber that was loaded with a tension of 960 nN for 30 mins, then relaxed with no load for 15 mins, and this load protocol was repeated through three cycles. The length of the fiber under tension is shown in Fig. 5 along with the applied force for each test. The length of the fiber increased with each subsequent loading period. Because the tension applied to the fiber was the same for all tests it is possible to compare the length of the fibers directly. Although the length overall of the fiber increased with each loading period, the viscoelastic, constant force extension response was similar for each pull. Data for an additional four Fn fibers that underwent similar repeat loading cycles are shown in Suppl. Fig. 1. These data suggest that plastic deformation occurs with slow loading, which is consistent with previous data using a slow force ramp[10].

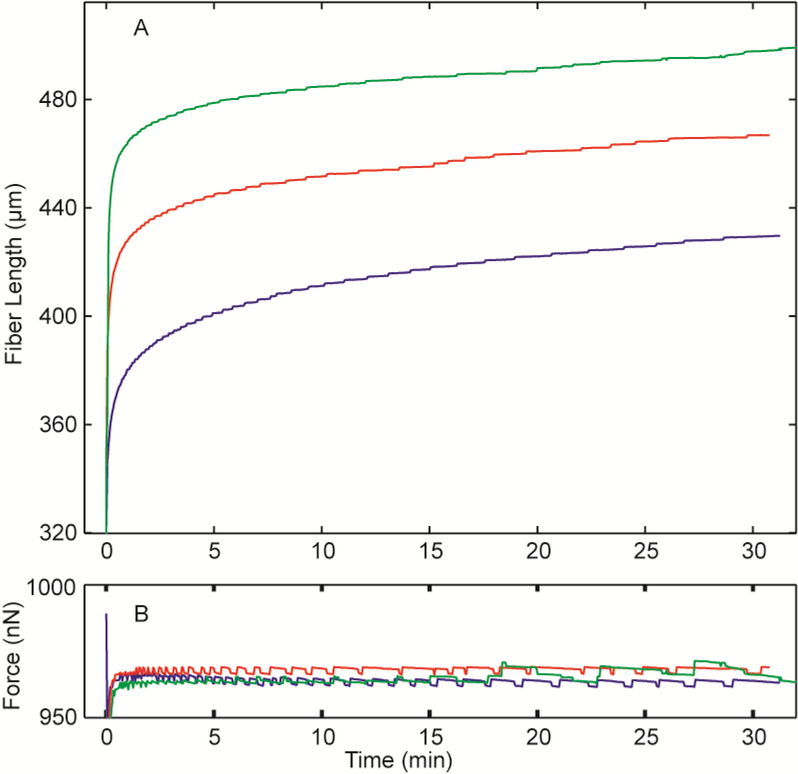
Figure 5.

Fn fibers exhibited permanent deformation after fiber creep testing. A single Fn fiber (initial length 107 μm) was stretched 3 times for 30 min at a constant force of 960 nN, shown in the subplot, and was allowed to relax for 15 min between tests. Stretch 1 is shown in blue, stretch 2 is shown in red, and stretch 3 is shown in green. Permanent deformation was observed as lengthening of the fiber after each creep test.

3.3. Fn fibers display creep on long time scales

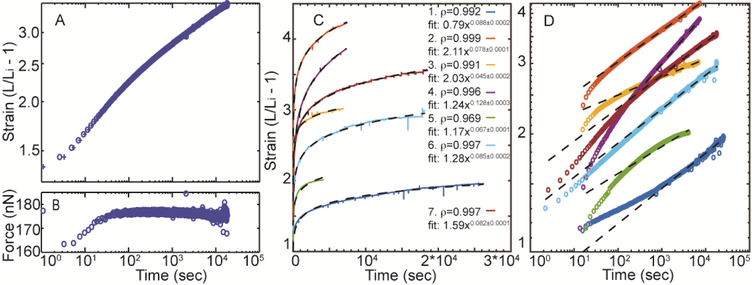
The results of a typical Fn fiber creep test is shown in Fig. 6A, B, and constant force creep is shown for 7 additional fibers in Fig. 6C, D. The fiber length initially increases rapidly then slows and continues to creep for the entire time course of the experiment (~5 hrs). In order to determine if these long-term creep experiments are well-described by a power law, we fit all curves to the form f(x) = ax^b. In addition, we sought to determine whether repeat cycles of constant force loading also follow a power law. These fits are shown in Suppl. Fig. 1, and note that the Pearson correlation coefficient was >0.95 for 17 out of 19 loading cycles provided herein. This suggests that Fn fibers continue to creep with a power law behavior even after repeat loading cycles.

Figure 6.

The strain of a typical Fn fiber under 5 hours of constant force extension plotted in log-log axes (A). The uncertainty in the data acquisition time is shown by bounding the time before (marked as ‘’) and after (marked as ‘✚’) the fiber displacement measurement. Note that these boundaries are almost overlapping and not visible after ~100 seconds. Time was set to zero at the first data point collected after the fiber was given a fast force ramp. The corresponding fiber tension is shown on log-linear axes (B). Representative strain versus time plots are shown for 7 additional fibers in (C) and (D) on linear and log-log scales. Power law fits for all fibers are provided in the inset of panel (C).

4. Discussion

Many ECM structures must resist mechanical loads that result from tissue stretch and application of cellular contractile forces. Developing tools to replicate these mechanical loads on reductionist ECM model systems and measure their response to strain or stress has been a major focus of the biomechanics and mechanobiology communities. Although Fn fibers have been characterized for their response to mechanical force when force is ramped at either fast[9] or slow rates[10, 11], this is the first study to determine the impact of constant force creep of Fn fibers. We measured constant force creep using a novel dual micropipette system with an optical feedback loop. This apparatus was implemented as a simple and low cost addition to an inverted microscope, yet this technique allows maintenance of a constant force on a single Fn fiber within a band of several nN. Using this apparatus, we tested the viscoelastic properties of Fn fibers drawn from solutions of purified Fn. These experiments demonstrated that Fn fibers continue to creep according to a power law for the temporal limit that we could achieve with our setup. Furthermore, this constant force extension resulted in plastic deformation of the Fn fibers. Future studies must determine if this plastic deformation also results in irreversible loss of the mechanobiological switching functions of Fn fibers. For example, an extended period of constant force extension of a Fn fiber may then render these fibers in an antiadhesive state for α₅β₁ integrins[7, 22] even after release of force and relaxation of the fiber.

Although classic studies of cellular rigidity sensation were performed on substrates with linearly elastic properties, it is now recognized that cells respond to the viscoelasticity of their local microenvironment[13, 14, 39]. Constant force creep of Fn matrix fibers may also stimulate a different biological response of cells in vivo than one might infer based on classic rigidity sensation studies. Early works on Fn matrix fibrillogenesis demonstrated that Fn fibers are mechanically loaded with an inward movement of fibrillary adhesions from focal contacts and adhesions at the cell perimeter[40, 41]. Cells apply tension to the substrate over the course of minutes to hours with fluctuations in traction force taking place on time scales of seconds[42, 43]. This study has shown that Fn, a major component of the in vivo cell environment, responds dynamically when stretched on these time scales. Importantly, this suggests viscoelasticity may be sensed by cells attached to fibrous Fn matrices in the same way that static mechanical properties influence cell behavior.

The breakage of intramolecular bonds that stabilize Fn type III domains in a folded conformation provides the mechanism for Fn fiber extension, but the molecular mechanism of plastic deformation is unknown. The mechanics of Fn matrix fibers are driven in large part by the dynamics of conformational changes at the molecular scale[5, 9, 27, 44]. Indeed, cryptic cysteine residues have been used as a reporter system to demonstrate unfolding of one or more of the four Fn type III domains that contain cysteine residues[8, 19, 25, 45]. The contribution of loss of intramolecular bonds and subsequent unfolding events to biomaterial viscoelasticity may be a more broadly relevant phenomenon, and the breakage of intermolecular bonds that stabilize the supermolecular architecture of the Fn fiber could also contribute to plastic deformation. For example, titin unfolding has been suggested to explain the viscoelastic behavior of skeletal myofibrils[46]. Since Fn type III domains found in Fn and titin are known to unfold with transition states that are proportional to the exponential of force, biophysical models of materials composed of these elements should predict constant force creep[19, 27]. Previously, repeated extension of Fn fibers demonstrated that these fibers are capable of full recovery of mechanical properties after relaxation times of greater than 1 min[9], although permanent deformation resulted when Fn fibers were stretched at lower rates of force ramping[10]. These differences may be due to the different manufacturing techniques used to generate the Fn fibers in these two studies, but we hypothesize that permanent deformation of Fn fibers is a slow, time dependent process that may depend on stretching rate. This dynamic response suggests that there are multiple micro-structural processes responsible for the creep response of the Fn fibers. Some of these processes appear to be reversible, while others responsible for the permanent deformation are not. Permanent deformation of the Fn fiber could occur due to sliding of Fn molecules past each other with crosslink rearrangement or loss of intermolecular bonds that stabilize the fiber or the stabilization of Fn type III domains in the unfolded state by interactions with neighboring molecules. Thus, plastic deformation could result from permanent changes to intermolecular bonds that stabilize supermolecular organization or intramolecular bonds that maintain Fn in a folded state. Indeed, previous work using atomic force microscopy has demonstrated that tandem modular proteins can misfold into a structure formed by two neighboring molecules[47]. As Fn fibers are protein dense structures[27], misfolding of neighboring modules could explain plastic deformation.

The temporal strain profile of Fn fibers remarkably resembles a power law over approximately three orders of magnitude of time (Fig. 6 and Suppl. Fig. 1). This may not be entirely unexpected as power law behavior appears in a variety of contexts in biomechanics studies. For example, the creep function of cells also behaves as a power law of elapsed time, indicating that there is a broad distribution of dissipation times in the cell[48]. Insight into the mechanism of power law creep of Fn fibers can be found through investigations of the viscoelasticity of skeletal muscle. Miller and colleagues demonstrated that tissue viscoelasticity arises due to the nature of molecular bonds[49] since bond lifetimes are distributed according to an inverse power law. Although skeletal muscle is a far more complex tissue than Fn fibers composed of only a single protein, a large number of mechanically distinct bonds are required to stabilize Fn fibers. Fn is a modular protein, and individual Fn type III domains have been shown to unfold according to a hierarchy[50, 51].

In conclusion, this study demonstrates that Fn fibers are viscoelastic materials that creep under constant force loads. Constant force creep causes permanent deformation of Fn fibers, although future work must determine if this impacts its biological functions. One final important contribution of this study is the development of an inexpensive technique that can be used to measure wet properties of micrometer-scale fibers. Often, mechanical measurements of fibers developed using wet spinning or electrospinning techniques are made under dry conditions for technical simplicity. However, measurements should be performed in submerged conditions due to the biological importance of measuring fiber properties in buffered solution or culture media.

Supplementary Material

1

Supplementary Figure 1. Fn fibers exhibited permanent deformation after fiber creep testing. Four Fn fibers were stretched 3 times for 30 min and were allowed to relax for 15 min between tests. Stretch 1 is shown in blue, stretch 2 is shown in red, and stretch 3 is shown in green. Permanent deformation was observed as lengthening of the fiber after each creep test. Power law fits and Pearson correlation coefficients are provided for all three loading cycles for all four fibers.