Skip to main content
PMC home page
Nature Communications logoLink to Nature Communications
. 2019 Oct 4;10:4515. doi: 10.1038/s41467-019-12530-w

Synthesis of magnesium-nitrogen salts of polynitrogen anions

Dominique Laniel 1,✉, Bjoern Winkler 2, Egor Koemets 3, Timofey Fedotenko 1, Maxim Bykov 3, Elena Bykova 4, Leonid Dubrovinsky 3, Natalia Dubrovinskaia 1
PMCID: PMC6778147  PMID: 31586062

Abstract

The synthesis of polynitrogen compounds is of fundamental importance due to their potential as environmentally-friendly high energy density materials. Attesting to the intrinsic difficulties related to their formation, only three polynitrogen ions, bulk stabilized as salts, are known. Here, magnesium and molecular nitrogen are compressed to about 50 GPa and laser-heated, producing two chemically simple salts of polynitrogen anions, MgN4 and Mg2N4. Single-crystal X-ray diffraction reveals infinite anionic polythiazyl-like 1D N-N chains in the crystal structure of MgN4 and cis-tetranitrogen N44− units in the two isosymmetric polymorphs of Mg2N4. The cis-tetranitrogen units are found to be recoverable at atmospheric pressure. Our results respond to the quest for polynitrogen entities stable at ambient conditions, reveal the potential of employing high pressures in their synthesis and enrich the nitrogen chemistry through the discovery of other nitrogen species, which provides further possibilities to design improved polynitrogen arrangements.

Subject terms: Solid-state chemistry, Materials chemistry, Materials for energy and catalysis

Polynitrogen compounds are potentially promising high energy density materials, but are difficult to synthesize due to their instability. Here, the authors observe the formation, under high pressure, of a Mg2N4 magnesium–tetranitrogen salt which remains stable at ambient conditions.

Introduction

Polynitrogen entities are recognized to be ideal constituents of high energy density materials (HEDM) on account of the tremendous energy released upon the conversion of singly or doubly bonded N–N atoms to triple-bonded molecular nitrogen1. As a direct consequence of their energetic potential, these low order bonds are highly unstable. So far, only three homonuclear polynitrogen species have been bulk stabilized at ambient conditions: N3−, N5+, and N5−2. In particular, the stabilization and isolation of the N5+ and N5− ions is arduous and typically achieved in salts with a complex, multi-elements, counter ion3–8. Other polynitrogen units are known to exist, such as N4+ and N4, but they are deemed unstable as they have a lifetime below the millisecond threshold9 and can only be kept intact by being trapped in inert matrices at ultralow temperatures10,11.

The application of pressure opens up unique possibilities to explore and produce polynitrogen entities. Indeed, pressure generally promotes electronic delocalization and thus favors the formation of extended and polymeric networks. As a matter of fact, the only bulk stable neutral energetic polynitrogen specie, cubic-gauche polymeric nitrogen (cg-N), was synthesized under pressure, at 110 GPa12. In that same pressure regime, other polynitrogen anions were discovered, such as infinite 1D armchair chains (in FeN4 and ReN8·xN2)13,14 and the pentazolate ring (N5−), found in CsN515. Despite numerous attempts, none of these compounds could be recovered at ambient conditions. The sole exception is the (Li)+(N5)− salt, produced near 50 GPa and retrieved at ambient conditions16. Unlike the vast majority of poly-N ions formed through classical chemistry methods, their pressure-formed counterparts have the significant advantage of being extremely simple, typically with a single element acting as the counter ion.

Atomistic model calculations highlight the outstanding potential of high pressure experiments, as a plethora of polynitrogen entities have been predicted to be stable17–19. Among them, the compression of magnesium and nitrogen was predicted to produce the MgN3, MgN4, and MgN10 salts comprised of exotic anionic benzene-like N6 rings, infinite 1D armchair chains and pentazolates, respectively17–19. To the best of our knowledge, these predictions have not been tested until now.

Here, we demonstrate that the (Mg)2+(N4)2− and the (Mg2)4+ (N4)4− salts are synthesized by compressing and laser-heating magnesium and molecular nitrogen samples above 50 GPa. Single-crystal X-ray diffraction measurements establish polynitrogen entities, namely infinite anionic polythiazyl-like 1D N-N chains and cis-tetranitrogen N44− species, to compose the MgN4 and Mg2N4 solids, respectively. Upon the full pressure release, the β-Mg2N4 compound undergoes an isosymmetric phase transition into the α-Mg2N4 salt, also comprised of cis-tetranitrogen N44− units. These results demonstrate the recoverability to ambient conditions of the pressure-produced N44−entity, emphasizing the potential and importance of the high pressure approach for the discovery and synthesis of improved polynitrogen species.

Results and discussion

Synthesis and characterization of the Mg-N compounds

With the goal of synthesizing nitrogen-rich Mg-N solids, we compressed micrometer-size pure magnesium pieces surrounded by a large volume of molecular nitrogen—used as both a pressure transmitting medium and a reagent—up to about 60 GPa in four diamond anvil cells (DACs). To facilitate a chemical reaction, samples were laser-heated using YAG lasers at pressures of 28.0, 33.0, 43.4, 52.2, 52.4, 52.7, and 58.1 GPa. The specific pressure-temperature paths followed for all samples are summarized in Supplementary Table 1. Metallic Mg served as a YAG laser absorber. Laser-heating at pressures below 52.2 GPa resulted in the formation of a previously known compound, Mg3N2 (space group C2/m),20 identified by both X-ray diffraction and Raman spectroscopy measurements (see Supplementary Figures 1 and 2 as well as Supplementary Table 2). Above the threshold pressure of 52.2 GPa, heating the samples to at least 1850 K led to the growth of the Mg piece—supposedly due to nitrogen diffusing into it—, the appearance of two sets of Raman modes and diffraction lines which did not correspond to known phases of either Mg3N220, pure Mg21, or pure N222,23 (Supplementary Figs. 4–7). Single-crystal X-ray diffraction revealed the crystal structures of two compounds with compositions Mg2N4 and MgN4 (crystallographic data are given in Supplementary Table 3 and Supplementary Table 4).

The MgN4 compound has an orthorhombic structure (Ibam space group) with the lattice parameters a = 3.5860(13) Å, b = 7.526(3) Å and c = 5.1098(17) Å at 58.5 GPa (see Table 1). The magnesium atoms are eight-fold coordinated by nitrogen atoms (see Fig. 1), which are arranged in exotic planar infinite zigzag N-N chains parallel to the a-axis, akin to those found in FeN4 and ReN8·xN2 near 110 GPa13,14. While the MgN4 compound’s crystal chemistry matches the theoretical calculations17–19, the measured lattice parameters do not, as the c parameter is double the predicted value and the structure adopts an I-type unit cell, opposite to the calculated C-type (see Supplementary Discussion). As shown in Supplementary Fig. 18, by drawing the reciprocal lattice corresponding to the predicted parameter c (c = 2.5549(17) Å), reflections appear at the mid-point of the lattice vector c*; weak but distinctly visible. This means that the c value is actually two times larger (c = 5.1098(17) Å) than the predicted one. The C-centering is contradicted by more than 130 experimentally observed reflections. Our DFT calculations reveal the Ibam MgN4 structure to have an enthalpy of about 10 kJ/mol lower than the predicted Cmmm MgN4 solid and to be dynamically stable at 50 GPa (see Supplementary Fig. 10). The full experimental crystallographic data and Raman spectra of Ibam MgN4 are presented in detail in the Supplementary Table 3 and the Supplementary Fig. 5, along with their further comparison to the theoretically computed data (see Supplementary Fig. 8)17,18.

Table 1.

Crystallographic data for the MgN4, β-Mg2N4 and α-Mg2N4 compounds

MgN4 β-Mg2N4 α-Mg2N4
Pressure (GPa) 58.5 58.5 0.0001 (1 bar)
Space group Ibam P21/n P21/n
a (Å) 3.5860(13) 7.113(5) 7.5182(9)
b (Å) 7.526(3) 5.828(6) 6.5426(11)
c (Å) 5.1098(17) 8.800(9) 13.4431(19)
β (°) 90 104.00(7) 130.080(17)
V (Å3) 137.90(9) 354.0(6) 505.95(18)
Fractional atomic coordinates (x; y; z) Mg: (0; 0; 0.25) Mg1: (0.49079; 0.7820;0.36972) Mg1: (−0.03444; −0.26972; −0.14194)
N1: (0.6584; 0.83344;0.5) Mg2: (0.87494; 1.0122;0.65121) Mg2: (0.19484; −0.24500; −0.43089)
N2: (0.2928; 0.3059; 0.5) Mg3: (0.27163; −0.0478; 0.08387) Mg3: (−0.15418; −0.47368; −0.39088)
Mg4: (0.73162; 1.0462; 0.26126) Mg4: (−0.05204; 0.03340; −0.31550)
N1: (0.9146; 0.7621; 0.4030) N1: (0.2053; 0.2398; −0.29135)
N2: (0.5752; 0.2424; 0.4128) N2: (0.0799; −0.2324; −0.32480)
N3: (0.5700; 0.4601; 0.3759) N3: (0.1944; −0.0551; −0.10797)
N4: (1.0672; 0.6905; 0.5081) N4: (−0.3561; −0.1649; −0.32605)
N5: (1.0586; 0.7188; 0.6557) N5: (−0.0018; −0.5637; −0.18680)
N6: (0.2820; 0.2132; 0.2432) N6: (0.1442; 0.3256; −0.39668)
N7: (0.4332; 0.1114; 0.3403) N7: (−0.3255; 0.2339; −0.45463)
N8: (0.7714; 0.8544; 0.4546) N8: (−0.4397; −0.2489; −0.43838)
Open in a new tab

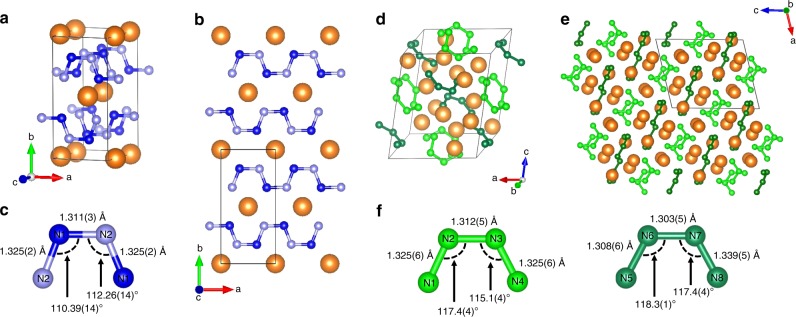
Fig. 1.

Fig. 1

Open in a new tab

The crystal structure of the MgN4 and β-Mg2N4 salts at 58.5 GPa. a The unit cell of MgN4 (the light blue, dark blue and orange spheres represent the N1, N2 and Mg atoms, respectively); b a projection of the MgN4 structure along the c-axis, emphasising 1D chains of nitrogen atoms aligned along the a-axis; c a repeating N42− subunit of a chain with the N-N distances and angles indicated; d the unit cell of β-Mg2N4 (the light green and dark green spheres represent the four distinct nitrogen atoms forming the a-N44− and b-N44− units, respectively, the orange spheres represent Mg atoms); e a projection of the β-Mg2N4 structure along the b-axis allowing to see the alternating layers of isolated a-N44− and b-N44− units, intercalated with Mg2+ ions. f The a-N44− (left) and b-N44− (right) entities with bond lengths and angles indicated

The structure of the high pressure Mg2N4 phase (Fig. 1) has a monoclinic P21/n symmetry with lattice parameters a = 7.114(3) Å, b = 5.824(2) Å, c = 8.804(4) Å and β = 104.04(3)° at 58.5 GPa (see Table 1). We name it β-Mg2N4, to distinguish from its ambient pressure modification α-Mg2N4 (see below). The unit cell of β-Mg2N4 contains twelve symmetrically independent atoms, four Mg and eight N. The atomic arrangement gives rise to an exotic poly-N entity: a N4 unit with a formal charge of 4−. The tetranitrogen anion has a surprising cis-like shape, analogous to the nitrogen skeleton in cis-tetrazene—here observed as an isolated molecule24,25. The eight nitrogen atoms form two discernable N44− units, hereafter named a-N44− and b-N44−, with slight variations in their N-N distances. At 58.5 GPa, a-N44− has bond lengths of 1.325(6), 1.312(5) and 1.325(6) Å while b-N44− has 1.308(6), 1.303(5), and 1.339(5) Å, for the first edge bond, the center bond, and the second edge bond, respectively. These modest differences underline a subtle but complex dissimilarity in their chemical environment, namely their proximity and coordination with the Mg2+ ions.

Theoretical insight on the β-Mg2N4 salt

The DFT model calculations confirm the β-Mg2N4 structural model in great detail and hence can confidently be employed to analyze its electronic structure (see Supplementary Table 5 for the complete analysis). The inspection of the total and partial density of states of β-Mg2N4 unambiguously exposes that there is only a very weak covalent bonding between N44− entities, and electron difference maps exhibits no charge accumulation between the Mg and N atoms. Instead, a strong ionic interaction between the Mg and N ions is observed: a Mulliken analysis shows that Mg is essentially in its charged formal state and a semi-quantitative comparison to MgCl2 implies that the bonding between Mg2+ and the N44− entities is even slightly more ionic than between Mg2+ and Cl−. Within the N44− entities, the edge and center bonds have the same Mulliken bond population, consistent with their similar bond lengths (~1.318 ± 0.015 Å). This theoretical insight exhibits the stark differences in electronic density configuration between the N44− entities in β-Mg2N4 and those previously observed in trans-tetrazene or tetrazadiene complexes, in which the N44− units are instead stabilized through strong covalent bonds and bond length disparities denote the single and double bond character of the edge and center bonds, respectively24,25.

As the P21/n β-Mg2N4 compound—and its crystal chemistry—had not been predicted by previous theoretical calculations, its enthalpy at 50 GPa was compared to the enthalpies of the P63/mcm and the Cmcm MgN2 structures that had been predicted17,18. We found that P21/n β-Mg2N4 is energetically competitive with the two predicted structure as all were found to be equal within 5 kJ/mol, which is less than the uncertainty of our calculations. The Raman spectrum of P21/n β-Mg2N4 was also computed and reproduces well the experimental spectrum recorded at 49.7 GPa, as seen in Supplementary Fig. 11.

Recovery of the α-Mg2N4 salt to ambient conditions

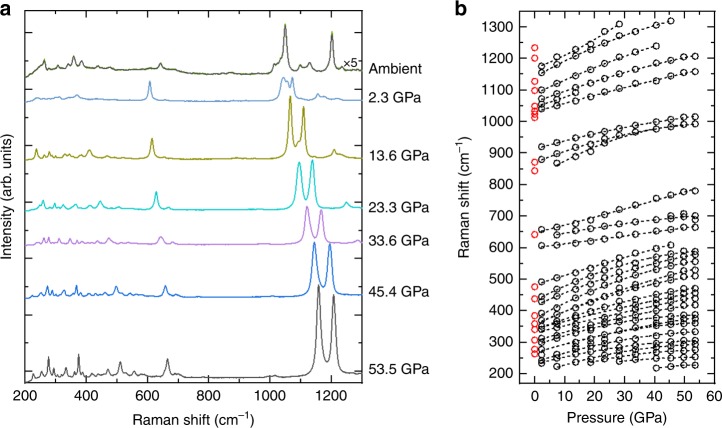
After the synthesis of the β-Mg2N4 compound, the DACs were slowly decompressed and Raman as well as XRD measurements were performed at each step of the decompression to track possible changes. Both the vibrational modes (Fig. 2) and the lattice parameters (Fig. 3 and Supplementary Tables 5–8) vary smoothly with pressure, displaying no sign of a chemical reaction, decomposition or phase transition down to 2.3 GPa. However, the opening of the DACs in air leads to the loss of the Raman signal from the sample,  caused by its deterioration, presumably following a chemical reaction with the water or the oxygen in air (see Supplementary Fig. 13). Therefore, at various pressures below 18 GPa, the DACs were opened in a glovebox under an inert atmosphere of argon. After the release of pressure, the DACs were closed, still in the glovebox, so that the samples were preserved in an inert atmosphere at ambient pressure. Microphotographs of a sample before and after the complete release of pressure are shown in Supplementary Fig. 12. The Raman spectra of these decompressed samples appeared to be different from those previously observed for β-Mg2N4. To clarify their structure and chemical composition, the samples were investigated employing single-crystal and powder XRD.

Fig. 2.

Fig. 2

Open in a new tab

Evolution of the Raman modes of the Mg2N4 compounds with pressure. a Typical Raman spectra of Mg2N4 taken during decompression from 53.5 GPa to ambient conditions. The spectra at ambient conditions is markedly different than those at higher pressures, evidencing a phase transition. b Pressure dependence of the Raman modes' frequencies, which evolve smoothly and continuously down to 2.3 GPa. Red dots indicate the modes at ambient pressure. The spectra are offset along the y-axis for clarity and ×5 indicates that the spectrum is five-times magnified

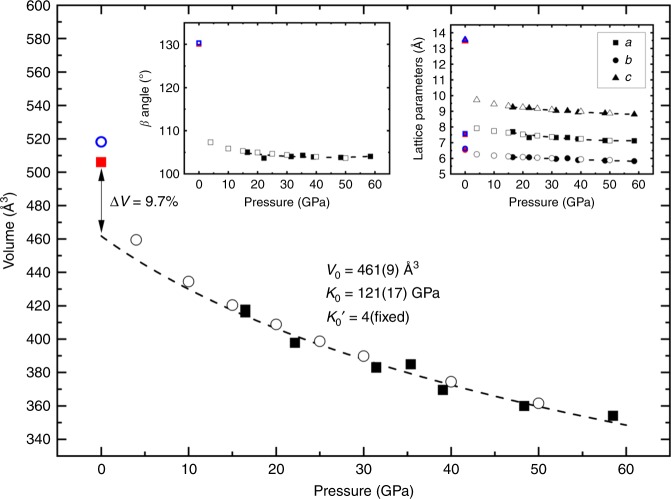
Fig. 3.

Fig. 3

Open in a new tab

Unit cell volume of the Mg2N4 compounds as a function of pressure. All solid and open symbols are experimental and theoretical data points, respectively, while the dashed line is the fit of the experimental PV data of the β-Mg2N4 compound using the second order Birch-Murnaghan equation of state (BM2 EoS) (V0 = 461(9) Å3 and K0 = 121(17) GPa). Red and blue symbols are the experimental and theoretical, respectively, unit cell volume of α-Mg2N4 at ambient pressure. The extrapolation of the experimental equation of state suggests a volume jump of 9.7% between the high pressure β-Mg2N4 and the ambient pressure α-Mg2N4 phases. The fit of the theoretical PV data using the BM2 EoS gives for β-Mg2N4 V0 = 470.23 Å3 and K0 = 110.83 GPa. The theoretical volume difference is thus of 10.2% between the calculated β-Mg2N4 and α-Mg2N4. The insets show the dependence of the unit cell parameters on pressure. The full (open) black and full red (open blue) symbols represent experimental (theoretical) data from the β and α phases of Mg2N4. The slightly higher volume obtained from the DFT calculations, compared to the experimental values, shows the underbinding in GGA26

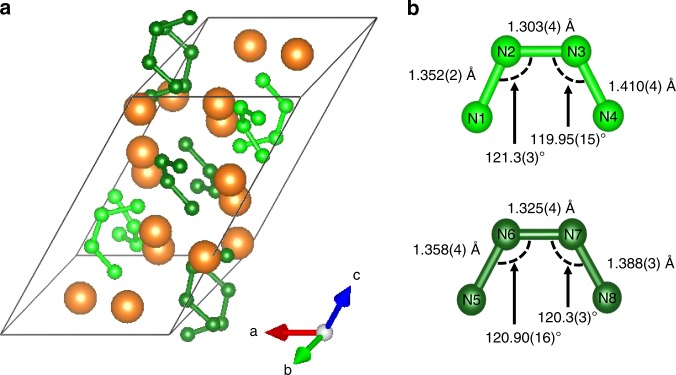
The single-crystal XRD analysis revealed a polymorph of Mg2N4 (α-Mg2N4), which still contains two distinct N44− units (Fig. 4). Its structural details are found in Table 1 while the full crystallographic data are provided in the Supplementary Table 9. A Le Bail refinement performed on a diffractogram collected from a α-Mg2N4 sample at ambient conditions (i.e., after the release of gaseous N2) revealed no other phases, as seen in Supplementary Fig. 15. The structure has the same monoclinic symmetry (P21/n space group) with lattice parameters of a = 7.5182(9) Å, b = 6.5426(11) Å, c = 13.4431(19) Å, and β = 130.080(17)°. The unit cell is strongly deformed in comparison to the high pressure polymorph, with a large increase of the unit cell parameters c and β as well as a decrease of the unit cell parameter a. The stacking of the N44− units in α-Mg2N4 also differs from that in the high pressure β-Mg2N4 phase, as shown in Supplementary Fig. 17. The structural model is again confirmed in great detail by DFT calculations, which also show that the α-Mg2N4 is more stable than the β-Mg2N4 by 10 kJ/mol at ambient conditions (see Supplementary Discussion).

Fig. 4.

Fig. 4

Open in a new tab

Crystal structure of the α-Mg2N4 salt at ambient conditions. a The unit cell of α-Mg2N4 (see also Supplementary Fig. 16). b The bond lengths and angles in the two distinct N44− entities: the a’-N44− (light green, top) and b’-N44− (dark green, bottom). The orange and green spheres represent Mg and N atoms, respectively

In the α-Mg2N4 phase, both of the N44− entities display slightly longer N-N distances. In a’-N44−, the bond lengths are of 1.352(2), 1.303(4) and 1.410(4) Å, while in b’-N44− they are 1.358(4), 1.325(4) and 1.388(3) Å, for the first edge bond, the center bond and the second edge bond, respectively. This resembles the bonds lengths measured in some tetrazadiene complexes (namely [Ir(RNNNNR)(CO)(PPh3)2][BF4], where R is 4-FC6H4)25. The DFT calculations show that there are essentially no differences in the character of chemical bonding between the Mg2+ and the N44−entities in α-Mg2N4 and β-Mg2N4, implying that it is still strongly ionic. The energy released upon the decomposition of α-Mg2N4 into Mg3N2 and molecular N2 is calculated to be about 1.9 kJ/g, which is about two times less than known for TNT27,28.

The α-Mg2N4 salt encapsulated in inert atmosphere persisted at ambient conditions for several months, as evidenced by single-crystal X-ray diffraction and Raman spectroscopy (see Supplementary Fig. 14). Although Raman spectroscopy measurements suggest the stability of the MgN4 compound at least down to 0.9 GPa (see Supplementary Fig. 9), it was not detected by XRD at a pressure other than 58.5 GPa. The DFT calculations suggest this compound to be elastically unstable at ambient conditions, as the c44 and c66 parameters were calculated to have values below 0 GPa. Further experiments and calculations are underway to conclusively determine the stability domain of MgN4.

The high pressure investigation of the Mg-N system unveiled an exotic and unexpected chemistry. First, a compound featuring infinite 1D polynitrogen chains was obtained near 50 GPa—half of the pressure previously thought to be required13,14. Second, in the same pressure domain, previously unknown (N4)4− polynitrogen anions were synthesized and stabilized in the simple Mg2N4 salt. Its high pressure polymorph (β-Mg2N4) undergoes a phase transition on pressure release, but the (N4)4− polynitrogen units persist in its low pressure polymorph (α-Mg2N4), adding a unique (N4)4− anion to a yet very short list of poly-N entities bulk stabilized at ambient conditions. The tetranitrogen anion can spark further research for producing improved energetic polynitrogen compounds. Moreover, these results underline the potential and possibilities that are enabled by high pressure chemistry, along with its applicability to produce compounds compatible with ambient conditions.

Methods

Sample preparation

A few pure magnesium flakes of typically about 10 × 10 × 5 µm3 in size were positioned on one of the diamond anvils, with culet diameter of 250 µm. Rhenium was used as the gasket material. A small ruby chip was loaded along with the sample and used to determine the pressure inside the pressure chamber29. The diamond anvil cell (DAC) pressure chamber was then loaded with pure molecular nitrogen (~1200 bars) in a high pressure vessel. Pure nitrogen, acting as both a pressure transmitting medium and a reagent, was always largely in excess with respect to magnesium.

Throughout the procedure, care was taken to minimize the exposure of Mg to air. On average, the magnesium flakes were exposed for about 20 min to air during the complete loading procedure. According to previous investigations30, an exposure of this time span is expected to produce a 20–50 nm protective oxide film at the surface of Mg, which prevents further chemical reaction between Mg and elements in the air. Considering the volume of the loaded Mg pieces (about 10 × 10 × 5 µm3), the very limited amounts of Mg oxides are not thought to play a role in the observed chemical reactions between nitrogen and magnesium. Indeed, sample characterization by Raman spectroscopy and X-ray diffraction never revealed vibrational modes or diffraction peaks that could be attributed to a solid other than a Mg-N compound.

Raman spectroscopy

Sample characterization was achieved in part by confocal Raman spectroscopy measurements performed with a LabRam spectrometer equipped with a ×50 Olympus objective. Sample excitation was accomplished using a continuous He-Ne laser (632.8 nm line) with a focused laser spot of about 2 μm in diameter. The Stokes Raman signal was collected in a backscattering geometry by a CCD coupled to an 1800 l/mm grating, allowing a spectral resolution of approximately 2 cm−1. At ambient pressure, after the release of gaseous molecular nitrogen, the full power Raman laser—4.6 mW incident on the DAC—resulted in the decomposition of the α-Mg2N4 crystallites; the irradiated spots becoming dark and no longer displaying the α-Mg2N4 vibrational modes. To avoid this, the laser power was reduced by employing neutral filters by a factor of approximately 6 (0.75 mW on the DAC).

X-ray diffraction

The X-ray diffraction studies were performed at the P02.2 beamline (λ = 0.2901 Å) at PETRA III. In order to determine the sample position on which the single crystal X-ray diffraction acquisition is obtained, a full X-ray diffraction mapping of the experimental cavity is performed. The sample position displaying the most single crystal reflections belonging to the phase of interest is chosen for the collection, in step-scans of 0.5° from −36° to +36° ω, of the single crystal X-ray diffraction data. The CrysAlisPro software31 is utilized for the single crystal data analysis. The analysis procedure includes the peak search, the removal of the diamond anvils’ parasitic reflections, finding reflections belonging to a unique single crystal, the unit cell determination and the data integration. The crystal structures are then solved and refined within the JANA2006 software32. The procedure for single crystal X-ray diffraction data acquisition and analysis was previously demonstrated and successfully employed13,14,33,34. Powder X-ray diffraction was also performed to verify the chemical homogeneity of the samples. The powder X-ray data was integrated with Dioptas35 and analyzed with the XRDA software36. Le Bail refinements employing a powder X-ray diffraction pattern was accomplished with the FullProf software37.

Laser-heating

The double-sided sample laser-heating was performed at our home laboratory at the Bayreuth Geoinstitut using two YAG lasers. Pure magnesium, which is metallic, was employed as the YAG laser absorber. Temperatures were accurately determined from the sample’s blackbody radiation38. Samples were heated between 10 and 15 min and moved under the YAG beams to evenly heat the whole magnesium piece.

Atomistic modeling

Density functional theory (DFT) calculations have been performed using the CASTEP code39. The code is an implementation of Kohn-Sham DFT based on a plane wave basis set in conjunction with pseudopotentials. The plane-wave basis set is unbiased (as it is not atom-centered) and does not suffer from the problem of basis-set superposition error unlike atom-centered basis sets. It also makes converged results straightforward to obtain in practice, as the basis set convergence is controlled by a single adjustable parameter, the plane wave cut-off. Pseudopotentials were either norm-conserving or ultrasoft, and were generated using the PBE exchange-correlation functional40 using the ‘on the fly’ parameters included in the CASTEP 2019 distribution. These pseudopotentials have been shown to be very accurate and are very well suited for the calculations carried out here41. The Brillouin-zone integrals were performed using Monkhorst-Pack grids42 with spacings between grid points of less than 0.02 Å−1. Full geometry optimizations of the unit cell parameters and the internal coordinates were performed until forces were converged to <0.01 eV/Å and the residual stress was <0.02 GPa. Phonon dispersion curves and Raman spectra were computed using linear response theory43 as implemented in CASTEP44. The population analysis was carried out as implemented in CASTEP45. Band gaps were obtained from band structure calculations. DFT-GGA calculations tend to systematically underestimate the band gap.

We benchmarked our model calculations by comparison of our results to the experimentally determined ambient conditions structure of Mg3N2, which adopts the space group Ia31 and has a lattice parameter of 9.9528(1) Å46. Our calculations gave a = 10.0127 Å, thus showing the often observed slight underbinding in GGA calculations. The experimental Raman spectrum47 is well reproduced, as shown in Supplementary Fig. 3.

Supplementary information

Supplementary Information (2.3MB, pdf)
Peer Review File (622.3KB, pdf)

Acknowledgements

The authors acknowledge the Deutsches Elektronen-Synchrotron (DESY, PETRA III) for provision of beamtime at the P02.2 beamline. Alexander Kurnosov is greatly thanked for helping with sample loadings employing the high pressure gas loader. D.L. thanks the Alexander von Humboldt Foundation for financial support. N.D. and L.D. thank the Federal Ministry of Education and Research, Germany (BMBF, grants no. 5K16WC1 and no. 05K19WC1) and the Deutsche Forschungsgemeinschaft (DFG projects DU 954–11/1, DU 393–9/2, and DU 393–13/1) for financial support. B.W. gratefully acknowledges funding by the DFG in the framework of the research unit DFG FOR2125 and within projects WI1232.

Author contributions

D.L., L.D. and N.D. conceptualized the research, D.L., E.K., T.F., M.B. and E.B. participated to the experimental data collection, B.W. performed all theoretical calculations and carried out their analysis, D.L., E.K, T.F. and M.B. conducted the sample laser-heating, D.L. analyzed the experimental results, wrote the original draft and created the figures, D.L., B.W., L.D. and N.D. reviewed and edited the draft.

Data availability

The details of the crystal structure investigations may be obtained from the Cambridge Crystallographic Data Centre (CCDC), 12 Union Road, CB2 1EZ Cambridge, United Kingdom (fax: + 44 (0)1223 336033; e-mail: admin@ccdc.cam.ac.uk) on quoting the deposition numbers CSD 1918150–1918155 and CSD 19182019. The data that support the findings of this study are available from the corresponding author upon reasonable request.

Competing interests

The authors declare no competing interests.

Footnotes

Peer review information Nature Communications thanks Karl Christe, Kamil Dziubek, and the other, anonymous, reviewer for their contribution to the peer review of this work. Peer reviewer reports are available.

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary information is available for this paper at 10.1038/s41467-019-12530-w.

References

  • 1.Klapötke, T. M. New Nitrogen-Rich High Explosives. in High Energy Density Materials 85–121 (Springer, 2007).
  • 2.Christe KO. Polynitrogen chemistry enters the ring. Science. 2017;355:351–351. doi: 10.1126/science.aal5057. [DOI] [PubMed] [Google Scholar]
  • 3.Vij A, Pavlovich JG, Wilson WW, Vij V, Christe KO. Experimental detection of the pentaazacyclopentadienide (pentazolate) anion, cyclo-N5- Angew. Chem. - Int. Ed. 2002;41:3051–3054. doi: 10.1002/1521-3773(20020816)41:16&#x0003c;3051::AID-ANIE3051&#x0003e;3.0.CO;2-T. [DOI] [PubMed] [Google Scholar]
  • 4.Christe KO, Wilson WW, Sheehy JA, Boatz JA. N5+: a novel homoleptic polynitrogen ion as a high energy density material. Angew. Chem. Int. Ed. 1999;38:2004–2009. doi: 10.1002/(SICI)1521-3773(19990712)38:13/14&#x0003c;2004::AID-ANIE2004&#x0003e;3.0.CO;2-7. [DOI] [PubMed] [Google Scholar]
  • 5.Xu Y, et al. A series of energetic metal pentazolate hydrates. Nature. 2017;549:78–81. doi: 10.1038/nature23662. [DOI] [PubMed] [Google Scholar]
  • 6.Jiang C, et al. Synthesis and characterization of the pentazolate anion cyclo-N5– in (N5)6(H3O)3(NH4)4Cl. Science. 2017;355:347–376. doi: 10.1126/science.aal5120. [DOI] [PubMed] [Google Scholar]
  • 7.Zhang W, et al. Stabilization of the Pentazolate Anion in a Zeolitic Architecture with Na20N60and Na24N60Nanocages. Angew. Chem. - Int. Ed. 2018;57:2592–2595. doi: 10.1002/anie.201710602. [DOI] [PubMed] [Google Scholar]
  • 8.Zhang C, et al. A symmetric Co(N5)2(H2O)4 4H2O high-nitrogen compound formed by cobalt(II) cation trapping of a cyclo-N5− anion. Angew. Chem. - Int. Ed. 2017;56:4512–4514. doi: 10.1002/anie.201701070. [DOI] [PubMed] [Google Scholar]
  • 9.Cacace F, de Petris G, Troiani A. Experimental detection of tetranitrogen. Science. 2002;295:480–481. doi: 10.1126/science.1067681. [DOI] [PubMed] [Google Scholar]
  • 10.Knight LB, et al. ESR and ab initio theoretical studies of the cation radicals 14N4+ and 15N4+: The trapping of ion-neutral reaction products in neon matrices at 4 K. J. Chem. Phys. 1987;87:885–897. doi: 10.1063/1.453243. [DOI] [Google Scholar]
  • 11.Thompson WE, Jacox ME. The vibrational spectra of molecular ions isolated in solid neon. II. O4+ and O4- J. Chem. Phys. 1989;91:3826–3837. doi: 10.1063/1.456868. [DOI] [Google Scholar]
  • 12.Eremets MI, Gavriliuk AG, Trojan IA, Dzivenko DA, Boehler R. Single-bonded cubic form of nitrogen. Nat. Mater. 2004;3:558–563. doi: 10.1038/nmat1146. [DOI] [PubMed] [Google Scholar]
  • 13.Bykov M, et al. Fe-N system at high pressure reveals a compound featuring polymeric nitrogen chains. Nat. Commun. 2018;9:2756. doi: 10.1038/s41467-018-05143-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Bykov M, et al. High-pressure synthesis of a nitrogen-rich inclusion compound ReN 8 ⋅ x N 2 with conjugated polymeric nitrogen chains. Angew. Chem. Int. Ed. 2018;57:9048–9053. doi: 10.1002/anie.201805152. [DOI] [PubMed] [Google Scholar]
  • 15.Steele BA, et al. High-pressure synthesis of a pentazolate salt. Chem. Mater. 2017;29:735–741. doi: 10.1021/acs.chemmater.6b04538. [DOI] [Google Scholar]
  • 16.Laniel D, Weck G, Gaiffe G, Garbarino G, Loubeyre P. High-pressure synthesized lithium pentazolate compound metastable under ambient conditions. J. Phys. Chem. Lett. 2018;9:1600–1604. doi: 10.1021/acs.jpclett.8b00540. [DOI] [PubMed] [Google Scholar]
  • 17.Yu S, et al. Emergence of novel polynitrogen molecule-like species, covalent chains, and layers in magnesium–nitrogen Mg x N y phases under high pressure. J. Phys. Chem. C. 2017;121:11037–11046. doi: 10.1021/acs.jpcc.7b00474. [DOI] [Google Scholar]
  • 18.Wei S, et al. Alkaline-earth metal (Mg) polynitrides at high pressure as possible high-energy materials. Phys. Chem. Chem. Phys. 2017;19:9246–9252. doi: 10.1039/C6CP08771J. [DOI] [PubMed] [Google Scholar]
  • 19.Xia K, et al. Pressure-stabilized high-energy-density alkaline-earth-metal pentazolate salts. J. Phys. Chem. C. 2019;123:10205–10211. doi: 10.1021/acs.jpcc.8b12527. [DOI] [Google Scholar]
  • 20.Hao J, et al. Structural phase transformations of Mg3N2 at high pressure: experimental and theoretical studies. Inorg. Chem. 2009;48:9737–9741. doi: 10.1021/ic901324n. [DOI] [PubMed] [Google Scholar]
  • 21.Stinton GW, et al. Equation of state and high-pressure/high-temperature phase diagram of magnesium. Phys. Rev. B. 2014;90:134105. doi: 10.1103/PhysRevB.90.134105. [DOI] [Google Scholar]
  • 22.Eremets MI, et al. Structural transformation of molecular nitrogen to a single-bonded atomic state at high pressures. J. Chem. Phys. 2004;121:11296–11300. doi: 10.1063/1.1814074. [DOI] [PubMed] [Google Scholar]
  • 23.Olijnyk H. High pressure x-ray diffraction studies on solid N2 up to 43.9 GPa. J. Chem. Phys. 1990;93:8968. doi: 10.1063/1.459236. [DOI] [Google Scholar]
  • 24.Holleman, A. F. & Wiberg, E. Lehrbuch der Anorganischen Chemie. (Walter de Gruyter, 1995).
  • 25.Moore DS, Robinson SD. Catenated nitrogen ligands part I.1 Transition metal derivatives of triazenes, tetrazenes, tetrazadienes, and pentazadienes. Adv. Inorg. Chem. 1986;30:1–68. doi: 10.1016/S0898-8838(08)60239-1. [DOI] [Google Scholar]
  • 26.Winkler B, Milman V. Density functional theory based calculations for high pressure research. Z. f.ür. Krist. – Cryst. Mater. 2014;229:112–122. [Google Scholar]
  • 27.Lindsay CM, Fajardo ME. The quest for greater chemical energy storage in energetic materials: grounding expectations. AIP Conf. Proc. 2017;1793:040023. doi: 10.1063/1.4971517. [DOI] [Google Scholar]
  • 28.Zhang J, Oganov AR, Li X, Niu H. Pressure-stabilized hafnium nitrides and their properties. Phys. Rev. B. 2017;95:020103. doi: 10.1103/PhysRevB.95.020103. [DOI] [Google Scholar]
  • 29.Dewaele A, Torrent M, Loubeyre P, Mezouar M. Compression curves of transition metals in the Mbar range: experiments and projector augmented-wave calculations. Phys. Rev. B. 2008;78:104102. doi: 10.1103/PhysRevB.78.104102. [DOI] [Google Scholar]
  • 30.Nordlien JH. Morphology and structure of oxide films formed on magnesium by exposure to air and water. J. Electrochem. Soc. 1995;142:3320. doi: 10.1149/1.2049981. [DOI] [Google Scholar]
  • 31.Rigaku Oxford Diffraction. CrysAlisPro Software system. (2015).
  • 32.Petrícek V, Dušek M, Palatinus L. Crystallographic computing system JANA2006: General features. Z. fur Krist. 2014;229:345–352. [Google Scholar]
  • 33.Bykov M, et al. Synthesis of FeN4 at 180 GPa and its crystal structure from a submicron-sized grain. Acta Crystallogr. Sect. E Crystallogr. Commun. 2018;74:1392–1395. doi: 10.1107/S2056989018012161. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Bykova, E. Single-crystal X-ray diffraction at extreme conditions in mineral physics and material sciences. (University of Bayreuth, 2015).
  • 35.Prescher C, Prakapenka VB. DIOPTAS: a program for reduction of two-dimensional X-ray diffraction data and data exploration. High. Press. Res. 2015;35:223–230. doi: 10.1080/08957959.2015.1059835. [DOI] [Google Scholar]
  • 36.Desgreniers S, Lagarec K. XRDA: a program for energy-dispersive X-ray diffraction analysis on a PC. J. Appl. Crystallogr. 1994;27:432–434. doi: 10.1107/S0021889893012610. [DOI] [Google Scholar]
  • 37.Rodriguez-Carvajal J. Recent advances in magnetic structure determination neutron powder diffraction. Phys. B Condens. Matter. 1993;192:55–69. doi: 10.1016/0921-4526(93)90108-I. [DOI] [Google Scholar]
  • 38.Mezouar M, et al. Methodology for in situ synchrotron X-ray studies in the laser-heated diamond anvil cell. High. Press. Res. 2017;37:170–180. doi: 10.1080/08957959.2017.1306626. [DOI] [Google Scholar]
  • 39.Clark SJ, et al. First principles methods using CASTEP. Z. fur Krist. 2005;220:567–570. [Google Scholar]
  • 40.Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  • 41.Lejaeghere K, et al. Reproducibility in density functional theory calculations of solids. Science. 2016;351:1–7. doi: 10.1126/science.aad3000. [DOI] [PubMed] [Google Scholar]
  • 42.Monkhorst HJ, Pack JD. Special points for Brillouin-zone integrations. Phys. Rev. B. 1976;13:5188–5192. doi: 10.1103/PhysRevB.13.5188. [DOI] [Google Scholar]
  • 43.Baroni S, de Gironcoli S, Dal Corso A, Giannozzi P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 2001;73:515–562. doi: 10.1103/RevModPhys.73.515. [DOI] [Google Scholar]
  • 44.Refson K, Tulip PR, Clark SJ. Variational density-functional perturbation theory for dielectrics and lattice dynamics. Phys. Rev. B - Condens. Matter Mater. Phys. 2006;73:1–12. doi: 10.1103/PhysRevB.73.155114. [DOI] [Google Scholar]
  • 45.Segall MD, Pickard CJ, Shah R, Payne MC. Population analysis in plane wave electronic structure calculations. Mol. Phys. 1996;89:571–577. doi: 10.1080/002689796173912. [DOI] [PubMed] [Google Scholar]
  • 46.Partin DE, Williams DJ, O’Keeffe M. The crystal structures of Mg3N2 and Zn3N2. J. Solid State Chem. 1997;132:56–59. doi: 10.1006/jssc.1997.7407. [DOI] [Google Scholar]
  • 47.Heyns AM, Prinsloo LC, Range KJ, Stassen M. The vibrational spectra and decomposition of α-calcium nitride (α-Ca3N2) and magnesium nitride (Mg3N2) J. Solid State Chem. 1998;137:33–41. doi: 10.1006/jssc.1997.7672. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information (2.3MB, pdf)
Peer Review File (622.3KB, pdf)

Data Availability Statement

The details of the crystal structure investigations may be obtained from the Cambridge Crystallographic Data Centre (CCDC), 12 Union Road, CB2 1EZ Cambridge, United Kingdom (fax: + 44 (0)1223 336033; e-mail: admin@ccdc.cam.ac.uk) on quoting the deposition numbers CSD 1918150–1918155 and CSD 19182019. The data that support the findings of this study are available from the corresponding author upon reasonable request.

Articles from Nature Communications are provided here courtesy of Nature Publishing Group

RESOURCES