Quantifying stochastic uncertainty in detection time of human-caused climate signals

Significance

Climate observations comprise one sequence of natural internal variability and the response to external forcings. Large initial condition ensembles (LEs) performed with a single climate model provide many different sequences of internal variability and forced response. LEs allow analysts to quantify random uncertainty in the time required to detect forced “fingerprint” patterns. For tropospheric temperature, the consistency between fingerprint detection times in satellite data and in 2 different LEs depends primarily on the size of the simulated warming in response to greenhouse gas increases and the simulated cooling caused by anthropogenic aerosols. Consistency is closest for a model with high sensitivity and large aerosol-driven cooling. Assessing whether this result is physically reasonable will require reducing currently large aerosol forcing uncertainties.

Abstract

Large initial condition ensembles of a climate model simulation provide many different realizations of internal variability noise superimposed on an externally forced signal. They have been used to estimate signal emergence time at individual grid points, but are rarely employed to identify global fingerprints of human influence. Here we analyze 50- and 40-member ensembles performed with 2 climate models; each was run with combined human and natural forcings. We apply a pattern-based method to determine signal detection time ${\mathit{t}}_{\mathit{d}}$ in individual ensemble members. Distributions of ${\mathit{t}}_{\mathit{d}}$ are characterized by the median ${\mathit{t}}_{\mathit{d}\left\{\mathit{m}\right\}}$ and range ${\mathit{t}}_{\mathit{d}\left\{\mathit{r}\right\}}$, computed for tropospheric and stratospheric temperatures over 1979 to 2018. Lower stratospheric cooling—primarily caused by ozone depletion—yields ${\mathit{t}}_{\mathit{d}\left\{\mathit{m}\right\}}$ values between 1994 and 1996, depending on model ensemble, domain (global or hemispheric), and type of noise data. For greenhouse-gas–driven tropospheric warming, larger noise and slower recovery from the 1991 Pinatubo eruption lead to later signal detection (between 1997 and 2003). The stochastic uncertainty ${\mathit{t}}_{\mathit{d}\left\{\mathit{r}\right\}}$ is greater for tropospheric warming (8 to 15 y) than for stratospheric cooling (1 to 3 y). In the ensemble generated by a high climate sensitivity model with low anthropogenic aerosol forcing, simulated tropospheric warming is larger than observed; detection times for tropospheric warming signals in satellite data are within ${\mathit{t}}_{\mathit{d}\left\{\mathit{r}\right\}}$ ranges in 60% of all cases. The corresponding number is 88% for the second ensemble, which was produced by a model with even higher climate sensitivity but with large aerosol-induced cooling. Whether the latter result is physically plausible will require concerted efforts to reduce significant uncertainties in aerosol forcing.

Large initial condition ensembles (LEs) are routinely performed by climate modeling groups (1–3). Typical LE sizes range from 30 to 100. Individual LE members are generated with the same model and external forcings, but are initialized from different conditions of the climate system (3). Each LE member provides a unique realization of the “noise” of natural internal variability superimposed on the underlying climate “signal” (the response to the applied changes in forcing).

Because internal variability in a LE is uncorrelated across realizations, averaging over ensemble members damps noise and improves estimates of externally forced signals (Fig. 1). LEs are a valuable test bed for analyzing the signal-to-noise (S/N) characteristics of different regions, seasons, and climate variables (1–5) and for comparing simulated and observed internal variability (6). Such information can inform “fingerprint” studies (7), which seek to identify externally forced climate change patterns in observations (8, 9).

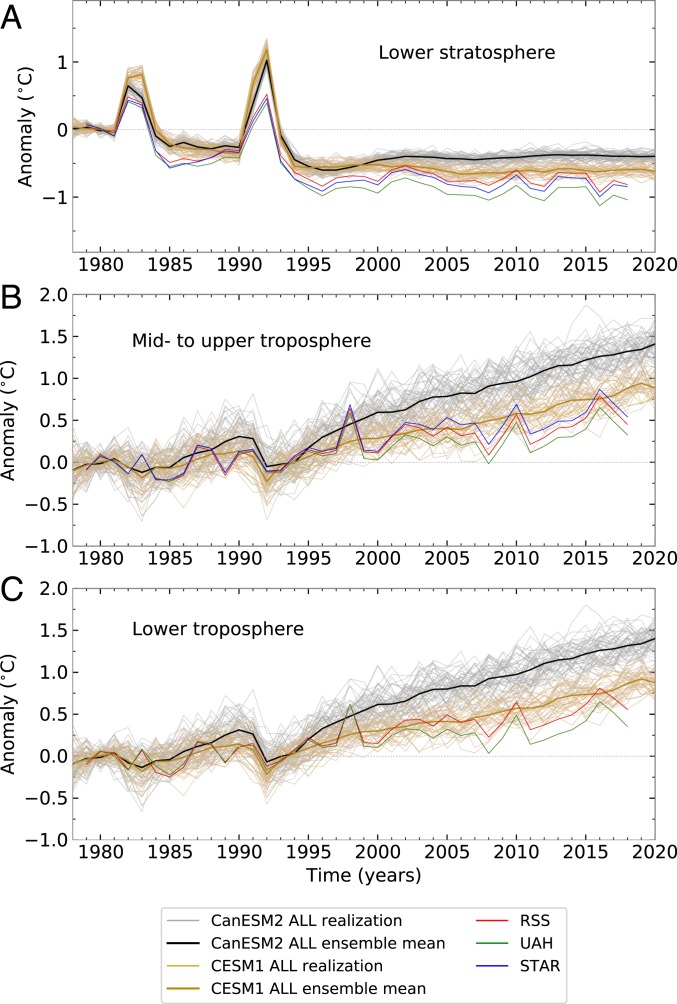
Fig. 1.

Time series of anomalies in annual-mean atmospheric temperature in the 50- and 40-member CanESM2 and CESM1 ALL ensembles (respectively) and in RSS, STAR, and UAH satellite data. (A–C) Results are for TLS (A), TMT (B), and TLT (C). Temperatures are spatially averaged over areas of common coverage in the simulations and satellite data (82.5°N to 82.5°S for TLS and TMT and 82.5°N to 70°S for TLT). The reference period is 1979 to 1981. STAR does not provide TLT data.

Few previous fingerprint studies have exploited LEs (5, 10). Our study uses LEs to quantify stochastic uncertainty in the detection time of global and hemispheric fingerprint patterns and assesses whether this stochastic uncertainty encompasses the actual fingerprint detection times in observations. We employ LEs performed with 2 different climate models for this purpose. We also compare information from local S/N analysis at individual grid points with results from the S/N analysis of large-scale patterns.

Most fingerprint studies rely on variability from a multimodel ensemble of control runs with no year-to-year changes in external forcings (8, 9, 11). Alternative internal variability estimates can be obtained from externally forced LEs performed with a single model (5). We evaluate here whether these estimates are similar and whether the type and size of external forcing in a LE modulate internal variability (12) and influence $t_d$.

Our focus is on the temperature of the lower stratosphere (TLS), the temperature of the mid- to upper troposphere (TMT), and the temperature of the lower troposphere (TLT), which have not been analyzed in previous LE studies. Satellite-based microwave sounders have monitored the temperatures of these 3 layers since late 1978 (13, 14). We calculate synthetic TLS, TMT, and TLT from a 50-member LE generated with the Canadian Earth System Model (CanESM2) (3, 5, 10) and from a 40-member LE performed with the Community Earth System Model (CESM1) (1, 2). In both LEs, the models were driven by estimated historical changes in all major anthropogenic and natural external forcings (henceforth “ALL”).

For CanESM2, additional 50-member LEs were available with combined solar and volcanic effects only (SV) and with individual anthropogenic forcing by ozone (OZONE), aerosols (AERO), and well-mixed greenhouse gases (GHG). These ensembles allow us to quantify the contributions of different forcings to temperature changes in the CanESM2 ALL experiment. Comparable LEs were not available from CESM1 at the time this research was performed.

Our fingerprint approach relies on a standard method that has been applied to many different climate variables (8, 9, 11, 15, 16). We calculate $t_d$ for global and hemispheric patterns. For each domain, the ensemble-mean CanESM2 or CESM1 ALL fingerprint is searched for in individual ALL realizations and in satellite temperature data from Remote Sensing Systems (RSS), the Center for Satellite Applications and Research (STAR), and the University of Alabama at Huntsville (UAH) (13, 14, 17). The data, model simulations, and fingerprint method are described in Materials and Methods and SI Appendix. Unless otherwise stated, results are for the 40-y satellite era (1979 to 2018).

Temperature Time Series and Patterns

The observations and CanESM2 and CESM1 ALL LEs are characterized by nonlinear cooling of the lower stratosphere (Fig. 1A). This nonlinearity is primarily driven by changes in ozone (18–20). After pronounced ozone depletion and stratospheric cooling in the second half of the 20th century, controls on the production of ozone-depleting substances led to gradual recovery of ozone and TLS in the early 21st century (18).

Observed lower stratospheric cooling over 1979 to 2018 ranges from −0.30 °C to −0.23 °C per decade (for UAH and RSS, respectively). TLS trends are always smaller in CanESM2, which has an ensemble range of −0.18 °C to −0.14 °C per decade. This difference may be partly due to underestimated ozone loss in the observational dataset used to prescribe CanESM2 ozone changes (21, 22). In CESM1, an offline chemistry–climate model was used to calculate the stratospheric ozone changes prescribed in the ALL simulation (22). The CESM1 ensemble range (−0.27°C to −0.23 °C per decade) includes 2 of the 3 satellite TLS trends.

In the troposphere, observations and both model ALL LEs show global warming over the satellite era (Fig. 1 B and C). Human-caused increases in well-mixed GHGs are the main driver of this signal (8, 9, 23). Simulated tropospheric warming is generally larger than in satellite data. In TMT, for example, the ensemble trend range is 0.35 °C to −0.43 °C per decade for CanESM2 and 0.20 °C to −0.28 °C per decade for CESM1, while the largest observational trend is −0.20 °C per decade.

Multiple factors contribute to these model-observed warming-rate discrepancies. One factor is possible differences between model equilibrium climate sensitivity (ECS) and the true but unknown real-world ECS (24, 25). Differences in anthropogenic aerosol forcing may also play a role (26). Other relevant factors include different phasing of simulated and observed internal variability (27–29), omission in the ALL simulations of cooling from moderate post-2000 volcanic eruptions (27, 30, 31), and residual errors in satellite data (13, 32).

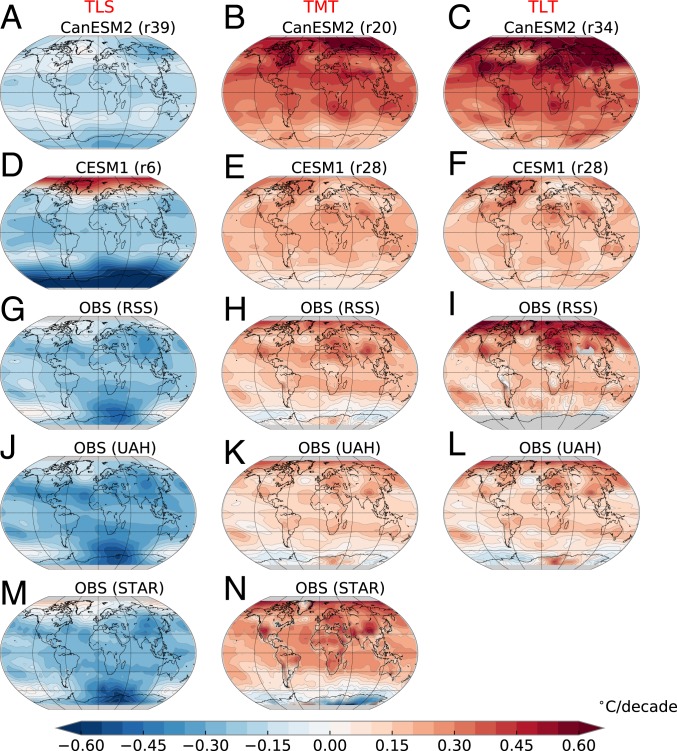
In terms of spatial patterns, both the observations and the model ALL ensembles show large-scale stratospheric cooling and tropospheric warming signals (Fig. 2). Even the CanESM2 and CESM1 ALL realizations with the smallest trends in global-mean temperature exhibit large-scale decreases in TLS and increases in TMT and TLT. There is also model–data agreement in hemispheric features of Fig. 2, such as the common signal of greater tropospheric warming in the Northern Hemisphere (NH).

Fig. 2.

(A–N) Least-squares linear trends over 1979 to 2018 in annual-mean TLS (A, D, G, J, and M), TMT (B, E, H, K, and N), and TLT (C, F, I, and L). Results are from 1 individual CanESM2 and CESM1 ALL realization (A–F) and from 3 different satellite datasets (RSS, UAH, and STAR) (G–N). Model results display the ensemble member with the smallest global-mean lower stratospheric cooling trend or tropospheric warming trend.

The CanESM2 LEs with individual forcings provide further insights into the causes of atmospheric temperature changes in the CanESM2 ALL simulation. The OZONE, AERO, SV, and GHG LEs confirm the dominant roles of ozone depletion in lower stratospheric cooling and of well-mixed GHG increases in tropospheric warming (SI Appendix and SI Appendix, Figs. S1 and S2).

Local S/N Ratios

We consider next the geographical distribution of local S/N ratios. As defined here and elsewhere (1, 33), local S/N is the ratio between the ensemble-mean trend at grid-point $x$ and the between-realization standard deviation of the trend at $x$. We focus on trends over 1979 to 2018 in the CanESM2 ALL ensemble (Fig. 3). The CESM1 ALL ensemble shows qualitatively similar patterns of local S/N (SI Appendix, Fig. S3).

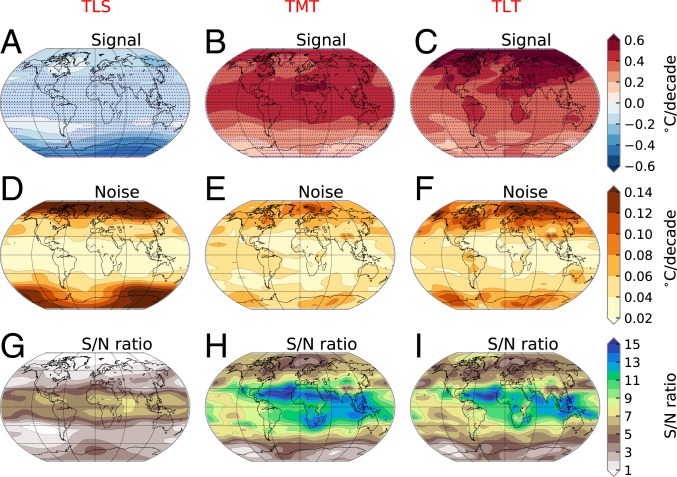
Fig. 3.

Signal, noise, and S/N ratios in the 50-member CanESM2 ALL LE. Results are for TLS (A, D, and G), TMT (B, E, and H), and TLT (C, F, and I). The signal (A–C) is the ensemble-mean trend in annual-mean atmospheric temperature over 1979 to 2018. The noise (D–F) is the standard deviation of the 50 individual temperature trends. G–I show the ratio between signal and noise. Stippling in A–C denotes grid points where S/N exceeds 2.

In the lower stratosphere, the maximum cooling signal is at high latitudes in the Southern Hemisphere (SH), where ozone depletion has been largest (Fig. 3A). Cooling is smaller but significant in the tropics. The between-realization variability of TLS trends is largest over both poles and smallest in the deep tropics (Fig. 3D). These signal and noise patterns explain why TLS S/N ratios reach maximum values in the tropics (Fig. 3G).

The tropics also have advantages for identifying tropospheric warming. As a result of moist thermodynamic processes (11), TMT trends are largest in the tropics. Tropical noise levels are relatively small. This spatial congruence of high signal strength and low noise yields large S/N ratios for tropical TMT trends (Fig. 3 B, E, and H). Because TLT is more directly affected by feedbacks associated with reduced NH snow cover and Arctic sea-ice extent, lower tropospheric warming is largest poleward of 60°N. S/N ratios for TLT trends reach maximum values between 30°N and 30°S, where signal strength is more moderate but noise levels are small (Fig. 3 C, F, and I).

The spatial average of the local S/N results in Fig. 3 is smallest for TLS. This suggests that the forced signal in ALL would be detected latest for TLS. Fingerprinting yields the opposite result, for reasons discussed in SI Appendix.

Fingerprints and Leading Noise Patterns

Our signal detection method relies on a pattern of climate response to external forcing (11). This is the fingerprint $F\left(x\right)$, defined here using ensemble-mean changes in annual-mean temperature in either the CanESM2 or the CESM1 ALL runs. We seek to determine whether $F\left(x\right)$ is becoming more similar over time to geographical patterns of temperature change in individual ALL realizations and satellite data. To address this question, we require internal variability noise estimates in which there is no expression of the fingerprint, except by chance. Noise information is taken from the single-model between-realization variability of the CanESM2 ALL and SV LEs and from a multimodel ensemble of control runs performed under phase 5 of the Coupled Model Intercomparison Project (CMIP5) (Materials and Methods and SI Appendix).

Before discussing fingerprint detection times, it is useful to examine basic features of the fingerprint and noise patterns. The CanESM2 ALL fingerprints capture global-scale lower stratospheric cooling and tropospheric warming (SI Appendix, Fig. S4). CESM1 ALL fingerprints (not shown) are very similar. The fingerprints are spatially dissimilar to smaller-scale, opposite-signed spatial features in the multimodel and single-model noise estimates (SI Appendix, Figs. S5 and S6). This is favorable for signal identification (34).

It was not evident a priori that the multimodel ensemble of CMIP5 control runs and the single-model between-realization variability in CanESM2 would yield similar internal variability patterns. This suggests that the patterns in SI Appendix, Figs. S4 and S5 are primarily dictated by large-scale modes of stratospheric and tropospheric temperature variability that are well captured in CanESM2 and the multimodel ensemble. It is also noteworthy that the magnitude and type of external forcing in the CanESM2 ALL and SV LEs do not appear to significantly modulate the large-scale spatial structure of the leading modes of atmospheric temperature variability. Forced modulation of certain modes of internal variability has been reported elsewhere (12, 35, 36).

Pattern-Based Signal-to-Noise Ratios

We estimate the fingerprint detection time $t_d$ with timescale-dependent S/N ratios (Materials and Methods and SI Appendix). We define $t_d$ as the year at which the time-increasing pattern similarity between the fingerprint and satellite data first rises above (and then remains above) time-increasing similarity between the fingerprint and patterns of internal variability.

Fig. 4 shows the individual components of the S/N ratios used to calculate $t_d$. In this example, the CanESM2 ALL fingerprints for global patterns of lower stratospheric and mid- to upper tropospheric temperature change are searched for in individual CanESM2 ALL realizations and in satellite data. The assumed start date for monitoring temperature changes is 1979, the beginning of satellite temperature records. As the trend length $L$ increases from 10 y to 40 y, the amplitude of signal trends decreases for TLS and increases for TMT (Fig. 4 A and B). Decreasing signal strength for TLS is primarily driven by partial recovery of ozone in the early 21st century (18, 37) (SI Appendix, Fig. S2). The increasing signal strength for TMT occurs because concentrations of well-mixed GHGs rise throughout the satellite era (38). As expected based on Fig. 1, signal strength for TLS is larger in satellite data than in the CanESM2 ALL LE; the converse holds for TMT.

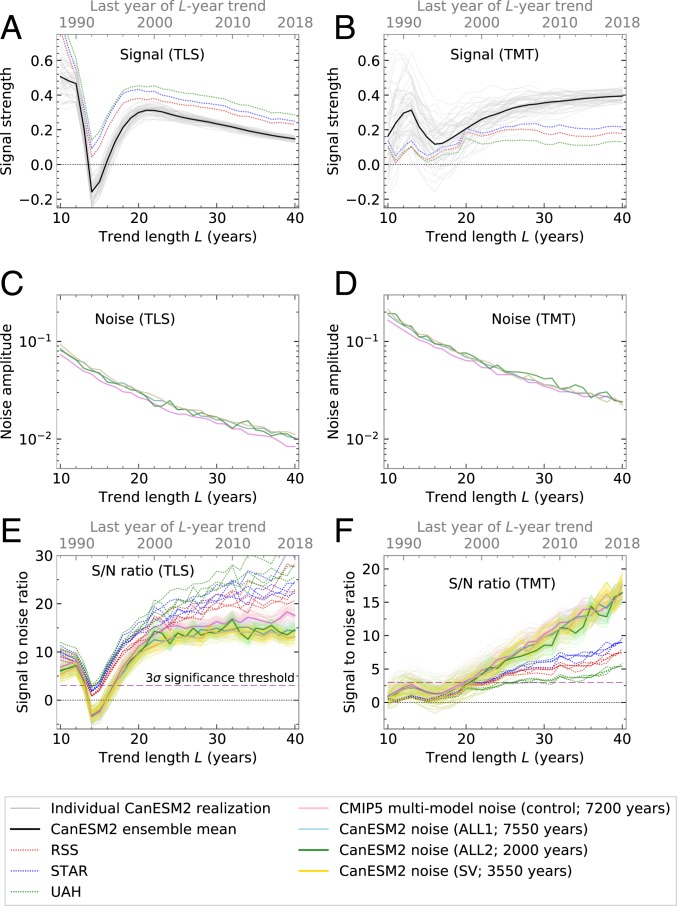
Fig. 4.

Signal, noise, and S/N ratios from a pattern-based fingerprint analysis of annual-mean atmospheric temperature changes in the CanESM2 ALL ensemble and in satellite data. Results are for TLS (A, C, and E) and TMT (B, D, and F) and are a function of the trend length $L$. The domain is near global ($80^{○}$N to $80^{○}$S for TLS and TMT). For definition of signal trends (A and B) and the standard deviation of the sampling distribution of noise trends (C and D), refer to Materials and Methods.

The sharp decrease in signal amplitude for trends ending in the early 1990s reflects stratospheric warming and tropospheric cooling caused by the 1991 Pinatubo eruption (11) (Fig. 1). Pinatubo’s effects are of opposite sign to the searched-for ALL fingerprints (SI Appendix, Fig. S4 A and B). Because the large thermal inertia of the ocean has greater influence on tropospheric than on stratospheric temperature, the signal strength minimum occurs earlier for TLS than for TMT, and recovery of signal strength to pre-eruption levels is faster in TLS than in TMT (compare Fig. 4 A and B).

As the trend-fitting period $L$ increases, the standard deviation of the null distributions of noise trends, $s\left\{b_{\text{N}}\right\}$, decreases in size (Fig. 4 C and D). This is expected: With increasing $L$, it is more difficult for internal variability to generate large warming or cooling trends (11). At all timescales considered, $s\left\{b_{\text{N}}\right\}$ is smaller in the stratosphere than in the troposphere. This difference in noise levels explains why the spread in signal trends is smaller in TLS than in TMT (Fig. 4 A and B).

The 4 different sources of internal variability information yield similar values of $s\left\{b_{\text{N}}\right\}$ across the range of timescales considered here (Fig. 4 C and D). This indicates that these variability estimates are not only similar in terms of the patterns of leading noise modes—they also have comparable amplitude.

For both the ALL ensemble and satellite data, exceedance of the $3\sigma$ signal detection threshold occurs earlier for TLS than for TMT (Fig. 4 E and F). The S/N ratios also reflect pronounced model vs. observed differences in signal strength. Implications of these results for $t_d$ are discussed below.

Detection Time Results

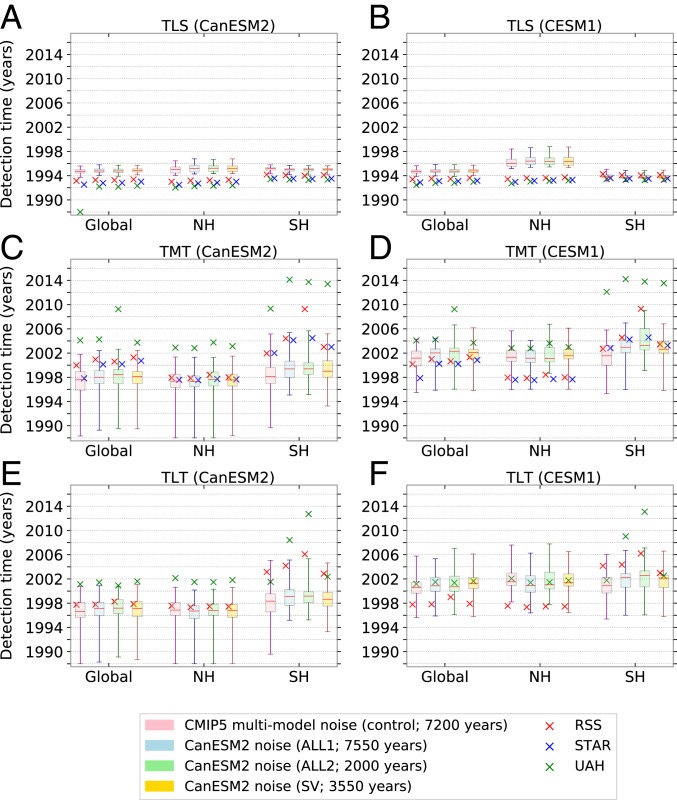
Two types of fingerprint detection time are shown in Fig. 5. The box-and-whiskers plots are detection times calculated solely with model simulation output. The colored crosses denote the times at which model fingerprints are statistically identifiable in satellite temperature data.

Fig. 5.

(A–F) Detection time $t_d$ for a pattern-based fingerprint analysis of TLS (A and B), TMT (C and D), and TLT (E and F). Results are for the globe, NH, and SH, with 4 different estimates of internal variability and a $3\sigma$ detection threshold. In A, C, and E, CanESM2 ALL fingerprints are compared with satellite temperature data (colored crosses) and with individual realizations of the CanESM2 50-member ALL ensemble (box-and-whiskers plots). The $t_d$ results in B, D, and F are analogous, but involve CESM1 fingerprints and individual realizations of the 40-member CESM1 ALL ensemble. Box-and-whiskers plots characterize basic statistical properties of the model-only $t_d$ distributions: the median $t_{d\left\{m\right\}}$ (horizontal red line), the interquartile range (shaded box), and the range $t_{d\left\{r\right\}}$ between the earliest and latest detection times in the ensemble (whiskers). Note that since the ALL fingerprints are very similar for CanESM2 and CESM1, observational detection times are similar for the 2 models.

In “model-only” $t_d$ results, we search for the CanESM2 ALL fingerprints in individual CanESM2 ALL realizations. CESM1 is treated analogously. There is a separate 50-member (CanESM2) or 40-member (CESM1) distribution of $t_d$ values for each model ALL LE, atmospheric layer, geographical domain, and noise estimate. The distribution properties of interest are the median $t_{d\left\{m\right\}}$ and the range $t_{d\left\{r\right\}}$ between the earliest and latest detection times.

There are 2 striking features of the model-only results. First, the CanESM2 and CESM1 ALL fingerprints are always detected earlier in the stratosphere than in the troposphere. Across regions, noise estimates, and the 2 model ALL LEs, $t_{d\left\{m\right\}}$ varies from 1994 to 1996 for TLS and from 1997 to 2003 for both TMT and TLT. These differences in fingerprint detection time are primarily related to the effects of the Pinatubo eruption, which temporarily mask anthropogenic cooling of the lower stratosphere and anthropogenic warming of the troposphere. Because ocean thermal inertia has a smaller effect on stratospheric than on tropospheric temperature, this masking effect decays more rapidly in TLS than in TMT or TLT.

A second notable feature of the model-only results is that $t_{d\left\{r\right\}}$ is smaller for lower stratospheric temperature (1 to 3 y) than for tropospheric temperature (8 to 15 y). Multiple factors contribute to this difference. The large external forcing caused by Pinatubo “synchronizes” individual realizations of the ALL LEs for several years after the eruption (Fig. 1). This synchronization effect is more pronounced in TLS because of its lower between-realization noise levels and because of the above-mentioned stratosphere–troposphere differences in the magnitude, timing, and recovery timescale of the Pinatubo temperature signal (Fig. 4 A and B). The result is a narrow time window during which S/N ratios for TLS cross the $3\sigma$ significance threshold (Fig. 4E).

In the lower stratosphere, the average value of $t_{d\left\{m\right\}}$ across regions and noise estimates is similar for both CanESM2 and CESM1 (ca. 1995). For TMT and TLT, however, the average of $t_{d\left\{m\right\}}$ lies between 1997 and 1998 for CanESM2 and between 2001 and 2002 for CESM1 (Fig. 5). Earlier fingerprint detection in CanESM2 is mostly due to the model’s larger global-mean tropospheric warming (Fig. 1 B and C).

Next, we seek to determine $P_1$, the percentage of the total number of observational $t_d$ values that lie within the stochastic uncertainty $t_{d\left\{r\right\}}$ (SI Appendix). In CanESM2, $P_1=0$ for TLS: Fingerprint detection time in observations is always earlier than the earliest $t_d$ value in the model ALL ensemble (Fig. 5A). This is likely due to the previously discussed underestimate of stratospheric ozone forcing in CanESM2 and the resulting underestimate of observed lower stratospheric cooling (Fig. 1A). For CESM1, $P_1=33\%$ for TLS, and it is only in the SH that observational $t_d$ values fall within the stochastic uncertainty inferred from the model (Fig. 5B).

In the troposphere, $P_1=88\%$ for CESM1 and 60% for CanESM2. These results primarily reflect larger tropospheric warming in CanESM2 than in CESM1 or observations (Fig. 1 B and C). This larger warming signal amplifies model-only S/N ratios in CanESM2 and shifts detection time earlier relative to CESM1 and observations (Fig. 5 C–F). A secondary (and partly countervailing) effect is that the decadal variability of tropospheric temperature is larger in CanESM2 than in CESM1 (11). This contributes to $t_{d\left\{r\right\}}$ values that are on average 2 to 3 y larger for CanESM2 than for CESM1.

Fig. 5 also provides information on the relative detectability of fingerprints in the 3 geographical domains. The most obvious differences are in the troposphere, where fingerprint detection occurs earlier in the NH than in the SH. This result reflects hemispheric differences in land–ocean distribution, heat capacity, and sea ice and snow cover changes.

Detection times for model TLS fingerprints are similar in the 3 satellite datasets (Fig. 5 A and B). This is due to 2 factors: long-term lower stratospheric cooling trends that differ by less than 25% in RSS, STAR, and UAH and the “synchronization” of TLS changes for several years after the Pinatubo eruption. In contrast, detection times for model TMT and TLT fingerprints are (in all but 2 cases) later in UAH than in RSS or STAR. Delayed detection occurs because UAH shows reduced long-term tropospheric warming relative to RSS and STAR (11, 13, 14, 32). Even in UAH data, however, detection of the model-predicted TMT and TLT fingerprints at a $3\sigma$ threshold invariably occurs by 2018.

Implications

CanESM2 and CESM1 have ECS values of 3.68 °C and 4.1 °C, respectively. The higher-ECS CESM1 yields global-mean tropospheric warming that is in closer agreement with satellite-derived warming rates. The lower-ECS CanESM2 overestimates observed tropospheric warming (Fig. 1 B and C). In accord with these global-mean results, our pattern-based analysis shows that fingerprint detection times in satellite tropospheric temperature data are more consistent with the range of $t_d$ values inferred from CESM1.

Clearly, ECS is not the sole determinant of consistency between fingerprint detection times in observations and in a model LE. The applied forcing must also have significant impact. The cooling associated with (highly uncertain) negative indirect anthropogenic aerosol forcing is substantially greater in CESM1 than in CanESM2 (26). Larger negative aerosol forcing compensates for the larger GHG-induced tropospheric warming arising from the higher ECS of CESM1.

This highlights the need for caution in interpreting apparent consistency between fingerprint detection times in observations and in a large ensemble. Consistency may mask underlying problems with both forcing and response. Such interpretational difficulties are not unique to our study—they also arise in comparing the local “time of emergence” (ToE) of an anthropogenic signal (33, 39, 40) in multiple models or in models and observations.

How might we determine whether CanESM2 or CESM1 has a more realistic estimate of the true tropospheric temperature response to combined anthropogenic and natural external forcing? One way of addressing this question involves applying pattern-based regression methods (8, 9, 41–43) to quantify the strength of the model-predicted GHG and AERO fingerprints in observational data. Ideally, single-forcing GHG and AERO LEs would be available for this purpose. This would facilitate direct comparison of the regression coefficients (typically referred to as “scaling factors”) for the CanESM2 and CESM1 fingerprints. At the time this research was performed, single-forcing GHG and AERO LEs were available from CanESM2 but not CESM1. Comparison of scaling factors in the 2 models was not feasible.

Scaling factor estimates are available for CanESM2. Three independent studies with hydrographic profiles of temperature and salinity (5), tropospheric temperature (44), and surface temperature (45) suggest that the CanESM2 GHG signal may be larger than in observations. This is in accord with the larger than observed tropospheric warming found here (Fig. 1 B and C). The evidence is more equivocal regarding the question of whether the CanESM2 anthropogenic aerosol signal is larger or smaller than in observations (SI Appendix).

In addition to such statistical analyses, it is imperative to improve our physical understanding of the forcing by (and response to) anthropogenic aerosols, particularly for aerosol indirect effects (26). Prospects for progress are promising. Results from relevant CMIP6 single-forcing simulations (and in some cases LEs) performed under the Detection and Attribution Model Intercomparison Project are now available for analysis by the scientific community (46). The Radiative Forcing Model Intercomparison Project will provide estimates of aerosol direct and indirect forcing from participating models (47). Finally, improved methods of diagnosing and comparing model-based and observationally based estimates of indirect forcing have the potential to reduce uncertainty in aerosol effects on climate (48, 49).

In terms of reducing climate sensitivity uncertainties, there are now more mature strategies for evaluating the robustness and physical plausibility of a wide array of “emergent constraints” on ECS (50–52). Additionally, Bayesian inference strategies are being employed for combining information from the often divergent results obtained with different emergent constraints.

The developments mentioned above provide grounds for cautious optimism regarding scientific prospects for narrowing uncertainties in aerosol forcing and ECS. In the future, we could (and should) be able to make more informed assessments of the relative plausibility of the CanESM2 and CESM1 fingerprint detection times found here.

Materials and Methods

Satellite Atmospheric Temperature Data.

We used gridded, monthly mean satellite atmospheric temperature data from RSS (13), STAR (14), and UAH (17). RSS and UAH provide satellite measurements of TLS, TMT, and TLT. STAR produces TLS and TMT data only. Temperature data were available for January 1979 to December 2018 for versions 4.0 of RSS, 4.1 of STAR, and 6.0 of UAH.

CanESM2 Model Output.

We analyzed simulation output from five 50-member LEs: ALL, SV, AERO, OZONE, and GHG. For the first 4 ensembles, CanESM2 was run over the 1950 to 2005 period with forcing by ALL, SV, AERO, and OZONE. After 2005 each of these 4 numerical experiments continued with the forcing appropriate for that ensemble from the Representative Concentration Pathway 8.5 (RCP8.5) scenario (38). The ALL, AERO, and OZONE LEs end in 2100; the SV ensemble ends in 2020 (3–5). Initialization of individual members for these 4 ensembles is described in SI Appendix.

CanESM2 did not perform a LE with historical changes in well-mixed GHGs alone. The GHG signal can be reliably estimated by subtracting from each ALL realization the local time series of the sum of the SV, AERO, and OZONE ensemble means (5).

CESM1 Model Output.

The 40-member CESM1-CAM5 ALL ensemble is described in detail elsewhere (1, 2). The initial 30-member ensemble was augmented with 10 additional realizations. All realizations have the same historical forcing from 1920 to 2005 and RCP8.5 forcing from 2006 to 2100. As for the CanESM2 LEs, only the atmospheric initial conditions were varied by imposing small random differences on the air temperature field of realization 1 (2).

CMIP5 Model Output.

One of our estimates of internal variability relied on multimodel output from CMIP5 (53). We analyzed 36 different preindustrial control runs with no year-to-year changes in external forcings. Control runs analyzed are listed in ref. 11.

Method for Correcting TMT Data.

Trends in TMT estimated from microwave sounders receive a large contribution from lower stratospheric cooling (54). We used a standard regression-based method to remove the bulk of this cooling component from TMT (SI Appendix).

Fingerprint Method.

Our fingerprint method relies on an estimate of the fingerprint $F\left(x\right)$, the true but unknown climate-change signal in response to an individual forcing or set of forcings (7, 11). Here, $F\left(x\right)$ is the leading empirical orthogonal function (EOF) of the ALL annual-mean ensemble-mean temperature changes over 1979 to 2018. Details of the method are given in SI Appendix.

Noise Estimates.

We rely on 4 different internal variability estimates, referred to here as CMIP5, ALL1, ALL2, and SV. Details of these estimates are given in SI Appendix.

Data Availability.

All primary satellite and model temperature datasets used here are publicly available. Synthetic satellite temperatures calculated from model simulations are provided at https://pcmdi.llnl.gov/research/DandA/.