Neuromuscular actuation of biohybrid motile bots

Significance

Biohybrid machines have been developed using muscles to actuate soft robotic structures. We envision that the integration of neurons into the embodiment of such systems can transform them into intelligent machines which, for instance, could use sensory neurons to detect environmental cues then adaptively respond and orchestrate various motor patterns through their neural circuitry. However, achieving such sensory-motor modalities relies on the ability of neural units to command muscle activity, making actuation through motor neurons the first milestone. Here, we achieve this milestone and demonstrate neuromuscular actuation of a biohybrid swimmer. This paves the way for the development of biohybrid embodied platforms as models to gain deeper understanding of motor control, with potentially broad impact in robotics, bioengineering, and health.

Abstract

The integration of muscle cells with soft robotics in recent years has led to the development of biohybrid machines capable of untethered locomotion. A major frontier that currently remains unexplored is neuronal actuation and control of such muscle-powered biohybrid machines. As a step toward this goal, we present here a biohybrid swimmer driven by on-board neuromuscular units. The body of the swimmer consists of a free-standing soft scaffold, skeletal muscle tissue, and optogenetic stem cell-derived neural cluster containing motor neurons. Myoblasts embedded in extracellular matrix self-organize into a muscle tissue guided by the geometry of the scaffold, and the resulting muscle tissue is cocultured in situ with a neural cluster. Motor neurons then extend neurites selectively toward the muscle and innervate it, developing functional neuromuscular units. Based on this initial construct, we computationally designed, optimized, and implemented light-sensitive flagellar swimmers actuated by these neuromuscular units. Cyclic muscle contractions, induced by neural stimulation, drive time-irreversible flagellar dynamics, thereby providing thrust for untethered forward locomotion of the swimmer. Overall, this work demonstrates an example of a biohybrid robot implementing neuromuscular actuation and illustrates a path toward the forward design and control of neuron-enabled biohybrid machines.

Biohybrid machines, developed through the integration of artificial and biological components, are emerging as platforms to understand and synthesize the processes that drive structure, function, and behavior in biological systems (1). The biohybrid approach is appealing in engineering due to unique advantages that biological components can offer, such as high energy efficiency, stimuli-responsive adaptation, and the ability to self-organize. Moreover, biohybrid systems may allow us to decipher fundamental design principles of natural organisms in simpler and controlled in vitro settings. These principles can in turn be applied to develop artificial, bioinspired designs (2–5). Consequently, the field of biohybrid machines has been gaining attention rapidly over the past decade (6). Pioneering studies have employed muscle cells or tissue constructs for actuation and demonstrated motile robots capable of swimming (7–9) and walking (10–12). These machines can also recapitulate notable abilities of biological muscle, such as adaptive strength through exercise (13), healing after mechanical damage (14), and modulation of enzymatic degradation and actuator lifetime (15).

However, in all of the biohybrid robots reported so far, 1 aspect that has been conspicuously lacking is neuronal control of muscle activity. A wide range of complex animal behaviors rely on the nervous system to interface the body and the environment through sensing and coordinated motor patterns (16). As such, the integration of neurons represents a critical milestone for biohybrid machines. The “neuronal infrastructure” that animals use to regulate movement involves neural networks (17) which interface with muscles via motor neurons. Communication between motor neurons and muscles is mediated by neuromuscular junctions (NMJs), whose development involves the extension of motor neuron axons toward muscle fibers and the subsequent formation of the synaptic structure (18). The expansion of biohybrid systems into the sensory-motor frontier must therefore begin with the realization of a biohybrid machine where muscle activity is evoked through motor neurons.

Here, we report a biohybrid swimmer actuated by neuromuscular units. We begin by establishing a design framework that highlights the requirements and principles to be considered for successful development of a neuromuscular bioactuator, and its implementation for locomotion. This includes the design of a scaffold and appropriate culture methods for the in situ formation of muscle tissues and NMJs, as well as the design of a propulsion mechanism. To realize the envisioned biohybrid system, we utilize an approach that combines experiments and predictive computational modeling. We first develop a test platform for neuron–muscle coculture on a free-standing soft scaffold and verify the functionality of the neuromuscular unit. Next, we design a flagellar swimmer architecture for locomotion at low Reynolds number, using a computational model that accounts for the actuator response, compliant body mechanics, and hydrodynamics. We then implement our computational blueprint to obtain a biohybrid swimmer capable of untethered forward locomotion actuated by neuromuscular units.

Results and Discussion

Biohybrid Design Framework.

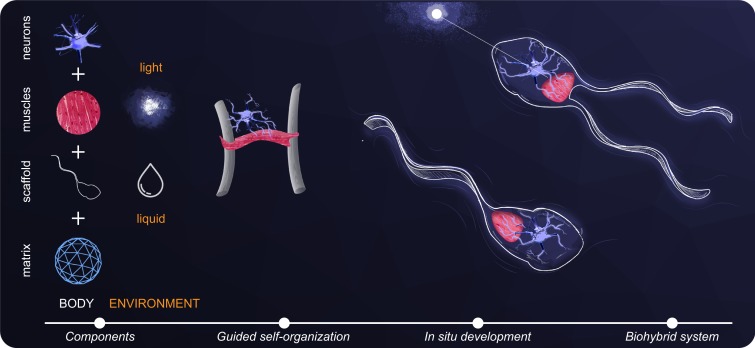
The swimmer that we envision (Fig. 1) consists of a soft scaffold on which muscles and neurons are embedded in reconstituted extracellular matrix (ECM) to develop functional neuromuscular units. Our choices regarding scaffold material and geometry, cell sources, and tissue culture techniques are based on 2 main principles, guided self-organization and in situ development, for the formation of muscle tissue constructs and NMJs, respectively. In terms of propulsion mechanism, we chose to utilize slender flagella since they are commonly encountered in natural swimmers at small scales, that is, at low Reynolds numbers (Re << 1) (19, 20).

Fig. 1.

Conceptual framework. The embodiment of the envisioned motile bot consists of an engineered scaffold, ECM, muscle tissue, and optogenetic motor neurons, operating in a fluid environment and responding to external light stimuli. Engineered muscle tissue is formed through self-organization of muscle cells and ECM, guided by the shape of the scaffold. Functional neuromuscular units develop in situ whereby motor neurons extend neurites and innervate the muscle tissue. Appropriate design choices can result in a biohybrid machine capable of locomotion actuated by neuromuscular units.

A common method of forming muscle tissue constructs is to embed myoblasts in an ECM gel cast in a well containing posts and allow the myoblast-laden gel to compact around the posts (21). A design principle that is implicitly used in this method is guided self-organization. Compaction of cell-laden ECM is a self-organization process driven internally by the traction forces that cells apply to the fibrous matrix (22). In the absence of a scaffold, gels compact uniformly, but when cast in a scaffold with posts gel compaction is restricted physically, yielding a longitudinal strip of tissue bridging between the posts. When the muscle strip twitches, it pulls on the posts, generating deflection (23). Hence, the synergy between scaffold geometry and biological self-organization defines both tissue morphology and actuation mode. In line with this principle, we designed a scaffold that has 2 flexible beams (“legs” in Fig. 2A) to guide the morphology and function of our muscle tissue.

Fig. 2.

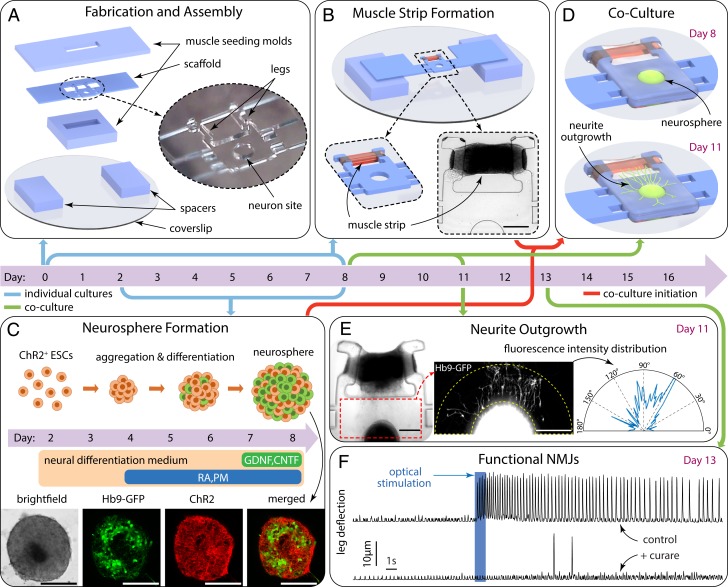
Biofabrication timeline. (A) Day 0: PDMS scaffold, spacers, and muscle-seeding molds are assembled on a glass coverslip. (B) Muscle strip bridging the 2 legs is formed during the first 2 d in culture then kept in differentiation medium for the following 6 d. (C) Optogenetic mouse ESCs are differentiated separately to obtain neurospheres, clusters of neural cells with photosensitive ChR2 ion channels and motor neurons expressing Hb9-GFP. (D) Day 8: Coculture is initiated by embedding neurosphere and muscle in a continuous ECM gel. (E) Day 11: Neurite outgrowth pattern after 3 d in coculture. Fluorescent intensity distribution around the neurosphere illustrates preferential neurite extension toward muscle strip. (F) Day 13 and onward: Optical stimulation of neurons induces muscle contractions. Evoked contractions are not observed in the presence of 25 µM curare. (Scale bars in B, C, and E: 250 µm.)

As scaffold material we chose polydimethylsiloxane (PDMS), since it can be used to build microscale structures that can be deformed sufficiently by contraction forces of engineered skeletal muscle (23). Furthermore, PDMS is also suitable for the fabrication of highly slender beams through capillary micromolding (24) which can be utilized as flagella for locomotion at low Re (8).

Regarding the formation of NMJs, the main principle we consider is in situ development. This affects the choice of cell source and tissue culture techniques. Advances in stem cell biology have enabled directed differentiation of pluripotent stem cells toward motor neurons (25), providing a viable source of motor neurons which can form functional NMJs with muscle cells in vitro (26). To facilitate in situ neuromuscular development, we chose to embed stem cell-derived neural cluster and the muscle strip together in ECM gel, thereby generating a continuous matrix connecting the 2 tissues through which motor neurons can extend neurites toward muscles and subsequently form NMJs.

In Situ Neuromuscular Development on Free-Standing Scaffolds.

We start by implementing our biohybrid design framework (Fig. 1) to build a neuromuscular actuator which will form the basis of the swimmer. Untethered locomotion inherently requires a free-standing scaffold, whereas in vitro NMJ models have only been demonstrated either on flat substrates or, more recently, on 3D but permanently anchored scaffolds (27–29). Thus, we first engineered a test platform to develop and characterize neuromuscular units on a free-standing PDMS scaffold. The scaffold (Fig. 2A) consists of a structure with a hollow cavity to facilitate the seeding of a neuronal cluster, 2 legs that serve as anchors to guide the formation of a muscle tissue, and spacers to raise this structure so that it is free-standing. Two temporary seeding molds are used to create a cavity around the legs which is seeded with skeletal myoblasts suspended in an ECM gel consisting of type I collagen and Matrigel (SI Appendix, Fig. S1). The myoblast-laden gel compacts during the first 2 d in culture, and this compaction is constrained by the scaffold legs, leading to the formation of a muscle strip bridging between the 2 legs (Fig. 2B and SI Appendix, Fig. S1). We designed the shape of the legs to groove inward at the free ends to trap the muscle strip at a prescribed location. Muscle cells are then allowed to differentiate for 6 d to form contractile myotubes. In separate culture, optically excitable motor neurons are obtained by directed differentiation of optogenetic mouse embryonic stem cells (28) using an established protocol (30) which produces neurospheres containing motor neurons (Fig. 2C).

To initiate neuron–muscle coculture, the scaffold with the muscle strip is covered with ECM and a neurosphere is seeded into the hollow cavity (Fig. 2D and SI Appendix, Fig. S1). During the first 3 d of coculture, we observe neurite outgrowth emanating from the neurosphere into the surrounding ECM. Neurite outgrowth was remarkably biased toward the muscle strip with very few neurites growing in other directions (Fig. 2E), most likely due to soluble factors secreted by muscle cells which have been shown to enhance neurite outgrowth in culture (31). Neurons then innervate the muscle cells, forming NMJs. We characterized the functionality of NMJs via a stimulation/inhibition assay. Under normal culture conditions, optical stimulation of motor neurons evoked periodic muscle contractions. This contraction pattern was absent when the NMJ inhibitor d-tubocurarine (curare) was applied. The occasional spontaneous twitches observed in the presence of curare show that its application did not hinder the contractility of muscle cells, indicating that NMJs are specifically targeted (Fig. 2F). Taken together, evoked muscle contractions by neural stimulation, and their absence under application of curare, confirm the formation of functional NMJs between motor neurons and muscles on our free-standing coculture scaffold.

Computationally Guided Design of the Swimmer.

Next, we proceeded to design swimmers powered by the neuromuscular actuator described above. For locomotion, the swimmer scaffold needs to meet additional requirements: produce net thrust, stabilize the swimmer against roll and pitch, and result in robust swimming gaits. We opted for a general blueprint characterized by a flat head to host the tissues and provide stabilization and flexible tails for biomimetic flagellar propulsion (19, 20). To account for the nonlinear interaction between fluid and soft elastic structures, we utilized a computational modeling approach based on assemblies of Cosserat rods (SI Appendix, Fig. S2). This approach has been established and validated against several benchmark problems (32) and recently demonstrated for the design of walking biohybrid machines (33).

We first modeled the muscle strip as a bundle of Cosserat rods and calibrated it based on the force outputs of neuromuscular units on the test platform of Fig. 2. Muscle strips generate rest tension by collective quasistatic contractility of the cells, and additional active contraction force when stimulated by neurons. To recapitulate these forces, the virtual muscle bundle was coupled to a virtual replica (same geometry and material properties) of the test scaffold (Fig. 3A). In the experimental test platform, muscle rest tension and cyclic contraction forces induced by periodic (1 Hz, 20% duty cycle) optical stimulation of neurons were characterized by resulting leg deflections (Fig. 3B). The total muscle force output was computationally modeled as a time-dependent combination of rest and active components and fit to experimental recordings (SI Appendix). This muscle force model, when applied to the simulated scaffold, produces leg deflections that closely match experimental data (Fig. 3B).

Fig. 3.

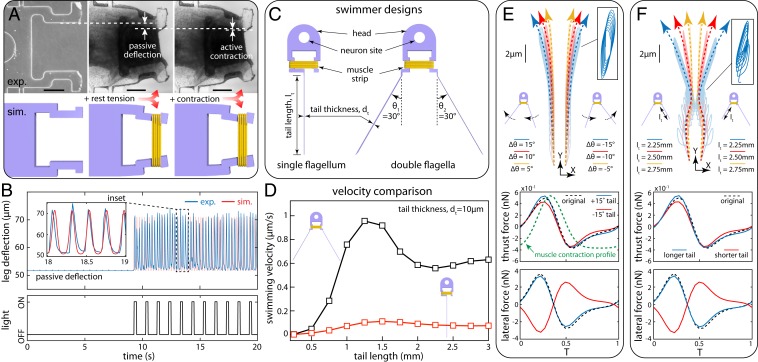
Computational modeling and design. (A) Virtual reconstruction of the test platform to capture muscle rest tension and contraction force. (Scale bar: 250 µm.) (B) Measured data used to calibrate muscle model and predict leg deflections. (C) Single-flagellum vs. double-flagella swimmer designs. (D) Predicted swimming velocity vs. tail length for fixed tail thickness. (E and F) Robustness of double-flagella design evaluated as the deviation of swimming trajectory from straight, due to tail angle (E, Top) or length (F, Top) perturbations. (E and F, Bottom) Corresponding deviations in propulsion force and lateral force.

Next, we numerically designed our swimmer blueprints (Fig. 3C): a single-flagellum design inheriting the spirit of our previous demonstration (8) and a double-flagella prototype that aims at larger thrust and reduced sensitivity to fabrication defects due to its compensating symmetry. For both prototypes, the head was designed based on the test platform, and the entire scaffold was modeled as a single Cosserat rod with varying radii, coupled to the calibrated muscle model. Since the fabricated scaffold has rectangular cross-sections, modeling it as a rod involves the calculation of equivalent radii for different components (i.e., tails, legs, and head) such that moment of inertia and mass are conserved. Hydrodynamics of the flagellar tails was modeled via slender body theory which simplifies the computation of fluid-induced loads when inertia is negligible (low Re) and length is much larger than cross-sectional dimensions (34, 35). As such, slender body theory is well established for modeling flagellar hydrodynamics (36–38) and has been applied to noncircular cross-sections, as exemplified by our previous work (8) and more recently by the magnetic swimmers of Huang et al. (39). The head and the surrounding tissues are approximated as a sphere of diameter equal to the head width, and the resulting hydrodynamic drag is computed via Stokes’ law. Details and validations of our modeling approach are presented and discussed in SI Appendix.

Using our computational model, we first explored the effect of tail thickness and length on swimming velocity for both candidate designs (single- and double-tailed). Simulations predicted up to an order of magnitude higher velocity for the double-tailed swimmer compared to the single-tailed design. Moreover, simulation results show that an optimum velocity can be achieved for an intermediate tail length (Fig. 3D and SI Appendix, Fig. S4), consistent with theoretical predictions (discussed in SI Appendix). We further examined the designs in terms of their robustness, that is, the ability to swim straight under the influence of experimental uncertainties. We anticipated that the symmetry of the design may be altered in experiment due to manual handling of the scaffold. This was simulated computationally by introducing a perturbation in either tail opening angle (Fig. 3E and SI Appendix, Fig. S5) or tail length (Fig. 3F and SI Appendix, Fig. S5), and the corresponding swimmer trajectories were compared, illustrating smaller deviations in the trajectory of the double-tail design relative to the single flagellum (SI Appendix, Fig. S5).

Neuromuscular Actuation of the Swimmer.

We then proceeded to build and test the double-tailed swimmer design, due to the better performance predicted by our computational model. We fabricated the swimmer scaffold and developed neuron–muscle coculture (SI Appendix, Fig. S6) using the methodology we had established for the test platform. First, functionality of the neuromuscular actuator was assessed by optical stimulation, verifying that muscle contractions can induce deflection of the tails (Movie S1). Then, the swimmer was released in a dish in culture medium and suspended by a layer of Percoll–medium mixture (Fig. 4A). Due to the higher density of Percoll, the Percoll–medium mixture forms a layer of fluid at the bottom of the dish (SI Appendix, Fig. S7), thereby generating buoyancy on the swimmer. Z-stack images (Movie S2) confirmed that the swimmer is suspended to a height that is ∼20 times the thickness of the swimmer scaffold (SI Appendix), ensuring that no physical friction with the substrate occurs. Moreover, this clearance reduces potential hydrodynamic boundary effects (40).

Fig. 4.

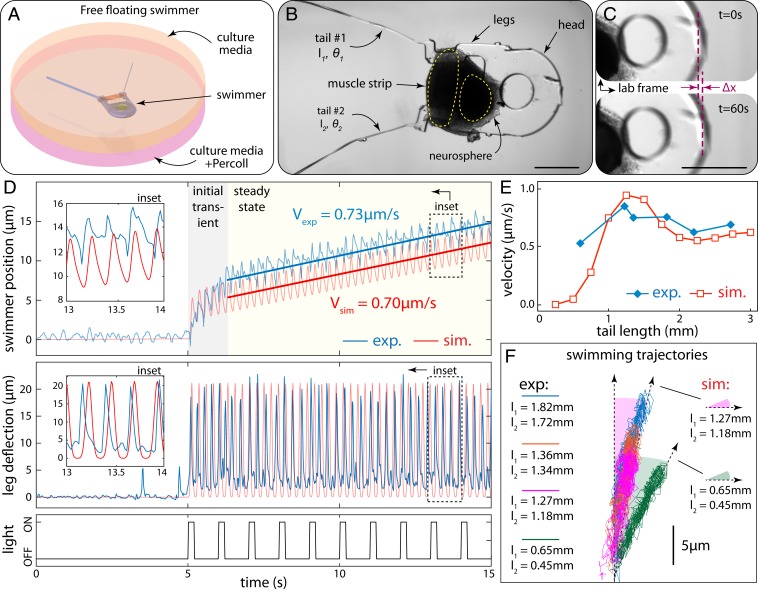
Free swimming driven by neuromuscular units. (A) Illustration of free-floating swimmer suspended by Percoll–culture media mixture. (B) Bright-field image of the swimmer after release from the anchors. The neurosphere is dislocated from its original seeding location due to tension generated between muscle and neurons. (C) Forward locomotion of the swimmer illustrated by comparison of snapshots at the beginning (Top) and end (Bottom) of a 60-s recording. (D) Experimental results and model predictions: (Top) swimmer position vs. time, (Middle) leg deflection due to muscle contraction, and (Bottom) input optical signal. (E) Experimental swimming velocity for different average tail lengths compared to model predictions. (F) Swimming trajectories for different tail lengths. (Scale bars in B and C: 500 µm.)

After the swimmer was released, we optically stimulated the motor neurons (1 Hz, 20% duty cycle) and the resulting periodic muscle contractions drove the motion of the flagella in a time-irreversible fashion, thereby propelling the swimmer forward (Fig. 4C and Movie S3). To quantify swimming velocity, we recorded videos of the swimmer and obtained its position in time by image processing. At rest the swimmer drifted slowly (0.17 µm/s) due to the flow of culture medium caused by handling of the dish. Thus, for all subsequent analysis, the experimentally recorded position data were corrected for drift (SI Appendix, Fig. S8). Upon the onset of muscle contractions, the swimmer initially displayed a brief (∼1 s) acceleration phase, followed by a steady-state phase with a constant time-averaged swimming velocity of ∼0.7 µm/s (Fig. 4D and Movie S4), corresponding to Re = 2 × 10⁻³. Swimming speeds are expected to be slow, given the targeted low Re regime, the relatively large body length of our swimmer (3.2 mm including head, legs, and tails), and the viscous drag associated with the voluminous head. While the elastohydrodynamic performance of our swimmer tails is optimized for the given neuromuscular actuator and double-tail swimmer design (SI Appendix), several strategies can be implemented to reduce drag and improve thrust, hence attaining higher speeds. Critical to these strategies are miniaturization and optimization of the neuromuscular construct, to increase compactness and force output. Possible options are discussed in SI Appendix. Moreover, we note that despite being slow the swimming velocity reported above is measured definitively, demonstrating actual untethered locomotion. Fluctuations in position recorded during the 5-s rest period had a root-mean-square amplitude of 0.45 µm, whereas the distance traveled during steady-state swimming over 5 s is ∼4.6 µm, an order of magnitude higher than the noise level. Furthermore, both the observed oscillatory behavior and the measured value of steady-state time-averaged swimming velocity were in close agreement with simulation predictions (Fig. 4D). The low swimming velocity therefore does not detract from the achievement of neuromuscular actuation of a motile device.

The steady-state swimming velocity shown in Fig. 4D was sustained for ∼20 s, after which muscles began to fatigue, and the swimmer decelerated, despite continuing optical stimulation of neurons (SI Appendix, Fig. S9). A possible reason for this fatigue is depletion of neurotransmitter vesicles at the NMJ, which can occur due to repetitive stimulation (41). Another possible reason is depletion of glucose or oxygen in the muscle cells. By allowing the system to rest, both resources can be replenished since neurotransmitter vesicles can be recycled at the synapse (42) and nutrients in the surrounding culture medium can diffuse into the muscle tissue. Indeed, when we performed a second recording after allowing the sample to rest for 1 min, we observed that the initial acceleration and steady-state velocity were recovered. This time, the steady-state velocity was sustained for ∼8 s. A third recording performed after an additional 10-min break showed that swimming performance was sustained intermittently for ∼30 s, comparable to the 20 s of our first recording. The distance traveled during this third recording (∼25 µm) was also consistent with that of the first session (SI Appendix, Fig. S9). Taken together, these results show that the decline in swimming performance after continuing repetitive stimulation is temporary and can be recovered by allowing the system to rest. This suggests that the duration for which performance can be continuously sustained is likely limited by the kinetics of neurotransmitter vesicle release and muscle metabolism. In the following analyses, only steady-state swimming velocities were considered.

To test our model predictions regarding the effect of tail length on swimming velocity, we cut the tails of the swimmer in small increments and measured steady-state swimming velocity after each cut. We tested various tail lengths ranging between 0.5 mm and 3 mm and observed that experimentally recorded velocities closely matched the trends predicted by our computational model (Fig. 4E). Next, we assessed the robustness of the swimming trajectory (Fig. 4F). Here, opening angles of both tails had ∼5° deflection from original design, as well as differences in length resulting from manual cutting of the tails. In 3 of the 4 cases tested, the difference in tail length was less than 10% of the average tail length. Consequently, the swimming trajectories in these cases followed similar paths and the major contribution to the deviation from straight line came from the angular difference. In the fourth case, the difference in tail length was 36% of the average tail length, resulting in a larger deviation. In all 4 cases, the experimental trajectories agree with simulations, further confirming the predictive power of our modeling approach (Fig. 4F).

Conclusion

Our present demonstration of a flagellar swimmer actuated by neuromuscular units was guided by a general conceptual framework derived from essential design principles and realized through enabling computational and experimental technologies. This biohybrid swimmer exemplifies a multicellular engineered living system that is developed via a synthesis of top-down engineering and bottom-up self-organization and development (1). The approach illustrated here of articulating general principles to guide the design of scaffolds and tissue culture techniques that work synergistically with natural processes may prove effective in the realization of future biohybrid and bioinspired systems.

The ability to command muscle activity through motor neurons paves the way for further integration of neural units in biohybrid systems. Given our understanding of motor control in animals (17), a possible design principle moving forward is the control of muscles by a hierarchical organization of neural networks with oscillatory firing patterns (43). Stem cell-derived neurons in culture have been shown to spontaneously develop networks with periodic bursting patterns (44). Advances in stem cell biology have enabled directed differentiation of pluripotent stem cells into neurons of spinal cord identity (25), cortical neurons (45), and, more recently, peripheral sensory neurons (46), thereby providing cell sources to possibly enhance functionalities of in vitro neural networks. These networks, in turn, may be leveraged to engineer autonomous biohybrid embodiments that exhibit adaptive motor patterns in response to environmental cues. Biohybrid systems with sensory-motor capabilities can have significant impact as platforms for deciphering mechanisms of embodied sensing and action (4), leading to novel advances in robotics, bioengineering, and medicine.

Methods

C2C12 mouse skeletal myoblasts (ATCC) and the optogenetic mouse embryonic stem cell (ESC) line ChR2^H134R-HBG3 Hb9-GFP (28), a generous gift from Roger Kamm’s laboratory, Massachusetts Institute of Technology, Cambridge, MA, were maintained and differentiated following established protocols (28, 30). PDMS scaffolds were created using standard microfabrication techniques and sterilized by autoclaving. Tissue seeding was performed by embedding cells in a mixture of type I collagen and Matrigel (Corning). Computational models were based on assemblies of Cosserat rods as previously described (32) and demonstrated (33). Further details of our experimental and computational methods are provided in SI Appendix. The solver used for numerical implementation of our Cosserat rod-based models is publicly available at https://github.com/mattialab/elastica.git.