Unexpected stretching of entangled ring macromolecules

Abstract

In the melt state at equilibrium, entangled non-concatenated ring macromolecules adapt more compact conformations compared to their linear analogues and do not form a network. We show here that, when subjected to uniaxial stretching, they exhibit a unique response, which sets them apart from any other polymer. Remarkably, whereas both linear and ring polymers strain harden, the viscosity of the rings increases dramatically (the melt thickens) at very low stretch rates due to the unravelling of their conformations along the stretching direction. At high rates, stretching leads to viscosity thinning similar to that of entangled linear polymers, albeit with subtle differences.

The state-of-the-art understanding of entangled flexible polymer chains is based on the concept of physical network formation (characterized by a plateau modulus) resembling microscopic spaghetti. Their motion, called reptation for linear polymers, reflects their ability to make conformational adjustments mediated by their free ends [1]. Incorporated into the tube model [2], the reptation concept has proven remarkably successful in predicting the linear and (in part) nonlinear rheology of linear polymers [1,2]. Linking the two free ends of a simple linear polymer has dramatic consequences, which have been explored in the last decade [3,4]. In brief, linked linear polymers, thereafter called rings, have compact conformation in the melt and reduced size compared to unlinked chains as shown by neutron scattering [5,6] and molecular dynamics simulations [7,8]. In fact, very large non-concatenated ring polymers in the entangled state approach an asymptotic state of compact conformations in which each polymer is compressed by surrounding rings because they cannot heavily overlap [7,8]. The resulting long-lived topological constraints between entangled non-concatenated rings do not form an entanglement network as linear chains do (hence, their stress relaxation modulus does not exhibit an entanglement plateau even at very large molar masses) and therefore their zero-shear-rate viscosity is much lower compared to that of their linear entangled counterparts [3,9]. This sets rings apart from any other macromolecule, with several implications in diverse disciplines. For example, DNA forms highly compact loopy conformations in constrained environments (chromosome territories) [10,11] and becomes knotted in the presence of appropriate enzymes [12].

In view of this background, an outstanding challenge is to unravel the nonlinear rheology of rings as it pertains to their processing conditions relevant to the macromolecular engineering applications [13,14] as well as to the fundamental understanding of polymer dynamics with respect to the relation between molecular details and macroscopic properties. In fact, the field of nonlinear ring rheology is virtually virgin [15,16]. Recent fragmental evidence from experiments and simulations with marginally entangled rings under moderate nonlinear shear deformation indicate a much weaker thinning response compared to their linear counterparts, reminiscent of that of unentangled linear chains [16,17]. Yet, the most relevant flow in processing involve strong extensional components which imparts substantial conformational changes on the macromolecules [13,18,19]. To date, entangled rings have never been subjected to extensional flows. Here, we present new experiments where we stretch well-characterized rings uniaxially under controlled conditions, using unique instrumentation, a filament stretching device [20]. We show that stretched entangled rings exhibit a hybrid response: At low rates they depart from linear viscoelasticity with substantial viscosity thickening (exceeding one order of magnitude), whereas at higher rates they behave similarly to their entangled linear counterparts (i.e., with the same molecular weight) with thinning viscosity exhibiting a power-law dependence on stretch rate with an exponent of about −1/2.

The main message from the analysis of the linear viscoelastic response is that ring purity is of utmost importance [3, 21]. Therefore, special emphasis was given to the purification process, which is based on liquid chromatography at the critical condition, LCCC [3, 22,23]. The specific polystyrene ring sample used here has a weight-average molar mass of 185,000 g/mol (referred to as 185k) and polydispersity of 1.01. This corresponds to Z=11 entanglements for the equivalent linear chains. Details about the synthesis, purification and characterization are given in the supplemental material (SM), Figure S1. Linear viscoelastic (LVE) measurements at 130°C were used to determine the frequency-dependent dynamic moduli and viscosities (see Figures S2, S3 and S4 of the SMAs implied by the measurements, and confirmed by differential scanning calorimetry measurements, the glass transition temperatures of this ring and its linear precursor are identical. The zero-shear-rate (Newtonian) viscosity values for the linear and ring polymers differ by factor 37.5 and are 7.05×10⁷ and 1.88×10⁶ Pas, respectively (see Figure S4 of SM). The LVE measurements were also used in order to determine the respective terminal times (τ_d and τ_Ring), the (same) Rouse time of an entanglement segment (τ_e) and the Rouse time (τ_R,linear and τ_R,ring) of the entire chain (see Table S1 of SM). They are listed in Table S1 of the SM. Interestingly, the terminal relaxation characterized by frequency-dependent storage and loss moduli G′~ ω² and G′′~ ω, respectively, occurs at a frequency corresponding to a terminal time τ_termianl >> τ_Ring. This is attributed to the presence of traces of unlinked linear chains in the purified ring sample [3,21,24,25]. The explored range of extensional rate $\dot{\epsilon }$ during the measurements was ${\tau }_d^{-1}\left(\mathrm{o}\mathrm{r}\mathrm{ }{\tau }_{terminal}^{-1}\right)<\dot{\epsilon }<{\tau }_e^{-1}$. In fact, the lowest rate used (3×10⁻³ s⁻¹) was slightly above ${\tau }_d^{-1}$ =2.3×10⁻³ s⁻¹ (or ${\tau }_{terminal}^{-1}$ =2.7×10⁻³ s⁻¹) and the highest rate (1 s⁻¹, well below ${\tau }_e^{-1}$= 17.2 s⁻¹) was determined by experimental considerations.

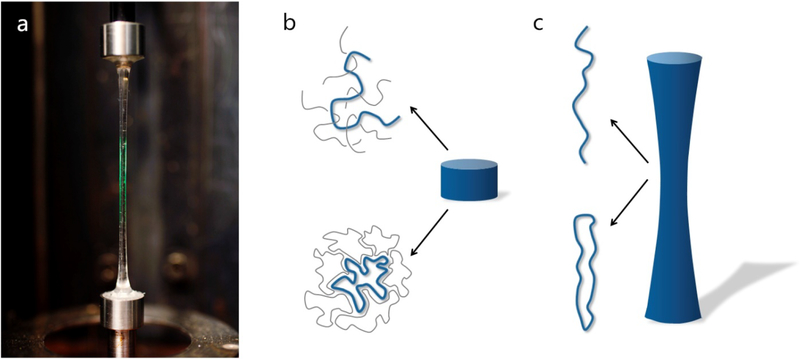
Uniaxial extension (often referred to as elongation but thereafter called simply extension) was achieved by means of the filament stretching rheometer [20], as shown in Figure 1. Given that melts are incompressible, we can calculate the local extension ratio λ in the mid-filament plane from the local reduction in diameter as λ = (D₀/D)² where D₀ is the initial equilibrium diameter of the sample at time t=0 and D its diameter at time t. The Hencky strain is defined as ε = ln λ and the extensional rate is defined as $\dot{\epsilon }= d\epsilon /dt$. In these experiments, the filament is stretched for t > 0 (see Figure 1a) such that the extension rate in the mid-filament plane is kept constant. The extensional stress difference $\mathrm{\Delta }\sigma (\dot{\epsilon },t)$ in the mid-filament plane is obtained from a force measurement and the stress growth coefficient is then defined as ${\eta }_E^{+}(\dot{\epsilon },t)=\mathrm{\Delta }\sigma /\dot{\epsilon }$. At steady state, Δσ becomes independent of time and we define the extensional viscosity function by ${\eta }_E\left(\dot{\epsilon }\right)=\mathrm{\Delta }\sigma /\dot{\epsilon }$. Further experimental details are presented in the SM.

Figure 1:

(a) Photo of stretched polystyrene in the perpendicular direction. (b) illustration of equilibrated specimens before stretching with different conformations of entangled linear (top) and ring (bottom) polymers. (c) illustration of stretched specimens with different conformations of the same (as in b) linear (top) and ring (bottom) polymers, showing the dramatic change in conformation due to stretching [18]. For clarity, we color one macromolecule with blue in each case, to emphasize its conformation in the melt.

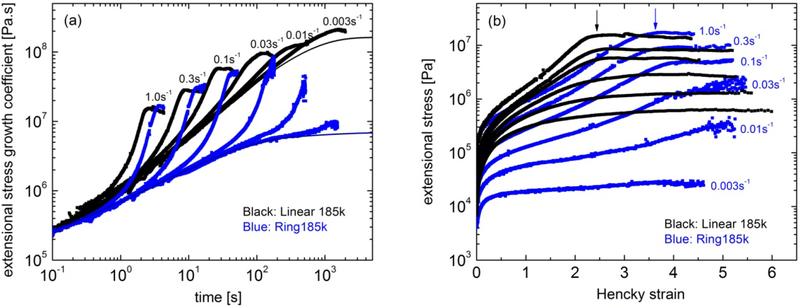
Figure 2a depicts the stress growth coefficient of the ring polymer and its linear precursor as functions of time for different values of the applied extensional rate. Based on knowledge from linear polymers [2], this range corresponds to orientation and stretching (see Figures 1b,1c). We observe that in the investigated range of extensional rates, the polymers exhibit initial extension hardening. It appears however that this effect is significantly more pronounced in the ring polymer and this will be further discussed below. The same data are plotted in the form of stress versus strain in Figure 2b. This log-linear representation emphasizes that steady-state values are reached, hence we assess the steady extensional viscosity as a function of rate below.

Figure 2:

(a) Stress growth coefficient of linear (185,000 g/mol) and ring (185,000 g/mol) polymers at 130°C and different extensional rates in the range 3×10⁻³ to 1 s⁻¹. The linear viscoelastic envelopes (from Figure S1) are depicted by solid lines. (b) the same data plotted as stress against Hencky strain in linear scale, showing that a steady state has been reached. The arrows indicate the start of steady state for the highest extensional rate.

A closer look at the data of Figure 2 reveals more features distinguishing rings from their linear counterparts. At the same extensional rate, the onset of stretching occurs earlier in linear polymers (see Figure 2a) which have longer relaxation times (see table S1 of the SM). Moreover, steady state is reached earlier in linear polymers (see arrows in Figure 2b). Note that, in the absence of an entanglement network it is difficult to transmit stress between different rings, hence the distribution of extensions may be broader and stretching may be delayed. Certainly, the strong extensional flow is imposed on two systems with markedly different equilibrium conformations, rings being more compact. This is documented in a recent single-molecule study of DNA ring and linear polymers which have been visualized when stretched in a cross-slot device [26].

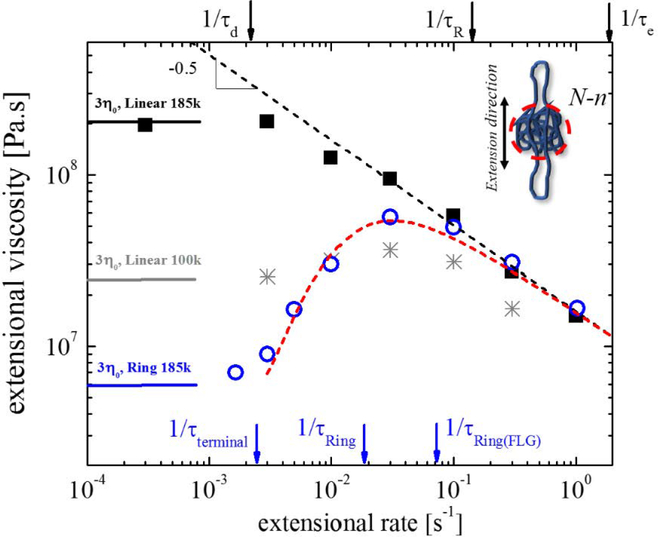
The extracted steady-state extensional viscosities are plotted against the extensional rate in Figure 3 together with the inverse relaxation time for the 185k linear and ring molecules respectively. We note first of all, that the linear chains exhibit a transition from constant viscosity to a power-law behavior at about the inverse reptation time (${\tau }_d^{-1}$) with no apparent change in behavior at the inverse Rouse time as previously observed [27]. By contrast, at low rates, the extensional viscosity of the ring is smaller than its linear counterpart by about a factor of 50 corresponding to the absence of entanglement network and much more collapsed nature of the equilibrium ring configurations compared to linear molecules [24]. At intermediate rates, there is a dramatic transition with an increase in extensional viscosity of the rings by about a factor of 10 over one to two decades of extensional rate. We interpret this increase as being due to the unravelling and elongation of the rings by the extensional flow. Due to the collapsed state of the rings, this transition becomes more dramatic for the rings than for the linear molecules. Finally, at high rates the extensional viscosity of the rings and the linear molecules are identical within experimental accuracy, both reaching a power-law behavior ${\eta }_{E }~{\dot{\epsilon }}^{-1/2}$.

Figure 3:

Steady-state uniaxial extensional viscosity extracted from Figure 2 at 130°C, as a function of the imposed extensional rate for the linear precursor (filled black squares), ring (open blue circles) and a linear polymer 100k (grey stars) with about half-molar mass (actually 54%). The respective zero-rate limiting viscosities extracted from the dynamic shear data (accounting for the Trouton ratio of 3 [14]) are indicated by the horizontal lines. The inverse relaxation times are shown for 185k linear at the top (black) and for the respective ring polymers at the bottom (blue). The high-rate data of 185k (linear and ring) polymers collapse within experimental uncertainty. The dashed line through the linear polymer data has a slope of −0.5 (see text). The dashed line through the ring data represents predictions of the phenomenological model (see text and the SM). Inset: illustration of the stretched ring comprising a globular head comprising N-n monomers and two double-folded tails with n monomers (see also SI). The vertical arrows represent different characteristic times (see also Table S1 of the SM).

The −1/2 exponent at high extensional rates has been observed with a range of polymer melts, albeit all with free ends, including model linear [27] and star [28] polystyrene, long-chain branched polyethylene [29,30] and unentangled linear chains [31]. However, even for the simplest monodisperse linear polymer melts it exponent is still debatable. Recent molecular dynamics simulations indicate that the confining tube elongates and thins with $\dot{\epsilon }$[32]. The original tube theory predicts orientation and stress saturation at rates exceeding the inverse reptation time, as discussed above, corresponding to a slope of −1 [33] and then a strong increase in stress as the rate overcomes the inverse Rouse time. Indeed, such a qualitative behavior is observed for polymer solutions [34] and can be explained by several modified tube models [34]. The monotonic behavior of the extensional viscosity function prompted initially the incorporation of the so-called interchain pressure effect into tube theories [33]. Also Nielsen et al. [35], have shown that the combination of anisotropic friction with finite chain extensibility leads to ${\dot{\epsilon }}^{-1/2}$ scaling. Lately the idea of friction reduction in extensional flow has been formulated [36,37], a concept that accommodates the difference between entangled melts and solutions [38,39] and describes unentangled linear chain behavior [31]. Ianniruberto and Marrucci [40] considered the balance between frictional and thermal equilibration forces at the onset of stretching and showed that branched polymers (e.g. combs) exhibit identical behavior with linear polymers in fast extensional flows, provided they have the same equivalent molar mass (i.e. same Rouse time). To test whether this prediction carries over to rings, we consider a folded ring with half molar mass as the equivalent linear chain. We show in Figure 3 the extensional viscosity of a linear chain 100k along with the ring 185k. It does exhibit thickening, which however is much less pronounced (less than a factor of two increase with respect to zero-rate viscosity) compared to the ring (factor of 10). The high-rate extensional viscosities of this polymer are clearly below the respective data of the 185k polymers, suggesting that this idea may not hold for rings (Figure 3, S5).

In view of the intriguing overlap of the asymptotic behavior of the ring and linear 185k polymers, we rationalize the ring behavior by a simple model where the asymptotic viscosity of the ring and the linear molecule is the same function of the number of monomers. Specifically, we assume that the ring polymer (with N Kuhn monomers [4]) in extensional flow has a shape of spherical globule with N − n monomers and two double-folded tails containing n Kuhn monomers, as illustrated in the inset of Figure 3. The number of monomers in the undistorted globule is determined by the condition that the reciprocal extensional rate is the relaxation time of this globular part of the ring (head): ${\dot{\epsilon }}^{-1}\approx {\tau }_{Ring}\left(N-n\right)$. The latter is estimated from the fractal loopy globule (FLG) model with N monomers, ${\tau }_{Ring}\left(N\right)=c_0{\tau }_m\frac{N^{7/3}}{N_e^{1/3}}$, where c₀ is a constant of order unity, τ_m corresponds to the monomer relaxation time and N_e the degree of polymerization of the entanglement segment. The total number of Kuhn monomers in the tails is n = 0 for low extensional rates and $n=N-{N_e^{1/7}\left(c_0{\tau }_m\dot{\epsilon }\right)}^{-3/7}\mathrm{ }\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{ }\mathrm{ }\dot{\epsilon }>{\tau }_{Ring}^{-1}\left(N\right)$. The extensional viscosity of ring melt is assumed to be the sum of the rate-dependent contributions from the globular head and from the double-folded tails: $\eta \left(\dot{\epsilon }\right)={\eta }_{head}\left(\dot{\epsilon },N-n\right)+{\eta }_{tail}\left(\dot{\epsilon },n\right).$ The former is the ring viscosity [4] multiplied by 3 (Trouton ratio), whereas the latter is equivalent to the extensional viscosity of linear polymers containing n monomers. Details including fitting of model parameters are presented in the SM. Whereas this expression fits the experimental data very well (Figure 3), its main value lies in the description of the ring unraveling process during extension and its relation to viscosity thickening. It is a rather simplified model, but may provide the ingredients for a deeper analysis of globular to double-folded conformation.

Despite this unique stretching behavior of ring polymers, two subtle points merit further discussion. First, the onset of extension thickening (Figure 3) occurs at a rate of about 3×10⁻³ s⁻¹, which corresponds to the inverse terminal time of the ring (τ_terminal⁻¹), i.e., the frequency where the terminal slope of 2 is reached in G′. However, it is much slower (by a factor of about 25) than the ring relaxation time based on the FLG model fit to the linear viscoelastic data (τ_FLG) or the experimental ring relaxation time (τ_Ring) based on the fit of low-frequency moduli with lines having slopes 1 and 2 (by a factor of 7). See also Figures S2, S3 and Table S1. It is also much slower than the inverse Rouse time of the linear precursor, which marks the onset its stretching (Table S1) [27,35]. This suggests the remarkable sensitivity of ring polymers to elongation. On the other hand, given that the probed terminal times of ring and linear precursor are similar (Figure S3 and Table S1), the role of remaining traces of unlinked linear chains, likely not been resolved by LCCC, cannot be ruled out. As discussed in the literature [3,21,24,25], even with the state-of-the-art fractionation (Figure S1) ring purification remains a challenge and the presence of traces of linear contaminants which thread the rings and alter their rheology cannot be excluded. With the equilibrium overlap concentration of 185k polystyrene being about 1.3 wt%, the possible presence of even 0.1wt% can be significant [3,21].

Secondly, the agreement of the model with the asymptotic viscosity at large rates should not be taken as independent support of the data since it comes from fitting. In fact, if one adopts the picture of ring unravelling into a double folded structure during extension, one could alternatively expect that at high extensional rates it behaves as a linear chain with half molar mass [40]. However, the data of Figure 3 indicate that this is not the case. Indeed, the 185k ring data are identical with those of linear 185k and different from the nearly half molar mass 100k (with molar mass 100,000 g/mol) linear data. To reconcile these two subtle points the conformational changes of the ring during the unravelling processes should be addressed. It is also worth considering the possible role of linear contaminants on both the onset of thickening and high-rate thinning. One could imagine that some of the compact ring structures even at equilibrium could be threaded by a linear molecule [3,5,21]. This structure would be much more sensitive to unravelling by extensional flow than an unthreaded one. This would explain the early onset of nonlinearity, coming from different mechanism compared to linear polymers. It is more difficult to imagine why a melt of ring molecules with less than 1% linear molecules would have the same asymptotic viscosity as 100% linear molecules. Certainly, if the early onset of thickening and the high-rate thinning behavior (collapse of thinning viscosity of ring and linear precursor) are due to less than 1% of a linear impurity, then the effect appears to be much more pronounced in nonlinear extension than in linear viscoelasticity (compare Figures 3 and S2). However, in lack of additional information we do not suggest at present that tiny impurities are responsible for this effect.

Resolving the above delicate issues represents the remaining grand challenge and calls for further investigations using rheo-SANS, stress relaxation after cessation of uniaxial extension and molecular dynamics simulations of pure rings in uniaxial extension. Nevertheless, it is now established that rings exhibit unique stretching behavior and can serve to tailor the flow of polymeric materials through their extreme sensitivity to extensional flow.

While the behavior of non-concatenated entangled rings near equilibrium is well documented after extensive studies, their transient strain hardening along with their strong viscosity thickening and linear polymer-like thinning behavior in strong extensional flow at very low and high rates, respectively, are suggestive of processes for polymeric extension and also novel applications. Polymer processing involves extensional deformation and in this regard, the present results shed light into the fascinating flow properties of polymeric loops, while advancing the state-of-the-art in polymer physics. More importantly, a new route opens for using this dual dynamic nature of rings in the design of composites with tunable properties (e.g., elastomers with controlled rolling resistance) or understanding the response of folded proteins and chromosome territories under strong external fields. Finally, uniaxial extensional rheology emerges as a highly sensitive and selective tool in polymer physics for diagnosing effects of macromolecular architecture under nonlinear response.