Analyzing the FFR: A tutorial for decoding the richness of auditory function

Abstract

The frequency-following response, or FFR, is a neurophysiological response to sound that precisely reflects the ongoing dynamics of sound. It can be used to study the integrity and malleability of neural encoding of sound across the lifespan. Sound processing in the brain can be impaired with pathology and enhanced through expertise. The FFR can index linguistic deprivation, autism, concussion, and reading impairment, and can reflect the impact of enrichment with short-term training, bilingualism, and musicianship. Because of this vast potential, interest in the FFR has grown considerably in the decade since our first tutorial. Despite its widespread adoption, there remains a gap in the current knowledge of its analytical potential. This tutorial aims to bridge this gap. Using recording methods we have employed for the last 20+ years, we have explored many analysis strategies. In this tutorial, we review what we have learned and what we think constitutes the most effective ways of capturing what the FFR can tell us. The tutorial covers FFR components (timing, fundamental frequency, harmonics) and factors that influence FFR (stimulus polarity, response averaging, and stimulus presentation/recording jitter). The spotlight is on FFR analyses, including ways to analyze FFR timing (peaks, autocorrelation, phase consistency, cross-phaseogram), magnitude (RMS, SNR, FFT), and fidelity (stimulus-response correlations, response-to-response correlations and response consistency). The wealth of information contained within an FFR recording brings us closer to understanding how the brain reconstructs our sonic world.

1. Introduction

1.1. What is the FFR?

The frequency-following response, or FFR, is a neurophysiological response to sound that reflects the neural processing of a sound’s acoustic features with uncommon precision.

Human scalp-recorded potentials to speech have been recorded for the past 25+ years (Galbraith et al., 1997; Galbraith et al., 1995; Galbraith et al., 1998; Krishnan, 2002; Krishnan & Gandour, 2009; Krishnan et al., 2004; Russo et al., 2004). FFRs can be recorded across the lifespan from infants through older adults (Jeng et al., 2011; Ribas-Prats et al., 2019; Skoe et al., 2015). By virtue of being generated predominately in the auditory midbrain (Bidelman, 2015; Chandrasekaran & Kraus, 2010; Sohmer et al., 1977; White-Schwoch et al., 2016b; White-Schwoch et al., in press), a hub of afferent and efferent activity (Malmierca, 2015; Malmierca & Ryugo, 2011), the FFR reflects an array of influences from the auditory periphery and the central nervous system. FFR can provide a measure of brain health, as it can index linguistic deprivation (Krizman et al., 2016; Skoe et al., 2013a), autism (Chen et al., 2019; Otto-Meyer et al., 2018; Russo et al., 2008), concussion (Kraus et al., 2016a; Kraus et al., 2017b; Kraus et al., 2016b; Vander Werff & Rieger, 2017), hyperbilirubinemia in infants (Musacchia et al., 2019), and learning or reading impairments (Banai et al., 2009; Hornickel & Kraus, 2013; Hornickel et al., 2009; Neef et al., 2017; White-Schwoch et al., 2015). The FFR has proven essential to answering basic questions about how our auditory system manages complex acoustic information and how it integrates with other senses (Anderson et al., 2010a; Anderson et al., 2010b; Musacchia et al., 2007; Selinger et al., 2016). It can reveal auditory system plasticity over short timescales (Skoe & Kraus, 2010b; Song et al., 2008) or lifelong experience, such as speaking a tonal language (Jeng et al., 2011; Krishnan et al., 2005), bilingualism (Krizman et al., 2016; Krizman et al., 2014; Krizman et al., 2012b; Krizman et al., 2015; Omote et al., 2017; Skoe et al., 2017) or musicianship (reviewed in Kraus & White-Schwoch, 2017; Parbery-Clark et al., 2009; Strait et al., 2009; Strait et al., 2013; Tierney et al., 2015; Tierney et al., 2013; Wong et al., 2007).

1.2. Purpose of this tutorial

This tutorial is not a review of the FFR’s history, origins, experience-dependence, nor its many applications, as those topics have been dealt with in detail elsewhere (Kraus & White-Schwoch, 2015; Kraus & White-Schwoch, 2017; Kraus et al., 2017a). How to record the response is well understood. There remains, however, a major gap in the current knowledge of how to analyze this rich response. Therefore, in this tutorial, we focus on data analyses. We touch on data collection parameters, but only insomuch as they affect FFR analyses. We aim to help clinicians and researchers understand the considerations that go into determining a protocol, based on the question at hand and the type of analyses best suited for that question, as there appears to be an interest in this within the field (e.g., BinKhamis et al., 2019; Sanfins et al., 2018). We provide an overview of the types of analyses that are appropriate for investigating the multifaceted layers of auditory processing present in the FFR and how some of that richness can be obscured or lost depending on how the data are collected. This tutorial is focused on the FFR we are most familiar with and the technique employed in our lab: a midline-vertex (i.e., Cz) scalp recording of an evoked response to speech, music, or environmental sounds (Figure 1). We originally chose this recording site to align the electrode with the inferior colliculus to maximize the capture of activity from subcortical FFR generators. We continue recording from here because we have developed a normative database over the years of FFRs recorded at this site to many different stimuli in thousands of individuals, many longitudinally, across a wide range of participant demographics (Kraus & Chandrasekaran, 2010; Kraus & White-Schwoch, 2015; Kraus & White-Schwoch, 2017; Krizman et al., 2019; Russo et al., 2004; Skoe & Kraus, 2010a; Skoe et al., 2015). In the ten years since our first tutorial (Skoe & Kraus, 2010a), we have employed many analysis techniques and what follows is a review of what we have learned and what we think constitutes the most effective ways of capturing what the FFR can tell us.

Figure 1.

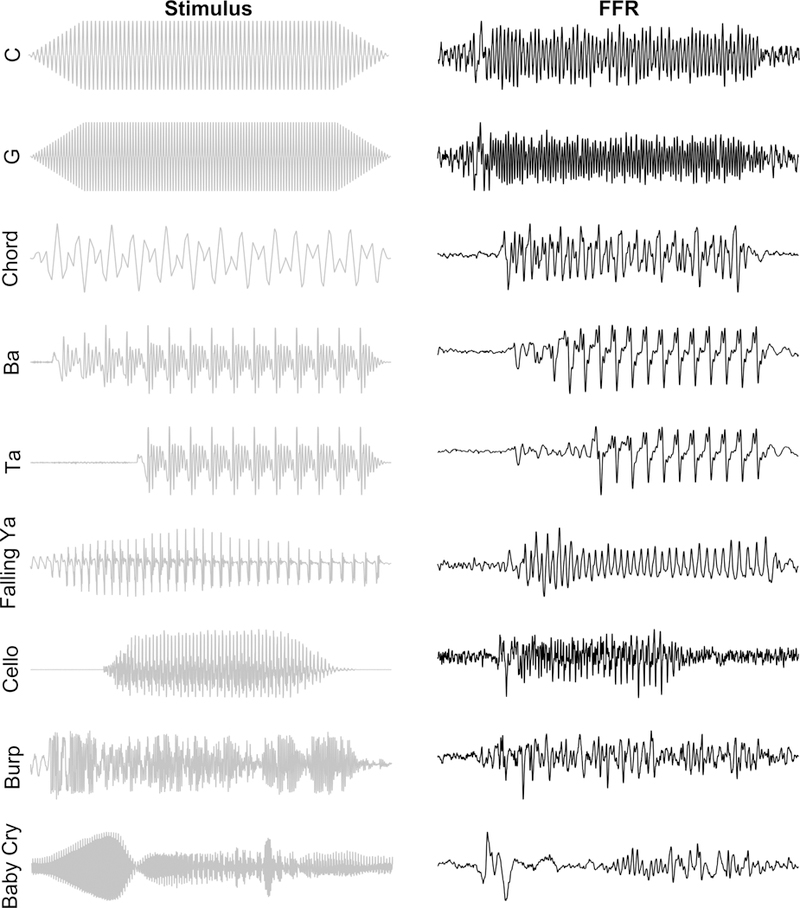
The FFR reflects transient and sustained features of the evoking stimulus. We have used a variety of stimuli to record FFRs. A few shown here include triangle waves of a single frequency (the notes C4 and G4), the notes G2 and E3 making a major 6th chord (chord), speech syllables with a flat (ba, ta) or a changing (falling ya) pitch, environmental sounds, like the bowing of a cello, a burp, or a baby’s cry. From the time domain FFRs on the right, it is evident that they contain much of the information found in the stimulus (left panel). The increase in frequency from C4 (262 Hz) to G4 (392 Hz) is mirrored in the FFR as is the later voice-onset time for ‘ta’ versus ‘ba’ and the falling frequency for the ‘ya’ from 320 to 130 Hz can be seen by the greater spacing of FFR peaks corresponding to the falling pitch.

2. FFR Components

The FFR provides considerable detail about sound processing in the brain. When talking about the FFR, we like to use a mixing board analogy, as each component of the FFR distinctly contributes to the gestalt, with each telling us something about sound processing. This processing of sound details distinguishes FFR from other evoked responses. When recording FFR to a complex sound, like speech or music, we typically consider three overarching features of the response: timing, fundamental frequency, and the harmonics. We also consider the accompanying non-stimulus-evoked activity. Each of these components contains a wealth of information (described in the data analyses section).

2.1. Timing

Amplitude deflections in the signal act as landmarks that are reflected in the response (Figure 1). These peaks occur at a specific time in the signal and should therefore occur at a corresponding time in the response. Generally, peaks fall into two categories. One is in response to a stimulus change, such as an onset, offset, or transition (e.g., onset to steady-state transition) while the other category reflects the periodicity of the stimulus. A term used to define a peak’s timing in the response is latency, which is referenced to stimulus onset, or less frequently, to an acoustic event later in the stimulus. One may also evaluate relative timing of peaks within a response or of peaks between two responses (e.g., to the same stimulus presented in quiet v. background noise). In addition to looking at timing via peaks in the time-domain response, one can look at the phase of individual frequencies within the response.

2.2. Fundamental frequency

The fundamental frequency (F0) is by definition the lowest frequency of a periodic waveform and therefore corresponds to the periodicity of the sound, or repetition rate of the sound envelope. For a speech sound, this corresponds to the rate at which the vocal folds vibrate. In music, the fundamental is the frequency of the lowest perceived pitch of a given note. The neural response to the F0 is rich in and of itself. We have a number of methods for extracting information about the phase, encoding strength, and periodicity of the F0 (Table 1).

Table 1.

Overview table of techniques for analyzing FFR. All of these measures can be performed on both the transient and sustained regions of the response. Additionally, peak-picking can provide information about the timing of onset and offset responses. On the technologies page of our website, (www.brainvolts.northwestern.edu), you can find links to get access to our stimuli and freeware.

Analytical Technique	Measure of	Polarity	Publications
Peak-picking	Broadband Timing	Single Added	Krizman et al., 2019 Kraus et al., 2016a; White-Schwoch et al., 2015; Anderson et al., 2013a; Hornickel et al., 2009; Parbery-Clark et al., 2009;
Autocorrelation	F0 Periodicity	Single Added	Kraus et al., 2016a; Carcagno & Plack, 2011; Russo et al., 2008; Wong et al., 2007; Krishnan et al., 2005;
Phase consistency	Frequency-specific timing consistency averaged over a response region or using a short-term sliding-window	Single Added Subtracted	Roque et al., 2019; Kachlicka et al., 2019; Omote et al., 2018; Ruggles et al., 2012; Tierney & Kraus, 2013; Zhu et al., 2013;
Cross-phaseogram	Frequency-specific timing differences between pairs of FFRs	Single Added Subtracted	Neef et al., 2017; Strait et al., 2013; Skoe et al., 2011;
RMS/SNR	Broadband response magnitude	Single Added Subtracted	Krizman et al., 2019 Kraus et al., 2016a; Marmel et al., 2013; Strait et al., 2009;
Fast Fourier transform (FFT)	Frequency-specific magnitude. May be short-term, slidingwindow, i.e., spectrogram	Single Added Subtracted	Krizman et al., 2019; Zhao et al., 2019; Musacchia et al., 2019; Skoe et al., 2017; Kraus et al., 2016a; White-Schwoch et al., 2015; Krizman et al., 2012b; Parbery-Clark et al., 2009;
Stimulus-response correlation	Fidelity of the response	Single Added Subtracted	Kraus et al., 2016a; Tierney et al., 2013; Marmel et al., 2013; Parbery-Clark et al., 2009;
Response-response correlation	Consistency and similarity of two FFRs (e.g., Quiet versus Noise). May be run in time-or frequency-domain	Single Added Subtracted	Anderson et al., 2013a; Parbery-Clark et al., 2009;
Response consistency	Broadband consistency across trials within a session	Single Added Subtracted	Otto-Meyer et al., 2018; Neef et al., 2017; White-Schwoch et al., 2015; Krizman et al., 2014; Tierney & Kraus, 2013; Skoe et al., 2013a;

2.3. Harmonics

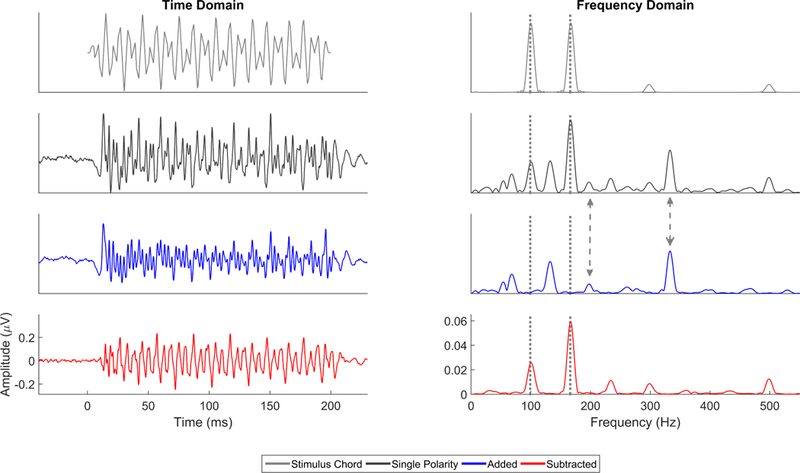
Harmonics are integer multiples of the F0. Typically all harmonics present in the stimulus are present in the FFR, at least up to about 1.2–1.3 kHz (Chandrasekaran & Kraus, 2010) and the ceiling frequency varies depending on whether you are looking at the response to a single stimulus polarity, or the added, or subtracted response to opposing-polarity stimuli (see Stimulus Polarity, below, and Figures 2 and 3). Non-linearities of the auditory system can introduce harmonic peaks in the FFR outside those present in the stimulus or at different strengths than one would predict from the stimulus composition (Warrier et al., 2011). In a speech stimulus, certain harmonics, called formants, are of particular importance phonetically and are somewhat independent of the F0 of the speech sound. Formants are harmonics that are larger in amplitude than surrounding harmonics, both in the stimulus and in the FFR. For example, the first formant of /a/ corresponds to a local peak at ~ 700–750 Hz, while /i/, will have a first formant in the 250–300 Hz range, regardless of the F0 of the utterance.

Figure 2.

Comparison of single polarity (black), added (blue), and subtracted (red) FFRs to the evoking stimulus (an E2G3 chord made from triangle waves (gray)) in the time (left) and frequency (right) domains. The frequencies of the stimuli, 99 and 166 Hz (gray dotted lines), are evident in the frequency domain of the subtracted and single polarity responses. However, in the single polarity response and added response, there are also peaks at double the frequencies of the two F0’s (i.e., 198 and 332 Hz, gray dashed arrows) which are the result of half-wave rectification in the extraction of the response envelope. The remaining peaks in the frequency domain are subharmonics and harmonics of the notes.

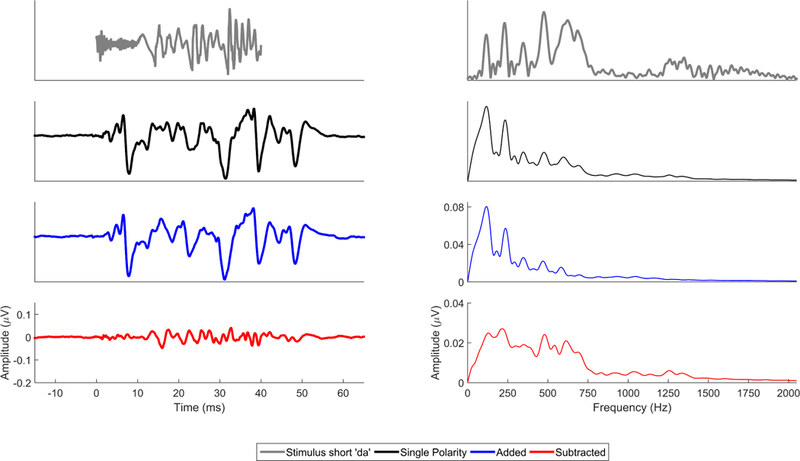
Figure 3.

Comparison of single polarity (black), added (blue), and subtracted (red) FFRs to the evoking stimulus ‘da’ (gray) in the time (left) and frequency (right) domains. The single polarity FFR contains responses to both the stimulus envelope and temporal fine structure. While the lower frequencies, especially the fundamental frequency and lower harmonics (H2, H3) are consequences of half-wave rectification and envelope encoding, the higher frequencies (particularly the local maxima at H7, H12) are likely the result of temporal fine structure encoding. The mid frequencies are likely a mix of both envelope and temporal fine structure encoding. This can be seen in the lower-frequency bias of the added response, which falls off in encoding strength after the 6th harmonic, and the more faithful representation in the subtracted domain of the frequencies present within the stimulus (e.g., unlike in the added response the encoding of first-formant peak H7 in the subtracted response is stronger than neighboring nonformant harmonics).

2.4. Non-stimulus activity

The stimulus used to evoke an FFR is presented multiple times and there is a gap of silence between each stimulus presentation. We measure the amount of neural activity that occurs during this silent interval to provide us with information about the neural activity that is not time-locked to the stimulus, which can be called non-stimulus activity, prestimulus activity, or neural noise.

3. Factors Influencing FFR

3.1. Stimulus polarity

In the cochlea, a periodic sound, such as a sine wave, will open ion channels on the hair cell stereocilia in one-half of its cycle, and close the channels during the other-half of its cycle, a process known as half-wave rectification. Additionally, the tonotopic arrangement of the cochlea causes earlier activation of auditory nerve fibers that respond to higher frequencies at the basal end of the cochlea compared to the nerve fibers that respond to lower frequencies at the apex (Greenberg et al., 1998; Greenwood, 1961; Ruggero & Rich, 1987). Consequently, the timing of auditory nerve responses will differ depending on whether they receive information from more basal or apical areas of the cochlea or whether the initial deflection of the stereocilia is hyperpolarizing or depolarizing. These timing differences will propagate to and be reflected in firing in central auditory structures, including the inferior colliculus (Liu et al., 2006; Lyon, 1982; Palmer & Russell, 1986).

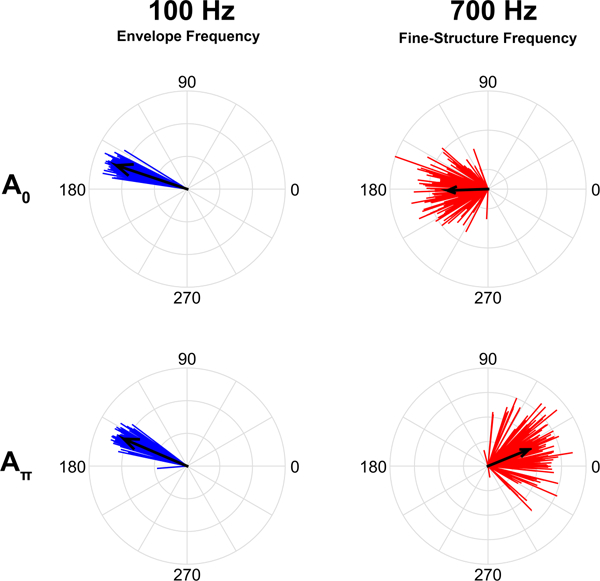
Because a sine wave can only depolarize a cochlear hair cell during one half of its cycle, the starting phase of the sine wave (i.e., where it is in its cycle) will affect FFR timing. If the initial deflection of the stereocilia is depolarizing, the initiation of an action potential in the auditory nerve will occur earlier than if the initial deflection is hyperpolarizing. If FFRs are recorded to two sine waves that are identical in frequency but start 180 degrees out of phase from one another (A₀ and A_π), these FFRs will maintain the phase difference between the two sinusoids. That is, the timing of the peaks in the response will also be shifted relative to one another so that the positive-deflecting peaks of the FFR for A₀ in the time-domain waveform will temporally align with the negative-deflecting troughs of the FFR to A_π (Figures 2 and 4).

Figure 4.

Unit circle histogram plots of phase of 100 Hz (left, blue) and 700 Hz (right, red) responses from FFRs recorded in the guinea pig inferior colliculus to two ‘a’s that start 180 degrees out of phase. The 100 Hz fundamental frequency is extracted from the envelope, which is phase invariant, while the 700 Hz first formant is extracted from the temporal fine structure, which varies with the phase of the stimulus. The 100 Hz responses maintain a consistent phase angle regardless of the stimulus polarity while the 700 Hz responses flip their phase angle by ~180 degrees, similar to the phase shift between the two ‘a’ stimuli. The average phase angle for each frequency and polarity are indicated by the black arrows, whose length indicates the consistency of that phase angle across trials (individual vectors).

FFRs are often obtained to both polarities by using stimuli presented in alternating-polarity. A common practice, then, is to add or subtract together the FFRs to each stimulus polarity. For a simple, unmodulated stimulus like a sinewave or a triangle wave, adding the FFRs to A₀ and A_π results in a doubling of the stimulus frequency due to the half-wave rectification of the signal as it is processed in the cochlea, while subtracting restores the original waveform and thus maintains the frequency of the stimulus (Figure 2, and see Aiken & Picton, 2008).

A periodic tone can be modulated by a lower frequency periodic wave, as occurs with speech. Speech can be thought of as many high frequency carriers of phonetic information being modulated by lower frequencies, bearing pitch information. When a higher, carrier frequency is modulated by a lower frequency, the modulation frequency acts as an ‘on/off switch, gating the intensity of the carrier frequency (Aiken & Picton, 2008; John & Picton, 2000). When this occurs, the region of the basilar membrane that responds to the carrier frequency will respond to that frequency at the rate of the modulation frequency. Thus, the carrier frequency will be maintained in the phase of firing, while the modulation frequency information will be maintained by the rate of firing (John & Picton, 2000).

With an amplitude-modulated stimulus, adding and subtracting A₀ and A_π responses will have different effects on the modulation and carrier frequencies. Because the modulation frequency acts as an ‘on/off switch that is coded in the rate of firing, the phase of the carrier frequency information is maintained in the response (Figure 4; John & Picton, 2000), while the modulation frequency is phase invariant (Aiken & Picton, 2008; Krishnan, 2002). For this reason, adding FFRs to the two stimulus polarities will emphasize the modulation frequency, while subtracting will emphasize the carrier frequency. On the other hand, both the modulation and carrier frequencies will be represented in the single polarity responses (Figure 2 and 3)¹.

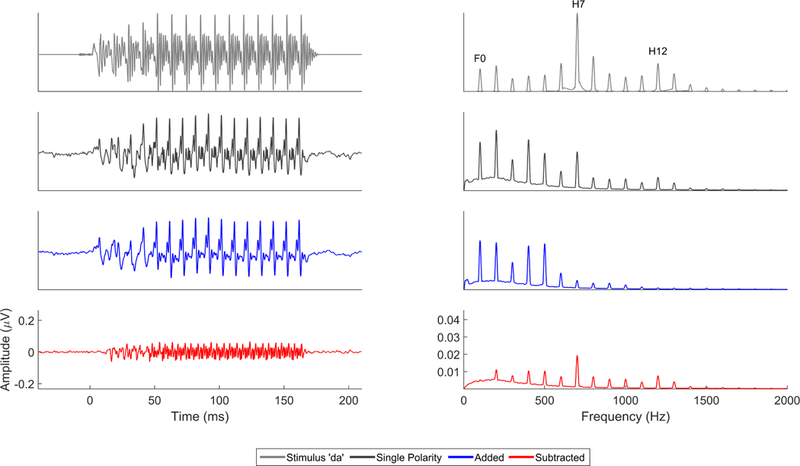
Expanding this to a more complex soundwave, a speech syllable, such as ‘da’, consists of multiple higher frequencies (the formants) that are modulated by a lower frequency (the fundamental) (Figure 3). Therefore, the same principle applies. Spectral energy from these higher frequencies is present in the syllable and are referred to as temporal fine structure (TFS) while the energy corresponding to the fundamental and some additional lower-frequencies that arise from cochlear rectification distortion components are referred to as the temporal envelope (ENV) (Aiken & Picton, 2008). Although the temporal envelope does not have its own spectral energy, it is introduced to the auditory system by the rectification process during cochlear transduction. FFRs to speech can capture both the temporal envelope and fine structure. Both are evident within an FFR to a single polarity, but can be semi-isolated by adding or subtracting alternating polarity responses ((Aiken & Picton, 2008; Ruggles et al., 2012); Figures 3 and 6). Because the temporal envelope is relatively phase invariant, the envelope response will show similar timing across the two polarities (i.e., da₀ and da_π). Adding the responses to da₀ and da_π biases the FFR to the envelope (FFR_ENV). In contrast, the FFR_tfs is phase dependent (Aiken & Picton, 2008; Krishnan, 2002) so subtracting the responses to da₀ and da_π biases the FFR to the fine structure (Figure 3).

Figure 6.

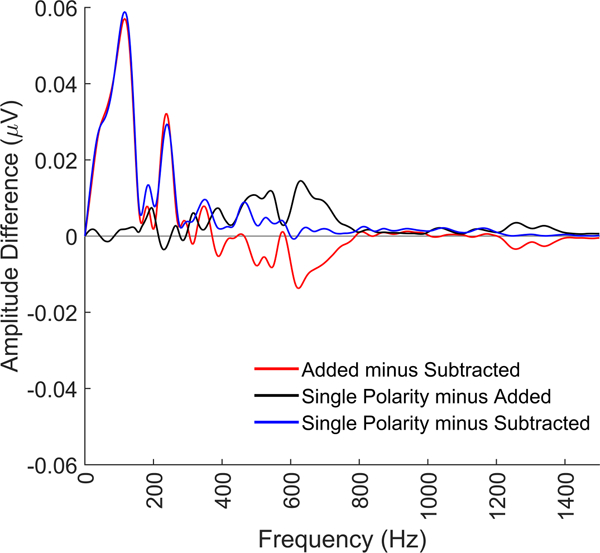
Comparison of single polarity, added, and subtracted frequency content for FFRs to the 40 ms ‘da’ stimulus. As can be seen in the blue difference line, the single polarity has a larger response than the subtracted response across all frequencies, while compared to the added FFR (black line), it shows similar magnitude responses for the lower frequencies (<400 Hz) and greater response magnitude for the mid frequencies (~500–800 Hz). That the single polarity response has the largest mid-frequency encoding suggests that the mid frequencies can be extracted from both the FFR_ENV and FFR_tfs and that there is not a clear frequency cutoff between ENV and TFS for a complex sound.

In our lab, we typically collect FFRs to alternating-polarity stimuli. Many of our previous findings were focused on the added polarity response, however single polarity and subtracted responses yield equally important information to consider. Choice of polarity should be dictated by the aspects of sound encoding under investigation and which stimuli you are using. For example in the case of unmodulated sound waves, such as the triangle wave chord in Figure 2 or our investigations into tone-based statistical learning (the C and G notes from Figure 1; Skoe et al., 2013b), single polarity or subtracted FFRs provide the ideal window into how the brain represents these sounds. This is because the frequencies in these stimuli, especially the lowest frequency that conveys the pitch information of interest, is contained predominantly within the temporal fine structure of the stimulus. If the energy of a given frequency is not present in the stimulus carrier freqeuncies, it will not be present in the temporal fine structure (i.e., subtracted) response (Figure 7). You might be wondering why we have devoted so much attention to stimulus polarity. As you will see, these polarities triple the amount of information that can be derived from a typical FFR recording.

Figure 7.

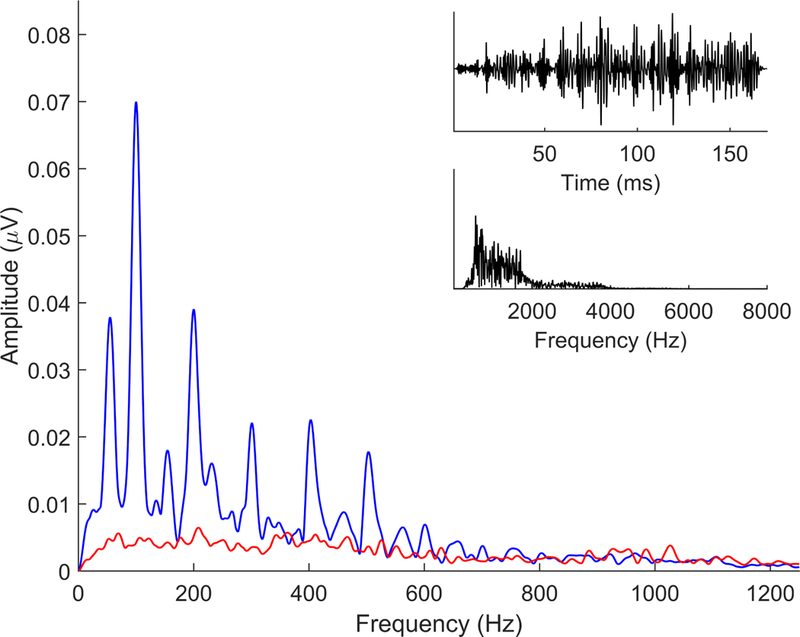
Comparison of added (blue) and subtracted (red) FFRs in response to a stimulus that consists of noise shaped by the ‘da’ envelope (black, top time domain, bottom frequency domain). Because the carrier is noise, there are no resolvable frequencies contained within the stimulus. The only spectral information can be extracted from the envelope. Therefore, the FFR to this stimulus is only an envelope response, no temporal fine structure is encoded. This demonstrates that the added response is an envelope response that consists of both the fundamental frequency (100 Hz in this case) and its lower harmonics, in this case, up to ~500 Hz. When there is no spectral energy in the stimulus, there is no subtracted response.

3.2. Averaging versus single-trial

Because the FFR is small, on the order of nanovolts to microvolts, the stimulus must be presented repeatedly to average the FFR above the noise floor (though see Forte et al., 2017 for methods to measure single-trial FFRs). When collecting these trials, some systems enable single trial data to be maintained for offline analyses. When collecting FFRs using these systems, we use open filters and a high sampling rate so that the responses can be processed offline according to the questions we are asking. This is especially important for calculating the consistency of the broadband response (see response consistency section) or the phase consistency of specific frequencies (see phase consistency section). Other systems will process the individual trials online, including filtering, artifact rejection, and averaging, typically providing us with an average of 4000 – 6000 artifact-free trials.

3.3. Stimulus presentation timing

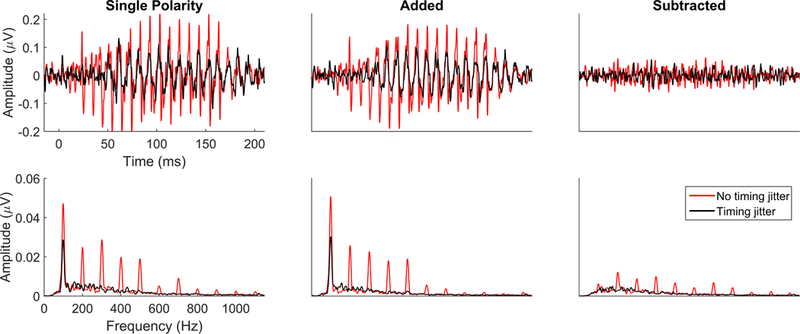
Collecting an FFR requires uncommon precision in the timing of stimulus presentation and the communication between the presentation and recording systems. The amount of jitter allowable for recording a cortical onset response will ablate the FFR. Egregious timing jitter will prevent FFR from forming. While this is bad, the silver lining is that it is very clear there is a problem with the presentation and recording setup. Smaller levels of jitter are much more insidious; they have greater consequences on higher frequency aspects of the FFR, while seemingly sparing the lower frequencies (Figure 8). The timing jitter will effectively low-pass filter the signal. If the lower frequencies are evident, though diminished, it can be harder to detect a timing problem, especially for someone new to FFR. This will severely impact the ability to make any statements about the strength of speech encoding, because the jitter prevents capture of the sound details typically contained in the FFR.

Figure 8.

FFRs collected from the same participants with (black) and without (red) jitter in the timing of the stimulus presentation. Subtle variations in the presentation timing of the stimulus can have catastrophic effects on the recorded response, serving to low-pass filter the response with a lower high-frequency cutoff as the jitter increases. Thus, as timing jitter increases, response peaks will be increasingly ablated, with the largest effects being on the highest frequencies. Magnitude of the response is severely diminished in the time domain in the single polarity, added, and subtracted responses (top), which makes peak-picking difficult. The frequency encoding is also affected. The response becomes almost entirely the F0, though the magnitude of F0 encoding is diminished compared to when there is no presentation jitter (bottom).

It is important to routinely check your system for jitter. There is no guarantee that a recording system will arrive out of the box jitter free or that presentation jitter will not arise over the life of the system. We loop our stimulus through the recording system (i.e., present the stimulus and then record it through our recording setup) to verify that no jitter is present. Another telltale sign of jitter in systems that average online is that the average’s amplitude will get smaller as the session progresses. An averaged response of a non-jitter setup will be as large in amplitude as any one single presentation. Minimizing presentation jitter is one of the most important aspects of good FFR data collection and so this verification process should never be skipped.

4. Analyzing the FFR

4.1. Overview

The FFR is a time-varying signal and can be analyzed as such. The same signal decomposition techniques used on other time-varying signals can be used here (the most common techniques we use are summarized in Table 1). These analyses are run on responses that have all been initially processed with baseline correction, filtering to an appropriate frequency range (typically at or around 70–2000 Hz), and artifact rejection (see Skoe & Kraus, 2010a or any of our publications for details on these steps). FFR analyses focus on measures of response timing, magnitude, and fidelity. These measures can be examined with broadband indices or we can focus on specific frequencies, like the fundamental frequency or its harmonics.

4.2. Timing

4.2.1. Broadband timing

One aspect of timing is the speed of one or more components of the neural response in the time-domain waveform. Specifically, we identify stereotyped peaks, which may be either positive or negative deflections in the FFR to determine their time of occurrence relative to stimulus onset. The neural transmission delay, or the difference in time between when something occurs in the stimulus and when it occurs in the FFR, is typically ~7–9 ms, due to the travel time from the ear to the midbrain. Therefore, if a stimulus onset takes place at time t=0 ms, the onset response will occur ~t=8 ms.

While we will often manually apply peak labels for our shorter stimuli, for longer stimuli that may have dozens of peaks, we employ an automatic peak-detection algorithm, which identifies local maxima and minima within a predefined window of the FFR. This predefined window for each peak is set with respect to the expected latency for a given peak based on our prior studies. These auto-detected peaks can then be manually adjusted by visual inspection of the response by an expert peak-picker. We use subaverages to guide in identifying reliable peaks in an individual’s final average response. We create two subaverages, comprising half the collected sweeps, each, and overlay them with the final average. Because many of the studies in our lab are longitudinal and the FFR is remarkably stable in the absence of injury or training (Hornickel et al., 2012; Song et al., 2010), we will also refer to a participant’s previous data to aid in peak picking.

In addition to the onset response, which all sounds generate, the number and morphology of FFR peaks is stimulus-dependent. For example, a speech sound that contains an F0 generates response peaks occurring at the period (i.e., the reciprocal of the frequency) of the F0, such that a stimulus with a 100 Hz F0 generates an FFR with major peaks occurring every ~10 ms with minor peaks flanking them, the periodicity of which relates to formant frequencies (Hornickel et al., 2009; Johnson et al., 2008). An irregular sound like an environmental noise or the baby cry illustrated in Figure 1 will have different acoustical landmarks that will inform the decision of the response peaks of interest. We often see FFR peaks that correspond to transition points in the stimulus (e.g., the onset of voicing) or the cessation of the sound.

Recording and processing parameters can also affect the morphology, timing, or magnitude of peaks in the FFR. Changes in stimulus intensity often affect the robustness and timing of FFR peaks differently, with onset peaks being the most robust to intensity reductions (Akhoun et al., 2008). Binaural stimuli evoke larger FFRs and, in some cases, earlier peak latencies than stimuli presented monaurally (Parbery-Clark et al., 2013). To elicit a robust response to all peaks across the largest number of individuals, we present monaural sounds at ~80 dB SPL and binaural sounds at ~70–75 dB SPL. Like ABR, rate can also affect FFR peak timing, with faster stimulus rates resulting in later peak latency, most notably observed for the onset peaks (Krizman et al., 2010). As a measure of periodicity of the F0, peak picking is only done on single-polarity or added-polarity responses. Peak timing appears to be consistent across polarities, which is expected given that they are largely determined by the phase-invariant temporal envelope, though there is a tendency for peaks in the added response to be earlier (Kumar et al., 2013).

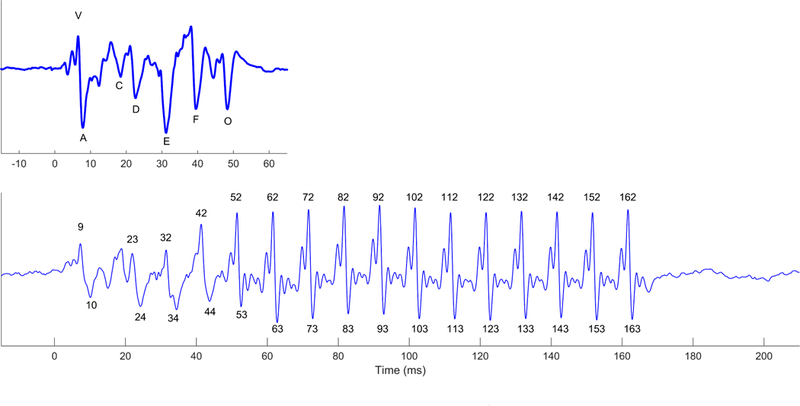
While we use the same procedure for peak-picking across stimuli, we have developed a particular nomenclature for our short, 40-ms ‘da’ stimulus. For our other stimuli we use the expected time to name the peak (e.g., peak 42 occurs ~42 ms post stimulus onset; Figure 9; (White-Schwoch et al., 2015)), or we will number the peaks sequentially (e.g., peak 1 is the earliest peak identified in the response (Hornickel et al., 2009)). On the other hand, the short ‘da’ has peaks named ‘V’, ‘A’, ‘C’, ‘D’, ‘E’, ‘F’, ‘O’ (Figure 9, King et al., 2002; Russo et al., 2004). As described previously (Krizman et al., 2012a), Peak V is the positive amplitude deflection corresponding to the onset of the stimulus and occurs ~7–8 ms after stimulus onset, A is the negative amplitude deflection that immediately follows V. Peak C reflects the transition from the onset burst to the onset of voicing. Peaks D, E, and F are negative amplitude deflections corresponding to the voicing of the speech sound, and as such are spaced ~8 ms apart (i.e., the period of the fundamental) occurring at ~22, ~31, and ~39 ms, respectively. O is the negative amplitude deflection in response to the offset of the sound and occurs at about 48 ms post stimulus onset (i.e., 8 ms after stimulus cessation). We have collected FFR to this stimulus in thousands of individuals across the lifespan and have created a published normative dataset (Skoe et al., 2015) that we refer to when picking peaks.

Figure 9.

Peak-naming conventions for peaks in the short-da (top) and long-da (bottom) FFRs. Other stimuli that we have used in the lab, such as ga or ba, use a naming convention similar to the long-da.

Several measures are available to analyze peaks. A primary measure is the absolute latency of a single peak, such as an onset peak. When looking at response peaks reflecting the periodicity of a sound, we will generally average these peaks over a specific region of the response, such as the formant transition. We will also compare relative timing across FFRs to different stimuli or to the same sound under different recording conditions, such as a ‘da’ presented in quiet or in the presence of background noise. Because noise delays the timing of peaks in the FFR, we can look at the size of these degradative effects by calculating latency shifts for specific FFR peaks (Parbery-Clark et al., 2009). Alternatively, we can calculate a global measure of timing shift by performing a stimulus-response correlation (see below), which provides a measure of the timing shift necessary to achieve the maximum absolute-value correlation between the stimulus and the response. We can similarly do this with two different FFRs (see response-response correlation below). These methods provide a measure of global timing in the subtracted FFR, while peak-picking can only be performed on added or single-polarity FFRs since the prominent peaks are responses to the temporal envelope.

4.2.2. Frequency-specific timing

4.2.2.1. Autocorrelation

Autocorrelation can be used to measure periodicity of a signal and so can be used to gauge pitch tracking in an FFR (e.g., see Carcagno & Plack, 2011; Wong et al., 2007). It is a standard procedure that time-shifts a waveform (W) with respect to a copy of itself (W’) and correlates W to W’ at many such time shifts. As a measure of F0 periodicity, it is meaningful on single polarity or added polarity FFRs (Figure 10). The goal is to identify the lag (L) at which the maximum correlation occurs (i.e., L_max), excluding a time shift of zero. The maximum correlation is referred to as r_max. The maximum lag occurs at the period of the fundamental frequency (i.e., F0 = 1/L_max Hz. Thus, for an FFR response to a speech syllable with a 100 Hz F0 we would expect a maximum autocorrelation between W and W’ at a lag of ~0.01 seconds, or 10 ms.

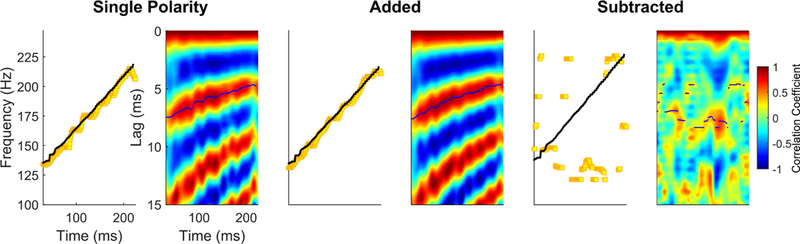
Figure 10.

Autocorrelation to extract the F0 of a rising ‘ya’ syllable. On the left is the pitch extraction over time (yellow squares) relative to the pitch of the stimulus (black dots). On the right is the autocorrelelogram of the FFR. The timing shift (i.e., lag, in ms) to achieve the maximum correlation (i.e., the darker red) corresponds to the periodicity of the fundamental frequency. As this periodicity is contained within the temporal envelope of the FFR, it is only evident on single polarity (left) or added (middle) responses. No F0 periodicity is evident in the subtracted (right) response.

If the stimulus has an F0 that changes over time or if there is a desire to examine changes over the duration of a response to a non-changing F0, you can use a sliding window to analyze the max lag and correlation at discrete points along the response. For example, for a 230 ms stimulus with an F0 that rises linearly from 130 Hz to 220 Hz, as in Figure 10, if we look at a specific time point for that stimulus, there will be a specific F0 value at that point, such as 130 Hz at t=0 ms, 175 Hz at t= 115 ms, and 220 Hz at t=230 ms. The instantaneous frequency at any given point can be derived by running an autocorrelation over small, overlapping segments of the waveform. Typically, we use a 40 ms window, with a 39 ms overlap, starting with a window centered over t=0 ms. An r_max and L_max are assigned to the center time point of each window to provide a measure of pitch tracking over time (Figure 10). As this measure can be run on both the stimulus and the response, we can use the output to determine the pitch-tracking accuracy of the brain response by computing the difference in extracted F0 between the stimulus and FFR at each time point. Because the response will always lag the stimulus by a fixed amount (about 8 ms), it is necessary to make that adjustment. So, the pitch of the stimulus at time = 50 ms would be compared to the pitch in the response at time = 58 ms. We then sum the absolute values of the frequency differences at each point to calculate a “frequency error”, where 0 indicates perfect pitch tracking and larger numbers indicate poorer pitch-tracking (i.e., greater differences between stimulus and response). A sliding-window fast-Fourier transform (FFT) approach (described below) can also be used to determine pitch-tracking accuracy (e.g., see Maggu et al., 2018; Song et al., 2008).

4.2.2.2. Phase consistency

Peak-picking on the time domain waveform requires averaging responses to a large number of stimulus presentations to generate a robust FFR with peaks sufficiently above the noise floor, operationally defined as peaks in the response that are larger in amplitude than the non-stimulus response activity. Moreover, while these peaks occur at the periodicity of lower frequency components of the stimulus, they are influenced by all frequencies in the stimulus and thus reflect broadband timing of the FFR. An alternative approach to looking at FFR timing is to analyze the phase of individual frequencies over the course of the response to determine how consistent the phase for a given frequency is across individual trials (i.e., responses to individual stimulus presentations). In addition to providing frequency-specific timing information, this technique has the added benefit of extracting meaningful information with fewer numbers of sweeps and is less susceptible to artifacts (Zhu et al., 2013), though we still encourage artifact rejection prior to processing to remove larger artifact. Furthermore, though it must be performed on data that has maintained single-trial responses, it can be performed on single polarity, added polarity, and subtracted polarity responses and can be examined by averaging over the whole FFR or by using a sliding-window approach. This measure has many names, including phase-locking value, phase-locking factor, but we prefer the term phase consistency or phase coherence, since the term ‘phase-locking’ implies that it is capturing phase-locking of a single neuron to a periodic stimulus, while the FFR is a population response reflecting periodicity encoding across a large number of subcortical neurons. Essentially, phase consistency analyses operate under the assumption that frequencies present in the stimulus envelope or temporal fine structure will demonstrate phase coherence across trials. In contrast, frequencies not present in the stimulus will behave randomly, resulting in no phase coherence for these frequencies (see Figure 11).

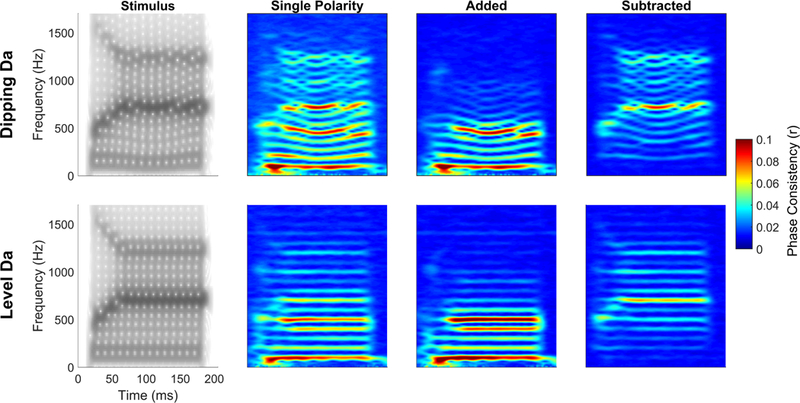
Figure 11.

Phase consistency of a ‘dipping da’ and a ‘level-F0 da’ using single polarity, added polarity, and subtracted polarity responses. For FFRs to either sound, in the single polarity, the fundamental frequency, second harmonic and formant frequencies all show the strongest phase coherence (red lines). Adding emphasizes the phase coherence of the lower frequencies, below ~600 Hz, and subtracting emphasizes the phase coherence of the higher frequencies above ~600 Hz.

On filtered, single-trial data we run our phase consistency analyses. In its simplest form, we calculate phase consistency by applying a fast-Fourier transform over a discrete time period, such as the formant transition or steady-state, of a single-trial FFR (e.g., see Tierney & Kraus, 2013). This transformation results in a vector that contains a length, indicating the encoding strength of each frequency, and a phase, which contains information about the timing of the response to that frequency. To examine the timing variability of the response, each vector is transformed into a unit vector by dividing the FFT by the absolute value of the FFT. This transformation sets the length component of the vector to one for all frequencies, thereby discarding the information about encoding strength but maintaining the phase information. A unit vector is generated for each response trial. We then average this unit vector across trials. When averaging, we can average the vectors obtained for a single polarity, we can add responses from both polarities, or we can subtract responses from the two polarities, to focus on phase consistency of either the lower frequency envelope or the higher frequency fine structure, respectively (e.g., see Kachlicka et al., 2019). The length of the resulting vector for each frequency provides a measure of intertrial phase consistency. Values range from 0 to 1, with a small number indicating poorer consistency and a higher number indicating greater phase consistency. In addition to looking at phase consistency over a single time period in the response, we also use a sliding window analysis to calculate phase consistency over small, overlapping time periods of the response to determine how encoding of a specific frequency changes over the duration of the response (Figure 11). Most often, we will use a 40 ms Hanning-ramped window with a 39 ms overlap, which results in phase consistency being calculated from 0–40 ms, 1–41 ms, 2–42 ms, etc. (e.g., see Bonacina et al., 2018; White-Schwoch et al., 2016a). The phase consistency of a single frequency of interest, for example, a 100 Hz F0, or an average of frequencies centered around a frequency of interest (e.g., 100 Hz ± 10 Hz) is then analyzed. Instead of using an FFT to examine phase consistency, other signal processing approaches to determine the instantaneous phase of the response at specific frequencies, such as wavelets, can also be used (e.g., see Roque et al., 2019).

4.2.2.3. Cross-phaseogram

The cross-phaseogram is a measure of relative timing between FFRs elicited by two different stimuli. It measures frequency-specific phase differences between two brain responses. Because of the tonotopic layout of the basilar membrane, with maximal excitation of higher frequencies occurring at the base and lower frequencies toward the apex, when sound enters the ear, higher frequencies reach their maximum peak of excitation milliseconds earlier than lower frequencies (Aiken & Picton, 2008; Kimberley et al., 1993). This timing information is maintained in the auditory pathway, as the auditory nerve fibers innervating the basal end of the cochlea will fire earlier than more apical fibers. It is because of this tonotopic arrangement that a high-frequency tone-burst will elicit an ABR peak V earlier than a lower frequency tone-burst (Gorga et al., 1988). When a more complex stimulus, such as an amplitude-modulated sinusoid, is used, modeling has shown that the envelope response entrains to the modulation frequency but the carrier frequency determines the phase of the response (John & Picton, 2000). Thus, an 85 Hz modulation of a 6000 Hz carrier frequency would have an earlier brain response to that modulation frequency than if the 85 Hz modulation was of a 750 Hz carrier frequency.

We can apply this knowledge to investigate subcortical speech-sound differentiation in individuals by recording their FFRs to minimally contrastive speech sounds. We often use the synthesized speech syllables ‘ba’ and ‘ga’, although other speech sounds that have time-varying spectral differences could be used. Our ‘ba’ and ‘ga’ have been synthesized to differ only on the trajectory of their second formant (F2, see Figure 12). The F2 of ‘ga’ begins 2480 Hz, descending linearly to 1240 Hz by t=50 ms, where it remains for the duration of the steady-state vowel. In contrast, the F2 of ‘ba’ begins at 900 Hz at t=0, then linearly ascends to 1240 Hz by t=50 ms, where, just like the ‘ga’, it remains over the vowel. We have shown that this manifests as differences in peak timing of both the envelope-and fine-structure-related peaks of the time-domain FFR waveform (Hornickel et al., 2009; Johnson et al., 2008).

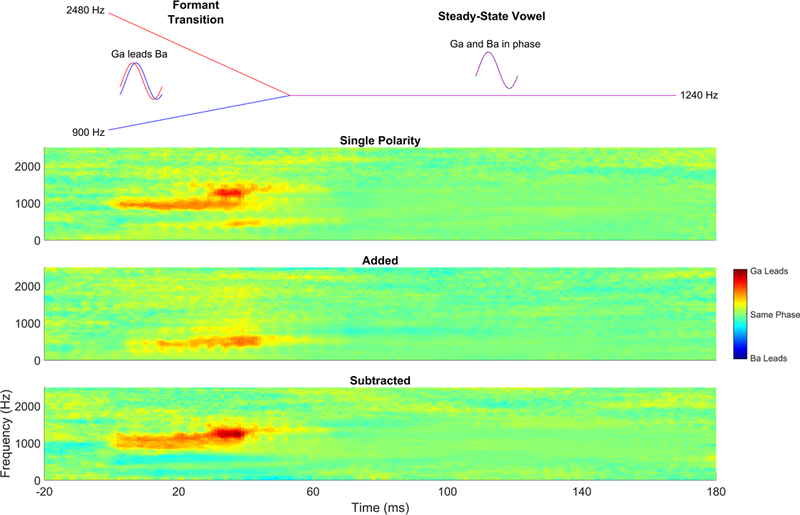
Figure 12.

Comparison of single polarity, added, and subtracted phaseograms comparing ba versus ga. Based on the frequency contents of ba and ga, it is expected that ga should phase-lead ba during the formant transition because it is higher in frequency, and thus activates more basal regions of the basal membrane than ba. We have typically reported it using ‘added’ polarity responses, which show a phase differences at a lower frequency than would be expected based on where in frequency these stimuli differ. Interestingly, however, if we compare the single polarity ba versus ga, which contain both the temporal envelope and fine structure, we see the greatest differences in the F2 frequencies (i.e., where they differ), however, there is also a ga phase lead in the lower frequency, suggesting that the second formant frequencies are encoded at that lower modulation rate. The modulation frequency differences become emphasized when we add polarities while the differences at the F2 frequencies become emphasized in the subtracted response. As expected, there are no phase or timing differences in the steady state ‘a’, which is where the two stimuli have equivalent spectral features. Phase differences (in radians) are indicated by color, with warmer colors indicating that ga phase leads ba. Green indicates no phase differences, and cooler colors would indicate ba phase leading ga.

The cross-phaseogram measures frequency-specific phase differences between an individual’s FFR to ‘ga’ and FFR to ‘ba’ and does so in an objective fashion that does not rely upon the identification of peaks in the waveforms. While the F2 of ‘ga’ is higher in frequency than the F2 of ‘ba’, we would expect ‘ga’ to phase-lead (i.e., be earlier in time) than ‘ba’ at these frequencies at the envelope frequencies modulating this information. To investigate these phase differences in the FFR, we use a sliding-window approach to determine phase angles for each frequency over successive time points. Typically, we will use a 20 ms window with a 19 ms overlap (Skoe et al., 2011). These windows are baselined and ramped before applying a cross-power spectral density function and converting the spectral estimates to phase angles (for additional details, see Skoe et al., 2011; Strait et al., 2013). When we plot this information, we can observe the frequency-specific phase differences between the ‘ga’-evoked and ‘ba’-evoked FFR (Figure 12). This measure can be applied to single polarity, added, or subtracted FFRs and because of the ratio of temporal envelope to temporal fine structure contained in each, these three polarity manipulations can reveal not only the phase differences between FFRs to ‘ba’ and ‘ga’, but also the phase relationships between frequencies in the FFR. Specifically, we see in the single polarity and subtracted FFRs that the ‘ba’ versus ‘ga’ phase differences are evident within the frequency ranges of F2 itself. However, in both the added polarity and single polarity, these differences also manifest at the lower frequencies that act as modulators of the higher F2 frequencies (Figure 12), consistent with the findings using amplitude modulated tones (John & Picton, 2000).

4.3. Magnitude

4.3.1. Broadband

4.3.1.1. RMS and SNR

The magnitude of the response can provide information on the robustness of auditory processing. To determine broadband response magnitude we calculate the root-mean-squared (RMS) amplitude of the response over a specified time region. This time region may vary depending on the goals of the analyses or the stimulus used, however, it must take into account the neural transmission delay (described in the peak-picking section). For our 40-ms ‘da’ stimulus, the time window we typically use is 19.5 to 44.2 ms, a region of the response that corresponds to the fully-voiced portion of the stimulus, omitting the unvoiced consonant release and the transient FFR component corresponding to the onset of voicing. This is the time region used in our published normative data because it encompasses the timing of peaks D, E, and F across all ages considered in those analyses (Skoe et al., 2015). We have also published results using slightly different FFR time ranges, such as beginning the window at ~11 ms, to include the onset of voicing (e.g., see Russo et al., 2004). Additional ranges, such as the entire response (e.g., see Marmel et al., 2013; Song et al., 2010), can always be considered.

As stimulus features inform our selection of the time region over which we measure RMS, we may use multiple time regions for a single FFR. For example, in our 170-ms ‘da’, we look at both the voiced portion of the consonant transition (typically the 20–60 ms region of the response), and the steady-state vowel portion (typically the 60–170 ms region of the response).

To generate a measure of relative magnitude, we calculate the signal-to-noise ratio (SNR) of the response by dividing the RMS amplitude of the response region of interest by the RMS amplitude of a non-stimulus-evoked portion of the response (i.e., non-stimulus activity, the time region prior to t=0 ms in Figures 2, 3, and 5). We can do this because we average the response at a timepoint prior to stimulus onset, providing us with a snapshot of non-stimulus-evoked brain activity during the time interval that spans the cessation of one stimulus presentation and the start of the next (i.e., the interstimulus interval, or ISI). This interstimulus-period response would be considered background activity of the brain, and so it is a measure of brain noise. While the SNR value is by definition unitless, we can take 20 times the base 10 log of the SNR to express it in decibels, which we refer to as dB SNR.

Figure 5.

Comparison of single polarity (black), added (blue), and subtracted (red) FFRs to the evoking stimulus, a short, 40-ms ‘da’ (gray) in the time (left) and frequency (right) domains.

While RMS is our go-to method for calculating broadband magnitude, other magnitude computations can be used, such as calculating the mean amplitude of the rectified waveform (Strait et al., 2009). Like RMS, these values can be calculated over the response and non-stimulus activity to create a ratio of signal to noise.

4.3.2. Frequency-specific magnitude

4.3.2.1. Fast Fourier transform

To examine the encoding strength of individual frequencies in the FFR, we apply a fast Fourier transform (FFT) to the averaged brain response (Figures 2, 3, and 5), converting the response from a series of voltages over time to a series of voltages over frequency. If the acoustic stimulus was presented to the participant in alternating polarities, then when creating an average of the response, it is possible to look at frequency-specific magnitude in the single polarity, the added polarity (which enhances temporal envelope frequencies, including the F0 and lower harmonics), and the subtracted polarity (which accentuates the response to the temporal fine structure, or middle and high harmonics) (Figures 3 and 5).

Our approach to generating the spectrum of a selected FFR time range involves if necessary, zero padding to increase the spectral resolution to at least 1 Hz, then, applying a Hanning window (other windowing approaches may be used) and a ramp equal to one half the time range over which the FFT was calculated (i.e., ramp up to the midway point of the selected time range and then ramp down to the end of the time range), though shorter ramps can be used. Any time region can be used to calculate the FFT, but like RMS calculations, the window needs to account for the neural transmission delay, and it should not extend beyond the response region. It should also contain, at minimum, one cycle of the period corresponding to the frequency of interest. For example, our long ‘da’ has an F0 of 100 Hz, the period of which is 10 ms, meaning the response window over which F0 encoding strength can be measured must be at least 10 ms in duration, but it is good practice to at least double this minimum time length.

There are a few approaches to extract the amplitude from the spectrum. When looking at F0 encoding, we may extract the amplitude at a single frequency, such as 100 Hz from the example above, or we may average over a range of frequencies (e.g., see Krizman et al., 2012a), especially if the F0 changes overtime, as in the case of our short ‘da’, whose F0 ramps from 103 to 125 Hz over the utterance. We may use an even broader range to capture the variation in frequency encoding near the F0 that is observed across individual responses (e.g., see Kraus et al., 2016a; Kraus et al., 2016b; Skoe et al., 2015). A similar method is used to investigate higher frequency encoding, where we measure harmonic encoding at individual harmonic frequencies (e.g., see Anderson et al., 2013b), or average across a range of frequencies centered at the frequency of interest (e.g., see White-Schwoch et al., 2015). Because, by definition, during the formant transition formants move across frequencies (e.g., the first formant of the 40-ms ‘da’ changes from 220–720 Hz), we average the amplitude across these frequencies to provide a snapshot of formant encoding (e.g., see Krizman et al., 2012a). We also average the amplitude of individual harmonics over a steady-state vowel to get a general measure of FFR harmonic strength (e.g., see Parbery-Clark et al., 2009).

Beyond examining a single time window, we can use a sliding window approach to explore changes in frequency encoding over the duration of the response. This short-term Fourier transform technique is especially informative for stimuli that have a changing F0 or if you want to examine a response to a formant transition. Similar to other sliding window procedures described above, we typically use a 40 ms window, centered beginning at t=0 ms and moving over the duration of the response with a 39 ms overlap across successive windows, providing 1 ms temporal resolution to frequency encoding. We plot these time-varying spectral powers as spectrograms (see Figure 13).

Figure 13.

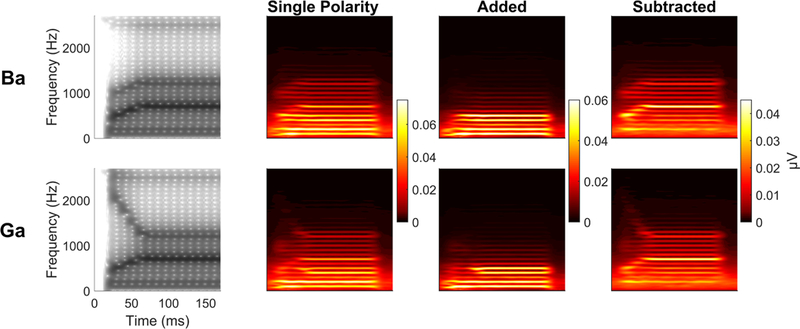
Spectrograms of the stimuli and single polarity, added, and subtracted FFRs for ‘ba’ (top) and ‘ga’ (bottom). The rising F2 of ‘ba’ and the falling F2 of ‘ga’ are maintained in the single polarity and subtracted responses while the added response highlights how these formant differences are reflected in the lower frequencies. These frequency differences can also be seen in the cross-phaseogram (Figure 12).

4.4. Fidelity

4.4.1. Broadband

Response fidelity is assessed by comparing FFR consistency within or across sessions, either to itself, another FFR, or the stimulus. Phase consistency may also be considered a frequency-specific measure of fidelity, but because it is also a timing-dependent measure, phase consistency has been discussed in the timing section. Additionally, while we typically perform the following measures in the time domain, any of these can be performed after transforming the time domain waveform into the frequency domain via a fast-Fourier transform (FFT).

4.4.1.1. Stimulus-to-response correlation

As the name implies, stimulus-to-response correlation assesses the morphological similarity of the response with its evoking stimulus. We first must filter the stimulus to match the response, generally, from 70–2000 Hz using a second-order Butterworth filter, but these parameters vary depending on the frequency content of the FFR being analyzed. For example, a lower cutoff value for the low-pass filter may be preferable for analyzing an added response, while a higher frequency may be used when analyzing a subtracted response. We do this to generate a stimulus waveform that will more highly correlate with the FFR, enabling better comparison of fidelity differences across participants.

We then run a standard cross-correlation between the filtered stimulus and response over a time region of interest (e.g., 19.5–44.2 ms for FFR to short ‘da’), which may vary depending on the acoustic features of interest, the stimulus used to evoke the FFR, or the research question. This procedure is similar to that described in the autocorrelation section, except the FFR waveform (W) is correlated with the stimulus (S) and not a copy of itself. W is correlated with S, across a series of time shifts for one of the two waveforms, such that at time-shift t=0, the original, unshifted waveforms W and S are correlated. At t=1, W has been shifted by one, while S remains unshifted and the cross-correlation for that lag is calculated, providing us with a Pearson product-moment correlation (though other correlation methods can be used). In theory, W can also be shifted by negative values in a similar manner, but because the brain response cannot temporally lead the stimulus, we do not perform stimulus-to-response calculations in this direction. The maximum absolute-value correlation (r) at a lag (t) that accounts for neural transmission delay, typically a 7–10 ms lag window, is obtained. Because the correlation values range from r = −1 (identical but 180° out of phase) to 0 (no correlation) to 1 (identical and in phase), it is possible for the maximum correlation to be negative. Once the maximum correlation is obtained, it is Fisher-transformed to z scores prior to statistical analyses. This natural-log-based transformation normalizes the r distribution so that the variance of r values across the range −1 to 0 to 1 are equivalently constant. The lag can provide an objective measure of broadband timing and so it too is analyzed (e.g., see Tierney et al., 2013).

4.4.2. Response-response correlation

Two FFRs can be correlated with one another. We often collect FFRs to the same stimulus under different listening conditions, for example, in quiet and background noise, and then cross-correlate the two responses (e.g., see Anderson et al., 2013a; Parbery-Clark et al., 2009). The method itself is identical to the cross-correlation method used for stimulus-to-response correlations described above. Here, an FFR to a stimulus in quiet (W^Q) is correlated to an FFR to that same stimulus in background noise (W^N) across a series of time shifts for W^N. For response-response correlations, however, it is appropriate to shift one of the FFRs both forward and backward in time when cross-correlating the waveforms. In this instance, a negative lag would indicate that the shifted waveform is earlier in time than the comparison FFR, while the opposite would be true for a positive lag. Again, r values are converted to z scores prior to statistical analyses.

4.4.3. Response consistency

We can also analyze the within-session correlation of FFR trials, an analysis that we refer to as response consistency or response stability. This supplies an index of how stable the FFR is from trial-to-trial. Response consistency calculations capitalize on the large number of trials presented to a participant during a session to generate an averaged FFR. To calculate response consistency, we correlate subsets of trials collected during a recording session, generating an r-value that is converted to a z-score prior to analyzing. The straight (i.e., lag = 0) calculation is performed over a time region relevant to the evoking stimulus and/or the question you are asking. The closer the r value is to 1, the more consistent the two FFR subaverages.

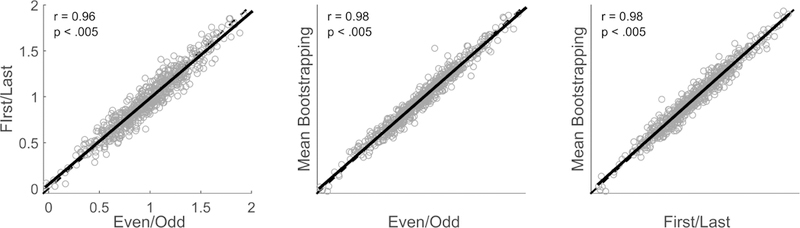
We have used several methods to examine response consistency. One method is to average the odd sweeps separate from the even sweeps (e.g., see Hornickel & Kraus, 2013). This approach was used to arbitrate whether a poor response consistency value was due to ongoing inconsistency of coding or to neural fatigue over the course of the recording session. A method comparing sweeps collected during the first half of the session with those collected during the last half of the session, could not by itself arbitrate between the two scenarios. We found that response consistency assessed by these two methods was highly correlated, suggesting that poorer response consistency was driven by across-trial differences in FFR morphology rather than fatigue (Hornickel & Kraus, 2013). The other method is to apply a bootstrapping approach to calculating response consistency within an individual. To do this, we randomly select and average half of the collected trials. We then average the remaining trials and correlate these two subaverages together over our time region of interest. These trials are then put back and the process is repeated some number of times, usually between 100 and 300 iterations. The correlation values of each iteration are averaged together to create an arithmetic mean of response consistency. Though it may be considered the most rigorous assessment of within-session response consistency, the consistency value obtained using this method correlates very strongly with the ‘first/last’ and ‘odd/even’ methods (Figure 14).

Figure 14.

Correlations among the response consistency methods. The dashed line represents the identity line, while the solid black line shows the z-transformed Pearson correlation of the response consistency calculated between two methods.

5. Other Considerations

5.1. Different recording methods

While it is beyond the scope of this tutorial, it is worthwhile to note that there are other methodologies to record an FFR. Traditionally, speech FFRs are recorded using insert earphones, however, recording FFRs in soundfield is another option (Gama et al., 2017). This opens up a number of possibilities for examining auditory processing in individuals who cannot be tested using an insert earphone (e.g., hearing aid and cochlear implant users) or for investigating neural mechanisms of the scalp-recorded FFR in animal models (Ayala et al., 2017). Secondly, recent research has found that FFR to continuous speech can be collected and analyzed (Etard et al., 2019; Forte et al., 2017), opening up the possibility of studying subcortical auditory processing in a way that most closely resembles how we listen in the real world.

Furthermore, the inferior colliculus, an auditory midbrain structure that is a major hub of both the ascending and descending auditory system (Ito & Malmierca, 2018; Malmierca, 2015; Mansour et al., 2019) and is capable of complex auditory processing (Malmierca et al., 2019), is thought to be the predominant generator of the electrophysiological recording of FFR collected using scalp electrodes at midline (i.e., EEG-FFR) (Chandrasekaran & Kraus, 2010; White-Schwoch et al., 2016b; White-Schwoch et al., in press). Using MEG, responses from cortical generators are evident (i.e., MEG-FFR, Coffey et al., 2016), opening new lines of research into cortical auditory processing. Recent studies reveal that changing the placement of electrodes on the scalp can alter the contribution of different sources to the FFR (Bidelman, 2018; Tichko & Skoe, 2017). Thus the sources of MEG-FFR, FFRs recorded using a single electrode, and responses obtained from multiple electrodes are likely not interchangeable. Indeed, we have found that the midline, scalp-recorded FFR is remarkably similar to the evoked response recorded directly from the inferior colliculus in experimental animals (White-Schwoch et al., 2016a), and that the inferior colliculus is necessary and sufficient for a midline EEG-FFR in humans (White-Schwoch et al., in press).

Along these lines, varying stimulus parameters, such as frequency content (Kuwada et al., 2002), presentation rate (Assaneo & Poeppel, 2018) or stimulus duration (Coffey et al., 2016) can also influence the contributors to a population response. It is possible that these effects may influence cortical and subcortical generators of the FFR differently. For example, while presentation rate can alter cortical responses to speech (Assaneo & Poeppel, 2018), only higher frequency encoding and onset timing in the FFR show a rate-sensitivity, while timing of periodic peaks and F0 encoding in the FFR are relatively unaffected by presentation rate (Krizman et al., 2010).

5.2. Click-ABR

The FFR has a different clinical scope than the click-evoked ABR. While the click-ABR reflects factors such as hearing loss and auditory neuropathy, the FFR can reveal other auditory processing deficits that have real-world consequences (Banai et al., 2009; Hornickel & Kraus, 2013; Hornickel et al., 2009; King et al., 2002; Musacchia et al., 2019; Russo et al., 2008). For these auditory processing deficits, the click-ABR is typically normal. For example, athletes who have sustained a concussion can have normal click-ABRs, yet the FFR can classify these individuals with 95% sensitivity and 90% specificity (Gallun et al., 2012; Kraus et al., 2016a; Kraus et al., 2016b). In children with normal ABRs, the FFR may also be a harbinger of future language problems (Kraus et al., 2017b; White-Schwoch et al., 2015). The clinical potential of the FFR is distinct from the ABR, offering new possibilities in auditory healthcare.

6. Summary and Conclusions

The FFR can help us understand, from a biological standpoint, how we make sense of sound. In this tutorial, we have delineated our most common data analysis strategies and have offered guidelines for aligning these analyses with specific applications. It is our hope that this tutorial will fuel the apparent global surge of interest in using the FFR in clinics and research laboratories. For the future, we are excited to learn how the FFR can help us get closer to discovering how our brains go about the formidable business of reconstructing our sonic world.

Highlights.

• FFR increasingly used for biological insight into hearing

• A gap remains in the current knowledge of the analytical potential of FFR

• The purpose of this tutorial is to bridge that gap

• Researchers using FFR can employ a unified analytical approach

• Analyses will allow deeper insights into how the brain reconstructs our sonic world