DIVERSE SPATIAL EXPRESSION PATTERNS EMERGE FROM UNIFIED KINETICS OF TRANSCRIPTIONAL BURSTING

SUMMARY

How transcriptional bursting relates to gene regulation is a central question that has persisted for more than a decade. Here, we measure nascent transcriptional activity in early Drosophila embryos and characterize the variability in absolute activity levels across expression boundaries. We demonstrate that boundary formation follows a common transcription principle: a single control parameter determines the distribution of transcriptional activity, regardless of gene identity, boundary position, or enhancer-promoter architecture. We infer the underlying bursting kinetics and identify the key regulatory parameter as the fraction of time a gene is in a transcriptionally active state. Unexpectedly, both the rate of polymerase initiation and the switching rates are tightly constrained across all expression levels, predicting synchronous patterning outcomes at all positions in the embryo. These results point to a shared simplicity underlying the apparently complex transcriptional processes of early embryonic patterning and indicate a path to general rules in transcriptional regulation.

INTRODUCTION

A central question in gene regulation concerns how discrete molecular interactions generate a continuum of expression levels observed at the transcriptome level (Lionnet and Singer, 2012; Scholes et al., 2016). A large set of molecular activities are required to elicit RNA transcription, including transcription factor binding, chromatin modifications, and long-range enhancer–promoter interactions (Voss and Hager, 2014). However, in most cases it is unclear which of these interactions predominantly regulate RNA synthesis rates and variability for a given gene (Coulon et al., 2013). In general, for genes whose transcription rates depend on levels of external inputs, we do not know which regulatory steps are preferably tuned to achieve required mRNA expression levels. Overall, it is unknown whether constraints exist that might select common mechanisms for modulating transcriptional activity across genes, space and time.

Addressing these questions requires measuring the kinetic rates of transcription, in absolute units. Many studies using single molecule counting approaches have documented the inherently stochastic nature of transcription (Little et al., 2013; Raj et al., 2006; Taniguchi et al., 2010; Zenklusen et al., 2008). In organisms ranging from bacteria to vertebrates, genes exhibit transcription bursts characterized by intermittent intervals of mRNA production followed by protracted quiescent periods (Bothma et al., 2014; Golding et al., 2005; Suter et al., 2011). This inherent stochasticity in gene activation results in higher cell-to-cell variability than expected from constitutive expression (Blake et al., 2003). A simple telegraph or two-state model has been used to explain the measured variability in the context of transcriptional bursting (Peccoud and Ycart, 1995). In this model a locus switches at random between inactive and active states, with only the latter permitting transcription initiation. Despite its prevalent use, it is largely unknown which molecular events determine the kinetic rates of this model (Coulon et al., 2013). Nor is it widely understood which of these kinetic rates are modulated by external input signals or to what extent. However, with precise measurements and quantitative modeling, it is possible to gain intuition for the mechanisms of transcriptional bursting based on their signature in the measured variability (Jones et al., 2014; Larson et al., 2013; Molina et al., 2013; Senecal et al., 2014; Zoller et al., 2015).

Drosophila embryos provide an ideal model to investigate transcriptional regulation (Gregor et al., 2014). Early embryos express many genes in graded patterns in response to modulatory inputs (Struhl et al., 1992). Spatial domains, where gene expression levels transition from highly active to nearly silent, are functionally the most critical for the developing embryo, as they determine specification of cell identities (Kornberg and Tabata, 1993). Among the earliest expressed genes in Drosophila development are the gap genes, which encode transcription factors responsible for anterior-posterior (AP) patterning (Jaeger, 2011). Each gap gene is expressed in its own unique domain, and the expression boundaries arise at distinct and precise positions (Dubuis et al., 2013). Gene expression levels are spatially graded across several cell diameters, and the intermediate levels of these gap genes confer patterning information necessary for segmentation (Lawrence, 1992). Thus the precise control of expression levels is essential for properly patterned cell fate specification.

The regulation of gap genes appears highly complex. Many activating and repressing factors determine expression boundaries through complex layers of homo- and heterotypic protein interactions at multiple promoters and enhancers (Estrada et al., 2016; Jaeger et al., 2004; Kvon et al., 2014; Perry et al., 2011; Segal et al., 2008). The collective activity of these factors generates expression rates that vary with position in the embryo (Briscoe and Small, 2015; Lawrence, 1992; Manu et al., 2009). Given the diversity of cis-regulatory architecture and trans-acting factors regulating these genes, an intuitive expectation is that expression rates emerge from carefully tuned transcription factor concentrations and binding affinities. Since various bursting kinetics could achieve such rates, a straightforward prediction is that the underlying bursting kinetics will differ between boundaries. This expectation is consistent with prior studies in cultured cells suggesting that many regulatory strategies exist (Carey et al., 2013; Molina et al., 2013; Senecal et al., 2014; Siddharth S et al., 2015). However, it is unknown how bursting rates are modulated across multiple expression boundaries in intact tissues.

To address these questions, we developed a single molecule fluorescent in situ hybridization (smFISH) method that generates accurate counts of nascent RNA molecules in individual nuclei. We applied this method to assess absolute transcriptional activity of the gap genes in terms of the number and variability of RNA polymerase II (Pol II) molecules at transcribing loci. This approach reveals a common principle that unifies transcriptional activity across expression boundaries. Surprisingly, a single common control parameter globally determines the distribution of transcriptional activity. We use a simple telegraph model to interpret our measurements. We show that the key regulatory parameter is the fraction of time a gene is in a transcriptionally active state, while the Pol II initiation rate is constant. Contrary to the expectation of diverse bursting kinetics, the promoter switching rates are tightly constrained across boundaries. This constraint highlights the conservation of the switching correlation time, and predicts synchronous transcriptional outcomes regardless of expression level, gene identity, or position in the embryo. We propose that this synchronicity is important for ensuring precise patterning. Moreover, our results suggest an emergent simplicity in the modulation of bursting that governs the apparently complex process of embryo segmentation. Overall, our quantitative approach provides a framework for uncovering unifying principles of transcriptional regulation that can be applied across genes in any biological context.

RESULTS

Precise measurements of transcriptional activity

During early fly development, gene expression boundaries arise from spatially varying transcription factor concentrations. Early embryos thus provide a natural context in which to ask how input factors shape transcription dynamics. Here we enhanced a previously developed smFISH method (Little et al, 2013) to yield a 3- to 4-fold increase in sensitivity, enabling precise counting of nascent transcripts and measurement of transcriptional activity across boundaries (STAR Methods). We performed confocal imaging with fluorescent oligonucleotide probes to label single mRNA molecules in fixed embryos followed by analysis to estimate intensities of transcription sites (i.e., spatially co-localized nascent transcripts) and individual cytoplasmic mRNAs. This method measures instantaneous activity per nucleus in terms of intensity units of individual cytoplasmic mRNAs, the “cytoplasmic unit” (C.U.) by normalizing the total intensity of each locus to that of cytoplasmic mRNAs (Fig. 1A, B).

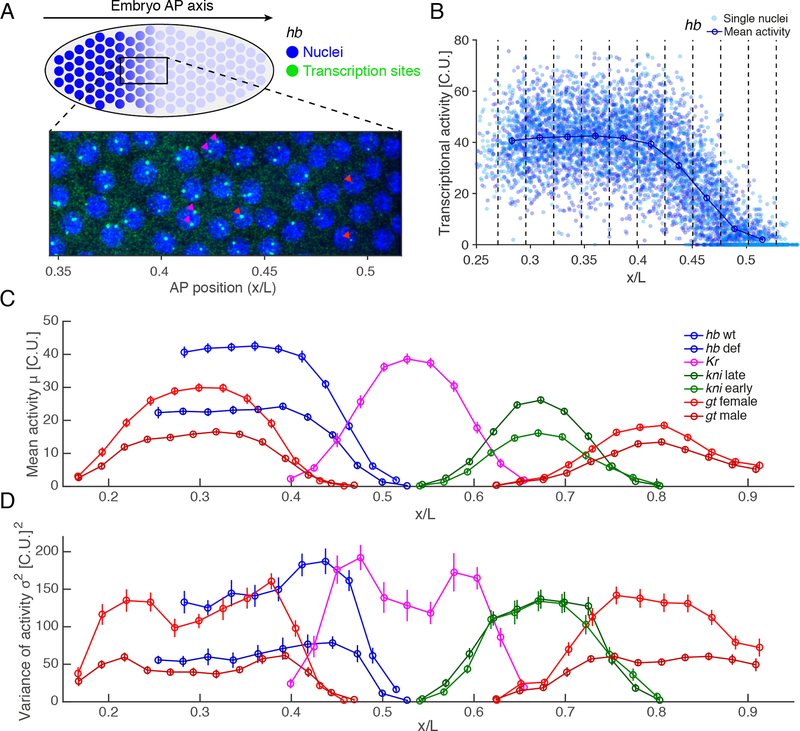
Figure 1: Absolute quantification of gap gene transcriptional activity.

(A) Activity of individual nuclei (blue) for the gene hunchback (hb) measured by single molecule mRNA-FISH (green) in nuclear cycle 13 (nc13) of the blastoderm embryo of length $L$. Red arrowheads: nuclei with two sites of transcription; magenta arrowheads: single site of transcription.

(B) Activity profile of hb as a function of AP position in % egg length for 18 embryos. Activity of individual nuclei from the summed intensity of all transcription sites per nucleus, normalized by the average intensity of a single cytoplasmic mRNA (cytoplasmic unit, C.U.). Blue dots: total mean intensity per nucleus. Vertical dashed lines define AP bins; circles: mean activity in each bin.

(C) Mean activity in C.U. as a function of AP position during nc13 for: hunchback in wild-type (labeled hb wt in blue, $N=18$ embryos); hunchback deficiency with half the hb dosage (hb def, light blue, $N=7$); Krüppel (Kr, magenta, $N=11$); knirps during early (kni early, green, $N=14$) and late nc13 (kni late, light green, $N=16$); giant in females with two alleles (gt female, red, $N=20$) and in males with one (gt male, light red, $N=16$).

(D) Total variance of transcriptional activity as a function of AP position (colorcode as in C).

All error bars are 68% confidence intervals. See also Figure S1.

We measured the transcriptional activity of the four major gap genes hunchback (hb), Krüppel (Kr), knirps (kni), and giant (gt) along the embryo’s AP axis. These genes are expressed early in development in broad spatial domains, permitting measurements of thousands of synchronized nuclei across small numbers of embryos; these factors all favor low measurement error (Fig. 1C and 1D, $N~15$ embryos per combination of gene/genotype). Analysis of expression levels in mid- to late interphase 13 ensures sufficient time to attain steady state levels of transcribing RNA polymerase II (Pol II; Fig. S1A–D, STAR Methods); and DNA replication occurs in early interphase (Blumenthal et al., 1974), such that these observations eliminate ambiguity arising from varying numbers of loci. Since loci on recently duplicated chromatids are often closely apposed in space, we measure total transcription per nucleus (Little et al, 2013), then infer properties of individual loci. As a control, we generated data from embryos heterozygous for a hb deficiency, and observed half the wild-type level of expression per nucleus (Fig. 1C). Importantly, we observe a corresponding decrease in variance to half of wild-type (Fig. 1D), supporting previous findings that all loci behave independently (Little et al., 2013). These results demonstrate the suitability of using total transcriptional activity per nucleus to infer the behavior of individual loci.

Since biological variance greatly constrains models of regulatory processes, we needed to determine how variability arises from measurement error, embryo-to-embryo differences, and intrinsic fluctuations in individual nuclei. The performance of our measurements was assessed by labeling each mRNA in alternating colors along the length of the strand. This allowed us to perform independent normalization in each channel, thus characterizing sources of measurement error, such as noise stemming from imaging and normalization (Fig. 2A). Estimation of the variance of the mean across embryos (Fig. 2B) enables further splitting of the variability in terms of embryo alignment along the anterior-posterior axis and inherent embryo-to-embryo variability (Fig. S1E–H, STAR Methods). For all genes and at all positions, measurement variability (imaging and spatial alignment) represents less than $7\%$ of the total variance on average (Fig. 2C), indicating that biological variability dominates our measurements (Dubuis et al., 2013). Importantly, this variability arises almost entirely from differences between nuclei, rather than differences between embryos (Fig. 2D); the low embryo-to-embryo variability in the maximally expressed regions ($16\pm 4\%$ CV, Fig. 2E) emphasizes that the mean expression levels across embryos are reproducible in absolute units (Fig. 1C). Thus the measured expression noise mainly stems from zygotic transcription, and is intrinsic to the molecular processes of transcription rather than from extrinsic sources of variability. Low measurement error and the predominance of intrinsic variability facilitates analysis of the noise–mean relationship, permitting inference of bursting kinetics from several hundred nuclei at each position along the AP axis (Fig. 1B), as detailed below.

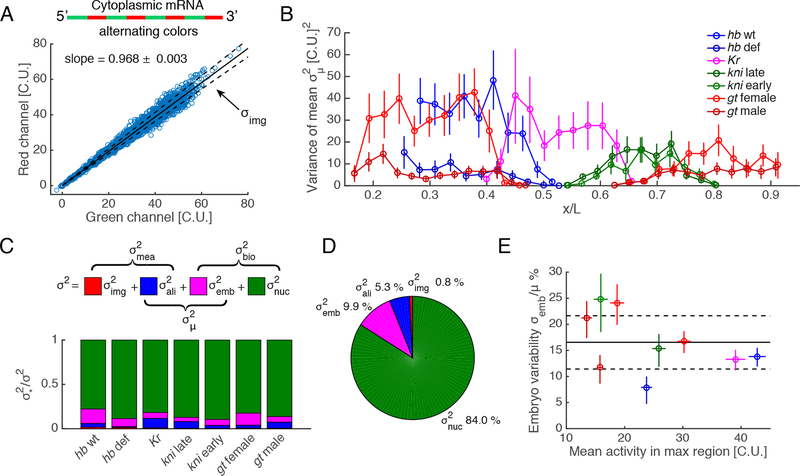
Figure 2: Decomposition of the total variance.

(A) Imaging noise estimation with dual-color smFISH. mRNA molecules are tagged with an alternating probe configuration. Blue circles: activity of single nuclei in 15 hb embryos. In absence of measurement noise or normalization error, both channels should perfectly correlate with slope 1. We characterized the spread along the fitted line (solid line) assuming error in both channels. Dashed lines: $1\sigma$ envelope.

(B) Variance of the mean ${\sigma }_{\mu }^2$ across embryos as a function of AP position (color code as in Figure 1C).

(C) Decomposition of the total variance ${\sigma }^2$ into measurement error and biological variability. Estimates of imaging error (red) alignment error (blue), embryo-to-embryo variability (magenta) are decoupled from the total variance. The remaining variance corresponds to biological variability and is termed intrinsic nucleus-to-nucleus variability in the text (green).

(D) Decomposition of total variance for all the genes pooled together. Nucleus-to-nucleus variability dominates ($~$84%).

(E) Fractional embryo-to-embryo variability (CV) as a function of mean activity (solid black line: mean ratio; dashed lines: 68% confidence intervals) reaches 16$\pm$4% (CV) in the maximally expressed regions that are the most reproducible. This represents absolute reproducibility as all embryos peak at comparable means.

Error bars are 68% confidence intervals. See also Figure S1.

Single parameter distribution of transcriptional activity across all expression boundaries

The expression patterns of the gap genes are determined by multiple enhancer elements at varying distances from their promoters (Kvon et al., 2014; Perry et al., 2011). Each enhancer contains a variable number of binding sites for multiple patterning input factors with cross-regulatory interactions (Ochoa-Espinosa et al., 2005; Schroeder et al., 2004). These features and evidence from genetic manipulations (Hoch et al., 1990; Jacob et al., 1991; Pankratz et al., 1992) indicate that many molecular processes regulate transcription rates generating observed mRNA levels with their stereotypical modulation as a function of position (Fig. 1C). Given the diversity of input factors and molecular control elements, it would appear likely that different genes should exhibit vastly different, uniquely defined transcriptional kinetics. To make progress in understanding these complex relationships, we capitalize on the fact that the kinetics of the processes underlying transcription determines not only mean expression levels but also the variability (Fig. 1D). Thus we can use the noise–mean relationship to characterize the transcription kinetics for individual genes.

To characterize noise–mean relationships in our system, we examined the dependence of variability on mean transcription levels (Fig. 3A). In agreement with prior measurements (Little et al., 2013), genes span a similar dynamic range of expression levels across boundaries, from nearly zero to a maximum value of $34\pm 6$ C.U. (Fig. 1C). Moreover, transcription is inherently variable: at all positions and for all genes, variability exceeds that expected from a simple model of constitutive activity, with noise (measured as CV²) approximately 10 times larger than Poisson for mean transcriptional activity below 10 C.U. (Fig. 3A). However, the noise–mean relationship follows an unexpectedly similar overall trend (Fig. 3A) (STAR Methods). Unlike many other systems (bacteria, yeast, mammalian cell culture), there is no clearly identifiable noise floor at high expression (Keren et al., 2015; Taniguchi et al., 2010; Zoller et al., 2015). The absence of such an extrinsic noise floor is likely a key feature of early embryo development: nuclei are highly synchronized within the cell cycle and share the same environment of the syncytial blastoderm. Sources of extrinsic noise that affect gene expression in cultured cells are thus minimized. Moreover, the collapse on a unique curve is unexpected and atypical given the different promoter–enhancer architectures (Hornung et al., 2012; Sanchez and Golding, 2013).

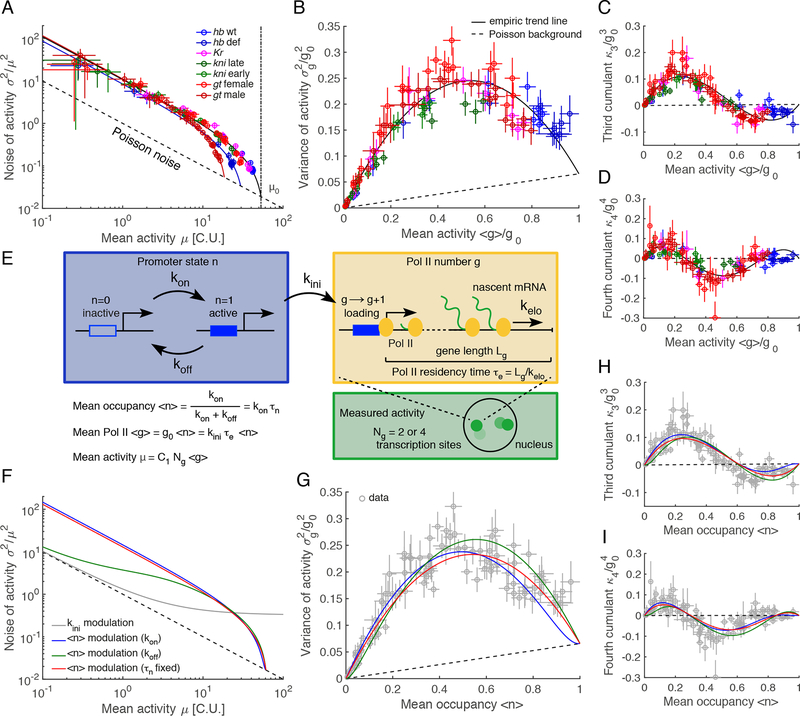
Figure 3: A two-state model recapitulates data collapse and single-parameter modulation.

(A) Noise-mean relationship (noise = CV²). Dashed line: Poisson background, the lowest attainable noise. Solid lines: fitting for each gene the following functional form of the noise $\text{C}{\text{V}}^2=\left(1+a\left(1-\mu /{\mu }_0\right)\right)/\mu$, where $a$ and ${\mu }_0$ are fitted parameters. The collapse of the trend to Poisson noise ($1/\mu$) at high expression implies an upper limit of attainable expression levels, ${\mu }_0$ (vertical dashed line). Color code as in Figure 1C.

(B-D) Normalized 2^nd, 3^rd and 4^th cumulant as a function of normalized Pol II counts for a single gene copy. Activities in C.U. were converted into Pol II counts $g$ by using fluorescent probe locations and gene lengths $L_g$. Assuming independence, the mean and the cumulant were divided by the gene copy number $N_g=\mathrm{2,4}$. Dashed lines: Poisson background. The solid lines: fitting the cumulants with 2^nd, 3^rd and 4^th order polynomials, respectively, constrained to match the Poisson level at maximum Pol II counts $g_0={\mu }_0\langle L_g\rangle /\left(C_1{N}_g{L}_g\right)$, where $\langle L_g\rangle$ is the average gene length and $C_1\in \left[\mathrm{0,1}\right]$ a conversion factor that depends on the probe locations on transcripts. Color code as in Figure 1C.

(E) Two-state model for measured transcriptional activity. The mean activity in Pol II counts is $\langle g\rangle =k_{\text{ini}}{\tau }_e\langle n\rangle$ with initiation rate $k_{\text{ini}}$, elongation time ${\tau }_e=L_g/k_{\text{elo}}$, and mean promoter activity $\langle n\rangle =k_{\text{on}}/\left(k_{\text{on}}+k_{\text{off}}\right)\in \left[0,1\right]$. The maximal Pol II count is given by $g_0=k_{\text{ini}}{\tau }_e$. The measured mean activity in C.U. is $\mu =C_1{N}_g\langle g\rangle$, where $N_g$ is the gene copy number and $C_1\in \left[\mathrm{0,1}\right]$ a conversion factor as in B-D.

(F) Noise-mean relationship and (G-I) normalized 2^nd, 3^rd and 4^th cumulants predicted by the two-state model under different single parameter mean activity modulation schemes: Pol II initiation rate $k_{\text{ini}}$ (gray), off-rate $k_{\text{off}}$ (green), on-rate $k_{\text{on}}$ (blue), and promoter occupancy $\langle n\rangle$ at constant switching correlation time ${\tau }_n=1/(k_{\text{on}}+k_{\text{off}})$ (red). Modulation of $\langle n\rangle$ by means of $k_{\text{on}}$ or at constant ${\tau }_n$ achieve numerical values that closely match the trends of our data.

Error bars are 68% confidence intervals. See also Figures S2 and S3.

This result is even more striking when we convert our units of transcriptional activity from C.U. to the actual number count of Pol II molecules, g. Such a conversion is necessary as the intensity at a given active transcription locus is dependent on the length of the individual gene, the copy number, and the probe arrangement (Fig. S2A, STAR Methods). Accounting for these factors, we can describe the shape of the distribution of Pol II counts per locus by calculating the 2^nd, 3^rd and 4^th cumulants for each gene across each boundary. While again the expectation is that Pol II counts should differ between different genes, an extra data collapse is observed instead: the 2^nd, 3^rd and 4^th cumulants for all data points are nearly uniquely determined by a single parameter, the mean activity $\langle g\rangle$ (Fig. 3B–D and Fig. S2B–D). Thus, transcriptional activity for all genes and across the entire expression range is characterized by a unique, common single-parameter distribution. This observation is model-free and indicates that a single parameter determines the generation of all gene expression boundaries. The uniqueness of the Pol II count distribution suggests that despite the well-documented diversity of cis-regulatory elements and trans-acting factors, a common conserved set of processes is regulated to determine transcription kinetics across all boundaries in the early embryo.

Two-state model identifies the unique control parameter

The shared Pol II count distribution suggests a common general model can describe the regulation of all gap genes. The observed intrinsic super-Poissonian variability in our data suggests that these genes operate in a bursting regime. While constitutive genes can be modeled by a single parameter, i.e. the effective initiation rate, multiple independent parameters are required to model transcription kinetics of bursting genes. A popular minimalist model accounting for bursting is the two-state or telegraph model (Peccoud and Ycart, 1995). It has been widely used to describe the distribution of mature mRNA and protein counts (Bar-Even et al., 2006; Raj et al., 2006; Zenklusen et al., 2008). Such a simple mechanistic model enables estimation of kinetic rates underlying bursting (Fig. 3E and Table 1), i.e. the switching rates between promoter states ($k_{\text{on}}$ and $k_{\text{off}}$) as well as the effective initiation rate $k_{\text{ini}}$ (Larson et al., 2013; Senecal et al., 2014; Suter et al., 2011).

Table 1:

Terminology and parameterization of transcription rates.

Kinetic rates	Units	Parameterization $\left\{k_{\text{ini}},k_{\text{on}},k_{\text{off}}\right\}$	Parameterization $\left\{k_{\text{ini}},\langle n\rangle ,{\tau }_n\right\}$
Pol II initiation rate $k_{\text{ini}}$	[min−1]	$k_{\text{ini}}$	$k_{\text{ini}}$
Promoter switching on-rate $k_{\text{on}}$	[min−1]	$k_{\text{on}}$	$\frac{\langle n\rangle }{{\tau }_n}$
Promoter switching off-rate $k_{\text{off}}$	[min−1]	$k_{\text{off}}$	$\frac{1-\langle n\rangle }{{\tau }_n}$
Bursting parameters	Units	Parameterization $\left\{k_{\text{ini}},k_{\text{on}},k_{\text{off}}\right\}$	Parameterization $\left\{k_{\text{ini}},\langle n\rangle ,{\tau }_n\right\}$
Promoter mean occupancy $\langle n\rangle$	#	$\frac{k_{\text{on}}}{\left(k_{\text{on}}+k_{\text{off}}\right)}=k_{\text{on}}{\tau }_n$	$\langle n\rangle$
Switching correlation time ${\tau }_n$	[min]	$\frac{1}{\left(k_{\text{on}}+k_{\text{off}}\right)}$	${\tau }_n$
Burst size $b$	#	$\frac{k_{\text{ini}}}{k_{\text{off}}}$	$\frac{k_{\text{ini}}{\tau }_n}{1-\langle n\rangle }$
Burst frequency $f$	[min−1]	$\frac{k_{\text{on}}{k}_{\text{off}}}{\left(k_{\text{on}}+k_{\text{off}}\right)}=k_{\text{off}}\langle n\rangle$	$\frac{\langle n\rangle \left(1-\langle n\rangle \right)}{{\tau }_n}$
Mean transcript synthesis rate	[min−1]	$\frac{k_{\text{ini}}{k}_{\text{on}}}{\left(k_{\text{on}}+k_{\text{off}}\right)}$	$k_{\text{ini}}\langle n\rangle$

Within the context of the two-state model the most intuitive parameterization is given by the kinetic rates $k_{\text{ini}},k_{\text{on}}$ and $k_{\text{off}}$. However, fluctuation analysis in transcriptional activity and inference approach both revealed that the three independent and uncorrelated variables $k_{\text{ini}},{\tau }_n$ and $\langle n\rangle$ provides a more natural parameterization, in which only $\langle n\rangle$ is modulated, while $k_{\text{ini}}$ and ${\tau }_n$ are both constant. Bursting parameters are clearly identified in both parameterizations.

Our measurements of nascent transcriptional activity represent instantaneous counts of the number of Pol II molecules engaged in transcription, providing a more direct measurement of transcriptional activity compared to counts of mature mRNAs or proteins. The two-state model presents a straightforward and parameter-sparse means to describe how discrete randomly occurring events generate a continuum of expression rates. Assuming the Pol II elongation rate $k_{\text{elo}}$ is constant and identical for all gap genes (Garcia et al., 2013; O’Brien and Lis, 1993), this model predicts the dependence of variability on mean activity for different scenarios of parameter modulation. Specifically, it predicts which kinetic rates are modulated to form gene expression boundaries.

Given that the first four cumulants of our data are uniquely determined by the mean activity, we sought to explore modulation of the mean arising from varying a single parameter, where such parameters could consist of combinations of the kinetic rates. When we solve the master equation for such a model (STAR Methods), a comparison of predicted noise (Fig. 3F) with our data (Fig. 3A) eliminates modulation of $k_{\text{ini}}$. Indeed, solely varying $k_{\text{ini}}$ leads to saturation of noise at high activity, which is not observed. This is true no matter the values of $k_{\text{on}}$ and $k_{\text{off}}$, which only affect the level of the plateau. Instead, our measurements are consistent with modulation of the fractional mean promoter occupancy $\langle n\rangle$, defined as $\langle n\rangle =k_{\text{on}}/\left(k_{\text{on}}+k_{\text{off}}\right)$. (Here occupancy refers to the active or “ON” state; thus $\langle n\rangle$ is bound between zero and one.) This value is the fraction of time spent in the active state and is equivalent to the probability of finding a locus in the active state (Lucas et al., 2013; Xu et al., 2015). Varying $\langle n\rangle$ is the only solution leading to a concave function for the variance observed in the data (Fig. 3B,G; STAR Methods Eq. 9). Modulation of the mean production rate is thus determined by $\langle n\rangle$ rather than the rate at which Pol II molecules enter into productive elongation.

In principle, either or both of the rates $k_{\text{on}}$ and $k_{\text{off}}$ may be tuned to modulate $\langle n\rangle$. To test which of these scenarios reproduces the noise and the shape of the cumulants (Fig. 3A–D), we first set the value of $k_{\text{ini}}$ to match the Poisson background in the data (Fig. 3B, dashed line, STAR Methods). For the special case in which both switching rates are modulated simultaneously, we achieved effective single parameter modulation by fixing the switching correlation time ${\tau }_n=1/(k_{\text{on}}+k_{\text{off}})$ the characteristic time-scale for changes in promoter activity. This quantity reveals how fast the switching occurs, how much time is required for the mean number of Pol II molecules engaged in transcription to reach steady state, and what fraction of the switching noise is filtered by the elongation process (STAR Methods). When ${\tau }_n$ is fixed, both switching rates, $k_{\text{on}}$ and $k_{\text{off}}$, are fully determined by $\langle n\rangle$, i.e.

$$k_{\text{on}}=\langle n\rangle /{\tau }_n\text{ and }{k}_{\text{off}}=\left(1-\langle n\rangle \right)/{\tau }_n$$ (Eq. 1)

In the three scenarios (tuning $k_{\text{on}},k_{\text{off}}$, or $\langle n\rangle$), the single free parameter (either $k_{\text{off}},k_{\text{on}}$ or ${\tau }_n$) was estimated by fitting the set of modeled cumulants to the data, assuming steady-state Pol II levels (Fig. 3G–I and Fig. S2E). Modulation of $k_{\text{off}}$ alone is ruled out, since this does not capture the noise below 10 C.U. (Fig. 3F). However, modulation of $k_{\text{on}}$ alone or of $\langle n\rangle$ at fixed ${\tau }_n$ recapitulates the noise and the cumulants (Fig. 3F–I). Thus, in addition to conserved $k_{\text{ini}}$, the model predicts a second conserved quantity across genes and positions, either $k_{\text{off}}$ alone or a combination of $k_{\text{on}}$ and $k_{\text{off}}$.

Finally, we examined whether the fitted cumulants assuming steady state are compatible with the finite duration of the nuclear cycle ($~$15 min). The time during which a gene relaxes from an inactive state devoid of elongating Pol II (start of interphase 13) to steady state is determined by the correlation time ${\tau }_n$ (Fig. S3A). Since each parameter modulation predicts a different dependency of ${\tau }_n$ on $\langle n\rangle$ (Fig. S3B), we tested under each scenario whether the mean and the cumulants at mid-cycle would be attained in time. It follows that modulation of $\langle n\rangle$ through $k_{\text{on}}$ alone or at fixed ${\tau }_n$ predicts a time-dependent solution at mid-cycle that is consistent with the steady state assumption above (Fig. S3C–G, STAR Methods). Thus the two-state model explains the data collapse and predicts that tuning only the mean occupancy $\langle n\rangle$ uniquely describes the formation of expression boundaries regardless of their position in the embryo.

Transcriptional bursting in absolute units

Further insight into transcriptional mechanisms requires the absolute scales of kinetic parameters. To go beyond arguments based on cumulants, we adopted an approach that is agnostic to the modulation strategy. To resolve whether $k_{\text{off}}$ or ${\tau }_n$ is constant and exclude other non-trivial forms of modulation (i.e., multiple rates changing simultaneously), we inferred all kinetic rates from the full distribution of transcriptional activity, for each gene and at each position independently. We performed dual-color smFISH, tagging the 5’ and 3’ regions of the transcripts with differently colored probe sets that provide two complementary readouts of nascent activity (Fig. 4A) (Brody et al., 2011; Xu et al., 2016). The measured activities are correlated via a finite Pol II elongation time (Fig. S4A–C, STAR Methods) and provide two snapshots of the state of the gene. Jointly measuring the 5’ and 3’ activities constrains the possible configurations of nascent transcripts and Pol II configurations at each locus (Fig 4B).

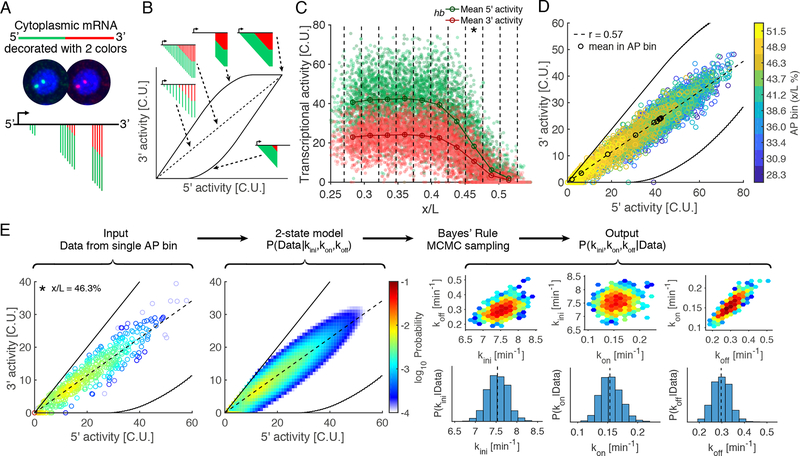
Figure 4: Estimation of transcription parameters via dual-color smFISH.

(A) Schematic of the dual-color single molecule mRNA-FISH technique. Two independent probe sets hybridized to different fluorophore target the 5’ (green) and 3’ region (red). The combination of readouts constrains the possible configurations of nascent transcript locations and numbers.

(B) Dual-color smFISH measurement space represented as 5’ vs. 3’ activity. Solid black line: border of possible measurements given probe set configuration, gene length, and maximal possible Pol II density (here we assumed a Pol II holoenzyme footprint of 90bp). Dashed black line: expected ratio of 3’ to 5’ activity defining the subset of configurations for which nascent transcripts are equally spaced along the entire gene length but at different densities.

(C) Activity profile for hb as a function of AP position for both 5’ and 3’ channels. Dots: total intensity of nascent transcripts in C.U. in a single nucleus. $N=18$ embryos aligned and overlaid. Vertical dashed lines: AP bins; circles: mean activity in each bin; error bars: 68% confidence intervals.

(D) Empirical distributions of 5’ versus 3’ activity for hb; colored circles: individual nuclei, color code represents different AP bins; black circles: mean of each AP bin (see B). The measurements are enclosed by the envelope of maximal Pol II density (black line, as in B).

(E) Inference of parameters defined by the two-state model. Parameters are estimated from the empirical distribution individually at each AP bin (the data, C and D). We calculated the likelihood of the data given a set of parameters $P\left(\text{Data}\right|k_{\text{ini}},k_{\text{on}},k_{\text{off}})$. By applying Bayes’ rule, we obtained the posterior probability $P(k_{\text{ini}},k_{\text{on}},k_{\text{off}}\left|\text{Data}\right)$, the probability of the parameters given the observed data; the posterior probability was sampled by Monte-Carlo Markov Chain (MCMC). Final estimates of the parameters are given by the median of the marginal posterior (vertical dashed line in histogram). The color code of the distributions stands for the log₁₀ probability.

See also Figures S4, S5 and S6.

Given a stochastic model of transcription, it is possible to extract the transcriptional parameters underlying the activities of each gene (Fig. 4C–D and Fig. S5). Using the two-state model, we calculated the likelihood of the joint distribution of 5’ and 3’ activities at each AP position while accounting for measurement noise (Fig. 4E, STAR Methods). The rate parameters $k_{\text{ini}},k_{\text{on}}$, and $k_{\text{off}}$ for each AP position were inferred from the likelihood of the data according to Bayes’ rule. We sampled the joint posterior distribution of the parameters (Hastings, 1970), which provides a probability for each parameter combination given the observed data. All inferred parameters with respective errors were estimated from the sampled joint posterior distribution (Fig. 4E and S5C). Validating our approach, inference on synthetic data clearly shows that the parameters are identifiable as long as the Pol II elongation rate is measured independently (Fig. S6A–F). Moreover, the previously measured Pol II elongation rate $k_{\text{elo}}=1.5$ kb/min (Garcia et al., 2013) provides an absolute time scale, enabling inference of endogenous kinetics from chemically cross-linked, inert embryos.

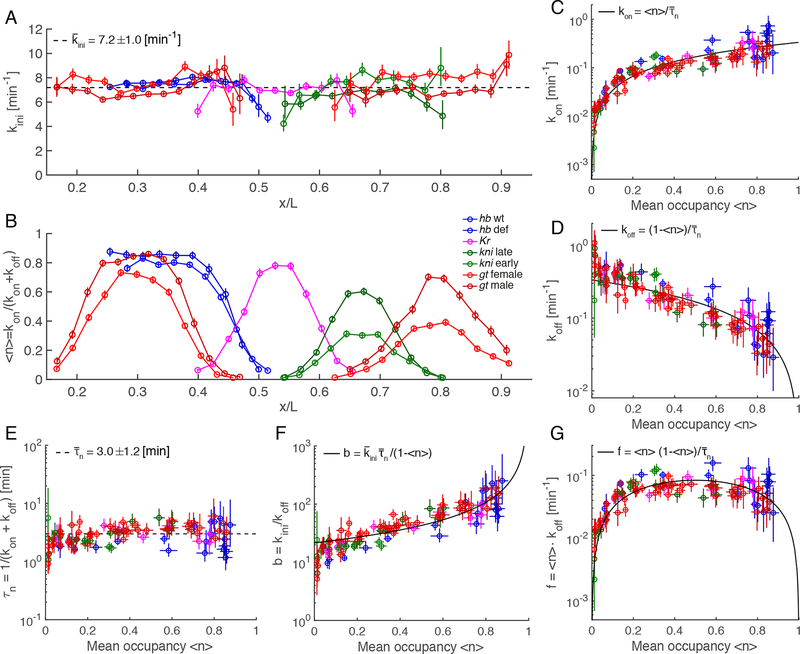
The inferred kinetic rates revealed nearly identical modulation across all expression boundaries, regardless of gene identity or boundary position (Fig. 5). Consistent with predictions based on cumulants (Fig. 3), the initiation rate $k_{\text{ini}}$ is constant at 7.2$\pm$1.0 Pol II initiations per minute and does not change across genes or positions (Fig. 5A). Thus while in the ‘ON’ state, these genes share the same rate-limiting step(s) in the cascade of molecular interactions leading to productive Pol II elongation, as reported for constitutive genes (Choubey et al., 2015). We also observe close agreement between measured and inferred mean activity, as well as good agreement between all other cumulants (Fig. S6G–J). Our inference confirms that all expression boundaries are generated through modulation of the mean promoter occupancy (Fig. 5B). This result supports the view that the processes that determine $k_{\text{ini}}$ are disfavored as mechanisms for controlling mRNA synthesis rates. Because these rates are determined by $\langle n\rangle$ for all genes, and span a similar dynamic range for all boundaries (Fig. S6K), we advocate that promoter occupancy represents the key control parameter describing expression boundary formation.

Figure 5: Inferred transcription parameters are tightly constrained across gap genes.

(A,B) Inferred Pol II initiation rate $k_{\text{ini}}$ (A), and promoter mean occupancy $\langle n\rangle$ (B) for all genes across AP position.

(C,D) Inferred on-rate $k_{\text{on}}$ (C) and off-rate $k_{\text{off}}$ (D) as a function of mean occupancy $\langle n\rangle$ for all genes. Solid black lines represent the global trend using the mean value of ${\tau }_n$ (see formula in inset).

(E) Inferred switching correlation time ${\tau }_n$ as a function of mean occupancy $\langle n\rangle$ for all genes with a mean value of ${\overline{\tau }}_n=3.0\pm 1.2$ min (dashed line).

(F,G) Inferred burst size $b$ (F) and burst frequency $f$ (G) as a function of the mean occupancy $\langle n\rangle$. Solid black lines represent the global trend using the mean value of $k_{\text{ini}}$ and ${\tau }_n$ (see formula in inset).

Color code as in Figure 1C. Error bars are the 10 to 90^th percentiles of the posterior distribution. See also Figure S6.

Current models of boundary formation imply a careful tuning of multiple input factor concentrations and DNA binding affinities (Briscoe and Small, 2015; Jaeger, 2011). The complexity and diversity of these inputs leads to an intuitive expectation that kinetic switching rates will differ between genes. This expectation seems all the more reasonable given that many combinations of $k_{\text{on}}$ and $k_{\text{off}}$ generate the same $\langle n\rangle$. Surprisingly, both $k_{\text{on}}$ and $k_{\text{off}}$ are tightly constrained for all genes and across all boundaries when portrayed as a function of mean occupancy $\langle n\rangle$ (Fig. 5C, D). This suggests that some combination of $k_{\text{on}}$ and $k_{\text{off}}$ must be conserved. Indeed, as predicted by the cumulant analysis above, our measurements confirm that the conserved combination is in fact the correlation time of the switching process ${\tau }_n=1/(k_{\text{on}}+k_{\text{off}})$, which is roughly constant at all positions over the entire expression range for every gene (Fig. 5E).

Our inference thus revealed that the more natural parameterization of this system is expressed in terms of the three independent, uncorrelated variables {$k_{\text{ini}},{\tau }_n$, $\langle n\rangle$}, in which only $\langle n\rangle$ is modulated (Table 1). The conservation of correlation time implies that $k_{\text{on}}$ and $k_{\text{off}}$ must be carefully coordinated such that all boundaries emerge from quantitatively identical modulation of switching rates. In addition, these conclusions are unaffected by changes in elongation rate, which only rescales the kinetic parameters (Fig. S6L–N, STAR Methods).

Our observation of constant $k_{\text{ini}}$ and ${\tau }_n$ has several implications. Much prior work has characterized bursting in terms of burst size $b=k_{\text{ini}}/k_{\text{off}}$ (the average number of transcripts produced per burst) and burst frequency $f=\langle n\rangle \cdot k_{\text{off}}$ (which reduces to $k_{\text{on}}$ for short burst durations, i.e. small $\langle n\rangle$) (Dar et al., 2012; Siddharth S et al., 2015). Interestingly, by virtue of the constancy of $k_{\text{ini}}$ and ${\tau }_n$, at high activity ($\langle n\rangle >0.5$) mainly the burst size changes (Figure 5F), while for $\langle n\rangle <0.5$, it is the burst frequency that changes (Figure 5G). These results recapitulate recent observations of frequency modulation (Bartman et al., 2016; Fukaya et al., 2016; Larson et al., 2013; Li et al., 2018; Senecal et al., 2014) and might explain previously observed global trends in burst size (Sanchez and Golding, 2013).

Provided all gene become transcriptionally competent at the same time following mitosis (Blythe and Wieschaus, 2015; Blythe et al., 2016), the conserved correlation time we measure here implies that all genes reach steady state simultaneously (Figure S3C,F). Consistent with prior observations (Dubuis et al., 2013; Garcia et al., 2013), synchronicity suggests that the relative mean synthesis rates are maintained (i.e. unmodulated) across the patterning boundaries during early development (Figure S3F). In addition, a short correlation time (${\overline{\tau }}_n=3.0\pm 1.2$ min, small relative to $~$15 min duration of interphase 13) ensures effective temporal averaging of the switching noise by accumulation of stable transcripts, further suggesting that both expression timing and noise minimization jointly constrain switching rates. These dynamic constraints may be essential for precise and reproducible patterning outcomes, affecting the range of permissible values of $k_{\text{on}}$ and $k_{\text{off}}$. Together these results show that for the gap genes, the apparently complex process of regulating expression rates is explained by a conceptually simple, shared modulation strategy of bursting kinetics. Our approach opens a path to uncovering general principles to unify the regulation of transcription across genes.

DISCUSSION

A multitude of processes influence eukaryotic transcription rates. It is unclear which events might be more likely than others to determine the kinetics of bursting—either globally or in a gene specific manner. Nor is it known how bursting kinetics compare across endogenous genes over a range of expression levels. Our quantitative bursting measurements reveal that all gap gene expression boundaries arise from the same underlying kinetics regardless of the differences in regulatory elements. Thus, from the complex combination of diverse interactions specific to each gene emerges a simple, common strategy for transcriptional regulation.

Our recognition of shared regulation surfaced only upon development of a highly precise single molecule method of quantification. Conclusions about bursting depend heavily upon understanding sources and extent of measurement error and minimizing variability from extrinsic sources. Extrinsic processes, such as cell growth and division, DNA duplication, and mRNA transport and decay, can significantly affect the apparent variability between cells, and thus also bursting rates (Battich et al., 2015; Halpern et al., 2015; Zopf et al., 2013). We minimize these effects by measuring transcription at nascent sites in an endogenous system with synchronized cell divisions. Moreover, explicit quantification of measurement error resulted in a noise model that significantly constrained our inference framework. All these approaches are generally applicable to enable precise quantification in any system.

The fundamental mean–cumulant relationships we uncovered demonstrate that a single parameter distribution globally determines transcriptional activity (Fig. 3B–D). Employing the telegraph model (Peccoud and Ycart, 1995), we find that the modulation of mean occupancy $\langle n\rangle$ predicts mean mRNA synthesis rates comparable with previous measurements (Fig. S6O, Garcia et al., 2013) and reproduces the distribution of nascent activity (Fig. S6G–J), whereas $k_{\text{ini}}$ and ${\tau }_n$ are conserved. The global behavior we observe is surprising, given that bursting is generally believed to be gene- and promoter-specific. Multiple factors and processes all impinge on bursting rates, including enhancer-promoter interactions, chromatin context, nucleosome occupancy, Pol II pausing, and transcription factor interactions (Bartman et al., 2016; Brown and Boeger, 2014; Carey et al., 2013; Dar et al., 2012; Fukaya et al., 2016; Molina et al., 2013; Senecal et al., 2014; Siddharth S et al., 2015; Suter et al., 2011; Weinberger et al., 2012; Zenklusen et al., 2008). It remains to be determined whether the same processes are modulated in the same manner, or conversely whether different regulatory strategies have converged, to generate identical transcriptional activity across genes.

These observations raise the question of whether the common transcriptional bursting kinetics carry a functional advantage (Eldar and Elowitz, 2010). In early embryos, the precise positioning of cell fates requires minimizing variability between nuclei, which is achieved by a combination of long mRNA lifetimes permitting accumulation and spatial averaging through the syncytial cytoplasm (Little et al., 2013). In principle, modulating $k_{\text{ini}}$ at a constitutive promoter would generate the theoretical minimal (Poisson) transcriptional noise at all levels (Sanchez et al., 2013). The fact that neither constitutive activity ($\langle n\rangle \le 0.85$) nor Pol II saturation (${k_{\text{elo}}/k}_{\text{ini}}~215$bp $\gg$ Pol II footprint) is ever observed suggests that some constraint prohibits this system from maintaining a continuous active state, and/or it is not straightforward to alter $k_{\text{ini}}$. Instead, a constant switching correlation time suggests that this value is important in facilitating robust patterning. We propose that both expression timing and noise minimization jointly constrain switching rates.

The mechanistic origins of the conserved parameters are unknown. One possibility is that protein–DNA affinities have been individually selected to confer the switching rates we observe. However, it is unclear how transient transcription factor interactions, usually on the order of seconds, could generate bursts on the order of minutes (Elf et al., 2007; Izeddin et al., 2014; Karpova et al., 2008). Another possibility is that the fast transcription factor binding kinetics is masked by the slower dynamics of common general factors involved in the transcription process. In fact, recent evidence suggests that Mediator and TBP binding, as well as the core promoter and its shape play a key role in bursting (Li et al., 2018; Schor et al., 2017; Tantale et al., 2016). Alternatively, processes of potentially even slower dynamics such as long-range enhancer–promoter interactions, chromatin modification, or Pol II pausing may determine common bursting kinetics (Chen et al., 2018; Henriques et al., 2018; Nicolas et al., 2018).

The observed constancy of ${\tau }_n$ will guide further modeling and identification of the molecular mechanisms. This constancy is connected to the binomial noise level (STAR Methods, Eq. 9). Extensions of the two-state model must provide similar filtering of the binomial noise, which will restrict the possible class of models. For example, we tested two particular extensions of the two-state model. One possibility is a 3-state model, consisting in a two-step reversible activation (Rieckh and Tkačik, 2014). Alternatively, a model with an additional noise term such as input noise stemming from input transcription factor diffusion (Kaizu et al., 2014; Tkačik et al., 2008) could explain dual modulation of switching rates observed under the two-state model. However, distinguishing these models will require live imaging.

The common transcriptional parameters of the gap genes highlight a form of complexity reduction: despite the variety of upstream regulatory elements, all expression boundaries result from similar bursting kinetics. Whether this signature results from an underlying molecular simplicity has yet to be determined. Regardless of the mechanistic means by which these similarities are achieved, the convergence suggests the general constraints that limit the range of permitted bursting rates and/or minimize transcription variability. The unexpected conservation of the initiation rate and the correlation time might indicate a path to general rules in transcriptional regulation. It is now possible to inquire about the breadth of these generalities and whether they apply to the same gene expressed in different cell types, or to the transcriptome as a whole, or even across organisms. Indeed, it appears plausible that other classes of genes share similarly constrained bursting kinetics (Sanchez and Golding, 2013). The methods we utilize here are applicable in a variety of systems and permit the discovery of the molecular mechanism(s) conferring unified transcription kinetics.

STAR METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Thomas Gregor (tg2@princeton.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Fly strains

Oregon-R (Ore-R) embryos were used as wild-type. Embryos heterozygous for a deficiency spanning hb were collected from crosses of heterozygous adults of the strain w¹¹¹⁸; Df(3R)BSC477/TM6C. Heterozygotes of the hb deficiency, as well as wild-type male and female embryos stained for gt, were distinguished from siblings by visual inspection of nascent transcription sites.

METHOD DETAILS

DNA oligonucleotides

Oligonucleotide sequences complementary to the open reading frames of each gene of interest were chosen using the Biosearch Technologies Stellaris RNA FISH probe designer (www.biosearchtech.com/support/tools/design-software/stellaris-probe-designer). Amine-modified oligonucleotides were obtained from Biosearch Technologies, chemically coupled to NHS-ester-Atto565 (Sigma-Aldrich; 72464) or -Atto633 (Sigma-Aldrich; 01464) and purified by HPLC. Probes are listed in Table S1.

smFISH protocol

We modified our smFISH protocol (Little et al., 2013) to minimize background and maximize signal. Embryos were crosslinked in 1xPBS containing 16% paraformaldehyde for 2 minutes before devitellinization. Embryos were washed four times in methanol, 5 minutes per wash, with gentle rocking at room temperature, followed by an extended 30–60 minute wash in methanol. Fixed embryos were then used immediately for smFISH without intervening storage. Embryos washed three times in 1X PBS, 5 minutes per wash, at room temperature with rocking. Embryos were then washed 3 times in smFISH wash buffer (Little et al. 2013), 10 minutes per wash, at room temperature. During this time, probes diluted in hybridization buffer (Little et al. 2013) were preheated to 37°C. Hybridization was performed for 1.5 hr at 37C with vigorous mixing every 15 minutes. During hybridization, smFISH wash buffer was preheated to 37C. Embryos were washed four times with large excess volumes of wash buffer for 3–5 minutes per wash, rinsed twice briefly in PBS, stained with DAPI, and mounted in VECTASHIELD (Vector Laboratories; H-1000). Imaging was performed within 48 hr to ensure high quality signal.

Imaging

Imaging was performed by laser-scanning confocal microscopy on a Leica SP5 inverted microscope. We used a 63x HCX PL APO CS 1.4 NA oil immersion objective with pixels of $76\times 76$ nm² and z spacing of $340$ nm. We typically obtained stacks representing $8$ μm in total axial thickness starting at the embryo surface. The microscope was equipped with “HyD Hybrid Detector” avalanche photodiodes (APDs) that we utilized in photon counting mode. This is in contrast to our prior approach (Little et al. 2013) in which standard photomultiplier tubes (PMTs) were used to collect two separate smFISH image stacks at two different laser intensities: a low power stack for measuring transcription intensities, and a high power stack to distinguish single mRNAs. The use of low-noise photon-counting APDs in place of standard photomultipliers provided sufficient dynamic range to capture high signal transcription sites and to separate relatively dim cytoplasmic single mRNAs from background fluorescence with a single laser power. This also abrogated the need to calibrate the high- and low-power stacks for comparison. The removal of the calibration step provided an additional reduction in measurement error.

Image analysis

Raw data are processed according to previously developed image analysis pipeline (Little et al., 2013). Briefly, raw images are filtered using a Difference-of-Gaussians (DoG) filter to detect spot objects. A master threshold is applied to separate candidate spots from background. True point-like sources of fluorescence are identified, as they appeared on multiple consecutive z-slices ($>3$) at the same location. All candidate particles are then labeled as transcription sites, cytoplasmic transcripts or noise based on global thresholds. The threshold separating cytoplasmic transcripts from noise is defined as the bottom of the valley between the two peaks on the particle intensity distribution. The threshold for transcription sites depends both on intensity and position, as transcription sites cluster in z and are enclosed in nuclei (segmented from DAPI staining). Intensity of transcription sites is obtained by integrating the signal over a fixed cylinder volume ($V_s=\pi \times {0.76}^2\times 3.06{\mu m}^3$, determined from the objective’s PSF).

Calibration in absolute units

We calibrated the integrated intensity of transcription sites $F_s$ by first characterizing the relationship between the fluorescence signal and the density of cytoplasmic transcripts. We defined summation volumes in the embryo ($V\cong 3.8\times 3.8\times 8{\mu m}^3$) avoiding region of high tissue deformation and excluding transcription site location. For each summation volume we counted the number of detected cytoplasmic transcripts and integrated the fluorescence intensity. At low count density, the fluorescence per summation volume $F$ scales linearly with density $D$ (Little et al., 2013). Fitting a simple linear relationship $F=\alpha D+\beta$, where $\beta$ corresponds to background, enables estimation of a scaling factor $\alpha$ to calibrate transcription sites in “cytoplasmic units” (C.U.) for each embryo. Namely, the intensity in C.U. is given by $f={(F}_s-b{V}_s)/\alpha$ where b is the background intensity per pixel in each nucleus. The resulting quantification of transcriptional activity for all gap genes is provided in Supplemental Data.

Measurement error

Embryo staging

In order to assess the timing of the different embryos, we first manually ranked the different embryos based on timing estimation from DAPI staining. We estimated the interphase stage relying on morphological features of the nuclei (shape and textures) in the DAPI channel. We then verified whether accumulation of cytoplasmic mRNAs correlates with our manual ranking (Fig. S1A). Both approaches lead to similar results and provide a decent proxy for timing. By comparing the average activity of the different embryos in the maximally expressed regions with the cytoplasmic density, we assessed the effect of timing on the mean activity (Fig. S1B). We estimated the Pearson correlation coefficient $\rho$ for the different genes and regions (gt anterior and posterior regions). Overall, timing explain up to ${\rho }^2$ = 44% of the embryo variability (defined as the variance of the mean activity among embryos ${\sigma }_{\mu }^2$) in the maximally expressed regions (Fig. S1C), with the exception of kni that is highly correlated $\rho ~0.8$. We thus separated the kni embryos in two sub-populations, early and late embryos. We performed the splitting by finding the cytoplasmic density threshold that minimizes the sum of within-population variance in mean activity. We then calculated the staging variability ${\sigma }_{\text{sta}}=\rho {\sigma }_{\mu }$, defined as the variability in mean activity explained by timing between late and early embryos (Fig. S1D). Given the overall small staging variability $<14\%$, the total mean activity is stable enough to warrant the assumption of steady-state.

Imaging noise model

We quantified measurements noise due to imaging and calibration using a two-color smFISH approach, labeling each mRNA in alternating colors along the length of the mRNA. We included 15 hb embryos in the analysis, which corresponds to approximately 4’000 nuclei activity measurements. We then normalized the activity (fluorescence signal) of the nuclei in cytoplasmic units independently in each channel. In absence of noise and provided accurate normalization, both channels would perfectly correlate with slope one. By plotting one channel against the other (Fig. 2A), we assessed the slope and characterized the spread of the data along the expected line.

We build a simple effective model to describe measurement noise:

$$P\left(S^{\left(5\right)},S^{\left(3\right)}\text{|}{G}^{\left(5\right)},G^{\left(3\right)}\right)=\mathcal{N}\left(S^{\left(5\right)}|\mu =G^{\left(5\right)},{\sigma }_5^2\left(G^{\left(5\right)}\right)\right)\cdot \mathcal{N}\left(S^{\left(3\right)}|\mu =G^{\left(3\right)},{\sigma }_3^2\left(G^{\left(3\right)}\right)\right)$$ (Eq. 2)

where $S$ stands for the fluorescent signal in cytoplasmic units and $G$ the total nascent transcripts (in C.U.) in absence of noise. We assumed that the measurement errors were normally distributed and independent in both channels, which was motivated by the absence of correlation in the background. We further assumed that the variance would depend on activities, consistent with the increasing spread observed in the data. In order to estimate the variance specific to each channel, we fitted a straight line $y=ax+h$ assuming error on both ${x\equiv S}^{\left(5\right)}$ and ${y\equiv S}^{\left(3\right)}$. We expanded the variance as a function of the scalar projection along the line $v$:

$${\sigma }^2\left(v\right)={\sigma }_b^2+b_{1}v+b_2{v}^2+\cdots$$

$$v=\frac{x+ay}{\sqrt{1+a^2}}$$

Assuming the same error along $x$ and $y$, we then maximized the following likelihood to estimate the parameters $\theta =\left\{a,h,{\sigma }_b,b_1,b_2,\cdots \right\}$:

$$P\left(\left\{x_i,y_i\right\}|\theta \right)=\prod _{i=1}^{N_d}\frac{1}{\sqrt{2\pi {\sigma }^2\left(v_i\right)}}\text{ exp}\left(-\frac{{\left(y_i-a{x}_i-h\right)}^2}{2\left(1+a^2\right){\sigma }^2\left(v_i\right)}\right)$$

Using the Akaike information criterion, we selected the best model which was parameterized by $\left(a,{\sigma }_b,b_1,b_2\right)$ with $h=0$. The best fitting parameters were: $a=0.968,{\sigma }_b=4.59\bullet {10}^{-2},b_1=9.31\bullet {10}^{-3}$ and $b_2=9.23\bullet {10}^{-4}$ (Fig. 2A). The variances in the noise measurement model (Eq. 2) are then given by:

$${\sigma }_5^2\left(G\right)={\sigma }^2\left(v=\sqrt{G^2+{\left(aG\right)}^2}\right)$$

$${\sigma }_3^2\left(G\right)={\sigma }^2\left(v=\sqrt{G^2+{\left(G/a\right)}^2}\right)$$

where ${\sigma }^2\left(v\right)={\sigma }_b^2+b_{1}v+b_2{v}^2$. The resulting imaging noise is shown in Figure S1E. In the maximally expressed regions, we measure transcriptional activity with an error of $5\%$ and relate it to absolute units with an uncertainty below $3.5\%$ (the largest deviation of the slope $0.968\pm 0.003$ from $1$). This represents an error reduction by 3- to 4-fold compared to our previous measurements (assuming multiplicative errors; $6\%$ vs $20\%$) (Little et al., 2013).

Splitting of the total variance

The Anterior-Posterior axis (AP) was determined based on a mid-sagittal elliptic mask of the embryo in the DAPI channel (Little et al., 2013). Position is obtained by registration of high- and low-magnification DAPI images of the surface. We then fitted constrained splines to approximate the mean activity as a function of the AP position. We used different features of the mean profiles such as maxima and inflection points to refine the alignment between the different embryos. Overall, this realignment procedure enables us to estimate an alignment error of the order of $2\%$ egg length.

After alignment, we defined spatial bins along the AP-axis with a width of $2.5\%$ of egg length. Such a width was a good compromise to balance the sampling and binning error. We next sought to decompose the measured total variance of the transcriptional activity ${\sigma }^2$ (Fig. 1D) into different components related to imaging, alignment, embryo and nuclei variability (Fig. 2B–D). We first estimated the variability of the mean across embryos ${\sigma }_{\mu }^2$ in each bin (Fig. 2B); we split the total variance ${\sigma }^2$ in each bin according to the law of total variance:

$${\sigma }^2=\underset{\langle {\sigma }_i^2\rangle }{\underbrace{\frac{1}{N_e}\sum _{i=1}^{N_e}{\sigma }_i^2}}+\underset{{\sigma }_{\mu }^2}{\underbrace{\frac{1}{N_e}\sum _{i=1}^{N_e}{\left({\mu }_i-\mu \right)}^2}}$$

where $N_e$ is the total number of embryos and $\mu$ the global mean.

Next we aimed to determine what fraction of ${\sigma }_{\mu }^2$ is explained by residual misalignment. Assuming that all the variability in the mean at boundaries results from spatial misalignment of the different embryos, one can find an upper bound on the residual alignment error ${\sigma }_x$:

$${\sigma }_{\mu }^2\ge {\sigma }_{\text{ali}}^2={\left(\frac{d\mu }{dx}\right)}^2{\sigma }_x^2$$

where $\mu$ is the global mean profile as function of AP position $x$. For each gene, we estimated the residual alignment error ${\sigma }_x$ required to explain as much embryo variability as possible (Fig. S1F, diagonal dash line). Overall we found that ${\sigma }_x$ is of the order of $1\%$ egg length. The total embryo variability in the maximally expressed regions cannot be explained by misalignment as $\left(\frac{d\mu }{dx}\right)\approx 0$ and leads to a noise floor (Fig. S1F, horizontal dash line). This noise floor can be partly explained by variability in the stage (early versus late interphase) of the different embryos (Fig. S1C–D). In the following we thus split ${\sigma }_{\mu }^2={\sigma }_{\text{ali}}^2+{\sigma }_{\text{emb}}^2$ where ${\sigma }_{\text{emb}}^2$ is the residual embryo to embryo variability.

Finally, we assessed what fraction of the total variance ${\sigma }^2$ corresponds to combined measurement noise ${\sigma }_{\text{mea}}^2={\sigma }_{\text{img}}^2+{\sigma }_{\text{ali}}^2$ where ${\sigma }_{\text{img}}^2$ was estimated in subsection (STAR Methods, Imaging noise model). Total measurement noise ${\sigma }_{\text{mea}}^2$ remains below $20\%$ of the total variance for all genes and all position (Fig. S1G), and on average reaches $6.1\pm 3.5\%$. The remaining variability corresponds to biological variability ${\sigma }_{\text{bio}}^2={\sigma }_{\text{nuc}}^2+{\sigma }_{\text{emb}}^2$ where ${\sigma }_{\text{nuc}}^2$ is the nuclei variability and was defined as:

$${\sigma }_{\text{nuc}}^2={\sigma }^2-{\sigma }_{\text{img}}^2-{\sigma }_{\text{ali}}^2-{\sigma }_{\text{emb}}^2$$

Overall, the non-nuclear variability $\left({\sigma }_{\text{img}}^2+{\sigma }_{\text{ali}}^2+{\sigma }_{\text{emb}}^2\right)$ remains below $33\%$ of the total variance for all genes and all position (Fig. S1H), and on average reaches $16.0\pm 6.4\%$. Thus, the nuclei variability ${\sigma }_{\text{nuc}}^2$ largely dominates in our data and represents $84\%$ of the total variance on average (Fig 1E–F).

Single parameter distribution of transcriptional activity

Noise mean-relationship in the FISH data

In practice, we measure transcriptional activity in cytoplasmic units (intensity in equivalent number of fully elongated transcripts) and not in Pol II counts $g$ directly. The measured mean activity $\mu$ in cytoplasmic units is proportional to the mean Pol II counts for a single gene copy $\langle g\rangle$, i.e. $\mu =C_1{N}_g\langle g\rangle$ where $C_1\in \left[\mathrm{0,1}\right]$ is a conversion factor accounting for the FISH probe locations on the gene and $N_g$ the number of gene copies (for most gap genes $N_g=4$, except for gt male and hb deficient that only have 2 copies). Assuming independence of loci, the measured variance ${\sigma }^2$ follows a similar relationship, i.e. ${\sigma }^2=C_2{N}_g{\sigma }_g^2$ with $C_2\in \left[\mathrm{0,1}\right]$. The conversion factors $C_1$ and $C_2$ are constant that are unique for each gene and are calculated further (STAR Methods, Conversion factor for Pol II counts).

As we will see later (Eq. 9), one can derive the following functional form for the variance in Pol II counts for a single gene copy:

$${\sigma }_g^2=\langle g\rangle +\langle g\rangle \left(g_0-\langle g\rangle \right)\Phi$$

where $g_0$ is the maximal mean Pol II counts on the gene that is determined by the Pol II initiation rate $k_{\text{ini}}$ and elongation time ${\tau }_e$, and $\Phi$ a quantity that is related to the dynamics of the promoter activity and bounded $\Phi \in \left[\mathrm{0,1}\right]$. Of note, $\Phi =0$ for a constitutively expressed gene such that the variance reduces to ${\sigma }_g^2=\langle g\rangle$ (Poisson variance). In principle, the values of both $g_0$ and $\Phi$ are gene-specific and could have specific dependency on $\langle g\rangle$. The interpretation of the equation above and the quantities $g_0$ and $\Phi$ will be discussed in greater details later on (STAR Methods, Two-state model of transcriptional activity). Using the relationships between the cytoplasmic units and Pol II counts for the mean and variance above, we can express the measured noise as:

$$\frac{{\sigma }^2}{{\mu }^2}=\frac{C_2}{C_1}\left(\frac{1}{\mu }+\frac{1}{C_1{N}_g}\frac{{\mu }_0-\mu }{\mu }\Phi \right)$$

where ${\mu }_0=C_1{N}_g{g}_0$ is the maximal mean expression level in cytoplasmic units. In practice, $C_2/C_1\approx 1$ and $C_1\approx 0.7$ (Table S2, 5’ probe location) such that the Poisson noise background in cytoplasmic units is approximately $1/\mu$. By setting $C_2/C_1=1$, we further simplify the equation above and obtain:

$$\frac{{\sigma }^2}{{\mu }^2}=\frac{1}{\mu }\left(1+a\left(1-\mu /{\mu }_0\right)\right)$$ (Eq. 3)

with $a=g_0\Phi$. By assuming $a$ and ${\mu }_0$ constant, we found that the above noise-mean relationship (Eq. 3) captures the overall trend in the data well (Fig. 3A), with $a=9.93\pm 0.35$ and ${\mu }_0=53.07\pm 1.73(R^2=0.99$). Although both gt male and hb deficient follow a similar trend, they deviate from the black line, ($a=10.66\pm 0.35,{\mu }_0=18.52\pm 0.28$) and ($a=7.68\pm 1.00,{\mu }_0=29.57\pm 1.59$) respectively. Interestingly, despite the fact that $g_0$ and $\Phi$ could a priori be gene-specific, $a$ is roughly conserved across genes and differences in ${\mu }_0$ can be explained by variation in gene copies ($N_g=2$ copies for gt male and hb deficient instead of $4$) and gene length (gt is shorter than hb, Table S3). This suggests that some key quantities underlying transcription are conserved among the gap genes and can be highlighted by proper normalization of the measured activity.

Normalized cumulants for a single gene copy

To further investigate the transcriptional commonalities of the gap genes, we calculated the 2^nd, 3^rd and 4^th cumulants from the data (Fig. 3B–D). For independent random variables, the cumulants have the property to be extensive, which is convenient as the measured transcriptional activities result from the sum of $2$ or $4$ independent gene copies. We first converted the $k$^th cumulants ${\tilde{\kappa }}_k$ computed from the data in cytoplasmic units to Pol II counts (or number of nascent transcripts) for a single gene copy with a normalized gene length:

$${\kappa }_k=\frac{1}{C_k{N}_g}{\left(\frac{\langle L_g\rangle }{L_g}\right)}^k{\tilde{\kappa }}_k$$

where ${\kappa }_k$ is the $k$^th cumulant in Pol II counts for a single gene copy, $L_g$ the gene length, $N_g$ the gene copy number ($4$ for most genes, except gt male and hb deficient that only have $2$ copies) and $C_k$ a conversion factor for the $k$^th cumulant to ensure proper normalization of the Poisson background (Eq. 4 and Table S2). The annotated gene length $L_g$ varies between $1.8$ to $3.6$ kb for the gap genes. In the following we used an effective gene length that is slightly larger and takes into account the possible lingering of fully elongated transcripts at the loci (Table S3). This effective gene length can be estimated from the dual color FISH data (STAR Methods, Dual color smFISH and effective gene length). For the normalization, we used a normalized gene length of $\langle L_g\rangle =3.3$ kb.

We then fitted a second order polynomial of the mean activity $\langle g\rangle$ to the variance ${\sigma }_g^2$ (Fig. S2A and Fig. 3B) in order to estimate the maximal activity $g_0$, which was defined as the second crossing point between the Poisson background (Fig. S2A dash line) and the fitted variance (solid line). We found $g_0=15.21\pm 0.20$ Pol II for a normalized gene length of $3.3$ kb. Similarly, we fitted 3^rd and 4^th order polynomial of the mean activity to the cumulants ${\kappa }_3$ and ${\kappa }_4$ (Fig. 3C–D), constrained to reach the Poisson limit at $g_0$. Of note, the cumulants of the Poisson distribution are all equal to the mean. As we observed in Figure 3B–D, the polynomial fits (solid lines) capture the main trend observed in the data, suggesting a simple relationship between the cumulants and the mean. It follows that the underlying activity distribution is essentially a universal single parameter distribution whose parameter is the mean activity. To test the extent of the universality, we repeated the analysis above of each gap gene individually (Fig. S2B–D). The individual fits (colored solid lines) remain relatively close to each other. Although the fits for hb slightly deviate from the other genes, the global shape of the cumulants is conserved.

Conversion factor for Pol II counts

As mentioned above, the cumulants of the transcriptional activity in cytoplasmic units are related to the cumulants in number of nascent transcripts or Pol II counts on the gene by conversion factors $C_k$. We calculated these conversion factors to ensure proper normalization of the Poisson background, meaning that the conversion of cumulants in C.U. for a constitutive gene would yield the correct cumulants in Pol II counts. Knowing the exact location of the fluorescent probe binding regions along the gene, one can calculate the contribution of a single nascent transcript to the signal in C.U. as a function its length $l$:

$$s\left(l\right)=\frac{1}{N}\sum _{i=1}^{N}H\left(l-l_i\right)=\frac{1}{N}b\left(l\right)$$

where $H$ is the unit step function, $l_i$ the end position of the $i^{\text{th}}$ probe binding region and $N$ the total number of probes. Here, we made the assumptions that each fluorescent probe contributes equally to the signal and each transcribed probe region bound. The number of probes bound to a transcript of length $l$ is given by $b\left(l\right)$ and will be denoted $b_i$ for $l\in \left(l_i,l_{i+1}\right]$ with $l_{N+1}=L_g$ the length of a fully elongated transcript. The total fluorescent signal $s$ in cytoplasmic units for $g$ transcripts is given by

$$s=\frac{1}{N}\sum _{i=1}^N{b}_i{g}_i$$

where $g={\sum }_{i=1}^N{g}_i$, with $g_i$ the number of transcripts whose length $l$ belongs to the length interval $\left(l_i,l_{i+1}\right]$. Assuming that $g_i$ follows a Poisson distribution with parameter ${\lambda }_i=k_{\text{ini}}{\tau }_i$ where ${\tau }_i=\left(l_{i+1}-l_i\right)/k_{\text{elo}}$, the mean fluorescent signal $\langle s\rangle$ is then given by

$$\langle s\rangle =\frac{1}{N}\sum _{i=1}^N{b}_i\langle g_i\rangle =\frac{1}{N}\sum _{i=1}^N{b}_i{k}_{\text{ini}}{\tau }_i=\underset{C_1}{\underbrace{\left(\frac{1}{N}\sum _{i=1}^N{b}_i{\tilde{\tau }}_i\right)}}{k}_{\text{ini}}{\tau }_e=C_1\langle g\rangle$$

where ${\tilde{\tau }}_i={\tau }_i/{\tau }_e=\left(l_{i+1}-l_i\right)/L$ and $C_1$ the conversion factor that relates the mean number of transcripts $\langle g\rangle$ to the mean fluorescent signal $\langle s\rangle$ in cytoplasmic units. This relation remains valid for the two-state model with $\langle g\rangle =k_{\text{ini}}{\tau }_e\langle n\rangle$ (Eq. 8).

As for the mean, one can calculate the conversion factors for the higher moments and cumulants assuming a Poisson background. The second moment is given by

$$\begin{gathered} \langle s^2\rangle =\frac{1}{N^2}\langle \sum _{ij}{b}_i{b}_j{g}_i{g}_j\rangle =\frac{1}{N^2}\left(\sum _{i\ne j}{b}_i{b}_j\langle g_i\rangle \langle g_j\rangle +\sum _i{b}_i^2\langle g_i^2\rangle \right) \\ =\frac{1}{N^2}\left(\sum _{i\ne j}{b}_i{b}_j{k}_{\text{ini}}^2{\tau }_i{\tau }_j+\sum _i{b}_i^2\left(k_{\text{ini}}^2{\tau }_i^2+k_{\text{ini}}{\tau }_i\right)\right) \\ =\frac{1}{N^2}\left(\sum _{ij}{b}_i{b}_j{k}_{\text{ini}}^2{\tau }_i{\tau }_j+\sum _i{b}_i^2{k}_{\text{ini}}{\tau }_i\right) \end{gathered}$$

where $\langle g_i{g}_j\rangle =\langle g_i\rangle \langle g_j\rangle$ since initiation events are assumed independent. This only holds for the Poisson background and is no longer exact for the two-state model as the switching process would introduce correlations. Nevertheless, the conversion factors for the higher moments and cumulants calculated below remain a good approximation under the two-state model, provided most probes are located in the 5’ region. The variance of the signal is finally given by

$$\langle {(s-\langle s\rangle )}^2\rangle =\langle s^2\rangle -{\langle s\rangle }^2=\frac{1}{N^2}\sum _{i=1}^N{b}_i^2{k}_{\text{ ini }}{\tau }_i=\underset{C_2}{\underbrace{\left(\frac{1}{N^2}\sum _{i=1}^N{b}_i^2{\tilde{\tau }}_i\right)}}\langle g\rangle =C_2\langle g\rangle$$

The calculation above can be generalized to the 3^rd and 4^th cumulants. We found the following correction factor for the Poisson background:

$$C_k=\frac{1}{N^k}\sum _{i=1}^N{b}_i^k{\tilde{\tau }}_i\text{ for }k=1,\cdots ,4$$ (Eq. 4)

Calculated values of $C_k$ for each gene and two different configurations of probe locations (5’ or 3’ region) are given in Table S2.

Two-state model of transcriptional activity

Master equation

Transcriptional activity of a single gene copy was modeled as a telegraph process (on-off promoter switching) with transcript initiation occurring as a Poisson process during the ‘on’ periods (Peccoud and Ycart, 1995). Within the two-state model (Figure 3E), the distribution of nascent transcripts on a gene results from random Pol II initiation in the active state coupled with elongation and termination (Choubey et al., 2015; Senecal et al., 2014; Xu et al., 2016). For simplicity, we combined elongation and termination as an effective process that was modeled as a deterministic progression (constant Pol II elongation rate). In addition, we assumed that all the kinetic rates of the model are constant in time and identical across embryos. The kinetic parameters of the model are the initiation rate $k_{\text{ini}}$, the promoter switching rates $k_{\text{on}}$ and $k_{\text{off}}$, and the elongation time ${\tau }_e=L_g/k_{\text{elo}}$.

The master equation that governs the temporal evolution of nascent transcripts at loci is given by

$$\frac{d}{dt}{P}_t\left(g,n\right)=k_{\text{ini}}{\delta }_{n1}\left(P_t\left(g-1,n\right)-P_t\left(g,n\right)\right)+k_n{P}_t\left(g,n-1\right)-k_{n+1}{P}_t\left(g,n\right)$$ (Eq. 5)

with $g$ the number of nascent transcripts (or alternatively the number of Pol II) on the gene and $n$ the promoter state. We used the convention that $n=1$ and $n=0$ correspond to the ‘on’ state and ‘off’ state respectively, and the following periodic conditions $n=-1\equiv 1$ and $n=2\equiv 0$. Here, $\delta$ stands for the Kronecker delta since initiation only occurs in the active state. Of note, we only considered the promoter switching and the initiation of elongation (Eq. 5); we did not explicitly model release of transcripts after termination. The rationale is the following; only the initiation events occurring during the time interval $\left[t-{\tau }_e,t\right]$ contributes to the signal at time $t$, i.e. the elongation time ${\tau }_e$ determined the ‘memory’ of the system. This is correct as long as the release events are instantaneous and termination is fast compared to elongation. Thus, the dynamics of nascent transcripts accumulation on the gene for $t\le {\tau }_e$ is obtained by solving the master equation with zero initial transcript on the gene $P_{t_0}\left(g\right)={\delta }_{g0}$ and an arbitrary initial distribution of promoter state.

Summary statistics

We can derive the temporal evolutions of the central moments from the master equation (Eq. 5) (Lestas et al., 2008; Sanchez and Kondev, 2008). The means of nascent transcripts $g$ and promoter states $n$ satisfy the following equations:

$$\{\begin{array}{c}\frac{d}{dt}\langle g\left(t\right)\rangle =k_{\text{ini}}\langle n\left(t\right)\rangle \\ \frac{d}{dt}\langle n\left(t\right)\rangle =k_{\text{on}}-\left(k_{\text{on}}+k_{\text{off}}\right)\langle n\left(t\right)\rangle \end{array}$$ (Eq. 6)

At steady state ($\frac{d}{dt}\langle n\rangle =0$), the mean occupancy of the promoter is simply given by $\langle n\rangle =k_{\text{on}}/\left(k_{\text{on}}+k_{\text{off}}\right)$. Similarly, the covariance satisfies the following set of equations:

$$\{\begin{array}{l}\frac{d}{dt}{\sigma }_g^2(t)=2k_{\text{ini}}{\sigma }_{gn}(t)+k_{\text{ini}}\langle n(t)\rangle \hfill \\ \frac{d}{dt}{\sigma }_{gn}(t)=k_{\text{ini}}{\sigma }_n^2(t)-\left(k_{\text{on}}+k_{\text{off}}\right){\sigma }_{gn}(t)\hfill \\ \frac{d}{dt}{\sigma }_n^2(t)=-2\left(k_{\text{on}}+k_{\text{off}}\right){\sigma }_n^2(t)+k_{\text{on}}(1-\langle n(t)\rangle )+k_{\text{off}}\langle n(t)\rangle \hfill \end{array}$$ (Eq. 7)

Assuming zero initial transcripts and promoter at steady state, one can solve both the mean and variance for $g$. Thus, the initial conditions are given by $\langle g\left(t_0\right)\rangle =0$, $\langle n\left(t_0\right)\rangle =k_{\text{on}}/\left(k_{\text{on}}+k_{\text{off}}\right)$, ${\sigma }_g^2\left(t_0\right)=0,{\sigma }_{gn}\left(t_0\right)=0$ and ${\sigma }_n^2\left(t_0\right)=\langle n\left(t_0\right)\rangle \left(1-\langle n\left(t_0\right)\rangle \right)$. Solving these equations (Eq. 6 & 7) for the elongation time $t={\tau }_e$ leads to:

$$\langle g\rangle =g_0\langle n\rangle$$ (Eq. 8)

$${\sigma }_g^2=g_0\langle n\rangle +g_0^2\langle n\rangle (1-\langle n\rangle )\Phi \left({\tau }_e/{\tau }_n\right)$$ (Eq. 9)

where $g_0=k_{\text{ini}}{\tau }_e$ is the maximal mean nascent transcript number or equivalently the mean number of transcripts in a constitutive regime (gene always ‘on’) and $\Phi \in \left[\mathrm{0,1}\right]$ a noise filtering function that takes into account the fluctuation correlation times. Here, the relevant time scales are the elongation time ${\tau }_e$ and the promoter switching correlation time ${\tau }_n=1/\left(k_{\text{on}}+k_{\text{off}}\right)$. The variance ${\sigma }_g^2$ results from the sum of two contributions; the Poisson variance $g_0\langle n\rangle$ stemming from the stochastic initiation of transcript and the propagation of switching noise:

$${\left(\frac{d\langle g\rangle }{d\langle n\rangle }\right)}^2{\sigma }_n^2\Phi \left({\tau }_e/{\tau }_n\right)=g_0^2\underset{\text{binomial variance}}{\underbrace{\langle n\rangle (1-\langle n\rangle )}}\Phi \left({\tau }_e/{\tau }_n\right)$$

For deterministic elongation, we find that the noise filtering function is given by:

$$\Phi (x)=2\frac{\text{exp}(-x)+x-1}{x^2}$$

In the limit of fast and slow promoter switching respectively, the noise filtering function reduces to

$${\tau }_e\gg {\tau }_n\underset{x\to \infty }{\text{lim}}\Phi (x)=0$$

$${\tau }_e\ll {\tau }_n\underset{x\to 0}{\text{lim}}\Phi (x)=1$$

Thus, the noise is minimal in the fast switching regime ${\tau }_e\gg {\tau }_n$ and reaches the Poisson limit ${\sigma }_g^2=g_0\langle n\rangle$. While in the slow switching regime ${\tau }_e\ll {\tau }_n$, none of the switching noise is filtered and the variance is described by a second order polynomial of the mean occupancy $\langle n\rangle$, i.e. ${\sigma }_g^2=g_0\langle n\rangle +g_0^2\langle n\rangle \left(1-\langle n\rangle \right)$. Of note, for exponentially distributed life-time of transcripts, such as cytoplasmic mRNA subject to degradation, the results above remain valid except that the noise averaging function becomes $\Phi \left(x\right)=1/\left(1+x\right)$ with ${\tau }_e$ the average life-time of the transcripts.

Following a similar approach as in the previous paragraph, higher order moments and cumulants are analytically calculated from the master equations (Eq. 5). The cumulants up to order 3 are equal to the central moments while higher order cumulants can be expressed as a combination of central moments. The 4^th cumulant is given by ${\kappa }_4={\mu }_4-3{\mu }_2^2$, where ${\mu }_4$ is the 4^th central moment and ${\mu }_2$ the variance. Assuming promoter at steady state, we solved the equations for 3^rd and 4^th moments of $g$ and derive the following analytical expressions for 3^rd and 4^th cumulants, ${\kappa }_3$ and ${\kappa }_4$:

$${\kappa }_3=g_0\langle n\rangle +3g_0^2\langle n\rangle (1-\langle n\rangle ){\Phi }_1\left({\tau }_e/{\tau }_n\right)+g_0^3\langle n\rangle (1-\langle n\rangle )(1-2\langle n\rangle ){\Phi }_2\left({\tau }_e/{\tau }_n\right)$$ (Eq. 10)

$${\kappa }_4=g_0\langle n\rangle +7g_0^2\langle n\rangle (1-\langle n\rangle ){\Phi }_1\left({\tau }_e/{\tau }_n\right)+6g_0^3\langle n\rangle (1-\langle n\rangle )(1-2\langle n\rangle ){\Phi }_2\left({\tau }_e/{\tau }_n\right)+g_0^4\langle n\rangle (1-\langle n\rangle )\left({\Phi }_3\left({\tau }_e/{\tau }_n\right)-6\langle n\rangle (1-\langle n\rangle ){\Phi }_4\left({\tau }_e/{\tau }_n\right)\right)$$ (Eq. 11)

where ${\Phi }_1,{\Phi }_2,{\Phi }_3$ and ${\Phi }_4$ are noise filtering functions that vanish in the fast switching regime (${\tau }_e\gg {\tau }_n$) and tend to one in the slow switching regime (${\tau }_e\ll {\tau }_n$):

$${\Phi }_1\left(x\right)=2\frac{\text{exp}\left(-x\right)+x-1}{x^2}$$

$${\Phi }_2\left(x\right)=6\frac{x\text{ exp}\left(-x\right)+2\text{ exp}\left(-x\right)+x-2}{x^3}$$

$${\Phi }_3\left(x\right)=12\frac{x^2\text{exp}\left(-x\right)+4x\text{ exp}\left(-x\right)+6\text{ exp}\left(-x\right)+2x-6}{x^4}$$

$${\Phi }_4\left(x\right)=2\frac{\text{exp}{\left(-x\right)}^2+4x^2\text{exp}\left(-x\right)+20x\text{ exp}\left(-x\right)+28\text{ exp}\left(-x\right)+10x-29}{x^4}$$

The above expressions for the cumulants are exact and were tested numerically. The cumulants are polynomials of the mean promoter activity $\langle n\rangle$, which follows from the propagation of the binomial cumulants from the switching process. Since the cumulants are extensive, the cumulants for $N_g$ independent gene copies are obtained by multiplying by $N_g$ the expression for a single gene copy (Eq. 9, 10 & 11).

Cumulant analysis

Noise-mean relationship and cumulants predicted by the two-state model

Within the context of the two-state model, we tested whether any transcriptional parameter modulations could explain the global trends in the noise and the cumulants (Figure 3A–D). Since we showed based on the cumulants that the distribution of activity is a single parameter distribution, we restricted the analysis to single parameter modulations of the mean activity (Fig. 3F–I). It is worth mentioning a few important observations that will simplify this task.

First, we see by close inspection of the steady state cumulants (Eq. 9, 10 & 11) that ${\tau }_e$ sets the scale, i.e. all parameters are defined with respect to ${\tau }_e$. In practice, the cumulants only depends on the three following independent parameters ${\tilde{k}}_{\text{ini}}=k_{\text{ini}}{\tau }_e,{\tilde{k}}_{\text{on}}=k_{\text{on}}{\tau }_e$ and ${\tilde{k}}_{\text{off}}=k_{\text{off}}{\tau }_e$. Thus, there is some freedom to set the scale of these rates. Here, we used ${\tau }_e=2.2$ min that is approximately the Pol II elongation time for the normalized gene length ($3.3$ kb and $k_{\text{elo}}=1.5$ kb/min; (Garcia et al., 2013)) and it will be considered fixed. Second, the magnitude of $k_{\text{ini}}$ determines whether the Poisson (first term $\propto k_{\text{ini}}$) or the binomial (second term $\propto k_{\text{ini}}^2$) components dominates in the expression of the variance (Eq. 7). We immediately see that increasing the mean Pol II number on the gene $\langle g\rangle$ by only modulating $k_{\text{ini}}$ cannot explain the data, since it would lead to a monotonic increase of the variance whereas the observed trend is concave with a global maxima at mid-expression levels. The only way of achieving such a trend is by modulating $\langle n\rangle$ provided the binomial term dominates the Poisson one. This condition implies that $k_{\text{ini}}$ has to be sufficiently large for intermediate value of $\langle n\rangle$, i.e. $k_{\text{ini}}\gg 1/\left({\tau }_e\left(1-\langle n\rangle \right)\Phi \left({\tau }_e/{\tau }_n\right)\right)$. Alternatively, if $k_{\text{ini}}$ is known, this inequality sets some constraints on the possible values of ${\tau }_n$. Third, it is possible to give an estimate of $k_{\text{ini}}$ from the polynomial fit of the measured variance (Fig. S2A and Fig. 3B). The second intercept of the fitted curve (black line) with the Poisson background (dash line), which should occur at $\langle n\rangle =1$, allows us to estimate $g_0$. Assuming $k_{\text{ini}}$ is maintained constant as $\langle n\rangle$ is modulated, we have $g_0=k_{\text{ini}}{\tau }_e=15.21$, which gives $k_{\text{ini}}=6.99$ min⁻¹ for ${\tau }_e=2.2$ min (see above).

We then investigated three different type of single parameter modulation to vary the mean Pol II number $\langle g\rangle$ consistent with the observation above, namely, modulations of the mean occupancy $\langle n\rangle$ from $0$ to $1$ by either varying $k_{\text{on}}$ alone, $k_{\text{off}}$ alone or both $k_{\text{on}}$ and $k_{\text{off}}$ while keeping the switching correlation time ${\tau }_n$ constant. The latter modulation also corresponds to single parameter modulation since $k_{\text{on}}=\langle n\rangle /{\tau }_n$ and $k_{\text{off}}=\left(1-\langle n\rangle \right)/{\tau }_n$ are then fully determined by $\langle n\rangle$. For each of these three types of modulation, one parameter is free (either $k_{\text{off}},k_{\text{on}}$ or ${\tau }_n$) and sets the amplitude of the cumulants (Fig. S2E). In order to infer these free parameters, we fitted (maximum likelihood) the measured cumulants with the modeled ones (Eq. 9, 10 & 11) predicted by each modulation strategy (Fig. 3G–I). We found:

1. $k_{\text{on}}$ modulation: $k_{\text{off}}=0.142$ min⁻¹ and $k_{\text{on}}=k_{\text{off}}\langle n\rangle /\left(1-\langle n\rangle \right)$

2. $k_{\text{off}}$ modulation: $k_{\text{on}}=0.075$ min⁻¹ and $k_{\text{off}}=k_{\text{on}}\left(1-\langle n\rangle \right)/\langle n\rangle$

3. $\langle n\rangle$ modulation at fixed ${\tau }_n:{\tau }_n=2.9993$ min with $k_{\text{on}}=\langle n\rangle /{\tau }_n$ and $k_{\text{off}}=\left(1-\langle n\rangle \right)/{\tau }_n$

We then calculated the noise-mean relationship (Eq. 3). We also show an example of a $k_{\text{ini}}$ modulation alone (Fig. 3F, gray line); no matter the value of $\langle n\rangle$ and ${\tau }_n$ this modulation cannot reproduce the trend in the data as explained above. The modulation of $k_{\text{off}}$ alone (green line) fails to capture the noise at low expression (Fig. 3F). On the other hand both the modulation of $k_{\text{on}}$ alone (blue line) and $\langle n\rangle$ at constant ${\tau }_n$ (red line) provides good qualitative agreement with the data (Fig. 3F–I). As mentioned above, it is important to keep in mind that the units of $k_{\text{ini}},k_{\text{on}},k_{\text{off}}$ and ${\tau }_n$ estimated here depends on the value of the elongation rate. Here, we used a conservative estimate of $k_{\text{elo}}=1.5$ kb/min (Garcia et al., 2013), which is possibly too small for the gap genes (Fukaya et al., 2017). A different elongation rate would simply imply a rescaling of the rates and the correlation time without affecting the fitting results (STAR methods, Effect of elongation rate on inference). Namely, the mean occupancy $\langle n\rangle$ would remain unchanged while the rates would be rescaled by a factor $k_{\text{elo}}^{*}/k_{\text{elo}}$ and the correlation time by $k_{\text{elo}}/k_{\text{elo}}^{*}$, where $k_{\text{elo}}^{*}$ corresponds to the new elongation rate.

Time-dependent cumulant analysis

Next, we investigated whether the single parameter modulation fitted above assuming steady state are consistent with the finite duration of the nuclear cycle (approximately 15 min in nc13). Namely, assuming all the data were taken at mid cycle, we asked under each modulation scenario whether steady state could be reached in a timely manner (mid cycle), as supported by our staging analysis (Fig. S1A–D) and other studies (Garcia et al., 2013). The relaxation time to steady state is determined by the switching correlation time ${\tau }_n$. By solving the equation for the temporal evolution of the mean Pol II number $\langle g\left(t\right)\rangle$ (Eq. 6) with initial condition $\langle g\left(t=0\right)\rangle =0$ (no Pol II on the gene) and $\langle n\left(t=0\right)\rangle =0$ (gene initially ‘off’), one finds:

$$\langle g(t)\rangle =\{\begin{array}{cc}{g}_0\langle n\rangle \left(\frac{t}{{\tau }_e}+\frac{{\tau }_n}{{\tau }_e}\left(\text{exp}\left(-t/{\tau }_n\right)-1\right)\right)& t\le {\tau }_e\\ g_0\langle n\rangle \left(1+\frac{{\tau }_n}{{\tau }_e}\text{exp}\left(-t/{\tau }_n\right)\left(1-\text{ exp}\left({\tau }_e/{\tau }_n\right)\right)\right)& t>{\tau }_e\end{array}$$

As mentioned above, the relaxation of the mean $\langle g\left(t\right)\rangle$ to its steady state value $\langle g\rangle =g_0\langle n\rangle$ is determined by the correlation time ${\tau }_n$ through the exponential factor $\text{exp}\left(-t{/\tau }_n\right)$. As ${\tau }_n$ increases, the relaxation gets slower and slower (Fig. S3A). It follows that the finite duration of nc13 should set some upper bound on the possible value of ${\tau }_n$. According to Fig. S3A, ${\tau }_n$ should not exceed 3 min for $\langle g\left(t\right)\rangle$ to reach approximately $90\%$ of the maximum activity $g_0$ ($\langle g\rangle =g_0$ for $\langle n\rangle =1$) at mid cycle as observed in the data (Fig. 3B).

Each of the three single parameter modulations fitted above predicts different dependency of ${\tau }_n$ on the mean occupancy $\langle n\rangle$ (Fig. S3B). Importantly, these values of ${\tau }_n$ were obtained for $k_{\text{elo}}=1.5$ kb/min (Garcia et al., 2013). A larger elongation rate would lead to smaller correlation times (Fukaya et al., 2017) (STAR methods, Effect of elongation rate on inference). The main benefit of using a potentially smaller elongation rate, it provides a stronger guarantee that the time-dependent solution reaches steady state in time (as the relaxation is slower). For each modulation (Fig. S3C), we estimated what fraction of the steady state value $\langle g\left(t\right)\rangle /\langle g\rangle$ is attained as a function of $\langle n\rangle$ at mid cycle ($t=7.5$ min). It turns out that the $k_{\text{off}}$ modulation clearly fails to reach steady state in time for higher occupancy, whereas both modulation of $k_{\text{on}}$ and $\langle n\rangle$ at fixed ${\tau }_n$ cover the measured range of activity at mid cycle ($0$ to $90\%$ of $g_0$). Each modulation predicts different boundary formation dynamics (Fig. S3D–F). For $k_{\text{on}}$, the highly expressed regions (large $\langle n\rangle$) relax much faster than the lowly expressed ones (small $\langle n\rangle$), whereas for $k_{\text{off}}$ it is the opposite. Interestingly, at fixed ${\tau }_n$, each position relaxes in synchrony and the activity ratio between them is conserved. The latter modulation appears more consistent with previous experimental observations (Dubuis et al., 2013; Garcia et al., 2013).

Next, we investigated the shape of the higher order time-dependent cumulants. Although the higher order time-dependent cumulants can be calculated from the moment equations, their analytical expressions are cumbersome. Alternatively, one can calculate the time-dependent cumulants directly from the time-dependent distribution of Pol II $P_t\left(g\right)$, which is easily computed numerically. With the same initial condition as the mean above, the time-dependent distribution of Pol II $P_t\left(g\right)$ is given by:

$$P_t\left(g\right)=\{\begin{array}{cc}\sum _n{P}_t(g,n|g\prime =0,n\prime =0)& t\le {\tau }_e\\ \sum _{n,n\prime }{P}_{{\tau }_e}\left(g,n\text{|}g\prime =0,n\prime \right)P_{t-{\tau }_e}\left(n\prime \text{|}n″=0\right)& t>{\tau }_e\end{array}$$

where $P_t(g,n|g\prime ,n\prime )$ is the propagator of the telegraph model (STAR Methods, Distribution of nascent transcripts, Eq. 13) and $P_t(n|n\prime )$ the propagator of the switching process alone:

$$P_t\left(n,n\prime \right)=\left({\delta }_{n1}\langle n\rangle +{\delta }_{n0}(1-\langle n\rangle )\right)\left(1-\text{ exp}\left(-t/{\tau }_n\right)\right)+{\delta }_{nn},\text{ exp}\left(-t/{\tau }_n\right)$$

We then computed the 2^nd, 3^rd and 4^th time-dependent cumulants from $P_t\left(g\right)$ for each fitted modulation (Fig. S3G). Provided the elapsed time is sufficiently large compared to the correlation time and the elongation time, the time-dependent cumulants closely follow the steady state solution. Thus, both the modulation of $k_{\text{on}}$ alone and $\langle n\rangle$ at fixed ${\tau }_n$ fitted assuming steady state predicts time-dependent mean versus cumulant curves at mid cycle ($t=7.5$ min) that are consistent with the data. In addition, under these conditions, the time-dependent mean activity closely reflect the time-dependent mean occupancy $\langle n\left(t\right)\rangle$:

$$\frac{\langle g(t)\rangle }{g_0}=\underset{\approx 1}{\underbrace{\frac{1+\frac{{\tau }_n}{{\tau }_e}\text{exp}\left(-t/{\tau }_n\right)\left(1-\text{ exp}\left({\tau }_e/{\tau }_n\right)\right)}{1-\text{ exp}\left(-t/{\tau }_n\right)}}}\langle n(t)\rangle t>{\tau }_e$$

Together it implies that even away from steady state, provided the elapsed time is sufficiently large ($t\gg {\tau }_e,{\tau }_n$), the inference based on steady state solutions should yield good estimates of the parameters. Indeed, for fixed ${\tau }_e$, the relationships between the mean and the cumulants at steady state are uniquely determined by $k_{\text{ini}}$, $\langle n\rangle$ and ${\tau }_n$. As long as time dependent-cumulants run along the steady state curves (Fig. S3G), the estimation of $k_{\text{ini}}$ and ${\tau }_n$ will be correct while the estimation of the mean occupancy will in fact corresponds to the instantaneous mean occupancy $\langle n\left(t\right)\rangle$ as $\langle g(t)\rangle /g_0\approx \langle n(t)\rangle$.

Inferring transcription kinetics of endogenous genes from dual color smFISH

Dual color smFISH and effective gene length

We performed dual-color smFISH tagging the 5’ and 3’ regions of the transcripts with different probe sets (Figure 4A, Table S1). After normalization in cytoplasmic units, both channels offer a consistent readout of the mean and the variability (Figure S4A,B). For each gene, given the 5’ and 3’ FISH probe configurations and assuming constant elongation rate, we calculated the expected ratio of 3’ over 5’ signal $r=C_1^{\left(3\right)}/C_1^{\left(5\right)}$ according to Eq. 4 using the annotated gene length (Fig. S4C–D, Table S3). The predicted ratios are consistent with the measured ones, albeit with small deviations likely stemming from termination (Fig. S4E). This suggests that nascent transcripts might be retained at transcription sites for a short duration. We then calculated for each gene, the effective length that would be consistent with the measured ratio (Fig. S4F, Table S3). Assuming an elongation rate $k_{\text{elo}}=1.5$ kb/min (Garcia et al., 2013), we estimated the lag consistent with the length difference between the effective and annotated length (Fig. S4F inset). Nascent transcripts remain at the loci for at most $35$ s, which remains small compared to the typical elongation time for the gap genes ${\tau }_e~2$ min. In this study, we used the effective elongation time for each gene that includes the short lingering time, which was calculated from the effective gene length.

The two channels enable estimation of the total nascent transcripts (5’ channel) and the fractional occupancy of transcripts along the 5’ and 3’ portions of the gene at each locus (Figure 4B,C). Because the 5’ and 3’ activities are temporally correlated through the elongation process additional information about transcription can be extracted that is not available with a single channel/color (Figure 4B,D). Combining measurements from multiple embryos (Figure 4C,D), we select nuclei at similar positions (bins of 2.5% egg length) to generate the joint distribution of 5’ and 3’ activity across AP position bins (Figure 4D).

Distribution of nascent transcripts

Modeling the joint distribution of 5’ and 3’ activity based on the two-state model requires first to calculate two key distributions, namely the steady-state distribution of nascent transcripts (or Pol II number) on the gene and the propagator that describes the temporal evolution of an arbitrary distribution of nascent transcripts. Both distributions can be derived from the master equation (Eq. 5). Although the master equation can be solved using generating functions (Xu et al., 2016), we followed another route that can be easily extended to multi-state system and remains computationally tractable. The master equation can be written in terms of an operator $\widehat{A}$ containing the propensity functions of the different reactions:

$$\frac{d}{dt}{P}_t\left(g,n\right)=\widehat{A}{P}_t\left(g,n\right)$$

After appropriate truncation on the transcript number (setting an upper bound for the maximum number of nascent transcripts) (Munsky and Khammash, 2006), the $\widehat{A}$ operator can be written in terms of a sum of tensor products of different matrices:

$$\widehat{A}=I_G\otimes N_2+K_G\otimes R_2$$ (Eq. 12)

with $I_G$ standing for the identity matrix of size $G+1$ where $G$ is the maximum number of transcripts after truncation. The matrix $N_2$ encodes the rates of the possible transitions for the two-state promoter and $R_2$ indicates in which promoter state initiation occurs:

$$N_2=\left[\begin{array}{cc}-k_{\text{on}}& k_{\text{off}}\\ k_{\text{on}}& -k_{\text{off}}\end{array}\right]R_2=\left[\begin{array}{cc}0& 0\\ 0& 1\end{array}\right]$$

while $K_G$ describes the initiation of transcripts:

$$K_G=\left[\begin{array}{cccc}-k_{\text{ini}}& 0& 0& 0\\ k_{\text{ini}}& \ddots & \ddots & 0\\ 0& \ddots & \ddots & 0\\ 0& 0& k_{\text{ini}}& -k_{\text{ini}}\end{array}\right]$$

The propagator of the resulting finite system can be expressed as a matrix exponential of the $\widehat{A}$ operator:

$$P_t\left(g,n\text{|}g\prime ,n\prime ,\theta \right)=\text{ exp}\left(\widehat{A}t\right)$$ (Eq. 13)

where $\theta$ stands for the set of kinetic parameters $(k_{\text{ini}},k_{\text{on}},k_{\text{off}})$. Although the propagator explicitly depends on the kinetic parameters, we chose to omit $\theta$ in the following for readability. The propagator dictates how an initial joint distribution of transcript and promoter state $P\left(g\prime ,n\prime \right)$ evolves after time $t$ in $P\left(g,n\right)$:

$$P\left(g,n\right)=\sum _{g\prime ,n\prime }{P}_t\left(g,n\text{|}g\prime ,n\prime \right)P\left(g\prime ,n\prime \right)$$

The distribution of nascent transcripts $P\left(g\right)$ for a gene of length $L_g$ is typically calculated using the propagator above with $t={\tau }_e\equiv L_g/k_{\text{elo}}$ the elongation time and the initial conditions. Since ${\tau }_e$ sets the ‘memory’ of the system, $P\left(g\right)$ can be calculated with initially zero nascent transcript on the gene and is then given by:

$$P\left(g\right)=\sum _{n,g\prime ,n\prime }{P}_{{\tau }_e}\left(g,n\text{|}g\prime ,n\prime \right){\delta }_{g\prime 0}P\left(n\prime \right)$$ (Eq. 14)

where $P\left(n\right)$ specifies the initial distribution of promoter state. The distribution $P\left(g\right)$ can be computed efficiently by directly estimating the action of the initial vector on the matrix exponential (Sidje, 1998). Assuming the promoter at steady state, $P\left(n\right)$ is then given by:

$$P\left(n\right)=\{\begin{array}{cc}\langle n\rangle & \text{for}n=1\\ 1-\langle n\rangle & \text{for}n=0\end{array}$$

with the mean occupancy $\langle n\rangle =k_{\text{on}}/\left(k_{\text{on}}+k_{\text{off}}\right)$.

Provided each gene copy is independent and undistinguishable, the combination of two and four gene copies can be represented by a three- and five-state promoter model. The corresponding $N$ and $R$ matrices are given by:

$$N_3=\left[\begin{array}{ccc}-2k_{\text{on}}& k_{\text{off}}& 0\\ 2k_{\text{on}}& -\left(k_{\text{off}}+k_{\text{on}}\right)& 2k_{\text{off}}\\ 0& k_{\text{on}}& -2k_{\text{off}}\end{array}\right]R_3=\left[\begin{array}{ccc}0& 0& 0\\ 0& 1& 0\\ 0& 0& 2\end{array}\right]$$

$$N_5=\left[\begin{array}{ccccc}-4k_{\text{on}}& k_{\text{off}}& 0& 0& 0\\ 4k_{\text{on}}& -\left(k_{\text{off}}+3k_{\text{on}}\right)& 2k_{\text{off}}& 0& 0\\ 0& 3k_{\text{on}}& -2\left(k_{\text{off}}+k_{\text{on}}\right)& 3k_{\text{off}}& 0\\ 0& 0& 2k_{\text{on}}& -\left(3k_{\text{off}}+k_{\text{on}}\right)& 4k_{\text{off}}\\ 0& 0& 0& k_{\text{on}}& -4k_{\text{off}}\end{array}\right]$$

$$R_5=\left[\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0\\ 0& 0& 2& 0& 0\\ 0& 0& 0& 3& 0\\ 0& 0& 0& 0& 4\end{array}\right]$$

The distribution of nascent transcripts is calculated according to Eq. 14, with the propagator $P_t\left(g,n\text{|}g\prime ,n\prime \right)$ computed from the updated $\widehat{A}$ operator (Eq. 12 & 13). The steady-state distribution of the $N_g$-gene copy system is given by:

$$P(n)=\left(\begin{array}{c}{N}_g\\ n\end{array}\right){\langle n\rangle }^n{(1-\langle n\rangle )}^{N_g-n}\text{ with }n\in \left\{0,1,2,\cdots ,N_g\right\}$$ (Eq. 15)

where $\langle n\rangle =k_{\text{on}}/\left(k_{\text{on}}+k_{\text{off}}\right)$ is the steady state mean occupancy of a single promoter.

Joint distribution of 5’ and 3’ activity

Here, we lay out the approach used to calculate the joint distribution of 5’ and 3’ activity for an arbitrary configuration of 5’ and 3’ FISH probes. Analytic solutions for steady-state distributions with idealistic single color probe configuration exist (Xu et al., 2016), but solutions for arbitrary probe configurations and multi-color FISH are cumbersome. Here, the computational approach is general enough and can be applied to a large class of transcription model, at or out of steady-state (transient relaxation), provided the elongation process is assumed deterministic.

The measured 5’ and 3’ transcriptional activities result from partially elongated nascent transcripts. Each fluorescent probe is assumed to be instantaneously bound and to contribute equally to the total fluorescence. Thus, the fluorescent signal of each nascent transcript is proportional to the number of probe binding regions that have been transcribed. In order to calculate the joint distribution, one needs to proceed backward in time. Starting from the 3’ end up to the 5’ end of the gene, we accumulate the contribution of nascent transcripts to the signal that could have been initiated in the interval separating two successive probe regions. Since we assumed elongation to occur at constant speed, the distance between two successive probe regions can be converted into a time. Doing so for each interval leads to the following temporal hierarchy (Fig. S4G). We used the following naming conventions for the durations $t_i^{\left(C\right)}$: the superscript $\left(C\right)\in \left\{\left(3\right),\left(5\right)\right\}$ stands for the probe channel, either $\left(3\right)$ for the 3’ probes (red channel) or $\left(5\right)$ for the 5’ probes (green channel), whereas the subscript $i$ denotes the interval separating probe $i$ from probe $i-1$ where increments are performed along the 3’ end to 5’ end direction.

For instance, if the 5’ and 3’ signal is measured at time $t={\tau }_e$, only transcripts initiated during the time interval $\left[0,t_1^{\left(3\right)}\right]$ fully contribute (1 C.U.) to the 3’ (red) signal, since only those get fully bound by 3’ FISH probes. On the other hand, transcripts initiated during $\left[t_1^{\left(3\right)},t_1^{\left(3\right)}+t_2^{\left(3\right)}\right]$ will contribute less to the signal since the last probe region has not yet been transcribed at the time of the measurement $t={\tau }_e$. Thus, the individual contribution of these transcripts to the total 3’ signal is $(k-1)/k$ C.U., where $k$ is the total number of probes for the 3’ channel. As we will see below, the probability to initiate $g$ nascent transcripts during any duration $t_i^{\left(C\right)}$ is given by the propagator $P_{t_i^{\left(C\right)}}\left(g,n\text{|}0,n\prime \right)$ (Eq. 13), where $n$ and $n\prime$ are the promoter states before and after $t_i^{\left(C\right)}$.

For any model of promoter activity that only consider the stochastic initiation of transcripts (as a Poisson process) and deterministic elongation with instantaneous release, the propagator will satisfy the following equality:

$$P_t\left(g,n\text{|}g\prime ,n\prime \right)=P_t\left(g-g\prime ,n\text{|}0,n\prime \right)$$

Thus, one only needs to calculate $P_t\left(g,n\text{|}0,n\prime \right)\equiv P_t\left(g,n\text{|}n\prime \right)$, which can be computed much faster than the matrix exponential (Eq. 13) (Sidje, 1998). It then follows that the Chapman-Kolmogorov equation for the time propagation reduces to a discrete convolution:

$$P_{t_2+t_1}\left(g_2,n_2\text{|}{n}_0\right)=\sum _{n_1}\sum _{g_1=0}^{g_2}{P}_{t_2}\left(g_2-g_1,n_2\text{|}{n}_1\right)P_{t_1}\text{(}{g}_1,n_1\text{|}{n}_0)$$

This property is used extensively in the following calculation of the joint distribution.

The computation of the joint distribution is performed according to a dynamic programming approach that can in principle be applied to an arbitrary number of color probes. We first calculate recursively the 3’ contribution (red probes) to the signal $P^{\left(3\right)}\left({\tilde{G}}_k,G_k,n_k\right)$, where ${\tilde{G}}_k$ stands for the total signal in probe space, $G_k$ the total number of nascent transcripts, $n_k$ the promoter state and $k$ the total number of probes covering the 3’ region. We then calculate the 5’ contribution in a similar fashion, $P^{\left(5\right)}\left({\tilde{G}}_k,n_0\right)$. Lastly, we combine both components to generate the final joint distribution $P\left({\tilde{G}}^{\left(5\right)},{\tilde{G}}^{\left(3\right)}\right)$ in probe space.

Step 1: calculate the 3’ contribution.

The initial distribution is given by:

$$\begin{gathered} P^{\left(3\right)}\left({\tilde{G}}_2,G_2,n_2\right)=P^{\left(3\right)}\left(\stackrel{{\tilde{G}}_2}{\overbrace{\left(k-1\right)g_2+k{g}_1}},\stackrel{G_2}{\overbrace{g_2+g_1}},n_2\right) \\ =\sum _{n_0,n_1}{P}_{t_2^{\left(3\right)}}\left(g_2,n_2\text{|}{n}_1\right)P_{t_1^{\left(3\right)}}\left(g_1,n_1\text{|}{n}_0\right)P\left(n_1\right)P\left(n_0\right) \end{gathered}$$

where $P\left(n_0\right)$ and $P\left(n_1\right)$ are the initial distributions of promoter state at time $t_0=0$ and $t_1^{\left(3\right)}$ respectively. Assuming promoters at steady state, both distributions are then given by Eq. 15 for a multi-gene system. We then perform the following recursion scheme for $i=\left\{3,\cdots ,k\right\}$:

$$P^{\left(3\right)}\left({\tilde{G}}_i,G_i,n_i\right)=\sum _{n_{i-1}}\sum _{g_i=0}^{g_{\text{max}}}{P}_{t_i^{\left(3\right)}}\left(g_i,n_i\text{|}{n}_{i-1}\right)P^{\left(3\right)}\left(\underset{{\tilde{G}}_{i-1}}{\underbrace{{\tilde{G}}_i-\left(k-i+1\right)g_i}},\underset{G_i}{\underbrace{G_i-g_i}},n_{i-1}\right)$$

where $g_{\text{max}}=\text{ min}\left(\lfloor {\tilde{G}}_i/\left(k-i+1\right)\rfloor ,G_i\right)$.

Step 2: calculate the 5’ contribution.

The initial distribution is given by:

$$P^{\left(5\right)}\left({\tilde{G}}_1,n_1|n_0\right)\equiv P^{\left(5\right)}\left(k{g}_1,n_1\text{|}{n}_0\right)=P_{t_1^{\left(5\right)}}\left(g_1,n_1|n_0\right)$$

We then perform the following recursion scheme for $i=\left\{2,\cdots ,k\right\}$:

$$P^{\left(5\right)}\left({\tilde{G}}_i,n_i|n_0\right)=\sum _{n_{i-1}}\sum _{g_i=0}^{g_{\text{max}}}{P}_{t_i^{\left(5\right)}}\left(g_i,n_i|n_{i-1}\right)P^{\left(5\right)}\left(\underset{{\tilde{G}}_{i-1}}{\underbrace{{\tilde{G}}_i-\left(k-i+1\right)g_i}},n_{i-1}|n_0\right)$$

where $g_{\text{max}}=\lfloor {\tilde{G}}_i/\left(k-i+1\right)\rfloor$. Lastly, we sum out $n_k$:

$$P^{\left(5\right)}\left({\tilde{G}}_k|n_0\right)=\sum _{n_k}{P}^{\left(5\right)}\left({\tilde{G}}_k,n_k|n_0\right)$$

Step 3: combine 3’ and 5’ contributions.

The final joint distribution of 5’ and 3’ activity in probe space is then given by:

$$P\left({\tilde{G}}^{\left(5\right)},{\tilde{G}}^{\left(3\right)}\right)=\sum _n\sum _{G=0}^{G_{\text{max}}}{P}^{\left(5\right)}\left({\tilde{G}}^{\left(5\right)}-kG|n\right)P^{\left(3\right)}\left({\tilde{G}}^{\left(3\right)},G,n\right)$$

where $G_{\text{max}}=\lfloor {\tilde{G}}^{\left(5\right)}/k\rfloor$. $P^{\left(3\right)}$ and $P^{\left(5\right)}$ are the joint distributions computed at step 1 and 2. Since the actual signal resolution is of the order of 1 cytoplasmic unit (a fully tagged transcript with $k$ fluorescent probes), the joint distribution can be coarse-grained by aggregating the states $\tilde{G}$ by a block of size $k$ corresponding to a single cytoplasmic unit. The coarse-grained distribution will be denoted $P\left(G^{\left(5\right)},G^{\left(3\right)}\right)$ in the following. In addition, it is possible to compute $P\left(G^{\left(5\right)},G^{\left(3\right)}\right)$ faster and with good accuracy using a reduced effective number of probes $k$, provided the original probe configuration is well approximated. Lastly, we remind the readers that $P\left(G^{\left(5\right)},G^{\left(3\right)}\right)$ implicitly depends on the kinetic parameters $(k_{\text{ini}},k_{\text{on}},k_{\text{off}})$ through the two-state model propagator, the elongation rate and the position of the probes through the temporal hierarchy (Fig. S4G).

Likelihood and inference

We modeled the joint distribution of 5’ and 3’ activity based on the two-state model and the exact probe location assuming steady state and constant Pol II elongation rate (Figure 4E; STAR Methods, Joint distribution of 5’ and 3’ activity). The resulting modeled activity distribution, together with the measurement noise model (Figure 2A; STAR Methods, Imaging noise model), enable calculating the likelihood of the 5’ and 3’ activities in C.U. (i.e. $\text{Data}$) given a set of kinetic parameters $(k_{\text{ini}},k_{\text{on}},k_{\text{off}})$. Specifically, the likelihood of the data $\text{Data}=\{S^{\left(5\right)},S^{\left(3\right)}\}$ given the parameters $\theta =(k_{\text{ini}},k_{\text{on}},k_{\text{off}})$ is expressed in terms of the measurement noise model $P\left(S^{\left(5\right)},S^{\left(3\right)}\text{|}{G}^{\left(5\right)},G^{\left(3\right)}\right)$ (Eq. 2) and the joint distribution $P\left(G^{\left(5\right)},G^{\left(3\right)}|\theta \right)$:

$$P\left(\text{Data|}\theta \right)={\displaystyle \prod }_{i=1}^{N_D}{\displaystyle \sum }_{G^{\left(5\right)},G^{\left(3\right)}}P\left(S_i^{\left(5\right)},S_i^{\left(3\right)}\text{|}{G}^{\left(5\right)},G^{\left(3\right)}\right)P\left(G^{\left(5\right)},G^{\left(3\right)}|\theta \right)$$

where $N_D$ is the total amount of data, i.e. the total number of measured nuclei per AP-bin for a given gene.

The general idea underlying “classical” inference is to maximize the probability of the data under some model, namely to find the parameters $(k_{\text{ini}},k_{\text{on}},k_{\text{off}})$ that maximize the likelihood of the data $P\left(\text{Data}|k_{\text{ini}},k_{\text{on}},k_{\text{off}}\right)$. In this manuscript we adopted a Bayesian approach, estimating the probability of the kinetic rate parameters of the two-state model given the observed data (i.e. the joint posterior distribution) $P\left(k_{\text{ini}},k_{\text{on}},k_{\text{off}}|\text{Data}\right)$ using Bayes’ rule:

$$P\left(k_{\text{ini}},k_{\text{on}},k_{\text{off}}\text{|Data}\right)=\frac{P\left(\text{Data|}{k}_{\text{ini}},k_{\text{on}},k_{\text{off}}\right)P\left(k_{\text{ini}},k_{\text{on}},k_{\text{off}}\right)}{P\left(\text{Data}\right)\equiv \int P\left(\text{Data|}{k}_{\text{ini}},k_{\text{on}},k_{\text{off}}\right)P\left(k_{\text{ini}},k_{\text{on}},k_{\text{off}}\right)d{k}_{\text{ini}}d{k}_{\text{on}}d{k}_{\text{off}}}$$

where $P(k_{\text{ini}},k_{\text{on}},k_{\text{off}})$ is the prior that encodes for prior knowledge about the parameter values. We used a non-informative and independent prior for each kinetic parameter, which was chosen as log-uniform $P\left(k_{\text{ini}},k_{\text{on}},k_{\text{off}}\right)=1/(k_{\text{ini}}\bullet k_{\text{on}}\bullet k_{\text{off}})$. Note that in absence of a prior $P(k_{\text{ini}},k_{\text{on}},k_{\text{off}})$, the most likely parameters are the ones that maximize $P\left(\text{Data}|k_{\text{ini}},k_{\text{on}},k_{\text{off}}\right)$. In that case, the Bayesian approach is essentially equivalent to “classical” maximum likelihood. The main advantage of the Bayesian approach over maximum likelihood is that it provides a natural way to estimate the uncertainty on the parameters through the joint posterior and allows us to determine whether the parameters are identifiable. Indeed, as the uncertainty grows, the posterior distribution becomes wider/flatter, which directly reflects on the range of the parameter confidence intervals.

Importantly, we set the elongation rate $k_{\text{elo}}$ to the experimentally measured value of $1.5$ kb/min (Garcia et al., 2013). At steady state, a known value of $k_{\text{elo}}$ is required to set the temporal scale of the other transcriptional parameters, which can be seen by inspecting the expressions of the various cumulants of the nascent transcript distribution (Eq. 9, 10 & 11). Since all cumulants can be parameterized by the three independent parameters $g_0=k_{\text{ini}}/k_{\text{elo}}$, $\langle n\rangle =k_{\text{on}}/\left(k_{\text{on}}+k_{\text{off}}\right)$ and the ratio ${\tau }_e/{\tau }_n=\left(k_{\text{on}}+k_{\text{off}}\right)/k_{\text{elo}}$, it follows that the model is not identifiable when the temporal scale is not set.

We then sampled the joint posterior distribution $P\left(k_{\text{ini}},k_{\text{on}},k_{\text{off}}|\text{Data}\right)$ using a Markov chain Monte Carlo (MCMC) algorithm (Hastings, 1970), for each gene and at each AP position individually. The sampled joint posterior distribution enables estimation of the marginal posterior distribution for each kinetic rate and any combination of these rates, such as $\langle n\rangle$ and ${\tau }_n$. All the parameters of the model and the error bars were estimated from the marginal posterior distribution, as the median and the percentiles respectively (Figure 4E). The best-fitting distributions predicted by the model match the data closely (Fig. S5B), and outliers are mainly explained by measurement and binning noise. Importantly, our inference approach does not require any a priori assumptions about the underlying parameter modulation, nor does it assume any continuity between datasets. In principle, the inferred parameters could be different for each gene and be modulated in any arbitrary way.

Parameter identifiability and performance

As mentioned above, the two-state model is fully identifiable (structural identifiability) as long as $k_{\text{elo}}$ is fixed. Indeed, in that case the steady state and time-dependent solution depend on three independent parameters, such as $(k_{\text{ini}},k_{\text{on}},k_{\text{off}})$ or $\left(k_{\text{ini}},\langle n\rangle ,{\tau }_n\right)$. In principle, provided one has enough data and measurement noise is small, each parameter can be resolved individually. On the other hand, it is true that some regimes might require a very large/infinite amount of data to infer the different parameters without ambiguity (practical identifiability). For instance, in the case of instantaneous bursts, namely when $k_{\text{off}}$ and $k_{\text{ini}}$ become large (i.e. approach infinity, but with finite ratio), only the burst size $b=k_{\text{ini}}/k_{\text{off}}$ and the burst frequency $f=k_{\text{on}}$ are well defined. Thus it is not possible to infer the exact values of $k_{\text{ini}}$ and $k_{\text{off}}$ individually. Such a scenario can be clearly diagnosed based on the marginal posterior distributions $P\left(k_{\text{ini}}|\text{Data}\right)$ and $P\left(k_{\text{off}}|\text{Data}\right)$ (from which the median and the error bars of the parameters are estimated). Indeed, since we used non-informative priors, the variance of these marginal posterior distributions would become extremely large and thus less informative. More intuitively, $k_{\text{ini}}$ and $k_{\text{off}}$ would no longer be sharply peaked around a mean value, but would take all possible values (consistent with the prior) that satisfy $b=k_{\text{ini}}/k_{\text{off}}\pm$ some error on $b$. This would consequently lead to to very large error bars on $k_{\text{ini}}$ and $k_{\text{off}}$. Thus, the error bars extracted from the marginal posterior distribution are indicative for whether or not we can estimate these parameters.

To validate our inference framework, we tested the inference on simulated data using a broad range of parameter values and in presence of measurement noise. Using the Gillespie algorithm (Gillespie, 1977), we generated simulated nuclei activity data based on 4 independent gene copies modeled by the telegraph model. We used the probe configuration and gene length of hb and assumed a typical elongation rate of $1.5$ kb/min (Garcia et al., 2013). Measurement noise was included in the simulated data according to the characterization performed previously on real data (Imaging noise model). We investigated different parameter regimes and modulation schemes of the mean activity $\langle g\rangle$, to test whether the input parameters used to generate the data could be inferred properly (Fig. S6A–E). Namely, we tested:

1. Modulation of the initiation rate $k_{\text{ini}}$ alone with ${\tau }_n=2$ min and $\langle n\rangle =0.35$ (cyan dash line).

2. Modulation of the on-rate $k_{\text{on}}$ alone with $k_{\text{ini}}=7$ min⁻¹ and $k_{\text{off}}=0.25$ min⁻¹ (green dash line).

3. Modulation of the off-rate $k_{\text{off}}$ alone with $k_{\text{ini}}=7$ min⁻¹ and $k_{\text{on}}=0.25$ min⁻¹ (blue dash line).

4. Modulation of the mean occupancy $\langle n\rangle$ alone with $k_{\text{ini}}=7$ min⁻¹ and ${\tau }_n=2$ min (red dash line).

For each scenario, we generated 8 batches of data covering the range of normalized activity $\langle g\rangle /g_0$. Each batch was made of 10 independently sampled datasets of 500 nuclei activity measurements. We performed the inference on each dataset individually and reported the mixture of posterior distribution over the 10 datasets to take into account the finite size variability in the generated data. We conclude that the inference framework performs well, since all the inferred quantities cover the true values within error bars. In addition, we estimated globally for all synthetic data the fractional inference error $\left|{\theta }_{\text{inf}}-{\theta }_{\text{true}}\right|/{\theta }_{\text{true}}$ from the MCMC sampled parameters ${\theta }_{\text{inf}}$. For all inferred parameters, the median of the error never exceeds $20\%$ (S6F). Overall, the inference allows us to distinguish the different tested modulation strategies without ambiguities. In addition, the sampled joint posterior distributions $P\left(k_{\text{ini}},k_{\text{on}},k_{\text{off}}|\text{Data}\right)$ are clearly peaked in the parameter space (S5C), indicating that practical identifiability is not an issue with real data.

Effect of elongation rate on inference

As discussed above, the elongation rate $k_{\text{elo}}$ sets the temporal scale of the transcriptional parameters, thus a different elongation rate would lead to different values of the parameters. In the manuscript, we used a value of $k_{\text{elo}}=1.5$ kb/min which we previously measured (Garcia et al., 2013). A recent study suggests that this value might be overall larger in the blastoderm embryo, of the order of $2.5$ kb/min (Fukaya et al., 2017). We thus sought to determine to which extent this new value would affect our results.

In principle, a different value of $k_{\text{elo}}$ rescales the transcriptional parameters in a very predictable way. No matter the elongation rate, the three quantities $k_{\text{ini}}$, $\langle n\rangle$ and ${\tau }_n$ should be perfectly identifiable. It follows that the new parameters (denoted by the * superscript) have to satisfy the following equations:

$$k_{\text{ini}}\frac{k_{\text{elo}}^{*}}{k_{\text{elo}}}=k_{\text{ini}}^{*}$$

$$\langle n\rangle ={\langle n\rangle }^{*}$$

$${\tau }_n\frac{k_{\text{elo}}}{k_{\text{elo}}^{*}}={\tau }_n^{*}$$

Inferring the transcriptional parameters from the data with $k_{\text{elo}}=2.5$ kb/min instead of $k_{\text{elo}}=1.5$ kb/min (as in the main text) confirms the rescaling above (Fig. S6L–N). As predicted, $k_{\text{ini}}$ and $k_{\text{ini}}$ are rescaled by a factor $2.5/1.5=1.67$ and $1.5/2.5=0.6$ respectively, whereas $\langle n\rangle$ is conserved.

QUANTIFICATION AND STATISTICAL ANALYSIS

We imaged hunchback wild-type (labeled hb wt) in $N=18$ embryos; a hunchback deficiency fly line with half the hb dosage (hb def) $N=7$; Krüppel (Kr) $N=11$; knirps during early (kni early) $N=14$ and late nc13 (kni late) $N=16$; giant females with two alleles (gt female) $N=20$ and giant males with one allele (gt male) $N=16$. On average the number of quantified nuclei per AP bin (2.5% egg length) is $n=499$ (hb wt), $n=157$ (hb def), $n=270$ (Kr), $n=354$ (kni early), $n=302$ (kni late), $n=397$ (gt female anterior region), $n=387$ (gt female posterior region), $n=310$ (gt male anterior region) and $n=277$ (gt male posterior region). The confidence intervals for all point estimators of the data (mean, variance, noise, third cumulant and fourth cumulant; Figures 1, 2 and 3) were built by bootstrapping the empirical distribution of activity in each individual embryo. We used the 68% confidence intervals for the point estimators. All the error bars for the inferred parameters (Figure 5) correspond to the 10 to 90^th percentiles of the marginal posterior distributions.

Supplementary Material

fs1

Figure S1: Temporal staging, measurement error and embryo-to-embryo variability, Related to Figure 1 and Figure 2. (A) Cytoplasmic mRNA density as a function of developmental stage during the 13^th interphase as estimated from DAPI staining by eye-inspection. Each data point corresponds to a single embryo; cytoplasmic density was measured for each gene in the maximally expressed spatial region along the AP axis. Good correlation between manual ranking and the cytoplasmic mRNA accumulation correlation justifies the latter as a convenient proxy for time, and thus the developmental age of the embryos within nuclear cycle 13.

(B) Mean activity in the maximally expressed regions as a function of the cytoplasmic mRNA density. Each data point corresponds to a single embryo. Color code as in Figure 1C.

(C) Pearson correlation coefficient ρ between the mean activity and the cytoplasmic mRNA density calculated over the population of embryos in (B). Values indicate that up to 44% (${\rho }^2$) of the variance in mean activity across embryos can be explained by staging uncertainty. The large correlation for kni (dark green) led to splitting the population of kni stained embryos into early and late stages to minimize the staging uncertainty in each subpopulation. We performed the splitting by finding the cytoplasmic density threshold that minimizes the sum of within-population variance in mean activity.

(D) Staging variability ${\sigma }_{\text{sta}}$ in percent of the total mean activity $\mu$ for each gene in the respective maximally expressed regions. The staging variability corresponds to the variability in mean activity among embryos, which is explained by staging uncertainty between early and late embryo as estimated from cytoplasmic mRNA density. The staging variability ${\sigma }_{\text{sta}}$ is defined as ${\sigma }_{\text{sta}}=\rho {\sigma }_{\mu }$, where ${\sigma }_{\mu }$ is the standard deviation of the mean activity across embryos. Note that the splitting of kni stained embryos into early and late stages was justified as the staging variability is significantly reduced. The overall small staging variability, which never exceeds 14%, indicates that the mean activity is sufficiently stable in time to warrant a steady state assumption.

(E) Modeled imaging noise (CV) as a function of the mean activity for both channels. The imaging noise model was built from dual-color smFISH data using an alternating probe configuration (see Figure 2A). Imaging error ${\sigma }_{\text{img}}$ was determined from the spread along the regression line between both channels (STAR Methods). Errors were assumed normally distributed, independent, and of equal magnitude in both channels. Thus, the modeled imaging error ${\sigma }_{\text{img}}$ is characterized as the orthogonal spread along the fitted regression line, which was parameterized as ${\sigma }_{\text{img}}\left(v\right)=\sqrt{{\sigma }_b^2+b_{1}v+b_2{v}^2}$, where (${\sigma }_b^2,b_1,b_2$) are fit parameters, and $v$ is the scalar projection of each data point onto the regression line. After fitting, the modeled imaging noise (CV) is given by ${\sigma }_{\text{img}}\left(v\right)/\mu$ with $v=\sqrt{{\mu }^2+{\left(a\mu \right)}^2}$ for the green channel (green line) and $v=\sqrt{{\mu }^2+{(\mu /a)}^2}$ for the red channel (red line), where $a$ is the slope of the fitted line and $\mu$ is the mean activity.

(F) Variability of the mean across embryos (CV²) as a function of alignment noise. Each data point corresponds to a single AP bin (2.5% egg length). The diagonal dashed line (slope $=1$) highlights the correlation between the two quantities at the boundaries while the horizontal dash line corresponds to the embryo variability in the maximally expressed regions for each gene (Figure 2E). The correlation indicates that most variability across embryos in the transition regions can be explained by alignment noise, whereas the remaining variability in the maximally expressed regions reflects staging variability (Figure S1C–D) and other extrinsic noise sources.

(G) Fraction of the total variance ${\sigma }^2$ corresponding to the measurement variance as a function of the AP position. Measurement variability ${\sigma }_{\text{mea}}^2$ is defined as the combination of imaging ${\sigma }_{\text{img}}^2$ and alignment variability ${\sigma }_{\text{ali}}^2$. The solid and dashed vertical lines are the overall mean fraction across genes and the 68% confidence interval, respectively.

(H) Fraction of the total variance ${\sigma }^2$ corresponding to the non-nuclear variance as a function of the AP position. The non-nuclear variance is the sum of the imaging ${\sigma }_{\text{img}}^2$, the alignment ${\sigma }_{\text{ali}}^2$ and embryo variability ${\sigma }_{\text{emb}}^2$. The remaining variance ${\sigma }_{\text{nuc}}^2={\sigma }^2-{\sigma }_{\text{img}}^2-{\sigma }_{\text{ali}}^2-{\sigma }_{\text{emb}}^2$ is defined as the nuclear variance and is deemed intrinsic to transcription. Overall, the nuclear variance largely predominates as it represents 84% of the total variance, on average. The solid and dashed vertical lines are the overall mean fraction across genes and the 68% confidence interval. Color code as in Figure 1C.

All error bars are the 68% confidence intervals.

fs2

Figure S2: Mean-cumulant activity relationships for a single gene copy, Related to Figure 3. (A–D) The mean and the cumulants were corrected for different gene length, probe configuration and copy number. Each data point corresponds to a single AP bin and the error bars are the 68% confidence intervals. The dashed line stands for the Poisson background. Color code as in Figure 1C.

(A) Estimation of the maximal activity $g_0$ by fitting a 2^nd order polynomial of the mean activity to the variance. The maximal activity $g_0$ is determined as the second intercept of the fit with the Poisson background (vertical dashed line). In Figures 3B–D and S2B–D the mean and the cumulants are normalized by the respective powers of $g_0$. Notably, $\langle g\rangle /g_0=\langle n\rangle$ for constant $k_{\text{ini}}$.

(B–D) Normalized cumulants as a function of normalized mean activity. The solid lines are 2^nd (B), 3^rd(C) and 4^th (D) order polynomial fits, respectively. Fits were performed for each gene independently (colored lines); black line corresponds to the global fit of all genes (Figure 3B–D). Individual fits are qualitatively similar, suggesting global trends in the data. (E) Steady state two-state model cumulants as a function of the mean occupancy $\langle g\rangle /g_0=\langle n\rangle$ for different scenarios of single parameter modulation (modulation of $\langle n\rangle$ through either $k_{\text{on}}$ or $k_{\text{off}}$ alone, or modulation of $\langle n\rangle$ at fixed correlation time ${\tau }_n$ by changing both $k_{\text{on}}$ and $k_{\text{off}}$; Figure 3G–I). For each considered modulation, only a single parameter is free since the value of $g_0$ (determined from A) has been fixed and the initiation rate $k_{\text{ini}}$ is assumed constant. Varying the free parameters (graded colored lines) mainly affects the amplitude of the cumulants. The solid black lines stand for the common maximal amplitude limit attained when the correlation time goes to infinity.

fs3

Figure S3: Time-dependent cumulant analysis, Related to Figure 3. All time dependent-solutions of the two-state model were calculated with initial conditions $g\left(t=0\right)=0$ (no Pol II on the gene) and $n\left(t=0\right)=0$ (gene initially in the ‘off’ state).

(A) Time-dependent mean activity $\langle g\left(t\right)\rangle$ normalized by its steady state value $\langle g\left(t\to \infty \right)\rangle \equiv \langle g\rangle$ at three different times ($t=2.5$ min, $t=5$ min and $t=7.5$ min) as a function of the switching correlation time ${\tau }_n$. At steady state, the ratio is thus equal to one (horizontal dashed line). The correlation time is the only parameter that affects the relaxation to steady state. As ${\tau }_n$ increases, the relaxation becomes slower. For $t=7.5$ min, a correlation time no larger than 3 min is required to reach approximately 90% of the maximal activity as observed in the data (Figure 3B).

(B) Correlation time ${\tau }_n$ as a function of the mean occupancy $\langle n\rangle$ for each best-fit single parameter modulation (from Figure 3G–I). Modulation of koff alone predicts a correlation time that is too large (${\tau }_n\gg 3$ min) at high $\langle n\rangle$ to reach the maximal activity of the data at mid cycle ($7.5$ min).

(C) Time-dependent relative activity as a function of the mean occupancy $\langle n\rangle$ for each best-fit single parameter modulation (as in Figure 3G–I). Same color code as in (B). The relative activity was calculated as the mean activity $\langle g\left(t\right)\rangle$ at $t=7.5$ min normalized by its steady state value $\langle g\rangle$. Modulation of $k_{\text{off}}$ alone clearly fails to reach steady state in time at high $\langle n\rangle$, as it only reaches 40% of the maximal activity. On the other hand, both modulation of $k_{\text{on}}$ alone and of $\langle n\rangle$ at fixed ${\tau }_n$ reach a sufficiently large maximal activity to explain the data (100% and 88%, respectively).

(D–F) Normalized time-dependent mean activity $\langle g\left(t\right)\rangle /g_0$ as a function of time for each best-fit single parameter modulation (as in Figure 3G–I). The circles correspond to the maximal attainable activity ($\langle n\rangle =1$) after $t=2.5,5$ and $7.5$ min (vertical dashed lines). Each modulation predicts different dynamics for boundary formation; for $k_{\text{on}}$ modulation high $\langle n\rangle$ regions relax faster than low $\langle n\rangle$ regions (D), while it is the opposite for $k_{\text{off}}$ (E). For fixed ${\tau }_n$, all regions relax in synchrony independently of $\langle n\rangle$ (F). In the latter case, during interphase 13 the ratio of any two curves is constant in time, and thus these ratios are conserved across the patterning boundaries, which are uniquely determined by $\langle n\rangle$.

(G) Normalized time-dependent cumulants as a function of the normalized time-dependent mean activity for each best-fit single parameter modulation. The solid black lines correspond to the steady state best fits in Figure 3G–I. The data in gray are identical to Figure 3B–D and the error bars are given by the 68% confidence intervals. For sufficiently large t (i.e. ${t>\{\tau }_n,{\tau }_e\}$), the time-dependent mean and cumulant relationships closely follow the steady state ones. In addition, at fixed elongation time ${\tau }_e$, the set of steady state cumulants are uniquely determined by $k_{\text{ini}}$, $\langle n\rangle$ and ${\tau }_n$. Together, these two observations imply that even when far from steady state, fitting the steady state cumulants would still provide good estimates of the parameters, except that the estimated $\langle n\rangle$ would instead corresponds to the instantaneous mean occupancy $\langle n\left(t\right)\rangle \approx \langle g\left(t\right)\rangle /g_0$ (STAR Methods).

fs4

Figure S4: Link between signal properties from dual-color smFISH and probe configuration for each gene, Related to Figure 4. (A) Mean 3’ versus 5’ activity for all gap genes. Each data point corresponds to the mean activity over all embryos in a single AP bin. The slopes for the different genes depend on the exact probe configuration. Error bars are the 68% confidence intervals.

(B) 3’ versus 5’ noise (CV). The excellent correlation and the slope close to one suggest that the switching correlation time ${\tau }_n$ is on the order of the elongation time ${\tau }_e$. Indeed, if ${\tau }_n<{\tau }_e$, one would have expected more buffering of the switching noise on the 5’ end compared to the 3’ end, whereas if ${\tau }_n\gtrsim {\tau }_e$ the magnitude of the noise should be similar on both ends. Error bars as in (A).

(C) Cumulative hb probe contribution to the fluorescence signal as a function of transcript length. The vertical dashed line corresponds to the length of a cytoplasmic mRNA for hb (3635 bp). Transcripts whose length is larger than 2667 bp would contribute as 1 cytoplasmic unit in both channels.

(D) Activity ratio (mean 3’ signal over mean 5’ signal) as a function of gene length for hb (blue line). Assuming elongation to occur at constant speed and instantaneous release of transcripts, the ratio is fully determined by the probes’ location and the gene length (transcribed region). The activity ratio results from the ratio of the integrals of the cumulative probe contribution in Figure C.

(E) Activity ratio for each gene. The circles stand for the measured ratio with error bars (both standard errors and standard deviations are shown) obtained from the propagation of the normalization errors in both channels for all embryos. The crosses correspond to the predicted ratio based on the annotated gene length. The squares are derived from Pol2 occupancy data (Pol2-ChIP; Blythe & Wieschaus, 2015). For Kr, kni and gt, Pol2 signal is found a few hundreds bp away from the annotated length suggesting extra processing related to termination. Similarly, the larger measured ratios (compared to the predicted ones based on annotated gene length (crosses)) likely reflect retention of nascent transcripts at the loci due to termination.

(F) Effective gene length for each gene as determined from the activity ratio. Symbols and error bars as in (E). Assuming an elongation speed of $1.5$ kb/min, the difference between the effective and annotated gene length can be translated in time (inset). The lag or extra residence time of transcripts at the loci is at most $35$ seconds.

(G) Temporal hierarchy used to calculate the 5’ and 3’ joint distribution of transcriptional activities. The measured signal result from partially tagged nascent transcripts and is proportional to the number of probe binding regions that have been transcribed. In order to calculate the joint distribution, we accumulate the distinct contribution of nascent transcripts, between each probe region, from the 3’ end up to the 5’ end of the gene. At constant elongation rate, the distance separating each successive probe region is converted into a time $t_i^{\left(C\right)}$, where the superscript $\left(C\right)\in \left\{\left(3\right),\left(5\right)\right\}$ stands for the probe channel and the subscript $i$ denotes the interval separating probe $i$ from probe $i-1$ (from the 3’ end to 5’ end direction). The joint distribution of activity is obtained by subsequent convolution of the distribution of Pol II initiated during each time $t_i^{\left(C\right)}$. Each of these convolutions are properly weighted to take into account the proper contribution of each probe region to the activity.

fs5

Figure S5: Parameter inference from dual-color smFISH activity distribution using the two-state model, Related to Figure 4. (A–B) The data correspond to the measured distribution of 3’ versus 5’ activity across AP position for hb. Data distributions were constructed based on the 2.5%-AP-bins defined in Figure 4C. Dashed black line represents the expected ratio of 3’ versus 5’ activity ($r=0.57$ for hb); black circle corresponds to the mean of the distribution and lies on the dashed line.

(A) Qualitative change of the distribution predicted by the 2-state model as the parameters vary for AP-bin at $x/L=38.6\%$ (top row) and at $x/L=48.9\%$ (bottom row). Changes in the transcriptional parameters $k_{\text{ini}},k_{\text{on}},k_{\text{off}}$, and in $\langle n\rangle$ at fixed ${\tau }_n$ set at the same mean activity $\langle g\rangle$ as in the data leads to qualitatively different distributions. Thus, all information regarding the kinetic parameters is contained in the distribution of 3’ versus 5’ activity, which enables inference of these rates.

(B) Side by side representation of the empirical (data, top row) and modeled (bottom row) distributions with best-fit parameters for different AP bins. The empirical distributions are used as input in our inference framework enabling precise inference of the underlying transcriptional kinetics at each AP position. Of note, the displayed modeled distributions are devoid of measurement noise and represent the theoretical output of the two-state model given the probe-set configuration and the effective elongation time. Thus, the likelihood of the data is essentially the convolution of the activity distribution calculated from the two-state model with the noise measurement distribution. Overall, the best-fit distributions reproduced the data well.

(C) Joint posterior distribution of the parameters given the data in (B) for each AP position. These distributions are generated as the output of our inference framework, namely we sampled the posterior distributions calculated from the likelihood according to Bayes’ rule using a Markov chain Monte Carlo (MCMC) algorithm. As the joint posterior distributions are highly peaked in the parameter space, it indicates that the parameters of the model are identifiable for all AP positions. The optimal kinetic rates $k_{\text{ini}},k_{\text{on}}$ and $k_{\text{off}}$, which were used to generate the modeled distribution in (B), are estimated from these joint posteriors as the median of the marginal posterior distributions.

fs6

Figure S6: Validation of the inference framework for dual-color smFISH and synthesis rates, Related to Figure 4 and Figure 5. (A-F) We simulated synthetic 3’ and 5’ nuclear activity data based on four gene copies (two alleles with two sister chromatids each) modeled by a two-state model with measurement noise, using the probe configuration for hb. To test the performance of our inference, we generated four different datasets by modulating the mean input activity $\langle g\rangle$ in the data through: 1) initiation rate $k_{\text{ini}}$ alone (cyan), 2) on-rate $k_{\text{on}}$ alone (green), 3) off-rate $k_{\text{off}}$ alone (blue) and the mean occupancy $\langle n\rangle$ at constant switching correlation time ${\tau }_n$ (red). The constant $g_0$ corresponds to the maximal activity for each dataset, defined as $g_0=\text{max}\left(k_{\text{ini}}\right){\tau }_e$, where the maximum is taken over the dataset when $k_{\text{ini}}$ varies (cyan) and ${\tau }_e$ is the elongation time. Importantly, the inference of the kinetic parameters was performed for each sub-dataset independently (individual circles; 500 nuclei), without assuming any continuity in the dataset. To take into account finite size sampling variation in the data, we inferred parameters on 10 replicates for each synthetic dataset. Thus, the estimated posterior distributions are aggregated over all replicates.

(A-E) Inferred kinetic rates $k_{\text{ini}}$ (A), $k_{\text{on}}$ (B), and $k_{\text{off}}$ (C), mean occupancy $\langle n\rangle =k_{\text{on}}/\left(k_{\text{on}}+k_{\text{off}}\right)$ (D) and switching correlation time ${\tau }_n=1/(k_{\text{on}}+k_{\text{off}})$ (E) as a function of the mean input activity $\langle g\rangle /g_0$. All quantities are estimated from the sampled joint posterior distribution of the kinetic rates. Colored circles stand for the inferred parameters as a function of input activity, i.e. the median of the marginal posterior distribution. Error bars correspond to the 10 and 90^th percentiles of the posterior distribution. The colored dashed lines represent the input (true) parameters used to simulate the data.

(F) Global relative inference error $\left|{\theta }_{\text{inf}}-{\theta }_{\text{true}}\right|/{\theta }_{\text{true}}$ calculated for each parameter $\theta$. These errors are estimated over all synthetic datasets and replicates and correspond to the median with error bars given by the 68% confidence intervals. Notably, $k_{\text{ini}}$ and $\langle n\rangle$ are easier to infer than the switching rates $k_{\text{on}}$ and $k_{\text{off}}$ or the correlation time ${\tau }_n$, which have more subtle effect on the shape of the activity distribution. Still, the inference is able to distinguish between small differences in parameter modulation. Overall, the errors remain small, as the medians of the inference errors never exceed 20% of the true values.

(G–J) Four first cumulants of data (unnormalized, in cytoplasmic units) as a function of the ones predicted by the two state-model with best fitting parameters for multiple gene copies ($N_g=\mathrm{2,4}$). Each data point corresponds to a single AP-bin. Error bars are the 68% confidence intervals. Overall, the slopes close to one and the large $R^2$ indicate that the model captures the first four cumulants of data well. Color code as in Figure 1C.

(K) Inferred mean synthesis rate $k_{\text{ini}}\langle n\rangle$ as a function of the mean occupancy $\langle n\rangle$ for all genes. Modulation of transcript mean synthesis rate across boundaries is fully determined by the mean occupancy. Color code as in Figure 1C. All error bars correspond to the 10 and 90^th percentiles of the posterior distribution.

(L-N) Comparison of the inferred transcriptional parameters $k_{\text{ini}}$, $\langle n\rangle$ and ${\tau }_n$ assuming two different elongation speeds $k_{\text{elo}}$ (1.5 kb/min vs. 2.5 kb/min). Both $k_{\text{ini}}$ and ${\tau }_n$ are rescaled while $\langle n\rangle$. remains the same. Thus, our results are unaffected by the exact value of $k_{\text{elo}}$; it only leads to a rescaling of the inferred parameters that have time units. Color code and error bars as in (K).

(O) Comparison of the estimated mean synthesis rate for a single gene copy of endogenous hb (wt and deficient) and the synthetic hb P2 reporter live-imaged by Garcia et al. (2013) during interphase 13. The reporter corresponds to a minimal version of the hb gene that is driven by the P2 promoter and the P2 (proximal) enhancer alone. The mean synthesis rate of the P2 reporter was obtained by multiplying the estimated effective initiation rate and the fraction of active nuclei divided by two (two sister chromatids per locus), as reported in Garcia et al. (2013). Excluding the posterior region ($x/L>0.45$), where the reporter shows ectopic expression, the estimated mean synthesis rates only differ by approximately 30 to 50%. This difference, in the case of the reporter, likely stems from both larger live-imaging measurement and calibration errors, and potentially reflects different expression rates between the endogenous gene and the synthetic reporter. Nevertheless, the reported synthesis rates estimated through different models and techniques are consistent. Error bars as in (K) except for the hb P2 reporter which are standard errors over multiple embryos.

ts1

Supplemental Table S1: Oligonucleotide sequences of smFISH probes used in this study, Related to STAR Methods.

ts2ts3

Supplemental Table S2: Conversion factors used to convert the k^th cumulants from cytoplasmic units to Pol II counts, Related to STAR Methods. The conversion factors were calculated according to Eq. 4 for each gene and two different configurations of probe locations (5’ and 3’ regions), using the effective gene length (see Table S3).

Supplemental Table S3: Gene length for the gap genes, Related to STAR Methods. The annotated gene length was obtained from UCSC Genome Browser (BDGP Release 6 + ISO1 MT/dm6) Assembly. The length estimated from Pol II ChIP density profiles is longer overall, suggesting that Pol II might be transcribing a few hundreds base pairs downstream during termination (Blythe and Wieschaus, 2015). We estimated an effective gene length from the ratio of 5’ and 3’ activity measurements assuming a constant elongation rate. Overall, the effective length is larger than the annotated one and consistent with the Pol II profiles, suggesting that transcripts might be retained at the loci for a short amount of time.

KEY RESOURCE TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Experimental Models: Organisms/Strains
D. melanogaster: Oregon-R, wild-type laboratory stock		Flybase: FBst1000077
D. melanogaster: chromosomal deletion spanning hb w[1118]; Df(3R)BSC477/TM6C, Sb[1] cu[1]	Bloomington Drosophila Stock Center	Flybase: FBab0045343 BDSC: 24981
Oligonucleotides
smFISH probes for hb, see Table S1	This paper	N/A
smFISH probes for Kr, see Table S1	This paper	N/A
smFISH probes for kni, see Table S1	This paper	N/A
smFISH probes for gt, see Table S1	This paper	N/A
Software and Algorithms
FiSH Toolbox	Little et al. (2013)	N/A