Unexpected Predictors of Antibiotic Resistance in Housekeeping Genes of Staphylococcus Aureus

Abstract

Methicillin-resistant Staphylococcus aureus (MRSA) is currently the most commonly identified antibiotic-resistant pathogen in US hospitals. Resistance to methicillin is carried by SCCmec genetic elements. Multilocus sequence typing (MLST) covers internal fragments of seven housekeeping genes of S. aureus. In conjunction with mec typing, MLST has been used to create an international nomenclature for S. aureus. MLST sequence types with a single nucleotide polymorphism (SNP) considered distinct. In this work, relationships among MLST SNPs and methicillin/oxacillin resistance or susceptibility were studied, using a public data base, by means of cross-tabulation tests, multivariable (phylogenetic) logistic regression (LR), decision trees, rule bases, and random forests (RF). Model performances were assessed through multiple cross-validation. Hierarchical clustering of SNPs was also employed to analyze mutational covariation. The number of instances with a known methicillin (oxacillin) antibiogram result was 1526 (649), where 63% (54%) was resistant to methicillin (oxacillin). In univariable analysis, several MLST SNPs were found strongly associated with antibiotic resistance/susceptibility. A RF model predicted correctly the resistance/susceptibility to methicillin and oxacillin in 75% and 63% of cases (cross-validated). Results were similar for LR. Hierarchical clustering of the aforementioned SNPs yielded a high level of covariation both within the same and different genes; this suggests strong genetic linkage between SNPs of housekeeping genes and antibiotic resistant associated genes. This finding provides a basis for rapid identification of antibiotic resistant S. arues lineages using a small number of genomic markers. The number of sites could subsequently be increased moderately to increase the sensitivity and specificity of genotypic tests for resistance that do not rely on the direct detection of the resistance marker itself.

Introduction

Drug resistance in Staphylococcus aureus has been recognized since the discovery and widespread use of antibiotics in the 1960s [1]. More recently, methicillin-resistant S. aureus (MRSA) infections have become pervasive both in hospital and community setting [2] and are responsible for significant morbidity and mortality worldwide [3]. In US hospitals, MRSA is currently the most commonly identified antibiotic-resistant pathogen and is a leading cause of hospital associated infections (HAI) [4]. These HAIs lead to increased length of stay, healthcare cost and mortality [5]. Worldwide, mortality rates of HAIs due to S. aureus are ~30%, and a MRSA infection doubles the risk of death [6]. Clinical syndromes of MRSA infection include non-invasive disease such as skin and soft tissue infections as well as invasive disease including bacteremia, endocarditis, septic arthritis, and osteomyelitis.

It has been proposed that methicillin resistance has repeatedly and independently evolved among several phylogenetically distinct lineages [7]–[9] The ability of S. aureus to develop resistance to antimicrobial agents has significantly contributed to the pathogen’s emergence and the difficulties treating infections in the clinical setting. The most recognized and epidemiologically important antibiotic class to which S. aureus can become resistant are β-lactam agents, notably methicillin and oxacillin. There are three known mechanism by which S. aureus may become resistant to methicillin. These include the production of β-lactamases [10], modification of normal penicillin binding proteins (PBPs) [11], and the presence of an acquired PBP [12]. Of these mechanisms, acquisition of PBP2a, encoded by the mecA gene, is the most common. The mecA gene is located on a mobile genetic element, the Staphylococcal Cassette Chromosome mec (SCCmec). The SCCmec additionally contains regulatory and recombinase genes which are important for drug resistance and pathogenicity [13]. While the role of SCCmec on antibiotic resistance is widely recognized, there are several other genes that may be interconnected with pathogenicity and resistance. Diep et al. demonstrated that the accessory gene regulator agr located on the arganine catabolic mobile element pathogenicity island was linked to increased expression of methicillin resistance genes and contributed to the evolution of highly pathogenic MRSA strains [14]. In addition, several other genes have been linked to increase antimicrobial resistance, including erm, vat, msrA and tet which are linked to rRNA methyltransferases, acetyltransferase, effluxing, and modification of the ribosomes or effluxing, respectively [15]–[17].

The current understanding of MRSA evolution is the result of advancement in molecular tools used to characterize S. aureus. Of these tools, multilocus sequence typing (MLST) is a widely utilized, highly discriminatory method of characterizing bacterial isolates. The MLST scheme for S. aureus uses ~450-base pair internal fragments of seven housekeeping genes to assign allelic profiles to isolates [Ref_ 18]. Variations in sequences are assigned as distinct alleles for each gene fragment. Each isolate is then identified by the alleles of the housekeeping loci. In conjunction with SCCmec typing, MLST has been used to create an international nomenclature for S. aureus and to trace its evolutionary history, showing that major MRSA strains have arisen repeatedly from successful epidemic methicillin-susceptible strains. Therefore, MLST types and single nucleotide polymorphisms (SNPs) of housekeeping genes are likely held in tight genetic linkage (i.e. hitchhiking) with SCCmec types and associated antibiotic resistance genes, which are thought to be generally stable in S. aureus lineages. In this study, we present an extensive analysis that characterizes the relations between MLST SNPs and their corresponding methicillin/oxacillin antibiogram profile, using several supervised and unsupervised statistical learning methods. We demonstrate that combinations of MLST SNPs are independently associated and able to predict resistance to methicillin or oxacillin.

Methods

MLST data, linked to clinical/epidemiological information and resistance values of antibiograms have been retrieved from the public domain internet repository of S. aureus MLST (http://saureus.mlst.net/). This repository is part of the MLST project (https://pubmlst.org/; formerly available at http://www.mlst.net/) that hosts MLST data of different organisms. The S. aureus MLST repository originally included isolates representing both methicillin-susceptible and MRSA allelic profiles of examples of the major epidemic strains circulating in the United Kingdom [18]. It now comprises isolates collected worldwide and provides services for MLST classification and isolate submission/storage. The S. aureus MLST scheme uses internal fragments of the following seven housekeeping genes: Carbamate kinase (arc); Shikimate dehydrogenase (aro); Glycerol kinase (glp); Guanylate kinase (gmk); Phosphate acetyltransferase (pta); Triosephosphate isomerase (tpi); Acetyle coenzyme A acetyltransferase (yqi). Additional details about the DNA extraction protocol, lysis solution, PCR conditions and primers are described on the website.

In this study, the concatenated, aligned, gap-free, nucleotide sequences of all seven aforementioned housekeeping genes were considered, retaining only alignment positions with a variable base content using binary dummy variables representing the 4 nucleotide bases at each position. This sequence encoding was then linked with the antibiogram values of methicillin, oxacillin and vancomycin. Antibiogram results were categorized into a susceptible or resistant class (or unknown if the datum was not present). Identical sequences were collapsed into one (retaining singletons), except for those identical sequences assigned to different antibiogram classes with at least one drug. The final data set was also linked with the following clinical/epidemiological information: patient’s age and gender, country and year of sampling, disease type (e.g. skin lesion, endocarditis, pyomyositis), source (e.g. nasal swab, blood, sputum, cow milk), and epidemiological classification (e.g. community-acquired, hospital-acquired). The genotypic information was used to independently infer a prediction model of resistance to methicillin, and another for oxacillin; vancomycin was not included due to the low prevalence of resistant isolates. Methicillin and oxacillin resistance were modeled separately because they are specified for each strain and we have no way of confirming the presence of mecA (MRSA). Considering the existence of oxacillin-susceptible MRSA (OS-MRSA), data entry errors can not be confidently inferred. The remaining information was used for descriptive statistics but not for identifying prognostic factors of resistance. The following machine learning models were used to classify the isolates into the resistant or susceptible class: decision trees (DT), random forests (RF), logistic regression (LR), and rule bases (RB) [19]. Decision trees are binary trees grown by inferring node splits upon a set of input predictors. The space of observations is recursively divided into two disjoint sub-spaces, thus inferring a node split, based on an optimal cut-off value of a predictor with respect to the outcome class. In practice, decision trees induce a partition of the space into quadrants and approximate a solution for each of the quadrants, thus being basic non-linear classifiers. Depending on the node split criteria (that include functions such as chi-square value, Gini index, or cross-entropy), variable sampling and tree growing policies, different implementations of DT are available. The one used in this study is the REPTree [20].

Random Forests [21] are ensemble of different decision trees grown on bootstrap samples of the data, where the predictors evaluated at each node split for each tree are subject to an additional random sampling. The output from a RF can be the majority vote, the average, the median or the mode of all outputs from the single trees (here set to 200). Although less interpretable, RF have been proven to have a higher discriminative power as compared to DT. LR is a generalized linear model used for binomial regression, which predicts the probability of occurrence of an event by fitting data to a logistic function. RB models are ensemble of if-then rules in natural language where the conditional part can be a combination of predictors, weights, logic and/or mathematical operators. The rules themselves can be inferred with a plethora of different methods. The algorithm chosen for this study was the PART decision list [22].

As goodness-of-fit functions, the accuracy (% of correctly predicted cases), the sensitivity (true positive rate), the specificity (true negative rate), and the area under the receiver operating characteristic (AUROC) were considered [23]. For two-class problems (say, resistant is class 1 and susceptible is class 0), the AUROC can be interpreted as the probability that the test result from a randomly chosen instance of class 1 is more indicative of class 1 than that from a randomly chosen instance of class 0. Robust extra-sample error estimation was obtained by repeated cross-validation [24]. A Student’s t-test, adjusted for repeated cross-validation [25], was used to assess differences in the average performance indicators of models, using a significance threshold of 0.05.

Since the input space comprised several thousands of covariates (n), and the sample size was a few thousands of instances (p), thus n>>p, we employed a feature selection scheme as follows (nested in the cross-validation to avoid a selection bias). First, all (binary) covariates were ordered by their chi-square value with respect to the outcome class. Then, DT, RF, LR, and RB were fit using all covariates whose chi-square value yielded a p-value below 0.01 or 0.05 (unadjusted for multiple testing), restricting the space to those variables with an observed frequency of at least 3%, and using half of the ordered input space. While DT, RF, and RB perform intrinsic feature selection, for LR we used and embedded algorithm called LogitBoost [26].

As the bacterial isolates considered might be subject to a strong non-independence, we employed a phylogenetic generalized least square (PGLS) analysis [27], [28] -with binomial link-parallel to the LR. PGLS requires a phylogenetic tree to be provided, upon which a covariance matrix is calculated. The phylogenetic tree for the MLST data was estimated here with a neighbor-joining approach and Jukes-Cantor distance. Also, phylogeny-trait (resistance and MLST types) association was tested via the Slatkin-Maddison test.

Finally, in order to assess base covariation across the MLST genes, a hierarchical clustering was performed, assessing node reliability via a multi-step, multi-scale bootstrap resampling [29]. The Waikato Environment for Knowledge Analysis (WEKA) software suite [20], the R software for statistical computing and graphics [30], and the MEGA5 software for phylogenetic analysis [31] were used to perform all analyses.

Results

The original, complete data set as downloaded from the public online S. aureus MLST repository comprised 3,940 instances whose attributes are described in Table 1. At the time of download, there were 128 MLST profiles with 3 or more members. The data were heterogeneously collected across different countries and healthcare facilities worldwide with clearly independent sampling strategies. Also, the epidemiological classification has not been recorded in a standard form, but rather in text fields with natural language description. By analyzing in detail all the epidemiological fields, we grouped the samples into colonization (22%), invasive infections (27%), non-invasive infections (12%) and other/unknown (39%) infection types. The prevalence of methicillin resistant strains differed significantly (chi-square test, p<0.0001) across these epidemiological groups (Figure 1). Out of the total, 623 (16%) were animal samples, of which 427 (68%) were classified as invasive infections.

Table 1.

Characteristics of the study population.

						Methicillin antibiogram profile
Factor/Strata		n (%)				Resistant			Susceptible	Unknown
	UK	722 (18.3%)				181 (25.1%)			451 (62.5%)	90 (12.5%)
	The Netherlands	386 (9.8%)				40 (10.4%)			87 (22.5%)	259 (67.1%)
	Norway	268 (6.8%)				51 (19%)			165 (61.6%)	52 (19.4%)
	Japan	245 (6.2%)				32 (13.1%)			190 (77.6%)	23 (9.4%)
	USA	234 (5.9%)				113 (48.3%)			53 (22.6%)	68 (29.1%)
	Switzerland	204 (5.2%)				34 (16.7%)			170 (83.3%)	0 (0%)
	Australia	195 (4.9%)				138 (70.8%)			51 (26.2%)	6 (3.1%)
	Germany	139 (3.5%)				56 (40.3%)			63 (45.3%)	20 (14.4%)
	France	131 (3.3%)				51 (38.9%)			55 (42%)	25 (19.1%)
	Spain	113 (2.9%)				64 (56.6%)			46 (40.7%)	3 (2.7%)
	China	100 (2.5%)				64 (64%)			30 (30%)	6 (6%)
	Gambia	100 (2.5%)				0 (0%)			100 (100%)	0 (0%)
	Iran	87 (2.2%)				82 (94.3%)			5 (5.7%)	0 (0%)
	Italy	79 (2%)				45 (57%)			27 (34.2%)	7 (8.9%)
	Thailand	64 (1.6%)				33 (51.6%)			15 (23.4%)	16 (25%)
	Ireland	56 (1.4%)				17 (30.4%)			34 (60.7%)	5 (8.9%)
	Portugal	56 (1.4%)				33 (58.9%)			9 (16.1%)	14 (25%)
	Denmark	51 (1.3%)				9 (17.6%)			35 (68.6%)	7 (13.7%)
	Bulgaria	51 (1.3%)				1 (2%)			0 (0%)	50 (98%)
	Poland	49 (1.2%)				13 (26.5%)			33 (67.3%)	3 (6.1%)
	Canada	48 (1.2%)				9 (18.8%)			37 (77.1%)	2 (4.2%)
	Brazil	42 (1.1%)				10 (23.8%)			22 (52.4%)	10 (23.8%)
	Sweden	38 (1%)				22 (57.9%)			2 (5.3%)	14 (36.8%)
	Taiwan	33 (0.8%)				20 (60.6%)			1 (3%)	12 (36.4%)
	Gabon	30 (0.8%)				0 (0%)			30 (100%)	0 (0%)
	Finland	30 (0.8%)				27 (90%)			3 (10%)	0 (0%)
	Other	374 (9.5%)				179 (47.9%)			106 (28.3%)	89 (23.8%)
Country	Unknown	15 (0.4%)				5 (33.3%)			4 (26.7%)	6 (40%)
Total		3940 (100%)				1329 (33.7%)			1824 (46.3%)	787 (20%)
	Female	586 (14.9%)				172 (29.4%)			360 (61.4%)	54 (9.2%)
	Male	633 (16.1%)				238 (37.6%)			326 (51.5%)	69 (10.9%)
Gender	Unknown	2721 (69.1%)				919 (33.8%)			1138 (41.8%)	664 (24.4%)
	<=2000	953 (24.2%)				335 (35.2%)			484 (50.8%)	134 (14.1%)
	2001 to 2004	1143 (29%)				465 (40.7%)			603 (52.8%)	75 (6.6%)
	2005 to 2007	945 (24%)				247 (26.1%)			390 (41.3%)	308 (32.6%)
	>=2008	685 (17.4%)				206 (30.1%)			277 (40.4%)	202 (29.5%)
Calendar year	Unknown	214 (5.4%)				76 (35.5%)			70 (32.7%)	68 (31.8%)
		Antibiogram results
				Oxacillin-
	Methicillin vs. Oxacillin				Resistant	Susceptible			Unknown
			Resistant		191	2			374
			Susceptible		47	306			606
	Methicillin-		Unknown		63	40			376

Figure 1.

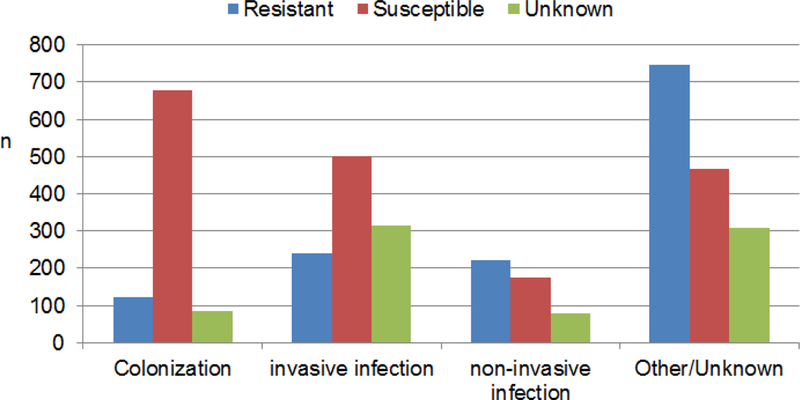
Epidemiological classification of the study population, stratified by methicillin resistance class.

The final data set accounted for 2005 instances with at least a known oxacillin, methicillin or vancomycin antibiogram result, as defined in the methods section. The number of instances with a known vancomycin antibiogram test result was 669; however, the number of isolates with a vancomycin-resistant profile was only 13 (1.9%), thus the vancomycin outcome was not included in the analyses. The number of instances with a known methicillin (oxacillin) antibiogram result was 1526 (649). All (193) but two (1.0%) methicillin-resistant isolates were also oxacillin-resistant, while among the oxacillin-resistant strains (238), 191 (80.2%) were also methicillin-resistant (Table 1). The number of variable alignment positions was 1478: 174 in arc, 204 in aro, 196 in glp, 129 in gmk, 262 in pta, 329 in tpi, and 184 in yqi, where the total gene lengths were 456, 456, 465, 429, 474, 402, and 516 bases, respectively. With the binary encoding, the input space comprised 3432 variable alignment positions encoded as binary indicators of nucleotides (383 in arc, 470 in aro, 440 in glp, 278 in gmk, 621 in pta, 840 in tpi, and 400 in yqi).

In order to determine the best prediction model, including an estimate of a relevant feature set, 25 independent runs of 5-fold cross-validation were executed using the data sets and fitting DT, RF, LR, and RB. Table 2 reports average (standard deviation, st.dev.) values for accuracy, sensitivity, specificity and AUROC, fitting the models with respect to the methicillin resistance class. The best model was a RF trained on the reduced set of input attributes with p-value from the chi-square test below 0.05 and a frequency filter of 3%. Thus, the input reduction based on a preliminary univariable/frequency test did not seem to affect the model performance, but instead improved the performance. The average (st.dev.) accuracy, AUROC, sensitivity and specificity of this RF model assessed to 74.661% (2.463), 0.789 (0.025), 0.611 (0.049), 0.827 (0.030), respectively, given the prevalence of the majority class (methicillin-susceptible) of 62.8%. For comparison, the usage of a linear model (LR), as well as DT or RB, in general did not lead to a significant reduction in terms of AUROC performance. Results were similar when applying the models to the oxacillin resistance, although the overall number of features selected by the chi-square test was higher (123 vs. 89 alignment positions at a raw p-value threshold of 0.05). Given a prevalence of 53.6% of instances belonging to the oxacillin-susceptible class (majority class), using a RF trained on the reduced set of input attributes with p-value from the chi-square test below 0.05 and a frequency threshold of 3%, the average the accuracy, AUROC, sensitivity and specificity were 62.804% (3.638), 0.705 (0.042), 0.639 (0.070), and 0.618 (0.063), respectively. LR, DT and RB behaved similarly.

Table 2.

Average (st.dev.) performance results of machine learning models in predicting the methicillin antibiogram profile. Class 1 is susceptibility (62.8%), class 0 is resistance (37.2%), after executing 25 independent runs of 5-fold cross-validation. The feature selection method filters the covariates according to their chi-square value subject to a cross-tabulation with the class (0.05 or 0.01 significance level, frequency threshold, or half of the ordered feature space). The best model in terms of AUROC is placed at the top rank of the table. Models whose average performance value is worse than that of the best one at the 0.05 level (by means of a Student’s t-test corrected for sample overlap) are marked with an asterisk.

model - filter	accuracy (%)	AUROC	sensitivity	specificity
RF – 0.05 – FT	74.661 (2.463)	0.789 (0.025)	0.611 (0.049)	0.827 (0.030)
RF - 0.05	74.505 (2.226)	0.768 (0.025)	0.615 (0.052)	0.822 (0.027)
RF - 0.01	74.621 (2.032)	0.764 (0.025)	0.626 (0.040)	0.817 (0.026)
RF - half	72.722 (2.463)	0.760 (0.024)	0.499 (0.077)*	0.862 (0.041)
DT – 0.05 – FT	73.194 (2.501)	0.739 (0.034)*	0.601 (0.066)	0.809 (0.033)
DT - 0.01	73.398 (2.215)	0.725 (0.027)*	0.608 (0.059)	0.809 (0.036)
DT - 0.05	72.939 (2.115)	0.719 (0.027)*	0.592 (0.058)	0.811 (0.034)
DT - half	73.409 (2.250)	0.718 (0.029)*	0.616 (0.056)	0.804 (0.035)
LR – 0.05 – FT	74.351 (2.591)	0.786 (0.026)	0.642 (0.050)	0.803 (0.032)
LR - 0.01	73.504 (2.106)	0.752 (0.023)*	0.637 (0.049)	0.793 (0.029)
LR - 0.05	72.033 (2.143)	0.743 (0.023)*	0.594 (0.054)	0.795 (0.033)
LR - half	74.111 (2.151)	0.757 (0.024)	0.653 (0.048)	0.793 (0.031)
RB – 0.05 – FT	74.581 (2.363)	0.770 (0.029)	0.634 (0.044)	0.812 (0.031)
RB - 0.01	74.286 (2.136)	0.744 (0.025)*	0.626 (0.049)	0.812 (0.027)
RB - 0.05	74.570 (2.137)	0.744 (0.023)*	0.634 (0.039)	0.812 (0.030)
RB - half	73.649 (2.214)	0.740 (0.021)*	0.628 (0.052)	0.801 (0.031)
OR	67.253 (2.006)*	0.602 (0.026)*	0.383 (0.116)*	0.844 (0.074)

RF: random forest; DT: decision tree; LR: logistic regression; RB: rule bases; OR: one rule; FT: frequency threshold of 3%.

Table 3 lists how many positions, re-compacted from binary indicators to 4-base alignment positions, were found significantly (unadjusted p-value<0.05) associated with either the methicillin or the oxacillin resistance class, by executing a chi-square test, stratified by the MLST gene. The list of the top 20 scoring positions is also included. By performing a Bonferroni correction for multiple testing, the number of positions with a p-value<0.05 drastically reduced, yielding 18 positions for methicillin and 5 for oxacillin. For each of these top-scoring positions, we executed a corresponding PGLS analysis to see if the strength of the association with resistance/susceptibility was confirmed. Of note, it was not possible to infer an extensive PGLS analysis, on the full set of positions, with feature selection in the same settings as for the LR analysis, given the limitations of the current software implementations (using the “ape”, “nlme”, and “phytools” R packages), which often crashed and was extremely slow given the large data set size. The results of the PGLS analysis were not fully in agreement with the LR estimations, both in coefficients and standard error estimates.

Table 3.

Summary and list of alignment positions associated to methicillin or oxacillin resistance across the 7 MLST genes. The numerator n is the number of positions whose unadjusted p-value resulting from a chi-square test made by cross-tabulating with the antibiogram class category was below 0.05. The denominator is the total number of variable positions in the gene alignment (first two columns), or the total number of variable positions across all genes (second two columns), or the total number of concatenated bases in the alignment (third two columns).

gene	n/gene_length; %			% over no. of variable positions		% over total no. of positions (3198)
	methicillin	oxacillin		methicillin	oxacillin	methicillin	oxacillin
arc	1¼56; (2.4%)	1¾56; (2.9%)		6.3%	7.5%	0.3%	0.4%
aro	18/456; (3.9%)	55/456; (12.1%)		8.8%	27.0%	0.6%	1.7%
glp	12/465; (2.6%)	17/465; (3.7%)		6.1%	8.7%	0.4%	0.5%
gmk	10/429; (2.3%)	5/429; (1.2%)		7.8%	3.9%	0.3%	0.2%
pta	9/474; (1.9%)	4/474; (0.8%)		3.4%	1.5%	0.3%	0.1%
tpi	14/402; (3.5%)	10/402; (2.5%)		4.3%	3.0%	0.4%	0.3%
yqi	15/516; (2.9%)	19/516; (3.7%)		8.2%	10.3%	0.5%	0.6%
total	89/3198; (2.8%)	123/3198; (3.8%)		6.0%	8.3%	2.8%	3.8%
Top 20 positions associated with resistance/susceptibility			methicillin	aro_153, aro_101, tpi_68, aro_86, glp_58, arc_183, aro_22, tpi_242, tpi_48, aro_141, aro_329, yqi_95, yqi_512, yqi_191, gmk_356, gmk_389, yqi_87, arc_202, pta_84, tpi_276
			oxacillin	aro_101, aro_153, aro_86, arc_183, tpi_68, glpf_58, yqi_504, yqi_95, yqi_512, aro_419, yqi_502, yqi_491, arc_77, arc_271, yqi_497, yqi_488, yqi_492, yqi_505, tpi_242, aro_361

Table 4 reports the odds ratios of positions from fitting multiple LR models (considering non-correlated variables at a frequency >3%, a preliminary filter based on a chi-square test, and a subsequent stepwise selection) on 500 bootstrap samples of the original data sets (excluding models with a non-convergent numerical fit from the final ensemble).

Table 4.

Summary of relevant predictors showing higher/lower odds towards methicillin/oxacillin susceptibility by fitting multiple multivariable logistic regression models (non-correlated variables at a frequency >3%, filtered by a chi-square test and stepwise selection) on bootstrap samples of the data sets (n=500). OR: odds ratio; CI: confidence intervals; *estimated averaging across all bootstrap samples

outcome	factor	bootstrap	OR (95% CI)*
Methicillin susceptibility	(Intercept)	100.0	1.75 (1.42–2.16)
	arc_271G	100.0	0.14 (0.13–0.14)
	pta_382T	99.4	2.49 (2.44–2.55)
	yqi_332T	99.4	4.43 (4.29–4.59)
	aro_153T	98.5	0.26 (0.26–0.27)
	tpi_276T	91.4	0.13 (0.12–0.15)
	tpi_48T	89.2	6.52 (5.96–7.14)
	yqi_494T	89.2	2.29 (2.24–2.34)
	yqi_95T	85.0	7.05 (6.41–7.75)
	gmk_356T	80.6	3.57 (3.44–3.72)
	glp_371T	75.7	13.32 (12.43–14.26)
	gmk_128T	74.9	2.26 (2.19–2.33)
	aro_131G	72.8	0.38 (0.37–0.39)
	aro_308C	71.9	3.74 (3.6–3.9)
	arc_183G	69.4	0.34 (0.33–0.36)
	gmk_357G	65.4	0.31 (0.3–0.32)
	glp_56G	65.2	0.09 (0.08–0.1)
	aro_22C	49.6	8.71 (7.72–9.84)
	gmk_401T	47.9	0.34 (0.32–0.35)
	glp_416T	46.8	0.16 (0.15–0.17)
	yqi_87G	46.8	0.16 (0.15–0.18)
	glp_194G	43.9	3.07 (2.93–3.22)
	yqi_191G	41.6	0.52 (0.51–0.53)
	glp_311G	38.2	0.18 (0.16–0.21)
	gmk_389G	37.1	3.52 (3.36–3.7)
	aro_86G	36.9	0.4 (0.38–0.41)
	aro_329T	36.7	3.11 (2.93–3.3)
	tpi_68T	36.3	1.68 (1.64–1.72)
	tpi_242G	32.1	1.6 (1.55–1.64)
	pta_84G	30.6	0.58 (0.57–0.59)
	gmk_317T	28.1	1.4 (1.28–1.53)
	aro_101T	26.4	1.82 (1.79–1.86)
	glp_58T	23.8	1.19 (1.1–1.28)
	pta_176T	18.1	1.47 (1.18–1.84)
	tpi_200T	17.9	0.57 (0.53–0.6)
Oxacillin susceptibility	(Intercept)	100.0	5.21 (3.79–7.17)
	aro_101C	98.3	12.68 (11.67–13.78)
	aro_101T	98.3	3.95 (3.8–4.1)
	arc_183G	83.2	0.25 (0.24–0.26)
	yqi_95T	79.3	5.87 (5.43–6.34)
	glp_58T	77.3	0.23 (0.22–0.24)
	aro_86G	65.3	0.39 (0.38–0.41)
	arc_271G	64.8	0.38 (0.37–0.4)
	pta_264T	64.2	3.15 (3.01–3.3)
	yqi_502T	57.4	0.04 (0.03–0.06)
	glp_194G	33.2	0.6 (0.57–0.63)
	aro_153T	26.7	0.62 (0.6–0.65)
	yqi_87G	25.3	1.08 (0.89–1.32)
	yqi_497G	24.7	7.74 (6.34–9.46)
	arc_77G	24.4	2.59 (2.51–2.68)
	tpi_242G	19.9	1.42 (1.36–1.49)
	tpi_35T	19.9	0.88 (0.8–0.97)
	tpi_68T	19.6	1.41 (1.37–1.46)
	tpi_53T	18.5	0.69 (0.64–0.74)
	gmk_317T	17.3	3.06 (1.64–5.68)
	gmk_285T	14.8	0.19 (0.1–0.37)
	yqi_504C	12.5	0.04 (0.03–0.06)

Finally, Figure 3 shows a bootstrapped hierarchical clustering that describes the base covariation across the MLST gene alignment positions that were significantly associated with the methicillin/oxacillin antibiogram profiles.

Figure 3.

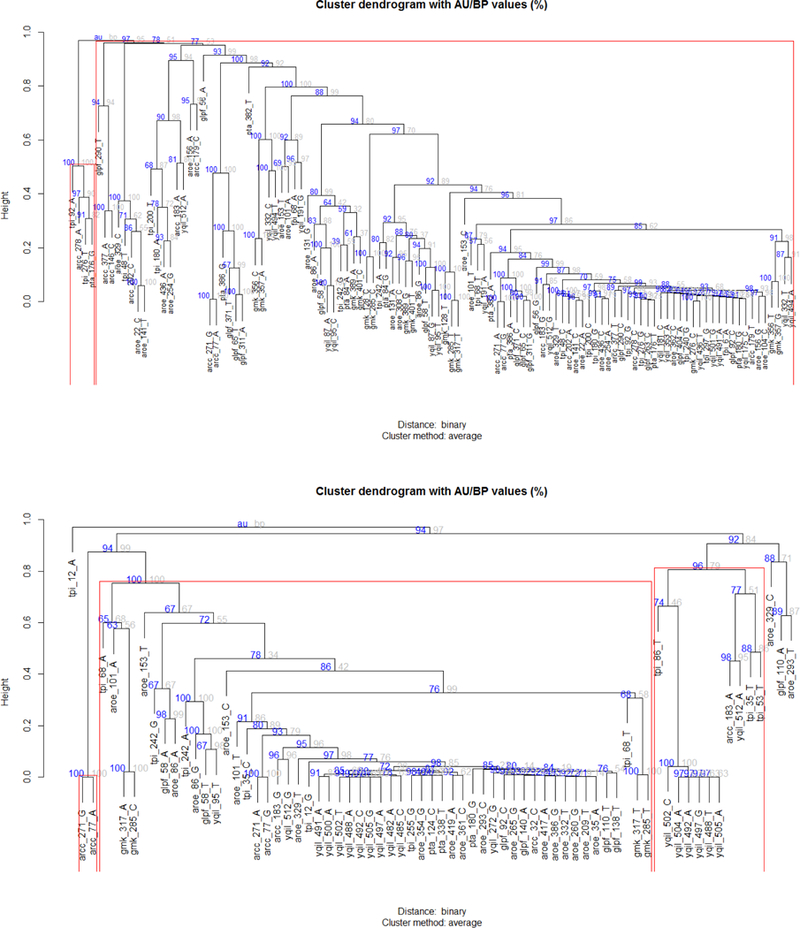
Hierarchical clustering of alignment positions from different MLST genes, significantly associated to methicillin (upper panel) and oxacillin (lower panel) resistance/susceptibility (base frequency>3%, chi-square p-value<0.025). Positions are progressively clustered together according to their binary correlation distance. Tree node reliability has been assessed by multi-step, multi-scale bootstrap resampling, obtaining approximately-unbiased (AU) p-values (expressed in %) from bootstrap percentages (BP).

As sensitivity analysis, since the observations were collected from multiple infection sources (both human and animals) and epidemiological categories (as invasive or non-invasive infections), the whole univariable and machine learning analysis was repeated on the subset of invasive infections. Results were comparable in terms of prediction and feature importance to those obtained in the main analysis (data not shown).

Discussion

This study applied statistical learning with phylogenetic correction to identify novel associations between single nucleotide polymorphisms (SNPs) within MLST regions of S. aureus and phenotypic antibiotic resistance. While several studies have recognized the direct association specific genes such as mecA which confer antibiotic resistance, the role of other regions, in this case among housekeeping genes, are not fully understood. Indeed, epistatic interactions may exist between housekeeping genes and antibiotic resistance determinants. Furthermore, genotypic markers of resistance do not always accurately correlate to phenotypic resistance [32]. This further suggests that other regions of the genome may be indirectly involved in phenotypic expression of drug resistance. This highlights the need for additional studies to identify unexplored or underappreciated regions of bacterial genomes which can subsequently be explored through in vitro studies and subsequent genome-wide statistical analysis. The supervised analysis showed that several SNPs are associated with resistance/susceptibility to oxacillin or methicillin: the highest scoring SNPs are common both to the methicillin and the oxacillin data sets, and this might be expected since those drugs belong to the same class of antibiotics and therefore are generally thought to behave similarly. However, the number of relevant SNPs was sensibly reduced after a Bonferroni correction (18 for methicillin and 5 for oxacillin). A phylogenetic generalized least square analysis, which should be able to correct for the non-independence of observations via a phylogenetic tree, did not confirm the findings of the LR method, although it could not be run extensively due to the large data set size. This was a key point of the analysis, because the phylogenetic relationships (i.e. non-independence of observations) among the bacterial isolates considered could massively impact the estimation of the statistical significance in associating SNPs and antibiotic resistance. However, also a PGLS analysis might not be affected by a wrong phylogeny estimation and the sampling bias.

All the statistical learning methods consistently showed predictions performances that significantly improved over the null reference model, although the overall accuracy and AUROC were not high. The covariation analysis highlighted several specific clusters of SNPs, comprising also positions in different genes. It would be interesting to see if results would be confirmed by a direct coupling analysis, which explicitly tests for genome-wide epistatic interactions. Unfortunately, the corresponding SCCmec profiles were not recorded in the data base, because it would have been interesting to see if clusters were related to different SCCmec types. Epidemiological strata such as the country or the disease type, along with the MLST types are themselves significantly associated with methicillin/oxacillin resistance. The first is attributable to the number of outbreaks per country and the sample correlation within outbreaks. The latter is obvious since the MLST types are defined by SNPs, and MLST types are used in conjunction with SCCmec types for MRSA nomenclature. Also, community-acquired and hospital-acquired infections are generally, although not uniquely, associated with specific MLST types. The observed differences of prevalence of resistant strains in different epidemiological classifications could be simply a result of a sampling bias, which cannot be ruled out in the studied data set. In the previous study by Enright et al. [7], emergence of MRSA strains was shown to arise repeatedly from successful epidemic methicillin-susceptible strains. This might suggest that the SNPs in housekeeping genes associated to different antibiotic profiles could be the effect of mutational hitchhiking. We have shown that there is a strong phylogeny-trait association both for antibiotic resistance and MLST types, and this might suggest that the hitchhiking hypothesis holds, i.e. we are detecting resistant strains rather than resistance signatures. In order to rule this out both a more accurate analysis is required, including a fine-tuned phylogeny estimation, with the appropriate choice of evolutionary model, evaluation of phylogenetic signal, and usage of parallel methods given the large sample size (>1,000 strains). On the other hand, this work establishes a basis for a subsequent, comprehensive, characterization of antimicrobial resistance by means of SNP analysis and antibiogram results. Given the expansion and decrease of costs of next-generation sequencing [33], we foresee the application of this framework on full-genomes, placed in the context of a rigorous prospective study design, and linked to a phylodynamic epidemiological characterization. Subsequent finding could directly be applied to the control of pathogenic strains and to the development of treatment policies.

Figure 2.

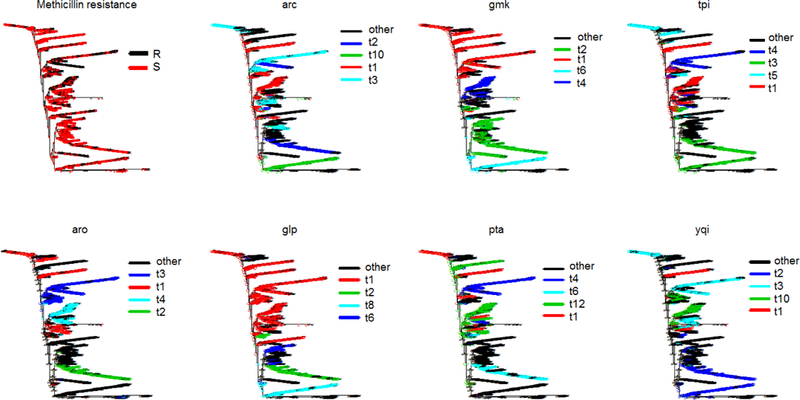
Phylogenetic trees of MLST alignment (1,526 taxa, neighbor-joining algorithm, Jukes Cantor distance) with ancestral trait reconstruction corresponding to methicillin resistance, and MLST types in different genes. All exhibit stron phylogeny-trait structure (p-value<0.0001)