MM Algorithms For Variance Components Models

Abstract

Variance components estimation and mixed model analysis are central themes in statistics with applications in numerous scientific disciplines. Despite the best efforts of generations of statisticians and numerical analysts, maximum likelihood estimation and restricted maximum likelihood estimation of variance component models remain numerically challenging. Building on the minorization-maximization (MM) principle, this paper presents a novel iterative algorithm for variance components estimation. Our MM algorithm is trivial to implement and competitive on large data problems. The algorithm readily extends to more complicated problems such as linear mixed models, multivariate response models possibly with missing data, maximum a posteriori estimation, and penalized estimation. We establish the global convergence of the MM algorithm to a Karush-Kuhn-Tucker (KKT) point and demonstrate, both numerically and theoretically, that it converges faster than the classical EM algorithm when the number of variance components is greater than two and all covariance matrices are positive definite.

1. Introduction

Variance components and linear mixed models are among the most potent tools in a statistician’s toolbox, finding numerous applications in agriculture, biology, economics, genetics, epidemiology, and medicine. Given an observed n × 1 response vector y and n × p predictor matrix X, the simplest variance components model postulates that Y ∼ N (Xβ, Ω), where $\Omega ={\sum }_{i=1}^m{\sigma }_i^2{V}_i$, and the V₁, …, V_m are m fixed positive semidefinite matrices. The parameters of the model can be divided into mean effects β = (β₁, …, β_p) and variance components ${\sigma }^2=\left({\sigma }_1^2,\dots ,{\sigma }_m^2\right)$. Throughout we assume Ω is positive definite. The extension to singular Ω will not be pursued here. Estimation revolves around the log-likelihood function

$$L\left(\beta ,{\mathit{\sigma }}^2\right)=-\frac{1}{2}\ln \det \mathbf{\Omega }-\frac{1}{2}{\left(\mathit{y}-\mathit{X}\mathit{\beta }\right)}^T{\mathbf{\Omega }}^{-1}\left(\mathit{y}-\mathit{X}\mathit{\beta }\right).$$ (1)

Among the commonly used methods for estimating variance components, maximum likelihood estimation (MLE) (Hartley and Rao, 1967) and restricted (or residual) MLE (REML) (Harville, 1977) are the most popular. REML first projects y to the null space of X and then estimates variance components based on the projected responses. If the columns of a matrix B span the null space of X^T, then REML estimates the ${\sigma }_i^2$ by maximizing the log-likelihood of the redefined response vector B^T Y, which is normally distributed with mean 0 and covariance ${\mathit{B}}^T\mathbf{\Omega }\mathit{B}={\sum }_{i=1}^m{\sigma }_i^2{\mathit{B}}^T{\mathit{V}}_i\mathit{B}$.

There exists a large literature on iterative algorithms for finding MLE and REML (Laird and Ware, 1982; Lindstrom and Bates, 1988, 1990; Harville and Callanan, 1990; Callanan and Harville, 1991; Bates and Pinheiro, 1998; Schafer and Yucel, 2002). Fitting variance components models remains a challenge in models with a large sample size n or a large number of variance components m. Newton’s method (Lindstrom and Bates, 1988) converges quickly but is numerically unstable owing to the non-concavity of the log-likelihood. Fisher’s scoring algorithm replaces the observed information matrix in Newton’s method by the expected information matrix and yields an ascent algorithm when safeguarded by step halving. However the calculation and inversion of expected information matrices cost O(mn³) + O(m³) flops and quickly become impractical for large n or m, unless V_i are low rank, block diagonal, or have other special structures. The expectation-maximization (EM) algorithm initiated by Dempster et al. (1977) is a third alternative (Laird and Ware, 1982; Laird et al., 1987; Lindstrom and Bates, 1988; Bates and Pinheiro, 1998). Compared to Newton’s method, the EM algorithm is easy to implement and numerically stable, but painfully slow to converge. In practice, a strategy of priming Newton’s method by a few EM steps leverages the stability of EM and the faster convergence of second-order methods.

In this paper we derive a novel minorization-maximization (MM) algorithm for finding the MLE and REML estimates of variance components. We prove global convergence of the MM algorithm to a Karush-Kuhn-Tucker (KKT) point and explain why MM generally converges faster than EM for models with more than two variance components. We also sketch extensions of the MM algorithm to the multivariate response model with possibly missing responses, the linear mixed model (LMM), maximum a posteriori (MAP) estimation, and penalized estimation. The numerical efficiency of the MM algorithm is illustrated through simulated data sets and a genomic example with 200 variance components.

2. Preliminaries

Background on MM algorithms

Throughout we reserve Greek letters for parameters and indicate the current iteration number by a superscript t. The MM principle for maximizing an objective function f (θ) involves minorizing the objective function f (θ) by a surrogate function g(θ | θ^(t)) around the current iterate θ^(t) of a search (Lange et al., 2000). Minorization is defined by the two conditions

$$\begin{gathered} f\left({\mathit{\theta }}^{\left(t\right)}\right)=g\left({\mathit{\theta }}^{\left(t\right)}|{\mathit{\theta }}^{\left(t\right)}\right) \\ f\left(\mathit{\theta }\right)\ge g\left(\mathit{\theta }|{\mathit{\theta }}^{\left(t\right)}\right),\hspace{1em}\hspace{0.17em}\hspace{0.17em}\mathit{\theta }\ne {\mathit{\theta }}^{\left(t\right)}. \end{gathered}$$ (2)

In other words, the surface $\theta \mapsto g\left(\theta |{\theta }^{\left(t\right)}\right)$ lies below the surface $\theta \mapsto f\left(\theta \right)$ and is tangent to it at the point θ = θ^(t). Construction of the minorizing function g(θ | θ^(t)) constitutes the first M of the MM algorithm. The second M of the algorithm maximizes the surrogate g(θ | θ^(t)) rather than f (θ). The point θ^(t+1) maximizing g(θ | θ^(t)) satisfies the ascent property $f\left({\theta }^{\left(t+1\right)}\right)\ge f\left({\theta }^{\left(t\right)}\right)$. This fact follows from the inequalities

$$f\left({\mathit{\theta }}^{\left(t+1\right)}\right)\ge g\left({\mathit{\theta }}^{\left(t+1\right)}|{\mathit{\theta }}^{\left(t\right)}\right)\ge g\left({\mathit{\theta }}^{\left(t\right)}|{\mathit{\theta }}^{\left(t\right)}\right)=f\left({\mathit{\theta }}^{\left(t\right)}\right),$$ (3)

reflecting the definition of θ^(t+1) and the tangency and domination conditions (2). The ascent property makes the MM algorithm remarkably stable. The validity of the descent property depends only on increasing g(θ | θ^(t)), not on maximizing g(θ | θ^(t)). With obvious changes, the MM algorithm also applies to minimization rather than to maximization. To minimize a function f (θ), we majorize it by a surrogate function g(θ | θ^(t)) and minimize g(θ | θ^(t)) to produce the next iterate θ^(t+1). The acronym should not be confused with the maximization-maximization algorithm in the variational Bayes context (Jeon, 2012).

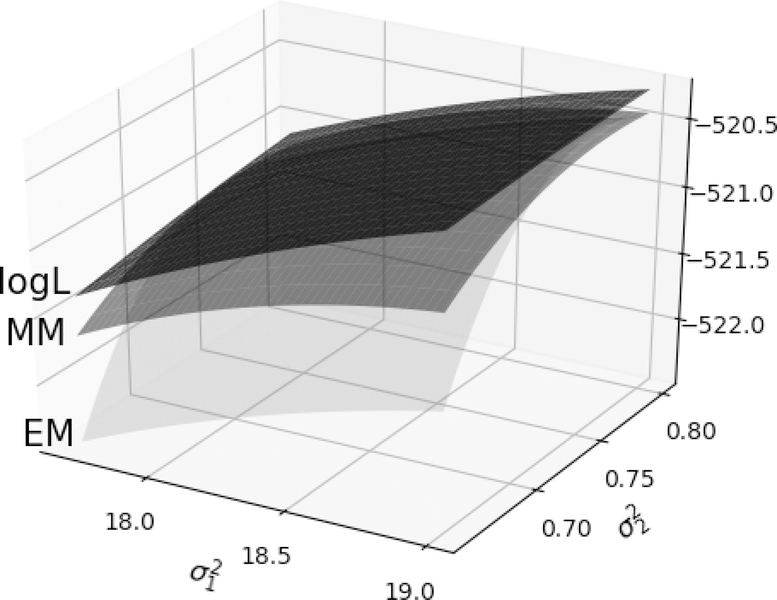
The MM principle (De Leeuw, 1994; Heiser, 1995; Kiers, 2002; Lange et al., 2000; Hunter and Lange, 2004) finds applications in multidimensional scaling (Borg and Groenen, 2005), ranking of sports teams (Hunter, 2004), variable selection (Hunter and Li, 2005; Yen, 2011), optimal experiment design (Yu, 2010), multivariate statistics (Zhou and Lange, 2010), geometric programming (Lange and Zhou, 2014), survival models (Hunter and Lange, 2002; Ding et al., 2015), sparse covariance estimation (Bien and Tibshirani, 2011), and many other areas (Lange, 2016). The celebrated EM principle (Dempster et al., 1977) is a special case of the MM principle. The Q function produced in the E step of an EM algorithm minorizes the log-likelihood up to an irrelevant constant. Thus, both EM and MM share the same advantages: simplicity, stability, graceful adaptation to constraints, and the tendency to avoid large matrix inversion. The more general MM perspective frees algorithm derivation from the missing data straitjacket and invites wider applications (Wu and Lange, 2010). Figure 1 shows the minorization functions of EM and MM for a variance components model with m = 2 variance components.

Figure 1:

Surrogate functions of EM and MM minorize the log-likelihood surface of a 2-variance component model at point $({\sigma }_1^{2(t)},{\sigma }_2^{2(t)})=(18.5,0.7)$. MM surrogate function hugs the log-likelihood surface tighter than EM.

Convex matrix functions

For symmetric matrices we write $A⪯B$ when B − A is positive semidefinite and $A\prec B$ if B − A is positive definite. A matrix-valued function f is said to be (matrix) convex if

$$f\left[\lambda \mathit{A}+\left(1-\lambda \right)\mathit{B}\right]⪯\lambda f\left(\mathit{A}\right)+\left(1-\lambda \right)f\left(\mathit{B}\right)$$

for all A, B, and λ ∈ [0, 1]. Our derivation of the MM variance components algorithm hinges on the convexity of the two functions mentioned in the next lemma. See standard text Boyd and Vandenberghe (2004) for the verification of both facts.

Lemma 1. (a) The matrix fractional function f (A, B) = A^T B⁻¹A is jointly convex in the m × n matrix A and the m × m positive definite matrix B. (b) The log determinant function f (B) = ln det B is concave on the set of positive definite matrices.

3. Univariate response model

Our strategy for maximizing the log-likelihood (1) is to alternate updating the mean parameters β and the variance components σ². Updating β given σ² is a standard general least squares problem with solution

$${\beta }^{\left(t+1\right)}={\left({\mathit{X}}^T{\mathbf{\Omega }}^{-\left(t\right)}\mathit{X}\right)}^{-1}{\mathit{X}}^T{\mathbf{\Omega }}^{-\left(t\right)}\mathit{y},$$ (4)

where Ω^−(t) represents the inverse of ${\mathbf{\Omega }}^{\left(t\right)}={\sum }_{i=1}^m{\sigma }_i^{2\left(t\right)}{V}_i$. Updating σ² given β^(t) depends on two minorizations. If we assume that all of the V_i are positive definite, then the joint convexity of the map $\left(\mathit{X},\mathit{Y}\right)\mapsto {\mathit{X}}^T{\mathit{Y}}^{-1}\mathit{X}$ for positive definite Y implies that

$$\begin{gathered} {\Omega }^{\left(t\right)}{\Omega }^{-1}{\Omega }^{\left(t\right)}=\left(\sum _{i=1}^m{\sigma }_i^{2\left(t\right)}{\mathit{V}}_i\right){\left(\sum _{i=1}^m{\sigma }_i^2{\mathit{V}}_i\right)}^{-1}\left(\sum _{i=1}^m{\sigma }_i^{2\left(t\right)}{\mathit{V}}_i\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}⪯\sum _{i=1}^m\frac{{\sigma }_i^{2\left(t\right)}}{{\sum }_j{\sigma }_j^{2\left(t\right)}}\left(\frac{{\sum }_j{\sigma }_j^{2\left(t\right)}}{{\sigma }_i^{2\left(t\right)}}{\sigma }_i^{2\left(t\right)}{\mathit{V}}_i\right){\left(\frac{{\sum }_j{\sigma }_j^{2\left(t\right)}}{{\sigma }_i^{2\left(t\right)}}{\sigma }_i^2{\mathit{V}}_i\right)}^{-1}\left(\frac{{\sum }_j{\sigma }_j^{2\left(t\right)}}{{\sigma }_i^{2\left(t\right)}}{\sigma }_i^{2\left(t\right)}{\mathit{V}}_i\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\sum _{i=1}^m\frac{{\sigma }_i^{4\left(t\right)}}{{\sigma }_i^2}{\mathit{V}}_i. \end{gathered}$$

When one or more of the V_i are rank deficient, we replace each V_i by V_i,ϵ = V_i + ϵI for ϵ > 0 small and let ${\mathbf{\Omega }}_{ϵ}^{\left(t\right)}={\sum }_i{\sigma }_i^{2\left(t\right)}{\mathit{V}}_{i,ϵ}$. Sending $ϵ$ to 0 in ${\mathbf{\Omega }}_{ϵ}^{(t)}{\mathbf{\Omega }}_{ϵ}^{-1}{\mathbf{\Omega }}_{ϵ}^{(t)}⪯{\sum }_{i=1}^m({\sigma }_i^{4(t)}/{\sigma }_i^2){\mathit{V}}_{i,ϵ}$ now gives the desired majorization ${\mathbf{\Omega }}^{\left(t\right)}{\mathbf{\Omega }}^{-1}{\mathbf{\Omega }}^{\left(t\right)}⪯{\sum }_{i=1}^m\left({\sigma }_i^{4\left(t\right)}/{\sigma }_i^2\right){\mathit{V}}_i$ in the general case. Negating both sides leads to the minorization

$$-{\left(\mathit{y}-\mathit{X}\beta \right)}^T{\mathbf{\Omega }}^{-1}\left(\mathit{y}-\mathit{X}\beta \right)⪰-{\left(\mathit{y}-\mathit{X}\beta \right)}^T{\mathbf{\Omega }}^{-\left(t\right)}\left(\sum _{i=1}^m\frac{{\sigma }_i^{4\left(t\right)}}{{\sigma }_i^2}{\mathit{V}}_i\right){\mathbf{\Omega }}^{-\left(t\right)}\left(\mathit{y}-\mathit{X}\beta \right)$$ (5)

that effectively separates the variance components ${\sigma }_1^2,\dots ,{\sigma }_m^2$ in the quadratic term of the log-likelihood (1).

The convexity of the function $\mathit{A}\mapsto -\log \det \mathit{A}$ is equivalent to the supporting hyperplane minorization

$$-\ln \det \mathbf{\Omega }\ge -\ln \det {\mathbf{\Omega }}^{\left(t\right)}-\text{tr}\left[{\mathbf{\Omega }}^{-\left(t\right)}\left(\mathbf{\Omega }-{\mathbf{\Omega }}^{\left(t\right)}\right)\right]$$ (6)

that separates ${\sigma }_1^2,\dots ,{\sigma }_m^2$ in the log determinant term of the log-likelihood (1). Combination of the minorizations (5) and (6) gives the overall minorization

$$\begin{gathered} g\left({\mathit{\sigma }}^2|{\mathit{\sigma }}^{2\left(t\right)}\right) \\ =-\frac{1}{2}\text{tr}\left({\mathbf{\Omega }}^{-\left(t\right)}\mathbf{\Omega }\right)-\frac{1}{2}{\left(\mathit{y}-\mathit{X}{\beta }^{\left(t\right)}\right)}^T{\mathbf{\Omega }}^{-\left(t\right)}\left(\sum _{i=1}^m\frac{{\mathit{\sigma }}_i^{4\left(t\right)}}{{\mathit{\sigma }}_i^2}{\mathit{V}}_i\right){\mathbf{\Omega }}^{-\left(t\right)}\left(\mathit{y}-\mathit{X}{\beta }^{\left(t\right)}\right)+c^{\left(t\right)} \\ =\sum _{i=1}^m\left[-\frac{{\mathit{\sigma }}_i^2}{2}\text{tr}\left({\mathbf{\Omega }}^{-\left(t\right)}{\mathit{V}}_i\right)-\frac{1}{2}\frac{{\mathit{\sigma }}_i^{4\left(t\right)}}{{\mathit{\sigma }}_i^2}{\left(\mathit{y}-\mathit{X}{\beta }^{\left(t\right)}\right)}^T{\mathbf{\Omega }}^{-\left(t\right)}{\mathit{V}}_i{\mathbf{\Omega }}^{-\left(t\right)}\left(\mathit{y}-\mathit{X}{\beta }^{\left(t\right)}\right)\right]+c^{\left(t\right)}, \end{gathered}$$ (7)

where c^(t) is an irrelevant constant. Maximization of g(σ² | σ^2(t)) with respect to ${\mathit{\sigma }}_i^2$ yields the simple multiplicative update

$${\sigma }_i^{2\left(t+1\right)}={\sigma }_i^{2\left(t\right)}\sqrt{\frac{{\left(\mathit{y}-\mathit{X}{\beta }^{\left(t\right)}\right)}^T{\mathbf{\Omega }}^{-\left(t\right)}{\mathit{V}}_i{\mathbf{\Omega }}^{-\left(t\right)}\left(\mathit{y}-\mathit{X}{\beta }^{\left(t\right)}\right)}{\text{tr}\left({\mathbf{\Omega }}^{-\left(t\right)}{\mathit{V}}_i\right)}},\hspace{1em}\hspace{0.17em}i=1,\dots ,m.$$ (8)

As a sanity check on our derivation, consider the partial derivative

$$\frac{\partial }{\partial {\sigma }_i^2}L\left(\beta ,{\mathit{\sigma }}^2\right)=-\frac{1}{2}\text{tr}\left({\mathbf{\Omega }}^{-1}{\mathit{V}}_i\right)+\frac{1}{2}{\left(\mathit{y}-\mathit{X}\beta \right)}^T{\mathbf{\Omega }}^{-1}{\mathit{V}}_i{\mathbf{\Omega }}^{-1}\left(\mathit{y}-\mathit{X}\beta \right).$$ (9)

Given ${\sigma }_i^{2\left(t\right)}>0$, it is clear from the update formula (8) that ${\sigma }_i^{2\left(t+1\right)}<{\sigma }_i^{2\left(t\right)}$ when $\frac{\partial }{\partial {\sigma }_i^2}L<0$. Conversely ${\sigma }_i^{2\left(t+1\right)}>{\sigma }_i^{2\left(t\right)}$ when $\frac{\partial }{\partial {\sigma }_i^2}L>0$.

Algorithm 1 summarizes the MM algorithm for MLE of the univariate response model (1). The update formula (8) assumes that the numerator under the square root sign is nonnegative and the denominator is positive. The numerator requirement is a consequence of the positive semidefiniteness of V_i. The denominator requirement is not obvious but can be verified through the Hadamard (elementwise) product representation $\text{tr}\left({\mathbf{\Omega }}^{-\left(t\right)}{\mathit{V}}_i\right)=1^T\left({\mathbf{\Omega }}^{-\left(t\right)}\odot {\mathit{V}}_i\right)1$. The following lemma of Schur (1911) is crucial. We give a self-contained probabilistic proof in Supplementary Materials S.1.

Lemma 2 (Schur). The Hadamard product of a positive definite matrix with a positive semidefinite matrix with positive diagonal entries is positive definite.

We can now obtain the following characterization of the MM iterates.

Proposition 1. Assume V_i has strictly positive diagonal entries. Then tr(Ω^−(t)V_i) > 0 for all t. Furthermore if ${\sigma }_i^{2\left(0\right)}>0$ and ${\mathbf{\Omega }}^{-\left(t\right)}\left(\mathit{y}-\mathit{X}{\beta }^{\left(t\right)}\right)\notin null\left({\mathit{V}}_i\right)$ for all t, then ${\sigma }_i^{2\left(t\right)}>0$ for all t. When V_i is positive definite, ${\sigma }_i^{2\left(t\right)}>0$ holds if and only if $y\ne \mathit{X}{\beta }^{\left(t\right)}$.

Proof. The first claim follows easily from Schur’s lemma. The second claim follows by induction. The third claim follows from the observation that null(V_i) = {0}.

In most applications, V_m = I. Proposition 1 guarantees that if ${\sigma }_m^{2\left(0\right)}>0$ and the residual vector y − Xβ^(t) is nonzero, then ${\sigma }_m^{2\left(t\right)}$ remains positive and thus Ω^(t) remains positive definite throughout all iterations. This fact does not prevent any of the sequences ${\sigma }_i^{2\left(t\right)}$ from converging to 0. In this sense, the MM algorithm acts like an interior point method, approaching the optimum from inside the feasible region.

Univariate response: two variance components

The major computational cost of Algorithm 1 is inversion of the covariance matrix Ω^(t) at each iteration. The special case of m = 2 variance components deserves attention as repeated matrix inversion can be avoided by invoking the simultaneous congruence decomposition for two symmetric matrices, one of which is positive definite (Rao, 1973; Horn and Johnson, 1985). This decomposition is also called the generalized eigenvalue decomposition (Golub and Van Loan, 1996; Boyd and Vandenberghe, 2004). If one assumes $\mathbf{\Omega }={\sigma }_1^2{\mathit{V}}_1+{\sigma }_2^2{\mathit{V}}_2$ and

lets $\left({\mathit{V}}_1,{\mathit{V}}_2\right)\mapsto \left(D,U\right)$ be the decomposition with U nonsingular, U ^T V₁U = D diagonal, and U ^T V₂U = I, then

$$\begin{gathered} {\mathbf{\Omega }}^{\left(t\right)}={\mathit{U}}^{-T}\left({\sigma }_1^{2\left(t\right)}\mathit{D}+{\sigma }_2^{2\left(t\right)}{\mathit{I}}_n\right){\mathit{U}}^{-1} \\ {\mathbf{\Omega }}^{-\left(t\right)}=\mathit{U}{\left({\sigma }_1^{2\left(t\right)}\mathit{D}+{\sigma }_2^{2\left(t\right)}{\mathit{I}}_n\right)}^{-1}{\mathit{U}}^T \\ \det \left({\mathbf{\Omega }}^{\left(t\right)}\right)=\det \left({\sigma }_1^{2\left(t\right)}\mathit{D}+{\sigma }_2^{2\left(t\right)}{\mathit{I}}_n\right)\det \left({\mathit{V}}_2\right). \end{gathered}$$ (10)

With the revised responses $\tilde{\mathit{y}}={\mathit{U}}^T\mathit{y}$ and the revised predictor matrix $\tilde{\mathit{X}}=U^T\mathit{X}$, the update (8) requires only vector operations and costs O(n) flops. Updating the fixed effects is a weighted least squares problem with the transformed data $\left(\tilde{y},\tilde{\mathit{X}}\right)$ and observation weights $w_i^{\left(t\right)}={\left({\sigma }_1^{2\left(t\right)}{d}_i+{\sigma }_2^{2\left(t\right)}\right)}^{-1}$. Algorithm 2 summarizes the simplified MM algorithm for two variance components.

Numerical experiments

This section compares the numerical performance of MM, EM, Fisher scoring, and the lme4 package in R (Bates et al., 2015) on simulated data from a two-way ANOVA random effects model and a genetic model. For ease of comparison, all algorithm runs start from σ²⁽⁰⁾ = 1 and terminate when the relative change (L^(t+1) − L^(t))/(|L^(t)|+ 1) in the log-likelihood is less than 10⁻⁸.

Two-way ANOVA:

We simulated data from a two-way ANOVA random effects model

$$y_{ijk}=\mu +{\alpha }_i+{\beta }_j+{\left(\alpha \beta \right)}_{ij}+{ϵ}_{ijk},1\le i\le a,1\le j\le b,1\le k\le c,$$

where ${\alpha }_i~N\left(0,{\sigma }_1^2\right)$, ${\beta }_j~N\left(0,{\sigma }_2^2\right)$, ${\left(\alpha \beta \right)}_{ij}~N\left(0,{\sigma }_3^2\right)$, and ${ϵ}_{ijk}~N\left(0,{\sigma }_e^2\right)$ are jointly independent. Here i indexes levels in factor 1, j indexes levels in factor 2, and k indexes observations in the (i, j)-combination. This corresponds to m = 4 variance components. In the simulation, we set ${\sigma }_1^2={\sigma }_2^2={\sigma }_3^2$ and varied the ratio ${\sigma }_1^2/{\sigma }_e^2$; the numbers of levels a and b in factor 1 and factor 2, respectively; and the number of observations c in each combination of factor levels. For each simulation scenario, we simulated 50 replicates. The sample size was n = abc for each replicate.

Tables 1 and 2 show the average number of iterations and the average runtimes when there are a = b = 5 levels of each factor. Based on these results and further results not shown for other combinations of a and b, we draw the following conclusions: Fisher scoring takes the fewest iterations; the MM algorithm always takes fewer iterations than the EM algorithm; the faster rate of convergence of Fisher scoring is outweighed by the extra cost of evaluating and inverting the information matrix. Table 1 in Supplementary Materials S.2 shows that all algorithms converged to same objective values.

Table 1:

Fisher scoring converges fastest and MM takes fewer iterations than EM. Shown below are average number of iterations until convergence for MM, EM, and FS for fitting a two-way ANOVA model with a = b = 5 levels of both factors. Standard errors are given in parentheses.

${\sigma }_1^2/{\sigma }_e^2$	Method	c = # observations per combination
		5	10	20	50
0.00	MM	143.12(99.76)	118.26(62.91)	96.26(50.61)	81.10(33.42)
	EM	2297.72(797.95)	1711.70(485.92)	1170.06(365.48)	788.10(216.60)
	FS	25.64(11.20)	21.10(7.00)	16.46(4.37)	13.88(2.88)
0.05	MM	121.86(98.52)	69.38(50.23)	55.88(37.34)	29.50(18.80)
	EM	1464.26(954.27)	538.04(504.42)	254.90(253.86)	104.98(157.97)
	FS	16.78(9.13)	12.62(6.22)	9.68(3.22)	8.10(1.34)
0.10	MM	84.74(59.33)	62.98(50.48)	40.46(31.43)	25.86(18.79)
	EM	985.46(830.49)	360.32(462.62)	157.70(231.91)	68.26(107.85)
	FS	15.20(10.10)	10.58(5.92)	8.58(3.56)	7.50(1.72)
1.00	MM	31.04(33.27)	29.60(27.66)	25.32(25.39)	24.90(20.76)
	EM	130.18(299.03)	161.14(290.23)	64.20(135.38)	84.88(137.88)
	FS	6.62(4.72)	6.32(3.64)	5.12(1.87)	5.36(1.50)
10.00	MM	29.80(35.42)	34.16(38.25)	28.82(28.44)	20.90(14.28)
	EM	115.94(274.33)	177.30(301.71)	80.12(155.67)	75.02(127.38)
	FS	12.72(5.14)	12.86(4.94)	11.66(3.95)	11.76(3.66)
20.00	MM	30.10(32.92)	32.72(39.02)	23.70(21.20)	19.62(15.67)
	EM	148.04(318.40)	85.86(180.28)	61.74(140.84)	37.36(83.89)
	FS	18.76(7.51)	17.40(5.21)	17.22(5.67)	16.28(5.03)

Table 2:

MM shows shortest run times than EM, Fisher scoring (FS), and lme4. Shown below are average run times (milliseconds) for fitting a two-way ANOVA model with a = b = 5 levels of both factors. Standard errors are given in parentheses.

${\sigma }_1^2/{\sigma }_e^2$	Method	c = # observations per combination
		5	10	20	50
0.00	MM	11.46(7.77)	10.06(5.29)	11.93(6.35)	10.44(3.99)
	EM	189.32(71.32)	148.20(48.13)	147.87(49.97)	96.28(24.97)
	FS	34.27(33.47)	24.89(8.55)	23.70(14.15)	20.46(4.54)
	lme4	25.84(12.10)	22.32(1.25)	27.34(4.06)	36.14(5.59)
0.05	MM	9.79(7.72)	6.19(4.22)	6.87(4.37)	4.45(2.20)
	EM	116.03(75.57)	47.72(45.35)	30.60(29.88)	14.23(19.68)
	FS	19.18(10.23)	15.37(7.48)	12.78(4.06)	12.39(2.35)
	lme4	22.76(1.96)	24.88(2.60)	28.72(3.10)	47.34(16.29)
0.10	MM	7.07(4.78)	6.29(4.94)	5.14(3.72)	3.95(2.23)
	EM	78.96(66.19)	35.48(45.81)	19.53(27.71)	9.67(13.56)
	FS	17.36(11.26)	14.44(9.00)	12.08(6.31)	11.47(2.40)
	lme4	22.66(1.83)	28.90(8.70)	30.16(4.43)	44.58(4.89)
1.00	MM	2.66(2.61)	3.22(2.91)	3.57(3.15)	3.85(2.50)
	EM	10.71(23.93)	15.88(27.52)	8.35(16.26)	11.34(16.65)
	FS	7.88(5.44)	9.10(4.95)	7.12(2.42)	8.46(2.27)
	lme4	23.12(1.75)	30.22(9.37)	29.96(4.47)	42.82(8.32)
10.00	MM	2.48(2.72)	3.24(3.19)	3.84(3.35)	3.35(1.71)
	EM	9.66(22.02)	15.98(26.57)	10.24(18.78)	10.27(15.40)
	FS	15.19(6.05)	16.39(6.11)	15.81(5.15)	18.14(5.46)
	lme4	35.02(3.83)	47.12(8.10)	63.24(15.33)	102.78(34.49)
20.00	MM	2.57(2.49)	3.13(3.53)	3.13(2.44)	3.07(1.81)
	EM	12.28(25.71)	8.44(16.89)	8.01(17.12)	5.47(9.76)
	FS	22.09(8.53)	22.03(6.14)	23.08(7.21)	23.99(7.38)
	lme4	37.34(12.91)	50.24(8.59)	63.62(17.39)	91.14(28.39)

Genetic model:

We simulated a quantitative trait y from a genetic model with two variance components and covariance matrix $\mathbf{\Omega }={\sigma }_a^2\widehat{\mathbf{\Phi }}+{\sigma }_e^2\mathit{I}$, where $\widehat{\mathbf{\Phi }}$ is a full-rank empirical kinship matrix estimated from the genome-wide measurements of 212 individuals using Option 29 of the Mendel software (Lange et al., 2013). In this example, MM had run times similar to Fisher scoring, and both were much faster than EM and lme4.

In summary, the MM algorithm appears competitive even in small-scale examples. Many applications involve a large number of variance components. In this setting, the EM algorithm suffers from slow convergence and Fisher scoring from an extremely high cost per iteration. Our genomic example in Section 7 reinforces this point.

4. Global convergence of the MM algorithm

The Karush-Kuhn-Tucker (KKT) necessary conditions for a local maximum ${\sigma }^2=({\sigma }_1^2,\dots ,{\sigma }_m^2)$ of the log-likelihood (1) require each component of the score vector to satisfy

$$\frac{\partial }{\partial {\sigma }_i^2}L\left({\mathit{\sigma }}^2\right)\in \{\begin{array}{c}\left\{0\right\}\\ \left(-\infty ,0\right]\end{array}\hspace{1em}\begin{array}{c}{\sigma }_i^2>0\\ {\sigma }_i^2=0.\end{array}$$

In this section we establish the global convergence of Algorithm 1 to a KKT point. To reduce the notational burden, we assume that X is null and omit estimation of fixed effects β. The analysis easily extends to the nontrivial X case. Our convergence analysis relies on characterizing the properties of the objective function L(σ²) and the MM algorithmic mapping ${\mathit{\sigma }}^2\mapsto M\left({\mathit{\sigma }}^2\right)$ defined by equation (8). Special attention must be paid to the boundary values ${\sigma }_i^2=0$. We prove convergences for two cases, which cover most applications. For example, the genetic model in Section 3 satisfies Assumption 1, while the two-way ANOVA model satisfies Assumption 2.

Assumption 1. All V_i are positive definite.

Assumption 2. V₁ is positive definite, each V_i is nontrivial, $\mathcal{H}=\mathit{\text{span}}\{{\mathit{V}}_2,\dots ,{\mathit{V}}_m\}$ has dimension q < n, and $\mathit{y}\notin \mathcal{H}$.

The key condition $\mathit{y}\notin \text{span}\left\{{\mathit{V}}_2,\dots ,{\mathit{V}}_m\right\}$ in the second case is also necessary for the existence of an MLE or REML (Demidenko and Massam, 1999; Grzadziel and Michalski, 2014). In Supplementary Materials S.4, we derive a sequence of lemmas en route to the global convergence result declared in Theorem 1.

Theorem 1. Under either Assumption 1 or 2, the MM sequence ${\left\{{\mathit{\sigma }}^{2\left(t\right)}\right\}}_{t\ge 0}$ has at least one limit point. Every limit point is a fixed point of M (σ²). If the set of fixed points is discrete, then the MM sequence converges to one of them. Finally, when the iterates converge, their limit is a KKT point.

5. MM versus EM

Examination of Tables 2 and 3 suggests that the MM algorithm usually converges faster than the EM algorithm. We now provide an explanation for this observation. Again for notational convenience, we consider the REML case where X is null. Since the EM principle is just a special instance of the MM principle, we can compare their convergence properties in a unified framework. Consider an MM map M (θ) for maximizing the objective function f (θ) via the surrogate function g(θ | θ^(t)). Close to the optimal point ${\mathit{\theta }}^{\infty }$,

$${\mathit{\theta }}^{\left(t+1\right)}-{\mathit{\theta }}^{\infty }\approx dM\left({\mathit{\theta }}^{\infty }\right)\left({\mathit{\theta }}^{\left(t\right)}-{\mathit{\theta }}^{\infty }\right),$$

where $dM\left({\mathit{\theta }}^{\infty }\right)$ is the differential of the mapping M at the optimal point ${\mathit{\theta }}^{\infty }$ of f (θ). Hence, the local convergence rate of the sequence θ^(t+1) = M (θ^(t)) coincides with the spectral radius of $dM\left({\mathit{\theta }}^{\infty }\right)$. Familiar calculations (Lange, 2010) demonstrate that

$$dM\left({\mathit{\theta }}^{\infty }\right)=\mathit{I}-{\left[d^{2}g\left({\mathit{\theta }}^{\infty }|{\mathit{\theta }}^{\infty }\right)\right]}^{-1}{d}^{2}f\left({\mathit{\theta }}^{\infty }\right).$$

In other words, the local convergence rate is determined by how well the surrogate surface $g\left(\mathit{\theta }|{\mathit{\theta }}^{\infty }\right)$ approximates the objective surface f (θ) near the optimal point ${\mathit{\theta }}^{\infty }$. In the EM literature, $dM\left({\mathit{\theta }}^{\infty }\right)$ is called the rate matrix (Meng and Rubin, 1991). Fast convergence occurs when the surrogate $g\left(\mathit{\theta }|{\mathit{\theta }}^{\infty }\right)$ hugs the objective f (θ) tightly around ${\mathit{\theta }}^{\infty }$. Figure 1 shows a case where the MM surrogate locally dominates the EM surrogate. We demonstrate that this is no accident.

Table 3:

MM and Fisher scoring (FS) show superior performance than EM and lme4. Shown below are average performance for fitting a genetic model. Standard errors are given in parentheses.

${\sigma }_a^2/{\sigma }_e^2$	Method	Iteration	Runtime (ms)	Objective
0.00	MM	198.02(102.23)	133.61(822.67)	−375.59(9.63)
	EM	1196.10(958.51)	29.71(12.34)	−375.60(9.64)
	FS	7.60(3.07)	19.34(33.77)	−375.59(9.63)
	lme4	–	401.02(142.04)	−375.59(9.64)
0.05	MM	185.86(99.41)	17.26(1.76)	−377.39(10.52)
	EM	1227.62(1030.07)	29.82(12.74)	−377.40(10.52)
	FS	7.84(2.74)	14.97(1.55)	−377.39(10.52)
	lme4	–	425.04(144.00)	−377.39(10.52)
0.10	MM	169.24(99.75)	16.97(1.59)	−378.40(11.44)
	EM	924.80(912.23)	26.06(11.26)	−378.41(11.45)
	FS	7.32(2.75)	15.06(1.38)	−378.40(11.44)
	lme4	–	435.14(128.87)	−378.40(11.44)
1.00	MM	58.96(23.69)	15.53(0.75)	−409.54(10.90)
	EM	105.10(79.65)	15.49(0.96)	−409.54(10.90)
	FS	5.80(1.05)	14.66(0.89)	−409.54(10.90)
	lme4	–	493.14(52.80)	−409.54(10.90)
10.00	MM	110.00(63.13)	16.22(1.12)	−532.48(8.77)
	EM	642.48(1470.38)	22.32(18.37)	−532.57(8.75)
	FS	14.98(5.21)	14.78(0.97)	−531.72(8.92)
	lme4	–	2897.12(15006.38)	−532.48(8.77)
20.00	MM	110.52(34.81)	16.07(0.91)	−590.87(7.15)
	EM	1014.22(1775.40)	27.03(22.33)	−590.89(7.15)
	FS	17.72(3.13)	14.79(0.93)	−588.46(7.27)
	lme4	–	5059.24(20692.67)	−590.79(7.15)

The Q-function in the EM algorithm

$$\begin{gathered} g_{\text{EM}}\left({\mathit{\sigma }}^2|{\mathit{\sigma }}^{2\left(t\right)}\right)=-\frac{1}{2}\sum _{i=1}^m\left[\text{rank}\left({\mathit{V}}_i\right)\cdot \ln {\sigma }_i^2+\text{rank}\left({\mathit{V}}_i\right)\frac{{\sigma }_i^{2\left(t\right)}}{{\sigma }_i^2}-\frac{{\sigma }_i^{4\left(t\right)}}{{\sigma }_i^2}\text{tr}\left({\mathbf{\Omega }}^{-\left(t\right)}{\mathit{V}}_i\right)\right] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-\frac{1}{2}\sum _{i=1}^m\frac{{\sigma }_i^{4\left(t\right)}}{{\sigma }_i^2}{\mathit{y}}^T{\mathbf{\Omega }}^{-\left(t\right)}{\mathit{V}}_i{\mathbf{\Omega }}^{-\left(t\right)}\mathit{y} \end{gathered}$$

minorizes the log-likelihood up to an irrelevant constant. Supplementary Materials S.6 gives a detailed derivation for the more general multivariate response case. Both surrogates g_EM(σ² | σ^2(∞)) and g_MM(σ² | σ^2(∞)) are parameter separated. This implies that both second differentials $d^2{g}_{\text{EM}}\left({\mathit{\sigma }}^{2\left(\infty \right)}|{\mathit{\sigma }}^{2\left(\infty \right)}\right)$ and $d^2{g}_{\text{MM}}\left({\mathit{\sigma }}^{2\left(\infty \right)}|{\mathit{\sigma }}^{2\left(\infty \right)}\right)$ are diagonal. A small diagonal entry of either matrix indicates fast convergence of the corresponding variance component. Our next result shows that, under Assumption 1, on average the diagonal entries of $d^2{g}_{\text{EM}}\left({\mathit{\sigma }}^{2\left(\infty \right)}|{\mathit{\sigma }}^{2\left(\infty \right)}\right)$ dominate those of $d^2{g}_{\text{MM}}\left({\mathit{\sigma }}^{2\left(\infty \right)}|{\mathit{\sigma }}^{2\left(\infty \right)}\right)$ when m > 2. Thus, the EM algorithm tends to converge more slowly than the MM algorithm, and the difference is more pronounced as the number of variance components m grows. See Supplementary Materials S.4 for the proof.

Theorem 2. Let ${\mathit{\sigma }}^{2\left(\infty \right)}\succ 0_m$ be a common limit point of the EM and MM algorithms. Then both second differentials $d^2{g}_{MM}\left({\mathit{\sigma }}^{2\left(\infty \right)}|{\mathit{\sigma }}^{2\left(\infty \right)}\right)$ and $d^2{g}_{EM}\left({\mathit{\sigma }}^{2\left(\infty \right)}|{\mathit{\sigma }}^{2\left(\infty \right)}\right)$ are diagonal with

$$\begin{gathered} d^2{g}_{EM}{\left({\mathit{\sigma }}^{2\left(\infty \right)}|{\mathit{\sigma }}^{2\left(\infty \right)}\right)}_{ii}=-\frac{\text{rank}\left({\mathit{V}}_i\right)}{2{\sigma }_i^{4\left(\infty \right)}} \\ {d}^2{g}_{MM}{\left({\mathit{\sigma }}^{2\left(\infty \right)}|{\mathit{\sigma }}^{2\left(\infty \right)}\right)}_{ii}=-\frac{{\mathit{y}}^T{\mathbf{\Omega }}^{-\left(\infty \right)}{\mathit{V}}_i{\mathbf{\Omega }}^{-\left(\infty \right)}\mathit{y}}{{\sigma }_i^{2\left(\infty \right)}}=-\frac{\text{tr}\left({\mathbf{\Omega }}^{-\left(\infty \right)}{\mathit{V}}_i\right)}{{\sigma }_i^{2\left(\infty \right)}}. \end{gathered}$$

Furthermore, the average ratio

$$\frac{1}{m}\sum _{i=1}^m\frac{d^2{g}_{MM}{\left({\mathit{\sigma }}^{2\left(\infty \right)}|{\mathit{\sigma }}^{2\left(\infty \right)}\right)}_{ii}}{d^2{g}_{EM}{\left({\mathit{\sigma }}^{2\left(\infty \right)}|{\mathit{\sigma }}^{2\left(\infty \right)}\right)}_{ii}}=\frac{2}{mn}\sum _{i=1}^m\text{tr}\left({\mathbf{\Omega }}^{-\left(\infty \right)}{\sigma }_i^{2\left(\infty \right)}{\mathit{V}}_i\right)=\frac{2}{m}<1$$

for m > 2 when all V_i have full rank n.

It is not clear whether a similar result holds under Assumption 2. Empirically we observed faster convergence of MM than EM, for example, in the two-way ANOVA example (Table 1). Also note that both the EM and MM algorithms must evaluate the traces tr(Ω^−(t)V_i) and quadratic forms (y − Xβ^(t))^T Ω^−(t)V_iΩ^−(t)(y − Xβ^(t)) at each iteration. Since these quantities are also the building blocks of the approximate rate matrices d²g(σ^2(t) | σ^2(t)), one can rationally choose either the EM or MM updates based on which has smaller diagonal entries measured by the ${\mathcal{l}}_1$, ${\mathcal{l}}_2$ or ${\mathcal{l}}_{\infty }$ norms. At negligible extra cost, this produces a hybrid algorithm that retains the ascent property and enjoys the better of the two convergence rates under either Assumption 1 or 2.

6. Extensions

Besides its competitive numerical performance, Algorithm 1 is attractive for its simplicity and ease of generalization. In this section, we outline MM algorithms for multivariate response models possibly with missing data, linear mixed models, MAP estimation, and penalized estimation.

6.1. Multivariate response model

Consider the multivariate response model with n × d response matrix Y, which has no missing entries, mean E Y = XB, and covariance

$$\mathbf{\Omega }=\text{Cov}\left(\text{vec}\mathit{Y}\right)=\sum _{i=1}^m{\mathbf{\Gamma }}_i\otimes {\mathit{V}}_i.$$

The p × d coefficient matrix B collects the fixed effects, the Γ_i are unknown d × d variance components, and the V_i are known n × n covariance matrices. If the vector vecY is normally distributed, then Y equals a sum of independent matrix normal distributions (Gupta and Nagar, 1999). We now make this assumption and pursue estimation of B and the Γ_i, which we collectively denote as Γ. Under the normality assumption, Roth’s Kronecker product identity vec(CDE) = (E^T ⊗ C)vec(D) yields the log-likelihood

$$\begin{gathered} L\left(B,\mathbf{\Gamma }\right)=-\frac{1}{2}\ln \det \mathbf{\Omega }-\frac{1}{2}\text{vec}{\left(\mathit{Y}-\mathit{X}B\right)}^T{\mathbf{\Omega }}^{-1}\text{vec}\left(\mathit{Y}-\mathit{X}B\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=-\frac{1}{2}\ln \det \mathbf{\Omega }-\frac{1}{2}{\left[\text{vec}\mathit{Y}-\left(I_d\otimes \mathit{X}\right)\text{vec}B\right]}^T{\mathbf{\Omega }}^{-1}\left[\text{vec}\mathit{Y}-\left(I_d\otimes \mathit{X}\right)\text{vec}B\right]. \end{gathered}$$ (11)

Updating B given Γ^(t) is accomplished by solving the general least squares problem met earlier in the univariate case. Update of Γ_i given B^(t) is difficult due to the positive semidefiniteness constraint. Typical solutions involve reparameterization of the covariance matrix (Pinheiro and Bates, 1996). The MM algorithm derived in this section gracefully accommodates the covariance constraints.

Updating Γ given B^(t) requires generalizing the minorization (5). In view of Lemma 1 and the identities (A ⊗ B)(C ⊗ D) = (AC) ⊗(BD) and (A ⊗ B)⁻¹ = A⁻¹ ⊗ B⁻¹, we have

$$\begin{gathered} {\mathbf{\Omega }}^{\left(t\right)}{\mathbf{\Omega }}^{-1}{\mathbf{\Omega }}^{\left(t\right)}=m\left[\frac{1}{m}\sum _{i=1}^m{\mathbf{\Gamma }}_i^{\left(t\right)}\otimes {\mathit{V}}_i\right]{\left[\frac{1}{m}\sum _{i=1}^m{\mathbf{\Gamma }}_i\otimes {\mathit{V}}_i\right]}^{-1}\left[\frac{1}{m}\sum _{i=1}^m{\mathbf{\Gamma }}_i^{\left(t\right)}\otimes {\mathit{V}}_i\right] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}⪯m\frac{1}{m}\sum _{i=1}^m\left({\mathbf{\Gamma }}_i^{\left(t\right)}\otimes {\mathit{V}}_i\right){\left({\mathbf{\Gamma }}_i\otimes {\mathit{V}}_i\right)}^{-1}\left({\mathbf{\Gamma }}_i^{\left(t\right)}\otimes {\mathit{V}}_i\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\sum _{i=1}^m\left({\mathbf{\Gamma }}_i^{\left(t\right)}{\mathbf{\Gamma }}_i^{-1}{\mathbf{\Gamma }}_i^{\left(t\right)}\right)\otimes {\mathit{V}}_i, \end{gathered}$$

or equivalently

$${\mathbf{\Omega }}^{-1}⪯{\mathbf{\Omega }}^{-\left(t\right)}\left[\sum _{i=1}^m\left({\mathbf{\Gamma }}_i^{\left(t\right)}{\mathbf{\Gamma }}_i^{-1}{\mathbf{\Gamma }}_i^{\left(t\right)}\right)\otimes {\mathit{V}}_i\right]{\mathbf{\Omega }}^{-\left(t\right)}.$$ (12)

This derivation relies on the invertibility of the matrices V_i. One can relax this assumption by substituting V_ϵ,i = V_i + ϵI_n for V_i and sending s to 0.

The majorization (12) and the minorization (6) jointly yield the surrogate

$$g\left(\mathbf{\Gamma }|{\mathbf{\Gamma }}^{\left(t\right)}\right)=-\frac{1}{2}\sum _{i=1}^m\left\{\text{tr}\left[{\mathbf{\Omega }}^{-\left(t\right)}\left({\mathbf{\Gamma }}_i\otimes {\mathit{V}}_i\right)\right]+{\left(\text{vec}{\mathit{R}}^{\left(t\right)}\right)}^T\left[\left({\mathbf{\Gamma }}_i^{\left(t\right)}{\mathbf{\Gamma }}_i^{-1}{\mathbf{\Gamma }}_i^{\left(t\right)}\right)\otimes {\mathit{V}}_i\right]\left(\text{vec}{\mathit{R}}^{\left(t\right)}\right)\right\}+c^{\left(t\right)},$$

where R^(t) is the n × d matrix satisfying vec R^(t) = Ω^−(t)vec(Y − XB^(t)) and c^(t) is an irrelevant constant. Based on the Kronecker identities (vec A)^T vec B = tr(A^T B) and vec(CDE) = (E^T ⊗ C)vec(D), the surrogate can be rewritten as

$$\begin{gathered} g\left(\mathbf{\Gamma }|{\mathbf{\Gamma }}^{\left(t\right)}\right)=-\frac{1}{2}\sum _{i=1}^m\left\{\text{tr}\left[{\mathbf{\Omega }}^{-\left(t\right)}\left({\mathbf{\Gamma }}_i\otimes {\mathit{V}}_i\right)\right]+\text{tr}\left({\mathit{R}}^{\left(t\right)T}{\mathit{V}}_i{\mathit{R}}^{\left(t\right)}{\mathbf{\Gamma }}_i^{\left(t\right)}{\mathbf{\Gamma }}_i^{-1}{\mathbf{\Gamma }}_i^{\left(t\right)}\right)\right\}+c^{\left(t\right)} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=-\frac{1}{2}\sum _{i=1}^m\left\{\text{tr}\left[{\mathbf{\Omega }}^{-\left(t\right)}\left({\mathbf{\Gamma }}_i\otimes {\mathit{V}}_i\right)\right]+\text{tr}\left({\mathbf{\Gamma }}_i^{\left(t\right)}{\mathit{R}}^{\left(t\right)T}{\mathit{V}}_i{\mathit{R}}^{\left(t\right)}{\mathbf{\Gamma }}_i^{\left(t\right)}{\mathbf{\Gamma }}_i^{-1}\right)\right\}+c^{\left(t\right)}. \end{gathered}$$

The first trace is linear in Γ_i with the coefficient of entry (Γ_i)_jk equal to

$$\text{tr}\left({\mathbf{\Omega }}_{jk}^{-\left(t\right)}{\mathit{V}}_i\right)=1_n^T\left({\mathit{V}}_i\odot {\mathbf{\Omega }}_{jk}^{-\left(t\right)}\right)1_n,$$

where ${\mathbf{\Omega }}_{jk}^{-\left(t\right)}$ is the (j, k)-th n × n block of Ω^−(t) and $\odot$ indicates elementwise product. The matrix M_i of these coefficients can be written as

$$M_i={\left(I_d\otimes 1_n\right)}^T\left[\left(1_n{1}_d^T\otimes {\mathit{V}}_i\right)\odot {\mathbf{\Omega }}^{-\left(t\right)}\right]\left(I_d\otimes 1_n\right).$$

The directional derivative of g(Γ | Γ^(t)) with respect to Γ_i in the direction Δ_i is

$$\begin{gathered} -\frac{1}{2}\text{tr}\left({\mathit{M}}_i{\mathbf{\Delta }}_i\right)+\frac{1}{2}\text{tr}\left({\mathbf{\Gamma }}_i^{\left(t\right)}{R}^{\left(t\right)T}{\mathit{V}}_i{R}^{\left(t\right)}{\mathbf{\Gamma }}_i^{-1}{\mathbf{\Delta }}_i{\mathbf{\Gamma }}_i^{-1}\right) \\ =-\frac{1}{2}\text{tr}\left({\mathit{M}}_i{\mathbf{\Delta }}_i\right)+\frac{1}{2}\text{tr}\left({\mathbf{\Gamma }}_i^{-1}{\mathbf{\Gamma }}_i^{\left(t\right)}{R}^{\left(t\right)T}{\mathit{V}}_i{R}^{\left(t\right)}{\mathbf{\Gamma }}_i^{\left(t\right)}{\mathbf{\Gamma }}_i^{-1}{\mathbf{\Delta }}_i\right). \end{gathered}$$

Because all directional derivatives of g(Γ | Γ^(t)) vanish at a stationarity point, the matrix equation

$$M_i={\mathbf{\Gamma }}_i^{-1}{\mathbf{\Gamma }}_i^{\left(t\right)}{\mathit{R}}^{\left(t\right)T}{\mathit{V}}_i{\mathit{R}}^{\left(t\right)}{\mathbf{\Gamma }}_i^{\left(t\right)}{\mathbf{\Gamma }}_i^{-1}$$ (13)

holds. Fortunately, this equation admits an explicit solution. For positive scalers a and b, the solution to the equation $b=X^{-1}a{X}^{-1}$ is $X=\pm \sqrt{a/b}$. The matrix analogue of this equation is the Riccati equation B = X⁻¹AX⁻¹, whose solution is summarized in the next lemma.

Lemma 3. Assume A and B are positive definite and L is the Cholesky factor of B. Then Y = L^−T (L^T AL)^1/2L⁻¹ is the unique positive definite solution to the matrix equation B = X⁻¹AX⁻¹.

The Cholesky factor L in Lemma 3 can be replaced by the symmetric square root of B. The solution, which is unique, remains the same. The Cholesky decomposition is preferred for its cheaper computational cost and better numerical stability.

Algorithm 3 summarizes the MM algorithm for fitting the multi-response model (3). Each iteration invokes m Cholesky decompositions and symmetric square roots of d × d positive definite matrices. Fortunately in most applications, d is a small number. The following result guarantees the non-singularity of the Cholesky factor throughout the iterations. See Supplementary Materials S.8 for the proof.

Proposition 2. Assume V_i has strictly positive diagonal entries. Then the symmetric matrix ${\mathit{M}}_i={\left(I_d\otimes 1_n\right)}^T\left[\left(1_d{1}_d^T\otimes {\mathit{V}}_i\right)\odot {\mathbf{\Omega }}^{-\left(t\right)}\right]\left(I_d\otimes 1_n\right)$ is positive definite for all t. Furthermore if ${\mathbf{\Gamma }}_i^{\left(0\right)}\succ 0$ and no column of R^(t) lies in the null space of V_i for all t, then ${\mathbf{\Gamma }}_i^{\left(t\right)}\succ 0$ for all t.

Multivariate response, two variance components

When there are m = 2 variance components Ω = Γ₁ ⊗V₁ + Γ₂ ⊗V₂, repeated inversion of the nd×nd covariance matrix Ω reduces to a single n×n simultaneous congruence decomposition and, per iteration, two d×d Cholesky decompositions and one d×d simultaneous congruence decomposition. The simultaneous congruence decomposition of the matrix pair (V₁, V₂) involves generalized eigenvalues d = (d₁, …, d_n) and a nonsingular matrix U such that U ^T V₁U = D = diag(d) and U ^T V₂U = I. If the simultaneous congruence decomposition of $\left({\mathbf{\Gamma }}_1^{\left(t\right)},{\mathbf{\Gamma }}_2^{\left(t\right)}\right)$ is $\left({\mathbf{\Lambda }}^{\left(t\right)},{\mathrm{\Phi }}^{\left(t\right)}\right)$ with ${\mathrm{\Phi }}^{\left(t\right)T}{\mathbf{\Gamma }}_1^{\left(t\right)}{\mathrm{\Phi }}^{\left(t\right)}={\mathbf{\Lambda }}^{\left(t\right)}=\text{diag}\left({\lambda }^{\left(t\right)}\right)$ and ${\mathrm{\Phi }}^{\left(t\right)T}{\mathbf{\Gamma }}_2^{\left(t\right)}{\mathrm{\Phi }}^{\left(t\right)}=I_d$, then

$$\begin{gathered} \hspace{0.17em}\hspace{0.17em}\hspace{1em}{\mathbf{\Omega }}^{\left(t\right)}={\left({\mathrm{\Phi }}^{-\left(t\right)}\otimes {\mathit{U}}^{-1}\right)}^T\left({\mathbf{\Lambda }}^{\left(t\right)}\otimes \mathit{D}+{\mathit{I}}_{\mathit{D}}\otimes {\mathit{I}}_n\right)\left({\mathrm{\Phi }}^{-\left(t\right)}\otimes {\mathit{U}}^{-1}\right) \\ \hspace{1em}{\mathbf{\Omega }}^{-\left(t\right)}=\left({\mathrm{\Phi }}^{\left(t\right)}\otimes \mathit{U}\right){\left({\mathbf{\Lambda }}^{\left(t\right)}\otimes \mathit{D}+{\mathit{I}}_{\mathit{D}}\otimes {\mathit{I}}_n\right)}^{-1}{\left({\mathrm{\Phi }}^{\left(t\right)}\otimes \mathit{U}\right)}^T \\ \det {\mathbf{\Omega }}^{\left(t\right)}=\det \left({\mathbf{\Lambda }}^{\left(t\right)}\otimes \mathit{D}+{\mathit{I}}_{\mathit{D}}\otimes {\mathit{I}}_n\right)\det \left[{\left({\mathrm{\Phi }}^{-\left(t\right)}\otimes {\mathit{U}}^{-1}\right)}^T\left({\mathrm{\Phi }}^{-\left(t\right)}\otimes {\mathit{U}}^{-1}\right)\right] \\ \hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\det \left({\mathbf{\Lambda }}^{\left(t\right)}\otimes \mathit{D}+{\mathit{I}}_{\mathit{D}}\otimes {\mathit{I}}_n\right)\det \left({\mathbf{\Gamma }}_2^{\left(t\right)}\otimes {\mathit{V}}_2\right) \\ \hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\det \left({\mathbf{\Lambda }}^{\left(t\right)}\otimes \mathit{D}+{\mathit{I}}_{\mathit{D}}\otimes {\mathit{I}}_n\right)\det {\left({\mathbf{\Gamma }}_2^{\left(t\right)}\right)}^n\det {\left({\mathit{V}}_2\right)}^{\mathit{D}}. \end{gathered}$$

Updating the fixed effects reduces to a weighted least squares problem for the transformed responses $\tilde{Y}={\mathit{U}}^T\mathit{Y}$, transformed predictor matrix $\tilde{\mathit{X}}={\mathit{U}}^T\mathit{X}$, and observation weights ${({\lambda }_k^{\left(t\right)}{d}_i+1)}^{-1}$. Algorithm 4 summarizes the simplified MM algorithm. The lengthy derivations are relegated to Supplementary Materials S.5.

6.2. Multivariate response model with missing responses

In many applications the multivariate response model (11) involves missing responses. For instance, in testing multiple longitudinal traits in genetics, some trait values y_ij may be missing due to dropped patient visits, while their genetic covariates are complete. Missing data destroys the symmetry of the log-likelihood (11) and complicates finding the MLE. Fortunately, MM algorithm 3 easily adapts to this challenge.

The familiar EM argument (McLachlan and Krishnan, 2008, Section 2.2) shows that

$$-\frac{n}{2}\ln \det {\mathbf{\Omega }}^{(t)}-\frac{1}{2}\text{tr}\{{\mathbf{\Omega }}^{-(t)}[\text{vec}(Z^{(t)}-\mathit{X}{B}^{(t)})\text{vec}{({\mathit{Z}}^{(t)}-\mathit{X}{\mathit{B}}^{(t)})}^T+{\mathit{C}}^{(t)}]\}$$ (14)

minorizes the observed log-likelihood at the current iterate $(B^{\left(t\right)},{\mathbf{\Gamma }}_1^{\left(t\right)},\dots ,{\mathbf{\Gamma }}_m^{\left(t\right)})$. Here Z^(t) is the completed response matrix given the observed responses $Y_{obs}^{\left(t\right)}$ and the current parameter values. The complete data Y is assumed to be normally distributed N (vec(XB^(t)), Ω^(t)). The block matrix C^(t) is 0 except for a lower-right block consisting of a Schur complement.

To maximize the surrogate (14), we invoke the familiar minorization (6) and majorization (12) to separate the variance components Γ_i. At each iteration we impute missing entries by their conditional means, compute their conditional variances and covariances to supply the Schur complement, and then update the fixed effects and variance components by the explicit updates of Algorithm 3. The required conditional means and conditional variances can be conveniently obtained in the process of inverting Ω^(t) by the sweep operator of computational statistics (Lange, 2010, Section 7.3).

6.3. Linear mixed model (LMM)

The linear mixed model plays a central role in longitudinal data analysis. Consider the single-level LMM (Laird and Ware, 1982; Bates and Pinheiro, 1998) for n independent data clusters (y_i, X_i, Z_i) with

$$Y_i={\mathit{X}}_i\beta +{\mathit{Z}}_i{\gamma }_i+{ϵ}_i,\hspace{1em}i=1,\dots ,n,$$

where β is a vector of fixed effects, the γi ∼ N (0, R_i(θ)) are independent random effects, and ${ϵ}_i\sim N\left(0,{\mathit{\sigma }}^2{I}_{n_i}\right)$ captures random noise independent of γi. We assume the matrices Z_i have full column rank. The within-cluster covariance matrices R_i(θ) depend on a parameter vector θ; typical choices for R_i(θ) impose autocorrelation, compound symmetry, or unstructured correlation. It is clear that Y_i is normal with mean X_iβ, covariance ${\mathbf{\Omega }}_i={\mathit{Z}}_i{\mathit{R}}_i\left(\theta \right){\mathit{Z}}_i^T+{\mathit{\sigma }}^2{\mathit{I}}_{n_i},$ and log-likelihood

$$L_i\left(\beta ,\theta ,{\mathit{\sigma }}^2\right)=-\frac{1}{2}\ln \det {\mathbf{\Omega }}_i-\frac{1}{2}{\left({\mathit{y}}_i-{\mathit{X}}_i\beta \right)}^T{\mathbf{\Omega }}_i^{-1}\left({\mathit{y}}_i-{\mathit{X}}_i\beta \right).$$

The next three technical facts about pseudo-inverses are used in deriving the MM algorithm for LMM and their proofs are in Supplementary Materials S.9-S.11.

Lemma 4. If A has full column rank and B has full row rank, then (AB)⁺ = B⁺A⁺.

Lemma 5. If A and B are positive semidefinite matrices with the same range, then

$$\underset{ϵ\downarrow 0}{\lim }\left(\mathit{B}+ϵ\mathit{I}\right){\left(\mathit{A}+ϵ\mathit{I}\right)}^{-1}\left(\mathit{B}+ϵ\mathit{I}\right)=\mathit{B}{\mathit{A}}^{+}\mathit{B}.$$

Lemma 6. If R and S are positive definite matrices, and the conformable matrix Z has full column rank, then the matrices ZRZ^T and ZSZ^T share a common range.

The convexity of the map $\left(\mathit{X},Y\right)\mapsto {\mathit{X}}^T{\mathit{Y}}^{-1}\mathit{X}$ and Lemmas 4–6 now yield via the obvious limiting argument the majorization

$$\begin{gathered} {\mathbf{\Omega }}^{\left(t\right)}{\mathbf{\Omega }}^{-1}{\mathbf{\Omega }}^{\left(t\right)}=\left({\mathit{Z}}_i{\mathit{R}}_i\left({\theta }^{\left(t\right)}\right){\mathit{Z}}_i^T+{\mathit{\sigma }}^{2\left(t\right)}{\mathit{I}}_{n_i}\right){\left({\mathit{Z}}_i{\mathit{R}}_i\left(\theta \right){\mathit{Z}}_i^T+{\mathit{\sigma }}^2{\mathit{I}}_{n_i}\right)}^{-1}\left({\mathit{Z}}_i{\mathit{R}}_i\left({\theta }^{\left(t\right)}\right){\mathit{Z}}_i^T+{\mathit{\sigma }}^{2\left(t\right)}{\mathit{I}}_{n_i}\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}⪯\left({\mathit{Z}}_i{\mathit{R}}_i\left({\theta }^{\left(t\right)}\right){\mathit{Z}}_i^T\right){\left({\mathit{Z}}_i{\mathit{R}}_i\left(\theta \right){\mathit{Z}}_i^T\right)}^{+}\left({\mathit{Z}}_i{\mathit{R}}_i\left({\theta }^{\left(t\right)}\right){\mathit{Z}}_i^T\right)+\frac{{\mathit{\sigma }}^{4\left(t\right)}}{{\mathit{\sigma }}^2}{\mathit{I}}_{n_i} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}=\left[{\mathit{Z}}_i{\mathit{R}}_i\left({\theta }^{\left(t\right)}\right){\mathit{Z}}_i^T{\mathit{Z}}_i^{T+}\right]{\mathit{R}}_i^{-1}\left(\theta \right)\left[{\mathit{Z}}_i^{+}{\mathit{Z}}_i{\mathit{R}}_i\left({\theta }^{\left(t\right)}\right){\mathit{Z}}_i^T\right]+\frac{{\mathit{\sigma }}^{4\left(t\right)}}{{\mathit{\sigma }}^2}{\mathit{I}}_{n_i}. \end{gathered}$$

In combination with the minorization (6), this gives the surrogate

$$\begin{gathered} g_i(\theta ,{\mathit{\sigma }}^2|{\theta }^{(t)},{\mathit{\sigma }}^{2(t)})=-\frac{1}{2}\text{tr}({\mathit{Z}}_i^T{\mathbf{\Omega }}_i^{-(t)}{\mathit{Z}}_i{\mathit{R}}_i(\theta ))-\frac{1}{2}{r}_i^{(t)T}{\mathit{R}}_i^{-1}(\theta )r_i^{(t)} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-\frac{1}{2}\text{tr}({\mathbf{\Omega }}_i^{-(t)})-\frac{{\mathit{\sigma }}^{4(t)}}{2{\mathit{\sigma }}^2}{({\mathit{y}}_i-{\mathit{X}}_i{\beta }^{(t)})}^T{\mathbf{\Omega }}_i^{-2(t)}({\mathit{y}}_i-{\mathit{X}}_i{\beta }^{(t)})+c^{(t)}, \end{gathered}$$

for the log-likelihood L_i(θ, σ²), where

$${\mathit{r}}_i^{\left(t\right)}=\left({\mathit{Z}}_i^{+}{\mathit{Z}}_i{\mathit{R}}_i\left({\mathit{\theta }}^{\left(t\right)}\right){\mathit{Z}}_i^T\right){\mathbf{\Omega }}_i^{-\left(t\right)}\left({\mathit{y}}_i-{\mathit{X}}_i{\beta }^{\left(t\right)}\right)={\mathit{R}}_i\left({\mathit{\theta }}^{\left(t\right)}\right){\mathit{Z}}_i^T{\mathbf{\Omega }}_i^{-\left(t\right)}\left({\mathit{y}}_i-{\mathit{X}}_i{\beta }^{\left(t\right)}\right).$$

The parameters θ and σ² are nicely separated. To maximize the overall minorization function ${\sum }_i{g}_i\left(\mathit{\theta },{\sigma }^2|{\mathit{\theta }}^{\left(t\right)},{\sigma }^{2\left(t\right)}\right)$, we update σ² via

$${\sigma }^{2\left(t+1\right)}={\sigma }^{2\left(t\right)}\sqrt{\frac{{\sum }_i{\left({\mathit{y}}_i-{\mathit{X}}_i{\beta }^{\left(t\right)}\right)}^T{\mathbf{\Omega }}_i^{-2\left(t\right)}\left({\mathit{y}}_i-{\mathit{X}}_i{\beta }^{\left(t\right)}\right)}{{\sum }_i\text{tr}\left({\mathbf{\Omega }}_i^{-\left(t\right)}\right)}}.$$

For structured models such as autocorrelation and compound symmetry, updating θ is a low-dimensional optimization problem that can be approached through the stationarity condition

$${\sum _i\text{vec}({\mathit{Z}}_i^T{\mathbf{\Omega }}_i^{(T)}{\mathit{Z}}_i-{\mathit{R}}_i^{-1}(\theta ){\mathit{r}}_i^{(t)}{\mathit{r}}_i^{(t)T}{\mathit{R}}_i^{-1}(\theta ))}^T\frac{\partial }{\partial {\theta }_j}\text{vec}\hspace{0.17em}{\mathit{R}}_i(\theta )=0$$

for each component θ_j. For the unstructured model with R_i(θ) = R for all i, the stationarity condition reads

$$\sum _i{\mathit{Z}}_i^T{\mathbf{\Omega }}_i^{\left(t\right)}{\mathit{Z}}_i={\mathit{R}}^{-1}\left(\sum _i{r}_i^{\left(t\right)}{r}_i^{\left(t\right)T}\right){\mathit{R}}^{-1}$$

and admits an explicit solution based on Lemma 3.

The same tactics apply to a multilevel LMM (Bates and Pinheiro, 1998) with responses

$$Y_i={\mathit{X}}_i\beta +{\mathit{Z}}_{i1}{\gamma }_{i1}+\cdot \cdot \cdot {\mathit{Z}}_{im}{\gamma }_{im}+{ϵ}_i.$$

Minorization separates parameters for each level (variance component). Depending on the complexity of the covariance matrices, maximization of the surrogate can be accomplished analytically. For the sake of brevity, details are omitted.

6.4. MAP estimation

Suppose β follows an improper flat prior, the variance components ${\mathit{\sigma }}_i^2$ follow inverse gamma priors with shapes α_i > 0 and scales γ_i > 0, and these priors are independent. The log-posterior density then reduces to

$$-\frac{1}{2}\ln \det \mathbf{\Omega }-\frac{1}{2}{\left(\mathit{y}-\mathit{X}\beta \right)}^T{\mathbf{\Omega }}^{-1}\left(\mathit{y}-\mathit{X}\beta \right)-\sum _{i=1}^m\left({\alpha }_i+1\right)\ln {\sigma }_i^2-\sum _{i=1}^m\frac{{\gamma }_i}{{\sigma }_i^2}+c,$$ (15)

where c is an irrelevant constant. The MAP estimator of (β, σ²) is the mode of the posterior distribution. The update (4) of β given σ² remains the same. To update σ² given β, apply the same minorizations (5) and (6) to the first two terms of equation (15). This separates parameters and yields a convex surrogate for each ${\mathit{\sigma }}_i^2$. The minimum of the ${\mathit{\sigma }}_i^2$ surrogate is defined by the stationarity condition

$$0=-\frac{1}{2}\text{tr}\left({\mathbf{\Omega }}^{-\left(t\right)}{\mathit{V}}_i\right)+\frac{{\sigma }_i^{4\left(t\right)}}{2{\sigma }_i^4}{\left(\mathit{y}-\mathit{X}{\beta }^{\left(t\right)}\right)}^T{\mathbf{\Omega }}^{-\left(t\right)}{\mathit{V}}_i{\mathbf{\Omega }}^{-\left(t\right)}\left(\mathit{y}-\mathit{X}{\beta }^{\left(t\right)}\right)-\frac{{\alpha }_i+1}{{\sigma }_i^2}+\frac{{\gamma }_i}{{\sigma }_i^4}.$$

Multiplying this by ${\sigma }_i^4$ gives a quadratic equation in ${\sigma }_i^2$. The positive root should be taken to meet the nonnegativity constraint on ${\sigma }_i^2$.

For the multivariate response model (11), we assume the variance components Γ_i follow independent inverse Wishart distributions with degrees of freedom ν_i > d − 1 and scale matrix ${\mathbf{\Psi }}_i\succ 0$. The log density of the posterior distribution is

$$\begin{gathered} -\frac{1}{2}\ln \det \mathbf{\Omega }-\frac{1}{2}\text{vec}{\left(Y-\mathit{X}\mathit{B}\right)}^T{\mathbf{\Omega }}^{-1}\text{vec}\left(Y-\mathit{X}\mathit{B}\right) \\ \hspace{0.17em}\hspace{0.17em}\hspace{1em}-\frac{1}{2}\sum _{i=1}^m\left(v_i+d+1\right)\ln \det {\mathbf{\Gamma }}_i-\frac{1}{2}\sum _{i=1}^m\text{tr}\left({\mathbf{\Psi }}_i{\mathbf{\Gamma }}_i^{-1}\right)+c, \end{gathered}$$ (16)

where c is an irrelevant constant. Invoking the minorizations (6) and (12) for the first two terms and the supporting hyperplane minorization for − ln det Γ_i gives the surrogate function

$$\begin{gathered} g\left(\mathbf{\Gamma }|{\mathbf{\Gamma }}^{\left(t\right)}\right)=-\frac{1}{2}\sum _{i=1}^m\text{tr}\left({\mathbf{\Omega }}^{-\left(t\right)}\left({\mathbf{\Gamma }}_i\otimes {\mathit{V}}_i\right)\right)-\frac{1}{2}\sum _{i=1}^m\text{tr}\left({\mathbf{\Gamma }}_i^{\left(t\right)}{\mathit{R}}^{\left(t\right)T}{\mathit{V}}_i{\mathit{R}}^{\left(t\right)}{\mathbf{\Gamma }}_i^{\left(t\right)}{\mathbf{\Gamma }}_i^{-1}\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-\frac{1}{2}\sum _{i=1}^m\left(v_i+d+1\right)\text{tr}\left({\mathbf{\Gamma }}_i^{-\left(t\right)}{\mathbf{\Gamma }}_i\right)-\frac{1}{2}\sum _{i=1}^m\text{tr}\left({\mathbf{\Psi }}_i{\mathbf{\Gamma }}_i^{-1}\right)+c^{\left(t\right)}. \end{gathered}$$

The optimal Γ_i satisfies the stationarity condition

$$\begin{gathered} {\left(I_d\otimes 1_n\right)}^T\left[\left(1_d{1}_d^T\otimes {\mathit{V}}_i\right)\odot {\mathbf{\Omega }}^{-\left(t\right)}\right]\left(I_d\otimes 1_n\right)+\left({\mathit{V}}_i+d+1\right){\mathbf{\Gamma }}_i^{-\left(t\right)} \\ ={\mathbf{\Gamma }}_i^{-1}\left({\mathbf{\Gamma }}_i^{\left(t\right)}{\mathit{R}}^{\left(t\right)T}{\mathit{V}}_i{\mathit{R}}^{\left(t\right)}{\mathbf{\Gamma }}_i^{\left(t\right)}+{\mathbf{\Psi }}_i\right){\mathbf{\Gamma }}_i^{-1}, \end{gathered}$$

which can be solved by Lemma 3.

6.5. Variable selection

In the statistical analysis of high-dimensional data, the imposition of sparsity leads to better interpretation and more stable parameter estimation. MM algorithms mesh well with penalized estimation. The simple variance components model (1) illustrates this fact. For the selection of fixed effects, minimizing the lasso-penalized log-likelihood $-L\left(\beta ,{\mathit{\sigma }}^2\right)+\lambda {\sum }_j\left|{\beta }_j\right|$ is often recommended (Schelldorfer et al., 2011). The only change to the MM Algorithm 1 is that in estimating β, one solves a lasso penalized general least squares problem rather than an ordinary general least squares problem. The updates of the variance components ${\sigma }_i^2$ remain the same. For estimation of a large number of variance components, one can minimize the ridge-penalized log-likelihood

$$-L\left(\beta ,{\mathit{\sigma }}^2\right)+\lambda \sum _{i=1}^m{\sigma }_i^2$$

subject to the nonnegativity constraints ${\sigma }_i^2\ge 0$. The variance update (8) becomes

$${\sigma }_i^{2\left(t+1\right)}={\sigma }_i^{2\left(t\right)}\sqrt{\frac{{\left(\mathit{y}-\mathit{X}{\beta }^{\left(t\right)}\right)}^T{\mathbf{\Omega }}^{-\left(t\right)}{\mathit{V}}_i{\mathbf{\Omega }}^{-\left(t\right)}\left(\mathit{y}-\mathit{X}{\beta }^{\left(t\right)}\right)}{\text{tr}\left({\mathbf{\Omega }}^{-\left(t\right)}{\mathit{V}}_i\right)+2\lambda }},\hspace{1em}i=1,\dots ,m,$$

which clearly exhibits shrinkage but no thresholding. The lasso penalized log-likelihood

$$-L\left(\beta ,{\mathit{\sigma }}^2\right)+\lambda \sum _{i=1}^m{\sigma }_i$$ (17)

subject to nonnegativity constraint ${\sigma }_i\ge 0$ achieves both ends. The update of σ_i is chosen among the positive roots of a quartic equation and the boundary 0, whichever yields a lower objective value. Next section illustrates variance component selection using lasso penalty on a real genetic data set.

7. A numerical example

Quantitative trait loci (QTL) mapping aims to identify genes associated with a quantitative trait. Current sequencing technology measures millions of genetic markers in study subjects. Traditional single-marker tests suffer from low power due to the low frequency of many markers and the corrections needed for multiple hypothesis testing. Region-based association tests are a powerful alternative for analyzing next generation sequencing data with abundant rare variants.

Suppose y is a n × 1 vector of quantitative trait measurements on n people, X is an n × p predictor matrix (incorporating predictors such as sex, smoking history, and principal components for ethnic admixture), and G is an n × m genotype matrix of m genetic variants in a pre-defined region. The linear mixed model assumes

$$Y=\mathit{X}\beta +G\gamma +ϵ,\hspace{1em}\gamma \sim N\left(0,{\sigma }_g^{2}I\right),\hspace{1em}ϵ\sim N\left(0,{\sigma }_e^2{I}_n\right),$$

where β are fixed effects, γ are random genetic effects, and ${\sigma }_g^2$ and ${\sigma }_e^2$ are variance components for the genetic and environmental effects, respectively. Thus, the phenotype vector Y has covariance ${\sigma }_g^{2}G{G}^T+{\sigma }_e^2{I}_n$, where GG^T is the kernel matrix capturing the overall effect of the m variants. Current approaches test the null hypothesis ${\sigma }_g^2=0$ for each region separately and then adjust for multiple testing (Lee et al., 2014; Zhou et al., 2016). Instead of this marginal testing strategy, we consider the joint model

$$\begin{gathered} \mathit{y}=\mathit{X}\beta +s_1^{-1/2}{\mathit{G}}_1{\gamma }_1+\cdot \cdot \cdot +s_m^{-1/2}{\mathit{G}}_m{\gamma }_m+ϵ, \\ {\gamma }_i\sim N\left(0,{\sigma }_i^2\mathit{I}\right),\hspace{1em}ϵ\sim N\left(0,{\sigma }_e^2{\mathit{I}}_n\right) \end{gathered}$$

and select the variance components ${\sigma }_i^2$ via the penalization (17). Here s_i is the number of variants in region i, and the weights $s_i^{-1/2}$ put all variance components on the same scale.

We illustrate this approach using the COPDGene exome sequencing study (Regan et al., 2010). After quality control, 399 individuals and 646,125 genetic variants remain for analysis. Genetic variants are grouped into 16,619 genes to expose those genes associated with the complex trait height. We include age, sex, and the top 3 principal components in the mean effects. Because the number of genes vastly exceeds the sample size n = 399, we first pare the 16,619 genes down to 200 genes according to their marginal likelihood ratio test p-values and then carry out penalized estimation of the 200 variance components in the joint model (17). This is similar to the sure independence screening strategy for selecting mean effects (Fan and Lv, 2008). Genes are ranked according to the order they appear in the lasso solution path. Table 4 lists the top 10 genes together with their marginal LRT p-values. Figure 1 in Supplementary Materials displays the corresponding segment of the lasso solution path. It is noteworthy that the ranking of genes by penalized estimation differs from the ranking according to marginal p-values. The same phenomenon occurs in selection of highly correlated mean predictors. This penalization approach for selecting variance components warrants further theoretical study.

Table 4:

Top 10 genes selected by the lasso penalized variance component model (17) are tallied with their marginal p-values in an association study of 200 genes and the complex trait height.

Lasso Rank	Gene	Marginal P-value	# Variants
1	DOLPP1	2.35 × 10−6	2
2	C9orf21	3.70 × 10−5	4
3	PLS1	2.29 × 10−3	5
4	ATP5D	6.80 × 10−7	3
5	ADCY4	1.01 × 10−3	11
6	SLC22A25	3.95 × 10−3	14
7	RCSD1	9.04 × 10−4	4
8	PCDH7	1.20 × 10−4	7
9	AVIL	8.34 × 10−4	11
10	AHR	1.14 × 10−3	7

8. Discussion

The current paper leverages the MM principle to design powerful and versatile algorithms for variance components estimation. The MM algorithms derived are notable for their simplicity, generality, numerical efficiency, and theoretical guarantees. Both ordinary MLE and REML are apt to benefit. Other extensions are possible. In nonlinear models (Bates and Watts, 1988; Lindstrom and Bates, 1990), the mean response is a nonlinear function in the fixed effects β. One can easily modify the MM algorithms to update β by a few rounds of Gauss- Newton iteration. The variance components updates remain unchanged.

One can also extend our MM algorithms to elliptically symmetric densities

$$f\left(\mathit{y}\right)=\frac{e^{-\frac{1}{2}\kappa \left({\delta }^2\right)}}{{\left(2\pi \right)}^{\frac{n}{2}}{\left(\det \mathbf{\Omega }\right)}^{\frac{1}{2}}}$$

defined for $\mathit{y}\in {ℝ}^n$, where δ² = (y − µ)^T Ω⁻¹(y − µ) denotes the Mahalanobis distance between y and µ. Here we assume that the function κ(s) is strictly increasing and strictly concave. Examples of elliptically symmetric densities include the multivariate t, slash, contaminated normal, power exponential, and stable families. Previous work (Huber and Ronchetti, 2009; Lange and Sinsheimer, 1993) has focused on using the MM principle to convert parameter estimation for these robust families into parameter estimation under the multivariate normal. One can chain the relevant majorization $\kappa \left(s\right)\le \kappa \left(s^{\left(t\right)}\right)+{\kappa }^{\prime }\left(s^{\left(t\right)}\right)\left(s-s^{\left(t\right)}\right)$ with our previous minorizations and simultaneously split variance components and pass to the more benign setting of the multivariate normal. These extensions are currently under investigation.