Competing Roles of Slow-Oscillations and Delta-Waves in Memory Consolidation Versus Forgetting

SUMMARY

Sleep has been implicated in both memory consolidation and forgetting of experiences. However, it is unclear what governs the balance between consolidation and forgetting. Here we tested how activity-dependent processing during sleep might differentially regulate these two processes. We specifically examined how neural reactivations during NREM sleep were causally linked to consolidation versus weakening of the neural correlates of neuroprosthetic skill. Strikingly, we found that slow oscillations (SO) and delta-waves (δ) have dissociable and competing roles in consolidation versus forgetting. By modulating cortical spiking linked to SO or δ waves using closed-loop optogenetic methods, we could respectively weaken or strengthen consolidation and thereby bidirectionally modulate sleep-dependent performance gains. We further found that changes in the temporal coupling of spindles to SO relative to δ waves could account for such effects. Thus, our results indicate that neural activity driven by SO and δ waves have competing roles in sleep-dependent memory consolidation.

Graphical Abstract

In brief

By selectively altering the balance between slow-oscillations and delta-waves during post-learning sleep in the rat brain, the forgetting or remembering of a new skill can be enhanced.

INTRODUCTION

Sleep is known to be important for both selective memory consolidation as well as forgetting of experiences (Born et al., 2006; Buzsáki, 1989; Marshall and Born, 2007; Poe, 2017; Sejnowski and Destexhe, 2000; Stickgold, 2005; Tononi and Cirelli, 2014), but we still do not know what governs the balance between the two. This question is of fundamental importance as the nervous system constantly faces the challenge of whether and how to selectively preserve the neural correlates of new experiences through memory consolidation, while simultaneous supporting the weakening of memories deemed to be less important. Examination of learning-induced activity patterns during sleep offers one potential clue regarding what might regulate the balance between consolidation versus weakening: there is consistent evidence for the reactivation of neural ensembles that represent awake experiences (Gulati et al., 2014; Ji and Wilson, 2007; Joo and Frank, 2018; Nadasdy et al., 1999; Peyrache et al., 2009; Ramanathan et al., 2015; Wilson and McNaughton, 1994). Reactivation of neural ensembles thus provides a possible substrate for selective consolidation of memories. Yet, despite the extensive study of ensemble reactivation in hippocampal (Ji and Wilson, 2007; Joo and Frank, 2018; Nadasdy et al., 1999; Wilson and McNaughton, 1994), prefrontal (Peyrache et al., 2009), and motor regions (Gulati et al., 2014; Ramanathan et al., 2015) during sleep, it remains an open question regarding how activity-dependent processing, in general, and reactivations, in specific, might differentially drive memory consolidation versus forgetting.

Here we show that neural reactivations differentially driven by slow-oscillations (SO) and delta-waves (δ) during non-rapid eye movement (NREM) sleep is essential for determining the extent of sleep-dependent performance gains through direct regulation of consolidation versus weakening of the neural traces of awake experiences. Previous studies have shown that during NREM sleep, SO, spindles, and their precise temporal interaction (i.e. “nesting”) play a role in memory consolidation (Bergmann and Born, 2018; Cairney et al., 2018; Diekelmann and Born, 2010; Genzel et al., 2014; Helfrich et al., 2018; Latchoumane et al., 2017; Maingret et al., 2016; Miyamoto et al., 2017; Navarro-Lobato and Genzel, 2019; Ngo et al., 2013; Peyrache et al., 2009; Sejnowski and Destexhe, 2000; Staresina et al., 2015); however, it remains unclear how reactivation of awake experiences are linked to them. Interestingly, NREM sleep is also enriched in δ waves as well as SO; it remains unclear how these two events might interact during memory consolidation. Classic studies initially distinguished SO and δ waves as two distinct neurophysiological phenomena consisting of low-frequency waves with different spatial and temporal properties (Steriade et al., 1993a; Steriade and Timofeev, 2003); subsequent studies have found evidence for the existence of two separate classes of “slow waves” during NREM sleep across species (Bernardi et al., 2018; Dang-Vu et al., 2008; Genzel et al., 2014; Molle et al., 2002; Siclari et al., 2014). While one class of slow waves are more global and have larger amplitudes, the other class has smaller amplitudes and are more local (Bernardi et al., 2018; Genzel et al., 2014; Siclari et al., 2014). Importantly, it remains unclear how these two phenomena might differentially drive activity-dependent processing and the reactivation of neural ensembles during sleep. Here we specifically classified SO (i.e. larger amplitude global slow waves) and δ waves (i.e. smaller amplitude local events) in NREM sleep. We then modulated spiking activity linked to SO or δ waves through a real-time closed-loop optogenetic system in rats. Furthermore, we examined how their respective coupling to spindles drove reactivations of novel awake experiences and thereby differentially drove selective memory consolidation versus memory weakening. Most remarkably, we found that SO and δ waves have dissociable and competing roles in determining the extent of memory consolidation during NREM sleep after learning of a neuroprosthetic skill.

RESULTS

SO are essential for sleep-dependent consolidation of a skill

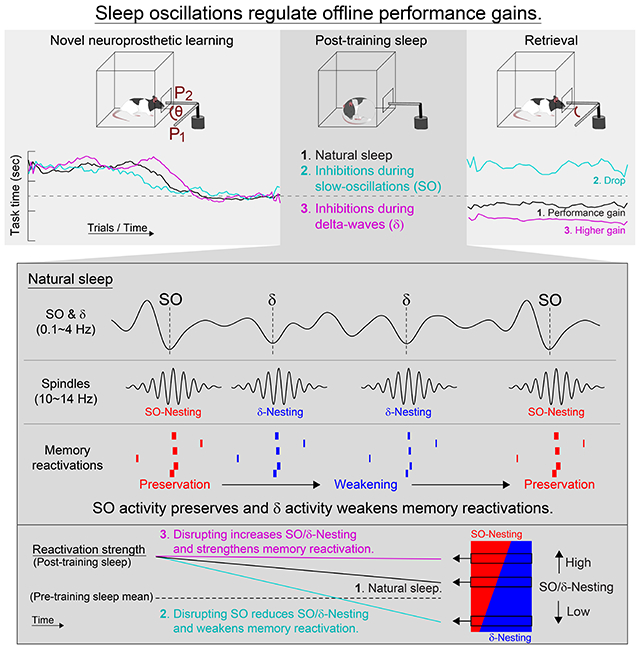
We implanted 32-channel microelectrode arrays with an attached cannula for fiber optic stimulation into primary motor cortex (M1) of twelve rats that were pre-injected with inhibitory opsins (see Table S1). We then monitored sleep waves, i.e. SO, δ waves and spindles, both before and after learning. In addition, we compared two types of electrophysiological recordings with one additional rat; namely, simultaneous DC-coupled recordings from the surface of M1 and AC-coupled recordings in layer 5 of M1 (Figure 1A). As shown, our detected SO and δ wave events in the AC recordings were also evident in the DC recordings. We neurophysiologically distinguished SO and δ waves using features previously described (Methods) (Bernardi et al., 2018; Dang-Vu et al., 2008; Genzel et al., 2014; Massimini et al., 2004; Ngo et al., 2013; Sela et al., 2016; Steriade et al., 1993a; Steriade and Timofeev, 2003). Notably, because SO and δ waveforms both contain 1-4 Hz spectral power (Steriade and Amzica, 1998), we distinguished the two based on their distinct waveforms (Figures 1B and 1C). Thus, slow waves with large positive and negative waves (see Methods) within 500 ms were labeled as SO, whereas slow waves with a significantly smaller preceding positive peak were labeled delta-waves/δ. For the analyzed sleep sessions (n = 72 sessions from the twelve rats), putative SO and δ waves could be discriminated using k-mean clustering; the peaks preceding up-states had a 12.5-fold stronger weight relative to the troughs of upstates for a discriminant line that was equidistant between the two k-means cluster centroids. Interestingly, consistent with past work, our SO showed more widespread synchronization in the region compared to δ waves (Figure 1D) (Bernardi et al., 2018). The inter-event intervals of SO and δ waves followed a log-normal distribution and the frequency of SO and δ waves was 0.41 and 1.12 Hz, respectively (Figure 1E). The autocorrelograms of SO and δ wave event times showed multiple major peaks which appeared to reflect their general rhythmicity (Figure 1F). Notably, our classification scheme appeared to detect phenomena that are remarkably similar to that identified by Steriade and colleagues using intracellular recordings (Steriade et al., 1993a; Steriade et al., 1993b).

Figure 1. Dissociation of SO and δ.

(A) Examples of raw and filtered traces with DC- and AC-coupled recordings. Traces were filtered using online (gray) and offline (black) digital filters (Methods). SO and δ waves marked by cyan and magenta hereafter.

(B) SO versus δ waves from all post-training sleep (n = 72 sessions, 12 rats). Distribution of peaks preceding upstates, troughs of up-states, and differences between SO power (in 0.1-1 Hz) and δ power (in 1.5-4 Hz) are shown.

(C) SO versus δ waves separated by red dashed line (determined by k-means clustering). Projections to axis orthogonal to separation line shown.

(D) Left, Examples of traces from 32 channels of a array. Mean traces above and single channel trace below. Right, comparison of detected SO versus δ waves in the array (mean ± s.e.m.; n = 72 sessions, mixed-effects model, t₁₄₂ = 5.13, ***P < 10⁻⁶).

(E) Distributions of inter-event intervals for SO and δ waves; dashed lines is geometric mean (n = 72 sessions; SO: 2.71 sec; δ: 0.96 sec).

(F) Autocorrelogram examples computed with bins of 100 ms (left) and 20 ms (right) from both SO and δ wave upstates for 1-hour sleep. Right histogram is an expansion of left histogram. Central peaks and lower values are truncated.

Each animal was also injected with a virus to express an inhibitory opsin in M1. More specifically, a red-shifted halorhodopsin, Jaws, was injected in order to silence neural activity (Chuong et al., 2014; Gulati et al., 2017); typically ~60% neurons (on average, 38.6% of putative excitatory and 34.8% of inhibitory neurons; Figure S1) responded to optical stimulation with a reduction in firing rate (Figure 2E). We then designed a closed-loop real-time system that could trigger the opsin in response to identified sleep slow waves features (Gulati et al., 2017). Closed-loop optogenetic inhibitions were delivered during up-states of the filtered LFP (in 0.1-4 Hz real-time digital filter; see Methods) to examine the role of cortical spiking activity in sleep-dependent memory processing. The online real-time filtering had delays of 41.2 ± 2.5 ms relative to offline zero-phase shift filtering in the up-states (Figure 1A).

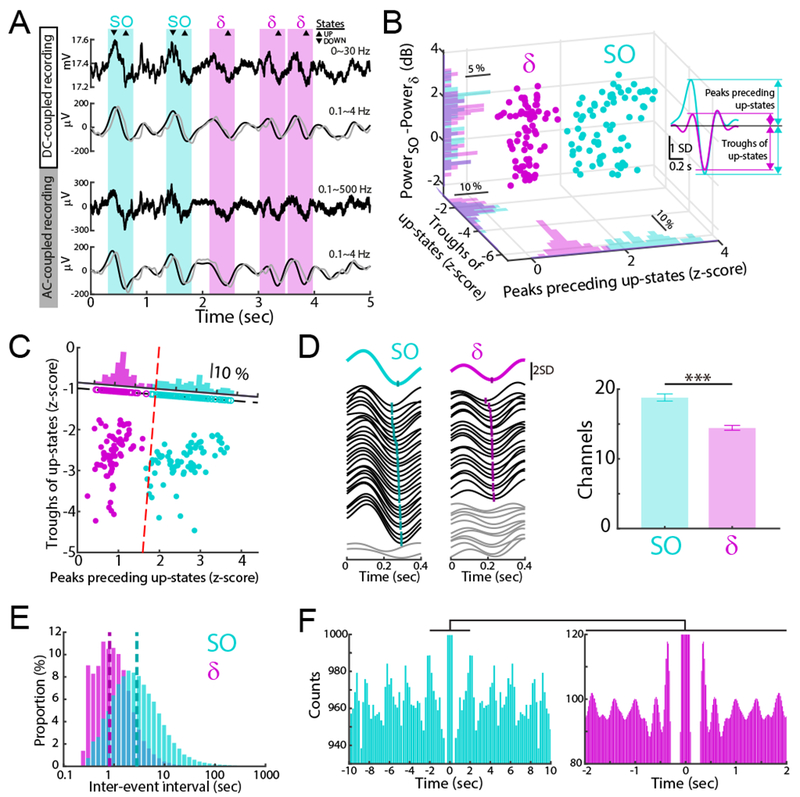
Figure 2. Optogenetic inhibitions during SO up-states.

(A) Flow charts for OPTO_SO and OPTO_SO+δ experiments.

(B) Rats learned direct neural control of a feeding tube (θ = angular position in ‘A’). Successful trials required movement from P₁ to P₂ within 15 sec.

(C and D) Examples of filtered traces (0.1-4 Hz) and stimulation periods (100 ms pulses) during up-states of SO and SO+δ for OPTO_SO (C) and OPTO_SO+δ experiments (D).

(E) Examples of 30 raw LFP traces and spike rasters (left: SO up-states; right: δ wave up-states). Scale bars indicates 100 ms on x-axis and 2 s.d. on y-axis of raw LFP.

(F) Example learning curves for OPTO_SO, OPTO_SO+δ and OPTO_OFF.

(G) Mean task time changes from BMI_1-Late to BMI_2-Early (mean in solid line ± s.e.m. in box; OPTO_SO: n = 13 sessions, 5 rats, mixed-effects model, t₂₄ = 6.99, ***P < 10⁻⁶; OPTO_SO+δ: n = 13 sessions, 7 rats, mixed-effects model, t₂₄ = 5.52, ***P < 10⁻⁴; OPTO_SO vs. OPTO_SO+δ: mixed-effects model, t₂₄ = −1.39, P = 0.18).

(H) Relationship of mean task time change in ‘G’ to the ratio of SO to δ-triggering (n = 26 sessions, 12 rats; linear regression, R² = 0.065, P = 0.208).

See also Figures S1 and S2.

We tested the effects of these optogenetic interventions on memory consolidation after learning of a neuroprosthetic skill, i.e. Brain-Machine Interface or BMI task (hereafter, BMI training block and BMI₂ retrieval block; Figures 2A and 2B) (Clancy et al., 2014; Ganguly et al., 2011; Gulati et al., 2017; Gulati et al., 2014; Jarosiewicz et al., 2008; Koralek et al., 2012; Moritz et al., 2008; Taylor et al., 2002). We have previously shown that BMI-based learning closely replicates the sleep-dependent reactivations linked to natural learning (Ramanathan et al., 2015); however, this system allows us to easily follow ensembles that are causally linked to actuator control. As prior, we used spiking activity from M1 to drive the angular velocity of a single degree-of-freedom mechanical actuator using a constant decoder. Thus, animals were required to explore and learn patterns of neural activity that could reliably control the actuator in order to deliver a liquid reward; over a typical training block (i.e. BMI₁), animals were able to learn the task. We also monitored the neural activity, both local field potential or LFP and spiking activity, during 1-hour periods of spontaneous behavior that included sleep (hereafter, pre-training sleep and post-training sleep); in offline analysis, sleep was detected using degree of movement based on video analysis (Pack et al., 2007) and NREM sleep was detected using power spectral density (Figure S2A and Methods).

We first assessed the role of SO in driving offline performance gains from BMI₁ to BMI₂. We thus triggered the optogenetic stimulations to perturb spiking activity during up-states of SO (hereafter, OPTO_SO; n = 13 sessions in 5 rats; Figure 2C). This was compared to a condition in which optogenetic inhibitions were delivered during both SO and δ waves (hereafter, OPTO_SO+δ: n = 13 sessions in 7 rats; Figure 2D); these experiments were partially presented in a previous study (Gulati et al., 2017) (also see Table S1 for details of sessions and rats). These interventions were delivered during the post-training sleep (Figure 2A). Amounts of total sleep time and NREM sleep time were not significantly different across conditions (Figure S2B). Typically, as in previous studies, we observed a performance gain during BMI₂ relative to the late trials of BMI₁ after natural unperturbed sleep (hereafter, OPTO_OFF) (Gulati et al., 2017; Gulati et al., 2014). For both the OPTO_SO and OPTO_SO+δ experiments, we observed significantly worse task performance upon awakening after the interventions during post-training sleep (Figures 2F and 2G).

Interestingly, the change in the mean task time from BMI_1-late to BMI_2-early for the OPTO_SO+δ experiments were not significantly different from perturbations primarily during SO, i.e. in the OPTO_SO experiments (OPTO_SO: 2.5 ± 0.4 sec; OPTO_SO+δ: 2.1 ± 0.4 sec; OPTO_SO vs. OPTO_SO+δ mixed-effects model, t₂₄ = −1.39, P = 0.18). Based on their respective frequencies of occurrence, the triggered optical pulses during the OPTO_SO+δ experiments were 2.2 times more frequent than during the OPTO_SO experiments. However, both experiments showed indistinguishable task performance changes after the perturbed sleep; this indicated that the laser light itself was unlikely to contribute to our observed effects (Methods; Figure S2C). In addition, we used offline analysis to detect the actual SO and δ waves affected by our respective interventions (Table S2); there are expected variations between the two because of differences between real-time filter implementation versus offline filtering methods. Therefore, based on offline detections, we examined whether the changes in performance could be predicted by the extent of δ waves and SO perturbations for the group of OPTO_SO and OPTO_SO+δ experiments (Figure 2H). Surprisingly, there was not a significant relationship between the extent of δ waves relative to SO perturbations on the change in task time after sleep (OPTO_SO and OPTO_SO+δ experiments, n = 26 sessions, 12 rats; linear regression, R² = 0.065, P = 0.208). Together, these results suggest that perturbations of spiking activity during up-states of SO is sufficient to prevent offline consolidation; the effect of SO perturbations appears to largely dominate the extent of corresponding perturbation to δ waves. This further suggests that SO are essential for memory consolidation.

Effects of targeting δ wave related activity

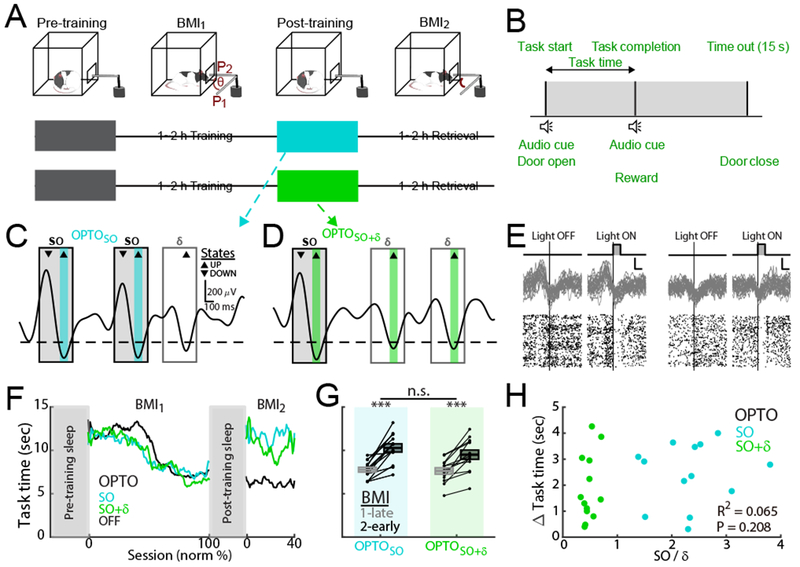
What then is the effect on consolidation of targeting δ waves? We examined the effects of interventions that were delivered predominantly during δ wave up states (hereafter, OPTO_δ; n = 14 sessions in 5 rats; Figures 3A and 3B). This was compared to a control condition (hereafter, OPTO_RAND) in which optogenetic inhibitions were delivered to time periods that were distinct from SO and δ wave up-states, inhibition was delivered with a random time delay following every detected up-state (n = 9 sessions in 3 rats; Figures 3A and 3C). Despite the perturbations of spiking activity during the post-training sleep, we observed an improvement of task performance in both the OPTO_δ and OPTO_RAND experiments (Figures 3D and 3E). Strikingly, however, in the OPTO_δ experiments the change in the mean task time was significantly greater in comparison to the OPTO_RAND group (OPTO_δ: −2.1 ± 0.4 sec; OPTO_RAND: −1.0 ± 0.2 sec; OPTO_δ vs. OPTO_RAND, mixed-effects model, t₂₁ = 2.63, P = 0.015). Moreover, the changes in the mean task time in the OPTO_RAND experiments were similar to natural sleep, i.e. in the OPTO_OFF experiments (OPTO_OFF: −1.1 ± 0.3 sec, n = 23 sessions in 12 rats; OPTO_RAND vs. OPTO_OFF, mixed-effects model, t₃₀ = −0.49, P = 0.63). Taken together, these results suggested that perturbations of spiking activity during δ wave up-states can boost the effects of sleep-dependent consolidation.

Figure 3. Optogenetic inhibitions during up-states of δ.

(A) Flow charts for OPTO_δ and OPTO_RAND experiments.

(B and C) Examples of filtered traces and stimulation periods during up-states of δ waves (magenta bars) and during period interleaving up-states (control; orange bars) for an OPTO_δ and OPTO_RAND.

(D) Learning curves for OPTO_δ,. OPTO_RAND and OPTO_OFF.

(E) Mean task time changes from BM_1-Late to BMI_2-Early (mean in solid line ± s.e.m. in box; OPTO_δ: n = 14 sessions, 5 rats, mixed-effects model, t₂₆ = −5.64, ***P < 10⁻⁵; OPTO_RAND: n = 9 sessions, 3 rats, mixed-effects model, t₁₆ = −4.19, ***P < 10⁻³; OPTO_δ vs. OPTO_RAND: mixed-effects model, t₂₁ = 2.63, *P = 0.015).

See also Figures S1 and S2.

Changes in the nesting of SO and δ waves to spindles

What might be the underlying neurophysiological basis for our observed set of performance changes? There is a growing body of literature indicating that the precise temporal coupling of spindles to SO, or “nesting” of the two events, is important for memory consolidation in both humans (Antony et al., 2018; Bergmann and Born, 2018; Cairney et al., 2018; Helfrich et al., 2018; Ngo et al., 2013; Staresina et al., 2015) and rodents (Latchoumane et al., 2017; Maingret et al., 2016; Peyrache et al., 2011). We further analyzed the effects of SO and δ wave triggered optogenetic inhibitions on the temporal coupling of sleep spindles to both SO and δ waves. We thus calculated the degree of nesting between SO and spindles (Figure 4A top) and δ waves and spindles (Figure 4A bottom); more specifically, we measured the distribution of temporal lags between a SO and its nearest spindle (ΔT_SO-Spindle). The ΔT_δ-Spindle was an analogous measure for δ waves. While a distribution of ΔT_SO-Spindle values can have large values (Figure S3A), the “SO-Nesting” focused on the distribution of events within −0.5 sec prior to 1 sec after the peak of the up-state (Figures 4B, 4C, and 4D). Similar metrics were calculated for δ waves and its closest spindle (ΔT_δ-Spindle; Figure S3B) and for “δ-Nesting”. Notably, consistent with the greater prevalence of δ waves, δ-Nesting was 1.3-fold greater than SO-Nesting under the CONTROL conditions. Interestingly, changes in the SO-Nesting index significantly explained the task performance changes (linear regression, R² = 0.085, P = 0.013). In contrast, changes in δ-Nesting index by itself did not predict task performance changes (linear regression, R² = 0.003, P = 0.644).

Figure 4. Spindle to SO nesting and changes in task performance.

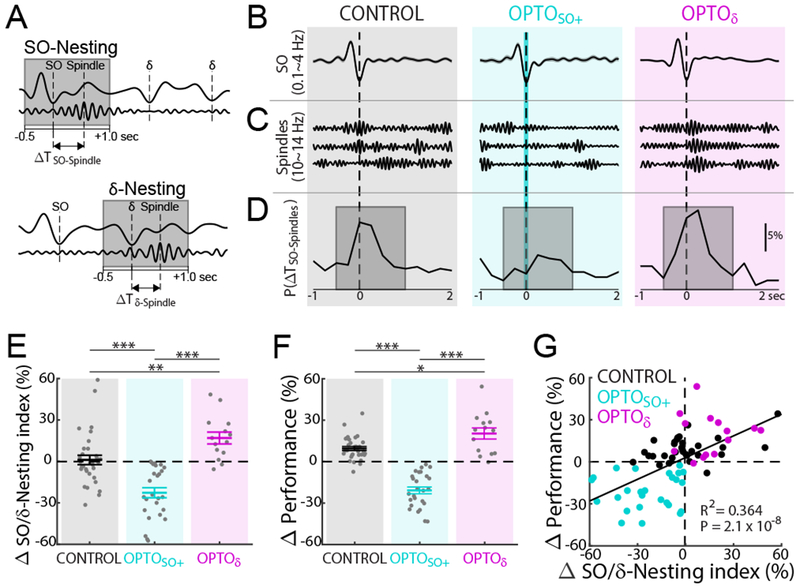
(A) Cartoon of nesting of spindle to SO (SO-Nesting; top) and δ (δ-Nesting; bottom). Gray boxes indicate the time window for ‘nesting’, −0.5 to 1.0 sec from up-state (same as ‘D’).

(B) Example of mean SO-up-state-triggered LFP (top, mean ± s.e.m., 0.1~4 Hz) for CONTROL, OPTO_SO+, and OPTO_δ.

(C) Single trial examples of detected spindles near SOs.

(D) Examples of probability distribution of spindle-peaks time from nearest SO up-state (Δ_SO-Spindles). Examples of probability distribution for ΔT_δ-Spindles are shown in Figure S3B.

(E) SO/δ-Nesting index changes from pre- to post-training sleep (mean ± s.e.m.; CONTROL: n = 32 sessions, 12 rats; OPTO_SO+: n = 26 sessions, 12 rats; OPTO_δ: n = 14 sessions, 5 rats; one-way ANOVA, F_2,69 = 25.36, P < 10⁻⁸; significant post hoc t tests, corrected for multiple comparison, **P < 0.01, ***P < 10⁻³).

(F) Task performance changes from BMI_1-Late to BMI_2-Early (positivity represents performance improvement) (CONTROL: n = 32 sessions, 12 rats; OPTO_SO+: n = 26 sessions, 12 rats; OPTO_δ: n = 14 sessions, 5 rats; one-way ANOVA, F_2,69 = 76.08, P < 10⁻¹⁷; significant post hoc t tests, corrected for multiple comparison, *P < 0.05, ***P < 10⁻³).

(G) Relationship between SO/δ-Nesting index changes and task performance changes (total n = 72 sessions, 12 rats; significant linear regression, R² = 0.354, P = 3.5 × 10⁻⁸; satisfies criteria for linear regression, see Methods).

See also Figures S3, S4, and S5.

How then can we reconcile the role of δ waves on changes in performance (Figure 3E)? One possibility is that while the absolute level of δ-Nesting is not predictive of performance, its abundance relative to SO-Nesting is more important. This might also be consistent with the results shown in Figure 2H, where δ wave perturbations did not contribute to the changes in performance levels when SO were also perturbed. We thus explored the possibility that the relative extent of δ wave and SO nested events is important for both reactivations and changes in performance. We calculated the “SO/δ-Nesting index”, it measures the ratio of the number of spindles nested to SO (i.e. within a −0.5-1s window) to the number of spindles nested to δ waves. This measure takes into account the relative extent of the respective nesting in a given sleep session. A lower SO/δ-Nesting index would indicate that there is lower temporal coupling between SO and spindles compared to between δ and spindles. Similarly, a higher SO/δ-Nesting index would indicate higher temporal coupling to SO in comparison to δ waves.

Interestingly, the OPTO_δ experiments were associated with a higher SO/δ-Nesting index during the intervention period (Figure 4E), indicating that spindles were more likely to be nested to a SO than a δ wave. We next compared the change in SO/δ-Nesting index for perturbations of SO. Notably, as outlined above, the OPTO_SO and OPTO_SO+δ groups were in a continuum, i.e. relative SO to δ wave perturbations. Consistent with this, the OPTO_SO and OPTO_SO+δ experiments were not significantly different for changes in SO/δ-Nesting index (mixed-effects model, t₂₄ = 1.47, P= 0.16); we thus combined them into an OPTO_SO+ group for this analysis. Overall, the OPTO_SO+ group experienced a relative drop in SO/δ-Nesting index. We also combined the OPTO_OFF and OPTO_RAND experiments as they were not significantly different from each other (hereafter referred to as CONTROL). For OPTO_δ, n = 14 sessions in 5 rats, the actual SO/δ-Nesting indices were 0.71 ± 0.05 during pre-training sleep and 0.87 ± 0.08 during post-training sleep (pre- vs. post-training sleep, mixed-effects model, t₂₆ = 2.15, p < 0.05). For OPTO_SO, n = 13 sessions in 5 rats, the SO/δ-Nesting indices were 0.76 ± 0.10 and 0.53 ± 0.07, respectively (pre- vs. post-training sleep, mixed-effects model, t₂₄ = −2.31, p < 0.05); for OPTO_SO+δ, n = 13 sessions in 7 rats, the values were 0.70 ± 0.06 and 0.44 ± 0.04, respectively (pre- vs. post-training sleep, mixed-effects model, t₂₄ = −3.93, p < 10⁻³). Finally, the SO/δ-Nesting indices for CONTROL conditions, n = 23 sessions in 12 rats, were 0.77 ± 0.06 and 0.77 ± 0.06, respectively (pre- vs. post-training sleep, mixed-effects model, t₆₂ = −0.002, p = 1.00). Together, this indicated that while OPTO_SO+ was more likely to have a decline in the nesting of spindles to SO, OPTO_δ appeared to have a higher nesting probability for SO. Similar to the direction of changes in the SO/δ-Nesting index values, we also found bidirectional shifts in task performance with optogenetic interventions (Figure 4F). In other words, the OPTO_SO+ interventions led to relative performance drops, while the OPTO_δ interventions led to relative performance gains.

We also observed that changes in the SO/δ-Nesting index significantly predicted the task performance changes when considering all three conditions (Figure 4G). Notably, the underlying data across these conditions met criteria that allowed us to perform regression analysis across conditions (see Methods; Figures S4A and S4B). In addition, we also examined the changes in the isolated SO-Nesting index and δ-Nesting index, i.e. not as a ratio but as an independent parameter. As noted above, although changes in the SO-Nesting index significantly explained the changes in task performance, the changes in the SO-Nesting index predicted the task performance changes 4.3-fold better than the isolated SO-Nesting index (see Methods; mean squared error of the regression; SO/δ-Nesting index: 255 ± 46%; SO-Nesting index: 374 ± 57%; SO/δ-Nesting index vs. SO-Nesting index, paired t test, t₇₁ = −3.09, P < 10⁻²). Moreover, in the analysis above, we used a time window of −0.5 to 1.0 sec relative to the up-state time of SO or δ waves to detect spindles (Figures 4D and S3). We also examined a broader set of time windows to detect spindles; we found very similar results with respect to changes in task performance (Figures S4C and S4D). Together, this suggested that the ratio of SO-nested spindles and δ-nested spindles play a role in determining sleep-dependent performance changes.

Do other detected changes in SO, δ wave, and spindle properties predict performance changes? The same regression analyses using the measured changes in either SO or δ wave peak-to-trough amplitudes were not able to explain the changes in task performance (linear regression, R² = 0.025, P = 0.334 for SO; R² = 0.015, P = 0.445 for δ; Figures S5A and S5B). Moreover, peak-amplitudes of spindles were not affected by the various interventions (Figure S5C). Together, these results further suggested that the temporal coupling of spindles to SO relative to δ waves was the most predictive of performance gains. Interestingly, our results also suggested that our suppression of δ up-state spiking activity had an effect on the nesting of SO to spindles.

Effects on ensemble reactivations during sleep

Using computational analyses of sleep-dependent “reactivation” of awake ensemble patterns (Methods) (Gulati et al., 2017; Gulati et al., 2014; Peyrache et al., 2009; Ramanathan et al., 2015), we further examined whether changes in neural ensemble reactivations could account for and predict the changes in task performances described above. This method uses principal components analysis (PCA) to identify the ensembles of neurons that become temporally correlated during learning and stable task performance. The output of this analysis are principle components (PCs), consisting of an array of weights assigned to each neuron in the ensemble, and the eigenvalue, a numerical value that represents the extent of total variance that is captured by a given PC. PCs with the largest eigenvalues capture the most variance. This approach allowed us to measure the strength of reactivations (Figures S6A, S6B, and S6C). Figure 5A shows examples of reactivation strengths during pre- and post-training sleep, which represents “template matching” using the first PC (Methods, PC1 was always significantly different from a random distribution). In other words, high reactivation values indicate that the sleep firing patterns are a closer match to awake firing patterns during BMI₁. Typically, we observed a significant mean increase in the strength of reactivation events during the post-training sleep period relative to the pre-training sleep in the CONTROL and OPTO_δ experiments. However, the mean reactivation strength during post-training sleep was significantly weaker for the OPTO_SO+ experiments (Figure 5B).

Figure 5. Strengthening and weakening of memory reactivation by optogenetic inhibitions.

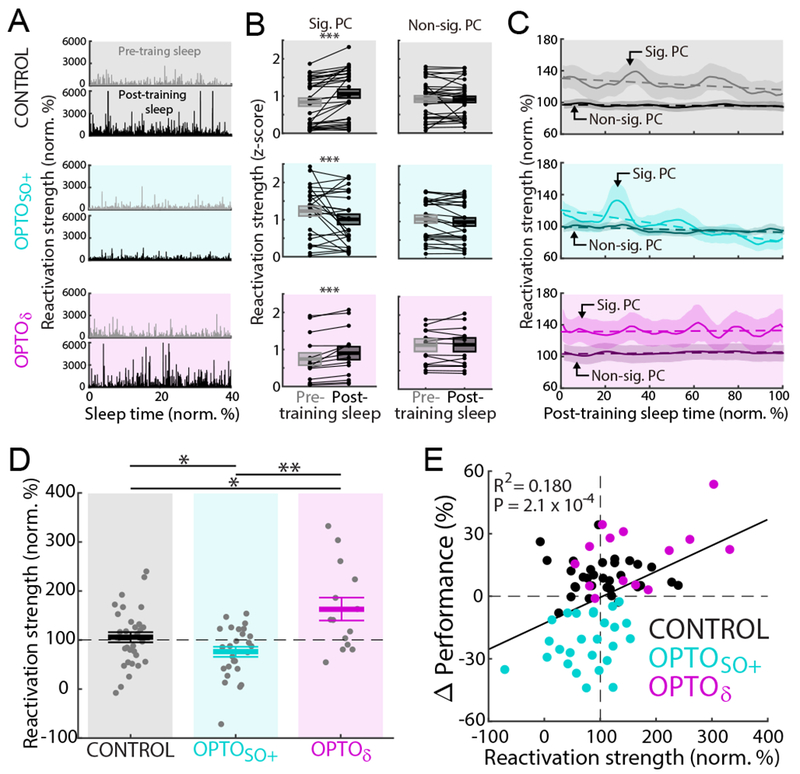
(A) Examples of top 10 percentile reactivation events during a pre- and a post-training sleep in each respective condition (CONTROL, OPTO_SO+, and OPTO_δ). Normalized to the mean reactivation strength during pre-training sleep. First 40% of sleep shown.

(B) Changes from pre- to post-training sleep in the mean reactivation strength for a significant PC (z-scored in each pre- and post-training sleep pair using the mean and the standard deviation during both pre- and post-training sleep; mean in solid line ± s.e.m. in box; CONTROL: n = 32 sessions, 12 rats, mixed-effects model, t₅₉₈₁₂₆ = 16.31, ***P < 10⁻⁵⁹; OPTO_SO+: n = 26 sessions, 12 rats, mixed-effects model, t₃₄₃₄₆₉ = −6.12, ***P < 10⁻⁸; OPTO_δ: n = 14 sessions, 5 rats, mixed-effects model, t₃₄₄₉₆₁ = 11.30, ***P < 10⁻²⁸; corrected for multiple comparison). Same analyses with a non-significant PC (mixed-effects model, P > 0.05, corrected for multiple comparison).

(C) Average time course of top 10 percentile reactivation events during post-training sleep (mean ± s.e.m.; averaged with moving window of 5% sleep time). Normalized to the mean reactivation strengths during pre-training sleep (that is 100% on y-axis). Dashed line represents linear fitting with the significant PC (CONTROL: n = 32 sessions, 12 rats, R² = 0.206, P = 2.1 × 10⁻⁶; OPTO_SO+: n = 26 sessions, 12 rats, R² = 0.626, P = 1.2 × 10⁻²²; OPTO_δ: n = 14 sessions, 5 rats, R² = 0.009, P = 0.36) and with the non-significant PC (CONTROL: n = 32 sessions, 12 rats, R² = 0.132, P = 2.0 × 10⁻⁴; OPTO_SO+: n = 26 sessions, 12 rats, R² = 0.353, P = 6.9 × 10⁻¹¹; OPTO_δ: n = 14 sessions, 5 rats, R² = 0.206, P = 2.1 × 10⁻⁶). Across “A-C,” top, middle, and bottom represent the CONTROL, OPTO_SO+, and OPTO_δ experiments, respectively.

(D) Mean reactivation strength at the end of post-training sleep (i.e. last 15% of sleep; CONTROL: 108.5 ± 11.2%, n = 32 sessions, 12 rats; OPTO_SO+: 75.7 ± 12.4%, n = 26 sessions, 12 rats; OPTO_δ: 162.9 ± 16.9%, n = 14 sessions, 5 rats; one-way ANOVA, F_2,57 = 8.42, P < 10⁻³; significant post hoc t tests, corrected for multiple comparison, *P < 0.05, **P < 0.01).

See also Figure S6.

(E) Relationship between the final mean reactivation strength of post-training sleep and task performance changes (total n = 72 sessions, 12 rats; significant linear regression, R² = 0.180, P = 2.1 × 10⁻⁴).

Interestingly, in the post-training sleep, the reactivation strength was found to weaken over time in sleep during CONTROL experiments (Figure 5C). Despite this apparent weakening of reactivation strength over the sleep period, the reactivation strengths at the end of observed period were still stronger than the mean reactivation strength during the pre-training sleep. In contrast, for the OPTO_SO+ experiments we noted a much more rapid reduction in reactivation strength at the end of post-training sleep (mean ± s.e.m.; CONTROL: 108.5 ± 11.2%, n = 32 sessions, 12 rats; OPTO_SO+: 75.7 ± 12.4%, n = 26 sessions, 12 rats; OPTO_δ: 162.9 ± 16.9%, n = 14 sessions, 5 rats; one-way ANOVA, F_2,57 = 8.42, P < 10⁻³; significant post hoc t tests, corrected for multiple comparison, CONTROL vs. OPTO_SO+: P = 0.024; CONTROL vs. OPTO_δ: P = 0.48; OPTO_SO+ vs. OPTO_δ: P < 10⁻³). Notably, we found that the OPTO_SO and the OPTO_SO+δ were not significantly different (mixed-effects model, t₂₄ = −0.54, P = 0.59), we therefore again combined them into the group OPTO_SO+. We confirmed that the changes in reactivation during the post-training sleep was not explained by a generalized change in firing rates (Figures 5C and S6D). We also found that a randomly selected non-significant PC (see Methods) reactivation did not change over time, suggesting that the neural ensemble identified by the first PC was selectively modified. Importantly, while previous research suggests that post-experience or learning-driven increases in reactivation strengths return to baseline values over time in sleep (Kudrimoti et al., 1999; Miyamoto et al., 2016; Miyamoto et al., 2017; Ramanathan et al., 2015; Tononi and Cirelli, 2014), our data suggests that our interventions can modify the rates of decline. In other words, while it is likely that any increases in reactivation strength will be back to baseline over time, their rates of decline may be important. Thus, we compared the mean reactivation strength at the end of the monitored period. The post-training sleep consisted of total sleep time of 58.9 ± 1.1 min, with a NREM sleep time of 31.1 ± 0.8 min, n = 72 in 12 rats for all conditions (Figure S2B). Interestingly, the OPTO_SO+ intervention resulted in significantly weaker reactivation at the end of the period compared to the CONTROL condition. Moreover, the OPTO_δ experiments had significantly stronger reactivation than the CONTROL conditions (Figure 5D). Taken as a group, the reactivation strengths at the end of the observed post-training sleep could also predict changes in task performance (Figure 5E).

SO-Nested spindles preserve memory reactivation

As described above, we found that the relative nesting of SO to δ waves, i.e. SO/δ-Nesting index, could account for both the offline gains and worsening of performance (Figure 4G). We thus wondered whether the nesting of spindles to either SO or δ waves was linked to the timing of reactivation. We thereby examined reactivation timing to each of these phenomena; we found that reactivation events were temporally linked to the up-states of both SO and δ waves as well as the peaks of spindles (Figures 6A, 6B, and 6C).

Figure 6. SO-nested spindles preserve and δ-nested spindles weaken memory reactivation.

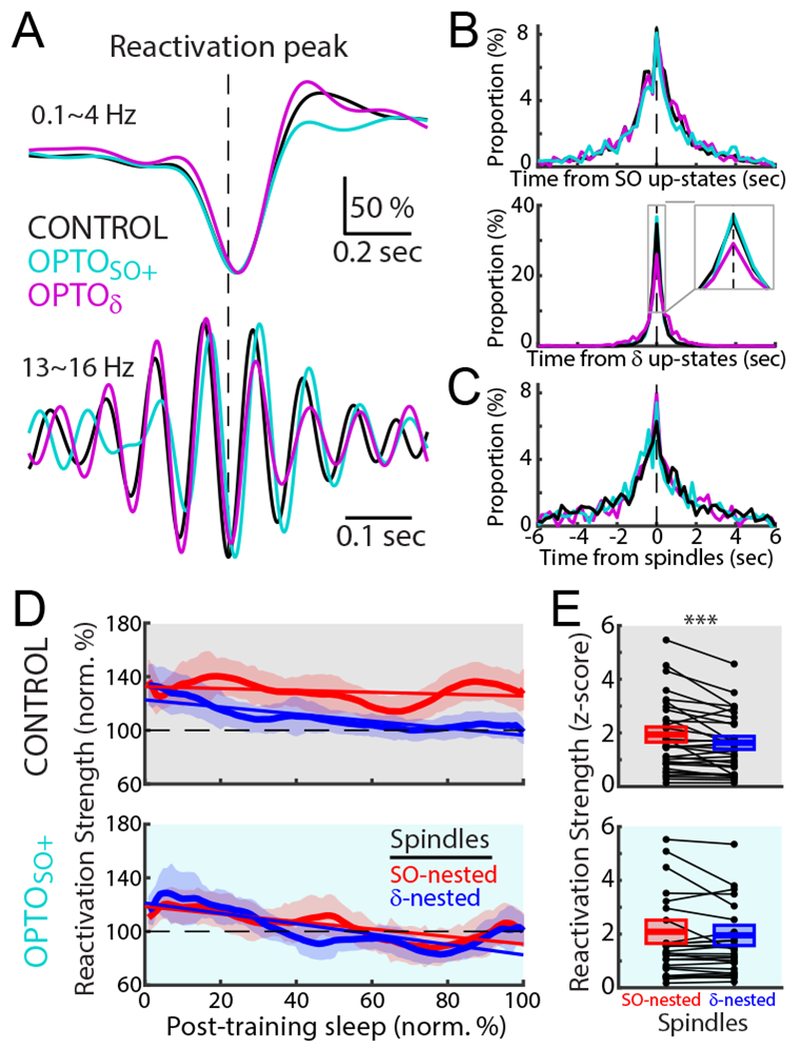
(A) Mean reactivation-peak-triggered LFPs in 0.1~4 H (top) and spindle band (13~16 Hz, bottom) in post-training sleep for CONTROL, OPTO_SO+, and OPTO_δ. Each trace was normalized to the maximum value.

(B and C) Probability distributions of reactivation peak time from the up-states of SO and δ waves (B) and the peaks of spindles (C). The top 10 percentile of reactivation peaks during post-training sleep was used in “A-C.”

(D) Average time courses of the reactivation strengths during SO-nested (red) and δ-nested spindles (blue) of post-training sleep in the CONTROL, and OPTO_SO+ experiments (mean ± s.e.m.; averaged with moving window of the 15% sleep time). Solid line represents the linear fitting (CONTROL: n = 32 sessions, 12 rats, R² = 0.042, P = 0.042 for the SO-nested spindles, R² = 0.536, P = 5.0 × 10⁻¹⁸ for the δ-nested spindles; OPTO_SO+: n = 26 sessions, 12 rats, R² = 0.407, P = 9.3 × 10⁻¹³ for the SO-nested spindles, R² = 0.491, P = 5.1 × 10⁻¹⁶ for the δ-nested spindles).

(E) Differences in mean reactivation strength during post-training sleep between SO-nested and δ-nested spindles (z-scored in each pair of pre- and post-training sleep pair using the mean and the standard deviation during pre-training sleep; mean in solid line ± s.e.m. in box; CONTROL: n = 32 sessions, 12 rats, mixed-effects model, t₁₃₁₃₇₀ = −6.55, ***P < 10⁻¹⁰; OPTO_SO+: n = 26 sessions, 12 rats, mixed-effects model, t₁₁₁₅₃₅ = −1.03, P = 0.31).

See also Figure S6.

Interestingly, in the CONTROL and OPTO_δ experiments, reactivation strengths during SO-nested spindles were sustained over the post-training sleep period (Figure 6D). In contrast to such preservation of the mean reactivation strength over sleep, reactivation strengths appeared to reduce over time for δ-nested spindles (comparison of the reactivation strength at the end of sleep between SO-Nesting and δ-Nesting; CONTROL: mixed-effects model, t₆₂ = −2.64, P = 0.01; OPTO_δ: mixed-effects model, t₂₆ = −3.47, P < 10⁻²). It is important to note that the majority of spindles were nested to either SO or δ waves (SO-Nesting: 40.7% vs. δ-Nesting: 52.8%). Notably, for the OPTO_SO+ experiments, reactivation strengths during the SO-nested spindles also weakened over the post-training sleep period (comparison between SO-Nesting and δ-Nesting, mixed-effects model, t₅₀ = 0.70, P = 0.49). Thus, the mean reactivation strength was significantly greater during the SO-nested spindles relative to the δ-nested spindles in the CONTROL experiments. However, for the OPTO_SO+ experiments, reactivations for the SO-nested spindles were not significantly different from that of the δ-nested spindles (Figure 6E). Remarkably, the mean reactivation strength during the SO-nested spindles was able to predict task performance changes (linear regression, R² = 0.206, P = 6.2 × 10⁻⁵; Figure S6E). This effect was similar to our observation that the changes in SO/δ-Nesting index significantly predicted the task performance changes. This was not the case for the reactivations linked to the δ-nested spindles (linear regression, R² = 0.001, P = 0.96). Taken together, our results suggest that SO-nested spindles have an important role in selectively preserving the strength of ensemble reactivations against weakening during NREM sleep.

Effects on sleep-dependent credit assignment

The BMI task allows us to readily distinguish neural activity that is causally linked to actuator movements (i.e. direct neurons) versus activity that is non-causal (i.e. indirect neurons) (Ganguly et al., 2011). Our previous study indicated that while task-related modulation of direct neurons was maintained, the task modulation of indirect neurons was significantly reduced after a period of sleep (Gulati et al., 2017). This phenomenon suggests that sleep may be important for identifying and selectively preserving activity that is causally linked to actions, i.e. “credit assignment”. Here, we repeated the same analysis and examined rescaling of activity of direct neurons and indirect neurons; we examined five rats that were trained for all three experiment types (Rat ID#1-5, Table S1). We specifically measured changes in peak-firing rate during a task relative to the baseline rate before the task start cue, i.e. modulation-depth/MD (Figure 7). In the CONTROL experiments, the direct neurons experienced a modest increase in MD compared to the net decrease in MD of indirect neurons (n = 13 sessions, 5 rats, mixed effect model, t₁₀₁ = −2.38, P = 0.038). This was also the case for the OPTO_δ experiments; however, in the OPTO_SO experiments, we did not observe significant rescaling (OPTO_SO: n = 13 sessions, 5 rats, mixed-effects model, t₁₀₆ = −1.44, P = 0.153; OPTO_δ: n = 14 sessions, 5 rats, mixed-effects model, t₁₁₆ = −4.16, P < 10⁻⁴). The estimated rescaling effect by the regression modeling in the mixed effect model (i.e. slope; see Methods) was 1.5-fold stronger in the OPTO_δ experiments compared to the CONTROL experiments. Interestingly, we also found that the mean peak time of neural firing of the direct+ neuron was closer to reward onset in comparison to the directδ neuron in the OPTO_δ experiment; it was the opposite in the CONTROL (Figure S7). What might this reveal about actuator control and performance gains? In general, it is likely that the animals learn actuator control by modulating the relative timing of the direct+ and the directδ neurons. Such temporal difference in neural firing might drive more precise modulation of the actuator. Together, these results suggest that our measured changes in sleep-dependent rescaling after learning is important for the observed performance changes.

Figure 7. Rescaling of task activations.

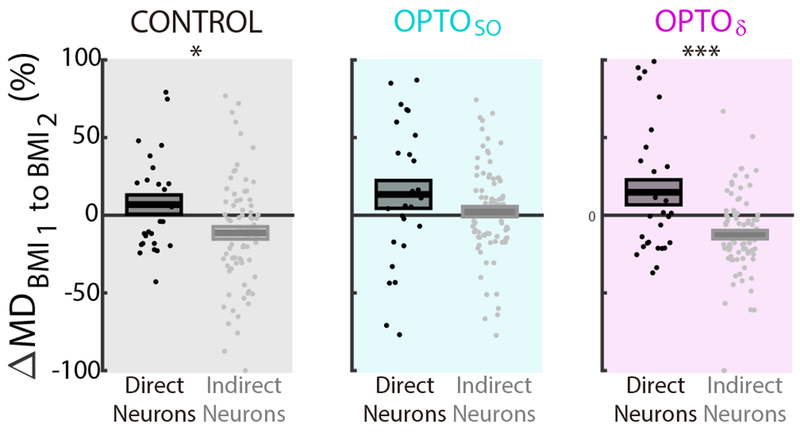
Rescaling of direct and indirect neurons measured through modulation depth changes (ΔMD) from BMI₁ to BMI₂ during CONTROL, OPTO_SO, and OPTO_δ (mean in solid line ± s.e.m. in box; CONTROL: n = 13 sessions, 5 rats, mixed-effects model, t₁₀₁ = −2.38, *P = 0.038; OPTO_SO: n = 13 sessions, 5 rats, mixed-effects model, t₁₀₆ = −1.44, P = 0.153; OPTO_δ: n = 14 sessions, 5 rats, mixed-effects model, t₁₁₆ = −4.16, ***P < 10⁻⁴; corrected for multiple comparison). Data from Rat ID 1-5 in Table S1 analyzed here.

See also Figure S7.

DISCUSSION

In summary, we found that neural reactivations differentially driven by SO and δ waves during NREM sleep determined the extent of sleep-dependent performance gains through competitive regulation of memory consolidation versus memory weakening. Our results indicate that the precise nesting of SO and spindles is particularly important for memory consolidation, likely through its ability to drive and maintain the reactivation of awake experiences. We also found that δ wave mediated reactivations typically decay over time in sleep; blocking such events appeared to then both enhance reactivations as well as improve performance gains. Overall, this suggests a model in which δ wave triggered processes, which promote weakening of memories, can modulate the efficacy of SO triggered processes, which promote memory consolidation.

Role of SO and spindles in sleep-dependent memory processing

Past work has highlighted the importance of SO, spindles and their precise temporal nesting as important for memory consolidation (Born et al., 2006; Buzsáki, 1989; Carr et al., 2011; Sejnowski and Destexhe, 2000; Stickgold, 2005). Spindle modulation by externally induced indirect stimuli in humans, e.g. task-related auditory cues (Antony et al., 2018; Cairney et al., 2018; Ngo et al., 2013), and internally induced stimuli in rodents (Latchoumane et al., 2017; Maingret et al., 2016) can influence nesting and performance gains. However, it remained unclear whether reactivation of awake experiences during nested SO and spindles is directly linked to consolidation. Our data demonstrate that the precise temporal coupling of spindles to SO is essential; we specifically found that it appears to be important for maintaining the reactivation strength of neural ensembles formed during the process of learning and for promoting offline performance gains. Interestingly, while the number of events in sleep was not significantly different for the various interventions, what changed was the temporal precision of nesting relative to SO and δ waves. Consistent with this notion was the finding that any disruption of spiking activity during SO, with a concomitant reduction in the precise nesting of spindles to SO, resulted in degradation of ensemble reactivation strength and worsening of performance upon awakening.

Interestingly, our optogenetic interventions suggests that cortical spiking activity may be an important drive for nesting (Bonjean et al., 2011; Steriade et al., 1993a), i.e. the brief silencing of cortical spiking during up-states altered the precise nesting of spindles to SO. Even though our optogenetic inhibitions affected both pyramidal and interneurons (Figure S1), it is possible that interneurons are particularly important for the precise temporal coupling of spindles to SO and for selective memory reactivation. For example, as recently shown, it is possible that concurrent peri-somatic inhibition of parvalbumin-positive interneurons during SO-nested spindles might be important for SO-spindle coupling (Niethard et al., 2017; Niethard et al., 2018). Future work can examine precisely how local cortical circuit elements regulate nesting and promote consolidation versus weakening of memories.

Role of δ wave activity in forgetting and weakening of memory traces

Our data also support a model in which δ waves triggers processes that weaken SO driven consolidation. Our control condition provides a clear contrast regarding how sleep waves might differentially contribute to either consolidation or “forgetting.” We found that δ waves appeared to drive weakening of ensemble reactivations over time in sleep. Intriguingly, with disruption of SO events, there was an apparent unopposed rapid weakening of all reactivations. Moreover, optogenetic inhibitions during δ waves (i.e. OPTO_δ) significantly increased reactivation strength and offline gains. Our analysis further indicated that the effects of OPTO_δ were best explained by an increase in the nesting of SO and spindles relative to the nesting of δ waves and spindles and increases in ensemble reactivation. Together, this suggests that δ waves support an activity-dependent process that can weaken reactivations of memory traces and promote forgetting.

What activity-dependent processes might be differentially recruited by δ waves during NREM sleep? While our study cannot resolve synaptic level modifications, past work might suggest mechanisms that could explain our results. For example, extensive past work on synaptic plasticity has shown that long-term depression (LTD) can be induced by low-frequency stimulation (0.5-3 Hz) (Lee et al., 2000; Malenka and Bear, 2004). Thus, it is possible that rhythmic δ waves at a frequency of 1.12 Hz (Figure 1E) might induce LTD and local weakening of synapses. Moreover, given the link of ensemble reactivations to δ waves, reactivations might drive selective LTD. In this model, SO-nested spindles could then serve to selectively strengthen and/or protect synapses that underlie a new experience; in other words, reactivation events linked to SO might support activity-dependent processes that either prevent LTD or trigger long-term potentiation (LTP). Intriguingly, a recent study in slices found that spike time-dependent plasticity during up-states is biased towards LTD. In contrast, precise temporal activation of presynaptic and postsynaptic neurons appeared to protect against synaptic depression (Gonzalez-Rueda et al., 2018). Moreover, given the repetitive interactions between SO and δ waves during NREM sleep, it is quite likely that systematic changes in synaptic activities occur over relatively long periods of time. Furthermore, it is quite possible that differences in neuromodulators could alter the type of plasticity triggered by reactivations during SO versus δ waves (Eschenko et al., 2012; Poe, 2017). They might also explain how relative weakening of synapses could still allow maintenance of ensemble reactivations during SO, i.e. by increasing excitability for SO as opposed to δ waves.

It is also possible that the phenomenon of homeostatic downscaling (Tononi and Cirelli, 2014) could be related to the reduction of reactivation strength during δ waves in NREM sleep. While again, measurement of firing rates and ensembles do not allow us to monitor synaptic level changes, the apparent reduction in ensemble reactivation strength over sleep could be related. Notably, however, we did not see changes in firing rates and the non-significant PC reactivation in the time period we monitored. Thus, it is quite possible that our identified process is more selective for newly encoded information. It is also possible that with addition monitoring over longer sleep, we would observe homogenizing of firing rates and reductions in delta power (Tononi and Cirelli, 2014; Watson et al., 2016). It remains to be seen whether our δ wave triggered reactivations could also support such changes with longer periods of time in NREM sleep.

Interactions between SO and δ waves

Classic studies initially distinguished SO and δ waves as two distinct neurophysiological phenomena consisting of low-frequency waves with different spatial and temporal properties (Steriade et al., 1993a; Steriade and Timofeev, 2003). Subsequent studies have found evidence for the existence of two separate classes of “slow waves” during NREM sleep ; one class of slow waves are more global and have larger amplitudes, the other class has smaller amplitudes and are more local (Bernardi et al., 2018; Dang-Vu et al., 2008; Genzel et al., 2014; Molle et al., 2002; Siclari et al., 2014). While there are multiple classification schemes, our definition of SO is perhaps consistent with the large global slow waves measured using EEG. Similarly, our defined δ waves are perhaps consistent with what is seen in EEG, i.e. δ waves as smaller amplitude local slow waves. Future work will have to definitively test for concordance of features across species and between invasive and non-invasive recording approaches.

One possibility is that cortical-subcortical structures support reciprocal interactions between SO and δ waves during NREM sleep; thus, we should not view activity-dependent processing during δ waves in isolation. Classic studies have proposed that a cortical SO (also called a K complex) may trigger complex waves within one oscillatory cycle; this can manifest as “clock-like” delta oscillations and spindles following slow oscillations through reciprocal connections between neocortex and thalamus (Hobson and Pace-Schott, 2002; Steriade et al., 1993a; Steriade and Timofeev, 2003). Our results suggest that such a temporal structure may be present, albeit not as clearly “clock-like”, in the rat motor cortex (Figure 1F). Moreover, while our identified SO was more global, i.e. perhaps supporting interactions between areas, δ wave was more local, i.e. more restricted to local circuits. Our results indicate that the interactions between the two are important for regulating the balance between consolidation and weakening. It is possible that global SO support “protection” of activity patterns across areas to support system consolidation (Genzel et al., 2014; Robertson, 2009). In contrast, δ waves are only able to drive local activity-dependent processes that appear to result in net weakening. In the absence of “protective” nested SO and spindles, local suppressive processes dominate. With a relative drop of local suppressive processes, global interactions are more likely to occur and promote consolidation. It is also possible that such repetitive exploration and competition between global versus local processes may be a key reason for the need for sleep, i.e. this may not be possible during awake states. Although we suggest an active role of δ waves in weakening of memory, there is also a possibility that δ waves exert their effects solely by diminishing SO-related consolidation processes and nesting of spindles. A past study found that artificially induced SO trigger a state of refractoriness in spindle generating networks; it is possible that δ waves may exert its effects by simply weakening the consolidation effects via its effects on SO and spindle generating networks (Ngo et al., 2015).

Past work in humans has also found that induction of new large slow waves using external stimulus (e.g. auditory pulses) can change the amplitude of the subsequent slow wave activity (Ngo et al., 2013; Papalambros et al., 2017). In this study, although the perturbations of SO activity did not change the following δ wave and even SO itself, the perturbations of δ waves decreased δ amplitude and increased the following SO peak amplitudes (i.e. down-states) (Figures S5A and S5B). This might be understood in terms of global versus local synchronization; i.e. local activity during δ waves might be more easily influenced by our local optogenetic perturbations. Moreover, a past study found that large slow waves tended to be smaller when preceded by another slow wave (Bernardi et al., 2018); this may explain why SO down-states were larger in the setting of smaller δ waves in our OPTO_δ experiments. Together, this suggests that natural interactions between SO and δ waves may trigger competing processes during sleep-dependent memory processing.

Our result may also have implications for phenomena seen with aging. For example, it is frequently noted that slow-wave activity is of lower amplitude in the elderly (McKillop et al., 2018). The elderly are less likely to have sleep-dependent consolidation benefits, perhaps because of a reduction in the nesting probability between SO and spindles (Helfrich et al., 2018). If our results also apply to the aging brain, it is possible that age related changes in the natural balance between SO and δ waves can determine whether offline gains can occur. This may also apply to the post-injured brain and the recovery process; there are known increases in δ waves after cortical injury (Carmichael and Chesselet, 2002; Gulati et al., 2015).

Conclusion

Our results show that NREM sleep appears to consist of processes that compete to promote consolidation versus weakening during sleep-dependent memory processing; they further suggest that SO and δ waves have dissociable and competing roles, respectively, in memory consolidation versus memory weakening.

STAR★METHODS

Lead contact and materials availability

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Karunesh Ganguly (karunesh.ganguly@ucsf.edu).

Experimental model and subject details

Mice

Experiments were approved by the Institutional Animal Care and Use Committee at the San Francisco VA Medical Center. We used a total of thirteen adult naïve healthy Long-Evans male rats that were approximately 3 months old (Charles River Labs); n=12 rats were used for optogenetic experiments and one rat was used for simultaneous AC- and DC-coupled recordings (Figure 1A). The animals were largely pair housed; however, after surgical procedures, animals were single housed during the recovery period. No statistical methods were used to pre-determine sample sizes, but our sample sizes are similar to those reported in previous publications (Gulati et al., 2017; Gulati et al., 2014; Ramanathan et al., 2015). Animals were kept under controlled temperature and humidity with a 12-h light/dark cycle; lights on at 06:00 a.m.

Method details

Surgery

For optogenetic experiments (n = 12 rats), viral injections were made at least 3 weeks before chronic microelectrode array implant surgeries. A red-shifted halorhodopsin, Jaws (AAV8-hSyn-Jaws-KGC-GFP-ER2, UNC Viral Core) was injected in each rat for neural silencing (Chuong et al., 2014; Gulati et al., 2017). Surgeries were performed under isofluorane (1-3%) anesthesia and body temperature was maintained at 37 °C with a heating pad. Atropine sulfate was also administered before anesthesia (0.02 mg/kg of body weight). Burr hole craniotomies were performed over injection sites, and the virus was injected using a Hamilton Syringe with 34G needle. 500 nl were injected (100 nl per min) into deep cortical layers (1.4 mm from surface of brain) at two sites in M1 (coordinates relative to bregma: posterior, 0.5 mm and lateral, 3.5 mm; and anterior, 1.5 mm and lateral, 3.5 mm). After the injections, the skin was sutured. The post-operative recovery regimen included administration of buprenorphine at 0.02 mg/kg and meloxicam at 0.2 mg/kg. Dexamethasone at 0.5 mg/kg and Trimethoprim sulfadiazine at 15 mg/kg were also administered post-operatively for 5 d. After at least 3 weeks recovery, probes with an attached cannula for optic fiber were implanted. Rats were anesthetized, and body temperature was maintained at 37 °C as described above. We used 32-channel microwire arrays; arrays were lowered down to 1,400–1,800 μm in the layer 5 of the primary motor cortex (M1) in the upper limb area (1-3 mm anterior to bregma and 2-4 mm lateral from midline). The reference wire was wrapped around a screw inserted in the midline over the cerebellum. Final localization of depth was based on quality of recordings across the array at the time of implantation. All animals were allowed to recover for 1-week with the same regimen as described above before start of experiments. Data collection and analysis were not performed blind to the conditions of the experiments. Viral expression was confirmed with fluorescence imaging. Optogenetic inhibition significantly reduced firing in Ml neurons, with a reduction in 50-70% of recorded cells (Figure 2E). Probes with an attached cannula for optic fiber were implanted after at least 2.5 weeks recovery. We also used one adult rat in Figure 1A and the same surgery procedure was done except electrode implantation. For this rat, we used Ag/AgCl electrodes; working and reference electrode were located on the surface of M1 and into the midline over the cerebellum, respectively. In the same rat, we also placed a twisted Platinum-Iridium wire (six-strand) into M1 and wrapped the reference wire around a screw inserted in the midline over the cerebellum.

Electrophysiology

We conducted AC-coupled and DC-coupled recordings at the same time for the case of Figure 1A, using Platinum-Iridium wire (A-M Systems) and Ag/AgCl electrode disks (World Precision Instruments; 4.0 mm diameter x 1 mm for working and 2.0 mm diameter x 4 mm for reference electrode) for AC- and DC-coupled recordings, respectively. Except for that single animal, we conducted AC-coupled recordings and recorded extracellular neural activity using 32-channel microwire electrode arrays (MEAs; 33-μm-length, 250-μm-spacing, 4-rows, standard polyimide-coated tungsten microwire arrays from Tucker-Davis Technologies (TDT) for two rats; and 25-μm-length, 200-μm-spacing, 6-rows, tungsten microwire arrays from Innovative Neurophysiology Inc. for ten rats). We recorded spike and LFP activity using a 128-channel RZ2 bioamp processor (TDT) and 128-channel neurodigitizer (digital PZ4 for AC-coupled and analog PZ5 for simultaneous AC- and DC-coupled recording).

Spike data was sampled at 24,414 Hz and LFP data at 1,018 Hz. ZIF-clip-based headstages with a unity gain and high impedance (~1 G) was used. Only clearly identifiable units with good waveforms and high signal-to-noise ratio were used. The remaining neural data (e.g. filtered LFP) was recorded for offline analysis at 1,018 Hz. Behavior related timestamps (that is, trial onset and trial completion) were sent to the RZ2 analog input channel using a digital board and synchronized to neural data. We initially used an online sorting program (SpikePac, TDT) for neuroprosthetic control. We then conducted offline sorting using Tucker-Davies Technologies’ OpenSorter for five rats and using MountainSort for seven rats (Chung et al., 2017). Briefly, MountainSort is spike-sorting software that uses an automatic algorithm, which compares clusters of data and identifies single units using one-dimensional projections. After the automatic sorting using MountainSort, a minimal manual merging and rejection of clusters were made.

Behavior

After recovery, animals were typically handled for several days before the start of experimental sessions. Animals were acclimated to a custom plexiglass behavioral box (Figure 2A) during this period. The box was equipped with a door at one end. Initially, water delivery from the actuator was not introduced and they were just acclimatized to the box for 3-4 days. Toward the end of the acclimation period, the rats typically fell asleep while in the box. Animals were then given water, such that water (from the feeding tube illustrated in Figure 2A) was available in a randomized fashion while in the behavioral box. We monitored body weights on a daily basis to ensure that the weight did not drop below 95% of the initial weight. Behavioral blocks were conducted in the morning, with second blocks conducted in the afternoon. We recorded neural data from the rats for a 1 to 2-h before start of BMI training (pre-training sleep). The rats were then allowed to perform the task training over a ~2-h block (BMI₁). Recorded neural data was entered in real-time from the TDT workstation to custom routines in Matlab. These then served as control signals for the angular velocity of the feeding tube. The rats typically performed ~180-200 trials per block. These blocks typically lasted from 90-120 min based on the rate of trial completion. Following this, we recorded neural data from animals for a 1-h period (post-training sleep). The animals then continued with another 90-120-min task retrieval block (BMI₂). Sorted units at the beginning of the recording before pre-training sleep were checked for maintenance throughout the next task and sleep blocks.

Neural control of the feeding tube

During the BMI training and retrieval blocks, we typically randomly selected two well-isolated units as “direct” and allowed their neural activity to control the angular velocity of the feeding tube. In two of the twelve rats, there was only one unit selected as the direct unit. The remaining neurons in all the experiments (that is, indirect) were recorded but not causally linked to the actuator movement. These direct and indirect units maintained their stability throughout the recording as evidenced by stability of waveform shape, inter spike interval histograms, and mean firing rate. We binned the spiking activity of each unit into 50 ms bins. We then established a mean firing rate (i.e. baseline) for each unit over a 3-5 min baseline period. During this period the animals were typically transitioning between walking, exploring and periods of rest. The mean firing rate was then subtracted from its current firing rate at all time bins. The specific transform that we used was

$${\theta }_{\text{v}}=\text{C}*[{\text{G}}_1*{\text{r}}_1(\text{i})+{\text{G}}_2*{\text{r}}_2(\text{i})]$$

where θ_v was the angular velocity of the feeding tube, r₁(i) and r₂(i) were firing rates of the direct neurons; G₁ and G₂ were +1 and −1 for direct+ and direct− neurons, respectively, and were held constant after initialization. C was a fixed constant that scaled the firing rates to arrive at a value of angular velocity. The animals were then allowed to control the feeding tube via modulation of neural activity of direct neurons. The tube started at the same start position every trial (P₁ in Figure 2A). The calculated angular velocity was added to the previous angular position at each time step (50 ms). During each trial, the angular position could range from −45 to +180 degrees. If the tube stayed in the “target zone” (P₂ in Figure 2A; spanned 10° area) for a period of 300 ms, a water reward was delivered. In the BMI block, the reward was delivered with a fixed delay of ~200 ms relative to task completion. In the beginning of a block, most rats were unsuccessful at bringing the feeding tube to the position P2. Most rats steadily improved control and reduced the time to completion of the task during the first training block (BMI₁). We obtained multiple learning blocks from each animal (Table S1). In the same animal, completely different units were selected for the direct neurons to ensure the independency in task performance across experiment sessions. These sessions were typically several days to 1 week apart to ensure that new units were recorded. Consistent with past studies, we also found that incorporation of new units into the control scheme required new learning (Ganguly et al., 2011; Gulati et al., 2017; Gulati et al., 2014).

Closed-loop optogenetics during post-training sleep

Five types of experiments were conducted using the twelve Jaws-injected animals, namely OPTO_SO (n = 13 sessions, 5 rats), OPTO_δ (n = 14 sessions, 5 rats), OPTO_SO+δ (n = 13 sessions, 7 rats), OPTO_RAND (n = 9 sessions, 3 rats) and OPTO_OFF (n = 23 sessions, 12 rats). These experiments were largely randomly interspersed for each animal. In general, we identified the phases of the LFP associated with “up” and “down” states based on the relationship of the neural spiking to the LFP. For example, as shown in Figure 1A, the negativity in our LFP signals was associated with neural spiking and thus consistent with an up-state, which are natural states of increased activity during slow waves. The positivity in our LFP signals was associated with silence of neural spiking and consistent with a down-state. The closed-loop stimulations were conducted by triggering the laser light based on real-time or online detection of cortical states. We used a custom script in the RPvdsEx program (TDT) to identify SO and δ in real-time during sleep. The raw data was filtered using a digital filter implemented in the RPvdsEx program. For the lowpass filter <4 Hz, we used the digital “biquad” filter with the 2nd order Butterworth filter coefficient. For the highpass filter >0.1 Hz, an exponential smoothing paradigm (i.e. MCSmooth component) was used. The laser light (625 nm, 100 ms; RLM638TA-200FC, Shanghai Laser & Optics Century) was delivered with 200 or 400 μm diameter optic fibers (Doric Lenses). In the OPTO_SO+ and OPTO_δ experiments, “filtering based” triggering was used to deliver the laser light during cortical up-states of SO and δ. Two manual thresholds (positive and negative) were placed on the filtered LFP trace (0.1-4 Hz) to detect up-states and down-states; down-states were detected when the filtered LFP trace crossed the positive threshold upward and up-states were detected when the filtered LFP trace crossed the negative threshold downward. The two manual thresholds were selected visually to approximate the respective phase of SO and δ waves based on the knowledge from other previous offline detections. As offline detection (see below), up-states were detected with the same criterion for both SO and δ. Then, an upstate preceded by down-state within 500 ms triggered a laser light pulse for SO, while an up-state which was not preceded by down-state within 500 ms triggered a light pulse for δ.

In the OPTO_RAND experiments, the above “filtering based” triggering was also used. In this control condition, light pulses were delivered during a state between up-states of SO and δ; a light pulse was triggered with time delay which was randomly generated from 0.3 to 1.3 sec after every up-state detection. However, this queued light pulse was not delivered, in the case that next up-state was detected before the onset time of the queued light. Moreover, to ensure that the light pulse with random delay did not disrupt subsequent up-states, the light was turned off as soon as up-states were detected during light on. In the OPTO_SO+δ experiments, two types of triggering were used (n = 3 power based; n = 10 filtering based). A light pulse was delivered during all SO and δ waves up-states in the same way stated above for the “filtering based” triggering. For the “power based” triggering, we used the following approach. The algorithm/workstation calculated the LFP power in the 0.1-4-Hz range and compared it to the threshold. Once the threshold was exceeded for >100 ms, LED illumination was triggered. The triggered light pulses during the OPTO_δ experiments had 1.7 times more incidences compared to the OPTO_SO experiments, but the task performance was improved with more inhibitions in OPTO_δ compared to OPTO_SO experiments. This indicated that the laser light itself was unlikely to contribute to our observed effects. Finally, a group of control experiments called OPTO_OFF (that is, where no stimulation was triggered) was also conducted in the Jaws-injected rats. Durations of total pre- and post-training sleep were similar in all experiment types (Figure S2B).

To examine the effect of optogenetic stimulations on putative excitatory (pE) versus putative inhibitory (pI) neurons, we conducted cell type classification as in the past studies (Figure S1) (Sirota et al., 2008; Stark et al., 2013). Units were sorted and only clearly identifiable units with good waveforms and high signal-to-noise ratio were used as stated above. A total of 894 units in 12 rats were used. For each unit, spike waveshape parameters were calculated; trough-to-peak amplitude and spike width. Spike width was calculated as inverse peak frequency of the spike spectrum, estimated by 1024-point FFT of the mean-padded waveforms. These two parameters created two separable clusters (pE: n = 759, 84.9% vs. pI: n =135, 15.1%). This analysis fulfilled the objective of the cell type classification; our optogenetic stimulations influenced on both pE and pI units with similar portion, 38.6% and 34.8 %, respectively.

BMI tasks and changes in performance

Analysis was performed in Matlab (Mathworks). A total of seventy-two BMI₁ training blocks recorded from the twelve rats were used for our analysis. All of these blocks demonstrated “robust learning” (that is, >3 s.d. drop in time to completion in the last 1/3 of trials or “late” trials (BMI_1-Late) in comparison to the first 1/3 of trials or ‘early’ trials; BMI_1-Early). These blocks were followed by a task retrieval block (i.e. BMI₂). In Figures 2A and 3A, we compared changes in mean task time across experimental sessions. Specifically, we compared the change in mean task time between BMI_1-Late and BMI_2-Early (the first 1/3 trials during BMI₂). For the comparison in task performance change in Figure 4F, we calculated performance by dividing the change in mean task time from the BMI_1-Late to the BMI_2-Early by the mean task time during the BMI_1-Late and then multiplying negative sign and number of 100 so that a positivity in performance represents a reduction in task time from the BMI_1-Late to the BMI_2-Early.

Task-related activity

The distinction between direct and indirect neurons was based on whether units were used for the direct neural control of the feeding tube. The modulation depth (MD) was calculated by comparing the peak activity around the task (in the 10 sec window before the task end/reward) over the baseline firing activity (averaged activity of 5 sec before task start) on the peri-event time histograms (PETH, bin length 50 ms). In other words, the MD is a measure of the modulation of firing rate relative to the pre-task start baseline rate. This was compared for direct and indirect neurons from BMI_1-Late to BMI_2-Early (change in MD from BMI_1-Late to BMI_2-Early; ΔMD; Figure 7). In a BMI block with approximately 200 trials, ΔMD were averaged across ~65 trials.

Identification of NREM sleep waves

The LFP activity was recorded using 32-channel microwire electrode arrays. The LFP was analyzed after removing obvious artifacts and excluding bad channels. Identification of NREM epochs was performed by classification based on power spectral density of LFP. LFP trace was segmented into non-overlapping 6 sec epochs. In each epoch the power spectral density was computed and averaged over the SO/δ (0.1-4 Hz) and gamma (30-60 Hz) frequency bands. Then a k-means classifier was used to classify epochs into two clusters, NREM sleep and REM/awake. Sleep epochs less than 30 sec were excluded from NREM sleep epochs. The identified NREM sleep epochs were verified by visual assessment of the LFP activity. This power-based sleep detections showed a close match to the video-based detections (Figure S2A) (Pack et al., 2007); the number of pixels which change intensity frame to frame in each pair of consecutive frames was computed from a recorded video during sleep block and then integrated those number of pixels during an epoch of 30 sec. If that integrated value was higher than threshold, that epoch was identified as sleep; the threshold was chosen by comparing detection results and visual assessment of the recorded video.

In offline analysis, SO, δ waves and spindles were detected using the algorithm used by Sela and colleagues (Sela et al., 2016). The LFP average across all recording channels excluding bad channels was filtered in the SO/δ band (0.1-4 Hz) through two independent filtering; the high pass Butterworth filter (2nd order, zero phase shifted, with a cutoff at 0.1 Hz) was applied and then followed by the low pass Butterworth filter (5th order, zero phase shifted, with a cutoff at 4 Hz). Next, all positive-to-negative zero crossings during NREM sleep were identified, along with the previous peaks, the following troughs, and the surround negative-to-positive zero crossings. Then the positive threshold (the top 15 percentile of the peaks) and the negative threshold (the bottom 40 percentile of the troughs) were respectively defined for the down-states and up-states. Each identified wave was considered a SO if the trough was lower than the negative threshold (i.e. up-state), the peak preceding that up-state was higher than the positive threshold (i.e. down-state), and the duration between the peak and the trough was between 150 ms and 500 ms (Figures 1B and 1C). On the other hand, a slow wave was considered a δ wave if the trough was lower than the negative threshold (i.e. up-states) and that the up-state was preceded by maximum voltage that was lower than the positive threshold within 500 ms. For spindle detection, the LFP was first z-scored in each channel and averaged across all good channels. The LFP average was filtered in spindle band (10-14 Hz) through two independent filtering; the high pass Butterworth filter (6th order, zero phase shifted, with a cutoff at 10 Hz) was applied and then followed by the low pass Butterworth filter (8th order, zero phase shifted, with a cutoff at 14Hz). We computed a smoothed envelope of this signal, the magnitude of the Hilbert transforms with convolving by a Gaussian window (200 ms). Next, we determined two thresholds for spindle detection based on the mean (μ) and standard deviation (σ) of the spindle band envelope during NREM sleep; the upper and lower thresholds were set μ + 2.5 χ σ and μ +1.5 χ σ, respectively. Epochs in which the spindle power exceeded the upper threshold for at least one sample and the spindle power exceeded the lower threshold for at least 500 ms were considered spindles. Each epoch where the spindle power exceeded the lower threshold was considered the start and stop of the spindle; the duration of each spindle was based on these values as well. For the reactivation analyses spindles was detected in 13-16 Hz based on the previous finding that fast spindles (13-16 Hz) play a key role for sleep-dependent memory reactivation (Molle et al., 2011; Ramanathan et al., 2015).

Spindle nesting analyses

We also analyzed the temporal coupling of spindles relative to SO and δ waves. For the nesting of spindles to SO (SO-Nesting; Figure 4A top), each spindle was linked to the closest SO. The time difference between the peak of spindle and the up-state of the linked SO was measured for each detected spindle (ΔT_SO-Spindle). If ΔT_SO-Spindle was between −0.5 sec and 1.0 sec (i.e. nesting time window), that spindle event was considered a SO-nested spindle. The nesting of spindles to δ (δ-Nesting; Figure 4B bottom) was identified in a manner analogous to the “SO-Nesting” value, i.e. time differences between the spindle peak time and the time of the δ up-state (ΔT_SO-Spindle). To quantitatively assess the changes in temporal coupling of spindles to SO, we specifically measured “nesting index” of spindles to SO (SO-Nesting index). Time lag of spindle from the closest SO (ΔT_SO-Spindle) was measured for each spindle event and the rate of spindles of which ΔT_SO-Spindle was within the nesting time window was measured; i.e. SO-Nesting index (Figures 4D and S2A). We also measured “nesting index” of spindles to δ (δ-Nesting index) the same way as the “SO-Nesting index” but using time lags between the peaks of spindles and the up-states of the linked δ (ΔT_SO-Spindle) (Figure S3B). Then SO/δ-Nesting index was calculated by the ratio of SO-Nesting index over δ-Nesting index (Figure 4E). SO-Nesting, δ-Nesting, and SO/δ-Nesting index were measured in a pair of pre-training and post-training sleep in a single session, then the change from the pre-training to the post-training sleep was computed (ΔSO-Nesting, Δδ-Nesting, and ΔSO/δ-Nesting index, respectively).

Ensemble reactivation analyses

To characterize ensemble reactivations following sleep, we performed an analysis that compared neural activity patterns during pre-training sleep and post-training sleep using a template that was created based on neural activity during task performance in BMI₁ (Gulati et al., 2017; Gulati et al., 2014; Peyrache et al., 2009; Ramanathan et al., 2015). We used principal component analysis (PCA) to convert a set of observations of neural activity during the task into a set of values of linearly uncorrelated variables called principal components (PC or “template”); the first PC accounts for the largest variance in the neural activity during task training in BMI₁. In detail, we first computed a pairwise unit activity correlation matrix during BMI₁ by concatenating binned spike trains (t_bin = 50 ms) for each neuron across trials (between −2.0 sec and 0.5 sec from the task end). This concatenated spike train was z-transformed to account for neurons with high firing rates. Then the z-transformed spike trains were placed into a 2-D matrix organized by neurons (x) and time (y for the number of time bins). From this spike count matrix, we calculated the correlation matrix (C_task), and then calculated the eigenvectors. This first eigenvector, or the first PC, was used as the template of ensemble activity during task training in BMI₁; this was projected back on to the neural activity during pre-training sleep and post-training sleep. This projection was a linear combination of z-scored binned neural activity from each pre- and post-training sleep, with the template (i.e. the eigenvector/PC) calculated from the C_task during the BMI₁. This linear combination has been termed as the “activation strength” in the awake task and “reactivation strength” during sleep of that particular neural ensemble. In this analysis we focused on the first eigenvector, as the first PC explained most task-related variance (Figure S6A). The first 1-2 PCs were found to be significant, that is their eigenvalues were greater than a threshold for random distributions defined using the Marcenko-Pastur distribution as in the previous studies (Gulati et al., 2014; Peyrache et al., 2009). Our reactivation analysis focused on the first significant PC. Moreover, we randomly selected one PC (which is non-significant, as defined above) as a means of measuring non-selective changes in firing rate.

The reactivation events that were chosen for the comparison with the task performance changes were those with a reactivation strength that was significantly greater in the post-training sleep than in the pre-training sleep; thus, in this study, top 10 percentile reactivation strengths was used to compare pre- and post-training sleep (Figure 5). However, typically the top 10-20 percentile reactivation strengths from the post-training sleep fulfilled this criterion (Figures S6B and S6C for the significant PC). We focused on the top 10 percentile peaks of reactivation strengths from the post-training sleep in order to examine the timing of reactivation relative to the NREM sleep waves (Figures 6A, 6B, and 6C). The average time courses of the reactivation strengths were smoothed using moving window of 5 and 20 percentage sleep period for Figure 5C and Figure 6D, respectively. We also focused on the reactivation events during the spindle epochs identified by the power-based lower threshold as described above (Figures 6D, 6E, and S7B) and the top 90 percentile reactivation strengths during the spindle epochs were used. We also confirmed that the change in reactivation strength in the post-training sleep was not explained by changes in the firing rates (Figure S7A).

Quantification and statistical analysis

Figures show mean ± s.e.m.; if this was not case, we specifically indicated it. Parametric statistics were generally used in this study (linear mixed-effect model, ANOVA, t-tests, linear regression, unless otherwise stated); they were implemented within MATLAB. The linear mixed-effects model (using MATLAB “fitlme”) was used to compare the differences in task performance, temporal coupling of spindles to SO, and reactivation strength. This model accounts for the fact that units, channels, events, or trials from the same animal are more correlated than those from different animals and is more stringent than computing statistical significance over all units, channels, events, and trials (Aarts et al., 2014). We fitted random intercepts for each rat and reported the P values for the regression coefficients associated with pre-training sleep or post-training sleep, BMI_1-late or BMI_2-early, SO-nested or δ-nested spindles, or stimulation types. The used random effects and fixed effects parameters are following; Figure 1D, random: rat, fixed: slow-wave type; Figures 2G and 3E, random: rat, fixed: experiment type; Figure 5B, random: rat and experiment session, fixed: sleep block; Figure 6E, random: rat and experiment session, fixed: spindle type; Figure 7, random: rat, fixed: neuron type. In Figures 5B and 6E, every reactivation event was used as the response parameter. In Figures 1D, 2G, 3E, and 7 mean in each experiment session was used as the response parameter, and in Figures 5B and 6E every value of reactivation events was used as the response paramenter. Regression modeling for fixed-effects provide intercept and slope in mixed-effects model comparison. In Figure 7, the estimated rescaling effect was compared using the slope coefficient of the fixed-effects between the CONTROL and OPTO_δ experiments.

Three optogenetic conditions were compared in Figures 4 and 5 after grouping OPTO_RAND with OPTO_OFF experiments and OPTO_SO+δ with OPSTO_SO experiments as stated main text (CONTROL: n = 32 sessions, 12 rats; OPTO_SO+: n = 26 sessions, 12 rats; OPTO_δ: n = 14 sessions, 5 rats). In order to compare across the three conditions, we performed one-way ANOVA (test of homogeneity of variances was done) and next performed two-tailed, two-sample t-tests for every possible pair of experiment type, which were followed by Bonferroni-Holm correction for family-wise error. Bonferroni-Holm correction was used for every multiple comparison. We used linear regression or correlation to evaluate the relationship between the changes in SO-Nesting index and the changes in task performance; between the changes in δ-Nesting index and the changes in task performance; between the changes in SO/δ-Nesting index and the changes in task performance; between the changes in top 10 percentile reactivation strength and the changes in task performance; between the changes in spindles peak amplitude and the changes in task performance; between the reactivation strength during SO-nested spindles or δ-nested spindles and changes in task performance (Figures 4G, 5E, and S7B). In these regression analyses using three conditions, four fundamental assumptions were tested (Osborne and Waters); normality of used parameters (Kolmogorov-Smirnov/KS test; Figures S4A and S4B); linearity between X and Y (visual assessment); homoscedasticity (Goldfeld-Quandt/GQ test); independence across observations (completely new units were used to modulate feeding tube across experiments). We also used linear regression to evaluate trends over sleep in the respective conditions (Figures 5C, 6D, and S7A).

We also compared the evidence for the linear regression model of ΔSO/δ-Nesting index to the model of ΔSO-Nesting index explaining the changes in task performance. The ‘odds’ are defined as the ratio of the probability of the data given one model to the probability of the data given the other model, which corresponds to the evidence favoring one model over another (Jaynes, 2003). We assumed that errors were normally distributed, and that the parameter σ was equivalent to the root mean squared error calculated from the model and sample data. Since it follows that the errors were conditionally independent, the probability of the 72 data points was the product of the 72 probabilities; here, that is equivalent to the R². The probability of the data was 4.3 times greater (i.e. odds) given the predictions of the linear regression model of ΔSO/δ-Nesting index relative the prediction based on the linear regression model of ΔSO-Nesting index, and thus the evidence for the linear regression model of ΔSO/δ-Nesting index was 4.3 times greater.

Data and code availability

The data and custom code that support the findings from this study are available from the corresponding author upon reasonable request.

Additional Resources

None

Supplementary Material

2

Figure S1. Optogenetic inhibitions influence on both putative excitatory and inhibitory cells. Related to Figures 2 and 3.

(A) Neurons in OPTO_SO+ and OPTO_δ experiments (n = 894, 12 rats) were classified as putative excitatory cells (pE) or inhibitory cells (pI) according to waveform shape (Sirota et al., 2008; Stark et al., 2013); cells were clustered according to the trough-to-peak time latency and mean spike width. Representative waveforms of a pE and a pI are shown with mean (thick traces) and individual waveforms (thin traces). Ellipses represents covariance error with 90% confidence interval. Filled circle represents the units that significantly changed firing rates with optogenetic stimulations (p<0.05).

(B) The proportion of putative excitatory (red bar; 84.9%) and inhibitory cells (blue bar; 15.1%) for all units shown in ‘A’. Black transparent bars indicate the proportion of significantly affected units for the pE and pI clusters. pE and pI were influenced by the optogenetic stimulations in similar proportion; 38.6 % and 34.8 %, respectively.

3

Figure S2. Sleep detections and optogenetic inhibitions during sleep. Related to Figures 2 and 3.

(A) Examples of detections of all sleep using degree of movement (red; see Methods) and NREM sleep using power spectral density in 0.1-4 Hz and gamma (30-60 Hz) bands.

(B) Mean NREM sleep time during pre- and post-training sleep. Total sleep time across all conditions: 59.1 ± 1.6 min during pre-training sleep, 58.6 ± 1.6 min during post-training sleep. NREM sleep time across all conditions: 29.8 ± 1.2 min during pre-training sleep, 32.7 ± 1.0 min during post-training sleep. A single square indicates NREM sleep time of a single session. Mean ± s.e.m. are shown.

(C) The number of optogenetic stimulations during post-training sleep. SO, SO+δ, and δ up-states triggered the optogenetic stimulations in the respective experiments of the OPTO_SO, OPTO_SO+δ, and OPTO_δ. In the OPTO_RAND experiment, the optogenetic stimulations were triggered by SO+δ up-states with random time delay (0.3-1.3 sec).

4

Figure S3. Spindles distributions relative to SO and δ waves. Related to Figure 4.

(A and B) Distributions of the time of spindle-peaks relative to SO up-states using bins of 200 ms (A; ΔT_SO-Spindles; longer time window relative to that in Figure 4D and for the spindle-peaks from the δ wave up-states (B; ΔT_δ-Spindles).

(C) Distribution of the probability time of spindles relative to SO (top) and δ waves (bottom). Top traces respectively show SO and δ wave up-states (mean ± s.e.m.). Below are the respective probability of spindle peak times. The distribution of values are from 72 sessions in 12 rats. Kolmogorov-Smirnov/KS test was used in shown statistics.

5

Figure S4. The relationship between the changes in SO-Nesting index and the performance changes. Related to Figure 4G.

(A and B) Distributions of the changes in SO/δ-Nesting index (A) and the changed in task performance (B) used for the linear regression shown in Figure 4G. Solid curves indicate fitted normal distribution. Here, normality for value of an independent (X) and a dependent parameter (Y) was validated for the fair linear regression analysis; Kolmogorov-Smirnov/KS test accepted normality for both X and Y (P>0.05) (see Methods).

(C and D) R² values (C) and P values (D) of the linear fittings to predict the task performance changes by the changes in SO/δ-Nesting index across the different time windows for nesting as shown in Figure 4G. Right-side time length of the nesting window was tested from 0 sec to 5 sec. An example of the up-state-triggered SO (0.1-4 Hz) is shown at top. Red circles indicate the nesting window used for the SO/δ-Nesting index in the present work. The period of the nesting window used in the present work showed nearly the best goodness of fit in the linear fitting between the SO/δ-Nesting index changes and the task performance changes.

6

Figure S5. Event-triggered LFPs for SO, δ waves, and spindles. Related to Figure 4.

Averages of event-triggered LFPs for SO (A), δ waves (B), and spindles (C) in the respective conditions of the CONTROL, OPTO_SO+, and OPTO_δ experiments. Mean peak-to-trough amplitudes were normalized to the mean during pre-training sleep. There were significant changes in the mean peak-to-trough amplitude of SO and δ from pre- to post-training sleep in the OPTO_δ experiments (OPTO_δ: n = 14, sessions, 5 rats, mixed-effects model, ***P < 10⁻³). ‘n.s.’ indicates non-significant change. Mean peak-to-trough amplitude during post-training sleep were compared across conditions and marked only for significant differences (**P < 0.01 and ***P < 0.001, corrected for multiple comparison).

7

Figure S6. Reactivation computations and relationship of reactivations to the firing rate during sleep and performance changes. Related to Figure 5 and 6.

(A) An example of a significant PC (the first principal component; left column) and a nonsignificant PC (a randomly selected PC from low-lank PCs; right column) weights. Red boxes indicate direct neurons (i.e. driving feeding tube).

(B) Examples of activation strengths during pre-training sleep, BMI₁, and post-training sleep (OPTO_OFF experiment).

(C) Differences in the distributions of the reactivation strengths between the pre-training sleep (gray) and the post-training sleep (black) shown in ‘B.’ Typically, the top 10-20 percentile reactivations (i.e. using the significant PC template) were greater in the post-training sleep.

(D) Average time courses of population mean firing rate during post-training sleep for CONTROL, OPTO_SO+, and OPTO_δ (mean ± s.e.m.; averaged with moving window of 5% sleep time). Normalized to population mean firing rate during pre-training sleep (that is 100% on y-axis). Solid lines represent linear fitting (CONTROL: n = 32 sessions, 12 rats, R² = 0.519, P = 2.8 × 10⁻¹⁷; OPTO_SO+: n = 26 sessions, 12 rats, R² = 0.062, P = 0.013; OPTO_δ: n = 14 sessions, 5 rats, R² = 0.014, P = 0.25). The last 10% sleep period did not show significant changes in the population mean firing rate compared to the first 10% sleep period in every condition (paired t test, P > 0.05).

(E) Relationships between the mean reactivation strength and the task performance changes during the SO-nested spindles (top) and during the δ-nested spindles (bottom) (total n = 72 sessions, 12 rats; linear regression, R² = 0.206, P = 6.2 × 10⁻⁵ for the SO-nested spindles, R² = 0.001, P = 0.96 for the δ-nested spindles; satisfying criteria for linear regression). The mean reactivation strength for each session was computed during the last 5% post-training sleep.

8

Figure S7. Spike activity timing of direct neurons. Related to Figure 7.

(A) Neural firing (peri-event time histogram; PETH) centered to task end/reward for an example session of BMI retrieval (BMI₂) in the two respective conditions of the CONTROL, and OPTO_δ experiments (mean ± s.e.m.; averaged with a Gaussian window of 3 seconds; CONTROL: n = 13 sessions, 5 rats; OPTO_δ: n = 14 sessions, 5 rats). Feeding tube is driven toward target/reward position when the firing difference of direct+ neuron (red) from direct− neuron (blue) is positive.

(B) Mean time difference between peak of firing relate relative fo task completion for the BMI₂ block. The timing relationship between direct+ and direct− neurons was inverted in the OPTO_δ compared to the CONTROL experiments. Mean in solid line ± s.e.m. in box.

(C) Time difference from peak firing of direct− to direct+ neuron in each session (mean in solid line ± s.e.m. in box; CONTROL: n = 13 sessions, 5 rats, −0.205 ± 0.131; OPTO_δ: n = 14 sessions, 5 rats, 0.163 ± 0.142; CONTROL vs. OPTO_δ: mixed-effects model, t₂₅ = 2.25, *P = 0.034).

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Bacterial and Virus Strains
AAV8-hSyn-Jaws-KGC-GFP-ER2	UNC Vector Core	N/A
Chemicals, Peptides, and Recombinant Proteins
Isoflurane	Baxter	NDC 10019-360-40
Atropine sulfate	American Regent Inc	NDC 0517-1010-25
Buprenorphine	Reckitt Benckiser Pharmaceuticals Inc	NDC 12496-0757-5
Meloxicam	Patterson Veterinary	NDC 14043-950-05
Dexamethasone	Mylan Institutional Llc	NDC 67457-423-12
Trimethoprim sulfadiazine	Teva Pharmaceuticals Ind	NDC 0703-9526-01
Experimental Models: Organisms/Strains
Long Evans Rat	Charles River Labs	Strain Code 006
Software and Algorithms
MountainSort	Chung et al., 2017	https://github.com/flatironinstitute/mountainsort_examples
SpikePac	Tucker-Davis Technologies (TDT)	https://www.tdt.com/support/downloads/
OpenSorter	Tucker-Davis Technologies (TDT)	https://www.tdt.com/support/downloads/
RPvdsEx	Tucker-Davis Technologies (TDT)	https://www.tdt.com/support/downloads/
MATLAB	Mathworks	https://www.mathworks.com/products/matlab.html
Sleep waves detection algorithm	Sela et al., 2016	N/A
Other
Bioamp processor (RZ2) and neurodigitizer (digital PZ4 and analog PZ5)	Tucker-Davis Technologies (TDT)	https://www.tdt.com
32-channel microwire electrode arrays	Tucker-Davis Technologies (TDT)	https://www.tdt.com/component/zif-clip-array-electrodes/
32-channel microwire electrode arrays	Innovative Neurophysiology Inc	http://www.inphysiology.com/optogenetic-applications/

HIGHLIGHTS.

• Reactivations during slow oscillations causally linked to memory consolidation.

• Delta-waves mediate weakening of memory reactivations and promote forgetting.

• Slow oscillations and delta-waves have competing roles in memory processing.