Identification of optimal prediction models using multi-omic data for selecting hybrid rice

Abstract

Genomic prediction benefits hybrid rice breeding by increasing selection intensity and accelerating breeding cycles. With the rapid advancement of technology, other omic data, such as metabolomic data and transcriptomic data, are readily available for predicting breeding values for agronomically important traits. In this study, the best prediction strategies were determined for yield, 1000 grain weight, number of grains per panicle, and number of tillers per plant of hybrid rice (derived from recombinant inbred lines) by comprehensively evaluating all possible combinations of omic datasets with different prediction methods. It was demonstrated that, in rice, the predictions using a combination of genomic and metabolomic data generally produce better results than single-omics predictions or predictions based on other combined omic data. Best linear unbiased prediction (BLUP) appears to be the most efficient prediction method compared to the other commonly used approaches, including least absolute shrinkage and selection operator (LASSO), stochastic search variable selection (SSVS), support vector machines with radial basis function and epsilon regression (SVM-R(EPS)), support vector machines with radial basis function and nu regression (SVM-R(NU)), support vector machines with polynomial kernel and epsilon regression (SVM-P(EPS)), support vector machines with polynomial kernel and nu regression (SVM-P(NU)) and partial least squares regression (PLS). This study has provided guidelines for selection of hybrid rice in terms of which types of omic datasets and which method should be used to achieve higher trait predictability. The answer to these questions will benefit academic research and will also greatly reduce the operative cost for the industry which specializes in breeding and selection.

Introduction

Rice, which is enriched with complex carbohydrates, vitamins, minerals, and fiber, is the main staple food for a large segment of the world population. Heterosis, defined as the superior performance of hybrids relative to their parents, has been reported as a major contributor to the increased productivity in rice (Jones 1926; Virmani et al. 1982). Only a small number of desirable hybrids can be selected through a large number of crosses in a traditional rice breeding program, which is labor intensive and time consuming (Collard and Mackill 2008; Spindel et al. 2015). Marker-assisted selection (MAS) has been used to facilitate rice breeding (Chen et al. 2000; 2001; Zhou et al. 2003), leading to genetic improvement and reduced number of generations needed. Quantitative trait loci (QTL) mapping is often used to identify DNA markers for breeding if these markers are in linkage disequilibrium (LD) with the genetic determinant of traits (Li et al. 2007). Genomic selection (Hayes and Goddard 2001) is a special form of MAS in which all markers on the genome are used for predicting expected breeding values (EBVs) for rice hybrids. A training set is used to build a genomic selection model, which can be applied to a breeding set (or validation set) for prediction of EBVs if this set share similar genetic architecture with the training set. Genomic selection models are often evaluated by trait predictability, a measurement of prediction accuracy that is calculated through cross validation (Riedelsheimer et al. 2012). A primary goal of genomic selection modeling is to optimize the trait predictability—a measure of predictive ability for a model.

In addition to genomic data, the rapid advancement of technology generates other types of omic datasets, such as transcriptomic data, proteomic data, and metabolomic data. An integrated analysis of these omic datasets may advance our knowledge of the underlying genetic and biochemical basis for agronomic traits. For example, the joint analysis of transcriptomic data and genomic data, called eQTL mapping, treats gene expression profiles as quantitative traits and maps these expression traits to genomic loci (Jansen and Nap 2001; Doerge 2002; Schadt et al. 2003; Bing and Hoeschele 2005; Rockman and Kruglyak 2006; Jia and Xu 2007; Keurentjes et al. 2007; Wang et al. 2014). Likewise, metabolomic expression profiles can be also treated as quantitative traits and mapped to genomic loci, i.e., mQTL mapping (Keurentjes et al. 2006; Schauer et al. 2006; Dumas et al. 2007; Gieger et al. 2008; Illig et al. 2010; Suhre et al. 2011; Wei et al. 2018). Both eQTL mapping and mQTL mapping are derivatives of QTL mapping. Genes and metabolites that are mapped to the same loci as a trait may be used to uncover the biological networks that govern the variability of the trait. Moreover, combining the additional omic datasets with genomic data has potential to improve prediction of trait.

Various omic datasets have been used for prediction of the EBVs of agronomic traits. For example, transcriptomic data have been used to predict hybrid performance (Stokes et al. 2010; Fu et al. 2012) and transcriptome-based prediction in hybrid maize appeared to be more precise than genome-based prediction (Frisch et al. 2010). Similarly, genomic data and metabolomic data of two backcross populations from 359 recombinant inbred lines (RILs) were used to predict biomass of Arabidopsis thaliana (Gärtner et al. 2009), in which the predictabilities for two prediction strategies were very close, i.e., 0.17 and 0.16 for genomic prediction and metabolomic prediction, respectively. A population was generated by testcrossing 285 diverse Dent inbred lines from worldwide sources with two testers and used to predict the combining ability for seven biomass- and bioenergy-related traits (Riedelsheimer et al. 2012). The average predictabilities of these seven traits for genomic prediction and metabolomic prediction were 0.54 and 0.33, respectively. A three-step prediction strategy was proposed and evaluated using a wheat dataset, which consists of 1604 hybrids and their 135 parents (Zhao et al. 2015). Their results showed that for hybrids without parental line in common, hybrids sharing one parental line, and hybrids sharing both parental lines, the genome-based prediction accuracies were 0.32, 0.65, and 0.89, respectively. Note the prediction accuracy, which is a different measure from predictability, was defined as the correlation between the predicted and the observed phenotypes divided by the square root of heritability. The corresponding metabolome-based prediction accuracies were 0.15, 0.42, and 0.74, respectively.

With the significant increase of omic data, how to appropriately use these resources to aid selection has become a heated topic. It has been indicated that inclusion of metabolomic data did not improve predictive value, but hampered the performance of genomic selection in hybrid wheat (Zhao et al. 2015). Prediction based on all available omic data (genomic, metabolomics, and transcriptomic data) rarely outperformed the best single omic data prediction in hybrid rice when various prediction models were compared (Xu et al. 2016). However, selection by combining transcriptomic data with genomic data resulted in a higher prediction accuracy than genomic selection in maize if the omic data (genomic, metabolomic, and transcriptomic data) were collected from parental lines at their early developmental stages (Westhues et al. 2017). The conflicting conclusions in the literature highlighted the need for further investigation on what combination of the omic datasets and what prediction model yields the best prediction for a trait. The answer to these questions will benefit academic research and will also greatly reduce the operative cost for the industry, which specializes in breeding and selection.

The goal of the study is to prove the concept that trait predictability may be optimized by using superior prediction models and selective omic datasets. For demonstration, we used a RIL sample of 210 lines and an immortalized F2 (IMF2) sample for which 278 hybrids were created by randomly paring these 210 lines (Hua et al. 2002; 2003). Three individual omic datasets, i.e., genomic dataset (G), transcriptomic dataset (T), and metabolomic dataset (M), and all possible combinations of these omic datasets were comprehensively analyzed for the comparison of trait predictability using eight widely adopted prediction methods.

Materials and methods

Rice data

Shanyou 63, an elite hybrid that has been widely cultivated in the last three decades in China, was derived from the cross between Zhenshan 97 and Minghui 63. A total of 210 RILs were derived by single-seed descent from this hybrid. An “immortalized F2” (IMF2) sample of 278 hybrids was derived from randomly crossing these 210 RILs (Hua et al. 2002; 2003). Field data of four traits were considered, including yield (YIELD), 1000 grain weight (KGW), number of grains per panicle (GRAIN) and number of tillers per plant (TILLER). For the RIL population, each trait was measured from four replicated experiments (1997 and 1998 from one location, 1998 and 1999 from another location). In each replicated experiment, eight plants were sampled from each line and the average trait value was treated as the phenotypic value for this line in this experiment (Xing et al. 2002; Yu et al. 2011). For the IMF2 sample, eight plants from each random cross were randomly collected and their average trait value was used as the phenotypic value for the F2 progeny of that cross. Trait values for each cross were measured twice in two consecutive years (1998 and 1999).

Three omic datasets, i.e., genomic dataset, transcriptomic dataset, and metabolomic dataset, were only collected from the 210 RILs. Xie et al. (2010) and Yu et al. (2011) derived an ultra-high-density linkage map for these RILs, yielding genotype data represented by 1619 genetic bins. For each RIL, a genetic bin takes genotype value of 1 if the DNA in this bin is from Zhenshan 97, and 0 from Minghui 63. The transcriptomic data consisted of 24,994 gene expression traits measured in tissues sampled from flag leaves of the 210 RILs in 2008 (Wang et al. 2014). RNAs were extracted from two biological replicates of each line, and then mixed in a 1:1 ratio for expression profiling by microarrays. Robust multi-array average (RMA) analysis was used for background correction and normalization. The metabolomic data for the 210 RILs consisted of 683 metabolites measured from flag leaves and 317 metabolites measured from germinated seeds (Gong et al. 2013). Two biological replicates were sampled for flag leaves in 2009, while for germinated seeds one biological replicate was sampled in 2009 and the second biological replicate was sampled in 2010. Metabolomic data in both tissues were log2-transformed for statistical analysis to meet with the normality assumption. The average of two replicated measurements for a metabolite was used for analysis.

The genotype of an IMF2 hybrid was deduced from the genotypes of two crossing parents. Let ${\pi }_j^m$ and ${\pi }_j^f$ be p × 1 vectors of the genotypes (1 for Zhenshan 97 and 0 for Minghui 63) for male and female RIL parents of the jth hybrid in the IMF2 sample, respectively, with j = 1, …, q, where q = 278, and p = 1619. Additive genotype of the IMF2 individual is defined as

$$z_j={\pi }_j^m+{\pi }_j^f$$ 1

and dominance genotype as

$$w_j=∣{\pi }_j^m-{\pi }_j^f∣$$ 2

Therefore, the additive genotypes for the IMF2 sample is defined as

$$Z={\left\{z_1,\dots ,z_q\right\}}^T$$ 3

and the dominance genotypes for the IMF2 population is defined as

$$W={\left\{w_1,\dots ,{\mathrm{w}}_q\right\}}^T$$ 4

For the IMF2 sample,

$$X=\left\{Z\mid \mid \mathrm{W}\right\}$$ 5

is a q × 2p genotype matrix. Likewise, the metabolomic and transcriptomic data for the IMF2 sample were not directly measured; rather, they were calculated from two crossing parents of each IMF2 hybrid in a similar way, with ${\pi }_j^m$ and ${\pi }_j^f$ representing metabolomic or transcriptomic measurements for the two RIL patents.

Prediction methods

Eight statistical methods were used for prediction: (i) LASSO developed by (Tibshirani 1996) and implemented by GlmNet R program (Friedman et al. 2010); (ii) Henderson’s BLUP implemented in the R program written by Xu et al. (2016); (iii) SSVS (also called Bayes B) developed by George and McCulloch (1993); (iv) support vector machine using the radial basis function and epsilon regressions (SVM-R(EPS)) implemented in the R package kernlab (Karatzoglou et al. 2004); (v) support vector machine using the radial basis function and nu regressions (SVM-R(NU)); (vi) support vector machine using the polynomial kernel function and epsilon regressions (SVM-P(EPS)); (vii) support vector machine using the polynomial kernel function and nu regressions (SVM-P(NU)); and (viii) partial least squares (PLS) implemented in the R package pls (Wehrens and Mevik 2007).

The first three methods (LASSO, BLUP, and SSVS) are all linear and use a random model. The single-omic data model is

$$y=X\beta +\epsilon$$ 6

where y is the trait values, predictor variables X may be one of X_SNP, X_MET, and X_EXP, with SNP, MET, and EXP denoting genomic, metabolomic, and transcriptomic datatypes, respectively, β is the vector of model effects, and ε is the vector of residual errors. The fully combined model including three omic datatypes becomes

$$y=X_{\mathrm{SNP}}{\beta }_{\mathrm{SNP}}+X_{\mathrm{MET}}{\beta }_{\mathrm{MET}}+X_{\mathrm{EXP}}{\beta }_{\mathrm{EXP}}+\epsilon$$ 7

whereas, other types of combined models have reduced format. Note in the BLUP method, more than one kinship matrix is needed to handle the mutually independent omic datasets. For IMF2 sample with fully combined model, six kinships matrices were included in the regression analysis, with one for the additive effects and the other one for the dominance effects for each omic datatype.

Kernel methods are a class of algorithms for pattern recognition in machine learning. The most commonly used kernel methods include support vector machine (SVM) in which various kernel functions may be used for describe the relationship between dependent variable y and explanatory variable X, i.e.,

$$y=f\left(X\mid \beta \right)+\epsilon$$ 8

Where

$$f\left(X\mid \beta \right)={\sum }_{j=1}^n{\beta }_j{K}_h\left(X,X_j\right)$$ 9

and K_h(X, X_j) is a kernel selected. In this study, the Gaussian kernel (SVM-RBF) and the polynomial kernel (SVM-POLY) were chosen for implementation of SVM functions.

The PLS method is a hybrid method between principal component analysis (PCA) and multiple regression analysis. However, the difference between PLS and PCA is that PLS calculate the weights of the latent scores by maximizing the covariance between y and the scores (Geladi and Kowalski 1986). The number of latent components was determined by a 10-fold cross-validation to minimize the prediction error.

Cross-validation

In this study, a 10-fold cross-validation was used to evaluate the predictability of each prediction scheme (a combination of omic datasets with a prediction method). The trait predictability is defined as the squared correlation between the observed trait values and the predicted EBVs in cross-validation setting. The predictability calculated for a sample depends on how the sample is partitioned into different subsets for cross-validation. Therefore, 100 repeated cross-validations were performed for each analysis by randomly partitioning data in different ways and the mean and the standard deviation of the values of predictability from the 100 repeated cross-validations were used in the study.

Results

Analysis of variance for predictabilities

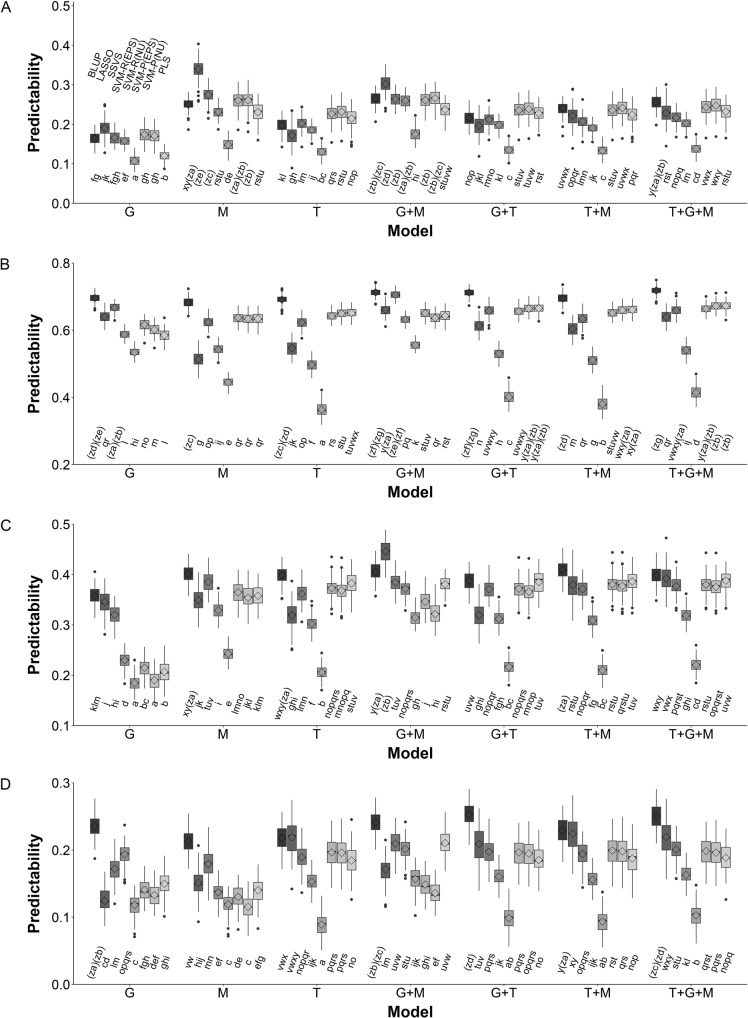
For each trait, a total of 5600 (7 × 8 × 100) values for predictability were calculated using all 7 possible combinations of omic datasets (G, M, T, G + M, G + T, T + M, and T + G + M) and 8 prediction methods with 100 replicates created by random cross-validation (Table S1; Table S2). The predictability was treated as the response variable, and 7 omic datasets combinations, 8 methods, and the interactions between the datatypes and the methods were treated as factor variables in an ANOVA. The results for the IMF2 sample (Table 1) show that all main and interaction effects were significant; thus, Turkey’s multiple comparisons were performed to test differences between these interactions (Fig. 1). The greatest predictabilities for YIELD, KGW, GRAIN and TILLER were achieved by using M with LASSO, G + M with BLUP, G + M with LASSO, and G + T with BLUP, respectively. For YIELD (Fig. 1a), the 56 data-method interactions were classified into 30 significant levels with label ‘a’ (worst prediction) through ‘ze’ (best prediction). For the other three traits (KGW, GRAIN, and TILLER also depicted in Fig. 1), 32, 27, and 29 significant interaction levels were detected. On average, G + M produced the best predictabilities and BLUP outperformed the other methods.

Table 1.

Analysis of variance of predictabilities for the four traits in a IMF2 sample with a 7 × 8 factorial design (seven combinations of omic datasets and eight prediction methods)

Trait	Source	d.f.	Sum of square	Mean square	F-test	P-value
YIELD	Method	7	5.209	0.7441	2074.3	<2e−16
	Predictor	6	5.286	0.8810	2455.8	<2e−16
	Method*predictor	42	1.686	0.0401	111.9	<2e16
	Residual	5544	1.989	0.0004
KGW	Method	7	32.17	4.596	17494	<2e−16
	Predictor	6	2.43	0.406	1544	< 2e−16
	Method*predictor	42	5.62	0.134	509	<2e−16
	Residual	5544	1.46	0.000
GRAIN	Method	7	12.594	1.7991	4812	<2e−16
	Predictor	6	6.771	1.1285	3018	<2e−16
	Method*predictor	42	4.538	0.1080	289	<2e−16
	Residual	5544	2.073	0.0004
TILLER	Method	7	5.733	0.8190	2473.6	<2e−16
	Predictor	6	1.258	0.2096	633.2	<2e−16
	Method*predictor	42	2.332	0.0555	167.7	<2e−16
	Residual	5544	1.836	0.0003

Fig. 1.

Multiple comparisons of the means of predictabilities by 56 interactions between seven combinations of omic datasets and eight prediction methods for the four traits in a IMF2 sample. a Result for YIELD. b Result for KGW. c Result for GRAIN. d Result for TILLER. The lower-case letters below the shaded boxes, for example, ‘a’ through ‘zg’ in YIELD (a), indicate differences between these interactions at the 0.05 level of significance. The 8 prediction methods are labeled above the shaded boxes for the analysis of genomic data (g) in a, and the order of these 8 methods remain the same in the analysis of other combinations of omic datasets with various traits

Similar results have been observed when the RIL sample has been analyzed. All main and interaction effects were significant in RILs (Table S3). The greatest predictabilities for YIELD, KGW, GRAIN, and TILLER were achieved by using G + M with SVM-R (EPS and NU), G + M with SSVS, G + M with SVM-P (EPS and NU) and G with BLUP, respectively. Consistently, G + M generally produced the best predictabilities for all four traits, and BLUP overall outcompeted the other prediction methods in the analysis of the RIL sample (Fig. S1).

Effects of variables in different prediction schemes

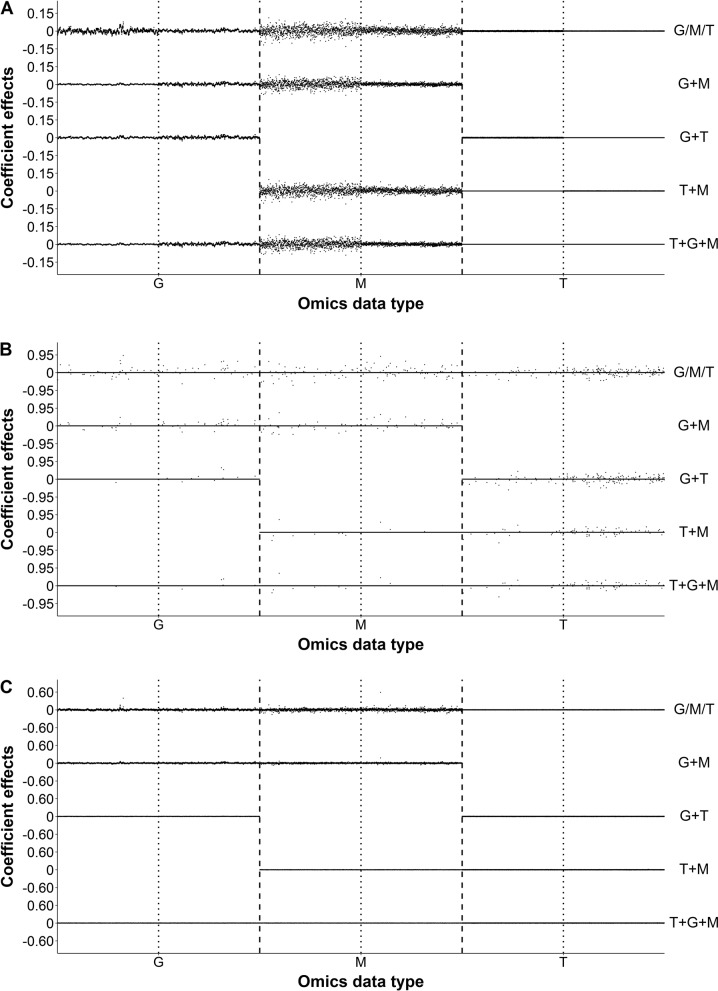
Since BLUP, LASSO, and SSVS are simple-linear-regression based methods, we compared the estimated effects of predictor variables in 7 omic combinations when these three methods were applied. All predictors, including 1619 genomic variables, 1000 metabolites, and 24,994 transcripts, had been standardized for the comparisons. Figure 2 shows the estimated additive effects and dominant effects for the variables when YIELD was analyzed in IMF2 sample. For BLUP and SSVS, the genomic effects and the metabolomic effects are generally larger than the transcriptomic effects. When multi-omic datasets were analyzed in a combined model (e.g., G + M or G + M + T), the estimated effects for each omic type are generally smaller than those estimated from the analysis of single omic dataset. For BLUP, the estimated genomic and metabolomic effects in the G + M + T model are very similar to those in the G + M model. When the same datatypes were analyzed, the transcriptomic effects estimated by LASSO are generally larger than those estimated by BLUP or SSVS, whereas, the number of variables with non-zero effects identified by LASSO are generally smaller than those by BLUP or SSVS. Similar results have been obtained when the other three traits (KGW, GRAIN, and TILLER) were analyzed in the same manner (Figs. S2–S4), and all four traits were analyzed in the RIL sample where only additive effects are applicable (Figs. S5–S8).

Fig. 2.

The estimated regression coefficients for YIELD in the hybrids by using three simple-regression based prediction methods with different omic datasets. a Estimated regression coefficients of BLUP. b Estimated regression coefficients of LASSO. c Estimated regression coefficients of SSVS. The dashed lines separate various omic-specific variables, with G, M, and T representing genomic, metabolomic, and transcriptomic variables, respectively. The dotted lines separate the additive (a) and dominance (d) variables within single omic-type variables

Computational efficiency

We evaluated the computational efficiency for each prediction method (in terms of computing time in hours) across various omic combinations on a regular personal computer (Intel Core i7 CPU 7700K, 4.20 GHz, Memory 16.00 G). Note that the numbers of variables used in the IMF2 sample are larger than those in the RIL sample because both additive and dominant effects are considered in the IMF2 sample while only additive effects are applicable in the RIL sample. For both the IMF2 sample (Table S4) and the RIL sample (Table S5), BLUP achieved the greatest computational efficiency on average. As the number of predictor variables grew when multi-omic datasets were analyzed, the computing time for BLUP only grew modestly, compared with the significant increase in computing time for the other methods.

Heritability vs. predictability

The values of overall heritability of the four traits (YIELD, KGW, GRAIN, and TILLER) are 0.4292, 0.7898, 0.6183, and 0.3097, respectively, in IMF2 sample, and are 0.4214, 0.8410, 0.7385, and 0.4222, respectively, in RIL sample, which were previously calculated (Xu et al. 2016) and used in the present study. The predictabilities for these four traits in the IMF2 sample (average across all methods and omic combinations) were 0.2134, 0.6102, 0.3378, and 0.1762, respectively. The correlation between the heritability and the predictability for these four traits was 0.9562 (P = 0.0438) in the IMF2 sample. Similarly, the predictabilities for these four traits in the RIL sample were 0.4162, 0.6567, 0.5094, and 0.3689, respectively, and the correlation between heritability and predictability was 0.9422 (P = 0.0578). As expected, trait predictability generally increases with trait heritability.

Overfitting

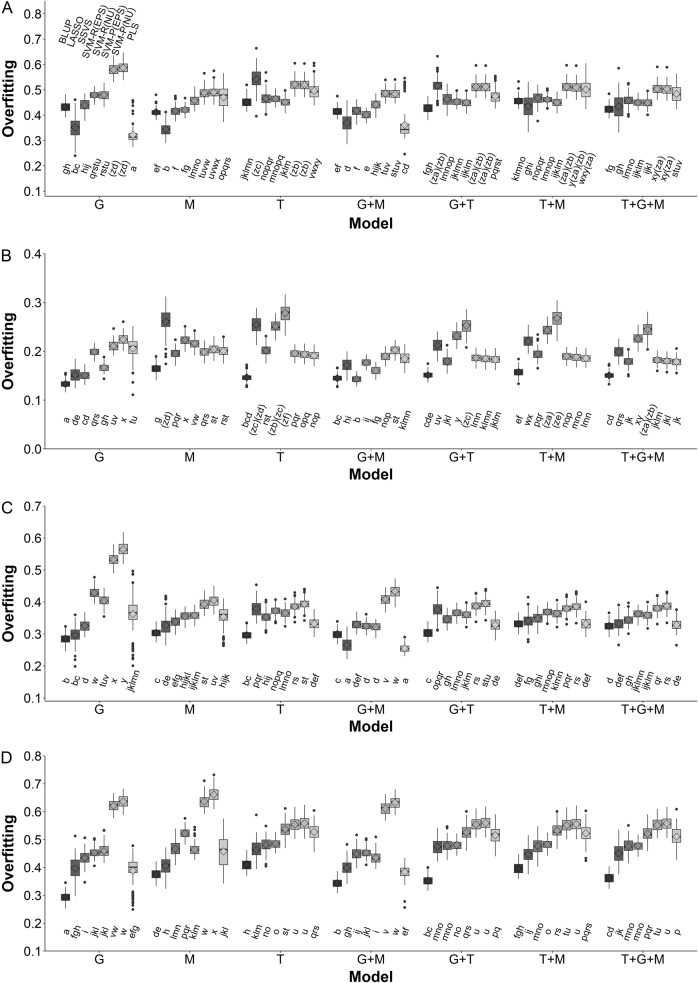
The squared Pearson correlation between the observed trait values and the predicted EBVs is called goodness of fit if no cross validation is applied, which is different from how predictability is defined. The measure of overfitting is the difference between the square root of goodness of fit and the square root of predictability. This is equivalent to the calculation of difference between the two correlation coefficients, one calculated between the observed trait values vs. the predicted EBVs without cross validation and the other one calculated with cross validation (Heslot et al. 2012). The levels of overfitting in the analyses of hybrids using various omics combinations and prediction methods are listed in Fig. 3 and Table S6. Overall, BLUP and G + M were least affected by overfitting for all four traits.

Fig. 3.

Multiple comparisons of the means of levels of overfitting by the 56 interactions between seven combinations of omic datasets and eight prediction methods for the four traits in the IMF2 sample. a Result for YIELD. b Result for KGW. c Result for GRAIN. d Result for TILLER

Comparison of metabolites in leaves and seeds

We further compared the predictabilities calculated using 683 metabolites in leaves, 317 metabolites in seeds, and all 1000 metabolites from two tissue sources, respectively, with various models involving metabolomic data, i.e., M, G + M, T + M, and T + G + M. For the IMF2 hybrids, the predictions based on the metabolites in leaves generally had the best predictability for YIELD, while the predictions based on metabolites in both leaves and seeds generally achieved the highest predictabilities for KGW, GRAIN and TILLER (Figs. S9–S12; Table S7). For the RIL sample, predictions based on metabolites in both tissue types generally achieved the highest predictabilities for YIELD, KGW and GRAIN, whereas, the metabolites in leaves provided best predictabilities for TILLER (Figs. S13–S16; Table S8).

Comparison of top selections in various prediction schemes

The 278 experimental hybrids only represent a small subset of a total of 21,945 possible crosses that could have been produced by the 210 RILs. For each trait, we therefore used the parameters estimated from the training samples (278 hybrids) to make trait predictions for all 21,945 crosses by each prediction scheme. The 21,945 possible crosses were then sorted based on the phenotypic values (from largest to smallest) predicted using various prediction scheme (different omic data combinations with different prediction methods). Example Data S1–S8 show part of the predicted phenotypic values of the 21,945 hybrids using the 8 prediction methods each with 7 omic combinations. The top 10 hybrids selected from the optimal scheme (BLUP with G + M) were compared with the sorted lists generated by other prediction schemes (either other prediction methods with G + M or BLUP with other omic combinations). The results in Table S9 indicated that the majority of these top selections by the optimal scheme were highly ranked in the lists sorted by other prediction schemes.

Discussion

With the rapid growth of omic datasets, there is an urgent need to find effective ways of using these data to assist in breeding programs. Efforts have been tried to compare different genomic prediction methods (Heslot et al. 2012; Thavamanikumar et al. 2015) or to investigate whether a simple combination of different types of omic datasets can improve prediction of hybrid performance in crops (Gärtner et al. 2009; Riedelsheimer et al. 2012; Xu et al. 2016; Schrag et al. 2018). This current study is the first to systematically compare various trait prediction schemes using all possible combinations of omic datasets with different prediction methods in order to identify the optimal strategy for predicting economically important traits in rice. The new knowledge gained from such analysis will help breeders avoid efforts and costs on unnecessary data that do not contribute to the prediction accuracy. Predictability, which is defined as the squared Pearson correlation coefficient between the observed and the predicted phenotypic values, has been preferred by many users in the evaluation of the predictive ability for genomic selection models (Xu et al. 2014; 2016). Predictability can objectively reflect the applicability of the models when they are applied to independent datasets, so it is equivalent to a combined use of goodness of fit and overfitting in model evaluation. Measurement of goodness of fit alone is not appropriate for assessing prediction models. For example, among the eight prediction methods, SVM-POLY (NU) has the goodness of fit of 100% (Table S10); however, the predictabilities associated with this method are unfavorable (Fig. 1, Table S1). In the study, predictability has been adopted as a principle measure to compare the predictive abilities of various prediction schemes.

Among all the prediction methods, the BLUP method generally provided the greatest predictabilities with smallest variation (Fig. 1 and Fig. S1), and was least impacted by overfitting in all four traits in both IMF2 sample and RIL sample (Fig. 3; Table S6), which echoes the previous research (Xu et al. 2016; 2017; Wei et al. 2018). In addition, BLUP appeared to be most computationally efficient to handle multi-omic datasets where many thousands of variables are jointly analyzed. The computational efficiency of BLUP mainly depends on the number of kinship matrices (covariance structures) rather than their sizes (number of variables in each matrix), therefore, it’s computing time increased modestly when multi-omic datasets were analyzed. Note that the number of kinship matrices for the IMF2 sample is twice as many as that for the RIL sample because for each omic datatype only additive effects are applicable in the RIL sample, whereas, both additive effects and dominant effects are involved in the IMF2 sample. In contrast, the computing time of the other seven methods substantially increases with the number of variables in the models (Tables S4 and S5). Although other prediction methods occasionally had the greatest predictability in single prediction scheme, for example, LASSO with M for YIELD in IMF2 sample or SSVS with G + M for KGW in RIL sample, on average they underperformed the BLUP method. LASSO, which penalizes many small effects by enforcing them to be zero, behaved differently from the other two simple-regression based methods (BLUP and SSVS) where the contributions from small effects are also integrated into the lump-sum prediction. Figure 2 and Figs. S2–S8 demonstrate that, LASSO only selected a small number of variables compared to BLUP and SVSS, but the estimated effects for these variables are fairly large. Form a Bayesian point of view, the penalty utilized in LASSO is equivalent to a Laplace (double exponential) prior over the regression coefficients, which assumes only a small number of these coefficients are non-trivial while many are close to zero and vanish with the penalty (Kyung et al. 2010). In all four traits, LASSO identified transcriptomic variables with large estimated effects, which is inconsistent with the estimation from BLUP or SVSS. These estimated large transcriptomic effects are likely to be inaccurate because the models involving the LASSO-selected transcriptomic variables had reduced predictabilities (Fig. 1 and Figure S1) and suffered from severe overfitting (Fig. 3; Table S6). These results suggest that LASSO may perform better in detection of major QTL/QTNs in GWAS than in genomic selection or in trait-prediction with multi-omic datasets, which are consistent with the conclusions of other studies (Wei et al. 2018).

The results showed that, in both the IMF2 sample and RIL sample, the combination of genomic data and metabolomic data (G + M) generally provided the best prediction (Fig. 1 and Fig. S1), and was least affected by overfitting in all four traits (Fig. 3; Table S6). Further inclusion of transcriptomic data (T), i.e., G + M + T, did not improve predictability; rather, the model performance decreased. Figure 2 and Figs. S2–S8 show that the estimated transcriptomic effects using BLUP are much smaller than the estimated genomic effects or metabolomic effects, which indicates that in rice (1) genome and metabolome may play more important roles in forming traits than transcriptome does, and (2) transcriptome does not provide additional information on the trait compared to genomic data (G), or metabolomic data (M), or both (G + M). Enclosing many transcriptomic variables of trivial or artificial effects impaired the performance of models by overfitting (Fig. 3; Table S6) and also by reducing the computational efficiency (Tables S4 and S5). Moreover, the estimated genomic effects and metabolomic effects in the G + M model were noticeably smaller than those estimated from single omic dataset model, i.e., G or M, which indicates that genome and metabolome provide complementary data that are useful for trait prediction and justifies the advantage of the combined model (G + M). On the other hand, the estimated genomic effects and metabolomic effects in the G + M model are very similar to those estimated in the fully combined model G + M + T, which supports our hypothesis that inclusion of transcriptomic data in the G + M model is unnecessary. In the study, the metabolomics (M) and transcriptomic (T) data were directly measured for RILs; however, such data were indirectly inferred, potentially subject to errors, for hybrids from their RIL parents (see Materials and methods), which is a major limitation for investigating the IMF2 sample. This may explain why the predictabilities for RILs were overall higher than those for IMF2 hybrids, especially in the prediction schemes involving metabolomic or transcriptomic data. It is expected that trait prediction for hybrids may be substantially enhanced if metabolomic data can be directly gauged from these hybrids.

A total of 1000 metabolites were obtained from two tissue sources, i.e., leaves and seeds, in the RIL sample. Generally, using metabolomic data from both types of tissues provided best prediction for majority of the traits (YILED, KGW, and GRAIN) in the RIL sample. Metabolites only from leaves on average had the greatest predictabilities for TILLER in the RIL sample. These results are very similar to that in the IMF2 sample where metabolomic data from both types of tissues provided best prediction for KGW, GRAIN, and TILLER but metabolites only from leaves had the greatest predictabilities for YILED. The data of year 1998 were separated from the data of year 1999, and were analyzed respectively using BLUP (the optimal prediction method) with various combinations of omic datasets. The predictabilities for individual years were lower than that can be achieved with the combined data (averaged trait values across years), indicating possible environmental variability in different years (Fig. S17). Inclusion of environmental data, if available, and their interaction with omic data has potential to produce better trait predictabilities than simply averaging the trait values across years.

Comparison among top selections by various prediction schemes has been utilized to test the reliability and prediction performance of these schemes (Xu et al. 2017). In the study, top-10 selections by BLUP with G + M (optimal prediction scheme) were compared with other schemes, either other prediction methods with G + M or BLUP with other combinations of omic datasets, to examine the ranks of these 10 top selections in the sorted lists by other prediction schemes (Table S9). In general, these top-10 selected hybrids by BLUP with G + M are well supported by the other prediction schemes because (1) many of these 10 hybrids are also included in the top-10 selections by the other prediction schemes (labeled in red), and (2) even some of these 10 hybrids are not in top-10 of the other sorted lists, they are still highly ranked in those lists. The consistency in these comparisons indicates the robustness and reliability of the optimal prediction scheme in this study, i.e., BLUP with G + M, while the slight differences between top-10 selections among various prediction schemes highlighted the potential advantage of the optimal prediction scheme.

In the study, the performances of various SVM approaches were carefully compared, including SVM-R(EPS), SVM-R(NU), SVM-P(EPS), and SVM-P(EPS). The SVM-R(EPS) generally outperformed SVM-R(NU) in terms of predictability in both IMF2 and RIL samples; whereas, the results of SVM-P(EPS) are close to those of SVM-P(NU). The SVM-P performed better than the SVM-R when handling large number of variants (for example, model with transcriptomic data). These SVM methods were implemented using the default parameters (cost = 1 and epsilon = 0.1/nu = 0.2) with the optimized parameters for gamma. The performances of these SVM methods were also compared with those using the optimal parameters (gamma, cost, and epsilon/nu). Trait predictability cannot always be improved with the optimal parameters, and prediction performance using the optimal parameters is not stable (Table S11). Moreover, the computational time spent on optimizing the parameters is significantly larger than that of adopting the default parameters. Thus, it appears that using the default parameters in the SVM methods is generally a good choice. The predictive ability with the SVM methods has been demonstrated in genomic selection research (Ogutu et al. 2011; Heslot et al. 2012; Xu et al. 2016; 2017), so further study is needed to exploit their potential in trait predictions with multi-omic data.

In conclusion, the BLUP method with the combined use of genomic data and metabolomic data will achieve the best prediction of economically important traits in rice, including YIELD, KGW, GRAIN, and TILLER, whereas transcriptomic data may not be necessary for this purpose. The study has provided a guideline for rice selection in terms of what types of omic datasets and what prediction model should be used to achieve the greatest predictability. The answer to this question will benefit academic research and will also greatly reduce the operative cost for the industry, which specializes in breeding and selection. The answer may vary when different traits in rice are considered. For other crops, such as maize and wheat, similar studies may be conducted to develop a selection guideline for industry practice or scientific research.

Compliance with ethical standards

Conflict of interest

The authors declare that they have no conflict of interest.

Supplementary information

The online version of this article (10.1038/s41437-019-0210-6) contains supplementary material, which is available to authorized users.