A local score approach improves GWAS resolution and detects minor QTL: application to Medicago truncatula quantitative disease resistance to multiple Aphanomyces euteiches isolates

Abstract

Quantitative trait loci (QTL) with small effects, which are pervasive in quantitative phenotypic variation, are difficult to detect in genome-wide association studies (GWAS). To improve their detection, we propose to use a local score approach that accounts for the surrounding signal due to linkage disequilibrium, by accumulating association signals from contiguous single markers. Simulations revealed that, in a GWAS context with high marker density, the local score approach outperforms single SNP p-value-based tests for detecting minor QTL (heritability of 5–10%) and is competitive with regard to alternative methods, which also aggregate p-values. Using more than five million SNPs, this approach was applied to identify loci involved in Quantitative Disease Resistance (QDR) to different isolates of the plant root rot pathogen Aphanomyces euteiches, from a GWAS performed on a collection of 174 accessions of the model legume Medicago truncatula. We refined the position of a previously reported major locus, underlying MYB/NB-ARC/tyrosine kinase candidate genes conferring resistance to two closely related A. euteiches isolates belonging to pea pathotype I. We also discovered a diversity of minor resistance QTL, not detected using p-value-based tests, some of which being putatively shared in response to pea (pathotype I and III) and/or alfalfa (race 1 and 2) isolates. Candidate genes underlying these QTL suggest pathogen effector recognition and plant proteasome as key functions associated with M. truncatula resistance to A. euteiches. GWAS on any organism can benefit from the local score approach to uncover many weak-effect QTL.

Introduction

After a decade of genome-wide association studies (GWAS), our understanding of the genetic bases of quantitative phenotypic variation in organisms has dramatically increased, the most advanced knowledge being acquired in humans (Timpson et al. 2018; Visscher et al. 2017) and in the workhorse plant models such as Arabidopsis thaliana, rice, and maize (Atwell et al. 2010; Bergelson and Roux 2010; Brachi et al. 2011; Han and Huang 2013; Yu and Buckler 2006; Yu et al. 2008). A large number of causal variants (mainly single nucleotide polymorphisms—SNPs) with meaningful effects have been finely mapped in an increasing number of species. However, for complex quantitative traits, the sum of the effects (or contribution) of the variants detected at a given genome-wide significance level in a GWAS generally do not match with heritability estimates; this was referred to as “missing heritability” (Manolio et al. 2009). The complexity of the genetics underlying complex traits such as allelic heterogeneity, genetic heterogeneity, and epistatic interactions between causal variants and epigenetic variation, which have been shown to be important for quantitative traits expression, could explain missing heritability (Brachi et al. 2011; Platt et al. 2010; Slatkin 2009). Various studies have also reported that rare variants with large effects that are not discovered or genotyped due to low sample sizes also contribute to missing heritability (Bandyopadhyay et al. 2017; Marouli et al. 2017; Zuk et al. 2014). Indeed, if undetected rare variants locate physically close to common variants that are genotyped, their effect can be detected, although necessarily underestimated due to incomplete linkage disequilibrium (LD) (Dickson et al. 2010; Marouli et al. 2017; Wang et al. 2010). Recently, however, the study of whole genome sequence data in a large human sample has shown that a significant part of the missing heritability in complex traits could be accounted for by rare variants particularly in genomic regions of low LD, where these variants are imperfectly tagged by common SNPs (Wainschtein et al. 2019).

As proposed earlier by R. A. Fisher in his “infinitesimal model” (Fisher 1918), another explanation of the lack of detection of causal variants in GWAS may lie in the fact that most complex quantitative traits are influenced by a substantial number of common variants with relatively small effects (Barton et al. 2017). As a consequence, they seldom pass the genome-wide significance thresholds in the frame of single-locus association tests (Shi et al. 2016; Yang et al. 2010), which have been reported typically to be near 10⁻⁸ for single tests, assuming a Bonferroni control for classical 5–20% genome-wide false-positive probability. The development of mixed linear models (MLMs) accounting for heterogeneous relatedness and population structure in a population sample have proven very efficient to reduce the false-positive rate and increase power to detect causal variants at the genome-wide level (Kang et al. 2010; Kang et al. 2008; Yu et al. 2006). However, a lack of genome-wide power was reported (i.e., <20%, assuming a p-value threshold of 10⁻⁵) when testing small-effect causal SNPs (i.e., explaining 5–10% of the phenotypic variation), with sample sizes of 34–38 for mouse, 95 for A. thaliana and 277 for maize data (Kang et al. 2008). Thus, assuming higher p-value thresholds (i.e., 10⁻⁵ or 10⁻⁶) may still not be adequate for detection.

In this study, we propose a method to solve the issue of detecting small-effect variants, namely the local score approach, which takes advantage of the cumulative association signals (i.e., the p-values) through LD between SNPs in a short genomic region containing a causal variant with small-to-moderate effect. The local score approach was recently applied for processing the statistical signature of positive selection in genome scans (Fariello et al. 2017). P-values generated by a sequence of single-marker statistical tests along the chromosome are turned into scores and the local score is defined as the maximum of a Lindley process over the sequence of scores (Mercier and Daudin 2001). The local score points a region that begins on the first non-zero score of a mountain and ends at the point where the maximum of the mountain is reached. The local score approach was compared with window-based approaches (Johansson et al. 2010; Myles et al. 2008) in a genome scan context and simulations showed consistently higher detection power with this approach (Fariello et al. 2017). Some studies have also suggested the use of such kind of approach in a GWAS context, especially when p-values are not too small and marker density is high (Guedj et al. 2006; Teyssèdre et al. 2012; Wiuf et al. 2016). Here we propose to extend the use of the local score in post-processing of the p-values of the MLM for association (Kang et al. 2010; Kang et al. 2008). We used simulations to evaluate the power of the local score approach to detect statistical signatures of association for quantitative trait loci (QTL) with small to large heritability, in a GWAS context with high marker density and moderate sample size (n = 200). We show that the power of the local score approach to detect small-effect QTL largely outperforms p-value-based tests and is competitive with regard to alternative methods, which also aggregate p-values (Guedj et al. 2006; Wiuf et al. 2016).

We apply the local score approach to a GWAS of Quantitative Disease Resistance (QDR) of the model legume Medicago truncatula to Aphanomyces euteiches, a major pathogen of grain and forage legumes such as pea or alfalfa. Plant QDR is a quantitative phenotypic trait potentially shaped by a mix of a few QTL with large effects and a variety of QTL with small-to-intermediate effects (Pilet-Nayel et al. 2017; Roux et al. 2014). Indeed, in M. truncatula, previous linkage-mapping analyses of QDR to the predominant pea-infecting isolates of A. euteiches (ATCC 201684 and RB84) identified the major locus prAe1/AER1 (Djébali et al. 2009; Pilet-Nayel et al. 2009). More recently, a GWAS approach in a collection of 174 M. truncatula accessions infected with the ATCC 201684 isolate, identified candidate genes underlying this major locus (Bonhomme et al. 2014). In addition, linkage-mapping analyses of QDR to other A. euteiches isolates (i.e., Ae109, MF-1, and NC-1) infecting pea and/or alfalfa identified numerous minor QTL (Hamon et al. 2010). Minor QTLs are commonly identified in linkage-mapping analyses of QDR in plants. However, only genes underlying major QDR loci (i.e., with >20% heritability) have been identified so far by GWAS (Roux et al. 2014). In this study, narrow-sense heritability for M. truncatula QDR to different A. euteiches isolates ranged from 0.1 to 0.8, thus making it an interesting trait for testing the local score approach. Using this approach, we confirmed major QTL, refined their mapping, but also identified a set of new minor QTL explaining QDR to multiple A. euteiches isolates that could otherwise not be detected using “classical” single-marker p-values of association. Candidate genes underlying these QTL suggest key roles for pathogen effector recognition and plant proteasome in the molecular mechanisms leading to M. truncatula resistance to A. euteiches. The translation of such kind of approach to crop species could help to improve plant breeding efficiency by adding newly detected minor QTL in marker-assisted selection programs.

Materials and methods

QTL simulations

As the power of the local score approach has only been tested in the context of genome scans for selection signatures (Fariello et al. 2017), we investigated its detection power in a GWAS context by simulating QTL of various effect sizes, located on a chromosomal sequence, using the QMSim software (Sargolzaei and Schenkel 2009). One QTL was simulated as one SNP (causal variant) on a chromosome of 100,000 SNPs, each randomly placed. A historical population of 10,000 diploid individuals was first generated, in which all SNPs (including the QTL) had equal allele frequencies (i.e., 0.5) and were in complete LD in the first generation, meaning that only two chromosomal haplotypes in equal frequencies were present in the first generation. Then, evolution through random mating and mutation-drift equilibrium was simulated over 1000 non-overlapping generations composed of equal numbers of males and females. To ensure a fixed number of SNPs as well as QTL segregation in the simulation outcome, a recurrent mutation rate per SNP was set up at 2.5 × 10⁻⁵ (following suggestion by QMSim user manual), assuming that recurrent mutation at SNP markers do not contribute significantly to the erosion of LD (Ardlie et al. 2002). The number of mutations per individual was sampled from a Poisson distribution with mean u (u = 2*number of loci*mutation rate) and then each mutation was assigned to a random locus on the chromosome. Recombination was fixed at one crossover per Morgan per generation and a chromosome of 100 cM was simulated. Assuming 1 cM equals 1 Mbp or 0.25 Mbp as in humans and A. thaliana, respectively (Nordborg et al. 2002), SNP density was on average one SNP per 250 bp to one SNP per kbp, and on average one recombination occurred on one chromosome at each generation. Finally, we sampled 200 individuals for subsequent association mapping and local score analyses, in order to correspond to a reasonable sampling for GWAS. Different QTL allele effects were simulated, each sampled from a normal distribution, and, assuming a phenotypic variance of 100, were scaled in the last historical generation to ensure the desired QTL heritability (see QMSim user manual). One thousand simulations were performed for each QTL heritability value (0%, 5%, 10%, 20%, or 40%).

Association mapping and local score analysis of simulated data

Simulated genotypic and phenotypic data were analyzed using a MLM implemented in the emma expedited (emmax) software (Kang et al. 2010). The MLM is used to estimate and then test for the significance of the allelic effect at each SNP, taking into account the genetic relationships between individuals to reduce the false-positive rate. Briefly, the MLM approach implemented in emmax proceeds in three steps. First, a kinship matrix K of pairwise genetic similarities (Identity By State) between individuals is calculated using the genotypic data (at the 100,000 SNPs generated at each simulation). Second, a variance component procedure is used to estimate σ²_a and σ²_e by restricted maximum likelihood from the relationship equation Var(Y) = σ²_aK + σ²_eI, with Var(Y) the phenotypic variance of the trait, σ²_a and σ²_e the genetic and residual variances, and I an identity matrix. Finally, for each of the 100,000 markers an F-test is used to test the significance of β_k, the allelic effect estimated in the following model: y_i = β₀ + β_kX_ik + η_i, with X_ik the allele found in individual i for the marker k, and η_i a combination of the random genetic and residual effects, with Var(η) proportional to Var(Y) (Kang et al. 2010). For each simulation, emmax generated a sequence of 100,000 p-values estimated from the F-test performed at each SNP. This association mapping method is hereafter referred to as p-value-based tests.

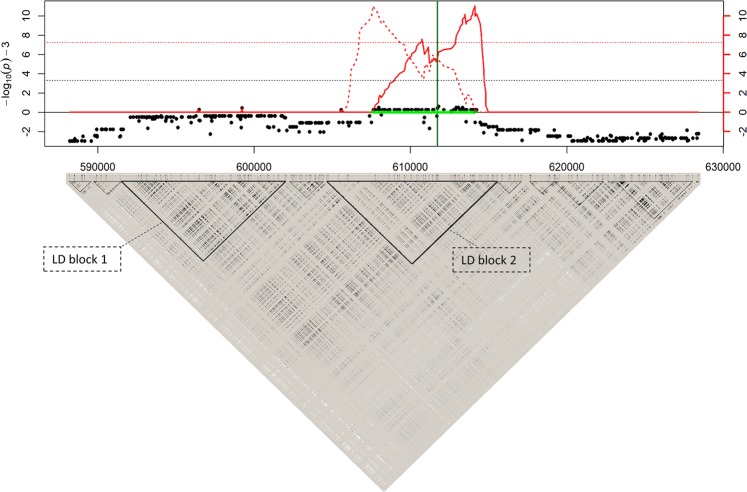
To find clusters of SNPs that are almost significant, we tested methods based on the local score theory, designed to cumulate local association signals based on p-values. The aim of the local score is to find segments of the genome that have a higher density of SNPs with medium to high signal, compared with the rest of the genome. This property is really useful, as the patterns of LD change through the genome and the local score does not rely on a fixed window size (Fig. 1), contrary to sliding windows approaches where the length of the window is fixed accounting for a general feature, such as the average LD decay for instance (e.g., 10 kbp windows).

Fig. 1.

Illustration of the local score approach based on p-values of a GWAS on a chromosome segment containing a QTL with 10% heritability. Top figure: Manhattan plot of the scores −log₁₀(p-value) − ξ (with ξ = 3; black dots) and the local score (i.e., the Lindley process, from left to right as indicated by the solid red curve, and from right to left as indicated by the dotted red curve) for 393 SNP markers on a chromosome segment containing a QTL (vertical green line). The horizontal green segment indicates the interval detected with the local score calculated in either direction, which contains the simulated QTL. The black and red horizontal dotted lines indicate the significance level for the scores (3.3; that is −log10(0.05/100,000) − 3) and for the Lindley process (7.25), respectively. Bottom figure: linkage disequilibrium plot of the 393 SNP markers (r² measure). The triangles indicate different blocks of LD on this chromosome segment (with pairwise SNP r²-values > 0.90), among which two large blocks of ~10 kbp. The LD plot was performed using the software Haploview (Barrett et al. 2005). These figures show that although two major LD blocks are present on this chromosome segment, only the LD block that cumulates the smallest p-values in cluster (i.e., the one containing the QTL) is detected by the local score approach, contrary to single-marker tests

We evaluated and compared three methods to p-value-based tests using the simulated data: the local score (Fariello et al. 2017), LHiSA (Local High-scoring Segment for Association; Guedj et al. 2006) and LandScape (Wiuf et al. 2016). In the local score approach (Fariello et al. 2017), individual scores X_i are assigned to each marker position. Over a SNP sequence of length M, given a sequence of scores X = (X₁, …, X_m, …, X_M), the local score is defined as $H=ma{x}_{1\le i\le j\le M}\sum _i^j{X}_k$. Finding the segment that accumulates the highest signal is equivalent to finding the maximum of a Lindley process defined as: h = (h₀, …, h_m,…, h_M), with h₀ = 0 and h_m = max(0, h_m − 1 + X_m) (see Fig. 1). Provided the expectation E(X) is negative and X has at least some positive values, the Lindley process will include at least one mountain above 0. It would not be possible to use the p-values as a score directly, because the expectation would never be negative and in addition we want that stretches of small p-values show higher scores than for higher p-values, so if p_i is the p-value of the i-th locus, then the score is taken as X_i = −log₁₀(p_i) − ξ. The proposed values for ξ are as follows: 1, 2, 3, or 4, depending on the range of the p-values. For ξ = 2, only p-values under 10⁻² will contribute positively to the score and p-values above will substract from the signal. In the LandScape method, a proposed score is Z_k = log₁₀(z_γ/p_i) = − log₁₀(p_i) + log₁₀(z_γ). They propose that z_γ is a quantile of the distribution of the p_i. If the p_i are p-values, they are supposed to have a uniform distribution, so a 0.01 quantile is 0.01 and log₁₀(0.01) = − 2. It is therefore equivalent to the ξ parameter in (Fariello et al. 2017). Then, finding high-scoring segments can be done by calculating A_k = max(0, A_k − 1 + Z_k). In the LHiSa approach the individual scores X_i are the same as in (Fariello et al. 2017) and ξ is the 0.05 quantile of the distribution of the scores.

There are mainly two differences between these approaches. The first one is that in the local score approach implemented in Fariello et al. (2017) we looked for segments of the genome whose score exceeds a certain threshold, whereas the aim of LHiSA is to identify the best k high-scoring segments (by removing iteratively the highest-scoring segment, once detected using H_i = max(0, H_i− 1 + X_i)), and to give their respective scores H⁽¹⁾, H⁽²⁾,…, H^(k). In Fariello et al. (2017) we prove that if there are more than one high-scoring segments that exceed the threshold, there is no need for computing a new threshold for each high-scoring segment. The LandScape method calls these segments independent segments and in addition considers dependent segments, which are high-scoring segments hidden within the signal of the high-scoring ones. In general, if there are dependent segments, using a higher ξ-value might transform an independent and a dependent segment into two independent ones. The other difference is the way that each method proposes to compute the threshold for a given score. When the LHiSA method was proposed, there were not very much datasets of genomic sequence data, so the marker density was quite low in general. They recall that if the X_i are independent and identically distributed, the distribution of H can be well approximated by a Gumbel distribution, based on the extreme values theory (Iglehart 1972; Karlin and Dembo 1992). In Wiuf et al. (2016), the computation of the threshold based on these ideas is called A0. When the sequence of scores is not independent, which is the case with high marker density, both of them propose to use permutations to obtain an empirical null distribution for no association with the trait. However, we previously showed empirically that if the number of SNPs is high and the p-values used to construct the score are uniformly distributed, and the autocorrelation is almost constant along the chromosome, then the local score follows a Gumbel distribution under the null, with parameters depending on the length and autocorrelation of the chromosome (Fariello et al. 2017). We provide formulas for computing the parameters of the Gumbel law for ξ-values of 1, 2, 3, and 4. Hence, performing computationally intensive permutations can be avoided. R scripts used to compute the local score and significance thresholds are available at https://forge-dga.jouy.inra.fr/projects/local-score/.

We provide a general view of the behavior of the local score (using ξ = 3), given a set of p-values in a GWAS context, in Fig. 1. We show the results of the simulation of a chromosome segment containing different SNP markers including a SNP QTL with 10% heritability, followed by GWAS, local score, and LD analyses. This figure shows that only the LD block containing the QTL, cumulating the smallest p-values in cluster, is detected as significant by the local score, contrary to p-value-based tests that tend to show a weaker association signal on a larger interval containing two LD blocks (including the LD block containing the QTL), and which would be considered as not significant, even using windowed statistics. The statistical properties of the local score in comparison with p-value-based tests and other local score approaches are evaluated in the subsection “Multiple false positives control and QTL detection power of local score methods in a GWAS context” of the Results and Discussion section.

Plant material and A. euteiches isolates

In this study, a collection of 174 M. truncatula accessions (extracted from http://www.medicagohapmap.org), representative of the overall genetic diversity of M. truncatula and belonging to the core collection CC192 (Ronfort et al. 2006), was used for phenotyping experiments (see Supplementary Table S1 in Burgarella et al. (2016)). The collection has already been used for GWAS of different traits (Bonhomme et al. 2014; Burgarella et al. 2016; Kang et al. 2015; Le Signor et al. 2017; Rey et al. 2017; Stanton-Geddes et al. 2013; Yoder et al. 2014). For QDR tests, five A. euteiches isolates from different geographical areas with different pathogenicity traits on pea and alfalfa were used. The pea-infecting isolates ATCC 201684 from Denmark and RB84 from France belong to pathotype I, and the Ae109 isolate to pathotype III, according to pathogenicity tests performed with pea differential genotypes (Wicker et al. 2003; Wicker and Rouxel 2001). ATCC 201684—previously studied by Bonhomme et al. (2014)—and RB84 belong to the main virulence group present in France, whichinfects a wide range of legume species. RB84 has been reported to be pathogenic on pea, alfalfa, M. truncatula, bean, faba bean, lentil, clover, and vetch (Moussart et al. 2008), whereas Ae109, isolated in Wisconsin (USA), was reported to be pathogenic to pea and alfalfa (Malvick et al. 1998). The alfalfa isolates MF-1 and NC-1, sampled in Wisconsin and North Carolina (USA), belong to race 1 (R1) and race 2 (R2) of A. euteiches, respectively (Malvick and Grau 2001). These two isolates have a narrow host range, as they were reported to be pathogenic on alfalfa, but not on pea, bean nor red-clover (Malvick et al. 1998), but they can also infect M. truncatula. The four isolates RB84, Ae109, MF-1, and NC-1 were used in a previous linkage-mapping analysis of QDR to A. euteiches in M. truncatula (Hamon et al. 2010).

Inoculation, phenotyping, and statistical modeling of QDR

Disease resistance tests were conducted in a growth chamber at 25 °C for a 16 h day and 23 °C for an 8 h night using the protocol described by Pilet-Nayel et al. (2009). For each A. euteiches isolate, the experiment was conducted using complete block design with four blocks per accession, each block testing all the 174 accessions at the same time with one pot of five plants per accession grown in a moistened vermiculite substrate. Zoospores were produced from each isolate for inoculations of 10-day-old plants with 5 ml of inoculum per plant adjusted to 2000 spores/ml and 100 spores/ml, for pea and alfalfa isolates, respectively, as described previously (Hamon et al. 2010). QDR was determined by a disease severity index, the Root Rot Index (RRI) scoring individual plants 14 days after inoculation on a 0–5 disease scoring scale, where 0 is an asymptomatic plant and 5 is dead plant (Pilet-Nayel et al. 2009).

To account for putative block effects on the disease severity, RRI adjusted means were calculated for each M. truncatula accession by fitting the following linear model with fixed effects, taking into account a block design: y_ijk = accession_i + block_j + ε_ijk, where y_ijk is the RRI for the k-th plant in the j-th block of the i-th accession, and ε_ijk is the residual. These adjusted means for each accessions were used for GWAS.

Association mapping and local score analyses of QDR

GWAS was performed on RRI-adjusted means obtained with isolates RB84, Ae109, MF-1, and NC-1 using the MLM approach implemented in the software emmax (Kang et al. 2010). Emmax computes the relationship between every pair of individuals from SNP data (called “kinship matrix”) and uses this kinship matrix to control for relatedness in the MLM of association. In this study, we used the Mt4.0 Medicago genome and SNP version to perform GWAS (see http://www.medicagohapmap.org/). We also re-analyzed phenotypic data from a previous GWAS that used the Mt3.5 genome version, which consisted of the RRI score and the PC1 (first principal component from a principal component analysis) parameter summarizing 11 in vitro measures, obtained following infection with A. euteiches ATCC 201684 (Bonhomme et al. 2014). A set of 5,328,852 genome-wide SNPs was selected with a minor allele frequency of 5% and at least 90% of the 174 accessions scored across the M. truncatula collection, to be used for calculating a kinship matrix of pairwise genetic similarities and to perform GWAS. Narrow-sense heritabilities (i.e., portion of the total phenotypic variation attributable to additive genetic effect, h²_ss) of the RRI-adjusted means obtained with isolates ATCC 201684, RB84, Ae109, MF-1, and NC-1 were calculated from estimates of σ²_a and σ²_e by restricted maximum likelihood accounting for the kinship matrix used in the MLM, using the Tassel software (Bradbury et al. 2007). As suggested by the simulation results in this study (see Results and Discussion section), to identify significant associations we used a relaxed chromosome-wide significance threshold α = 20% for p-value-based tests and for the local score approach (i.e., the probability to get at least one false-positive peak on the chromosome is 20%). For p-value-based tests we applied a Bonferroni correction for the number of blocks of SNPs in LD previously estimated in M. truncatula genome, leading to a p-value threshold of 4 × 10⁻⁶ (Bonhomme et al. 2014). For the calculation of the local score, a conservative value of ξ = 2 was chosen, in order to efficiently control for multiple false-positive peaks along a chromosome. Finally, to estimate chromosome-specific significance threshold values for the local score applied to M. truncatula data, we took into account the autocorrelation (ρ, ranging from 0.16 to 0.18) of p-values along each chromosome of length L to estimate the coefficients a_L,ρ and b_L,ρ of the Gumbel law used to model maxima of stochastic processes (see Materials and Methods) and hence to get the significance threshold value for each chromosome we used equation 4 following Fariello et al. (2017), namely threshold_L,ρ,α = (log(−log(α)) − a_L,ρ)/b_L,ρ. R functions to calculate the local score and associated significance thresholds on real data assuming ξ = 1, 2, 3, or 4 are available at https://forge-dga.jouy.inra.fr/projects/local-score/.

Results and discussion

Multiple false positives control and QTL detection power of local score methods in a GWAS context

In order to investigate whether our simulations produced a LD decay consistent with standards observed in real data (i.e., Human-like or Arabidopsis-like chromosomes), r² between pairs of SNPs was calculated over different distances (Fig. S1). Assuming 1 cM equals 0.25 Mbp in A. thaliana (Nordborg et al. 2002), the one-half LD decay was ~27–37 kbp, in accordance with several estimates ranging from 10 to 50 kbp in this species (Kim et al. 2007; Nordborg et al. 2002; Nordborg et al. 2005; Plagnol et al. 2006). LD in the human genome is known to be highly variable and to show block-like structures. Still, using the standard assumption of 1 cM, which equals 1 Mbp in human (Nordborg et al. 2002), in our simulations the one-half LD decay was ~7–9 kbp, which is in line with influential estimates of useful LD ranging from 3 to 10 kbp (Kruglyak 1999; Pritchard and Przeworski 2001; Shifman et al. 2003). Hence, the simulated LD decay was consistent with the average LD decay found at the chromosome scale in real data. We could thus evaluate different methods to be applied at the chromosome level in a GWAS context, for statistical detection of QTL.

Based on the simulated data assuming either “no QTL effect” or the different QTL heritability values (5%, 10%, 20%, or 40%) at a single SNP position, we evaluated QTL detection power and the probabilities of multiple false positives along the chromosome, while controlling for different chromosome-wide significance thresholds (i.e., 0.2, 0.1, 0.05, 0.01, and 0.001), for the four methods: p-value-based tests, the local score, LHiSA, and LandScape. To do this, we used the empirical distributions of the maximum along the chromosome of −log₁₀(p), h (Fariello et al. 2017), H (Guedj et al. 2006), and A_k, (Wiuf et al. 2016), respectively, in the simulations with no QTL effect.

By controlling for the family-wise error rate (FWER) along the simulated chromosome, which we called here “chromosome-wide FWER,” we could calculate the proportion of simulations of the null hypothesis of “no QTL effect” in which one false-positive peak or more than one false-positive peak occurred on the chromosome. A comparison for the different methods is shown in Fig. 2. From this figure, one can see that p-value-based tests as well as the local score with ξ = 4 make poor control of multiple false-positive peaks along the simulated chromosome, whereas the best control is done by the local score with ξ = 2, followed by LandScape. In practice, ξ must be chosen between the average and the maximum of the set of −log₁₀(p_i) (Fariello et al. 2017). In these simulations of the null hypothesis, the average and the maximum of the set of −log₁₀(p_i) was 0.414 and 3.82, on average across 1000 simulations, respectively. A value of ξ = 4 is out of range, thus not advisable, and we showed that this is because it makes poor control of multiple false-positive peaks. As also shown for selection scans (Fariello et al. 2017), we show here that the local score is equivalent to the single-marker approach (i.e., p-value-based tests) for large values of ξ, as the only scores that remain positive are those corresponding to very low p-values, so the detected regions would contain just one or a few SNPs.

Fig. 2.

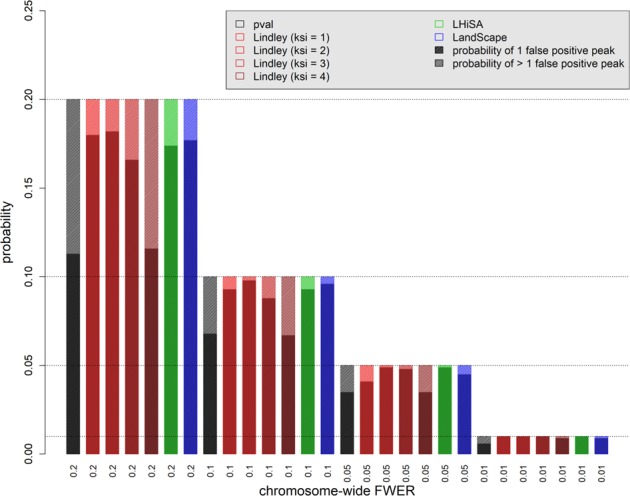
Proportion of unique or multiple false-positive peaks across the simulated chromosome, detected with p-value-based tests (emmax method) and methods based on aggregation of p-values (Local Score, LHiSA, and LandScape). The empirical distributions of the maximum along the chromosome of −log₁₀(p), A_k, H, and h, based on 1000 simulations of the null hypothesis of “no QTL effect,” were used to control the chromosome-wide FWER, by setting significance thresholds at the 80%, 90%, 95%, or 99% quantiles. Hence, the corresponding proportions of simulations showing at least one false positive was 20%, 10%, 5%, or 1%, respectively. Among these, we distinguished the proportion of simulations showing either unique or multiple false positive peaks across the simulated chromosome

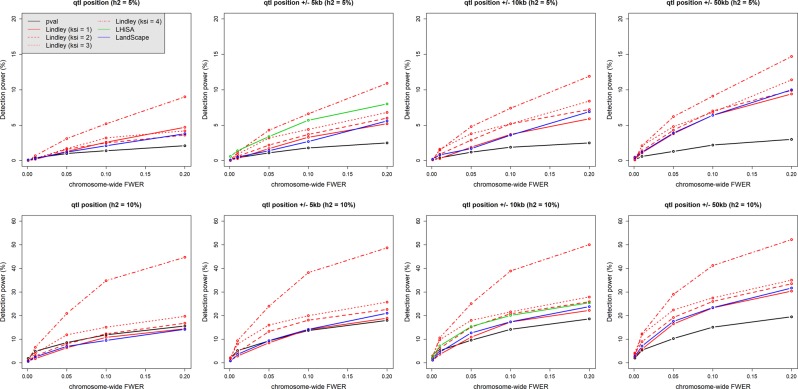
A comparative power analyses was carried out between the four methods. The power of each statistic (−log₁₀(p), h, H, and A_k) was determined as the proportion of the simulations with “QTL effect” for which the statistics at the QTL position (or on an interval including the QTL position) was greater than a given quantile of the distribution under the “no QTL effect.” The results for low QTL heritability values of minor QTL explaining 5–10% of the phenotypic variation are shown in Fig. 3. Detection power was calculated while controlling for different chromosome-wide FWER, at the QTL position but also in windows of ±5, ±10, ±50, and ±100 kbp centered on the QTL position. This way of computing power penalizes the local score approaches with regard to single-marker tests, because if a significant segment reaches its maximum out of the considered window, the segment could be considered as not significant, thus will not count for the power computation.

Fig. 3.

Minor QTL detection power by p-value-based tests (emmax method) and methods based on aggregation of p-values (Local Score, LHiSA, and LandScape). Two different QTL heritability values, 0.05 (top row) and 0.1 (bottom row), were each simulated 1000 times (see the simulation settings in the Materials and Methods section “QTL simulations”). The detection power was calculated as the proportion of simulations in which the simulated QTL was detected at a given chromosome-wide FWER set up using simulations of the “no QTL hypothesis.” Power estimation at the QTL position used the value of each statistic (−log₁₀(p), A_k, and h) at the simulated QTL position, whereas estimations on windows of ±5, ±10, or ±50 kbp on both sides of the QTL position used the maximum of each statistic in the window. As LHiSA does not provide a marker-based statistic, rather the score H of the highest-scoring segment, power was calculated as the proportion of simulations in which the highest-scoring segment contained the QTL position and had an H-value superior to the significance threshold. In addition, as the highest-scoring segment had variable size across simulations, LHiSA power curves were compared with power curves of the other methods on windows thatwere the closest to the mean interval size given by LHiSA; i.e., 13,593 and 28,598 bp, for QTL heritability values of 0.05 and 0.1, respectively. This method penalizes the other local score methods, as we considered that the QTL was detected if the maximum in the considered window is higher than the detecting thresholds. Situations where the local score is higher than the threshold but is outside the window are not considered as cases of QTL detection, even if the QTL falls in the segment

From this figure, one can see a general trend for methods based on aggregation of p-values (i.e., local score, LHiSA, and LandScape) to show more detection power of minor QTL than p-value-based tests, for FWER ranging from 5 to 20%. This illustrates the ability of such methods to capture efficiently the LD surrounding the QTL position through autocorrelation of p-values and therefore the local association signal. However, a clear limit to the detection of minor QTL (QTL heritability of 5%) occurs. For instance, for a relaxed chromosome-wide FWER of 20%, power ranges approximately from 5% to 15% maximum, depending on the method, but it largely outperforms the power of p-value-based tests, which is 3% maximum. The other trend is that the local score approach tends to show (i) higher power than either LandScape (although it depends on the chosen ξ-value) or to a lesser extent LHiSA, and (ii) increased power for large ξ-values. In addition, the power of approaches based on the local score does not increase dramatically when considering increased interval sizes on either side of the position tested. This emphasizes again the ability of these statistics to capture local LD surrounding the position tested. Finally, the detection power for major QTL (i.e., explaining 20–40% of the phenotypic variation) is illustrated in Fig. S2. This analysis clearly shows that p-value-based tests largely outperforms the local score, LHiSA, and LandScape to detect major QTL in a GWAS, notably for low chromosome-wide FWER. However, it should be noted that under the hypothesis of the presence of a QTL with intermediate effect (i.e., heritability of 20%), the local score is competitive with regard to the single-marker approach (i.e., p-value-based tests) provided large values of ξ are used. In other words, it can be argued that the local score with a large ξ-value could be used to finely map such type of QTL once they have been detected using p-value-based tests with low chromosome-wide FWER. For the detection of major QTL (i.e., heritability of 40%), p-value-based tests are unequaled by any method that aggregates p-values (Fig. S2).

In summary, we recommend the use of the local score approach when the objective is to detect minor QTL (i.e., heritability from 5% to 10%), because, as it accounts for all the variants in the QTL region accumulating the information and accounting for LD, its power outperforms p-value-based tests. With the goal to increase chances to map minor QTL as precisely as possible in the context of GWAS with high marker density while decreasing efficiently the probability of multiple false-positive peaks along a chromosome, ξ-values of 2 to 3 seem to be a good compromise especially for chromosome-wide FWER ≥5%. Although the local score might not be required for efficient detection of major QTL, we suggest as a general recommendation to apply this approach without a priori knowledge of the genetic architecture of the trait, but using larger ξ-values (i.e., ≥3) to allow fine mapping of major QTL once they have been detected.

M. truncatula QDR varies in response to the inoculated A. euteiches isolate

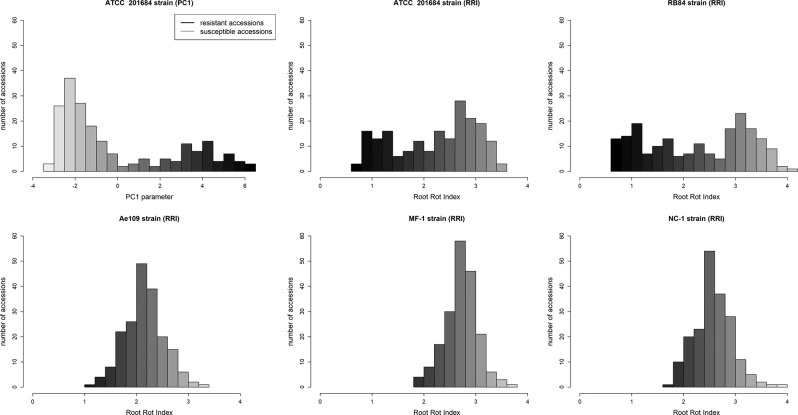
Frequency distributions of the RRI adjusted means obtained for the 174 M. truncatula accessions in response to five A. euteiches isolates (ATCC 201684, RB84, Ae109, MF-1, and NC-1), plus the distributions of the PC1 parameters in response to ATCC 201684 previously described (Bonhomme et al. 2014), are shown in Fig. 4. For the pea isolates ATCC 201684 and RB84 from pathotype I, RRIs were similarly distributed, following a bimodal curve with a mean (±SD) of 2.21 (±0.8) and 2.26 (±1), respectively, with 11% and 14% of very resistant accessions showing RRI values lower than 1 (Fig. 4, Supplementary File S1). The distribution of the PC1 parameter (i.e., in vitro responses to isolate ATCC 201684) also showed a bimodal distribution and 15% of very resistant accessions showed PC1 values higher than 4. In contrast, the frequency distribution of RRI obtained with the pea isolate Ae109 from pathotype III showed a unimodal distribution with mean 2.15 (±0.39). No highly resistant accession with RRI values lower than 1 was detected, but 32% of accessions were partially resistant with RRI values <2. Likewise, the responses of the accessions to alfalfa isolates MF-1 and NC-1 also showed unimodal distributions with means of 2.72 (±0.32) and 2.57 (±0.36), respectively, and only a few (2–6%) partially resistant accessions were identified with RRI values <2 (Fig. 4). Bimodal vs. unimodal distributions of RRI scores for resistance to RB84 vs. Ae109, MF-1, and NC-1 of A. euteiches in a RIL population of M. truncatula were also previously reported (Hamon et al. 2010). Narrow-sense heritability (h²_ss) of QDR to isolates ATCC 201684 and RB84 in this M. truncatula collection was very high (h²_ss of RRI = 0.72 and 0.78, respectively). It was lower in response to the Ae109, MF-1, and NC-1 (h²_ss of RRI = 0.38, 0.10, and 0.22, respectively) in accordance with smaller phenotypic variances of RRI observed for accessions of M. truncatula infected with these three isolates (Fig. 4). Hence, QDR phenotypic distributions as well as high heritability values suggest that the genetic architecture of QDR of M. truncatula is dominated by a few QDR loci with major effects in response to ATCC 201684 and RB84. On the other hand, the genetic architecture of QDR of M. truncatula seems to be governed by small-effect QDR loci in response to isolates Ae109, MF-1, and NC-1, which were reported to be pathogenic to a narrower host range, i.e., alfalfa and/or pea (Malvick et al. 1998). The isolates Ae109, MF-1, and NC-1, originating from alfalfa production fields in the central United States (Malvick et al. 2009), showed to be more adapted to M. truncatula, which is closely related to alfalfa, than the ATCC 201684 and RB84 isolates originating from pea growing areas in Europe.

Fig. 4.

Phenotypic distributions of the Root Rot Index (RRI) and/or the PC1 scores across a collection of 174 M. truncatula accessions in response to five different A. euteiches isolates. The distributions of RRI and PC1 scores for the ATCC 201684 isolate were retrieved from Bonhomme et al. (2014)

GWAS and local score analyses of an integrative parameter of QDR

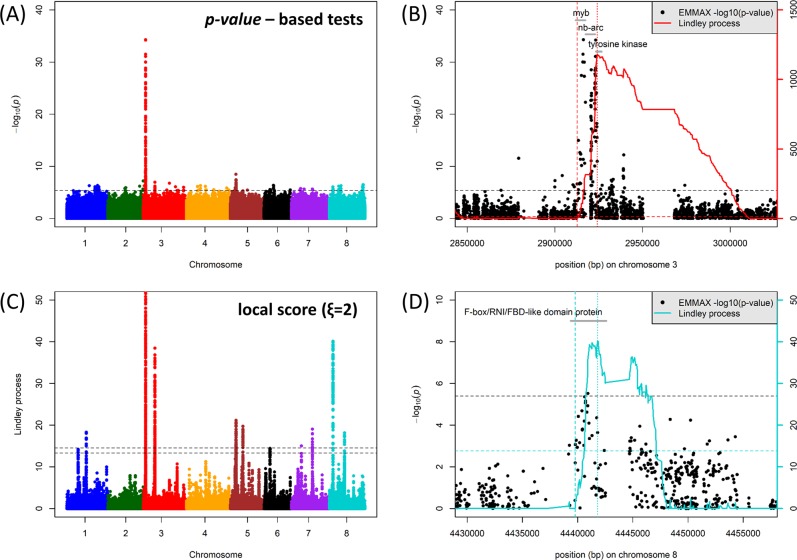
The PC1 parameter (h²_ss = 0.72) integrates both plant symptoms and developmental variation of the root system in response to A. euteiches ATCC 201684 (Bonhomme et al. 2014). Unlike in the previous study, we conducted here a GWAS of the PC1 parameter using (i) SNPs mapped onto the latest (Mt4.0) version of the M. truncatula genome, (ii) the MLM approach implemented in the software emmax—as for the analyses of simulated data—and (iii) a kinship matrix estimated on the basis of the genome-wide SNP dataset used for GWAS (i.e., 5,328,852 SNPs with a minor allele frequency of 5%), which clearly implies population structure and heterogeneous relatedness in the M. truncatula collection (see Fig. S3). GWAS and local score analysis of the PC1 parameter revealed a strong association peak at the top of chromosome 3, ranging from position 2.913 to 2.924 Mb over ~10 kbp, with a peak corresponding to p-values ~ 10⁻³⁵ (Fig. 5a). Inspection of this region indicates the presence of three closely spaced genes encoding a MYB transcription factor, an NB-ARC (a Resistance Gene Analog), and a tyrosine kinase protein encoding gene (Fig. 5b, Supplementary Table S1). The local score (using ξ = 2) reached very high values in this region (up to 1179), also indicating an extremely significant association signal. A close look at the p-values in this short genomic region does not clearly pinpoint one of these three genes as the best candidate, as they are very close to each other (Fig. 5b). In the previous GWAS of the PC1 parameter, only one significant SNP located next to the MYB transcription factor was detected in this region (Bonhomme et al. 2014), but the SNP dataset used, similar to the one used in this study, was mapped onto the former version of the M. truncatula genome (Mt3.5), which lacked robust coverage, gene annotation, and SNP data in this genomic region at that time (Bonhomme et al. 2014). However, the other main QDR locus found in the previous GWAS, the F-box protein coding gene Medtr3g011020, is still detected in this study with the new genome version but less significantly (p-values ~ 10⁻⁸) than the MYB/NB-ARC/tyrosine kinase locus (Fig. S4).

Fig. 5.

GWAS and local score analysis of M. truncatula PC1 parameter (Bonhomme et al. 2014) for quantitative disease resistance to A. euteiches isolate ATCC 201684. a Manhattan plot of the p-value-based tests (emmax) performed on the PC1 parameter. The horizontal dashed line indicates the significance threshold (4 × 10⁻⁶). b Magnification of the highest significant peak at the top of chromosome 3 at the MYB/NB-ARC/tyrosine kinase QDR locus. Gray segments indicate the different gene models in the region. The solid red curve indicates the Lindley process (local score method with ξ = 2) calculated from left to right and the two red dashed vertical lines indicate the interval detected, with the curve right of the peak not taken into account. The horizontal black and red dashed lines indicate the significance threshold (FWER = 20%) for p-value-based tests (4 × 10⁻⁶) and for the local score (13.92), respectively. c Manhattan plot of the Lindley process (local score method with ξ = 2). The two horizontal dashed lines indicate the minimum and maximum of the eight chromosome-wide significance thresholds. Note that the range of values on the y-axis is limited to 0–50 in order to highlight minor QDR loci, whereas the main association peak on chromosome 3 shows very high local score values (up to 1179: see Fig. 5b). d Magnification of the highest significant peak on chromosome 8 at the F-box/RNI/FBD-like domain protein. The legend is the same as in Fig. 5b, except that curves and lines relative to the Lindley process are highlighted in light blue

The genome-wide local score analysis of the PC1 parameter also highlighted at least seven other significant QDR loci, which were marginally significant (10⁻⁴ to 1.5 × 10⁻⁶) according to p-value-based tests (Fig. 5c, Supplementary Table S1). Among these QDR loci, one on chromosome 3 spanned a DEAD-box RNA helicase family protein encoding gene, which was also detected in the previous GWAS using the PC1 parameter (Bonhomme et al. 2014). The main peak on chromosome 5 mapped upstream of an ubiquitin-conjugating enzyme coding gene, whereas the main peak on chromosome 8 mapped within a F-box/RNI/FBD-like domain protein encoding gene (Fig. 5c, d). This new GWAS of the PC1 parameter, powered by a local score approach, allowed to detect, among other candidates, two new QDR loci with molecular functions related to proteasome, a biological pathway already pinpointed to play a major role in QDR to A. euteiches (Bonhomme et al. 2014; Djébali et al. 2009). None of these loci was detected by using solely the p-value-based tests.

GWAS and local score analyses of QDR to five A. euteiches isolates

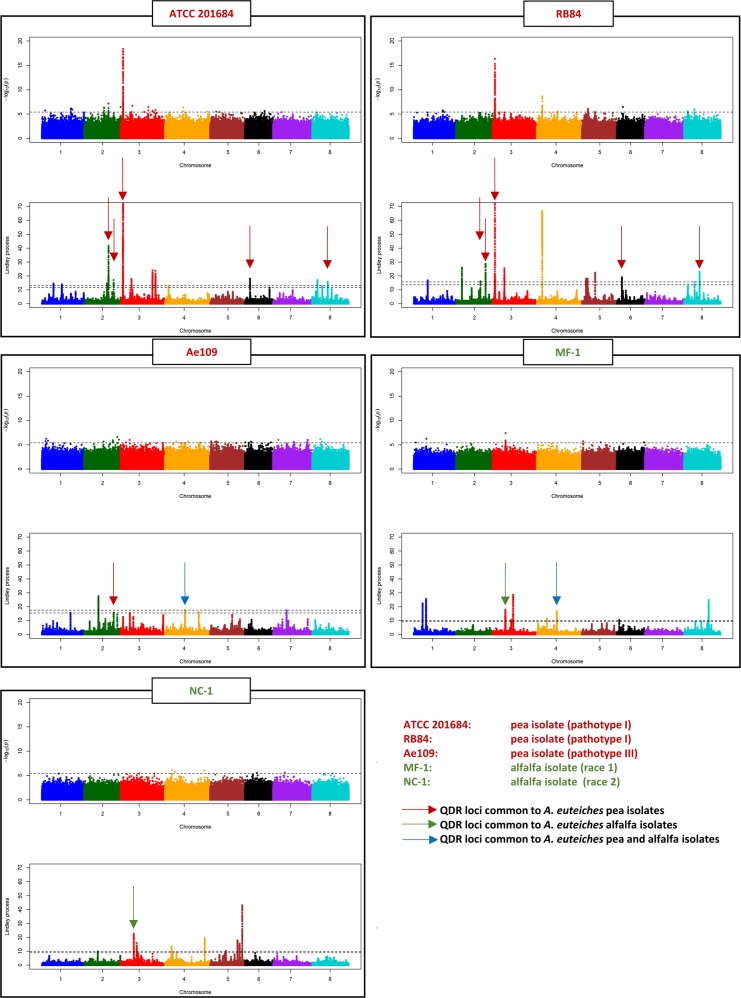
GWAS and local score analyses were also conducted with RRI-adjusted mean scores in response to the five different A. euteiches isolates previously described. Assuming a relaxed genome-wide significance threshold of 20% for p-value-based tests (i.e., p-value ≤ 4 × 10⁻⁶), seven significant QDR loci were identified, regardless of the A. euteiches isolate to which they were associated. Among these loci, the MYB/NB-ARC/tyrosine kinase major locus, already identified by GWAS of the PC1 parameter, was also detected in response to both A. euteiches isolates ATCC 201684 and RB84 (Fig. 6, Supplementary Table S1). This result highlights both (i) the robustness of different experimental designs (in vitro vs. semi-natural conditions for plant phenotyping) to detect major loci (Bonhomme et al. 2014) and (ii) the identification of a major locus controlling resistance to two A. euteiches pea isolates belonging to the same pathotype. Also assuming a relaxed genome-wide significance threshold of 20% for peak detection using the local score approach, a total of 46 QDR loci were identified. A proportion of 91% (i.e., 42/46) of them showed p-value > 4 × 10⁻⁶, indicating that they could be considered as marginally or not significant according to p-value-based tests, but clearly significant with regard to local score values (Fig. 6, Supplementary Table S1). This result supports our simulations showing that the local score approach is more powerful to detect minor QTL (i.e., with less significant effect) than p-value-based tests. The genetic bases of M. truncatula QDR to A. euteiches highly depend on the origin of the different A. euteiches isolates and—apart from the major locus MYB/NB-ARC/tyrosine kinase identified with p-value-based tests in response to the pea isolates ATCC 201684 and RB84—only the local score analyses could highlight other common QDR loci in response to the different isolates.

Fig. 6.

GWAS and local score analysis of M. truncatula Root Rot Index parameter for quantitative disease resistance to five A. euteiches isolates. Each box represents the Manhattan plots of the p-value-based tests (top) and the Lindley process (bottom) performed on M. truncatula RRI phenotypic parameter, in response to each of the five different A. euteiches isolates. The horizontal dashed line in each Manhattan plot of the p-value-based tests indicates the significance threshold (4 × 10⁻⁶). The two horizontal dashed lines in each Manhattan plot of the Lindley process indicate the minimum and maximum of the eight chromosome-wide significance thresholds. For the first two Manhattan plots of the Lindley process (QDR to isolates ATCC 201684 and RB84), the range of values on the y-axis is limited to 0–70 in order to highlight small-effect QDR loci outside of chromosome 3, on which the main association peak shows very high local score values (600 and 463 for ATCC 201684 and RB84, respectively; see Supplementary Table S1). Brown, green, and blue arrows highlight QDR loci (mainly identified using the local score approach), which are common to (i) A. euteiches pea isolates, (ii) A. euteiches alfalfa isolates, and (iii) A. euteiches pea and alfalfa isolates

The genetic bases of M. truncatula QDR to A. euteiches pea isolates was strongly dependent on the A. euteiches pathotype (pathotype I for ATCC 201684 and RB84, pathotype III for Ae109). Only one significant QDR locus was detected in response to the three A. euteiches pea isolates, the three association signals all pointing the same ~1 kbp region located ~4 kbp next to two genes among which a serine/threonine–protein phosphatase BSL2-like on chromosome 2 (Fig. 6, Supplementary Table S1). A reciprocal best hit blast between M. truncatula and A. thaliana genomes indicates that the identified serine/threonine–protein phosphatase BSL2-like from M. truncatula (Medtr2g087530) and a paralog of this gene (Medtr4g050540) are the closest homologs of BRI1 suppressor 1 (BSU1)-like 2 (AT1G08420) and BSU1-like 3 in A. thaliana (AT2G27210). Interestingly, the Solanum demissum BSL1 protein was reported to form a complex with Phytophthora infestans RxLR effector Avr2 and with the NB-LRR immune receptor R2 to trigger disease resistance to the oomycete (Saunders et al. 2012). It could be hypothesized that a similar mechanism takes place in the disease resistance of M. truncatula to pea isolates of A. euteiches, involving BSL2 and one of the NB-LRR identified in this study. The NB-ARC gene of the major QDR locus MYB/NB-ARC/tyrosine kinase in response to ATCC 201684 and RB84 pea isolates (pathotype I) could be such a candidate gene. This locus was not detected in response to pea isolate Ae109 (pathotype III), but a small peak occurred in this region at only 57 kbp away from the MYB/NB-ARC/tyrosine kinase locus (see Fig. 6; local score = 12.55, with the most significant SNP at position 2,970,777 with p-value = 7.7 × 10⁻⁵). This could represent a borderline case of detection due to phenotypic inaccuracies that may occur when using scoring scales to assess QDR and when the variation of phenotypes is tightened in a collection.

QDR to pathotype I pea isolates of A. euteiches (i.e., ATCC 201684 and RB84) shared the most similar genetic bases, with three additional common QDR loci identified (Fig. 6, Supplementary Table S1), whose gene contents suggest again a key role for proteasome functions in QDR of M. truncatula to A. euteiches. Interestingly, the local score analysis notably identified one additional highly significant QDR locus on chromosome 4 (Medtr4g020590), specific to the RB84 isolate, which contained a disease resistance protein TIR-NBS-LRR, suggesting that the two strains do not use exactly the same set of effectors to attack their host (Fig. 6, Supplementary Table S1). Overall, these results showed that QDR against A. euteiches pea isolates involved common large-effect as well as small-effect loci, but also additional QDR loci that are pathotype specific (i.e., pathotype I vs. pathotype III) or even isolate-specific within a given pathotype (i.e., ATCC 201684 vs. RB84).

In fact, very little correlation exists between QDR in response to pea vs. alfalfa isolates. Indeed, only one putative common QDR locus was detected in response to one of the pea (Ae109) and one of the alfalfa (MF-1) isolate, the two association signals being 115 kbp distant, on chromosome 4 (Fig. 6, Table S1). Interestingly, previous works have shown that the Ae109 and MF-1 A. euteiches isolates, both sampled in Wisconsin (USA) where pea and alfalfa were grown intensively, were genetically close (Malvick et al. 1998), suggesting that they may have recently derived from a common ancestral isolate and then evolved through their adaptation to different hosts (pea and alfalfa). The genetic bases of M. truncatula QDR to A. euteiches alfalfa isolates (MF-1 and NC-1) are also weakly correlated, as only one putative QDR locus was detected in response to both isolates, the two association signals being ~90 kbp distant, on chromosome 3 (Fig. 6, Supplementary Table S1).

Conclusions

This study provides new methodological and scientific knowledge for dissecting genetic architecture of complex traits, such as QDR to pathogens in plants. By simulations, we showed that the local score approach is better than single SNP p-value-based tests for detecting weak (h²_ss = 5–10%) marker–phenotype associations in GWAS with high marker density. This approach is also competitive with regard to alternative methods, which aggregate p-values, typically the window-based methods. One feature is that the local score is flexible with regard to the changing LD patterns along the genome (see Fig. 1), contrary to fixed window lengths. In addition, we show that the local score efficiently controls for multiple false-positive peaks along chromosomes, provided that the value of its tuning parameter ξ is correctly set up (typically 2 or 3). Although the local score approach provides increased power relative to p-value-based tests or alternative local score approaches, the power itself remains low (up to 15%) to detect QTL with small heritability (i.e., <10%), but it can be applied to find statistical signals of association along a segment, whatever the haplotype structure surrounding the causal markers. Future works should investigate the way to increase power while maintaining efficient control of multiple false-positive peaks along the chromosomes.

By applying the method to the GWAS of QDR to multiple A. euteiches isolates in M. truncatula, we refined the position of a previously reported major locus (Bonhomme et al. 2014), which conferred resistance to two A. euteiches isolates from pea pathotype I. The major locus, underlying MYB/NB-ARC/tyrosine kinase candidate genes, would be involved in recognition or signaling pathway triggering resistance to A. euteiches. We also discovered a diversity of minor QTL—not detected using p-value-based tests—associated with resistance to A. euteiches isolates from pea pathotype I and III, and alfalfa race 1 and 2, some of which being putatively common among isolates according to their pathotypes and the legume hosts grown in their regions of origin. These results raise new issues on adaptation of A. euteiches populations to leguminous hosts and their genetic resistance factors.

More broadly, our study suggests that the local score is a promising approach to improve GWAS resolution and to uncover genetic variants with weak effects that contribute to the heritability of quantitative traits in model (e.g., human, A. thaliana, M. truncatula) as well as in non-model and domesticated species displaying variable levels of LD, and in which high marker density is available.

Data archiving

Supplementary File S1 contains RRI-adjusted mean for each accession, obtained following infection with A. euteiches isolates ATCC 201684, RB84, Ae109, MF-1, and NC-1, plus the PC1 values obtained following infection with isolate ATCC 201684 (Bonhomme et al. 2014). These values were used as phenotypic data in the GWAS of M. truncatula QDR to A. euteiches. The M. truncatula SNP dataset (hapmap format) used for GWAS can be found at http://www.medicagohapmap.org/downloads/mt40.

Compliance with ethical standards

Conflict of interest

The authors declare that they have no conflict of interest.

Supplementary information

The online version of this article (10.1038/s41437-019-0235-x) contains supplementary material, which is available to authorized users.