Abstract
Livestock production both contributes to and is affected by global climate change, and substantial modifications will be required to increase its climate resilience. In this context, reliance on dominant commercial livestock breeds, featuring small effective population sizes, makes current production strategies vulnerable if their production is restricted to environments, which may be too costly to support under future climate scenarios. The adaptability of animal populations to future environments will therefore become important. To help evaluate the role of genetics in climate adaptation, we compared selection strategies in dairy cattle using breeding simulations, where genomic selection was used on two negatively correlated traits for production (assumed to be moderately heritable) and adaptation (assumed to have low heritability). Compared with within-population breeding, genomic introgression produced a more positive genetic change for both production and adaptation traits. Genomic introgression from highly adapted but low production value populations into highly productive but low adaptation populations was most successful when the adaptation trait was given a lower selection weight than the production trait. Genomic introgression from highly productive population to highly adapted population was most successful when the adaptation trait was given a higher selection weight than the production trait. Both these genomic introgression schemes had the lowest risk of inbreeding. Our results suggest that both adaptation and production can potentially be improved simultaneously by genomic introgression.
Subject terms: Genetic variation, Animal breeding
Introduction
Adaptation of livestock to environmental challenges is becoming increasingly important in cost-effective animal production, especially as the climate becomes warmer, conditions for diseases are more favourable and production costs are set to rise (FAO 2015; Phocas et al. 2016). Heat stress is one of the most pressing factors affecting livestock production (Niyas et al. 2015) and has been shown to cause a decrease in milk production (5–15%) and lower conception rates (Berman 2011) in cattle. In addition, chronic stress triggers metabolic changes that result in stress-related disease and suppression of innate immunity (Das et al. 2016). However, selection can compensate for thermal stress with, e.g., the slick hair coat phenotype being implicated in the thermoregulation of tropically adapted cattle breeds (Pitt et al. 2019).
In practice, adaptation comprises many traits including those influencing fitness, such as longevity and disease resistance. These traits typically have low heritability and have declined when milk production has increased (e.g., Mirkena et al. 2010). Genetic correlations have been estimated to range from −0.11 to −0.84 between milk yield and functional longevity (e.g., Sasaki 2013; Pritchard et al. 2013a, 2013b). As adaptation to the local environment generally has a low heritability and possibly has antagonistic genetic correlations with milk production, long-term and efficient breeding strategies are required. In a rapidly changing environment, one approach is to introgress locally adaptive genes found in autochthonous breeds into major production breeds or vice versa (Nardone et al. 2006; Hoffmann 2010; Berman 2011; Hoffmann 2013). Thus, an efficient strategy may be needed to introduce adaptive traits quickly into commercial breeds or these breeds may need to be replaced with better adapted populations (Åby and Meuwissen 2014).
Introgression strategies commonly assume that one or more alleles in genes of interest or associated markers have been located in a donor population but are missing in the recipient population (e.g., Visscher et al. 1996). The aim is to select these favourable alleles from individuals within the donor population and use backcrossing and selection to introduce them into the recipient population, such that the favourable allele becomes fixed in the recipient population with as small as possible proportion of the rest of the donor’s genome included. However, the allele(s) of interest need to be known and to be of large effect, which is unfortunately seldom the case.
Knowing the location of important genes affecting traits of interest may be unnecessary for introgression to succeed. Ødegård et al. (2009a) simulated a fish breeding population where introgression was applied for a major quantitative trait locus (QTL) affecting disease resistance by backcrossing a production line (PL) with a resistant donor line. In their study, classical selection, i.e., without genomic information, was inefficient but genomic selection without specific knowledge of the target QTL was usually effective in preserving favourable alleles. Gaspa et al. (2015) investigated introgression of polledness in Holstein Friesian cattle by using simulations and concluded that a single gene strategy, applying genomic selection helped to speed up the process of introgression, while simultaneously increasing the genetic gain of other important traits and reducing inbreeding.
Adaptation and production can be both assumed to be polygenic traits. Ødegård et al. (2009b) simulated a fish breeding scheme where both production and disease resistance were polygenic with either low or high heritability. The authors concluded that in contrast to classical selection, genomic selection increased genetic gain in introgression backcrossing schemes, with the largest gain being for low heritability traits and on traits not recorded in selection candidates.
Åby and Meuwissen (2014) simulated two divergent populations according to production and fitness profiles of livestock with pure and crossbreeding in discrete generations. Both production and fitness were polygenic traits having moderate heritability but no genetic correlation. According to their results, selection using breeding values estimated by genomic best linear unbiased prediction (GBLUP) outperformed conventional BLUP in terms of genetic increase in production and fitness. In general, results from the simulation studies suggest that genomic selection can be effective in introgression of a lowly heritable trait to a target population with high production when traits (i.e., the introgressed trait and production) are polygenic and uncorrelated.
The aim of this study was to evaluate breeding strategies for the selection of rapid environmental (e.g., temperature) adaptation and production using dairy cattle as a model, by stochastic simulation. Breeding strategies include pure breeding and crossbreeding schemes involving a poorly adapted but high production population and a well-adapted population but of low milk yield. Adaptation and production traits were assumed to be negatively correlated and governed by many loci. We assumed production to have a higher heritability than adaptation and use bivariate genomic BLUP to estimate breeding values to improve both adaptation and production. A variety of breeding strategies using selection and introgression were considered. Introgression schemes included selection from well-adapted to poorly adapted population and vice versa when selection strategies applied different selection weights to the traits.
Material and methods
Simulation of breeding programmes followed two phases. First, QMSim (Sargolzaei and Schenkel 2009) was used to simulate an initial historic population (HP) and the subsequent selection of two divergent lines, a PL and an adaptation line (AL). Second, the final breeding animals from these populations were available as breeding animals for alternative selection schemes. Five replicates were simulated using QMSim, i.e., five sets of final breeding animals. Within a replicate, the studied breeding schemes selected the first breeding animals from the same population, although different schemes could use different sets of animals. Table 1 shows the simulation parameters used.
Table 1.
Parameters to simulation
| Parameter | Number |
|---|---|
| N breeding males | 200 |
| N breeding females | 2800 |
| N progeny per mating | 1 |
| N females per male | 14 |
| h2, adaptation | 0.1 |
| h2, production | 0.3 |
| Genetic correlation | −0.3 |
| N chromosomes | 30 |
| Chromosome length | 100 cM |
| N QTL simulated | 900 |
| N markers | 54,000 |
Simulation of two populations using QMSim
The HP in QMSim generates initial values of linkage disequilibrium, mutation and drift. The simulated genome was assumed to have 30 chromosomes of 100 cM each. To mimic a commercial Bovine 54 K SNP chip, the genome had 54,000 evenly distributed bi-allelic SNP (Single Nucleotide Polymorphic) markers with equal frequencies (0.5) for the two alleles in the base population (1800 bi-allelic SNP markers per chromosome). The HP consisted of 1000 individuals that were randomly mated for 95 generations (Fig. 1). During the following 5 generations, the population was expanded to 12,000 individuals, to allow selection of two populations.
Fig. 1.

QMSim simulation scheme
QMSim allows selection of one trait in the populations descending from the HP and here this trait was chosen to represent milk production in dairy cattle. The production trait was assumed to have 30 randomly positioned QTLs within each chromosome, i.e., in total 900 QTLs. The mutation rate used was 2.5 × 10−5 per generation (e.g., Solberg et al. 2008). The number of recombinations per Morgan was sampled from a Poisson distribution with a mean of one and the crossovers were randomly placed on the chromosomes. QTL effects of the production trait were introduced in the last generation of the HP for a trait with a heritability of 0.30, which is close to heritability of 305-day milk yield in dairy cattle. The allelic effects were sampled from a gamma distribution with a shape parameter of 0.4 as implemented in QMSim, so that the QTLs explained all genetic variation. QTL allelic effects were scaled in QMSim such that the phenotypic variance in the last HP generation was one.
Animals for two populations or breeds (AL and PL) were selected from the HP and subsequent breeding in QMSim was carried out separately within these breeds (Fig. 1). For both populations, 2800 females and 200 males were selected from the last generation of the HP to be used as breeding animals. The AL population animals were randomly selected but the PL population bulls (cows) had the highest pseudo breeding values (phenotypes) for production. No animal was used in both populations. Within both populations each sire was mated to 14 dams, with each mating producing one offspring (50:50 birth sex ratio). This procedure yielded a total of 2800 offspring (1400 males and 1400 females). In the following ten generations in QMSim, selection of breeding animals in the AL population was random but in the PL population animals with highest pseudo estimated breeding values (EBVs) were selected for breeding.
Selection within the AL and PL populations allowed for overlapping generations. The breeding animals in each generation were selected from the current breeding animals and from the youngest mature generation. From the 200 current breeding males, 60% (120 sires) were kept and 40% (80 sires) were replaced. In the AL population, the 80 new sires were randomly selected from the youngest mature generation and they replaced a randomly selected 80 older breeding males. In the PL population, the selection used the pseudo EBVs calculated by QMSim based on 20 daughter records. The breeding animals replaced had the lowest pseudo EBV among the current breeding males and the selected new males had the highest pseudo EBV in the youngest mature generation. Correspondingly, 20% (560 females) were replaced among the 2800 breeding females. In the AL population, the selection of replacements and replaced females were random. In the PL population, the selection used the pseudo EBVs based on the cow’s own information. Thus, the two populations had the same random drift base population from which the PL population was selected for higher production, but the AL population continued with random selection. The AL population depicts a random drift population where there has been no efficient selection for production or adaptation which reflects the prevailing situation for many small local breeds. The breeding scheme was continued for ten generations separately within AL and PL to produce two genetically different populations.
After this set of simulations, QTL effects for the adaptation trait were further simulated as a correlated trait to production. In the simulations, all the production QTL positions and effects were used to generate a correlated trait, which had a genetic correlation of −0.30 and heritability of 0.10 for all animals after the HP. Heritability of 0.10 is close to lowly heritable adaptation traits such as functional longevity that have moderately negative genetic correlation with milk production (Sasaki 2013). In practice, there can be adaptation traits having lower heritability and possibly weaker or stronger genetic correlation with production, but the use of different values would affect only absolute values, not the observed trends. The adaptation trait’s QTL effects were scaled the same way as in QMSim for production in order to get the wanted genetic correlation of −0.3 between production and adaptation. However, the scaling of adaptation QTLs used information from one generation later than for the production QTLs, because that was the first available generation with data from QMSim. Correlations of true breeding values (TBVs) between the traits indicated that the wanted correlation of −0.3 was realised. TBV of an animal was calculated using the true QTL values and the QTL genotypes of animal.
Breeding programme simulations
Different breeding schemes were simulated for an additional ten simulation years after the QMSim simulation. These schemes used the final breeding animals from the QMSim simulation (Fig. 1) but, due to restrictions in the QMSim program, subsequent breeding programme simulations were performed using a different set of computer programs. In every simulation scheme, a simulation year used current breeding animals to produce calves. A new set of breeding animals were selected from the current breeding animals and calves maturing from previous year according to their EBVs (Table 2), i.e., breeding animals could be from a number of birth years. The basic principles in the simulation followed those described for QMSim. However, animals were simulated to mature after 1 year instead of immediately being available as in QMSim.
Table 2.
Steps in one simulation year after the QMSim simulation
| Step | Operation |
|---|---|
| 1) | Search genotypes of breeding animals from all animals |
| 2) | Make random mating pairs to the breeding animals in (1) |
| 3) | Generate random recombination positions for the mating pairs in (2) |
| 4) | Offspring genotypes by mating pairs in (2) using recombination positions in (3) |
| 5) | Calculate true breeding values to the new genotypes in (4) |
| 6) | Generate phenotypes to the maturing cows |
| 7) | Generate pseudo phenotypes to the maturing bulls |
| 8) | Extract all phenotype data for genetic evaluation by SNP-BLUP |
| 9) | Extract genotypes for animals in (8) |
| 10) | Calculate estimated breeding values by SNP-BLUP using data from (8) and (9) |
| 11) | Calculate index (A1P1, A2P1 or A1P2) using estimated breeding values |
| 12) | Select new breeding animals from the current breeding and the mature animals |
Each step was a program in a script. In steps 1–5, current breeding animals are mated to produce calves. In steps 6–12, previous year calves mature and are included in genetic evaluation. These mature animals and current breeding animals are selection candidates for a new set of breeding animals.
Selection was based on EBVs that used genomic information and observations from the final breeding animals in QMSim and subsequent years. EBVs were calculated using a two-trait SNP-BLUP where the variance components were equal to the simulation parameters. This is equivalent to using GBLUP (Strandén and Garrick 2009). A variety of breeding strategies were considered: (1) selection within a population; (2) selection within a new synthetic breed made from the AL and PL populations; and (3) selection of females within a population but allowing selection of males from another population, i.e., genomic introgression by crossbreeding.
For the within-population selection (strategies 1 and 2), selection of breeding animals was from the current breeding animals and mature calves. There were three types of breeding schemes denoted A, P and AP. Scheme A used the current AL breeding animals, scheme P used the PL individuals and scheme AP used the combined AL and PL individuals. In AP, the first-generation males were selected according to the selection index from the F1 individuals, which were the offspring of male AL to female PL or male PL to female AL matings. As the number of female F1 individuals was only 2800, another 2800 cows were selected from the current AL and PL population cows. Thus, the A and P schemes continued to use 200 males and 2800 females but the AP scheme doubled the breeding population to 400 males and 5600 females keeping the same selection intensity.
Genomic introgression (strategy 3) was used to introduce favourable alleles of a trait from a donor population to a target population (Fig. 2). A pure breed donor population was maintained along with the target population. In introgression from the AL to PL population (AiP), a pure AL population was maintained to allow selection of AL sires. Half of the selected breeding sires used in the target population were from the AL population and the other half were from the current PL population. Thus, after 4 years, some of the PL population individuals were backcrossed. It is noteworthy that the candidates for the next-generation PL sires were the current PL sires and the mature PL male calves, which (in both cases) were not necessarily pure PL breed animals either. The same logic was followed in the introgression breeding scheme from the PL to AL population (PiA). It is noteworthy that in both introgression schemes, selection in the pure line used the same selection index weights as in the target population. However, in practice, the AL population is expected to continue its own selection scheme in AiP. Thus, a genomic introgression scheme named rAiP was simulated where random selection was continued in the AL population.
Fig. 2.

Repeated introgression backcrossing scheme of the production line (PL) with the adaptation line (AL) for the first 3 years. For simplicity of presentation, calves mature here after birth but in simulation after 1 year
Simulation and the statistics calculated
Each of the five QMSim simulations gave a set of final AL and PL breeding animals (Fig. 1). The final breeding animals were available for the breeding schemes described. Unlike in the QMSim simulation schemes, the subsequent selection of animals in these breeding schemes was based on an index of EBVs by SNP-BLUP. Three alternative indices were used where the standardised EBVs of the adaptation and production traits were weighted differently. The EBVs were standardised trait wise by dividing by trait genetic SDs. The adaptation (A2P1) selection index had a weight 2 for adaptation and 1 for production EBVs. The equal weight (A1P1) selection index had equal weights for both of the EBVs. The production (A1P2) selection index weighted 1 for adaptation and 2 for production EBVs.
Two statistics were computed for both traits using the TBVs of the progeny to breeding animals after the QMSim simulation: adjusted genetic level (G) and genetic change during the last nine simulation years (ΔG). Both statistics are reported in genetic SD of trait. If selection is random or very mild, genetic change ΔG stays at zero. When two traits are studied, selection of one of the traits will change the other, as well due to correlated response. Genetic change (ΔG) in the target population was computed as the difference in the mean genetic level over replicates between the final and the first year of the breeding scheme simulation, i.e., genetic change during the last 9 years. Adjusted genetic level (G) was computed as the average difference over replicates in genetic level between the last simulation year in the target population and the control level, which was the last generation AL individuals of the QMSim simulation. Genetic level in a simulation year was mean of TBVs of animals born that year in the target population.
The adjusted genetic level (G) allowed comparison of the absolute genetic level, which illustrates changes in production and adaptation levels compared with the control level. After the QMSim simulation, the AL and PL lines were on different genetic levels. Consequently, comparisons according to the genetic change would provide a false impression on the short-term genetic consequences of selection. As the control level is the same for all schemes within a replicate, differences in absolute genetic level between the replicates could be corrected. The control level calculated from the last generation AL individuals of QMSim is from the random selection scheme and is close to the genetic level after HP. Thus, e.g., in AiP, the genetic change ΔG has been calculated using the target PL population individuals only, but calculating the adjusted genetic level G we used the genetic level values of the last generation PL population and the last QMSim generation AL population. It is noteworthy that the difference in G and ΔG will not be the same in a single population (e.g., P) and introgression schemes (e.g., AiP), because the starting level in ΔG is based on the genetic level of the progeny to the selected individuals. In a single population, the parents of progeny come from one of the pure lines but in the introgression schemes the parents come from both of the lines.
The rate of inbreeding per generation (ΔF) describes the risk of a breeding scheme. Inbreeding rate was estimated using pedigree information following the method of Gutierrez et al. (2009). The method used pedigree inbreeding coefficients to calculate individual rates of inbreeding, which are averaged to estimate the population inbreeding rate.
Existing and new programs were combined in several Linux shell scripts. The first phase of the script was based on the QMSim software, which generated the two breeding lines to be used in the subsequent breeding scheme simulation. Then, each breeding scheme used a script that was a set of programs written in Perl, R (all steps needing random numbers) or Fortran. Existing programs included RelaX2 (Strandén and Vuori 2006) for rate of inbreeding calculation and MiX99 (Strandén and Lidauer 1999) for breeding value estimation by two-trait SNP-BLUP.
Results
Genetic level in the final year of QMSim quantifies initial genetic level in the AL and PL populations before selection using the studied selection indices in the contrasted breeding schemes. In the final year of QMSim, the average differences across replicates in adjusted genetic levels of adaptation and production between the AL and PL populations were 1.10 and −2.99 genetic SDs of the traits, respectively. The positive and negative differences for adaptation and production reflect genetic differences in the populations; genetically, the AL population had higher adaptation but poorer production than in the PL population. The genetic level of the AL population can be considered a control level. Thus, adjusted genetic level values below 0 means that the trait has not reached the same level as in the AL population at the time the breeding scheme was started.
Genetic change and level were positive and high for adaptation in all schemes when the selection index A2P1 was used (Table 3). The genomic introgression and synthetic breeding schemes were able to achieve a higher genetic level for adaptation than the within-line selection schemes. Genetic progress for adaptation was highest in the introgression scheme from AL to PL (AiP). However, as genetic change for production trait was negative in AiP, this scheme may be unrealistic in practice. In contrast, introgression from PL to AL (PiA) gave high genetic progress for both production and adaptation. Furthermore, the adjusted genetic level achieved for production was high and was moderately high for adaptation. The highest genetic increase in adaptation in the non-introgression schemes was achieved by the combined AP scheme, with genetic progress being higher than in the rAiP and PiA schemes. Similarly, genetic change and adjusted genetic level were good in production in the AP scheme. The other non-introgression schemes showed low genetic increases in production. However, the P scheme, while giving the highest adjusted genetic level for production, gave the lowest for adaptation.
Table 3.
Genetic change in last 9 years (ΔG) and genetic level in the last year (G)
| Production | Adaptation | |||||
|---|---|---|---|---|---|---|
| Schemea | Index | ΔG (SE) | G (SE) | ΔG (SE) | G (SE) | ΔF |
| A | A2P1 | 0.45 (0.05) | 0.45 (0.05) | 1.22 (0.04) | 1.21 (0.03) | 0.12 (0.004) |
| P | A2P1 | 0.25 (0.02) | 3.86 (0.02) | 1.33 (0.06) | 0.22 (0.08) | 0.17 (0.011) |
| AP | A2P1 | 1.08 (0.10) | 2.89 (0.10) | 2.22 (0.03) | 1.66 (0.01) | 0.07 (0.004) |
| rAiP | A2P1 | −0.94 (0.06) | 1.56 (0.05) | 1.08 (0.05) | 0.58 (0.03) | 0.03 (0.002) |
| AiP | A2P1 | −0.96 (0.09) | 1.52 (0.07) | 2.37 (0.04) | 1.86 (0.03) | 0.05 (0.004) |
| PiA | A2P1 | 1.76 (0.08) | 3.00 (0.09) | 1.34 (0.05) | 1.24 (0.06) | 0.04 (0.001) |
| A | A1P1 | 1.87 (0.06) | 1.87 (0.06) | 1.38 (0.05) | 1.38 (0.05) | 0.13 (0.006) |
| P | A1P1 | 1.81 (0.07) | 5.42 (0.07) | 1.37 (0.05) | 0.26 (0.06) | 0.20 (0.007) |
| AP | A1P1 | 2.82 (0.03) | 4.63 (0.04) | 0.92 (0.05) | 0.36 (0.07) | 0.09 (0.007) |
| rAiP | A1P1 | −0.20 (0.04) | 2.39 (0.01) | 0.56 (0.03) | −0.01 (0.06) | 0.04 (0.001) |
| AiP | A1P1 | 0.39 (0.06) | 2.98 (0.07) | 1.46 (0.06) | 0.88 (0.07) | 0.05 (0.003) |
| PiA | A1P1 | 2.93 (0.09) | 4.27 (0.10) | 0.45 (0.10) | 0.28 (0.12) | 0.04 (0.003) |
| A | A1P2 | 1.72 (0.08) | 1.71 (0.07) | 0.13 (0.04) | 0.14 (0.04) | 0.11 (0.009) |
| P | A1P2 | 1.63 (0.06) | 5.24 (0.07) | 0.16 (0.04) | −0.95 (0.10) | 0.19 (0.007) |
| AP | A1P2 | 3.67 (0.04) | 5.48 (0.05) | −0.13 (0.07) | −0.69 (0.10) | 0.10 (0.005) |
| rAiP | A1P2 | 0.09 (0.05) | 2.76 (0.03) | 0.21 (0.03) | −0.47 (0.06) | 0.04 (0.001) |
| AiP | A1P2 | 1.12 (0.04) | 3.79 (0.04) | 0.50 (0.03) | −0.18 (0.07) | 0.05 (0.003) |
| PiA | A1P2 | 3.50 (0.05) | 4.92 (0.07) | −0.28 (0.09) | −0.55 (0.12) | 0.04 (0.003) |
Genetic change in last 9 years (ΔG) and genetic level in the last year (G) within scheme measured in genetic SD units of the trait (production or adaptation), and rate of inbreeding per generation (ΔF) in percentages with standard error (SE) over five replicates. The selection index weighted adaptation and production equally in A1P1, by 2:1 ratio in A2P1, respectively, and by 1:2 ratio in A1P2, respectively
aThe A, P and AP schemes used only adaptation line (AL), production line (PL), or combined AL and PL synthetic line individuals, respectively. The AiP scheme used introgression from AL to PL, and the PiA scheme used introgression from PL to AL. In the rAiP scheme, there was no selection in the AL donor line used in introgression
When production and adaptation were weighted equally in the selection index, all schemes were able to make positive genetic change for both production and adaptation (Table 3), except rAiP, which showed a −0.20 change in production. Thus, in contrast to the A2P1 index selection, introgression from AL to PL (AiP) gave positive genetic change in both of the studied traits. The final genetic level of adaptation was not as high as with A2P1 but the genetic level for production was quite high. The positive genetic progress of adaptation in the AiP scheme was due to applying the same selection index in the donor AL population scheme. When the selection was random in the donor population (rAiP), genetic progress in production was negative. Introgression from PL to AL (PiA) gave lower genetic progress in adaptation than in AiP, but the genetic level reached was still positive. However, both the genetic progress and level for production were very high. Thus, as the relative weight of adaptation decreased in the selection index (from A2P1 to A1P1), genetic change and the level of adaptation decreased. In this context, genomic introgression did not prove to be the best strategy. Instead, continuing selection within the PL population (P) gave a high genetic increase in adaptation and a high genetic level in production. Likewise, the joint population AP scheme was competitive.
When the selection index A1P2 was used, genetic change and level in adaptation tended to be very low or even negative. Scheme P achieved minor improvement in adaptation, but the final level of adaptation was very low. Scheme A was able to maintain reasonable increases in adaptation, although at a low level. The introgression scheme from AL to PL (AiP) gave the highest genetic increase in adaptation with the final genetic level value of adaptation being almost 0. In AiP, the genetic progress in production was lower than in the non-introgression schemes. However, the final genetic level of production was still high due to the high genetic level of production at the beginning of the breeding scheme. Thus, when the index weight for production increased, scheme AiP became more favourable than PiA, because genetic change in both production and adaptation was positive.
Performance of the breeding schemes under different selection indices is illustrated in Figs. 3–6. The P and PiA introgression schemes had the highest genetic change in production (Fig. 3). The PiA scheme seemed superior when adaptation was given high weight. The AiP introgression scheme had the highest genetic change in adaptation, although different non-introgression schemes were often close (Fig. 4). The synthetic AP scheme reached highest genetic level in production but the single population P and the introgression PiA schemes were competitive when production was given higher weight than adaptation (Fig. 5). The A and AiP schemes achieved the highest genetic level in adaptation (Fig. 6).
Fig. 3.
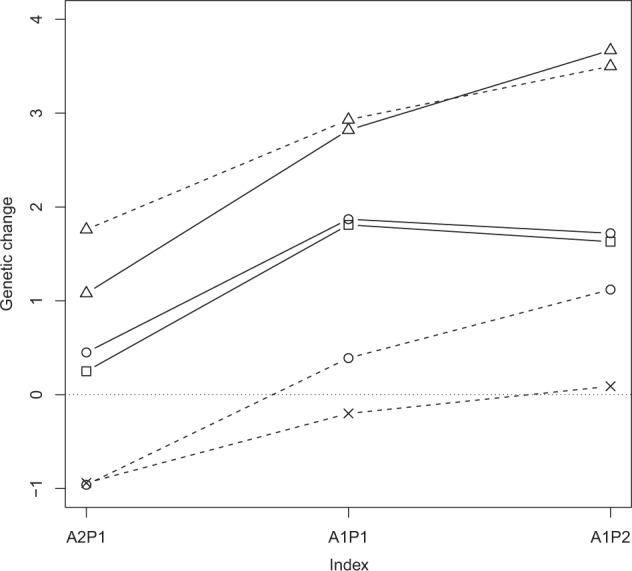
Genetic change of production in genetic standard deviation by selection index. The selection index weighted adaptation and production equally in A1P1, by 2:1 ratio in A2P1, respectively, and by 1:2 ratio in A1P2, respectively. The non-introgression schemes A (circle), AP (square) and P (triangle) have solid lines, and the introgression schemes rAiP (cross), AiP (circle) and PiA (triangle) have dashed lines
Fig. 6.
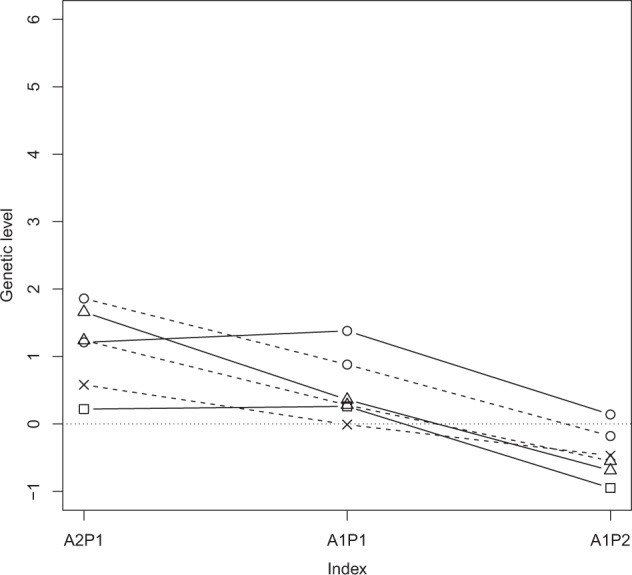
Genetic level of adaptation in genetic SD by selection index. The selection index weighted adaptation and production equally in A1P1, by 2:1 ratio in A2P1, respectively, and by 1:2 ratio in A1P2, respectively. The non-introgression schemes A (circle), AP (square) and P (triangle) have solid lines and the introgression schemes rAiP (cross), AiP (circle) and PiA (triangle) have dashed lines
Fig. 4.

Genetic change of adaptation in genetic SD by selection index. The selection index weighted adaptation and production equally in A1P1, by 2:1 ratio in A2P1, respectively, and by 1:2 ratio in A1P2, respectively. The non-introgression schemes A (circle), AP (square) and P (triangle) have solid lines and the introgression schemes rAiP (cross), AiP (circle) and PiA (triangle) have dashed lines
Fig. 5.

Genetic level of production in genetic standard deviation by selection index. The selection index weighted adaptation and production equally in A1P1, by 2:1 ratio in A2P1, respectively, and by 1:2 ratio in A1P2, respectively. The non-introgression schemes A (circle), AP (square) and P (triangle) have solid lines and the introgression schemes rAiP (cross), AiP (circle) and PiA (triangle) have dashed lines
The introgression schemes from the AL donor population (AiP) used AL sires. The proportion of genes originating from the AL population depended on the selection index (Fig. 7). The more adaptation was weighted in the selection index, the higher the influence of the AL population proved to be. The continued use of random selection in the AL population decreased the gene proportion of the original AL population considerably. In the last simulation year, the proportion of the AL population genes in AiP (rAiP) was 58% (39%) using A2P1, 44% (24%) using A1P1 and 34% (19%) using A1P2. These numbers were similarly ranked in AiP and rAiP as the genetic level G for adaptation in Table 3. When introgression was from the PL donor population (PiA), the proportion of AL genes decreased from the original 100% rapidly. In the final simulation year, the proportion of AL genes in PiA was 36% using A2P1, 29% using A1P1 and 27% using A1P2. For A2P1 and A1P1, these numbers were lower than those in AiP.
Fig. 7.

Average proportion of AL population genes in cows by simulation year in different introgression schemes from AL to PL (AiP). In the target population selection index, adaptation and production were weighted by ratio 2:1 (black), 1:1 (blue) and 1:2 (red). Selection index in the donor population (AL) was the same as in the target population (solid line) or random (dashed line)
The rate of inbreeding per generation ΔF was highest in the within-population schemes A and P (Table 3). The AP scheme showed a lower ΔF and the genomic introgression schemes had an even lower ΔF. These results can be expected, because the genomic introgression schemes introduced animals with a lower than average relatedness to the target population and the combined breeding population AP had double the population size in comparison with the within-line selection schemes A and P. Differences in ΔF within schemes using different selection indices were small.
Discussion
It should be anticipated that selection for a trait with high heritability will produce a higher genetic change than selection for a trait with low heritability when all the other conditions are the same. Thus, it should be easier to change a highly heritable trait such as production in this study than a less heritable trait such as adaptation. Consequently, PiA introgression should be preferred over AiP, because it should be easier to breed high production into locally adapted animals than the other way around. Indeed, we found that PiA crossbreeding was more successful than AiP, but only when adaptation had a high weight in the selection index. In contrast, when production had a high weight, AiP exceeded PiA, because adaptation increased in the former but decreased in the latter. This result is logical, because when production is given a high weight in the selection index, PiA is efficient as adaptation is of less importance. However, when production has a high weight, AiP will lead to selection of favourable adaptive genes from the AL line, while maintaining a high genetic level of production.
In our study, the synthetic breed scheme AP combined the two divergent lines into one common population. This was the most successful non-introgression strategy in terms of inbreeding rate and genetic change in production. Overall, genetic diversity decreased most when only one of the original populations was maintained. When the selection index weighted the traits equally, the AP scheme reached similar genetic change in production and higher genetic change in adaptation than the best introgression strategy (PiA). In some cases, the AP scheme may be the only way to conserve genes from both of the populations when either or both of the populations have too low number of animals to make a viable population. As the potentially positive effects of heterosis were not considered in our study, the AP scheme may show even more positive results. However, heterosis effects would be expected to be lost rapidly in the AP scheme. In contrast, heterosis would contribute for a longer duration in the crossbreeding scheme, where each new generation would results in some heterosis, because a separate donor line is maintained.
The rate of inbreeding ΔF depends on the effective population size. The synthetic breed scheme AP increased population size by combining two breeds, leading to a lower rate of inbreeding than in the within breed schemes, which is expected. Similarly, genomic introgression schemes increase effective population size by incorporating genetic diversity from another population. However, in the simulated introgression schemes, the donor population remained separate during the simulation and allowed continuous crossbreeding and thus featured a much lower rate of inbreeding than in the AP scheme.
Repeated crossbreeding or backcrossing between a locally adapted breed and a more productive breed has been used to breed locally adapted high milk yield cows. For example, in Yakutia, north-eastern Siberia, the locally adapted Yakutian cattle, which tolerate Siberian harsh cold environment, has been crossed with Simmental and Russian Kholmgor breeds to establish the Siberian Simmental and Siberian Kholmogor cattle populations, respectively (Li et al. 2005). These crossbreds have been backcrossed with the native Yakutian cattle to further develop two hybrid cattle populations. Breeding selection can be used for adaptation to local warm climate (e.g., Berman 2011). In Ethiopia, the aim of crossbreeding native breeds to Holstein is to produce cows with at least 25% native and at most 75% Holstein breed proportions such that production is increased and adaptation is maintained (Negussie et al. 1999). Simulation results in our study support genomic introgression schemes from high production to adaptation (PiA) breeds to be reasonable when local adaptation is of high importance. However, the extent of crossbreeding varies in Africa even to such an extent that there is a risk of introgression into indigenous populations and subsequent erosion of local genetic resources (Leroy et al. 2016). These risks are supported by our simulation results, where proportion of the AL population genes decreased more rapidly in PiA than they increased in AiP, particularly when production was given a high weight.
In practice, any given farm is likely to have either high production or high adaptation animals. This influences the type of introgression preferred and possible. When a farm has high adaptation-level animals and increasing production is desired, then the PiA scheme could be used. However, although increasing production and lowering adaptation may provide short-term gains, it incurs risks that will present themselves later. This is another reason to proceed cautiously using the PiA scheme. The use of AiP introgression is likely to show lower production but has the long-term benefit of adaptation. Climate change has direct and indirect effects on dairy cattle (Nardone et al. 2006; Kantanen et al. 2015). Indirect effects may be apparent earlier via extreme temperature or rainfall affecting feed production, which may require population replacement. The choice may then favour robust cattle that do not require high cost maintenance. The AL population had an adaptation level of zero at the beginning of the breeding scheme simulations. All schemes that showed a positive genetic level in adaptation in the last simulation year achieved the same level as the AL population at the beginning of the simulation. When adaptation was given a high weight, the genetic levels in adaptation were always positive. Even the PL population achieved high adaptation and was able to maintain high production during the simulation time of 10 years.
Our simulation assumed a 2-year generation interval and 10 years of selection. In practice, the absolute genetic levels and genetic change are unlikely to be this favourable over such a short period. First, we assumed that all animals were genotyped and genomic evaluation is in use. High but less efficient genetic change is likely to be achieved using single-step genomic evaluation (Aguilar et al. 2010; Christensen and Lund 2010) when only some of the animals, e.g., all bulls, are genotyped. However, a basic assumption for the results to be applicable in practice is that an efficient breeding scheme is in place. Second, both traits in the simulation were assumed to be observed after the animal become mature, i.e., at the age of 2 years. In practice, first lactation milk yield is at the earliest available at the age of 3, whereas adaptation data are available much later, depending on the defined trait (e.g., longevity). When genomic evaluation is used, it is important that the genotyped reference animals and their progeny have a sufficient number of observations. Thus, the more animals that have been genotyped, the higher the accuracy of genetic evaluation will be, and individual record information is less important. Third, the importance of genomic evaluation extends to the rate of inbreeding as well. When breeding value estimation is based on genomic information instead of pedigree information, using an animal model, selecting animals from different families becomes more likely, which translates to a lower rate of inbreeding. Fourth, the use of young 2-year-old animals to selection allows short generation interval and is feasible due to the use of genomic evaluation. However, calving at the age of 24 months may be too early. If a year in the simulation was extended to be 15 months, then the first calving would be at 30 months. This would extend the simulation by 25% from 10 to about 13 years. Finally, it was assumed that both of the populations had an equally good recording system, and that there were always breeding animals available. In practice, conserved local breeds may have too low a number of bulls with breeding values as accurate as in the major breed for an introgression scheme to succeed as well as in the simulations.
Our study design is quite unique and genomic introgression simulations including two selected traits have not been presented for dairy cattle. However, our results are similar to those in Ødegård et al. (2009b) where pure breed, synthetic breed and genomic introgression were simulated for fish. In particular, genetic increase in the simulated 5 years in production was higher (6.81 vs. 4.02) in the backcrossed scheme they used, similar to our PiA scheme (3.50 vs. 1.63) than in the pure breed scheme, but the opposite was the case for adaptation. As each mating in fish produced 20 offspring, selection intensity was higher and the absolute values for genetic change were higher than achieved in our dairy cattle simulation.
All schemes featured a fairly low rate of inbreeding (Table 3). The major reason for this result was that even for the within-population schemes, the number of selected males was quite high and selection of females had low intensity. However, the low rate of inbreeding also indicates moderate accuracy of the EBVs. Accuracy of genomic evaluation by SNP-BLUP depends on the number of genotyped reference animals with records. The simulated population had many reference animals but only breeding bulls had a reasonable amount of information (20 daughter records). In practice, the reference animals are likely to have more accurate genomic evaluation, which may give larger genetic differences between the schemes and higher rates of inbreeding.
We assumed a genetic correlation of −0.3 between adaptation and production. In addition, all loci affecting these traits were assumed to be shared. In practice, this would not be the case. However, this allowed a more realistic simulation than, e.g., in Ødegård et al. (2009b) where no pleiotropic effects for QTL were assumed. The use of non-zero genetic correlations made selection to increase both the traits simultaneously more challenging, which also contributed to the lower genetic responses we found than were detected in the previous study of Ødegård et al. (2009b).
Changing genetic correlations and heritabilities will affect the absolute values achieved in our study. In particular, if heritability for production traits is higher and for adaptation traits is lower, increasing the genetic level of adaptation becomes more difficult, especially if the genetic correlation is more negative. However, the observed trends between the schemes under different selection index weights and conclusions should remain. For example, our results confirm the value of conserving genetic resources for the benefit of introgressing their favourable characteristics into commercial breeding programmes when the production trait has a high value.
Our simulations show that accelerated progress was achieved most efficiently by genomic introgression from the locally adapted into the production populations when (as is likely to be the case) production had a high weight in the selection index. This approach led to the selection of favourable locally adapted genes, while still maintaining a high level of production. Practical application of this scheme, however, should proceed in caution, especially focusing on locally adapted genes, ensuring that they are preserved in a separate local population. Knowing some or all of the favourable alleles of genes affecting the selected traits and using this information in the genetic evaluation can increase selection accuracy but further research is needed to quantify the change in genetic level and the likely increase in rate of inbreeding.
Supplementary information
Acknowledgements
This study is part of ClimGen (“Climate Genomics for Farm Animal Adaptation”) project funded by FACCE-JPI ERA-NET Plus on Climate Smart Agriculture.
Compliance with ethical standards
Conflict of interest
The authors declare that they have no conflict of interest.
Footnotes
The members of Climate Genomics Consortium are listed in Appendix.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
The online version of this article (10.1038/s41437-019-0207-1) contains supplementary material, which is available to authorised users.
References
- Åby BA, Meuwissen THE (2014) Selection strategies utilizing genetic resources to adapt livestock to climate change. In: 10th World Congress on Genetics Applied to Livestock Production, Vancouver, Canada, 17–22 August 2014.
- Aguilar I, Misztal I, Johnson DL, Legarra A, Tsuruta S, Lawlor TJ. Hot topic: a unified approach to utilize phenotypic, full pedigree, and genomic information for genetic evaluation of Holstein final score. J Dairy Sci. 2010;93:743–752. doi: 10.3168/jds.2009-2730. [DOI] [PubMed] [Google Scholar]
- Berman A. Invited review: are adaptations present to support dairy cattle productivity in warm climates? J Dairy Sci. 2011;94:2147–2158. doi: 10.3168/jds.2010-3962. [DOI] [PubMed] [Google Scholar]
- Christensen O, Lund MS. Genomic prediction when some animals are not genotyped. Genet Sel Evol. 2010;42:2. doi: 10.1186/1297-9686-42-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das R, Sailo L, Verma N, Bharti P, Saikai J, Imtiwati, Kumar R. Impact of heat stress on health and performance of dairy animals: a review. Vet World. 2016;9:260–268. doi: 10.14202/vetworld.2016.260-268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Food and Agriculture Organisation of the United Nations (2015). Coping with climate change - the roles of genetic resources for food and agriculture. Rome.
- Gutierrez JP, Cervantes I, Goyache F. Improving the estimation of realized effective population sizes in farm animals. J Anim Breed Genet. 2009;126:327–332. doi: 10.1111/j.1439-0388.2009.00810.x. [DOI] [PubMed] [Google Scholar]
- Gaspa G, Veerkamp R, Calus MPL, Windig JJ. Assessment of genomic selection for introgression of polledness into Holstein Friesian cattle by simulation. Livest Sci. 2015;179:86–95. doi: 10.1016/j.livsci.2015.05.020. [DOI] [Google Scholar]
- Hoffmann I. Climate change and the characterization, breeding and conservation of animal genetic resources. Anim Genet. 2010;41(Suppl. 1):32–46. doi: 10.1111/j.1365-2052.2010.02043.x. [DOI] [PubMed] [Google Scholar]
- Hoffmann I. Adaptation to climate change – exploring the potential of locally adapted breeds. Animal. 2013;7:346–362. doi: 10.1017/S1751731113000815. [DOI] [PubMed] [Google Scholar]
- Kantanen J, Løvendahl P, Strandberg E, Eythorsdottir E, Li MH, Kettunen-Præbel A, Berg P, Meuwissen T. Utilization of farm animal genetic resources in a changing agro-ecological environment in the Nordic countries. Front Genet. 2015;6:52. doi: 10.3389/fgene.2015.00052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leroy G, Baumung R, Boettcher P, Scherf B, Hoffman I. Review: sustainability of crossbreeding in developing countries; definitely not like crossing a meadow. Animal. 2016;10:262–273. doi: 10.1017/S175173111500213X. [DOI] [PubMed] [Google Scholar]
- Li MH, Nogovitsina E, Ivanova Z, Erhardt G, Vilkki J, Popv R, Ammosov I, Kiselyova T, Kantanen J. Genetic contribution of indigenous Yakutian cattle to two hybrid populations, revealed by microsatellite variation. Asian Aust J Anim Sci. 2005;18:613–619. doi: 10.5713/ajas.2005.613. [DOI] [Google Scholar]
- Mirkena T, Duguma G, Haile A, Tibbo M, Okeyo AM, Wurzinger M, Sölkner J. Genetics of adaptation in domestic fam animals: a review. Livest Sci. 2010;132:1–12. doi: 10.1016/j.livsci.2010.05.003. [DOI] [Google Scholar]
- Nardone A, Ronchi B, Lacetera N, Bernabucci U. Climatic effects on productive traits in livestock. Vet Res Commun. 2006;30(Suppl. 1):75–81. doi: 10.1007/s11259-006-0016-x. [DOI] [Google Scholar]
- Negussie E, Brännäng E, Rottmann OJ. Reproductive performance and herd life of dairy cattle at Asela livestock farm, Arsi, Ethiopia. II: crossbreds with 50, 75 and 87.5% European inheritance. J Anim Breed Genet. 1999;116:225–234. doi: 10.1046/j.1439-0388.1999.00191.x. [DOI] [Google Scholar]
- Niyas PA, Chaidanya K, Shaji S, Sejian V, Bhatta R, Bagtah M, Roa GSLHVP, Kurien EK, Girish V. Apadtatoin of livestock to environmental challenges. J Vet Sci Med Diag. 2015;4:3. [Google Scholar]
- Ødegård J, Sonesson AK, Yazdi MH, Meuwissen THE. Introgression of a major QTL from an inferior into a superior population using genomic selection. Genet Sel Evol. 2009;41:38. doi: 10.1186/1297-9686-41-38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ødegård J, Yazdi MH, Sonesson AK, Meuwissen THE. Incorporating desirable genetic characteristics from an inferior into a superior population using genomic selection. Genetics. 2009;181:737–745. doi: 10.1534/genetics.108.098160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phocas F, Belloc C, Bidanel J, Delaby L, Dourmad JY, Dumont B, Ezanno P, Fortun-Lamothe L, Foucras G, Frappat B, González-García E, Hazard D, Larzul C, Lubac S, Mignon-Grasteau S, Moreno CR, Tixier-Boichard M, Brochard M. Review: towards the agroecological management of ruminants, pigs and poultry through the development of sustainable breeding programmes: I-selection goals and criteria. Animal. 2016;10:1749–1759. doi: 10.1017/S1751731116000926. [DOI] [PubMed] [Google Scholar]
- Pitt D, Bruford MW, Barbato M, Orozco-terWengel P, Martínez R, Sevane N. Demography and rapid local adaptation shape Creole cattle genome diversity in the tropics. Evol Apps. 2019;12:105–122. doi: 10.1111/eva.12641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard T, Coffey M, Mrode R, Wall E. Genetic parameters for production, health, fertility and longevity traits in dairy cows. Animal. 2013;7:34–46. doi: 10.1017/S1751731112001401. [DOI] [PubMed] [Google Scholar]
- Pritchard T, Coffey M, Mrode R, Wall E. Understanding the genetics of survival in dairy cows. J Dairy Sci. 2013;96:3296–3309. doi: 10.3168/jds.2012-6219. [DOI] [PubMed] [Google Scholar]
- Sargolzaei M, Schenkel FS. QMSim: a large-scale genome simulator for livestock. Bioinformatics. 2009;25:680–681. doi: 10.1093/bioinformatics/btp045. [DOI] [PubMed] [Google Scholar]
- Sasaki O. Estimation of genetic parameters for longevity traits in dairy cattle: a review with focus on the characteristics of analytical models. Anim Sci J. 2013;84:449–460. doi: 10.1111/asj.12066. [DOI] [PubMed] [Google Scholar]
- Solberg TR, Sonesson AK, Woolliams JA, Meuwissen THE. Genomic selection using different marker types and densities. J Anim Sci. 2008;86:2447–2454. doi: 10.2527/jas.2007-0010. [DOI] [PubMed] [Google Scholar]
- Strandén I, Lidauer M. Solving large mixed models using preconditioned conjugate gradient iteration. J Dairy Sci. 1999;82:2779–2787. doi: 10.3168/jds.S0022-0302(99)75535-9. [DOI] [PubMed] [Google Scholar]
- Strandén I, Vuori K (2006). RelaX2: pedigree analysis program. In: 8th World Congress on Genetics Applied to Livestock Production, Belo Horizonte, MG, Brazil, Volume 27.30, 13–18 August 2006.
- Strandén I, Garrick DJ. Technical note: derivation of equivalent computing algorithms for genomic predictions and reliabilities of animal merit. J Dairy Sci. 2009;92:2971–2975. doi: 10.3168/jds.2008-1929. [DOI] [PubMed] [Google Scholar]
- Visscher PM, Haley CS, Thompson R. Marker-assisted introgression in backcross breeding programs. Genetics. 1996;144:1923–1932. doi: 10.1093/genetics/144.4.1923. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


