Understanding Missing Entropy in Coarse-Grained sSystems: Addressing Issues of Representability and Transferability

Abstract

Coarse-grained (CG) models facilitate efficient simulation of complex systems by integrating out the atomic, or fine-grained (FG), degrees of freedom. Systematically-derived CG models from FG simulations often attempt to approximate the CG potential of mean force (PMF), an inherently multidimensional and many-body quantity, using additive pairwise contributions. However, they currently lack fundamental principles that enable their extensible use across different thermodynamic state points, i.e., transferability. In this work, we investigate the explicit energy-entropy decomposition of the CG PMF as a means to construct transferable CG models. In particular, despite its high-dimensional nature, we find for liquid systems that the entropic component to the CG PMF can similarly be represented using additive pairwise contributions, which we show is highly coupled to the CG configurational entropy. This approach formally connects the missing entropy that is lost due to the CG representation, i.e., translational, rotational and vibrational modes associated with the missing degrees of freedom, to the CG entropy. By design, the present framework imparts transferable CG interactions across different temperatures due to the explicit definition of an additive entropic contribution. Furthermore, we demonstrate that transferability across composition state points, such as between bulk liquids and their mixtures, is also achieved by designing combining rules to approximate cross-interactions from bulk CG PMFs. Using the predicted CG model for liquid mixtures, structural correlations of the fitted CG model were found to corroborate a high-fidelity combining rule. Our findings elucidate the physical nature and compact representation of CG entropy and suggest a new approach for overcoming the transferability problem. We expect this approach will further extend the current view of CG modeling into predictive multiscale modeling.

Graphical Abstract:

Computer simulations have enabled the scientific community to understand chemical and physical phenomena at the molecular level in recent years.^1–7 Coarse-grained (CG) models have further extended the spatiotemporal scales of simulations by removing or “integrating out” unnecessary degrees of freedom in the system of interest.^8–15 In bottom-up CG models that are systematically parameterized from fine-grained (FG) simulations,^15–18 the CG Hamiltonian is equivalent to the potential of mean force (PMF), and the resultant CG internal energy from summing up the CG Hamiltonian does not correspond to the FG internal energy. This is because the many-body PMF of the CG system is essentially the configuration-dependent free energy that necessarily contains an entropic contribution, i.e., it is not entirely an energetic quantity.^19–22 However, due to its many-body nature, the configuration-dependent (e.g., pair distances) free energy depends on other thermodynamic variables (e.g., temperature, pressure, or chemical potential), and thus the so-called transferability problem limits the predictive ability of multiscale models for systems investigated in different state points.^{14, 23, 24} Despite the somewhat limited success of understanding and resolving the transferability problem using systematic approaches,^25–32 no general method to solve the transferability problem, to our knowledge, has been proposed. Therefore, a fundamental theory to construct transferable bottom-up CG models needs to be explored.

In pursuit of this direction, a key barrier for transferability of CG interactions is the entropic contribution to the many-body PMF (free energy) of the CG variables,²⁸ as it will change throughout different state points. Since the exact form of the entropic contribution to the many-body PMF is difficult to determine, we instead endeavor to understand its relationship to the configurational entropy of the CG system. Since multiple atomic entities may be mapped into a single pseudo-atom, i.e., a CG site or “bead”, it seems clear that the entropy of the CG system is inherently reduced compared to that of the FG system since the entropic contribution from different motions (or modes) within the CG bead are no longer resolved. This inequality is part of the general representability problem in which naïvely predicting thermodynamic quantities of the CG system based on FG expressions may result in significant deviations from the true FG values.^{18, 33–37} While such inequalities can be analytically reformulated in simple CG models,¹⁸ the generalization to physical systems with more complex interactions is quite challenging.

As such, an understanding of the CG entropy and its relation to the FG entropy is of utmost importance for not only constructing a systematic bottom-up CG model but also addressing challenges in coarse-graining, i.e., representability and transferability. We note that a previous theoretical study has addressed this issue for the first time and further derived a representability relationship with analytical analyses on global expressions for the entropy in CG systems.³⁸ A central result from Ref 38 is that the entropic contribution to the CG PMF is a conditioned relative entropy that quantifies information loss upon CG mapping. This prior work demonstrated that decreasing CG resolution increased the entropic contribution to the PMF in the case of simple models.³⁸ An important consequence of this analysis is that a practical yet accurate representation of the entropic contribution is likely necessary for transferable CG models. In this work, we aim to define and interpret the entropy within CG systems and provide a compact representation of the microscopic contributions to the CG entropy. After retrieving the missing entropy from the CG observable expression, we propose procedures for constructing transferable CG models using: (1) various temperatures and (2) different chemical environments (system transferability).

In general, the coarse-graining (CG) procedure is applied to a fine-grained (FG) system having configurations rⁿ by applying the mapping operator M: rⁿ → R^N, yielding reduced configurations R^N. Namely, a set of configurational states at the FG, ω_FG, is renormalized to the set of CG configuration states ω_CG. The exact configurational entropy of the CG configurational states in the canonical ensemble $S_{\text{CG}}\left({\omega }_{\text{CG}}\right)={\langle S_{\text{CG},{\text{ω}}_{\text{CG}}}\left(R^{\text{N}}\right)\rangle }_{\text{CG}}$, which should be identical to the all-atom configurational entropy (S_AA(ω_FG)), is formulated by taking the ensemble average of the CG entropy estimator S_{CG,ωFG (R}^N₎ defined as

$$S_{{\text{CG,ω}}_{\text{CG}}}(R^{\text{N}})=-k_B\text{ln}{p}_{{\text{ω}}_{\text{CG}}}(R^{\text{N}})-\frac{\partial W_{\text{CG}}(R^{\text{N}})}{\partial T}$$ (1)

In eq (1), p_ωCG(R^N) denotes the probability of CG configuration R^N among ω_CG, and w_CG(Rⁿ) is the CG many-body potential of mean force (PMF).^{21, 39} Detailed derivations for the many-body PMF case were first suggested by Ref 38 and also were given in Ref 18 – please refer to Section S1 of the Supporting Information (SI) for details. To reiterate, eq (1) shows that the naïvely observed entropy of the CG system $S_{\text{CG}}^{\text{naïve }}\left({\omega }_{\text{CG}}\right)={\langle -k_B\text{ln}{p}_{{\omega }_{\text{CG}}}\left(R^{\text{N}}\right)\rangle }_{\text{CG}}$ is not equivalent to that of the FG entropy S_AA (ω_FG,). For instance, simple polymer models can demonstrate this mismatch between FG and CG entropies where the total entropy is completely mapped to the CG model while the naïve expression yields zero entropy.¹⁸ In this sense, we denote the missing (or excess) entropy term 〈−∂ΔW_CG(R^N)/∂T〉_CG as the entropy (S_map) that is mapped into the CG system. From eq (1), estimated S_map by taking a canonical ensemble average (constant NVT) over CG space, such that $S_{\text{map}}={\langle \frac{-\partial W_{\text{CG}}\left(R^{\text{N}}\right)}{\partial T}\rangle }_{\text{CG}}$. In practice, it is difficult to ascertain the exact functional form of S_map in complex systems, but certain approximations may prove to be useful.

Assuming that the CG PMF is adequately represented in a pairwise-decomposable form (which may not always be the case), the S_map term can also be decomposed in a pairwise form as below:

$$S_{\text{map}}=\langle \frac{-\partial W_{\text{CG}}(R^{\text{N}})}{\partial T}\rangle \approx \langle \sum _{IJ}\frac{-\partial \mathrm{\Delta }{W}_{\text{CG}}(R_{IJ})}{\partial T}\rangle =\langle \sum _{IJ}{S}_{\text{map}}^{\left(2\right)}(R_{IJ})\rangle$$ (2)

Equation (2) suggests that one can recover the missing entropy by calculating and averaging the pairwise mapping entropy $S_{\text{map}}^{(2)}(R)$, which is the temperature derivative of the CG PMF. This is in line with the preceding work that connects the missing entropy to the mapping entropy.³⁸ In practice, we introduce a free energy decomposition scheme, which is commonly referred to as energy-entropy decomposition in eq (3) below.^{28, 40–42}

$$\mathrm{\Delta }{W}_{\text{CG}}\left(R_{IJ};T\right)=\mathrm{\Delta }{U}_{\text{CG}}\left(R_{IJ}\right)-T\mathrm{\Delta }{S}_{\text{CG}}\left(R_{IJ}\right)$$ (3)

The symbol Δ here refers to the thermodynamic quantity in reference to R_IJ at infinite distance. Thus, the pairwise entropy function can be expressed as $\mathrm{\Delta }{S}_{\text{CG}}(R)=-\frac{\partial \mathrm{\Delta }{W}_{CG}(R;T)}{\partial T}$. We note that we explicitly consider the energy-entropy decomposition of the many-body PMF since we restrict ourselves to the canonical ensemble in this work, such that the free energy is indeed the Helmholtz free energy. Due to the entropic contribution, the PMF has an explicit dependence on temperature, which also provides a useful framework for constructing temperature transferable CG models.^{28, 40–42} Hence, S_map approximately becomes 〈Σ_IJ ΔS_CG(R_IJ)〉 giving $S_{\text{map}}^{(2)}\left(R_{IJ}\right)=\mathrm{\Delta }{S}_{\text{CG}}\left(R_{IJ}\right)$. This relationship clearly demonstrates a link between the missing entropy (due to coarsening) and the entropic contribution to the CG PMF, i.e., the entropy associated with FG configurations that are degenerate in CG configuration space is encoded in the CG PMF. Here, we note that we expect S_map to exactly correspond with the entropic contribution to the CG PMF in the limit of perfectly expressive basis functions and infinite sampling. For practical reasons, we instead represent the CG PMF in a pairwise form, and further decompose it into energy and entropy contributions. We then approximate S_map on the basis of the pairwise entropy integrated over all CG configurations using eq (2). Therefore, one goal of the present work is to verify the correspondence shown in eq (2) and further utilize this pairwise entropy function to construct a transferable CG force field.

Even if one can recover an entropy from utilizing eqs (1)–(3), a problem still remains: to accurately relate it to the corresponding entropy at the FG resolution (the “missing” entropy) and to understand its physical meaning. We find that the missing entropy term becomes clearer when applied to single-site CG fluid models. In the single-site model, the CG system will only have translational motion, while at the FG resolution various rotational and vibrational motions exist and are coupled with the translational motions. In other words, the single-site CG model can clearly differentiate the mapped entropy (rotational or vibrational motion) with the naïvely observed entropy (only translational motion). Yet, this argument necessitates a procedure to separate the entropies originating from different motions in the system.

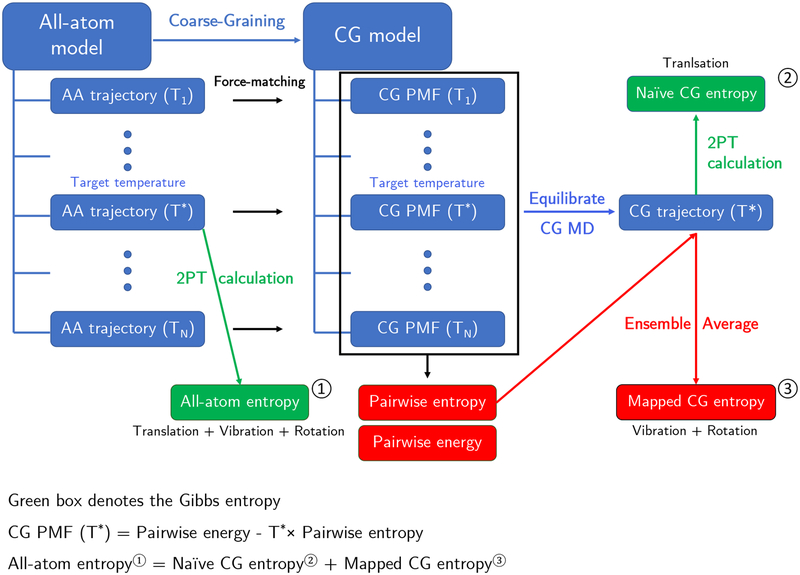
Our strategy is to leverage the two-phase thermodynamic (2PT) method⁴³ and to further decompose the entropy into its modal contributions. In 2PT, the partition function is constructed by partitioning the density of states of the system into translational, rotational, and vibrational contributions. Thermodynamic properties are then obtained by applying quantum statistics to the solid-like component and classical statistics to the gas-like component. Due to its simplicity and efficiency, the 2PT model has been widely applied from simple Lennard-Jones fluid⁴³ to liquid states^{44, 45} with complex phenomena.^{46, 47} Notably, the 2PT method can provide very accurate thermodynamic quantities for liquid states even with the use of short trajectories.^{44, 48} By utilizing the 2PT framework, we can distinguish the translational contribution from the rotational and vibrational contributions and relate them to the configurational entropy at the FG resolution (see Fig. 1). However, any other free energy methodology, such as quasiharmonic analyses, that can extract different modal contributions would work under the suggested framework and would not be limited to only the 2PT method.

Figure 1:

Schematic diagram describing the procedure for calculating different entropy quantities in all-atom and CG systems. The entropy of a single-site CG liquid system consists of two components: the naïve (translation) and mapped CG entropies (vibration and rotation). Both all atom entropies and naïve CG entropies (based on the Gibbs definition) are directly obtained by 2PT calculations using MD trajectories. The mapped CG entropy is calculated separately using the pairwise entropy function from the CG PMF using eq (4). The representability relationship for entropy (bottom) asserts that the all-atom entropy should be identical to the sum of naïve and mapped CG entropies.

Overall, simulations are carried out for both FG and CG systems where the CG models are effectively constructed by the Multiscale Coarse-Graining (MS-CG) formalism,¹⁹‘²²·⁴⁹ although alternative bottom-up CG methods could be used. In practice, the CG parameterization is performed by variational force-matching to minimize the force residuals between the FG and CG ensembles (a detailed procedure is described in Section 5–3 in SI). From the N sets of CG PMFs generated from force-matching, ΔS_CG(R) is obtained by a finite difference derivative of the pairwise potential at temperature T_t and T_N given by²⁸·⁵⁰ $\mathrm{\Delta }{S}_{\text{CG}}(R)\approx -\frac{\mathrm{\Delta }{W}_{\text{CG}}\left(R,T_N\right)-\mathrm{\Delta }{W}_{\text{CG}}\left(R,T_1\right)}{T_N-T_1}$.

Finally, we obtain a complete expression for the mapped entropy as a function of the CG variables. Additional smoothing or filtering can also be performed to the differences in the pairwise forces before the integration step in eq (S12). At the target temperature T = T*, the FG entropy and naïve CG entropy is calculated using the 2PT entropy. The missing CG entropy is subsequently recuperated by utilizing the mapped entropy and the configurations of the CG system at T = T* as an ensemble average of the pairwise mapping entropy function: $S_{\text{map}}=\langle \sum _{IJ}{S}_{\text{map}}^{(2)}\left(R_{IJ}\right)\rangle =\langle {\sum }_{IJ}\mathrm{\Delta }{S}_{\text{CG}}\left(R_{IJ}\right)\rangle$.

The current framework has certain limitations from the approximations that we have introduced. First, we assumed that the CG force fields are adequately pairwise decomposable. However, higher-order correlations may not be captured and thus our present approach may not directly work in systems with non-negligible many-body effects. Further improvements of the present algorithm may be feasible by using stable numerical algorithms to calculate the finite difference, e.g., self-consistent basis sets,⁵⁰ and post-processing the numerical noise from the force-matched profile,⁵¹ e.g., using the Bayesian regularization approach.⁵² These numerical issues are not as evident in this work for liquid mixtures, but certain approaches should be considered for complex systems such as lipids or polypeptides.

Representability: Application to bulk liquids

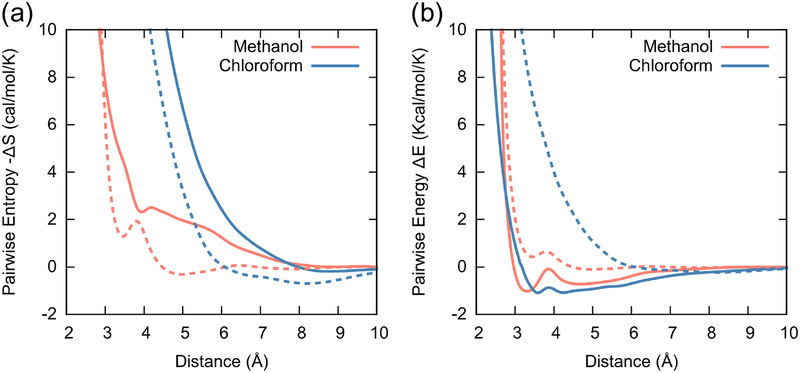
For single-site CG models where the configurational entropy of the CG system originates from translational motion, we hypothesize that the entropic contributions from rotational and vibrational motions are mapped to the CG PMF. It follows that the value of the mapping entropy is dependent on the vibrational and rotational motions at the FG resolution. For example, the mapping entropy should increase as the vibrational or rotational entropies increase. In order to test our hypothesis, we first designed a proof-of-concept study by investigating the pairwise entropy function in different single-site CG neopentane moieties by gradually tuning the length and stiffness of its C-C bonds. We find that the value of the pairwise entropy functions from different CG neopentane systems gradually increases as the C-C bonds become longer or softer (SI Section S2). With this in mind, we now present results for more complex liquid systems: methanol and chloroform molecules. Using the schemes and details that are described above, the pairwise thermodynamic quantities are obtained and plotted in Fig. 2.

Figure 2:

Pairwise thermodynamic quantities for liquids systems: methanol (red) and chloroform (blue). (a) The pairwise mapping entropy function $S_{\text{map}}^{(2)}(R)$ (solid lines) calculated from the scheme depicted in Fig. 1. (b) The pairwise energy function (solid lines) calculated from differences between the PMF and the pairwise entropy function. For comparison, the pairwise PMFs of both liquids are shown as dashed lines in each figure. For (a), the PMF values are additionally scaled by a factor of 1/T with T = 300 K.

As is immediately evident, the pairwise entropy functions (Fig. 2a) demonstrate approximately positive definite behavior and vanish at large distances. While the energetic profile of methanol has features that are representative of non-spherical interactions, such as the Gay-Berne interaction,⁵³ the profile of chloroform is closer to spherical interactions, which is evident from the small separation between the two potential minima. These features will be further addressed in the next section.

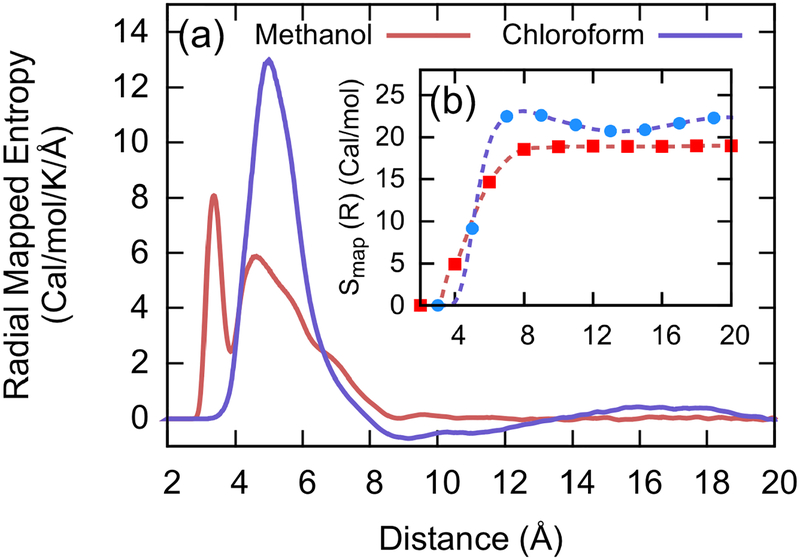
Using the pairwise entropy function $S_{\text{map}}^{(2)}(R)$ from Fig. 2a, the global mapped entropy of the methanol and chloroform systems is readily calculated and shown in Fig. 3. Here, we introduce the radial distribution function g(R) and a change of variables to calculate the radial mapped entropies and integrate them to obtain the overall mapped entropies:

$$S_{\text{map}}=\rho \int dR\cdot 4\pi R^{2}g(R)\cdot S_{\text{map}}^{(2)}(R)$$ (4)

This approach gives consistent values to other numerical techniques, such as averaging the quantity −∂Δ〈W_CG(R_IJ)〉/∂T over the ensemble (SI Section 3). In Fig. 3a, the major peaks with non-negligible intensities occur in regions with large g(R) values, but soon the radial entropy $S_{\text{rad }}(R):=4\pi R^2\rho g(R)\cdot S_{\text{map}}^{(2)}(R)$ decays to zero because $\underset{R\to R_{\text{cut}}}{\text{lim}}{S}_{\text{map}}^{(2)}(R)=0$. To check convergence of the mapped entropy, we integrate S_rad(R) from R = 0 to R = R_cut by varying R_cut from 3 to 20 Å. The changes to the overall mapped entropy are depicted in Fig. 3b, demonstrating that the value quickly converges beyond the first coordination shell. It is worth noting that the current approach is mainly suitable for systems without strong long-range correlations due to the contribution from $R^{2}g(R)\cdot S_{\text{map}}^{(2)}(R)$.

Figure 3:

Mapped entropy for methanol (red) and chloroform (purple) system using the pairwise entropy function. (a) The radial mapped entropy component $S_{rad}(R)=4\pi R^2\rho g(R)\cdot S_{\text{map}}^{(2)}(R)$. (b) The global mapped CG entropy obtained by integrating the radial mapped entropy with different cutoff radii for methanol (red, square) and chloroform (blue, circle).

To establish a connection between the CG entropy and its correspondence at the FG resolution, we first computed the all-atom configurational entropies of methanol and chloroform at T = 300 K by utilizing the 2PT method.⁴³ Here, liquid systems were modeled using the Optimized Potential for Liquid Simulations (OPLS) force field as listed in Table 1.⁵⁴ The all-atom entropies are first validated by comparison to previously reported entropy values using same method⁴⁴ and the OPLS force field. Slight differences observed for the methanol system likely arise due to differences in simulated temperatures, resulting in consistently larger entropy values than the reported values (Ref 44 used T = 298 K). For chloroform, we used a modified version of the OPLS force field from Ref 55, but the general trends remain consistent.

Table 1:

Comparison of average molar entropy for methanol and chloroform with different contributions: Molar entropies calculated at all-atom resolution, naïve CG entropies (translation only) from the 2PT calculation, and mapped (or missing) CG entropy from Fig. 3b (due to rotation and vibration).

Entropy	All-atom		MS-CG		Reference 2PT44
(Cal mol−1 HK−1)			Naïve	Missing
Methanol
Translation	16.12		21.11		16.03
Rotation	11.53	13.26	0.00	18.95	11.38	13.09
Vibration	1.73		0.00		1.71
Chloroform
Translation	20.32		24.96		21.12
Rotation	18.95	24.62	0.00	22.33	19.20	24.85
Vibration	5.67		0.00		5.65

For the CG systems, the naïve CG entropy similarly calculated from the 2PT method is shown in Table 1, which corresponds to the translational entropy given the absence of intramolecular vibrations and rotations due to our CG mapping. Likewise, we approximate the entropy that is folded into the CG PMF from Fig. 3b, which corresponds to the rotational and vibrational entropies that are lost due to the CG mapping. In comparing the all-atom and CG translational entropies, we note larger values in the latter case, which likely arise due to the following factor. First, we restrict ourselves to a pairwise basis set²² to represent the effective CG potential, which may not capture the complete many-body PMF; for instance, single-site methanol is inherently non-spherical at the atomistic level, which can only be approximated to a certain extent with simple pairwise interactions (see Fig. 2). More importantly, we also find that our approximations of the mapped (i.e., missing) CG entropies for both systems recapitulates reasonably well the rotational and vibrational contributions at the FG resolution, even though the CG model for methanol somewhat overestimates the mapping entropy contribution. This analysis therefore suggests that our approach can faithfully represent the entropy of CG systems in a pairwise decomposable manner by explicitly including the missing entropy, in which the latter quantity corresponds to the FG entropy that is lost from CG mapping.

Transferability: Temperature transferability of bulk liquids

As mentioned previously, the transferability problem arises due to difficulty in capturing the many-body PMF, especially since the PMF will change in unknown ways for new systems given its state-point dependency.^{14, 15, 24} In particular, one must consider the non-trivial contribution of the CG entropy to the PMF, which has been challenging to unambiguously quantify. An end goal of this work is to enable a general CG potential that retains high-fidelity in different molecular environments and thermodynamic state points.¹⁴ We will focus on two different cases: (i) different temperatures and (ii) different systems or chemical environments, i.e., bulk liquid and liquid mixtures. As a first step in constructing transferable CG interactions for a given system at different state points, the most direct approach is to interpolate the PMFs at different temperatures by leveraging the energy-entropy decomposition expressed in eq (3) within valid temperature ranges, i.e., within a given phase. In practice, we estimate the pairwise terms in the CG PMF at different temperatures, where the pairwise thermodynamic functions ΔU_CG(R) and ΔS_CG(R) are from Fig. 2 and assumed here to be temperature independent (i.e., a simple linear dependence on temperature of ΔW_CG(R; T)).

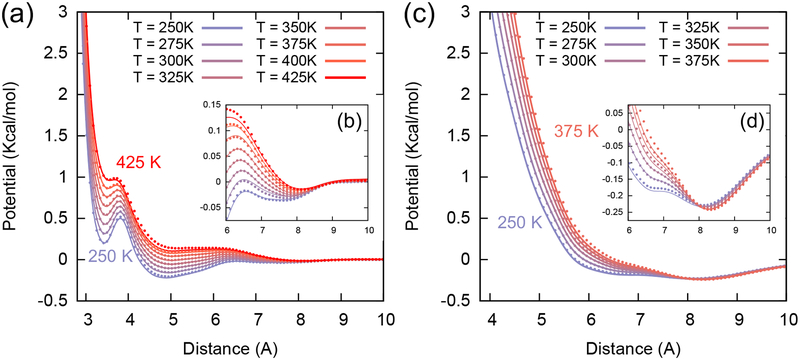
We find that the analytically-fitted effective CG interactions (using eq (3)) for methanol and chloroform are in excellent agreement with respect to the interactions derived from MS-CG at each state-point, as shown in Fig. 4. A nearly linear dependence of the CG PMF on temperature is consistent with previous reports.^{28, 56, 57} It is worthwhile to note that we used the following ranges to obtain the pairwise entropy functions of each system: 250–350 K for methanol and 250–325 K for chloroform. However, in Fig. 4, we not only interpolated the PMFs at temperatures within the training range but also extrapolated them to even higher temperatures outside of our training set. For methanol, we find that the range of extrapolation can be much larger than those reported in previous works (330 K for Ref 28 and 300 K for Ref 56). Remarkably, the extrapolated CG interactions can also reproduce the effective PMF correctly, even in the long-range regimes (Fig. 4b and 4d), while assuming only linear temperature dependence: ΔW_CG(R;T) = ΔU_CG(R) — TΔS_CG(R). This success in extrapolating the CG PMF suggests that we can extend this approach and construct “phase-transferable” CG models by combining pairwise energy and entropy functions from different phases. We are, for example, currently pursuing the development of CG force fields that are transferable between liquid and vapor phases for a future publication.

Figure 4:

Effective CG interactions of the methanol and chloroform systems for different temperatures by comparing the fitted PMFs (dots) with the conventional MS-CG PMFs (lines). (a) Methanol-Methanol CG PMFs at selected temperatures from 250 K to 425 K. (b) Magnified CG PMFs of methanol at the long-range region between 6 and 10 Å. (c) Chloroform-Chloroform CG PMFs at selected temperatures from 250 K to 375 K. (d) Magnified CG PMFs of chloroform at the long-range region between 6 and 10 Å.

Transferability to different chemical environments: “Liquid mixtures”

In order to transfer the effective CG interactions to different chemical environments, we construct liquid mixtures composed of methanol and chloroform. Constructing bottom-up CG models that are transferable from bulk to mixed-liquid states has been recognized as a difficult problem, and has therefore been the focus of recent research efforts.^{30, 32} However, recently suggested methods remain system-dependent, thereby limiting their applicability. However, as is common practice in all-atom and top-down models, a “combining rule” for arbitrary CG models is one potential solution. Even though combining (or mixing) different PMFs may seem nearly impossible due to their complex nature, we seek to predict effective CG interactions between two different molecules by solely utilizing information derived from bulk states.

To address the aforementioned challenges, we show that the energy-entropy decomposition of bulk state PMFs can be utilized to predict the PMFs associated with single-site CG liquid mixtures, especially cross-interactions, in a systematic way. Rather than combining the PMF naïvely, our framework discriminates and combines the energetic and entropic terms separately. Finally, the interpolated (or mixed) PMF of the system is readily obtained by adding these two functions. To more effectively predict the interaction between methanol and chloroform CG beads, we approximate the methanol CG bead as a spherocylindrical particle and the chloroform CG bead as a spherical particle. These choices were motivated by the energetic interaction profiles calculated in Fig. 2b, which suggest that methanol has a rod-like interaction⁵⁸ while chloroform retains spherical symmetry with a small degree of anisotropy.³⁰ By adopting this assumption, the methanol-chloroform cross-interaction was simplified to a rod-sphere interaction. Based on previous statistical mechanical developments of rod-sphere interactions using Gay-Berne and Lennard-Jones functional forms^{59, 60}, we first extracted effective Gay-Berne^{53, 58} and Lennard-Jones (LJ 6–4)⁶¹ parameters from the self-interaction PMFs and projected the cross-interaction onto an approximated pairwise form (please refer to the SI Section 6). As a result, we then obtained a simplified expression of the rod-sphere energetic interaction term as:

$$\mathrm{\Delta }{U}_{\text{MeOH}-{\text{CCl}}_3\text{H}}(R)\approx \frac{27}{4}\sqrt{{ϵ}_{\text{MeOH}}\cdot {ϵ}_{{\text{CCl}}_3\text{H}}}[{(\frac{{\sigma }_{{\text{CCl}}_3\text{H}}}{R})}^6-{(\frac{{\sigma }_{{\text{CCl}}_3\text{H}}}{R})}^4]$$ (5)

with ${\sigma }_{{\text{CCl}}_3\text{H}}={\sigma }_{r-s}=3.1893$ Å and ${ϵ}_{r-s}=\sqrt{{ϵ}_{\text{MeOH}}\cdot {ϵ}_{{\text{CCl}}_3\text{H}}}=0.9503$ kcal/mol. The pairwise self-interactions (methanol-methanol, chloroform-chloroform) were modeled using the procedure detailed in the previous section, with additional details in the SI.

While mixing the energetic interactions is similar to conventional combining rules for interaction parameters, mixing the entropic functions is relatively different. Specifically, we point out that the entropic mixing discussed in this work is a pairwise quantity that is a function of pair distance (i.e., not the conventional entropy of mixing), which, to our knowledge, is seldomly explored. Here, we suggest a combining rule for pairwise entropy functions. Due to the near-positive definite nature of the obtained entropy function from the single-site CG mapping, we take a geometric average of the entropy functions at a given distance R. This expression is given by $\mathrm{\Delta }{S}_{\text{MeOH}-{\text{CCl}}_3\text{H}}^{\text{mix}}(R)=\sqrt{\left(\mathrm{\Delta }{S}_{\text{MeOH}}^{\text{bulk}}(R)\right)\cdot \left(\mathrm{\Delta }{S}_{{\text{CCl}}_3\text{H}}^{\text{bulk}}(R)\right)}$ (Note that ΔS_CG(R) >0). In turn, we note that such an entropic combining rule is consistent with the conventional Lorentz-Berthelot mixing rules^{62, 63} (see the SI). From the proposed mixing protocol, we can compute the pairwise energy and entropy functions for the methanol-chloroform interaction and compare them to the actual MS-CG interactions from force-matching the mixture system (Fig. 5a). Notably, excellent agreement is observed for both the energetic and entropic contributions in Fig. 5a, which suggests that the interpolated model can be transferred to other temperatures as well. We next perform CG simulations using the fitted CG interactions to evaluate the fidelity of the mixed CG model.

Figure 5:

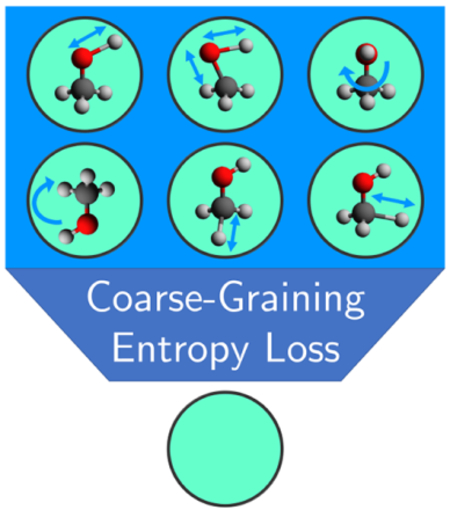
Assessment of the transferability of CG models in the liquid mixture utilizing a proposed combining rule based on energy-entropy decomposition. Here, each liquid molecule was mapped to single CG bead, (a) Thermodynamic quantities of the methanol-chloroform CG cross interaction: energetic (orange) and entropic (green) interactions from the proposed combining rule (dotted lines) comparing to the actual MS-CG (solid lines), (b) Methanol-chloroform g(r) for CG mapped atomistic and interpolated MS-CG simulations. The g(r) function obtained from the actual MS-CG model for the CG mixture is also depicted (dotted lines) to provide the upper limit of possible CG models. Histograms of observed methanol (red, magenta) and chloroform (blue, cyan) cluster sizes in mapped all-atom and interpolated CG models in (c) natural (averaged) scales and (d) log scales.

To evaluate the structural correlations of methanol-chloroform pairs, we calculated the radial distribution function (RDF), or g(r), of methanol-chloroform and compared it to the exact CG mapped all-atom reference as shown in Fig. 5b. The RDF of the interpolated CG model is smoother than the mapped all-atom reference due to the use of simple CG energetic functions for combining. In particular, it deviates in the first peak width that can be interpreted as smoothing over underlying structure that appears in the all-atom structure. Nonetheless, the structural agreement is quite reasonable (the peak value near 4.5 Å is almost identical), given the fact that the interpolated CG PMF was constructed without any prior information of the exact CG cross-interaction.

In order to investigate higher-order correlations, especially given the inhomogeneous nature of this system,⁶⁴ we perform cluster analysis of methanol and chloroform clusters based on a previously reported protocol that utilizes connected graphs within the first coordination shell to identify clusters.²⁹ Surprisingly, we find that the cluster distribution of the interpolated CG models and the CG mapped atomistic system matches almost perfectly in both methanol and chloroform regardless of the observation scheme (averaged observation in Fig. 5c and logarithm of overall clusters in Fig. 5d). Altogether, both thermodynamic and structural properties derived from our proposed strategy to construct transferable CG interactions appear to faithfully reproduce the actual CG properties of the mixture as directly obtained by force-matching to the mixture.

To summarize, our work elucidates the nature of CG entropy as the mapped (missing) entropy from the many-body CG PMF determined by the CG mapping. Using single-site CG models, we clarify the implicit embedding of vibrational and rotational entropies within the CG PMF, while only the translational entropy is captured by naïve arguments. Furthermore, we demonstrate the use of a free energy decomposition framework to impart transferable bottom-up CG force fields for non-parameterized state points. Our findings in the methanol/chloroform mixture system suggest a high-fidelity combining rule to approximate CG PMFs for different chemical environments by separately mixing the energetic and entropic components of the bulk-phase CG PMFs.

In order to combine CG PMFs, an entropic combining rule is suggested based on mixing rules that are introduced in this work. Nevertheless, it is evident that much of the physical nature of the pairwise entropy function and its combining rules remains unexplored, suggesting that the proposed framework will have various potential applications and future directions. A natural extension of the proposed combining rule for simple liquids would be to model complex interacting systems that necessitate CG modeling: protein-protein interactions or proteins in water. For example, we plan to integrate the current approach with a recently proposed bottom-up CG modeling framework for complex biomolecules in water (e.g., lipids), which represent solvent effects through the use of virtual sites.⁶⁵ After successfully applying the approach to more complex biomolecules, the next step will be to investigate the correct combining rules for pairwise thermodynamic quantities in such systems. We also note that the pairwise entropy function obtained from different temperatures might be useful to compare and validate different CG models. In contrast to more ad hoc top-down CG models, the present framework is expected to facilitate bottom-up CG modeling by providing a systematic procedure to transfer CG force fields to different thermodynamic state points and compositions.