Somatic Recording of GABAergic Autoreceptor Current in Cerebellar Stellate and Basket Cells

Abstract

Patch-clamp recordings were performed from stellate and basket cells in rat cerebellar slices. Under somatic voltage clamp, short depolarizing pulses were applied to elicit action potentials in the axon. After the action potential, a bicuculline- and Cd²⁺-sensitive current transient was observed. A similar response was obtained when eliciting axonal firing by extracellular stimulation. With an isotonic internal Cl⁻ solution, the peak amplitude of this current varied linearly with the holding potential, yielding an extrapolated reversal potential of −20 to 0 mV. Unlike synaptic or autaptic GABAergic currents obtained in the same preparation, the current transient had a slow rise-time and a low variability between trials. This current was blocked when 10 mm BAPTA was included in the recording solution. In some experiments, the current transient elicited axonal action potentials. The current transient was reliably observed in animals aged 12–15 d, with a mean amplitude of 82 pA at −70 mV, but was small and rare in the age group 29–49 d. Numerical simulations could account for all properties of the current transient by assuming that an action potential activates a distributed GABAergic conductance in the axon. The actual conductance is probably restricted to release sites, with an estimated mean presynaptic current response of 10 pA per site (−70 mV, age 12–15 d). We conclude that in developing rats, stellate and basket cell axons have a high density of GABAergic autoreceptors and that a sizable fraction of the corresponding current can be measured from the soma.

The axonal membrane of brain neurons is responsible for the generation and propagation of action potentials as well as for the consequent depolarization of nerve terminals and associated Ca²⁺ entry. In addition, axon terminals and adjacent areas contain receptors for neurotransmitters, called presynaptic receptors (for review, see McGehee and Role, 1996; Langer, 1997; Wu and Saggau, 1997). Presynaptic receptors can be activated by the release of neurotransmitter coming from the same neurons, in which case they act as autoreceptors, by stimulation of axo-axonic synapses, or by spillover of neurotransmitter released from nearby neurites belonging to other neurons. Activation of presynaptic receptors in turn can potently modify the strength of neurotransmitter release.

Among the many subtypes of presynaptic receptors that are believed to exist, GABA_A receptors are perhaps the most extensively studied. Activation of presynaptic GABA_A receptors has been proposed as the cause of presynaptic inhibition first at the crayfish neuromuscular junction (Dudel and Kuffler, 1961), and since then in a number of preparations, notably in the mammalian brain (for review, seeMcGehee and Role, 1996). The mode of action of presynaptic GABA_A receptors has been best studied in two preparations where the size of the presynaptic structure is large enough to allow intracellular recording: the sensory axons in the mammalian spinal cord (for review, see Rudomin, 1990) and mammalian peptidergic pituitary terminals (Zhang and Jackson, 1993). In both cases, presynaptic inhibition is associated with a depolarization of the presynaptic element. In most brain neurons, however, the size of axons and terminals is very small. Although successful presynaptic recordings have recently been obtained in certain brain preparations [calyx of Held: Forsythe (1994); cerebellar basket cells: Southan and Robertson (1998)], such recordings remain difficult, so that alternative approaches to the study of brain autoreceptors would be desirable.

In the present work, we present such an approach, which developed from the chance observation of an unconventional current response when recording from cerebellar stellate and basket cells under voltage clamp. If action potentials are elicited in the axon by applying short depolarizing pulses in the soma, two distinct bicuculline-sensitive current signals are obtained during repolarization. One of these signals corresponds to the activation of somatodendritic autaptic currents, as reported earlier (Pouzat and Marty, 1998). The second component is described in the present study. As we shall see, it corresponds to the activation of GABAergic autoreceptors in the axon of the recorded cell.

MATERIALS AND METHODS

Preparation. Rats were decapitated under deep anaesthesia (metofane; Mallinckrodt Veterinary, Bray, Ireland), and parasagittal cerebellar slices were prepared as described (Llano and Gerschenfeld, 1993). Slices were used 1–5 h after preparation. Two groups of rats (12- to 15-d-old, and 29- to 49-d-old) were used in the present study. The data base used to determine the proportion of cells displaying autoreceptor currents or/and autaptic currents overlapped with that used in Pouzat and Marty (1998).

Compositions of intracellular and extracellular recording solutions. The intracellular recording solution contained (in mm): 150 KCl, 4.6 MgCl₂, 0.1 CaCl₂, 1 EGTA, 10 KHEPES, 0.4 NaGTP, and 4 NaATP. The external solution contained (in mm): 125 NaCl, 2.5 KCl, 2 CaCl₂, 1 MgCl₂, 1.25 NaH₂PO₄, 26 NaHCO₃, and 10 glucose. Bicuculline methochloride (10 μm; Tocris Cookson, Bristol, UK) was used in some experiments to block GABA_A receptors.

Recording from stellate and basket cells. The procedures described by Llano and Gerschenfeld (1993) were used to identify interneurons in the molecular layer and to record from them. Series resistance values during recording ranged from 10 to 35 MΩ and were partially compensated (50–75%). Currents were recorded with a sample interval of 50 or 100 μsec and were filtered at one-fifth of the sampling frequency. To subtract leak and capacitive currents, a series of hyperpolarizing voltage pulses were applied from the resting potential with a fraction of the amplitude of the test depolarizing pulse, and the resulting currents were added to the response to the depolarizing pulse.

All experiments were performed at room temperature (20–23°C).

Morphology. Neurobiotin (2 mg/ml) was included to the pipette solution in some experiments. Slices were then processed after the end of the recordings as explained (Pouzat and Hestrin, 1997). In other experiments, Lucifer yellow (saturating concentration) was included in the pipette solution; cells were then examined under epifluorescence during the experiment, and results were stored using a CCD camera. Unlike neurobiotin staining, Lucifer yellow staining was always successful. However, the morphology that was obtained with Lucifer yellow (e.g., see Fig. 9) was less precise than that obtained after processing neurobiotin-filled cells (e.g., see Fig. 8).

Fig. 9.

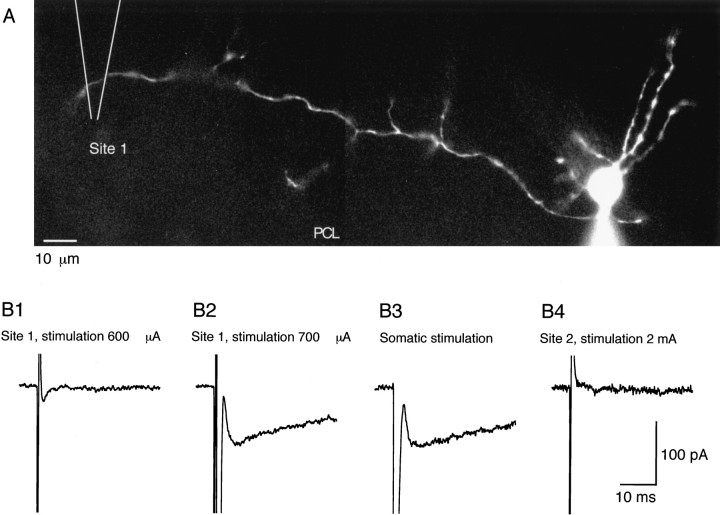
The delayed current transient can be obtained by extracellular stimulation. A, Morphology of the recorded interneuron (a basket cell) with Lucifer yellow staining. The Purkinje cell layer (PCL) corresponds roughly to the lower border of the field. The location of the stimulation pipette was alternated between a position 160 μm left of the soma of the recorded cell (Site 1) and another position 160 μm right of the soma of the recorded cell (Site 2; data not shown). B, Current traces obtained for different stimulation conditions. Series of pulses of 0.2 msec in duration and of various amplitudes were delivered with a frequency of 0.25 Hz at each site. Between each series of pulses, responses to somatic depolarizations were recorded. B1, A 600 μA stimulation at Site 1 failed to elicit any response. Only the stimulation artifact is obtained. B2, Increasing the stimulation intensity to 700 μA resulted in a large Na⁺ current (which just saturated the recording amplifier at 2 nA; data not shown) and a 90 pA delayed current transient. B3, Response to somatic stimulation. Na⁺ current amplitude = 1.75 nA (data not shown). Note the similarity of the amplitude and time course of the delayed current transient with that obtained by direct axon stimulation. B4, Lack of response at Site 2, with a stimulation intensity largely beyond the threshold at Site 1.

Fig. 8.

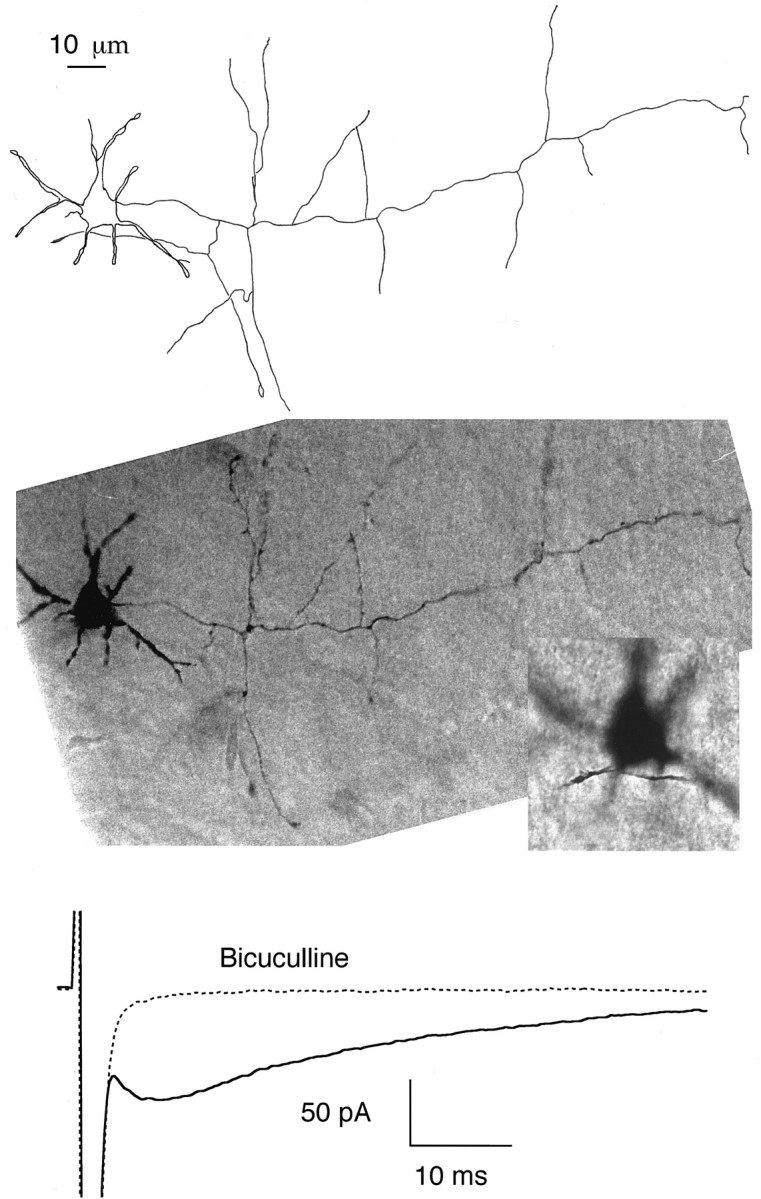
The delayed current transient does not require close contact or extensive overlap between the axonal and dendritic domains. Top, Camera lucida drawing of a basket cell (14-d-old animal) that was filled with neurobiotin during recording and processed for histology. The short thick neurites radiating from the soma are dendrites. The axon leaves the soma on the right and takes an almost straight course, sending several collaterals along the way. It is prolonged beyond the boundary of the drawing. The Purkinje cell layer is roughly horizontal and is located at the level of the tips of the axon collaterals at the lower boundary of the cell.Middle, Composite photograph from the same cell. In the lower scale photograph the dendrites are in focus; the axon collateral that appears to overlap with the dendritic field in the drawing of thetop panel is then not in focus. Insert, Blowup of the somatodendritic region with the axon collateral in focus. The shortest distance between axonal and dendritic domains in this cell was 2 μm. Bottom, Average responses to depolarizing pulses from the same cell, with and without bicuculline, showing the presence of a normal size, delayed current transient.

Numerical methods for simulation of an active cable. We assume here a uniform cable of length l and radius a (both in centimeters), voltage-clamped at the origin, with a sealed end at x = l. This cable has voltage-dependent Na⁺ and K⁺ conductances, as well as a synaptic conductance, which is either localized or uniformly distributed. The electric parameters of the cable are R_i, the cytoplasmic resistivity (in kΩ·cm); R_m, the resistance of a unitary surface of membrane (in kΩ·cm²); C_m, the capacitance of a unitary surface of membrane (in μF/cm²); G_K, the density of K⁺conductance (in mS/cm²); G_Na, the density of Na⁺ conductance (in mS/cm²); G_s, the density of synaptic conductance (in mS/cm²). E_K, E_Na, E_s, and E_L (all in mV) are, respectively, the reversal potential of the K⁺current, the Na⁺ current, the synaptic current, and the leak current. The voltage dependence of the K⁺and Na⁺ currents are modeled following Hodgkin and Huxley (1952). V(x, t) (in mV) is the membrane potential. To have a consistent set of units, times are in milliseconds.

With the assumptions outlined above the cable equation takes the form (Hodgkin and Huxley, 1952; Rall, 1977):

$$C_{\text{m}} \frac{\partial }{\partial t} V=\frac{a}{2·R_{\text{i}}}·\frac{{\partial }^2}{\partial x^2} V-\frac{V-E_L}{R_{\text{m}}}-G_K·n^4·(V-E_K)-G_{\text{Na}}·m^3·h·(V-E_{\text{Na}})-G_{\text{s}}·(V-E_{\text{s}}),$$ Equation 1

with:

$$\frac{\partial }{\partial t} n=(1-n)·{\alpha }_{\text{n}}(V)-n·{\beta }_{\text{n}}(V),$$ Equation 2

$$\frac{\partial }{\partial t} m=(1-m)·{\alpha }_{\text{m}}(V)-m·{\beta }_{\text{m}}(V),$$ Equation 3

$$\frac{\partial }{\partial t} h=(1-h)·{\alpha }_{\text{h}}(V)-h·{\beta }_{\text{h}}(V).$$ Equation 4

Here, n, m, h, α_n, β_n, α_m, β_m, and α_h, β_hare defined as in Hodgkin and Huxley (1952). The boundary conditions are:

$$V(x=0,t)=V_{\text{c}}(t),$$ Equation 5

where V_c(t) is the command potential applied in the soma, and:

$$\frac{\partial }{\partial x} V(x=l,t)=0.$$ Equation 6

The initial conditions are:

$$V(x,t=0)=v(x),$$ Equation 7

where v(x) is the potential profile at time 0 (usually, v(x) = −70).

The Crank–Nicolson method (Moore et al., 1975; Hines, 1984; Mascagni, 1989) was used to solve numerically this system of equations. “Staggered time grids” (Hines, 1984; Mascagni, 1989) were used to compute the last three terms in Equation 1. The algorithm was implemented on Igor (Wavemetrics) and run on a Pentium computer (266 MHz). The integration steps, dx and dt were chosen smaller than one-tenth of the minimal length constant and of the minimal time constant, respectively. The minimal length and time constants are computed when the sum of the Na⁺, K⁺, and synaptic conductances is maximum. To obtain the value of the minimal constants a guess was made, the simulation was run, and the minimal constants were computed from the stored values of the activation parameters (n(x, t), m(x, t), and h(x, t)). If the guess was larger than the computed value, the simulation was repeated with the computed value as a new guess. This procedure was repeated until convergence was reached.

The following parameter values were used for the simulations of Figures10-12: R_i = 0.1 kΩ·cm, R_m = 50 kΩ·cm², C_m = 1 μF/cm², G_K = 400 mS/cm², G_Na = 50 mS/cm², E_L = −70 mV, E_K = −95 mV, E_Na = +90 mV. The simulations were always started from −70 mV, so that the initial conditions were: v(x) = −70 mV.

Fig. 10.

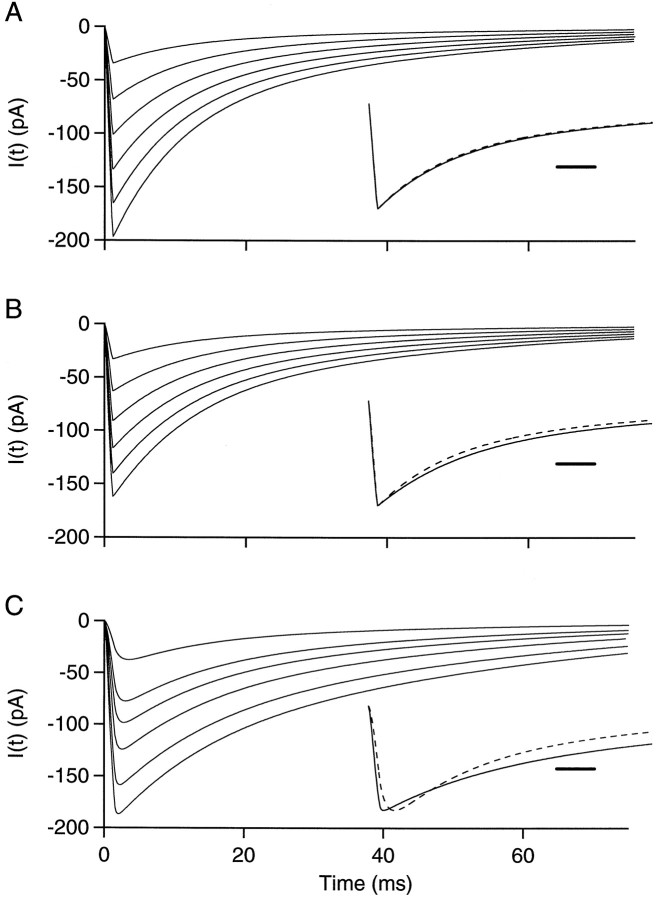
Currents recorded in response to synaptic conductance changes in passive cables. A, B,Dendrite-like cable voltage-clamped at the origin with localized synaptic inputs. The cable is uniform, with a length of 50 μm and a radius of 0.4 μm. Its electrical parameters are R_i = 100 Ω·cm, R_m = 50 kΩ·cm², C_m = 1 μF/cm². The synaptic conductance has a rise time of 1.1 msec and a bi-exponential decay with τ_fast = 9 msec, τ_slow = 40 msec, and a weight of 0.6 for the fast component. Six different peak conductances are simulated: 0.5, 1.0, 1.5, 2.0, 2.5, and 3 nS. The reversal potential of the synaptic current is at 0 mV. The origin of the cable is clamped at −70 mV. The conductance is located 10 μm away from the origin in A and 48 μm away in B. Inset, Scaled largest current (continuous line) and scaled smallest current (dashed line); Calibration, 5 msec. C, Axon-like cable voltage-clamped at the origin with homogeneous synaptic input. The cable is 200 μm long and has a radius of 0.25 μm. Its electrical parameters are the same as in A and B. The synaptic conductance has a rise time of 1.5 msec and the same bi-exponential decay as above. Six different autoreceptor conductance densities are simulated: 0.25, 0.64, 0.89, 1.27, 1.91, and 2.55 mS/cm². As above, the reversal potential of the synaptic conductance is 0 mV, and the origin is maintained at −70 mV. As the autoreceptor current density increases, the time to peak decreases from 3.5 to 2.0 msec, whereas the half decay time increases from 14.2 to 21.8 msec. Inset, As above, scaled largest (continuous line) and smallest (dashed line) currents. Calibration, 5 msec.

Fig. 11.

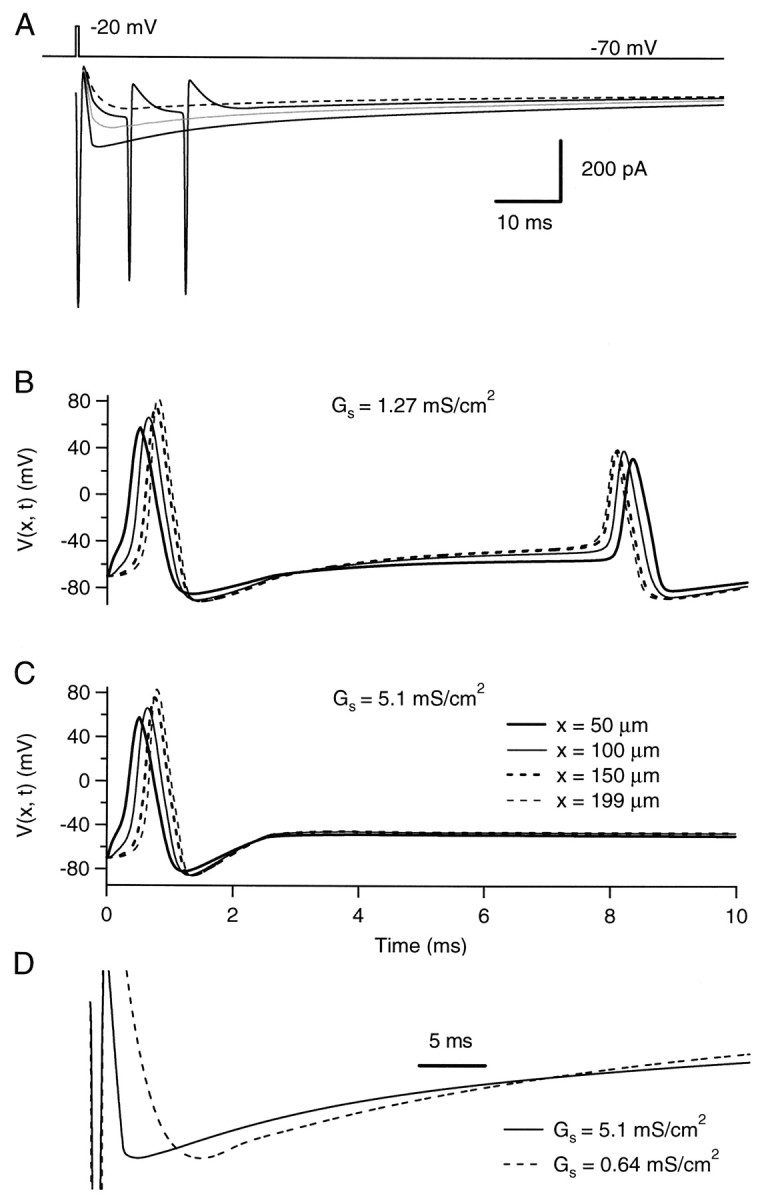
Axon-like cable with homogeneous autoreceptor current input. Simulations of a cable 200 μm long with a radius of 0.25 μm. The parameters describing the passive electrical properties of the cable are as in Figure 10. The cable has a uniform Na⁺ conductance density (50 mS/cm² with a reversal potential at +90 mV) and a uniform K⁺ conductance density (400 mS/cm² with a reversal potential at −95 mV). The kinetic parameters of these conductances are given in Materials and Methods. Results of simulations are displayed with different uniform autoreceptor conductance densities. The kinetic parameters and reversal potential of the autoreceptor conductance are the same as in Figure 10. A, Currents elicited by a short voltage pulse (duration, 0.5 msec; amplitude, 50 mV) at the origin of the cable. Traces are “leak-subtracted” (see Materials and Methods). The autoreceptor conductance is activated 1 msec after the beginning of the pulse. Autoreceptor densities of 0.64 mS/cm² (dashed trace), 1.27 mS/cm² (continuous trace with the two secondary spikes), 2.55 mS/cm² (gray trace), and 5.1 mS/cm² (continuous trace without secondary spikes) are represented. B, C, Voltage time courses at four different locations along the cable with two different autoreceptor conductance densities: 1.27 mS/cm² for B and 5.1 mS/cm² for C. Here only 10 msec are shown. The first spike is the one evoked by the voltage pulse at the origin. The second, antidromic spike in B corresponds to the first of the two secondary spikes in A. D, Peak-scaled traces corresponding to autoreceptor conductance density values of 0.64 mS/cm²(dashed line) and 5.1 mS/cm²(continuous line). Times to peak are, respectively, 8.4 and 3.6 msec, and half-decay times are 25 and 28 msec. Calibration, 5 msec.

Fig. 12.

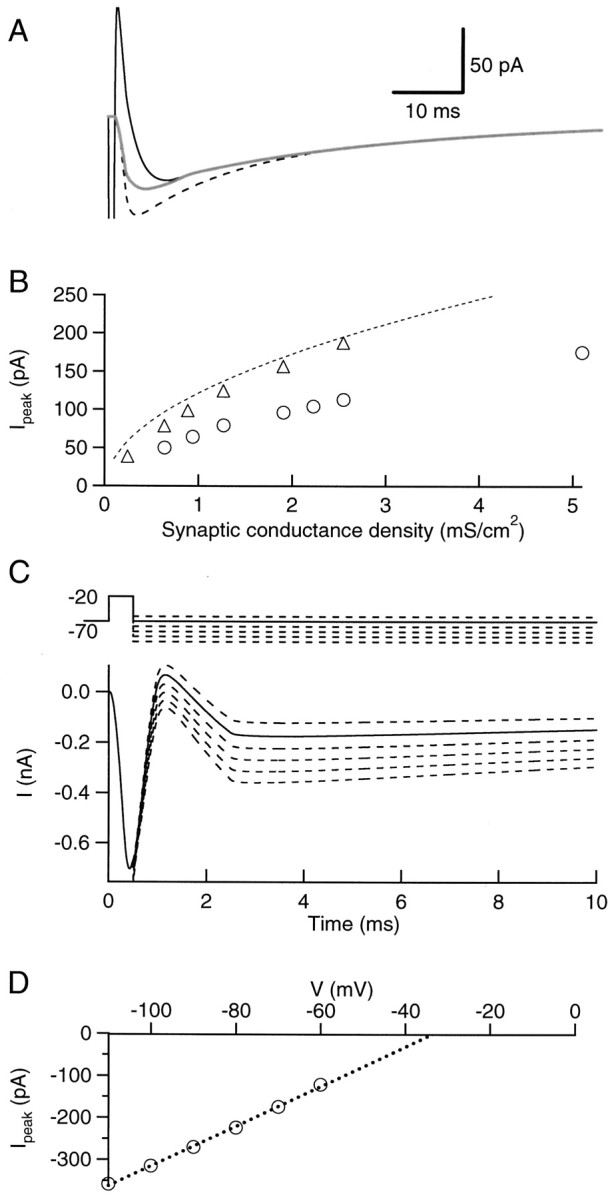
Effects of active conductances on the kinetics and peak amplitude of the delayed current transients. A, Superimposed traces representing simulations of the delayed current transient for a 200 μm long homogeneous cable containing an autoreceptor conductance density of 0.64 mS/cm², without (dashed trace, from Fig. 10C) and with (thin continuous trace, from Fig. 11A) voltage-dependent conductances. The thick trace represents the subtraction of the currents obtained with and without autoreceptors, in the presence of voltage-dependent conductances. B, Peak delayed current transient as a function of autoreceptor conductance density, as calculated with the analytical model of a semi-infinite passive cable (dashed line), with the numerical simulation of a passive cable (triangles, from Fig. 10C) and with the numerical simulation of an active cable (circles, from Fig. 11A). C, Simulations of the experiments performed to estimate the reversal potential of the delayed current transient. Top part, schematic representation of the voltage command applied at the origin of the cable. Bottom part, current traces obtained with an autoreceptor conductance density of 5.1 mS/cm²(these traces are leak-subtracted). D, Plot of the peak delayed current transient versus repolarization potential. The extrapolated reversal potential is −33 mV.

The functions describing the voltage dependence of the rate constants α and β in Equations 2-4 were taken from Traub et al. (1994), except that the reference potential was taken as the bath potential instead of the resting potential of the cell (−60 mV) as in Traub et al. (1994), and that it was necessary to shift the activation rate constant of the K⁺ conductance (α_n) by 5 mV to the left to reduce the window of activation of action potentials by the autoreceptor current (see Fig.11). The synaptic conductance was described as the product of the peak conductance with a kinetic factor comprised between 0 and 1:

$$G_{\text{s}}(t)=G_{\text{peak}}·g_{\text{s}}(t),$$ Equation 8

where g_s rises linearly from 0 to 1 and decays with bi-exponential kinetics. The rise time (τ_rise) was 1.1 or 1.5 msec, and the decay kinetics were taken from Llano and Gerschenfeld (1993):

$$g_{\text{s}}(t)=\left\{\begin{array}{c}\frac{t}{{\tau }_{\text{rise}}},0\le t\le {\tau }_{\text{rise}}\\ 0.6·e^{-\frac{t-{\tau }_{\text{rise}}}{9}}+0.4·e^{-\frac{t-{\tau }_{\text{rise}}}{40}},t\ge {\tau }_{\text{rise}}\end{array}.\right.$$ Equation 9

Results of numerical calculations were compared with analytical solutions for the recorded somatic current and the potential along the cable in response to three types of perturbations. The first one was a step change of the voltage command. The second perturbation was a current injection at one position along the cable. The analytical solutions for these two situations were taken from Rall and Segev (1985). The last perturbation was a step increase of a distributed synaptic conductance. The derivation of the analytical solution in this last case is presented in the Appendix. In all three cases, numerical calculations reproduced the predictions of the analytical solutions (data not shown).

Leakage and capacitive current subtraction was simulated for the calculations of Figures 11A and 12B as during the real experimental protocol. That is, the response to a voltage pulse from −70 to −80 mV was computed, and the resulting current trace was multiplied by 5 before being added to the responses to pulses from −70 to −20 mV.

RESULTS

Characterization of a novel bicuculline-sensitive current in cerebellar interneurons

A delayed current transient associated with axonal excitability

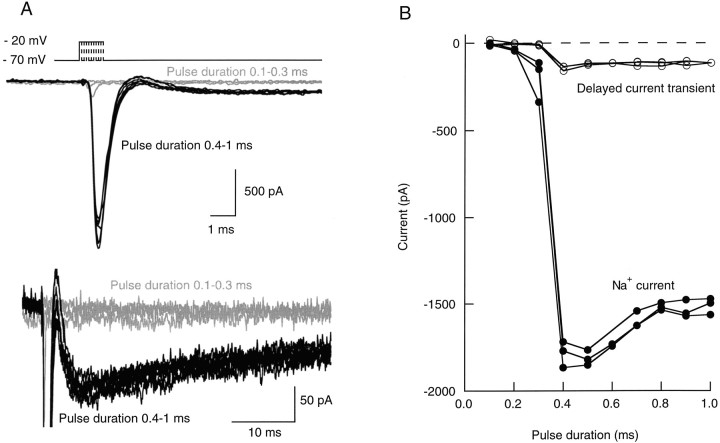
If somatic depolarizing pulses of increasing duration were applied from a holding potential of −70 mV in interneurons, a large amplitude, quickly decaying inward current was observed past a certain threshold, reflecting the activation of voltage-dependent Na⁺channels (Fig. 1A) (Llano and Gerschenfeld, 1993). Because the site of initiation of action potentials in central neurons is located in the axon (for review, see Stuart et al., 1997), it was assumed that this current reflects the initiation of an action potential in the axon. Confirmation of this point will be presented below (see Fig. 9). In many experiments, this early signal was followed after a short time gap by a delayed inward current transient having an amplitude of up to several hundreds of picoamperes (Fig. 1A). The delayed current transient had much slower onset (10–90% rise-time; 1.9 msec in the example shown) and decay (half-decay time, 41 msec) kinetics than the early Na⁺ current, as may be seen in the bottom panel of Figure 1A. Like the Na⁺ early transient, it was an all-or-none event. The activation thresholds for the two components were identical (Fig.1B; n = 4). If during the course of one experiment the threshold of the Na⁺ current activation changed as a result of an alteration of the series resistance, the threshold of the delayed current transient changed in parallel. After application of tetrodotoxin (TTX, 100 nm), the amplitude of the Na⁺ current was first gradually reduced, without any marked associated change in the delayed current transient. Then, the Na⁺ current suddenly failed, and the delayed current transient was simultaneously abolished (results not shown; n = 4). Taken together, the results show that there is a tight coupling between the delayed current transient and the early Na⁺ current and therefore indicate that the delayed current transient is a consequence of an axonal regenerative depolarization.

Fig. 1.

Voltage pulses elicit two distinct inward current signals with the same threshold. A, Leak-subtracted current traces obtained in an interneuron in response to successive voltage pulses (test potential, −20 mV; pulse frequency, 0.5 Hz) of increasing duration (0.1–1.0 msec, with 0.1 msec increments). For the three shortest pulses (0.1–0.3 msec, gray traces) no regenerative current was elicited. For all other stimuli (0.4–1 msec pulses,black traces), a regenerative Na⁺ current was obtained. For these stimuli, a slow, delayed current transient (mean amplitude, 118 pA) was also obtained. The bottom panelshows the same set of traces as the top panel, with different time and current amplitude scales, to illustrate the delayed current transient; Na⁺ currents are truncated. B, Peak amplitudes of (early) Na⁺ current (filled symbols) and of delayed current transient (open symbols) as a function of pulse duration, from three consecutive runs like the one illustrated in A. Both components are all-or-none, and they have the same threshold. The slight decrease of the Na⁺ current amplitude for pulse durations ≥0.5 msec is attributable to the fact that the peak of the Na⁺ conductance occurs after the pulses for shorter durations and during the pulses for longer durations. In the latter case, the corresponding Na⁺ current is reduced because the driving force is less.

The delayed current transient is mediated by GABA_Areceptors and is blocked by extracellular Cd²⁺

To study the properties of the delayed current transient further, the protocol shown in Figure 2 was adopted. The amplitude and duration of the voltage pulse were adjusted such that axonal Na⁺ currents were reliably activated. However, these parameters were maintained in such a range that somatic K⁺ current activation was kept at a minimum. In this way, voltage-dependent currents returned quickly toward baseline after the offset of the voltage pulse, allowing the full time course of the delayed current transient to be resolved. Such voltage pulses were repeated at a frequency of 0.2–1 Hz. The amplitude of the delayed current transient ran down during the course of whole-cell recording (Fig. 2A,B), as will be discussed below. However, this rundown had a relatively slow time course, so that it was possible to test the action of potential blockers by exchanging rapidly the bath.

Fig. 2.

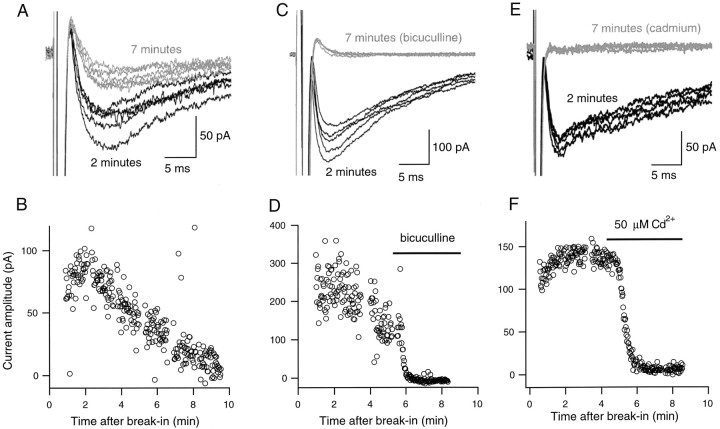
The delayed current transient is abolished by bicuculline and by Cd²⁺. A, Two series of five representative current responses to depolarizing somatic voltage pulses (test potential, −30 mV; pulse duration, 0.8 msec; pulse frequency, 0.67 Hz), one obtained shortly after breaking into the whole-cell recording mode (black traces), and the other obtained after 7 min of whole-cell recording (gray traces). B, Decay of the peak amplitude of delayed inward current transients as a function of time in whole-cell recording, from the same cell as in A. Six points deviate strongly from the main decay curve: they correspond to traces that were contaminated with a spontaneous IPSC. C, In another cell, responses to depolarizing somatic voltage pulses (test potential, −30 mV; pulse duration, 1 msec; pulse frequency, 0.67 Hz), shortly after breaking into the whole-cell recording mode (black traces), and after 7 min of whole-cell recording (gray traces), in the presence of bicuculline. D, Plot of the peak amplitude of delayed inward current transients as a function of time, from the same cell as in C. E, F, Same experiment as in C and D, except that the current was here challenged by a solution containing 50 μmCd²⁺.

We have recently reported that depolarizing somatic voltage pulses elicit autaptic currents in a fraction of stellate and basket cells (Pouzat and Marty, 1998). Autaptic currents and delayed current transients are triggered by the same stimulation protocols and are superficially similar. However, as will become apparent later, they can be unambiguously distinguished, and they reflect separate cellular mechanisms. Autaptic currents may be blocked by bicuculline and are sensitive to the extracellular Ca²⁺ concentration (Pouzat and Marty, 1998). Therefore, the effects of bicuculline and of the nonselective Ca²⁺ channel blocker Cd²⁺ were next tested on the delayed current transient. If the bath solution was exchanged to one containing 10 μm bicuculline, a rapid decay of the delayed current transient was observed (Fig. 2C,D; n = 4). After washout of bicuculline, partial recovery was obtained (data not shown). These results show that the delayed current transient is mediated by GABA_A receptors.

Rapid bath exchange with a solution containing 50 μmCd²⁺ similarly led to an abolition of the delayed current transient (Fig. 2E,F; n = 4), indicating that Ca²⁺ entry through voltage-gated Ca²⁺ channels was involved. Thus autaptic currents and delayed current transients share the same sensitivity to depolarization-induced Ca²⁺entry.

The delayed current transient depends linearly on potential

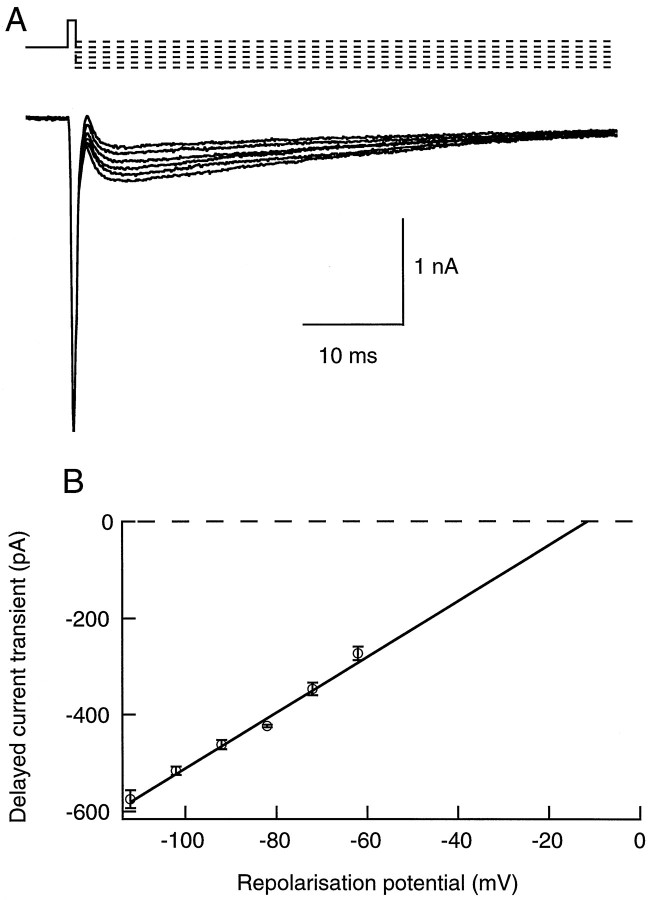
To obtain information on the I–V characteristics of the delayed current transient, the repolarization potential was altered (Fig. 3A). Over a range from −110 to −60 mV, the dependence of the peak amplitude of the transient on repolarization potential was linear (Fig.3B). From the intersect of the linear fit of this I–V curve with the voltage axis, values of reversal potentials comprised between −18 and 0 mV (n = 4; values corrected for the junction potential arising between the pipette and the bath solutions) were inferred. The results indicate that the delayed current transient reflects a conductance increase with a depolarized reversal potential and are consistent with the notion that the transient involves the activation of Cl⁻-selective GABAergic channels. However, because the pipette solution was loaded with a high Cl⁻solution, the expected Cl⁻ reversal potential assuming full equilibration is very close to 0 mV, whereas negative values were usually found for the extrapolated reversal potential. Furthermore, data obtained with more depolarized repolarization potentials indicated an upward bend of the I–V curve, leading to even more negative extrapolated reversal potential values (results not shown). This deviation from linearity, as well as the discrepancy between the expected value of E_Cland the value obtained by extrapolation of the I–V curve, can be explained by the model proposed later in this study (see Fig.12).

Fig. 3.

The delayed current transient depends linearly on potential. A, In this experiment the repolarization potential was changed from −110 to −60 mV. Depolarizing pulse was −20 mV (0.8 msec duration; repetition rate, 0.5 Hz). Traces were leak-subtracted. B, Plot of the peak amplitude of the delayed current transient (mean ± SEM) as a function of the repolarization potential, from four consecutive series such as the one shown in A. The regression line yields an extrapolated reversal potential of −13 mV.

The delayed current transient runs down during whole-cell recording

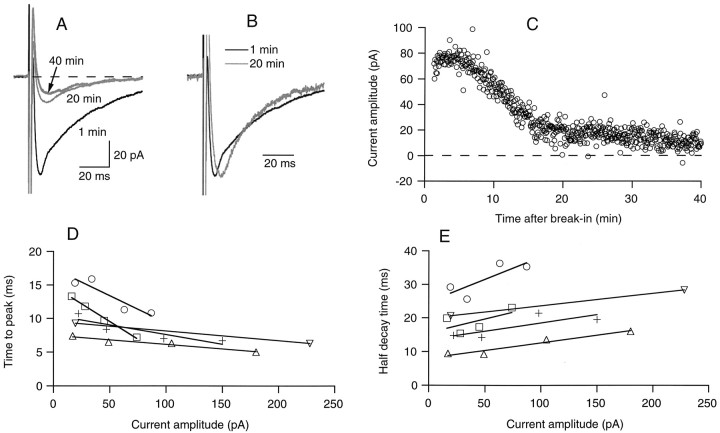
The variation of the amplitude of the delayed current transient as a function of time in whole-cell recording followed several phases (Figs. 2B,4C). Directly after the onset of whole-cell recording, there was a short period of increase with a modest and variable amplitude (“run up”), which lasted for up to 3 min. We presume that this increase at least in part reflects the equilibration of the Cl⁻-rich pipette solution with the cell compartment (the axon, see below) where the GABA receptors are located. The transient then reached a maximum, and irreversibly decreased thereafter (“run down”; Fig. 2B). When examined over a longer period, the run down appeared as biphasic (Fig.4C). The main part of the current decreased rather abruptly after 10–30 min of whole-cell recording, leaving a small amplitude component of up to 20 pA, which was almost totally insensitive to run down. This component, like the main component, was abolished by bicuculline (results not shown).

Fig. 4.

The delayed current transient fades during prolonged whole-cell recording. A, Mean delayed current transient at three distinct periods of whole-cell recording, showing a marked decay during the initial 20 min period, followed by a stabilization at a low level (gray traces). B, Superimposed normalized traces at 1 and 20 min of whole-cell recording, showing that the reduction of amplitude with time is accompanied by a lengthening of the time to peak and a decrease of the time of decay. C, Kinetics of washout, from the same data (stimulation frequency, 0.25 Hz; series resistance during recording, 14 MΩ). D, E, Relation of time to peak (D, measured from the onset of the voltage pulse) and half decay time (E) on peak current amplitude. Data are from four cells as the one illustrated in A and B, and from a fifth cell in which the current was inhibited by addition of bicuculline. Each data point corresponds to averages of ∼10–20 traces with homogeneous amplitudes. Results for individual cells are indicated by specific symbols and have been fitted by individual regression lines. Note that the slopes of the regression lines are all negative in D and positive in E.

Changes in kinetics associated with a reduction of the delayed current transient

A characteristic kinetic change occurred during washout, as became apparent after scaling up the reduced current (Fig.4B). As the peak amplitude was reduced, the rise time was increased and the decay time was decreased. Summary data from five cells including that illustrated in Figure 4B are presented in Figure 4D,E. Four of the data sets represent washout experiments, and the fifth plots the results of a cell where the current was reduced by addition of bicuculline. In each case the regression line through the data indicates a positive correlation between amplitude and decay time, and a negative one between amplitude and time to peak. Similar trends were obtained in other experiments with either bicuculline or Cd²⁺ (results not shown). Thus the correlations apparent in Figure 4D,E apply regardless of whether the delayed current transient was reduced as a result of rundown or after addition of bicuculline or Cd²⁺.

The delayed current transient is blocked by dialyzing the cell with 10 mm BAPTA

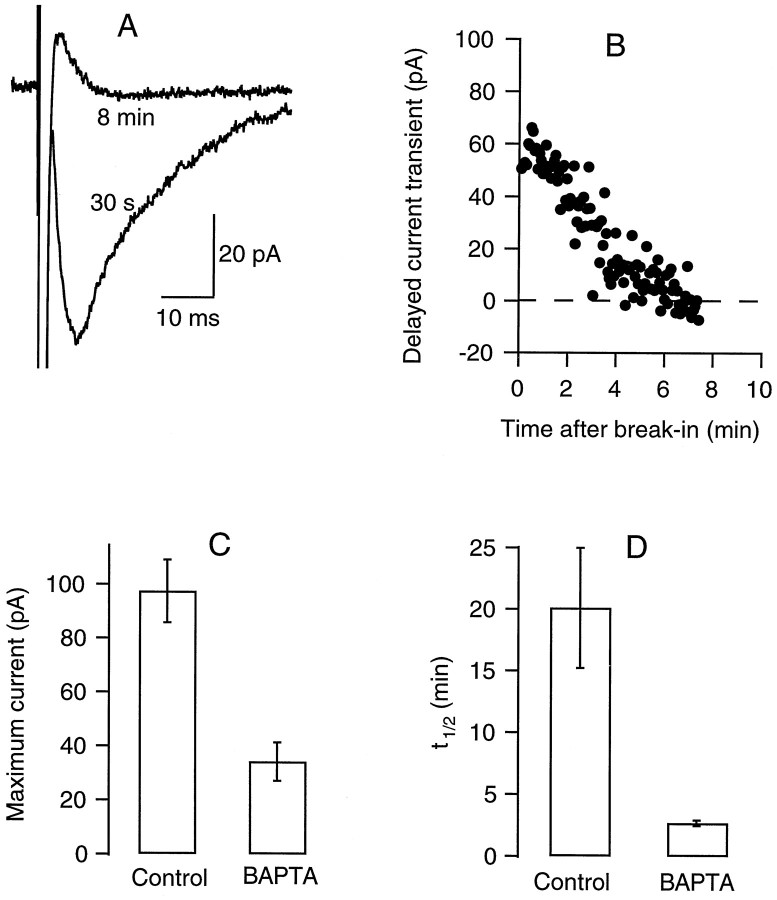
When an intracellular solution including 10 mm BAPTA was used instead of the usual 1 mm EGTA, the relation of the delayed current transient amplitude on whole-cell recording time changed drastically (Fig. 5). There was no run up, and the maximum current amplitude was less than in control conditions. The kinetics of rundown was monophasic and markedly accelerated with respect to control experiments. These results show that the delayed current transient is sensitive to the Ca²⁺ homeostasis of the recorded cell.

Fig. 5.

The delayed current transient is blocked by intracellular BAPTA. A, Mean delayed current transient (6 consecutive traces each; stimulation frequency, 0.25 Hz) recorded shortly after break-in (labeled 30 s) and after approximately 8 min of whole-cell recording. The pipette solution contained 10 mm BAPTA instead of the usual 1 mmEGTA. B, Time course of decay of the peak amplitude; series resistance during recording, 24 MΩ. C, D, Summary results for six control cells and six BAPTA-dialyzed cells, showing values (mean ± SEM) for the maximum peak delayed current transient (obtained during the first minutes of whole-cell recording) and for the time to half decay of this current. Average series resistance values were 24 ± 5 MΩ for the control cells and 36 ± 6 MΩ for the BAPTA-dialyzed cells.

The rise-time and decay of the delayed current transient are longer than those of IPSCs

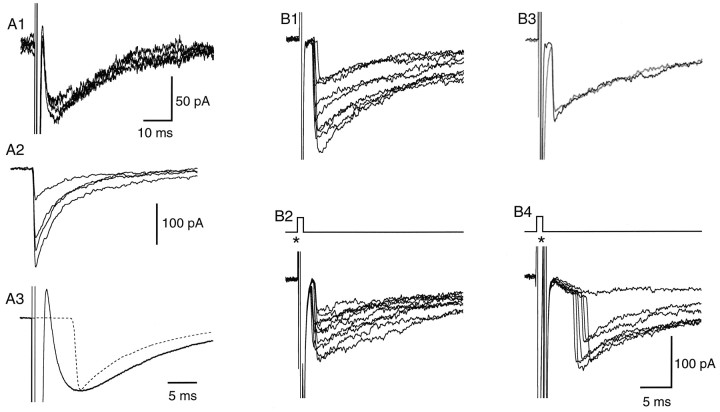
Spontaneous IPSCs recorded in stellate or basket cells have sharp rising phases, with a mean time to peak of 1.1 msec at room temperature (Llano and Gerschenfeld, 1993). In each cell where measurements of the delayed current transient were performed, the slow rise of the delayed current transient contrasted strikingly with the fast rise-times of the spontaneous IPSCs (Fig.6A). In addition, decay times were systematically slower for the delayed current transient than for IPSCs (Fig. 6A3). We considered the possibility that the conductances accompanying the axonal action potential might decrease the quality of the voltage clamp, leading to a distortion of the delayed current transient. This seemed unlikely because autaptic currents, when observed, have fast rise-times (Pouzat and Marty, 1998), although they are triggered by the same stimulations as delayed current transients, and furthermore because spontaneous IPSCs with fast rise-times are occasionally superimposed with the delayed current transient (data not shown). Nevertheless, the possibility of a distortion through the stimulated action potential was examined in a series of experiments in which extracellularly evoked IPSCs and delayed current transients were elicited in the same cell with variable intervals. When the stimuli were timed such that the extracellularly evoked IPSCs occurred near the onset of the delayed current transients, the IPSCs retained their fast rise-times (Fig. 6B ). These results suggest that the slow kinetics of the delayed current transient is not simply derived from a deterioration of the voltage clamp after the axonal action potential.

Fig. 6.

The delayed current transient has slow onset and decay kinetics. A1, A2 , Examples of superimposed traces of delayed current transient (A1) and of spontaneous IPSCs taken in the same recording (A2). A3, Comparison between scaled averages of the autoreceptor current (continuous line, average of 142 sweeps) and of the spontaneous IPSCs (dotted line, average of 150 IPSCs; peak amplitude before scaling: 210 pA). B1, Examples of extracellularly evoked IPSCs, from another cell. B2, Here extracellular stimulations (at the time indicated by the star) were combined with somatic depolarizations. B3, Comparison of single evoked IPSCs obtained without (black trace) or with (gray trace) somatic depolarization. Rise-times are rapid in both cases. B4, A further series of evoked IPSCs, obtained with another location of the stimulation pipette. Here the evoked IPSCs are seen to superimpose on slowly rising delayed current transients.

The delayed current transient is developmentally regulated

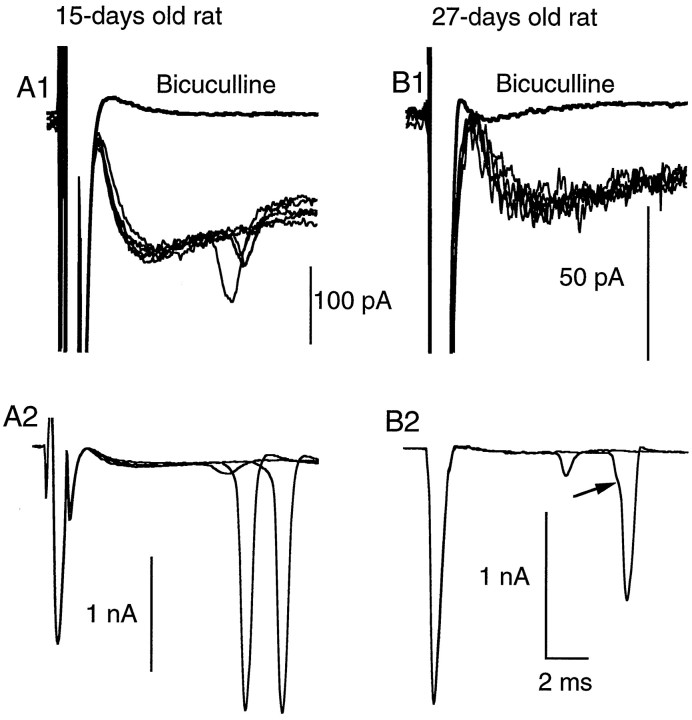
It was reported recently that activation of AMPA receptors increases the rate of miniature IPSCs in mouse cerebellar stellate and basket cells, indicating the presence of axonal ionotropic glutamate receptors in this preparation (Bureau and Mulle, 1998). This effect wanes during development, suggesting a downregulation of presynaptic AMPA receptors. In view of these results, we compared the properties of the GABAergic delayed current transient during two age periods: 12–15 d and 29–49 d. Results presented so far correspond to the first of these periods. For this age group, the delayed current transient was consistently observed (92% of the recordings, n = 41; estimated threshold for detection: 10 pA). When observed, the delayed current transient had a mean amplitude of 82 ± 17 pA. By contrast, delayed current transients in the older age group were observed much more sparingly, with an incidence rate of 14% (n = 35). When observed, they were of smaller amplitude, with a mean amplitude of only 15 ± 3 pA (Fig.7B1).

Fig. 7.

The delayed current transient is associated with enhanced axonal excitability. A1, Superimposed exemplar traces of delayed current transient; regenerative responses are present in three traces out of six. No such responses were seen in the presence of bicuculline (thick line; average trace). A2, Three further traces from the same experiment, shown with a less expanded vertical scale. Two of the traces contained large amplitude regenerative responses. B1, B2, Similar results obtained from an experiment with an older animal (27-d-old instead of 15-d-old in A1, A2). In this case the amplitude of the delayed current transient is small (∼30 pA), but regenerative responses are nevertheless observed before application of bicuculline.

Autapses were observed in the same series of experiments. As reported earlier (Pouzat and Marty, 1998), autapses are rather frequent in the group 26–49 d, with an incidence rate of 26%. In two cells from this group (6% of the cases), autaptic currents and autoreceptor currents were superimposed. At age 12–15 d, autapses occurred in only 5% of the recordings (2/42 cells). In these two cases the probability of failure of the autaptic currents was very low, as expected from a previous study on the evolution of the probability of release at the interneuron–Purkinje cell synapse (Pouzat and Hestrin, 1997). Because of the high activity of autaptic currents, it could not be decided in these two cells whether an autoreceptor current was also present.

Active responses associated with the delayed current transient

In some experiments, fast inward current signals were superimposed on the early part of the decay phase of the delayed current transient (Fig. 7). These signals occurred often with two different amplitudes, one of the order of a few tens of picoamperes, and the other on the order of 1 nA (Fig. 7 A1,A2). The time course and amplitude of the larger signals were similar to those of the Na⁺ current transients directly associated to the voltage pulse, suggesting that the delayed current transient induced voltage-clamp escape in the axon. The smaller events appeared earlier than the larger ones (Fig. 7A2,B2), and occasionally a transition was observed from the smaller to the larger level (Fig.7B2, arrow). Although in most recordings each delayed current transient produced maximally a single spike, in one experiment up to three spikes were obtained, with regular interspike intervals of ∼10 msec (data not shown).

Such regenerative signals were found in both of the age groups studied. However, they were more prominent in the older age group, where they occurred in 60% of the recordings displaying delayed current transients (3/5 cells), compared with a proportion of 8% in the younger age group (3/36 cells). Furthermore, in accordance with the general difference in peak amplitudes between the two groups, spikes were associated with delayed current transients of a few tens of picoamperes in the older age group, as opposed to 100 pA or more in the younger age group (compare Fig. 7, A1 and B1; note vertical scale difference). In all recordings where delayed current transients elicited spikes, spontaneous IPSCs (occurring at ordinary synapses) with amplitudes similar to or larger than that of the delayed current transient were present; none of these IPSCs elicited active currents. These observations show that the active currents are not caused by voltage escape resulting from current flow across the series resistance to the cell, and that they are specifically associated with the delayed current transient.

After application of bicuculline, the secondary axonal spikes were abolished in parallel with the delayed current transients (Fig.7A1,B1).

All of these observations indicate that the delayed current transient elicits voltage-clamp escape in the axon and that this occurs more readily in the older than in the younger age group.

Results with neurobiotin-filled cells

In a series of experiments, neurobiotin was included in the pipette solution, and the slices were processed with the hope of recovering the morphology of the cells. However, the proportion of interneurons that gave good stainings was low (<10%), whereas parallel staining of Purkinje cells was almost always successful. Success rates were particularly low if the intracellular solution was rich in Cl⁻ ions, as required for the measurement of autaptic currents and delayed current transients. As a result, only three cells yielded electrophysiological recordings together with satisfactory staining. One of these cells had an autaptic current, and the two others had only an autoreceptor current. Two of the cells, including the cell with autaptic currents, had regions of close apposition between axonal and dendritic domains, with potential autaptic sites. The third cell is illustrated in Figure8. There is clearly no autaptic site in this cell, and yet a substantial delayed current transient was measured. This demonstrates that the delayed transient current does not require an autapse in the recorded cell. In addition, the axonal and dendritic domains are largely distinct in the cell of Figure 8; this also applied to other cases in which large delayed transient currents were recorded (Fig. 9). One branch of the axon does appear to overlap with the dendritic tree in Figure8A, but close inspection reveals that this branch was above the plane of the dendrites and remained at a distance of ≥2 μm of the nearest dendrite. At such distances dilution by diffusion from a point source is expected to reduce the local GABA concentration below the threshold for activation of GABA_A receptors (Clements, 1996; Barbour and Häusser, 1997). This evidence suggests that the extent of overlap between axonal and dendritic domains of interneurons is quite limited and that one cannot account for the current on the basis of spillover from the axonal to the dendritic region.

Extracellular stimulation of the delayed current transient

It was reasoned that if the delayed current transient was caused by activation of the axon, it should be obtainable by suitable extracellular stimulation in the axon domain. Interneurons tend to send their axon in the parasagittal plane, along an axis parallel to the Purkinje cell layer. However, the direction of the course of the main axon of any given cell along the Purkinje cell layer cannot be predicted. After establishing a whole-cell recording on a target cell, extracellular stimulations were therefore applied in alternation on one side and on the other. At both locations, the stimulation pipette was positioned in the proximal part of the molecular layer, where basket cell axons are normally found, at a distance of ∼150 μm from the soma. It was found that although no response was obtained on one side, an action potential could be elicited from the other side beyond a well defined threshold (Fig. 9B1,B2). This was monitored under somatic voltage clamp as a rapid inward current transient resembling that obtained with somatic stimulation. After the rapid inward current, a delayed current transient very similar to that obtained with somatic stimulation was also obtained (Fig. 9, compare B2 and B3). This signal decreased during prolonged whole-cell recording in parallel to the somatically evoked delayed current transient. When stimulating on the other side of the soma, neither an action potential nor a delayed current transient was obtained, even if the stimulation intensity was increased to three times the threshold value on the responsive side (Fig. 9B4; n = 3). For these experiments, Lucifer yellow was included in the pipette solution, and the morphology of the recorded neuron was determined by epifluorescence after completion of the measurements. The axon was found on the side where stimulations had been successful (Fig.9A; n = 3).

These experiments show that direct stimulation of the axon under steady somatic voltage clamp, like somatic depolarization, elicits the same sequence of fast Na⁺ current and delayed current transient. Under the conditions of Figure 9, somatic voltage clamp uncouples the dendrites from the axon, effectively preventing activation of somatodendritic voltage-dependent channels. Therefore, the Na⁺ channels activated in Figure 9B2 are axonal rather than somatodendritic. The similarity with the results obtained when depolarizing the soma confirms that the fast Na⁺ current elicited on somatic stimulation reflects the activation of axonal Na⁺ channels and that the delayed current transient requires firing of an action potential in the axon.

Simulations

This section presents simulations of somatic currents elicited in a voltage-clamped neuron by activation of synaptic conductances located either in dendrites or in the axon. In performing these simulations, particular attention was given to the following features of the delayed current transient: (1) slow onset and decay kinetics compared with that of spontaneous IPSCs; (2) link between peak amplitude and kinetics, whereby large events have short rise-times and slow decay times, whereas small events have long rise-times and short decay times; (3) negative extrapolated reversal potential; and (4) presence of spikes on the decay phase in some experiments.

Dendritic receptors

Feature 1 suggests at first that the delayed current transient could be a filtered version of the autaptic currents reported previously (Pouzat and Marty, 1998) and that they could arise from axodendritic contacts of the interneuron onto itself. Morphological data (Llano et al., 1997, their Fig. 5; Pouzat and Hestrin, 1997, their Fig. 1A2, B5) suggest that autaptic contacts are highly localized. Consequently, simulations were performed with one localized input along an otherwise uniform cable. The length and radius of the cable were set at 50 and 0.4 μm, respectively, corresponding to the upper and lower bounds of values for interneuron dendrites at the age 12–15 d (Llano et al., 1997, their Fig. 5; Pouzat and Hestrin, 1997, their Fig. 1A2; this work, Figs. 8, 9). Such a cable therefore should represent maximum dendritic filtering in this preparation. The passive electrical parameters of the dendrites were as given in Materials and Methods. No active conductance was included. Synaptic inputs with a reversal potential at 0 mV were positioned at various locations along the dendrite. The synaptic conductance had a rise-time of 1.1 msec (Llano and Gerschenfeld, 1993) and bi-exponential decay kinetics (Eq.9). Figure 10 shows the results of such simulations for an input located close to the soma (A) and for an input located near the tip of the dendrite (B). Each graph presents several traces corresponding to various peak conductances. The insets show scaled versions of the largest (continuous line) and smallest (dashed line) current. In all traces, including those generated at the distal site, current kinetics are almost identical to those of the underlying conductance and do not depend significantly on current amplitude. In particular, no change in rise-time is observed. These results strongly argue against dendritic filtering as the explanation of the slow kinetics of the delayed current transient. Nevertheless, we considered the possibility that the cytosol of interneurons may have an unusually low conductivity, thus leading to more severe filtering than predicted in Figure 10A,B. Therefore, additional simulations were performed assuming larger values of R_i (0.25 and 0.5 kΩ·cm instead of 0.1 kΩ·cm). With these values of R_i, a significant attenuation of the peak amplitude was observed for the largest currents at the distal input and was associated with a slower decay time course. However, even in these extreme conditions, no significant increase in rise-time was observed (data not shown).

We conclude from these simulations that cable filtering generated at interneuron dendrites cannot account for the slow rise of the delayed current transient.

Distributed axonal receptors without active conductances

Having rejected a dendritic site of origin for the delayed current transient, we performed next a series of simulations on the assumption that it is generated in the axon. This hypothesis is immediately compatible with the association of axonal spikes with the delayed current transient (feature 4). The possibility was considered that the delayed current transient could be generated at axo-axonic autapses. However, such autapses have not been observed morphologically in any preparation. Furthermore, examination of the available data at interneurons (Llano et al., 1997, their Fig. 5; C. Pouzat, unpublished results) fails to reveal any apposition between distinct regions of the axonal tree and thus does not support this possibility. Finally, axo-axonic autapses would be expected to yield widely fluctuating currents including failures, whereas the delayed transient current varied little from trial to trial. Overall, it seemed highly unlikely that the delayed current transient would be caused by axo-axonic contacts. We next considered the possibility that this current would reflect the activation of autoreceptors along the axon, after the activation of many release sites. We therefore performed simulations of an axon-like cable with a length of 200 μm, a radius of 0.25 μm, and a uniformly distributed autoreceptor conductance. Passive cable properties were as described in Materials and Methods. Autoreceptor conductance densities were empirically set at 0.25, 0.64, 0.89, 1.27, 1.91, and 2.55 mS/cm² to cover the range of experimentally observed amplitudes of the delayed current transient. (These numbers correspond to conductances of 0.2, 0.5, 0.7, 1, 1.5, and 2 × 10⁻¹⁰ S per site, assuming one site every 5 μm; see below.) The rise-time of the conductance was somewhat increased with respect to the previous simulation (1.5 msec instead of 1.1 msec) to take into account the jitter expected among release sites attributable to the propagation of the action potential. (The propagation time of 0.4 msec was taken in view of the results of Fig.11B,C.) Decay kinetics were the same as above. A first set of simulations was run without active conductances (Fig. 10C). Simulated currents have many of the qualitative features of the delayed current transients. Their kinetics are slower than those of spontaneous IPSCs, as may be seen in Figure 10 (compare traces in C with those in A and B) and are within the range of the observed kinetics of the delayed current transient (Fig.4D,E). The simulations display correlations between amplitude and rise-time on the one hand, and between amplitude and decay time on the other, which match those observed experimentally (compare Fig. 10C, inset with Fig. 4B).

To obtain insight into the factors that determine the characteristics of the delayed current transient, an analytical solution was derived for a simplified but closely related situation: a semi-infinite cable with an instantaneously rising distributed conductance (Appendix ). The analytical solution shows that for large synaptic conductance densities, the peak current grows like the square root of the synaptic conductance density (Eq. EA.20) and furthermore that the rise-time is proportional to the inverse of the square of the peak current amplitude (Eq. EA.22).

Other simulations were performed with different cable lengths ranging from 100 to 600 μm (data not shown). In general, the results were almost totally independent of the cable length over this range, except that with the shortest cable length (100 μm), peak amplitudes for small synaptic current densities were somewhat reduced, and decay kinetics were accelerated. This acceleration was the same for all autoreceptor conductance densities, so that the correlation between amplitude and kinetics was left unchanged. Consistent with these simulations, an analytical solution for a finite cable submitted to a step increase in distributed conductance predicts that the amplitude of the recorded current saturates as a function of cable length (Appendix). These results indicate that somatic recordings gather information from the proximal end of the cable only, essentially from the first 100 μm. Therefore, attaching axon collaterals to the main axon should have no major consequence on the predicted currents. Other simulations were performed changing the values of R_i (range, 0.1–0.25 kΩ·cm) and R_m (range, 50–100 kΩ·cm²): the qualitative features apparent in Figure 10C were maintained throughout this range of parameters.

Distributed axonal receptors with active conductances: secondary spikes

In the next series of simulations, voltage-dependent Na⁺ and K⁺ conductances were included. Because quantitative information on axonal voltage-dependent conductances in this preparation is almost totally lacking, the choice of the parameters describing these conductances was largely arbitrary. We chose a set of parameters derived from simulations performed byTraub et al. (1994) for the axonal membrane of hippocampal pyramidal cells, as detailed in Materials and Methods. The chief goal of these simulations was to see whether the features apparent in Figure10C would be conserved with a more realistic set of axonal conductances, and also whether features 3 and 4 of the delayed current transient could be duplicated with reasonable parameters for Na⁺ and K⁺ conductances. Again, the cable length was set at 200 μm and its radius at 0.25 μm. The responses of such a cable to a voltage pulse having a duration of 0.5 msec and an amplitude of 50 mV were computed. The synaptic conductance was triggered 1 msec after the beginning of the voltage pulse, and its kinetic parameters were the same as in Figure 10C.

Figure 11A shows the computed currents for a series of autoreceptor conductance densities. It is immediately apparent that the model accounts for the presence of spikes on the decay phase of the current (feature 4). The presence of spikes was critically dependent on the properties of voltage-dependent conductances as well as on the autoreceptor conductance density. The interplay between voltage-dependent and GABAergic conductances may be appreciated by examination of the time course of the voltage at different locations along the cable (here 50, 100, 150, and 199 μm from the soma; Fig.11B,C). Figure 11B illustrates such voltage profiles for an autoreceptor conductance density value (1.27 mS/cm²) within the critical range where secondary spikes occur during the decay of the delayed current transient. The secondary spike, which is triggered by the autoreceptor conductance, is generated at the end of the cable and is therefore an antidromic spike. Figure 11C shows similar voltage profiles for a higher density of axonal GABAergic channels. Comparison between B and C reveals the reasons why some synaptic conductance densities give rise to secondary spikes whereas others do not. If the density is too large, it maintains the membrane potential too depolarized to allow Na⁺ conductance to recover from inactivation, as exemplified in Figure 11C. If it is too small, the depolarizing autoreceptor current is not strong enough to bring the membrane to threshold. In Figure 11, only one autoreceptor conductance density (1.27 mS/cm²) gave rise to spikes, whereas smaller and larger densities did not. Increasing the Na⁺ conductance density (to 100 or 200 mS/cm²) and/or reducing the K⁺conductance density (to 200 mS/cm²) increased the range of synaptic conductance densities that led to spike generation (down to 0.75 and up to 2 mS/cm²). Slowing down the kinetics of the voltage-dependent conductances (by a factor of 2) had the same consequence (data not shown). Changing the length of the cable (range, 100–600 μm) did not substantially alter the results (data not shown).

It should be noted that in the simulations, secondary spikes were not assumed to generate any autoreceptor conductance increase. In reality, however, a secondary spike would be followed by its own autoreceptor current.

Distributed axonal receptors with active conductances: amplitude and kinetics of the delayed current transient

Figure 11D shows a peak scaling of two of the currents of Figure 11A. The continuous line is from the autoreceptor conductance density of 5.1 mS/cm², and the dashed line is from the autoreceptor conductance density of 0.64 mS/cm². It may be seen that the higher peak amplitude gives rise to faster onset and slower decay. Thus the model reproduces the correlation between peak amplitude and kinetics that is observed experimentally (Fig. 4).

Figure 12 illustrates the effects of active conductances on the measured delayed current transient. In Figure 12A, currents corresponding to a conductance of 0.64 mS/cm² are compared without (dashed line) and with (thick continuous line) active conductances. Inclusion of voltage-dependent channels results in a reduction of the peak amplitude of the delayed current transient and in a lengthening of its rise-time.

Figure 12B compares the peak delayed current transient values obtained from the analytical solution of the infinite passive cable (dashed line, from Eq. EA.17), from the passive cable simulation (triangles, from Fig. 10C), and from the active cable simulation (circles, from Fig.11A). At any density of autoreceptor currents, addition of voltage-dependent conductances results in a strong reduction of the peak amplitude of the delayed current transient.

Finally, Figure 12C,D is a simulation of the experiments used to evaluate the reversal potential of the delayed current transient. The reduction of the apparent peak amplitude of the delayed current transient increases with depolarization because of the voltage dependence of the K⁺ conductance, leading to an apparent negative reversal potential (Fig. 12D). The I–V curve nevertheless remains approximately linear in the voltage range used in the tail experiments (−110 to −60 mV; Fig.12D). The deviation is actually larger in Figure12D than experimentally observed, probably because the K⁺ conductance assumed in the simulation is larger than in reality.

An estimate of the contribution of each individual release site to the total autoreceptor current

The simulations presented in Figure 12A (circles) indicate that a somatically recorded delayed current transient of 80 pA (the average value at age 12–15 d) corresponds to an axonal conductance of 1.4 mS/cm². This is not an accurate estimate because it depends on specific assumptions concerning the voltage-dependent K⁺conductances in the axon, which are poorly characterized. Nevertheless, this estimate is rather consistent when changes of the K⁺ current characteristics are performed within the frame of parameters compatible with the known properties of interneuron currents (size of somatically measured K⁺ currents, kinetic properties of the delayed current transient, etc.), so that it provides a useful indication of the order of magnitude of the autoreceptor current.

Because of the steep dependence of the concentration on distance during diffusion from a point source, and of the relatively low affinity of GABA_A receptors for GABA, the transmitter that is released at one varicosity is unlikely to activate GABA_A receptors that are much beyond the limits of the synaptic cleft (Clements, 1996;Barbour and Häusser, 1997). For this reason, the currents that are measured most likely reflect the activation of receptors that belong to the presynaptic membrane of each varicosity. Assuming an axon radius of 0.25 μm and a spacing between varicosities of 5 μm (Pouzat and Kondo, 1996), the above current density translates to a mean current value (at −70 mV) of ∼10 pA per varicosity.

Because the simulation performed in Figures 10-12 assumes an axon 200 μm in length, the same current density corresponds to a total maximum current (assuming a driving force of 70 mV, and a homogeneous distribution of one varicosity every 5 μm of axon length) of 400 pA, five times larger than the value of the delayed current transient. This estimate needs to be corrected upward to account for the presence of side branches in the axonal tree (Bishop, 1993; Pouzat and Kondo, 1996), leading to a corrected value on the order of 1–2 nA.

It is instructive to compare the value of 10 pA per varicosity with an estimate of the postsynaptic current obtained under symmetrical Cl⁻ conditions. The average quantal size obtained at single-site interneuron–interneuron synapses is 61 pA, and the corresponding release probability is 0.28 [Kondo and Marty (1998); the latter value is derived from their Table 1]. Thus one release site gives on average a postsynaptic current of 17 pA per action potential, a value only slightly larger than the estimate for the presynaptic autoreceptor current. These estimates suggest that the number of presynaptic receptors may be only slightly smaller than that of postsynaptic receptors in the present preparation.

Although the estimated density of 1.4 mS/cm² is much smaller than the values assumed for axonal Na⁺ and K⁺ conductances, it may have a significant effect on axonal excitability. In pituitary gland nerve terminals, the density of presynaptic GABA_A conductance was estimated (under symmetrical Cl⁻ conditions) at only 0.38 mS/cm², yet this density was shown to significantly inhibit action potential firing by interfering with Na⁺ current inactivation (Zhang and Jackson, 1995a;Jackson and Zhang, 1995).

DISCUSSION

The delayed current transient: a Ca²⁺-dependent GABAergic current with unconventional properties

The delayed current transient is blocked by bicuculline, indicating that it is mediated by GABA_A receptors. It is blocked by extracellular Cd²⁺, indicating that it depends on voltage-dependent Ca²⁺ entry. On the basis of these criteria, the delayed current transient is similar to the many examples of GABAergic IPSCs that have been described in CNS preparations. However, in other respects the delayed current transient has quite unusual properties. It is blocked by perfusion of the recorded cell with BAPTA, suggesting that the release of GABA takes place in the very cell in which currents are recorded. It also has remarkable kinetic properties: it displays a slow rise-time, suggesting attenuation through cable filtering, and a unique correlation between peak amplitude and the kinetics of both onset and decay. Finally, its fluctuations from one trial to the next are much smaller than for ordinary GABAergic IPSCs of comparable mean amplitude. We will next examine various possible interpretations of the delayed current transient in the light of these observations.

The delayed current transient is not an autaptic current

We demonstrated recently the presence of functional autapses in cerebellar stellate and basket cells by using essentially the same experimental protocol as that of the present study (Pouzat and Marty, 1998). Like the delayed current transient, autaptic currents are triggered by an axonal spike, they are blocked by bicuculline, and they depend on voltage-dependent Ca²⁺ entry (Pouzat and Marty, 1998). However, autaptic currents in interneurons have sharply rising onsets that contrast with the slow rise of the delayed current transient. Furthermore, autaptic currents fluctuate widely from one trial to the next. Quantal sizes ranging from 21 to 178 pA (symmetrical Cl⁻ conditions) have been estimated from these fluctuations, and failure rates average 80%. In all these respects, autaptic currents resemble ordinary interneuron–interneuron IPSCs, but differ markedly from the delayed current transients described here. A further difference concerns developmental regulation: whereas the rate of occurrence of autaptic currents grows during development, the delayed current transient is much less prominent in adult animals than at 2 weeks.

This series of differences between delayed current transient and autaptic currents suggests that the underlying cellular mechanisms are distinct.

The delayed current transient is not mediated by electrical junctions among interneurons

It is conceivable that delayed current transients could reflect the detection of IPSCs elicited in neurons that would be postsynaptic to the recorded cell if presynaptic and postsynaptic neurons were linked by electrical junctions. In previous publications, we have investigated the possible presence of electrical junctions among interneurons. Although there is some evidence for the presence of electrical junctions, these junctions are rare and when present are associated with a small conductance [on the order of 1 nS at most; seeVincent and Marty (1996); Pouzat and Marty (1998)]. The rare occurrence of electrical junctions, compared with the very high rate of occurrence of delayed current transients, make it unlikely that one could be the source of the other. Second, the conductance of electrical junctions, when present, is much too low to ensure action potential transfer from one cell to the next [as discussed in Pouzat and Marty (1998)]. Third, if delayed current transients were caused by the detection of IPSCs elicited in neighboring postsynaptic interneurons through gap junctions, the high variability and high failure rate of interneuron–interneuron IPSCs (Kondo and Marty, 1998) would be expected to yield a corresponding high variation in the delayed current transients including occasional failures. This contrasts with the low variability that is experimentally observed for delayed current transients. Finally, if delayed current transients were generated by IPSCs in neighboring cells, they should occur randomly because of the ongoing firing of interneurons. However, no delayed current transient was ever observed between stimulations. Altogether, the hypothesis of a participation of electrical junctions in the generation of delayed current transients can be safely dismissed.

The delayed current transient is attributable to activation of axonal GABA_A receptors

A telltale property of delayed current transients is that they are often associated with signs of active responses (Fig. 7). This escape cannot occur in the dendrites because the triggering current is only on the order of 100 pA. Simulations similar to those illustrated in Figure10 indicate that injections of such currents in the dendrites elicit only minor voltage changes (≤6 mV), which are clearly insufficient to trigger action potentials. Therefore it can be concluded that delayed current transients elicit voltage escape in the axon. These signals occur only during the decay phase of the delayed current transients, and they tend to be larger if they occur later, probably because the Na⁺ channels are still recovering from the inactivation caused by the initial axonal spike. We propose that these signals are caused by the activation of axonal GABA_Areceptors. Because the entire neuron is loaded with the high Cl⁻ solution, activation of axonal receptors induces local depolarization and may lead to voltage escape.

The axonal receptor hypothesis readily accounts for the other unusual properties of the delayed current transient. Because the axon is thin and long, and because it contains a high density of voltage-dependent channels, severe distortions are expected to occur when the axonal current is monitored in a somatic voltage-clamp recording. This, according to the simulations of Figures 10-12, accounts for the difference between the kinetics of the delayed current transient and that of dendritic IPSCs. Because the axon has many release sites, as opposed to one or a few release sites in any specific interneuron–interneuron synapse, relative fluctuations in the total number of releasing sites are expected to be much less in the first case than in the second.

Physiological relevance of the autoreceptor current

As in the case of any presynaptic receptor, several functional roles can be envisaged for the GABAergic autoreceptors of cerebellar interneurons. The first possibility is a participation in axo-axonic synapses, as occurs at the crayfish neuromuscular junction, in the mammalian spinal cord, and in retinal bipolar cells of fish (for review, see Rudomin, 1990; McGehee and Role, 1996). In the present case, however, such a mechanism is unlikely, for reasons that have already been discussed. Alternatively, presynaptic GABA_A receptors could be activated by spillover from nearby GABAergic terminals, as occurs at peptidergic terminals in the pituitary (Zhang and Jackson, 1995b). In cerebellar slices, presynaptic GABAergic receptors could be sensitive to the buildup of the bulk concentration of GABA in the molecular layer after sustained activity of interneurons, leading to a negative feedback curtailing excessive inhibitory activity. A final possibility is that presynaptic GABAergic receptors are sensitive to the phasic release of GABA from the cell that carries the receptors (autoreceptors), as proposed earlier in hippocampal cultures (Vautrin et al., 1994). The fact that autoreceptor currents can be measured gives strong support to this possibility. The currents that are generated in the axon could contribute to regulate the firing rate. However, it is difficult to predict the exact consequences of the activation of the autoreceptor current, because this necessitates a knowledge of the position of the reversal potential of the GABAergic channels under physiological conditions, which is presently unknown.

Another open question is whether the axonal and dendritic GABA channels have the same properties. In fish retinal bipolar cells, GABA_C channels underlie the presynaptic GABA conductance (for review, see McGehee and Role, 1996). In the present work, however, as in the pituitary and the spinal cord of mammals, the presynaptic autoreceptor current is blocked by low concentrations of bicuculline and thus appears to be carried by GABA_Achannels. In the pituitary, presynaptic GABA_A channels have unique single-channel properties: subconductance states are much less prominent than in somatodendritic channels (Zhang and Jackson, 1995b), raising the intriguing possibility that axonal and somatodendritic GABA_A currents could be attributable to different combinations of channel subunits.

Current delivered by the amplifier in response to a step increase of a distributed conductance for a semi-infinite cable

We consider here a semi-infinite cable voltage-clamped at its resting value at the origin. We call V the deviation of the membrane voltage from its resting value, and we assume that at t = 0 the cable is uniformly at rest. At rest, the cable has a cytoplasmic resistivity R_i, a membrane resistivity R_m, and a membrane capacitance C_m. At t = 0, a uniformly distributed conductance density G_s, with a reversal potential E_s, is activated. Once activated, G_s remains constant.

To simplify calculations, we use dimensionless parameters (Rall, 1977). Then the cable equation takes the form:

$$\frac{\partial }{\partial T} V=\frac{{\partial }^2}{\partial X^2} V-V-R_{\text{m}}·G_{\text{s}}·(V-E_{\text{s}}),$$ Equation EA.1

with the boundary conditions:

$$V(X=0,T)=0,$$ Equation EA.2

and

$$V(X,T)\underset{X\to \infty }{\overset{}{\to }} 0,$$ Equation EA.3

and the initial condition:

$$V(X,T=0)=0.$$ Equation EA.4

We use the Laplace transform method to solve the problem. Applying the Laplace operator:

$$\underset{T=0}{\overset{\infty }{\int }}\text{dT}·e^{-\text{p}·T},$$ Equation EA.5

on both sides of Equation EA.1 and using the initial conditions (Eq. EA.4) and the boundary condition (Eq. EA.3), we get:

$$p·V_L(X,p)=\frac{{\partial }^2}{\partial X^2} V_L(X,p)-(1+R_{\text{m}}·G_{\text{s}})·V_L(X,p)+\frac{R_{\text{m}}·G_{\text{s}}·E_{\text{s}}}{p},$$ Equation EA.6

where:

$$V_L(X,p)=\underset{T=0}{\overset{\infty }{\int }}\text{dT}·e^{-\text{p}·T}·V(X,T).$$ Equation EA.7

Applying the Laplace operator (Eq. EA.5) to the boundary conditions (Eqs. EA.2 and EA.3) gives:

$$V_L(0,p)=0$$ Equation EA.8

and:

$$V_L(X,p)\underset{X\to \infty }{\overset{}{\to }} 0.$$ Equation EA.9

The solution of the inhomogenous ordinary differential equation (A.6), with the boundary conditions (Eqs. EA.8 and EA.9), is (Tuckwell; 1988, pp 139–141):

$$V_L(X,p)=-\frac{R_{\text{m}}·G_{\text{s}}·E_{\text{s}}}{p·(1+R_{\text{m}}·G_{\text{s}}+p)}·\left(e^{-X·\sqrt{1+R_{\text{m}}·G_{\text{s}}+p}}-1\right).$$ Equation EA.10

The inverse transform of Equation EA.10 is not easy to find but is not needed here. Rather, we have to calculate the current delivered by the amplifier. This is given, according to Equations 3.6 and 3.7 ofRall (1977), by:

$$i_{\text{c}}(T)=-G_{\infty }·\frac{\partial }{\partial X} V(X=0,T),$$ Equation EA.11

$$G_{\infty }=\frac{\pi ·\sqrt{2}·a^{\frac{3}{2}}}{\sqrt{R_{\text{i}}·R_{\text{m}}}},$$ Equation EA.12

where G_∞ is the input conductance of the semi-infinite cable. In view of the identity:

$$\underset{T=0}{\overset{\infty }{\int }}\text{dT}·e^{-\text{p}·T}·\frac{\partial }{\partial X} V(X,T)=\frac{\partial }{\partial X} V_L(X,p),$$ Equation EA.13

the problem of calculating i_c(t) amounts to finding the inverse transform of the partial derivative (with respect to X) of V_L at X = 0. This is, according to Equation EA.10:

$$\frac{\partial }{\partial X} V_L(X=0,p)=\frac{R_{\text{m}}·G_{\text{s}}·E_{\text{s}}}{p·\sqrt{1+R_{\text{m}}·G_{\text{s}}+p}}.$$ Equation EA.14

Using a table of Laplace transforms (Gaskell, 1970, Eq. 44), we obtain:

$$\frac{\partial }{\partial X} V(0,T)=\frac{R_{\text{m}}·G_{\text{s}}·E_{\text{s}}}{\sqrt{1+R_{\text{m}}·G_{\text{s}}}}·\text{erf}\left(\sqrt{1+R_{\text{m}}·G_{\text{s}}}·\sqrt{T}\right),$$ Equation EA.15

where:

$$\text{erf}(X)=\frac{2}{\sqrt{\pi }}\underset{0}{\overset{X}{\int }}\text{dY}·e^{-Y^2}.$$ Equation EA.16

Combining with Equation EA.11 leads to the solution:

$$i_{\text{c}}(T)=-G_{\infty }·\frac{R_{\text{m}}·G_{\text{s}}·E_{\text{s}}}{\sqrt{1+R_{\text{m}}·G_{\text{s}}}}·\text{erf}\left(\sqrt{1+R_{\text{m}}·G_{\text{s}}}·\sqrt{T}\right).$$ Equation EA.17

When T → ∞, i_c(T) takes the value:

$$i_{\text{p}}=-G_{\infty }·\frac{R_{\text{m}}·G_{\text{s}}·E_{\text{s}}}{\sqrt{1+R_{\text{m}}·G_{\text{s}}}}.$$ Equation EA.18

Because the resting conductance of the axon is usually much smaller than that prevailing at the peak of the delayed current transient, R_m· G_s ≫ 1. With this simplification, Equations EA.17 and EA.18 may be rewritten, respectively, as:

$$i_{\text{c}}(T)\approx -G_{\infty }·E_{\text{s}}·\sqrt{R_{\text{m}}·G_{\text{s}}}·\text{erf}\left(\sqrt{R_{\text{m}}·G_{\text{s}}·T}\right).$$ Equation EA.19

and

$$i_{\text{p}}\approx -G_{\infty }·E_{\text{s}}·\sqrt{R_{\text{m}}·G_{\text{s}}}.$$ Equation EA.20

The rise-time of the current corresponds to the value of T, T_r, for which the argument of the erffunction takes a certain value (which may be chosen close to 1 if the rise-time is defined as the time to peak amplitude). Hence:

$$T_{\text{r}}·R_{\text{m}}·G_{\text{s}}=C^{\text{t}},$$ Equation EA.21

where C^t is a constant. Combining Equations EA.19 and EA.21 yields:

$$T_{\text{r}}=C^{\text{t}}·\frac{G_{\infty }^2·E_{\text{s}}^2}{i_{\text{p}}^2}.$$ Equation EA.22

Equation EA.22 shows that the rise-time of the delayed current transient is proportional to the inverse of the square of its peak amplitude.

Steady-state solution of the equation of a finite cable with a uniform autoreceptor conductance density

We consider a finite cable voltage-clamped at its resting value at the origin. The electrical parameters of the cable are as defined in Appendix . As in Appendix , we assume that the cable is uniformly at rest until at time T = 0; a synaptic (or autoreceptor) conductance is activated and remains constant thereafter. The reduced length of the cable, L, is related to the actual length, l, and to the cable length constant, λ, by the equation:

$$L=\frac{l}{\lambda }.$$ Equation EB.1

Finally, a sealed-end boundary condition is used at the end of the cable. The voltage escape (from the resting value), V, follows the equation:

$$\frac{\partial }{\partial T} V=\frac{{\partial }^2}{\partial X^2} V-V-R_{\text{m}}·G_{\text{s}}·(V-E_{\text{s}}),$$ Equation EB.2

with the boundary conditions:

$$V(X=0,T)=0$$ Equation EB.3

and

$$\frac{\partial }{\partial X} V(X=L,T)=0$$ Equation EB.4

and the initial condition:

$$V(X,T=0)=0.$$ Equation EB.5

We aim here at calculating V_∞, the steady-state solution of Equation EB.2. From Equation EB.2, we obtain:

$$\frac{{\partial }^2}{\partial X^2} V_{\infty }-(1+R_{\text{m}}·G_{\text{s}})·V_{\infty }=-R_{\text{m}}·G_{\text{s}}·E_{\text{s}}.$$ Equation EB.6

The solution of the inhomogeneous Equation EB.6 with the boundary conditions (B.3 and B.4) is (Tuckwell, 1988, pp 139–141):

$$V_{\infty }(X)=\frac{R_{\text{m}}·G_{\text{s}}·E_{\text{s}}}{1+R_{\text{m}}·G_{\text{s}}}·\left[1-\text{cosh}\left(X·\sqrt{1+R_{\text{m}}·G_{\text{s}}}\right)+\text{tanh}\left(L·\sqrt{1+R_{\text{m}}·G_{\text{s}}}\right)·\text{sinh}\left(X·\sqrt{1+R_{\text{m}}·G_{\text{s}}}\right)\right].$$ Equation EB.7

From Equations EB.7 and EA.18, one obtains the expression of the steady-state current delivered by the amplifier:

$$i_{\infty }=-G_{\infty }·\frac{R_{\text{m}}·G_{\text{s}}·E_{\text{s}}}{\sqrt{1+R_{\text{m}}·G_{\text{s}}}}·\text{tanh}\left(L·\sqrt{1+R_{\text{m}}·G_{\text{s}}}\right),$$ Equation EB.8

which, for R_m· G_s≫ 1, simplifies to:

$$i_{\infty }\approx -G_{\infty }·\sqrt{R_{\text{m}}·G_{\text{s}}}·E_{\text{s}}·\text{tanh}\left(L·\sqrt{R_{\text{m}}·G_{\text{s}}}\right).$$ Equation EB.9

In Equation EB.9, the length of the cable influences only the argument of the tanh function. This function rises first proportionally to its argument but then abruptly saturates at 1 as the argument grows further. Because of the shape of the tanh function, the amplitude of the current delivered by the amplifier saturates for large values of the cable length. Let us consider a specific case in which the density of autoreceptor conductance, G_s, is 1 mS/cm². Taking our standard values for R_i (0.1 kΩ·cm), R_m(50 kΩ·cm²), and a (0.25 μm), we find that the length constant of the cable is λ = 791 μm. Applying Equations EB.9 and EB.1, it follows that the currents for the cable lengths of 200 and 400 μm are −116 and −123 pA, respectively (with E_s = +70 mV).