Increased Synchronization of Neuromagnetic Responses during Conscious Perception

Abstract

In binocular rivalry, the observer views two incongruent images, one through each eye, but is conscious of only one image at a time. The image that is perceptually dominant alternates every few seconds. We used this phenomenon to investigate neural correlates of conscious perception. We presented a red vertical grating to one eye and a blue horizontal grating to the other eye, with each grating continuously flickering at a distinct frequency (the frequency tag for that stimulus). Steady-state magnetic fields were recorded with a 148 sensor whole-head magnetometer while the subjects reported which grating was perceived. The power of the steady-state magnetic field at the frequency associated with a grating typically increased at multiple sensors when the grating was perceived. Changes in power related to perceptual dominance, presumably reflecting local neural synchronization, reached statistical significance at several sensors, including some positioned over occipital, temporal, and frontal cortices. To identify changes in synchronization between distinct brain areas that were related to perceptual dominance, we analyzed coherence between pairs of widely separated sensors. The results showed that when the stimulus was perceived there was a marked increase in both interhemispheric and intrahemispheric coherence at the stimulus frequency. This study demonstrates a direct correlation between the conscious perception of a visual stimulus and the synchronous activity of large populations of neocortical neurons as reflected by stimulus-evoked steady-state neuromagnetic fields.

When two incongruent visual images are simultaneously presented one through each eye, only one image is consciously perceived at a time, with the percept alternating between the two images every few seconds (Levelt, 1966; Walker, 1978). This phenomenon, called binocular rivalry, provides a useful experimental paradigm for identifying aspects of brain function that are closely correlated with conscious experience. Because conscious perception changes over time while the stimuli remain constant, this paradigm offers a way to distinguish between neural activity related to the physical features of the stimuli and neural activity directly related to conscious experience.

Psychophysical studies have demonstrated that a perceptual competition between incongruent visual stimuli can occur even when both stimuli are presented through the same eye (Raushchecker et al., 1973) or when they are rapidly alternated between eyes (Logothetis et al., 1996). This suggests that rivalry occurs between percepts rather than between eyes or between monocular visual channels (LeGrand, 1967; Kovacs et al., 1996). Consistent with these observations, single-unit recordings during binocular rivalry in monkeys have demonstrated that the firing of a large majority of neurons in the primary visual cortex correlates with the stimulus but not with the percept (Leopold and Logothetis, 1996). By contrast, the firing of cortical units in higher visual areas, such as the inferior temporal cortex and the superior temporal sulcus (Sheinberg and Logothetis, 1997), is highly correlated with the visual percept. On the other hand, in strabismic cats, in which there is competition between monocular visual channels, the stimulus that is perceptually dominant during rivalry is associated with increased synchronization between neurons in early visual areas without changes in individual neural firing rates (Fries et al., 1997).

While unit recordings offer high spatial and temporal resolution as well as stimulus specificity, they are not practical for obtaining global coverage of neural responses. Although limited by low spatial resolution, whole-head magnetoencephalography (MEG) and electroencephalography (EEG) offer the advantage of high temporal resolution, which is essential for comparing neural responses to the same stimulus during the short episodes of perceptual dominance in binocular rivalry. MEG and EEG signals are believed to reflect the synchronous activity of large populations of neocortical neurons (Hamalainen et al., 1993; Nunez, 1995; Srinivasan et al., 1998).

Previous EEG studies have demonstrated that perceptual dominance increases the amplitude of visually evoked potentials at occipital electrodes (Lansing, 1964; Cobb et al., 1967; MacKay, 1968; Brown and Norcia, 1997). In an initial MEG study of binocular rivalry in humans, we directly compared steady-state–evoked responses when subjects viewing a stimulus were consciously perceiving it and when they were not (Tononi et al., 1998). Two competing stimuli were flickered at a different frequency in the range of 7–12 Hz, and the magnetic fields at the frequency specific to each stimulus (“frequency tags”) were detected at 148 sensors. We found that that power over the entire array was significantly modulated at the stimulus frequency when that stimulus was perceptually dominant. This suggests that conscious perception is associated with increased local synchronization of neural activity.

The main goal of the present study was to determine whether conscious perception of the stimulus was associated with increased synchronization between neural populations distributed in different cortical areas (Edelman, 1989; Tononi et al., 1992; Tononi and Edelman, 1998). Synchronization between distinct populations of neurons can be evaluated by measuring the coherence between the responses measured at widely separated pairs of MEG or EEG sensors (Niedermeyer and Lopes da Silva, 1987; Nunez, 1995; Srinivasan et al., 1998). This coherence reflects the level of functional integration between large populations of neurons in distant areas of the brain. In this study, we examined the modulation of coherence between MEG sensors at the frequency specific to the stimulus that is associated with its perceptual dominance during binocular rivalry. The finding of coherence modulation independent of power modulation points to a role for interareal neural synchronization in conscious perception.

MATERIALS AND METHODS

Experimental methods. Eleven right-handed subjects (nine males and two females) aged 25–49 participated in this study. Each had a corrected visual acuity of 20/20 and could see large-disparity random-dot stereograms. All subjects gave informed consent. Neuromagnetic data were collected using a Magnes 2500WH MEG system from Biomagnetic Technologies (San Diego, CA). This array provides coverage of the entire scalp by means of 148 magnetometer coils (1 cm in diameter) that are spaced 3 cm apart on an approximately ellipsoidal surface located ∼3 cm from the scalp surface. MEG recordings were performed in a magnetically shielded room, and noise cancellation was performed in real time with respect to a set of reference sensors. A set of reference coils for detecting background noise signals was located ∼18 cm above the head. There were eight reference coils: three orthogonal magnetic field coils identical to the MEG sensors and five gradient coils for detecting the five off-axis components of the field gradient tensor. The output from any given sensor channel was the sum of the output directly from the pickup magnetometer coil plus a weighted sum of the outputs from all of the reference channels. The weights used for a given channel were determined by conducting an MEG recording with no subject present and selecting the set of weights that minimized the output from that channel.

Computer-generated stimuli were projected from a Proxima 4200 video projector through a porthole and onto a screen in front of the subjects. In each trial, subjects viewed high-contrast (>95%) square-wave gratings of 1.7 cycles/° in a square field subtending a visual angle of 13° at the fovea over a uniform dark gray background. A red vertical grating was presented to one eye and a blue horizontal grating was presented to the other eye by having subjects wear correspondingly colored lenses. The intensity of the red stimulus was adjusted such that each subject reported that the two stimuli were of comparable brightness under conditions of binocular rivalry, with sufficiently long dominance episodes (at least 2 sec) of each grating. Average luminance of the flickering stimulus after passing through the colored lenses was 0.02 cd/m². Subjects were instructed to fixate on a dim gray point at the center of the superimposed gratings.

In rivalry trials, stimulus s₁ was flickered continuously at frequency f₁, and stimulus s₂ was flickered at a different frequency, f₂. The two frequencies were selected from the following list: 7.41, 8.33, 9.50, or 11.12 Hz. These frequencies correspond to one grating image every 9, 8, 7, or 6 video frames, respectively. On the other video frames a black field was projected. A photodiode recorded the flicker ofs₁ and s₂ on a computer screen driven in parallel with the projector. Subjects were asked to activate one switch with their left index finger whenever the red grating was perceptually dominant and a second switch with the right index finger whenever the blue grating was dominant. They were instructed to activate neither switch if neither of the two percepts was clearly dominant, i.e., when they saw a mixture of red vertical and blue horizontal gratings. The activation of the switches was recorded in an additional channel. After a brief exposure to the stimuli, subjects had no trouble categorizing the percepts as red, blue, or mixed. When asked, all of the subjects reported perceiving the stimulus flicker, but they did not comment on any difference in frequency between f₁ and f₂. During each trial, MEG data were collected for 315 sec. Stimulus presentation began 30–60 sec before the onset of data collection to establish a steady-state response.

To emphasize the effect of perceptual dominance or nondominance over stimulus-specific factors, we counterbalanced grating–frequency and grating–eye pairings for each subject so that, for each frequency pair, each grating was presented at each frequency and to each eye for a total of four trials. Two different frequency pairs were used successively in the rivalry condition, with one frequency common to both pairs, yielding eight trials at that frequency. The common frequency used for each subject was either 7.41 or 8.33 Hz. Data analysis was limited to the common frequency (f_c) across the eight rivalry trials. This sample size of n = 8 provided sufficient data for the statistical tests described below.

Two additional types of trials were used as controls. The first type, stimulus alternation, was used to compare differences between perceptual dominance and nondominance caused by binocular rivalry with differences attributable to the physical presence or absence of the stimulus. Stimulus s₁ alone was presented to one eye at frequency f₁ for a random interval of time, after which stimulus s₂ alone was presented to the other eye at frequency f₂ for another random interval, and so on for 315 sec. The time intervals were drawn from a γ distribution with a mean of 2 sec and an SD of 1 sec. This distribution has been observed in binocular rivalry experiments in humans using a similar stimulus (cf. Logothetis et al., 1996). Stimulus-alternation trials were performed with both stimulus–frequency and stimulus–eye pairings for a total of four trials.

A second control, the “fusion” trial, was used to assess the effect of orientation shifts on the MEG signals. The red and blue gratings were presented in the same orientation, either both vertical or both horizontal, but flickered at distinct frequencies. Under these conditions, subjects did not experience binocular rivalry but instead perceived a single fused image of a flickering purple grating. After a random interval of time drawn from the same γ distribution used in the stimulus-alternation trials, both gratings switched to the other orientation. Because the perceptual shifts resulting from binocular rivalry are accompanied by shifts in the orientation of the perceived grating, it was useful to examine the effect of this explicit orientation shift on the power observed at each grating’s frequency.

A total of 14 trials (8 rivalry, 4 stimulus alternation, and 2 fusion) were performed in a session that lasted 2–3 hr.

Power analysis. The MEG time series were bandpass filtered at 1–50 Hz and digitized at 254 Hz. For each sensor channelm, the Fourier transformF_m(f) of the entire 315 sec–recording interval (Δf = 0.0032) was calculated using a fast Fourier transform (FFT) algorithm (MATLAB, Natick, MA). From these Fourier coefficients, the power spectrum was calculated asP_m(f) =F_m(f) ×F_m*(f). Peaks at frequencies f₁ and f₂were identified in the spectrum of the photodiode signal, and the presence of peaks in the MEG data at the same frequencies was verified. In every trial, a peak was present at f₁ andf₂ in the power spectrum of many MEG channels.

The signal-to-noise ratio (SNR) was computed at each MEG channel as the ratio of the power at the stimulus frequenciesf₁ and f₂ to the average power of the 20 surrounding bins. The choice of the number of bins was arbitrary; we found that the SNR estimate was not sensitive to it. Simulations confirmed that at the SNR typically observed atf₁ and f₂, any sidebands caused by phase drift of the steady-state response were likely to be obscured by broad-band spontaneous MEG activity. This can be seen by comparing carefully steady-state auditory and visually evoked potentials to simulations of random phase variation as presented by Regan (1989, pp 94–96). An SNR threshold of 5 was used to emphasize stimulus-related neuronal activity over spontaneous MEG. At an SNR of 5, on average 80% of the variance in the signal atf₁ or f₂ is expected to be stimulus related. By assuming that the data from all the sensors at each stimulus frequency and from the 20 surrounding bins were drawn from a single exponential distribution, it was estimated that, at an SNR >5, all of the peaks had a probability of p < 0.005 (Press et al., 1992).

The recording of the switch positions indicated which stimulus was being perceived by the subject. The two response functions r₁ and r₂ were defined to have a value of 1 during the intervals when the subject signaled that stimuluss₁ or s₂, respectively, was perceptually dominant and a value of 0 otherwise. The values of r₁ or r₂ during episodes of perceptual dominance lasting <250 msec were also set to 0 to limit the analysis to stable percepts. To obtain the power corresponding to the periods when the subject was consciously perceiving s₁ (perceptual dominance), we multiplied the MEG data sample-by-sample by r₁before the FFT. The power corresponding to the periods when the subject was not conscious of s₁ (perceptual nondominance, defined as the periods when the subject was conscious ofs₂) was calculated by multiplying the MEG data by r₂ before applying the FFT. Multiplying the MEG time series by the response function corresponds to convolving the respective frequency spectra, resulting in some contamination of a given spectral peak by neighboring frequency bins. At the signal-to-noise ratios observed in the MEG data, numerical simulations indicated that the contamination of the power at the stimulus frequencies was negligible compared with the size of the effects observed in this study. The power values at f₁and f₂ were normalized by the total duration of dominant intervals in r₁ andr₂. The power difference atf₁ and f₂ was obtained by subtracting the power during perceptual nondominance from the power during perceptual dominance for each trial. The power difference at the common frequency f_c was averaged over the eight rivalry trials for each subject.

Coherence analysis. The coherence between two signals is a correlation coefficient (squared) that measures the phase consistency of the two signals as a function of frequency (Nunez, 1995). Coherence at a given frequency measures the fraction of variance in either channel that has amplitude and phase predicted by the other channel across many recording epochs. To obtain the coherence γ_mn² between two channels m andn from Q epochs, we first compute the average cross spectrum C_mn at each frequencyf (Bendat and Piersol, 1986):

$$X_{\text{mn}}(f)=\frac{1}{Q} \sum _{q=1}^Q F_{\text{mq}}(f)F_{\text{nq}}(f)*,$$ Equation 1

whereF_mq(f) is the Fourier transform of the qth epoch of channel mat frequency f. The cross spectrum is squared and normalized by the average power spectrum of the individual channels to obtain the coherence γ_mn² that is highly sensitive to the consistency of the phase difference between the channels (Bendat and Piersol, 1986):

$${\gamma }_{\text{mn}}^2(f)=\frac{\Vert X_{\text{mn}}(f){\Vert }^2}{\langle P_{\text{m}}(f)\rangle \langle P_{\text{n}}(f)\rangle },$$ Equation 2

where <P_m(f)> = ‖X_mm(f)‖ is the power spectrum of the mth channel averaged over theQ epochs. Note that the form of this equation closely resembles that of a correlation coefficient, in which the cross spectrum is analogous to covariance and the power spectrum is analogous to the variance (squared SD).

At frequency f, a coherence value of 1 indicates that the two channels maintain the same phase difference on every epoch, whereas a coherence value near 0 indicates that the phase difference is random from epoch to epoch. Robust coherence estimates require sufficient epochs for averaging, so each of the eight rivalry trials was subdivided into five epochs of duration 63 sec to obtain a total ofQ = 40 epochs.

To compute coherence during perceptual dominance and nondominance, we multiplied the MEG data by the response functions before applying the FFT, as described in the power analysis. The average coherence difference between dominance and nondominance was computed from the eight rivalry trials at the common frequencyf_c.

For every coherence estimate γ_mn², the SEM ε_mn was computed based on the assumption that the time-series values are samples of a Gaussian random process (Bendat and Piersol, 1986):

$${\varepsilon }_{\text{mn}}=\sqrt{\frac{2}{Q}}\left(\frac{1-{\gamma }_{\text{mn}}^2}{\Vert {\gamma }_{\text{mn}}\Vert }\right).$$ Equation 3

These SEs were used to construct 95% confidence intervals on the actual value of coherence (Γ_mn²) from the estimated coherence (γ_mn²) as:

$${\gamma }_{\text{mn}}^2(1-2{\varepsilon }_{\text{mn}})<{\mathrm{\Gamma }}_{\text{mn}}^2<{\gamma }_{\text{mn}}^2(1+2{\varepsilon }_{\text{mn}}).$$ Equation 4

Traditionally, coherence analysis has been used in EEG and MEG to study spontaneous rhythmic activity, e.g., the α rhythm (Srinivasan et al., 1998). In this study, we applied coherence analysis to a steady-state MEG signal that reflects the brain’s response to an external stimulus flickering at a given frequency. It is possible that the signal at each channel is perfectly locked to the stimulus, i.e., maintains a constant phase difference with the stimulus, so that measured coherence is <1 only because of the addition of spontaneous MEG at the same frequency. In this case, coherence between channels at the stimulus frequency merely reflects the SNRs of the channels. In particular, if the signals at channels m and n consist of pure sine waves, each with a fixed phase added to uncorrelated noise, the coherence between the channels at the sinusoidal frequency can be estimated directly from the SNR of each channel as (Bendat and Piersol, 1986):

$${\gamma }_{\text{mn}}^2=\frac{1}{\left(1+\frac{1}{{SNR}_{\text{m}}}\right)\left(1+\frac{1}{{SNR}_{\text{n}}}\right)}.$$ Equation 5

(Note that in this formula the SNR estimate should be based on the same epoch length on which the coherence estimate is based: 63 sec.) For every subject, a coherence estimate was obtained from this formula for every channel pair, based on the SNR of each channel, and its 95% confidence interval was computed by the use of Equation 4. If the coherence between channels were accounted for by the SNR at the stimulus frequency, the observed values would fall within this interval. If coherence values were lower than the predicted interval, the signals at the stimulus frequency must vary in phase over time. In this case, coherence analysis can be used to study modulation of the phase relationship between two channels by the perceptual dominance or nondominance of the stimulus.

The physical constraints of extracranial recording of MEG or EEG also influence coherence estimates (Srinivasan et al., 1998). In MEG, high coherence between two sensors may be a consequence of a single-current source contributing to both sensors. A single-current source in the brain produces a widespread magnetic field pattern at the extracranial sensors. Even if all of the active populations of neocortical neurons are uncorrelated with each other, the MEG sensors can exhibit high coherence, because a given population contributes signal to multiple sensors. Thus, measured coherence between MEG sensors reflects a mixture of genuine phase correlation between distinct populations of neurons and the artificial correlation by one population contributing to multiple sensors. This artificial coherence should be consistently observed independent of frequency. In the case of EEG, theoretical models, simulations, and comparisons with experimental data have demonstrated that it is possible to segregate genuine correlation from volume conduction effects by identifying the common pattern of coherence across the entire frequency spectrum (Srinivasan et al., 1998). To determine the minimum sensor separation that ensures that coherence is a measure of correlated activity between distinct neuronal populations, we also examined coherence between channels at nonstimulus frequencies.

Statistical analysis of perceptual dominance and nondominance. The statistical significance of the contrast between perceptual dominance and nondominance in power and coherence was determined on a subject-by-subject basis by a permutation test (Efron and Tibshirani, 1993). For each subject, each rivalry trial yielded an MEG data set and an associated response function. Permutation samples were computed by randomly reassigning each response function to an MEG data set across the eight rivalry trials, thereby randomizing the contrast between perceptual dominance and nondominance in the MEG data. All of the total of 8! (= 40320) possible pairings, including the observed pairing, were used to yield statistics on the null hypothesis that no power or coherence difference is present at the common frequency f_c. If the null hypothesis were true, the observed pairing of response functions to MEG data would not be expected to yield a significantly larger magnitude difference than does a random assignment of response functions to MEG data. For each permutation sample, the average power or coherence difference at frequency f_c was computed in the same manner used for the observed data but with the randomly assigned response functions.

The omnibus difference was defined as the sum of squared power or coherence differences across all the sensors. The statistical significance of the observed omnibus difference was established by comparing it with the distribution of the omnibus differences obtained from the permutation samples. The proportion of permutation samples with a higher omnibus difference than the observed value determined the significance level.

After the significance of whole-array (overall) differences was established, local significance tests were run on the power difference at each channel. The population of power differences obtained for each sensor by the permutation sampling was used to determine the individual-sensor significance after a Bonferroni correction for multiple comparisons was applied.

The coherence data were further examined to determine which channel pairs demonstrated robust coherence differences. A Bonferroni correction could not be applied to test individual channel pairs because the typical data set consisted of >2000 channel pairs. Instead, an overall coherence was first computed for each sensor pair using the entire time series. Channel pairs in which the magnitude of the coherence difference between periods of perceptual dominance and nondominance was more than twice the SE of the overall coherence were deemed to be robust and plotted topographically. For any coherence estimate, the SD ς = γ²ε is always smaller than the SE, resulting in a highly conservative criterion.

RESULTS

Behavioral analysis

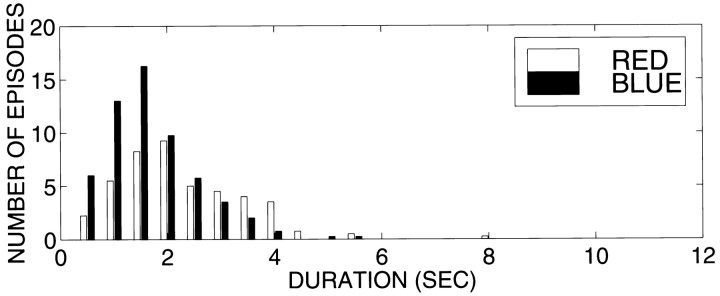
Across all 11 subjects, the average duration of an episode of perceptual dominance in rivalry trials was 2.3 ± 0.9 sec, with an average of 53 episodes each of red- and blue-grating dominance per trial. In most subjects, the number and length of intervals in which the red and blue gratings were dominant were comparable. For 5–25% of the total recording time, neither stimulus was perceptually dominant. As an example, Figure 1 shows the average distribution of red- and blue-grating episode durations of one subject (J.S.).

Fig. 1.

Episode durations of perceptual dominance of the red vertical and blue horizontal gratings, averaged over the eight rivalry trials of subject (J.S.).

Power analysis

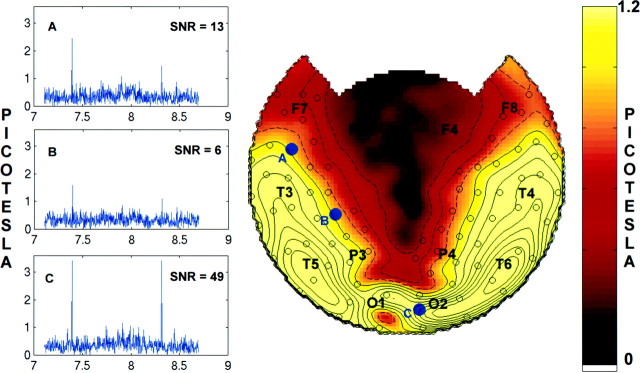
In every subject, steady-state responses were detected at the stimulus frequencies; these responses were absent when the corresponding eye was occluded. Amplitude spectra of the MEG signals recorded over posterior and anterior brain regions during a single rivalry trial of subject J.S. are shown in Figure2, left. Two single-bin (Δf = 0.0032 Hz) peaks are clearly visible, one at 7.41 Hz and the other at 8.33 Hz, corresponding to the two stimulus frequencies. Peaks were also present at the harmonics of the stimulus frequency but were not analyzed in this study. Figure 2,right, shows the topographic distribution of the average amplitude at the common frequency (f_c = 7.41 Hz) of the eight rivalry trials for this subject. (Average amplitude, given as the square root of power, is plotted rather than the power to reduce the dynamic range of the plots and facilitate visualizing features of the topography. All statistical analysis was performed on the power values.) In all subjects, power typically extended bilaterally from posterior sites, where it was at a maximum, to anterior and lateral sites.

Fig. 2.

Left, Amplitude spectra of a single rivalry trial in subject J.S. at MEG sensors located over the left frontal (A), left parietal-central (B), and right occipital (C) cortex. Note the sharp peak at 7.41 Hz, the flicker frequency of the red grating, and at 8.33 Hz, the flicker frequency of the blue grating. The peaks are confined to one frequency bin, Δf = 0.0032 Hz (aliasing artifacts by the graphing software sometimes create the appearance of additional bins). The SNR, defined as the ratio of the power at the peak to the average power in a 0.06 Hz band (20 bins) surrounding it, is indicated on each plot for the 7.41 Hz peak. Only those peaks satisfying a criterion of SNR >5 were submitted to further analysis. Right, Topographic display of the signal amplitude at the common stimulus flicker frequency of f_c = 7.41 Hz, averaged across all eight rivalry trials. Although signal power is discussed in the text, the square root of the power, equivalent to the absolute magnitude of the field amplitude, is plotted here to increase the displayed dynamic range. The topographic maps were generated by interpolating the amplitude values at the 148 sensors on a best-fit sphere with a three-dimensional spline. The map is then projected from the sphere onto a plane. The positions on the best-fit sphere of sensors with SNR >5 are indicated by open circles. A few points are designated based on the 10–20 EEG electrode placement system: F, frontal; C, central;P, parietal; O, occipital; andT, temporal. The channels labeledA–C (filled blue dots) correspond to the amplitude spectra shown on theleft. Contours of constant amplitude (A) are indicated in steps of 0.2 picotesla;dashed lines are for A < 1 picotesla, and solid lines are for A≥ 1 picotesla.

The power difference between perceptual dominance and nondominance of the stimulus associated with f_c was computed for each sensor. The average power difference values atf_c were calculated with the subject’s response functions offset from the MEG data by an offset time τ ranging from −2.5 to +2.5 sec in steps of 0.25 sec. The offsets were introduced to take into account the variable delay between the motor output when the subject signals the onset of conscious perception and the establishment of the steady-state response. The former depends on the reaction time and the strategy used for the perceptual decision, whereas the latter depends on the rate at which the steady-state response is modulated, and both may vary across subjects.

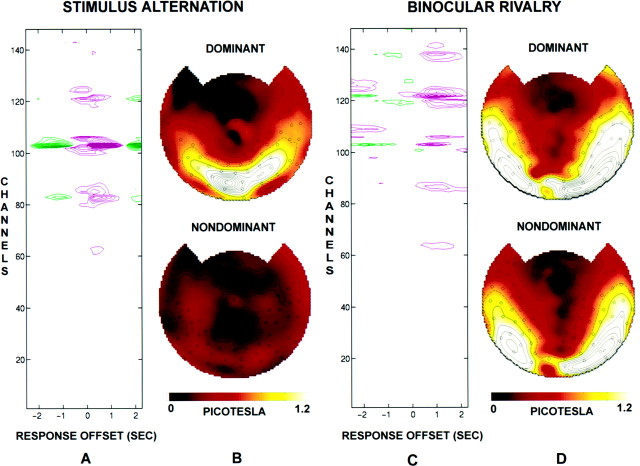
The average power difference at frequencyf_c = 7.41 Hz as a function of offset time τ for the four stimulus-alternation trials is shown for subject J.S. in Figure 3A. In most sensors, a large positive power difference extends from τ = −0.5 sec to τ = +1.25 sec, with the maximum at τ = +0.25 sec. A negative difference of smaller amplitude is noticeable at earlier and later offsets. Such negative differences occur because of the pseudoperiodicity of the episodes of stimulus presentation (dominance) caused by the fact that every interval in which the stimulus associated with f_c is dominant is preceded and followed by an interval during which the other stimulus is dominant. The average interval between these episodes is 2 sec, which corresponds to the interval between positive and negative peaks. The time course of the amplitude difference suggests that the steady-state response takes time to develop and that its peak value can occur after the onset of the behavioral response. Figure 3B shows topographic maps of the amplitude (square root of the power) atf_c during episodes of perceptual dominance and of perceptual nondominance, both at offset τ = 0.25 sec, which corresponds to the peak of the power difference. During stimulus-alternation trials, nondominance corresponds to periods during which no stimulus was presented at this frequency and, as expected, there was negligible power. The response offset for stimulus-alternation trials was τ = 0.25 sec in every subject.

Fig. 3.

Analysis of the temporal offset between subject J.S.’s response functions and steady-state power differences. The power spectrum was calculated with the response function offset from the MEG data by an offset time τ ranging from −2.5 to +2.5 sec in steps of 0.25 sec. All plots show power at the single frequencyf_c = 7.41 Hz that was used in all eight rivalry trials and four stimulus-alternation trials. A, Power difference as a function of offset time and channel number for the stimulus-alternation trials. The contour lines inmagenta indicate positive power differences (power is greater during episodes reported as dominant by the subject);green lines indicate negative differences in power.Contour lines are shown at 0.05 picotesla² and are higher in steps of 0.025 picotesla². B, Topographic display of amplitude corresponding to perceptual dominance (top) and to perceptual nondominance (bottom) for stimulus-alternation trials, at the offset for which the difference was maximal (τ = 0.25 sec). There is essentially no power during nondominance, because no stimulus is presented at that frequency during those intervals. C, Power difference for the rivalry trials, plotted as described in A. D, Topographic display of amplitude for the rivalry trials, plotted as described in B. During rivalry the offset for which the difference was maximal was τ = 1.0 sec. Note that for rivalry trials there is still considerable power during nondominance, even though the stimulus is not perceived.

Figure 3C shows the average power difference of the eight rivalry trials at f_c = 7.41 Hz in the same subject. In this case, there was also a positive power difference in many sensors, which was again surrounded by earlier and later (data not shown) negative differences (mean perceptual alternation interval of 2.3 sec). The magnitude of the power difference was reduced in comparison with that of the stimulus-alternation trials, and the number of sensors involved was greater than that in the stimulus-alternation trials. The maximum power difference occurred at a longer time offset than that in the stimulus-alternation trials (τ = 1.0 sec). In each of the 11 subjects, the optimal rivalry response offset was different, presumably reflecting differences between subjects in reaction time as well as in the strategy adopted in deciding when a percept was dominant. In 9 of the 11 subjects, the peak magnitude of differences occurred at the same offset τ in all eight rivalry trials; the individual offsets ranged from 0 to 1 sec. Of these nine subjects, one did not show a peak at the stimulus frequency corresponding to the red grating in any of the trials. All subsequent analyses were performed on data from the remaining eight subjects using the value of τ for each subject that gave the maximum magnitude of power difference.

Figure 3D shows topographic maps for subject J.S. of the magnetic field amplitude at f_c during episodes of perceptual dominance and of perceptual nondominance. The signal was distributed in a similar way during perceptual dominance and nondominance. However, a marked difference in power was observed according to whether the stimulus was consciously perceived or not. In many sensors, power was higher during perceptual dominance than during perceptual nondominance, whereas in a few sensors, the converse was true. (In stimulus-alternation trials, power was always higher during dominance because there was no stimulus during nondominance.) In fusion trials, in which the two gratings were always presented in the same orientation, alternating together every few seconds, the difference between horizontal and vertical presentation of the two gratings resulted in negligible modulation of power.

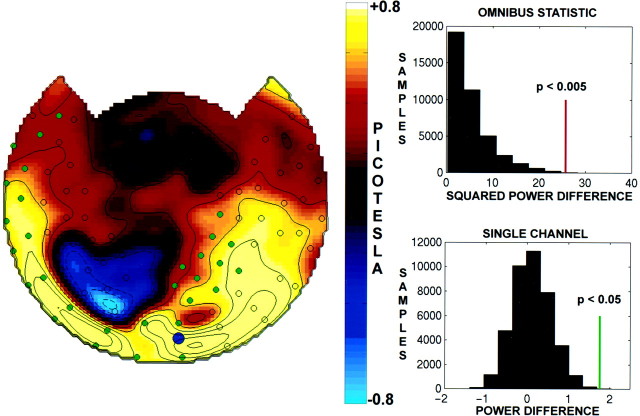
The average amplitude difference at f_cacross all eight rivalry trials is topographically mapped for the same subject in Figure 4, left. The difference in power between dominance and nondominance extended to many but not all the sensors showing a stimulus-related response. In this subject, a positive difference is observed bilaterally over the occipital, temporal, and frontal cortex. Smaller negative differences are observed in a few sensors over the left parietal cortex. Several sensors in which a consistent stimulus-related response was observed, as indicated by the circles specifying SNR >5, showed minimal modulation.

Fig. 4.

Left, Topographic display of amplitude differences (ΔA) atf_c = 7.41 Hz between perceptual dominance and nondominance for subject J.S. Contours of constant ΔA are indicated in steps of 0.2 picotesla;dashed lines are for ΔA < 0 picotesla, and solid lines are for ΔA ≥ 0 picotesla. The circlesindicate channels with SNR >5. The circles filled ingreen indicate channels that were individually significant after Bonferroni correction (p< 0.05). Top right, Distribution of permutation samples of the summed squared power difference. Permutation samples were obtained by randomizing the pairing between MEG records and the response functions, yielding 8! (= 40320) samples including the observed pairing. The power difference was squared and summed over all channels with SNR >5 (n = 80). The red bar indicates the observed power difference that has significance p < 0.005, as determined from the permutation distribution. Bottom right, Histogram of permutation samples of the power difference at a single channel. The observed difference is indicated by a green bar. After Bonferroni correction, this difference was significant atp < 0.05. The channel shown is indicated by ablue dot on the topographic map.

The summed squared power difference was found to be statistically significant (p < 0.005) using a conservative randomization test (see Materials and Methods). Figure 4, top right, shows the distribution of the summed squared power differences obtained from the permutation-sampling procedure for this subject. Only sensors with SNR >5 were included in the omnibus statistic. After omnibus significance was established, a significance test was run on each channel with SNR >5, with a Bonferroni correction. Figure 4, bottom right, shows the distribution of power differences obtained from permutation samples at one of the channels showing a significant positive difference. In this subject, many channels with small positive power differences were individually significant. (Channels that are significant after Bonferroni correction are indicated by filled green circles.)

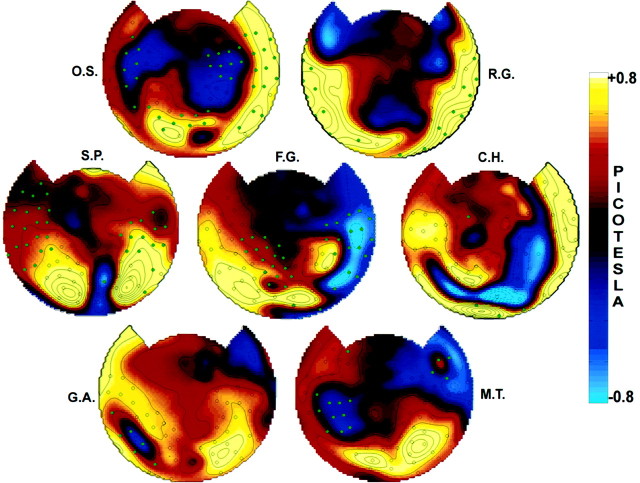
Maps of amplitude difference values between perceptual dominance and nondominance for the seven other subjects are shown in Figure5. Each subject showed a statistically significant (p < 0.05) omnibus power difference, and many individual sensors showed power differences that were significant after Bonferroni correction. In each subject, anterior sensors with small power differences were individually significant. By contrast, in each subject, many posterior sensors that showed a large power difference were not individually significant. (However, without a Bonferroni correction, these channels showed power differences that were significant.)

Fig. 5.

Topographic display of the average amplitude differences between perceptual dominance and nondominance in seven subjects. The common frequency was 7.41 Hz for all subjects except R.G., for whom it was 8.33 Hz. The omnibus significance of the maps, which was calculated using only channels with SNR >5 (indicated by acircle), was p < 0.005 for all subjects except G.A. and M.T. For these two subjects the overall SNR was lower. Using the channels with SNR >2, their omnibus significance was p < 0.05. Individual channels that reached a Bonferroni-corrected significance of p < 0.05 are indicated in all subjects by a filled green circle.

Marked power differences as a function of perceptual dominance were observed in different subjects at sensors over the occipital, parietal, temporal, and frontal cortex, although the particular set of modulated sensors varied between subjects. These effects were sometimes left or right lateralized, even though the power was distributed bilaterally in all of the subjects. In every subject, power increases were observed at occipital and parietal sensors, even though they were not individually significant in every subject. Sensors over the temporal and frontal cortex showed individually significant modulation in six of the eight subjects. Several subjects (O.S., S.P., C.H., F.G., and M.T.) showed sensors with negative power differences (i.e., higher power during perceptual nondominance) that were individually significant.

Coherence analysis

The overall coherence was computed from the entire time series between every pair of MEG sensors with SNR >5. To obtain enough data epochs for averaging, we subdivided each rivalry trial into five epochs to obtain a total of 40 epochs. Although this reduced the frequency resolution by a factor of five to Δf = 0.016 Hz, we verified that the spatial distribution of power was unchanged. The data from two subjects with only a few high-SNR channels (G.A. and M.T.) were excluded from the coherence analysis.

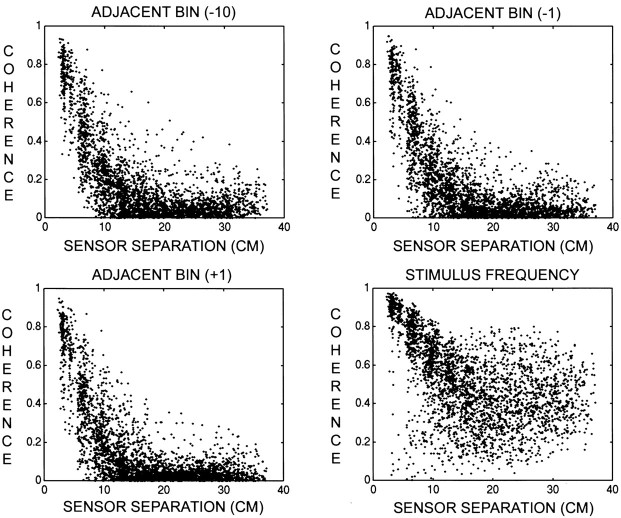
Coherence was first examined as a function of sensor separation at several frequencies. Figure 6 presents scatter diagrams of coherence versus sensor separation atf_c = 7.41 Hz, at the two adjacent frequency bins (f_c ± Δf), and at f_c − 10Δf in one subject (S.P.). At the three nonstimulus frequencies, coherence was high between nearby sensors and decreased with increasing sensor separation. This pattern was present across most frequencies and was likely caused by the widespread magnetic field pattern at the extracranial sensors. A similar pattern is observed in EEG and has been modeled from the volume conduction properties of the head (Srinivasan et al., 1998). In the case of MEG, the large separation between sources and sensors (>4 cm) is the primary reason for the artificial coherence. Data from one subject (O.S.) exhibited high coherences at all sensor separations at the bins adjacent to the common frequency and were therefore excluded from further analysis.

Fig. 6.

Scatter diagrams of coherence versus sensor separation for subject S.P. Sensor-separation distances were calculated on the best-fit sphere to the sensor positions. This sphere has a radius of 12 cm, and the typical separation between neighboring sensors is 3 cm. The stimulus frequency isf_c = 7.41 Hz. The frequency resolution for the coherence calculations was Δf = 0.016 Hz. Only sensors with SNR >5 were included. Top left, Scatter plot for the frequency f_c − 10Δf. Top right, Scatter plot for the frequency f_c − Δf.Bottom left, Scatter plot for the frequencyf_c + Δf. Bottom right, Scatter plot for the frequencyf_c. Note that at all three unstimulated frequencies the coherence exhibits the same steep decrease with sensor separation, becoming negligible at sensor separations of >12 cm. At the stimulus frequency, coherence is generally >0.5 at all separations.

At the stimulus frequency, many nearby and distant sensors demonstrated high coherence with values as high as 0.8 (Fig. 6, bottom right). In closely spaced sensor pairs, the observed coherence is likely to be a mixture of artificial and genuine coherence. To emphasize genuine coherence between neocortical regions, we restricted further statistical analysis of coherence to sensors separated by at least 12 cm.

We then tested whether coherence between the remaining channel pairs could be accounted for by the SNR of each channel. As explained in Materials and Methods, if we assume that each channel consists of a constant phase sinusoid added to uncorrelated noise, coherence between channels can be estimated from their SNRs (see Eq. 5). For each sensor pair, the 95% confidence interval on this coherence estimate was constructed to test whether the observed coherence could be predicted from the SNR. Comparison with the data revealed that none of the observed coherences were higher than predicted by the SNRs of the channels. On the other hand, in every subject, a large percentage of the coherences (44–91%; mean = 66%) were significantly lower than predicted by the SNRs of the channels. This result would be expected if the signal at the stimulus frequency were varying in phase over time rather than maintaining a consistent phase with respect to the stimulus. Thus, the observed coherence value between two channels measures the consistency of the phase difference between signals at the stimulus frequency that are varying in phase over time.

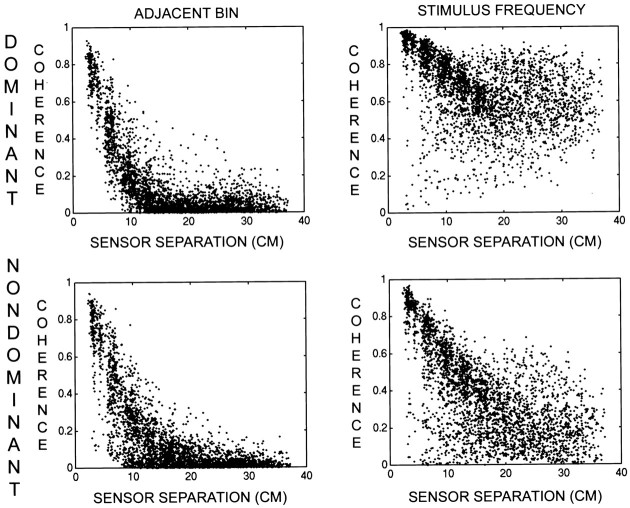
Coherence was computed for episodes of perceptual dominance and nondominance by multiplying the MEG data by the respective response functions before Fourier analysis (see Materials and Methods). The response function was offset by the characteristic time for each subject, determined from the power analysis described above. Figure7 presents scatter diagrams of coherence versus sensor separation in one subject (S.P.) during perceptual dominance and nondominance at f_c and at the adjacent frequency bin (f_c − Δf). In general, sensors separated by >12 cm demonstrated increased coherence during perceptual dominance. Differences in coherence were observed at shorter sensor separations, but they appeared to be smaller because of the presence of the common pattern of coherence. At nonstimulus frequencies, we found that coherence was unaffected by the perceptual switch in every subject.

Fig. 7.

Scatter diagrams of coherence versus sensor separation corresponding to perceptual dominance and nondominance for subject S.P. The scatter plots are described in Figure 6. Top left, Scatter plot for the frequencyf_c − Δf during perceptual dominance. Top right, Scatter plot for the frequency f_c during perceptual dominance.Bottom left, Scatter plot for the frequencyf_c − Δf during perceptual nondominance. Bottom right, Scatter plot for the frequency f_c during perceptual nondominance. Note that at the unstimulated frequency the coherence is not modulated by perceptual dominance.

To test the significance of the total difference in coherence, the summed squared coherence difference among sensors separated by >12 cm was used as an omnibus statistic and compared with permutation samples obtained by randomizing the pairing of the response function with the MEG (see Materials and Methods). In this subject, the overall coherence difference was statistically significant (p < 0.005). For each sensor pair separated by >12 cm, the coherence difference was identified as robust if the magnitude of the coherence difference between perceptual dominance and nondominance was more than twice the SE in the overall coherence. For example, with 40 trials an overall coherence of 0.65 has an SE of 0.12. Thus, a coherence difference of magnitude 0.25 (e.g., 0.50 during nondominance and 0.75 during dominance) was considered to be robust.

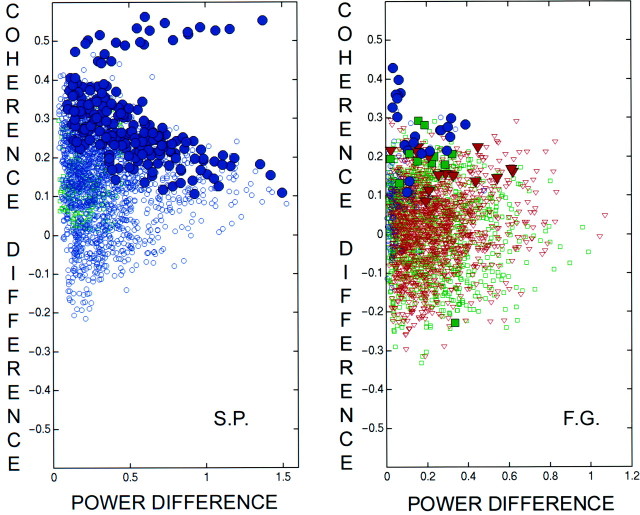
In most subjects, power increased at most sensors during perceptual dominance so that the SNR increased correspondingly. If the observed coherences were mainly the result of different brain regions responding passively to the periodic stimulus, that is, maintaining a fixed phase relationship to the stimulus throughout the recording interval, increased power would always result in increased coherence. Figure8 shows all of the coherence differences for sensor pairs separated by >12 cm (1972 pairs for subject S.P. and 2361 pairs for subject F.G.) plotted as a function of the geometric mean of the magnitudes of the power difference at each sensor. In both of these subjects, the summed squared coherence difference was significant (p < 0.05). In these plots,blue circles represent pairs in which both sensors increased power during perceptual dominance of the stimulus, red triangles represent pairs in which both sensors decreased power, and green squares represent pairs in which one increased power while the other decreased power. Robust increases in coherence are indicated by the correspondingly colored filled symbols. These plots demonstrate that the coherence modulation was not simply correlated with power modulation. We also verified that coherence modulation was not directly related to fractional power modulation.

Fig. 8.

Scatter diagrams of the coherence difference versus the geometric mean of the magnitude of the power difference between perceptual dominance and nondominance for subjects S.P. and F.G. The coherences shown are between sensors with SNR >5 and separated by at least 12 cm. In each plot, the blue circles correspond to sensor pairs in which perceptual dominance increased the power at both sensors. The red triangles correspond to sensor pairs in which power decreased at both sensors. The green squares correspond to sensor pairs in which one increased power and one decreased power. Thefilled symbols indicate robust coherence differences.Left, Coherence differences versus the geometric mean of the magnitude of power differences in subject S.P. For each sensor pair, the geometric mean is the square root of the product of the absolute values of the power differences. Right, A plot the same as left for subject F.G. The figures demonstrate that the size and direction of coherence modulation do not depend on the power modulation.

In most subjects, most of the channels showed increases of power and coherence, but the magnitude of the absolute or fractional power difference did not predict the magnitude of the coherence difference (e.g., subject S.P.). In those subjects that showed negative power differences, coherence sometimes increased during perceptual dominance between channels one or both of which decreased in power, and vice versa. For example, in subject F.G. the perceptually dominant state was characterized by robustly increased coherence between many distant sensor pairs (only one pair exhibited a decrease), including sensor pairs in which power either increased in both, decreased in both, or increased in one and decreased in the other.

Figure 9, top, shows the coherence during dominance and nondominance for subject S.P. between 78 channels with SNR >5 (2953 pairs). In these matrix plots, the channels are organized into four regional groups: LA, left anterior;LP, left posterior; RP, right posterior; andRA, right anterior. In both conditions, coherence values were high near the diagonal because neighboring sensors are numbered consecutively. During perceptual dominance, high coherences were observed between sensors over opposite hemispheres and between anterior and posterior sensors within each hemisphere. Interhemispheric coherences involving at least one anterior sensor were somewhat lower, but there were some coherences >0.5. During nondominance, the coherences were generally reduced.

Fig. 9.

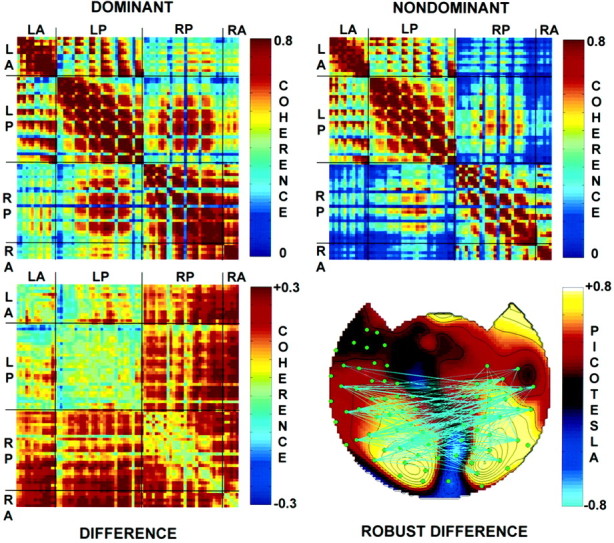
Topography of coherence during perceptual dominance and nondominance in subject S.P. Top left, Coherence matrix during perceptual dominance. In this channel-by-channel matrix, the channels are sorted into groups:LA, left anterior; LP, left posterior;RP, right posterior; and RA, right anterior. Top right, Coherence matrix during perceptual nondominance. Bottom left, Coherence difference matrix obtained by subtracting coherence during perceptual nondominance from coherence during perceptual dominance. Note that most of the coherences are higher during dominance. The summed squared coherence differences were significant (p < 0.005) as determined by the use of a randomization test. Bottom right, Topography of robust coherence differences. The topographic map shows the amplitude difference between dominance and nondominance.Filled green circles indicate channels with SNR >5 and a coherence >0.3 with at least one other channel. Robust differences between perceptual dominance and nondominance are indicated bycyan lines for positive differences and blue lines for negative differences. Robust differences in coherence were defined as those in which the difference exceeded twice the SE of the overall coherence.

Figure 9, bottom left, shows the coherence differences between dominance and nondominance. In this subject, most of the coherence differences were positive, and coherences involving right hemisphere sensors appeared to be more strongly modulated by perceptual dominance. Figure 9, bottom right, shows the power difference map of subject S.P. with the robust coherence differences indicated. The green filled circles indicate sensors whose overall coherence with at least one other sensor was >0.3. The cyan lines connect sensors that showed a robust gain in coherence during perceptual dominance. Most of these pairs involved one sensor over each hemisphere, although there were some sensor pairs within each hemisphere that also showed robust increases in coherence.

Each of the five subjects analyzed showed a significant overall difference in coherence between perceptual dominance and nondominance (p < 0.05). Figure10, left, shows the coherence difference matrices for the other four subjects. Although most of the coherences were higher during perceptual dominance, many of the subjects showed a reduction in coherence between some sensor pairs. Although the largest power differences occurred over posterior sites, coherences within the left posterior and right posterior sensors were less modulated than were coherences between these sensor groups. Coherences between anterior and posterior sensors also appeared to increase during perceptual dominance.

Fig. 10.

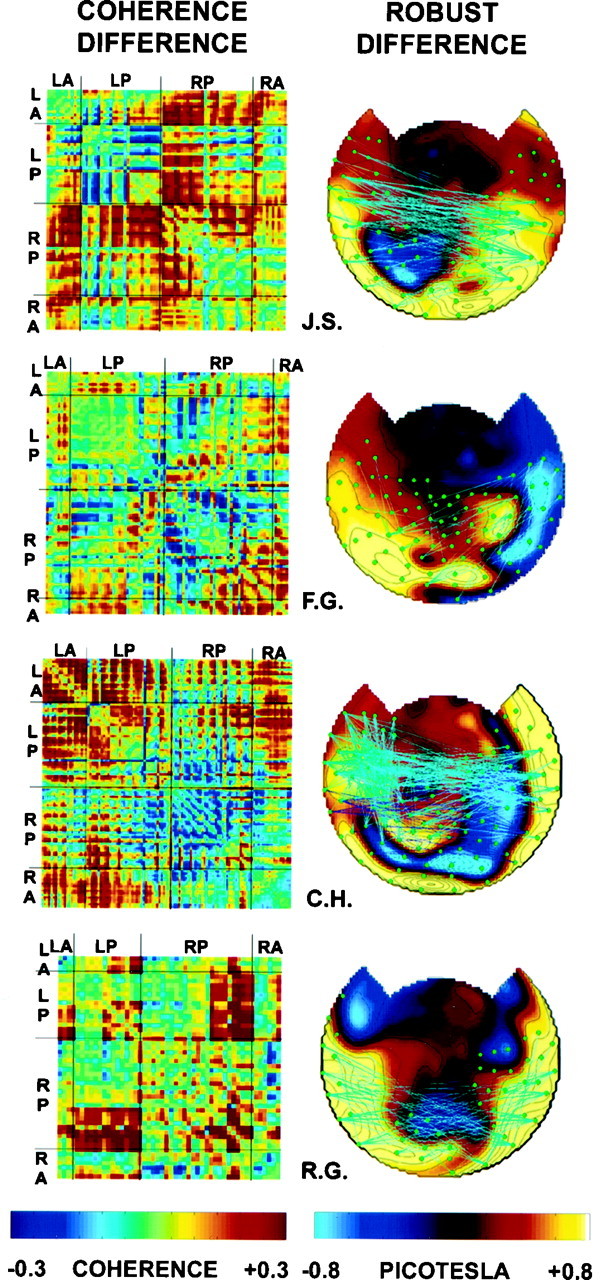
Coherence differences in four subjects.Left, Coherence difference matrices, plotted as described in Figure 9. Note that most coherences are higher during dominance. The summed squared coherence differences were significant (p < 0.05) in each subject as determined by the use of a randomization test. Right, Topographic map of robust coherence differences, plotted as described in Figure9.

Figure 10, right, shows topographic maps of the power differences and robust changes in coherences between dominance and nondominance. Most of the robust changes were increases of coherence between sensors over opposite hemispheres, although many subjects showed some increase in intrahemispheric coherences as well.

DISCUSSION

In this study, human subjects experienced binocular rivalry between two stimuli and continuously reported which stimulus was perceived. The stimuli were presented one to each eye and frequency tagged by flickering each stimulus at a different frequency. Stimulus-evoked steady-state magnetic fields at each stimulus frequency were simultaneously recorded over many cortical areas with an MEG sensor array covering the whole head. The power and coherence of these signals were used to determine how stimulus-related brain activity differs when human subjects are conscious of a visual stimulus and when they are not.

The present results demonstrate that the conscious perception of a stimulus is associated not only with a change in stimulus–frequency power but also with a significant increase in stimulus–frequency coherence between distant MEG sensors. Robust differences in coherence primarily involved interhemispheric sensor pairs, both between occipital and parietal sensors and between temporal or frontal sensors of one hemisphere and temporal, parietal, or occipital sensors of the other hemisphere. There was also an increase in coherence between frontal/temporal and occipital/parietal sites within each hemisphere, but fewer of these pairs were robust. These increases in coherence were found to be independent of the modulation of power at each sensor, which points to a role for increased interactions between distinct neuronal populations during conscious perception.

Power analysis

The results presented here confirm and extend our previous finding that the amplitude of the response at the stimulus frequency is strongly modulated over the entire MEG array by perceptual dominance (Tononi et al., 1998). In this study, a statistical analysis of power differences between dominance and nondominance was performed on a channel-by-channel basis. The largest absolute increase of power during perceptual dominance was observed at sensors over posterior (occipital) areas, consistent with previous EEG studies using a few occipital electrodes (Lansing, 1964; Cobb et al., 1967; MacKay, 1968; Brown and Norcia, 1997). However, in several subjects these channels were often not significant after a Bonferroni correction for multiple observations. At these channels, the fractional modulation of power was smaller than that at other channels. By contrast, in the same subjects many channels located at more anterior sites, which showed predictably smaller magnitude power differences, showed a statistically significant modulation even after Bonferroni correction. This observation can be related to the results of single-unit recordings in monkeys during binocular rivalry (Sheinberg and Logothetis, 1997). In these studies, the firing of neurons in the inferotemporal cortex and other late visual areas dealing with higher order features of the stimulus was tightly correlated with perceptual dominance. By contrast, only a small fraction of the neurons recorded in early visual areas such as V1 were modulated by the percept (Leopold and Logothetis, 1996).

Sensors showing a modulation of power that depended on whether or not the stimulus was consciously perceived were located bilaterally over occipital, temporal, parietal, and frontal cortical regions. However, the topography of power modulation because of perceptual dominance differed considerably from subject to subject. Although most channels increased power in association with perceptual dominance, in many subjects there were channels that decreased power.

What are the neural processes leading to an increase in power at the majority of MEG sensors during perceptual dominance? MEG is primarily sensitive to synchronous synaptic activity (Hamalainen et al., 1993). An increase in power at an MEG sensor can be either a consequence of the recruitment of additional synchronous neurons or a consequence of increased precision of the synchronization of neurons (i.e., the phases of the active neurons within the population become the same). This “local” synchronization could be a result of increased phase locking to the stimulus or be mediated by intra-areal connections (cf.Rager and Singer, 1998). In agreement with the latter interpretation, multiunit recordings in strabismic cats indicate that perceptual dominance under conditions of binocular rivalry is associated with increased synchronization in early visual areas of stimulus-independent neuronal activity, whereas perceptual suppression is associated with reduced synchronization (Fries et al., 1997). Our results indicate that an increase in local synchronization during perceptual dominance is observed not just over the occipital cortex but also bilaterally over more anterior cortical sites, including frontal areas that are not part of the visual system.

Coherence analysis

Although power at any given sensor reflects the amount of locally synchronized activity, coherence between distant MEG sensors reflects the level of synchronization between different brain regions. Changes in coherence among brain regions during the performance of various cognitive tasks have been reported using EEG and local field potentials (Bressler et al., 1993; Gevins, 1995). Recent studies have shown an increase in coherence (in the 40 Hz frequency range) associated with the switching of percepts when subjects were viewing bistable perceptual objects such as the Necker cube (Gaetz et al., 1998). The present results provide a direct demonstration that when a stimulus is consciously perceived, coherence between brain regions increases in comparison with when it is not consciously perceived. This finding is consistent with certain theoretical proposals (Edelman, 1989; Tononi et al., 1992; Tononi and Edelman, 1998) suggesting that the conscious perception of a stimulus is associated with an increase in the level of long-range synchronization between distinct populations of neurons located in distant parts of the brain.

Several neural mechanisms may be responsible for the observed increase in coherence among brain regions when a subject is conscious of a stimulus. Enhanced synchronization of subcortical inputs to each area can indirectly result in increased coherence between areas. Alternatively, increases in long-range coherence between distinct areas may result from reentrant interactions between neuronal populations facilitated by corticocortical fiber systems (Edelman, 1989; Lopes da Silva, 1991; Tononi et al., 1992; Nunez, 1995). The observation of increased power in the absence of a predictable increase in coherence and evidence of increased coherence while power decreased both support the latter interpretation, because increased synchronous input to two populations would necessarily increase both power and coherence.

In pilot experiments, we determined that widespread coherent responses were only evident with stimuli having a half-period of at least 50–100 msec (corresponding to 5–10 Hz). At higher flicker rates, responses were only observed at posterior MEG sensors located over visual cortical areas. Because the transmission delays in the fiber systems linking anterior and posterior cortical sites are estimated in the 50–100 msec range (Katznelson, 1981), these observations are consistent with the hypothesized role for reentrant interactions between early visual and temporal/frontal areas in generating coherent oscillations in the latter areas. However, it is likely that at least part of the coherence is caused by synchronization by feed-forward thalamocortical or corticocortical afferents (Rager and Singer, 1998).

Methodological considerations

The “frequency-tagging” method used in this study offers excellent temporal resolution coupled with a remarkable signal-to-noise ratio. Unlike functional magnetic resonance imaging (fMRI) or other methods based on hemodynamics (Lumer et al., 1998), this approach allowed us directly to compare brain responses when the subject was conscious and not conscious of the same stimulus. The high signal-to-noise ratio obtained via frequency tagging enabled us to analyze the responses of individual subjects and to establish the existence of distinct topographic features in each subject that would have been masked by subject averaging. At the same time, within-subject statistical comparisons consistently verified the occurrence of power modulation over anterior sites.

Despite these advantages, MEG recordings of brain activity have certain limitations. A precise correspondence between MEG or EEG signals recorded at different sensors and neural activity in underlying cortical areas cannot be established unless further assumptions are made (Hamalainen et al., 1993). However, previous studies achieving whole-head coverage with dense arrays of EEG electrodes have demonstrated that steady-state visual-evoked responses in areas other than occipital visual areas are attributable at least in part to local generators and are not merely volume-conducted potentials (Nunez, 1995). Sensitivity analysis of MEG sensors suggests that current sources located at a tangential distance of 7–8 cm from the sensor will contribute only 20% as much as sources located at a distance of 1 cm (Malmivuo and Plonsey, 1995). This implies that signals recorded at sensors separated by >10–12 cm should predominantly reflect distinct sources of neural activity rather than the same sources. The observation of negligible coherence between sensors separated by >12 cm at unstimulated frequencies further supports this conclusion.

In every subject examined, at least a few sensors showed significantly increased power during perceptual nondominance. The location of these sensors was typically over more anterior regions and more consistently on the right side of the brain. A recent study of binocular rivalry in humans using fMRI suggests that neural populations in right frontal and parietal areas may be involved in the active suppression of the nondominant stimulus (Lumer et al., 1998). Single units responding when their preferred stimulus was not being consciously perceived have also been reported (Leopold and Logothetis, 1996). However, a straightforward interpretation of this result is complicated by the physical limitations of MEG, which is preferentially sensitive to sources tangential to the sensors, i.e., along the sulcal walls. If temporally correlated synaptic activity in opposite sulcal walls increases, the magnetic fields will partially cancel because of their opposite orientations (Nunez, 1986). The observation that some sensors that lost power during perceptual dominance still exhibited increased coherence with other sensors suggests that the loss of power may in part result from geometric cancellation effects.

Finally, it should be mentioned that the frequency-tagging method is intrinsically limited, in that it can only be used to evaluate the responses of cortical populations that respond at the stimulus flicker frequency. For instance, at flicker rates above 50 Hz, a frequency tag cannot be detected (Regan, 1989), although subjects still experience binocular rivalry. In the present study, most subjects showed robust and widespread modulation of power and coherence involving both anterior and posterior sensors at the tag frequency. However, two subjects showed high signal-to-noise ratios only at a few channels, rendering coherence analysis impractical. Because of the power of the frequency-tagging method in identifying stimulus-specific responses in many brain areas, it will be important to overcome this limitation by optimizing the selection of tag frequencies depending on the subject’s response and on the modality of stimulus administration.

Conclusion

By using a binocular rivalry paradigm in conjunction with whole-head MEG and frequency tagging, this study demonstrates that it is possible to contrast directly the neural responses to the same stimulus when it is consciously perceived and when it is not. The results indicate that conscious perception is associated with distributed changes in the intensity of both local (intra-areal) and global (interareal) synchronization in the brain. Such changes in local and global synchronization are observed not only in visual areas but extend to and are often more prominent in more anterior areas, including frontal areas that are not part of the visual system. Further studies using frequency tags to keep track of the brain’s responses to competing stimuli may help in delineating the dynamic processes involved in consciousness and cognition.