A Neurotrophic Model of the Development of the Retinogeniculocortical Pathway Induced by Spontaneous Retinal Waves

Abstract

The development of the retinogeniculate pathway or the geniculocortical pathway, or both, occurs either before birth or before eye opening in many species. It is widely believed that spontaneous retinal activity could drive the segregation of afferents into eye-specific laminae or columns and the refinement of initially diffuse receptive fields and the emergence of orderly, retinotopic organization. We show that a recent computational model that generates a phenomenologically accurate representation of spontaneous retinal activity can indeed drive afferent segregation and, more particularly, topographic and receptive field refinement in the retinogeniculocortical system. We use a model of anatomical synaptic plasticity based on recent data suggesting that afferents might compete for limited amounts of retrograde neurotrophic factors (NTFs). We find that afferent segregation and receptive field formation are disrupted in the presence of exogenous NTFs. We thus predict that infusion of NTFs into the lateral geniculate nucleus should disrupt normal development and that the infusion of such factors into the striate cortex should disrupt receptive field refinement in addition to the well known disruption of ocular dominance column (ODC) formation. To demonstrate that the capacity of our model of plasticity to drive normal development is not restricted just to spontaneous retinal activity, we also use a coarse representation of visually evoked activity in some simulations. We find that such simulations can exhibit the formation of ODCs followed by their disappearance, reminiscent of the New World marmoset. A decrease in interocular correlations stabilizes these ODCs. Thus we predict that divergent strabismus should render marmoset ODCs stable into adulthood.

The development of the retinogeniculocortical pathway in Old World primates occurs largely prenatally (Rakic, 1976, 1977, 1981; LeVay et al., 1980; Rakic and Riley, 1983; Horton and Hocking, 1996a), whereas the development of the retinogeniculate but not the geniculocortical pathway in carnivores such as the cat (Shatz, 1983) and the ferret (Linden et al., 1981) occurs largely prenatally or before eye opening. In the retinogeniculate system, such development consists in, for example, the segregation of initially overlapping afferents into eye-specific laminae in the lateral geniculate nucleus (LGN) (Rakic, 1977; Shatz, 1983) and the establishment of an orderly, topographic representation of the retinas in the LGN (Sanderson, 1971; Malpeli and Baker, 1975). The segregation of retinogeniculate afferents into eye-specific laminae appears to be a competitive, activity-dependent process (Rakic, 1981;Sretavan and Shatz, 1986; Penn et al., 1998), and comparison of the retinogeniculate system with the developing or regenerating retinotectal system in lower vertebrates such as amphibia and fish suggests that the establishment of refined receptive fields and topography is an activity-dependent process (Meyer, 1983; Schmidt and Edwards, 1983; Schmidt and Eisele, 1985). In the geniculocortical system, the prenatal development in Old World primates results in, for example, the segregation of initially overlapping geniculocortical afferents into a mosaic of eye-specific regions called ocular dominance columns (ODCs) (Hubel and Wiesel, 1962; Rakic, 1976, 1977; LeVay et al., 1980; Horton and Hocking, 1996a) and, again, an orderly, topographic representation of the retinas on the striate cortex (Van Essen et al., 1984; Tootell et al., 1988). The segregation of geniculocortical afferents into ODCs, like the segregation of retinogeniculate afferents into eye-specific laminae in the LGN, is believed to be an activity-dependent, competitive process (Guillery and Stelzner, 1970; Hubel and Wiesel, 1970; Guillery, 1972; LeVay et al., 1978, 1980; Shatz and Stryker, 1978; Reiter et al., 1986; Stryker and Harris, 1986).

Because these developmental processes occur in the absence of vision, with some early processes occurring even before the development of photoreceptors in the retina, it is thought that spontaneous neuronal activity could drive the early development of the visual system. One possible candidate for such activity is the spontaneous waves of activity that sweep across the retinal ganglion cell layer of the developing retina (Galli and Maffei, 1988; Maffei and Galli-Resta, 1990; Meister et al., 1991; Wong et al., 1993, 1995; Feller et al., 1996, 1997; Penn et al., 1998). Spontaneous retinal waves are known to be transmitted to the LGN (Mooney et al., 1996), and they could also be relayed to the striate cortex. Very recently, the blockade of such waves in one eye before eye opening in the ferret has been shown to lead to an increased representation of the active eye and a decreased representation of the inactive eye in the LGN (Penn et al., 1998). The spatiotemporal correlations that exist in retinal waves are thought to be suitable for driving not only afferent segregation but also receptive field and topographic refinement (Katz and Shatz, 1996). However, to date, no experimental or theoretical approach has demonstrated this, although some computational models using phenomenologically inaccurate representations of spontaneous retinal activity have been shown to lead to topographic refinement or ODC formation, or both, as have coarse representations of visually evoked activity (von der Malsburg and Willshaw, 1976; Fraser and Perkel, 1989;Montague et al., 1991; Goodhill, 1993; Sirosh and Miikkulainen, 1997).

If spontaneous retinal activity might underlie the activity dependence of these developmental processes, then what underlies their competitive nature? At least in the ocular dominance system, much evidence strongly implicates retrograde neurotrophic factors (NTFs), particularly the neurotrophins. For example, intraventricular infusion of nerve growth factor prevents or tempers a response to monocular deprivation in the rat (Maffei et al., 1992; Berardi et al., 1993; Domenici et al., 1993;Yan et al., 1996) and the cat (Carmignoto et al., 1993). In ferret kits, neurotrophin-4, but no other neurotrophin, prevents the atrophy of LGN cell bodies controlled by the deprived eye during monocular deprivation (Riddle et al., 1995). Finally, cortical infusion of brain-derived neurotrophic factor or neurotrophin-4 (Cabelli et al., 1995) or substances that scavenge these factors (Cabelli et al., 1997) prevents the formation of ODCs. The production of some NTFs in the striate cortex is activity dependent (Castren et al., 1992; Bozzi et al., 1995; Schoups et al., 1995), and in the hippocampus the production and release of NTFs depend on neuronal activity (Zafra et al., 1991;Gwag and Springer, 1993; Lindholm et al., 1994; Blöchl and Thoenen, 1995, 1996; Griesbeck et al., 1995; Goodman et al., 1996). Taken together, these results suggest that a limited supply of NTFs might be the source of competitive dynamics (Purves, 1988).

In this paper, we apply a mathematically well characterized neurotrophic model of anatomical synaptic plasticity (Elliott and Shadbolt, 1998a,b) to the development of the retinogeniculocortical pathway. For most of our simulations, we use a recently developed model that generates a phenomenologically accurate representation of spontaneous retinal waves (Feller et al., 1997) to provide retinal stimulation to the simulated visual pathway. Our aim is to demonstrate that, at least in the context of small simulations, realistic spontaneous retinal activity can indeed drive normal development, specifically the refinement of receptive fields and initially coarse topography. We also seek to demonstrate that a neurotrophic model can account for a wide range of developmental processes at different stages in the visual system. To demonstrate that the utility of our neurotrophic model is not restricted to simulations using just spontaneous retinal activity, we also use a coarse representation of visually evoked retinal activity.

MATERIALS AND METHODS

In this section we first discuss the construction of patterns of retinal activity, using either realistic spontaneous retinal activity or coarse, visually evoked retinal activity. We also discuss the anatomical architecture of both a simple model of one retinal sheet innervating one LGN sheet and a full model of the retinogeniculocortical pathway in which two retinal sheets, two LGN sheets, and one cortical sheet are simulated. We describe how retinal activity propagates through these networks to the LGN and the cortex. We next discuss our model of anatomical synaptic plasticity, based on our neurotrophic theory. Finally we discuss the visualization of target-sheet topography.

Anatomical architecture and activity patterns. We typically simulate two patches of visuotopically equivalent retina, one for the left eye and one for the right eye. For most simulations we construct spontaneous patterns of activity in these retinas following closely the model of Feller et al. (1997). We will also present some simulations in which we use, instead, patterns of retinal activity that are a coarse representation of visually evoked activity, following closely the approach of Goodhill (1993). For our current purposes, we do not distinguish between different cell types, for example between X and Y cells or between ON- and OFF-type cells, because we are interested in more general issues of topographic refinement and afferent segregation.

In brief, the model of spontaneous retinal activity presented by Feller et al. (1997) has the following components. The retinal ganglion cell layer is modeled as a 96 × 70 triangular, close-packed lattice of cells, and the amacrine cell layer as a triangular 48 × 35 lattice of cells. Only cholinergic amacrine cells are considered in the amacrine cell layer because spontaneous wave propagation depends on cholinergic transmission (Feller et al., 1996). This represents a patch of retina of dimensions 1.4 mm × 1.2 mm (Feller et al., 1997). Both classes of neuron are modeled as leaky, integrate-and-fire spiking neurons with an integration time τ_int of 100 msec, and they receive input of fixed, unit efficacy from only amacrine cells within a distance of 120 μm (which corresponds to a distance of approximately 3.5 amacrine cell spacings). The change in activation level X of each type of cell over the basic time step of the model Δt = 100 msec is given by:

$$X_{\text{new}}^C=X_{\text{old}}^C{e}^{-\mathrm{\Delta }t/{\tau }_{\text{int}}}+N^A,$$ Equation 1

where C ∈ {A, G} for amacrine (A) or ganglion (G) cells, and N^A is the number of active amacrine cells within the cell’s input radius. If a ganglion cell’s activation level reaches the threshold θ_G = 10 units, it fires for one time step and then its activation level is set to zero. The threshold for amacrine cell firing is θ_A = 6 units. After firing for 10 time steps (1 sec), its activation level is also set to zero. However, the amacrine cell is then refractory and unable to fire for a period of time. This amacrine cell refractory period is introduced to account for the facts that retinal waves have boundaries, finite regions of propagation, and to some degree are determined by refractory regions of tissue. The refractory period of each amacrine cell is drawn from a normal distribution with mean 120 sec, SD 38 sec. In addition to being capable of being driven to threshold by excitatory input from neighboring amacrine cells, each amacrine cell can spontaneously fire, with a probability p_spont = 0.035 sec⁻¹. Cell firing is considered, for simplicity, as a state in which the cell’s output is unity; when not firing, its output is zero. Such a model can be shown to generate patterns of activity on the retinal ganglion cell layer that are phenomenologically accurate in several respects, including accounting for the distribution of sizes of active domains and the distribution of interwave intervals (Feller et al., 1997). The model is, however, very sensitive to the values of some of its parameters, particularly p_spont and θ_A. The values of these parameters, given above, are selected so that the model’s output reproduces the experimental data. Whether or not the model’s postulated mechanisms of wave generation are correct, its phenomenologically realistic output on the simulated retinal ganglion cell layer is all that concerns us here.

Were we to permit all 96 × 70 = 6720 ganglion cells to arborize over all cells in a simulated LGN sheet of the same size, our simulation would contain ∼45 million variables representing the number of synapses between each ganglion cell and each LGN cell. Each variable would need updating at each simulated time step Δt = 100 msec for millions of time steps. Such numbers are intractably large given current computational resources. Restricting the extent of arborization would defeat the purpose of determining whether realistic waves can drive topographic refinement. Thus, because 96 × 70 ≈ 80 × 80, we change dimensions to an 80 × 80 array and simply discard every other ganglion cell in all rows and columns to leave a triangular 40 × 40 array of cells, each cell being in register with an amacrine cell. This does not affect, for example, the distribution of domain sizes (except to scale the waves by a factor of 2) or the distribution of interwaves intervals. For a one-retina, one-LGN sheet system, this still leaves us with 40⁴ = 2.56 × 10⁶ variables. We discuss one simulation of such a system, but for full retinogeniculocortical simulations, this number is still intractably hard. Thus, we reduce further from 40 × 40 arrays to 20 × 20 triangular arrays by threshold-averaging the activities of neighboring ganglion cells in 2 × 2 parallelograms. If three or four cells are active in each parallelogram, then the representative “average” cell is active; if one or no cell is active, then the representative is inactive; if two cells are active, then the representative’s activity is randomly set to zero (inactive) or one (active). Again, such manipulations alter the scale of the system without altering the dynamics in any other way. Because the model of Feller et al. (1997) is very sensitive to the values of some of its parameters, reducing the size of their simulated patch of retina by reducing, for example, the amacrine cell input radius would then require us to demonstrate that the resulting parameter region still faithfully reproduces the experimental data. Because our focus here is not on constructing models of realistic spontaneous waves but rather on determining whether such waves can drive normal development, we opt for the simpler, averaging strategy.

A significant problem that we find with the model of Feller et al. (1997) is that there tend to exist “hot spots” on the simulated retina that initiate spontaneous wave propagation more frequently than average, and corresponding “cold spots” that initiate wave propagation less frequently than average. Such regions become topographically overrepresented or underrepresented in our simulations. The experimental data, however, indicate that wave initiation sites are consistent with a random, uniform distribution (Feller et al., 1997). Thus, some way must be found of overcoming this lack of uniformity in the model. To this end, after a fixed number of simulated time steps, we re-randomize the refractory periods of amacrine cells. This is repeated each time the fixed number of time steps elapses. We find that this measure ensures an approximately uniform distribution of wave initiation sites without, again, altering in any other way the dynamics of the waves.

Because full simulations of retinal waves would often contain “dead time” during which no waves propagate, and thus the simulations would not progress, we instead construct waves “off line” and store them in data files, discarding any periods of inactivity. These data files are then used to reconstruct retinal wave activity patterns, which are “played back” to full simulations. Although this eliminates periods of inactivity within each simulated retina and thus speeds up simulation, it increases interocular correlations in simulations with two retinas. The effect of this in our model of plasticity is possibly to increase the degree of binocularity at the boundaries of ODCs and to decrease the spacing of ODCs (Elliott and Shadbolt, 1998b). However, despite its challenge to our simulations with a harder problem than natural development normally poses, we find that segregation of afferents and topographic refinement still occur. This demonstrates that, with reduced interocular correlations, normal development would proceed properly.

In generating the spontaneous retinal waves for two-eye simulations, we assume that the wave-generating mechanisms in each retina are independent of those in the other retina. Wave data files consist of 50,000 periods of activity played and replayed to simulations, with amacrine refractory period reinitialization occurring every 250 periods of activity. To avoid edge effects, periodic boundary conditions are imposed on the simulated retinas, so that opposite edges of the retinal sheets are identified.

To simulate visually evoked activity patterns, we follow the method used by Goodhill (1993). First, each ganglion cell in the left retina is randomly assigned to be active (unit activity) or inactive (zero activity). Then, for each ganglion cell in the left retina with activity a, the visuotopically equivalent cell in the right retina is assigned the same activity a with probability p; otherwise it is assigned the opposite activity 1 − a. This permits the introduction of well defined interocular correlations. These binary activity patterns are then separately convolved with a suitably normalized Gaussian, with parameter ς_r. This smears out the binary activity patterns and introduces well defined intraocular correlations (Goodhill, 1993). Such a model attempts to capture the intraocular and interocular correlations that are likely to exist in visually evoked activity. We will always take ς_r = 0.75. The dependence of, for example, ODC width on this parameter is discussed in Elliott and Shadbolt (1998b).

We simulate the LGN as two sheets of cells that initially receive innervation from both eyes. For computational tractability, each sheet is taken as a triangular, close-packed array of cells of the same dimensions as each retina, and periodic boundary conditions are imposed. Because the number of cells in the LGN is of the same order as the number of ganglion cells in the retina, this is not a bad approximation (cf. Sanderson, 1971). To set up the initial pattern of connectivity between each retina and each LGN sheet, we again follow the method used by Goodhill (1993). Let the maximum distance (in units of cell spacings) between any two cells in an LGN sheet be denoted by d_max. Given a perfect one-to-one mapping, each retinal ganglion cell would project to a unique LGN cell in each sheet, the LGN cell that would be in register with the ganglion cell were the appropriate LGN sheet superimposed on the ganglion sheet. Let d denote the distance between this LGN cell and some other LGN cell in the same sheet. Then, initially, the number of synapses projected from the retinal ganglion cell to an LGN cell is taken to be proportional to β(1 − d/d_max) + (1 − β)n, where n ∈ [0, 1] is a randomly selected number for each LGN cell. The parameter β ∈ [0, 1] determines the initial topographic bias in the projections (Goodhill, 1993). For β = 0 there is no bias at all, whereas for β = 1 the bias is greatest. Following Goodhill (1993), we take β = 0.5, which provides a small, initial bias for the topographic mapping. This can be imagined to be established, for example, by activity-independent mechanisms during target innervation. Small decreases in the value of β do not affect our results.

Cells in each simulated LGN sheet are initially binocularly innervated. However, experimentally, although the segregation of retinogeniculate afferents appears to be an activity-dependent, competitive process (Rakic, 1981; Sretavan and Shatz, 1986; Penn et al., 1998), the outcome of this process is always predictable: each LGN lamina will end up being innervated only by a particular, predictable eye. Several mechanisms can be imagined to account for this behavior. Perhaps the simplest, and the one that we shall use in simulation, is that an initial contralateral-eye bias in some laminae and an ipsilateral-eye bias in the others would tilt the competition in favor of the dominating set of inputs. Such biases again could be imagined to be initially established by activity-independent mechanisms during target innervation. Thus, to achieve such a bias in simulation, in the presumptive left eye-controlled LGN sheet, we multiply the initial number of synapses from the left eye, set up as described above, by a factor 1 + γ, and the initial number of synapses from the right eye by a factor 1 − γ. This is reversed for the presumptive right eye-controlled LGN sheet. In simulations presented below, we always take γ = 0.5, although, in fact, γ can be taken surprisingly close to zero (γ ∼ 0.1) without the predictable nature of the segregation breaking down.

Because we are interested in more general developmental issues, we use a very simple model of LGN neurons. If the input ganglion cells of a particular LGN cell are indexed by the label i and have activity a_i ∈ [0, 1], and if the number of synapses the LGN cell receives from those cells is s_i, then, in each time step, Δt, we take the instantaneous firing rate of the LGN cell to be (∑_is_ia_i)/(∑_is_i). The numerator is standard in simple models of neural networks. This is then divided by the total number of synapses for two reasons. First, we want to keep the instantaneous firing rate bounded in the interval [0, 1], the same interval used for ganglion cells. Second, because we simulate a developing system, the number of synapses can change. It would be expected, for example, that a neuron would adjust its firing threshold in a manner that depends on the number of its inputs (cf.Bienenstock et al., 1982). The form that we use is the simplest, parameter-free form that satisfies these requirements. Other forms are possible, such as a logistic function of the numerator, but this would introduce additional parameters. Furthermore, the form that we use permits a thorough mathematical analysis of our neurotrophic model of plasticity (see below). Here, for simplicity, we do not model any explicit lateral interactions between LGN cells, although we will discuss this possibility in Results.

Our model of the geniculocortical pathway is similar to that of the retinogeniculate pathway. The striate cortex contains one or two orders of magnitude more cells than the LGN (cf. Beaulieu and Colonnier, 1983). It would be computationally intractable to model such large numbers. We therefore simulate a patch of layer IV of the cortex that is the same size as the retinal and LGN sheets, that is, a 20 × 20 triangular, periodic, close-packed array of cells. The projections from each LGN sheet to the cortical sheet are established in an identical manner to the projections from each retina to the LGN sheets. We use the same bias index β = 0.5. However, in contrast to the retinogeniculate projection, we do not permit an ipsilateral or contralateral bias in the geniculocortical projection, so that each cortical cell is initially almost exactly binocularly driven. This is likely to be a reasonable model for monkeys, although the possible importance of a contralateral bias in cats has recently been discussed (Crair et al., 1998). The mechanisms that allow the ipsilateral projection to the striate cortex in cats to develop and gain ground in territory initially heavily dominated by the contralateral eye are likely to be non-Hebbian and perhaps not activity dependent (Crair et al., 1998). In the absence of further experimental characterization of these mechanisms, and because we are concerned here with the activity-dependent component of development, we use a generic, bias-free geniculocortical projection in our simulations. This means that we restrict our study to the development of the primate geniculocortical pathway. The model of cortical activity that we use is identical to the model of LGN activity; again, no explicit lateral interactions on the cortex are modeled, although we discuss this possibility in Results.

Thus, for typical, full retinogeniculocortical simulations, we use two simulated retinas that usually produce spontaneous waves of activity, but we also run simulations with visually evoked activity. These two retinas innervate two LGN sheets (a presumptive left eye-controlled sheet and a presumptive right eye-controlled sheet), and the activity in the retinas excites the cells in the LGN sheets. The two LGN sheets innervate a patch of striate cortex, which is similarly excited by LGN activity. All of these sheets are 20 × 20, so our full simulations consist of 6 × 20⁴ = 960,000 variables representing the numbers of synapses from afferent cells to target cells. All synapses are purely feed forward, and cortical activity has no impact on LGN activity via feedback synapses to the thalamus in our simulations. To produce decent receptive field refinement, good topographic refinement, and the complete segregation of retinogeniculate and geniculocortical afferents, our simulations run for of order 10⁶ time steps of Δt = 100 msec. This represents a little more than 1 d of simulated development, but each simulation runs on our computers (DEC Alphas) for ∼1 month. Thus, reducing the rate at which the system develops, so that simulated development takes of order a simulated month, would be intractable. We also run simpler simulations of a projection from one retinal sheet to one LGN sheet. Most of these are on 20 × 20 sheets and run comparatively quickly (a few days), but we discuss one simulation on 40 × 40 sheets that is much slower.

In modeling the continuous development of the full retinogeniculocortical pathway as a one-stage process, we could be accused of disregarding the basic developmental data. For example, in the cat, retinogeniculate segregation is well underway even before geniculocortical afferents invade the cortical plate (Shatz, 1983;Shatz and Sretavan, 1986; Allendoerffer and Shatz, 1994). In fact, we find in our simulations that the geniculocortical pathway does not begin changing significantly until the retinogeniculate pathway has nearly completed its development, that is, until retinogeniculate afferents are well segregated and topographic refinement is largely over. Thus, although our model is simplified for reasons of computational convenience in some respects, its behavior is faithful to the developmental data in that the model breaks up development into an essentially two-stage process.

The neurotrophic model of plasticity. To permit anatomical remodeling, we use our previously used model of synaptic plasticity based on competition for neurotrophic support. This model is well characterized mathematically (Elliott and Shadbolt, 1998a) and has been successfully applied to the development of ODCs, in which system a number of predictions were made (Elliott and Shadbolt, 1998b). We use the same neurotrophic model for both retinogeniculate and geniculocortical synapses. This thus commits us to the view that neurotrophic interactions play an important role in the activity-dependent development of the retinogeniculate as well as the geniculocortical pathway, but not, of course, to the view that precisely the same class of neurotrophic molecules is important in both systems. Nevertheless, for notational and computational convenience, we shall discuss the model as if only one neurotrophic molecule is involved.

We consider a generic sheet or set of sheets of afferent cells (either the retinas or the LGN sheets) and a generic sheet of target cells (either an LGN sheet or the cortical sheet). Let afferent cells be indexed by letters such as i and j and target cells be labeled by letters such as x and y. The number of synapses between afferent i and target x is denoted by s_xi(t); for notational convenience, we will not indicate the time dependence explicitly. Let the activity of afferent cell i be denoted by a_i ∈ [0, 1]. The basic equation for our model of neurotrophic interactions is then given by:

$$\frac{{\text{ds}}_{\text{xi}}}{\text{dt}}=\epsilon s_{\text{xi}}\left[\sum _{\text{y}} {\mathrm{\Delta }}_{\text{xy}}\left(T_0+T_1 \frac{\sum _{\text{j}}{s}_{\text{yj}}{a}_{\text{j}}}{\sum _{\text{j}} s_{\text{yj}}}\right)\frac{(a+a_{\text{i}}){\rho }_{\text{i}}}{\sum _{\text{j}}{s}_{\text{xj}}(a+a_{\text{j}}){\rho }_{\text{j}}}-1\right],$$ Equation 2

where the number of NTF receptors ρ_i expressed on each afferent terminal is given by:

$${\rho }_{\text{i}}={\overline{a}}_{\text{i}}/\sum _{\text{x}} s_{\text{xi}},$$ Equation 3

with $\overline{a}$_i in the expression for ρ_i denoting the recent time average of the activity of afferent i, assumed to be given by:

$${\overline{a}}_{\text{i}}(t)=\frac{1}{\tau }\underset{-\infty }{\overset{t}{\int }}{\text{dt}}^{\prime }{a}_{\text{i}}(t^{\prime })e^{-(t-t^{\prime })/\tau }.$$ Equation 4

The parameter ε determines the overall rate at which the number of synapses changes and is related to τ through ε = 1/τ. For full retinogeniculocortical simulations using spontaneous retinal activity, we use the value ε = 5.0 × 10⁻⁴, although for simulations using visually evoked activity we use, for computational convenience, the value ε = 0.02, for reasons explained in Results. For simulations of a one-retina, one-LGN sheet system, we can take ε to be a little smaller than the smallest value in full simulations; we take it to be ε = 10⁻⁴. These smaller values of ε correspond to values of τ representing time scales of a few minutes of simulated time. The parameters T₀ and T₁ represent activity-independent and the maximum activity-dependent levels, respectively, of release of NTFs from target cells (Blöchl and Thoenen, 1995, 1996; Griesbeck et al., 1995; Goodman et al., 1996). Uptake by afferents of NTFs depends on a resting, constitutive uptake parameter, a, and also on the level of activity of the afferent. This latter assumption, that the uptake of NTFs by afferents contains an activity-dependent component, is a specific postulate of our model, and it is a critical feature in allowing for competitive interactions between afferents. The function Δ_xy permits NTF diffusion through the target field and depends only on the separation between target cells x and y. We assume it to be a simple, suitably normalized Gaussian function with parameter ς_t. We take ς_t= 0.75; the dependence of, for example, ODC width on this parameter is discussed in Elliott and Shadbolt (1998b).

We have discussed extensively the derivation, justification, analysis, and predictions of this model in previous publications (Elliott and Shadbolt, 1998a,b). We therefore only briefly describe the critical assumptions underlying the model here.

The first assumption is that the production and release of NTFs from target cells depends on neuronal activity. If the activity-dependent component is removed from the model, then the model ceases to be capable of inducing competition between afferents and thus cannot induce their segregation. The production and release of many NTFs in the cortex and hippocampus is regulated by activity (Zafra et al., 1991; Castren et al., 1992; Gwag and Springer, 1993; Lindholm et al., 1994; Blöchl and Thoenen, 1995, 1996; Bozzi et al., 1995;Griesbeck et al., 1995; Schoups et al., 1995; Goodman et al., 1996), so this assumption seems quite reasonable. The released NTFs are assumed to diffuse rapidly through the target field, with diffusion characterized by the function Δ_xy. For the parameters given above, the assumed diffusion is not extensive, amounting only to significant diffusion to nearest-neighbor target cells (i.e., only six cells in our simulations). Although not critical for inducing competition, the diffusion of NTFs in our model is critical for inducing ODCs of finite, non-zero width. Without diffusion, each target cell would become dominated by one eye or the other, but there would be no ordering into columns or patches of nearby cortical cells dominated by the same eye.

A second critical assumption is that the uptake of NTFs by afferents depends on their activities. Without this assumption, our model does not lead to competition. Presently no data bear directly on this assumption. It is therefore a central prediction of our model that NTF uptake depends on afferent activity, with more active afferents being able to take up greater levels of NTFs than less active afferents. If this prediction is wrong, then our model is wrong. Our model also requires that there is an activity-independent component to afferent NTF uptake, governed by the parameter a.

Perhaps the most critical pair of assumptions is that the number of synapses that an afferent projects into a region of tissue determines the level of NTF uptake from that region of tissue (in addition to other factors such as afferent activity), and that the time-average level of uptake of NTFs from a region of tissue determines how many synapses an afferent projects to that region of tissue. The first of this pair of assumptions appears to be quite plausible. Much evidence supports some version of the second of this pair of assumptions. For example, the level of NTFs appears to affect the size of axonal arborization (Campenot, 1982a,b; Cohen-Cory and Fraser, 1995; Causing et al., 1997; Kimpinski et al., 1997). Furthermore, the influence of NTFs appears to be local, with local excess supply promoting local sprouting and local shortage promoting local retraction (Campenot, 1982a,b; Gallo and Letoureau, 1998). The interaction between these two assumptions results in competitive interactions through a feedback mechanism. Elevated NTF uptake results in elevated synaptic numbers, which in turn enhances the capacity for further uptake while depleting other afferents of NTFs that they otherwise would have taken up. If NTF uptake does not depend on the number of synapses, then competition does not occur in our model.

Finally, although not critical, because many other forms are possible, we assume that the number of NTF receptors expressed on each afferent terminal is given by Equation 3 and that the uptake of NTF also depends on this number, in addition to the number of synapses and afferent activity. This form requires that the receptors are expressed in an activity-dependent manner (Birren et al., 1992; Bengzon et al., 1993;Cohen-Cory et al., 1993, Dugich-Djordjevic et al., 1995, Salin et al., 1995) and that the larger the total number of synapses supported by an afferent, the fewer the number of receptors per synapse.

Together, these various assumptions lead to the mathematical form of the model exhibited in Equation 2, as described in detail elsewhere (Elliott and Shadbolt, 1998a,b). This neurotrophic model is very different in character from the previous, much simpler neurotrophic models that we have built (Elliott et al., 1996). For example, although an earlier model (Elliott et al., 1996) was formulated in energy-minimization terms (interpreted as NTF maximization), it can be shown that the differential equations in Equation 2 cannot be derived by assuming (gradient descent) minimization of some energy function (our unpublished observations). Thus, mathematically, the present model is very different from energy-minimization models, either our own earlier model of anatomical plasticity based on competition for neurotrophic support (Elliott et al., 1996) or other forms of models, such as models of physiological plasticity in which competition is imposed using synaptic normalization (Miller et al., 1989).

In addition to these mathematical differences, our present model is also different, in terms of biology, from other types of models (Miller et al., 1989). For example, our model seeks to shed light on the mechanisms of synaptic competition, a ubiquitous phenomenon in the developing vertebrate nervous system (Purves, 1988). This is reflected, for example, in our postulate concerning the possible activity dependence of NTF update by afferents. In contrast, many other models (Miller et al., 1989; Goodhill, 1993) enforce competition by imposing synaptic normalization. They can therefore shed no light on the mechanisms of competition because they merely assume it rather than show how it can emerge from underlying processes. Although some evidence hints at the possibility that certain types of synaptic normalization, in fact, do operate in the normal, developing cortex (Turrigiano et al., 1998), the form is not that required by models of the development of the visual system (Elliott and Shadbolt, 1998b). Finally, our model makes biological predictions or replicates experimental results that some other models do not. For example, simple correlation-based models of physiological synaptic plasticity (Miller et al., 1989) do not exhibit any change in ODC width in response to changes in either intraocular or interocular image correlations, unlike the present model or, for example, Goodhill’s model [(Goodhill, 1993) whether Goodhill’s model exhibits shifts in ODC width in response to changes in intraocular image correlations is unclear, because Goodhill did not consider this possibility]. Thus, both mathematically and biologically, our present model is different from previous models (Miller et al., 1989; Goodhill, 1993; Elliott et al., 1996).

It can be shown that a critical quantity in our model of anatomical plasticity is the ratio T₀/(aT₁) (Elliott and Shadbolt, 1998a,b). When this is less than 1, afferent segregation (which could be topographic and receptive field refinement or eye-specific afferent segregation) always occurs, even for very highly (although not perfectly) correlated afferent activity. However, when this quantity exceeds unity, afferent segregation never occurs. T₀ represents the amount of NTF released from target cells in an activity-independent manner, or, alternatively, the amount of exogenous NTF infused into the target system. Thus, when T₀ exceeds a critical threshold, afferent competition breaks down, consistent with the experimental result that the infusion of excess quantities of NTFs eliminates or tempers competitive interactions (Carmignoto et al., 1993; Cabelli et al., 1995; Riddle et al., 1995).

The quantity T₁, representing the maximum activity-dependent release of NTFs from target cells, essentially sets the scale for the number of synapses from afferent cells to target cells. We shall always take it to be T₁ = 20 without loss of generality. The value of the quantity a, representing the capacity for resting uptake of NTFs by afferents, is required to be neither too large (a ≫ 1) nor too small (a ≪ 1) (Elliott and Shadbolt, 1998a). We therefore always take it to be a = 1. The value of T₀ will always be T₀ = 0, unless indicated otherwise. That is, we shall assume for most simulations that there is no exogenous infusion of NTFs into target sheets. These values apply to both retinogeniculate and geniculocortical synapses.

The representation of topography. To display the representation of a sheet of afferent cells on a sheet of target cells, we use two similar measures. In the first measure, which we denote by M^CoM, we determine the “center of mass” in space of the input to a target cell from all its afferent cells, where this is always calculated relative to perfect projections. Thus, for target cell x, this measure is defined as:

$${\vec{M}}_{\text{x}}^{\text{CoM}}=\frac{\sum _{\text{i}}{\vec{p}}_{\text{xi}}{s}_{\text{xi}}}{\sum _{\text{i}}{s}_{\text{xi}}},$$ Equation 5

where p⃗_xi is the spatial position of afferent i relative to the spatial position of the afferent that would uniquely project to target cell x were topography perfect. When two afferent sheets are considered, the sums can be extended over both so that an “average” afferent point is obtained. When a sheet projects no synapses to a target cell, then the measure is left undefined at that cell. To visualize this center of mass measure, the positions defined by these vectors are plotted in space and connected according to the neighborhood relations on the target sheet. This measure is used, for example, by Goodhill (1993). Intuitively, this center of mass projection simply determines which afferent cell a target cell best represents by determining where, on the afferent sheet, the average synaptic input (in terms of numbers of synapses, not neuronal activity) comes from.

However, this first measure can be quite misleading. When periodic boundary conditions are used, for example, every target cell that is initially innervated according to the method described above at first has a roughly symmetrical input in afferent space, and the randomness implicit in the initial projections is averaged out by Equation 5. Thus, initially, this measure gives the impression that topography is nearly perfect, despite highly unrefined receptive fields and large scatter. If periodic boundary conditions are not used, so that edge effects are significant and initial projections are for the most part highly unsymmetrical, then the measure gives the impression of a badly disrupted topography that slowly “unfolds” as development proceeds (Goodhill, 1993). However, this unfolding is equally misleading, because it is principally an artifact. To overcome these difficulties, we use a second measure.

Instead of considering only the average, center of mass projection, we also consider the maximum projection. That is, a cell on the target sheet is defined as best representing the cell on the afferent sheet that sends the maximum number of synapses to it, rather than the cell that is closest to where the center of mass of projected synapses lies (when multiple such cells exist, we average over the locations, although this situation does not arise in our simulations). The visualization of this measure is performed in the same manner as the for center of mass measure.

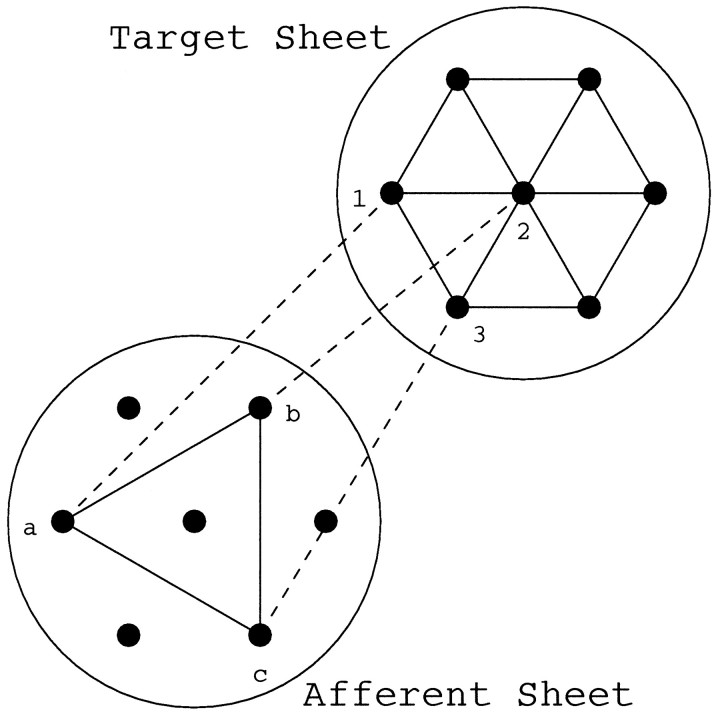
Figure 1 illustrates schematically the visualization of topography for a small system of seven afferent cells innervating seven target cells. For each cell on the target sheet, we determine which afferent cell it best represents, using either measure described above. Thus, although target cell 1 might receive input from all afferent cells, it might best represent afferent cell a, and similarly for target cells 2 and 3. Because target cells 1 and 2 are neighbors, a line is drawn to connect the two afferent cells, a and b, that these target cells best represent, and similarly for every pair of nearest target neighbors and the afferents that they best represent. When topography is perfect, the neighborhood relations on the target sheet will map without distortion onto the connections constructed as described on the afferent sheet. Hence, in this case, the hexagonal nearest neighbor pattern illustrated on the target sheet will be perfectly reproduced on the afferent sheet. When topography is not perfect, the connections constructed on the afferent sheet will be distorted. The extent of distortion will indicate how badly afferent topography is represented on the target sheet.

Fig. 1.

A schematic illustration of the visualization of topography in a small system containing seven afferent and seven target cells. The connections between cells in the target sheet denote nearest neighbor relations. For each target cell, the afferent cell that it best represents is determined. Thus target cells 1, 2, and3 best represent afferent cells a, b, and c, respectively. Because target cells 1 and2 are neighbors, the afferent cells a and b that they best represent are connected with aline, similarly for all other pairs of nearest target neighbors (only 3 such pairs are shown for clarity). The resulting pattern of connections among the afferent cells illustrates the representation of the afferent sheet on the target sheet.

After sufficient topographic refinement, both measures of topography should converge to approximately the same result, although they differ significantly at the outset. Neither measure, however, gives much information about the extent of receptive field refinement, so, in addition to showing representations of topography, we will also show typical examples of the development of some target cells’ receptive fields.

RESULTS

We now present results of simulations of our model. First we present results for the simple, one-eye, one-LGN sheet simulations. Then we present results for the full retinogeniculocortical simulations.

One-eye, one-LGN sheet simulations

We first present simulations run on one-eye, one-LGN sheet systems. The primary purpose of this is to establish whether the model of spontaneous retinal waves presented by Feller et al. (1997) is capable of inducing topographic and receptive field refinement.

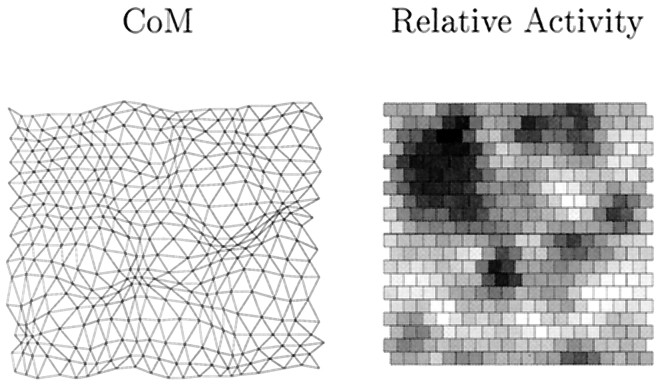
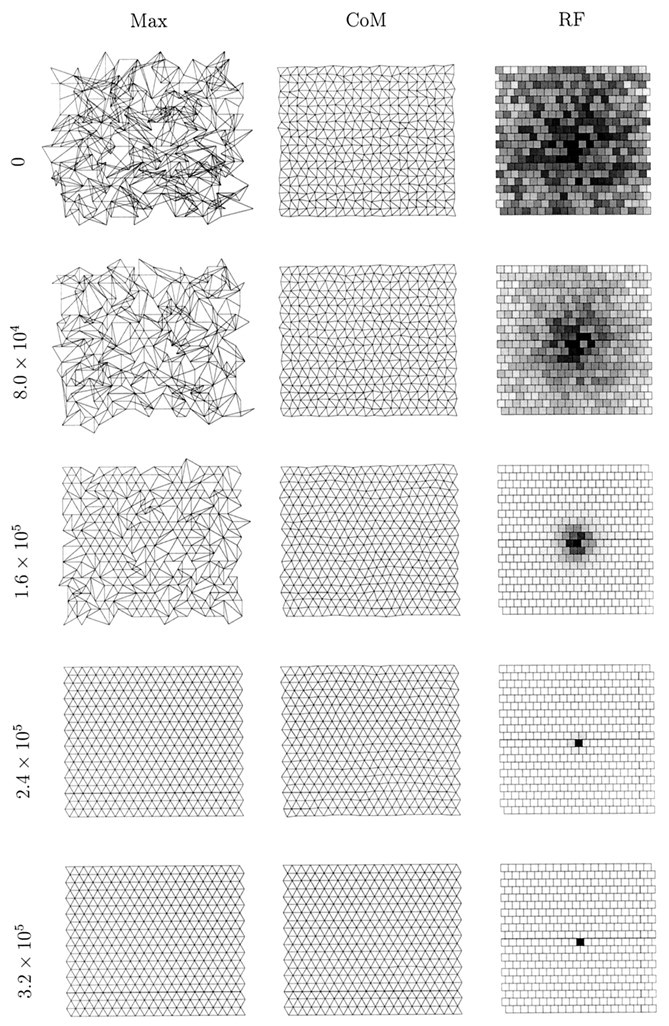
In Figure 2, we show the state of one simulation at various time steps with the retinal wave model in which regular re-randomization of amacrine cell refractory periods is not performed. Except for averaging to reduce the size of the system and the use of periodic boundary conditions to avoid edge effects, this model is identical to that presented by Feller et al. (1997). Initially, the center of mass measure of topography is almost perfect, for reasons explained in Materials and Methods. However, the maximum measure shows significantly disrupted topography, and the sample receptive field shows little bias. As development proceeds, the maximum topography measure becomes increasingly disrupted, whereas the center of mass measure changes slowly while retaining its orderliness.

Fig. 2.

An example of a one-eye, one-LGN sheet simulation using spontaneous retinal waves. In this simulation, regular re-randomization of amacrine cell refractory periods is not performed.Left to right, in the first column, the maximum projection measure (Max) for topography is shown; in the second column, the center of mass measure is shown; in the third column, the receptive field (RF) of the LGN cell at position (11,11) (near the center of the sheet) is shown. Each row represents the state of the system after a given number of time steps, the first being 0 time steps, the second 2.5 × 10⁵, the third 5.0 × 10⁵, the fourth 7.5 × 10⁵, and the last 1.0 × 10⁶. The visualization of topography is described in Materials and Methods and Figure 1. To visualize a target cell’s receptive field, we calculate the number of synapses from all afferents to that cell as a percentage of the maximum number of synapses sent by an afferent. This percentage value is then displayed as a gray scale (white = 0%,black = 100%); each square represents one afferent cell.

The initial collapse of the maximum measure at a few retinal positions occurs for two reasons. First, a well known feature of neural network simulations is their undesirable capacity for overgeneralization. During the very early stages of simulated development, the system experiences only a small subset of the ensemble of afferent activity patterns that it will eventually experience. The system therefore tends to collapse around this early subset. This behavior is a function of the parameter ε, with larger values making the behavior even more extreme. This is why we use a small value, ε = 10⁻⁴. Although an even smaller value would be desirable for a number of reasons, this would make the simulations intractably slow. Second, when amacrine cell refractory periods are not re-randomized regularly, hot and cold spots of activity exist on the simulated retina. These further accentuate the problem of overgeneralization, because the data are not uniformly distributed.

The existence of the retinal activity hot and cold spots is revealed as the simulation progresses. The maximum measure of topography slowly unfolds after its initial disruption as receptive field refinement occurs, and this measure gradually converges on the center of mass measure. However, both measures reveal overrepresented regions of the retina (regions of dense packing of points) where LGN cell receptive fields change slowly, and underrepresented regions of retina (regions of loose packing of points) where LGN cell receptive fields change rapidly. Nevertheless, despite these disruptions, topography and receptive fields are finally such that the retinal sheet is represented fairly continuously without large jumps on the LGN sheet.

The connection between the distortions of the final topography measures in Figure 2 and retinal activity hot and cold spots is revealed in Figure 3. Regions of overrepresentation correspond exactly to the most active patches of retina, whereas regions of underrepresentation correspond exactly to the least active patches. For the retinal wave data used to generate Figure 2, there is no indication that the distribution of wave initiation sites becomes more uniform as time progresses up to the maximum number of time steps used: 50,000. Indeed, by dividing this interval into five consecutive intervals of 10,000 time steps and determining in each the mean and SD of the ganglion cell activity rate, in addition to the minimum and maximum values per interval, all of these quantities simply scale linearly with time. Thus, the failure of the neurotrophic model of plasticity to eliminate the remaining topographic distortions does not invalidate the model but rather shows that the model of spontaneous retinal activity does not generate retinal waves that are phenomenologically realistic in all respects (Feller et al., 1997). Thus, to make the distribution of retinal wave initiation points more uniform, we find that the simplest method is regularly to re-randomize the amacrine refractory periods. Whether or not this is biophysically realistic, we are only concerned here with using phenomenologically realistic patterns of spontaneous retinal activity in our simulations.

Fig. 3.

The connection between disrupted topography and retinal activity hot spots. The left map is the bottom center of mass topography measure in Figure 2. Next to it is agray scale representation of relative activities of retinal ganglion cells in the simulation. The least active cells are shown aswhite, whereas the most active cells are shown asblack; shades of gray interpolate between these extremes. Because the topography measure is in retinal coordinates, these two maps are superimposable. For the 50,000 periods of activity in the simulated retinal waves used in the simulation in Figure 2, we find that the least active ganglion cell is active only 493 times (white squares in right map), whereas the most active ganglion cell is active 1760 times (black squares in right map). On average, each ganglion cell is active 968 times (SD 254).

Figure 4 shows a simulation in which amacrine cell refractory period reinitialization does occur regularly. We see, again, a slight tendency for the maximum measure of topography to collapse, but the tendency is not nearly so dramatic as in Figure 2, in which refractory period reinitialization does not occur. Both measures of topography develop and converge quite closely. After 1.25 × 10⁶ time steps, both measures of topography are nearly identical and almost perfect (data not shown). This result rules out the possibility that the behavior exhibited in Figure 2 is largely caused by playing and replaying only a finite set (50,000) of preconstructed episodes of retinal wave activity to the simulation, because, were this so, we would expect to observe similar behavior in the simulation presented in Figure 4. In this figure, we observe a near-uniform representation of the retinal sheet on the LGN sheet, with only faint hints of differences in the extent of representation of different regions of retina. Further simulations described below that use spontaneous retinal waves will always be with amacrine refractory reinitialization.

Fig. 4.

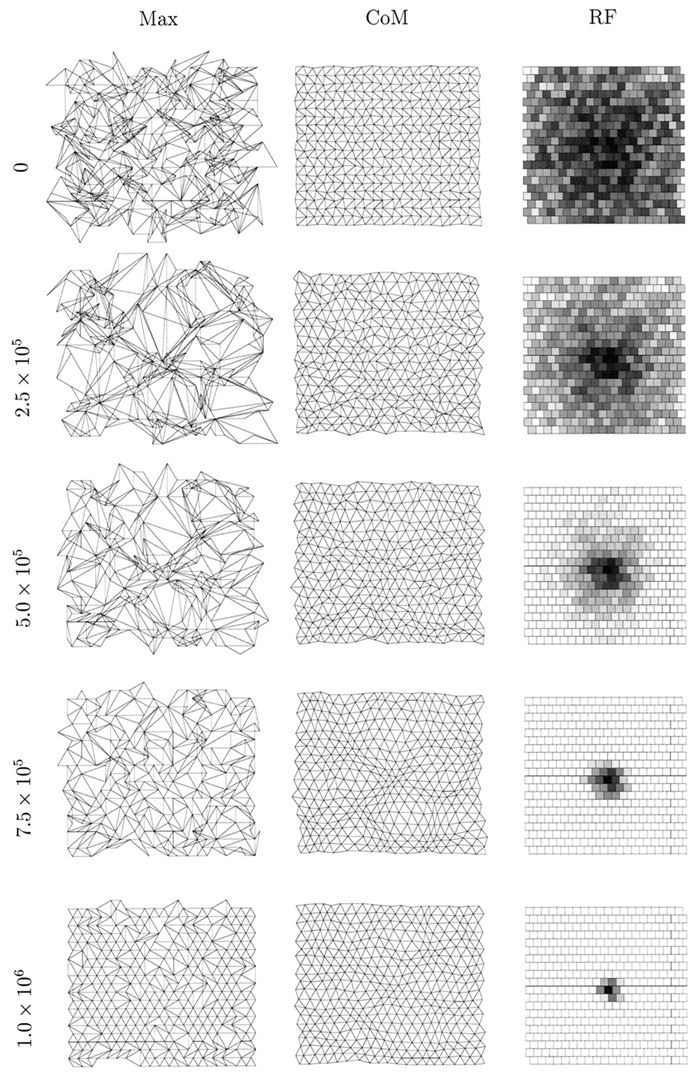
An example of a one-eye, one-LGN sheet simulation using spontaneous retinal waves in which amacrine cell refractory period reinitialization occurs regularly. The details of this Figure are otherwise identical to Figure 2.

To determine whether the averaging procedure used to reduce 40 × 40 arrays of cells to 20 × 20 arrays has any impact either on the capacity of our neurotrophic model of plasticity to permit topographic refinement or on the capacity of the simulated retinal waves to drive such refinement, we examined one simulation in which such averaging was not performed. As expected, topographic and receptive field refinement proceeded normally, as in the smaller simulations, but naturally this larger simulation took much longer to run to completion (data not shown).

In Figure 5, we simulate the infusion of exogenous NTFs by setting T₀ = 100. We see that topography and receptive fields remain in unrefined states. Thus, infusion of exogenous NTFs in this simulation has eliminated the competitive mechanisms that result in the refinement of connections.

Fig. 5.

An example of a one-eye, one-LGN sheet simulation in which the infusion of exogenous neurotrophic factors is simulated by setting T₀ = 100. The details of this Figure are otherwise identical to Figure 4.

To establish whether the capacity of our neurotrophic model of synaptic plasticity to permit the development of refined topography and receptive fields depends on the use of a particular form of retinal activity, we now consider a simulation in which we use visually evoked activity. We may safely take ε = 0.02 to speed up simulations. Such a simulation is shown in Figure 6. Despite the increase in the value of ε, we find that a comparable number of time steps is required for simulated development to occur as are needed when retinal waves are used. This demonstrates that the use of distributed retinal activity patterns makes the task of topographic and receptive field refinement much harder. One noticeable difference between this simulation and the simulation using retinal waves shown in Figure 4 is that there is no further disruption of the initially bad topography attributable to overgeneralization. This is because the model uses distributed and not local patterns of retinal activity, so that all retinal points are approximately equally active from the outset.

Fig. 6.

An example of a one-eye, one-LGN sheet simulation in which visually evoked activity is used rather than spontaneous retinal waves. The details of this Figure are otherwise identical to Figure 4, except for the time steps, which are as indicated.

The above simulations did not use any lateral interactions on the LGN sheet, except for those that relate to the diffusion of NTFs on the target sheet. The major difference between simulations using explicit lateral connections and those that do not is the rate at which the systems develop. Lateral interactions tend to increase the rate at which receptive field and topographic refinement occur (data not shown). This increase in not so marked in the case of spontaneous retinal activity, because the activity patterns are already narrowly focused and do not give rise to significantly distributed patterns of activity on the LGN sheet. However, in the case of visually evoked activity, the presence of explicit lateral interactions dramatically increases the rate of development (cf. Goodhill, 1993).

Full retinogeniculocortical simulations

We now turn to full retinogeniculocortical simulations. In addition to attempting to establish whether spontaneous retinal waves can drive topographic and receptive field refinement, we are now interested in whether such waves, in simulation, can drive the segregation of retinogeniculate and geniculocortical afferents.

In Figure 7, we show the state of the retinogeniculate pathway after 2.5 × 10⁵ time steps. At this stage, the afferents have already segregated cleanly into eye-specific layers in the LGN (data not shown), so that the presumptive left eye-controlled LGN sheet is entirely controlled by the left eye and the presumptive right eye-controlled LGN sheet is entirely controlled by the right eye. Both measures of topography reveal an ordered, smooth mapping of each retina onto its appropriate LGN sheet, and receptive fields are well refined. As the simulation progresses further, both measures of topography continue to converge to an almost perfect state.

Fig. 7.

The state of the retinogeniculate pathway after 2.5 × 10⁵ time steps in a full, retinogeniculocortical simulation using spontaneous retinal activity. The top row shows projections from the left eye to the presumptive left eye-controlled LGN sheet, and the bottom row shows the projections from the right eye to the presumptive right eye-controlled LGN sheet. The two receptive fields are taken from the LGN cells at position (11,11) in each LGN sheet. Conventions are as in Figure 2.

To obtain predictable but competitive segregation of retinal afferents into eye-specific layers in the LGN, we have, as described in Materials and Methods, used an ipsilateral projection bias in one lamina and a contralateral projection bias in the other. The extent of the bias is determined by the value of the parameter γ. In the simulation in Figure 7 we have used a large value, γ = 0.5, so that, for example, left eye inputs project ∼75% of all synapses to the presumptive left eye-controlled LGN. We have used such a large value for reasons of computational convenience only, so that the rate of segregation of afferents in the LGN is speeded up. In fact, even a bias value as low as γ = 0.1 (giving ∼55% control to the dominant input) still leads to predictable segregation (data not shown). Nevertheless, for γ = 0, so that there is no bias, segregation ceases to be predictable, and each eye can end up controlling distinct regions of the same LGN lamina, producing LGN equivalents of ocular dominance “patches” (data not shown). Thus, a prediction of this approach is that for the segregation of afferents in the LGN to be predictable, a (perhaps small) bias in the initial projections must exist. Other, alternative possibilities might exist, however. For example, cell surface cues might be such that the projections to a lamina from the eye that are destined to retract are less stable than those that are destined to remain, or the avidity of uptake of NTFs by the afferent terminals that will remain is greater than the avidity of uptake by those that will retract. Nevertheless, for the outcome of a competitive process to be completely predictable, as is the case in the LGN, it seems necessary that some intrinsic difference between the ipsilateral and contralateral projections must exist.

Recent experimental data indicate that the blockade of spontaneous retinal activity in one eye leads to an expansion of the LGN territory controlled by the active eye and a reduction in the territory controlled by the inactive eye (Penn et al., 1998). By eliminating activity in one eye in our simulations, we find that the active eye develops more synapses and retains synapses in the lamina that would otherwise have been controlled by the other eye, whereas the inactive eye retracts synapses not only from the “inappropriate” LGN lamina but also from the lamina that it would otherwise have controlled (data not shown). Thus, despite tilting competition in favor of the initially dominating input attributable to differences in the ipsilateral and contralateral projections, the competition can still be significantly influenced by other factors, such as relative levels of electrical activity in the two projections.

At the same point in simulated development as shown in Figure 7 for the retinogeniculate pathway, the geniculocortical pathway remains disordered and has progressed little (data not shown). Thus, although we do not explicitly model the two-stage process of retinogeniculate and geniculocortical development, our simulations essentially break development up into two phases. This occurs because geniculocortical development cannot progress significantly until LGN cell receptive fields have been refined. After 5.0 × 10⁵ time steps, the geniculocortical pathway in the same simulation has achieved quite sharply focused receptive fields and well ordered topographic refinement. However, although significant fluctuations in ocular dominance are beginning to emerge, no cortical cell is entirely dominated by input from only one eye (data not shown).

After further 2.5 × 10⁵ time steps, shown in Figure 8, the segregation of geniculocortical afferents into ODCs is nearly complete. Both measures of topography have largely stabilized and converged, with holes representing regions of no control by a particular eye. Comparing the CoM measure of topography for both LGN sheets (middle map, second row) with the map of ocular dominance, we see very ordered topography within ODCs and a “doubling back” across boundaries, consistent with the experimental data (Hubel and Wiesel, 1977). This is also a feature of the Max measure (middle map, top row), although it is a little harder to observe in this case.

Fig. 8.

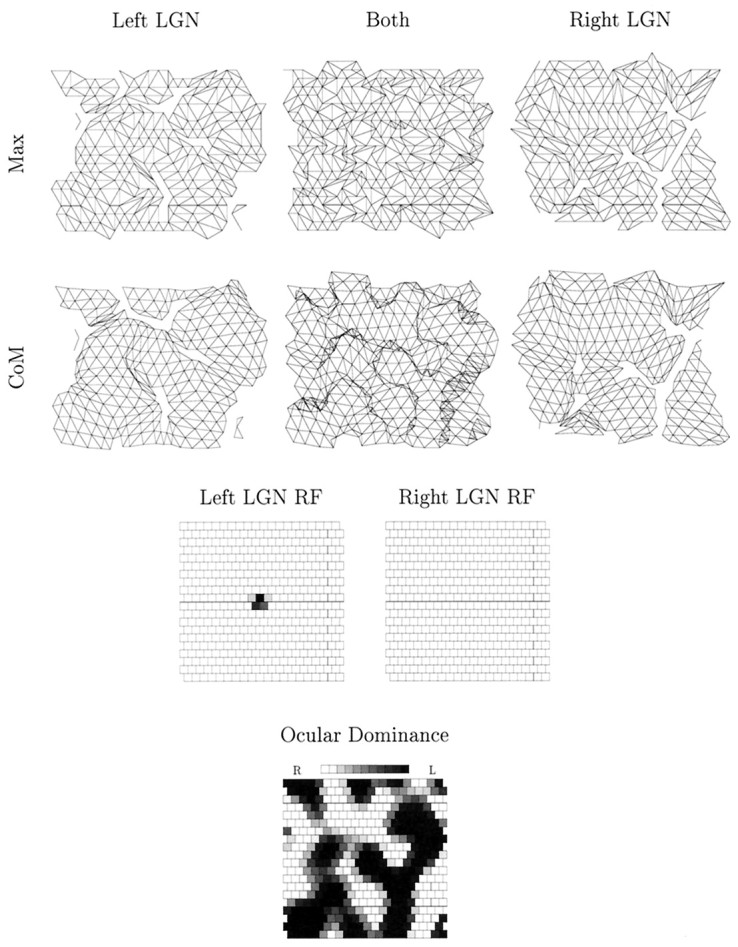
The state of the geniculocortical pathway after 7.5 × 10⁵ time steps for the same simulation shown in Figure 7. The top row shows the Maxmeasure of topography, whereas the second row shows theCoM measure. In these two rows, the first maps show the representation of only the left LGN sheet on the cortex; the third maps show the representation of only the right LGN sheet on the cortex; and the second maps show the representation of both LGN sheets on the cortex. The third row shows the receptive field of the cortical cell at position (11,11) in the cortical map, showing the left and right LGN connections separately (there are no synapses from the right LGN sheet, hence all squares are white). The last row shows a representation of ocular dominance on the simulated cortex. Each square represents a cortical cell, with the assigned gray scale value denoting the percentage control by the left eye. White represents complete control by the right (R) eye, and black represents complete control by the left (L) eye;shades of gray interpolate between.

The single retinogeniculocortical simulation using spontaneous retinal waves presented here is representative. We always observe that retinogeniculate development precedes geniculocortical development, and that cortical ODCs largely emerge after cortical topography and cortical cell receptive fields become refined. Simulating the infusion of excess quantities of NTFs into the LGN by increasing the value of T₀ prevents topographic and receptive field refinement, in a manner identical to that shown for one-eye, one-LGN simulations (Fig. 5). Furthermore, the segregation of retinogeniculate afferents into eye-specific laminae does not occur under this regime, and, in addition, the geniculocortical pathway fails to develop properly, despite a simulated infusion localized to the LGN (data not shown). Simulating the infusion of excess quantities of NTFs into the cortex at a sufficiently early, prenatal stage would prevent both the formation of ODCs (cf. Elliott and Shadbolt, 1998b) and topographic and receptive field refinement, although the development of the retinogeniculate pathway would not be disrupted in this case.

Many factors interact to determine the width of the ODCs shown in Figure 8, and these have been explored numerically and partially analyzed mathematically elsewhere (Elliott and Shadbolt, 1998b). One factor is the spatial NTF diffusion function Δ. For the values of the parameters determining this function used here (stated in Materials and Methods), the diffusion of NTF, in both the LGN and the cortex, is significant only to a cell’s six nearest neighbors. Increasing the extent of diffusion increases the width of the ODCs. Another factor is the extent of intraocular activity correlations. Our previous work predicted for the first time that alterations in intraocular correlations alters the width of ODCs; specifically, increasing the correlations increases ODC width (Elliott and Shadbolt, 1998b). Here, the spatial extent of spontaneous retinal activity is therefore a critical variable in determining the resulting periodicity of ODCs, with larger domains resulting in wider ODCs. Thus, should it be possible to manipulate the size of spontaneous retinal activity domains by pharmacological means in an animal such as an Old World monkey, in which the development of the geniculocortical pathway occurs largely prenatally (Horton and Hocking, 1996a), then we would predict that the width of the resulting ODCs would change. The final factor that affects ODC width is the extent of interocular activity correlations. As first predicted in the biologically relevant model of Goodhill (1993) and subsequently verified experimentally (Löwel, 1994; Goodhill and Löwel, 1995; Tieman and Tumosa, 1997), in our neurotrophic model, decreasing interocular correlations increases ODC width (Elliott and Shadbolt, 1998b). Thus, the size of interocular correlations between the spontaneous activity in both retinas also determines, in part, the width of ODCs. In the present simulations, however, for reasons of computational tractability, we have discarded periods of inactivity in each retina (see Materials and Methods). The effect of this will be to increase the interocular correlations beyond the level that would be expected to exist in the natural system, although it is likely that the correlations never become much stronger than uncorrelated. Our neurotrophic model can segregate afferents in the presence of even very strong interocular correlations (Elliott and Shadbolt, 1998a,b), so even mildly correlated interocular activity patterns do not present any difficulty for our model. Nevertheless, all other things being equal, were we to reinstate the inactive periods in simulation, we would expect a mild increase in the ODC width in Figure 8, together with a decrease in the binocularity of cortical cells at ODC boundaries.

We now consider a simulation in which we use visually evoked activity rather than spontaneous retinal waves. As before, we take ε = 0.02. We set p, the probability that visuotopically equivalent retinal ganglion cells are assigned the same activity, to p = 0.5, so that the two retinal images are uncorrelated. The development of the system using the model of visually evoked activity patterns is quite similar to that using spontaneous retinal waves. By 2.5 × 10⁵ iterations, perfect segregation of retinogeniculate afferents has occurred, and the topographic representation of an eye on its appropriate LGN sheet is almost perfect, as is receptive field refinement (data not shown). At 5.0 × 10⁵ time steps, the geniculocortical pathway is well on its way to successful topographic and receptive field refinement, although there is at this stage very little indication of the segregation of geniculocortical afferents into ODCs. This is shown in Figure 9. By 7.5 × 10⁵ time steps, development is almost over. However, ODCs are largely not present. In fact, following the time course of the segregation of ODCs more closely reveals that ODCs begin to form but then gradually disappear. This is illustrated in Figure10.

Fig. 9.

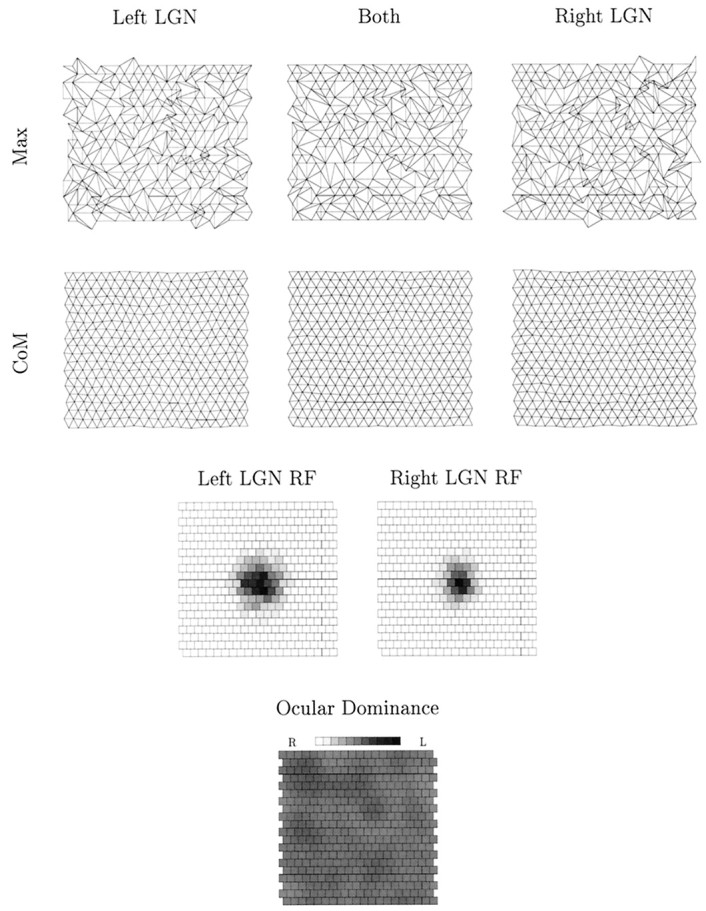
The state of the geniculocortical pathway after 5.0 × 10⁵ time steps in a simulation in which visually evoked activity rather than spontaneous retinal waves is used. The format of this Figure is otherwise identical to Figure 8.

Fig. 10.

The emergence and then disappearance of ocular dominance columns in the simulation using visually evoked activity shown in Figure 9. Each map represents the state of cortical ocular dominance at the time pointindicated immediately above it.

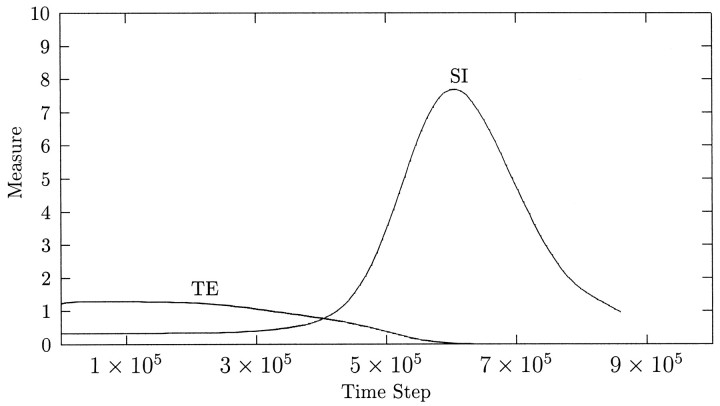
To establish why ODCs in this simulation are transient, we plot, in Figure 11, measures of the extent of geniculocortical afferent segregation and the extent of topographic refinement in the geniculocortical system against time. The average topographic error is non-zero when the segregation of afferents into ODCs begins. However, while this segregation is under way, the topographic error reduces to very close to zero. This has the result that topographically equivalent pairs of cells in the LGN sheets are competing only for one, topographically appropriate cortical cell. Because cell death does not occur at this stage of development, the competition cannot be resolved, so each pair of LGN cells can only end up balancing their control of the appropriate cortical cell. Hence, any disparity in innervation that accrued while the topographic error was non-zero is slowly removed as the LGN cells equalize their control.

Fig. 11.

The time course of the emergence of ocular dominance columns and topographic refinement in the simulation in Figures 9 and 10. The first measure, labeled SI (for segregation index), represents the deviation of cortical cells from perfectly balanced, binocular control, averaged over all cortical cells in the simulation. Each cell is assigned an ocular dominance index, between 0 and 100; 0 represents complete control by the right eye, and 100 represents complete control by the left eye. The magnitude of the deviation of this index from 50, representing equal control, is then calculated and averaged over all cortical cells; this is the number SI. The second measure, labeled TE (for topographic error), represents the error in the representation of the LGN sheets on the cortex. For each cortical cell, the Max measure of topography is used to determine which LGN cell (in either sheet) that cortical cell represents. The distance between this LGN cell and the LGN cell that the cortical cell would represent were topography perfect is then calculated (in units of lattice spacing). This distance is then averaged over all cortical cells to give a measure of the overall extent of topographic error; this is the numberTE.

This account of the washing away of ODCs in the simulation shown in Figures 9-11 suggests that reducing the interocular image correlations by reducing the value of p, which increases the rate of segregation, should result in stable segregation. This is shown in Figure 12, in which we have taken p = 0.25. In this simulation, ODCs emerge and stabilize before the topographic error has a chance to reduce to zero. Analysis of the widths of the ODCs in Figures 10 and 12 by two-dimensional Fourier methods reveals that the ODCs in Figure 12 are approximately 1.5 times wider than those in Figure 10 (data not shown). Thus, reduced interocular correlations increase ODC width, consistent with previous results (Goodhill, 1993; Elliott and Shadbolt, 1998b).

Fig. 12.

The maintenance of ocular dominance columns in a simulation using visually evoked activity but with a lower value of the interocular image correlation parameter, p,than used in Figure 10.

The use of explicit lateral interactions in these full, retinogeniculocortical simulations differs in one major respect from simulations without them. In simulations using visually evoked activity, the presence of lateral interactions has the effect, as with the smaller, one-eye, one-LGN simulations, of increasing the overall rate of development. But in this case, the rate of the development of ODCs is also increased, with the result that they are always stable and never partially form and then disappear (cf. Goodhill, 1993). This is in contrast to simulations in which explicit lateral interactions are not modeled.

DISCUSSION

We have shown that a neurotrophic model of synaptic plasticity using a model that generates a phenomenologically accurate representation of spontaneous retinal activity can robustly lead to the segregation of retinogeniculate afferents into eye-specific laminae in the LGN and geniculocortical afferents into ODCs in the striate cortex. Furthermore, such activity patterns can successfully drive the refinement of an initially coarse topography and initially diffuse receptive fields into adult-like states. The use of visually evoked activity also led to the intriguing observation that ODCs can partially form but then slowly disappear.

What features of the simulated spontaneous retinal activity used here are critical in our model for driving normal development? We have already discarded interwave intervals for computational reasons. For receptive field and topographic refinement, interwave intervals are not likely to be important, although they will be important, as argued in Results, in helping to determine, for example, the periodicity of ODCs in the striate cortex. The intrawave temporal information—correlations in firing times of cells as a wave sweeps over a patch of retina—could be very important in real, developing systems. For example, very recent data indicate, at least in the retinotectal system, that there is a critical window of ∼40 msec during which the temporal coincidence of spikes from different afferents arriving at the same tectal cell can lead to either cooperative or competitive interactions between those synapses (Zhang et al., 1998). Unfortunately, the model of spontaneous retinal activity presented by Feller et al. (1997) uses a basic time step size of 100 msec, which is much too large to resolve interactions between synapses that occur over a few milliseconds. In addition, our neurotrophic model of plasticity is formulated in terms of instantaneous firing rates, not as a spiking model of neurons, and thus at present does not lend itself to addressing temporal issues over very short time scales. To attempt to take such temporal issues seriously, although highly desirable, would at present be computationally intractable, given that we are already very close to the limits of our computational resources (with each simulation taking 1 month to run). Thus, at least for our current simulations, intrawave temporal data play no role in simulated development. We are therefore left with the spatial distribution of activity on the retinas at each simulated time step. These spatial data, and the way that they change from one time step to the next, play the key role in driving normal development in our simulations. Other models have used approximations to these spatial correlations, but ours is the first, to our knowledge, that uses spontaneous retinal activity with phenomenologically realistic spatial properties.

Our simulations of the full, retinogeniculocortical pathway using spontaneous retinal activity would seem to be particularly applicable to the development of Old Monkey monkeys, which, for example, exhibit an adult-like pattern of ODCs at birth (Horton and Hocking, 1996a). Presumably, the prenatal development of the visual system of Old World monkeys is driven by such spontaneous activity. Our simulations of at least the retinogeniculate pathway using spontaneous retinal activity are also applicable to the development of animals such as cats and ferrets, for which the development of the retinogeniculate pathway is essentially complete by the time of eye opening.

Although NTFs are strongly implicated in the development of ODCs in the striate cortex (Carmignoto et al., 1993; Cabelli et al., 1995; Riddle et al., 1995), so far as we are aware no work implicates NTFs in the post-target-innervation development of the retinogeniculate pathway or in the development and refinement of receptive fields and topography in the cortex. Just as NTFs are implicated in the segregation of geniculocortical afferents into ODCs in the striate cortex, our model predicts that they are also involved in the competitive dynamics that lead to the segregation of retinogeniculate afferents into eye-specific laminae in the LGN. An immediate consequence of this is that prenatal cranial infusion of excess quantities of the appropriate NTFs in an animal such as the cat (cf. Sretavan et al., 1988) or postnatal infusions in a late-developing animal such as the ferret (cf. Penn et al., 1998) should either eliminate or temper the segregation of retinogeniculate afferents into eye-specific laminae.

Our simulations also reveal that the development of receptive fields and topography in both the LGN and cortex is a process that is competitive in character, and one that therefore can be interfered with by application of excess, exogenous NTFs. Thus, our simulations predict that, in addition to the absence of ODCs in the striate cortex of animals that have experienced exogenous cortical infusion of excess NTFs, receptive fields would be large and unrefined and topography would be substantially disrupted. This result would also be applicable to the retinotectal system of the frog, in which it has been demonstrated that exogenous application of antibodies to another class of molecules that are implicated in plasticity, the cell adhesion molecules, significantly disrupts topography (Fraser et al., 1988).

However, perhaps the most intriguing of our results relates to the disappearance of ODCs in simulations using visually evoked activity. Such results would be applicable to those animals in which the geniculocortical pathway remodels largely after eye opening, such as cats, ferrets, and some New World monkeys. However, the emergence and then disappearance of ODCs in cats or ferrets has never been observed. In contrast, the marmoset does exhibit the development of ODCs in the presence of vision, which then slowly disappear (DeBruyn and Casagrande, 1981; Spatz, 1989; Sengpiel et al., 1996).

This result is only obtained in our simulations when explicit lateral connections between cortical cells are not modeled; when lateral circuitry is present, ODCs are stable. In fact, it has recently been suggested that the relative timing of the development of geniculocortical versus intracortical circuitry might be different in New World monkeys than in other species in which ODCs are present and stable (Livingstone, 1996). The reasoning behind this suggestion is that in Livingstone’s study (1996) of the New World squirrel monkey, no anatomical evidence for ODCs was found using standard techniques (Hubel et al., 1976; Tigges et al., 1977; Hendrickson et al., 1978;Rowe et al., 1978; Hendrickson and Wilson, 1979; Humphrey and Hendrickson, 1983; Hendrickson and Tigges, 1985), but physiological recordings from layer IV revealed that each cell was dominated by input from one or the other eye, but with no order to the distribution of such cells, leading to so-called “salt-and-pepper” segregation (Livingstone, 1996). However, Horton and Hocking (1996b) have recently used anatomical techniques to demonstrate the existence of ODCs of width ∼225 μm in the squirrel monkey. It is difficult to reconcile the salt-and-pepper physiological results of Livingstone (1996) with the normal although rather narrow anatomical ODCs seen by Horton and Hocking (1996b).

Salt-and-pepper segregation is precisely the developmental outcome that would be predicted by many models in the absence of lateral cortical connectivity; even if ODCs are present in the squirrel monkey, then models would typically predict that rather short-range lateral cortical connectivity would be necessary to induce the formation of narrow ODCs (Swindale, 1980; Miller et al., 1989; Goodhill, 1993; Elliott and Shadbolt, 1998b). (In our model, large-scale order in the ocularity of cortical cells derives not from explicit lateral connections but from the diffusion of NTFs through the cortex.) Our model thus exhibits the appearance and then disappearance of ODCs in the presence of vision and in the absence of explicit (although perhaps only long-range) lateral cortical connectivity, precisely the conditions that have been hypothesized to exist in the early development of New World monkeys (Livingstone, 1996). Hence, our simulations in this case might reasonably be taken as an account of the development of ODCs in the New World marmoset.

Our results therefore give an understanding of the disappearance of marmoset ODCs. They form when the topographic error is still sufficiently large, but as the topographic error reduces, topographically equivalent pairs of LGN cells end up, at least in simulation, competing only for one cortical cell. This has the result that the competition cannot be resolved, and pairs of LGN cells equalize their control of cortical cells, causing any existing ocular segregation to vanish. So far as we are aware, only one other model has been shown to reproduce the phenomenology of marmoset ODCs (Swindale, 1996). However, the parameter regime in which this model behaves as required is unintuitive and seems to consist in very specific selections of parameter values without much explanation, justification, or attempt to relate them to biologically relevant variables. It is therefore difficult to assess how seriously to take its results.

Our account of the disappearance of marmoset ODCs could be criticized on the grounds that it is obtained in a simulation in which the number of cortical cells equals the number of LGN cells in each sheet. Were there a disparity in the numbers of cells—in particular, were the number of cortical cells much larger than the number of LGN cells, as is actually the case in real animals—then topographically equivalent pairs of LGN cells would not end up innervating just one cortical cell. Instead their arbors would be spread over a number of cells, and segregation between these cells could then occur. This is indeed the case in simulations in which we reduce the number of LGN cells but leave all other parameters unchanged (data not shown). However, the introduction of short-range lateral excitation into simulations would cause nearby cortical cells to behave cooperatively, leading to competition for clusters of mutually excitatory cortical cells rather than individual cells. This is equivalent to the statement that, in our simulations, each simulated cortical unit would in fact represent a cluster of connected cells, and this would be the justification for considering so few cortical units (aside from the issue of computational tractability).

By reducing interocular correlations in our simulations of marmoset development, we found that ODCs were stabilized into adulthood. This is reminiscent of the recent finding that strabismic squirrel monkeys possess ODCs, unlike normal squirrel monkeys [Livingstone (1996); but see Horton and Hocking (1996b)], and that monocular deprivation in marmosets permits the maintenance of ODCs into adulthood (DeBruyn and Casagrande, 1981). If monocular deprivation decorrelates the activity between the two eyes, then the effects of divergent strabismus in the marmoset might be similar to the effects of monocular deprivation, at least in terms of the maintenance of ODCs. Because our simulation in which ODCs disappear assumed uncorrelated activity between the two eyes, we cannot strictly claim that the simulation in which ODCs were maintained represents strabismic development. Nevertheless, the introduction of short-range, mutually excitatory lateral connections as discussed above would enable the same results to be obtained with increased intereye correlations. We thus predict that the induction of divergent strabismus in marmosets should result in permanent ODCs.

In addition to predicting that strabismus might maintain marmoset ODCs into adulthood, we also predict that strabismus, whether or not marmoset ODCs are in fact maintained into adulthood, increases ODC periodicity (determined by the combined widths of adjacent pairs of columns). This prediction is consistent with previously established results, namely that reduced interocular correlations increase ODC periodicity (Goodhill, 1993; Elliott and Shadbolt, 1998b). This result has been verified in the cat (Löwel, 1994; Tieman and Tumosa, 1997). In Old World monkeys, however, although manipulations of visual experience can alter the widths of ODCs (specifically, monocular deprivation achieves this), recent evidence suggests that alterations in visual experience do not affect their periodicity (Crawford, 1998;Murphy et al., 1998). The reason for this difference between cats and Old World monkeys is that Old World monkey ODCs typically form and are adult-like before birth (Horton and Hocking, 1996a), and it is therefore likely that their basic periodicity is already well established and unchangeable at birth. In contrast, in the cat, it is precisely visual experience that influences the development of ODCs and therefore could also help to determine their basic periodicity (Löwel, 1994; Goodhill and Löwel, 1995). The ODCs of the New World marmoset, in contrast to the Old World macaque, are shaped by visual experience, so this monkey seems a better candidate for testing the prediction that strabismus alters ODC periodicity in a monkey rather than a feline model.

In summary, we have shown that a model that generates a phenomenologically realistic representation of spontaneous retinal activity can be used to drive the normal development of the retinogeniculocortical pathway in the context of a mathematically well characterized neurotrophic model of synaptic plasticity. Such a model induces the segregation of retinogeniculate and geniculocortical afferents, the refinement of receptive fields and the establishment of an ordered topography in register, at the level of the striate cortex, with ODCs. The use of visually evoked activity reveals the surprising result that ODCs can be transient, suggesting parallels with the development of the striate cortex of marmosets.