Effects of Gravitational Load on Jaw Movements in Speech

Abstract

External loads arising as a result of the orientation of body segments relative to gravity can affect the achievement of movement goals. The degree to which subjects adjust control signals to compensate for these loads is a reflection of the extent to which forces affecting motion are represented neurally. In the present study we assessed whether subjects, when speaking, compensate for loads caused by the orientation of the head relative to gravity. We used a mathematical model of the jaw to predict the effects of control signals that are not adjusted for changes to head orientation. The simulations predicted a systematic change in sagittal plane jaw orientation and horizontal position resulting from changes to the orientation of the head. We conducted an empirical study in which subjects were tested under the same conditions. With one exception, empirical results were consistent with the simulations. In both simulation and empirical studies, the jaw was rotated closer to occlusion and translated in an anterior direction when the head was in the prone orientation. When the head was in the supine orientation, the jaw was rotated away from occlusion. The findings suggest that the nervous system does not completely compensate for changes in head orientation relative to gravity. A second study was conducted to assess possible changes in acoustical patterns attributable to changes in head orientation. The frequencies of the first (F1) and second (F2) formants associated with the steady-state portion of vowels were measured. As in the kinematic study, systematic differences in the values of F1 and F2 were observed with changes in head orientation. Thus the acoustical analysis further supports the conclusion that control signals are not completely adjusted to offset forces arising because of changes in orientation.

Movements arise from the interaction of muscle forces, loads external to the body, and forces attributable to dynamics. This interaction complicates the job of controlling movement, because the relationship between muscle activity and a resulting movement or posture may change, perhaps dramatically, depending on the force environment in which movement is produced. External loads, in combination with intrinsic properties of the musculo-skeletal system and forces arising from dynamics, effectively define the physical system with which a controller must deal. Hence motor commands that successfully control movement or posture under one set of force conditions (e.g., free motion) may fail under different force conditions (e.g., when coupled to a load). To maintain movement accuracy neural commands to muscles must be appropriately adjusted.

A number of studies have examined motor adaptation in the context of external loads (Lackner and DiZio 1992; Fisk et al., 1993; Shadmehr and Mussa-Ivaldi, 1994). The typical approach is to impose a novel force environment (i.e., a force field), which perturbs the limb and requires subjects to modify commands to muscles to achieve accurate control. The studies involve relatively large imposed forces and large movements, thus maximizing the impact of inappropriate motor planning (i.e., large end point and trajectory errors) and hence necessitating compensation.

Little is known, however, about compensation in motor systems in which everyday interaction with the environment is more subtle than in limb movements. In this paper we describe a study that examines compensation in the control of jaw movement during speech to changes in head orientation relative to gravity. Whereas limb movements commonly occur in the context of strong mechanical interactions with the environment, one of the only external loads experienced during speech is the gravitational force. In the context of this load, the motor system produces the movements appropriate to the acoustical and perceptual requirements of speech.

Studies to date on human arm movements are generally consistent with the idea that the gravitational force is compensated for in motor planning. Fisk et al. (1993) examined one-joint arm movements executed inside an aircraft that followed a parabolic flight path. The results indicate that for rapid movements produced when forces were either minimal (0 g) or maximal (1.8 g) subjects adapt successfully as indicated by similar movement accuracy in both force conditions. This suggests that subjects incorporated the change in force to successfully plan movements under these changing force conditions. Papaxanthis et al. (1998) arrived at a similar conclusion in their investigation of the kinematics of vertical and horizontal drawing movements. They showed that despite differences in gravitational torque at the shoulder attributable to the direction of movement, observed movements in all directions were relatively straight and showed no differences in duration or peak velocity. In contrast, data reported by Smetanin and Popov (1997) suggest that subjects may not in fact compensate for changes in the direction of gravitational force when making pointing movements to remembered targets; movement accuracy was systematically affected by whole-body orientation relative to gravity.

Electromyographic activity during movement has been shown to change systematically depending on body orientation, leading some researchers to conclude that control signals are adjusted to take forces arising as a result of orientation into account. This has been shown in both movements about the shoulder (Michiels and Bodem, 1992) and elbow (Virji-Babul et al., 1994) and for activity of abdominal wall, tongue, and velopharyngeal muscles during speech (Hoit et al., 1988; Moon et al., 1994; Niimi et al., 1994).

The approach in the present paper was to use a simulation model to predict the changes in the kinematics of jaw movements that arise when motor commands are not adjusted to compensate for changes in the orientation of the head relative to the gravitational load. We compare model predictions with results of an empirical study in which jaw movement kinematics were recorded during speech in upright, supine (face up) and prone (face down) orientations. We report that in all but one case the empirically observed movements match the predictions of the model, supporting the hypothesis that subjects do not completely compensate for loads arising from changes in head orientation. This conclusion is supported by a second study in which we examine the changes to acoustics that result from speaking in these same three orientations. Systematic changes are observed in the spectral distribution of vowels that depend on head orientation relative to gravity.

MATERIALS AND METHODS

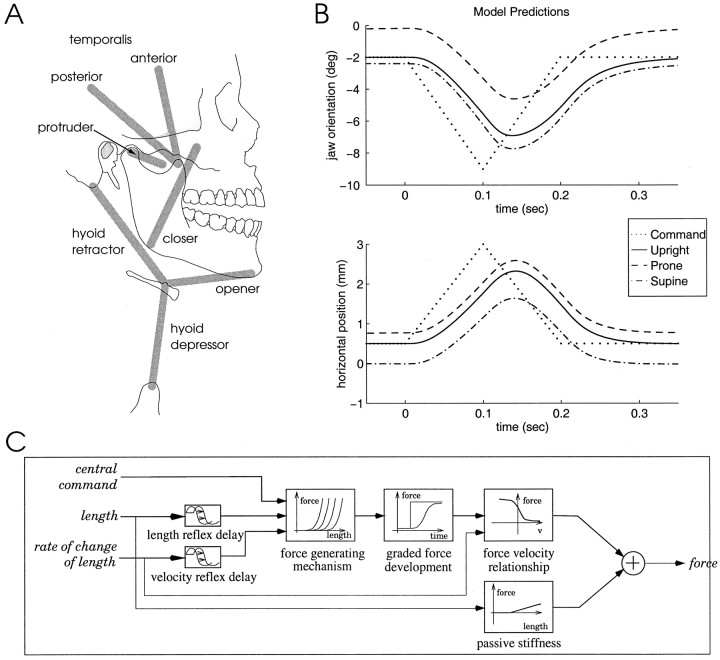
The jaw model. In the simulation studies we used a model of sagittal plane human jaw and hyoid motion based on the λ version of the equilibrium point (EP) hypothesis. The model used in the present study is described in detail by Laboissière et al. (1996). The model includes seven muscle groups (see Fig.1A) and four kinematic degrees of freedom: sagittal plane jaw orientation (rotation about an axis through the mandibular condyle center), horizontal jaw position (protrusion and retraction), hyoid vertical position, and hyoid horizontal position. There are also modeled neural control signals and reflexes, muscle mechanical properties, jaw and hyoid bone dynamics, and realistic musculoskeletal geometry. The anthropometry implemented in the model is based on measures reported by Scheideman et al. (1980). Muscle origins and insertions are based on those of McDevitt (1989). The muscle model is a variant of the Zajac (1989) model and includes activation and contraction dynamics and passive tissue properties (Fig.1C). Model dynamics are derived using a Lagrangian procedure.

Fig. 1.

A, Schematic of the modeled muscle groups and their attachments to the jaw and hyoid bone. B, Predicted jaw orientation and horizontal position for an opening–closing movement. The same constant rate equilibrium shift (dotted line) underlies movements in the three different orientations relative to gravity: upright (solid line), prone (dashed line), and supine (alternating dots anddashes). Compared with the upright orientation, simulated jaw movement in a prone orientation is rotated closer to occlusion and translated in an anterior direction. In contrast, the simulated jaw movement in a supine orientation is rotated away from occlusion and translated in a posterior direction. C, Muscle model.

According to the EP hypothesis, movements result from shifts in the equilibrium state of the motor system. In the λ version of the model, shifts in equilibrium arise from centrally specified changes in threshold muscle lengths, λ values, at which motoneuron (MN) recruitment and hence muscle activation begins. When the value of λ is changed, muscle activation and force vary in proportion to the difference between the actual and threshold muscle length. Through the coordination of individual muscle λ values, motion to a new equilibrium position may be achieved (for a detailed description of the λ model, see Feldman et al., 1990).

Human jaw muscles generally contribute to motion in more than one kinematic degree of freedom. For example, masseter, a jaw-closer muscle, acts to move the jaw toward occlusion and in a posterior direction. In the model, commands to individual muscles, shifts or changes to the values of λ, are coordinated to produce independent movement in each of the degrees of freedom of the jaw (Laboissière et al., 1996). These commands are analogous to the “R” command described in previous formulations of the model (Feldman, 1986; Feldman et al., 1990).

In addition to the set of λ shifts that produce movement through a change in the equilibrium position of the jaw, an independent set of λ shifts change the muscle coactivation level and hence jaw stiffness without producing movement. The ability to cocontract muscles independent of motion is well documented in both behavioral and physiological studies (Humphrey and Reed, 1981; Milner and Cloutier, 1993). The cocontraction command used here is analogous to the “C” command described in earlier versions of the model.

The simulations presented here use coordinated jaw rotation and translation commands to produce speech-like jaw opening and closing movements. The simulated movement commands specify a constant rate change in the equilibrium jaw orientation and a corresponding constant rate change in the equilibrium jaw horizontal position. A constant coactivation command is used throughout the simulated movements. Jaw rotation and translation commands begin and end simultaneously in each opening and closing phase of movement. This is consistent with the empirical finding that jaw rotation and translation during speech are time synchronized (Ostry and Munhall, 1994).

To predict the kinematic effect of using control signals that do not take into account changes in head orientation relative to gravity, simulations were carried out in which the same commands were used to produce jaw movement in different simulated orientations. Three different head orientations were tested, upright, supine, and prone.

Empirical studies. In a first study examining jaw kinematics, five subjects with no known history of speech motor disorder or temperomandibular joint dysfunction were tested. Each subject produced a series of speech-like utterances in the same orientations as in the simulations: upright (seated), supine, and prone. In the supine orientation, subjects lay flat on their backs. In the prone orientation, subjects lay face down on an elevated surface such that the body and forehead were supported and the jaw was able to move freely. In each orientation the head and trunk were aligned.

Subjects repeated speech-like utterances embedded in a carrier phrase. Data were collected in 15 sec blocks, which allowed the subjects to produce approximately seven repetitions of the test phrase. Six phonetic conditions involving different consonant–vowel–consonant (CVC) combinations were tested. Subjects were instructed to maintain a normal speaking rate and volume. Volume and rate were monitored by the experimenter during the course of the experiment, with feedback provided verbally to the subject. We subsequently verified that volume and speech rate were not correlated with the kinematic variables that were used to assess the effects of head orientation on jaw position (see Results).

The six CVCs involved the combination of the consonants s, r, and k with the vowel sounds a, as in “bat,” and e, as in “bet.” The first and last consonants were the same, for example, sas orkek. The two vowels were chosen to vary the movement amplitude, whereas the consonants were chosen to vary the position of the jaw at the beginning and end of the movement. Each CVC sequence was embedded in a carrier sentence to produce test utterances such as “see sasy again” or “see keky again”. This served to balance the immediate phonetic context before and after the CVC. The data collection for each subject was blocked within the three body orientation conditions. The order of tested body orientations was varied across subjects. Approximately 15 repetitions of each utterance were obtained in each experimental condition.

Jaw movements were recorded using Optotrak (Northern Digital), an optoelectronic position measurement system. The system consists of three single-axis CCD sensors which track the three-dimensional (3D) motion of infrared-emitting diodes (IREDs) attached to the head and jaw. Four IREDs used to track head motion were attached to an acrylic and metal dental appliance (weight, 10 gm) custom made for each subject and fixed with a dental adhesive (Iso-Dent; Ellman International) to the buccal surface of the maxillary teeth. Similarly, four IREDs used to track motion of the jaw were attached to an appliance glued to the mandibular teeth. The four IREDs were in each case arranged in a rectangular configuration in the frontal plane. The appliances had little effect on the intelligibility of the utterances tested in this study. IRED motion was recorded at 200 Hz.

To aid in data scoring and to provide information about speech volume levels, the acoustical signal was recorded digitally at 1000 Hz using a small microphone (Audio-Technica) taped to the bridge of the nose.

A second study examined speech acoustics. Six subjects were tested, four of whom were participants in the previous study. Subjects produced speech utterances in the same orientations relative to gravity: upright, supine, and prone. The speech task was identical to that described above and consisted of six CVC combinations embedded in a carrier phrase. Trial order and duration were also the same. Subjects were instructed to maintain a normal speaking rate and volume, both of which were monitored by the experimenter. The dental appliances used in the kinematic study were not worn by the subjects.

Speech acoustics were recorded in a sound-attenuating testing room (Industrial Acoustics Company) which served to isolate the subject from environmental noise as well as to reduce acoustical resonance. Subjects wore a head-mounted directional microphone (AKG Acoustics) placed ∼5 cm from the mouth. The acoustical signal was analog low-pass-filtered with a 7.5 kHz cutoff (Rockland Systems), amplified (Mackie Designs), and sampled at 22,050 Hz using a 16 bit analog-to-digital board (Turtle Beach) installed on a Pentium PC workstation.

Data analysis. In the kinematic study, the three-dimensional position data for each IRED were digitally low-pass-filtered using a second-order zero phase lag Butterworth filter with a cutoff frequency of 10 Hz (chosen on the basis of Fourier analysis and then verified by comparison of raw and filtered data). Using vendor-supplied software, the representation of jaw and head motion was transformed from its original 3D camera coordinates into a 6D rigid body representation of jaw position and orientation in a head-centered coordinate system. The origin of this transformed coordinate system was the position of the condyle center (projected onto the midsagittal plane) at occlusion. The horizontal axis was aligned with the occlusal plane. Quantitative analyses were restricted to sagittal plane jaw orientation (about the condyle center) and horizontal position, because movements in these two degrees of freedom constitute the primary motions of the jaw during speech (Ostry and Munhall, 1994; Ostry et al., 1997).

An interactive computer program was used to isolate jaw movements associated with the CVC from the remainder of the carrier phrase. Movements in each of the two kinematic degrees of freedom were scored separately. The CVC segment was first located on the basis of the acoustical signal. Start and end points of the CVC were scored as the point at which the velocity of the jaw (measured in each degree of freedom separately) was closest to zero. Once isolated, the kinematic data were time-normalized by using linear interpolation.

The kinematic data were examined in two ways. To visualize the form of jaw movement trajectories, mean jaw orientation and mean jaw position at each of the interpolated time points were computed to yield a mean jaw movement trajectory for each experimental condition. For purposes of statistical analysis, three points in the jaw movement record were scored on a trial-by-trial basis—the initial consonant, the maximum opening corresponding to the vowel, and the final consonant—and then means were computed at each of these points for each head orientation.

To examine data across subjects, an additional normalization procedure was performed. The procedure involved subtracting the mean initial measurement (first sample) for the upright orientation from all records on a subject-by-subject basis. This had the effect of shifting all records up or down in value so that the first sample of the upright condition has a value of zero, although preserving any differences between experimental conditions. This reduced the variability among subjects attributable to the procedure for locating the coordinate system origin (Ostry et al., 1997). It also corrected for any other differences between subjects arising from the specific region of the work space of the jaw in which the test utterances were produced. Typical corrections were less than 2° in jaw orientation and 2 mm in jaw position.

For the modeling results the orientation angle is given in degrees relative to the jaw orientation at occlusion, whereas horizontal position is shown in millimeters relative to the jaw position at occlusion. The same convention is used for the empirical data, except that all values are given relative to the position and orientation of the jaw at the first sample in the upright condition (see above).

In the acoustical study, the analysis focused on the spectral distribution of the vowel in each CVC segment. Unlike consonants, vowels are typically characterized by relatively stable peaks in their spectral distributions (formants). Different vowels are characterized acoustically by different formant values. The values of the formant peaks thus provide a basis for assessing acoustical changes associated with different head orientations.

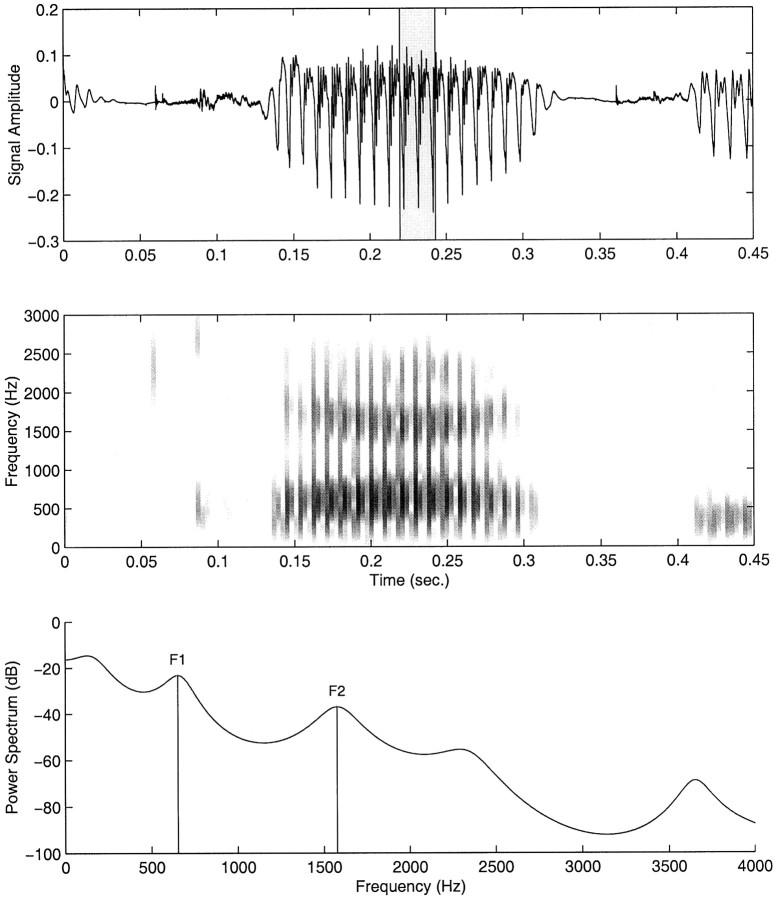
An interactive computer program was used to score and analyze the acoustical data. The portion of the signal associated with each CVC was first isolated from the carrier phrase. A 512 sample segment (∼23 msec) was then selected during the steady-state portion of the vowel (Fig. 2).

Fig. 2.

Scoring procedure for acoustical data. Top panel, Acoustic signal during the CVC. A 20 msec analysis window (shown in gray) is selected during the steady-state portion of the vowel, located on the basis of a frequency spectrogram (middle panel). F1 and F2 frequencies are determined from an estimate of the power spectral density computed across the analysis window (bottom panel).

For each utterance, an estimate of the power spectral density (PSD) function was computed using the Yule–Walker autoregression method (Marple, 1987). The PSD estimates typically exhibited two peaks associated with the first formant (F1, between 500 and 1000 Hz) and the second formant (F2, between 1400 and 2200 Hz), respectively. Values for formant peaks were scored and analyzed as described below.

The effect of head orientation on formant values was assessed for each vowel separately and averaged over consonants. To compare data across subjects, a normalization procedure was carried out. The procedure involved calculating mean formant frequencies across all 18 conditions (six CVCs × three body orientations) for each subject. Each observed value of F1 and F2 was then transformed into a deviation score by subtracting the overall mean for a given subject. This had the effect of preserving differences in formants attributable to the experimental manipulations but eliminating overall differences between subjects.

Statistical analyses were performed separately for F1 and F2 using a two-way, repeated measures ANOVA (three orientations × two vowels). Post hoc comparisons of pair-wise means were carried out using Tukey’s method.

As a control, we verified that acoustical differences were not attributable to aspects of the recording setup or environment. We performed a study in which we simulated the testing procedure by playing a prerecorded signal through a loudspeaker, which had a position and orientation in the recording chamber comparable with those of the experimental subjects. The aim was to replicate the testing procedure but to hold the acoustical source constant. Any observed differences in spectral characteristics would be attributable to properties of the recording procedure or acoustical characteristics of the testing room.

A series of test utterances was recorded using a single subject in an upright body orientation. All aspects of the recording procedure were identical to those described above. The acoustical signal was analog low-pass-filtered (7.5 kHz cutoff) and then recorded at 44.1 kHz on a digital audiotape. The signal was then played through a loudspeaker to replicate the position of an experimental subject in the recording chamber. The signal was rerecorded using a microphone that was fixed to the speaker. Analysis of the rerecorded signals showed no statistically significant differences in estimates of F1 and F2 frequencies as a function of orientation of the loudspeaker.

RESULTS

Simulated opening–closing movements in three head orientations are shown in Figure 1B. The coordinate system is similar to that used in the empirical study: the origin is at the condyle center at occlusion; the horizontal axis is parallel to the occlusal plane. The modeled control signals (dotted lines) are identical in the three orientations and involve constant rate changes in equilibrium jaw orientation and horizontal position. The predicted movements are shown as smooth curves. Compared with a movement with the head upright (solid line), movement in a prone orientation (dashed line) is rotated closer to occlusion and translated in an anterior direction. Movement in a supine orientation (alternating dots and dashes) is rotated away from occlusion and translated in a posterior direction.

A value of 10 N was used as the cocontraction level (average modeled muscle force). This value was chosen on the basis of previous unrelated work (Laboissière et al., 1996) in which this level of cocontraction was found to produce modeled kinematic results that matched empirical data. In the present study, an analysis of the sensitivity of the model predictions to the value of the cocontraction command was carried out. Cocontraction commands ranging from 5 to 50 N were found to influence the overall magnitude of the predicted effect, with larger values of cocontraction predicting smaller differences attributable to head orientation. Nevertheless, the order of predicted effects was in all cases the same as that in Figure 1.

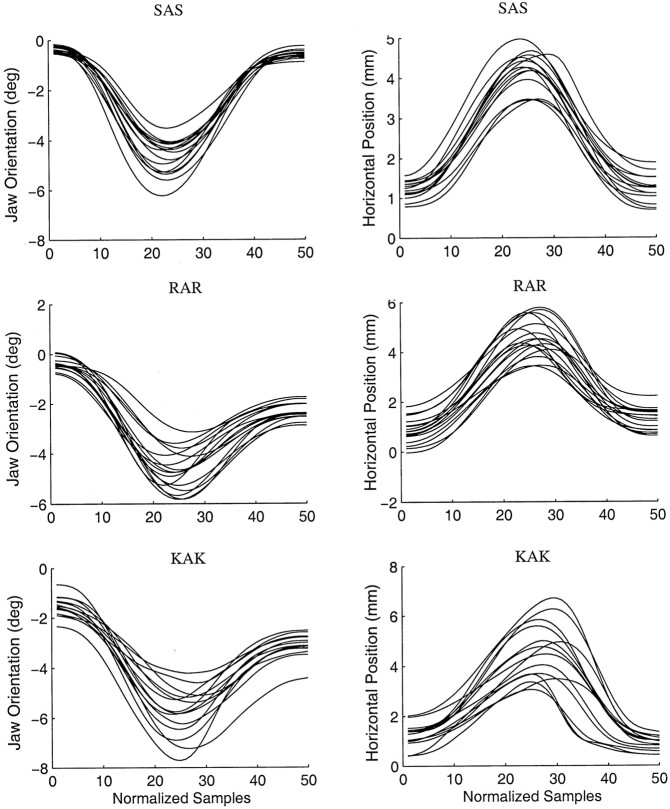
Examples of empirically observed patterns of jaw opening and closing are shown in Figure 3, which gives jaw orientation and horizontal position traces for a single subject. The data are normalized to 50 samples (average duration, 250–300 msec). The typical pattern of jaw motion is shown for a number of different CVC utterances produced in an upright orientation. During the opening phase of movement the jaw simultaneously rotates away from occlusion and translates in an anterior direction. During the closing phase the jaw rotates toward occlusion and translates in a posterior direction.

Fig. 3.

Individual movement traces for three CVC conditions in the upright orientation for one subject. Traces have been time-normalized to 50 samples by linear interpolation. Jaw orientation angle is measured in degrees relative to the jaw angle at occlusion, whereas horizontal position is measured in millimeters relative to the jaw position at occlusion.

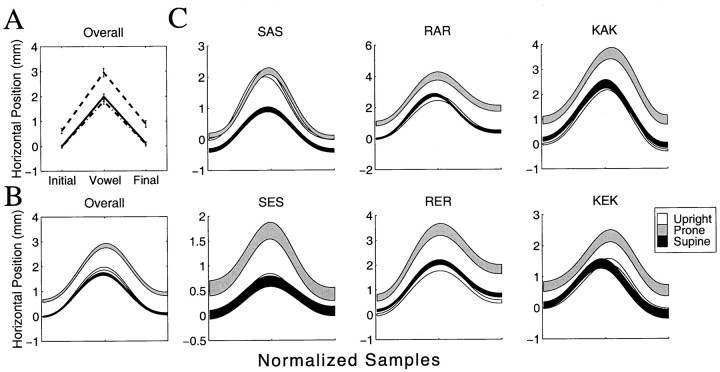
Figure 4, A and B, shows mean jaw orientation across all subjects and phonetic conditions for each head orientation. Figure 4A gives point estimates of jaw orientation at the initial consonant, vowel and final consonant, whereas Figure 4B shows the mean trajectory ±1 SE over the entire movement. The pattern of results closely matches the predictions of the model under conditions in which control signals are not modified to compensate for changes in head orientation relative to gravity. Compared with the upright condition, in the prone orientation the jaw is rotated closer to occlusion, whereas in the supine orientation the jaw is rotated further from occlusion.

Fig. 4.

Mean jaw orientation across all subjects and phonetic conditions for each head orientation. A, Point estimates ±1 SE at the initial consonant, vowel, and final consonant;B, mean trajectory over the entire movement ±1 SE;C, mean jaw orientation angle during movement across all subjects for each phonetic condition. The basic pattern of results predicted by the model is observed in each condition. Note that all values are given relative to the orientation of the jaw at the first sample in the upright condition (see Materials and Methods).

To test the significance of differences in jaw orientation in the three head orientations, statistical tests were performed using ANOVA at each of the three measurement points in the movement (initial consonant, vowel, and final consonant). Differences between pairs of means (upright vs prone, upright vs supine, and supine vs prone) were tested using Tukey’s method. All pair-wise differences at each measurement point were found to be reliable (p < 0.01).

Figure 4C shows mean jaw orientation across all subjects for each phonetic condition. Although there is some variability across conditions, the basic pattern of results predicted by the model is observed in each condition. As above, statistical comparisons were performed at each measurement point (initial consonant, vowel, and final consonant), this time for each phonetic condition separately. Of the 54 comparisons in total (6 phonetic conditions × 3 measurement points × 3 contrasts per measurement point), all but 6 were significant at p < 0.01.

Figure 5, A and B, shows the average horizontal jaw position across all subjects and phonetic conditions in each head orientation. The pattern of results for prone and supine conditions matches the predictions of the model under conditions in which control signals are not modified to account for changes in head orientation. In the prone orientation the jaw is consistently translated more forward than in the upright orientation. In the supine orientation the jaw is translated backward compared with the prone orientation. No difference is observed between the supine and upright orientations.

Fig. 5.

Mean horizontal jaw position across subjects and phonetic conditions for each head orientation. A, Point estimates at the initial consonant, vowel, and final consonant;B, mean jaw position over the entire movement; C, mean horizontal jaw position during movement for each phonetic condition separately. All values are given relative to the position of the jaw at the first sample in the upright condition.

Differences in jaw horizontal position were tested using ANOVA and Tukey tests. Reliable differences were observed between mean jaw position in the prone and supine orientations and between prone and upright orientations (p < 0.01). No differences were observed between mean jaw positions in the supine and upright orientations.

Figure 5C shows mean jaw horizontal position across all subjects for each phonetic condition separately. Although there is some variability, the basic pattern of results is preserved within individual phonetic conditions. Statistical comparisons were performed between all pairs of means at each measurement point. Differences between means in the prone and supine orientations were reliable at all three measurement points (p < 0.01) with a single exception: means for the final consonant position in ses. In four of six phonetic conditions, differences between means in the prone and upright orientations were also reliable at the three measurement points (p < 0.01). Differences between supine and upright orientations were obtained only for sas(p < 0.01).

Separate analyses were undertaken for the acoustical data. Figure6 shows the effect on F1 and F2 values of different head orientations. Data for each vowel are given separately, averaged over consonants. Values represent deviation scores from subjects’ average formant frequencies (see Materials and Methods). Theellipses show 1 SEM. Original values of F1 and F2 are shown for each subject in Table 1.

Fig. 6.

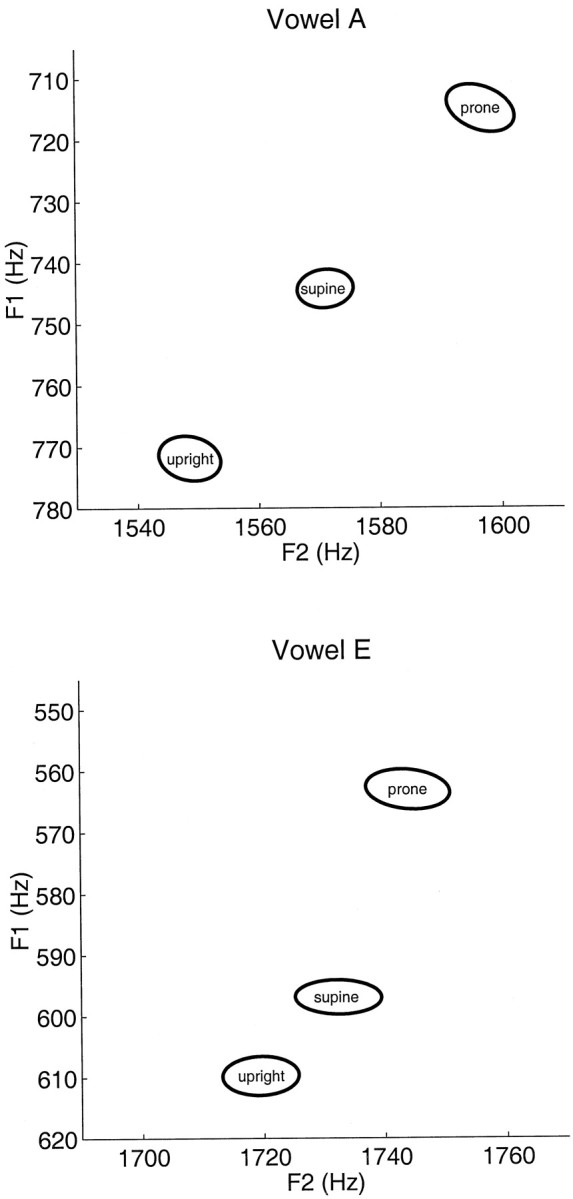
Mean change in F1 and F2 frequency associated with different head orientations. Values represent deviation scores from subjects’ average formant frequencies (see Materials and Methods). Theellipses show 1 SEM. Following the convention in speech acoustics, the F1 axis (plotted on the ordinate) is inverted such that low values are at the top and high values are at the bottom.

Table 1.

Mean F1 and F2 frequencies (hertz) for each subject shown for each vowel and head orientation

Vowel	Orientation	Subject 1		Subject 2		Subject 3		Subject 4		Subject 5		Subject 6
		F1	F2	F1	F2	F1	F2	F1	F2	F1	F2	F1	F2
A	Upright	915.4	1926.5	703.9	1535.3	821.3	1568.8	854.0	1555.6	675.0	1502.8	799.7	1625.5
		(7.38)	(16.16)	(5.76)	(7.24)	(13.04)	(9.93)	(12.03)	(7.35)	(5.69)	(13.12)	(6.51)	(14.03)
	Supine	855.1	1991.6	688.1	1547.8	796.1	1664.7	821.9	1551.4	692.0	1462.8	751.0	1632.1
		(7.59)	(16.44)	(3.65)	(7.33)	(11.79)	(9.65)	(8.74)	(7.42)	(6.25)	(11.42)	(6.16)	(11.00)
	Prone	875.8	2070.6	645.7	1556.2	757.4	1646.0	809.3	1572.6	681.4	1506.2	662.2	1656.8
		(10.69)	(24.08)	(2.98)	(5.63)	(9.84)	(14.52)	(13.44)	(9.37)	(7.62)	(8.31)	(8.34)	(11.92)
E	Upright	712.1	2105.6	599.9	1653.6	642.1	1790.3	619.0	1736.9	560.4	1502.4	634.0	1922.5
		(5.28)	(24.33)	(8.36)	(11.35)	(8.16)	(7.52)	(10.49)	(7.16)	(5.09)	(10.16)	(6.13)	(19.54)
	Supine	700.0	2117.3	583.0	1620.8	649.4	1847.3	617.3	1772.6	556.1	1505.8	590.0	1941.5
		(4.26)	(28.72)	(6.32)	(8.63)	(9.90)	(10.09)	(8.88)	(7.36)	(6.01)	(11.67)	(4.50)	(24.61)
	Prone	695.4	2184.1	554.0	1663.4	592.8	1849.9	602.3	1786.2	538.6	1539.7	510.0	1846.4
		(4.33)	(25.41)	(5.48)	(11.26)	(8.00)	(10.27)	(12.52)	(9.45)	(5.38)	(11.78)	(8.07)	(23.26)

SE is shown in parentheses. Subject 1 is female; the remainder are male.

Systematic differences in the values of F1 and F2 are seen to accompany changes in head orientation. For both a and e, the mean F1 frequency is highest in the upright orientation and lowest in the prone orientation (p < 0.01). F2 frequencies are highest in the prone orientation and lowest in the upright orientation (p < 0.01). Tukey tests were performed to assess differences between formant frequencies in both vowels. Changes to F1 and F2 associated with different head orientations were in all cases statistically reliable (p < 0.05) with the exception of contrasts involving the supine condition for the vowele.

In two separate control studies, we examined the extent to which jaw kinematic data and estimates of formant frequencies were correlated with speech volume and speech rate. The tests involving jaw kinematic data were performed as follows. As a measure of volume the average value of the rectified acoustical signal was computed over the voiced portion of the vowel. As a measure of rate, we used the duration of the CVC segment for each trial. For each subject, we calculated means for volume and rate in each phonetic condition and each head orientation. Pearson product–moment correlation coefficients were computed across all subjects and experimental conditions to assess the relationship between volume and rate and jaw orientation. It was found that volume and rate were not correlated with jaw orientation at any of the three measurement points during the CVC (p > 0.05).

A second analysis examined the dependence of formant frequencies on speech rate and volume. For this analysis, the 22,050 Hz acoustical recording used to determine formant frequencies was also used to obtain rate and volume estimates on a per trial basis. Volume was assessed as the averaged value of the rectified signal during the voiced portion of the vowel. The duration of voicing was taken as the measure of rate. As in the kinematic analysis described above, correlation coefficients were calculated across subjects and experimental conditions. No relationship was found between measures of rate and volume and either of the two formant frequencies (p > 0.05). These analyses suggest that differences in jaw orientation and formant frequencies that accompanied changes in head orientation were not attributable to either speech volume or rate.

A possible concern related to the interpretation of the findings is that the loads to the jaw resulting from the manipulation of head orientation may not elicit compensation because they do not result in jaw positions or acoustical patterns that lie outside the normal range of variation observed in the upright orientation. To test this possibility, we compared the variation in kinematic and acoustical values observed in the upright condition with that observed when head and body orientation were varied. Measures of SD were calculated for each subject and phonetic condition in the upright orientation. Corresponding measures were calculated across the three head orientations to provide a global measure of variation resulting from changes to the direction of the gravitational load. Measures of variation were calculated for jaw orientation, horizontal jaw position, and first and second formant frequencies. A comparison of variability across orientations with variability in the upright condition alone provided a measure of the extent to which the effect of the gravitational manipulation exceeded the normal range of variation. SDs averaged across subjects and phonetic conditions for jaw orientation, horizontal jaw position, and F1 and F2 frequencies are provided in Table 2. In all cases, variation introduced by differences in head orientation was substantially greater than the variation observed under normal speaking conditions.

Table 2.

SDs averaged across subjects and phonetic conditions for kinematic variables (jaw orientation and horizontal jaw position) and acoustical variables (F1 and F2 frequencies)

	Variable	Upright	Overall	Ratio
Kinematic (consonant)	Jaw orientation	0.286	0.660	2.31
	Horizontal position	0.217	0.681	3.14
Kinematic (vowel)	Jaw orientation	0.515	0.999	1.94
	Horizontal position	0.207	0.712	3.44
Acoustic	F1	21.00	41.36	1.97
	F2	29.00	57.48	1.98

Jaw orientation is given in degrees; horizontal position is given in millimeters, and acoustical frequency is given in hertz. Values are shown for the upright condition alone (upright column) and across all three gravitational conditions (overall column). In every case, the ratio of SD across orientations to SD in the upright condition (ratio column) shows that variation attributable to changes in head orientation is substantially greater than the variation under normal speaking conditions.

DISCUSSION

In this study, we used a mathematical model of the jaw to predict the effects of using motor commands that are not adjusted to compensate for loads arising as a result of head orientation relative to gravity. The simulations predicted orientation-dependent changes in jaw position relative to the upper skull. The results of a comparable empirical study were consistent with the pattern predicted by the model, with one exception. The jaw was rotated toward occlusion and translated forward in the prone orientation and was rotated away from occlusion in the supine orientation. In contrast to the simulations, horizontal jaw position was similar in upright and supine head orientations. The results suggest that subjects do not completely compensate for differences in gravitational load.

One reason why subjects may fail to account for orientation relative to gravity when making jaw movements during speech is that other articulators such as the tongue, velum, and larynx may compensate for the effect of changing orientation. However, our acoustical analyses suggest that this is not the case; F1 and F2 frequencies vary systematically depending on head orientation relative to gravity. A recent study by Tiede (1997) is consistent with this possibility. Tiede reports data suggesting that tongue height during speech (measured using electromagnetometry) is systematically affected by changes in orientation relative to gravity (upright vs supine). The direction of change in tongue position is consistent with the idea that there is little compensation for changes to articulator position caused by gravity.

The observation that the horizontal position of the jaw was the same in the upright and supine orientations could arise for a variety of reasons. The finding is consistent with the possibility of compensation for load in this one orientation and one degree of freedom. However, this is difficult to reconcile with the systematic differences observed for movements in other orientations (e.g., prone) and in other degrees of freedom (e.g., pitch). Another possibility is that passive tissue properties of the temporomandibular joint constrain motion of the jaw differentially depending on the direction of the load (Baragar and Osborn, 1984). Constraints such as these are not included in the jaw model presented here.

The apparent lack of compensation demonstrated in the present study stands in contrast to a number of studies, primarily involving arm movements, in which subjects compensate for the effects of artificial force environments (Lackner and DiZio, 1992; Shadmehr and Mussa-Ivaldi, 1994) as well as for changes in load associated with movement in different directions (Fisk et al., 1993; Papaxanthis et al., 1998).

The naturally occuring loads that accompany orofacial movement are smaller than those usually associated with movement of the limbs. Nevertheless the typical absence in the present case of adjustments to offset the effects of load indicates that compensation for external loads is not a universal property of motor systems. Indeed, in studies of arm movement using gravitational manipulations, compensation for loads is at times not observed (Smetanin and Popov, 1997). Moreover, whereas a number of examples of compensation for artificial motion-dependent loads have been reported, evidence of compensation for naturally occuring loads has been more limited. This includes demonstrations of grip force adjustment in the context of loads arising as a result of arm movement (Flanagan and Wing, 1997), anticipatory postural adjustments (de Wolf et al., 1998; van der Fits and Hadders-Algra, 1998), and predictive changes to muscle activity in the context of loads arising as a result of multijoint dynamics (Gribble and Ostry, 1999). By better understanding the natural conditions under which load compensation occurs, we can determine how loads and dynamics are incorporated in motion planning.

The general absence of corrections to jaw position with changes in load may reflect the nature of the goals in speech production. Whereas factors such as end point accuracy, the shape of the motion path, and postural maintenance may be of primary importance in producing arm movements, intelligibility is presumably the main consideration in speech. Thus although loads caused by the gravitational force affect both orofacial movement and acoustics, corrections may be expected only when intelligibility is compromised. Indeed, in the case of orofacial movements, this lack of compensation may contribute to the high variability associated with speech.

Although the jaw model used in this study is relatively complete, it lacks an account of several other systems that may be relevant to jaw motion in speech. These include the vestibular system, which is known to send reflex input to orofacial MNs (Hickenbottom et al., 1985), and the respiratory system, whose activity is associated with the volume and timing of speech production and other orofacial behaviors (McFarland et al., 1994; Hoit et al., 1988). Motions of the tongue and lips may also affect jaw position (Sanguineti et al., 1998) and are not included in the present model.