The Spectral Main Sequence of Human Saccades

Abstract

Despite the many models of saccadic eye movements, little attention has been paid to the shape of saccade trajectories. Some investigators have argued that saccades are driven by a rectangular “bang-bang” neural control signal, whereas others have emphasized the similarity to fast arm movement trajectories, such as the “minimum jerk” profile. However, models have not been tested rigorously against empirical trajectories. We examined the Fourier transforms of saccades and compared them with theoretical models. Horizontal saccades were recorded from 10 healthy subjects. The Fourier transform of each saccade was accurately computed using a padded fast Fourier transform (FFT), and the frequencies of the first three minima (M1, M2, M3) in each energy spectrum were measured to a precision of 0.12 Hz. Each subject showed near-linear trends in the relationships among M1, M2, and M3 and the reciprocal of duration (1/T), which we call the “spectral main sequence.” Extrapolation of plots did not pass through the origin, indicating a subtle departure from self-similarity. Bivariate confidence regions were established to allow for slope-intercept variability. The nonharmonic relationships seen cannot arise from a rectangular saccadic pulse driving a linear ocular plant. The relationships are also incompatible with minimum acceleration, minimum jerk, or higher-order minimum square derivative trajectories. The best fits were made by trajectories that minimize postmovement variance with signal-dependent noise (Harris and Wolpert, 1998). It is concluded that the spectral main sequence is exquisitely sensitive to the saccade trajectory and should be used to test objectively all present and future models of saccades.

Saccades are the fastest type of eye movement, reaching hundreds of degrees per second and are usually completed in tens of milliseconds. Despite their speed, saccade trajectories tend to be remarkably stereotyped both within and across individuals. The duration, T, and peak velocity,PV, of saccades increase monotonically with amplitude,A, of the movement in a more-or-less consistent way, which has been called the “main sequence” (Bahill et al., 1975b). Over the range of amplitudes typically made in everyday viewing (<20°) (Bahill et al., 1975a), velocity profiles tend to have a similar quasi-symmetric shape that appears to be simply scaled in velocity and time according to the amplitude. This self-similarity breaks down for larger saccades as velocity trajectories become more asymmetrical with a protracted decelerating phase (Collewijn et al., 1988).

Despite the numerous models of the saccadic system, there has been surprisingly little attention paid to the precise shape of velocity profiles. Descriptively, Yarbus (1967) fitted them by a symmetric truncated cosine for small saccades. Others have used a gamma function, which has a skew parameter that allows larger saccades to be fitted (Van Opstal and Van Gisbergen, 1987).

In terms of explanatory models, probably the most common view is that trajectories are time-optimal by bringing the eye to its final position in the shortest possible time (Clark and Stark, 1975; Lehman and Stark, 1979; Enderle and Wolfe, 1987). For linear systems this is achieved by “bang-bang” control (BB), in which the driving signal is switched between maximum permissible signal levels. The trajectories generated by such models of the neural driving signal are dependent on the dynamic response of the extraocular muscles (the “ocular plant”), on which there is currently no consensus.

An alternative, kinematic approach to explain trajectories, which consequently is independent of the choice of plant, can be adopted. The similarity between the trajectories of saccades and fast arm movements has been emphasized previously (Abrams et al., 1989; Harris, 1998b), and for fast arm movements it has been proposed that trajectories are selected to maximize smoothness, for example by minimizing the square of jerk integrated over the duration of the movement. This “minimum-jerk” profile (jerk = rate of change of acceleration) fits arm trajectories well (Hogan, 1984; Flash and Hogan, 1985), although a minimum “snap” profile may provide a better fit (snap = rate of change of jerk) (Wiegner and Wierzbicka, 1992). These minimum square derivative (MSD) velocity profiles are self-similar and symmetrical.

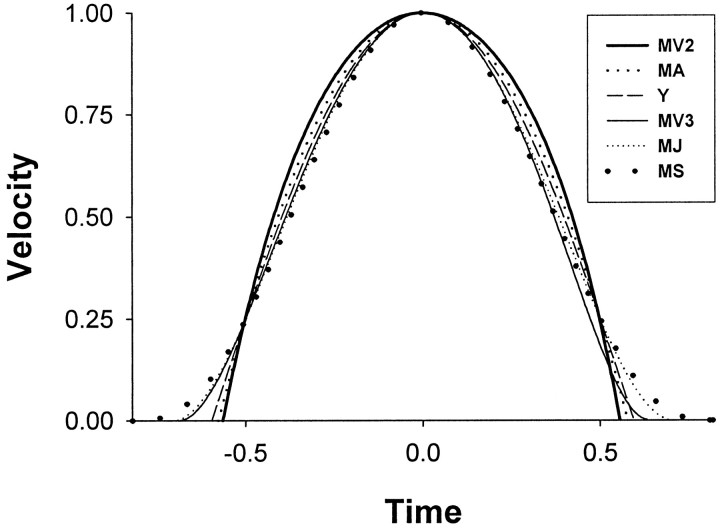
Although temporal MSD profiles appear to fit saccades well, why movements should be selected for smoothness is unclear. Recently Harris and Wolpert (1998) have proposed that the trajectories of saccades and arm movements may minimize end-point variance in the presence of signal-dependent motoneuron noise. For fast movements, minimum variance (MV) trajectories tend to be similar to MSD profiles (Fig.1), but a quantitative comparison has not yet been made.

Fig. 1.

Similarities of MSD and MV model trajectories (see Materials and Methods). Shown are velocity profiles of minimum acceleration, jerk and snap (MA, MJ, MS), minimum variance second and third order (MV2, MV3 with third time constant = 10 msec); the descriptive Yarbus model (Y) is also shown for its similarity to MA. The time-origin is centered at peak velocity, which has been normalized to unity. Trajectories have been scaled in time so that velocity is 0.25 at ±0.5 time units, except in MV3 where a slight asymmetry precluded the alignment at +0.5 time units. For clarity, the order with which the profiles reach zero velocity has been mirrored in the legend. The MV profiles are based on an amplitude of 5° and duration 38 msec.

It is difficult to discriminate between these models by conventional means because of the smoothness of movements, recording noise and limited bandwidth, and the uncertain plant. Defining trajectories with higher derivatives, such as acceleration, jerk, or snap, becomes virtually impossible because of noise and the distortion caused by the low-pass filtering of any eye movement recording equipment.

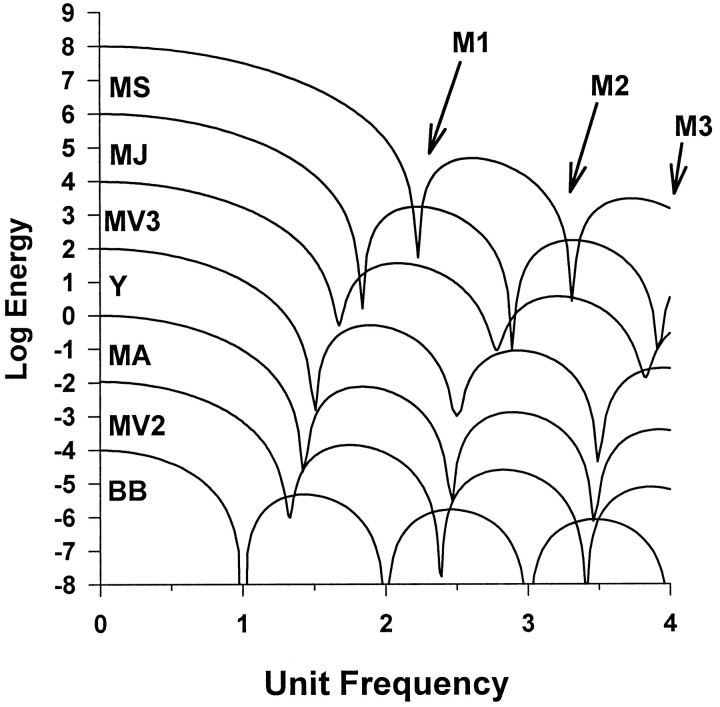
In this study we compared actual saccade trajectories with model trajectories using Fourier transforms. The Fourier energy spectra of a primate saccade has a characteristic and distinctive sequence of sharp local minima at frequencies that depend on the duration and overall shape of the trajectory (Harris et al., 1990; Harris, 1998a,b). For a linear plant, the frequencies of these minima, M1, M2, M3 etc., should coincide with minima in the frequency domain of the driving signal. Thus, the minima allow us to compare models based purely on the neural control signal (BB) or purely on the output (MSD), without reference to a specific plant model. The minima do not define the trajectory absolutely, but any plausible descriptive or explanatory model must be able to at least reproduce these minima. For example, the gamma function does not have any minima, and so we can reject this model at the outset. The other model trajectories have energy spectral minima at different frequencies (Fig. 2). They cannot all be correct. In this study we sought to establish the empirical relationship among saccade spectral minima and saccade duration, which we shall call the “spectral main sequence” (SMS), and then to compare it with the predictions of the models.

Fig. 2.

Fourier energy spectra of velocity profiles plotted on log₁₀-linear axis. Energy plots are shown for the models in Figure 1 and for the rectangular pulse bang-bang model (BB). For clarity the sharpness of the minima has been reduced, and the ordinates have been offset. The minima frequencies and their ratios are summarized in Table 3.

MATERIALS AND METHODS

Horizontal eye movements were recorded using an infrared limbus eye-tracker (IRIS, Skalar Medical, Delft, The Netherlands). This apparatus has a horizontal linear range of ±25° with an accuracy of 3 minarc. The frequency response has a 3 dB attenuation at 100 Hz and can readily detect the first three minima for saccades over 4°.

The experimental protocol was approved by the Institute of Child Health Ethics Committee, and informed consent was obtained from all volunteers. Saccades were recorded from 10 healthy adults (6 males, 4 females) with normal vision aged 25–35 years (mean = 29.3 years). Subjects sat facing a white flat screen in dimmed room lighting (2 cd/m²); their heads were supported in a chin rest and stabilized by a pair of ear muffs. Only recordings from the left eye were analyzed.

The stimulus was a red (670 nm) laser circular spot with a diameter of 1 mm projected onto the screen via a galvanometer mirror, which was under computer control. The screen was 89 cm from the subject, and the spot subtended an angle of 4 minarc at the retina.

Each trial started with the target spot in the center, which after a random time delay (1.1–2.5 sec) stepped to a peripheral position, where it remained for 1.5 sec before returning to the center for the start of the next trial. Each subject was presented with 100 trials, with 10 trials for each of 10 different peripheral target positions: 2.5, 5, 10, 15, and 20° to the left and right of the central fixation target. Trials were presented in a fixed pseudorandom order. Only saccades to centrifugal target jumps were recorded.

Before trials were presented, a calibration procedure was performed in which the subject was asked to fixate the spot at 12 different predetermined horizontal locations between +20° and −20°. A linear regression was produced on-line, and if necessary, the apparatus was readjusted and the calibration procedure repeated until a linear relationship between eye position and target position was obtained.

Analysis. All saccades were previewed to exclude trials with anticipatory saccades and blink artifacts. Eye position was sampled at 1 kHz. Eye velocity and acceleration were estimated from the eye position using a zero-phase low-pass digital filter (3 dB point = 64 Hz). The onset of a saccade was defined as the first point at which the velocity was continuously above 10°/sec for at least 10 msec. Similarly, the offset was defined as the last point after the peak velocity to be above 10°/sec. To ensure that the saccade trajectory was always fully captured for Fourier analysis, the extracted data segment went 5 msec beyond the identified start and end points of the saccade.

The Fourier transform of a saccade was computed from the unfiltered position signal using a standard fast Fourier transform (FFT). This involved extending (“padding”) the extracted data segment at either end to form a dataset comprising 8192 points, then multiplying by a cosine window, and then applying the FFT. This avoided problems associated with truncation and wrap-around (Harris, 1998a). The first three minima in the energy spectra were measured to the resolution of 0.12 Hz. Although most minima were sharply defined, occasionally this was not the case. In these circumstances the energy spectra were multiplied by ω², ω⁴, ω⁶, or ω⁸ (equivalent to taking successive derivatives in the time-domain; ω = angular frequency), whereupon the minima became readily detectable. It was found that the minima frequencies were highly variable for saccades below 4° in amplitude. This was because the minima for short saccades occur at very high frequencies and become buried in noise. Thus, only saccades above 4° were considered in this study.

SMS confidence regions. To study possible relationships among the four variables (M1–M3 and reciprocal duration, 1/T), linear regressions were performed for each subject. Given the presence of unavoidable measurement errors and biological variability in the frequencies and durations, the best unbiased intrasubject estimate of the slopes and intercepts was obtained by bivariate linear regressions of M1, M2, and M3 versus 1/T, M2 and M3 versus M1, and M3 versus M2.

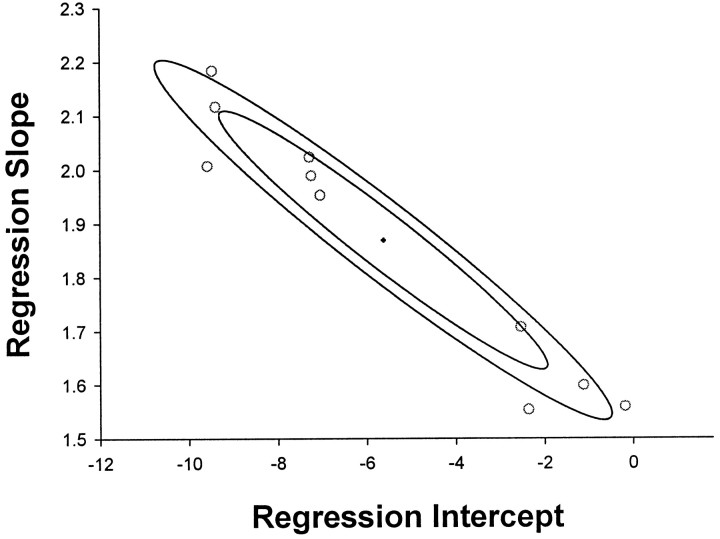
Sample differences in the linear regression will lead to covariance between the individual samples of slope and intercept. The codependence can be seen in the example in Figure 3, where higher regression slopes are associated with lower regression intercepts, and vice versa. To obtain an overall estimate of the population intercept and slope, bivariate confidence regions were constructed according to n(μ −m)^TS⁻¹(μ − m) < F_α(p,n − p) p(n − 1)/(n − p), where μ and m are the population and sample mean vectors of the two groups (p = 2) slope and intercept; n is the sample size (n = 10); S is the covariant of the n × p matrix, withS⁻¹ its inverse. Decomposing the vectors into slope (y = μ_y − y) and intercept (x = μ_x − x) components, we have for two dimensions a region bounded by the ellipse of the form ay² + bxy + cx² = d, centered on ( x, y). Using Hotelling’sT², the 95 and 99% confidence regions shown in Figure 3 indicate the probability of finding the population intercept and slope within them.

Fig. 3.

Illustration of bivariate confidence regions. Ellipses show 95% (inner) and 99% (outer) confidence regions for the estimate of the population slope and intercept of the individual M1 versus 1/T regressions (○). The center, ( x, y), is shown by thecross-hair.

Models. Eight models were considered: the descriptive Yarbus model (Y); MSD profiles that minimize the square of acceleration (MA; a parabola), the square of jerk (MJ), and the square of snap (MS); the bang-bang rectangular pulse; and minimum variance profiles with second-order and two with third-order ocular plants. The gamma function model was not considered because it has no local minima in its energy spectrum.

The Fourier energy spectra of the Yarbus and MSD models can be found analytically and are shown in Table 1. Each of these models inherently assumes that velocity profiles of saccades for different amplitudes have the same basic shape but differ only in velocity- and time-scales. Such profiles are self-similar because it is possible to find individual scale factors in velocity and time so that the set of functions would superimpose (for a given model) (Fig. 4A). The Fourier transform preserves self-similarity. Therefore, the ratios of the minima to each other and to reciprocal duration (1/T) are invariant to changes in amplitude, peak velocity, and duration of the trajectory. Linear plots of the minima against each other or against 1/T must yield straight lines passing through the origin. This can be seen in Figure 4B, where scaling amplitude scales the overall energy for a given duration but does not affect the frequencies at which the minima occur; scaling duration has an inverse relationship on the minima frequencies, but the ratios between the minima are constant, as demonstrated for M1 and M2 in the inset. In this study only the ratios among M1, M2, and M3 and the relationship with M1–M3 and 1/T were investigated.

Table 1.

Model velocity formulae and their analytical Fourier energy spectra

Model	Velocity	Fourier energy spectrum
Yarbus (1967)	$$\frac{\pi }{2}cos(\pi t)$$	$${\left[\frac{{\pi }^{2}cos(\omega /2)}{({\pi }^2-{\omega }^2}\right]}^2$$
Minimum acceleration	$$\frac{3}{2} [1-4t^2]$$	$$144{\left[\frac{2sin(\omega /2)}{{\omega }^3}-\frac{cos(\omega /2)}{{\omega }^2}\right]}^2$$
Minimum jerk	$$\frac{15}{8} [1-4t^2{]}^2$$	$$14,400{\left[\frac{12sin(\omega /2)}{{\omega }^5}-\frac{6cos(\omega /2)}{{\omega }^4}-\frac{sin(\omega /2)}{{\omega }^3}\right]}^2$$
Minimum snap	$$\frac{35}{16} [1-4t^2{]}^3$$	$$2,822,400\left[\frac{120sin(\omega /2)}{{\omega }^7}-\frac{60cos(\omega /2)}{{\omega }^6}-\frac{12sin(\omega /2)}{{\omega }^5}+\frac{cos(\mathbf{\omega }\mathbf{/}\mathbf{2})}{{\mathbf{\omega }}^{\mathbf{4}}}\right]$$
Rectangular pulse	$$h(t)\otimes \text{rect}(T)$$	$$‖H(\omega )‖{}^2·{\left[\frac{Tsin(\omega T/2)}{\omega T/2}\right]}^2$$

Equations of velocity trajectories and their Fourier energy spectra for Yarbus, MSD, and rectangular pulse models. Trajectories are normalized for unit amplitude and unit duration with time origin at peak velocity.

Fig. 4.

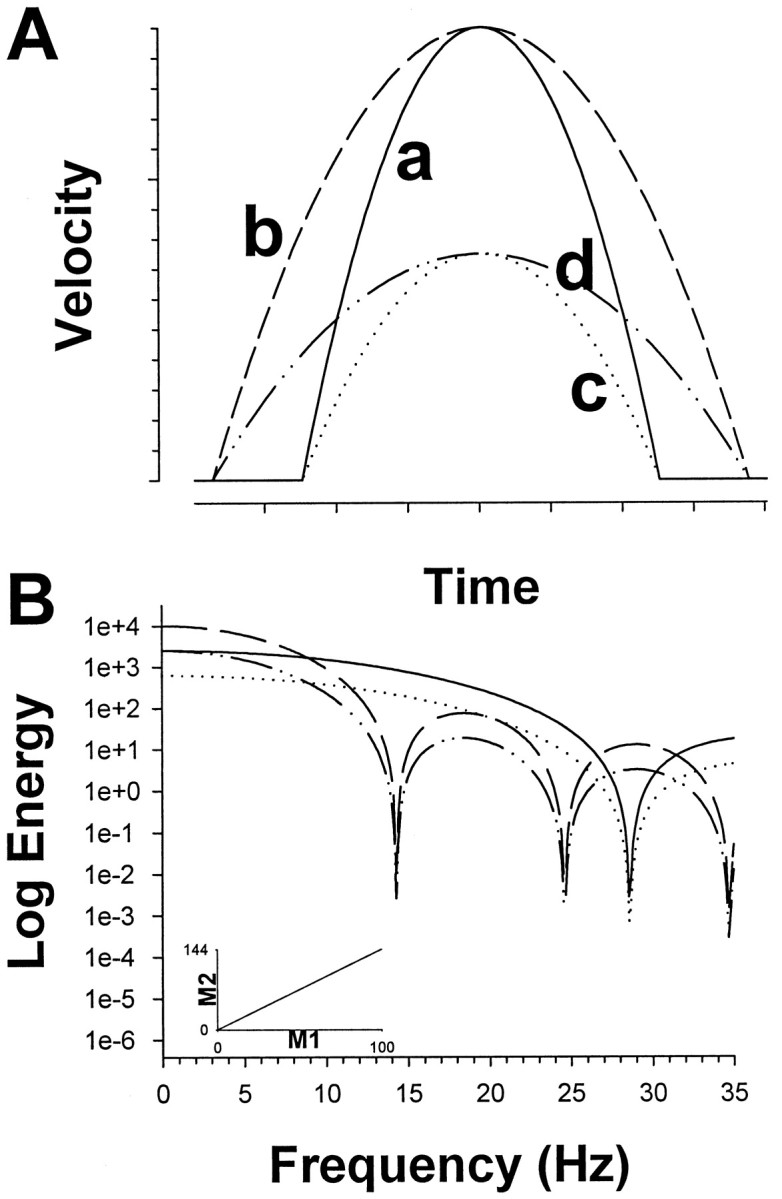
Illustration of self-similarity using a parabola as an example. A, The basic temporal shape (curvea) remains the same with arbitrary scaling in time (curveb) or in velocity (curvec) or both (curved). B, The Fourier transform of the curves in A. Scaling in velocity amplitude scales the overall energy without affecting the frequency at which the minima occur, whereas scaling in time has an inverse relationship on the minima frequencies. The ratios between the minima are unaffected by the time or amplitude scaling for a given shape, as shown in theinset for the first two minima (see Materials and Methods).

Bang-bang control theory is the optimal strategy to reach the target in the minimum time with the inherent assumption that the ocular plant is linear. Bang-bang control has been proposed previously (Enderle and Wolfe, 1987). To investigate whether bang-bang control is a tenable model for the saccadic system, the model’s assumption of a linear plant is accepted. Then, the energy spectrum of the output (i.e., eye position) is the product of the energy spectrum of the input (aggregate neural driving signal) and the energy transfer function of the ocular plant. If the input energy spectrum goes to zero at some frequency, then the output must also have zero energy at the same frequency. Even if energy does not go to zero but has a moderately sharp minimum and the plant characteristics are smooth, then energy minima are also virtually invariant to linear plants (Harris, 1998a). Thus, the energy minima of position or velocity will occur at frequencies very close to the minima of the pulse. The simplest bang-bang control signal is a rectangular pulse, in which the pulse height remains the same and increases in duration with saccade amplitude. Thus, for this model the pulse shapes and their energy spectra are self-similar (although eye velocity output profiles are not) (Fig.5A,B). Thus, as for the MSD models, linear plots of the minima against each other or against 1/T must also yield straight lines passing through the origin, and the slopes of these plots must be integral multiples of each other (harmonics) as determined by the energy spectrum of a rectangle (Table 1).

Fig. 5.

Illustration of bang-bang control with a second-order ocular plant. A, Simplest control is a rectangular pulse in which maximum agonist signal is maintained. Different amplitudes are achieved by changing the duration of the rectangle (dotted line); hence pulses are self-similar (see Materials and Methods). B, Velocity trajectories resulting from A are not self-similar.

Minimum variance trajectories have velocity profiles that minimize the position variance over a postmovement period, where the SD of the noise on the control signal increases with the magnitude of the mean control signal (signal-dependent noise). The optimal profiles were found numerically, assuming that the SD of the noise was proportional to the mean of the control signal, and using the same parameter values used byHarris and Wolpert (1998), namely a postmovement period of 50 msec and a second-order plant with time constants of 224 and 13 msec, or a third-order plant with an additional time constant of 10 ms. Optimal profiles with the third time constant set to 4 msec were also modeled. (Further details of the numerical techniques used can be found atwww.hera.ucl.ac.uk.)

RESULTS

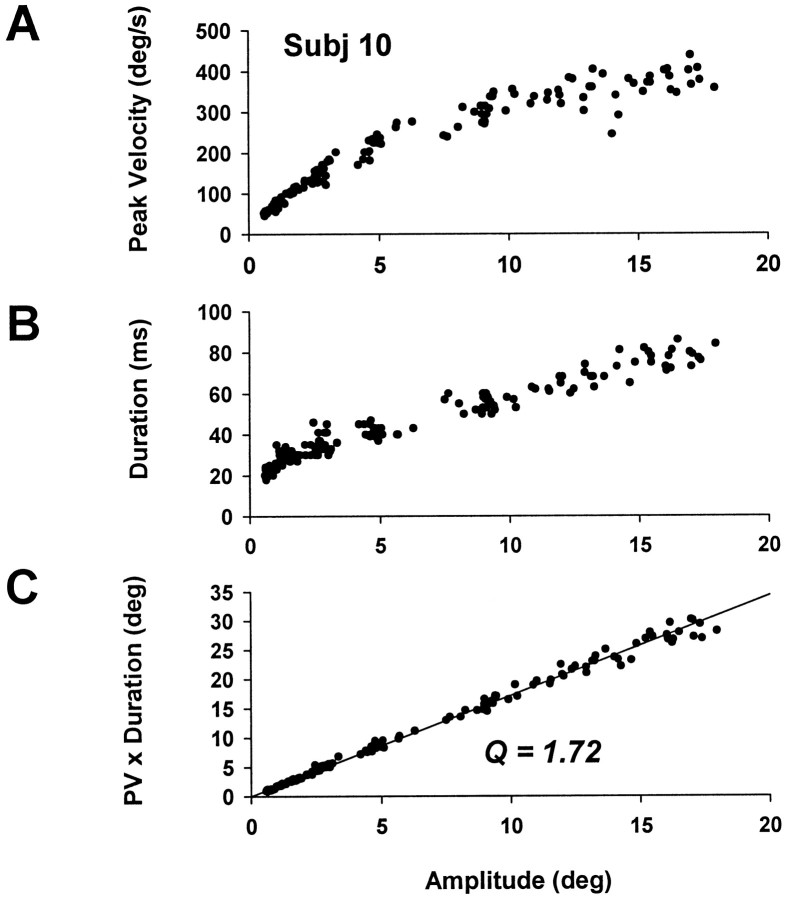
All subjects produced saccades with the typical temporal main sequence (TMS) (Fig. 6) as described by many previous investigators. In particular, duration was always a linearly increasing function of amplitude for saccades over ∼4°, and linear regression over the linear portion (4–20°) gave a slope (T-A slope) range of 2.22–3.37 msec/° and an intercept (T-A incpt) range of 20.3–30.4 ms (Table 2). The ratio of peak velocity to mean velocity, which we call Q, tended to be roughly constant for different amplitudes, with a value ranging from 1.54 to 1.80. These temporal measures are similar to other reports (Becker, 1989). Velocity trajectories of saccades showed the typical quasi-symmetrical profile for amplitudes of 5–10°, with a subtle change toward positively skewed profiles for large saccades (Fig. 7), as reported by others (Collewijn et al., 1988). Thus, there was no indication of any systematic deviations in our measures of velocity profiles or duration from previously published data.

Fig. 6.

Time-domain analysis of saccades showing typical temporal main sequence relationships. A, Peak velocity versus amplitude. B, Duration versus amplitude.C, Peak velocity × duration versus amplitude. Regression line constrained through origin gives the ratio of peak velocity to mean velocity, Q.

Table 2.

Summary of individual temporal and spectral main sequence parameters

ID	n	T-A			Q	M1–1/T			M2–1/T			M3–1/T			M2–M1			M3–M1			M3–M2
		Incpt	Slope	r		Incpt	Slope	r	Incpt	Slope	r	Incpt	Slope	r	Incpt	Slope	r	Incpt	Slope	r	Incpt	Slope	r
1	70	28.3	3.37	0.91	1.80	−7.29	2.02	0.93	−7.76	3.24	0.90	−15.5	4.82	0.86	3.90	1.60	0.91	4.16	2.30	0.86	−0.99	1.42	0.94
2	77	20.5	3.15	0.95	1.71	−9.40	2.12	0.98	5.52	2.46	0.95	0.62	3.69	0.92	16.4	1.16	0.96	17.2	1.73	0.95	−7.73	1.50	0.95
3	70	23.5	2.22	0.96	1.61	−9.58	2.04	0.97	−6.97	3.05	0.88	−13.4	4.51	0.83	7.60	1.52	0.88	8.40	2.24	0.85	−2.74	1.47	0.90
4	73	21.6	3.00	0.95	1.60	−0.19	1.56	0.91	0.89	2.72	0.89	1.34	3.77	0.82	1.03	1.75	0.89	4.76	2.33	0.86	3.18	1.33	0.87
5	71	20.3	2.83	0.98	1.64	−2.53	1.70	0.99	1.79	2.64	0.97	13.7	3.14	0.90	5.68	1.55	0.96	18.4	1.83	0.90	11.8	1.18	0.93
6	73	29.5	2.54	0.91	1.64	−7.25	1.99	0.97	0.33	2.67	0.93	−5.55	1.09	0.88	10.2	1.34	0.94	10.8	2.00	0.90	−4.13	1.49	0.93
7	79	20.7	2.42	0.96	1.60	−1.12	1.60	0.97	1.08	2.71	0.97	17.7	3.10	0.92	2.92	1.70	0.96	19.8	1.93	0.91	16.6	1.14	0.94
8	57	28.0	2.71	0.90	1.54	−2.36	1.55	0.96	−16.8	3.54	0.88	−16.2	4.72	0.86	−11.3	2.28	0.88	−8.64	3.02	0.87	6.22	1.33	0.93
9	80	30.4	2.66	0.96	1.60	−9.47	2.18	0.98	−3.02	2.93	0.87	2.41	3.55	0.87	10.0	1.32	0.87	18.6	1.60	0.86	6.48	1.21	0.90
10	78	24.2	3.14	0.91	1.72	−7.05	1.95	0.98	−3.48	2.83	0.96	−6.11	4.05	0.91	6.74	1.45	0.96	8.76	2.06	0.91	−0.77	1.42	0.92
Mean	72.8	24.7	2.80		1.65	−5.62	1.87		−2.84	2.88		−2.11	3.94		5.32	1.57		10.2	2.11		2.78	1.35

Regressions of duration–amplitude main sequence (T-A) intercept (incpt) and slope, the ratio of peak to mean velocity Q, and the spectral main sequence bivariate regressions (see Materials and Methods) are shown along with the respective correlation coefficients and number of saccades scored for each subject (n).

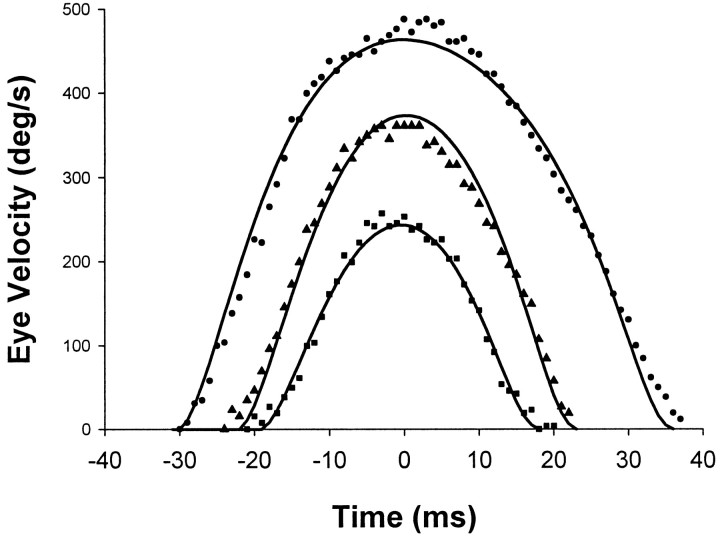
Fig. 7.

Typical velocity trajectories of saccades with superimposed MV trajectory. Shown is near symmetry for low amplitudes, becoming more skewed for large amplitudes. Plots were aligned approximately with peak velocity, and amplitudes were 5.4° (▪), 10.3° (▴), and 20.0° (●). The lines show the MV (with third time constant of 4 msec) profiles for matched amplitudes and durations.

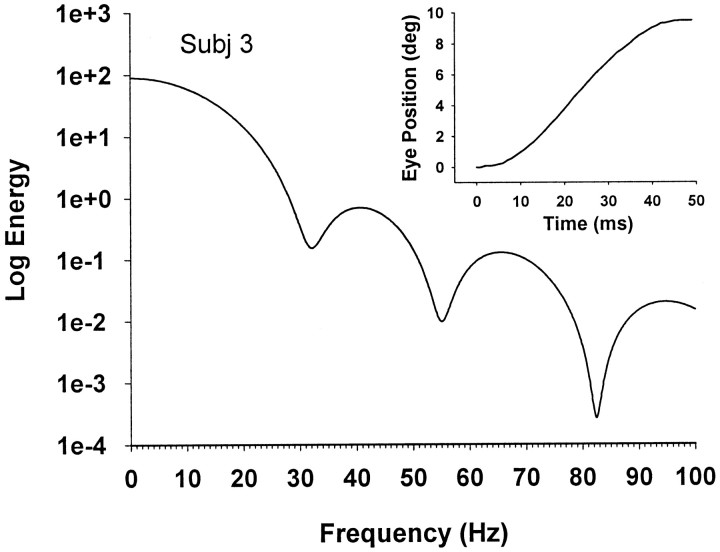
Fourier analysis showed energy spectra with usually clearly defined minima occurring at nonharmonic frequencies, as shown by the typical example in Figure 8. These energy spectra were similar to those published previously (Harris et al., 1990;Harris, 1998a,b).

Fig. 8.

Typical energy spectrum of the velocity profile of a saccade (inset) with amplitude 9.5°, durationT = 47 msec (1/T ∼ 21 Hz). Log energy is plotted against linear frequency. Only the first three minima are shown.

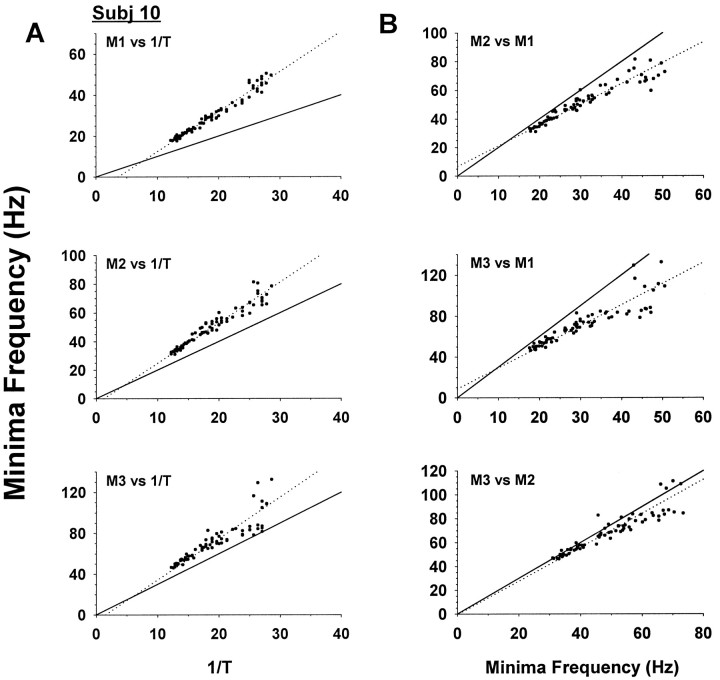
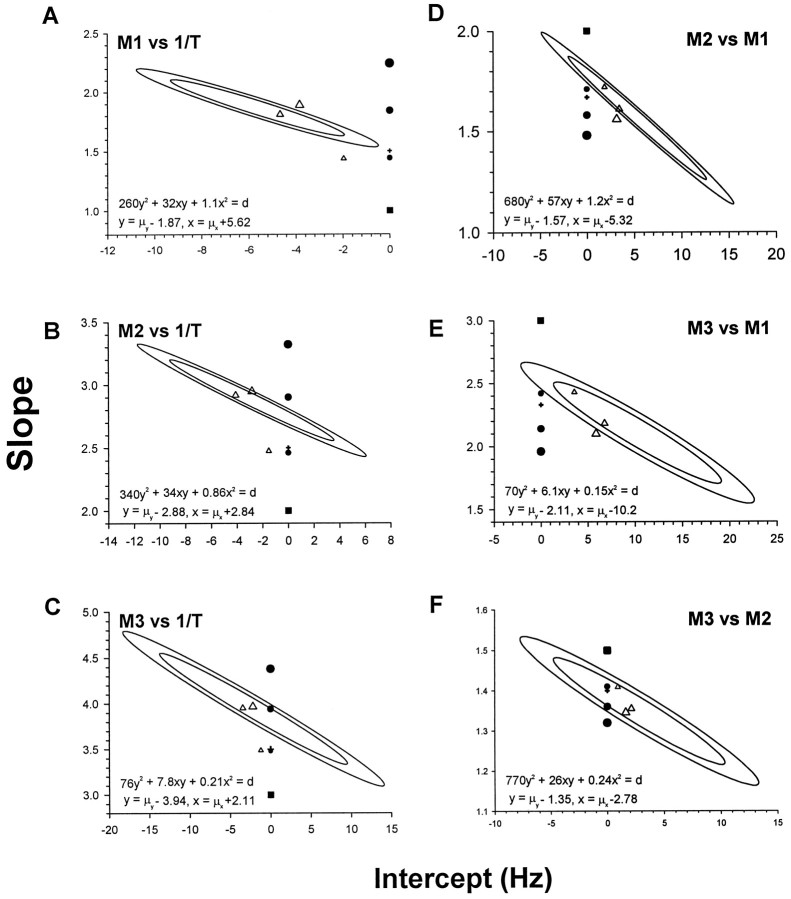
Plots between M1–M3 and the reciprocal of duration (1/T), as well as between M2–M3 and M1, and M3 and M2, revealed approximately linear relationships, as seen in Figure9A,Bfor a typical subject. To compare these results with model predictions, the slope and intercept were estimated by bivariate linear regressions (see Materials and Methods) and are summarized in Table 2. Subjects showed broadly similar results for each regression, but to take account of intersubject variability in estimating the population slope and intercept, bivariate confidence regions were plotted (Fig.10) (see Materials and Methods).

Fig. 9.

Typical SMS for an individual subject.A, Plots of minima frequencies M1, M2, and M3 versus reciprocal duration of saccade (1/T) for the same subject as in Figure 6. B, Plots of M2 and M3 versus M1, and M3 versus M2. Note near-linear relationships in all plots.Dotted lines show bivariate linear regressions.Solid lines indicate predicted harmonic relationships for the rectangular bang-bang control pulse.

Fig. 10.

Comparison of SMS confidence regions with models. Ellipses show 95% (inner) and 99% (outer) confidence regions for the group SMS (see Materials and Methods). Predicted rectangular BB model (square), MSD models (circles, size in increasing order of derivative: acceleration, jerk, snap), Yarbus model (cross-hair), and MV models (triangles, size in increasing order of third time constant:t₃ = 0, 4, 10 msec) are plotted. The equations for the 95% (d = 1.004) and 99% (d = 1.946) ellipses are also shown. All model slopes and intercepts are summarized in Table 3.

Comparison with bang-bang control

The simplest bang-bang control signal is the rectangular pulse, which has energy minima at harmonics of the reciprocal of the pulse duration (Fig. 9, solid lines; Fig. 10, squares). It was clear from individual SMSs that there is no harmonic relationship among the minima. The predicted rectangular pulse slopes and intercepts consistently fell far outside the 99% confidence regions and were rejected at the p < 0.001 level.

Comparison with MSD profiles

Inspection of MJ slopes alone suggests a close fit to the observed means (Tables 2, 3). However, with the exception of MJ in Figure 10C (p = 0.065), and MJ and MA in Figure 10F(p_MJ = 0.037,p_MA = 0.34), all MSDs fell outside of the 99% confidence regions. Moreover, the M3 versus M2 ratio seen in Figure 10F is the least discriminating of the SMS relationships studied because all the models predict very similar values (note scale in Fig. 10F). Although MA provides a poor fit, it can be seen to fall closer than MJ to the confidence regions in all but B and C in Figure 10, which in turn was much closer to the confidence regions than MS. The MS model was consistently rejected at the p < 0.001 level, and higher-order MSD models diverge farther from the confidence regions. It can be seen that the descriptive Yarbus model is very close to MA. This is not surprising because the cosine function in Table 1 can be quite well approximated by a parabola (Fig. 1). Five out of six of the predicted slopes and intercepts for MA, MJ, and Y models were rejected at the p < 0.05 level.

Table 3.

Comparison of model regressions

	Rectangle	Minimum acceleration	Yarbus model	Minimum jerk	Minimum snap	Minimum variance
						T3 = 0 msec		T3 = 4 msec		T3 = 10 msec
						Incpt	Slope	Incpt	Slope	Incpt	Slope
M1 versus 1/T	1.00	1.44	1.50	1.84	2.24	−1.97	1.44	−4.66	1.81	−3.84	1.89
M2 versus 1/T	2.00	2.46	2.50	2.90	3.32	−1.52	2.48	−4.10	2.92	−2.83	2.95
M3 versus 1/T	3.00	3.48	3.50	3.94	4.38	−1.21	3.49	−3.43	3.95	−2.19	3.97
M2 versus M1	2.00	1.71	1.67	1.58	1.48	1.87	1.72	3.42	1.61	3.15	1.56
M3 versus M1	3.00	2.42	2.33	2.14	1.96	3.57	2.43	6.77	2.18	5.87	2.10
M3 versus M2	1.50	1.41	1.40	1.36	1.32	0.93	1.41	2.12	1.36	1.63	1.35

The predicted regression slopes and intercepts (incpt) are summarized for all eight models. Only the MV models have non-zero intercepts. The zero intercepts for the other models are not shown.

Comparison with MV profiles

MV profiles depend on the type of signal-dependent noise in the motoneuron signal and the specific dynamic response of the ocular plant. We tested examples as described by Harris and Wolpert (1998)(see Materials and Methods). It was found that regressions of the MV minima did not pass through the origin but showed intercepts that were similar to the empirical observations (Tables 2, 3). The implication of the MV regression intercepts is that MV profiles are not exactly self-similar. The change in shape is subtle, as shown by the temporal velocity profiles [Fig. 7 and Harris and Wolpert (1998)].

The sensitivity of the theoretical SMS can be seen particularly clearly in Figure 10. A change in the plant model from second to third order with a time constant of just 4 msec had a substantial effect on predicted slope and intercept. Increasing the third time constant to 10 ms had a further significant effect on how well the observed SMS was fitted. The second-order model fell within the 95% confidence bounds for all the interminima ratios but was rejected at p < 0.01 for all the minima against 1/T. The intermediate plant provided a good fit of all the observed SMSs, being within the 95% confidence regions and close to the sample mean. The third model showed varying agreement with the empirical data. It was just outside the 99% confidence regions for half of the relationships, but was never far from the mean slope and intercept.

DISCUSSION

All subjects showed systematic relationships among the frequencies of the energy minima and the reciprocal of the duration of the saccade (1/T). We have called these empirical relationships the SMS, which is quite distinct from the traditional TMS that relates peak velocity and duration to amplitude (Bahill et al., 1975b). The SMS is based purely on temporal measures (duration and frequency) and is independent of the amplitude or peak velocity of a movement. Consequently, there is no trivial reason why the SMS should depend on the TMS. The SMS arises from the whole shape of the trajectory (Harris 1998a).

Explanatory models of the neural pulse

The saccadic pulse has often been assumed to be rectangular in shape, reflecting the belief that it is the optimal bang-bang control signal (Enderle and Wolfe, 1987). The energy spectrum of a rectangular pulse has zeroes at harmonic frequencies of the reciprocal of the pulse duration (Table 1). Importantly, we have shown that M2 and M3 are not harmonics of either M1 or 1/T. This demonstrates conclusively that saccades cannot result from a rectangular pulse driving any linear ocular plant.

In the theory of optimal control of saturated linear systems, bang-bang control may require more elaborate driving signals, where one or more switches occur between maximum agonist activity and maximum antagonist activity during the movement (Bryson and Ho, 1975). After a rectangular driving pulse (no switches), the next simplest bang-bang control signal has one switch, where the driving signal is switched from its maximum agonist value to its maximum antagonist value at some optimal switching time to brake the movement. Small “braking pulses” at the end of saccades have been observed in abducens motoneuron discharges (Van Gisbergen et al., 1981) and in muscle fibers (Sindermann et al., 1978), but the magnitude of these braking pulses are far less than the peak antagonist activity. There is no evidence of two or more switches during saccades, so we conclude that saccades are not driven by any kind of bang-bang control. However, this does notmean that saccades are not time-optimal because bang-bang optimal control applies only to linear systems with simple saturating control signals.

Explanatory kinematic models

Kinematic models assume that a movement trajectory optimizes some trajectory parameter rather than being constrained by the driving signal or muscle dynamics. On the basis of the smoothness and symmetry of fast arm movement trajectories, Hogan (1984) proposed that the kinematic goal was to maximize smoothness by minimizing the integrated square of jerk. This MJ constraint provided a good fit to the observed symmetric velocity profiles. In view of the similarity of saccade velocity profiles to wrist movements (Abrams et al., 1989), the possibility that saccades may also be governed by the same kinematic constraint has been raised (Harris, 1998b). However, the minima of the MJ model fall outside the 95% confidence region for all but one of the six relationships investigated (Fig. 10). Minimizing the integrated square of acceleration also produces a smooth parabolic symmetrical trajectory and is similar to the descriptive truncated cosine profile originally proposed by Yarbus (1967). Again, both of these models fall outside the 95% confidence bounds on all but one measure and cannot account for velocity asymmetries and SMS non-zero intercepts.

Wiegner and Wierzbicka (1992) reported that arm movement trajectories were better fit by a minimum snap profile, which is similar to but slightly smoother than the MJ profile (Fig. 1). From Figure 10, we see that the minima ratios for the MS profile are even farther away from the confidence regions than those of the MJ profile. Saccades cannot be described by higher-order MSD profiles, because higher-order MSD profiles have minima at even higher frequencies. We conclude that MSDs do not give a good description of saccade trajectories in the frequency domain. Consequently, if fast arm movements truly minimize jerk or snap, saccades and fast arm movements do not minimize the same kinematic quantity. Spectral analysis of arm movements would confirm this.

Explanatory MV models

Apart from the poor fit to the SMS, a serious conceptual problem with the above MSD models (whether for arm or saccadic movements) is their assumption that “smoothness” is the fundamental kinematic goal of the movement. Although both fast arm and eye movements do indeed appear to be smooth, it is not obvious why smoothness should be so important, and it can hardly be considered to be an “explanation.” Instead, we have argued that smoothness would arise if the goal of the movement were to minimize position variance at the end of the movement of a given duration in the presence of signal-dependent noise (Harris, 1998b; Harris and Wolpert 1998). MV profiles depend on the duration of the movement, the dynamics of the plant, and the type of signal dependency of the noise, and in principle there are many MV profiles. Clearly, unlike bang-bang control or kinematic control, the minima of MV trajectories are dependent on the plant model, especially the order of the plant. Here we have examined only simple models as described by Harris and Wolpert (1998).

Although the MV profiles appear similar to MSD profiles (Fig. 1), they become increasingly asymmetric with duration (Harris and Wolpert, 1998), as seen in the real data (Fig. 7). In the frequency domain, the subtle lack of self-similarity in the MV profiles appears as regression lines among minima that do not pass through the origin. Minor alterations in the simple plant dynamics are sufficient to capture all of the details found in the SMS. In particular, the third-order model with a 4 msec time constant fits the observed SMS quite well, being within the 95% confidence region for all tested relationships (Fig.10).

We emphasize that the good fit of this MV trajectory does not prove that saccades follow this MV trajectory; rather, we have failed to reject this model on the basis of the SMS. Other models may fit the data as well. We also emphasize that the SMS characterizes the shape of trajectories and not how they are generated. One could doubtless conceive of an internal feedback controller to realize MV trajectories, but this remains to be explored.

In addition, there are two important caveats to be aware of. First, by constructing a confidence region we are in effect “averaging” across individuals and hence generating a composite SMS. Individual differences in saccade trajectories could reflect optimal trajectories with different constraints (e.g., slightly different plants), but they could also reflect failure to find the precise optimum. Indeed, we have argued that some variability around the optimum would be essential to allow the optimum to be reached on average (Harris, 1998b). Thus, examining how and why trajectories differ among individuals may be a more fruitful line of enquiry than producing ever narrower confidence regions by increasing sample size.

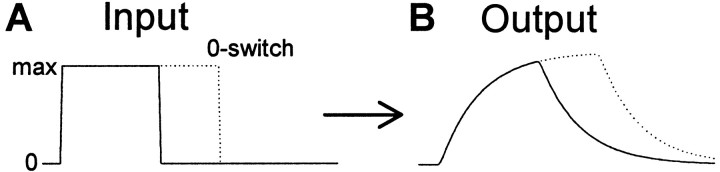
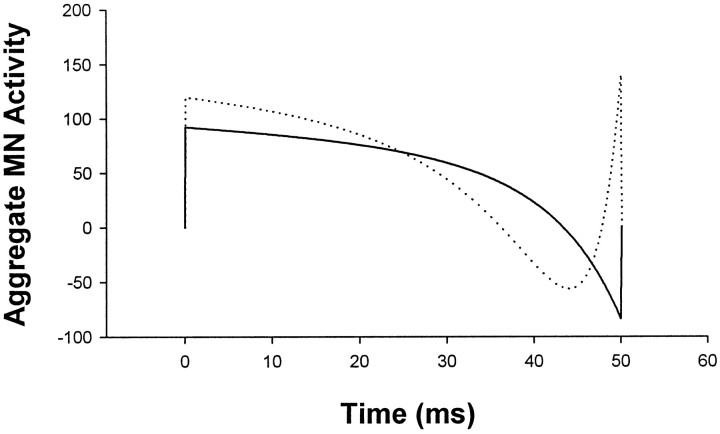
Second, our ultimate goal is to understand and model not only saccade trajectories but also their neural commands. In principle, if we have a potentially good model of trajectories we can ask what neural command would give rise to such a trajectory. Thus, Figure11 shows the aggregate neural command for a second- and third-order MV model. Unfortunately, even for these relatively simple lumped linear models, there are serious difficulties. First, we do not know the time course of the aggregate neural command during a saccade, because it depends on all active excitatory and inhibitory burst units and how they are delivered by the agonist and antagonist motoneurons to their respective extra-ocular muscles. A single motoneuron burst signal may give the impression of a bang-bang control signal, but averaging across burst units has revealed the presence of a small braking pulse (Van Gisbergen et al., 1981), which is similar to but not as sharp as the theoretical second-order MV command in Figure 11 (Harris and Wolpert, 1998). It is also highly questionable whether the CNS can deliver very sharp aggregate neural commands as seen in the braking pulse of the theoretical second- or third-order MV profiles in Figure 11. We have placed no limits on the control signals for these models, and no attempt has been made to model the tonic step component. A more complex nonlinear plant is probably required for realistic modeling of the very end of the pulse signal.

Fig. 11.

Neural control signals for MV models. Predicted combined agonist and antagonist motoneuronal firing rate for the second-order MV (solidlines) and third-order MV (dottedlines,t₃ = 4 msec) models.

Summary

In summary, we have shown that the Fourier energy spectra of human horizontal saccades in the range of 4–20° in amplitude have minima at frequencies that depend nearly linearly on the reciprocal of saccade duration, which we call the SMS. Unlike the traditional temporal main sequence (Bahill et al., 1975b), the SMS depends on the whole shape of the saccade trajectory. The SMS allows us to confidently reject the bang-bang control model of saccades as well as the possibility that saccades have minimum jerk or snap profiles, as proposed for fast arm movements. The original trigonometric model (Yarbus, 1967) or the minimum acceleration profile (parabola) are also rejected. Among the models considered, the minimum variance model with a third-order plant provides the best fit that also captures the subtle lack of self-similarity seen in actual data. However, it must be recognized that the SMS does not uniquely define the shape of saccade trajectories, and in principle, there could be other velocity profiles that fit the SMS at least as well. The SMS provides a stringent and essential test for all models of saccade trajectories.